Review of quantitative ultrasound: envelope statistics and backscatter coefficient imaging and contributions to diagnostic ultrasound

Abstract

Conventional medical imaging technologies, including ultrasound, have continued to improve over the years. For example, in oncology, medical imaging is characterized by high sensitivity, i.e., the ability to detect anomalous tissue features, but the ability to classify these tissue features from images often lacks specificity. As a result, a large number of biopsies of tissues with suspicious image findings are performed each year with a vast majority of these biopsies resulting in a negative finding. To improve specificity of cancer imaging, quantitative imaging techniques can play an important role. Conventional ultrasound B-mode imaging is mainly qualitative in nature. However, quantitative ultrasound (QUS) imaging can provide specific numbers related to tissue features that can increase the specificity of image findings leading to improvements in diagnostic ultrasound. QUS imaging techniques can encompass a wide variety of techniques including spectral-based parameterization, elastography, shear wave imaging, flow estimation and envelope statistics. Currently, spectral-based parameterization and envelope statistics are not available on most conventional clinical ultrasound machines. However, in recent years QUS techniques involving spectral-based parameterization and envelope statistics have demonstrated success in many applications, providing additional diagnostic capabilities. Spectral-based techniques include the estimation of the backscatter coefficient, estimation of attenuation, and estimation of scatterer properties such as the correlation length associated with an effective scatterer diameter and the effective acoustic concentration of scatterers. Envelope statistics include the estimation of the number density of scatterers and quantification of coherent to incoherent signals produced from the tissue. Challenges for clinical application include correctly accounting for attenuation effects and transmission losses and implementation of QUS on clinical devices. Successful clinical and pre-clinical applications demonstrating the ability of QUS to improve medical diagnostics include characterization of the myocardium during the cardiac cycle, cancer detection, classification of solid tumors and lymph nodes, detection and quantification of fatty liver disease, and monitoring and assessment of therapy.

I. Introduction

Imaging has fundamentally transformed the practice of medicine since the first X-rays were produced more than a 100 years ago [1]. Since that time medical imaging techniques have continued to evolve in their capabilities, expanded in their applications and have grown in their importance to medical practice. X-ray, X-ray CT, magnetic resonance imaging (MRI), ultrasound, nuclear imaging, and optical imaging techniques have all been adapted for specific applications in medicine. Each of these imaging modalities has associated tradeoffs in terms of spatial resolution, frame rate, contrast, imaging depth, cost, safety and portability.

The improvements in biomedical imaging have, for the most part, been beneficial to the practice of medicine. For example, in recent years, the high quality of imaging has resulted in higher sensitivity to suspicious tissue features for cancer imaging and detection, although gains in sensitivity remain an important medical problem. Unfortunately, in the case of cancer, these improvements in sensitivity have not always been paralleled by improvements in specificity, i.e., the ability to determine if a suspicious image finding is benign or malignant. As a result, a cancer “overdiagnosis” problem has occurred [2,3] in which many biopsies are being conducted because of suspicious image findings with the vast majority of these biopsies having negative findings [4]. Therefore, currently there is a need to improve cancer imaging by improving the specificity as well as sensitivity of imaging techniques. This in turn would reduce the number of biopsies, which would thereby reduce the cost of medical care, reduce the anxiety of, and additional risks posed to, patients undergoing these procedures, and reduce the time burden of physicians and pathologists.

In order to improve the specificity of biomedical imaging, quantitative imaging techniques have been developed [5,6]. A mapping of physical quantities in the image space generated from the signals can provide new sources of image contrast. In ultrasound, quantitative ultrasound (QUS) techniques include spectral-based parameterization of ultrasound signals, flow estimation through Doppler, tissue elastography techniques, shear wave imaging and envelope statistics. Some of these techniques have already been adopted on clinical devices while some of these techniques are still under development. In this paper, the history and successes in spectral-based parameterization and envelope statistics will be reviewed for their ability to produce new sources of contrast and provide improved diagnostics for soft tissue imaging. These techniques are still under development and not available on most current clinical ultrasound imaging systems. Pre-clinical and clinical reports of soft-tissue QUS include: characterization of cyclical variation in the ultrasound backscatter from the myocardium, breast and prostate cancer detection, thyroid cancer diagnosis, diffuse liver disease quantification, detection of micrometastases in lymph nodes, detection of cervical ripening, detection of cell death and response of tumors to therapy and monitoring of thermal therapies. Roadblocks that have been identified in past years include practical implementation of calibration procedures and accounting for attenuation and transmission losses in vivo.

II. Historical Development of QUS

Ultrasound signals from tissues are based on the scattering of ultrasound from changes in the mechanical properties of tissue structures. Scattering from interfaces between two different kinds of tissues or large structures (on the order of a wavelength or larger) can result in large specular echoes. However, within certain tissue structures and organs, regions of uniform scattering may occur giving rise to scattering from many sub-resolution structures. In B-mode, this scattering appears as speckle. Many image processing techniques aim to reduce the presence of speckle. However, the signals giving rise to speckle are associated with the underlying tissue microstructure. Currently, the gold standard for disease classification is based on optical histology, which is able to characterize the microstructure of tissue. Therefore, if the ultrasound signals depend on tissue microstructure, then it is hypothesized that characterization of these signals could noninvasively provide information about tissue microstructure to assist in classifying disease without the need for optical histology in all cases. To properly characterize these signals, it is mandatory to model the signals associated with ultrasonic backscatter from tissues. Two methods of analyzing these signals have gained prominence: spectral-based parameterization of the signals, and characterization of the envelope statistics.

A. Spectral-Based Parameters

Spectral-imaging techniques in ultrasound are based on parameterizing the backscatter coefficient (BSC) of a tissue. The BSC is related to the underlying tissue structure and is a fundamental property of tissue similar to the attenuation and sound speed of a tissue. Because the BSC is a fundamental property of the tissue, the BSC can be both operator and system independent. Nevertheless, accurately estimating the BSC from experimental data is not a straightforward task and several methods exist as described below.

One of the earliest attempts at using spectral-based ultrasonic imaging was from Holasek et al. [7]. In that work they developed an analog filter technique to break the bandwidth of backscattered ultrasound into three bands. They color coded each band and displayed the different colors as an image in an attempt to tissue type based on ocular images. At the same time, the BSC was being evaluated as a means of characterizing the scattering from blood [8].

A few years later, Lizzi et al. [9] developed a theoretical framework for spectrum analysis of ultrasound signals for the purposes of characterizing ocular tissues. Their work allowed for a calibration spectrum to account for system-dependent effects. Since the early days of spectral-based ultrasound analysis, many researchers have applied these techniques to ultrasonic imaging and improved technology has brought about a renewed interest in further developing these techniques.

Modern spectral-based ultrasonic imaging focuses on estimation of the BSC as a starting point to further modeling and parameterization. The BSC, assuming far field, can be used as the basis for spectral-based QUS estimates and is defined by [10],

$${\sigma }_{\mathit{bsc}}\left(f\right)=\frac{R^2}{V}\frac{\langle I_{sc}\left(f\right)\rangle }{I_{\mathit{inc}}\left(f\right)}\propto W\left(f\right)$$ (1)

where R is the distance to the scattering volume of interest, V is the scattering volume defined by the beamwidth and range gate length, I_sc (f) and I_inc (f) are the scattered and incident fields, respectively, and W(f) is the normalized power spectrum. The normalized power spectrum is found by estimating the periodogram of signals windowed from some tissue region and dividing by some reference spectrum. In regions where the scattering is uniform, the BSC can be parameterized to yield estimates of the scatterer properties, which can then provide a geometrical interpretation of the underlying tissue microstructure.

To normalize the power spectra used in calculating the BSC, two different methods have been developed: 1) a planar reference method when using single-element transducers [9,11] and 2) a reference phantom technique allowing the use of clinical array systems [12,13]. Figure 1 illustrates the techniques for obtaining a calibration spectrum. Normalization methods effectively correct the effects of focusing, time-gain compensation, and diffraction because these factors affect the experimental data and the normalization data in the same fashion.

Fig. 1.

(Left) Illustration of the planar reflector technique and (right) illustration of the reference phantom technique.

In the planar reference technique, a smooth plate (i.e., roughness much smaller than a wavelength) of material with known reflectivity is used to provide a reference signal from the surface. The power spectrum of the reference signal is calculated through the magnitude squared of the Fourier transform of the reflected signal, |S_planar (ω)|². Similarly, the power spectrum from the sample is estimated for a particular scan line (designated by subscript n) in a data block through the magnitude squared of the Fourier transform of the windowed signal, |S_n (ω)|² A data block consists of a number of sequential scan lines of windowed radio frequency (RF) data. The size of the data block in the axial direction is determined by the length of the windowing function and normalized to the number of pulse lengths. The lateral width is determined by the number of scan lines in the data block and can be normalized to width as a number of beamwidths. The normalized power spectrum for a data block is given by [14]

$$W\left(f\right)=\frac{1}{N}\frac{{\Re }^2}{4}A\left(f,L\right)\sum _{n=1}^N\frac{{\left|S_{s,n}\left(f\right)\right|}^2}{{\left|S_{\mathit{planer}}\left(f\right)\right|}^2}$$ (2)

where A(f, L) is an attenuation compensation function, ℜ is the reflection coefficient of the reference material and N is the number of scan lines in the data block. The normalized power spectrum represents an average of the normalized spectra within the data block. The planar reference technique is suited for weakly-focused single-element transducers.

In the reference phantom technique, Yao et al. [12] derived the BSC from a sample by comparing the echo data acquired from the sample to data from a reference phantom with a known BSC and attenuation coefficient. The BSC from a sample using the reference phantom technique is given by

$${\sigma }_b^2\left(f\right)={\sigma }_b^{\mathit{RPM}}\left(f\right)e^{-4z\left[{\alpha }_{\mathit{RPM}}\left(f\right)-{\alpha }_s\left(f\right)\right]}\frac{{\left|S_s\left(f\right)\right|}^2}{{\left|S_{\mathit{RPM}}\left(f\right)\right|}^2}$$ (3)

where z is the depth, ${\sigma }_b^s\left(f\right)$ and α_s (f) are the BSC and attenuation coefficients of the sample, respectively. Similarly, ${\sigma }_b^{\mathit{RPM}}\left(f\right)$ and α_RPM (f) are the known BSC and attenuation coefficients of the reference sample, respectively. The frequency domain signal from the sample and the reference sample are denoted by S_s (f) and S_RPM (f), respectively. The data acquired from the sample and reference phantom are presumed to come from the same range depth using the same system settings. Furthermore, the scatterers in the reference phantom should not be too large with respect to a wavelength in order to avoid specular reflections. This technique is applicable for any transducer geometry such as single-element focused/unfocused transducers and array systems including different beamforming techniques [15,16].

Spatial resolution of spectral-based imaging depends on the size of the data blocks. Assuming uniform scattering properties throughout a data block, then larger data blocks sizes result in lower variance and bias of estimates at the tradeoff of spatial resolution in QUS imaging [14–18]. In one study where these tradeoffs were analyzed, it was suggested that data block sizes of 10 pulse lengths by five beamwidths (50 resolution cells) would provide adequate spatial resolution with low estimate bias and variance (< 10%) [17].

Separate studies have developed and explored different techniques to further expand the tradeoffs between data block size and estimate bias and variance. In one study a filter function was created to mitigate bias introduced by small gating functions [20]. This technique was later combined with Welch’s technique [21] to further improve both bias and variance of scatterer property estimates [22]. Smoothing techniques involving multi-taper methods and Welch’s technique have also been explored in the context of BSC estimation further expanding the tradeoffs between QUS spatial resolution and the quality of scatterer property estimates [23–27]. Another method for improving spectral-based estimates is angular compounding [28–29].

If implemented correctly, spectral-based QUS can provide operator- and system-independent imaging biomarkers. Several studies have been conducted to demonstrate the ability to accurately estimate the BSC from tissue-mimicking phantoms and rat tumors using multiple ultrasonic imaging platforms [30–33]. These studies established that the BSC and attenuation can be accurately determined in a system-independent manner and consistently when using different clinical machines. Therefore, the ability to conduct spectral-based QUS imaging has been demonstrated on multiple clinical ultrasound scanners.

In order to better quantify the BSC for imaging, the BSC is often parameterized. An approach used by Lizzi et al. was to parameterize the normalized backscatter power spectrum converted to a decibel scale by fitting a line to the normalized power spectrum versus frequency [34,35]. The spectral slope, mid-band fit and spectral intercept were then used to parameterize the normalized power spectrum.

The linear approach may not capture all of the structure in the normalized power spectrum or BSC representing scattering from tissues. Therefore, approaches using models of tissue microstructure have also been implemented. Specifically, based on the Born approximation for weak scattering, the BSC has been modeled using an intensity form factor approach [10,36,37]. Based on the form factor models, estimates of scatterer properties (i.e., effective scatterer diameter (ESD) and effective acoustic concentration (EAC)) related to the underlying tissue microstructure can be obtained [38, 39]. This is accomplished through an estimator that compares the BSC calculated from measurements to a theoretical BSC and minimizes some cost function versus trial values of ESD and EAC. The most common estimator used is the minimum average squared deviation (MASD) [10]. In most instances, an estimator will provide a single value for the ESD. However, this value in tissue will most likely represent a distribution of scatterer sizes and the width and shape of this scatterer size distribution will influence the final ESD estimate [40]. Different estimators can be used to reduce the effects of scatterer size distribution on the final ESD estimate [41]. Furthermore, different frequencies are sensitive to different scales of structure [42, 43]. This suggests that for a particular application, the choice of appropriate frequency range may be warranted.

The appropriate choice of a form factor model describing the underlying tissue structure is a subject of continued research. The most commonly used form factor model for QUS remains the Gaussian form factor [10,14]. However, new form factor models may arise based directly off of modelling of ultrasonic scattering from tissues using the impedance map approach [44,45]. In the impedance map approach, stained tissue histology slides are converted to acoustics impedance values and combined to form a three dimensional map of impedance, from which ultrasonic scattering can be modelled. The impedance map approach also helps in identifying structures that are responsible for scattering. Assigning the impedance value to optical histology slides is not without uncertainty and the exact impedance values that should be assigned to different structures remains an open question. Other modeling of ultrasound backscatter will be discussed later in the paper.

In addition to estimating scatterer properties such as ESD and EAC, the attenuation coefficient of the tissue can be estimated using spectral analysis. Several techniques have been developed to estimate the attenuation from the spectra of backscattered ultrasound [46–48]. Estimation of the frequency-dependent attenuation is important as a parameter for characterizing tissue and for compensating for other spectral based estimates [49].

B. Envelope Statistics

The shape and attributes of the envelope of the backscattered ultrasound also contain information about the underlying tissue microstructural properties. A number of models for the statistics of the envelope have been proposed over the past few decades with applications to sea echo, medical ultrasound, and laser [50]. Some of these distributions include the Rayleigh distribution, the Rician distribution, the K distribution, the homodyned K distribution, and the Nakagami distribution. Derivations of these distributions have been covered extensively in the literature, e.g., [51]. Therefore, these distributions are only briefly covered here.

The most basic distribution describing the envelope of backscattered ultrasound and subsequently the distribution providing the least amount of information is the Rayleigh distribution. The Rayleigh distribution arises when a large number of nearly identical and randomly located scatterers contribute to the echo signal. If the signal follows a Rayleigh distribution, the only information about a sample that can be extracted from the envelope of the backscattered ultrasound is the mean backscattered power. Pre-Rayleigh scattering conditions occur when the number of nearly identical scatterers per resolution is low, i.e., less than 10.

The Rician distribution extends the Rayleigh distribution to include a coherent signal, which could be the result of periodically located scatterers or specular scatterers in the signal [52, 53]. The Rician distribution provides an estimate of strength of the coherent signal.

Jakeman and Pusey [54] introduced the use of the K distribution, a generalization of the Rayleigh distribution, in the context of microwave sea echo to model situations where the number of scatterers per resolution cell is assumed to be small. A parameter introduced by the K distribution is the number of scatterers per resolution cell, μ. The K distribution approaches the Rayleigh distribution in the limit μ → ∞. If the resolution cell of the ultrasound source can be calculated, the actual number density of scatterers can be estimated from μ.

The homodyned K distribution was first introduced by Jakeman [55]. Besides incorporating the capability of the K distribution to model situations with low effective scatterer number densities, the homodyned K distribution can also model situations where a coherent signal component exists due to periodically located scatterers. The homodyned K distribution is the more versatile of the models discussed, but also the most complicated. The probability distribution function of the homodyned K distribution does not have a closed-form expression; however, it can be expressed in terms of an improper integral as

$$p_A\left(A\right)=A\underset{0}{\overset{\infty }{\int }}x{J}_0\left(sx\right)J_0\left(Ax\right){\left(1+\frac{x^2{\sigma }^2}{2\mu }\right)}^{-\mu }dx$$ (6)

Where J₀(●) is the modified zeroth order Bessel function of the first kind, s² is the coherent signal energy, σ² is the diffuse signal energy, and μ is the same as in the K distribution. The derived parameter k = s/σ is the ratio of the coherent to diffuse signal energy and can be used to describe the level of structure or periodicity in scatterer locations. To estimate the parameters of the homodyned K distribution, two efficient algorithms were recently developed [50,56].

The Nakagami distribution, or m-distribution, was developed by Nakagami after extensive experiments on long distance multipath propagation of radio waves via the ionosphere and/or troposphere [57,58]. The use of the Nakagami for characterization of ultrasound signals was introduced by Shankar et al. [59,60]. The Nakagami probability distribution function is given by

$$p_A\left(A\right)=\frac{2m^m{A}^{2m-1}}{\mathrm{\Gamma }\left(m\right){\mathrm{\Omega }}^m}exp\left(\frac{-m{A}^2}{\mathrm{\Omega }}\right)$$ (7)

where m is called the Nakagami parameter and Ω is called the scaling factor. The two parameters of the Nakagami pdf are calculated from

$$\mathrm{\Omega }=\langle A^2\rangle$$ (8)

and

$$m=\frac{{\mathrm{\Omega }}^2}{\langle {\left(A^2-\mathrm{\Omega }\right)}^2\rangle }.$$ (9)

The value of the estimated Nakagami parameter, m, allows the classification of the signal, and therefore the sample or tissue, into one of four categories: 1) m < 0.5 – the distribution is considered to be a Nakagami-Gamma (i.e., few scatterers per resolution cell with Gamma-distributed scattering cross sections), 2) 0.5 ≤ m ≤ 1 – pre-Rayleigh scattering conditions, 2) m ≈ 1 – Rayleigh distributed and 3) m > 1 – the distribution is considered Rician or post-Rayleigh. Therefore, the Nakagami distribution is useful for classifying tissues or samples by designating the type of scattering condition associated with the envelope distribution. Nakagami imaging has been explored for tissue characterization, where maps of the Nakagami parameter are constructed [61–64].

The quality of estimates based on the envelope statistics depend on several factors. Similar to spectral-based estimates, the bias and variance of estimates from the envelope statistics also depend on the number of samples available for estimation, i.e., the larger the data block size the better the bias and variance of the estimates [50]. In addition, when estimating the number of scatterers per resolution cell, μ, the accuracy of the estimate depends on the actual number of scatterers per resolution cell. When using the homodyned K distribution method and fractional order moments, the μ is only accurate when the number of scatterers per resolution cell is less than 10 [52]. Finally, parameters based on the envelope statistics are also dependent on the frequency of ultrasound and on attenuation, which causes a spreading of the beam with depth [65, 66]

III. Successful Applications of Quantitative Ultrasound

Spectral-based QUS and envelope statistics have been utilized successfully to improve diagnostics for several important clinical applications. In this section we review several recent notable successful applications of QUS in soft tissues.

A. Characterization of the Myocardium

One of the earliest applications of QUS techniques to clinical medicine was the ability to characterize cyclical variations in the myocardium over a cardiac cycle. Numerous studies have been conducted to quantify QUS parameters in the heart [67–79]. These studies have demonstrated that quantification of the cyclical variation of myocardial ultrasonic backscatter over the heart cycle can be used to identify the early onset of cardiac abnormalities.

More recent application of these studies has been to characterize diabetes [80–81]. In one study, comparisons between normal subjects and patients with type 2 diabetes demonstrated that parameterization of the ultrasonic backscatter from the myocardium could differentiate between the hearts of diabetic patients based on their diabetic control. Specifically, the rise time and slew rate of cyclical rise in backscatter parameters over the cardiac cycle could differentiate diabetic control. The clinical impact is to potentially provide a noninvasive technique to monitor patients at higher risk of type 2 diabetic cardiomyopathy.

B. Pre-Clinical and Clinical Breast Lesion Characterization

Pre-clinical studies were conducted to determine if QUS could differentiate between benign and malignant tumors, and between different kinds of malignant tumors in rodent models of breast cancer [12,82,83]. QUS analysis was conducted over a broad ultrasonic frequency range of 5 to 25 MHz using single-element weakly-focused transducers. The first tumors examined were spontaneous mammary fibroadenomas in rats, the second kind of tumor examined was the 4T1 MMT carcinoma for mice and the third kind of tumor examined was a mammary sarcoma (EHS sarcoma) for mice. Tumors were grown to a little over a centimeter in size and then examined using QUS techniques.

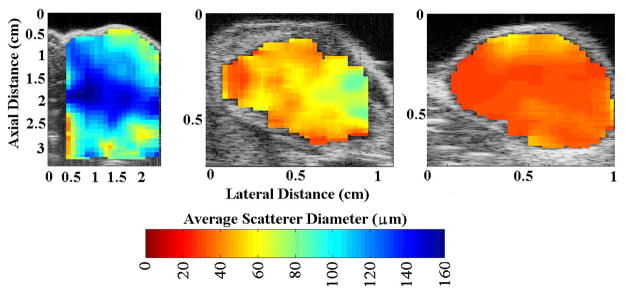
QUS parameters (i.e., ESD, EAC, k and μ) were used to distinguish and classify the three kinds of rodent models of mammary cancer. Statistically significant differences were observed between the three kinds of tumors examined based on the QUS parameters [84]. The parameters were related to underlying tissue structures by comparing to optical photomicrographs of the tumors. For example, the glandular acini in the fibroadenoma were identified as the dominant sources of scattering in the fibroadenomas [85]. Figure 2 shows examples of QUS images of the tumors using the ESD parameter.

Fig. 2.

Ultrasound grey-scale B-mode images superimposed with estimates of ESD for (left) rat fibroadenomas, (center) mouse carcinomas, and (right) mouse sarcomas. Figure reproduced from [5].

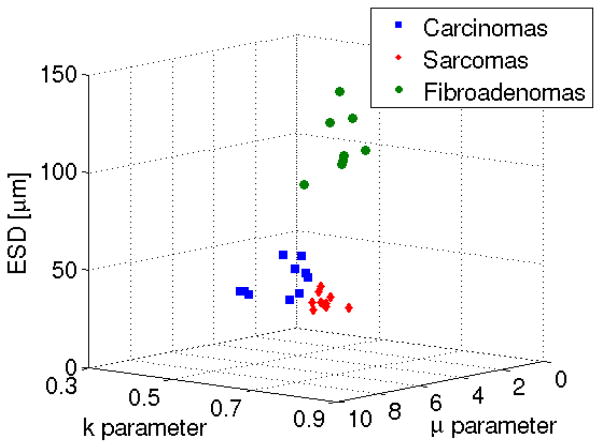
Figure 3 shows a feature analysis plot of QUS estimates for the three different kinds of tumors (ESD from Gaussian form factor and parameters of the homodyned-K distribution). Based on the QUS parameters, no overlap existed between the fibroadenomas, carcinomas and sarcomas allowing a clear distinction between the tumors based on the QUS parameters. As more parameters are added yielding a higher dimensional set, the ability to separate tissues can increase.

Fig. 3.

Feature analysis plot of the ESD versus μ versus k parameter. Figure from [5].

A few studies involving QUS for clinical breast cancer detection have been published. Studies have utilized spectral-based QUS to characterize breast cancer and detect the response of breast cancer to therapy [86,87]. Another study utilized parameters from the homodyned-K to characterize breast lesions [88].

C. Pre-Clinical Thyroid Cancer Lesion Characterization

A high-frequency single-element ultrasonic scanning system was used to scan thyroids extracted from mice that had spontaneously developed thyroid lesions (cancerous or benign) [89]. Four sets of mice were acquired having different predispositions to developing thyroid anomalies. The first set of balb/c mice were not expected to develop thyroid lesions and were used as controls. Another set of mice were from the Rb 1+/− mouse strain [90] with approximately 50% of these mice developing benign C-cell adenomas or C-cell hyperplasia in the thyroid. The third set of mice was from the TG-BRAF mouse line [91] that develop papillary thyroid carcinomas (PTCs), i.e., the most common type of thyroid cancer. The final set of mice [92] consisted of mutant mice that had introduced a dominant negative mutant thyroid nuclear receptor gene, TRβPV, into the TRβ gene locus. As a result of this mutation, as the mice aged they developed metastatic thyroid tumors consistent with follicular (variant) pattern papillary thyroid carcinomas (FTC).

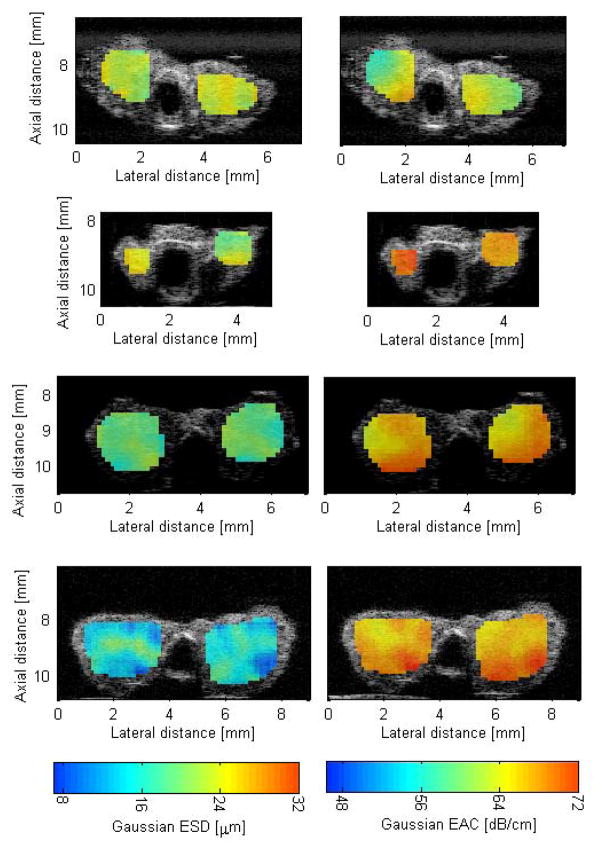
Figure 4 shows QUS images of mice thyroids (normal and cancerous) enhanced by either the ESD or EAC. From B-mode images it would be difficult to differentiate between different thyroids based on their visible appearance. Statistically significant differences were observed between the cancerous thyroids (PTC and FTC) and the normal thyroids using the ESD, EAC, and μ parameters. The k parameter did not yield statistically significant differences between groups. No parameter was able to differentiate the C-cell adenomas from the normal thyroids. Only the ESD and EAC could differentiate the cancerous thyroids from the C-cell adenomas. Finally, the ESD and EAC provided the ability to distinguish the PTC from the FTC. The μ parameter did not provide statistically significant differences between the PTC and FTC thyroids.

Fig. 4.

QUS images of thyroids enhanced by ESD (left column) and EAC (right column). The top row is normal thyroid (no tumor observed), the second row is a C-cell adenoma, the third row is PTC, and the last row is a FTC.

D. Detection of Prostate Cancer

QUS methods have been investigated in a wide range of studies to image and characterize prostate cancer. If successful, QUS methods could enable more-effective biopsy and treatment guidance and could also provide non-invasive treatment monitoring. Unfortunately, current imaging methods cannot reliably detect cancerous regions and as a consequence, biopsies sample prostatic tissue based on the gland anatomy, but blindly with respect to cancerous regions. For example, transrectal ultrasound (TRUS) which is the most common means of prostate imaging is unable to detect cancerous regions reliably. Therefore, current standard of care usually involves treating the entire gland and therapy monitoring is based on serum prostate-specific antigen (PSA) levels.

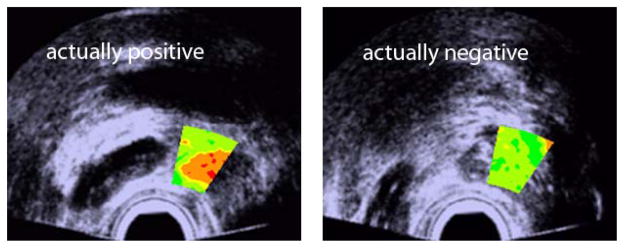
To date the most successful QUS studies involving the prostate were performed by Feleppa et al [93–96]. In these studies, spectral-based QUS estimates (i.e., midband and intercept) were computed from a wide range of clinical instruments providing RF data. One of the interesting results of these studies was the comparison between the performance of the urologist and QUS at detecting cancer. The urologist used his experience, the patient record, the PSA, and the conventional TRUS B-mode image to assign a level of suspicion for cancer at the biopsy site. The QUS results were obtained by training classifiers (support vector machines and artificial neural networks) that use two QUS estimates in addition to PSA for identifying cancerous tissue [97, 98]. The AUC value obtained using the B-mode was 0.638 +/− 0.031 compared to the QUS-based AUC of 0.844 +/− 0.018. Figure 5 illustrates how the QUS methods could be adapted to a clinical setting by a urologist with no background in QUS. The color-coded information simply displays the likelihood of cancer from green to red and is applied over the biopsied region of the gland.

Fig. 5.

QUS images utilizing a level of cancer suspicion metric overlaid on B-mode images of the prostate. (Reproduced from [79])

E. Detection of Micrometastases in Excised Lymph Nodes

Cancer involvement in lymph nodes near a primary tumor is important for proper staging, treatment, and patient management. Specifically, if metastases exist in lymph nodes, it is a strong indication that the cancer has spread and should be aggressively treated as systemic.

In current standard of care, several lymph nodes are typically excised during the same surgical procedure performed to treat the primary tumors. The exact protocol is different for different primary cancer organs, but the lymph nodes are always sent to a pathology laboratory where they are typically evaluated by looking at one or two sections within each node. Therefore, the current pathology protocol is labor-intensive, time-consuming, and results in false-negative determinations due to inadequate sampling of the lymph nodes. In particular, small but clinically-significant micrometastases (i.e., 0.2 to 2 mm in size) can be missed.

High-frequency QUS techniques were investigated to see whether they could be used to asses lymph nodes in their entirety and possibly guide pathologists toward suspicious regions[99–101]. In these studies, RF data were acquired in 3D from individual, freshly-excised lymph nodes from breast-, colorectal-, or gastric-cancer patients using a single-element transducer operating at 26-MHz center frequency. In total, 13 QUS estimates (4 spectral-based and 9-envelope based) were combined using classifiers (i.e., support vector machines or linear discriminant) to detect cancers. The classifiers were trained using gold-standard histology. Discriminant scores from the classifiers were also used to compute cancer probability maps throughout the lymph node.

Results showed excellent classification performance for nodes harvested from colorectal- and gastric-cancer patients with area under the receiver operator curve (AUC) greater than 0.95 [99]. Results were also satisfactory for the more complex nodes obtained from breast-cancer patients with AUC values around 0.84.

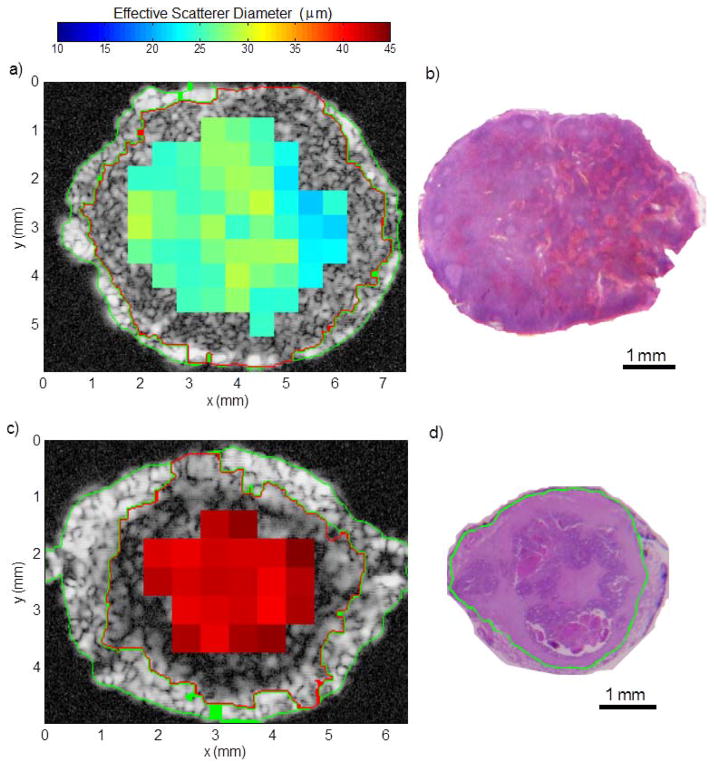
To visually illustrate the results, Fig. 6 shows representative ESD images obtained from lymph nodes harvested from colorectal patients. The ESD estimates are found to be much smaller in the non-cancerous node (Fig. 6a) than in the completely-metastatic node (Fig. 6c).

Fig. 6.

Illustrative results obtained with a non-metastatic lymph node (a and b) and a nearly entirely metastatic lymph node (c and d). a) and c): parametric cross-sectional images displaying effective scatterer-size estimates. b) and d) histologic thin section approximately corresponding to a) and c), respectively. Metastatic region is highlighted in green in d) and segmentation results are shown by the green and red highlights in a) and c). (Adapted from [102]).

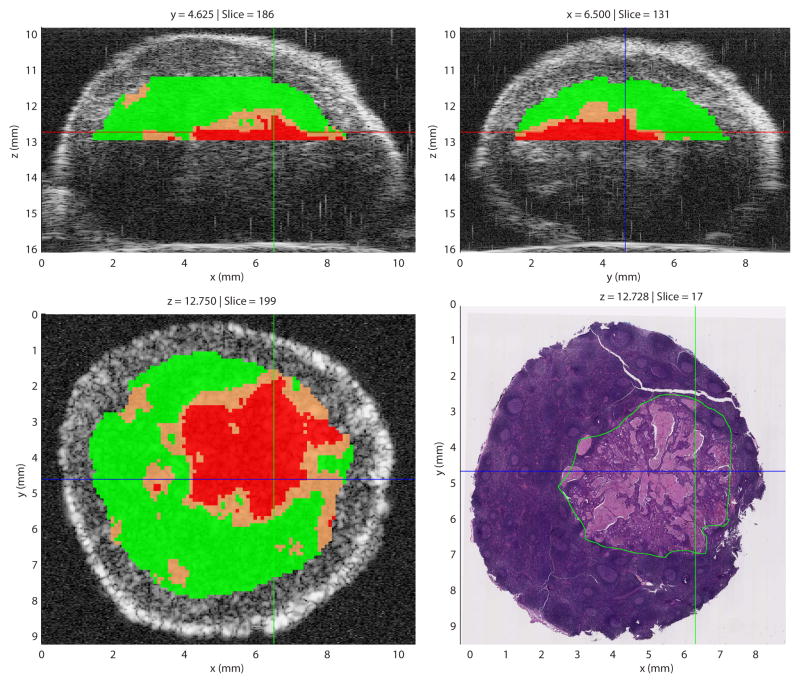
A graphical user interface (GUI) was developed to allow pathologists to investigate the 3D data and visualize the QUS-based cancer probabilities [103]. An illustrative screen capture (Fig. 7) demonstrates how the GUI (called Lymph Explorer) could be used to guide pathologist towards suspicious regions in lymph nodes. (The co-registered image demonstrates the accuracy of the methods, but would not be available in the clinical use of the Lymph Explorer.)

Fig. 7.

Illustrative Lymph Explorer screen capture showing cancer probabilities. Results were obtained from a partially-metastatic lymph node of a colorectal-cancer patient. In the three QUS images, regions highlighted in red indicate cancer probability greater than 75%; those in green indicate a cancer probability smaller than 25% and those in orange indicate a cancer probability between 25% and 75%. In the co-registered histology image, the green outline indicates the metastatic region. (Adapted from [102,103])

In the case of a lymph node containing a micrometastases, Lymph Explorer could prove to be an invaluable tool, because a random section through the lymph node could likely miss the cancer foci. Even If some small lesions go undetected, Lymph Explorer would provide guidance on how to cut through a suspicious region, then the stained section would be evaluated by a pathologist. This approach could greatly reduce false-negative determinations in lymph nodes containing small cancer foci. In addition, although these QUS methods are under investigation for their ability at detecting micrometastases, they are already capable of increasing the current rate of true-negative determinations.

F. Quantifying Liver Steatosis

The idea of BSC-based and attenuation QUS techniques to quantify diffuse liver disease has been around for several decades [104–106]. Early work successfully examined attenuation as a key indicator of liver steatosis [104]. While BSC and attenuation change with steatosis, concomitant factors in the liver besides steatosis may lead to changes in these parameters, e.g., fibrosis.

In a more recent study, fresh liver samples were extracted from male New Zealand white rabbits [107]. The rabbits had been on a special fatty diet or normal diet (control). The BSC was calculated to obtain spectral estimates using an analysis bandwidth of 8 to 15 MHz from excised rabbit livers. The ESD and EAC were calculated from the BSC. The k and μ parameters were estimated from the envelope statistics of the backscattered ultrasound. To correlate the QUS parameters with the grade of fatty liver, QUS parameters were compared to the total liver lipids. The total liver lipids were estimated by the Folch method [108].

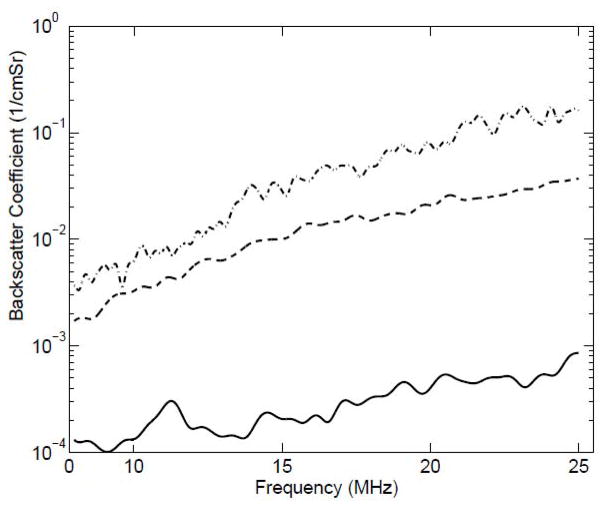
The BSCs from the liver samples extracted from animals on normal diet, three weeks of fatty diet and six weeks of fatty diet are shown in Fig. 8. Statistically significant differences from QUS parameters were quantified through a p-value < 0.05. The ESD decreased significantly and EAC increased with increasing lipid content. Specifically, the mean ESD was observed to be 30 μm, 25 μm and 19 μm in liver samples from animals on normal diet, three weeks of fatty diet and six weeks of fatty diet, respectively. The k parameter estimated from the liver samples of animals on normal diet and fatty diet did not provide statistically significant differences. However, the μ parameter, which is related to the density of scatterers per resolution cell, increased significantly with increasing lipid content. Therefore, QUS has demonstrated the ability to detect and grade the fatty liver. Furthermore, these QUS methods may complement shear wave imaging that is sensitive to liver fibrosis but not to fatty liver.

Fig. 8.

Backscatter coefficients from liver samples extracted from animals on different diets with (solid line) zero days on fatty diet, (dashed line) three weeks on fatty diet, and (dot-dashed line) six weeks on fatty diet.

In a more recent study in humans, QUS techniques were used to grade steatosis [109]. In that study, 204 patients were scanned with an ultrasound scanner (Siemens S3000) using the Ultrasound Research Interface (URI) and 4C1 curved array probe. Participants fasted four hours before analysis. The BSC was calculated from the acquired data using a reference phantom approach. QUS results were compared to MRI proton density fat fraction and body mass index. ROC analysis indicated that the BSC provided 91% specificity, 76% negative predictive values and 95% positive predictive value.

G. Detection of Cervical Ripening

Several groups have explored QUS techniques for the detection of cervical ripening both in animal models of pregnancy and in humans. The goal of developing these techniques is to find an early indication of the likelihood of preterm birth. In the U.S. more than 12% of births are preterm [110]. The consequences of preterm birth are many and prematurity is responsible for 20% of retardation, 30% vision impairment and 50% of cerebral palsy [111,112]. Therefore, the development of imaging markers that can predict preterm birth before the onset of labor and before irreversible changes occur would dramatically improve the ability to intervene.

Initial studies of QUS parameters of the rat cervix using high-frequency ultrasound (30 to 70 MHz) were used to predict the gestational age of pregnant rats [113]. ESD and EAC were found to relate to the gestational age of the rats, i.e., ESD increased and EAC decreased for days 15 to 21 of pregnancy. These results suggested that QUS parameters of the cervix at high ultrasonic frequency could predict the stage of pregnancy in rats.

In a subsequent study, McFarlin et al. [114] utilized the ultrasonic attenuation estimated from the power spectrum to predict the onset of labor in pregnant humans. Specifically, RF data were acquired from pregnant human cervices. Estimates of attenuation were acquired using a Zonare ultrasound system with an array having a bandwidth of 4 to 9 MHz. Regression analysis of the attenuation estimates demonstrated that attenuation could predict the interval between ultrasound examination and delivery. However, attenuation could not predict the gestational age at the time of examination.

Other groups have explored different QUS biomarkers for quantifying the ripening of the cervix including shear modulus, backscatter power loss, anisotropy and backscatter heterogeneity [115–117]. These studies further corroborated the role of attenuation in predicting cervical ripening and also showed that anisotropy of the cervix could be an important indicator. Further studies examined second harmonic generation imaging with optical microscopy to examine collagen structure and successfully compared these results to corresponding QUS estimates of tissue microstructure [118].

H. Detection of Cell Death and Tumor Response to Therapy

Increased tumor cell death is a good prognostic indicator of a treatment outcome especially in the early stages of therapy [119,120]. Spectral-based QUS techniques have demonstrated the ability to detect cell death in both in vitro and in vivo experiments. Specifically, early experiments were carried out to detect cell death in cell samples and tissues exposed to various cancer therapies (e.g., radiation, chemotherapy and photodynamic therapy) using high-frequency ultrasound (20–50 MHz) [121–123]. In the experiments performed on cell samples in vitro exposed to a chemotherapeutic drug, apoptotic cells exhibited up to a sixteen fold increase in ultrasound integrated backscatter (UIB) in comparison with viable cells. Other measurable changes in ultrasonic spectral-based parameters were also observed [111,124,125].

In more recent experiments, two spectral-based QUS parameters, UIB and spectral slope were used to monitor the responses of tumors exposed to cancer treatment [126–128]. Tumor cell death can be characterized by significant changes in the microstructure associated with tumor cells (nuclear condensation and fragmentation) and also cellular organization. The studies showed that ultrasonic backscatter was sensitive to the structural organization of the tumors. In research conducted by Vlad et al. [126], radiotherapy effects were characterized by QUS methods in preclinical mouse cancer models as early as 24 hours post treatment. Ultrasonic images enhanced by spatial maps of ultrasound spectral parameters enabled non-invasive assessment of cell death in tumor regions responding to radiotherapy. The contrast provided by the QUS parameters was hypothesized to come from the changes in the tissue microstructure due to therapy response and did not require the injection of exogenous contrast agents.

Recently, QUS at clinical frequency ranges was used to study treatment response monitoring in breast cancer xenograft tumors [129] and human breast tumors treated with chemotherapy [86]. Tumors demonstrated approximately an 8 to 9- fold increase in mid-band fit and spectral intercept after cancer therapy initiation. These techniques were then applied to detecting response and predicting survival in breast cancer patients receiving chemotherapy [87]. In the study, the EAC parameter was observed to increase in patients responding to treatment as early as one week post treatment initiation, which further increased at week 4 and reached a maximum value at week 8 of therapy initiation. In contrast, non-responding patients did not exhibit changes in the QUS parameters. The best predictor of treatment response was through the combination of EAC and ESD parameters at week 4 achieving a sensitivity of 82% and specificity of 100%. The results demonstrate that backscatter parameters extracted from ultrasound data are predictive of ultimate clinical chemotherapy response, as early as 1 week after treatment initiation. The improved predictive capabilities provided by QUS could allow clinicians to further customize cancer therapies and to change ineffective treatments within days to weeks of starting therapy.

I. Monitoring of Thermal Therapies

In vivo and ex vivo studies were conducted to monitor high-intensity focused ultrasound (HIFU) application and microwave ablation using QUS techniques [130,131]. For HIFU, rat mammary adenocarcinoma tumors (MAT) were exposed to HIFU to create thermal lesions.

During the treatments, an ultrasonic linear array (14L5/38) connected to an Ultrasonix RP was used to scan the tissues and record RF data. The BSC was estimated from the data corresponding to the treatment region and two parameters were estimated from the backscatter coefficient (ESD and EAC) and two parameters were estimated from the envelope statistics (k and μ) of the backscattered echoes.

Tumors were exposed to a spatial peak temporal average intensity (I_SPTA) of 335 W/cm² with 75% duty cycle, as measured in degassed water using a needle hydrophone (Precision Acoustics, Dorchester, UK). Data was collected with the RP system during exposure by synchronizing capture of RF data with periods between HIFU exposure tone-bursts. HIFU exposure time of 60 sec was used in all experiments.

B-mode images of the scanned areas were constructed. Regions of interest in the B-mode images and data blocks were defined in the first image. Spectral-based parameters and envelope statistics were estimated for each data block for each frame acquired during the therapy. For example, the percentage changes in EAC versus time were estimated using

$$\mathrm{\Delta }\text{EAC}(10sec)=\frac{\text{EAC}(10sec)-\text{EAC}(0sec)}{\text{EAC}(sec)}.$$ (10)

These parameters were then compared to temperature readings from a thermocouple placed behind the tumor. The placement of the thermocouple behind the tumor placed it outside of the HIFU beam focus and therefore represents a lower bound for the actual temperature in the treatment area.

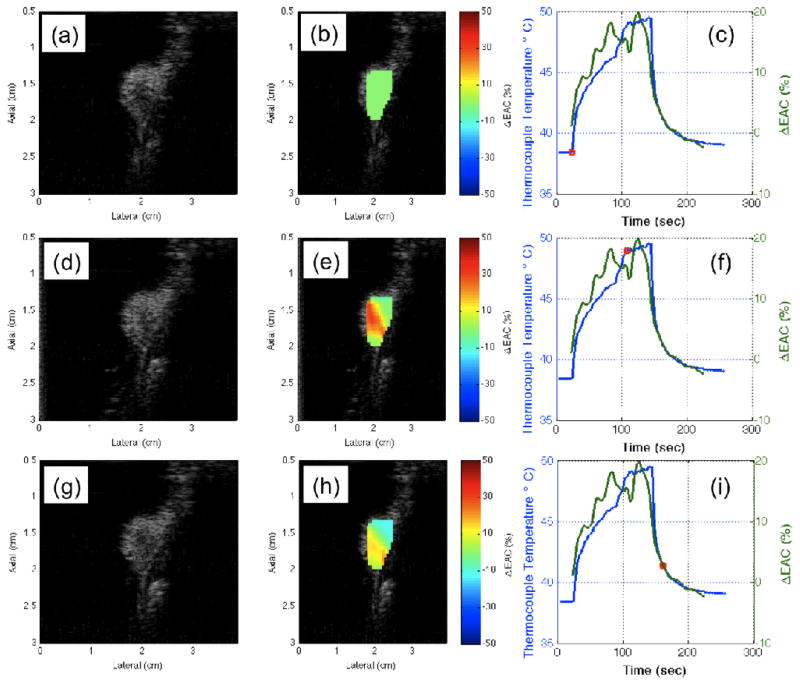
An example of the B-mode images of the tumors at different time points of HIFU application are shown in Fig. 9(a), (d) and (g) and the corresponding parametric images enhanced by ΔEAC are shown in Fig. 9(b), (e) and (h). The temperature profiles recorded by the thermocouple are shown as the blue curves in Fig. 9(c), (f) and (i). The red circles indicate the time points corresponding to the displayed B-mode and parametric images. The three rows in the figure represent the results at three different time points of 0 sec, 60 sec and 80 sec, respectively during the treatment. The percentage changes in ΔEAC(%) are shown in Fig. 9(c), (f) and (i) denoted in green color. An attenuation correction of 0.4 dB/cm/MHz was used to obtain the BSCs at different time points of HIFU application. It is expected that the lesion created by the HIFU application will have spatially varying attenuation, but the current results shown do not account for attenuation changes in the lesion because the depth of the tumors was small and attenuation changes would not affect the BSC estimate greatly.

Fig. 9.

B-mode and parametric images at different times during the HIFU treatment on rat R1.

The B-mode images in Fig. 9 do not show visible B-mode brightening as the HIFU therapy is applied. The EAC was observed to increase with increasing temperature and then decrease with decreasing temperature when the HIFU was turned off. Therefore, these curves indicate that BSC-based parameters can be correlated to temperature changes induced in tissues during thermal treatment. Small fluctuations due to tumor motion in an out of the imaging plane did not disrupt the ability to track temperature with the QUS parameters.

J. Blood characterization

Using QUS methods for the precise characterization of blood or more specifically red-blood cells (RBCs) and RBC aggregation has been an active area of research since the early 1970s [8, 132,133]. A typical human RBC can be assumed to be biconcave with a diameter of 8 μm and a thickness of 2.8 μm. However, the shape of RBCs can vary under normal and pathological conditions (e.g., sickle cell anemia, malaria, etc) and they can interact with each other to form rouleaux, i.e., isotropic aggregates, or complex 3D structures. In most cases, aggregates will significantly alter the BSC because of the increased scattering cross section. Even under healthy conditions, rouleaux will form and deform depending on shear rate.

From the clinical point of view, the ability to precisely characterize blood (e.g., hematocrit, aggregate shape and concentration, etc.) can yield a powerful tool for diagnosing a wide range of blood diseases and conditions. For example, high levels of RBC aggregation (e.g., compact spherical clumps) can be indicative of inflammation [134]. Although rouleaux formation is a common physiological phenomenon in healthy human blood, abnormal aggregation or hyperaggregation is associated with several circulatory conditions. Therefore, modeling RBC scattering is both medically significant and challenging, which is why it has been so heavily researched and why many different modeling approaches have been investigated [134–137].

One of the key challenges to properly modeling blood scattering is that most current QUS scattering models assume sparse media, or that individual scatterers are sufficiently far from each other that their spatial positions are completely random. Such an assumption becomes less valid as the volume fraction of scatterer increases or if scatterers become close to each other (e.g., rouleaux or RBC aggregates). Therefore, several theoretical studies have investigated how to model dense media or media where scatterer locations are not completely random [136, 138,139].

Some of the more recent successes have been accomplished with the use of the structure factor model (SFM) [140]. Conceptually, the SFM is an additional frequency-dependent multiplicative term modelling RBCs interactions, which is added to the conventional “sparse” BSC. In the case of RBC scattering, the SFM depends heavily on the hematocrit and on the RBCs spatial organization. In the case of high concentration and randomly-located RBCs, the SFM converges to unity as the hematocrit decreases, i.e., the BSC converges to that of a sparse model as expected when the number density of RBC decreases.

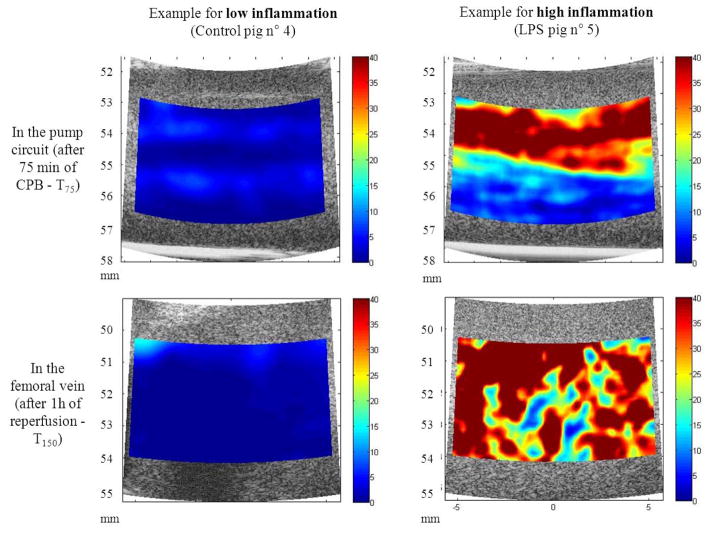
The first practical use of SFM for the ultrasound characterization of RBCs was performed using a Taylor series expansion of the SFM to develop the so-called structure factor size estimator (SFSE) [141]. In this fundamental study, the authors used the known values of the acoustic impedance of RBC and plasma, hematocrit, and RBC size to estimate two quantitative parameters using the SFSE (i.e., the packing factor and aggregate diameter). The results of the study demonstrated the efficacy of the approach at discriminating different levels of aggregation. A follow-up study from the same group refined the model by including compensating for the total attenuation between the probe and the blood in the model [142]. Figure 10 illustrates the strength of the approach to assess blood physiological state. The SFSE was demonstrated successfully to assess real-time variations of RBC aggregation as a surrogate marker of inflammation in a cardiopulmonary bypass swine model [143], and to assess the pro-thrombotic impact of RBC aggregation [144] in preclinical studies. The same model compensated for attenuation and instrument properties allowed assessing the higher level of flowing RBC aggregation in superficial veins of diabetic patients compared with normal individuals [145].

Fig. 10.

Examples of Structure Factor Size and Attenuation Estimator parametric images of red blood cell aggregation (W, longitudinal views) in case of low (left) and high inflammation (right). Data were acquired within the pump circuit deviation (top) and the femoral vein (bottom). The color maps vary from 0 (blue) to 40 (red). Variable W has no unit. LPS = lipopolysaccharide; CPB = cardiopulmonary bypass. (Adapted from [143]).

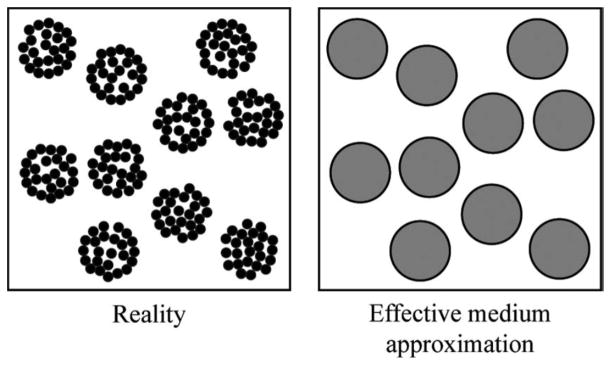
While the Taylor series approaches led to efficient QUS estimation methods and provided meaningful preclinical and clinical results, the physical interpretation of the QUS estimates is more challenging. Therefore, recently researchers proposed combining an effective medium theory with SFM (EMTSFM) [146,147] to model very specific cases of aggregation as illustrated in Fig. 11. This approach allowed the efficient modelling of blood by characterizing the aggregate size, and for the first time in the QUS field, the compactness of RBC aggregates. In clinical hemorheology, assessing the compactness of RBC aggregates is of high clinical importance because it is related to the binding energy between cells. The physical interpretation of EMTSFM is therefore straightforward and could prove useful for clinical studies where hematocrit and RBC aggregation are possible markers of a wide range of conditions. Another aspect of these methods is their ability at tracking aggregation dynamics because rouleaux are typically associated with healthy state, they can aggregate and disaggregate more easily than spherical clumps which are typically associated with diseased state.

Fig 11.

Schematic representation of aggregates treated as individual scatterers. The aggregates of red blood cells in blood (left side) are assumed to be homogeneous particles (right side) with effective properties that depend on the internal hematocrit and on the density and compressibility of the red blood cells within them. (Adapted from [146]).

IV. Current Roadblocks to Widespread Use and Clinical Acceptance

A. Radio-frequency data

For the most part, QUS methods rely on elegantly processing RF data. Therefore, manufacturers must be willing to provide the RF data or more generally the so called IQ data which can readily be used to regenerate RF data (though some investigators claim that the fidelity of RF data reconstructed from IQ data is compromised). Although access to RF data was initially a challenge for QUS, it is clearly not the case anymore. As ultrasound technology has progressed tremendously in the last 10 years, most systems are now completely digital and all manufacturers can now easily provide IQ data without significantly increasing hardware costs. Therefore, in modern ultrasonic devices accessibility to RF data is no longer a roadblock.

B. BSC Estimation and Calibration

Although QUS techniques based on the BSC clearly provide valuable information about tissues independent of the instrument and user, the need for proper estimation and calibration can be cumbersome in the fast-paced clinical environment. The BSC is an efficient tissue parameter to describe how a tissue will interact with ultrasound. Nevertheless, several estimation methods resulting in slightly different values for BSC exist [11]. Some early controlled studies performed on well-calibrated phantoms by several laboratories also illustrate the challenges remaining in the estimation of the BSC [148,149].

Most clinical systems use linear or phased arrays and therefore, the only available way to properly calibrate for QUS is with the use of the reference phantom method [12]. In this regard, a reliable and well-characterized phantom must be available that has a long shelf life during which acoustical features are stable. Reference data must be collected with all the probes and all possible settings which could be used during a clinical examination. In addition, these reference data must be collected regularly to insure robustness of the QUS estimates and also must be collected every time maintenance is performed on the system. Another approach could be to acquire the clinical data first, optimizing all the settings on the system to get the best possible image, and then take data from the phantom without changing any of the settings. This would marginally increase the examination time, but could prove to be a viable option.

Nevertheless, the need for accurate calibration remains a challenge to widespread clinical implementation of QUS methods. Over the past 20 years, several research groups have developed new reliable phantoms which could be mass produced and used as reliable reference phantoms for QUS studies [33, 150, 151]. In addition, just like manufacturers test systems and ultrasound probes before shipping them out to a customer, an extra step could be implemented to collect data from reference phantoms and save it into the system so that it could readily be used for QUS calibration with the same system. Finally, although theoretically it is better to collect calibration data with all probes and all possible settings, it is likely that the burden of data collection could be reduced by collecting data at key settings and potentially simulating and interpolating reference data from the skipped settings. Therefore, the added clinical value of QUS methods far outweighs the burden associated with acquiring calibration data.

C. Attenuation

Acoustic attenuation can strongly affect the shape of the backscattered signal and will therefore bias QUS estimates if it is not properly compensated [49]. Attenuation compensation techniques are well established and several methods exist to obtain reliable estimates of the BSC when the attenuation values are known. The challenge is that often attenuation values remain unknown, attenuation is spatially heterogeneous and an error in the acoustic attenuation coefficient used for correcting the BSC will result in a bias in QUS estimates as a function of depth even when the tissue properties are uniform.

In recent years a large number of researchers have developed several techniques to estimate both local and total attenuation. Local attenuation refers to estimates of attenuation in some defined region of interest and maps of local attenuation can be used for diagnostics. Local attenuation algorithms have demonstrated success in several applications. The approaches include the spectral shift method, spectral difference method, and the hybrid method (used to remove weaknesses of the spectral fit and difference methods) [47,48,152–155]. Local attenuation has been demonstrated to have good accuracy and precision in phantom studies and consistency among clinical systems have been demonstrated in phantoms and animal studies [155]

Total attenuation refers to the attenuation of signal up to some specified depth. Total attenuation is important for correcting for frequency-dependent losses when calculating the BSC. Several approaches have been explored for estimating the total attenuation including integrating local attenuation estimates from the surface of the transducer up to some targeted region [156]. Other approaches include time domain techniques [157], techniques using multiple sources [158,159] and techniques that estimate a scattering form factor or a structure factor simultaneously with the total attenuation [46,48, 142] These techniques have demonstrated the ability to correct for frequency-dependent losses and improve spectral-based QUS estimates. The success of the total attenuation techniques provides further confidence that attenuation compensation issues for QUS have been largely overcome and may no longer be a roadblock to clinical translation.

D. Computational complexity

Satisfactory clinical use of QUS methods would require real-time display of the QUS-based information. Therefore, the computational complexity of the algorithm used to generate images such as Fig. 8 must be taken into account. For the most part, the estimation of spectral-based QUS estimates is extremely fast because it requires only computing FFTs and fitting models to the data (some methods do not even use model-based approaches). Therefore, these QUS methods are less complex than the Doppler-based approaches used in most clinical scanners.

Envelope-statistics-based QUS methods have varied complexity depending on the model used. For example, fitting a Nakagami distribution to an experimentally-derived probability-density function is very fast because it only requires computing the first two moments of the empirical PDF (Eqs. (8) and (9)). However, using more advanced models, such the homodyned-K may require more-complex estimators. Nevertheless, overall QUS methods remain computationally-efficient and with the development of ultrasound systems with powerful processors and memory, the computational complexity of nearly all QUS methods still allows for real-time implementation on clinical scanners.

E. Model-based approaches

Most of the presented QUS methods are model-based. A quantity (e.g., BSC, empirical PDF, etc.) is estimated and is fit to a model to yield the QUS estimates. The attractiveness of these model-based approaches is that associated parameters can provide a geometrical and physical interpretation of microstructure.

While model-based approaches are very attractive for QUS, inaccurate models could ultimately yield unreliable QUS estimates. For example, the use of a Gaussian form factor for the estimation of ESD and EAC is very common, and yet, it is quite unlikely that a biological tissue would behave as an ensemble of low number density of randomly located spherical structures with a Gaussian decay in acoustical impedance. The key reason why the Gaussian form factor is so heavily used is the computational efficiency with which EAC and ESD can be estimated [13]. Ultimately, the Gaussian form factor can be considered to have been empirically validated considering the amount of successful studies performed with this unrealistic scattering model. More-accurate models exist and for example, exact form factors can be computed for solid or fluid spheres using first principles as outlined by Faran [160]. However, these form factors are cumbersome, rely on infinite series of Bessel functions which must be truncated and have no efficient fitting algorithm in existence.

Tissue-specific form factors (which model the scattering from a scatterer) and structure factors (which model the organization and interaction effects of scatterers) can also be derived from impedance maps and theoretical and experimental studies have been performed based on these ideas [44, 161–164]. Of course, using accurate models would provide QUS estimates that better quantify tissue microstructure which in turn would enhance the clinical value of such estimates. For example, in the case of cancer imaging, using better models could enhance sensitivity and specificity.

In the case of envelope statistics, models of increased complexity (e.g., homodyned-K distribution) can provide rich physical interpretation and may be preferred to other simpler models (e.g., Nakagami distribution), but estimators can be difficult to implement, thereby compromising the QUS estimates. Recent studies in lymph nodes also showed that envelope-statistics models having limited physical meaning may actually fit the experimental data better [165].

Finally, it should also be mentioned that QUS can be used in a model-free approach. One example of this is in the liver studies outlined above, where fat content was found to be highly correlated to the BSC at 8 to 15 MHz. In the lymph-node studies, the authors used an envelope-statistics methods which essentially obtained QUS estimates by quantifying the experimental PDF divergence from a Rayleigh PDF. We therefore conclude that the use (or not) of a model is not a limiting factor for clinical transition of QUS methods.

V. Conclusion

The future of biomedical imaging lies in the continued improvement of imaging devices, developing multi-modality imaging techniques, finding new sources of contrast and developing quantitative imaging technologies.

To this end, QUS techniques have demonstrated potential for improving diagnostic ultrasound for a number of different applications. Similar QUS techniques could also be used for photoacoustic imaging and have recently been demonstrated [166, 167]. The new sources of contrast and the ability to correlate specific quantitative values to tissue state will help improve medical diagnostics and improve specificity. Roadblocks to implementation on clinical devices have been largely overcome in recent years due to the work of several different groups demonstrating the techniques can be both operator and system independent. Issues with attenuation compensation have been largely overcome by improved techniques to estimate attenuation. Therefore, because of the demonstrated successes of QUS techniques for a plethora of applications, QUS is poised to appreciably enhance diagnostic ultrasound.