Molecular origin of constant m-values, denatured state collapse, and residue-dependent transition midpoints in globular proteins

Abstract

Experiments show that for many two state folders the free energy of the native state ΔG_ND([C]) changes linearly as the denaturant concentration [C] is varied. The slope, $m=\frac{d\mathrm{\Delta }{G}_{\mathit{\text{ND}}}([C])}{d[C]}$, is nearly constant. According to the Transfer Model, the m-value is associated with the difference in the surface area between the native (N) and the denatured (D) state, which should be a function of $\mathrm{\Delta }{R}_g^2$, the difference in the square of the radius of gyration between the D and N states. Single molecule experiments show that R_g of the structurally heterogeneous denatured state undergoes an equilibrium collapse transition as [C] decreases, which implies m also should be [C]-dependent. We resolve the conundrum between constant m-values and [C]-dependent changes in R_g using molecular simulations of a coarse-grained representation of protein L, and the Molecular Transfer Model, for which the equilibrium folding can be accurately calculated as a function of denaturant (urea) concentration. In agreement with experiment, we find that over a large range of denaturant concentration (> 3 M) the m-value is a constant, whereas under strongly renaturing conditions (< 3 M) it depends on [C]. The m-value is a constant above [C]> 3 M because the [C]-dependent changes in the surface area of the backbone groups, which make the largest contribution to m, is relatively narrow in the denatured state. The burial of the backbone and hydrophobic side chains gives rise to substantial surface area changes below [C]< 3 M, leading to collapse in the denatured state of protein L. Dissection of the contribution of various amino acids to the total surface area change with [C] shows that both the sequence context and residual structure are important. There are [C]-dependent variations in the surface area for chemically identical groups such as the backbone or Ala. Consequently, the midpoint of transition of individual residues vary significantly (which we call the Holtzer Effect) even though global folding can be described as an all-or-none transition. The collapse is specific in nature, resulting in the formation of compact structures with appreciable populations of native-like secondary structural elements. The collapse transition is driven by the loss of favorable residue-solvent interactions and a concomitant increase in the strength of intrapeptide interactions with decreasing [C]. The strength of these interactions is non-uniformly distributed throughout the structure of protein L. Certain secondary structure elements have stronger [C]-dependent interactions than others in the denatured state.

The folding of many small globular proteins is often modeled using the two-state approximation in which a protein is assumed to exist in either the native (N) or the denatured (D) states [1]. The stability of N relative to D, ΔG_ND(0), is typically obtained by measuring ΔG_ND([C]) as a function of the denaturant concentration [C], and extrapolating to [C]=0 using the linear extrapolation method (LEM) [2]. The denaturant-dependent change in native state stability, ΔG_ND([C]), for these globular proteins is usually a linear function of [C] [2–9]. Thus, ΔG_ND([C]) = ΔG_ND(0) + m[C], where m = ∂ΔG_ND([C])/∂[C] is a constant [5], which by convention is referred to as the m-value. However, deviations from linearity, especially at low [C], have also been found [10], indicating that the m-value is concentration dependent. In this paper we address two inter-related questions: (1) Why are m-values constant for some proteins, even though there is a broad distribution of conformations in the denatured state ensemble (DSE)? (2) What is the origin of denatured state collapse, that is the compaction of the DSE, with decreasing [C] that is often associated with non-constant m-values [10–12]?

Potential answers to the first question can be gleaned by considering the empirical Transfer model (TM) [13–15], which has been remarkably successful in accurately predicting m-values for a large number of proteins [15, 16]. The revival in the TM as a practical tool in analyzing the effect of denaturants (and more generally osmolytes) comes from a series of pioneering studies by Bolen and coworkers [15–17]. Assuming that proteins exist in only two states [8, 15], the TM expression for the m-value is

$$m=\frac{1}{[C]}{\displaystyle \sum _{k=1}^{N_S}\frac{n_k\delta g_k^S([C])}{{\alpha }_{k,G-k-G}^S}\mathrm{\Delta }{\alpha }_k^S}+\frac{1}{[C]}{\displaystyle \sum _{k=1}^{N_B}\frac{n_k\delta g_k^B([C])}{{\alpha }_{k,G-k-G}^B}\mathrm{\Delta }{\alpha }_k^B,}$$ (1)

where the sums are over the side chain (S) and backbone (B) groups of the different amino acid types (Ala, Val, Gly, etc.), n_k is the number of amino acid residues of type k in the protein, and $\delta g_k^S$ and $\delta g_k^B$ are the experimentally measured transfer free energies for k [13, 17, 18] (Fig. 1a). In Eq. 1, $\mathrm{\Delta }{\alpha }_k^P=\langle {\alpha }_{k,D}^P\rangle -\langle {\alpha }_{k,N}^P\rangle$ (P = S or B), where $\langle {\alpha }_{k,D}^P\rangle$ and $\langle {\alpha }_{k,N}^P\rangle$ are the average solvent accessible surface areas [19] of group k in the D and N states respectively, and ${\alpha }_{k,G-k-G}^P$ is the corresponding value in the tripeptide glycine-k-glycine. There are two fundamentally questionable assumptions in the TM model: (1) The free energy of transferring a protein from water to aqueous denaturant solution at an arbitrary [C] may be obtained as a sum of transfer energies of individual groups of the protein without regard to the polymeric nature of proteins. (2) The surface area changes $\mathrm{\Delta }{\alpha }_k^P$ are independent of [C], residual denatured state structure, and the amino-acid sequence context in which k is found.

Figure 1.

(a) The transfer free energy of the backbone (the glycine residue) and side chain groups as a function of urea concentration. The lines are a linear extrapolation of the experimentally measured δg_k upon transfer from 0 M to 1 M urea [15]. The amino acid corresponding to a given line is labeled using a three letter abbreviation. Blue labels are for hydrophobic side chains, while red labels indicate polar or charged side chains according to the hydrophobicity scale in [63]. (b) The native state stability (black circles) of protein L as a function of urea concentration, [C], at 328 K. ΔG_ND([C]) = −k_BTln(P_N([C])/(1 − P_N([C]))), where P_N([C]) is the probability of being folded as a function of [C]. The midpoint of the transition C_m = 6.56 M urea. The red line is a linear fit to the data in the range of 5.1 to 7.9 M. At [C] < 3 M there is a departure from linearity (i.e. a [C]-dependent m-value). Inset in the upper left is a ribbon diagram of the crystal structure of protein L [48]. Inset in bottom right shows P_N([C]) versus [C] at 328 K (blue line). In addition, |dP_N/d[C]|, the absolute value of the derivative of P_N versus [C] is shown (green line). The full width at half the maximum value of |dP_N/d[C]| (denoted 2δC) is 2.8 M and is defined as the ‘transition region’ given by C_m ± δC.

The linear variation of ΔG_ND([C]) as [C] changes can be rationalized if (i) $\delta g_k^P([C])$ is directly proportional to [C], and (ii) $\mathrm{\Delta }{\alpha }_k^P$ is [C]-independent. Experiments have shown that $\delta g_k^P([C])$ is a linear function of [C] [7] while the near-independence of $\mathrm{\Delta }{\alpha }_k^P$ on [C] can only be inferred based on the accuracy of the TM in predicting the m-values [15, 16]. In an apparent contradiction to such an inference, small angle X-ray scattering experiments [20–23] and single molecule FRET experiments [24–29] show that the denatured state properties, such as the radius of gyration R_g and the end-to-end distance (R_ee), can change dramatically as a function of [C]. These observations suggest that the total solvent accessible surface area of the protein, $\mathrm{\Delta }{\alpha }_T(={\displaystyle {\sum }_{k=1}^{N_S}\mathrm{\Delta }{\alpha }_k^S+}{\displaystyle {\sum }_{k=1}^{N_B}\mathrm{\Delta }{\alpha }_k^B)}$, and the various groups must also be a function of [C], since we expect that Δα_T must be a monotonically increasing function of $\mathrm{\Delta }{R}_g^2$, which is the difference between $R_g^2$ of the D and N states [26, 30]. For compact objects $\mathrm{\Delta }{\alpha }_T\propto \mathrm{\Delta }{R}_g^2$ but for fractal structures the relationship is more complex [31]. Furthermore, NMR measurements have found that many proteins adopt partially structured or random coil-like conformations at high [C] [32–35], which necessarily have large fluctuations in global properties such as $\mathrm{\Delta }{\alpha }_k^P$ and R_g. Thus, the contradiction between the constancy of m-values and the sometimes measurable changes in denatured state properties is a puzzle that requires a molecular explanation.

Bolen and collaborators have already shown that quantitative estimates of m can be made by using measured transfer free energies of transfer free energies of individual groups [15, 16]. More importantly, these studies established the dominant contribution to m arises from the backbone [15, 16]. However, only by characterizing the changes in the distribution of $\mathrm{\Delta }{\alpha }_k^S$ and $\mathrm{\Delta }{\alpha }_k^B$ as a function of [C] can the reasons for success of the TM in obtaining the global property m be fully appreciated. This is one of the goals of the present study. In addition, we correlate m with denatured state collapse, [C]-dependent changes in residual structure, and the solution forces acting on the denatured state - properties that cannot be analyzed using the TM.

The denatured, and perhaps even the native state should be described as ensembles of fluctuating conformations, and will be referred to as the DSE and NSE (native state ensemble), respectively. As a result, it is crucial to characterize the distribution of various molecular properties in these ensembles and how they change with [C] in order to describe quantitatively the properties of the DSE. Because the D state is an ensemble of conformations with a distribution of accessible surface areas, Eq. 1 should be considered an approximate expression for the m-value. Even if the basic premise of the TM is valid, we expect that $\mathrm{\Delta }{\alpha }_k^P$ should depend on the conformation of the protein and the denaturant concentration. Consequently, the m-value should be written with an explicit concentration dependence as

$$\begin{array}{c}\hfill m([C])=\frac{1}{[C]}{\displaystyle \sum _{k=1}^{N_S}}\frac{n_k\delta g_k^S([C])}{{\alpha }_{G-k-G}^S}\{\langle {\alpha }_{k,D}^S([C])\rangle -\langle {\alpha }_{k,N}^S([C])\rangle \}\hfill \\ \hfill +\frac{1}{[C]}{\displaystyle \sum _{k=1}^{N_B}\frac{n_k\delta g_k^B([C])}{{\alpha }_{G-k-G}^B}}\{\langle {\alpha }_{k,D}^B([C])\rangle -\langle {\alpha }_{k,N}^B([C])\rangle \}\hfill \end{array}$$ (2)

where $\langle {\alpha }_{k,j}^P([C])\rangle ={\displaystyle {\int }_0^{\infty }{\alpha }_{k,j}^{P}P({\alpha }_{k,j}^P;[C])d{\alpha }_{k,P}}$ (j = D or N and P = S or B). In principle, the denominator in Eq. 2 should also be [C]-dependent, however, we ignore this for simplicity. In contrast to Eq. 1, the conformational fluctuations in the DSE and NSE are taken into account in Eq. 2 by integrating over the distribution of surface areas $(P({\alpha }_{k,j}^P;[C]))$. Moreover, we do not assume that the surface area distributions are independent of [C] as is done in Eq. 1. Such an assumption can only be justified by evaluating $P({\alpha }_{k,j}^P;[C])$ using molecular simulations or experiments.

We use the Molecular Transfer Model (MTM) [36] in conjunction with coarse-grained simulations of protein L using the C_α side chain model (C_α-SCM) (see Methods) to test the molecular origin of the constancy of m-values. Because the conformations and energies are known exactly in the C_α-SCM simulations, we can determine how an ensemble of denatured conformations, with a distribution of solvent accessible areas in the DSE, gives rise to a constant m-value. We show that the m-values are nearly constant for two reasons: (1) As previously shown [15, 16], the bulk of the contribution to ΔG_ND([C]) changes come from the protein backbone. (2) Here, we establish that the distribution of the backbone solvent accessible surface area is narrow, with small changes in $\mathrm{\Delta }{\alpha }_k^B$ as [C] decreases.

Determination of the molecular origin of denatured state collapse, often associated with a concentration dependent m-value, requires characterizing the DSE of protein L at low [C] (< 3 M urea) where the NSE is thermodynamically favored. Under these conditions we find that the radius of gyration (R_g) DSE undergoes significant reduction as [C] decreases. Urea-induced collapse transition of protein L is continuous as a function of [C], and results in native-like secondary structural elements. We decompose the non-bonded energy into residue-solvent and intrapeptide interactions and show that (1) these two opposing energies govern the behavior of R_g of the DSE, and (2) the strength of these interactions are non-uniformly distributed in the DSE and correlate with regions of residual structure. Thus, different regions of the DSE can collapse to varying degrees as [C] changes.

Methods

C_α-side chain model for protein L

In order to ascertain the conditions under which Eq. 1 is a good approximation to Eq. 2, we use the coarse-grained C_α-side chain model (C_α-SCM) [37] to represent the sixty-four residue protein L. In the C_α-SCM, each residue in the polypeptide chain is represented using two interaction sites, one that is centered on the α-carbon atom and another at the center-of-mass of the side chain [37]. The potential energy (E_P) of a given conformation of the C_α-SCM is a sum of bond-angle (E_A), backbone dihedral (E_D), improper dihedral (E_I), backbone hydrogen bonding (E_HB) and non-bonded Lennard-Jones (E_LJ) terms (E_P = E_A + E_D + E_C + E_HB + E_LJ). The functional form of these terms, and derivation of the parameters used are explained in the supporting information of reference [36].

Sequence information is included in the C_α-SCM by using non-bonded parameters that are residue dependent. We take into account the size of a side chain by varying the collision diameter used in the E_LJ term. The interaction strength between side chains i and j, that are in contact in the native structure, depends on the amino acid pair and is modeled by varying the well-depth (ε_ij) in E_LJ [36]. Thus, the C_α-SCM incorporates both sequence variation and packing effects. Numerous studies have shown that considerable insights into protein folding can be obtained using coarse-grained models [38–40], thus rationalizing the choice of the C_α-SCM in this study.

Simulation details

Equilibrium simulations of the folding and unfolding reaction using the C_α-SCM are performed using Multiplexed-Replica Exchange (MREX) [41, 42] in conjunction with low friction Langevin dynamics [43] at [C]=0. We used CHARMM to carry out the Langevin dynamics [44], while an in-house script handles the replica exchange calculation. In the MREX simulations, multiple independent trajectories are generated at several temperatures. In addition to the conventional replica exchange acceptance/rejection criteria for swapping conformations between different temperatures [41], MREX also allows exchange between replicas at the same temperature [42]. Replicas were run at eight temperatures: 315, 335, 350, 355, 360, 365, 380, 400 K. At each temperature four independent trajectories were simultaneously simulated. Every 5,000 integration time-steps the system configurations were saved for analysis. Random shuffling occurred between replicas at the same temperature with 50% probability. Exchanges between neighboring temperatures were attempted using the standard replica exchange acceptance criteria [41]. A Langevin damping coefficient of 1.0 ps⁻¹ was used, with a 5 fs integration time-step. In all, 90,000 exchanges were attempted, of which the first 10,000 discarded to allow for equilibration. All trajectories were simulated in the canonical (NVT) ensemble.

Analysis with the Molecular Transfer Model

We model the denaturation of protein L by urea using the Molecular Transfer Model [36]. Previous work [36] has already shown that the MTM quantitatively reproduces experimentally measured single molecule FRET efficiencies [27–29] as a function of [C] (GdmCl) for protein L and the cold shock protein, thus validating the methodology. The MTM combines simulations at [C]=0 with the TM [13, 14], experimentally measured transfer free energies [15, 16], and a reweighting method to predict protein properties at any urea concentration of interest [36, 45–47]. Our previous work has shown that the MTM accurately predicts a number of molecular characteristics of proteins as a function of denaturant or osmolyte concentration [36]. The MTM equation, which has the form of the Weighted Histogram Analysis Method [46], is

$$\langle A([C],T)\rangle =Z{([C],T)}^{-1}{\displaystyle \sum _{l=1}^R{\displaystyle \sum _{t=1}^{n_l}\frac{A_{l,t}{e}^{-\beta \{E_P(l,t,[0])+\mathrm{\Delta }{G}_{tr}(l,t,[C])\}}}{{\displaystyle {\sum }_{n=1}^R{n}_n{e}^{f_n-{\beta }_n{E}_P(l,t,[0])}}},}}$$ (3)

where 〈A([C], T)〉 is the average of a protein property A at urea concentration [C] and temperature T, and Z([C], T) is the partition function. The sums in Eq. 3 are over the R different replicas from the MREX simulations, that vary in terms of temperature, and n_l protein conformations from the l^th replica. The value of A from replica l at time t is A_l,t, and E_P(l, t, [0]) is the potential energy of that conformation at [C]=0, β = 1/(k_BT), where k_B is Boltzmann’s constant. In Eq. 3, ΔG_tr(l, t, [C])), the reversible work of transferring the l, t protein conformation from 0 M to [C] M urea solution, is estimated using a form of the TM, and is given by

$$\mathrm{\Delta }{G}_{tr}(l,t,[C]))={\displaystyle \sum _{k=1}^{N_S}\frac{n_k\delta g_k^S([C])}{{\alpha }_{G-k-G}^S}\langle {\alpha }_k^S(l,t,[C])\rangle }+{\displaystyle \sum _{k=1}^{N_B}\frac{n_k\delta g_k^B([C])}{{\alpha }_{G-k-G}^B}\langle {\alpha }_k^B(l,t,[C])\rangle .}$$ (4)

All terms in Eq. 4 are the same as in Eq. 2 except instead of computing a difference in surface areas, only the surface areas from conformation l, t $(\langle {\alpha }_k^P(l,t,[C])\rangle )$ are included. In the denominator of Eq. 3, the sum is over the different replicas and n_n, β_n and f_n are, respectively, the number of conformations from replica n, β_m = 1/(k_BT_m) where T_m is the temperature of m^th replica, and the free energy f_m of replica m is obtained by solving a self-consistent equation (see reference [45]).

In computing $\langle {\alpha }_k^P(l,t,[C])\rangle$ for use in Eq. 4 we use the radii listed in Table I where the backbone group corresponds to the glycine. These parameters are different from the ones reported in [36]. They result in better agreement between predicted m-values using the MTM and predicted m-values from Auton and Bolen’s implementation of the TM [15, 18]. The values for ${\alpha }_{G-k-G}^S$, used in Eq. 4, are reported in Table II.

TABLE I.

van der Waals radius of the side chain beads for various amino-acids based in part on measured partial molar volumes [62].

Residue	Radius (Å)
Ala	2.14
Cys	2.33
Asp	2.37
Glu	2.52
Phe	2.70
Gly	2.70
Hsda	2.63
Ile	2.63
Lys	2.70
Leu	2.63
Met	2.63
Asn	2.33
Pro	2.36
Gln	2.56
Arg	2.79
Ser	2.20
Thr	2.39
Val	2.49
Trp	2.88
Tyr	2.75

^aThe same value of the radius was used regardless of the protonation state.

TABLE II.

Solvent accessibility of the backbone and side chain groups of residue k in the tripeptide Gly − k − Gly (α_{Gly−k−Gly})

αGly−k−Gly (Å2)
k	Backbone	Side chain
Ala	62.5	108.3
Met	50.3	164.7
Arg	46.2	186.0
Gln	52.1	155.4
Asn	55.6	138.7
Gly	85.0	0.0
Tyr	47.3	179.9
Asp	56.7	133.7
Trp	43.8	198.7
Phe	48.3	174.6
Cys	57.7	128.6
Pro	56.9	132.7
Lys	48.3	174.6
Hsda	51.4	159.2
Hse	51.6	159.2
Hsp	51.4	159.2
Ser	60.9	114.9
Thr	56.2	135.7
Val	53.8	147.1
Ile	50.3	164.7
Glu	53.0	150.8
Leu	50.3	164.6

^aHsd - Neutral histidine, proton on ND1 atom. Hse - Neutral histidine, proton on NE2 atom. HSP - Protonated histidine.

We calculate the average of a number of properties of protein L using Eq. 3. The end-to-end distance (R_ee) of a given conformation is the distance between the C_α sites at residues one and sixty-four. The radius of gyration, R_g, is computed using $\sqrt{R_g^2}=\frac{1}{2N-N_G}\langle {\displaystyle {\sum }_{i=1}^{2N-N_G}{(r_i-r_{\mathit{\text{CM}}})}^2\rangle }$, where N is the number of residues, N_G is the number of glycines in the sequence, r_i is the position of interaction site i, and $r_{\mathit{\text{CM}}}=1/(2N-N_G){\displaystyle {\sum }_{i=1}^{2N-N_G}{r}_i}$ is the mean position of the 2N − N_G interaction sites of the protein. The solvent accessible surface area of a backbone or a side chain $({\alpha }_k^P)$ in residue k in a given conformation was computed using the CHARMM program [44], which computes the analytic solution for the surface area. A probe radius of 1.4 Å, equivalent to the size of a water molecule, was used.

The extent to which a structural element is formed (denoted f_S) in a conformation of protein L is defined by Q_p, the fraction of native backbone contacts formed by structural element p, where p = β-hairpin S12 or S34, or β-strand pairing between S1 and S4. We define Q_p as

$$Q_p={\displaystyle \sum _j^{N-4}{\displaystyle \sum _{k=j+4}^N\frac{\mathrm{\Theta }(R_C-d_{jk})}{C_p}},}$$ (5)

where the sum is over the N = 64 C_α sites, R_C(= 8 Å) is a cutoff distance, and d_jk is the distance between interaction sites j and k, and Θ(R_C − d_jk) is the Heaviside step function. Strand 1 (S1) corresponds to residues 4–11, S2 between 17–24, S3 corresponds to 47–52, and S4 between 57–62 (Fig. 2b). In Eq. 5, C_p is the maximum number of native contacts for structural element p. The extent of helix formation in a conformation r of protein L is computed as the ratio N_ϕ(r)/N_ϕ(N), where N_ϕ(r) is the number of neighboring dihedral pairs, between residues 26 and 44, that have dihedral angles within ±20° of the dihedral’s value in the native state, and N_ϕ(N) = 15.

Figure 2.

(a) $\langle {\alpha }_{k,j}^P\rangle$ versus urea concentration for the backbone and the side chains alanine, phenylalanine, and glutamate, computed using $\langle {\alpha }_{k,j}^P([C])\rangle ={\displaystyle {\int }_0^{\infty }{\alpha }_{k,j}^{S}P({\alpha }_{k,j}^P;[C])d{\alpha }_{k,S}}$ (j = D or N and P = S or B). For the backbone $\langle {\alpha }_{k=\mathit{\text{all}},j}^B([C])\rangle =N^{-1}{\displaystyle {\sum }_{k=1}^{N_B}\langle {\alpha }_{k,j}^B([C])\rangle }$, where N = 64, the number of residues in the protein. $\langle {\alpha }_{k,N}^P\rangle$ and $\langle {\alpha }_{k,D}^P\rangle$ are displayed as green and blue lines respectively. Brown dashed lines show $\langle {\alpha }_{k,D}^P\rangle$ for individual residues of type k, the residue indices are indicated by the numbers in red. For the backbone only six groups (from residues 1, 10, 20, 30, 40, and 50) out of sixty-four backbone groups are shown. (b) Linear secondary structure representation of protein L. β-strands are shown as red arrows, the α-helix as a green cylinder, and unstructured regions as a solid black line. Secondary structure assignments were made using the STRIDE program [64]. The residues corresponding to each secondary structure element are listed below the representation. (c) $n_k\mathrm{\Delta }{\alpha }_k^P$ (Eq.2) as a function of urea concentration for the backbone (green line, with corresponding ordinate on right), and all other sixteen unique amino acid types in protein L (with corresponding ordinate on left). For clarity, labels for Met and Ser residues are not shown. Met and Ser have $n_k\mathrm{\Delta }{\alpha }_k^P$ values close to zero in this graph. $\mathrm{\Delta }{\alpha }_k^P=\langle {\alpha }_{k,D}^P\rangle -\langle {\alpha }_{k,N}^P\rangle$ (P = S or B). For the backbone we plot ${\displaystyle {\sum }_{k=1}^{N_B}{n}_k\mathrm{\Delta }{\alpha }_k^B}$. The inset shows Δα_T as a function of urea concentration. The red arrow indicates C_m.

The non-bonded interaction energy E_I in the C_α-SCM is E_I = E_LJ + E_HB. We include only the Lennard-Jones (LJ) and hydrogen bond (HB) energies in E_I [36]. The urea solvation energy, E_S, of a given conformation is set equal to Eq. 4; E_M is a simple sum of E_I and E_S. The values of E_I and E_S for the various structural elements of protein L were computed by neglecting non-bonded and solvation energies of residues that were not part of the structural element of interest.

The time-series of the various properties were inserted into Eq. 3 to compute their averages as a function of [C]. To compute averages 〈A_D〉 and 〈A_N〉 of the DSE and NSE respectively, a modification to Eq. 3 was made. The numerator was multiplied by Θ_n(l, t), where Θ_n(l, t) is the Heaviside step function that is equal to Θ(5 − Δ(l, t)) when the average of the NSE is computed (i.e. n =NSE) and is equal to Θ(5 + Δ(l, t)) when the average of the DSE is computed (i.e. n =DSE). Here, Δ(l, t) is the root mean squared deviation between the C_α carbon sites in the C_α-SCM of conformation l, t and the C_α carbon atoms in the crystal structure (PDB ID 1HZ6 [48]). When Δ(l, t) is greater than 5 Å then Θ(5 + Δ(l, t)) = 0 and Θ(5 − Δ(l, t)) = 1, and when Δ(l, t) is less than 5 Å then Θ(5 + Δ(l, t)) = 1 and Θ(5 − Δ(l, t)) = 0.

Probability distributions were computed using P(A ± δ_A; [C]) = Z(A ± δ_A, [C], T)/Z([C], T), where Z(A ± δ_A, [C], T) is the restricted partition function as a function of A. Due to the discrete nature of the simulation data, a bin with finite width ±δ_A, whose value depends on A, is used. $Z(A\pm {\delta }_A,[C],T)={\displaystyle {\sum }_{l=1}^R{\displaystyle {\sum }_{t=1}^{n_l}\frac{f_A(l,t)e^{-\beta \{E_P(l,t,[0])+\mathrm{\Delta }{G}_{tr}(l,t,[C])\}}}{{\displaystyle {\sum }_{n=1}^R{n}_n{e}^{f_n-{\beta }_n{E}_P(l,t,[0])}}}}}$, where all terms are the same as in Eq. 3 except for f_A(l, t), which is a function that we define to equal 1 when the protein conformation l, t has a value of A in the range of A ± δ_A, and zero otherwise.

Results and Discussion

ΔG_ND([C]) changes linearly as urea concentration increases

We chose the experimentally well characterized B1 IgG binding domain of protein L [27, 28, 49] to illustrate the general principles that explain the linear dependence of ΔG_ND([C]) on [C] for proteins that fold in an apparent two-state manner. In our earlier study [36], we showed that the MTM accurately reproduces several experimental measurements including [C]-dependent energy transfer as a function of guanidinium chloride (GdmCl) concentration. Prompted by the success of the MTM, we now explore urea-induced unfolding of protein L. The MTM predictions for urea effects are expected to be more accurate than for GdmCl, since the experimentally measured $\delta g_k^P([C])$ urea data, used in Eq. 1, includes activity coefficient corrections while the GdmCl data does not [13, 15]. The calculated ΔG_ND([C]) as a function of urea concentration for protein L shows linear dependence above [C] > 4 M (Fig. 1b) with m = 0.80 kcal mol⁻¹ M⁻¹, and a C_m (obtained using ΔG_ND([C_m]) = 0) ≈ 6.6 M. The consequences of the deviation from linearity, which is observed for [C] < 3 M, are explored below. It should be stressed that the error in the estimated ΔG_ND([0]) is relatively small (~0.8 kcal mol⁻¹) if measurements at [C] > 4 M are extrapolated to [C]= 0 (Fig. 1b). Thus, from the perspective of free energy changes the assumption that ΔG_ND([C]) = ΔG_ND([0]) + m[C], with constant m, is justified for this protein.

Molecular origin of constant m-values

Inspection of Eq. 2 suggests that there are three possibilities that can explain the constancy of m-values, thus making Eq. 1 a good approximation to Eq. 2: (1) Both $\langle {\alpha }_{k,D}^P([C])\rangle$ and $\langle {\alpha }_{k,N}^P([C])\rangle$ in Eq. 2 have the same dependence on [C], making $\mathrm{\Delta }{\alpha }_k^P$ effectively independent of [C]. (2) The distributions $P({\alpha }_{k,D}^P;[C])$ in Eq. 2 are sharply peaked about their mean or most probable values of ${\alpha }_{k,D}^P([C])$ at all [C], thus making $\mathrm{\Delta }{\alpha }_k^P$ independent of [C]. In particular, if the standard deviation in ${\alpha }_{k,D}^P$ (denoted σ_αk) is much less than $\langle {\alpha }_{k,D}^P([C])\rangle$ for all [C]’s then the $\mathrm{\Delta }{\alpha }_k^P$’s would be effectively independent of [C]. (3) One group in the protein, denoted l (backbone in proteins), makes the dominant contribution to the m-value. In this case, only the changes in $\mathrm{\Delta }{\alpha }_l^P$ and $P({\alpha }_{l,D}^P;[C])$ matter, thereby making $\mathrm{\Delta }{\alpha }_l^P$ insensitive to [C]. The MTM simulations of protein L allow us to test the validity of these plausible explanations for the constancy of m-values, especially when [C]> 3 M (Fig. 1b). Only by examining these possibilities, which requires changes in the distribution of various properties as [C] changes, can the observed constancy of m be rationalized.

$\langle {\alpha }_{k,D}^P([C])\rangle$ and $\langle {\alpha }_{k,N}^P([C])\rangle$ do not have the same dependence on [C]

The changes in $\langle {\alpha }_{k,D}^P\rangle$ and $\langle {\alpha }_{k,N}^P\rangle$ as a function of [C] show that as [C] increases, both $\langle {\alpha }_{k,D}^P\rangle$ and $\langle {\alpha }_{k,N}^P\rangle$ increase (blue and green lines in Fig. 2a). However, $\langle {\alpha }_{k,D}^P([C])\rangle$ has a stronger dependence on [C] than $\langle {\alpha }_{k,N}^P([C])\rangle$ for both the backbone and side chains (Fig. 2a). Thus, the observed linear dependence of ΔG_ND([C]) on [C] cannot be rationalized in terms of similarity in the variation of $\langle {\alpha }_{k,D}^P([C])\rangle$ and $\langle {\alpha }_{k,N}^P([C])\rangle$ as [C] changes. The stronger dependence of $\langle {\alpha }_{k,D}^P([C])\rangle$ on [C] arises from the greater range and magnitude of the solvent accessible surface areas available to the DSE (see below). The greater range allows larger shifts in $\langle {\alpha }_{k,D}^P([C])\rangle$ than $\langle {\alpha }_{k,N}^P([C])\rangle$ with [C]. Equally important, the strength of the favorable protein-solvent interactions is positively correlated with the magnitude of the surface area and [C] (see Eq. 4 and Fig. 1a). Thus, the DSE conformations with larger surface area are stabilized to a greater extent than the NSE conformations with increasing [C] and subsequently $\langle {\alpha }_{k,D}^P([C])\rangle$ shows a stronger dependence on [C].

Surface area distributions are broad in the DSE

The variation of $\mathrm{\Delta }{\alpha }_{k,D}^S$ and $\mathrm{\Delta }{\alpha }_{k,D}^B$ with [C] suggests that the $P({\alpha }_{k,D}^P;[C])$ are not likely to be narrowly peaked, and must also depend on [C] (Eq. 2). As urea concentration increases, the total backbone surface area distribution in the DSE, $P({\alpha }_D^B;[C])$, shifts towards higher values of ${\alpha }_D^B$ and becomes narrower (Fig. 3a). A similar behavior is observed in the distribution of the total surface area (Fig. 3b) and for the side chain groups (data not shown). It should be noted that the change in ${\alpha }_D^B$ with [C] is about five times smaller than the corresponding change in α_T (compare Figs. 3a and 3b). Thus, the distribution of surface areas for the various protein components are moderately dependent on [C], and Δα_T is more strongly dependent on [C] (Fig. 2c inset). These findings would suggest that m should be a function of [C] above 4 M (Eq. 2), in contradiction to the finding in Fig. 1b.

Figure 3.

(a) The probability distribution of the total backbone surface area in the DSE $(P({\alpha }_D^B))$ at various urea concentrations, indicated by the number above each trace. For comparison, $P({\alpha }_N^B)$ for the native state ensemble at 6.5 M urea is shown (solid brown line) as well as the average distribution over both the NSE and DSE at 6.5 M urea (black line). (b) Same as (a) except distributions are of the accessible surface area of the entire protein.

We characterize the width of the denatured state $P({\alpha }_{k,D}^P)$ distributions by computing the ratio ${\rho }_k={\sigma }_{{\alpha }_{k,D}}/\langle {\alpha }_{k,D}^P\rangle$, where ${\sigma }_{{\alpha }_{k,D}}=\sqrt{\langle {{\alpha }_{k,D}^P}^2\rangle -{\langle {\alpha }_{k,D}^P\rangle }^2}$. Fig. 4a shows ρ_k as a function of [C] for the various protein components (backbone, side chains, and the entire protein). As with the backbone $P({\alpha }_D^B)$ distribution (Fig. 3a), ρ_k indicates that $P({\alpha }_{k,D}^P)$ becomes narrower at higher urea concentrations for most k (Fig. 4a). At 8 M urea, the width of $P({\alpha }_{k,D}^P)$ ranges from 5 to 25 % of the average value of ${\alpha }_{k,D}^P$ for all groups, except k = Trp which has an even larger width. Clearly, ρ_k is large at all [C], which accounts for the dependence of $\mathrm{\Delta }{\alpha }_k^P$ on [C]. The results in Fig. 4 show that there are discernible changes in ρ_k which reflects the variations in $P({\alpha }_{k,D}^P;[C])$ as [C] is changed. Consequently, the constancy of the m-value cannot be explained by narrow surface area distributions.

Figure 4.

(a) The ratio ${\rho }_k={\sigma }_{{\alpha }_{k,D}}/\langle {\alpha }_{k,D}^P\rangle$ (see text for explanation) as a function of urea concentration for the entire protein (black line), the backbone (blue line), and all other amino acid types found in protein L. (b) The quantity m[C] versus urea concentration for the full protein (black circles), the backbone groups (red squares), and the Phe, Leu, Ile, and Ala side chains. Solid lines correspond to linear fits to the data in the range of 5.1 to 7.9 M urea.

The weak dependence of changes in accessible surface area of the protein backbone on [C] controls the linear behavior of ΔG_ND([C])

Plots of m[C], at several urea concentrations for the entire protein, the backbone groups (second term in Eqs. 1 and 2), and the hydrophobic side chains Phe, Leu, Ile, and Ala are shown in Fig. 4b. The slope of these plots is the m-value, which in the transition region (i.e. from 5.1 M to 7.9 M urea) is 0.80 kcal mol⁻¹ M⁻¹ for the entire protein. The contribution from the backbone alone is 0.76 kcal mol⁻¹ M⁻¹, and from the most prominent hydrophobic side chains (Phe, Leu, Ile, and Ala) is a combined 0.04 kcal mol⁻¹ M⁻¹. Thus, the largest contribution to the change in the native state stability, as [C] is varied, comes from the burial or exposure of the protein backbone (95%). The simulations directly support the previous finding that the protein backbone contributes the most to the stability changes with [C] [16]. Thus, for [C] > 3 M the magnitude of the m-value is largely determined by the backbone groups. However, only by evaluating the [C]-dependent changes in the distribution of surface areas can one assess the extent to which Eq. 2 be approximated by Eq. 1.

The relative change in accessible surface area of the backbone $\mathrm{\Delta }{\alpha }_D^B$ has a relatively weak urea dependence between 4 M to 8 M urea, increasing by only 75 Ų (Fig. 2c). Such a small change in $\mathrm{\Delta }{\alpha }_D^B$ with [C] has a negligible effect on the m-value. These results show that m is effectively independent of [C] in the transition region because $\mathrm{\Delta }{\alpha }_k^B([C])$ associated with the backbone groups change by only a small amount as [C] changes, despite the fact that Δα_T can change appreciably (Δα_T(4M → 8M) ≈ 300 Ų Fig. 2c inset). Thus, the third possibility is correct, namely that the weak dependence of $\mathrm{\Delta }{\alpha }_k^B([C])$ on [C] results in m being constant.

Residual denatured state structure leads to the inequivalence of amino acids

In applying Eq. 1 to predict m-values, it is assumed that all residues of type k, regardless of their sequence context, have the same solvent accessible surface area in the DSE [15, 16]. Our simulations show that this assumption is incorrect. Comparison of ${\alpha }_{k,D}^P$ for individual residues of type k, and the average $\langle {\alpha }_{k,D}^P\rangle$ as a function of urea concentration (Fig. 2a) shows that both sequence context and the distribution of conformations in the DSE determine the behavior of a specific residue. Large differences between ${\alpha }_{k,D}^P$ values are observed between residues of the same type, including alanine, phenylalanine and glutamate groups, even at high urea concentrations (Fig. 2a). The inequivalence of a specific residue in the DSE is similar to NMR chemical shifts that are determined by the local environment. As a result of variations in the local environment not all alanines in a protein are equivalent. Thus, ignoring the unique surface area behavior of individual residues in the DSE could lead to errors in the predicted m-value. Because the backbone dominates the transfer free energy of the protein (Fig. 4b), errors arising from this assumption may be small. However, the dispersions in the backbone ${\alpha }_{k,D}^B$ suggests that different regions of the protein may collapse in the DSE at different urea concentrations, driven by differences in $\mathrm{\Delta }{\alpha }_{k,D}^B$ from residue to residue (see below).

The simulations can be used to calculate [C]-dependent changes in surface areas of the individual backbone groups as well as side chains. Interestingly, even for the chemically homogeneous backbone group, significant dispersion about $\langle {\alpha }_{k,D}^B\rangle$ is observed when individual residues are considered (Fig. 2a). For example, ${\alpha }_{k,D}^B$ for residue 10 changes more drastically as [C] decreases than it does for residues 20 or 50. Thus, the connectivity of the backbone group can not only alter the conformations as [C] is varied but also the contribution to the free energy.

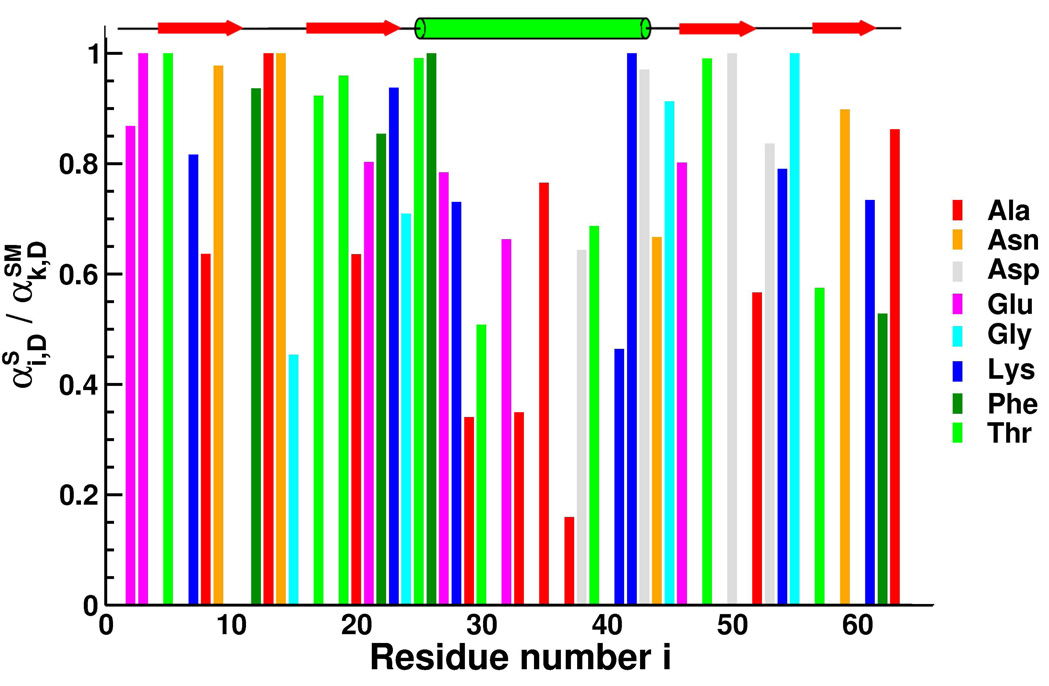
Even more surprisingly, the changes in ${\alpha }_{k=\mathit{\text{Ala}},D}^S$ depends on the sequence location of a given alanine residue and the associated secondary structure adopted in the native conformation. The changes in ${\alpha }_{k=\mathit{\text{Ala}},D}^S$ for residues 8 and 20, both of which adopt a β-strand conformation in the native structure (Fig. 2b), exhibit similar changes upon a decrease in [C] (Fig. 2a). By comparison, surface area changes in alanine residues 29 and 33, that are helical in the native state (Fig. 2b), are similar as [C] varies, while the changes in ${\alpha }_{k=\mathit{\text{Ala}},D}^S$ for alanines that are in the loops (residues 13 and 63) are relatively small. Examining the probability distribution of surface areas for the individual alanines ($P({\alpha }_{\mathit{\text{Ala}},D}^S)$ in Fig. 5), which is related to the average surface area and higher order moments, a wide variability between different residues is observed. Similar conclusions can be drawn by analyzing the results for the larger hydrophobic residue Phe and the charged Glu (Fig. 2a). Thus, for a given amino acid type, both sequence context as well as the heterogeneous nature of structures in the DSE lead to a dispersion about the average $\langle {\alpha }_{k,D}^S\rangle$ and higher order moments of $P({\alpha }_{k,D}^S)$ as urea concentration changes. Much like the chemical shifts in NMR, the distribution functions of chemically identical individual residues bear signatures of their environment and the local structures they adopt as [C] is varied!

Figure 5.

The distribution $(P({\alpha }_{\mathit{\text{Ala}},D}^S))$ of the solvent accesible surface area of side chains from the nine individual alanine residues in the denatured state ensemble of protein L at various urea concentrations. Black, red and green lines correspond to 1 M, 4 M and 8 M urea respectively. The corresponding alanine for each graph is given by its residue number. The large changes in $(P({\alpha }_{\mathit{\text{Ala}},D}^S))$ for the chemically identical residue shows that environment and local structures affect the structures and energetics of the side chains.

The total surface area difference between N and D (Δα_T) changes by about 1,200 Ų as [C] decreases from 8 M to 0 M (see inset of Fig. 2c). Decomposition of Δα_T into contributions from backbone and side chains (Eqs. 1 and 2) shows that the burial of the backbone groups contributes the most (up to 38%) to Δα_T (Fig. 2c). Not unexpectedly, hydrophobic residues (Phe, Ile, Ala, Leu), which are buried in the native structure, also contribute significantly to Δα_T, which supports the recent all atom molecular dynamics simulations [50]. Among them, Phe, a bulky hydrophobic residue, makes the largest side chain contribution to Δα_T (Fig. 2c). For example, as urea concentration increases from 4 M to 8 M the total backbone $\mathrm{\Delta }{\alpha }_D^B$ increases by 75 Ų, and $n_k\mathrm{\Delta }{\alpha }_{k,D}^S$ for k =Phe, Leu, Ala, Ile increase by 21–42 Ų.

The dispersion in ${\alpha }_{k,D}^P$ could be caused by residual structure in the DSE [51, 52]. We test this proposal quantitatively by plotting ${\alpha }_{k,D}^S/{\alpha }_{k,D}^{SM}$ for each residue, where ${\alpha }_{k,D}^{SM}$ is the maximum ${\alpha }_{k,D}^S$ value for residue type k in 8 M urea. If residual structure causes the dispersion in ${\alpha }_{k,D}^P$ then we expect that ${\alpha }_{k,D}^S/{\alpha }_{k,D}^{SM}$ should depend on the secondary structure element that residue k adopts in the native state. We find that there is a correlation between ${\alpha }_{k,D}^S$ and the helical secondary structure element (residues 26 to 44, Fig. 6). The helical region tends to have smaller ${\alpha }_{k,D}^S/{\alpha }_{k,D}^{SM}$ values compared to other regions of the protein. Of the nine alanines in protein L, four are found in the helical region of the protein. These four residues have some of the smallest ${\alpha }_{k,D}^S/{\alpha }_{k,D}^{SM}$ values out of the nine alanines. The [C]-dependent fraction of residual secondary structure in the DSE shows that at 8 M urea the helical content is 32% of its value in the native state (Fig. 7a). Taken together, these data show that ${\alpha }_{k,D}^P$ depends not only on the residue type, but also on the residual structure present in the DSE, which at all values of [C], is determined by the polymeric nature of proteins.

Figure 6.

The ratio ${\alpha }_{i,D}^S/{\alpha }_{k,D}^{SM}$ (see text for an explanation) as a function of residue number i at 8 M urea. The legend indicates the amino acid type for each residue. Only amino acid types that occur at least four times in protein L, and have at least two of those residues separated by more than twenty five residues along sequence space, are plotted. For reference, the linear secondary structure representation of protein L is shown above the graph.

Figure 7.

(a) The residual secondary structure content in the DSE versus urea concentration. (b) The interaction energy (E_M) in the DSE divided by the number of residues in the secondary structural element, in units of k_BT, versus urea concentration for the entire protein and various secondary structural elements. The inset shows E_I, E_S, and E_M for the entire protein versus urea concentration in units of kcal mol⁻¹.

Residue-dependent variations in the transition midpoint - The Holtzer Effect

Globally, the denaturant-induced unfolding of protein L may be described using the two state model (Fig. 1b). However, deviations from an all-or-none transition can be discerned if the residue-dependent transitions C_m,i can be measured. For strict two-state behavior, C_m,i = C_m for all i, where C_m,i is the urea concentration below which the i^th residue adopts its native conformation. The inequivalence of the amino acids, described above (Fig 2a), should lead to a dispersion in C_m,i. The values of C_m,i are determined by specific interactions, while the dispersion in C_m,i is a finite-size effect [53, 54]. In other words, because the number of amino acids (N) in a protein is finite, all thermodynamic transitions are rounded instead of being infinitely sharp. Finite-size effects on phase transitions have been systematically studied in spin systems [55] but have received much less attention in biopolymer folding [54]. Klimov and Thirumalai [53] showed that the dispersion in the residue-dependent melting temperatures T_m,i, denoted ΔT (ΔC), for temperature (denaturant) induced unfolding scales as ΔT/T_m ~ 1/N (ΔC/C_m ~ 1/N). The expected dispersion in C_m,i or T_m,i is the Holtzer effect.

In the context of proteins, Holtzer and coworkers [56] were the first to observe that although globally thermal folding of the 33-residue GCN4-lzK peptides can be described using the two state model, there is dispersion in the melting temperature throughout the protein’s structure. In accord with expectations based on the finite size of GCN4-lzK, it was found, using one-dimensional NMR experiments, that T_m,i depends on the sequence position. The deviation of T_m,i from the global melting temperature is as large as 20% [56]. More recently, large deviations in T_m,i from T_m have been observed for other proteins [57].

We have determined, for protein L, the values of C_m,i using Q_i(C_m,i) = 0.5, where Q_i is the fraction of native contacts for the i^th residue. The distribution of C_m,i show the expected dispersion (Fig. 8a), which implies different residues can order at different values of [C]. The precise C_m,i values are dependent on the extent of residual structure adopted by the i^th residue, which will clearly depend on the protein. Similarly, the distribution of the melting temperature of individual residues T_m,i, calculated using Q_i(T_m,i) = 0.5, also show variations from T_m. However, the width of the thermal dispersion is narrower then obtained from denaturant-induced unfolding (Fig. 8b). This result is in accord with the general observation that thermal melting is more cooperative than denaturant-induced unfolding [58]. It should be emphasized that the Holtzer effect is fairly general, and only as N increases will ΔC and ΔT decrease.

Figure 8.

The histogram of residue-dependent midpoints of unfolding as a function of (a) urea concentration at 328 K and (b) temperature at 0 M urea. The C_m for the entire protein is ~6.6 M, while the melting temperature is 356 K at 0 M urea.

Specific protein collapse at low [C], and the balance between solvation and intraprotein interaction energies

As [C] is decreased below 3 M there is a deviation in linearity of ΔG_ND([C]) (Fig. 1b) and the m-value depends on [C]. At low [C] values the characteristics of the denatured state change significantly relative to the denatured state at 8 M. The radius of gyration $R_g^D$ and Δα_T change by up to 6 Å (Fig. 9) and 1,150 Ų (Fig. 2c) respectively, indicating that the denatured state undergoes a collapse transition. We detail the consequences of the [C]-dependent changes and examine the nature and origin of the collapse transition.

Figure 9.

The average R_g (open black circles) and R_ee (x’s) as a function of [C] for protein L at 328 K. The values of $R_g^{\mathit{\text{DSE}}}$ (open black circles, dashed line, left axis) and $R_{\mathit{\text{ee}}}^{\mathit{\text{DSE}}}$ (x’s, dashed line, right axis) as a function of urea concentration are also shown. Lines are a guide to the eye. The gray vertical line at 6.56 M urea denotes the C_m.

Surface area changes

Above 4 M urea, the α_k,D values change only modestly (Fig. 2a). However, below 4 M much larger changes in α_k,D occur (Fig. 2a). In particular, Δα_T decreases by 850 Ų going from [C]=4 M to [C]=0 M urea, compared to ≈300 Ų upon decreasing [C] from 8 M to 4 M urea (Fig. 2c inset). The backbone is the single greatest contributor to Δα_T, accounting for 24% to 38% of Δα_T at various [C]. Thus, a significant amount of backbone surface area in the DSE is buried from solvent as [C] is decreased, and the protein becomes compact (Fig. 2c). The next largest contribution to Δα_T, as measured by n_kΔα_k(= n_k(〈α_k,D([C])〉 − 〈α_k,N([C])〉)), arises from the hydrophobic residues Phe, Ile, and Ala (Fig. 2c). These residues also exhibit relatively large changes in the DSE surface area as [C] is decreased. The large change in surface area of Phe as [C] decreases shows that dispersion interactions also contribute to the energetics of folding [50]. On the other hand, for side chains that are solvent exposed in the native state, such as the charged residue Asp, n_kΔα_k is small and does not change significantly with [C] (Fig. 2c). The results in Fig. 2, and the surface area dependence of the TM, suggests that the changes in surface area at low [C] are related to changes in solvation energy of the backbone (see below).

R_g and R_ee changes

Decreasing [C] below 4 M leads to a $R_g^D$ change of up to 4 Å, and an end-to-end distance (R_ee) change of up to 10 Å (Fig. 9). Such a large change in $R_g^D$ shows that a collapse transition occurs in the DSE. We find no evidence (e.g. a sigmoidal transition in $R_g^D$ versus [C]) that the DSE at 0 M $(\langle R_g^D\rangle =15.5\mathrm{\AA })$ and the DSE at 8 M urea $(\langle R_g^D\rangle =21.5\mathrm{\AA })$ are distinct thermodynamic states. This suggests that the urea-induced DSE undergoes a continuous second order collapse transition as urea concentration decreases.

Residual structure changes

To gain insight into secondary structure changes that occur during the collapse transition we plot the residual secondary structure $(f_S^D)$ in the DSE versus [C] (Fig. 7a). Above 4 M urea only β-hairpin 3–4 and the helix are formed to any appreciable extent. However, below 4 M β-hairpin 1–2 and β-sheet interactions between strands 1 and 4 can be found in the DSE. For example, at 1 M urea β-hairpin 1–2 and strands 1 and 4 are formed 21% and 16% of the time, while there is 56% helical and 74% β-hairpin 3–4 content in the DSE (Fig. 7a). Thus, as [C] is decreased, the residual structure in the DSE increases, contributing to changes in R_g, R_ee, and the surface areas. This finding suggests that the collapse transition is specific in nature, leading to compact structures with native-like secondary structure elements.

Solvation versus intraprotein interactions

Neglecting changes in protein conformational entropy, two opposing energies control the [C]-dependent behavior of $R_g^D$; the interaction of the peptide residues with solvent (the solvation energy, denoted E_S), and the intraprotein non-bonded interactions between the residues (denoted E_I). For denaturants, such as urea, E_S favors an increase in $R_g^D$ and a concomitant increase in solvent accessible surface area, while E_I typically is attractive and hence favors a decrease in $R_g^D$. Because E_S in the TM model is proportional to a surface area term, and E_I is likely to be approximately proportional to the number of residues in contact (which increases as the residue density increases upon collapse), we expect $E_S([C])\propto -[C]{\langle R_g^D([C])\rangle }^2$ and $E_I([C])\propto -1/{\langle R_g^D([C])\rangle }^3$. The behavior of these two functions (increasing $\langle R_g^D([C])\rangle$ leads to a more favorable E_S([C]) and unfavorable E_I([C])) suggests that there should always be some contraction (expansion) of the DSE with decreasing (increasing) [C]. The molecular details in the C_α-SCM allow us to exactly determine E_S([C]) and E_I ([C]) as a function of [C], and thereby get an understanding of the energy scales involved in the specific collapse of the DSE.

In the inset of Fig. 7b we plot E_S([C]), E_I ([C]), and E_M([C])(≡ E_S([C]) + E_I ([C])) in the DSE. As indicated by the Flory-like argument given above, E_S([C]) becomes more favorable with increasing [C], and E_I ([C]) becomes more unfavorable with increasing [C] (Fig. 7b Inset). The behavior of E_M([C]) is important to examine, as this quantity governs the behavior of $R_g^D([C])$. Above 4 M, E_M([C]) is relatively constant, varying by no more than 1 kcal/mol. This finding is consistent with the small changes in $R_g^D$, R_ee, and $\mathrm{\Delta }{\alpha }_k^P$ above 4 M urea (Fig. 9 and Fig. 2c). Below 4 M, the E_M([C]) strength increases and is dominated by the attractive intrapeptide interactions (E_I([C])) at low [C] (Fig. 7b Inset), driving the collapse of the protein as measured by $R_g^D$.

We dissect the monomer interaction energies further by computing the average monomer interaction energy per secondary structural element (Fig. 7b). Above 4 M urea, the monomer interaction energies change by less than 0.4 k_BT, except for the β-hairpin 3–4 which changes by as much as ~ 0.9 k_BT. Below 4 M the monomer interaction energies change by as much as 1.5 k_BT, with the helix exhibiting the smallest change with [C]. These findings, which are in accord with changes in residual secondary structure (Fig. 7b), indicate that the magnitude of the driving forces for specific collapse $(\text{defined as}\frac{d{E}_M([C])}{d[C]})$ are (from greatest to least) associated with β-hairpin 3–4 > β-strands 1–4 > β-hairpin 1–2 > helix. Thus, the forces driving collapse are non-uniformly distributed throughout the native state topology.

Concluding remarks

The major findings in this paper reconcile the two-state interpretation of denaturant m-values with the broad ensemble of conformations in the unfolded state, and resolves an apparent conundrum between protein collapse and the linear variation of ΔG_ND([C]) with [C]. The success of the TM model in estimating m-values [15, 16] suggests that the free energy of the protein can be decomposed into a sum of independent transfer energies of backbone and side chain groups (Eq. 1). However, in order to connect the measured m-values to the heterogeneity in the molecular conformations it is necessary to examine how the distribution of the DSE changes as [C] changes. This requires an examination of the validity of the second, more tenuous assumption in the TM, according to which the denatured ensemble surface area exposures of the backbone and side chains do not change as [C] changes. This assumption, whose validity has not been examined until the present work, implies that neither the polymeric nature of proteins, the presence of residual structure in the DSE, nor the extent of protein collapse alters $\langle {\alpha }_{k,D}^P([C])\rangle$ or $\langle {\alpha }_{k,N}^P([C])\rangle$ significantly. Our work shows that as urea concentration (or more generally any denaturant) changes there are substantial changes in P(α_T) (Fig. 3b), R_g, and R_ee (Fig. 9). However, because backbone groups, whose ${\alpha }_{k,D}^B$ values are more narrowly distributed than almost all other groups (see Fig. 4a), make the dominant contribution to the m-value (see Fig. 4b), the m-value is constant in the transition region. Therefore, approximating Eq. 2 using Eq. 1 causes only small errors in the range of 3 M to 8 M urea for protein L.

The utility of the TM in yielding accurate values of m using measured transfer free energies of isolated groups, without taking the polymer nature of proteins into account, has been established in a series of papers [15, 16]. The success of the empirical TM (Eq. 1), with its obvious limitations, has been rationalized [15, 16] by noting that the backbone makes the dominant contribution to m. The present work expands further on this perspective by explicitly showing that the total backbone surface changes (Δα_B) area changes weakly with [C] (for [C] > 3M for protein L). We conclude that Eq. 1, with the assumption that changes in surface areas are approximately [C]-independent, is reasonable. This finding, to our knowledge, has not been demonstrated previously. We ought to emphasize that m, a single parameter, is only a global descriptor of the properties of a protein at [C] ≠ 0. Full characterization of the DSE requires calculation of changes in the distribution functions of a number of quantities (see Figs. 3a and 3b) as a function of [C]. This can only be accomplished using MTM-like simulations and/or NMR experiments, which are by no means routine. The paucity of NMR studies that have characterized [C]-dependent changes in the DSE, at the residue level, shows the difficulty in performing such experiments.

The MTM simulations show discernible deviations from linear behavior at [C] < 3 M (Fig. 1b), which can be traced to changes in the backbone surface area in the DSE. The structural characteristics of the unfolded state under such native conditions are different from those at [C] >> [C_m]. The values of $\mathrm{\Delta }{\alpha }_{k,D}^P$ are relatively flat when [C] > [C_m] (Fig. 2b) but decrease below [C_m] because of protein collapse. Because $\delta g_k^B([C])$ dominates even below [C_m] (Fig. 4b) it follows that departure from linearity in ΔG_ND([C]) is largely due to burial of the protein backbone. The often-observed drift in baselines of spectroscopic probes of protein folding may well be indicative of the changes in $\mathrm{\Delta }{\alpha }_{k,D}^B$, and reflect the changing distribution of unfolded states [5, 59]. Single molecule experiments [24–27, 29], that directly probe changes in the DSE even below [C_m], exhibit large shifts in the distribution of FRET efficiencies with [C]. Our simulations are consistent with these observations. The logical interpretation is that the DSE and, in particular, the distribution of α_T, α_B, and the radius of gyration R_g must be [C]-dependent. The present simulations suggest that only by carefully probing these distributions, can the replacement of Eq. 2 by Eq. 1 be quantitatively justified. In particular, large changes in the DSE occur under native conditions. Therefore, it is important to characterize the DSE under native conditions to monitor the collapse of proteins.

Equilibrium SAXS experiments on protein L at various guanidinium chloride concentrations found that R_g does not change significantly above [C_m] [60]. The ~2 Å change in $R_g^D$ above [C_m] observed in these simulations is within the ≈ ±1.8 Å error bars of the experimentally measured R_g above [C_m] [60]. Our findings also suggest that the largest change in $R_g^D$ occurs well below [C_m] (3 M urea or less). Under these conditions the fraction of unfolded molecules is less than 1% (Fig. 1b inset), which implies it is difficult to accurately measure the R_g of the DSE using current SAXS experiments and explains why the equilibrium collapse transitions are not readily observed in scattering experiments. The present work and increasing evidence from single molecule FRET experiments show that the denatured state can undergo a continuous collapse transition that is modulated by changing solution conditions. This finding underscores the importance of quantitatively characterizing the DSE in order to describe the folding reaction. In order to establish if the collapse transition is second order, which is most likely the case, will require tests similar to that proposed by Pappu and coworkers [61].

Figure 10.

Abbreviations

TM

Transfer Model

MTM

Molecular Transfer Model

D

Denatured state

N

Native state

DSE

Denatured state ensemble

NSE

Native state ensemble

C_α-SCM

C_α side chain model

MREX

Multiplexed Replica Exchange

GdmCl

Guanidinium Chloride

NMR

Nuclear Magnetic Resonance

FRET

Forster Resonance Energy Transfer