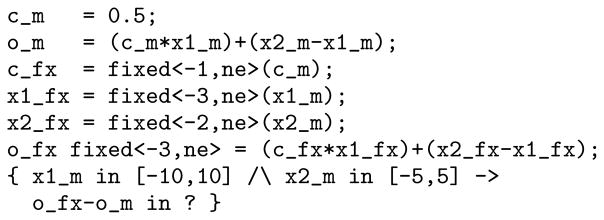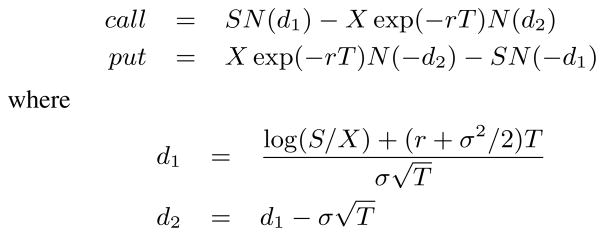Towards Program Optimization through Automated Analysis of Numerical Precision

Abstract

Reducing the arithmetic precision of a computation has real performance implications, including increased speed, decreased power consumption, and a smaller memory footprint. For some architectures, e.g., GPUs, there can be such a large performance difference that using reduced precision is effectively a requirement. The tradeoff is that the accuracy of the computation will be compromised. In this paper we describe a proof assistant and associated static analysis techniques for efficiently bounding numerical and precision-related errors. The programmer/compiler can use these bounds to numerically verify and optimize an application for different input and machine configurations. We present several case study applications that demonstrate the effectiveness of these techniques and the performance benefits that can be achieved with rigorous precision analysis.

1. Introduction

For many programmers numerical precision is an afterthought; developers choose the numerical type with the maximum practical precision for their variables (typically double) and treat these operands as real numbers. Floating and fixed point numbers are only an approximation to the real numbers. In the worst case this approximation manifests itself in subtle bugs [17]. And so programmers over-provision, using a more precise representation than is necessary, with the goal of preventing numerical precision errors. The choice of numerical types has real impacts on application performance, though, and should not be made casually.

The absence of tools for program-driven analysis of numerical errors makes it difficult for programmers to rigorously evaluate performance-accuracy trade-offs. We encountered this absence first-hand when re-implementing a Bayesian network inference application [1] (described in Section 4) that targets modern general purpose processors (GPPs), graphics processing units (GPUs) and programmable logic (FPGAs). This work grew out of efforts to verify and optimize this application for the different kinds of fixed and floating arithmetic available on those platforms.

On GPPs, GPUs and FPGAs reducing precision can improve application performance. When targeting FPGAs, or designing custom application-specific hardware (ASICs), reduced precision directly translates to fewer gates and narrower datapaths, and thus potentially to reduced energy consumption and increased maximum clock rate [14]. On GPPs, reduced precision can reduce functional unit latency, e.g. division, and improve memory and arithmetic throughput [13]. Switching from 64 to 32-bit floating point potentially improves memory bandwidth and cache utilization (measured in operands per time or volume) by 2× and the throughput of the 128-bit SIMD SSE unit by 2× as well. The difference is even more striking for GPUs: 32-bit arithmetic throughput is 933 GigaFLOPs peak vs. 78 GigaFLOPs for 64-bit floating point on the 2009 NVIDIA Tesla C1060.

The challenge is to determine when precision reduction is possible. Detailed simulation and testing, along with hand analysis, is the most commonly used technique. However simulation is time consuming, requires both working “ideal” and test implementations, and does not guarantee the absence of problems in cases not tested. Compile-time program-driven static analysis, which can efficiently and accurately bound numerical errors in a computation without considering a potentially unbounded set of inputs, offers a desirable alternative. In contrast to simulation, static analysis provides comprehensive coverage and guaranteed bounds on rounding errors. These bounds will by definition be pessimistic; our goal is to ensure that they are accurate enough to be useful for program verification and optimization.

In this paper we introduce Gappa++, an enhanced version of the Gappa proof assistant¹ [6], and a set of accompanying techniques that enable automated analysis of numerical errors in fixed and floating point, linear and non-linear, computations. Gappa++ extends Gappa’s interval arithmetic (IA)-based proof engine with an affine arithmetic (AA)-based engine that can more accurately bound linear computations with correlated errors. Using Gappa++ we verify the correctness and optimize the performance for several real-world applications.

This paper makes the following contributions:

• We describe Gappa++, a novel static precision analysis tool that enhances the Gappa proof assistant with: 1) an AA-based extension that computes more accurate bounds for linear computations; 2) better support for transcendental functions; and 3) support for rounding modes on NVIDIA GPUs.

• We present analysis techniques for verifying and optimizing applications using the proof assistant for GPPs, FPGAs and GPUs. We detail the GPU assembly-to-Gappa transformations used to accurately model the GPU’s hardware intrinsics.

• We present three representative application case studies: Bayesian network inference [1], neural prosthetics [25], and Black-Scholes stock option pricing [2], that demonstrate the effectiveness of the proof assistant, and the performance benefits that can be achieved with rigorous precision analysis.

The remainder of the paper is organized as follows: Section 2 provides relevant background on fixed and floating point arithmetic, IA and AA; Section 3 describes the Gappa++ proof assistant; Section 4 presents several application case studies; and finally Section 5 concludes.

2. Background and Related Work

2.1 Floating and Fixed Point Error

Evaluating a computation includes two primary sources of error: 1) approximation errors (often termed methodical errors), such as approximating e^x as 0 for x ≪ 0; and 2) rounding errors, produced when using an insufficiently precise numerical representation.

Rounding errors result from having only finite precision to represent real numbers. Fixed point numbers are represented as m·2^e, where m is the signed mantisaa and 2^e is an implicit, constant scaling factor determined by the format. Floating point numbers (following the IEEE 754 standard [21]) are implemented as sign·1.m·2^(e−bias), where m is the unsigned mantissa and e is the variable exponent².

The maximum fixed point rounding error is a function of the format and independent of the magnitude of the number. The floating point rounding error is dependent on both the format and magnitude of the number. An approximate error model for round-nearest-even (RNE) is given by:

$$\begin{array}{lll}\hfill x_f& =\hfill & x+x·2^{-(t+1)}·\epsilon \hfill \\ \hfill x_f\circ y_f& =\hfill & (x_f•y_f)+(x_f•y_f)·(2^{-(t+1)}·\epsilon \hfill \end{array}$$ (1)

where x_f is the floating point representation of a real number x, ∘ is the floating point implementation of the operation •, t is the mantissa bit width, and ε ∈ [−1, 1] is the error term [24] (2^−(t+1) corresponds to .5 ULPs, or unit in the last place, which is the difference between adjacent floating point numbers). Note that not all floating point conversions or arithmetic operations introduce rounding errors. Some numbers, e.g. .5, and operations, e.g., subtraction of numbers of similar magnitude [24], can be represented exactly.

To bound numerical errors programmers can run exhaustive simulations comparing different implementations to an “ideal” version. However, as discussed earlier, these simulations can be difficult and time-consuming to prepare and run and provide limited test coverage. While simulation will continue to be a part of the verification workflow, we would like to reserve that effort for the end of the design process, where we test an implementation already optimized and checked by other means. Static analysis bounds errors at compile time using the application source code, user-supplied bounds on the inputs, and error models similar to Equation (1). Unlike simulation, static analysis can produce provable error bounds, and since these approaches require much less effort by the programmer, can be used to efficiently and even automatically explore the design space. The trade-off is that by their nature static analysis techniques are conservative, often overly so.

Static analysis tools seem to be split between those used for program verification [3, 15, 10, 4], and those designed for program optimization [19, 7, 8, 23, 14, 16, 5]. There are numerous techniques for static analysis. In general, these techniques attempt to construct a transfer function for the computation [19, 3, 15], use a form of range-based arithmetic [7, 8, 14], e.g, interval or affine, through which errors are propagated, or both [5]. Often, the static analysis is combined with simulation in hybrid static-dynamic approaches [23]. In this work, we propose a static analysis approach using a combination of range arithmetic and algebraic rewriting that provides high accuracy, i.e., tight error bounds, efficient evaluation, and is suitable for integration into the compiler.

The most similar work is the Caduceus static analyzer for C programs [4]. Caduceus integrates Gappa (along with other tools) into its back-end proof infrastructure for proving assertions about C applications. The focus of Caduceus is verification, while the focus of this work is program optimization, and extending Gappa to support a broader set of computations.

2.2 Interval and Affine Arithmetic

Interval arithmetic (IA) [18] represents a number, x̄, by an inclusive interval, [x.lo, x.hi] such that x.lo ≤ x ≤ x.hi. For each operation there is a corresponding IA implementation, e.g. IA addition is given as

$$\overline{z}=\overline{x}+\overline{y}=[x.lo+y.lo,x.hi+y.hi].$$

Similar formulas can be derived for other common mathematical operations. The primary weakness of IA is overestimation, particularly in the presence of correlated variables. In the simplest example, if x̄ = [−1, 1], x̄ − x̄ will result in [−2, 2] instead of 0. Overestimation accumulates throughout the computation, potentially resulting in an exponential growth in the range estimates.

Affine arithmetic (AA) [9] is a refinement to IA that addresses the above problem by keeping track of correlations between variables. Instead of an interval, a number, x, is represented by an affine expression, given as

$$\widehat{x}=x_0+x_1{\epsilon }_1+x_2{\epsilon }_2+\dots +x_n{\epsilon }_n\text{where}{\epsilon }_i=[-1,1].$$ (2)

Each ε_i is an independent source of uncertainty, and may contribute to the uncertainty of more than one variable. Thus correlations are preserved. In the simple example above, if x̂ = x₀ + x₁ε₁, the expression x̂ − x̂ will return 0.

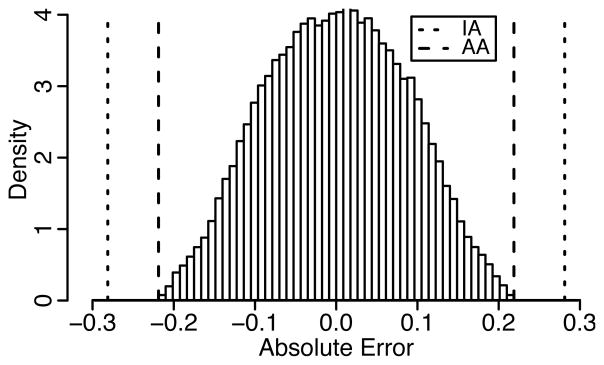
As a more complex example, consider the fixed-point expression y = c·x₁ + (x₂ − x₁) adapted from [7], where x₁ = [−10, 10] RNE with 3 fractional bits, x₂ = [−5, 5] RNE with 2 fractional bits and all operations are RNE with 3 fractional bits. The AA expression for o is

$$\begin{array}{lll}\hfill \widehat{x_1}& =\hfill & 10{\epsilon }_1+2^{-4}{\epsilon }_{e1}\hfill \\ \hfill \widehat{x_2}& =\hfill & 5{\epsilon }_2+2^{-3}{\epsilon }_{e2}\hfill \\ \hfill \widehat{c·x_1}& =\hfill & 5{\epsilon }_1+2^{-5}{\epsilon }_{e1}+2^{-4}{\epsilon }_{e3}\hfill \\ \hfill \widehat{x_2-x_1}& =\hfill & -10{\epsilon }_1+5{\epsilon }_2-2^{-4}{\epsilon }_{e1}+2^{-3}{\epsilon }_{e2}\hfill \\ \hfill \widehat{y}& =\hfill & -5{\epsilon }_1+5{\epsilon }_2-2^{-5}{\epsilon }_{e1}+2^{-3}{\epsilon }_{e2}+2^{-4}{\epsilon }_{e3}\hfill \end{array}$$

where ε_e1, ε_e2, ε_e3 are the rounding errors in x₁, x₂, c · x₁ respectively. Figure 1, shows both the IA bound on the rounding error (as computed with Gappa), the AA bounds, and a histogram of simulated errors for 100,000 trials³. IA does not capture the correlated error in x₁and as a result produces less accurate bounds.

Figure 1.

IA and AA bounds, along with a histogram of simulated errors for c · x₁ + (x₂ − x₁)

For affine, i.e., linear, operations, the resulting affine forms can be derived from Equation (2). The results of a non-linear operation, f(…), are no longer affine. To obtain an affine expression, f is replaced with a linear approximation f^*, and a new ε term is added to the expression to capture the approximation error. Many AA implementations use Chebyshev approximations, f(x) = Ax + B + δε for non-affine operations [9]. For large input ranges, the added error term δε can be larger than the numerical errors we are trying to analyze. Thus IA or AA alone are often ill suited for nonlinear computations; in these cases alternative techniques, such as algebraic rewriting (described in Section 3), are needed.

3. Gappa++ Proof Assistant

Gappa++ extends the Gappa proof assistant [6] to better support transcendental functions and linear computations. This section describes both Gappa and our extensions.

3.1 Gappa

Gappa proves the validity of logical properties involving the bounds of mathematical expressions. The initial application for Gappa was verifying libm implementations of elementary functions.

Gappa only manipulates expressions on real numbers. Floating or fixed point arithmetic is expressed with separate “rounding operators”, functions that map a real number x to its rounded value ⋄(x). Rounding is captured explicitly and specifically for each operand. Bounds on the rounding or numerical error are computed from ⋄(x) − x, the enclosure of the difference of the approximate and ideal value.

The Gappa input script for the computation in Figure 1 is shown in Figure 2. Each script has four parts: 1) the code segment with rounding operators of the form

Figure 2.

Gappa input script for bounding the rounding error in the expression from Figure 1. A note about syntax and convention: the rounding operator on the left-hand side of the equals is applied to all operations, but not variables, on the right-hand side; we use the suffixes _m, _f, and _fx to represent mathematically ideal, floating and fixed point variables, respectively.

[fixed|float]<precision,direction>

2) a set of hypotheses, e.g., x1_m in [−10,10]; 3) a set of enclosures to be proved, e.g., o_fx-o_m in ?; and 4) an optional set of hints (not shown). Using this script Gappa computes the bounds on absolute error in o_fx - o_m = [−.28125,.28125], given the hypotheses on x1_m, x2_m.

All values within Gappa are expressed as intervals, and IA plays a key role in ensuring that Gappa proofs are machine checkable. Enclosures are only one type of predicate. Floating and fixed point numbers are actually discrete sets; Gappa includes FIX and FLT predicates, which indicate a number is uniquely representable at a given precision. These predicates are to identify situations, cited in Section 2, in which numbers or expressions are uniquely representtable, and thus no rounding errors are introduced. This capability separates Gappa from other tools that use a simpler error model.

As discussed previously, IA fails to capture correlations between expressions with shared terms. Gappa uses algebraic rewriting to expose correlated errors. For example, ∘(a)−b can be rewritten as (∘(a) − a) + (a − b)), which separates the rounding error from the difference of a and b. IA without rewriting would compute the enclosures of ∘(a) and b separately, then subtract them, potentially leading to a much larger bound on the difference. In contrast to AA, which also captures correlations, algebraic rewriting can be used to generate tight bounds over large input ranges for non-linear operations, such as log, that have well-known algebraic properties. Adding additional support for transcendental functions to Gappa was a key part successfully applying Gappa++ to the applications in Section 4.

3.2 Operator, Rewriting and Rounding Extensions

Several of the case study applications make use of log and exp functions. We added these operators, along with their base-2 variants, exp2 and log2 to Gappa.

We incorporated new rewriting rules for these operations, including

$$\begin{array}{lll}\hfill log(a)-log(b)& \to \hfill & log(1+(a-b)/b)\hfill \\ \hfill exp(a)-exp(b)& \to \hfill & exp(b)·(exp(a-b)-1)\hfill \\ \hfill a+log(b)& \to \hfill & log(exp(a)·b)\hfill \end{array}$$

and many similar variants. These rewriting rules help isolate the rounding errors in expressions with transcendental functions, even when using large input ranges.

Along with new operators and rewriting rules, we also added a new rounding operator, cuda_32, which implements the semantics of 32-bit floating point arithmetic on NVIDIA GPUs. cuda_32 is similar to ieee_32, but without subnormal numbers [20].

3.3 Affine Extension

In theory, algebraic rewriting should be sufficient to capture correlated errors. As practical matter, however, Gappa often does not rewrite aggressively enough, as shown by the loose bounds in Figure 1. For linear expressions, AA is more effective at capturing correlated errors, and so we developed an AA extension to the Gappa proof engine to improve accuracy in these cases. The AA engine is invoked with a hint in the input script. At each invocation Gappa++ passes to the AA extension hypotheses on input variables and rounding errors; the AA extension returns a new bound for the expression, computed with AA, that is added to Gappa++ as a hypothesis. The AA result is one of several potential bounds computed within Gappa++; if the AA engine fails to return a tighter bound, it is ignored by Gappa++. Thus there is no risk, other than to execution time, for using the AA hint.

The AA extension only supports addition, subtraction and multiplication (with both single and dual variable terms); expressions with other operators are ignored by the AA extension. The above operations are implemented as suggested in [9], using the MPFR multiple precision floating point library [11] to implement the co-efficients with the same extended precision used within Gappa++ itself.

At creation, the AA engine reports to Gappa++ dependencies on the enclosures of all input, e.g., x1_m, and on the magnitude of all rounding errors, e.g.,

fixed<ne,-16>(x1_m)-x1_m

The latter information is used to generate the error epsilons for rounding operations. Thus the AA extension can leverage Gappa++’s best bounds on the error (and its predicate system, etc.) Sometimes, however, the AA extension has more accurate information about the magnitude of variables than Gappa++, and so separate AA-based error bounds are computed. The tighter of these two errors bounds is chosen for each rounding operator.

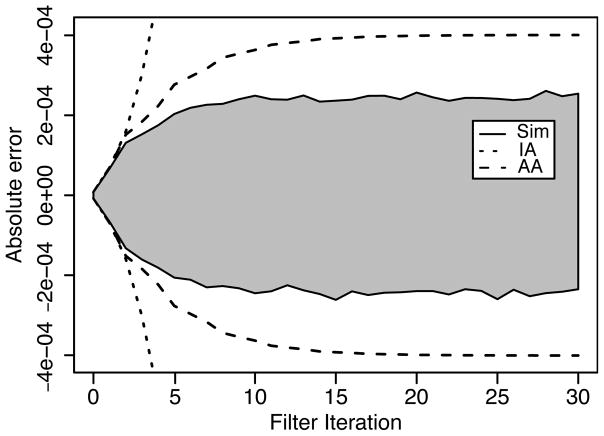
Using the affine extension in Gappa++, we can calculate more accurate bounds for linear expressions. For example, for the script in Figure 2, Gappa++ computes more accurate bounds of [−.21875,.21875]. The difference in accuracy is even more pronounced for more complex computations, particularly those with feedback. Figure 3 shows the IA, AA and simulated errors for the simple filter

Figure 3.

AA and IA error bounds along with simulated error (gray region) for simple IIR filter in Equation (3)

$$y_n=x_n+c_1{y}_{n-1}+c_2{y}_{n-2}$$ (3)

where $c_1=\frac{1}{\sqrt{2}}$, c₂ = .5, x_n = [−64, 64] and all computations and operands are RNE with 16 fractional bits (adapted from [7]). As the simulation shows, since the filter is stable, the error is also stable (after some number of iterations). The AA error is also stable, while the IA error is not. The IA error, computed with an unmodified version of Gappa, grows exponentially and is too large to be usable.

The trade-off for using the AA extension is execution time. AA maintains significantly more information for each variable, and is thus slower to compute enclosures than IA methods. However, computing bounds for 30 filter iterations took only .38s using Gappa++ vs. .35s for plain Gappa⁴. For contrast the corresponding simulation took 130s.

In general, the affine extension increased the execution time of Gappa++ by up to 12× and memory usage by up to 10×. However, even the largest affine problem we ran (Section 4.2) completed in less than 125s, and most took less than a minute. So even with the AA extension, the static analysis techniques are still faster than simulation. We are working to improve the performance of the AA extension and believe significant reductions in execution time can be made by reducing the number of times Gappa invokes the affine engine.

4. Case Studies

The development of Gappa++ was motivated by several informatics applications, presented as case studies in this section. Each application demonstrates a different Gappa++ usage model, including: optimizing numerical approximations (network inference, Section 4.1); comparing different sources of error (neural prosthetics, Section 4.2); and verifying that an application satisfies an absolute error bound (option pricing, Section 4.3).

4.1 Bayesian Inference

The inside of a cell is a complex dynamical environment in which proteins interact in complex causal networks. Understanding the causal structures of these networks on a per-individual basis is important for advancing both basic biological and clinical knowledge. The structure of these networks can be inferred using Bayesian techniques; however, the algorithm is extremely computationally demanding [1].

Previous efforts have achieved > 10× speedups using specialized accelerators, such as GPUs and FPGAs. Porting this application to these platforms is challenging. Incorporating rigorous precision analysis into our workflow helped us improve the performance of the FPGA version by 33% plus 4× better precision, and speedup the baseline CPU implementation by 15% without reducing overall accuracy.

The algorithm uses Monte-Carlo Markov Chain sampling to explore the space of potential graphs. Inside the inner-most loop is the accumulation of local scores, ls_n, which represent the log probabilities of particular parent-child relationships. The accumulation is implemented as

acc += log(1+exp(ls[i]-acc));

The log(1 + exp(x)) expression is only non-linear over a small region around 0 and can be approximated as 0 or x for x ≪ 0 and x ≫ 0 respectively. The approximations are much faster than the actual computation, and so it is beneficial to set the boundaries within which we actually do the computation as tight as possible.

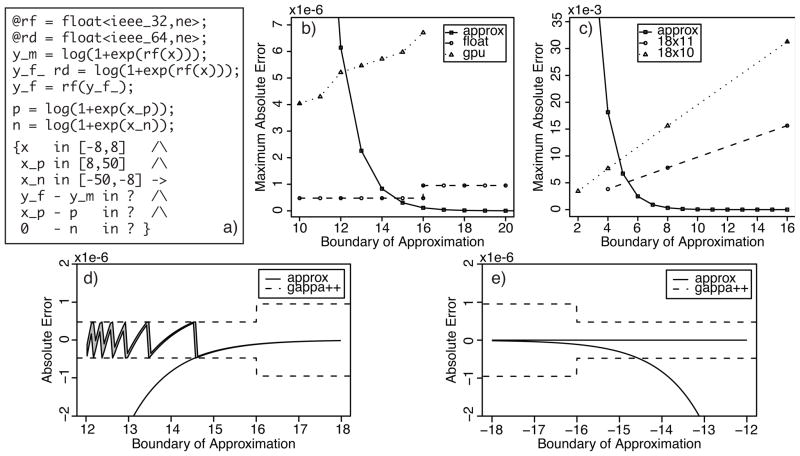
The original implementation used [−30,30] as the approximation boundary, chosen to be conservative with respect to accuracy. However, using Gappa++ we can show that those bounds are too conservative, and do not actually improve overall accuracy. The baseline implementation already used float precision; however, that does not mean that 32-bit computations are being performed. GCC with optimization level 3 (−O3) actually emits double precision operations for log(1 + exp(x)), only rounding to 32-bits at the end. Our Gappa++ analysis (an example script is shown in Figure 4a) is driven from the assembly, and accurately models the actual precision in use.

Figure 4.

Gappa++ and simulation-based analysis of the approximation of score accumulation in inference algorithm: a) Gappa++ script used in panel b; b), c) absolute error vs. boundary of approximation for CPU, GPU (b) and FPGA-based (c) implementation; negative and positive approximations overlap and are represented by a single line; d), e) simulation and Gappa++-computed errors at the positive (d) and negative (e) approximation boundaries.

Figure 4b compares the error in the positive and negative approximations, i.e. x − log(1 + exp(x)), and the rounding error introduced in the log(1+exp(x)) computation for both “float” implementation on the CPU and the same code compiled for an NVIDIA GPU (Gappa++ analysis of GPU applications is described in more detail in Section 4.3). The “crossover” point where the rounding error exceeds that of the approximation is much less than 30. Continuing to perform the actual computation beyond the cross-over point only reduces performance. Setting the boundary to a still conservative [−16,16] improves GPP performance on our benchmark platform by 15%. Tightening the approximation boundary only requires modifying a single constant, making this an effort-efficient optimization in an already heavily optimized application.

The above results are verified with detailed simulation. Figure 4d,e shows simulated errors (gray region) vs. the approximation vs. the Gappa++ estimates. Note that the Gappa++ estimate is computed over the entire non-approximated range, i.e. [−12,12], and thus represents the maximum error over that space. Gappa++ accurately captures the error at the positive boundary. The analytical “crossover” point matches the simulated convergence of the computation and approximation errors. Interestingly, this convergence occurs when there is insufficient precision to capture the effect of the 1+ operation. Above this threshold the computation effectively simplifies to the approximation.

At the negative boundary, where the result is near 0 and floating point numbers are much more precise, the absolute errors are very small and the actual computation and approximation only converge for very negative inputs. Although the actual computation is more precise in the region, that additional precision does not necessarily improve overall accuracy (which is set by the positive boundary) and so maintaining the more conservative boundary only slows the application (small, subnormal, numbers are slower on modern x86 processors).

A second interesting feature is the step function increase at 16 in the Gappa++ error bounds. This results from a limitation in the range-based analysis being performed. The bulk of the Gappa++ error results from the double-to-single rounding operation occurring at the end of the computation. At large x, however, because the input x is rounded to single precision, the output of log(1 + exp(x)) is effectively rounded to single precision; a fact that Gappa++ does not capture in its predicates and rewriting. This is a subtle effect, and one that we are actively working to handle in future iterations of Gappa++.

Precision analysis plays an even larger role in the FPGA porting effort. On the FPGA, the algorithm is implemented using fixed point arithmetic and block RAM-implemented lookup tables (LUT) for the log(1 + exp(x)) accumulation. Our goal is to maximize performance and accuracy (compared to baseline CPU implementation). Performance on the FPGA is a direct function of the amount of aggregate bandwidth we can extract from the block RAM (BRAM) macros distributed throughout the chip. Specifically, the peak FPGA performance can be modeled as

$$\frac{\text{Number}\text{of}\text{RAMs}}{0.5+\text{RAMs}\text{per}\text{LUT}}·\text{Clock}\text{Rate}$$ (4)

and thus we need to minimize the RAMs per LUT we use.

The Xilinx Virtex5 FPGAs we are using for this application have several BRAM configurations: 36×10 (10 bits of address, 36-bit words); 18×11; and 2× 18×10. The original implementation used 36×9 with a boundary of −12,16, which translates to .5 BRAM per LUT (each BRAM is dual ported). This configuration truncates the input to the LUT to 4 fractional bits to form the address (5 integer bits, 4 integer bits). The truncation is the dominant source of error in the FPGA implementation, since the actual accumulation is performed with 16+ fractional bits.

The first optimization is to use the entire address to pick up an additional factional bit. Using Gappa++ we can do better. Since the error is dominated by the truncation, we can use the narrower 18 bit configurations to get more address space (18×11) or more ports (2× 18×10). Shrinking the range over which we use the LUT reduces the number of integer bits needed, and thus increases the precision of the truncation. Figure 4c shows the error for different boundaries and BRAM configurations; the optimal boundaries are [−8,8] for both configurations. The latter trades away an additional fractional bit for a 33% increases in performance (.25 RAM per LUT vs. .5 RAM per LUT). Since we already have increased precision over the original, we choose the faster 18×10 configuration. Thus as a result of this analysis, the performance of the FPGA implementation improves 33% over the original 36×9 configuration, with 2 bits (4×) more precision, all within the same resource usage.

This case study helps demonstrate Gappa++’s effectiveness as a backend analysis tool for performance optimization. We identified a join (ϕ node) in the dataflow graph with unequal error incoming on each branch. Using Gappa++ we are able to optimize the boundary of the approximation to equalize the error on each branch. Similar analyses and optimizations could be performed in situations where the same variable is being computed in different ways on different branches.

4.2 Neural Prosthetics

Neural prosthetics systems seek to restore lost movement or communication functionality to patients with neural deficits [25]. These systems translate the electrical messages sent between neurons, recorded with electrodes implanted in the brain, into commands for the prosthetic device. Reducing the power consumption of a future implantable prosthetic processor (IPP) is a key challenge. Previous estimates show that the IPP can be built within the allotted power budget if implemented with energy-efficient fixed point arithmetic [25]. Our goal is to use static analysis to help verify and optimize that implementation.

One of largest power consumers is the front-end digital fil-ter (4^th order high-pass infinite impulse response (IIR) filter with f_c = Hz implemented as two second-order-sections in series; difference equations for direct form (DF) I and II implementations are shown in Table 1). Using Gappa++ we can explore the effects of rounding on the noise properties of the filter. Table 2 summarizes the Gappa++ and simulated errors for both 32-bit floating point and fixed point with 16 fractional bits, RNE, for DF I and II implementations. The Gappa++ results are obtained by unrolling the loop into straight-line code until the errors stabilize (300 iterations in this case).

Table 1.

Difference equations for filter second-order sections used in neural prosthetic system

DF I	yn = b0xn + b1xn−1 + b2xn−2 − a1yn−1 − a2yn−2
DF II	wn = xn − a1wn−1 − a2wn−2
	yn = b0wn − b1wn−1 − b2wn−2

Table 2.

Summary of Gappa++ (above) and simulated (below) error bounds for IIR filter. Uniformly distributed [0,1] input rounded to model data from 12-bit ADC.

DF I	Actual	Ideal Coeffs.	Ideal Arith.
32-bit float	±9.77e-4	±9.71e-4	±1.10e-5
	±2.02e-5
16-bit fix	±5.77e-2	±5.51e-2	±2.76e-3
	±3.15e-3
DF II	Actual	Ideal Coeffs.	Ideal Arith.
32-bit float	±9.70e-4	±9.64e-4	±1.10e-5
	±6.15e-5
16-bit fix	±2.94e-3	±2.61e-4	±2.76e-3
	±6.42e-4

Published results indicate that the root mean square (RMS) electrical noise observed in the filtered signal would be ~ ±3.9e-3 in the above scenario [22]. The results in Table 2 suggest that a 16-bit fixed point DF II implementation would be sufficient. Further, for the DF II filter, the arithmetic appears to be a lesser source of error than coefficient quantization. If the user is comfortable with the filter performance with quantized coefficients, the arithmetic precision could potentially be further optimized to improve performance and energy-efficiency.

Our goal in this initial work is not to perform optimized float-to-fixed (F2F) translation, but instead just to demonstrate that Gappa++ can accurately bound errors for non-trivial linear and non-linear computations. And thus could serve as the back-end analysis tool for an optimizing F2F translator. Although not shown here, Gappa++ can compute enclosures for individual variables (not just differences) and thus can also be used to set the number of integer bits to avoid overflow (a key part of F2F translation).

The difference between the DF I and II implementations is an example of how otherwise functionally equivalent code can have different numerical properties. The compiler could play a role in helping the programmer smartly select among different implementations for the same computation. In this case it is among variants that have similar performance; in the next case study, Black-Scholes, it is among variants with very different performance characteristics.

4.3 Black-Scholes Stock Option Pricing

The Black-Scholes [2] algorithm, defined in Figure 5, analytically computes the value of European-style stock options. Each option can be computed independently and in parallel, and so Black-Scholes is often used as a performance benchmark for different processors, particularly x86 SSE extensions and GPUs. As described earlier, GPUs can provide a 10× boost in computing power – if – the application can be implemented using 32-bit floating point. In the case of Black-Scholes, the programmer would like to verify without time-consuming simulation that the GPU implementation, for example, is accurate to less than one cent.

Figure 5.

Definition of Black-Scholes algorithm where S: stock price, X: strike price, r: risk-free interest rate, T: time to expiration, σ: voltatility, and N(x): fifth-order approximation of the cumulative normal distribution function.

Using Gappa++ we verified that 64 and 32-bit IEEE-compliant and 32-bit GPU-based implementations all are accurate to much less than one cent relative to a mathematically ideal implementation. The Gappa++ and simulated error bounds are summarized in Table 3. The analytical bounds are typically 1–3 orders of magnitude larger than the simulated enclosures; however, in all cases, Gappa++ produces sufficiently accurate bounds to verify that the different implementations meet the penny threshold.

Table 3.

Summary of Gappa++ and simulated error bounds for Black-Scholes. Inputs: stock price = [5,30]; strike price = [1,100]; time = [.25,10]; R = .02; and volatility = .3.

Puts	Gappa++	Simulation
double	[−1.202e-12, 1.187e-12]	[−3.064e-15, 2.998e-14]
float	[−6.585e-4, 6.738e-4]	[−1.286e-5, 1.349e-5]
gpu	[−2.990e-3, 3.090e-3]	[−2.196e-5, 1.367e-5]
Calls	Gappa++	Simulation
double	[−1.198e-12, 1.183e-12]	[−1.399e-15, 1.323e-14]
float	[−6.572e-4, 6.816e-4]	[−6.335e-6, 6.246e-6]
gpu	[−3.0e-3, 3.1e-3]	[−8.319e-6, 1.093e-5]

In the case of float and double the Gappa++ scripts are purposely conservative. When compiled for sequential execution, the compiler will often produce 64-bit floating point instructions for the “float” implementation. When compiled for SSE units, however, most of the operations will be performed at 32-bit precision. Thus by using a uniform ieee_32 rounding operator in the Gappa++ script we can ensure the application meets the required error bounds even if all operations were computed using the SSE unit.

Switching to 32-bit arithmetic can yield real performance benefits. Table 4 summarizes the execution time for various implementations of Black-Scholes, including sequential float and double, SSE float and double [12], and a NVIDIA 9800 GTX GPU [20]. Note that all implementations were compiled with icc -fast.

Table 4.

Execution for different Black-Scholes implementations pricing 1,000,000 put and call options

	Time (ms)	Speedup
double	118	1.0
float	125	0.95
double SSE	104	1.13
float SSE	66	1.8
GPU	14	8.4

The float and double Gappa++ scripts are direct translations of the application source code to Gappa syntax and rounding operators. The GPU script is the product of a separate translation pass, taking CUDA PTX assembly as input, that introduces additional error terms and rounding operators to faithfully model GPU operations.

The most relevant operations for Black-Scholes are multiply-add (MAD), log and exp. The GPU’s MAD operator truncates the intermediate result, and thus must be modeled as

float<cuda_32,ne>(a+float<cuda_32,zr>(b*x))

The GPU provides hardware support for the elementary functions exp2 and log2, among others. “Fast” versions of exp and log are synthesized from these intrinsic by multiplying the input or output by the appropriate constant. The intrinsics have an additional error compared to the correctly rounded single precision result (2 ULPs for exp2, 3 ULPs for log2). We model this additional error by introducing additional hypotheses that express the actual result as an approximation of the correctly rounded result. Specifically, y=exp2(x) is modeled as

Y_ = float<cuda_32,ne>(exp2(x));
…
{(y-y_)/y_ in [-2b-23,2b-23] /\ …

log2 and other intrinsics are modeled similarly, using the errors reported in the CUDA programming guide [20].

Although mostly straight-line code, the Black-Scholes implementation has two branches that require dataflow-style analysis. At each branch we “decouple” the analysis by computing magnitude and error enclosures for all live variables. These enclosures are modified by the conditional statement and used as hypotheses for two new scripts (one for each branch). The enclosures computed by the branch scripts are merged together with a ∪ operation at the dataflow join.

In computing the bounds in Table 3 we made extensive use of Gappa’s bisection feature. Bisection attempts to produce more accurate error bounds by splitting the input ranges into disjoint sub-ranges, computing the bounds on each sub-range, and merging the results with the ∪ operator. The trade-off is increased runtime. We bisected the ranges before the control flow decoupling into 500 uniform sub-ranges, and 100 sub-ranges after the decoupling. For ieee_32 bisection improved the bounds from ~ ±2.6e-2 to ~ ±6.8e-4 with the total runtime increasing from ~1s to ~90s. Analyses at other precisions showed similar trade-offs.

The Black-Scholes case study demonstrates Gappa++’s effectiveness in bounding the error in complex, non-linear computations, and the performance benefits that result from being able to confidently reduce the arithmetic precision.

5. Conclusion

In this paper we have presented Gappa++, an enhanced version of the Gappa proof assistant, and a set of techniques for using Gappa++ to analyze numerical and precision-related errors in real informatics applications. In a series of case studies we demonstrated the effectiveness of Gappa++ across a range of applications and hardware platforms, and showed the kinds of performance improvements that can be achieved with rigorous precision analysis.

Motivated by these results we argue that precision analysis should be a more regular part of a programmer’s workflow. Although Gappa++ was not directly integrated with the compiler in this initial work, both the tool and analysis techniques described in this work could be readily used as part of a compiler-based static analysis suite. Gappa is already in use as a back-end in the Caduceus static analyzer [4]. And none of the analysis performed in this work required Gappa’s interactive features, such as hints; the scripts were direct translation of the source code-under-test and thus could be generated and invoked automatically.

Much of the precision analysis and optimization is effectively dataflow-based, and could be integrated alongside similar passes in an optimizing compiler. For example, in the Bayesian Inference case study we used Gappa++ to equalize the error on the different incoming branches at a join in the dataflow graph. The compiler could readily notify the programmer that such situations might present optimization opportunities. With annotations to indicate functional equivalence and acceptable error bounds, the compiler could automatically compare and contrast different implementations and or verify correctness, as was done in the neural prosthetic and Black-Scholes case studies.

We imagine and are actively working towards a future in which the compiler helps the programmer verify and optimize the numerical aspects of their application.

Both short and long-term hardware trends will make this kind of tool support increasingly important. For example, GPUs have already begun to support 64-bit floating point operations, although, as discussed, with 2–10× less throughput than 32-bit arithmetic. Selectively making use of 64-bit operations may enable additional applications to use GPUs that for precision reasons were not able to do so previously. A key challenge for the programmer and the compiler is to identify the minimum set of operations that must be performed at increased precision, so as to maximize performance.

Long-term, more and more applications will be implemented on high-performance heterogeneous systems (CPUs plus SSE, GPUs, FPGAs, etc.) and high-efficiency embedded platforms; all of which introduce non-trivial accuracy-performance trade-offs. As a result, there will be a growing need to help developers automatically verify and optimize the numerical behavior of their applications for these new and different platforms.