Adsorption and encapsulation of flexible polyelectrolytes in charged spherical vesicles

Abstract

We present a theory of adsorption of flexible polyelectrolytes on the interior and exterior surfaces of a charged vesicle in an electrolyte solution. The criteria for adsorption and the density profiles of the adsorbed polymer chain are derived in terms of various characteristics of the polymer, vesicle, and medium, such as the charge density and length of the polymer, charge density and size of the vesicle, electrolyte concentration and dielectric constant of the medium. For adsorption inside the vesicle, the competition between the loss of conformational entropy and gain in adsorption energy results in two kinds of encapsulated states, depending on the strength of the polymer-vesicle interaction. By considering also the adsorption from outside the vesicle, we derive the entropic and energy contributions to the free energy change to transfer an adsorbed chain in the interior to an adsorbed chain on the exterior. In this paper, we have used the Wentzel-Kramers-Brillouin (WKB) method to solve the equation for the probability distribution function of the chain. The present WKB results are compared with the previous results based on variational methods. The WKB and variational results are in good agreement for both the interior and exterior states of adsorption, except in the zero-salt limit for adsorption in the exterior region. The adsorption criteria and density profiles for both the interior and exterior states are presented in terms of various experimentally controllable variables. Calculation of the dependencies of free energy change to transfer an adsorbed chain from the interior to the exterior surface on salt concentration and vesicle radius shows that the free energy penalty to expel a chain from a vesicle is only of the order of thermal energy.

I. INTRODUCTION

Packaging of charged macromolecules into vesicular carriers in aqueous media and their subsequent release into the exterior region are of common occurrence. The manifestation of this phenomenon in the context of biology and technological applications is well documented in the literature exhibiting very rich phenomenology.^1,2 Yet, even the elementary aspects of the packing/unpacking of charged macromolecules by carriers are not fully understood, although some progress is being made in the study of viruses.^3–8 The ubiquitous feature of this phenomenon is that both the macromolecular cargo and the vesicular interface are electrically charged. The interactions between the cargo and the oppositely charged vesicle arise primarily from the long-range electrostatic forces. Furthermore the macromolecular cargo itself is topologically correlated, mediated by the electrostatic interactions among various segments of the molecule. In addition, the whole process occurs in aqueous electrolyte solutions with cargo-vesicle interaction being significantly modulated by changes in the electrolyte concentration. A full understanding of this packing-unpacking phenomenon continues to be a challenge due to the combined effects from the long-range electrostatic forces, topological connectivity of the macromolecules, confinement of the cargo inside the vesicle, and adsorption of the cargo at the vesicle interface.

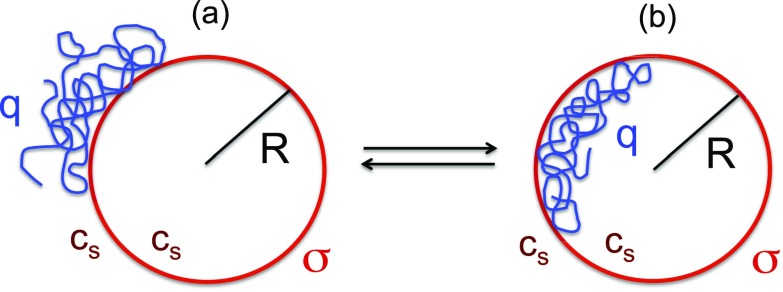
In efforts to make progress towards a fundamental understanding of this packing-unpacking process and to ascertain the energetics of this process, we consider the initial and final states of the macromolecule in this process (Fig. 1): (1) The polymer is captured on the exterior of the vesicle as an adsorbed chain, and (2) the polymer is adsorbed on the interior of the vesicle.

FIG. 1.

Cartoon of an adsorbed flexible polyelectrolyte chain of uniform charge number density q on the exterior (a) and interior (b) of a charged spherical vesicle of radius R with uniform charge number density $\sigma$. The salt concentration c_s is the same in both the interior and exterior regions.

Naturally, there are several fundamental questions that arise regarding these two states. For the exterior state [Fig. 1(a)], identification of the critical condition of adsorption and the monomer density profile of the adsorbed polymer in terms of various experimental variables is of interest. The critical condition emerges as a compensation between attractive interaction favoring adsorption and loss of conformational entropy disfavoring adsorption. If the attraction between the polymer and the vesicle is weak, the adsorption would not occur at all due to the severe entropic penalty. For sufficiently strong attraction, adsorption would occur. It is therefore necessary to accurately evaluate the conformational entropy of a flexible polyelectrolyte chain that is partially adsorbed to a curved charged interface in order to obtain the adsorption criterion. For the interior state [Fig. 1(b)], if the attraction between the polymer and vesicle is sufficiently weak, the cargo will merely be confined inside the vesicle. For sufficiently strong attractive interaction, the polymer would coat the interior wall of the vesicle. The adsorption criterion delineating these two limits in the interior is obtained by evaluating the conformational entropy of the polyelectrolyte chain under confinement inside an electrostatically interactive vesicle. In addition, due to confinement effects, an optimum radius of the vesicle may arise for coating the polyelectrolyte chain in the interior. The adsorption criteria, density profiles, and optimum vesicle radii are dictated by various experimental variables.

The experimental variables pertinent to the process are the polymer charge number density q, polymer length L, vesicle surface charge number density $\sigma$, vesicle radius R, and the uniform electrolyte concentration c_s. The temperature T and the presumed uniform dielectric constant $𝜖$ of the medium are expressed in terms of the Bjerrum length ${\ell }_B=e^2∕(4\pi {𝜖}_0𝜖k_{B}T)$, where e is the electronic charge, ${𝜖}_0$ is the permittivity of vacuum, and k_B is the Boltzmann constant. The Bjerrum length sets the scale for the strength of the electrostatic interaction energy. The spatial range of the electrostatic interaction is captured roughly by the Debye length ${\kappa }^{-1}$ which is proportional to $1∕{\sqrt{c}}_s$. The adsorption criteria and the density profiles for both the exterior and interior states and the optimum vesicle radii for the interior state are to be calculated in terms of the experimental parameters $q,L,\sigma ,R,{\ell }_B$, and $\kappa$. Calculation of the free energy difference $\mathrm{\Delta }F$ between the exterior and interior states of the polyelectrolyte chain would enable the estimation of energy costs for translocating the chain from the interior state to the exterior state, and their relative thermodynamic stabilities.

Adsorption of a polyelectrolyte chain onto a spherical charged surface from its exterior has attracted considerable effort based on theoretical approaches,^9–27 computer simulations,^28–43 and experiments,^44–49 as nicely described in a recent review.¹² Planar and cylindrical interfaces for the exterior state and confinement of a polyelectrolyte chain inside a spherical cavity have also been investigated, although not as extensively as the exterior state for spherical cavities.^10,12,17 In general, the conclusions deduced from these studies are inconclusive and various theoretical predictions appear to depend on the specifics of the model and the approximations used in the calculations. Since the primary focus of the present paper is in the context of adsorption onto spherical vesicles, we now briefly summarize the current status in this context only.

According to all previous theoretical works,^14–27 starting from the pioneering work of Wiegel,¹³ the adsorption phase transition can be triggered by any of the experimental variables as follows: surface charge number density $\sigma$, vesicle radius R, polymer charge number density q, temperature and dielectric constants in terms of the Bjerrum length ${\ell }_B$, salt concentration in terms of $\kappa$, and the polymer length L. For example, an increase in surface charge number density above a critical value ${\sigma }_c$ would result in adsorption when all other experimentally relevant quantities are held constant. Similarly lowering the temperature or decreasing the salt concentration would lead to adsorption. Almost all experiments reported so far in the literature^44–49 are conducted at a fixed room temperature and the critical condition for adsorption is determined experimentally by relating surface charge density and salt concentration. By considering the adsorption of synthetic polyelectrolytes on micelle, proteins, and dendrimers, the empirically suggested critical condition is^12,44–49

$$\left|{\sigma }_c\right|\sim {\kappa }^a,a\simeq 1-1.4.$$ (1)

On the other hand, various theoretical predictions¹² for the value of the exponent a range from 6/5 to 3 for the experimental conditions pertinent to Eq. (1), namely, $\kappa R>>1$. In the other limit, $\kappa R<<1$, corresponding to the low salt limit, the range of a predicted by theories¹² is from 1 to 3. However, this latter limit is not relevant to experimental situations establishing Eq. (1). Briefly, the models and assumptions behind the previous theoretical approaches are as follows.

The probability distribution function $G(\mathbf{r},{\mathbf{r}}^{\prime };N)$ for a flexible polyelectrolyte chain of contour length $L=N\ell$ with its ends at r and ${\mathbf{r}}^{\prime }$, in the proximity of a charged surface is given by the Edwards path integral,¹⁴

$$\begin{array}{rcl}G(\mathbf{r},{\mathbf{r}}^{\prime };N)& =& {\int }_{\mathbf{r}(0)={\mathbf{r}}^{\prime }}^{\mathbf{r}(N)=\mathbf{r}}D\left[\mathbf{r}(s)\right]exp\left\{\right.-\frac{3}{2{\ell }^2}{\int }_0^{N}ds{(\frac{\partial \mathbf{r}(s)}{\partial s})}^2\\ & & -\frac{1}{k_{B}T}{\int }_0^{N}ds{V}_p\left[\mathbf{r}(s)\right]-\frac{1}{k_{B}T}{\int }_0^N{V}_s\left[\mathbf{r}(s)\right]\left.\right\},\end{array}$$ (2)

where r(s) is the position vector of the arc length variable s ($0\le s\le L$), and $\ell$ is the Kuhn length. V_p denotes various inter-segment interactions of the chain acting on the segment at r(s). V_s is the electrostatic potential from the charged surface acting on the polymer segment at r(s). The symbol $\int D\left[\mathbf{r}(s)\right]$ denotes the functional integration representing the sum over all possible chain configurations subjected to constraints from all intrachain interactions and interaction with the surface. The path integral representation of Eq. (2) can be equivalently written as

$$\begin{array}{rcl}\left[\frac{\partial }{\partial N}-\frac{{\ell }^2}{6}{\nabla }_{\mathbf{r}}^2+\frac{V_p(\mathbf{r})}{k_{B}T}+\frac{V_s(\mathbf{r})}{k_{B}T}\right]G(\mathbf{r},{\mathbf{r}}^{\prime };N)=\delta (\mathbf{r}-{\mathbf{r}}^{\prime })\delta (N).& & \\ & & \end{array}$$ (3)

By drawing an analogy with the time-dependent Schrödinger equation for a particle in a potential, the time-independent version is

$$G(\mathbf{r},{\mathbf{r}}^{\prime };N)=\sum _m{\psi }_m(\mathbf{r}){\psi }_m^{*}({\mathbf{r}}^{\prime })e^{-{\mathrm{\lambda }}_{m}N}$$ (4)

with

$$\left[-\frac{{\ell }^2}{6}{\nabla }_{\mathbf{r}}^2+\frac{V_p(\mathbf{r})}{k_{B}T}+\frac{V_s(\mathbf{r})}{k_{B}T}\right]{\psi }_m(\mathbf{r})={\mathrm{\lambda }}_m{\psi }_m(\mathbf{r}).$$ (5)

For a chosen set of potentials, V_p and V_s, and appropriate boundary conditions, the eigenvalue problem of Eq. (5) is solved for ${\psi }_m(\mathbf{r})$ and ${\mathrm{\lambda }}_m$, from which the probability distribution function $G(\mathbf{r},{\mathbf{r}}^{\prime };N)$ is obtained from Eq. (4). Various experimentally relevant features, such as the adsorption criteria and density profiles of the adsorbed chain, follow from $G(\mathbf{r},{\mathbf{r}}^{\prime };N)$. Based on the quantum analogy with a particle in a potential, the adsorption criterion corresponds to the condition at which at least one bound state is allowed by Eq. (5). If the combined potential (V_p + V_s)/k_BT is attractive and sufficiently strong, the polymer chain would adsorb corresponding to the occurrence of bound states. If the combined potential is weaker than a critical value, then only scattering states are allowed by Eq. (5) representing unadsorbed states of the polymer chain. Once the adsorption criterion is established, the density profile in the adsorbed state is calculated from the eigenfunctions ${\psi }_m$ and eigenvalues ${\mathrm{\lambda }}_m$. Since the contour length of the polymer $L=N\ell$ is usually very large, the leading term in Eq. (4) representing the ground state is often sufficient in the calculation of $G(\mathbf{r},{\mathbf{r}}^{\prime };N)$.

The simplest situation of an infinitely thin and infinitely large planar charged interface somewhere in the middle of an electrolyte solution and an adsorbing Gaussian chain was initially treated by Wiegel.¹³ For a uniform surface charge number density $\sigma$ and linear polymer charge number density q, the electrostatic interaction energy between the surface and a polymer segment at a distance z perpendicular to the interface is

$$\frac{V_s(z)}{k_{B}T}=-2\pi |\sigma q|\frac{\ell {\ell }_B}{\kappa }{e}^{-\kappa z},$$ (6)

based on the linearized Poisson-Boltzmann description. Ignoring the intra-chain interaction, namely, by taking V_p = 0, Wiegel derived the exact adsorption criterion for this idealized model as¹³

$$|{\sigma }_c|=\frac{{\kappa }^3\ell }{48\pi {\ell }_B\left|q\right|}{j}_{\mathrm{0,1}}^2\sim {\kappa }^3,$$ (7)

where $j_{\mathrm{0,1}}\simeq 2.4048$ is the first zero of the Bessel function J₀(x) for $x>0$.

Since isolated flexible polyelectrolyte chains do not obey Gaussian chain statistics (where the radius of gyration $R_g\sim \sqrt{N}$), due to the electrostatic repulsion between segments, Eq. (7) is not relevant to experimental situations. In view of this, one of the present authors¹⁴ addressed the role of V_p in Eqs. (3) and (5). Even in the absence of an adsorbing interface, the chain statistics of an isolated polyelectrolyte chain is not exactly solvable. Using the Debye-Hückel potential for the screened Coulomb interaction among the segments of a flexible chain and a variational procedure, the square of the radius of gyration of the chain was derived as¹⁴

$$R_g^2=\frac{L{\ell }_{eff}}{6},$$ (8)

where ${\ell }_{eff}$ depends on $N,{\ell }_B$, and $\kappa$ and other excluded volume parameters pertinent to short-range interactions. The approximation of uniform expansion was used in deriving the above result. For a Gaussian chain, ${\ell }_{eff}$ is simply the Kuhn length $\ell$. When electrostatic interactions dominate over the short-ranged excluded volume interactions, the limiting behaviors of ${\ell }_{eff}$ for the low salt and high salt limits were derived by Muthukumar as¹⁴

$${\ell }_{eff}\sim \left\{\begin{array}{cc}N\hfill & \kappa R_g<<1\hfill \\ {\ell }_B^{2∕5}{\kappa }^{-4∕5}{N}^{1∕5}\hfill & \kappa R_g>>1\hfill \end{array}.\right.$$ (9)

With this approximation of uniform electrostatic swelling of the chain, Eqs. (2)–(5) yield

$$\left[-\frac{\ell {\ell }_{eff}}{6}{\nabla }_{\mathbf{r}}^2+\frac{V_s(\mathbf{r})}{k_{B}T}\right]{\psi }_m(\mathbf{r})={\mathrm{\lambda }}_m{\psi }_m(\mathbf{r}),$$ (10)

where the effective Kuhn length ${\ell }_{eff}$ absorbs V_p/k_BT. As a result, the adsorption criterion for the potential in Eq. (6) becomes¹⁴

$$|{\sigma }_c|=\frac{{\kappa }^3{\ell }_{eff}}{48\pi {\ell }_B|q|}{j}_{\mathrm{0,1}}^2.$$ (11)

Combining Eqs. (9) and (11),

$$|{\sigma }_c|\sim \left\{\begin{array}{cc}{\kappa }^3\hfill & \kappa R_g<<1\hfill \\ {\kappa }^{11∕5}\hfill & \kappa R_g>>1\hfill \end{array}.\right.$$ (12)

This prediction at higher salt concentrations ($\kappa R_g>>1$) is consistent with experimental results for planar interfaces.⁹

The adsorption of a flexible polyelectrolyte chain onto a spherical vesicle of radius R, with the electrolyte concentration being the same both inside and outside, was originally addressed by von Goeler and Muthukumar,¹⁵ and the analog of Eq. (5) for this situation is

$$\left[-\frac{{\ell }^2}{6}\frac{1}{r^2}\frac{d}{dr}(r^2\frac{d}{dr})+\frac{V_p(\mathbf{r})}{k_{B}T}+\frac{V_s(\mathbf{r})}{k_{B}T}\right]{\psi }_m(\mathbf{r})={\mathrm{\lambda }}_m{\psi }_m(\mathbf{r}),$$ (13)

where radial symmetry is used and

$$\frac{V_s(r)}{k_{B}T}=-4\pi |\sigma q|\ell {\ell }_{B}Rsinh(\kappa R)\frac{e^{-\kappa r}}{\kappa r},r>R.$$ (14)

By absorbing the effect of intra-chain electrostatic interaction into the renormalized effective Kuhn length as ${\ell }_{eff}$, Eq. (13) becomes

$$\left[-\frac{\ell {\ell }_{eff}}{6}\frac{1}{r^2}\frac{d}{dr}(r^2\frac{d}{dr})+\frac{V_s(\mathbf{r})}{k_{B}T}\right]{\psi }_m(\mathbf{r})={\mathrm{\lambda }}_m{\psi }_m(\mathbf{r}),$$ (15)

where V_s(r) is given by Eq. (14). Using a variational procedure on Eq. (15), von Goeler and Muthukumar derived the adsorption criterion as¹⁵

$$|{\sigma }_c|=\frac{{\kappa }^3{\ell }_{eff}}{12\pi {\ell }_B|q|}\frac{1}{(1-e^{-2\kappa R})}.$$ (16)

The limits of the dependence of critical surface charge density on the salt concentration follows from Eqs. (12) and (16) as

$$|{\sigma }_c|\sim \left\{\begin{array}{cc}{\kappa }^2,\hfill & \kappa R<<1\text{and}\kappa R_g<<1\hfill \\ {\kappa }^{6∕5},\hfill & \kappa R<<1\text{and}\kappa R_g>>1\hfill \\ {\kappa }^{11∕5},\hfill & \kappa R>>1\text{and}\kappa R_g>>1\hfill \\ {\kappa }^3,\hfill & \kappa R>>1\text{and}\kappa R_g<<1\hfill \end{array}.\right.$$ (17)

The critical condition $|{\sigma }_c|\sim {\kappa }^{6∕5}$ is consistent with the experimental results summarized in Eq. (1) for the adsorption of synthetic polyelectrolytes on micelles.^12,44–49 Also, in general, if $R>>R_g$, then the limit of planar surface with ${\sigma }_c\sim {\kappa }^3{\ell }_{eff}$ is recovered.

The above potential V_s(r) in Eq. (14) is pertinent to the situation of vesicles where the dielectric constant and salt concentration are the same in both the interior and exterior regions. In the limit of vesicle radius $R\to \infty$, Eq. (14) reduces to the result of Eq. (6) for planar interfaces. On the other hand, if we were to consider a colloidal situation of adsorption of a polyelectrolyte chain to a spherical solid with no salt inside the sphere, then the potential is given by the Debye-Hückel theory as

$$\frac{V_s(r)}{k_{B}T}=\frac{V_{DH}(r)}{k_{B}T}=-4\pi |\sigma q|\ell {\ell }_B{R}^2\frac{e^{-\kappa (r-R)}}{(1+\kappa R)r},r>R.$$ (18)

For this potential, it must be noted that the corresponding planar limit ($R\to \infty$) is twice the result given in Eq. (6). Since the difference between V_s(r) in Eq. (14) and the Debye-Hückel potential is merely in the prefactor (not dependent on r), the variational result of von Goeler and Muthukumar gives the critical condition for the Debye-Hückel surface potential as

$$|{\sigma }_c|=\frac{{\kappa }^2{\ell }_{eff}(1+\kappa R)}{24\pi {\ell }_B|q|R},$$ (19)

and with the use of Eq. (9), we get

$$|{\sigma }_c|\sim \left\{\begin{array}{cc}{\kappa }^2,\hfill & \kappa R<<1\text{and}\kappa R_g<<1\hfill \\ {\kappa }^{6∕5},\hfill & \kappa R<<1\text{and}\kappa R_g>>1\hfill \\ {\kappa }^{11∕5},\hfill & \kappa R>>1\text{and}\kappa R_g>>1\hfill \\ {\kappa }^3,\hfill & \kappa R>>1\text{and}\kappa R_g<<1\hfill \end{array}.\right.$$ (20)

Again, the prediction $|{\sigma }_c|\sim {\kappa }^{6∕5}$ for salt concentrations pertinent to experimental conditions on adsorption onto solid-like spheres is also consistent with the experimental findings given in Eq. (1).^12,44–49 These conclusions are also in qualitative agreement with simulation results.^28–43 Therefore, the major conclusions for the dependence of ${\sigma }_c$ on $\kappa$ are insensitive to whether V_s(r) in Eq. (14) or V_DH in Eq. (18) is used in the variational procedure.

The solution of Eq. (13) with V_p = 0 and V_s = V_DH has been extensively investigated by Cherstvy and Winkler in a series of publications^12,25–27 using the non-variational procedure of the Wentzel-Kramers-Brillouin (WKB) approximation in quantum mechanics.⁵⁰ In addition, they exactly solved Eq. (13)^22–24 by taking V_p = 0 and V_s as the Hulthén potential which is an approximation for the Debye-Hückel potential. Based on these analyses, the authors derived the critical condition for adsorption as

$$|{\sigma }_c|\sim \left\{\begin{array}{cc}\kappa \hfill & \kappa R<<1\hfill \\ {\kappa }^3\hfill & \kappa R>>1\hfill \end{array}.\right.$$ (21)

As described above, the intra-chain electrostatic interaction energy V_p must be taken into account for the dependence of ${\sigma }_c$ on $\kappa$. By simply adopting the procedure of Muthukumar, the above equation becomes

$$|{\sigma }_c|\sim \left\{\begin{array}{cc}\kappa \hfill & \kappa R<<1\hfill \\ {\kappa }^{11∕5}\hfill & \kappa R>>1\hfill \end{array}.\right.$$ (22)

The high salt limit is the same as that in the variational theory of von Goeler and Muthukumar. However, there is a discrepancy between the variational theory and the WKB method for the low salt concentration limit. Although the WKB method was used for V_DH and not for V_s in Eq. (14), we do not expect any change in the scaling laws of Eq. (22) for V_s using the WKB method. As discussed below, the variational result is only a bound and the low salt limit requires careful numerical analysis in resolving this discrepancy. However, in the experimentally relevant regime of high salt, both the variational calculation and the numerical WKB methods lead to the same scaling law between ${\sigma }_c$ and $\kappa$.

For the interior state, where a polyelectrolyte chain adsorbs to the interior surface of the vesicle, the attractive electrostatic potential V_s(r) between the polyelectrolyte and the surface is given by

$$\frac{V_s(r)}{k_{B}T}=-4\pi |\sigma q|\ell {\ell }_{B}R\frac{e^{-\kappa R}sinh(\kappa r)}{\kappa r},r<R.$$ (23)

In obtaining this potential, the salt concentration and the dielectric constant are taken to be the same both inside and outside the vesicle. Combined Eqs. (15) and (23) were solved by Wang and Muthukumar¹⁶ using a variational method, and the authors identified two regimes of polyelectrolyte encapsulation and preferred radii of vesicles for encapsulation. When V_s is weak, the encapsulation is entropy-dominated and the chain is delocalized inside the vesicle. In this regime, the optimum radius of the encapsulating vesicle decreases with increasing strength of V_s. When V_s is strong, the encapsulation is adsorption-dominated and the polyelectrolyte is localized near the interface. In this regime, the optimum radius of the encapsulating vesicle increases with an increase in the strength of V_s. There are no other theoretical calculations for the interior state addressed here, although there have been some interesting works on virus-like particles.^3–8 Since the validity of the variational procedure is questionable for low salt concentrations, we address here the interior state with the WKB approximation and compare with our previous variational results. Accurate calculation of the free energies of the exterior and interior states of the adsorbed polyelectrolyte chain allows an understanding of the relative stabilities of these two states in terms of various parameters $\sigma ,q,{\ell }_B,N,R$, and $\kappa$.

The outline of the rest of the paper is as follows. Section II describes the model and the theoretical method based on the WKB approximation. In Sec. III, our main results on the exterior state, the interior state, and the exchange between these states are discussed. The main conclusions are summarized in Sec. IV.

II. MODEL AND THEORETICAL METHOD

A. Polyelectrolyte chain and interacting vesicle

The vesicle is taken as a thin spherical shell of uniform charge density $\sigma e$, with both the interior and exterior regions containing the same salt concentration and hence the same Debye length ${\kappa }^{-1}$. The radius of the vesicle is R. The adsorbing polyelectrolyte chain is taken to be flexible, described by the Edwards path integral representation, as given by Eq. (2), for the probability distribution function $G(\mathbf{r},{\mathbf{r}}^{\prime };N)$. By integrating out the degrees of freedom of all dissociated small ions and solvent molecules in the system, V_p[r(s)] in Eq. (2) due to the intra-chain inter-segment interactions is given by¹⁴

$$\begin{array}{rcl}\frac{V_p[\mathbf{r}(s)]}{k_{B}T}& =& \frac{{\ell }^3}{2}{\int }_0^{N}d{s}^{\prime }(\frac{1}{2}-\chi )\delta [\mathbf{r}(s)-\mathbf{r}(s^{\prime })]\\ & & +\frac{q^2{\ell }_B{\ell }^2}{2}{\int }_0^{N}d{s}^{\prime }\frac{e^{-\kappa |\mathbf{r}(s)-\mathbf{r}(s^{\prime })|}}{|\mathbf{r}(s)-\mathbf{r}(s^{\prime })|},\end{array}$$ (24)

where the Debye-Hückel theory is assumed to be valid for the dissociated ions. Here q is the uniform linear charge number density along the backbone of the chain. If there are z_p effective charged groups per Kuhn length, then $q=z_p∕\ell$. The first term in the right hand side of Eq. (24) represents the usual short-ranged excluded volume interaction, with $\chi$ being the Flory-Huggins parameter. The potential energy arising from the attractive interaction between the interface and a segment of the polyelectrolyte chain is

$$\frac{V_s(r)}{k_{B}T}=\left\{\begin{array}{cc}-{\tilde{V}}_0\frac{R}{r}{e}^{-\kappa (r-R)},\hfill & r>R\hfill \\ -{\tilde{V}}_0\frac{R}{r}\frac{sinh(\kappa r)}{sinh(\kappa R)},\hfill & r<R\hfill \end{array},\right.$$ (25)

where

$${\tilde{V}}_0=2\pi |\sigma q|\frac{\ell {\ell }_B}{\kappa }(1-e^{-2\kappa R}).$$ (26)

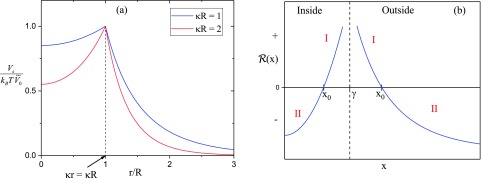
As already pointed out, Eqs. (25) and (26) are valid for uniform salt concentration both inside and outside the vesicle and within the Debye-Hückel theory. It is to be noted that V_s(r) in Eq. (25) is continuous at the vesicle interface (r = R), unlike that in Eq. (18), and a plot of V_s(r) against r/R is given in Fig. 2(a) for $\kappa R=1$ and 2, as typical examples, in units of ${\tilde{V}}_0$.

FIG. 2.

(a) Reduced potential as a function of the vesicle radius R. (b) Sketch of $\mathcal{R}$, given by Eq. (35), as a function of radius for both inside and outside of the vesicle. I and II refer to $\mathcal{R}>0$ and $\mathcal{R}<0$, respectively, to be distinguished in the WKB method.

As in the original approximate treatment of the intra-chain excluded volume and electrostatic interaction by Muthukumar with a variational procedure, we take these interactions in terms of only a renormalized effective Kuhn length ${\ell }_{eff}$ given by¹⁴

$$\begin{array}{rcl}& & {(\frac{{\ell }_{eff}}{\ell })}^{5∕2}-{(\frac{{\ell }_{eff}}{\ell })}^{3∕2}\\ & & =\frac{4}{3}{(\frac{3}{2\pi })}^{3∕2}(\frac{1}{2}-\chi )\sqrt{N}+\frac{2\sqrt{6}}{3}{z}_p^2\frac{{\ell }_B}{\ell }\frac{{\ell }_{eff}}{\ell }\frac{N^{3∕2}}{a^{5∕2}}\\ & & \times \left[(a^2-4a+6)e^{a}erfc(\sqrt{a})-6-2a+\frac{12\sqrt{a}}{\sqrt{\pi }}\right],\end{array}$$ (27)

where

$$a\equiv {\kappa }^2{R}_g^{2}with{R}_g^2=\frac{N\ell {\ell }_{eff}}{6}.$$ (28)

As already noted, the limiting values of ${\ell }_{eff}$ for the low-salt and high-salt limits are¹⁴

$${\ell }_{eff}=\left\{\begin{array}{cc}\frac{2}{3}{(\frac{2}{5})}^{2∕3}\frac{1}{{\pi }^{1∕3}}{(z_p^2\frac{{\ell }_B}{\ell })}^{2∕3}N\ell ,\hfill & \kappa R_g<<1\hfill \\ \frac{6^{1∕5}}{{\pi }^{3∕5}}{\left[(\frac{1}{2}-\chi )+\frac{4\pi z_p^2{\ell }_B}{{\kappa }^2{\ell }^3}\right]}^{2∕5}{N}^{1∕5}\ell ,\hfill & \kappa R_g>>1\hfill \end{array}.\right.$$ (29)

When electrostatic interactions dominate over the short-range excluded volume interaction, the above equation reduces to Eq. (9). In the numerical calculations presented in Sec. III, the full crossover formula, Eq. (27), is used.

Using the effective Kuhn length to account for the intra-chain interaction, Eq. (15) can be rewritten as

$$\left[-\frac{\ell {\ell }_{eff}}{6}\frac{1}{x^2}\frac{d}{dx}(x^2\frac{d}{dx})+\frac{V_s(x)}{k_{B}T{\kappa }^2}\right]{\psi }_m(x)=\frac{{\mathrm{\lambda }}_m}{{\kappa }^2}{\psi }_m(x),$$ (30)

where $x=\kappa r$. With the change of variable, ${\psi }_m=\varphi ∕x$, we get

$$\frac{d^2\varphi (x)}{d{x}^2}-\frac{6}{\ell {\ell }_{eff}}\frac{V_s(x)}{k_{B}T{\kappa }^2}\varphi (x)=\mu \varphi (x),$$ (31)

where

$$\mu =-\frac{6{\mathrm{\lambda }}_m}{\ell {\ell }_{eff}{\kappa }^2}\equiv -\mathrm{\lambda }.$$ (32)

Therefore, in general for both inside and outside the vesicle,

$$\frac{d^2\varphi (x)}{d{x}^2}+\mathcal{R}(x)\varphi (x)=0,$$ (33)

where

$$\mathcal{R}(x)=-\frac{6}{\ell {\ell }_{eff}}\frac{V_s(x)}{k_{B}T{\kappa }^2}-\mu .$$ (34)

Combining Eqs. (25) and (34),

$$\mathcal{R}(x)=\left\{\begin{array}{cc}B\gamma sinh(\gamma )\frac{e^{-x}}{x}-\mu ,\hfill & x>\gamma \hfill \\ B\gamma e^{-\gamma }\frac{sinh(x)}{x}-\mu ,\hfill & x<\gamma \hfill \end{array},\right.$$ (35)

where $\gamma =\kappa R$ and

$$B=\frac{24\pi \left|\sigma q\right|}{{\kappa }^3}\frac{{\ell }_B}{{\ell }_{eff}}.$$ (36)

Our objective is to solve Eq. (33) for $\varphi (x)$ and get $\psi =\varphi ∕x$ and then $G(\mathit{r},{\mathit{r}}^{\prime };N)$ from Eq. (4), from which the adsorption criteria and density profiles are to be computed.

B. WKB procedure

We solve Eq. (33) using the WKB method.⁵⁰ In view of the spatial dependence of V_s(r) given in Fig. 2(a), a sketch of $\mathcal{R}$ is given in Fig. 2(b) for both inside and outside of the vesicle. For interesting values of $\mu$ given by Eq. (32) enabling possibilities of bound states, $\mathcal{R}$ has a simple root [$\mathcal{R}\sim (x-x_0)$] at the turning point x₀, as sketched in Fig. 2(b). For each of the inside and outside regions of the vesicle, there are two scenarios: region I with $\mathcal{R}>0$ and region II with $\mathcal{R}<0$.

In region I ($\mathcal{R}>0$), the WKB solution is⁵⁰

$${\varphi }_1(x)=\frac{{\xi }_1^{1∕6}}{\sqrt{k_1}}\left[{\alpha }_{1}Ai(-z_1)+{\beta }_{1}Bi(-z_1)\right],\mathcal{R}>0,$$ (37)

where

$$k_1^2=\mathcal{R},k_1>0,$$ (38)

$$z_1={(\frac{3}{2}{\xi }_1)}^{2∕3},$$ (39)

$${\xi }_1=\left\{\begin{array}{cc}{\int }_{x_0}^{x}d{x}^{\prime }{k}_1(x^{\prime }),\hfill & x<\gamma \hfill \\ {\int }_x^{x_0}d{x}^{\prime }{k}_1(x^{\prime }),\hfill & x>\gamma \hfill \end{array},\right.$$ (40)

and Ai and Bi are the Airy functions of first kind and second kind, respectively.⁵¹ ${\alpha }_1$ and ${\beta }_1$ are coefficients to be determined by using boundary conditions.

Analogously in region II ($\mathcal{R}<0$), the WKB solution is⁵⁰

$${\varphi }_2(x)=\frac{{\xi }_2^{1∕6}}{\sqrt{k_2}}\left[{\alpha }_{2}Ai(z_2)+{\beta }_{2}Bi(z_2)\right],\mathcal{R}<0,$$ (41)

where

$$k_2^2=-\mathcal{R},k_2>0,$$ (42)

$$z_2={(\frac{3}{2}{\xi }_2)}^{2∕3},$$ (43)

$${\xi }_2=\left\{\begin{array}{cc}{\int }_x^{x_0}d{x}^{\prime }{k}_2(x^{\prime }),\hfill & x<\mathrm{\gamma }\hfill \\ {\int }_{x_0}^{x}d{x}^{\prime }{k}_2(x^{\prime }),\hfill & x>\mathrm{\gamma }\hfill \end{array},\right.$$ (44)

and ${\alpha }_2$ and ${\beta }_2$ are coefficients to be determined using the boundary conditions. The unknowns are the coefficients ${\alpha }_1,{\beta }_1,{\alpha }_2$, and ${\beta }_2$, and the turning point x₀. These are determined for the exterior and interior states as follows.

C. Exterior state

For this situation, we follow the same steps as those taken by Cherstvy and Winkler^12,25–27 and so only a brief derivation is given here. In this case,

$$\mathcal{R}(x)=B\gamma sinh(\gamma )\frac{e^{-x}}{x}-\mu .$$ (45)

Since $\mathcal{R}(x_0)=0$ at the turning point, $\mu$ is

$$\mu =B\gamma sinh(\gamma )\frac{e^{-x_0}}{x_0},$$ (46)

so that

$$\mathcal{R}(x)=B\gamma sinh(\gamma )(\frac{e^{-x}}{x}-\frac{e^{-x_0}}{x_0}).$$ (47)

As Bi(z) is an increasing function of z diverging at $z\to \infty$, ${\beta }_2$ in Eq. (41) must be zero. At the turning point x₀, ${\varphi }_1(x_0)={\varphi }_2(x_0)$ and ${\varphi }_1^{\prime }(x_0)={\varphi }_2^{\prime }(x_0)$, resulting in

$$\begin{array}{cc}& {\alpha }_{1}Ai(0)+{\beta }_{1}Bi(0)={\alpha }_{2}Ai(0)\hfill \\ \hfill and& \\ & -{\alpha }_{1}Ai(0)+{\beta }_{1}Bi(0)=-{\alpha }_{2}Ai(0).\hfill \end{array}$$ (48)

Therefore ${\beta }_1=0$ and ${\alpha }_1={\alpha }_2$. As a result,

$${\varphi }_1(x)=\frac{{\xi }_1^{1∕6}}{\sqrt{k_1}}{\alpha }_{1}Ai(-z_1),x<x_0$$ (49)

and

$${\varphi }_2(x)=\frac{{\xi }_2^{1∕6}}{\sqrt{k_2}}{\alpha }_{1}Ai(z_2),x>x_0.$$ (50)

The only unknown coefficient ${\alpha }_1$ is absorbed into the normalization of the eigenfunction and hence into the density profile. The remaining unknown x₀ is determined from the boundary condition

$${\varphi }_1(x=\gamma )=0.$$ (51)

Therefore, it follows from Eqs. (39), (40), and (49) that

$$Ai(-z_{1\gamma })=0,$$ (52)

where

$$z_{1\gamma }={(\frac{3}{2}{\xi }_{1\gamma })}^{2∕3},{\xi }_{1\gamma }={\int }_{\gamma }^{x_0}d{x}^{\prime }{k}_1(x^{\prime }).$$ (53)

Denoting the first zero of $Ai(-z_{1\gamma })$ as −ai₁ ($a{i}_1\simeq 2.33811$), we get

$${\int }_{\gamma }^{x_0}d{x}^{\prime }\sqrt{\mathcal{R}}=\frac{2}{3}{(a{i}_1)}^{3∕2}.$$ (54)

Substitution of Eq. (47) for $\mathcal{R}$ in Eq. (54) yields the desired expression for x₀ as

$$\sqrt{B\gamma sinh(\gamma )}{\int }_{\gamma }^{x_0}d{x}^{\prime }{(\frac{e^{-x}}{x}-\frac{e^{-x_0}}{x_0})}^{1∕2}=\frac{2}{3}{(a{i}_1)}^{3∕2}.$$ (55)

This equation is solved numerically and ${\varphi }_1$ and ${\varphi }_2$ are computed subsequently. The density profile $\mathcal{P}(x)=x^2{\psi }^2(x)={\varphi }^2(x)$ is then constructed with the normalization condition

$$4\pi {\int }_{\gamma }^{\infty }dx\mathcal{P}(x)=4\pi {\int }_{\gamma }^{\infty }dx{x}^2{\psi }^2(x)=4\pi {\int }_{\gamma }^{\infty }dx{\varphi }^2(x)=1.$$ (56)

The condition for polyelectrolyte adsorption on the exterior surface of the vesicle corresponds to $\mu =0$, that is, $x_0\to \infty$, according to Eq. (46). Therefore, it follows from Eq. (55) that the critical condition in terms of B_c for a given $\gamma$ is

$$\sqrt{B_c\gamma sinh(\gamma )}{\int }_{\gamma }^{\infty }\frac{d{x}^{\prime }}{\sqrt{x^{\prime }}}{e}^{-x^{\prime }∕2}=\frac{2}{3}{(a{i}_1)}^{3∕2},$$ (57)

so that

$$B_c={(\frac{2}{3})}^2\frac{{(a{i}_1)}^3}{2\pi {\left[erfc(\sqrt{\frac{\gamma }{2}})\right]}^2}\frac{1}{\gamma sinh(\gamma )}.$$ (58)

Substituting Eq. (36) for B, the critical surface charge density for adsorption is

$$|{\sigma }_c|=\frac{{(a{i}_1)}^3}{108{\pi }^2}\frac{{\kappa }^3{\ell }_{eff}}{{\ell }_B\left|q\right|}\frac{1}{\gamma sinh(\gamma )}\frac{1}{{\left[erfc(\sqrt{\frac{\gamma }{2}})\right]}^2}.$$ (59)

The numerically computed results on the density profile and adsorption criteria are discussed in Sec. III.

D. Interior state

The previous analysis of this situation was performed using only variational methods.^16,17 Here, we use the WKB method. For this situation,

$$\mathcal{R}(x)=B\gamma e^{-\gamma }\frac{sinh(x)}{x}-\mu .$$ (60)

Defining the turning point x₀ in terms of $\mu$,

$$\mu \equiv B\gamma e^{-\gamma }\frac{sinh(x_0)}{x_0},$$ (61)

we have

$$\mathcal{R}(x)=B\gamma e^{-\gamma }(\frac{sinh(x)}{x}-\frac{sinh(x_0)}{x_0}).$$ (62)

Therefore, we get from Eqs. (37)–(40) and (62) valid for region I ($\mathcal{R}>0$)

$${\varphi }_1(x)=\frac{{\xi }_1^{1∕6}}{\sqrt{k_1}}{\alpha }_1\left[Ai(-z_1)+(\frac{{\beta }_1}{{\alpha }_1})Bi(-z_1)\right],\mathcal{R}>0,$$ (63)

where

$$\begin{array}{c}\hfill z_1={(\frac{3}{2}{\xi }_1)}^{2∕3},\hfill \\ \hfill {\xi }_1={\int }_{x_0}^{x}d{x}^{\prime }{(B\gamma e^{-\gamma })}^{1∕2}{\left[\frac{sinh(x)}{x}-\frac{sinh(x_0)}{x_0}\right]}^{1∕2}.\hfill \end{array}$$ (64)

For region II ($\mathcal{R}<0$), we get from Eqs. (41)–(44) and (62),

$${\varphi }_2(x)=\frac{{\xi }_2^{1∕6}}{\sqrt{k_2}}{\alpha }_2\left[Ai(z_2)+(\frac{{\beta }_2}{{\alpha }_2})Bi(z_2)\right],\mathcal{R}<0,$$ (65)

where

$$\begin{array}{c}\hfill z_2={(\frac{3}{2}{\xi }_2)}^{2∕3},\hfill \\ \hfill {\xi }_2={\int }_x^{x_0}d{x}^{\prime }{(B\gamma e^{-\gamma })}^{1∕2}{\left[\frac{sinh(x_0)}{x_0}-\frac{sinh(x)}{x}\right]}^{1∕2}.\hfill \end{array}$$ (66)

The objective is to determine the coefficients ${\alpha }_1,{\beta }_1,{\alpha }_2$, and ${\beta }_2$, and the turning point x₀ appearing in Eqs. (63) and (65) for $\mathcal{R}$ in Eq. (62). This is performed by imposing continuity of $\varphi$ and its slope at the turning point x₀,

$${\varphi }_1(x=x_0)={\varphi }_2(x=x_0),$$ (67)

$${\varphi }_1^{\prime }{|}_{x\to x_0}={\varphi }_2^{\prime }{|}_{x\to x_0},$$ (68)

and from the boundary conditions,

$$\varphi (\gamma )=0,\frac{d{\varphi }_2(x)}{dx}{|}_{x\to 0}=0,$$ (69)

and the normalization condition for the density profile,

$$4\pi {\int }_0^{\gamma }dx{\varphi }^2(x)=1.$$ (70)

Now, ${\varphi }_1(x_0)$ is given by Eq. (63) as

$${\varphi }_1(x_0)=C_{1}Ai(0)({\alpha }_1+\sqrt{3}{\beta }_1),$$ (71)

where we have used $Bi(0)=\sqrt{3}Ai(0)$ and

$$C_1=\underset{x\to x_0}{lim}\frac{{\xi }_1^{1∕6}}{\sqrt{k_1}}={(\frac{2}{3})}^{1∕6}{(\frac{1}{{\mathcal{R}}^{\prime }{|}_{x_0}})}^{1∕6}.$$ (72)

Similarly ${\varphi }_2(x_0)$ follows from Eq. (65) as

$${\varphi }_2(x_0)=C_{2}Ai(0)({\alpha }_2+\sqrt{3}{\beta }_2),$$ (73)

where

$$C_2=\underset{x\to x_0}{lim}\frac{{\xi }_2^{1∕6}}{\sqrt{k_2}}={(\frac{2}{3})}^{1∕6}{(\frac{1}{{\mathcal{R}}^{\prime }{|}_{x_0}})}^{1∕6}=C_1.$$ (74)

Therefore, the continuity condition ${\varphi }_1(x_0)={\varphi }_2(x_0)$ yields from Eqs. (71) and (73)

$${\alpha }_1-{\alpha }_2+\sqrt{3}({\beta }_1-{\beta }_2)=0.$$ (75)

The derivative ${\varphi }_1^{\prime }(x)$ from Eq. (63) is

$$\begin{array}{rcl}{\varphi }_1^{\prime }(x)& =& \left\{\right.\frac{1}{6}\frac{{\xi }_1^{\prime }}{{\xi }_1}-\frac{1}{2}\frac{k_1^{\prime }}{k_1}\\ & & -\frac{\left[{\alpha }_{1}A{i}^{\prime }(-z_1)+{\beta }_{1}B{i}^{\prime }(-z_1)\right]}{\left[{\alpha }_{2}Ai(-z_1)+{\beta }_{1}Bi(-z_1)\right]}\frac{{\xi }_1^{\prime }}{{(\frac{3}{2}{\xi }_1)}^{1∕3}}\left.\right\}{\varphi }_1(x),\end{array}$$ (76)

where the prime denotes the derivative d/dx. Taking the limit $x\to x_0$ and noting

$$\underset{x\to x_0}{lim}(\frac{1}{6}\frac{{\xi }_1^{\prime }}{{\xi }_1}-\frac{1}{2}\frac{k_1^{\prime }}{k_1})=-\frac{1}{6}\frac{{\mathcal{R}}^{\prime }}{\mathcal{R}}{|}_{x\to x_0}\equiv C_3,$$ (77)

we get from Eqs. (40), (63), (74), and (77)

$${\varphi }_1^{\prime }(x=x_0)=C_3{\varphi }_1(x_0)-\frac{(-{\alpha }_1+\sqrt{3}{\beta }_1)}{3^{1∕3}\mathrm{\Gamma }(1∕3)}{(\frac{2}{3})}^{1∕3}\frac{1}{C_1},$$ (78)

where the values of the Airy functions for zero argument have been used. $\mathrm{\Gamma }(1∕3)$ is the gamma function, $\mathrm{\Gamma }(1∕3)\simeq 2.6789$. By following the same procedure for ${\varphi }_2(x)$ in Eq. (65),

$$\begin{array}{rcl}{\varphi }_2^{\prime }(x)& =& \left\{\right.\frac{1}{6}\frac{{\xi }_2^{\prime }}{{\xi }_2}-\frac{1}{2}\frac{k_2^{\prime }}{k_2}\\ & & +\frac{\left[{\alpha }_{2}A{i}^{\prime }(z_2)+{\beta }_{2}B{i}^{\prime }(z_2)\right]}{\left[{\alpha }_{2}Ai(z_2)+{\beta }_{2}Bi(z_2)\right]}\frac{{\xi }_2^{\prime }}{{(\frac{3}{2}{\xi }_2)}^{1∕3}}\left.\right\}{\varphi }_2(x).\end{array}$$ (79)

At the turning point x = x₀,

$${\varphi }_2^{\prime }(x=x_0)=C_3{\varphi }_2(x_0)-\frac{(-{\alpha }_2+\sqrt{3}{\beta }_2)}{3^{1∕3}\mathrm{\Gamma }(1∕3)}{(\frac{2}{3})}^{1∕3}\frac{1}{C_1}.$$ (80)

The continuity conditions ${\varphi }_1^{\prime }(x=x_0)={\varphi }_2^{\prime }(x=x_0)$ and ${\varphi }_1(x=x_0)={\varphi }_2(x=x_0)$ yield from Eqs. (78) and (80)

$$-{\alpha }_1+\sqrt{3}{\beta }_1=-{\alpha }_2+\sqrt{3}{\beta }_2.$$ (81)

Combining Eqs. (75) and (81), we get

$${\alpha }_1={\alpha }_2=\alpha and{\beta }_1={\beta }_2=\beta .$$ (82)

Using the boundary condition ${\varphi }_1(\gamma )=0$, Eqs. (63) and (64) give

$$\frac{\beta }{\alpha }=-\frac{Ai\left[-{(\frac{3}{2}{\xi }_1(x=\gamma ))}^{2∕3}\right]}{Bi\left[-{(\frac{3}{2}{\xi }_1(x=\gamma ))}^{2∕3}\right]},$$ (83)

as a function of x₀. From the other boundary condition, ${(d{\varphi }_2(x)∕dx)}_{x\to 0}=0$, Eq. (79) yields

$$\frac{1}{6}{(\frac{3}{2})}^{1∕3}{\xi }_2^{-2∕3}(x\to 0)=-\frac{\left[A{i}^{\prime }(z_{20})+\frac{\beta }{\alpha }B{i}^{\prime }(z_{20})\right]}{\left[Ai(z_{20})+\frac{\beta }{\alpha }Bi(z_{20})\right]},$$ (84)

where

$$\begin{array}{c}\hfill z_{20}={(\frac{3}{2}{\xi }_{20})}^{2∕3},\hfill \\ \hfill {\xi }_{20}={(B\gamma e^{-\gamma })}^{1∕2}{\int }_0^{x_0}d{x}^{\prime }{\left[\frac{sinh(x_0)}{x_0}-\frac{sinh(x^{\prime })}{x^{\prime }}\right]}^{1∕2}.\hfill \end{array}$$ (85)

Combining Eqs. (63), (65), (83), and (85), the eigenfunction $\varphi$ is computed numerically and the density profiles are constructed.

The critical condition for adsorption inside the vesicle is given by the minimum value B_c of the quantity $B=24\pi {\ell }_B\left|\sigma q\right|∕{\kappa }^3{\ell }_{eff}$ above which there are solutions to Eqs. (63) and (65). In general, for $B>B_c$, there can be more than one solution satisfying the boundary conditions. However, only one of these solutions satisfies the physical result of the density profile being non-zero everywhere inside the vesicle. For $B<B_c$, there are no solutions to Eqs. (63) and (65). The methodology of computing B_c is as follows. The critical adsorption condition for the polymer inside the sphere is defined as the minimum value of B for a given $\gamma$ at which the turning point, x₀, is at the center of the sphere. Although this does not define the condition $\mu =0$, it gives a minimal value for it. To get this critical value, B_c, we use the two boundary conditions for the density profile. Adsorbing boundary conditions of the surface, $\varphi (\gamma )=0$, gives us the value of one of the coefficients, namely, $\beta$. Since the density profile should be smooth at x = 0, we take $\varphi (0)=0$. This condition is satisfied only when B is some discrete value for a given $\gamma$. The minimum and positive value of B is the critical condition.

III. RESULTS AND DISCUSSION

Using the equations derived above, we have computed the density profiles and adsorption criteria for the exterior and interior states. One of the key quantities which appear in these equations is the effective Kuhn length representing the electrostatic swelling of the chain due to intra-chain interactions. This is presented first. Next, the density profiles and adsorption criteria are discussed. Finally the free energy of the system and the relative stabilities of the exterior and interior states are discussed.

A. Electrostatic swelling of an isolated chain

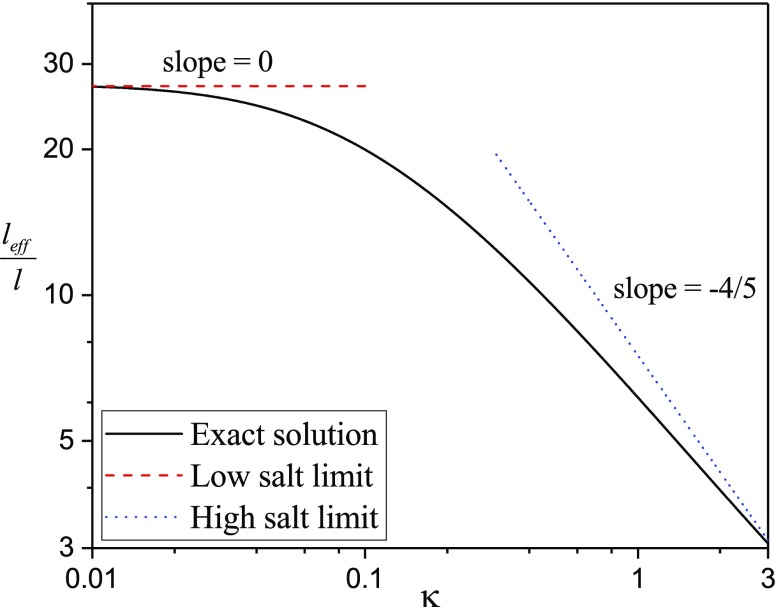
As shown in Eqs. (27)–(29), ${\ell }_{eff}$ depends on $\chi ,{\ell }_B,\kappa ,q=z_p∕\ell$, and N. The full crossover behavior is given in Fig. 3, where ${\ell }_{eff}$ is plotted against $\kappa \ell$ for $N=100,\chi =0.5$, and z_p = 1. All lengths are in units of the bare Kuhn length $\ell$. The dashed and dotted lines correspond to the limiting behaviors for low salt (red) ($\kappa R_g<<1$) and high salt (blue) ($\kappa R_g>>1$), respectively, given by Eq. (29). While the asymptotic results are used in drawing qualitative conclusions, the full crossover is used in all numerical results discussed below.

FIG. 3.

Dependence of the effective Kuhn length ${\ell }_{eff}$ on $\kappa$, for N = 100 and $w_c=0.4$. The black curve is the exact result from Eq. (27); red dashed line and blue dotted line denote the low salt and high salt limits, respectively.

B. Density profiles

The density profile $P(x)={\varphi }^2(x)$ for the exterior state is given by Eqs. (49), (50), and (56) as

$$P(x)=\mathcal{N}\left\{\begin{array}{cc}\frac{{\xi }_1^{1∕3}(x)}{\sqrt{\mathcal{R}}}{Ai}^2(-{(3{\xi }_1∕2)}^{2∕3}),\hfill & x<x_0\hfill \\ \frac{{\xi }_2^{1∕3}(x)}{\sqrt{-\mathcal{R}}}{Ai}^2({(3{\xi }_2∕2)}^{2∕3}),\hfill & x<x_0\hfill \end{array}\right.$$ (86)

with $\mathcal{R}$ given by Eq. (35). The normalization constant $\mathcal{N}$ is determined from the normalization condition of Eq. (56). Defining the radial distance X away from the surface of the vesicle,

$$\kappa X=x-\gamma =\kappa (r-R),$$ (87)

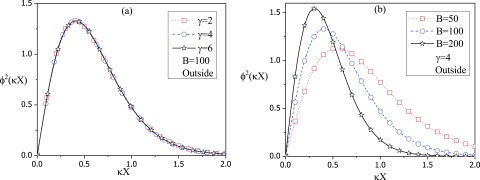
the density profile $\mathcal{P}$ is plotted in Fig. 4 as a function of X for a set of vesicle radii at fixed interaction strength B = 100 and for a set of interaction strength B at fixed vesicle radius ($\gamma =4$). As seen in Fig. 4(a), the density profile is independent of the vesicle radius for B = 100. On the other hand, P is strongly dependent on B for $\gamma =4$, as shown in Fig. 4(b). As expected, as the attractive interaction strength parameter B increases, the polymer is closer to the surface. These profiles are entirely equivalent to the variational results for the same V_s and the WKB results for V_DH.

FIG. 4.

The density profile of the polymer in the exterior region, ${\varphi }^2=\mathcal{P}$, as a function of $\kappa X$ with X being the distance from the interface: (a) Three different values of $\gamma$ for B = 100. (b) Three different values of the strength of the potential, B, for $\gamma =4$.

For the scenario of adsorption on the inside surface of the vesicle, the density profile $P={\varphi }^2(x)$ is given by

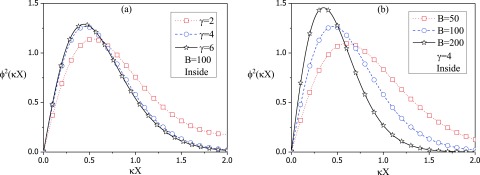
$$P=\mathcal{N}\left\{\begin{array}{cc}\frac{{\xi }_1^{1∕3}(x)}{\sqrt{\mathcal{R}}}{(Ai[-{(\frac{3{\xi }_1}{2})}^{2∕3}]+\frac{\beta }{\alpha }Bi[-{(\frac{3{\xi }_1}{2})}^{2∕3}])}^2,\hfill & x>x_0\hfill \\ \frac{{\xi }_2^{1∕3}(x)}{\sqrt{-\mathcal{R}}}{(Ai[{(\frac{3{\xi }_2}{2})}^{2∕3}]+\frac{\beta }{\alpha }Bi[{(\frac{3{\xi }_2}{2})}^{2∕3}])}^2,\hfill & x>x_0\hfill \end{array},\right.$$ (88)

where $\mathcal{R}$ is given by Eq. (62) and the normalization constant is determined from Eq. (70). Following the computational protocol described in Sec. II, a few examples of the density profile are given in Fig. 5, where $\mathcal{P}$ is plotted against the distance $\kappa X=\kappa (R-r)$ from the surface of the vesicle towards its center. As seen in Fig. 5(a), for B = 100, the density profile is closer to the surface for higher values of the vesicle radius, essentially independent of $\kappa R$. On the other hand, for smaller vesicles, the chain is more spread out into the interior. Similarly for a given value of $\gamma =4$, the polymer is adsorbed closely at the interface as the strength of the interaction between the polymer and the interface is increased, as shown in Fig. 5(b). These results are in excellent agreement with the variational results presented earlier.

FIG. 5.

The density profile of a polymer inside the sphere, ${\varphi }^2=\mathcal{P}$, as a function of $\kappa X$ with X being the distance from the surface: (a) Three different values of $\gamma$ for B = 100. (b) Three different values of the strength of the potential, B, for $\gamma =4$.

C. Adsorption criteria

The WKB result of the adsorption criterion for the exterior state is given by Eq. (59) as

$$|{\sigma }_c|=\frac{|a{i}_1{|}^3}{108{\pi }^2}\frac{{\kappa }^2{\ell }_{eff}}{{\ell }_B\left|q\right|R}\frac{1}{sinh(\kappa R)}\frac{1}{{\left[erfc(\sqrt{\frac{\kappa R}{2}})\right]}^2}.$$ (89)

The asymptotic limits of this WKB result for the low salt ($\kappa R_g<<1$) and high salt ($\kappa R_g>>1$) limits are

$$|{\sigma }_c|=\frac{|a{i}_1{|}^3{\ell }_{eff}}{108{\pi }^2{\ell }_B|q|}\left\{\begin{array}{cc}\frac{\kappa }{R^2},\hfill & \kappa R<<1\hfill \\ \pi {\kappa }^3,\hfill & \kappa R>>1\hfill \end{array}.\right.$$ (90)

When the $\kappa$-dependence of ${\ell }_{eff}$ is taken into account from Eq. (29), the above equation gives

$$|{\sigma }_c|\sim \left\{\begin{array}{cc}\kappa ,\hfill & \kappa R<<1\hfill \\ {\kappa }^{11∕5},\hfill & \kappa R>>1\hfill \end{array}.\right.$$ (91)

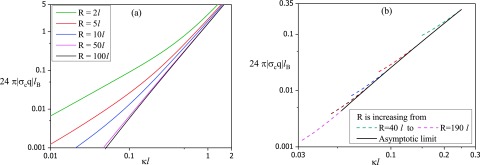
The calculated results for the critical surface charge density, above which there is adsorption in the exterior state, from Eqs. (27) and (91), are given in Fig. 6(a). Here $24\pi \left|{\sigma }_{c}q\right|{\ell }_B$ is plotted against $\kappa$ for different values of the vesicle radius R. The full crossover formula for ${\ell }_{eff}$ is used in getting these results. As seen in Fig. 6(a), the critical charge density crosses over from ${\sigma }_c\sim \kappa$ behavior at small values of $\kappa R$ to ${\sigma }_c\sim {\kappa }^{11∕5}$ behavior at large values of $\kappa R$. The values 1 and 11/5 are the bounds for the exponent a in Eq. (1). The apparent value around 6/5 is in the crossover region.

FIG. 6.

Critical charge $24\pi \left|{\sigma }_{c}q\right|l_B$ as a function of $\kappa \ell$. (a) Outside the sphere, all curves approach the asymptotic limit of a planar surface, $\kappa R>>1$. (b) Inside the sphere, the critical conditions are given for values of vesicle radius from $R=40\ell$ (top curve) to $R=190\ell$ (lowest curve), with the asymptotic limit denoted by the black line with a slope of 5/2.

Thus there is no difference between the WKB result and the variational result of Eq. (20) for high salt concentrations. However, in the low salt limit, which is not readily accessible to experiments, there is a discrepancy between the variational result ${\sigma }_c\sim {\kappa }^2$ and the WKB result ${\sigma }_c\sim \kappa$, as already pointed out by Winkler and Cherstvy.¹² This discrepancy can be traced to the numerical difficulty in identifying the critical condition in the variational procedure of von Goeler and Muthukumar for the limit of $\kappa \to 0$. In addition, the variational procedure gives a bound and the numerical values of ${\sigma }_c$ from the WKB method are bounded by the variational result. This difference goes away at higher salt concentrations of experimental relevance, and in fact both the WKB and the variational calculations give equivalent results (${\sigma }_c\sim {\kappa }^{11∕5}$) within a numerical factor of order unity [$(2∕27){(ai)}^3\simeq 0.95$].

For the interior state, the critical condition of adsorption is computed by finding the minimum value $B_c=24\pi {\ell }_B\left|{\sigma }_{c}q\right|∕{\kappa }^3{\ell }_{eff}$ below which there are no solutions to Eqs. (63) and (65). A plot of $24\pi {\ell }^2\left|{\sigma }_{c}q\right|{\ell }_B$ versus $\kappa$ is given in Fig. 6(b) for different values of the vesicle radius R (from $40\ell$ to $190\ell$). For all values of R, ${\sigma }_c$ approaches an asymptotic behavior as illustrated by the solid line in the figure, corresponding to $\gamma =\kappa R\sim 5\text{–}10$. For smaller values of $\kappa R$, there is a deviation from the asymptotic behavior with a weaker dependence of ${\sigma }_c$ on $\kappa$. In the asymptotic limit (high salt concentration, $\kappa R\ge 5$), the slope of the solid line is close to 5/2,

$$|{\sigma }_c|\sim {\kappa }^{5∕2}.$$ (92)

This result is in very good agreement with the result of variational calculation of Ref. 16.

D. Free energy of adsorption

The entropic and energy contributions to the free energy of the adsorbed chain can be calculated from the equation for the eigenfunction $\varphi (x)$ by following the procedure given in Refs. 16 and 17. For the exterior state, Eqs. (31) and (35) give

$$\frac{{\partial }^2\varphi (x)}{\partial x^2}-B\gamma sinh(\gamma )\frac{e^{-x}}{x}=-\mathrm{\lambda }\varphi (x),x>\gamma ,$$ (93)

where $x=\kappa r,\gamma =\kappa R,\mathrm{\lambda }=6{\mathrm{\lambda }}_0∕({\kappa }^2\ell {\ell }_{eff})$, and $B=24\pi \left|\sigma q\right|{\ell }_B∕({\kappa }^3{\ell }_{eff})$. Multiplying Eq. (93) by $\varphi (x)$ and integrating over x, and in view of the normalization condition for the density profile, we get

$$\mathrm{\lambda }={\mathrm{\lambda }}_u+{\mathrm{\lambda }}_s,$$ (94)

where the energy part of the free energy is

$${\mathrm{\lambda }}_u=-B\gamma sinh(\gamma ){\int }_0^{\gamma }dx{\varphi }^2(x)\frac{e^{-x}}{x},$$ (95)

and the entropic part of the free energy is

$${\mathrm{\lambda }}_s=-{\int }_{\gamma }^{\infty }dx\varphi (x)\frac{{\partial }^2}{\partial x^2}\varphi (x).$$ (96)

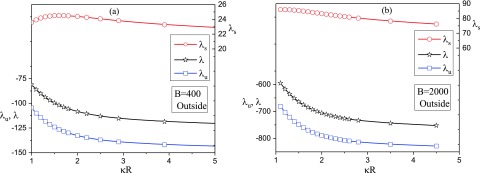
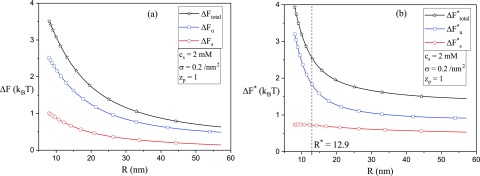
The contributions from the energy and entropy to the total free energy of the exterior state are given in Fig. 7, as a function of $\gamma =\kappa R$ for two examples of the polymer-surface interaction energy parameter B = 400 and 2000. As expected from the reduction of conformational entropy of the chain in the adsorption process, the entropic part ${\mathrm{\lambda }}_s$ (data in red with the ordinate on the right hand side) is positive and is roughly independent of the vesicle radius. On the other hand, the energy part ${\mathrm{\lambda }}_u$ (data in blue) is considerably larger than ${\mathrm{\lambda }}_s$ and is inevitably close to the total free energy $\mathrm{\lambda }$ (data in black). These features are observed for both B = 400 and B = 2000, except that the energy contribution to the free energy is much stronger for higher values of the strength of the polymer-surface interaction. The dependence of the total free energy on the vesicle radius is monotonic and the free energy of the adsorbed exterior state decreases continuously with a decrease in the curvature of the vesicle.

FIG. 7.

The entropic part, the energy part, and the total free energy of the system, ${\mathrm{\lambda }}_s$, ${\mathrm{\lambda }}_u$, and $\mathrm{\lambda }$, respectively, in the exterior state, as a function of $\kappa R$ for two values of the strength of the potential, B: (a) B = 400 and (b) B = 2000. Free energy F is related to $\mathrm{\lambda }$ as $F={\kappa }^2\ell {\ell }_{eff}\mathrm{\lambda }∕6$.

The decomposition of the free energy into the energy and entropy contributions can be similarly accomplished for the interior state as well. Now, Eqs. (31) and (35) give

$$\frac{{\partial }^2\varphi (x)}{\partial x^2}-B\gamma e^{-\gamma }\frac{sinh(x)}{x}\varphi (x)=-\mathrm{\lambda }\varphi (x),x<\gamma ,$$ (97)

where various symbols are already defined. Multiplying Eq. (97) by $\varphi (x)$ and integrating over x, and in view of the normalization condition of Eq. (70), we get $\mathrm{\lambda }={\mathrm{\lambda }}_u+{\mathrm{\lambda }}_s$ with the energy part given by

$${\mathrm{\lambda }}_u=-B\gamma e^{-\gamma }{\int }_0^{\gamma }dx{\varphi }^2(x)\frac{{\partial }^2}{\partial x^2}\frac{sinh(x)}{x}$$ (98)

and the entropy part given by

$${\mathrm{\lambda }}_s=-{\int }_0^{\gamma }dx\varphi (x)\frac{{\partial }^2}{\partial x^2}\varphi (x).$$ (99)

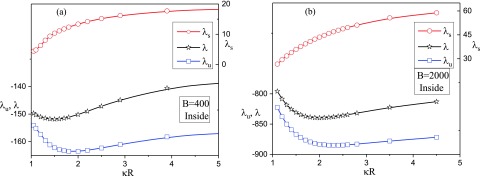
The total free energy and the contributions from energy and entropy are given in Fig. 8 as functions of $\gamma =\kappa R$, for two illustrative values of B. By considering the case of B = 400 [Fig. 8(a)], the entropic part ${\mathrm{\lambda }}_s$ (data in red with the ordinate on the right hand side) is positive as expected due to reduction of chain conformations. Also, ${\mathrm{\lambda }}_s$ increases monotonically as $\kappa R$ is increased, eventually reaching an asymptotic value (comparable to the value for the exterior state in this limit). On the other hand, the energy contribution ${\mathrm{\lambda }}_u$ (data in blue) is negative and is an order of magnitude stronger than ${\mathrm{\lambda }}_s$, thus dominating its contribution to the total free energy (data in black). More significantly, the free energy and ${\mathrm{\lambda }}_u$ is non-monotonic with $\kappa R$ as was obtained by the variational calculation in Ref. 16. The free energy of the vesicle with the chain adsorbed inside is a minimum at an optimum value of the ratio of vesicle radius to the Debye length, denoted by $\kappa R^{*}$. The same features are seen for higher strengths of polymer-surface interaction as shown in Fig. 8(b) for B = 2000, except that the free energy minimum is shifted towards a higher value of $\kappa R^{*}$. The dependence of $\kappa R^{*}$ on the strength parameter B is given in Fig. 9 which shows approximately a logarithmic dependence,

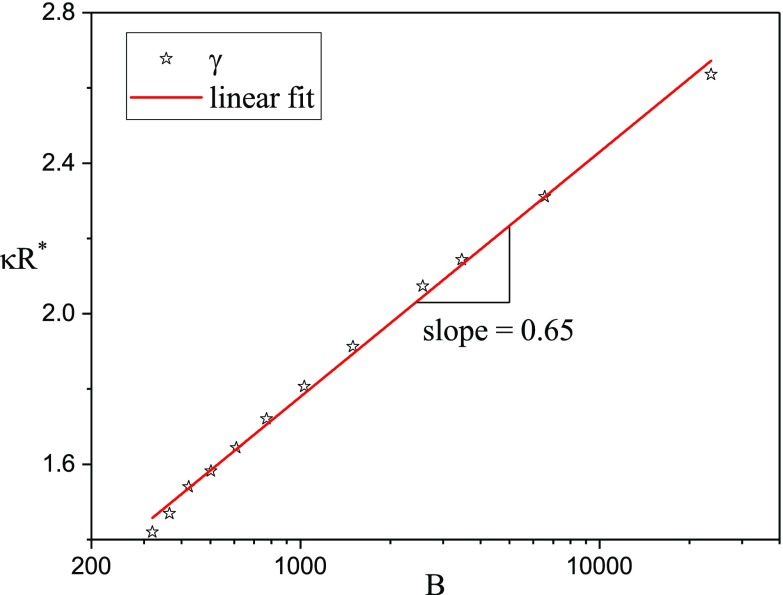
$$\kappa R^{*}=0.65{log}_{10}B-0.17.$$ (100)

Therefore, there exists an optimum radius of vesicle for the adsorption of a polyelectrolyte chain on its inside surface for a given set of parameters. As long as the adsorption criterion is met, all vesicle radii have net negative free energy and hence the adsorbed encapsulation is a thermodynamically favorable process. However, if the vesicle radius is allowed to vary, then the vesicle with the adsorbed chain is expected to adapt itself towards the global free energy minimum corresponding to $\kappa R^{*}$. The optimum vesicle radius $R^{*}$ depends on $\kappa$ and other parameters such as $\sigma ,q,{\ell }_B$, and N depend on B, as given by Eq. (36). Any of these parameters can be used to tune the optimum vesicle radius for encapsulating a flexible polyelectrolyte chain as an adsorbed interior state.

FIG. 8.

The free energy of the polyelectrolyte chain inside the vesicle, $\mathrm{\lambda }$, and its energy and entropic parts, ${\mathrm{\lambda }}_u$ and ${\mathrm{\lambda }}_s$, as a function of $\kappa R$. (a) B = 400 and (b) B = 2000. Free energy F is related to $\mathrm{\lambda }$ as $F={\kappa }^2\ell {\ell }_{eff}\mathrm{\lambda }∕6$.

FIG. 9.

Dependence of the optimum radius $R^{*}$ on the strength of the potential, B. Solid line is the fitted approximation with a slope of 0.65.

E. Stabilities of exterior and interior states

The free energy F (in units of k_BT) is related to the eigenvalue $\mathrm{\lambda }$ by Eqs. (32) and (33) as

$$F=\frac{{\kappa }^2\ell {\ell }_{eff}}{6}\mathrm{\lambda }.$$ (101)

From the values of $\mathrm{\lambda }$ in the exterior and interior regions, the free energy change can be computed. We define the relative thermodynamic stabilities of the interior and exterior states by defining the change in free energy associated with the exchange of an adsorbed chain from the interior to the exterior region as

$$\mathrm{\Delta }F=F_{exterior}-F_{interior}.$$ (102)

$\mathrm{\Delta }{F}_u$ and $\mathrm{\Delta }{F}_s$ are the corresponding values of the energy and entropy contributions to the change in free energy. In our definition, all parameters are the same for the initial and final states. Representative results are given in Fig. 10(a) for $B=400,{\ell }_B∕\ell =1$, and N = 100, where $\mathrm{\Delta }F,\mathrm{\Delta }{F}_u$, and $\mathrm{\Delta }{F}_s$ are plotted against R. As is evident from the figure, an encapsulated adsorbed chain inside a vesicle is more stable than the ejected adsorbed chain on the exterior surface of the vesicle. Therefore, energy must be supplied to eject the adsorbed chain out of the vesicle. This free energy cost decreases monotonically with R, when all other parameters are fixed. The precise value of the energy cost depends on the values of all relevant parameters and can be computed using the computational protocol described above. For aqueous systems with $\sigma =0.2∕{nm}^2,q=1∕nm$, and c_s = 2 mM, $\mathrm{\Delta }F$ values are comparable to a few k_BT as shown in Fig. 10(a).

FIG. 10.

The free energy difference of the polyelectrolyte translocation from a vesicle for the strength of the potential, B = 400. $\mathrm{\Delta }F$ is the total free energy difference, while $\mathrm{\Delta }{F}_u$ and $\mathrm{\Delta }{F}_s$ are the energy and entropic parts for $c_s=2\mathrm{\text{mM}},\sigma =0.2∕{\mathrm{\text{nm}}}^2$, and q = 1/nm. (a) Vesicle radius is held constant. (b) The initial vesicle radius is the optimum radius, $R^{*}=12.9\mathrm{\text{nm}}$, and the final vesicle radius can be different from $R^{*}$.

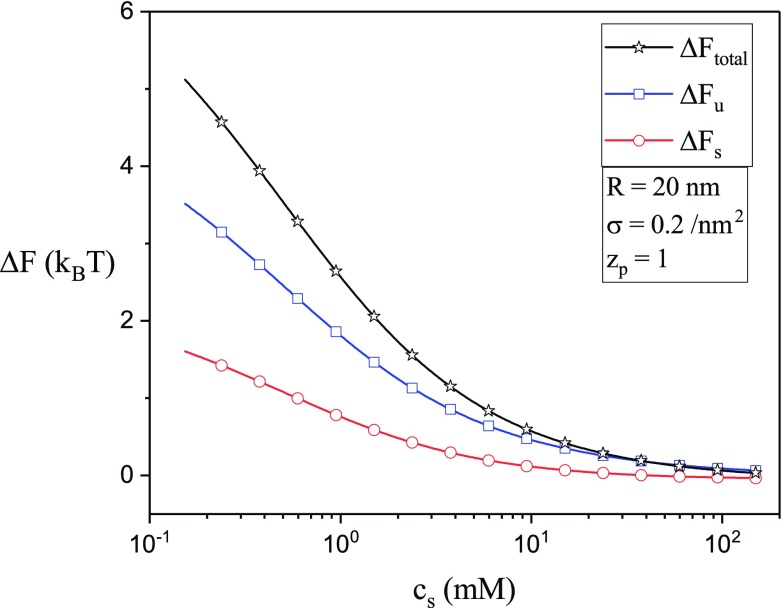
An alternative scenario to the case of Fig. 10(a), where R is fixed for both the initial and final states, is to consider the initial state corresponding to the optimum vesicle radius $R^{*}$ and the final state corresponding to the vesicle radius R. The dependencies of $\mathrm{\Delta }{F}^{*},\mathrm{\Delta }{F}_u^{*}$, and $\mathrm{\Delta }{F}_s^{*}$ on R, corresponding to this alternate scenario, are given in Fig. 10(b). Here, the initial value of the vesicle radius is $R^{*}=12.9\mathrm{\text{nm}}$ and the vesicle radius in the final state is R. Again, $\mathrm{\Delta }{F}_u^{*}$ is the dominant contributor to $\mathrm{\Delta }{F}^{*}$. The entropic part $\mathrm{\Delta }{F}_s^{*}$ is essentially independent of R. Furthermore, $\mathrm{\Delta }{F}^{*}$ decreases continuously with R if $R>R^{*}$ and increases continuously with R if $R<R^{*}$. These results suggest that the free energy cost to eject an adsorbed chain from the inside of a vesicle to the exterior adsorbed state can be mitigated if the vesicle can spontaneously expand into bigger radii. Again, for aqueous systems with $\sigma =0.2∕{\mathrm{\text{nm}}}^2,q=1∕\mathrm{\text{nm}}$, and c_s = 2 mM, $\mathrm{\Delta }F$ values are comparable to a few k_BT as shown in Fig. 10(b). The above calculations can readily be repeated to compute the free energy cost associated with the chain expulsion when another variable such as $T,\sigma ,q,𝜖$, or c_s is tuned. As an example, the dependencies of $\mathrm{\Delta }F,\mathrm{\Delta }{F}_u$, and $\mathrm{\Delta }{F}_s$ on the salt concentration are given in Fig. 11 for $R=20\mathrm{\text{nm}},\sigma =0.2∕{\mathrm{\text{nm}}}^2$, and q = 1/nm. The free energy difference is seen to decrease with salt concentration and the magnitude is of the order of thermal energy, k_BT.

FIG. 11.

The dependencies of $\mathrm{\Delta }F,\mathrm{\Delta }{F}_u$, and $\mathrm{\Delta }{F}_s$ on c_s for $R=20\mathrm{\text{nm}},\sigma =0.2∕{\mathrm{\text{nm}}}^2$, and q = 1/nm.

IV. CONCLUSIONS

Using the WKB method, we have derived adsorption criteria and density profiles for a flexible polyelectrolyte chain adsorbing to the interior and exterior surfaces of a charged vesicle with uniform surface charge number density $\sigma$. The other experimentally controllable variables used in the derivation are the polymer linear charge number density, the polymer length, the vesicle radius, the Debye length ${\kappa }^{-1}$, and the Bjerrum length ${\ell }_B$. The ionic strength and the dielectric constant of the medium are assumed to be the same in both the interior and exterior regions of the vesicle, without regard to the Donnan equilibrium. The intrachain electrostatic interaction among various segments is also included in deriving the final expressions.

For adsorption inside the vesicle, two regimes are identified as in our earlier variational theory. For weaker polymer-interface attraction, the polymer is unadsorbed and is merely delocalized inside the vesicle. For strong enough attraction with the interface, the chain is in an adsorbed state. The adsorption criterion is written in terms of the critical surface charge number density ${\sigma }_c$ as

$$|{\sigma }_c|\approx \frac{1}{24\pi {\ell }^2|q|{\ell }_B}{\kappa }^{5∕2},$$ (103)

in the high salt limit of $\kappa R\ge 5$. The adsorption occurs for $\left|\sigma \right|>\left|{\sigma }_c\right|$, which can be tuned by any of the variables $q,{\ell }_B$, and $\kappa$. In addition, we find that there is an optimum vesicle radius for forming an adsorbed interior state.

For adsorption outside the vesicle, the critical surface charge density required for adsorption in experimentally relevant conditions, where there is a finite amount of electrolyte ions, is given by

$$|{\sigma }_c|\sim {\kappa }^a,$$ (104)

where

$$a=\left\{\begin{array}{cc}\frac{6}{5},\hfill & \kappa R<1\text{and}\kappa R_g>1\hfill \\ \frac{11}{5},\hfill & \kappa R>1\text{and}\kappa R_g>1\hfill \\ 3,\hfill & \kappa R>1\text{and}\kappa R_g<1\hfill \end{array}\right.$$ (105)

with R and R_g being the vesicle radius and the radius of gyration of the polyelectrolyte chain, respectively. These conclusions for the exterior state are valid also for adsorption to spherical solid-like particles or proteins, except that the numerical prefactor in the scaling law of Eq. (103) is different. This difference in the numerical prefactor arises from the difference between V_s in Eq. (14) and the Debye-Hückel potential in Eq. (18).

The experimental results summarized in Eq. (1) are obtained under the conditions satisfying $\kappa R<1$ and $\kappa R_g>1$. Therefore, our theoretical result, $\left|{\sigma }_c\right|\sim {\kappa }^{6∕5}$, appears to be in agreement with the experimental results. In general, the results for the interior state from the WKB and variational methods are equivalent, except for a slight difference of order unity in the numerical prefactors. For the exterior state, similar agreement is seen except in the narrow region of zero-salt limit.

The entropic and energy contributions to the free energy of the adsorbed chain are calculated for both the interior and exterior states. The energy contribution dominates over the entropic part by an order of magnitude. Using the free energy of the chain in these two states, we find that the interior state is more stable and that the energy cost to eject the chain to the exterior with chain adsorption decreases monotonically with the size of the vesicle and also with salt concentration. Unloading of the polymer from a vesicle with its initial optimum radius can be facilitated by allowing the vesicle to expand. The typical values of the free energy cost are comparable to a few k_BT.

Although the situation of an encapsulated flexible polyelectrolyte chain inside a charged sphere appears to be similar to single stranded RNA viruses, there are significant differences between these two systems, as exhibited by polyelectrolyte-brush-like interior surface of the capsid and the corresponding monomer density profiles for RNA with a depletion zone near the surface.^3–8

The theory and calculations presented here are based on an idealized model. Several extensions such as the incorporation of the elasticity of the vesicle surface and the Donnan equilibrium for partitioning of electrolyte ions, and kinetics of ejection of the polymer are of further interest.