Abstract
We present the Mesoscopic Membrane with Proteins (MesM-P) model, an extension of a previously developed elastic membrane model for mesoscale simulations of lipid membranes. MesM-P employs a discrete mesoscopic quasi-particle approach to model protein-facilitated shape and topology changes of the lipid membrane on length and time scales inaccessible to all-atom and quasimolecular coarse-grained molecular dynamics simulations. We investigate the ability of MesM-P to model the behavior of large lipid vesicles as a function of bound protein density. We find four distinct mechanisms for protein aggregation on the surface of the membrane, depending on membrane stiffness and protein spontaneous curvature. We also establish a connection between MesM-P and the results of higher resolution coarse-grained molecular dynamics simulations.
I. INTRODUCTION
The inherent multiscale nature of many biological processes, e.g., those that take place on the cell membrane, presents great challenges for computational modeling techniques. Highly coarse-grained (CG) modeling provides a way of overcoming the challenge of simulating systems that manifest at large time and length scales. A highly CG model can either be derived from finer resolution atomistic simulations (a bottom-up approach)1–6 or by reproducing a set of experimental observations (top-down approach).7,8 In principle, the two approaches can be combined to produce a set of models that span the range from near-atomistic to mesoscopic resolutions, consistent with both all-atom simulations and experimental results. While the finer-grained models can provide detailed information on atomistic and molecular interactions underlying the phenomenon of interest, the coarser (mesoscopic) description of the system will provide at least a qualitative understanding of the system on large time and length scales. In such a hierarchical setup, the information from all-atom simulations and experiments can be passed back and forth from one scale to another to ensure consistency and to enable the understanding of the underlying processes from multiple perspectives.
A problem that is particularly suited for such a multi-scale approach is the remodeling of lipid membranes under the influence of proteins. Protein-driven membrane remodeling plays important roles in many biological processes such as intracellular trafficking, endocytosis, cell division, etc.9–13 While occurring on relatively larger length scales (typically 100s of nm or larger), membrane remodeling is initiated and largely influenced by much smaller interactions at the protein-lipid interface. One of the best-known membrane remodeling proteins are a family of Bin/Amphiphysin/Rvs (BAR) domain proteins that have an elongated, crescent-shaped structure. They bind to the membrane by a combination of electrostatic interactions between lipids and BAR domain, and in most cases by a shallow insertion of the protein’s amphipathic helices.14,15 Despite the similarities in their structure, there is a large diversity among BAR domains based on length, charge, and the intrinsic curvature of the BAR domain. They can roughly be classified as three groups: BAR/N-BAR, F-BAR, and I-BAR domains. BAR/N-BAR and F-BAR domains induce positive membrane curvature, while I-BAR domains induce negative membrane curvature.14,15 However, the mechanism by which they generate complex membranous structures has only recently begun to emerge. A key understanding of their mode of action is that the way they operate depends on physical parameters, such as protein surface density, membrane tension, or membrane shape;16 therefore, the same BAR protein may have a sensing role in one process and a curvature-generating or scission role in others.17
In light of recent advances in our understanding how membrane proteins assemble and influence membrane behavior, developing large-scale simulation models is key. While many CG models that represent lipids and proteins at molecular resolution1–3,5,6,18 have been developed, a number of models that operate beyond molecular resolution have also been presented in the recent years. For example, Ramakrishnan et al. model the membrane as a dynamically triangulated surface that can couple with an in-plane nematic field that represents anisotropic inclusions, such as BAR proteins.19–21 In another work, Noguchi et al. model a solvent-free membrane using a collection of spin particles, embedded by banana-shaped rods representing BAR proteins.22–25 The elastic membrane version 2 (EM2) model,26–29 developed in our group prior to the aforementioned papers, is largely based on Smooth Particle Applied Mechanics (SPAM).30–33 SPAM is a closely related method to Smooth Particle Hydrodynamics (SPH).30,34,35 However, it avoids instability and consistency issues related to SPH and can be more naturally linked to molecular dynamics.26 EM2 provides a computationally tractable approach for solving continuum equations in a grid-free way. The membrane and the surrounding solvent are partitioned into a collection of particles that each represent the properties of the volume they occupy, such as position, mass, and velocity. However, they are also characterized by protein density and lipid composition that can be exchanged with nearby particles, thus giving a more realistic model of a fluctuating membrane and its underlying molecular composition. EM2 has been shown to model large-scale membrane topological changes,28,29,36 lipid domain formation,26 as well as the coupling between them through a free-energy formalism. Moreover, the inclusion of explicit mesoscopic solvent provides the correct hydrodynamic description and makes it possible to study protein density variations around the membrane.
Here, we present a new development of the EM2-like approach, which we also extend and re-implement in a computationally efficient and highly scalable manner in the framework of the widely used LAMMPS open source molecular dynamics (MD) package.37 This new model that we call Mesoscopic Membrane with Proteins (MesM-P) enables us to study protein assembly and its effect on membrane shape on experimental length and time scales and under a wide variety of conditions, such as different membrane composition, membrane stiffness, and protein concentration. In particular, modeling membranes at intermediate protein concentrations was a key limitation of the previous model; only simulations with maximal protein coverage were possible. Thus, in this work we study the assembly of proteins on large lipid vesicles at low protein concentrations, similarly to previous CG MD simulations of N-BAR proteins on the membrane.38,39 Unlike the molecular-based CG models, with the MesM-P model, we do not need to undergo complex CG parameterization each time when changing the protein or studying different membrane compositions and so we can explore a much wider range of experimental systems.
The remainder of this paper is organized as follows: Sec. II gives the detailed description of the model and the simulation setup, and it emphasizes the novelties of the MesM-P framework. Section III presents results from the MesM-P simulations at low protein concentration and compares them to our previously published highly CG simulations of N-BAR proteins on the membrane. Section IV provides further discussion and conclusions.
II. METHODS
The MesM-P model is based on the EM2 model26–29 that successfully represented topological remodeling of the membrane at maximal protein densities.29 Here, we give a detailed description of the MesM-P model, emphasizing the changes and additions we have made.
A. MesM-P model
In the MesM-P model, the membrane and the surrounding solvent are represented by a collection of quasi-particles that, in a sense, constitute a movable grid that evolves with the motion of the individual quasi-particles. Each quasi-particle carries information on the physical properties of the medium with a corresponding set of variables. The quasi-particles associated with the membrane, besides mass, position, and velocity, are described with a normal and an in-plane vector, as well as with the protein and lipid composition fields. The normal vector, , gives the local orientation of the membrane that is used to calculate the instantaneous local curvature in a corresponding area of the membrane (Fig. 1). The in-plane vector, , signifies the average orientation of proteins along which the spontaneous curvature is applied (Fig. 1). The protein and lipid composition fields (denoted as ϕB and ϕM, respectively) represent the local protein density and the local charged lipid density, respectively. They take values from −1 to 1, with −1 corresponding to the largest possible density and 1 to the absence of proteins in the case of ϕB or minimally charged membrane in the case of ϕM. The quasi-particles that represent the solvent are only characterized with mass, position, velocity, and the protein composition field.
FIG. 1.
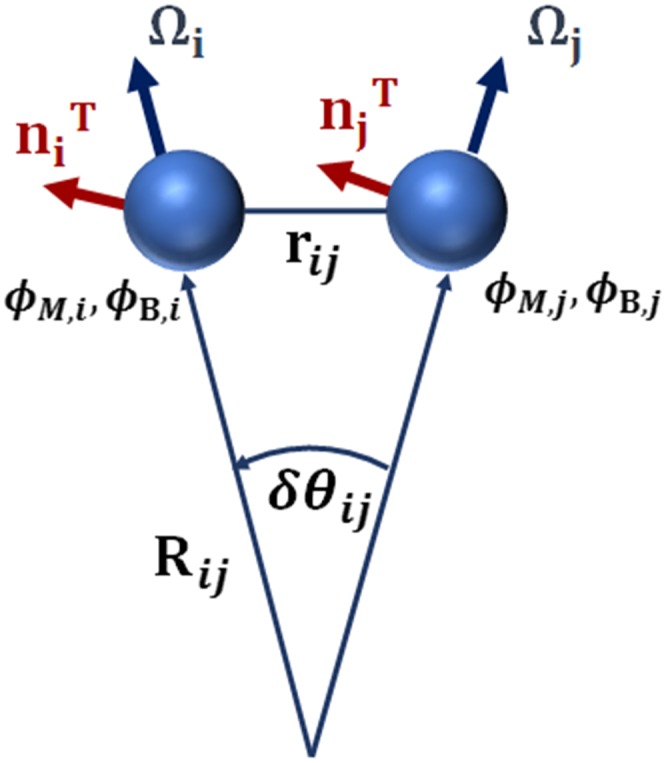
Schematic representation of the MesM-P model, where each quasi-particle is characterized by its position, normal and in-plane vectors ( and , respectively), protein density (ϕB), and lipid composition (ϕM).
1. Hamiltonian
The dynamics of the system are determined by the following Hamiltonian:
| (1) |
Here, N is the total number of membrane and solvent quasi-particles (N = NM + NS), while rN are their positions.
Below we present and describe in detail each term of Eq. (1).
2. Excluded volume interactions
The excluded volume potential, Hexcl, includes a 2-16 Lennard-Jones term that acts between membrane quasi-particles and a soft repulsion term for solvent-solvent and membrane-solvent interactions that is based on a Lucy function,30
| (2) |
The former has the following form and sets the size of the quasi-particles that constitute the membrane:
| (3) |
| (4) |
where is the distance between quasi-particles i and j. The 1/r16 term makes membrane quasi-particles incompressible, while the 1/r2 term, in principle, allows for formation of holes and defects on the membrane that makes it possible to model topology breaking, as seen in the transformation of membrane vesicles into tubular networks.36 The σLJ216 parameter defines the quasi-particle size and must be equal to discretization length σ in Hbend (see below).
The functional form and strength of the membrane-membrane excluded volume interaction must be chosen so that it does not affect the rigidity of the membrane, which should instead be controlled by the Hbend term (see below). In the previous formulation of the model, the strength of the HLJ216 term was modulated by a high protein concentration. While coupling high protein concentration with this term does not pose an issue at a maximal (and thus uniform) protein concentration, at low protein densities on the membrane, such dependence has undesirable consequences: (1) the excluded volume interactions themselves stiffen the membrane in the areas of higher protein concentrations, and (2) it influences the influx of proteins to the membrane. Thus, here we use membrane-membrane excluded volume interactions that are independent of protein concentration, with membrane stiffness and protein coverage controlled by other terms in the Hamiltonian. The parameter εLJ216 was chosen to be 6.5 kJ/mol for this study, which gives reasonable stability to the membrane while allowing for ruptures and topological transformations.
The HLucy terms allow for overlap between two quasi-particles, allowing free movement of solvent in the media,
| (5) |
| (6) |
Based on the previous studies, we have chosen , , and σLucy = 9.0 nm, where the latter defines the discretization length scale for composition fields.26 In terms of the former, it is more energetically unfavorable for a solvent particle to overlap with a membrane than with other solvent particles.
An important consequence of using the two potentials above is that the membrane in the MesM-P model has a well-defined area and is practically incompressible beyond it, while the soft Lucy potential allows for a change in volume for a closed membrane system.
3. Bending potential
Bending energy, Hbend, is a discretized version of a continuum elastic description of the membrane that accounts for symmetry breaking due to the presence of membrane inclusions.40 The detailed derivation of Hbend expression can be found elsewhere.27 We also briefly discuss this derivation in the Appendix. Similar to EM2, in the MesM-P model Hbend has the following form:
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
where is a unit vector in the direction of rij and σ is the discretization length scale. It can be shown that ; ; δθij/rij = 1/Rij = Cij, where δθij is the angle between and (see Fig. 1), and 1/Rij = Cij is the local curvature. The term C0 is the spontaneous curvature at maximal protein concentration and optimal alignment. Changing its value essentially changes the type of protein modeled. We will refer to C0 as “spontaneous curvature coefficient” for simplicity. The formula given in Eq. (10) for γ expresses the fact that the effective spontaneous curvature increases with increasing density of proteins and as proteins align in the same direction in nearby cells represented by quasi-particles i and j. It is worth noting that the function here is different from the one used in the previous work,29 where was set to zero if protein local density was smaller than 50% of the maximal value. By contrast, here the spontaneous curvature gradually increases in the full range of protein densities.41
The discretization length σ was chosen here to equal 6.8 nm, in line with previous work.28 However, σ can be varied to model the membrane at different resolutions, if necessary.
The overall strength of the bending energy is given by εbend that can be expressed in terms of the protein density dependent bending modulus, kc, as
| (13) |
where ρA = Nm/A is the initial area density of the membrane, and Nc,i is the average number of quasi-particles found within the interaction cutoff near the quasi-particle i. The bending modulus, kc, depends on protein density in a linear manner, consistent with the previous work,
| (14) |
In the current work, we choose k0 = 1, implying that the membrane gradually becomes stiffer when protein concentration exceeds 50% of the maximal density. However, both positive and negative values of k0 can be considered, while the bending modulus can vary in the full range of the protein density, if needed.
For future discussion, we also define the protein density independent parameter as
which we further refer to as the “strength of the bending energy,” for simplicity. In the current work, we have extensively studied the effect of and C0 on protein aggregation and associated membrane remodeling (see Results and Discussion and Table I), as they represent the two most important parameters that define the physical properties of the membrane and proteins, respectively, in this case.
TABLE I.
MesM-P model parameters.
| εLJ216 | 6.5 kJ/mol | σLJ216 | 6.8 nm |
|---|---|---|---|
| 5 kJ/mol | σLucy | 9.0 nm | |
| 1 kJ/mol | |||
| εE12a | 5 kJ/mol | σE12 | 5.0 nm |
| 5−100 kJ/mol | σ | 6.8 nm | |
| C0 | 0.07−0.40 nm−1 | k0 | 1.0 |
| 0.251 kJ/mol | 5 nm2 kJ/mol | ||
| εξ,B | 1 nm2 kJ/mol | εwell,B | 0.001 kJ/mol |
| εξ,M | 1 nm2 kJ/mol | εwell,M | 0.001 kJ/mol |
| εO | 5−15 kJ/mol | ν | 1 or 2 |
By E12 we denote the 1/r12 excluded volume potential between membrane and solvent quasiparticles that acts at shorter distance.
4. Coupling potentials
The Hcoupl term represents various coupling mechanisms between the membrane and the proteins, namely, intrinsic curvature coupling (IC), and composition coupling (CC). In case of IC, the coupling is achieved through the curvature of the membrane. In other words, the proteins have a higher affinity to the areas of the membrane that have their preferred curvature. In the case of CC, the coupling is through charged lipid distribution on the membrane. This corresponds to the fact that many membrane-binding proteins have positively charged residues on their binding surfaces, and, thus, the distribution of negatively charged lipids will play a role in the positioning of the proteins on the membrane. Below we give the explicit expressions for IC and CC coupling potentials.
The IC potential has the following form:
| (15) |
where Nc,i is the instantaneous count of quasi-particles that are within the cutoff distance from particle i, while φij is the same as defined in Eq. (9).
The IC potential consists of two terms. The first term is responsible for a uniform attraction of proteins to the membrane, which is usually due to the electrostatic interactions. The second term explicitly couples the protein composition to the membrane curvature. The relative strength of those two terms, controlled by parameters and , will decide if protein density is uniform over the surface of the membrane or if proteins aggregate in the areas where the curvature matches the intrinsic (spontaneous) curvature of the proteins. In line with previous work, we have chosen and that favor the aggregation of proteins at corresponding curvature on the membrane.29
The CC potential has the following form:
| (16) |
| (17) |
| (18) |
where εCC defines the strength of the coupling and ζ0 is a non-negative constant that describes the uniform attraction of the proteins to the membrane. For ζ0 = 0, there will be no influx of proteins to an uncharged membrane. However, for any value of ζ0, the CC potential will favor higher protein concentration in the areas of the membrane with higher density of negatively charged lipids, while this difference will relatively decrease with increasing ζ0.
In the current work, we only use the IC coupling. While either IC or CC coupling can be used, it is also theoretically possible to use them at the same time and this will be explored in the future.
5. Composition potentials
A discretized form of the Landau model42 is employed to represent the energy (which is in fact a free energy) as a function of the spatial variation of membrane and protein composition fields. The corresponding expressions for protein density and lipid composition are
| (19) |
| (20) |
where the first terms, that have square of ϕ gradients, drive the system to uniform composition (i.e., ϕ = 0), while the second terms represent the tendency of the system to mix or phase separate. In this paper, we are not interested in spontaneous phase separation neither in protein or lipid compositions; single well potentials centered at ϕ = 0 were chosen in accordance to the previous work.29 However, if the phase separation behavior in the effective binary system is of interest, double well potentials can be used instead. The overall strengths of potentials must be chosen so that the spatial distributions of protein and charged lipid densities are consistent with the characteristic behavior of the system at hand in the absence of coupling and other composition-dependent terms. The relative values of εξ and εwell can be chosen based on quantitative experimental observables, such as the width of the interface between phases.29 Here, we used values of 1 nm2 kJ/mol and 0.001 kJ/mol for εξ and εwell, respectively. We have also tested values within two orders of magnitude difference from those and did not find any significant effect on our findings. This is expected for the study carried out here because in the absence of a CC potential, the membrane composition does not play any role and because the dynamics of protein density is dominated by IC and bending terms.
The gradients in Eqs. (19) and (20), as was shown in Ref. 26, can be calculated as
| (21) |
where is either N or NM, m is the mass of the quasi-particle, ρij = 0.5(ρi + ρj) is the average density with , and W(r) is a smooth weight function, for which the Lucy function30 is used,
| (22) |
where σLucy is a fundamental length scale and A is a normalization constant.
6. Oligomerization potential
The oligomerization energy favors the alignment of proteins on the surface of the membrane at their high densities. It has the following form:
| (23) |
where fO(ϕB,i, ϕB,j) is defined as
| (24) |
and ν is an integer that takes values of 1 and 2, where ν = 1 favors the alignment of the in-plane vectors in the same direction, while for ν = 2, both parallel and anti-parallel alignments are likely.
In the current study, we have tried a number of combinations of εO and ν values, as indicated in Table I (results not shown). However, we did not find this term to have a statistically significant effect on our results, which is due to the fact that the protein field (represented by the orientations of in-plane vectors) was already well aligned due to the anisotropic form of bending and curvature coupling potentials. In the future, however, this potential can be modified to favor different alignments of the proteins, for example, to distinguish between end-to-end and side-by-side oligomerization.
7. Biasing protein density on the membrane
Hp−bias is a new potential that is added here to control (or bias) the total protein coverage on the surface of the membrane relative to the maximal value. The coverage is defined as
| (25) |
and takes the values from 0 to 1. It equals 1 only if ϕB,i = 1 for all quasi-particles associated with the membrane. The potential itself has the following simple form:
| (26) |
where εp−bias is the strength of the bias, and η0 is the target value (that also takes values from 0 to 1).
8. System evolution in time
The MesM-P system is propagated in time by calculating forces and torques using the Hamiltonian described above and by varying the composition fields according to Landau-Ginzburg (LG) dynamic equation43 that is given in Lagrangian form26 as
| (27) |
Here, Γ is a positive phenomenological coefficient that must be chosen to have the maximum value that results in stable dynamics. vi is the velocity of the quasi-particle. Finally, α is a so-called “composition-stat” that constrains the total composition of the system to be constant. The LG dynamics themselves do not conserve the composition; thus, α term has to be added, which evolves according to the following equation:
| (28) |
where Q is a constant that defines the relaxation rate of total composition to the average value of zero.
In the current work, the Nose-Hoover integration scheme (similar to the one implemented in LAMMPS under ASPHERE package) is used to propagate the translational and rotational degrees of freedom associated with the quasi-particles based on calculated forces and torques.
It is worth noting that composition field dynamics given by Eq. (28) is deterministic, and in the absence of spatial movement, it will drive the system to the free-energy minima. However, a noise term can be explicitly added to Eq. (28) that will introduce thermal fluctuations in accordance to the fluctuation-dissipation theorem. At the given quasi-particle resolution, we expect those fluctuations to be negligible relative to the indirect thermal driving from the translational and rotational degrees of freedom. We will explore the possibility of including explicit thermal fluctuations in the LG dynamics in the future.
B. New features of MesM-P
The MesM-P addresses the biggest limitation of the EM2 model by allowing for simulations of membrane remodeling under a wider range of protein densities, which is very important for modeling various experimentally relevant situations. With the EM2 model, only two situations could have been modeled, namely, when the spontaneous curvature of the proteins was suited for binding onto the membrane, giving close to 100% coverage, and when the spontaneous curvature was too high and the coverage was zero.36 Besides adding an explicit potential that can control the amount of protein on the membrane, which corresponds to an experimental setup where limited number of proteins are injected near the membrane and their binding is directly observed, a number of changes have been applied to MesM-P potentials (that are described in Subsection II A) that allow simulating the dynamic binding of proteins at low concentrations, relevant for endocytosis and many other membrane-remodeling phenomena.
Several other additions have been made that naturally followed from either the new implementation of the model or its integration into LAMMPS.37 Below we list some of them:
-
1.
It is now possible to have more than one type of membrane and solvent quasi-particles. One example of how this can be used is to have two types of solvent, where one can carry protein density, while the other one cannot. This capability was used here to model a typical experimental situation when proteins are present only on one side of the membrane.
-
2.
The MD integration for MesM-P was implemented as a collection of separate modules that can be individually controlled and turned on or off, allowing for the use of different integration schemes depending on the problem. Moreover, this can be combined with other standard LAMMPS modules. One important implication of this is the ability to now perform constant NPT (constant number of particles, pressure, temperature) simulation of flat membranes using the combination of MesM-P specific modules and the pressure controls native to LAMMPS.
-
3.
The MesM-P potential was implemented as LAMMPS pair style (which does not necessarily mean that all interactions are pairwise), in a highly scalable and modular way. Besides accelerating the computations orders of magnitude, this makes it possible to individually switch on and off any of the terms and combine the MesM-P potential with other standard or custom potentials.
-
4.
Along with the MesM-P force field and integration routines, a number of supporting compute modules were implemented that allow an on-the-fly computation and output of different observables. Examples of such observables are the per-term energy, the total protein density on the membrane, the per-particle composition gradient, or normal and in-plane vectors.
C. Simulation setup
The simulations reported below were performed with LAMMPS open source MD package,37 using custom implementations of MesM-P interaction potentials, corresponding atom vector style, integration routines, and various supporting compute procedures. The MesM-P source code is available for download as open source software from https://github.com/uchicago-voth/MesM-P/.
The vesicle simulations were run in a cubic box with dimensions of 360 nm, under constant volume and constant temperature of 308 K. The system contained 95 016 quasi-particles in total, 5882 of which belonged to the membrane. For stability purposes, the temperature control was performed separately for the translational degrees of freedom of solvent quasi-particles, the translational degrees of freedom of membrane quasi-particles, and the rotational degrees of freedom associated with the membrane, using the Nose-Hoover thermostat.
As was described above, two different types of solvents were used in the vesicle simulations. The solvent that was enclosed inside the membrane could not carry protein density, while the solvent outside the membrane could. An additional 1/r12 excluded volume potential that acted only at very short distances was added between the membrane and the solvent quasi-particles to prevent the solvent from crossing the membrane. Also, in the initial configuration, the protein density on the membrane was zero (ϕB,i = 1 for all i = 1 … NM), while the lipid composition on the membrane and the protein density in the outer solvent were randomly assigned values from −1 to 1. Starting from a spherical membrane configuration, with a diameter of 300 nm, each simulation was performed for half a million time steps. All simulation parameters are summarized in Table I.
III. RESULTS AND DISCUSSION
We have performed MesM-P simulations of a membrane vesicle, starting from a membrane devoid of proteins on its surface. We varied membrane stiffness and the spontaneous curvature coefficient associated with the proteins to simulate different lipid compositions and essentially different membrane-curving proteins. Two sets of results will be discussed; for the first set, the protein spontaneous curvature was always positive, while for the second set, it was negative. The motivation behind each case will be discussed below.
A. Case of positive spontaneous curvature
Many proteins, including N-BAR and F-BAR, are known to exert positive membrane curvature along their principle axis. Here, we model such a simple case of positive curvature induction. We varied the stiffness of the membrane by taking values of the strength of the bending energy from 5 kJ/mol to 100 kJ/mol. Simultaneously, we also varied the spontaneous curvature coefficient C0 from 0.07 nm−1 to 0.4 nm−1.
For all combinations of the parameter values, we found that the local protein density was well correlated with the local curvature of the membrane, with areas of the membrane with higher positive curvature typically having higher protein concentration. Also, the distribution of proteins on the membrane surface dynamically changed over the course of the simulations as the shape of the vesicle was changing. Additionally, we found that, in the absence of any control over the protein coverage on the membrane (i.e., when Hp−bias was off), the total protein density on the surface after the equilibrium was established varied in the approximate range from 5% to 25% for different values of the parameters. As this range corresponds to the protein densities that are often studied experimentally,44–46 we decided not to use any explicit control over the membrane coverage for this case. Thus, the total density of the proteins bound to the membrane varied according to the shape changes that the membrane was undergoing. Another approach where the total protein density is controlled will be discussed in Subsection III B.
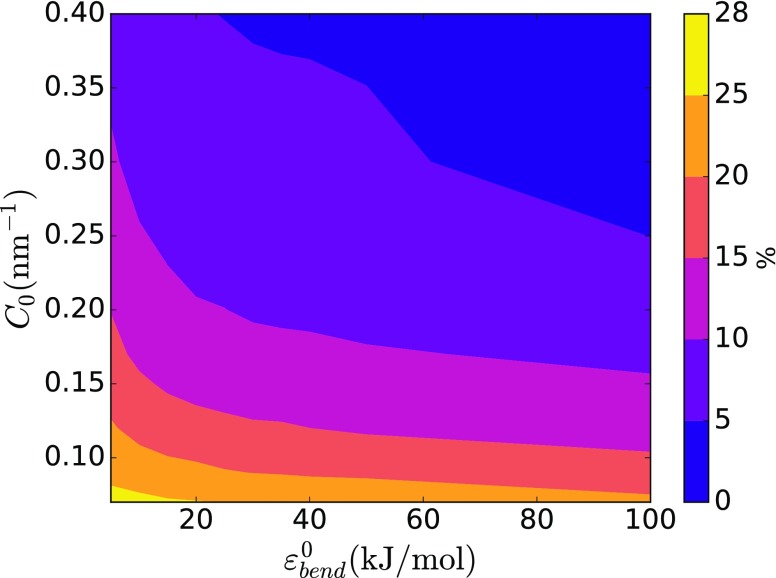
According to our model, the total bound protein density inversely correlates with and C0, as shown in Fig. 2. Under the same simulated conditions, the stiffer membranes will be more difficult to bend and therefore attract less of the curvature-sensing proteins. At the same time, highly curving proteins are less likely to find the optimal or near-optimal binding spot. In both cases, this will result in a decrease in binding of the proteins to the membrane. However, it is worth noting that the situation described here, where there is no initial protein density on the membrane, is different from in vitro experiments that are done at some quasi-static protein density. In this setup, when the membrane has initial protein density and proteins are not allowed to bind and unbind (or binding/unbinding events are rare), the proteins may even break the membrane and cause a topological transformation.28,29,36 As we will show later, the same happens when protein density is biased to a specific value in our simulations.
FIG. 2.
Dependence of the total protein density on the surface of the vesicle at equilibrium on membrane bending energy strength () and spontaneous curvature coefficient (C0).
Remarkably, in all cases of positive spontaneous curvature, therefore representing BAR/N-BAR and F-BAR proteins, protein density on the membrane formed distinct linear aggregates and meshes at lower and higher protein densities, respectively, similarly to highly CG molecular-scale MD simulations of N-BAR proteins on membranes.38,39 This observation confirms that the MesM-P model captures the collective molecular-level behavior of the CG model and, importantly, it further demonstrates the physical robustness of the linear aggregation phenomenon. Nevertheless, some differences in the way the proteins aggregate and the membrane is locally bent are seen for various cases of stiffness and spontaneous curvature.
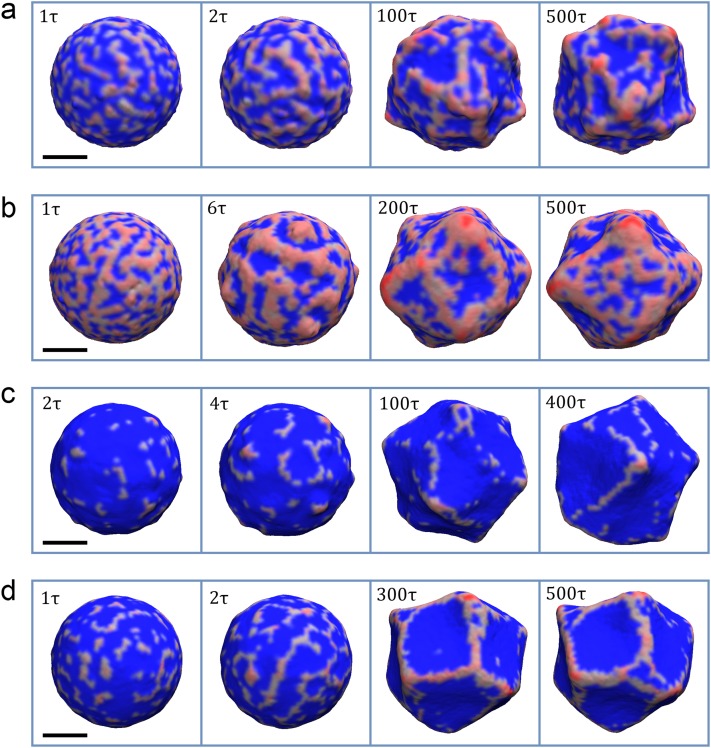
For the case of and C0 = 0.20 nm−1, the proteins induce high local membrane curvature, resulting in a positively curved budding [Fig. 3(a)]. Initially, the proteins form disconnected, but tightly packed oligomers that rapidly grow both in length and width, connecting into a semi-regular mesh [see the left two snapshots of Fig. 3(a)]. The surface enclosed by the mesh is usually flat or has small negative curvature. With time, the proteins continue to aggregate, transforming the membrane both locally and globally into a highly irregular shape [see the right two snapshots of Fig. 3(a)].
FIG. 3.
The evolution of membrane vesicle and local protein density (reddish shading) on its surface for the cases of (a) and C0 = 0.20 nm−1, (b) and C0 = 0.07 nm−1, (c) and C0 = 0.40 nm−1, and (d) and C0 = 0.20 nm−1. For (a) the semi-regular protein mesh forms from initially disconnected oligomers that span the whole surface of the vesicle. At this relatively low membrane stiffness, the mesh transforms the membrane both locally and globally. At the local scale, the aggregation of the protein results in positive curvature and budding, while the areas of the membrane that are enclosed in the mesh bend inwards, giving rise to negative curvature. The total protein density for the final state is about 15%. For (b), the interconnected protein mesh forms from the very start and coarsens over time. The total protein density for the final state is about 26%. For (c), the small amount of protein aggregates form on the membrane in the beginning, giving rise to oligomerization. However, the influx of the protein is not enough to form an interconnected mesh. Toward the end of the simulation, the long oligomers, with length scale comparable to vesicle diameter, form and break dynamically. The total protein density for the final state is only about 5%. For (d), the short oligomers that first appear start to interconnect into a mesh that spans the whole surface of the vesicle. The areas that are encircled by such mesh start to bend inward. As time progresses, the mesh continues to evolve and the areas with negative curvature tend to aggregate into larger ones. Towards the end of the simulation, the global equilibrium is established, while protein density continues to evolve locally on the membrane surface. The total protein density for the final state is about 9%. The time progresses from left to right. The label in the top left indicates the step in thousand time steps (in some time units τ). The areas of the membrane with non-zero protein local density are colored red, while the rest is colored blue. The scale bar marks 100 nm.
For the case of and C0 = 0.07 nm−1, proteins bind and form the mesh more rapidly than in the previous case. This mesh coarsens with time, where the sizes of the protein-free and the protein-rich areas grow [see the left two snapshots of Fig. 3(b)]. The membrane covered by the proteins becomes positively curved, while the areas devoid of proteins bend toward the interior, thus giving rise to negative curvature [see Fig. 3(b)]. Over the time, the sizes of protein-rich (positively curved) and protein-free (negatively curved) domains grow even further. However, at longer times, a dynamic equilibrium establishes between the protein-free and protein-rich domains that split and join over time [see the right two snapshots of Fig. 3(b)].
For the case of and C0 = 0.40 nm−1, proteins bind much slower than in the cases above, and the total density after reaching the equilibrium is below 5%. We initially see the formation of very short oligomers that dynamically move around the membrane [see the left two snapshots of Fig. 3(c)]. At longer times, the oligomers that came into close proximity to each other merge, forming longer linear oligomers and “Y” shaped formations. This eventually results in a dynamic equilibrium, where longer oligomers form and break, occasionally giving rise to circular structures and oligomers with length scales on the order of the vesicle diameter [see the right two snapshots of Fig. 3(c)].
Finally, for the case of and C0 = 0.20 nm−1, like in the previous case, we initially see the formation of short oligomers, although comparatively faster with significantly longer chains appearing on the same time scale [see the left snapshot of Fig. 3(d)]. However, unlike the previous case, those oligomers start to interconnect, forming regions of negative curvature, outlined by linear protein aggregates [see the second snapshot from the left of Fig. 3(d)]. At later times, the protein density evolves into a sparse network that outlines larger areas of inwardly bent buds. Also, contrary to the previous case, the protein network reaches a global equilibrium, maintaining its shape, while local variations in protein density occur [see the right two snapshots of Fig. 3(d)].
Next, we tested how changing the spontaneous curvature and the membrane’s bending stiffness affects protein distribution on the vesicle. We found that with increasing from 5 kJ/mol to 25 kJ/mol, proteins form a more regular mesh, with fewer loose proteins (Figs. 4 and 5). Interestingly, this tendency starts to reverse with increased bending stiffness (Figs. 6 and 7). Most likely, this behavior is a consequence of fewer proteins in general binding to stiffer membranes. Finally, while locally the membrane becomes smoother, i.e., the curvature variation is smaller at short length scales, its global shape, generally, becomes less regular with increasing . This effect can be seen by comparing simulations with different values of while keeping the same C0. However, one can see that for and C0 values of 0.30 and 0.40 nm−1, the membrane shape is nearly spherical. This result is not surprising as the final protein density on the membrane was low, 1%-2%, therefore in line with experimental observations.44–46
FIG. 4.
The final configuration of the vesicle for and C0 values of 0.07, 0.09, 0.12, 0.15, 0.17, 0.20, 0.30, and 0.40 nm−1, which appear from left to right and top to bottom, respectively. The areas of the membrane with non-zero protein local density are colored red, while the rest is colored blue. The scale bar marks 100 nm.
FIG. 5.
The final configuration of the vesicle for and C0 values of 0.07, 0.09, 0.12, 0.15, 0.17, 0.20, 0.30, and 0.40 nm−1, which appear from left to right and top to bottom, respectively. The areas of the membrane with non-zero protein local density are colored red, while the rest is colored blue. The scale bar marks 100 nm.
FIG. 6.
The final configuration of the vesicle for and C0 values of 0.07, 0.09, 0.12, 0.15, 0.17, 0.20, 0.30, and 0.40 nm−1, which appear from left to right and top to bottom, respectively. The areas of the membrane with non-zero protein local density are colored red, while the rest is colored blue. The scale bar marks 100 nm.
FIG. 7.
The final configuration of the vesicle for and C0 values of 0.07, 0.09, 0.12, 0.15, 0.17, 0.20, 0.30, and 0.40 nm−1, which appear from left to right and top to bottom, respectively. The areas of the membrane with non-zero protein local density are colored red, while the rest is colored blue. The vesicle shape becomes more asymmetric with increasing protein density (decreasing C0). The scale bar marks 100 nm.
In experiments, at high enough protein surface density and low enough membrane tension, BAR proteins induce tubules from the surface of the membrane.45 In our simulations, we did not observe tubule formation following the protein assembly. One possibility is that our simulation time scale is below the multi-second time scales at which tubules are formed in vitro. Another important thing to consider is that curvature sensing of BAR proteins depends on their surface density in a non-trivial way and the formation of tubules may be a consequence of localized aggregation. Modeling this behavior in our simulation method will be a subject of future investigation.
B. A case of negative spontaneous curvature
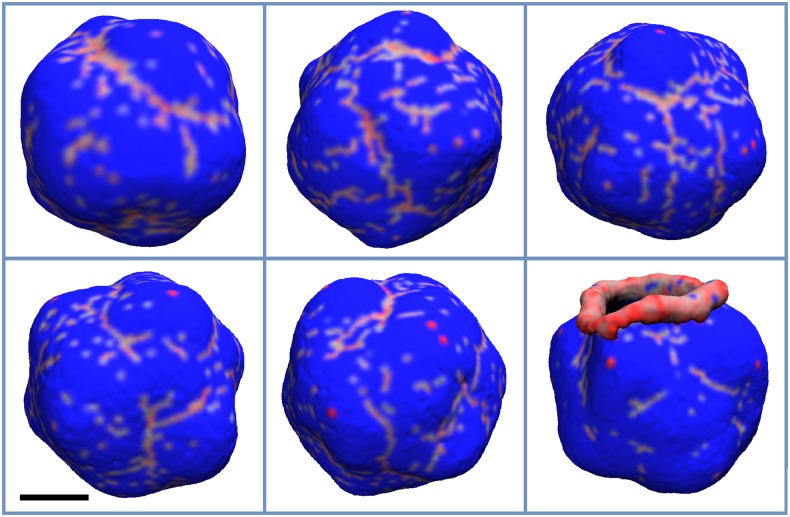
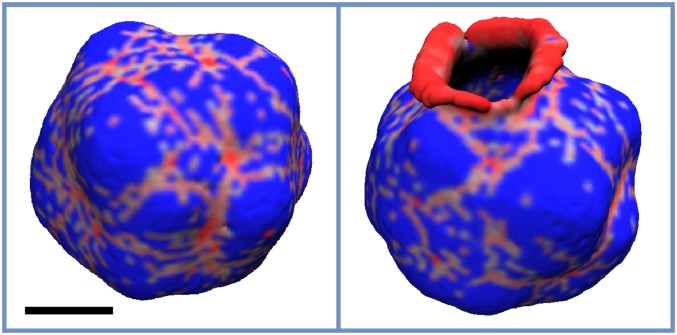
To simulate the assembly of I-BAR proteins on the membrane, we used negative C0, while assuming that the in-plane vector points perpendicularly to the protein’s main axis. Also, to closer mimic the experimental system where an equilibrium protein density was ensured by encapsulating the protein in a giant vesicle,47 we biased the total protein density at 10% and 20% (see Sec. II A 7 in Methods).
For the case of the lower protein density, where the average density settled at ∼7.5%, and for C0 ranging from −0.07 to −0.17 nm−1, we mostly see long oligomers that extend to the scale comparable to the vesicle diameter, with shorter ones appearing as well (Fig. 8). At a higher protein density (Fig. 9), ∼17%, a mesh appears as seen with positively curving proteins and in CG MD simulations. In both cases of the negative curvature here and in the CG MD simulations, the membrane has a negative curvature in the vicinity of protein aggregates, perpendicular to the direction of oligomerization, while forming positively curved buds in the areas between the oligomers or encircled by the mesh (see Figs. 8 and 9). Lastly, for smaller negative C0, the membrane breaks in one or multiple locations (see last snapshots of Figs. 8 and 9), starting to role on itself. In other words, the membrane undergoes a topological transition due to an excessive local buildup of proteins. Such a possibility was discussed in Subsection III A.
FIG. 8.
The final configuration of the vesicle for , η0 = 0.1, and C0 values of −0.07, −0.09, −0.12, −0.15, −0.17, and −0.20 nm−1, which appear from left to right and top to bottom, respectively. The areas of the membrane with non-zero protein local density are colored red, while the rest is colored blue. The scale bar marks 100 nm.
FIG. 9.
The final configuration of the vesicle for εbend = 15 kJ/mol, η0 = 0.2, and C0 values of −0.07 and −0.09 nm−1, which appear from left to right. The areas of the membrane with non-zero protein local density are colored red, while the rest is colored blue. The scale bar marks 100 nm.
IV. CONCLUSIONS
In this work, we have presented a new generation of a mesoscopic simulation model for membrane-protein systems, termed MesM-P, and its highly scalable and computationally efficient implementation. The MesM-P model extends on the EM2 model; however, it is better suited for simulations at any protein density. Moreover, new capabilities of MesM-P allow for a more realistic modeling of a typical experimental setup. For example, the P-Bias potential allows for an explicit control of protein density on the surface of the membrane, while two types of solvent particles can be used to model the asymmetric composition of solutions inside and outside the vesicle.
By simulating positively and negatively curving proteins interacting with a lipid vesicle at lower protein concentrations, we found that MesM-P simulations recapitulate the membrane-mediated formation of linear aggregates as observed for N-BAR proteins using molecular-scale CG MD simulations.38,39 Going beyond that study, we show that linear aggregation takes place over a wide range of protein spontaneous curvature and membrane bending stiffness, albeit with different binding and assembly dynamics. Therefore, we confirm the prediction39 that essentially all BAR proteins should show the same assembly behavior, although forming oligomers at different length scales.
Some differences were observed when varying membrane and protein physical parameters. Namely, the shape of the membrane enclosed by protein aggregates appeared different than in CG MD simulations. There are two important differences stemming from the molecularity between CG MD and MesM-P simulations: (1) the in-plane vectors for quasi-particles with non-zero protein density align parallel to one another, corresponding to side-by-side oligomerization rather than end-to-end in CG MD and (2) the CG simulations showed that protein oligomers induce negative local curvature in a perpendicular direction and alternating positive and negative local curvatures at length scale of one protein in a parallel direction (that is positive on average). We tested the influence of directionality of oligomerization in the case of negative C0 where the curvature was set perpendicular to the oligomers, ultimately recapitulating the same budding behavior as seen in CG MD.
Our results also have a certain resemblance to the findings of dynamically triangulated surface models that represent anisotropic protein inclusions using membrane-surface nematogens. The recent extension of such models to inhomogeneous protein concentrations at fixed surface coverage in some cases show similar aggregation behavior for corresponding surface coverage as we have explored above.20 However, there are a number of critical differences between the two models, most importantly, including explicit isotropic and anisotropic interactions between nematogens in dynamically triangulated surface models and the ability of MesM-P to model a variable protein coverage on the surface of the membrane that we have explored in this paper.
MesM-P, unlike CG models, is easier to parameterize in order to phenomenologically model different kinds of proteins or membrane compositions, thus making it possible to simulate a wide range of experimental systems. MesM-P and EM2 also accurately model the hydrodynamic behavior, protein, and lipid diffusion on mesoscopic scales, and permit topological transitions by using a grid-free and bond-free approach. These advances open possibilities to realistically simulate a variety of interesting systems that have been inaccessible to previous mesoscopic or CG models as well as to attain unprecedented length and time scales for them.
However, perhaps the biggest potential of the MesM-P approach is in its role as a link between molecular interactions and macroscopic phenomena. It has been previously demonstrated how molecular details of large scale membrane remodeling can be understood using a combination of bottom-up CG and mesoscopic modeling.48 While the molecular-level CG description does not allow for a direct observation of shape and topology changes that the membrane undergoes on realistic (experimental) length and time scales, the packing and molecular interactions of proteins and proteins with the membrane can be studied quantitatively using the membrane conformations obtained from mesoscopic simulations. This is done by back-mapping parts of the system that are of interest to CG representation and equilibrating them. The obtained CG system can then be used to study molecular details, including of protein aggregation and membrane-protein interactions.48 This approach in essence transfers high length scale information obtained from mesoscopic simulations back to the molecular scale CG model. However, the opposite can also be done. If the CG model was obtained using a bottom-up approach and recapitulates the important details of the atomistic system, one can imagine passing those details further into the mesoscopic model by their systematic incorporation into MesM-P. This can be done by either reparameterization of the existing parts of MesM-P Hamiltonian or by the addition of the new terms into it that control “short-range” properties of the system, such as protein oligomerization or local curvature generation and sensing. Together, those two approaches will allow for a deep understanding of phenomena such as protein-facilitated membrane remodeling both qualitatively and quantitatively. This will be a subject of future research.
ACKNOWLEDGMENTS
This work was supported by the National Institute of General Medical Sciences (NIGMS) of the National Institutes of Health (NIH) under Award No. R01GM063796. We acknowledge the contribution of Dr. John Grime for helpful discussions on implementation of the MesM-P model in LAMMPS, and the contribution of Dr. Jesper Madsen for help with vector visualization and analysis. For computational resources, this work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the National Science Foundation (Grant No. ACI-1053575).
APPENDIX: DERIVATION OF MesM-P
Similar to its predecessor EM2, the MesM-P model can be derived from the continuum elastic model of the membrane using the SPAM framework. Such a derivation was discussed in detail in several of the previous publications.26,27 Here, we briefly describe the continuum field-theory model that MesM-P is based on and discuss its derivation.
The free energy of undulating membrane with protein inclusions can be written as
| (A1) |
where the first three terms describe the elastic properties of the membrane and correspond to mean and deviatoric (Gaussian) bending energies, and bulk expansion/contraction contribution, respectively,26,27,40,49
| (A2) |
| (A3) |
| (A4) |
In Eq. (A2), kc is the bending modulus, c1,2 = 1/R1,2 are the two local principal curvatures, H = (c1 + c2)/2 is the mean curvature, and C0 is the spontaneous curvature. For n = 2, the spontaneous curvature, C0, is isotropic, applied equally to all the directions, while n = 1 corresponds to the case of anisotropic spontaneous curvature that is applied only in the direction of in-plane vector . For C0 = 0, Eq. (A2) provides the free-energy of the membrane relative to its flat conformation. In Eqs. (A3) and (A4), Ba is the deviatoric modulus, λ is the bulk modulus, h is the thickness of the membrane, and 2ε is the local, in-plane, strain, which is zero for flat membrane. It is worth noting that the integrals in Eqs. (A2) and (A3) are calculated in some local coordinate system defined at the area element dAm, while the integral in Eq. (A4) is evaluated along the initial flat membrane (thus the area element dA0) is used.
Equations (A2)–(A4) can be discretized by defining the local density of the initially flat membrane as
| (A5) |
where δM(r − ri) is the weight function that satisfies the condition drδM(r − ri) = 1 and NM is the number of mesoscopic quasi-particles that will be used to represent the membrane. The exact expression for δM(r − ri) does not matter as long as it becomes zero beyond some distance σ from ri, which defines the fundamental discretization length scale of the membrane. Then, with the assumptions of nearly uniform density, ρ(r)/ρ0 1, and flat membrane, C0 = 0, the effective discretized expressions can be obtained,27
| (A6) |
| (A7) |
where ρA = Nm/A is the initial area density of the membrane, Nc,i is the average number of quasi-particles found within the interaction cutoff near quasi-particle i, and rij and are the instantaneous initial separations between quasi-particles i and j.
Equation (A6) represents contributions from both mean and deviatoric bending energies28 [Eqs. (A2) and (A3)], and Eq. (A7) corresponds to the bulk expansion/contraction energy given in Eq. (A4). Then, the effect of anisotropic inclusions can be added in a straightforward manner to obtain the expression given in Eqs. (7)–(12). The quadratic form of Eq. (A7) implies a harmonic bonding between the nearest quasi-particles. However, such a bonding term will be prohibitive for topological transformation of the membrane and it is more general to replace it with a dissociable potential, like the one given in Eqs. (3) and (4).
The term Fϕ in Eq. (A1) represents the free energy of spatially varying protein and lipid composition fields that are given by the standard Landau model,
| (A8) |
where the first term always drives the system to the uniform composition, while the second term can be chosen to represent the tendency of the system to either mix (presented by a single well form) or phase separate (two- or multi-well form). Similar to the previous case, Eq. (A8) can be discretized by defining a local density function. Using a specific form of the density function defined as
| (A9) |
with W(r) as a Lucy function30 [see Eq. (22)], one can obtain Eqs. (19) and (20).26 The last term in Eq. (A1), Fϕ,H, is responsible for coupling between the protein composition and curvature,26
| (A10) |
Being quadratic in curvature and linear in composition, this term does not favor either direction of bending. Its contribution is divided between the modulation of the bending stiffness of the membrane [see Eq. (14)] and IC potential [Eq. (15)]. The former represents the membrane stiffening or softening under the influence of the proteins, while the latter creates a feedback between membrane bending and local concentration of the proteins.
REFERENCES
- 1.Ayton G. S. and Voth G. A., J. Phys. Chem. B 113, 4413 (2009). 10.1021/jp8087868 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Izvekov S. and Voth G. A., J. Phys. Chem. B 113, 4443 (2009). 10.1021/jp810440c [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ayton G. S., Lyman E., and Voth G. A., Faraday Discuss. 144, 347 (2010). 10.1039/b901996k [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wang Z.-J. and Deserno M., J. Phys. Chem. B 114, 11207 (2010). 10.1021/jp102543j [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Srivastava A. and Voth G. A., J. Chem. Theory Comput. 9, 750 (2012). 10.1021/ct300751h [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Srivastava A. and Voth G. A., J. Chem. Theory Comput. 10, 4730 (2014). 10.1021/ct500474a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Brannigan G., Philips P. F., and Brown F. L., Phys. Rev. E 72, 011915 (2005). 10.1103/physreve.72.011915 [DOI] [PubMed] [Google Scholar]
- 8.Cooke I. R., Kremer K., and Deserno M., Phys. Rev. E 72, 011506 (2005). 10.1103/physreve.72.011506 [DOI] [PubMed] [Google Scholar]
- 9.Slepnev V. I. and De Camilli P., Nat. Rev. Neurosci. 1, 161 (2000). 10.1038/35044540 [DOI] [PubMed] [Google Scholar]
- 10.Doherty G. J. and McMahon H. T., Annu. Rev. Biochem. 78, 857 (2009). 10.1146/annurev.biochem.78.081307.110540 [DOI] [PubMed] [Google Scholar]
- 11.Arasada R. and Pollard T. D., J. Cell Sci. 128, 2259 (2015). 10.1242/jcs.162974 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Boucrot E., Ferreira A. P., Almeida-Souza L., Debard S., Vallis Y., Howard G., Bertot L., Sauvonnet N., and McMahon H. T., Nature 517, 460 (2015). 10.1038/nature14067 [DOI] [PubMed] [Google Scholar]
- 13.Renard H.-F., Simunovic M., Lemière J., Boucrot E., Garcia-Castillo M. D., Arumugam S., Chambon V., Lamaze C., Wunder C., and Kenworthy A. K., Nature 517, 493 (2015). 10.1038/nature14064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Frost A., De Camilli P., and Unger V. M., Structure 15, 751 (2007). 10.1016/j.str.2007.06.006 [DOI] [PubMed] [Google Scholar]
- 15.Qualmann B., Koch D., and Kessels M. M., EMBO J. 30, 3501 (2011). 10.1038/emboj.2011.266 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chen Z., Atefi E., and Baumgart T., Biophys. J. 111, 1823 (2016). 10.1016/j.bpj.2016.09.039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Simunovic M., Voth G. A., Callan-Jones A., and Bassereau P., Trends Cell Biol. 25, 780 (2015). 10.1016/j.tcb.2015.09.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Monticelli L., Kandasamy S. K., Periole X., Larson R. G., Tieleman D. P., and Marrink S.-J., J. Chem. Theory Comput. 4, 819 (2008). 10.1021/ct700324x [DOI] [PubMed] [Google Scholar]
- 19.Ramakrishnan N., Ipsen J. H., and Kumar P. B. S., Soft Matter 8, 3058 (2012). 10.1039/c2sm07384f [DOI] [PubMed] [Google Scholar]
- 20.Ramakrishnan N., Kumar P. B. S., and Ipsen J. H., Biophys. J. 104, 1018 (2013). 10.1016/j.bpj.2012.12.045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sreeja K., Ipsen J. H., and Kumar P. B. S., J. Phys.: Condens. Matter 27, 273104 (2015). 10.1088/0953-8984/27/27/273104 [DOI] [PubMed] [Google Scholar]
- 22.Shiba H. and Noguchi H., Phys. Rev. E 84, 031926 (2011). 10.1103/physreve.84.031926 [DOI] [PubMed] [Google Scholar]
- 23.Noguchi H., Europhys. Lett. 108, 48001 (2014). 10.1209/0295-5075/108/48001 [DOI] [Google Scholar]
- 24.Noguchi H., Sci. Rep. 6, 20935 (2016). 10.1038/srep20935 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Noguchi H., Phys. Rev. E 93, 052404 (2016). 10.1103/PhysRevE.93.052404 [DOI] [PubMed] [Google Scholar]
- 26.Ayton G. S., McWhirter J. L., McMurtry P., and Voth G. A., Biophys. J. 88, 3855 (2005). 10.1529/biophysj.105.059436 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ayton G. S., McWhirter J. L., and Voth G. A., J. Chem. Phys. 124, 064906 (2006). 10.1063/1.2165194 [DOI] [Google Scholar]
- 28.Ayton G. S., Blood P. D., and Voth G. A., Biophys. J. 92, 3595 (2007). 10.1529/biophysj.106.101709 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ayton G. S., Lyman E., Krishna V., Swenson R. D., Mim C., Unger V. M., and Voth G. A., Biophys. J. 97, 1616 (2009). 10.1016/j.bpj.2009.06.036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lucy L. B., Astron. J. 82, 1013 (1977). 10.1086/112164 [DOI] [Google Scholar]
- 31.Kum O., Hoover W. G., and Posch H. A., Phys. Rev. E 52, 4899 (1995). 10.1103/physreve.52.4899 [DOI] [PubMed] [Google Scholar]
- 32.Hoover W. G. and Hoover C. G., Mol. Phys. 101, 1559 (2003). 10.1080/0026897021000026647 [DOI] [Google Scholar]
- 33.Hoover W. G., Hoover C., Kum O., Castillo V., Posch H., and Hess S., Smooth Particle Applied Mechanics (World Scientific, 2006). [Google Scholar]
- 34.Monaghan J. J., Annu. Rev. Astron. Astrophys. 30, 543 (1992). 10.1146/annurev.aa.30.090192.002551 [DOI] [Google Scholar]
- 35.Ellero M., Kröger M., and Hess S., J. Non-Newtonian Fluid Mech. 105, 35 (2002). 10.1016/s0377-0257(02)00059-9 [DOI] [Google Scholar]
- 36.Simunovic M., Mim C., Marlovits T. C., Resch G., Unger V. M., and Voth G. A., Biophys. J. 105, 711 (2013). 10.1016/j.bpj.2013.06.039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Plimpton S., J. Comput. Phys. 117, 1 (1995). 10.1006/jcph.1995.1039 [DOI] [Google Scholar]
- 38.Simunovic M., Srivastava A., and Voth G. A., Proc. Natl. Acad. Sci. U. S. A. 110, 20396 (2013). 10.1073/pnas.1309819110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Simunovic M. and Voth G. A., Nat. Commun. 6, 7219 (2015). 10.1038/ncomms8219 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Fischer T. M., J. Phys. II 2, 337 (1992). 10.1051/jp2:1992137 [DOI] [Google Scholar]
- 41.Leibler S., J. Phys. 47, 507 (1986). 10.1051/jphys:01986004703050700 [DOI] [Google Scholar]
- 42.McWhirter J. L., Ayton G., and Voth G. A., Biophys. J. 87, 3242 (2004). 10.1529/biophysj.104.045716 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Metiu H., Kitahara K., and Ross J., J. Chem. Phys. 65, 393 (1976). 10.1063/1.432779 [DOI] [Google Scholar]
- 44.Sorre B., Callan-Jones A., Manzi J., Goud B., Prost J., Bassereau P., and Roux A., Proc. Natl. Acad. Sci. U. S. A. 109, 173 (2012). 10.1073/pnas.1103594108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Shi Z. and Baumgart T., Nat. Commun. 6, 5974 (2015). 10.1038/ncomms6974 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Simunovic M., Evergren E., Golushko I., Prévost C., Renard H.-F., Johannes L., McMahon H. T., Lorman V., Voth G. A., and Bassereau P., Proc. Natl. Acad. Sci. U. S. A. 113, 11226 (2016). 10.1073/pnas.1606943113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Prévost C., Zhao H., Manzi J., Lemichez E., Lappalainen P., Callan-Jones A., and Bassereau P., Nat. Commun. 6, 8529 (2015). 10.1038/ncomms9529 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lyman E., Cui H., and Voth G. A., Phys. Chem. Chem. Phys. 13, 10430 (2011). 10.1039/c0cp02978e [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Helfrich W., Z. Naturforsch., C: J. Biosci. 28, 693 (1973). 10.1515/znc-1973-11-1209 [DOI] [PubMed] [Google Scholar]