A Functional Subnetwork Approach to Designing Synthetic Nervous Systems That Control Legged Robot Locomotion

Abstract

A dynamical model of an animal’s nervous system, or synthetic nervous system (SNS), is a potentially transformational control method. Due to increasingly detailed data on the connectivity and dynamics of both mammalian and insect nervous systems, controlling a legged robot with an SNS is largely a problem of parameter tuning. Our approach to this problem is to design functional subnetworks that perform specific operations, and then assemble them into larger models of the nervous system. In this paper, we present networks that perform addition, subtraction, multiplication, division, differentiation, and integration of incoming signals. Parameters are set within each subnetwork to produce the desired output by utilizing the operating range of neural activity, R, the gain of the operation, k, and bounds based on biological values. The assembly of large networks from functional subnetworks underpins our recent results with MantisBot.

1. Introduction

The development of robotic control that can closely match the dexterity and adaptability found in the animal kingdom has so far remained elusive. This is because the control of locomotion is a complex process controlled by dynamic systems which are not fully understood. However, recent advances in neural imaging and recording has lead to an increase in the abundance and detail of our knowledge of how an animal’s nervous system controls its body within the context of its environment (for a recent review, see Buschmann et al. (2015)).

These advances have lead to an explosion of bio-inspired robotic systems in recent years (for a review, see Ijspeert (2014)). These models can be broadly categorized into a range of template and anchor models. In a template model, biological principles are abstracted, such using as a spring-loaded inverted pendulum (SLIP) model to investigate bipedal locomotion (Blickhan, 1989) or using Whegs to investigate insect locomotion (Allen et al., 2003; Schroer et al., 2004). These models seek to explain how specific characteristics of animal locomotion lead to desired behaviors, or they exploit certain principles of animal locomotion for more agile robotic systems. Anchor models, in contrast, seek to directly mimic particular mechanical or control mechanisms from animals, in order to understand how they function. Robots such as Pleurobot (Karakasiliotis et al., 2016), Puppy (Hunt et al., 2017), MantisBot (Szczecinski and Quinn, 2017; Szczecinski et al., 2017a), and others are relevant anchor models, because they seek to use highly articulated robots with central pattern generator controllers to understand how specific animals are capable of providing adaptable locomotion with their unique morphology and physical constraints.

The template versus anchor model distinction is not limited to physical models; it can also be applied to control systems. The majority of robotic controllers so far have been template models, either mathematical abstractions of neural systems, or black box artificial neural networks. This is because effective tools for setting parameters in more realistic, dynamic neural models to produce reliable behavior in a robotic system do not yet exist. In spite of growing knowledge about the neural connectivity that underlies locomotion control, detailed data for tuning these systems (neural time constants, ion channel conductivities, synaptic conductivities, etc.) remain largely unavailable, requiring the modeler or engineer to tune these parameter values. However, this is an inherently difficult task because there are many parameters to be tuned in a model, and likely many different parameter combinations that lead to indistinguishable performance (Prinz et al., 2004; Marder and Taylor, 2011). Thus, the emphasis in choosing parameter values should not be on selecting the singular “correct” values, but rather sufficiently “effective” values. In this work, we tune parameter values in functional subnetworks for addition, subtraction, multiplication, division, differentiation, and integration of incoming signals and use analytical techniques to identify constraints on the parameter values that must be met for the intended calculations to occur. Larger networks can then be assembled from these subnetworks with no additional tuning (Szczecinski and Quinn, 2017; Szczecinski et al., 2017a). In this manuscript, “tuning” refers to selecting the static parameter values for a network; “learning” refers to changing the parameter values while the model performs a task, either in simulation or in a robot, based on its performance; and “adapting” refers to a model qualitatively changing its behavior (e.g., walking more slowly), either with or without “learning.”

Neuromechanical models may be tuned in a supervised or unsupervised way. A supervised tuning method adjusts the parameters of the model until the model replicates animal data. This includes tuning the model by hand (Daun-Gruhn and Tóth, 2010; Szczecinski et al., 2014; Markin et al., 2016), which is a time-consuming and imprecise process. Such imprecision may be acceptable in simulation studies, but provides many difficulties for robots that must interact with real environments. Techniques do exist for tuning controllers based on animal locomotion data (Schilling et al., 2013; Hunt et al., 2015b, 2017; Karakasiliotis et al., 2016). However, collecting kinematic and dynamic data from animals is time-consuming and expensive, and once collected, must be further processed to scale the dynamics of the animal to the robot (Karakasiliotis et al., 2016; Hunt et al., 2017). In addition, using cross-individual average values for tuning dynamical neural models may fail in many cases, because the average may not represent any one individual (Golowasch et al., 2002; Marder and Taylor, 2011). Large amounts of animal data may be used to tune a control network of abstracted artificial neural networks (Schilling et al., 2013). Methods like back-propagation can be used to adjust synaptic weights in the network until it captures the animal data arbitrarily closely, if it has enough connections (Trappenberg, 2009). However, because the control network is abstracted, so are the biological insights gained from the model.

Unsupervised tuning methods, in contrast, tune the model based on how well the model accomplishes a task, such as navigating toward a goal, without comparison to animal data. These methods frequently use genetic algorithms (GAs) (Beer and Gallagher, 1992; Haferlach et al., 2007; Agmon and Beer, 2013; Izquierdo and Beer, 2013) or reservoir computing (RC) (Dasgupta et al., 2015) to test many different networks and parameter values, based on a simulated agent’s performance. GAs can be effective at finding networks that perform specific operations, such as oscillating (Beer and Gallagher, 1992), navigating (Haferlach et al., 2007), or switching between foraging tasks (Agmon and Beer, 2013). However, this approach has some drawbacks. Specifically, the evolution process is slow, requiring the simulation of hundreds or thousands of parameter combinations (Agmon and Beer, 2013), which may take days without great computing power. The speed and likelihood of success can be increased by embedding functional subnetworks in the network (Pasemann et al., 2001; Haferlach et al., 2007), which may be identified by brute-force (Prinz et al., 2003), dynamical systems analysis (Hunt et al., 2017), or constraints on network connectivity and parameter values (Haferlach et al., 2007). In this paper, we analytically derive parameter constraints to eliminate the need for GAs altogether, and guarantee network performance.

RC methods simulate large “reservoirs” of randomly connected dynamical neuron models, and then use optimization methods to map reservoir activity to learned useful values. While this method can produce capable robotic controllers (Dasgupta et al., 2015), the final system is likely more complicated than is ultimately necessary, increasing its computational cost to implement. In addition, the final system is a black box, which does not provide any insights about nervous system function. The methods in this paper enable the direct assembly and tuning of dynamical networks without the need of large reservoirs of neurons.

This work analytically derives constraints that govern the behavior of synthetic nervous systems (SNSs) built from dynamical neural networks. These constraints were derived as a result of our previous network design work (Szczecinski et al., 2017b) and have enabled the rapid assembly and testing of our recent robot control networks (Szczecinski and Quinn, 2017; Szczecinski et al., 2017a). An SNS designer can apply these constraints to find parameter values needed for a functional network. Section 2 presents the neural and synaptic models and explains how the neural system encodes mechanical inputs and outputs. Section 3 derives two basic synapse types, “signal transmission” and “signal modulation,” and uses them to derive constraints on synaptic parameters in networks performing addition, subtraction, multiplication, and division of two incoming signals. Section 4 derives constraints on neural and synaptic parameters in networks that differentiate and integrate incoming signals as a function of time. Results showing that the networks perform as intended are provided throughout the manuscript, and Tables 1 and 2 summarize the design constraints. Finally, Sec. 6 explores how these techniques may be used to tune robot controllers and neuromechanical models of animals, and how they may be improved in the future.

Table 1.

This table assumed that the designer has already selected a value of R for the subnetwork.

Operation	Componentpathways	Constraint equations	Free parameters
Addition	Syn. 1,	${\mathit{g}}_{\mathit{s}\text{,1}}=\frac{{\mathit{k}}_{\mathit{syn}\text{,1}}\cdot \mathit{R}}{\mathrm{\Delta }{\mathit{E}}_{\mathit{s}\text{,1}}-{\mathit{k}}_{\mathit{syn}\text{,1}}\cdot \mathit{R}}$	ksyn,1
	transmission	ΔEs,1 − ksyn,1⋅R > 0	ΔEs,1, maximize
	Syn. 2,	${\mathit{g}}_{\mathit{s}\text{,2}}=\frac{{\mathit{k}}_{\mathit{syn}\text{,2}}\cdot \mathit{R}}{\mathrm{\Delta }{\mathit{E}}_{\mathit{s}\text{,2}}-{\mathit{k}}_{\mathit{syn}\text{,2}}\cdot \mathit{R}}$	ksyn,2
	transmission	ΔEs,2 − ksyn,2⋅R > 0	ΔEs,2, maximize
Subtraction	Syn. 1,	${\mathit{g}}_{\mathit{s}\text{,1}}=\frac{{\mathit{k}}_{\mathit{syn}}\cdot \mathit{R}}{\mathrm{\Delta }{\mathit{E}}_{\mathit{s}\text{,1}}-{\mathit{k}}_{\mathit{syn}}\cdot \mathit{R}}$	ksyn
	transmission	ΔEs,1 − ksyn⋅R > 0	ΔEs,1, maximize
	Syn. 2,	${\mathit{g}}_{\mathit{s}\text{,2}}=\frac{\mathrm{\Delta }{\mathit{E}}_{\mathit{s}\text{,1}}}{\mathrm{\Delta }{\mathit{E}}_{\mathit{s}\text{,2}}}\cdot \frac{-{\mathit{k}}_{\mathit{syn}}\cdot \mathit{R}}{\mathrm{\Delta }{\mathit{E}}_{\mathit{s}\text{,1}}-{\mathit{k}}_{\mathit{syn}}\cdot \mathit{R}}$	ΔEs,2, minimize
	transmission
Division	Syn. 1,	${\mathit{g}}_{\mathit{s}\text{,1}}=\frac{{\mathit{k}}_{\mathit{syn}}\cdot \mathit{R}}{\mathrm{\Delta }{\mathit{E}}_{\mathit{s}\text{,1}}-{\mathit{k}}_{\mathit{syn}}\cdot \mathit{R}}$	csyn
	transmission	ksyn = 1	ΔEs,1, maximize
		ΔEs,1 − ksyn⋅R > 0
	Syn. 2,	${\mathit{g}}_{\mathit{s}\text{,2}}=\frac{{\mathit{c}}_{\mathit{syn}}\cdot \mathit{R}-\mathit{R}}{\mathrm{\Delta }{\mathit{E}}_{\mathit{s}\text{,2}}-{\mathit{c}}_{\mathit{syn}}\cdot \mathit{R}}$
	modulation	ΔEs,2 = 0
		0 < csyn < 1
Multiplication	Syn. 1,	${\mathit{g}}_{\mathit{s}\text{,1}}=\frac{{\mathit{k}}_{\mathit{syn}}\cdot \mathit{R}}{\mathrm{\Delta }{\mathit{E}}_{\mathit{s}\text{,1}}-{\mathit{k}}_{\mathit{syn}}\cdot \mathit{R}}$
	transmission	ksyn = 1
		ΔEs,1 − ksyn⋅R > 0	ΔEs,1, maximize
	Syn. 2,	${\mathit{g}}_{\mathit{s}\text{,2}}=\frac{-\mathit{R}}{\mathrm{\Delta }{\mathit{E}}_{\mathit{s}\text{,2}}}$
	modulation	ΔEs,2 < 0	ΔEs,2, maximize
	Syn. 3,	gs,3 = gs,2
	modulation	ΔEs,3 = ΔEs,2

In this table, “minimize” refers to making a value as negative as possible and “maximize” refers to making a value as positive as possible.

Table 2.

This table assumed that the designer has already selected a value of R for the subnetwork.

Operation	Components	Constraints and useful relations	Free parameters
Differentiation	Neuron 1	Cm,1 < Cm,2	τd
	Neuron 2	Cm,2 = τd	kd
		Cm,1 = Cm,2 − kd
	Syn. 1,	ksyn = 1/kd	ΔEs,1, maximize
	transmission	${\mathit{g}}_{\mathit{s}\text{,1}}=\frac{{\mathit{k}}_{\mathit{syn}}\cdot \mathit{R}}{\mathrm{\Delta }{\mathit{E}}_{\mathit{s}\text{,1}}-{\mathit{k}}_{\mathit{syn}}\cdot \mathit{R}}$
		ΔEs,1 − ksyn⋅R > 0
	Syn. 2,	${\mathit{g}}_{\mathit{s}\text{,2}}=\frac{\mathrm{\Delta }{\mathit{E}}_{\mathit{s}\text{,1}}}{\mathrm{\Delta }{\mathit{E}}_{\mathit{s}\text{,2}}}\cdot \frac{-{\mathit{k}}_{\mathit{syn}}\cdot \mathit{R}}{\mathrm{\Delta }{\mathit{E}}_{\mathit{s}\text{,1}}-{\mathit{k}}_{\mathit{syn}}\cdot \mathit{R}}$	ΔEs,2, minimize
	transmission
Integration	Neuron 1	Iapp,1 = R	ki,mean
		${\mathit{C}}_{\mathit{m}\text{,1}}=\frac{\text{1}}{\text{2}\cdot {\mathit{k}}_{\mathit{i},\text{mean}}}$
	Neuron 2	Iapp,2 = R
		Cm,1 = Cm,2
	Syn. 1,	$\mathrm{\Delta }{\mathit{E}}_{\mathit{s}\text{,1}}=\frac{-\mathit{R}}{{\mathit{g}}_{\mathit{s}\text{,1}}}$	ki,range
	transmission	${\mathit{g}}_{\mathit{s}\text{,1}}=\frac{\text{2}\cdot {\mathit{C}}_{\mathit{m}\text{,1}}}{\text{1}∕{\mathit{k}}_{\mathit{i}\text{,range}}-{\mathit{C}}_{\mathit{m}\text{,1}}}$
	Syn. 2,	gs,2 = gs,1
	transmission	ΔEs,2 = ΔEs,1

In this table, “minimize” refers to making a value as negative as possible and “maximize” refers to making a value as positive as possible.

2. Methods: Models and Approach

We model neurons as non-spiking Hodgkin–Huxley compartments (Cofer et al., 2010), the same basic model as used in continuous-time recurrent neural networks (Haferlach et al., 2007; Agmon and Beer, 2013). The leaky integrator dynamics capture the most basic behavior of neurons and allow more complex behaviors to be added with additional ion channels, if desired. This work is not concerned with the specifics on how action potentials are generated and have left out Hodgkin–Huxley sodium and potassium currents. The membrane voltage, V, may be seen as a proxy for the spiking frequency of a spiking neuron. V varies according to the differential equation

$$C_m\frac{\mathit{dV}}{\mathit{dt}}=I_{\mathit{leak}}+I_{\mathit{syn}}+I_{\mathit{app}}$$ (1)

where

$$I_{\mathit{leak}}=G_m\cdot \left(E_r-V\right),$$ (2)

$$I_{\mathit{syn}}={\displaystyle \sum _{i=1}^n}{G}_{s,i}\cdot \left(E_{s,i}-V\right),$$ (3)

and I_app is an optional external stimulus. Equations (2) and (3) define the leak and synaptic currents, respectively. Both follow the same basic form of a conductance G multiplied by the difference between the current membrane voltage, V, and a constant reference voltage (i.e., reversal potential), E. E_r is the resting potential of the neuron, and C_m and G_m are the capacitance and conductance of the cell membrane, respectively. Unless otherwise noted, all units in this paper are scaled to nA for current, mV for potentials, nF for capacitances, and μS for conductances.

Neurons communicate via synapses. The conductance, G_s,i in equation (3), is a threshold linear function of the ith incoming (i.e., presynaptic) neuron’s voltage. Synapses communicate via piecewise-linear functions described as

$$G_{s,i}=\left\{\begin{array}{ll}0,\hfill & \text{if}{V}_{\mathit{pre}}<E_{\mathit{lo}},\hfill \\ g_{s,i}\cdot \frac{V_{\mathit{pre}}-E_{\mathit{lo}}}{E_{\mathit{hi}}-E_{\mathit{lo}}},\hfill & \text{if}{E}_{\mathit{lo}}<V_{\mathit{pre}}<E_{\mathit{hi}},\hfill \\ g_{s,i},\hfill & \text{if}{V}_{\mathit{pre}}>E_{\mathit{hi}}.\hfill \end{array}\right.$$ (4)

The parameters g_s,i, E_lo, and E_hi are constants representing the synapse’s maximum conductance, its lower threshold, and its upper threshold, respectively. The relationship between the presynaptic neuron voltage, synaptic conductance, and postsynaptic neuron voltage is illustrated in Figure 1A.

Figure 1.

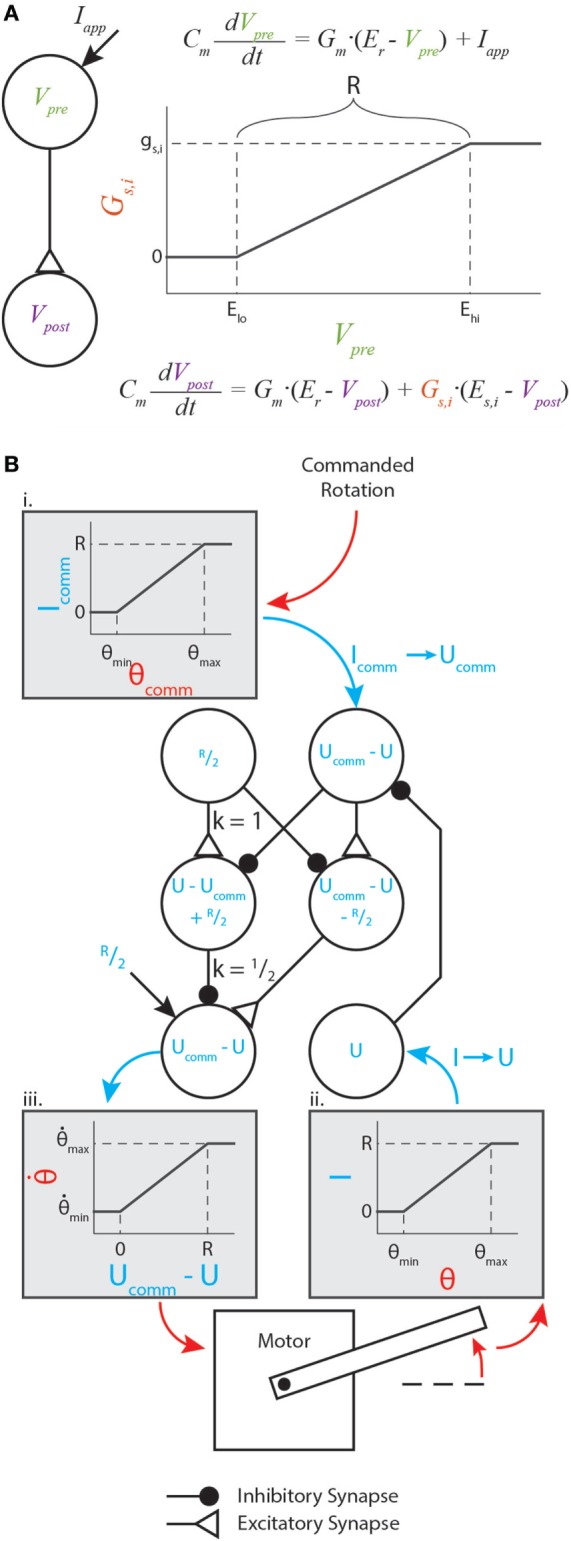
Graphical representation of synaptic dynamics and mapping between mechanical and neural values. (A) Graphical representation of how synapses couple neural dynamics. Note that R is marked on the plot. (B) Enhanced version of the motor control network from Szczecinski et al. (2017b), showing how R relates mechanical and neural values. Mechanical values are drawn in red, and neural values are drawn in blue. Gray shaded boxes map from mechanical to neural values (i. and ii.), or from neural to mechanical values (iii.).

We prefer this piecewise-linear representation better than a sigmoidal function for several reasons. First, the thresholds ensure that for low activations, synapses conduct exactly 0 current. This could represent a reduced model of a spiking neuron, which transmits no information while it is not spiking. Second, equation (4) contains no transcendental terms, facilitating analytical manipulation of the equations. A discontinuous system does complicate traditional gradient-based optimization methods, but this structure can be exploited to make these methods unnecessary. In the following sections, we show how networks of three or four neurons with synapses between them can be constructed and analytically tuned to perform mathematical operations on the input signals, such as addition or differentiating with respect to time.

Instead of analyzing V when designing these networks, we shift the neural activity to simplify analysis. For each neuron, we substitute U = V − E_r, the activation level above the resting voltage. A typical value is E_r = −60 mV, but using U for analysis rather than V lets us apply the same analysis no matter what E_r is. We also set G_m = 1 μS, which is a typical value (Daun-Gruhn et al., 2009; Daun-Gruhn, 2010).

For the synapses, we set E_lo = E_r of the presynaptic neuron, and introduce a new parameter R = E_hi − E_lo. Thus, a synapse’s conductivity rises as the presynaptic neuron’s voltage rises above its resting potential, and exhibits an “operating range” of R mV. The constraints we apply ensure that U_pre ∈ [0, R], meaning that the synapse is always active, but never saturates. Thus, we can replace G_s with the second line of equation (4). Applying the substitutions described so far,

$$G_s=g_s\cdot \frac{V_{\mathit{pre}}-E_{\mathit{lo}}}{E_{\mathit{hi}}-E_{\mathit{lo}}}=g_s\cdot \frac{U_{\mathit{pre}}}{R}=\frac{g_s}{R}\cdot U_{\mathit{pre}}.$$ (5)

For each synapse, we also introduce the parameter ΔE_s,i = E_s,i − E_r,post, where E_r,post is the resting potential of the postsynaptic, or receiving neuron.

Making all of these substitutions in equations (1)–(3) gives the response

$$C_m\frac{\mathit{dU}}{\mathit{dt}}=-U+{\displaystyle \sum _{i=1}^n}\frac{g_{s,i}}{R}\cdot U_{\mathit{pre},i}\cdot \left(\mathrm{\Delta }{E}_{s,i}-U\right)+I_{\mathit{app}}.$$ (6)

When U = R, the neuron is fully active, and when U = 0, the neuron is inactive. We can use this knowledge to categorize synapses as excitatory or inhibitory, depending on the sign of ΔE_s,i. If ΔE_s,i ≥ R, then the ith synapse will always transmit positive current, no matter the instantaneous value of U. Thus, this synapse will cause U to increase and is, therefore, excitatory. Similarly, if ΔE_s,i ≤ 0, then the ith synapse will always transmit negative current, no matter the instantaneous value of U. Thus, this synapse will cause U to decrease and is, therefore, inhibitory.

2.1. Mapping between Neural and Mechanical Values

The nervous system encodes physical quantities as neural activity. In insects, the firing rate of sensory neurons encode the stretch of chordotonal organs (Field and Matheson, 1998) and the strain of campaniform sensilla (Zill et al., 2004), among other physical quantities. Typical robot controllers perform operations on these signals to provide meaningful information for control actions. These operations may include the subtraction of measured and reference values, differentiation or integration of error values, or gain adjustments. Neural systems perform these same operations, but in a transformed space. The exact transformation that nervous systems use is not known, but for reliable behavior, it is necessary that sensory information is mapped to neural activity in apredictable way. Thus, we map any sensory input, θ, to an applied current

$$I_{\mathit{app}}=R\cdot \frac{\theta -{\theta }_{\min }}{{\theta }_{\max }-{\theta }_{\min }},$$ (7)

where R is the “operating range” specified in the previous section. Figure 1B illustrates such a transformation within a diagram of a neural feedback loop that controls the position of a motor. The purpose of this paper is not to analyze how this particular network functions; for a detailed analysis of this network and its function, see Szczecinski et al. (2017b). Instead, the purpose is to show how R and other functional values (time constants, gains, etc.) may be used to constrain neural and synaptic parameter values.

Figure 1B (i,ii) graphically illustrate the mapping in equation (7), and Figure 1B (iii) graphically illustrates the inverse relationship (i.e., neural value to mechanical value). If a sensory neuron has only this applied current and leak current, equation (6) shows that

$$C_m\frac{\mathit{dU}}{\mathit{dt}}+U=R\cdot \frac{\theta -{\theta }_{\min }}{{\theta }_{\max }-{\theta }_{\min }}.$$ (8)

This means that the sensory neuron acts as a low-pass filter with time constant τ = C_m. It is trivial to show that, when the neuron is at equilibrium (i.e., dU/dt = 0),

$$U^{\ast }=R\cdot \frac{\theta -{\theta }_{\min }}{{\theta }_{\max }-{\theta }_{\min }},$$ (9)

where the superscript “∗” specifies the equilibrium value. (Throughout this manuscript, the equilibrium activation of neuron U will be referred to as U*, and the neuron itself will be referred to as U.) Equation (9) means that the neuron’s activation above its rest potential encodes the sensory signal. In addition to perceiving sensory information, commands must be issued in the same transformation. Thus, we map the commanded sensory quantity, θ_comm, to the commanded neural activation, U_comm, with the inverse function of equation (9),

$${\theta }_{\text{comm}}={\theta }_{\min }+\frac{U_{\text{comm}}}{R}\cdot \left({\theta }_{\max }-{\theta }_{\min }\right).$$ (10)

In this way, the nervous system may specify an intended motion, such as the rotation of a joint, encoded in neural activity. In our synthetic nervous systems, R specifies how mechanical quantities and neural activation are related. Thus, the tuning of every functional subnetwork described in this work relies on R, which the designer specifies before tuning the rest of the network. Two other parameters are critical for tuning these subnetworks: the amplification of synaptic transmission, k_syn (discussed in Sec. 3.1), and the synaptic reversal potential, ΔE_s. From these values, biological parameters such as synaptic conductance and neural tonic drive can be directly calculated. This makes network design intuitive, enabling the designer to select biological parameter values based on functional ones.

3. Methods: Arithmetic Subnetworks

This section describes how to use typical engineering quantities to design neural and synaptic pathways. We can understand how these pathways work by manipulating their equilibria, something that naive optimization does not leverage. The steady-state activation U* is calculated by solving for U when dU/dt = 0

$$0=-U^{\ast }+{\displaystyle \sum _{i=1}^n}\frac{g_{s,i}}{R}\cdot U_{\mathit{pre},i}\cdot \left(\mathrm{\Delta }{E}_{s,i}-U^{\ast }\right)+I_{\mathit{app}}.$$ (11)

Moving all U* terms to the left hand side

$$U^{\ast }\cdot \left(1+{\displaystyle \sum _{i=1}^n}\frac{g_{s,i}}{R}\cdot U_{\mathit{pre},i}\right)={\displaystyle \sum _{i=1}^n}\frac{g_{s,i}}{R}\cdot U_{\mathit{pre},i}\cdot \mathrm{\Delta }{E}_{s,i}+I_{\mathit{app}}.$$ (12)

Solving for U*,

$$U^{\ast }=\frac{{\sum }_{i=1}^n\frac{g_{s,i}}{R}\cdot U_{\mathit{pre},i}\cdot \mathrm{\Delta }{E}_{s,i}+I_{\mathit{app}}}{1+{\sum }_{i=1}^n\frac{g_{s,i}}{R}\cdot U_{\mathit{pre},i}}.$$ (13)

This solution is the basis for the remainder of Sec. 3.

3.1. Signal Transmission Pathways

The goal of a signal transmission pathway is to cause the postsynaptic neuron’s voltage to be some ratio of the presynaptic neuron’s voltage. We call this ratio k_syn. The U_pre,i terms in the denominator of the right hand side of equation (13) mean that k_syn changes as U_pre changes, so we approximate k_syn as U_post/U_pre when the presynaptic neuron is fully activated (i.e., U_pre = R). The steady-state response of a neuron with a single synaptic input and no applied current can be written based on equation (13), as below:

$$U_{\mathit{post}}^{\ast }=\frac{\frac{g_s}{R}\cdot U_{\mathit{pre}}\cdot \mathrm{\Delta }{E}_s}{1+\frac{g_s}{R}\cdot U_{\mathit{pre}}}.$$ (14)

To find k_syn for this synapse, we first divide both sides of equation (14) by U_pre,

$$\frac{U_{\mathit{post}}^{\ast }}{U_{\mathit{pre}}}=\frac{\frac{g_s}{R}\cdot U_{\mathit{pre}}\cdot \mathrm{\Delta }{E}_s}{U_{\mathit{pre}}\cdot \left(1+\frac{g_s}{R}\cdot U_{\mathit{pre}}\right)}.$$ (15)

Next, we want to find k_syn, which can be calculated for any value of U_pre. To simplify analysis and improve the clarity of this derivation, we set find k_syn when U_pre = R. Then, we show how to set parameter values to keep k_syn nearly constant, even as U_pre changes. Making this substitution,

$$\frac{U_{\mathit{post}}^{\ast }}{R}=k_{\mathit{syn}}=\frac{\frac{g_s}{R}\cdot R\cdot \mathrm{\Delta }{E}_s}{R\cdot \left(1+\frac{g_s}{R}\cdot R\right)}.$$ (16)

Finally, reducing R/R terms reveals

$$k_{\mathit{syn}}=\frac{g_s\cdot \mathrm{\Delta }{E}_s}{R\cdot \left(1+g_s\right)}.$$ (17)

Rearranging to solve for g_s,

$$g_s=\frac{k_{\mathit{syn}}\cdot R}{\mathrm{\Delta }{E}_s-k_{\mathit{syn}}\cdot R}.$$ (18)

Because g_s must be positive, and the numerator of equation (18) is always positive, equation (18) is also subject to the constraint

$$\mathrm{\Delta }{E}_s>k_{\mathit{syn}}\cdot R.$$ (19)

Equation (18) will be used to tune addition, subtraction, multiplication, and division networks (Secs. 3.3 through 3.6).

3.2. Signal Modulation Pathways

We may also use synapses to modulate a neuron’s sensitivity to other inputs. Based on equation (13), the steady-state response of a neuron with only an applied current I_app is simply

$$U_{\mathit{post}}^{\ast }=I_{\mathit{app}},$$ (20)

if we set G_m = 1. For example, this is the case for a sensory neuron that receives applied current proportional to a sensor’s state, such as a joint angle (Figure 1B), muscle stretch, or touch sensor. However, the nervous system may need to actively increase or reduce the sensitivity of the sensory neuron depending on context. Hyperpolarizing or depolarizing the neuron, however, would cause sensory information to be truncated (i.e., V_pre < E_lo). We can change the sensitivity of this neuron without losing sensory information by adding a synaptic input to the response from equation (20):

$$U_{\mathit{post}}^{\ast }=\frac{\frac{g_s}{R}\cdot U_{\mathit{pre}}\cdot \mathrm{\Delta }{E}_s+I_{\mathit{app}}}{1+\frac{g_s}{R}\cdot U_{\mathit{pre}}}.$$ (21)

To quantify how U_pre modulates $U_{\mathit{post}}^{\ast }$ for a given I_app, we introduce the parameter c_syn, which quantifies this degree of modulation. We define c_syn as $U_{\mathit{post}}^{\ast }∕U_{\mathit{pre}}$, the same as k_syn, but with the understanding that U_pre will decrease $U_{\mathit{post}}^{\ast }$ in this case. Dividing both sides of equation (21) by U_pre and using the definition of c_syn,

$$\frac{U_{\mathit{post}}^{\ast }}{U_{\mathit{pre}}}=c_{\mathit{syn}}=\frac{\frac{g_s}{R}\cdot U_{\mathit{pre}}\cdot \mathrm{\Delta }{E}_s+I_{\mathit{app}}}{U_{\mathit{pre}}\cdot \left(1+\frac{g_s}{R}\cdot U_{\mathit{pre}}\right)}.$$ (22)

As in the previous section, we will solve for c_syn when U_pre = R to simplify analysis. Making this substitution and reducing R/R terms,

$$c_{\mathit{syn}}\cdot R=\frac{g_s\cdot \mathrm{\Delta }{E}_s+R}{1+g_s}.$$ (23)

Multiplying both sides by the denominator of the right hand side and expanding,

$$c_{\mathit{syn}}\cdot R+c_{\mathit{syn}}\cdot R\cdot g_s=g_s\cdot \mathrm{\Delta }{E}_s+R.$$ (24)

Collecting g_s terms on the left hand side,

$$c_{\mathit{syn}}\cdot R\cdot g_s-g_s\cdot \mathrm{\Delta }{E}_s=R-c_{\mathit{syn}}\cdot R.$$ (25)

Solving equation (25) for g_s,

$$g_s=\frac{c_{\mathit{syn}}\cdot R-R}{\mathrm{\Delta }{E}_s-c_{\mathit{syn}}\cdot R}.$$ (26)

Just as in Sec. 3.1, g_s > 0 depends only on R, which the designer specifies beforehand, ΔE_s, which is limited by biological constraints, and c_syn, which the designer picks based on network function. ΔE_s should be negative, and as close to 0 as possible to minimize hyperpolarization of the postsynaptic neuron. Equation (26) will be used to tune division and multiplication networks (Secs. 3.5 and 3.6).

3.3. Addition

A subnetwork that approximates linear addition of the form $U_{\mathit{post}}^{\ast }=k_{\mathit{syn}}\cdot \left(U_{\mathit{pre},1}+U_{\mathit{pre},2}\right)$ may underlie positive feedback mechanisms, which increase motor neuron activation proportional to sensory inputs such as force sensing organs (Zill et al., 2004), or used to sum sensory signals from different body segments (Mittelstaedt, 1957). We construct such a network by using two Signal Transmission pathways as presented in Sec. 3.1.

Let us rewrite equation (13) here, for clarity:

$$U^{\ast }=\frac{{\sum }_{i=1}^n\frac{g_{s,i}}{R}\cdot U_{\mathit{pre},i}\cdot \mathrm{\Delta }{E}_{s,i}+I_{\mathit{app}}}{1+{\sum }_{i=1}^n\frac{g_{s,i}}{R}\cdot U_{\mathit{pre},i}}.$$ (27)

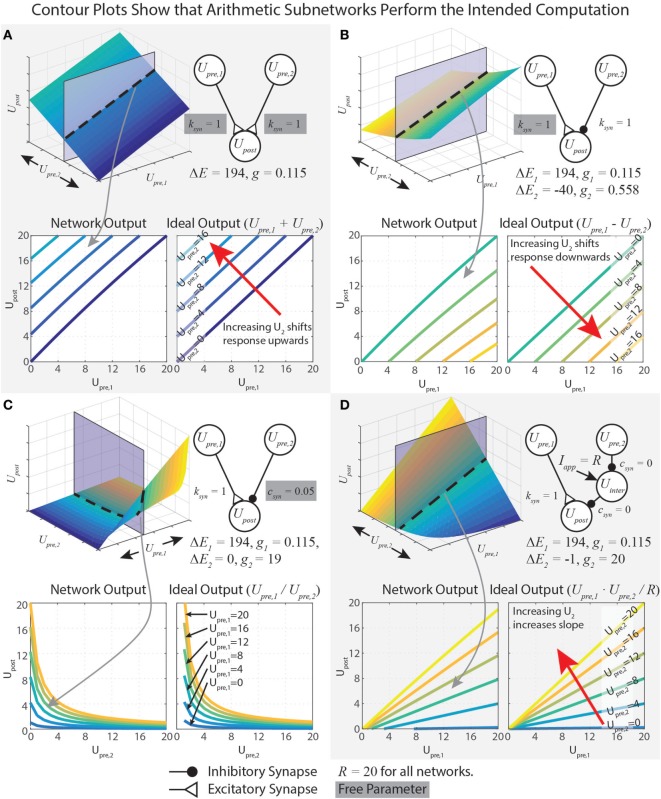
This equation shows U_pre,i in both the numerator and denominator. To capture addition, we wish to minimize the impact of U_pre,i on the denominator. This is accomplished by minimizing g_s. However, if g_s = 0, then the network will not function at all. Therefore, we instead maximize ΔE_s, which yields a small g_s (equation (18)). Mathematically, there is no limit on ΔE_s, but synaptic potentials are limited in biological systems. In our work, we choose the reversal potential of calcium (E_s = 134 mV), which yields ΔE_s = E_s − E_r = 134 − (−60) = 194 mV, and specify R = 20 mV. To design a pathway where k_syn = 1, for example, we plug these values into equation (18), which gives g_s = 115 nS. The contour plots in Figure 2A show that the network matches the ideal behavior very closely over the operating range U_sum ∈ [0, R]. These design constraints are summarized in Table 1.

Figure 2.

Data demonstrating the function of arithmetic networks. Each contour plot represents cross sections of the response surface, as depicted at the top. The network diagram, relevant parameters, and data are shown for addition (A), subtraction (B), division (C), and multiplication (D). Triangular synaptic terminations stand for excitatory inputs, and filled round terminations stand for inhibitory inputs. For each operation, the contour on the right is the ideal output, and the contour on the left is the actual operation for the parameter values listed. Free parameters from Table 1 are highlighted in gray.

3.4. Subtraction

A subnetwork that approximates linear subtraction of the form $U_{\mathit{post}}^{\ast }=k_{\mathit{syn}}\cdot \left(U_{\mathit{pre},1}-U_{\mathit{pre},2}\right)$ may underlie negative feedback mechanisms, which are important for controlling many parameters in locomotion (Pearson, 1993; Peterka, 2003; Buschmann et al., 2015). Just as in the previous section, equation (18) is used to find g_s for each pathway.

Designing a subtraction network requires that we pay attention to how the two synapses affect one another. Since the reversal potentials of hyperpolarizing ion channels are not much more negative than typical resting potentials, larger g_s,2 values are required to transmit information than for depolarizing ion channels. This makes it harder to minimize g_s like we did in the previous section. Equation (13) enables us to constrain g_s,2 such that when U_pre,1 = R and U_pre,2 = R, $U_{\mathit{post}}^{\ast }=0$. Starting with the neuron response in equation (13) for two synaptic currents and no applied current,

$$U_{\mathit{post}}^{\ast }=\frac{g_{s,1}∕R\cdot U_{\mathit{pre},1}\cdot \mathrm{\Delta }{E}_{s,1}+g_{s,2}∕R\cdot U_{\mathit{pre},2}\cdot \mathrm{\Delta }{E}_{s,2}}{1+g_{s,1}∕R\cdot U_{\mathit{pre},1}+g_{s,2}∕R\cdot U_{\mathit{pre},2}}.$$ (28)

Substituting in U_pre,1 = R, U_pre,2 = R, and $U_{\mathit{post}}^{\ast }=0$,

$$0=\frac{g_{s,1}∕R\cdot R\cdot \mathrm{\Delta }{E}_{s,1}+g_{s,2}∕R\cdot R\cdot \mathrm{\Delta }{E}_{s,2}}{1+g_{s,1}∕R\cdot R+g_{s,2}∕R\cdot R}$$ (29)

$$0=\frac{g_{s,1}\cdot \mathrm{\Delta }{E}_{s,1}+g_{s,2}\cdot \mathrm{\Delta }{E}_{s,2}}{1+g_{s,1}+g_{s,2}}$$ (30)

$$0=g_{s,1}\cdot \mathrm{\Delta }{E}_{s,1}+g_{s,2}\cdot \mathrm{\Delta }{E}_{s,2}$$ (31)

$$g_{s,2}=\frac{\mathrm{\Delta }{E}_{s,1}}{\mathrm{\Delta }{E}_{s,2}}\cdot -g_{s,1}.$$ (32)

Substituting equation (18) for g_s,1,

$$g_{s,2}=\frac{\mathrm{\Delta }{E}_{s,1}}{\mathrm{\Delta }{E}_{s,2}}\cdot \frac{-k_{\mathit{syn}}\cdot R}{\mathrm{\Delta }{E}_{s,1}-k_{\mathit{syn}}\cdot R}.$$ (33)

To be physically realizable, g_s,2 > 0. Because g_s,1 > 0 and ΔE_s,1 > 0, g_s,2 > 0 if and only if ΔE_s,2 < 0. Thus, it is critical that ΔE_s,2 < 0.

Just as for the addition network, we minimize g_s,1 by maximizing ΔE_s,1. If R = 20 mV and k_syn = 1, then g_s,1 = 115 nS and ΔE_s,1 = 194 mV. To tune g_s,2, we first select ΔE_s,2 = −40 mV, then we solve equation (33) to find g_s,2 = 558 nS. These design constraints are summarized in Table 1, and Figure 2B graphically shows the accuracy of the subtraction network.

3.5. Division

A subnetwork that approximates division of the form

$$U_{\mathit{post}}^{\ast }=\frac{U_{\mathit{pre},1}}{1+\frac{1-c_{\mathit{syn}}}{c_{\mathit{syn}}\cdot R}\cdot U_{\mathit{pre},2}}$$ (34)

replicates the function of GABA synapses that regulate activity in the brain. A key reason for this behavior is that the reversal potential of GABA-ergic synapses is about equal to the resting potential of the postsynaptic neuron (Trappenberg, 2009). Equation (26) is used to find g_s for the division pathway.

The synapse from U_pre,1 to U_post is tuned as an excitatory Signal Transmission pathway with k = 1, as in Sec. 3.1. In our work, R = 20 mV, ΔE_s,1 = 194 mV, and equation (18) tells us that g_s,1 = 115 nS. Such a small g_s ensures that the signal from U_pre,1 to U_post is transmitted without greatly affecting the sensitivity of U_post to inputs. That is, the effect of U_pre,1 on the denominator of $U_{\mathit{post}}^{\ast }$ is very nearly 0.

The synapse from U_pre,2 to U_post is tuned as a Signal Modulation pathway, as analyzed in Sec. 3.2. Setting ΔE_s,2 = 0 will eliminate U_pre,2’s influence on the numerator of $U_{\mathit{post}}^{\ast }$. Substituting this case into equation (26) and reducing,

$$g_{s,2}=\frac{1-c_{\mathit{syn}}}{c_{\mathit{syn}}},$$ (35)

where $U_{\mathit{post}}^{\ast }=c_{\mathit{syn}}\cdot R$ when U_pre,1 = U_pre,2 = R, their maximal value. Equation (35) also reveals that since g_s,2 > 0, 0 < c_syn < 1.

The steady-state response of the network is the result of these two synaptic inputs, as written in equation (28). Substituting equation (35), and specifying that k_syn,1 = 1, $U_{\mathit{post}}^{\ast }$ simplifies to

$$U_{\mathit{post}}^{\ast }=\frac{{\overline{)g_{s,1}∕R\cdot \mathrm{\Delta }{E}_{s,1}\cdot }}^1{U}_{\mathit{pre},1}+g_{s,2}∕R\cdot {\overline{)\mathrm{\Delta }{E}_{s,2}\cdot }}^0{U}_{\mathit{pre},2}}{1+{\overline{)g_{s,1}\cdot }}^0{U}_{\mathit{pre},1}∕R+\frac{1-c_{\mathit{syn}}}{c_{\mathit{syn}}}\cdot U_{\mathit{pre},2}∕R}\approx \frac{U_{\mathit{pre},1}}{1+\frac{1-c_{\mathit{syn}}}{c_{\mathit{syn}}\cdot R}\cdot U_{\mathit{pre},2}}$$ (36)

In our network, we wished $U_{\mathit{post}}^{\ast }=1$ when U_pre,2 = R, so we set c_syn = 1/R = 0.05, which makes g_s,2 = 19 μS. When c_syn is close to 0, U_pre,2 can strongly reduce U_post’s sensitivity to inputs. When c_syn is close to 1, U_pre,2 can only weakly reduce U_post’s sensitivity to inputs. Figure 2C shows that this network performs the intended division of the signals. Table 1 summarizes these design constraints.

3.6. Multiplication

A subnetwork that approximates multiplication of the form $U_{\mathit{post}}^{\ast }=U_{\mathit{pre},1}\cdot U_{\mathit{pre},2}∕R$ can be used to control the gain of a sensory feedback loop, a frequently observed characteristic of neural systems that control locomotion (Cruse, 1981; Gabriel and Büschges, 2007) and posture (Peterka and Loughlin, 2004).

A multiplication network can be assembled by replacing the Modulatory Pathway in the division network with two identical Modulatory Pathways in series, connected into a disinhibitory network (see Figure 2D). This works because the product of two numbers, a⋅b = a/(1/b). However, tuning the Modulatory Pathway for the multiplication network differs from tuning the division network. This is because the right-side pathway of the network in Figure 2D must make $U_{\mathit{post}}^{\ast }=0$, no matter how active U_pre,1 becomes (because a⋅0 = 0, no matter the value of a). Thus, according to equation (22), c_syn = 0, unlike the division network, for which 0 < c_syn < 1. Solving equation (26) when c_syn = 0 reveals that

$$g_{s,2}=-R∕\mathrm{\Delta }{E}_{s,2}.$$ (37)

To solve for g_s,2, we must first select ΔE_s,2. If ΔE_s,2 = 0 like for the division network, then equation (37) divides by 0. If ΔE_s,2 > 0, then g_s,2 < 0, which is physically not realizable. Therefore, we must choose a value ΔE_s,2 < 0. The more negative ΔE_s,2 is, the more small-amplitude signals are clipped; however, the less negative it is, the larger g_s,2 must be. Therefore, g_s,2 is the limiting factor to maintain biological realism. We have chosen g_s,2 = 20 μS and R = 20 mV, making ΔE_s,2 = −1.

Now that we have designed one of the Modulatory synapses, we can calculate the response of the complete multiplication network seen in Figure 2D, which includes two identical Modulatory Pathways in series. When U_pre,2 is inactive, then it does not inhibit U_inter, which is tonically active. In this case, U_inter’s activity completely desensitizes U_post to inputs. When U_pre,2 is active, then it inhibits U_inter. In this case, U_inter is hyperpolarized, and cannot desensitize U_post to inputs. To show that this is the case, let us find the full response of the system. We first calculate $U_{\mathit{inter}}^{\ast }$, which has one Modulatory Pathway input and a tonic applied current I_app = R. Its response is the same as in equation (21), with the constraint from equation (37), which causes terms to cancel:

$$U_{\mathit{inter}}^{\ast }=\frac{\frac{g_{s,2}}{R}\cdot U_{\mathit{pre},2}\cdot -\frac{R}{g_{s,2}}+R}{1-\frac{U_{\mathit{pre},2}}{\mathrm{\Delta }{E}_{s,2}}}=\frac{R-U_{\mathit{pre},2}}{1-\frac{U_{\mathit{pre},2}}{\mathrm{\Delta }{E}_{s,2}}}.$$ (38)

U_post has two presynaptic neurons, U_pre,1 and U_inter. The synapse from U_pre,1 is a Signal Transmission synapse, and the synapse from U_inter is a Signal Modulation synapse. Its response is found via equation (13),

$$U_{\mathit{post}}^{\ast }=\frac{\frac{g_{s,3}}{R}\cdot U_{\mathit{inter}}\cdot \mathrm{\Delta }{E}_{s,3}+\frac{g_{s,1}}{R}\cdot U_{\mathit{pre},1}\cdot \mathrm{\Delta }{E}_{s,1}}{1+\frac{g_{s,3}}{R}\cdot U_{\mathit{inter}}+\frac{g_{s,1}}{R}\cdot U_{\mathit{pre},1}}.$$ (39)

We showed in Sec. 3.3 that equation (18) can be used to design a synapse that transmits the presynaptic neuron’s activity to the postsynaptic neuron, while minimizing its impact on the denominator of the postsynaptic neuron’s steady-state response, $U_{\mathit{post}}^{\ast }$. This enables us to approximate U_pre,1’s effect on $U_{\mathit{post}}^{\ast }$ as an applied current I_app ≈ U_pre,1. Making this substitution in equation (39),

$$U_{\mathit{post}}^{\ast }\approx \frac{\frac{g_{s,3}}{R}\cdot U_{\mathit{inter}}\cdot \mathrm{\Delta }{E}_{s,3}+U_{\mathit{pre},1}}{1+\frac{g_{s,3}}{R}\cdot U_{\mathit{inter}}}.$$ (40)

Because we previously specified that the Modulatory Pathways are identical, we can apply the constraint from equation (37),

$$U_{\mathit{post}}^{\ast }=\frac{U_{\mathit{pre},1}-U_{\mathit{inter}}}{1-\frac{U_{\mathit{inter}}}{\mathrm{\Delta }{E}_{s,3}}}.$$ (41)

We can now substitute equation (38) for U_inter,

$$U_{\mathit{post}}^{\ast }=\frac{U_{\mathit{pre},1}-\frac{R-U_{\mathit{pre},2}}{1-\frac{U_{\mathit{pre},2}}{\mathrm{\Delta }{E}_{s,2}}}}{1-\frac{1}{\mathrm{\Delta }{E}_{s,3}}\cdot \frac{R-U_{\mathit{pre},2}}{1-\frac{U_{\mathit{pre},2}}{\mathrm{\Delta }{E}_{s,2}}}}.$$ (42)

This expression can be simplified. First, as noted previously, synapses 2 and 3 are identical, so ΔE_s,2 = ΔE_s,3 = ΔE_s. Second, we can multiply the first term in both the numerator and denominator by the factor (1 − U_pre,2/ΔE_s), which enables us to combine terms. Performing these simplifications,

$$U_{\mathit{post}}^{\ast }=\frac{U_{\mathit{pre},1}-U_{\mathit{pre},1}\cdot U_{\mathit{pre},2}∕\mathrm{\Delta }{E}_s-R+U_{\mathit{pre},2}}{1-U_{\mathit{pre},2}∕\mathrm{\Delta }{E}_s-R∕\mathrm{\Delta }{E}_s+U_{\mathit{pre},2}∕\mathrm{\Delta }{E}_s},$$ (43)

$$U_{\mathit{post}}^{\ast }=\frac{-U_{\mathit{pre},1}\cdot U_{\mathit{pre},2}∕\mathrm{\Delta }{E}_s+U_{\mathit{pre},1}+U_{\mathit{pre},2}-R}{1-R∕\mathrm{\Delta }{E}_s}.$$ (44)

Equation (44) contains a lot of information about how the multiplication network functions. First, U_post’s response indeed contains a term that multiplies U_pre,1 and U_pre,2. When ΔE_s = −1, then $U_{\mathit{post}}^{\ast }$scales with U_pre,1⋅U_pre,2 in a 1:1 fashion. Second, the numerator will be ≤ 0 if either U_pre,1 = 0 or U_pre,2 = 0, $U_{\mathit{post}}^{\ast }\le 0$. This is because U_pre,1 and U_pre,2 must each be less than or equal to R. If either input is greater than R, then their synaptic inputs to U_post will saturate (see equation (4)), preventing this condition from being violated. Third, the denominator does not depend on the input values. Technically, because of the approximation made in equation (40), the denominator does change slightly with U_pre,1. However, with our chosen values of R (20), ΔE_s (−1), and g_s,1 (0.115), this change is less than 1%, justifying this approximation. Figure 2D demonstrates that this network multiplies the two inputs.

Table 1 summarizes the function, component pathways, constraint equations, and free parameters of each network from this section. This analysis enables direct construction and parameter selection for functional subnetworks that can be assembled into more complex networks capable of performing real-time robotic control (e.g., Szczecinski and Quinn (2017) and Szczecinski et al. (2017a)). Additionally, one of the key advantages to using dynamic neural systems for motor control is the handling of time varying signals. The next section examines how the dynamics of these neurons can be exploited to perform calculus on signals.

4. Methods: Dynamic Networks

The differential equation for a single neuron’s response (equation (1)) can be solved analytically. Solving an equation dx/dt = f (x) is simplified if the equilibrium state is x* = 0, so as in Sec. 3, the substitution U = V − E_r is made. Additionally, the membrane conductance G_m and capacitance C_m can be combined into a new parameter τ = C_m/G_m, which is a more intuitive parameter when discussing dynamic networks. This section uses analysis from the previous section, plus additional analysis, to derive design constraints for networks that differentiate or integrate input signals over time.

4.1. Differentiation

One dynamic response neural systems are known to utilize is differentiation of signals. Early examination of neural networks led to the discovery of the Reichardt detector network (Reichardt, 1961), an autocorrelation network with delays that approximates the differential of an incoming signal. Other examples include human balance, which relies on feedback proportional to the position, velocity, and acceleration of the center of mass (Peterka, 2003; Safavynia and Ting, 2012). Also, positive velocity feedback plays an important role in insect muscle control (Cruse, 1981).

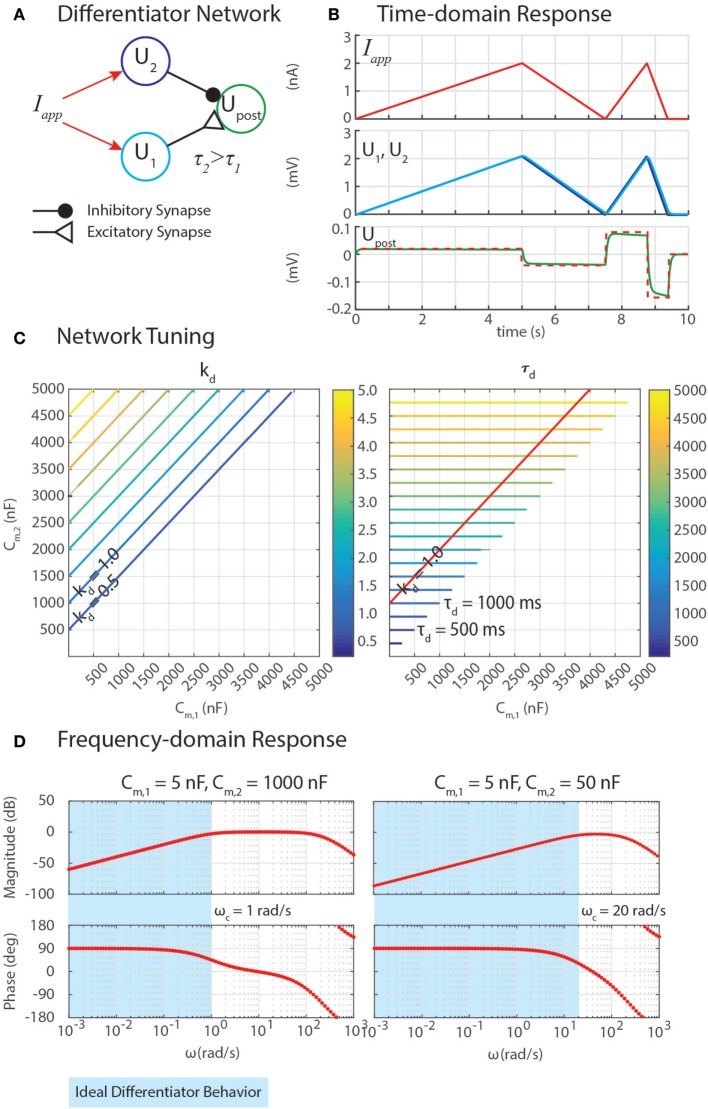
We have developed differentiation networks based on the Reichardt detector network, shown in Figure 3A. We can understand its function by examining a neuron’s response to a ramp input, I_app = A⋅t, where A is an arbitrary slope of the ramp. The response of the network should be a step with a magnitude proportional to A, as shown in Figure 3B. Inserting this applied current into equation (6), a single neuron’s response is

$$C_m\cdot \frac{\mathit{dU}}{\mathit{dt}}=-U+A\cdot t$$ (45)

$$C_m\cdot \frac{\mathit{dU}}{\mathit{dt}}+U=A\cdot t.$$ (46)

Figure 3.

(A) A network can exploit neural dynamics to compute the differential of an incoming signal. (B) When given an applied current in the form of ramps, the network returns steps whose heights are proportional to the slopes of the ramps. (C) The amplification of the differential, k_d, and the time constant of the network, τ_d, depend on the capacitance of the neurons, C_m,1 and C_m,2. (D) Frequency domain analysis enables the identification of the cutoff frequency ω_c, enabling the network to naturally filter out high-frequency noise.

The response of the neuron, U(t), is the sum of the particular and homogeneous solutions to equation (46), U_p(t) and U_h(t), respectively. Simulating the dynamics of equation (46) suggests that the particular solution is a ramp of slope A, which lags behind the input with a time constant C_m. To confirm this, we can substitute a candidate solution and its derivative into equation (46), and check for equality. The result is the particular (i.e., steady-state) response,

$$U_p\left(t\right)=A\cdot \left(t-C_m\right)$$ (47)

This means that if the same I_app were injected into neurons with different C_m values, and then their outputs were subtracted from one another with a network from Sec. 3.4, the network would perform a finite-difference approximation of the derivative of I_app, once the transient response decays (illustrated in Figures 3A,B).

Calculating the homogeneous solution, U_h(t), informs us how quickly the transient response decays. The homogeneous solution to first-order linear equation like equation (46) is well-known, U_h(t) = b⋅exp(− t/C_m). The constant b is found by plugging the initial condition into the full response, U(t) = U_p(t) + U_h(t),

$$b=A\cdot C_m.$$ (48)

To tune this network, the response of U_post is written as the difference between neuron U_pre,1 with C_m,1 and neuron U_pre,2 with C_m,2 > C_m,1,

$$\begin{array}{ll}\hfill U_{\mathit{post}}\left(t\right)& =U_{\mathit{pre},1}\left(t\right)-U_{\mathit{pre},2}\left(t\right)\\ & =A\cdot t-A\cdot C_{m,1}\cdot \left(1-\exp \left(-t∕C_{m,1}\right)\right)-\left(A\cdot t-A\cdot C_{m,2}\cdot \left(1-\exp \left(-t∕C_{m,2}\right)\right)\right).\end{array}$$ (49)

Canceling the terms that are linear in t and expanding,

$$U_{\mathit{post}}\left(t\right)=A\cdot \left(C_{m,2}-C_{m,1}\right)+A\cdot \left(C_{m,1}\cdot \exp \left(-t∕C_{m,1}\right)-C_{m,2}\cdot \exp \left(-t∕C_{m,2}\right)\right).$$ (50)

Properly tuning a differentiator network requires tuning C_m,1 and C_m,2 to obtain the intended gain of the network, k_d, and an appropriately high cutoff frequency, ω_c. Equation (50) reveals how these may be tuned. First, the steady-state response of this network to a ramp input defines k_d = (C_m,2 − C_m,1). Second, the cutoff frequency ω_c = 1/τ_d quantifies the frequency of incoming signals (i.e., I_app = A⋅sin(ω⋅t)) above which the network’s response has less than half the energy of a lower-frequency signal. This is especially useful because although differential calculations amplify high-frequency noise, this network filters out noise with a frequency ω > ω_c. Because C_m,2 > C_m,1, the time constant τ_d = C_m,2.

Figure 3C shows contours of k_d and τ_d as C_m,1 and C_m,2 change. The plots show that increasing C_m,2 relative to C_m,1 increases k_d, which may be valuable for amplifying signals. However, this also increases τ_d, making ω_c impractically low, which will cause the network’s output to lag behind the input substantially. The contour for k_d = 1 is drawn on the contour of τ_d, showing that the smallest τ_d achievable for this gain value is 1,000 ms, which would filter out all incoming signals for which ω > ω_c = 1/(1 s) = 1 rad/s (0.159 Hz).

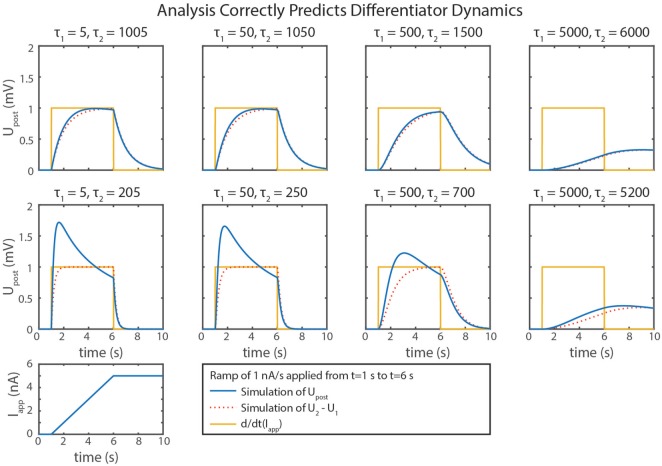
We can gain further insight into tuning τ_d using our FeedbackDesign tool (Szczecinski et al., 2017b). Figure 3D shows Bode plots for this network’s response, given two different values for C_m,2. When C_m,2 = 1,000 nF, like in Figure 3B, the network functions properly for inputs with ω < 1 rad/s, as predicted in the previous paragraph. Lowering C_m,2 to 50 nF increases ω_c to 20 rad/s (3.18 Hz). Lowering C_m,2 also lowers the magnitude response as a function of ω, that is, it decreases k_d. To regain this lost gain, we may increase k_syn in the subtraction network. Figure 4 shows simulation data that explores this tradeoff. Table 2 lists how to use τ_d and k_d to tune the entire differentiation network.

Figure 4.

Simulation data from eight trials with the differentiator network are shown. Different values of C_m,1 and C_m,2 were used in each. ${\mathit{U}}_{\mathit{post}}^{\ast }$ is plotted in blue, U₂ − U₁ is plotted in dotted red, and the actual rate of change of the input, d/dt(I_app), is plotted in gold.

4.2. Integration

Our neuron model is a leaky integrator, which means that the membrane voltage will integrate an applied current, but “leak” current to return to its resting potential. As a result, data cannot be stored in individual neurons, because neurons only have one stable equilibrium point. A network that is constructed to have a marginally stable equilibrium curve (or subspace) will not leak. A network will have this property if the determinant of the Jacobian matrix is 0, or in other words, if it is not full rank (Khalil, 2002). Instead of leaking, it will maintain its activation when no external currents are applied; when currents are applied, the state of the system will change continuously. This is analogous to the position of a box on a table with friction; it will remain wherever it is placed indefinitely, unless an external force is applied. In this section, we expand on previous work (Szczecinski et al., 2017a) to show how to construct a network that is marginally stable by applying constraints to reduce the rank of its Jacobian matrix; demonstrate that such a network can be used to integrate signals over time; and relate the integration rate, k_i, to the parameter values of the network, such that $\dot{U_1}=k_i\cdot I_{\mathit{app}}$.

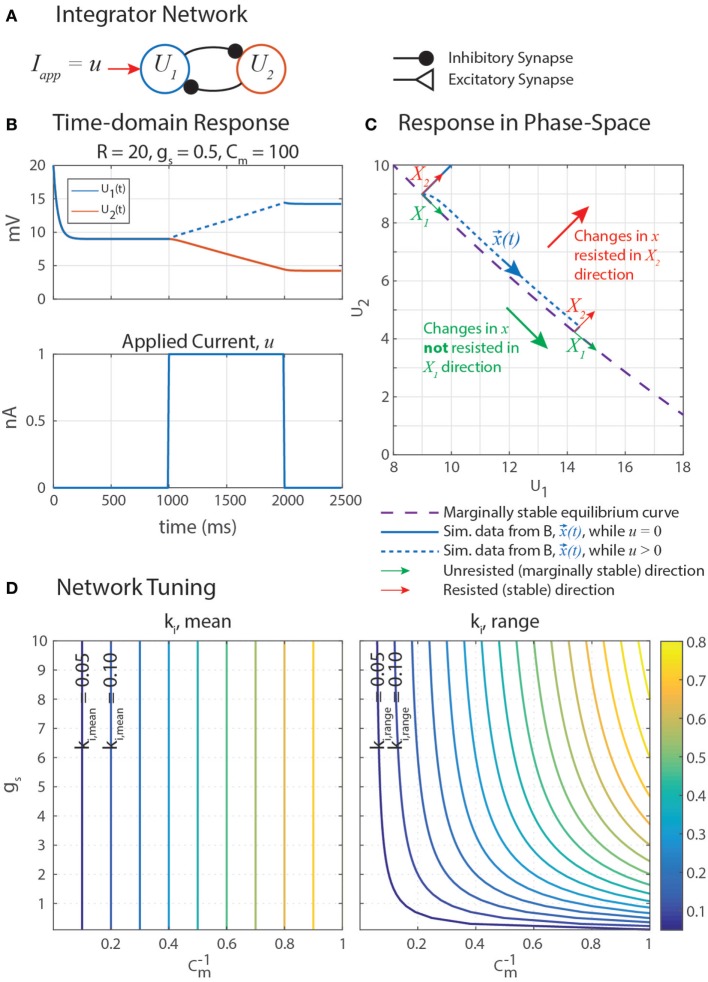
Marginally stable networks are hypothesized to play an important role in navigation (Haferlach et al., 2007) and the regulation of muscle forces in posture (Lévy and Cruse, 2008). Some memory models use carefully tuned self-excitation to cancel the leak current with excitatory synaptic current (Seung et al., 2000). In a similar vein, our network uses self-disinhibition (Figure 5A) to produce a line-attractor network in which a continuum of marginally stable equilibrium states exist. Simulation data in Figure 5B shows that stimulating U₁ with an applied constant current u causes U₁ to increase at an apparently constant rate, and when u is removed, neither U₁ nor U₂ leak to their rest potentials. This is the behavior of an integrator, as described in the previous paragraph.

Figure 5.

(A) A disinhibitory network can exploit neural dynamics to compute the integral of an incoming signal. (B) When given an applied current in the form of a step, the network response is a ramp whose slope is proportional to the amplitude of the step. (C) A plot of this data in the (U₁, U₂) phase space shows that when stimulated by applied current u, the system state, x(t) = [U₁(t), U₂(t)]^T (blue), moves in the X₁ direction (green) while maintaining a constant distance from the equilibrium subspace (dashed violet) in the X₂ direction (red). This difference in behavior in each direction is because the eigenvalue associated with eigenvector X₁, λ₁ = 0, and the eigenvalue associated with eigenvector X₂, λ₂ < 0. X₁ and X₂ are drawn in multiple places because they depend on x(t), as shown in Appendix. (D) The mean rate of integration, k_i,mean (left), and the range of the rate of integration, k_i,range (right), depend on the synaptic conductance of mutual inhibition, g_s, and the membrane capacitance of the neurons, C_m. Note that the x-axis of these plots are 1/C_m, to better space the contour lines.

Let us write the response of the integrator network as shown in Figure 5A to find its equilibrium states. Each neuron has leak current, synaptic current, and a constant applied current. Let all parameter values be symmetrical between the two neurons. We make the same substitutions as before; U = V − E_r, E_r = E_lo, ΔE_s = E_s − E_r, and R = E_hi − E_lo. If I_app = R,

$$C_m\cdot \frac{{\mathit{dU}}_1}{\mathit{dt}}=-U_1+g_s\cdot \frac{U_2}{R}\cdot \left(\mathrm{\Delta }{E}_s-U_1\right)+R$$ (51)

$$C_m\cdot \frac{{\mathit{dU}}_2}{\mathit{dt}}=-U_2+g_s\cdot \frac{U_1}{R}\cdot \left(\mathrm{\Delta }{E}_s-U_2\right)+R.$$ (52)

Moving dynamical terms to the left hand side, and applied current to the right hand side,

$$\frac{{\mathit{dU}}_1}{\mathit{dt}}+\frac{1}{C_m}\left(U_1-g_s\cdot \frac{U_2}{R}\cdot \left(\mathrm{\Delta }{E}_s-U_1\right)\right)=\frac{R}{C_m}$$ (53)

$$\frac{{\mathit{dU}}_2}{\mathit{dt}}+\frac{1}{C_m}\left(U_2-g_s\cdot \frac{U_1}{R}\cdot \left(\mathrm{\Delta }{E}_s-U_2\right)\right)=\frac{R}{C_m}$$ (54)

Solving equation (53) when dU₁/dt = 0 reveals the equilibrium curve

$$U_2=\frac{R\cdot \left(U_1-R\right)}{g_s\cdot \left(\mathrm{\Delta }{E}_s-U_1\right)}.$$ (55)

Solving equation (54) when dU₂/dt = 0 reveals the equilibrium curve

$$U_1=\frac{R\cdot \left(U_2-R\right)}{g_s\cdot \left(\mathrm{\Delta }{E}_s-U_2\right)},$$ (56)

which can be algebraically rearranged to be the same as equation (55) as long as g_s and ΔE_s are constrained such that

$$g_s\cdot \mathrm{\Delta }{E}_s=-R.$$ (57)

Multiplying both sides of equation (56) by the denominator of the right hand side, and expanding,

$$g_s\cdot \mathrm{\Delta }{E}_s\cdot U_1-g\cdot U_1\cdot U_2=R\cdot U_2-R^2.$$ (58)

Collecting multiples of U₂ and applying equation (57),

$$U_2=\frac{R\cdot \left(U_1-R\right)}{g_s\cdot \left(\mathrm{\Delta }{E}_s-U_1\right)}.$$ (59)

Thus, equations (55) and (56) are the same equilibrium curve if g_s and ΔE_s satisfy equation (57). This curve, drawn on the phase-space diagram in Figure 5C, describes every equilibrium state that this network can have. In other words, a [U₁, U₂] pair is an equilibrium state of the system if and only if it satisfies equation (55). In the coming paragraph, we will use eigenvalue analysis to show that this network always functions as an integrator, as long as equation (57) is satisfied.

To find the system’s eigenvalues, let us write equations (53) and (54) together in matrix form,

$$\left[\begin{array}{c}\hfill \dot{U_1}\hfill \\ \hfill \dot{U_2}\hfill \end{array}\right]+\frac{1}{C_m}\cdot \left[\begin{array}{cc}\hfill 1+U_2\cdot \frac{g_s}{R}\hfill & \hfill \frac{-g_s}{R}\cdot \left(\mathrm{\Delta }{E}_s-U_1\right)\hfill \\ \hfill \frac{-g_s}{R}\cdot \left(\mathrm{\Delta }{E}_s-U_2\right)\hfill & \hfill 1+U_1\cdot \frac{g_s}{R}\hfill \end{array}\right]\cdot \left[\begin{array}{c}\hfill U_1\hfill \\ \hfill U_2\hfill \end{array}\right]=\frac{1}{C_m}\cdot \left[\begin{array}{c}\hfill R\hfill \\ \hfill R\hfill \end{array}\right],$$ (60)

in which the square matrix is J, the system Jacobian. Because J contains U₁ and U₂ terms, it is not constant, but still describes the stability of the system, given specific values of U₁ and U₂. To construct a marginally stable equilibrium subspace for the network, we must show that J has insufficient rank (i.e., the rows are identical) when U₁ and U₂ are at equilibrium (i.e., equation (55) is satisfied). However, the rows are identical, no matter the values of U₁ and U₂, if we apply the constraint from equations (57) to (60),

$$\left[\begin{array}{c}\dot{U_1}\hfill \\ \dot{U_2}\hfill \end{array}\right]+\frac{1}{C_m}\cdot \left[\begin{array}{cc}1+\frac{g_s}{R}\cdot U_2\hfill & 1+\frac{g_s}{R}\cdot U_1\hfill \\ 1+\frac{g_s}{R}\cdot U_2\hfill & 1+\frac{g_s}{R}\cdot U_1\hfill \end{array}\right]\cdot \left[\begin{array}{c}{U}_1\hfill \\ U_2\hfill \end{array}\right]=\frac{1}{C_m}\cdot \left[\begin{array}{c}R\hfill \\ R\hfill \end{array}\right].$$ (61)

Thus, the system will always have one null direction, and we do not need to calculate J for specific equilibrium conditions to determine the system’s stability. To make notation more compact, let us define

$$a=1+g_s∕R\cdot U_1$$ (62)

$$b=1+g_s∕R\cdot U_2$$ (63)

These expressions let us write equation (61) as simply

$$\left[\begin{array}{c}\dot{U_1}\hfill \\ \dot{U_2}\hfill \end{array}\right]+\left[\begin{array}{cc}b∕C_m\hfill & a∕C_m\hfill \\ b∕C_m\hfill & a∕C_m\hfill \end{array}\right]\cdot \left[\begin{array}{c}{U}_1\hfill \\ U_2\hfill \end{array}\right]=\left[\begin{array}{c}R∕C_m\hfill \\ R∕C_m\hfill \end{array}\right].$$ (64)

Plotting the simulation data of the network’s forced response from Figure 5B on a phase-space diagram (Figure 5C) suggests that u causes U₁ and U₂ to change in such a way that the state of the system ($\overrightarrow{x}\left(t\right)$, blue) moves tangent to the equilibrium curve (dashed violet), with some constant distance away from it. These curves do not overlap because the forced response is not the same as the equilibrium condition while the external current u is applied. Motion in the X₂ direction is resisted by the neural dynamics, much how a spring resists the translation of an object with an applied force.

Nonetheless, these direction-dependent responses suggest that the state can be generalized into two decoupled degrees of freedom in the phase-space: unresisted, marginally stable motion parallel to the equilibrium curve (X₁, green in Figure 5C); and resisted, stable motion away from the equilibrium curve (X₂, red). The natural coordinates, $\overrightarrow{x}={\left[U_1,U_2\right]}^T$, are transformed into generalized coordinates, $\overrightarrow{q}={\left[q_1,q_2\right]}^T$, by a matrix X comprised of the eigenvectors of J. This same transformation matrix is used to transform J into the generalized coordinate system, yielding J_q. J_q is diagonal, decoupling the dynamics of the generalized coordinates and enabling us to quantify how quickly $\overrightarrow{x}$ moves parallel to the equilibrium curve.

Appendix shows the calculation of X, with q₁ representing the marginally stable mode and q₂ representing the stable mode. Using X, we can transform the system into generalized coordinates. First, we write the dynamics from equation (64) in a compact format.

$$\dot{\overrightarrow{x}}+J\overrightarrow{x}=\overrightarrow{F},$$ (65)

where J is the square matrix in equation (64) and

$$\overrightarrow{F}=\left[\begin{array}{c}\hfill R∕C_m+u∕C_m\hfill \\ \hfill R∕C_m\hfill \end{array}\right].$$ (66)

The generalized coordinates, $\overrightarrow{q}$, are defined as

$$\overrightarrow{x}=X\overrightarrow{q}.$$ (67)

To transform equation (65) into generalized coordinates, premultiply both sides of equation (65) by X⁻¹,

$$\dot{\overrightarrow{q}}+J_q\overrightarrow{q}=\overrightarrow{Q},$$ (68)

where J_q = X⁻¹JX and $\overrightarrow{Q}=X^{-1}\overrightarrow{F}$. The top and bottom rows of equation (68) are decoupled because J_q is a diagonal matrix. Furthermore, $J_q^{i,i}={\mathrm{\lambda }}_i$, meaning that $J_q^{1,1}=0$, so the system simplifies even further.

To find the particular solution of this system, we can guess the form of q_p,1 and q_p,2, and substitute those in to equation (68). We observe that ${\dot{q}}_1\left(t\right)=B\cdot u$ in steady state, where B is a constant that relates ${\dot{q}}_1\left(t\right)$ and u. q₁(t) would be the integral of ${\dot{q}}_1\left(t\right)$, but because the top row of J_q is zeros, it will not appear in the particular solution, and thus need not be explicitly included. We also observe that ${\dot{q}}_2\left(t\right)=0$ in steady state, so q₂(t) = D, a constant. We can calculate $\overrightarrow{Q}=X^{-1}F$ using X⁻¹, which is calculated in Appendix (equation (A9)). Solving for the particular solution of this system, ${\dot{\overrightarrow{q}}}_p\left(t\right)$,

$$\begin{array}{lll}\hfill {\dot{\overrightarrow{q}}}_p\left(t\right)+J_q\overrightarrow{q_p}& =\left[\begin{array}{c}B\cdot u\\ 0\end{array}\right]+\left[\begin{array}{cc}0& 0\\ 0& \frac{a+b}{C_m}\end{array}\right]\cdot \left[\begin{array}{c}{q}_{p,1}\\ D\end{array}\right]& \hfill =\left[\begin{array}{c}\frac{a\cdot d}{C_m\cdot \left(a+b\right)}\cdot u\\ \frac{R\sqrt{2}}{C_m}+\frac{b\sqrt{2}}{C_m\cdot \left(a+b\right)}\cdot u.\end{array}\right]\end{array}$$ (69)

$$B=\frac{a\cdot d}{C_m\cdot \left(a+b\right)},$$ (70)

where d is defined in equation (A5). B describes how quickly q_p,1 varies with u, but we want to know how quickly U₁ varies with u. Therefore, we use equation (67) to transform ${\overrightarrow{\dot{q}}}_p={\left[B\cdot u,0\right]}^T$ into natural coordinates to find $\dot{\overrightarrow{x}}$,

$$\dot{\overrightarrow{x_p}}=X\dot{\overrightarrow{q_p}}$$ (71)

$$\begin{array}{ll}\hfill \left[\begin{array}{c}{\dot{U}}_{1,p}\left(t\right)\\ {\dot{U}}_{2,p}\left(t\right)\end{array}\right]& =\left[\begin{array}{cc}1∕d& 1∕\sqrt{2}\\ -b∕\left(\mathit{ad}\right)& 1∕\sqrt{2}\end{array}\right]\cdot \left[\begin{array}{c}\frac{a\cdot d}{C_m\cdot \left(a+b\right)}\cdot u\\ 0\end{array}\right]\end{array}$$ (72)

$${\dot{U}}_{1,p}\left(t\right)=\frac{a}{C_m\cdot \left(a+b\right)}\cdot u$$ (73)

$$k_i=\frac{a}{C_m\cdot \left(a+b\right)}.$$ (74)

Recall that a and b are functions of U₁ and U₂, respectively. This means that k_i, the integral gain of the network, is not a constant. To place bounds on k_i, let us substitute equations (62) and (63) into equation (74),

$$k_i=\frac{1+g_s∕R\cdot U_1}{C_m\cdot \left(2+g_s∕R\cdot \left(U_1+U_2\right)\right)}.$$ (75)

We can now plug in different values of U₁ and U₂ to see how k_i varies. Using equations (55) and (56), we find that the most extreme cases are when [U₁, U₂] = [0, R] and [U₁, U₂] = [R, 0]. We can plug these cases into equation (75) to find the minimum and maximum values for k_i,

$$k_{i,\min }=\frac{1+g_s∕R\cdot 0}{C_m\cdot \left(2+g_s∕R\cdot \left(0+R\right)\right)}=\frac{1}{C_m\cdot \left(2+g_s\right)}$$ (76)

and

$$k_{i,\max }=\frac{1+g_s∕R\cdot R}{C_m\cdot \left(2+g_s∕R\cdot \left(R+0\right)\right)}=\frac{1+g_s}{C_m\cdot \left(2+g_s\right)}.$$ (77)

The difference between k_i,min and k_i,max:

$$k_{i,\text{range}}=\frac{1+g_s}{C_m\cdot \left(2+g_s\right)}-\frac{1}{C_m\cdot \left(2+g_s\right)}=\frac{g_s}{C_m\cdot \left(2+g_s\right)}.$$ (78)

To find the mean rate of integration, we can calculate k_i,mean = (k_i,min + k_i,max)/2,

$$k_{i,\text{mean}}=\frac{1}{2\cdot C_m}.$$ (79)

This is the same value of k_i obtained from computing k_i when U₁ = U₂. This simple expression is a useful relationship for tuning the integrator network. One may select C_m to obtain the intended mean integration rate, and then minimize the variation of the integration rate by minimizing g_s, as long as equation (57) is satisfied.

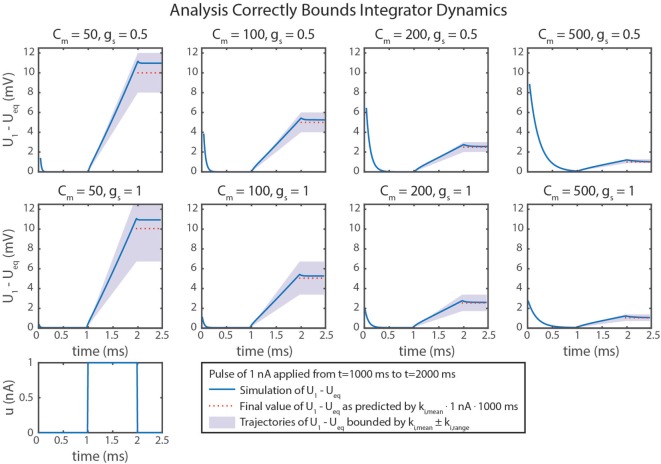
Figure 5D graphically demonstrates how k_i,mean and k_i,range determine C_m and g_s. Just as in equation (79), k_i,mean is a function only of C_m. Therefore, the contour only shows vertical lines. The value of k_i,range is minimized by decreasing either g_s or $C_m^{-1}$ (i.e., increasing C_m). Figure 6 shows simulation data of the integrator’s response to a step input with eight different parameter value combinations. In every case, the change in U₁ is bounded by the values of k_i,mean and k_i,range. As shown in Figure 5D, increasing C_m decreases the integration rate, and increasing g_s increases the variation in the integration rate.

Figure 6.

Simulation data from eight trials are shown. Different values of C_m and g_s were used in each. Neural dynamics are plotted as blue lines. The expected final values of the simulations are plotted in dotted red lines. Regions bounded by k_i,mean ± k_i,range are shaded in violet. In every case, the actual outcome is correctly bounded. As demonstrated mathematically in the text, k_i,mean only depends on C_m. In addition, k_i,range depends on g_s, leading to more variation in k_i, as indicated by larger shaded areas.

Table 2 summarizes the design approach for this integrator network. The mean and range of the integration rate are free parameters that are determined by the intended network performance. Using these values and the constraint in equation (57), the neurons’ C_m value and the synapses’ g_s and ΔE_s values can be fully specified.

5. Application to a Robot Controller

We have used the methods in this paper to tune (i.e., select parameter values for) several different networks that control robotic stepping (Szczecinski and Quinn, 2017; Szczecinski et al., 2017a) and visual tracking (Szczecinski et al., 2017a). Once a network layout is determined, whether hypothetical or based on neurobiological findings, individual subnetworks can be identified and tuned to work together. Figure 7 shows a simplified joint-control network in which different functional pathways are color-coded. This illustrates how these functional subnetworks enable the direct assembly of control networks based on neurobiology. The neurobiological inspiration for these networks and the results of robotic experiments are presented in Szczecinski and Quinn (2017) and Szczecinski et al. (2017a), and so are omitted here.

Figure 7.

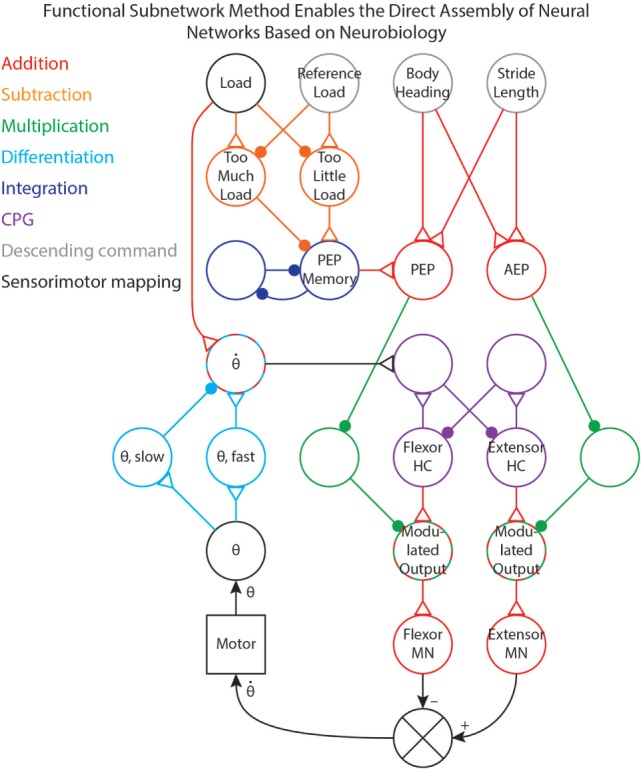
A simplified joint-control network from our previous work (Szczecinski and Quinn, 2017; Szczecinski et al., 2017a), with pathways color-coded based on the functional subnetwork.

The joint network in Figure 7 uses three simple descending commands (body heading, stride length, and reference leg load) to control the walking motion of one joint of a leg. The descending commands modulate the output of a central pattern generator (CPG) to control the speed of the motion, and sensory feedback is used to adjust both the timing and amplitude of motor output. Addition pathways are drawn in red. These include the mapping between body heading and stride length (i.e., descending commands, drawn in gray) to the PEP and AEP (Szczecinski and Quinn, 2017). The PEP can also be modulated by force feedback, which compares the load on the leg to a reference value (Szczecinski and Quinn, 2017, in review). This requires a subtraction network, drawn in orange, to compute if there is too much or too little load on the leg. The difference is used to adjust the PEP Memory network, which is an integration network, drawn in blue. This network adjusts the PEP over time, and remembers the motor command that produces the intended force.

The output of the CPG, drawn in purple, excites the motor neurons. Tuning CPG dynamics is discussed in our previous work (Szczecinski et al., 2017b). The PEP and AEP neurons adjust the motor output via multiplication pathways, drawn in green, which scale CPG output to the motor neurons based on the intended range of motion. Motor neuron activity controls the motor velocity, and the θ neuron receives position feedback from the motor via the mappings in Figure 1B. The motor velocity, computed by the cyan differentiation pathway, reinforces ongoing CPG behavior through the $\dot{\theta }$ neuron (Szczecinski et al., 2017b). A division pathway (not shown) can be used to normalize the velocity feedback to the joint’s commanded range of motion, simplifying the control of stepping frequency. The $\dot{\theta }$ neuron also receives some input from the Load neuron, ensuring that stance phase is stable (Szczecinski and Quinn, 2017, accepted). By using the functional subnetworks and the design constraints presented in this paper, we can rapidly and directly assemble models of neural systems that perform as intended without hand-tuning or optimization methods.

How are the “Free Parameters” in Tables 1 and 2 chosen? The free parameters fall into two classes: reversal potentials (i.e., ΔE_s) and dynamical constants (e.g., k, τ, etc.). The reversal potentials are informed by biology. In this paper, we kept −40 < ΔE_s < 194 mV (i.e., −100 < E_s < 134 mV). The modeler could use reversal potentials from specific synapses if that data were available. The dynamical constants are informed by the function of the robot. For example, the k_syn of the subtraction network in Figure 1B controls the stiffness of the controller, and may destabilize the system if not tuned to match the mechanical properties of the robot (Szczecinski et al., 2017b).

As another example, τ_d and k_d of the differentiator network in Figure 7 determines the robustness of CPG rhythms, and how well it entrains to sensory feedback (Szczecinski et al., 2017b). A slow, adaptively-walking robot may want a high k_d to regularize CPG oscillations, whereas a fast running robot may want a low k_d to be less sensitive to sensory feedback. Picking specific values for these free parameters ultimately depends on the intended behavior of the robot. The constraints in this paper enable the designer to think in terms of more traditional robotics quantities, and use these to set neural and synaptic parameter values, which may be less intuitive.

6. Discussion

In this paper, we presented analytical methods for setting parameters in dynamical neural networks that can add, subtract, multiply, divide, differentiate, and integrate incoming signals. Such operations are at the core of control, and these techniques enable control networks to be assembled rapidly and tuned directly. This work primarily identifies constraint equations, not unique values, that govern how parameters should be tuned. Thus, many different networks may perform the same function with different parameter values, as observed in real neural circuits (Prinz et al., 2004). Since these results are analytical, not based on machine learning or optimization, there is no concern about these networks over- or under-fitting training data, and their behavior is provable. These techniques build on our previous analysis of synthetic nervous systems (Szczecinski et al., 2017b) and have been validated through several studies with our robot, MantisBot (Szczecinski and Quinn, 2017; Szczecinski et al., 2017a).

All of the results from this paper make it easier to tune neuromechanical models of animals, as well. Many such models have been created to study the principles underlying insect (Daun-Gruhn and Tóth, 2010; Szczecinski et al., 2014) and mammalian (Hunt et al., 2015a; Markin et al., 2016) locomotion alike. Oftentimes, parameters of these models are tuned by hand to obtain the intended motion, which is a painstaking, slow, and imprecise process. The analysis in this paper can make neuromechanical models come together more quickly, and have more predictable behavior, leading to more thorough scientific investigations. More precise tuning methods enable more thorough validation or invalidation of hypotheses. Faster tuning methods enable more rapid validation or invalidation of hypotheses. For example, these methods could be used to improve the coordination our previous cockroach model (Szczecinski et al., 2014). In the model, curve walking of varying radii was achieved by modulating muscle activations with broad descending commands. However, the coordination, reliability, and repeatability of such motion could be improved with the methods of this paper, enabling us to improve or reject the model.

6.1. Simplifications

Some of the calculations in this paper are based on approximations, which lead to inaccuracies in the calculations of the subnetworks. One example is that the subtraction network does not produce linear output. This non-linearity occurs because the reversal potentials of synapses are rarely much lower than the resting potentials of neurons, requiring large values of g_s,2 to build a subtractor where k_syn = 1. A large g_s,2 value increases U_pre,2’s effect on the denominator of $U_{\mathit{post}}^{\ast }$’s response, causing the synaptic input to reduce U_post’s sensitivity to inputs. This is particularly noticeable in the differentiator’s response (Figure 4), especially as k_syn increases.

Another example of a simplification we made is that our calculation of k_i only used the particular solution of the system. This means that a transient response also exists, which we did not compute. In addition, k_i is a function of U₁ and U₂. This means that k_i is not a constant for this network. However, the impact of U₁ and U₂ on k_i can be minimized by minimizing g_s and maximizing R, as we showed in Sec. 4.2.

However, the developed networks are not intended to act as perfect analogs to their mathematical counterparts. These networks are intended to act as representations of real neural circuits, which likely do not act as perfect adders, multipliers, differentiators, etc. Dynamic and transient effects are a real part of biological control systems, and effective neural controllers have developed around these idiosyncrasies and have likely evolved to even exploit many of these aspects. In spite of these issues, the methods in this paper are valuable. Our recent robotics work (Szczecinski and Quinn, 2017; Szczecinski et al., 2017a), as well as related work in progress, is proof of the effectiveness of this approach.

6.2. Why Put Neurons in the Way?

The methods in this paper enable the direct construction of networks that perform arithmetic and dynamic calculations. Why bother building neural networks just to recreate mathematical operators? We believe there are several reasons to take this approach. From a neurobiology perspective, the constraints that we have identified may help explain why certain structures are common in the nervous system (David Friel, personal correspondence). For instance, mutually inhibitory parallel pathways are common in the thoracic control of insect locomotion (Büschges and Wolf, 1995), which may function as subtraction networks in negative feedback loops. As another example, networks in the retina of the rabbit are selectively sensitive to motion in one direction or the other (Barlow and Levick, 1965). Such a network could be constructed by using adjacent cells in the retina as inputs to differentiator networks. This would be consistent with both the function of direction-sensitivity, as well as the laterally inhibitive structure. Even though such consistency does not guarantee that the animal’s nervous system functions precisely this way, the design methods in this paper may aid in understanding the function of neural networks found in animals.

Additionally, the constraints that we identified may be used to constrain parameter values in large brain models. Rather than using global search techniques to understand the dynamics of a large pool of neurons, we believe it may be faster to begin with a number of functional subnetworks, and then use local search techniques to tune the connections between them. In this way, the designer is certain that parts of the network perform specific, useful computations, rather than naively optimizing a large network (Haferlach et al., 2007; Agmon and Beer, 2013; Izquierdo and Beer, 2013). The end result is something like a genetic program, but in a neuroscience context.

Author Contributions

NS led research on functional subnetworks and led the preparation of the manuscript. AH aided in the preparation of the manuscript. RQ provided critical oversight of the research and aided in the preparation of the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Appendix

A. Derivation of Integrator Eigenvalues and Eigenvectors

We find the eigenvalues λ₁ and λ₂ and the associated eigenvectors X₁ and X₂ of the Jacobian matrix by the eigenvalue problem,

$$\det \left(J-{\mathrm{\lambda }}_i\cdot I\right)=0$$ (A1)

$$J\cdot X_i={\mathrm{\lambda }}_i\cdot X_i,$$ (A2)

where i is the index of the eigenvalue (1 or 2), $I\in {\mathbb{R}}^{2\times 2}$ is an identity matrix, and J is the square matrix from equation (64). Solving for λ,

$${\mathrm{\lambda }}_1=0,{\mathrm{\lambda }}_2=\frac{a+b}{C_m}>0.$$ (A3)

Because J is on the same side of the equation as $\dot{\overrightarrow{x}}$ (see equation (65)), λ₂ > 0 indicates a stable system (e.g., as the stiffness matrix of a physical system). ${\mathrm{\lambda }}_2>0\forall \overrightarrow{x}$, because a > 0 and b > 0. The definition of a in equation (62) shows that a > 0 because g_s > 0 (it is a physical quantity) and U₁/R ∈ [0, 1]. The same reasoning applies to b.

We use the eigenvalues to find their associated eigenvectors,

$$X_1=\left[\begin{array}{c}\hfill 1\hfill \\ \hfill -b∕a\hfill \end{array}\right].$$ (A4)

Normalizing X₁ to 1,

$$X_1=\left[\begin{array}{c}\hfill \frac{1}{\sqrt{1^2+{\left(-b∕a\right)}^2}}\hfill \\ \hfill \frac{-b∕a}{\sqrt{1^2+{\left(-b∕a\right)}^2}}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 1∕d\hfill \\ \hfill -b∕\left(\mathit{ad}\right)\hfill \end{array}\right],d=\sqrt{1^2+{\left(-b∕a\right)}^2}.$$ (A5)

Next, we calculate

$$X_2=\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \end{array}\right].$$ (A6)

Normalizing X₂ to 1,

$$X_2=\left[\begin{array}{c}\hfill 1∕\sqrt{2}\hfill \\ \hfill 1∕\sqrt{2}\hfill \end{array}\right].$$ (A7)

We now know the transformation matrix between the natural coordinates, $\overrightarrow{x}={\left[U_1,U_2\right]}^T$, and the generalized coordinates, $\overrightarrow{q}={\left[q_1,q_2\right]}^T$:

$$\overrightarrow{x}=X\cdot \overrightarrow{q},X=\left[X_1,X_2\right]=\left[\begin{array}{cc}\hfill 1∕d\hfill & \hfill 1∕\sqrt{2}\hfill \\ \hfill -b∕\left(\mathit{ad}\right)\hfill & \hfill 1∕\sqrt{2}\hfill \end{array}\right].$$ (A8)

We will also make use of X⁻¹ when transforming between natural and generalized coordinates. We can analytically invert X from equation (A8),

$$X^{-1}=\frac{a\cdot d\cdot \sqrt{2}}{a+b}\cdot \left[\begin{array}{cc}\hfill 1∕\sqrt{2}\hfill & \hfill -1∕\sqrt{2}\hfill \\ \hfill b∕\left(\mathit{ad}\right)\hfill & \hfill 1∕d\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill \frac{a\cdot d}{a+b}\hfill & \hfill \frac{-a\cdot d}{a+b}\hfill \\ \hfill \frac{b\cdot \sqrt{2}}{a+b}\hfill & \hfill \frac{a\cdot \sqrt{2}}{a+b}.\hfill \end{array}\right]$$ (A9)