Resolving multicopy duplications de novo using polyploid phasing

Abstract

While the rise of single-molecule sequencing systems has enabled an unprecedented rise in the ability to assemble complex regions of the genome, long segmental duplications in the genome still remain a challenging frontier in assembly. Segmental duplications are at the same time both gene rich and prone to large structural rearrangements, making the resolution of their sequences important in medical and evolutionary studies. Duplicated sequences that are collapsed in mammalian de novo assemblies are rarely identical; after a sequence is duplicated, it begins to acquire paralog specific variants. In this paper, we study the problem of resolving the variations in multicopy long-segmental duplications by developing and utilizing algorithms for polyploid phasing. We develop two algorithms: the first one is targeted at maximizing the likelihood of observing the reads given the underlying haplotypes using discrete matrix completion. The second algorithm is based on correlation clustering and exploits an assumption, which is often satisfied in these duplications, that each paralog has a sizable number of paralog-specific variants. We develop a detailed simulation methodology, and demonstrate the superior performance of the proposed algorithms on an array of simulated datasets. We measure the likelihood score as well as reconstruction accuracy, i.e., what fraction of the reads are clustered correctly. In both the performance metrics, we find that our algorithms dominate existing algorithms on more than 93% of the datasets. While the discrete matrix completion performs better on likelihood score, the correlation clustering algorithm performs better on reconstruction accuracy due to the stronger regularization inherent in the algorithm. We also show that our correlation-clustering algorithm can reconstruct on an average 7.0 haplotypes in 10-copy duplication data-sets whereas existing algorithms reconstruct less than 1 copy on average.

1 Introduction

Advances in single-molecule sequencing (SMS) by Pacific Biosciences (Menlo Park, CA), and Oxford Nanopore (Cambridge, UK) have recently enabled the assembly of draft de novo mammalian genomes [35, 21] nearing the quality of the original release of the human genome. The goal of de novo fragment assembly is to estimate the sequence of a genome given overlaps of relatively short sequencing reads, and is a well-studied problem. While there are multiple formulations of the fragment assembly problem [27, 31], the common challenge is that repeats in the genome longer than the length of sequenced DNA fragments make a unique reconstruction of the genome impossible [30]. Reads produced by SMS are advantageous for de novo assembly because the read length is at least two orders of magnitude greater than other high-throughput sequencing methods, so that genome order may be uniquely resolved when repeats are small.

SMS reads are characterized by a raw read accuracy between 75% and 90% with read lengths that follow a log-normal distribution. Initial development in de novo assembly of SMS reads focused on efficient methods to detect overlaps between long but noisy reads [28, 6]. Consistent with information theory [26], regions of genomes without sufficiently long repeats are contiguously assembled [24] with SMS reads. A type of repeat not well represented in human and other de novo SMS assemblies are segmental duplications: sequences 1 to 400 kilobases in length that are duplicated with at least 90% identity [18]. Segmental duplications are at the same time both gene rich and prone to large structural rearrangements, making the resolution of their sequences important in medical and evolutionary studies [37]. Comparing an SMS-based assembly of a Yoruban individual [38] to the human reference (GRCh38) reveals that only 64.2% of known segmentally duplicated bases in the human genome are present in the assembly. Due to the low raw-read accuracy of SMS sequences, reads from different duplication paralogs are frequently merged together into the same sequence in an assembly. As a result, human assemblies of SMS reads contain large contigs with correctly resolved unique sequence, and shorter contigs containing the collapse of multiple copies of a duplication into one sequence.

Segmental duplications that are collapsed in real de novo assemblies are rarely identical; after a sequence is duplicated, over generations it begins to acquire paralog specific variants (PSVs): single-nucleotide variants that distinguish different duplication paralogs. To put this in an evolutionary context, sequences that have duplicated shortly after the human-chimpanzee divergence (6 million years ago) have acquired up to roughly one PSV per thousand bases [17]. Although the ultimate goal of de novo assembly is to completely resolve the sequence of a genome, an intermediate goal is to resolve the individual sequences that are collapsed in the assembly. We propose resolving sequences by estimating the number of duplications collapsed into an individual sequence in an assembly, and determining the PSVs belonging to each duplication.

Given S segmental-duplication paralogs of the same length containing V variants, one may represent all paralogs as an S × V matrix P with entries in {0, 1}, where each entry P(i, j) is 0 if the repeat paralog i is in the consensus state at site j, or 1 if it is a PSV. The set of N reads from all repeat paralogs may be aligned to the consensus sequence, and represented as an N × V read-fragment matrix X with entries in {0, 1, −} corresponding to consensus, variant, or absent (since reads only give information about certain positions). The goal is to reconstruct the paralog matrix P given only the read matrix X, where there are also sequencing errors creating erroneous entries in X. Let us assume that the error probability is ε at any position, i.e., with probability 1−ε, the location is read correctly and with probability ε, the location is read incorrectly (0 is read as a 1 and vice-versa).

For S = 2, this problem is identical to haplotype phasing of a diploid genome [25, 4, 29]. Defining a read conflict as two overlapping reads that are non-gap and disagreeing at a site, haplotype phasing with error-free reads may be determined by grouping all conflict-free reads. To handle sequencing errors, a common formulation for haplotype phasing is Minimal Error Correction (MEC), where a minimal number of base changes are applied to reads so that they may be partitioned into two conflict-free sets. For S = 2, there has also been an exact information theoretic characterization of when it is possible to phase the genome correctly [36, 13], along with efficient algorithms. This is based on connections to a problem called “community detection” [20] where the goal is to cluster users into communities based on positive or negative interactions between individuals.

When S > 2 this corresponds to the much less studied problem of polyploid phasing, which was discussed in pioneering work by Aguiar and Istrail [1]. Beginning with Hapcompass [1], there has been some work on polyploid phasing using algorithms based on branch-and-extend [5], belief propagation [32] and semi-definite programming [14]. In a recent theoretical work [7], the hardness of optimizing the MEC for S > 2 has also been proven, indicating that algorithms for this problem need to be necessarily approximate or tailored to some assumptions. A major drawback of existing works is that they consider only S = 3, 4 and none have been developed, optimized, or tested for the high ploidy that is encountered in segmental duplications, where S can be potentially larger than 10, and to the low error-rate in Illumina sequencers. Thus algorithms that are robust to the high error rates and can handle the high poly-ploidy are imperative in solving the segmental duplication problem, and in this paper, we will design such algorithms.

In particular, we propose two algorithms for solving the problem. The first approach is based on a discrete matrix completion paradigm where the goal is to maximize the likelihood of the observed data given the underlying haplotypes. The second approach is based on a correlation-clustering framework with an inherent assumption that each haplotype has a paralog-specific variant (which holds in many types of segmental duplications). By performing detailed simulations, we demonstrate the superior performance of the proposed algorithms over existing algorithms, especially in the high ploidy regime.

2 Haplotype phasing via Discrete Matrix Completion

2.1 A probabilistic model

In order to represent the matrices in real-valued arithmetic, we adopt the following mapping f: {0, 1,−} → {−1, 1, 0}, i.e., we represent the consensus allele as −1, variant as 1 and undisclosed locations as 0. To model the read matrix X, we first consider an idealized matrix M, which does not contain any noise nor does it contain any undisclosed position. If read n is sampled from the s-th paralog, then the n-th row of this matrix M is given by the s-th row of the paralog matrix, i.e., M_n. = f(P_s.). The disclosed locations of the matrix are represented by a set Ω which comprises of the set of tuples (n, v) where read n contains information about variant v. Given M and Ω, the matrix X is not a deterministic function since there are independent read errors, which convert a 1 into a −1 with probability ε and vice versa. The probability of observing X given M and Ω is therefore given as follows,

$$\begin{gathered} log\mathbb{P}(X\mid M,\mathit{\Omega })=\sum _{(n,v)\in \mathit{\Omega }}log\mathbb{P}(X_{n,v}\mid M,\mathit{\Omega }) \\ =\sum _{(n,v)\in \mathit{\Omega }}log\left((1-\epsilon ){𝟙}_{X_{n,v}=M_{n,v}}\right)+log\left(\epsilon {𝟙}_{X_{n,v}\ne M_{n,v}}\right) \\ =d_H(X,M)\ast log(\epsilon )+(\mid \mathit{\Omega }\mid -d_H(X,M))\ast log(1-\epsilon ) \\ =-d_H(X,M)\ast log(\frac{1-\epsilon }{\epsilon })+(\mid \mathit{\Omega }\mid )\ast log(1-\epsilon ), \end{gathered}$$

where d_H(X,M) is the Hamming distance between the two matrices X and M in the locations Ω, i.e., where X ≠ 0. Different haplotype assembly algorithms have sought to minimize varied objective criteria in order to obtain the correct clustering of reads belonging to the respective haplotypes [34]. Some of the noteworthy objectives are minimum edge removal (MER), minimum SNP removal (MSR) and minimum error correction (MEC). The quantity d_H(X,M) is called the error criterion, and in our approach, maximizing the likelihood is equivalent to minimizing this error criterion referred to as MEC.

We observe that the ideal matrix M has repeated rows, since all rows sampled from the same paralog are identical. This implies that the matrix M has low-rank. Indeed the matrix M can be factorized as the product of two matrices M = A · B, where A ∈ ℝ^N×S with A_ij ∈ {0, 1} ∀i, j and B ∈ ℝ^S×V with B_ij ∈ {−1, 1} ∀i, j. Each row of A is an elementary vector of length S denoting which paralog the read is from and matrix B is identical to f(P) (represented in {−1, 1}).

The observed matrix X is a noisy partial observation of the low-rank matrix M, and the goal is to reconstruct the matrices A and B given X. If each read spanned the entire segmental duplication, the problem would be trivial, since similar reads can be grouped together and taking a consensus inside clusters reveals the segmental duplications. The difficulty is posed by the fact that read lengths are much smaller and do not span all variant positions.

Each read only provides partial phasing information. The resulting X matrix is thus sparse, and our goal can be formally stated as follows:

$${\text{argmin}}_{A,B}{d}_H(X,A·B).$$ (1)

Real-valued versions of this problem has received much attention and is called the matrix completion problem. While this problem has a rich history, there is a significant difference in our setting, since the matrices A and B have structure (i.e., A has only elementary row vectors and B has binary entries) and the matrix X is ternary. We therefore have to develop new algorithms that exploit the discrete structure of the problem.

The problem of finding missing entries in a matrix arises in diverse research domains. One of the most illustrative examples is the Netflix challenge where users rate a small fraction of movies at random and the task is to predict user preferences for an unrated movie; a key assumption in this domain is that the true matrix of preferences is low-rank. While low-rank matrix-completion problem is known to be NP-Hard, there are methods that can give provably correct reconstruction under probabilistic rather than worst-case assumptions [10, 33]. Popular techniques for this problem include convex relaxation of the rank to nuclear norm [33], singular value thresholding [9] and alternating minimization [22], all of which have theoretical guarantees as well. The key difference between these works and our problem is that they consider real-valued matrix-completion, whereas, in this paper, we adapt and extend the algorithms to the discrete setting inherent to the phasing problem.

In a recent paper [8], Cai et al. formulate haplotype phasing as a low rank matrix completion problem and use structure constrained alternating minimization for obtaining the haplotypes. In the paper, they demonstrate improved performance over HapCompass for diploid and simulated polyploid data (with S = 3, 4). We show in this paper that while that method has good performance with small S, the performance starts deteriorating with higher S. The main reason for the deteriorating performance is the inability of the algorithm to exploit the discrete structure of the problem (for example, the algorithm does not use the fact that the B matrix is binary, instead treating it as a real-valued matrix). We alleviate this problem in the present paper by proposing an algorithm that explicitly exploits this fact.

2.2 Iterative Two Stage Matrix Completion

Our problem stated in (1) is a hard combinatorial problem. One can design alternating minimization based techniques for this problem, where A and B are optimized alternatively while keeping the other variable fixed. While such methods monotonically increase likelihood, they are not guaranteed to find the global optimum of the problem and display high sensitivity to initial conditions. The key idea in our approach is to first neglect the discrete nature of our problem, and view it as a real-valued matrix completion problem. We then “round” the results obtained from this real valued matrix completion to obtain a feasible solution for the discrete problem. This rounded solution then becomes the initial value of a discrete matrix completion routine designed based on the alternative minimization technique. While this method already has superior performance compared to existing approaches, we found that in the regime when the ploidy is high, the algorithm is able to extract some dominant haplotypes correctly while being incorrect on the other haplotypes. In order to overcome this barrier, in iteration i, we only fix the best i − 1 haplotypes based on the current MEC, and optimize for the rest. A schematic representation of this algorithm is depicted in Fig. 1, and the detailed pseudocode is in Algorithm 1, Algorithm 2 and Algorithm 3.

Fig. 1.

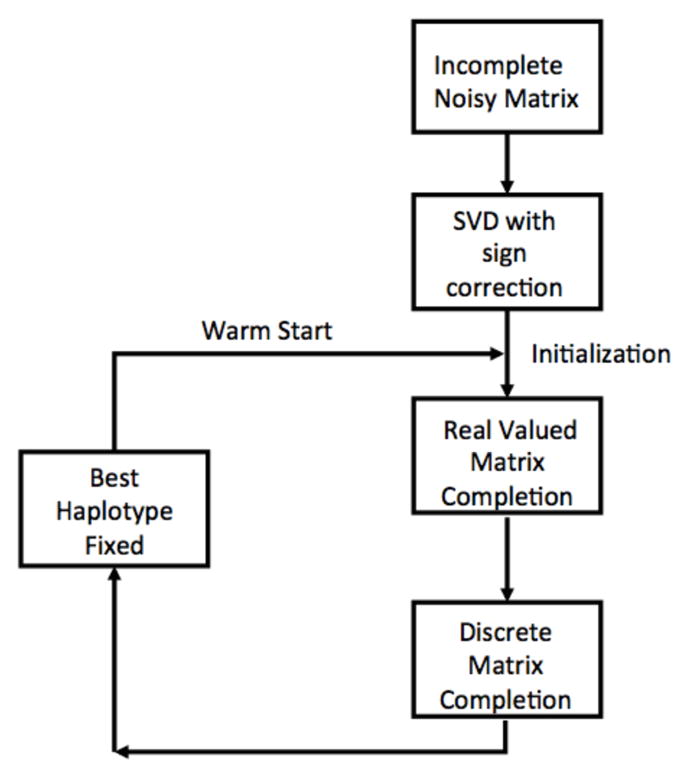
The initialization and iteration workflow for MCP

Algorithm 1.

Iterative Matrix Completion

	Input : Noisy incomplete Matrix X, Rank Estimate S
1:	Initialize Ainit ∈ ℝN×S and Binit ∈ ℝS×V with sign corrected SVD.
2:	e ← Error rate
3:	k ← S
4:	while k ≥ 2 and MEC Score decreases do
5:	Best ← RealMatCom(Ainit, Binit, X, k)
6:	Aest, Best ← DiscreteMatCom(Best, X, e)
7:	Choose the best segment based on individual scores
8:	Ainit ← Aest
9:	Binit ← Best
10:	k ← k − 1
11:	end while
	Output : Estimated Haplotypes Best

Algorithm 2.

Real Valued Matrix Completion

1:	procedure RealMatCom(Ainit, Binit, X, k)
2:	A ← Ainit
3:	B ← Binit
4:	while stopping criterion not satisfied do
5:	Minimize A using projected gradient descent
6:	Minimize B1:k using projected gradient descent
7:	end while
8:	return sign(B)
9:	end procedure

Algorithm 3.

Discrete Valued Matrix Completion

1:	procedure DiscreteMatCom(Best, X, e)
2:	while MEC Score decreases do
3:	for each row i of X do
4:	for each segment s of Best do
5:	d(i, s) ← Hamming distance of Xi and Best,s for known entries
6:	Wi ← Window size of revealed entries of Xi
7:	Aest,is ← (1 − e)Wi−d(i,s) · ed(i,s)
8:	end for
9:	Update overall MEC score and score for each individual segment
10:	Normalize Aest,i to be a probability distribution
11:	end for
12:	Initialize Best,new ∈ ℝS×V with zeros
13:	for each row i of X do
14:	$B_{\text{est},\text{new}}\leftarrow B_{\text{est},\text{new}}+{\mathcal{P}}_{\mathit{\Omega }}(A_{\mathit{est},i}^T·X_i)$
15:	end for
16:	Best ← sign(Best,new)
17:	end while
18:	return Aest, Best
19:	end procedure

A standard approach in combinatorial optimization is to relax the integer constraints in the problem in order to get a real-valued optimization problem, and then to round the obtained results to get a feasible solution. We follow a similar approach here by relaxing our discrete problem to a continuous optimization problem, and along with it, we relax the objective too. Instead of optimizing according to the Hamming distance objective with the discrete constraints on A,B (see (1)), we instead minimize the Frobenius norm of the difference while at the same time assuming that A and B are real valued.

The noisy low rank matrix completion can be formally stated as an optimization problem.

$$\underset{A,B}{min}\frac{1}{2}{\Vert {\mathcal{P}}_{\mathit{\Omega }}(A·B-X)\Vert }_F^2$$

The objective function is a squared sum of errors over all the known entries of X. ℘_Ω(·) is the projection operator and Ω is the set of known incides of X. So, ℘_Ω(Z_ij) = Z_ij if (i, j) ∈ Ω and 0 otherwise. While we relax the integer constraints of the problem, we assume the following linear constraints to hold.

$$0\le A_{ij}\le 1\forall i\in [N],j\in [S]$$ (2)

$$-1\le B_{ij}\le 1\forall i\in [S],j\in [V]$$ (3)

Since the optimization is over unknown matrices A and B in a product form, the problem is non-convex. However, alternating minimization algorithms are known to have guaranteed reconstruction performance in certain regimes [22] and therefore we resort to using such algorithms. Thus we first solve the optimization over A, keeping B fixed, which makes the problem convex in A and vice-versa.

2.3 Projected Gradient Descent

The alternating minimization for our problem therefore can be stated as follows: min

$$\begin{array}{l}\underset{A}{min}\frac{1}{2}{\Vert {\mathcal{P}}_{\mathit{\Omega }}(A·B-X)\Vert }_F^2\\ s.t.0\le A_{ij}\le 1\forall i,j\end{array}$$

and similarly

$$\begin{array}{l}\underset{B}{min}\frac{1}{2}{\Vert {\mathcal{P}}_{\mathit{\Omega }}(A·B-X)\Vert }_F^2\\ s.t.-1\le B_{ij}\le 1\forall i,j\end{array}$$

To incorporate the constraints on the variables, we use a projected gradient descent to minimize each of the convex formulations.

2.4 Initialization

Since the overall problem is non-convex, it is required to choose a suitable initialization for better performance. For this purpose, we use the singular value decomposition (SVD). This is a factorization of a m × n rectangular matrix of rank r in the form 𝒰Σ𝒱^T, where 𝒰 is a m×r unitary matrix, Σ is a r×r diagonal matrix with non-negative diagonal entries and 𝒱 is a n × r unitary matrix. The columns of 𝒰 and 𝒱 are called the left and right singular vectors respectively. Prior theoretical results [22] suggest taking the S singular vectors of ℘_Ω(X) as the initial guess for A and B. While this is a reasonable initialization, the signs of the singular vectors obtained from SVD decomposition may not be consistent with our problem since we require the entries of A to be strictly non-negative. We note that the signs of the singular vectors can be swapped without affecting the SVD. Therefore, in our algorithm, in order to ensure this sign consistency, we reverse the signs of certain rows of B to ensure that all columns of A have a positive sum.

$${\mathcal{P}}_{\mathit{\Omega }}(X)=\mathcal{U}·\mathit{\sum }·{\mathcal{V}}^T\mathit{\Gamma }=\text{sign}({𝟙}^T\mathcal{U})A_{\text{init}}=\mathcal{U}\ast \text{diag}(\mathit{\Gamma })B_{\text{init}}={(\mathcal{V}\ast \text{diag}(\mathit{\Gamma }))}^T$$

For details of the projected gradient descent, we refer the reader to Appendix I.

2.5 Discrete Matrix Completion

We round the output of the real-valued matrix completion to satisfy the discrete constraints of A and B and utilize this to run a discrete alternating minimization algorithm to solve (1). The optimization of A given a fixed B is easy to solve: the basic idea is to assign each read to the segment which minimizes the Hamming distance with the read. To optimize B given a fixed A, we find the consensus of all the reads which are informative about a given position. In our algorithm, instead of having A to be a hard decision of which segment a given read belongs to, each row i of A encodes the probability that read i belongs to segment j. Therefore, while optimizing over B, we utilize the weighted consensus rather than the plain consensus of the read assignments. This procedure of refinement comes under the purview of a broader class of algorithms called the Expectation Maximization (EM) algorithm [16] as well as Variational Bayes [40]. The matrix A can be viewed as hidden variables encoding the membership of read fragments to duplication copies and B as the parameters for the exact underlying segments. We refer the reader to Algorithm 3 for a detailed description of the algorithm.

2.6 Choosing the best segment and Effective Rank Reduction

As pointed out earlier, the algorithm as stated above works well with small polyploid instances; however, in the presence of higher ploidy, the algorithm returns only the top few haplotypes correctly. For example, consider the cascading topology of repeats in Figure 2, it is easier to resolve segment 7 but the other segments are more easily confused. Therefore, we propose an iterative algorithm, where in each iteration, the best haplotype is fixed and then the algorithm is run to optimize over possibilities of the other haplotypes. Thus in order to do matrix completion with S haplotypes, the algorithm is iterated over S−1 times. Such algorithms have a precedent even in real-valued matrix completion. For example, stagewise alternating minimization is shown to have better theoretical guarantees in [22]. In our implementation, at iteration i, the best i − 1 haplotypes are chosen as the ones which have minimum Hamming distance from their assigned reads.

Fig. 2.

Examples of topologies of duplication simulations. In total there are 12 structured trees and 50 random topologies. The divergence between any two simulated duplications is given by the mutation rate r×the shortest path between the duplications in the tree.

3 Haplotype phasing with correlation clustering

One limitation of the MEC objective function and therefore of the discrete matrix completion algorithm is that the ploidy must be known a priori or estimated. Since the MEC objective itself decreases monotonically with ploidy, it is not possible to estimate the ploidy using the MEC objective. This can be potentially remedied using regularized alternatives that account for model complexity like AIC, BIC or MDL. We propose an alternative algorithm here that can jointly estimate the ploidy while estimating the haplotypes themselves. This algorithm is based on a key assumption, distinct from the assumptions of the discrete matrix completion problem: that each of the haplotypes have uniquely identifying variants. While this assumption is stronger, it can lead to stronger regularization of the problem by restricting the search space and therefore leads to better estimates, especially when the ploidy is high.

The basic idea of the algorithm is the following: each locus is represented as a vertex and reads that straddle multiple vertices create edges between the vertices that have either positive or negative weight based on whether reads share the variant or not. The goal is then to cluster the nodes into groups which share the same variant, with each cluster representing a haplotype and each locus (node) in the cluster representing a haplotype-specific variant.

To formally define our algorithm, we begin with an alternative formulation for polyploid phasing through correlation clustering [3], with the premise that a metric defines how similar or dissimilar two objects are, and clusters maximize the amount of similarity within each cluster and dissimilarity between clusters. Importantly, in correlation clustering the number of clusters is discovered as a result of clustering and not as a parameter.

We use an augmented form of the SNP conflict graph 𝒢_𝒮 introduced in [25], denoted 𝒢_PSV = (V,E),E = {E⁺,E⁻}. The construction of 𝒢_PSV requires the fragment matrix M, and some data-dependent parameters: the expected range of coverage per haplotype c_min and c_max, and a distance d that is the maximum distance reads are expected to overlap variants. A vertex exists for each of the columns (sites) in the fragment matrix M, connected by an edge (u, v) ∈ E⁺ if u and v are overlapped by between c_min and c_max reads that are variant (e.g., 1) at both sites, or an edge (u, v) ∈ E⁻ if the sites corresponding u and v are within d bases and (u, v) ∉ E⁺. A weight W(u, v) is assigned to each edge.

Correlation clustering on 𝒢_PSV corresponds to finding clusters C = c₁, … , c_n that minimize the sum of weighted negative edges within each cluster and weighed positive edges between clusters: Score_CC = Σ_ci (Σ_{(u,v)∈ci,(u,v)∈E⁻} w(u, v)+Σ_{(u∈ci,v ∉ci),(u,v)∈E⁺}w(u, v)), where w(u, v) may reflect certainty of clustering, or more simply w(u, v) = 1 to count edges. Each cluster defines a set of sites that belong to a haplotype. This was shown to be APX-hard [15, 12, 19], and approximations based on linear programming (LP) were described in [15, 12]. We developed an implementation of the LP approach that was successful at clustering smaller datasets, however the number of constraints grows with |E|², and |E| grows by p²v², for ploidy p and number of paralog specific variants v, which requires excessive resources for larger datasets.

To evaluate correlation clustering on larger datasets, we developed a simple randomized heuristic to search similar to the method of [2] for clusters that provide acceptable values for Score_CC that follows the steps:

1. Define clusters likely to represent repeat paralogs through a random search.

2. Merge clusters with sufficient overlap, and assign nodes to unique clusters.

3. Optimize clusters by swapping vertices from adjacent clusters.

Define the neighbor similarity Sim(u, v) of two vertices to be the number of neighbors shared between u and v connected by edges in E⁺, and Score(V, E, c) to be the Score_CC of a single cluster c assuming all vertices V\c are in a separate cluster. First, clusters are formed by iteratively adding vertices neighboring a cluster as long as the neighbor similarity is sufficient and addition of the vertex decreases Score_CC, described in 4.

Given parameters for neighbor similarity s, a maximal number of search iterations max search it and swap iterations max swap it, and fraction cluster overlap f^ovp, the method FindCluster is used to find a set of clusters C by first initializing C = ∅, and iteratively selecting a vertex v_i ∉ C, and adding the result of FindCluster(V, v_i, E, s) to C until C contains all vertices in V or max_it iterations are reached. The resulting clusters in C are not disjoint, and so any cluster c_i with a fraction of vertices overlapping with a cluster c_j > f^ovp is first merged into c_j, then remaining vertices belonging to more than one cluster are assigned to the largest cluster for which they are a member. Finally, the clusters are further optimized by selecting edges (u, v) ∈ E⁺ where u ∈ c_i and v ∈ c_j and swapping u and v if this improves Score_CC for up to max swap it iterations.

Algorithm 4.

Find cluster

procedure FindCluster(V, vi, E, s)

c ← vi

repeat

for all v ∈ c do

for all n ∈ Neighbors(v) ∉ c do

if Sim(v, n) ≥ s and Score(V, E, c ∪ n) < Score(V, E, c) then

c ← c ∪ n

end if

end for

end for

until c has not grown

return c

end procedure

4 Results

We benchmarked our methods on a dataset of simulated collapsed segmental duplications. It is difficult to simulate the complex mosaic architecture of segmental duplications [23], and so we elected to use a simplified model of 100kbp nonmosaic duplications. While this lacks the complexity of mosaic duplication architecture, the length is greater than the average duplication unit (~30kbp), ensuring evaluation on challenging problems. Starting with an ancestral sequence, sequences are duplicated according to a specified tree topology T and mutation rate r, where each child node is a copy of a parent node mutated at a rate of r random SNV mutations per base. In real data, duplications arise with many complex histories [17, 39]. To capture the complexity of evolution, we used two classes of trees: 12 simulations from well defined topologies such as flat, bifurcating, and cascading resulting in four to eight duplicated sequences, and 50 simulations from random tree topologies that have 10 duplicated sequences. Examples of the duplication toplogies are shown in Figure 2. The mutation rate was varied from between 0.01, 0.005, and 0.001, and 0.0005 mutations per base to simulate various ages of duplications. For each set of duplications we simulated 50× read coverage using the Alchemy SMS read simulator [11], a model based simulator that emulates a sequencing run by Pacific Biosciences, and mapped reads back to the ancestral sequence. PSV sites are detected as sites that contain between 25 and 60 non-ancestral bases.

For each of the simulated topologies and mutation rates, we evaluated the Discrete Matrix Completion (DMP), Correlation Clustering (CC), and Structure Constrained Gradient Descent (SCGD). The SCGD method has been shown to outperform other previously developed methods in polyploid phasing [8].

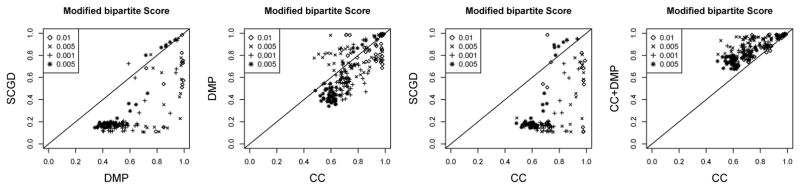
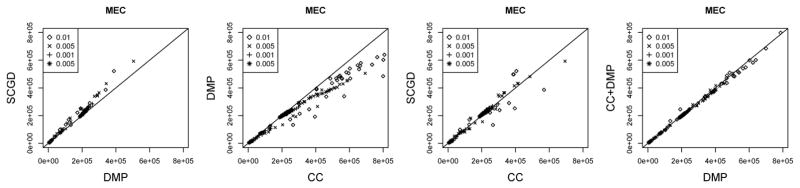
We report Minimum error correction (MEC) values by computing the sum of Hamming distance between each read and the consensus sequence for each haplotype. For CC, we assign reads to each haplotype according to the minimal Hamming distance from the read to each haplotype. For duplications simulated under models of high mutation rates (0.01 and 0.005), the DMP method is able to obtain a lower MEC than the other methods. Out of the 128 datasets for which every method is able to run within the time constraint set on our server, we compare the performance. We observe that CC obtains the best MEC score 11% of the datasets, DMP 85%, and SCGD 3.9%.

For each haplotype we count the number of reads in the haplotype that are shared with the reads simulated in each duplication, and define a matching statistic as the sum of number of reads in the maximally matched duplication divided by the total number of reads. This statistic ranges between 1 for perfect reconstruction of haplotypes down to a 1/p when all of them are collapsed into a single reconstructed haplotype. The results are shown in Figure 4. CC had the greatest matching score 67.7% of the datasets, DMP 26.1% of the datasets, and SCGD on 6.1% of the datasets. Interestingly, while the CC method has a higher MEC statistic, it has a greater number of correctly partitioned reads when compared with the ground truth. We reason that this is because the CC method exploits the assumption that the positions are variant specific explicitly resulting in stronger regularization, so that even though the likelihood score is somewhat lower for CC method than other methods, it is able to fit the data more accurately. The other methods DMP and SCGD are unable to exploit this assumption and therefore overfit more severely to the data. The DMP method is sensitive to the initialization conditions for B_est, and so we used a solution derived by CC as initial conditions for DMP. We measured improvements on this combination (CC+DMP) relative to DMP on MEC (Figure 3, right), and CC for matching score. While the MEC score was largely unchanged, 220 of the 224 simulations where both CC and CC+DMP had a solution had a greater matching score in CC+DMP (Figure 4).

Fig. 4.

Matching statistics for the DMP, CC, SCGD, and CC+DMP methods. A perfect reconstruction of haplotypes shows a score of 1, while a random assignment will score 1/ploidy. Higher matching score is better.

Fig. 3.

MEC scores for the DMP, CC, SCGD, and CC+DMP methods. The DMP method is shown to produce haplotpyes with lower MEC than either method, particularly for the high mutation rate simulations. Lower MEC score is better.

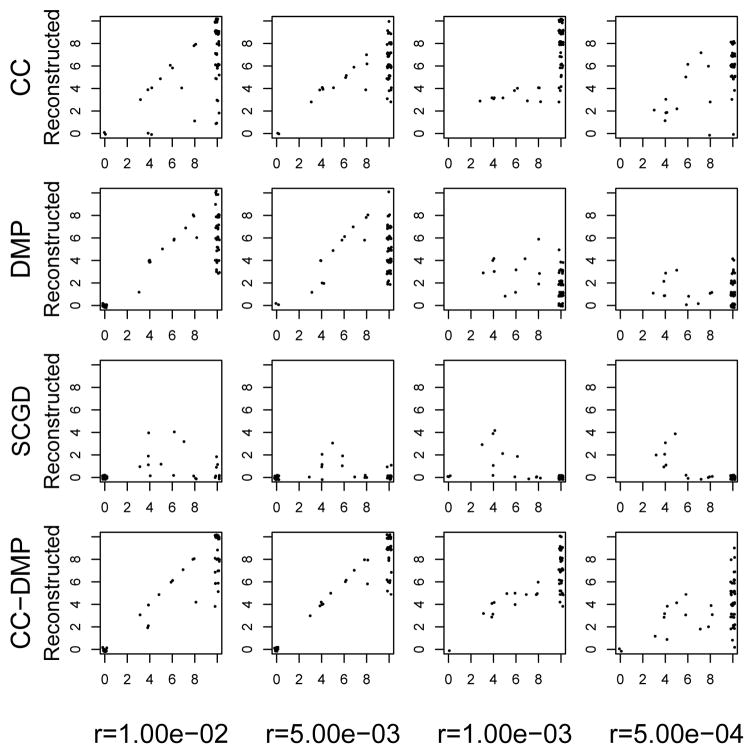
We also measure a more stringent quality of reconstruction accuracy: we ask for what fraction of the true haplotypes there is a reconstructed cluster into which 90% of the correct reads are assigned. Formally, for each simulated duplication we determined which haplotype had the most reads overlapping with the reads simulated from that duplication, and counted how many such haplotypes had at least 90% of the reads from that haplotype reciprocally assigned to that duplication. This gives an indication of the number of copies of a segmental duplication that would be correcly assembled given the phased haplotypes. For the 48 simulations with duplication copy number between 3 and 8, the CC method resolves 70% of duplication copies, while the DMP and SCGD methods resolve 66% and 26%, respectively (Figure 5). For duplications of ploidy 10, the CC method resolves on average 7.0 copies of each duplication, whereas the DMP and SCGD methods resolve on average 3.3 and 0.03 copies, respectively. The CC+DMP combined method resolved 80% of duplications for simulations of copy number between 3 and 8. However for copy number 10 duplications this provided marginal improvements over CC alone, providing solutions for 24 fewer simulations than CC, resolving on average 7.1 duplications per simulation.

Fig. 5.

Correctly assembled haplotypes for the DMP, CC, SCGD, and CC+DMP methods. Each point is the number of correctly phased genotypes per simulation, with points jittered for display

5 Conclusions

The resolution of segmental duplications remains problematic in de novo assemblies. Deviating from the typical formulations of de novo assembly, we present a new formulation and two novel algorithms for resolving high copy collapsed duplications that rely on polyploid phasing. We demonstrated that while it is possible to optimize for minimal error correction, methods that focus on resolving clusters with unique paralog specific variants actually resolve more duplications despite having a higher minimal error correction value, perhaps due to less over-fitting of results to variants present in ancestral copies of a duplication. In future work we hope to improve the the rank estimation for the discrete matrix completion method, possibly leveraging the clusters discovered by correlation clustering, and characterizing the conditions under which correlation clustering converges to the correct clusters. Finally we plan on applying these methods to resolving duplications in published human assemblies [35, 38].

6 Appendix

After each gradient step, the resultant matrix is projected onto the box. The updates for A and B are as follows :

$${\stackrel{\sim }{A}}^{(t+1)}\leftarrow A^{(t)}-{\alpha }_A{\nabla }_{A}f(A)$$

Then $A_{ij}^{(t+1)}=\{\begin{array}{ll}0,\hfill & \text{if}{\stackrel{\sim }{A}}_{ij}^{(t+1)}<0\hfill \\ {\stackrel{\sim }{A}}_{ij}^{(t+1)},\hfill & \text{if}0\le {\stackrel{\sim }{A}}_{ij}^{(t+1)}\le 1\hfill \\ 1,\hfill & \text{if}{\stackrel{\sim }{A}}_{ij}^{(t+1)}>1\hfill \end{array}$

$${\stackrel{\sim }{B}}^{(t+1)}\leftarrow B^{(t)}-{\alpha }_B{\nabla }_{A}f(B)$$

Then $B_{ij}^{(t+1)}=\{\begin{array}{ll}-1,\hfill & \text{if}{\stackrel{\sim }{B}}_{ij}^{(t+1)}<-1\hfill \\ {\stackrel{\sim }{B}}_{ij}^{(t+1)},\hfill & \text{if}-1\le {\stackrel{\sim }{A}}_{ij}^{(t+1)}\le 1\hfill \\ 1,\hfill & \text{if}{\stackrel{\sim }{A}}_{ij}^{(t+1)}>1\hfill \end{array}$

where f(·) is the objective function. The projected gradient descent allows us to incorporate additional constraints on the problem as well. If we further enforce that the sum of each row of A equals 1, then we would have the projection as $A_{ij}^{(t+1)}=max\{0,{\stackrel{\sim }{A}}_{ij}^{(t+1)}-{\nu }_i\}$ where ν_i can be computed for each row i using the equality

$$\sum _{j=1}^{S}max\{0,{\stackrel{\sim }{A}}_{ij}^{(t+1)}-{\nu }_i\}=1$$

We allow a maximum of 50 iteration steps for minimizing each of A and B, and 100 iteration steps for alternating minimization. We exit the iterations if the change in norm is insignificant (1e − 02) or if the objective value change is below a tolerance (1e − 04). The learning rate values have to be computed in order to ensure that gradient steps do not diverge. Our choices of learning rates have been

$${\alpha }_A=C\frac{{\Vert \nabla f(A^{(t)})\Vert }_F^2}{{\Vert {\mathcal{P}}_{\mathit{\Omega }}(\nabla f(A^{(t)})·B^{(t)})\Vert }_F^2}$$

and

$${\alpha }_B=C\frac{{\Vert \nabla f(B^{(t)})\Vert }_F^2}{{\Vert {\mathcal{P}}_{\mathit{\Omega }}(A^{(t)}·\nabla f(B^{(t)}))\Vert }_F^2}$$

where C ∈ (0, 1).