Monte Carlo simulations of randomized clinical trials in epilepsy

Abstract

Background

The placebo response in epilepsy randomized clinical trials (RCTs) has recently been shown to largely reflect underlying natural variability in seizure frequency. Based on this observation, we sought to explore the parameter space of RCT design to optimize trial efficiency and cost.

Methods

We used one of the world's largest patient reported seizure diary databases, SeizureTracker.com to derive virtual patients for simulated RCTs. We ran 1000 randomly generated simulated trials using bootstrapping (sampling with replacement) for each unique combination of trial parameters, sweeping a large set of parameters in durations of the baseline and test periods, number of patients, eligibility criteria, drug effect size, and patient dropout. We studied the resulting trial efficiency and cost.

Results

A total of 6,732,000 trials were simulated, drawing from 5097 patients in the database. We found that the strongest regression predictors of placebo response were durations of baseline and test periods. Drug effect size had a major impact on trial efficiency and cost. Dropout did not have a major impact on trial efficiency or cost. Eligibility requirements impacted trial efficiency to a limited extent. Cost was minimized while maintaining statistical integrity with very short RCT durations.

Discussion

This study suggests that RCT parameters can be improved over current practice to reduce costs while maintaining statistical power. In addition, use of a large‐scale population dataset in a massively parallel computing analysis allows exploration of the wider parameter space of RCT design prior to running a trial, which could help accelerate drug discovery and approval.

Introduction

Epilepsy affects about 1% of the US population.1 Medications are only able to fully protect about ⅔ of patients 2 from seizures, a number that has remained relatively stable for many years. Indeed, over 22 medications and two implanted devices have been approved by the FDA over the decades. However, enthusiasm in industry for epilepsy is now tempered by soaring costs for drug development.3 Therefore, there is a critical need for improved trial efficiency in order to accelerate drugs to market.

Our group showed recently that the so‐called placebo effect in epilepsy may in fact reflect underlying variability of seizure rates, rather than a true response to placebo.4 If so, then detailed trial parameters are critical factors influencing success or failure. Features such as number of patients per treatment arm, inclusion/exclusion criteria, and duration of various trial phases may play a major role in determining outcome because these same parameters will influence to what extent natural variability will be sampled. In the case of diseases where natural variability is low, such decisions might be made on other grounds, but there is now evidence to suggest that in epilepsy, the selection of these parameters may dictate the likelihood of trial success to an extent.

This project's goal is therefore to quantify the consequences of those parameter choices on randomized clinical trials (RCT) outcomes.

Methods

Overview

Using patient reported seizure diaries from SeizureTracker.com,4, 5 we generated a series of virtual patients. The virtual patients were used to form simulated trials, which included patient dropout. In each trial, 50% of patients had simulated “drug”, while the other 50% had a “placebo.” For each unique combination of RCT parameters considered, a set of 1000 simulated RCTs were simulated. Parameters were then tested systematically, allowing a “parameter sweep” across multiple trial dimensions. The methods are summarized in Figure 1. The characteristics of these simulated trials were then analyzed for efficiency and cost. Simulation was conducted on the NIH HPC Biowulf cluster in Matlab 2016b and trial outcomes were calculated in R 3.3.0. Source code available on request. The raw data is provided through the International Seizure Diary Consortium.

Figure 1.

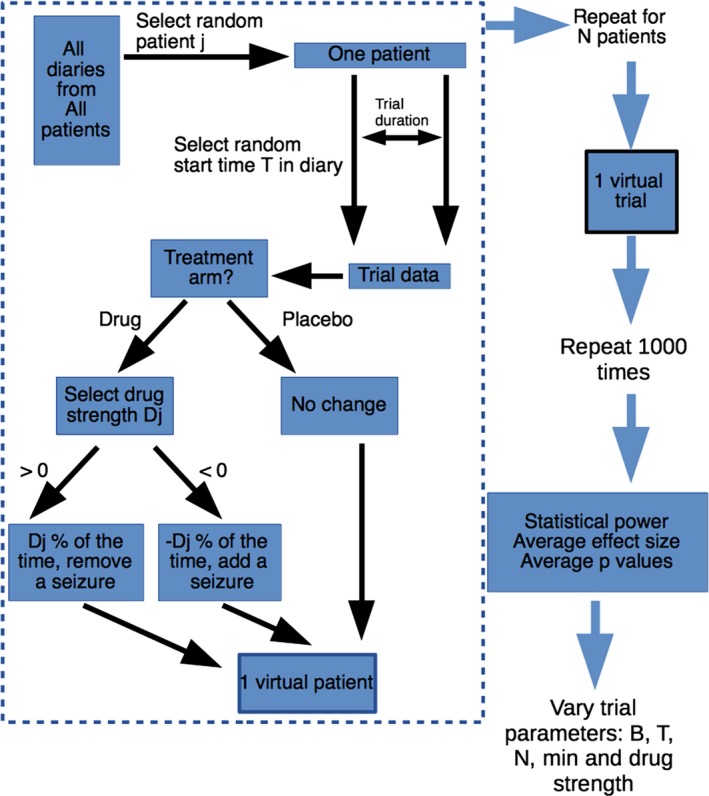
Simulation flow chart. A single virtual patient was constructed according to the area inside the dashed lines. First, patient j was selected from a uniform random distribution (with replacement). A starting time T was selected from a uniform random distribution (with replacement) within that patient's diary, and one trial duration was copied out of that patient's original diary to form the basis for the trial data. Note that the order of events was preserved. If the patient was assigned to placebo, the trial data was unchanged. If assigned to drug, then a single randomly selected drug strength, D _j, was chosen from a normal distribution (Equation (1)). If Dj >= 0, then D _j % of the time seizures were removed from the trial data. If D _j < 0, then D _j % of the time seizures were added to the trial data. This entire process was repeated for all N patients to produce a single virtual trial. The trial with identical parameters was repeated 1000 times to obtain summary values for power, effect size and P values. Then parameter values were changed systematically to test the impact of each parameter on summary statistics.

Generating a virtual patient

Each virtual patient was generated using data from one of the world's largest patient reported seizure diary databases, SeizureTracker.com.4, 6 A deidentified, unlinked data export from SeizureTracker was created on June 31, 2016, in accordance with the NIH Office of Human Protection protocol #12301. Demographic data was used to exclude any patient with unlisted or impossible ages. Similarly, seizures with dates that predated the patient's birth date or occurred after the data export were excluded from further analysis. Any patient diary with >=6 seizures recorded over at least 6 months was considered. Of note, an additional minimum eligibility requirement was imposed later in the processing (see Parameter sweeps).

The trial duration was simply the sum of the baseline phase duration (a trial parameter) and the test period duration (another trial parameter). In these simulations, no “titration” phase was included.

For each individual virtual patient, data was derived from a single randomly chosen unique patient diary in SeizureTracker (uniform random selection with replacement). A randomly selected starting position was chosen from a uniform distribution from the first recorded seizure until the last possible time that would allow a full simulated trial's worth of data. In this way, even if the same patient were chosen multiple times, different virtual diaries would be obtained. Essentially, the technique employed was a form of bootstrapping (sampling with replacement). From the selected starting time, an uninterrupted record of “trial duration” of data was used. For example, if patient 25 was selected, and the selected starting time was day 45, and a 120‐day trial duration was required, then days 45–164 from patient 25 would be assigned as the requested virtual patient diary, now called day 1 through day 120.

With the diary data, 2‐week blocks of time were counted out, resulting in a set of seizure counts for the trial duration, (C _i,j, the ith count from patient j). For example, if patient number 6 had 12 seizures in the first 2‐weeks, then eight seizures in the second 2‐weeks, and 13 seizures in the third 2‐week period, we would write: C _1,6 = 12; C _2,6 = 8; C _3,6 = 13.

Simulating “drug”

During the experimental phase of “drug” exposed patient, a simulated drug was applied by randomly removing seizures from the diary. There was one drug effect size, (D ₀) per simulated trial. The drug effect size for each patient (D _j) was modeled as a normally distributed random variable with mean D ₀ and standard deviation 10%. Any D _j > 100% was forced to 100%, and any D _j < −100% was forced to −100%. Therefore, each patient experienced a unique drug effect size:

$$D_j\sim N\left(D_0,10\right),\text{where}{D}_j\in [-100\%,100\%]$$ (1)

Thus, if the trial's drug effect size D ₀ was 20%, then a patient's personally experienced drug effect size might be 15%. A second patient exposed to that same drug might experience a drug effect size of 25%. It is apparent from the above that some patients may indeed have negatively valued D _j, which matches clinical experience that a minority of patients paradoxically experience a worsening of seizures with some anti‐seizure drugs. Thus, D _j values can be as high as 100% (i.e. complete seizure‐freedom) or as low as −100% (i.e. doubling of baseline seizure rate).

The 2‐week seizure counts (C _i,j, the ith count from patient j) during the drug testing phase were modulated by the simulated drug. When D _j was positive, C _i,j was reduced by a random amount. When D _j was negative, C _i,j was increased by a random amount. The amount of increase or decrease was determined using the sum of C _i,j random indicator variables that with probability of being equal to 1 given by D _j

Dropout

Dropout rates of 0 through 40% were tested, though typical the dropout rates reported in the literature range 20–30%. Dropout was simulated using a set expected level for the trial, meaning it was included as one of the trial parameters. For example, if dropout was set to 10%, then each virtual patient was given a 10% probability of experiencing dropout. Dropout patients then had a uniformly distributed random number chosen between 1 and the number of 2‐week segments in the trial. That number represented the segment when the patient would experience dropout. For example, if a virtual patient had a total of 12 2‐week segments, and the number 4 was chosen randomly, then the first three segments would remain intact, and all subsequent segments would become missing values.

Simulated trial

For a given set of N virtual patients (see section Generating a virtual patient) required for a simulated trial, 50% were assigned to “placebo” and 50% to “drug”. The latter group had a virtual “drug” applied, as described in section Simulating “drug”, and dropout assigned as described in Dropout. The former group had no change to their diary data during the “placebo” testing phase, but did ‘experience’ dropout. The trial outcome was assessed using the two commonly selected primary endpoints in epilepsy clinical RCTs: the 50% responder rate (RR50), and the median percentage change (MPC).7 RR50 represents the proportion of each trial arm that experienced a 50% or greater reduction in seizures during the testing phase compared to the baseline phase. MPC represents the median value, across patients, of the percentage change in the normalized seizure rate between baseline and experimental phases. The statistical comparison between the “drug” and “placebo” arm was conducted using Fisher's Exact test for RR50 and the Wilcoxon Rank Sum test for MPC in the typical fashion.7

Parameter sweeps

Each unique set of parameters was tested in a set of 1000 simulated trials. A set of parameter combinations was tested such that a “sweep” across multiple possible values could be evaluated. The parameters considered were: baseline phase duration (B), testing phase duration (T), number of patients (N), minimum number of seizures during baseline (min), dropout (R), and drug effect size (D).

Parameter sweeps were conducted such that each of variables were explored through commonly and less commonly encountered values. Three parameter sweeps were conducted across four values of D, R and min, respectively. For each value within the sweep, a complete set of B, T and N were also generated. A complete set comprised B=(2,4,6,8,10,12), T = (2,4,6,8,10,12) and N=(100,150,…900), totaling 612 combinations.

The drug effect size (D) sweep tested D = 10%,20%,30% and 40%, using min=4 and dropout=0%. The eligibility minimum value (min) sweep tested min=2,4,6,8, using D = 30% and dropout=0%. The dropout sweep tested dropout=10%,20%,30%,40% using min=4 and D = 30%. Thus, the complete set of simulated trials comprised (612 × 4x3 – 612) and 1000 repetitions per parameter set, thus 6,732,000 trials.

Cost analysis

To compare the relative costs of the different parameter combinations, we used a simplified model based on recent costs from three recent trials (personal communication, Eisai) that considered the cost of a phase II/III trial to be reduced to fixed costs (average= $20,261,142) and price per patient per month (average=$1,295). Using the latter figure, the duration of the baseline phase (B) in months, and the duration of the testing phase (T) in months, and the number of patients (N), the cost for a trial can be estimated as follows:

$$\text{trial cost}=20,261,142+\text{variable costs}$$ (2)

$$\text{variable costs}=1295\times (B+T)\times N$$ (3)

Given a set of 1000 simulated trials with identical trial parameters, if 90% of the trials are able to achieve an RR50 difference between “drug” and “placebo” with P < 0.05, then such parameters would be considered to possess 90% statistical power, a commonly chosen initial condition for trial design. If a set of 1000 simulated trials achieve less than that, a higher number of patients is likely required to achieve 90% power. Therefore, we sought to calculate the variable costs for different combinations of drug, B and T with the minimum N required to achieve 90% power. For example, suppose that for a 20% effective drug and trial parameters including N = 150 patients, 800 simulated trials detected the difference between drug and placebo (i.e. 80% power). In that case, an increase in N to perhaps 250 may be sufficient to increase the power to 90%. On the other hand, if the drug were 40%, the number of patients may be sufficient at N = 150 to achieve >90% power.

Within the parameter sweep for min, we sought to find the lowest value for min required. To achieve this, for each combination of B and T, we found the lowest value of N required to achieve 90% power. Within this subset of trials, the lowest possible value of min was reported for that combination of B and T. In this way, across all given values of B and T, the least restrictive value of min was obtained that would still result in an optimal trial cost.

Regression models

In order to better characterize the outcomes of the simulated trials across multiple parameters, a series of linear regression models were developed. The models included all possible interaction terms. They were tested to identify relationships between the trial parameters in predicting several outcomes: the RR50 value for placebo, the power of RR50, the MPC value for placebo, and the power of MPC. The R function GLM was used for the regression, and STEP was used to test forward and backward elimination to minimize Bayesian information criterion (BIC), thus identifying the most parsimonious linear model required for the fit. For the drug model, covariates B, T, N and drug were used. For the minimum eligibility model, covariates B, T, N and min were used. For the dropout model, covariates B, T, N and dropout were used.

Results

The full SeizureTracker.com database includes over 22,000 unique patients, of which over 14,000 patients reported at least one seizure. After inclusion criteria were met, the largest set of possible patients was 5097, meaning all virtual patients were derived from that reduced pool of patients. The demographic composition of the SeizureTracker cohort has been previously described.4

The placebo arm values from a sweep of baseline (B) and test (T) values are shown in Figure 2. For that figure, following fixed parameters were used: number of patients (N)=900, minimum monthly baseline seizure rate (min)=4 and percentage of patients that drop out of the study (dropout)=0. Each grid location represents the average value of placebo RR50 across 1000 trials with a given value of B and T. The figure was produced with parameter N = 900, however any value of N from 100 to 900 produced nearly identical results. From the figure, it is apparent that the choice of B and T play a major role in the expected placebo responder rate, due to the natural variability in seizure frequency. For example, when B = 12, T = 2 the placebo RR50 value was 96.5%, whereas when B = 2 and T = 12, the placebo RR50 was 6.7%. In the case of the commonly used B = 8 and T = 12, the rate was 19.2%. Another common combination, B = 6, T = 12 yielded an RR50 rate of 14.7%. Also shown, many combinations of B and T resulted in negative MPC values, which may not be desirable for a placebo. Of note, many grid locations with low RR50 values correspond to grid locations with negative MPC values. Both RR50 and MPC was correlated with baseline duration (B) and negatively correlated with test duration (T).

Figure 2.

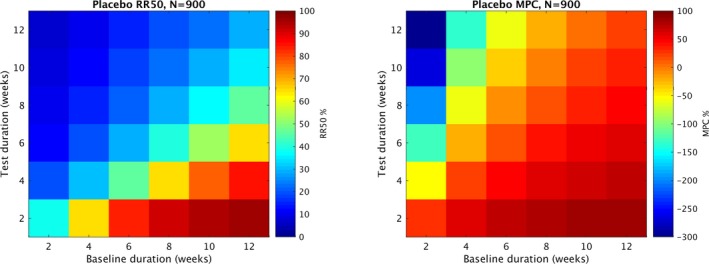
Expected values of placebo RR50 and MPC. Each grid location represents the average value (RR50 or MPC) in the placebo arm of 1000 trials with identical parameters. All trials used number of patients (N) = 900, percentage of patients that drop out (dropout) = 0, and minimum monthly seizure rate during baseline required for inclusion (min) = 4. The different grid locations represent different combinations of baseline weeks (B) and test weeks (T) values for the trial duration. RR50 and MPC were both correlated with B and inversely correlated with T. Note that the color scales differ in the MPC figure and the RR50 figure. The lowest values of RR50 correspond to the most negative values of MPC.

Figure 3 summarizes several analyses related to the parameter sweep over drug. By displaying the minimum value of N that obtains a power ≥90% from the RR50 Fisher Exact test, the images along the left side of Figure 2 show the relationship between the choice of B, T and the subsequent required trial N. Trials with roughly balanced values of B and T with B 2‐4 weeks longer than T require fewer patients than other combinations. Using the N from each grid position and Equation (3), the right hand side plots the variable costs of the trial depending on the choice of B and T, for several different drug effect sizes. Of note, very short trials such as B = 4 and T = 2 appear to be quite cost‐effective for drugs of effect size 20% and higher.

Figure 3.

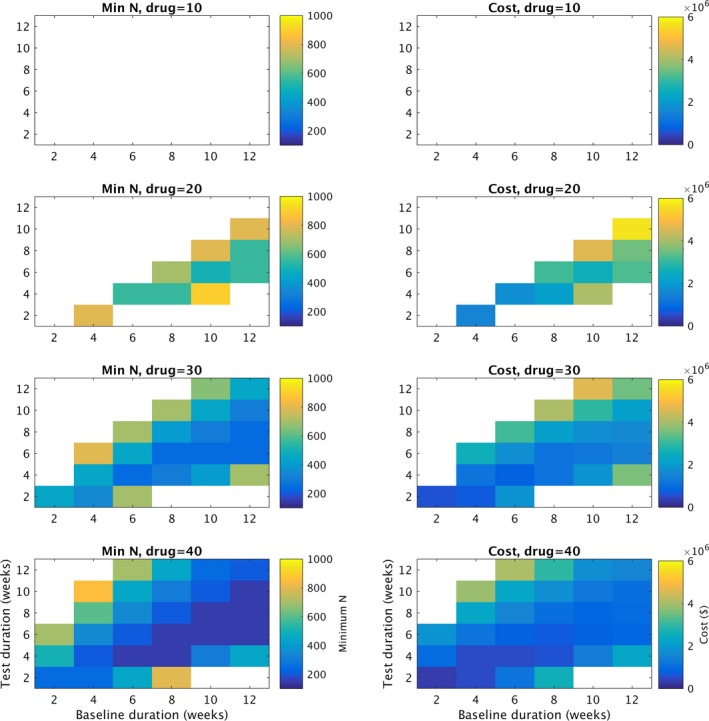
Cost analysis. Along the left hand side a summary of the drug parameter sweep is shown, including drug effect size (drug) of 10,20,30 and 40%. Of note, for all the simulations in this figure, the minimum monthly seizure rate during baseline (min) = 4, and the percentage of patients that dropped out (dropout)=0. The x axis for all graphs represents number of baseline weeks (B). For each grid position in the left graphs (combination of B and T), number of patients in the trial (N) was tested for N = 100,150,200,…,900. The lowest value of N required to achieve 90% or better power at distinguishing “drug” from “placebo” is represented by the color of the grid position. Thus, for drug effect sizes 20% or higher, trials with baseline 2–4 weeks longer than test appear to be more efficient than other combinations. With stronger drugs, more trial baseline (B) and test (T) combinations can reliably distinguish drug from placebo. Of note, the highest number of patients (N) tested was N = 900, therefore grid elements in white represent combinations that did not fulfill the 90% power requirement at N = 900. Along the right hand side, Equation (3) was used to calculate the variable cost of a trial with a given B and T, using the N obtained from the figures on the left. Of note, very low combinations such as B = 4, T = 2 appear to be very cost‐efficient while retaining 90% statistical power.

Figure 4 summarizes the least restrictive value of min required to obtain the optimal trial cost for a given combination of B and T. Of note, this plot does not require min = 8 for each combination, suggesting that in many cases a lower value of min would be reasonable.

Figure 4.

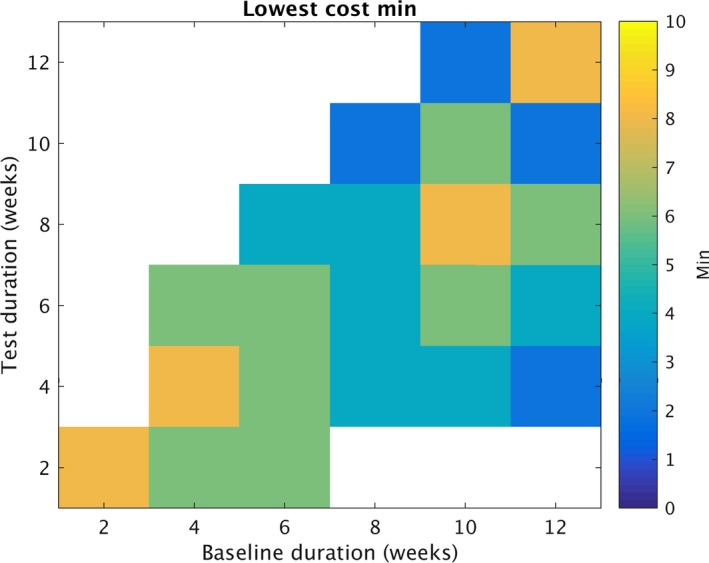
Optimizing “min”. Similar to figures 1 and 2, each grid element represents a summary of numerous simulated trials. Each color element represents the lowest value for the minimum monthly seizure rate during baseline (min) selected. To be selected, all combinations of min and N were evaluated for cost (Equation (3)), requiring >=90% statistical power for a chosen combination. The value of min that optimized cost is displayed for each grid element. To identify the values displayed, N was tested for N = 100,150,200,…,900. Min was tested at 2,4,6 and 8. The x axis for all graphs represents number of baseline weeks (B). Of note, values greater than 8 were not tested, therefore white represents situations in which the lowest min value is unknown.

To better summarize the outcomes of the many simulations, linear regression models were developed (Table 1). For the RR50 of the placebo arm (RR50placebo), the terms B, T and the B:T interaction were sufficient without requiring drop or N. When min was considered for RR50placebo, it was useful alone and as an interaction with B. The MPC for placebo (MPCplacebo) required only B, T and the B:T interaction terms, without requiring N, or drop.

Table 1.

Linear fit models to represent the average response of the 1000 trials, given various input trial parameters

Inputs	Output	Best fit model
B,T,N,drug	RR50placebo	B + T + B:T
	RR50power	B + T + drug + N + B:T + B:drug + T:drug + B:N + T:N + drug:N + B:T:drug + B:T:N + B:drug:N + T:drug:N + B:T:drug:N
	MPCwilcox	T + drug + N + T:drug + T:N + drug:N + T:drug:N
	MPCplacebo	B + T + B:T
B,T,N,min	RR50placebo	B + T + min + B:T + B:min
	RR50power	B + T + min + N + B:T + B:min + T:min + B:N + T:N + B:T:min + B:T:N
	MPCwilcox	T + min + B + T:min + T:N + min:N + T:min:N
	MPCplacebo	B + T + B:T
B,T,N,drop	RR50placebo	B + T + B:T
	RR50power	B + T + N + B:T + B:N + T:N + B:T:N
	MPCwilcox	T + N + T:N
	MPCplacebo	B + T + B:T

Three different parameter sweeps were considered, and within those, 4 outcomes were predicted by the linear models. RR50placebo represents the RR50 in the placebo arm. RR50power is the statistical power of the RR50 comparison between drug and placebo using the Fisher Exact test. MPCwilcox is the statistical power of the MPC comparison between drug and placebo using the Wilcoxon Rank Sum test. MPCplacebo is the MPC value from the placebo arm. The best fit model listed represents the model chosen from the model selection analysis. B = baseline duration in weeks. T = test duration in weeks. Drug = drug effect size. N = total number of patients in a trial. Min = minimum monthly seizure rate for inclusion criteria. Drop = dropout rate.

The three models for RR50power included either min, drug, or dropout. Higher drug effect size increased the RR50power. Higher values of min increased the RR50power. All three models of RR50 included N, and it served to increase RR50power. The relationship of B and T to RR50power depended on if drug was included; when not included, B and T had negative beta values, when drug was included, B and T had positive betas. Table 2 lists all the beta values for the 3 RR50power models. The details of these models are highlighted because of their importance in determining the sample size for the overall trial, as it is known that RR50 is generally of lower statistical power than MPC outcomes.7 Of note, the model for dropout did not find that the dropout rate was a significant factor, rather it favored combinations of B, T, and N alone.

Table 2.

The details of the 3 linear regression models for RR50power are shown, including the terms and estimated coefficients for each

Factor	Estimate
DRUG model: RR50power
intercept	−5.22E‐01
B	4.38E‐03
T	5.89E‐02
drug	4.23E‐02
N	9.08E‐04
B:T	−8.30E‐03
B:drug	−3.10E‐03
T:drug	−4.91E‐03
B:N	−5.63E‐05
T:N	−1.53E‐04
drug:N	−9.84E‐06
B:T:drug	6.58E‐04
B:T:N	1.74E‐05
B:drug:N	1.74E‐06
T:drug:N	5.13E‐06
B:T:drug:N	−6.06E‐07
MIN model: RR50power
intercept	5.75E‐01
B	−2.68E‐02
T	−7.18E‐02
min	2.45E‐02
N	9.70E‐04
B:T	8.94E‐03
B:min	−2.45E‐03
T:min	−4.02E‐03
B:N	−4.42E‐05
T:N	−3.93E‐05
B:T:min	4.25E‐04
B:T:N	5.38E‐06
DROPOUT model: RR50power
intercept	6.84E‐01
B	−3.82E‐02
T	−9.09E‐02
N	1.00E‐03
B:T	1.11E‐02
B:N	−4.65E‐05
T:N	−3.88E‐05
B:T:N	5.19E‐06

B=baseline duration in weeks. T=test duration in weeks. Drug=drug effect size. N=total number of patients in a trial. Min=minimum monthly seizure rate for inclusion criteria. Drop=dropout rate.

Discussion

This study explored the complex relationship between RCT trial parameters, statistical efficiency, expected placebo responses, and economic consequences. Using a big data Monte Carlo simulation approach, we explored the parameter space for trial design including duration of baseline and test periods, minimum monthly seizure rate required for eligibility, number of patients needed, dropout, and drug effect size. We found evidence that shorter trials can still achieve sufficient power with dramatically lower cost. We found that the strongest predictors of placebo response were durations of baseline and test periods. Drug effect size, but not dropout rate, had a major impact on trial efficiency and cost. The least restrictive minimum seizure rate was found to depend on the trial durations selected. The close relationship between trial parameters and expected placebo response indicates that care must be taken in selecting parameters that lead to optimal outcomes, depending on what factors are deemed most important for the trial (i.e. low cost, high statistical power, etc.).

It is a widely held view that long treatment arms (such as 3 months) are required to demonstrate efficacy of a drug. Under the assumption that the effect size of a drug within an individual is stable, at least in a probabilistic fashion, we demonstrated that statistical power can be achieved with much shorter trial durations. This means that a drug that is truly effective can be proven to be so in a shorter time, and ineffective drugs can be disproven quickly as well. Conversely, if one rejects the stable effect size assumption, then one must also conclude that a 3‐month treatment phase is also too short. Indeed, without the stability assumption, one must test drugs for years to be certain of ongoing effectiveness.

Prior work in modeling the consequences of different trial parameters is consistent with our findings here, particularly that very short trials (baseline=4 weeks, test=3 weeks) may be sufficiently powered.8 In that study, trial data was used from a specific drug trial, meaning that they were unable to vary drug effect size and eligibility criteria as we did. In contrast, our study was able to explore a much wider segment of the parameter space because our dataset had less restrictions upon it initially. We also were able to draw from a much larger initial sample of patients due to the large database we used, allowing for additional population features to enter our results. We feel that the findings of this study validate but also expand the original findings of the work by French et al.8

Limitations

Our approach here is predicated on the premise that natural variability in seizure frequency is the dominant force in producing a placebo response.4 There are certainly other possible forces, such as psychological influence, regression to the mean, and geographic variation.9, 10 It currently remains unknown to what extent each factor plays a role in epilepsy trials. Studies suggest at least some relationship may be present between seizure rates and stress,11, 12 though the details remain unclear. This study certainly finds placebo response values that are consistent with historical studies, supporting the hypothesis that natural variability may be dominant, however further work in this area is needed. Future RCT simulation models could include psychological or other influences, as new empirical evidence becomes available.

The primary dataset utilized in this simulation study is derived from patient reported outcomes, from a self‐selected group of patients. Although it is certainly true that such data has some reliability concerns, it is important to reflect on the fact that all outpatient epilepsy drug trials to date rely on self‐reported seizure records, almost always recorded on paper diaries. Paper diaries are likely less reliable than electronic diaries for seizures, though this has yet to be demonstrated conclusively.5, 13 SeizureTracker.com data has the additional limitation that diagnoses are by self‐report, rather than with physician review, raising the possibility that at least some of the data used for this study may have come from patients who do not truly have epilepsy.10 In one study, up to 30% of patients who were treated for years with anti‐seizure medication found that after video‐EEG that they do not truly have epilepsy.14 Moreover, video‐EEG monitoring is not a common screening test for trial entry. This suggests that clinical trials likely suffer from the same mis‐diagnosis issue. It is financially impractical to correct this potential source of mis‐diagnosis in RCTs with present technology. Thus, although the primary dataset may have certain imperfections resulting in a lower signal‐to‐noise ratio, typical epilepsy clinical trials may have similar concerns.

An assumption about dropout occurring with uniform distribution any time during the trial duration was employed here. We acknowledge that there may be a systematic bias for patients to drop out of epilepsy RCTs when their seizure rates go above some level. Similarly, drug side effects may result in nonrandom dropout. We are not aware of any systematic analysis demonstrating this in epilepsy, therefore, we used the simpler assumption for our initial investigation of the parameter space. An interesting area for further study is how various types of systematic reasons for dropout would affect the outcome of clinical trials, and the relationship of this to other trial parameters.

This study did not account for the added cost and delays associated with a titration period typical of clinical trials.15 Some drugs require very long titration periods, while others can be initiated quite rapidly. It is likely that the general trends seen in these simulations regarding the impact of trial parameters are similar with or without the inclusion of titration periods, though this remains to be further investigated.

Newer trial outcome metrics, such as the time‐to‐prerandomization,16 would be affected in different ways by trial parameter selection. The results found here cannot be readily generalized to other outcome metrics, and further simulation would be required.

Future directions

This study suggests future large‐scale trial simulations that can further elucidate the optimal selection of trial parameters a priori. In future work, additional parameters can be explored individually and in a multivariable fashion. For example, inclusion/exclusion criteria involve seizure clustering, age, and subtype of epilepsy should be further investigated. In addition, using other datasets or statistical modeling that can generate datasets would increase the confidence in the results found in simulation studies of this kind. Investigating newer trial analysis methods, such as the time‐to‐prerandomization technique would require further simulation as well.

Author Contributions

Dr. Goldenolz planned the study, analyzed and interpreted the data, and wrote the manuscript. Mr. Tharayil assisted with analysis and edited the manuscript. Mr. Moss collected the data, and edited the manuscript. Dr. Myers assisted with study planning, data interpretation, and editing the manuscript. Dr. Theodore assisted with study planning, data interpretation, and editing the manuscript.

Conflicts of Interest

Mr. Moss is the cofounder/owner of Seizure Tracker which was used for the data in this study. Mr. Moss has received personal fees from Cyberonics and UCB, both of which are companies that conduct randomized clinical trials in epilepsy, though they did not participate in any way with this study. We have no other conflicts to disclosure.

Funding Statement

This work was funded by National Institute of Neurological Disorders and Stroke (NINDS) NIH Division of Intramural Research grant ; Cyberonics grant ; UCB grant ; Courtagen grant ; Tuberous Sclerosis Alliance grant .