A New Wavelet Denoising Method for Experimental Time-Domain Signals: Pulsed Dipolar Electron Spin Resonance

Abstract

We adapt a new wavelet-transform-based method of denoising experimental signals to pulse-dipolar electron-spin resonance spectroscopy (PDS). We show that signal averaging times of the time-domain signals can be reduced by as much as 2 orders of magnitude, while retaining the fidelity of the underlying signals, in comparison with noiseless reference signals. We have achieved excellent signal recovery when the initial noisy signal has an SNR ≳ 3. This approach is robust and is expected to be applicable to other time-domain spectroscopies. In PDS, these time-domain signals representing the dipolar interaction between two electron spin labels are converted into their distance distribution functions P(r), usually by regularization methods such as Tikhonov regularization. The significant improvements achieved by using denoised signals for this regularization are described. We show that they yield P(r)’s with more accurate detail and yield clearer separations of respective distances, which is especially important when the P(r)’s are complex. Also, longer distance P(r)’s, requiring longer dipolar evolution times, become accessible after denoising. In comparison to standard wavelet denoising approaches, it is clearly shown that the new method (WavPDS) is superior.

Graphical abstract

1. INTRODUCTION

1.A. Background

Pulsed dipolar ESR spectroscopy (PDS) is a powerful biophysical method for the study of the structure and function of biological systems.^1–9 It has been applied mainly to proteins and protein complexes, which possess either endogenous paramagnetic centers^10–12 or engineered sites to which paramagnetic tags (spin-labels) are covalently attached.^13,14 PDS measures the strength of the magnetic dipole–dipole interaction between electron spins,^1,2,4 usually carried by the attached spin-labels. However, in many cases studying the system of interest by PDS is a challenging task due to several factors, such as low protein concentrations available in a particular experiment, and/or short phase memory relaxation times (T_m’s) causing a fast decay of the dipolar signal over a few microseconds, particularly in the case of membrane proteins. All these obstacles lead to dipolar evolution signals in the time domain often with insufficient signal-to-noise ratios (SNR). Thus, very long time-averaging of the PDS signals is frequently needed to obtain reliable data for further analysis to reconstruct accurate distances and distance distributions that report on the protein structure. Several approaches have been used to overcome these challenges: solvent deuteration,^3,15,16 and also partial¹⁷ or complete¹⁸ protein deuteration; the building of spectrometers with increasing sensitivity, either by several research groups^19–22 or by commercial means; and the development of new pulse sequences that enhance the accessible distance range and allow samples with reduced protein concentration to be used.^23,24 Yet, new methods for improving the SNR of PDS experiments remain needed.

Herein we report our development of a novel wavelet-transform denoising method,²⁵ which provides significant noise removal in time-domain signals while preserving the fidelity of the underlying original signals. It is a powerful approach and can be used to obtain good PDS data from noisy signals. The method provides multiresolution analysis that enables time-frequency decomposition of the signal; i.e., it informs which frequencies occur at what time instances, which helps to separate the signal from the noise.^26–30 The method significantly improves on existing wavelet denoising methods by providing a much larger increase in SNR with virtually no distortion of the underlying signal.

Although we focus on the application to time-domain ESR, we note that it is equally applicable to other physical chemical techniques that examine time-domain signals.

To demonstrate the new denoising method as applied to PDS, we used data for doubly spin-labeled cysteine mutants of T4 Lysozyme (T4L) as well as model data of unimodal and bimodal Gaussian distance distributions.

We show that with this new method of denoising the time-domain signal improves the stability of the reconstruction of the interspin distance distributions, and therefore the reliability of the results. Also, we demonstrate that signal acquisition times can be reduced by at least an order of magnitude and still yield high-quality results after denoising. The results from denoising of the bimodal model and bimodal experimental data show that the method can be applied with very high accuracy to more complex PDS signals typical of multiple interspin distance distributions. Thus, the challenge of obtaining PDS time-domain signals with high SNR is much reduced, so that systems at low spin concentration and systems that produce rapidly decaying PDS signals due to short T_m’s become more amenable to study. We strongly believe that the denoising method described here will greatly benefit the field of PDS studies. In addition, this method should apply to other experimental fields where noisy time-decay signals are observed, such as nuclear magnetic resonance spectroscopy,³¹ infrared spectroscopy,³² optical spectroscopy,³³ and others.

1.B. Conversion of Pulse-Dipolar Signals to Distance Distributions

The signal from an ensemble of proteins with two spin labels each is given as

$${\int }_{R_{\text{min}}}^{R_{\text{max}}}\kappa (r,t)P(r)\mathrm{d}r=S(t)$$ (1)

where κ(r,t) represents an orientationally averaged signal from a spin pair at a given r, P(r), is the distribution in distance between the spin pairs, and S(t) is the PDS signal. In discrete matrix form, it can be written as

$$\mathbf{K}P=S$$ (2)

which is especially appropriate for discrete time data acquisition. The signal S(t) is acquired from the PDS experiment. To obtain the distance distribution P(r), the inversion of K is required (i.e., P = K⁻¹S), which is an ill-posed problem. As the determinant of K is zero or near zero, there are many possible solutions for the distance distribution P. Also, this inversion is easily corrupted by the noise in the experimental results. To overcome these problems and obtain a stable and desirable solution P, methods like Pake pattern function,³⁴ direct conversion,³⁵ singular value decomposition (SVD),³⁶ model fitting,^37–48 polynomial interpolation,⁴⁹ coordinate transformation,⁵⁰ Tikhonov regularization (TIKR),^{36,41,49,51,52} and regularization using Monte Carlo calculations⁵³ have been used. The basic SVD used to invert K and to obtain P is given by

$$P=\mathbf{\sum }_{i=1}^p\frac{{u_i}^{\mathrm{T}}S}{{\sigma }_i}{\nu }_i$$ (3)

where u_i and ν_i are column vectors of unitary matrices U and V, obtained in the SVD of the matrix K, and the σ_i are the individual singular values of the diagonal matrix Σ obtained from K, and p is the length of the input signal S(t).³⁶ Given the instability of eq 3, the TIKR method is often used.^36,41,49,51 It minimizes the function

$${\varphi }_{\text{TIKR}}[P]\equiv \text{min }{\Vert \mathbf{K}P-S\Vert }^2+{\lambda }^2{\Vert \mathit{\text{LP}}\Vert }^2$$ (4)

where λ is the regularization parameter and L is the differentiation operator. Equation 4 leads to the unique distance distribution given by

$$P_{\lambda }={({\mathbf{K}}^{\mathrm{T}}\mathbf{K}+{\lambda }^2)}^{-1}{\mathbf{K}}^{\mathrm{T}}S$$ (5)

For practical implementation, eq 5 can be rewritten in terms of the SVD (cf. eq 3) as

$$P_{\lambda }={({\sum }^2+{\lambda }^{2}I)}^{-1}\mathbf{V}\sum {\mathbf{U}}^{\mathrm{T}}S$$ (6)

Equation 6 can be rewritten and solved as a sum of singular value contributions:^36,51

$$P_{\lambda }=\mathbf{\sum }_{i=1}^{\text{Rank}(\mathbf{K})}{f}_i\frac{{u_i}^{\mathrm{T}}S}{{\sigma }_i}{\nu }_i,\text{where}{f}_i\equiv \frac{{{\sigma }_i}^2}{{{\sigma }_i}^2+{\lambda }^2}$$ (7)

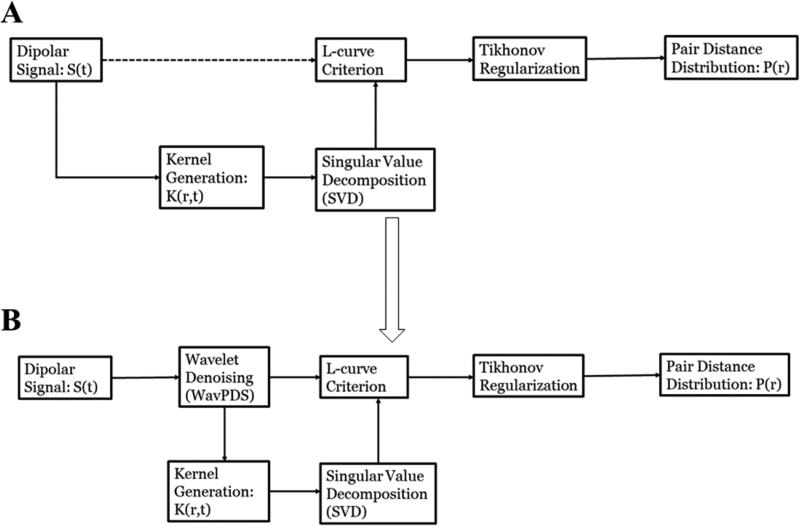
Figure 1A shows the block diagram of the standard approach. Limitations:

1. The ill-posed problem of eq 3 is highly sensitive to noise present in the signal, for which the method of eq 7 has some effectiveness. In suppressing noise, this method tends to lead to broader distance distributions. The broadening of the distance distribution is attributed to the removal of the contributions from the smaller singular values, for which σ_i² ≪ λ², by the filter function f_i. But incorporating contributions of smaller singular values, which are substantially corrupted by noise, would yield an unstable solution. Hence, there is a trade-off between an unstable solution and a reduction of resolution in the distance distribution due to the presence of noise, which requires the removal of contributions of smaller singular values.

2. It is difficult to obtain a high SNR using longer dipolar evolution times. At longer evolution times, the SNR becomes poorer by increasing the instability in the distance distribution. Hence, smaller evolution times are typically used with relatively higher SNR to obtain a more stable distribution, but at a loss of resolution in the distance distribution. This is especially a problem for longer distances.

Figure 1.

Block diagrams for determining distance distribution P(r) from the dipolar signal by Tikhonov regularization using L-curve criterion: (A) standard approach; (B) new approach after WavPDS denoising.

In this paper, we present our method to denoise the dipolar signal to retrieve a noise-free signal, and subsequently yield stable and accurate distance distributions. Figure 1 shows the block diagram of the TIKR process with and without applying wavelet denoising.

1.C. Wavelet Transform and Discrete Wavelet Transform

A wavelet transform (WT) provides the time-frequency decomposition of a signal. This helps to separate noise and signal, as they typically do not possess the same time-frequency patterns. The wavelet transform of a signal S(t) is given as^26,28,29

$$F(\tau ,s)=\frac{1}{\sqrt{|s|}}{\int }_{-\infty }^{+\infty }S(t){\psi }^{\ast }\left(\frac{t-\tau }{s}\right)\mathrm{d}t$$ (8)

where τ (a time) and s (an inverse frequency) are respectively known as the translation and scale parameters, S(t) is the input signal, F(τ,s) is the WT of the signal as a function of τ and s, and ψ*(t) is the complex conjugate of the wavelet function ψ(t); for real wavelets, ψ*(t) = ψ(t). As can be seen from eq 8, τ and s allow the study of time–frequency information on the input signal by varying the window width s and its translation τ. However, it is computationally cumbersome to perform the WT calculation for all the possible values of τ and s.

By analogy to the fast Fourier transform, the discrete wavelet transform (DWT) is used to calculate the wavelet transform in a computationally less expensive manner. The DWT is given as^26,29,54

$$D_j[n]=\mathbf{\sum }_{m=0}^{p-1}S[t_m]2^{j/2}\psi [2^j{t}_m-n]$$ (9)

where now s = 2^−j and τ = n2^j, with j and n integers, t_m is the discretized time, S[t_m] is the discretized input signal, p = length(S[t_m]), and D_j[n] is the discrete wavelet transform (also called the Detail component) of S[t_m] at scale 2^j, also known as the Decomposition level j. This represents an expansion of the function S(t) in an orthonormal set of wavelet functions expressed in eq 10.²⁹

$$\mathbf{\sum }_{m=1}^L\psi \left(\frac{t_m-n{2}^j}{2^j}\right)\psi \left(\frac{t_m-n\prime 2^j\prime }{2^j\prime }\right)=\{\begin{array}{cc}1,\hfill & \text{if }j=j\prime \text{and }n=n\prime \hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (10)

Here L is the discrete length of the wavelet function that is a characteristic of the particular wavelet used. The number of Decomposition levels allowed is N, where N = |log₂ p|, i.e., 1 ≤ j ≤ N, where N refers to the lowest frequency sub-band. The dyadic scale (i.e., s = 2^−j) is selected so that the Detail components D_j[n] represent nonoverlapping frequency bands.³⁰ However, at Decomposition levels 1 to j, only frequency sub-bands represented by them are wavelet-transformed, requiring that the remaining frequency band to reconstruct the original signal also be obtained. Even at j = N, there is a low-frequency sub-band that is not covered because j is still constrained by the discrete finite signal of step length given by p. The remaining low-frequency information contained in the wavelet transform of the signal is given by the Approximation component, which is defined as

$$A_j[n]=\mathbf{\sum }_{m=0}^{p-1}S[t_m]2^{j/2}\varphi [2^j{t}_m-n]$$ (11)

where A_j[n] is the Approximation component at the jth Decomposition level, and ϕ[t_m] is the discrete scaling function that allows the calculation of the low-frequency part of the wavelet transform of the input signal. The wavelet function ψ[2^jt_m − n] and the scaling function ϕ[2^jt_m − n] derived from it are orthogonal and of the same length.^26,29 The input signal can be recovered using the inverse discrete wavelet transform (IDWT) from the D_j[n] of eq 9 and the A_j[n] of eq 11.^26,29,54

We show in Figure S1 the decomposition of an actual PDS signal into a sequence of Detail and Approximation components.

2. METHOD

2.A. Wavelet Denoising

The Detail components in the DWT allow the separation of signal and noise.^54,55 Moreover, given a good choice of wavelet family, the signal, which is coherent, will have a large magnitude in a few wavelet coefficients and will occur at the same location at the different Detail components. By contrast, random noise will have many wavelet coefficients with small magnitudes that vary in location at the different Detail components. To denoise the signal in the DWT, the following four general steps are required,⁵⁶ which we describe in terms of our new method.²⁵

1. The selection of an appropriate wavelet. We use “db6” from the Daubechises wavelet family⁵⁷ in this study. They are illustrated in Figure S2. This wavelet correlates very well with the signal properties of decaying oscillatory time-domain signals. This results in effective separation of signal and noise by increasing the difference between their wavelet coefficient patterns.

2. The selection of the maximum Decomposition level needed to properly denoise the Detail components and the Approximation component. Smaller or greater maximum Decomposition levels can result in underdenoising or signal distortion, respectively. We use the criterion {S_j < T_r, S_j > T_r, when k = j}, where k is the maximum Decomposition level needed, T_r is the criterion to distinguish between noisy and noise-free Detail components discussed below, and S_j is the “peak-to-sum ratio”, given as

   $$S_j=\frac{\text{max}(D_j)}{{\mathbf{\sum }}_{n=1}^{q_i}{D}_j[n]}$$ (12)

   Thus, S_j is a measure of the sparsity of the jth Decomposition level. It is calculated separately for negative and positive coefficients (S_j,L and S_j,H, respectively) at the jth Decomposition level.

3. To separate the noise coefficients from the signal coefficients, selection of noise thresholds for each Detail component. As mentioned above, the noise coefficients will have smaller magnitudes than the signal coefficients; i.e., the maximum magnitude of noise coefficients should be less than the minimum magnitude of signal coefficients. We use two thresholds, lower and upper, for negative and positive coefficients. They are calculated as λ_j,M = μ_j − κ_j,Mσ_j, where M = L or H corresponding to the lower and upper thresholds, respectively, for the Detail component at the jth Decomposition level, μ_j and σ_j are the mean and standard deviation, respectively, of the Detail component at the jth Decomposition level, and κ_j,L and κ_j,H are adjustable parameters; our previous paper²⁵ describes how to obtain these values on the basis of the associated S_j,L and S_j,H values.

4. The selection of the noise thresholding function to apply to the noise thresholds: We have devised a condition in ref 25 that leads to the use of wavelets such that a coefficient in a Detail component is either a noise or a signal coefficient provided the SNRs are above some minimum value. We have carefully confirmed that the wavelets in this study as well as those in ref 25 satisfy this condition, resulting in successfully denoising at a minimum SNR compared to the cases of other standard wavelet families. This enables us to use as the thresholding function

   $${D^{\prime }}_j[n]=\{\begin{array}{cc}0,\hfill & \text{for }{\lambda }_{j,\mathrm{L}}<D_j[n]<{\lambda }_{j,H}\hfill \\ D_j[n],\hfill & \text{otherwise}\hfill \end{array}$$ (13)

   where D_j[n] and $D_j^{\prime }[n]$ are the noisy and denoised Detail component, respectively, at the jth Decomposition level.

In addition, we carry out two more steps tailored to the needs of a rapidly decaying signal versus time. First, the signal is flipped from left to right in time (i.e., time is reversed) before taking the DWT to avoid distorting the initial (t = 0) signal. Reversing the signal results instead in having small, near-zero, magnitudes at the start, allowing more accurate DWT of the stronger part of the signal. The DWT of the flipped signal, of course, contains the same information as that of the nonflipped signal.

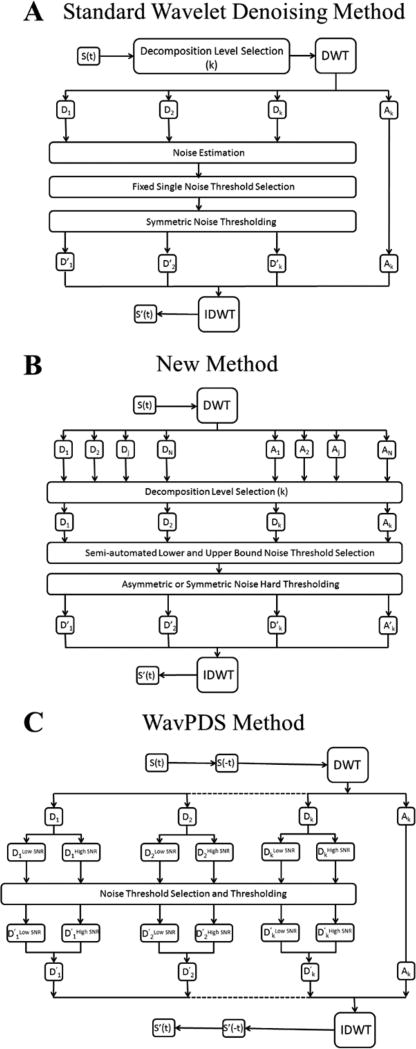
Second, the signal is divided into two parts: higher SNR and lower SNR regions. Although the noise content is the same, the higher SNR part for earlier times contains signal that is less affected by noise, whereas noise tends to be dominant in the low-SNR part. Therefore, the number of Detail components to denoise is different for both. Moreover, the separation into lower and higher SNR parts avoids an overlap between the signal wavelet coefficients of the higher SNR part and the noise wavelet coefficients of the lower SNR part, preventing under-denoising or signal distortion. Figure 2 compares in block diagram form a standard wavelet denoising method (2A) with our new denoising process (2B)²⁵ and the modified version for time-domain signals (2C).

Figure 2.

(A) Block diagram of a standard wavelet denoising method. (B) Block diagram of the new wavelet denoising method.²⁵ (C) Block diagram of WavPDS. S(t) and S′(t) are the noisy and denoised signal, respectively; D_j and D′_j are the noisy and denoised Detail components at the jth Decomposition level, respectively; A_j and A′_j are the noisy and denoised Approximation components at the jth Decomposition level, respectively; DWT and IDWT represents discrete wavelet transform and inverse wavelet transform, respectively. (Parts A and B of Figure 2 are reprinted with permission from ref 25. © 2016 IEEE.)

We call our denoising method with the additional modifications “WavPDS” for PDS signals.

2.B. Difference between the New Method and Standard Methods

Standard wavelet denoising methods are vulnerable to signal distortion and under-denoising, as they are not able to effectively remove some noise coefficients and/or may remove some signal coefficients in the wavelet domain (Figures S3–S8).^27,56,58,59 WavPDS avoids this by using our new method,²⁵ which objectively selects the number of Decomposition levels to denoise, calculates the adaptive noise thresholds on the basis of statistics of wavelet coefficients using a new formula, uses separate noise thresholds for positive and negative wavelet coefficients, and removes low-frequency noise by denoising the Approximation component (cf. the block diagrams in Figure 2A–C).²⁵ The upshot of these features as discussed in section 4, item 5 is that WavPDS is more successful in removing the noise coefficients in the Detail components representing high-frequency sub-bands and only WavPDS removes the lowest frequency noise present in the final Approximation component.

2.C. Spurious Peaks

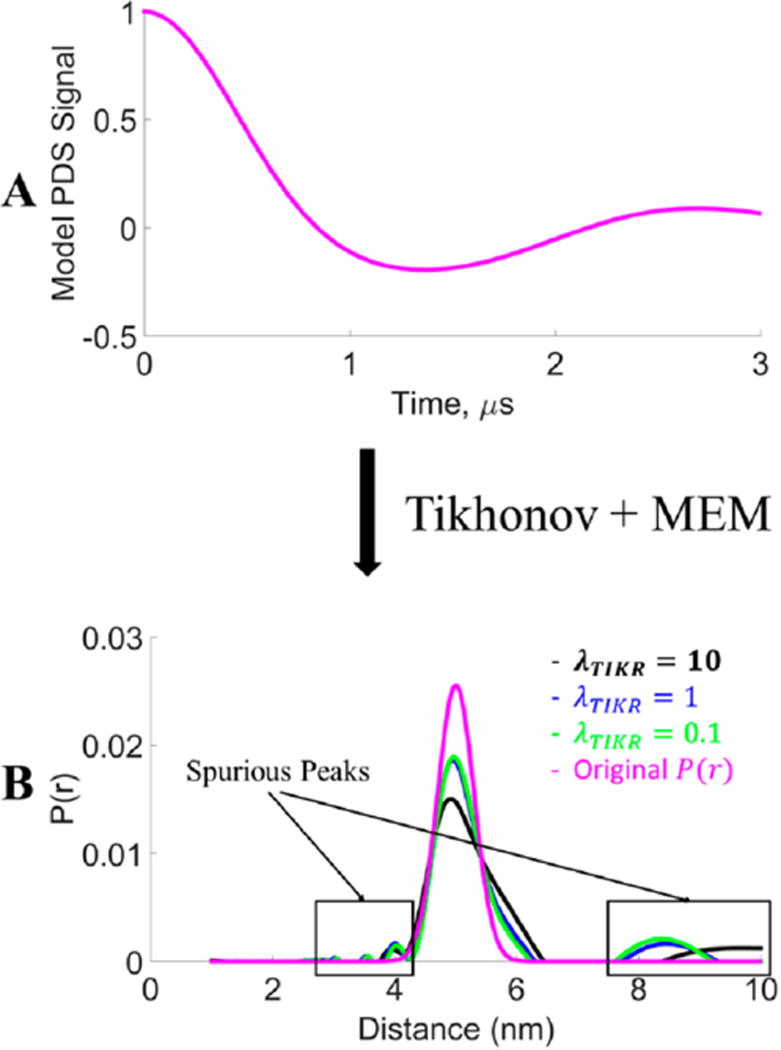
Although noise in the signal is a source of spurious or unwanted peaks in the distance distribution, the removal of the smaller of singular values, which are corrupted by the noise, also contributes to the spurious peaks. To demonstrate this, we generated a model unimodal Gaussian distribution centered at 5 nm with a standard deviation 0f 0.3 nm. Then, a model signal was generated for 3 µs using this model distance distribution. The distance distributions were reconstructed by using different λ_TIKR values in the TIKR³⁶ followed by the maximum entropy method (MEM).⁵¹ MEM was used largely to remove negative values of P(r) that emerged from the TIKR.⁵¹ Figure 3 shows different P(r)’s generated using different λ_TIKR values. The original P(r) (in pink) is given by the model and is also obtained from the model S(t) as expected (Figure 3A) after TIKR using the L-curve³⁶ (cf. sections 3.A and 3.B). Figure 3 shows that the distribution narrows with smaller λ_TIKR values, i.e., more contributions from smaller singular values. This result is also expected. However, Figure 3 also shows the presence of spurious peaks despite using a noise-free model. These spurious peaks (and negative values not shown in Figure 3 because MEM has been applied) are due to the removal of contributions of the smaller singular values. Thus, spurious peaks are generated not only due to the presence of noise but also due to the absence of contributions of the smaller singular values, which are expunged by the TIKR method for singular values where for σ_i² ≪ λ_TIKR².

Figure 3.

Comparison of distance distributions with different λ values for Tikhonov regularization of the model signal. The model signal was generated from a Gaussian distribution centered at 5 nm with a standard deviation of 0.3 nm. (Note: MEM⁵¹ was used to constrain P(r) ≥ 0.)

2.D. Objective Measures

The SNR, χ², and structural similarity index measure (SSIM)^60,61 are used as objective measures to compare the results of noisy and denoised signals with respect to a reference signal. The SNR provides the estimate about the noise in the noisy or denoised signal, χ² provides the closeness of fit, and the SSIM provides the similarity of the noisy or denoised signal with respect to a reference signal in terms of their shape and structure. The SNR is calculated as

$$\text{SNR}=\frac{{\text{signal}}_{\text{peak}}}{{\text{noise}}_{\text{RMS}}}$$ (14)

Also χ² is the root-mean-square (RMS) error defined as

$${\chi }^2\equiv \sqrt{\frac{1}{p}\mathbf{\sum }_{i=1}^p{(Y[i]-X[i])}^2}$$ (15)

where X and Y are input and reference signals, respectively. The SSIM is calculated as

$$\text{SSIM}(X,Y)=\frac{(2{\mu }_X{\mu }_Y+c_1)(2{\sigma }_{\mathit{\text{XY}}}+c_2)}{({{\mu }_X}^2+{{\mu }_Y}^2+c_1)({{\sigma }_X}^2+{{\sigma }_Y}^2+c_2)}$$ (16)

where μ and σ are mean and standard deviation, respectively, and c₁ and c₂ are positive integers used to stabilize each term. They are given in the standard MATLAB package. The SSIM values range from −1 to 1, where an SSIM of 1 means X is identical to Y.⁶⁰

2.E. ESR Method and Sample Preparation

DEER experiments at 17.3 GHz were conducted on several samples of double cysteine mutants of bacteriophage T4 lysozyme (T4L) spin-labeled with MTSL ((1-oxyl-2,2,5,5-tetramethyl-d₃-pyrroline-3-methyl)methanethiosulfonate). These T4L mutants were generated by site-directed mutagenesis using the Quick-Exchange Multi Site-Directed Mutagenesis Kit (Agilent Technologies, Stratagene Products Division), expressed in E. coli BL21(DE3) cells, and purified and spin-labeled as previously described.⁶² After spin-labeling and removal of unreacted MTSL, the protein concentration was determined from the UV absorbance at 280 nm.⁶² The following samples of spin-labeled T4L were studied: (i) sample 1, 63 µM of mutant 44C/135C; (ii) sample 2, mixture of mutants 8C/44C and 44C/135C at concentrations of 44 and 47 µM, respectively. In both cases, the buffer composition was 25 mM Tris/25 mM MOPS pH 7.6, 1 mM EDTA and 10% Gly (w/v); before freezing for PDS measurements, an extra 20% Gly-d8 (w/v) was added to the samples. Therefore, it should be noted that the protein concentrations given above are those before the extra 20% Gly-d8.

Four-pulse DEER^2,63 measurements at 17.3 GHz and 60 K were performed using a home-built Ku-band pulse spectrometer under standard experimental conditions.^1,3,19 The spectrometer tune-up was, as usual, done by using both the primary and refocused echoes, which are much stronger than the DEER signal, so there was no difficulty tuning up even for a very dilute sub-micromolar concentration sample of labeled protein (Figure S9). The π/2−π−π DEER pulse widths were 16, 32, and 32 ns, respectively, and the π pump pulse was 32 ns. A frequency separation of 70 MHz between detection and pump pulses was used. The detection pulses were applied at the low-field edge and the pump pulse was positioned near the center of nitroxide spin-label spectrum, close to the maximum. DEER time-domain signals of 4–5 µs dipolar evolution times were collected. Three data sets at different DEER signal averaging times were produced for each sample, resulting in widely different SNR. From these time-domain DEER data, interspin distance distributions were reconstructed using TIKR³⁶ and refined by MEM⁵¹ to constrain P(r) ≥ 0. Because sample 1 contained just one doubly spin-labeled protein mutant, it produced a unimodal distance distribution, whereas sample 2 produced a bimodal distance distribution due to the superposition of two unimodal distributions.

3. RESULTS

3.A. Model Data

3.A.1. Unimodal Distance Distribution

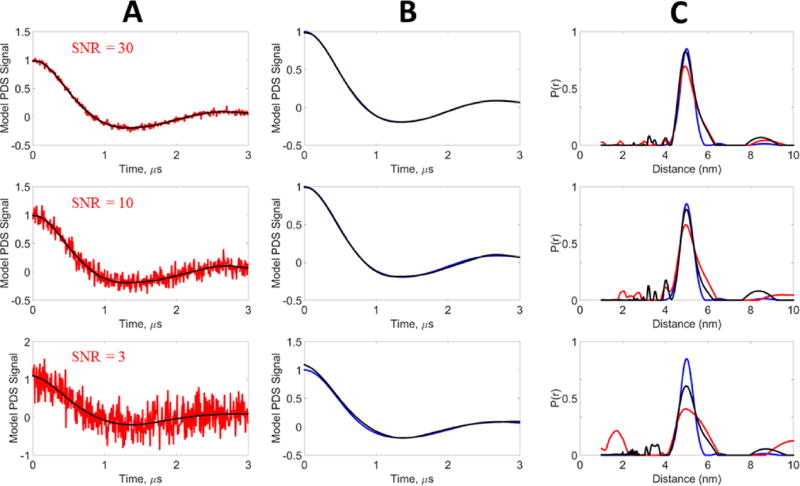
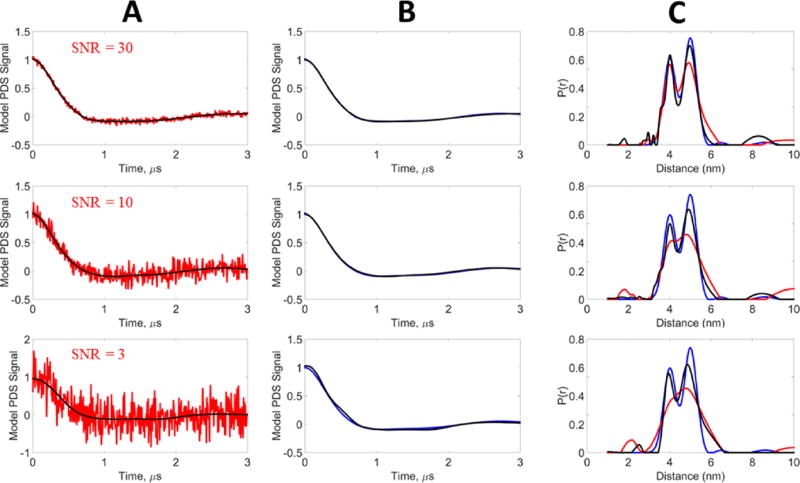
A 3 µs signal was generated for a unimodal Gaussian distribution centered at 5 nm with a standard deviation of 0.3 nm. Gaussian noise was added to the model signal to generate SNRs of 3, 10, and 30. Denoising was performed on the noisy data, resulting in SNRs of the denoised signals of 278, 848, and 1883, respectively. Figure 4A shows the denoised time-domain signals along with the original noisy signals, whereas Figure 4B compares the denoised signal with the model. All curves are normalized. It can be seen that for SNR 10 and 30, the denoising is able to (nearly) perfectly recover the model data. At SNR 3, the denoised signal shows only a small discrepancy with respect to the model. Table 1 shows the χ², SNR, and SSIM values of the noisy signals and how they are greatly improved by denoising. The SNR is improved by almost 2 orders of magnitude and the χ² values are also greatly reduced. The SSIM values are significantly increased, approaching unity from much poorer comparisons of the noisy signals to the model.

Figure 4.

Model data, unimodal distribution: blue, model signal (reference); red, noisy signal; black, WavPDS denoised signal. The model signal was generated from a Gaussian distribution centered at 5 nm with a standard deviation of 0.3 nm. White Gaussian noise was added to generate the noisy signals at SNRs 30, 10, and 3. (A) Comparison of noisy and denoised signals. (B) Comparison of the reference signal with the denoised signal obtained by WavPDS. (C) Distance distributions from noisy, denoised, and reference signals.

Table 1.

Comparison of Noisy and WavPDS Denoised Signals with Respect to the Model Signal, Unimodal Distribution at SNRs of 30, 10, and 3 (Figure 4)

	SNR	χ2	SSIM
noisy → denoised	30 → 1880	0.03 → 0.0005	0.5836 → 0.994
	10 → 850	0.10 → 0.0011	0.1194 → 0.959
	3 → 276	0.33 → 0.0036	0.010 → 0.938

The distance distributions of the model, noisy, and denoised signals were obtained using TIKR³⁶ followed by MEM.⁵¹ The regularization parameter value λ_TIKR was first obtained using the L-curve method.^36,64–66 However, at low SNR (i.e., the noisy signals), the L-curve method is not very reliable³⁶ and led either to a very broad distribution or to an unstable solution. Moreover, it was observed that the λ_TIKR value obtained from the L-curve using the criterion of maximum curvature was not at the elbow of the L-curve for these noisy signals, because there was no well-defined elbow. In fact, for SNRs of 3 and 10 the L-curve plot was very distorted. Therefore, the λ_TIKR value was then manually selected for the noisy signals (after trial and error) for optimal distance distribution, i.e., ${\lambda }_{\text{TIKR}}^{\text{OPT}}$. The optimal distance distribution was easy to determine as it could be compared with the model distribution. A larger λ_TIKR yielded a broader distance distribution, whereas a smaller λ_TIKR yielded an unstable distribution and/or enhanced artificial peaks. However, once denoised, the standard shape of the L-curve was restored (i.e., a clear elbow), so the optimal λ_TIKR selected for the denoised signal was obtained directly from the L-curve. For the noisy signals, the ${\lambda }_{\text{TIKR}}^{\text{OPT}}$ values obtained manually decreased after denoising ( ${\lambda }_{\text{TIKR}}^{\text{OPT}}=15\to 0.01,{\lambda }_{\text{TIKR}}^{\text{OPT}}=10\to 0.5$, and ${\lambda }_{\text{TIKR}}^{\text{OPT}}=5\to 0.5$ for SNR of 3, 10, and 30, respectively). For the original model signal, the optimal ${\lambda }_{\text{TIKR}}^{\text{OPT}}=1\times {10}^{-6}$ was obtained by using the L-curve method. Because the model data are noise-free, λ_TIKR is near zero to eliminate the contributions of the zero singular values that arise because the K matrix is singular.³⁶ Though they should be exactly zero, due to computational error they are only near zero. The denoised signals consistently have much smaller optimal λ_TIKR than the noisy signals. This means that, when denoised, a significant number of contributions from the smaller singular values could be included according to eq 7.

Figure 4C compares the distance distributions from the noisy, denoised, and model signals. At SNR = 30, the distance distribution of the denoised signal and the model are very nearly identical, whereas that for the noisy signal has a slightly reduced normalized intensity and is somewhat broader at its larger distances. For SNRs of 3 and 10, the distance distributions P(r) of the denoised signals accurately provide the peak location and distribution width, whereas the P(r) of the noisy signals possess broader peaks of lower amplitude. Especially for an SNR of 3, the distance distribution is no longer reliable.

3.A.2. Bimodal Distance Distribution

A 3 µs signal was generated for a bimodal Gaussian distribution, centered at 4 and 5 nm, each with a standard deviation of 0.3 nm. The peak height at 4 nm was 80% of the peak height at 5 nm. Similar to the unimodal model, Gaussian noise was added to the model signal to generate SNRs of 3, 10, and 30 and then the model was denoised. Table 2 shows the χ², SNR, and SSIM values of the noisy and denoised signals. Parts A and B of Figure 5 show the denoised signals along with noisy and model signals, all of which are normalized. For the SNR of 30, the denoising is able to virtually perfectly recover the model data; the SSIM is very close to unity. For the SNRs of 10 and 3, the denoising is almost as good, as reflected in the SSIM values as well as in the χ²’s. The denoised signals significantly increase in SNR by about 2 orders of magnitude for all the noisy signals, just as we found for the unimodal case.

Table 2.

Comparison of Noisy and WavPDS Denoised Signals with Respect to the Model Signal, Bimodal Distribution at SNRs 30, 10, and 3 (Figure 5)

	SNR	χ2	SSIM
noisy → denoised	30 → 3186	0.03 → 0.0003	0.5412 → 0.997
	10 → 1850	0.10 → 0.0005	0.1068 → 0.953
	3 → 378	0.33 → 0.0026	0.0077 → 0.945

Figure 5.

Model data, bimodal distribution: blue, model signal (reference); red, noisy signal; black, WavPDS denoised signal. The model signal was generated from two Gaussian distributions centered at 4 and 5 nm and each with a standard deviation of 0.3 nm. White Gaussian noise was added to generate the noisy signals at SNRs 30, 10, and 3. (A) Comparison of noisy and denoised signals. (B) Comparison of the reference signal with the denoised signal obtained by WavPDS. (C) Distance distributions from noisy, denoised, and reference signals.

Similar to example 3.A.1, the L-curve plot λ_TIKR value needed to be manually adjusted for noisy signals, whereas the optimal λ_TIKR for the denoised signals was obtained directly from the L-curves (cf. Figure S10). The optimal λ_TIKR values were reduced from those for the noisy signals to those for the denoised signals ( ${\lambda }_{\text{TIKR}}^{\text{OPT}}=60\to 5,{\lambda }_{\text{TIKR}}^{\text{OPT}}=20\to 3$, and ${\lambda }_{\text{TIKR}}^{\text{OPT}}=5\to 1$ for SNR 3, 10, and 30, respectively; cf. Figure S10). For the model signal itself, the optimal λ_TIKR = 5 × 10⁻⁶ was simply obtained using the L-curve.

In Figure 5C, the distance distributions of noisy, denoised, and model signals at SNRs 3, 10, and 30 are shown. At SNR = 30, the P(r) of the denoised signal is very close to the model P(r), whereas the P(r) of the noisy signal has a broader distribution and lower peak height. Moreover, the first peak incorrectly appears to be about the same height as the second peak. For an SNR of 10, the noisy signal results in a broad distribution with the two peaks almost indistinguishable. Meanwhile, the denoised signal is able to resolve both peaks along with maintaining their height difference. The noisy signal at SNR = 3 provides only a single broad distribution, thereby failing to resolve the peaks. On the contrary, its denoised version is successfully able to clearly resolve the two peaks.

3.A.3. Short Evolution Time vs Long Evolution Time

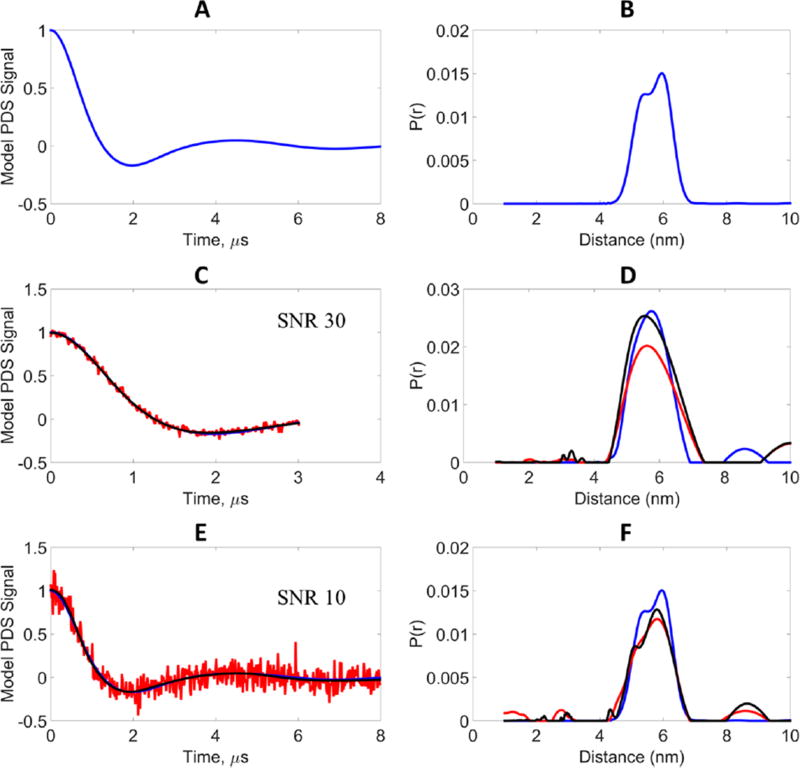
High SNR at short evolution times can frequently be obtained but at the cost of poor peak resolution and broader widths in the distance distributions. In these cases, not enough time has been allowed for a reasonably complete dipolar oscillation. On the contrary, due to the reduced SNR at longer evolution times, one is also not able to resolve the peaks due to the presence of increased noise. A major challenge in PDS is to obtain a high-SNR signal for longer evolution times. We created a model system to illustrate the effectiveness of WavPDS in denoising the lower SNR signal at a longer evolution time. A model was created, which corresponds to a distance distribution containing two close Gaussian peaks between 5.3 and 6 nm. As shown in Figure 6, this distribution is recovered from an 8 µs dipolar evolution time signal. This signal was then shortened to 3 µs, which resulted in a single peak in the P(r), showing the resolution loss at short evolution time. Noisy signals were generated at SNR = 30 for 3 µs and at SNR = 10 for 8 µs, i.e., a factor of 3 increase of noise assuming the same total signal acquisition times. In many experimental cases one often encounters even greater reduction in SNR by doubling the dipolar evolution times due to effects of phase memory decay. As can be seen in Figure 6, the model, noisy, and denoised signals at 3 µs yield a single distance distribution. For longer evolution times at SNR = 10, the denoised signal resolves the two peaks, whereas the noisy signal is unable to. The optimal µ_TIKR’s for the noisy signals at 3 and 8 µs are 10 and 20, respectively. For the denoised signals, the optimal λ_TIKR was obtained directly from the L-curve and was 1 and 0.01, respectively, for 3 and 8 µs evolution time. The optimal λ_TIKR’s for the model signal are 4.2 × 10⁻⁶ and 2.7 × 10⁻⁶ for the 3 and 8 µs evolution times, respectively. As mentioned earlier, the near-zero λ_TIKR values are due to computational error and are used to eliminate the contributions of the zero singular values due to the singular nature of the matrix K.

Figure 6.

Model data, results of longer evolution time at higher noise (low SNR) compared to shorter evolution time at lower noise (high SNR): blue, model signal (reference); red, noisy signal; black, WavPDS denoised signal. (A) Model signal at evolution time 8 µs generated from bimodal distance distribution. (B) Bimodal distance distribution generated from two Gaussian distributions centered at 5.3 and 6 nm, each with standard deviation 0.3 nm, and peak heights of 0.8 and 1, respectively. (C) Comparison of noisy, denoised, and Model signals at 3 µs evolution time for the bimodal distance distribution. (D) Distance distributions from noisy, denoised, and model signals at 3 µs evolution time. (E) Comparison of noisy, denoised, and model signals at 8 µs evolution time for the bimodal distance distribution. (F) Distance distributions from noisy, denoised, and model signals at 8 µs evolution time.

3.B. Experimental Data

3.B.1. Unimodal Case

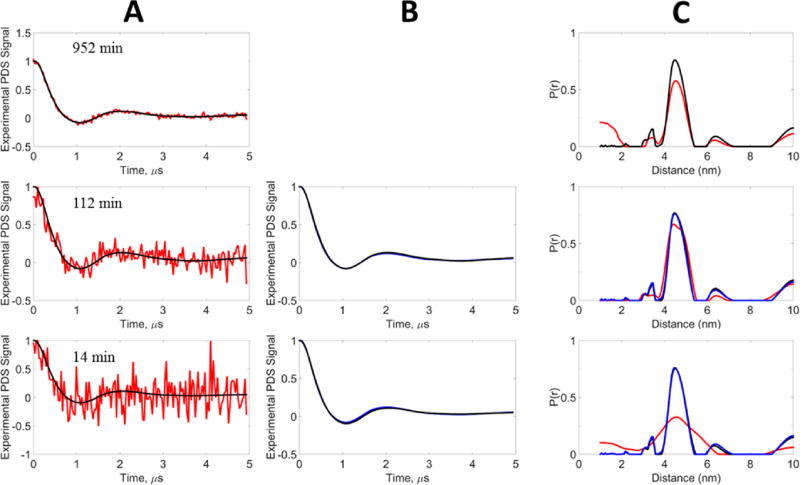
To test WavPDS in experimental signals, the sample was signal-averaged for three different acquisition periods generating small, medium, and large SNRs. Denoising was applied after the baseline was subtracted from the original signal. This was done for simplicity of presentation in this paper. However, we illustrate in Figure S10 how performing the denoising before baseline subtraction greatly aids in its removal for noisy signals, a matter we plan to discuss elsewhere. This unimodal signal is illustrated in Figure 7A where the DEER signal is averaged for 14, 112, and 952 min on the protein sample. At 952 min excellent SNR is achieved in the DEER signal (Table 3), although some residual noise still affects the longer time, lower SNR part of the DEER signal. The P(r)’s shown in Figure 7C were obtained as in the model cases. A mild sharpening of the P(r) is observed after applying WavPDS, wherein most of the residual noise has been removed in the denoised time-domain signal. It was not practical to average for acquisition times much greater than ca. 1000 min. Given the good signal obtained after 952 min, we chose to use its denoised form as the reference to compare with the cases of reduced acquisition time. When the signal acquisition time is reduced by almost an order of magnitude (from 952 to 112 min), the noise increases significantly but our denoised signal and P(r) are almost identical to those of the reference (cf. Figure 7A–C), whereas this is not the case for the result obtained from the noisy data (Table 3). The last case involves nearly another order of magnitude reduction in signal averaging time to 14 min. This yields a very noisy signal that is too noisy for a P(r) to be recovered using λ_TIKR, but the result shown in Figure 7C is for ${\lambda }_{\text{TIKR}}^{\text{OPT}}$ and is clearly too broad. However, after our wavelet denoising procedure we recover very nearly identical results as compared to the reference.

Figure 7.

Experimental data, unimodal distribution: blue, reference signal; red, noisy signal; black, WavPDS denoised signal. The experimental signal was generated from T4 Lysozyme spin-labeled at mutant 44C/135C with 63 µM concentration at acquisition times 952, 112, and 14 min (section 2.E). (A) Comparison of noisy and denoised signals. (B) Comparison of reference signal with denoised signals after applying WavPDS. (C) Distance distributions from noisy, denoised, and reference signals. The denoised signal at 952 min was used as the reference.

Table 3.

Comparison of Noisy and WavPDS Denoised Signals with Respect to the Experimental Reference Signal (952 min WavPDS Denoised Signal), Unimodal Distribution at Signal Acquisition Times 952, 112, and 14 min (SNRs 37, 6.8, and 3.8, Respectively; Figure 7)

	SNR	χ2	SSIM
noisy → denoised	37 → (reference)	0.027 → 0 (reference)	0.676 → 1 (reference)
	6.8 → 909	0.190 → 0.0011	0.135 → 0.995
	3.8 → 488	0.263 → 0.0021	0.038 → 0.967

Similar to model data results, the λ_TIKR values were optimized by manual adjustment for noisy signals, whereas the optimal λ_TIKR for the denoised signals was obtained directly from the L-curves (Figure S11). The ${\lambda }_{\text{TIKR}}^{\text{OPT}}$ value reduced from the noisy signals to denoised signals: ${\lambda }_{\text{TIKR}}^{\text{OPT}}=30\to 0.08,{\lambda }_{\text{TIKR}}^{\text{OPT}}=8\to 0.07$, and ${\lambda }_{\text{TIKR}}^{\text{OPT}}=3\to 0.09$ for signal acquisition times 14, 112, and 952 min, respectively (Figure S11). It must be noted that denoising improved the L-curve shape to give a sharp elbow and directly resulted in the optimal λ_TIKR values, which was not possible for the noisy signal (Figure S11).

3.B.2. Bimodal Case

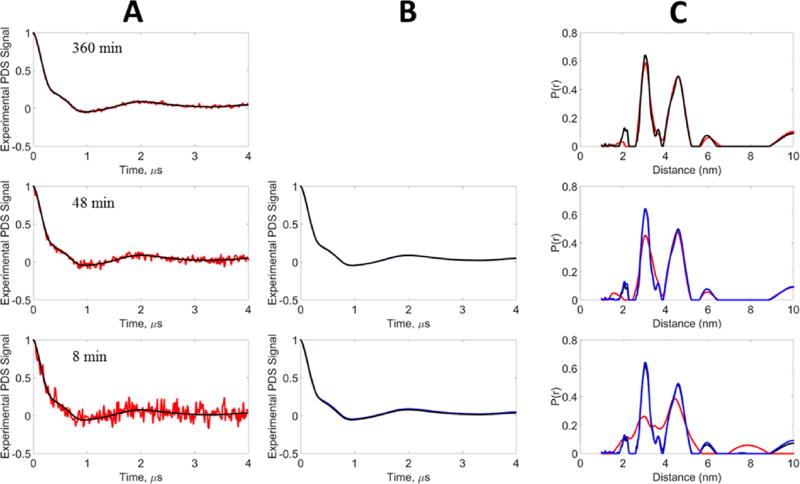
Like the unimodal case, the bimodal signal was obtained at different signal averaging times (8, 48, and 360 min), generating different SNRs (Table 4). Figure 8 shows the noisy and denoised signals and their respective distance distributions. It can be seen that at 360 min the signal is nearly noiseless, so the “noisy” and denoised P(r) are very similar. As in the unimodal case, the denoised 360 min case is taken as the reference for the bimodal signals. For the 48 min noisy signal, the distance distribution is able to retrieve the two peaks but the first peak is now smaller and broader than the second peak, whereas the denoised signal is able to perfectly retrieve both peaks. For 8 min, the noisy signal yields a very broad P(r) that is barely able to reveal the existence of two peaks. On the contrary, the denoised signal at 8 min is successfully able to retrieve the two peaks, and it is very nearly identical to that of the reference.

Table 4.

Comparison of Noisy and WavPDS Denoised Signals with Respect to the Experimental Reference Signal (360 min WavPDS Denoised signal), Bimodal Distribution at Signal Acquisition Times 360, 48, and 8 min (SNRs 80, 31, and 11, Respectively; Figure 8)

	SNR	χ2	SSIM
noisy → denoised	80 → (reference)	0.013 → 0 (reference)	0.8815 → 1 (reference)
	31 → 3333	0.032 → 0.0003	0.573 → 0.999
	11 → 1046	0.086 → 0.0009	0.156 → 0.961

Figure 8.

Experimental data, bimodal distribution: blue, reference signal; red, noisy signal; black, WavPDS denoised signal. The experimental signal was generated from the T4 lysozyme spin-labeled admixture of mutants 8C/44C and 44C/135C at concentrations of 44 and 47 µM, respectively, at acquisition times 360, 48, and 8 min. (A) Comparison of noisy and denoised signals. (B) Comparison of denoised signals after WavPDS with reference. (C) Distance distributions from noisy, denoised, and reference signals. The denoised signal at 360 min was used as the Reference.

Like the unimodal signal, the λ_TIKR values had to be manually adjusted for the noisy signals, whereas the optimal λ_TIKR values for the denoised signals were obtained directly from the L-curves (Figure S11). The ${\lambda }_{\text{TIKR}}^{\text{OPT}}$ values decreased from those of the noisy signals to those of the denoised signals as ${\lambda }_{\text{TIKR}}^{\text{OPT}}=10\to 0.09,{\lambda }_{\text{TIKR}}^{\text{OPT}}=5\to 0.08$, and ${\lambda }_{\text{TIKR}}^{\text{OPT}}=2.48\to 0.1$ for signal acquisition times 8, 48, and 360 min, respectively. It must again be noted that denoising improved the L-curve shape to give a sharp elbow and directly resulted in the optimal λ_TIKR values, which was not possible for the noisy signals.

4. DISCUSSION

This work on denoising time-domain PDS signals, and how this affects the distance distributions that are obtained from them, has led to the following:

1. The SNR of the time-domain signal is increased by a factor of about 100 for both model and experimental signals using our new denoising procedure.

2. When the SNR ≳ 10, virtually perfect time-domain signals are obtained after denoising, when compared to a standard; for SNR ~ 3, very good denoised signals are obtained.

3. Although standard procedures such as SVD followed by TIKR to obtain the P(r) do a partial denoising by discarding contributions from the heavily noise-corrupted smaller singular values, the prior denoising of the time-domain signals yields significantly better P(r)’s especially for initially noisy signals where the SNR ≲ 30.

4. By denoising the time-domain signals, one can employ longer dipolar evolution times, which is important for determining longer distances and/or separating overlapped distance distributions.

5. Standard wavelet denoising methods are typically much less effective in denoising noisy time-domain signals than is WavPDS and hence in obtaining the correct P(r), but they become more satisfactory for less noisy signals.

We now discuss these points in more detail.

1. Improvement in SNR: We have shown that denoising improves the SNR of the time-domain signal by a factor of approximately 100 in the model and experimental cases of unimodal and bimodal distributions. In the model cases, we considered noisy SNRs of 3, 10, and 30. The factor of approximately 100 is true in all three SNR scenarios, except that in the unimodal model the SNR increase is about 82. Thus, substantial reductions in signal averaging times can be achieved by denoising. Because signal averaging improves the SNR by √N, a factor of just 10 in SNR improvement by denoising reduces the signal averaging time by a factor of 100. When we considered SNR ~ 1 for both model cases, we found that denoising became unreliable, so we recommend denoising for SNR ≳ 3.

2. Accuracy of the denoised signal: Here we find the SSIM parameter best reflects the accuracy of the fit. One needs to compare the time-domain signal to that of a reference to apply this parameter. For the model cases, the original model is the appropriate reference. For the experimental cases it was not feasible to average for long enough periods to obtain ideal references, so we used very long averaging times (ca. 16 and 6 h for the unimodal and bimodal cases, respectively), yielding good SNRs (of 37 and 80, respectively), and then denoised them to serve as the references. For the two model cases for which the SNR = 30, nearly perfect agreement (SSIM of 0.994 and 0.997) with the reference was achieved from the initial noisy SSIM values of 0.58 and 0.54, respectively. When the SNR = 10, almost perfect agreement of 0.96 and 0.95, respectively, was achieved from initial values for SSIM of ~0.12, 0.11, whereas for SNR = 3 initial values of SSIM 0.01 and 0.008 became 0.95 and 0.945. For the experimental cases for SNRs of 3.8 and 11, SSIM values of 0.97 and 0.96 were achieved after denoising, whereas for SNRs of 6.8 and 31, SSIM values of 0.995 and 1.00 were achieved. Thus, for an SNR ~ 3–4, excellent results can be achieved, whereas for SNR ~ 7–10 virtually perfect results are achieved in the time-domain data.

3. Improvement in Distance Distributions: Here we consider the implications of denoising the time-domain signals on the P(r) obtained from them. Although there are other possible approaches to illustrate this, we used TIKR followed by MEM largely to remove negative P(r) values that emerge from TIKR.^36,51 It is well-known that for SNR ≲ 30 this approach, using the L-curve “elbow” to determine the regularization parameters, ${\lambda }_{\text{TIKR}}^{\text{OPT}}$, is inadequate.³⁶ We show in Figures S10 and S11 the L-curve plots. Though these plots yielded satisfactory values of λ for the denoised signals, this was not the case for the noisy spectra; we therefore used a trial and error approach to determine the optimum λ for the latter. This was only possible in this present study because we had the reference P(r)’s for all the cases. In general, determining an optimum λ for noisy cases becomes rather uncertain. But by prior denoising, we find the L-curve works quite well. We show in Figures 4–8 how the P(r)’s derived from the noisy and denoised time-domain signals compare with the respective reference P(r)’s. Here, because of spurious contributions to the P(r)’s that appear (some of which were negative before applying MEM), we did not employ the quantitative measures (i.e., χ², SNR, SSIM) that we employed for the time-domain data but rather relied on visual inspection. It is clear from these figures (Figures 4–8) that the denoised time-domain results all yield very good to excellent agreement with the reference P(r). This is especially true for initial SNR ≳ 10; for SNR ~ 3 the results still tend to be very good. The experimental denoised results are particularly good. However, for the noisy spectra we see significantly poorer P(r) results, especially for SNR ~ 3 and even for SNR ~ 10, even when the optimum λ is used. This is true for both the bimodal model and the experimental results, where the noisy results have difficulty in resolving both peaks. That is, they show broadened P(r)’s.

   Why is depending on just the partial denoising by TIKR less satisfactory than first denoising the time-domain signal before applying TIKR? Because we had to use optimized regularization parameters, ${\lambda }_{\text{TIKR}}^{\text{OPT}}$, to obtain satisfactory P(r)’s for the noisy results, that is not the issue. We have indeed found that prior denoising yields significantly smaller λ values than even the optimized values from the noisy signals. These smaller λ values bring into the P(r) the contributions from smaller singular values in the SVD decomposition of P(r) (eq 7) because they are no longer corrupted by noise, and they provide greater resolution (e.g., narrower and more accurate P(r)’s) and detail that is important for P(r)’s with more complex structure (e.g., separation of two close distances).

4. Longer Distances May be Studied: In the model example shown in Figure 6 we illustrate that when one needs longer dipolar evolution times to distinguish subtle features in the P(r), but one is limited by the increase in noise, the denoising method can help to overcome this problem. This is clearly also true when longer dipolar evolution times are needed for the measurement of longer distances.

5. Comparison of WavPDS with Standard Methods: Results from the use of standard wavelet denoising methods^58,59 are shown in Figures S3–S8 and Tables S1–S6 using the same “db6” wavelets. They cover six of the examples: the model bimodal case (Figures S3 and S4; Tables S1 and S2) and the experimental unimodal (Figures S5 and S6; Tables S3 and S4) and bimodal (Figures S7 and S8; Tables S5 and S6) cases. These include a range of initial SNRs. We find that these other methods are much less effective in improving the SNR, i.e., typically only by a factor of 2–3 (except for cases S1 and S2, where the factor is as great as 5) compared to the factor of order 100 for WavPDS. It appears that they are not as successful in removing the noise coefficients in the Detail components representing high-frequency sub-bands nor do they remove any low-frequency noise present in the final Approximation component. The WavPDS method, as we have seen, is very successful in rendering a good P(r) in all these cases. For the noisiest cases (model bimodal SNR = 3 and experimental unimodal SNR = 3.8), using the standard methods yields poor fits to the double peak model P(r) (Figure S3) and better, but not good, fits to the unimodal P(r) (Figure S5). These cases also demonstrate that a simple unimodal P(r) is more easily fit with lesser quality data than a more complex P(r), such as in the bimodal case. This is because contributions from fewer of the smaller singular values are needed to describe the rather simple unimodal distribution. And according to the requirement ${\sigma }_i>{\lambda }_{\text{TIKR}}^{\text{OPT}}$ (eq 7) so that the contribution from the ith singular value is included, the larger λ’s reduce the number of these significant contributions. Even for a somewhat higher SNR = 11 for the bimodal experimental result (Figure S6) and an SNR = 10 (Figure S4) for the bimodal model, the results from the other methods do not yield satisfactory P(r)’s. However, where one has less noisy signals (e.g., Figure S8), these other methods do yield more satisfactory P(r)’s, although not as good as WavPDS.

Low-pass filters are frequently used in denoising, but it is well-known that the standard wavelet denoising methods are superior.^26,29,56 We demonstrate this fact with an example from this work in Figure S12.

Overall, we can conclude that WavPDS is much more effective at denoising the time-domain signals, but as the SNR of the original noisy signal increases and/or the “simplicity” of the actual P(r) increases, the results from these other methods become more satisfactory. However, this last comment is only true because instead of using the λ-value obtained directly from the elbow of the L-curves, which we find are still poorly defined, we used trial-and-error searches to obtain the optimum λ (which is always considerably different; cf. Tables S1–S6). In this study we have a reference P(r) for optimizing the choice of λ, but in actual practice, where the true P(r) is not known a priori, the determination of a good λ still remains a challenge. As we have shown, however, after denoising by WavPDS, the L-curve-obtained λ is indeed at or near the optimum λ.

We now wish to note some additional aspects related to the methodology.

1. Spin–Echo Detection: The experimental time-domain decay signals discussed above are actually obtained as a series of points which themselves represent spin–echo heights obtained as a function of the dipolar evolution time but with the (refocused) spin–echo kept at a fixed time after the initial π/2 pulse.^4,67 Each such point is the average of many spin–echo repeats. One can in fact first denoise each of these averaged spin–echo signals. We show an example in Figure S13 how the spin–echo signal can be very successfully denoised. We plan to investigate this approach further.

2. Baseline Subtraction from Weak PDS Signals: This is a standard issue in processing PDS data. In the present study we have chosen to first remove the baseline from the original noisy data using our standard procedure^3,68 before denoising, largely to simplify the presentation of the denoising methodology and the comparisons between the various sets of results. Indeed, prior denoising of the raw data, which does include the baseline, would aid significantly in identifying and removing it. This is another matter we plan to address elsewhere, but we do show a preliminary example of this in Figure S9. This is an example of a very weak PDS signal from sub-micromolar concentration of labeled protein. Nevertheless, the denoising is very effective in enabling the removal of the baseline and recovering the denoised signal.

3. Spurious Peaks in the P(r): Even after denoising, spurious peaks still arise in the P(r). As we showed in Figure 3, it is not only noise but also truncation of the smaller singular values that contributes to the TIKR procedure. This is an effect that remains even after denoising by WavPDS. We plan to study this matter further.

4. What is the minimum SNR of the original data that can still be usefully denoised by WavPDS? Our results on both model and experimental data show success with an SNR ~ 3, but unreliable results SNR ~ 1 with model data. Further studies are needed to best answer this question.

5. CONCLUSIONS

In this study, we have shown that by greatly enhancing the SNR of time-domain signals, while retaining the fidelity of the underlying signals by means of our new wavelet denoising method, WavPDS, it is possible to reduce signal averaging times by as much as 1–2 orders of magnitude. This was demonstrated with the use of both model and experimental pulse-dipolar ESR signals. Once denoised, they may be readily inverted by standard methods into distance distributions more conveniently and more accurately than for the original noisy signals.