False fMRI activation after motion correction

Abstract

Motion correction of echo‐planar imaging (EPI) data used in functional MRI (fMRI) is an essential preprocessing step performed prior to statistical analysis. At ultra‐high resolution fMRI, current requirements regarding translational and rotational motion may no longer be acceptable. This prompts the need for a systematic investigation of the effects of motion correction procedures with in vivo fMRI data. Here we systematically evaluated the effect of retrospective motion correction with freely available fMRI analysis software packages (FSL, AFNI, and SPM) on activation maps using fMRI data acquired with prospective motion detection, to identify and quantify confounding effects of retrospective motion correction, and to evaluate its dependence on spatial resolution and motion correction algorithms. Brain activation maps were obtained for two different resolutions, an ultrahigh, that is, 0.65³ mm³, and a more widely used 2.0³ mm³ isotropic resolutions at 7 T. The EPI data were acquired using simultaneous non‐image‐based optical moiré phase tracking (MPT) of physical motion. The results showed that image‐based motion detection, performed by SPM8 software package, may be erroneous in high‐field fMRI data with partial brain coverage and can introduce spurious motion leading to false‐positive and false‐negative activation. Further analyses demonstrated that limited acquisition field of view has the dominant influence on the effect. Hum Brain Mapp 38:4497–4510, 2017. © 2017 Wiley Periodicals, Inc.

INTRODUCTION

fMRI is a widely used neuroimaging tool for assessing brain activity. BOLD fMRI is one of the main techniques, which has gained widespread application due to its ease of use and noninvasiveness. In fMRI, a series of imaging volumes is usually acquired at time intervals of a few seconds. Several preprocessing steps are required before the data can be analyzed statistically to evaluate brain activation. The validity of each of the preprocessing steps is very important. This study focuses on the validity of one of these steps, that is, motion correction.

The quality of fMRI data is strongly affected by the presence of head movements. Typically fMRI users implement various criteria when accepting data based on head movement during the acquisition, with some limits as strict as translational movement <1 mm in any direction and rotational movement <1° around any axis for data acquired with voxel side dimensions of 2–3 mm [Chang et al., 2013; Dumontheil et al., 2016; Wu et al., 2016]. The effects of substantial movements can be so large, that the analysis results may become unreliable. This situation is exacerbated in some clinical studies with certain patients, for example, diagnosed with Parkinson's disease, and generally in all clinical studies when scan time is limited and subjects are not always easily available for repeat scans.

Head motion causes a degradation of the quality of fMRI in many ways. Mainly, many methods of analyzing fMRI data are performed under the assumption that the same voxel in subsequent repetitions corresponds to the same location in the brain. Head motion invalidates this assumption. Also, head motion can cause changes in magnetic field [Deichmann et al., 2002], leading to varying distortions in the acquired images [Jezzard and Clare, 1999; Andersson et al., 2001], intensity variations due to spin history effects [Friston et al., 1996] and T2*, and therefore local BOLD sensitivity, which further degrade the quality of fMRI data. There are many ways to alleviate the effects associated with head motion. They can be broadly categorized, depending on when the correction took place with respect to image acquisition, that is, prospective and retrospective motion‐correction, and on whether the correction is based on the acquired MR images or on other information, that is, image‐ and non‐image‐based motion‐correction.

Retrospective image‐based motion‐correction has gained wide usage among fMRI researchers due to its availability and ease of use. Many fMRI analysis software packages include motion‐correction tools, such as Analysis of Functional NeuroImages (AFNI), FMRIB Software Library (FSL), SPM, and BrainVoyager. The performance of the freely distributed software packages, namely, SPM, FSL, and AFNI, will be studied. Prospective motion‐correction methods are not as easily available, as they require modifications to standard scanning sequences (Prospective Acquisition CorrEction (PACE) [Thesen et al., 2000] and navigator‐based methods [Fu et al., 1995]) and in some cases an additional complicated mechanical set‐up (Advanced RealTime Tracking (ARTTrack3) [Zaitsev et al., 2006], Moiré Phase Tracking (MPT) [Maclaren et al., 2012] motion‐correction). It has been demonstrated in Speck et al. [2006] that a prospective real‐time optical slice‐by‐slice motion‐correction method is far superior to image‐based motion correction methods in recovering the correct slice positions in some cases, reducing residual Nyquist artifact and geometric distortions. Furthermore, fMRI analysis showed that data acquired with prospective optical motion‐correction had more activated voxels and less false positive and false negative voxels [Speck et al., 2006]. MPT motion‐correction may be considered to be the gold standard in motion correction, as it is nonimage based and provides highly precise (up to 0.01 mm in three directions and better than 0.01° in all three rotations) and accurate (up to 0.1 mm in three directions and better than 0.07° in all three rotations) [Maclaren et al., 2012] pose tracking at a very high rate (up to 80 frames per second). It should be noted that this high level of precision is strongly dependent on the precision of scanner‐camera cross‐calibration procedure, as calibration errors affect motion detection precision of the MPT motion correction system [Zaitsev et al., 2006; Zahneisen et al., 2014]. The cross‐calibration procedure typically takes 1–2 h to perform. Importantly, however, no subject‐specific calibration is required. The procedure can be performed once to the desired level of precision, and the obtained scanner‐camera transformation can be used for as long as the reference marker's position remains unchanged [Maclaren et al., 2012]. In addition to highly precise intrascan motion correction, prospective motion correction also corrects for head motion between scans. Interscan motion correction provides a further advantage as it prevents head motion from shifting regions of interest outside the acquisition box, which is of particular relevance when precise positioning and coverage of the acquisition field of view is of great importance. Furthermore, almost instant adjustments of the acquisition box keep the phase‐encoding direction constant relevant to the head, which improves the efficacy of the subsequent distortion correction.

Especially image‐based approaches to motion correction are imperfect to some extent. As already mentioned, head motion introduces variations in the signal time course due to signal coming from different parts of the brain at different moments of time. This effect introduces false‐negative activations due to increased unexplained signal variance. Head motion also has an opposite, much more significant, effect when head motion is correlated with the stimulus. This kind of motion may mimic truly activated voxels and therefore can impose difficulties on image‐based retrospective motion‐correction methods. In fact, it has previously been shown with simulations that image‐based retrospective motion‐correction algorithms may mistake brain activation related changes for motion related changes in the images [Freire et al., 2001], and correct for them accordingly. Not only can this ruin the assumption that the signal comes from the same location in the brain, thus reducing the strength of true activation, but also it may introduce false positive brain activation in regions with high local image intensity gradients, for example, edges of the brain, as this erroneous motion and related signal changes are highly correlated with the stimulus.

More advanced hardware and methods have allowed researches to increase fMRI spatial resolution. This, however, comes at the price of reduced imaged brain volume. Higher resolution requires more for each slice to acquire, thus reducing the number of slices acquired due to repetition time (TR) constraints. Each slice is also thinner, further reducing the brain volume acquired. For ultra‐high‐resolution cases, there is even the need to reduce in‐plane FOV to fulfill TR requirements. Additionally, higher resolution fMRI data are more susceptible to motion related problems than low resolution even at the same magnitude of motion because the spatial shift becomes larger relative to the voxel size. Smaller voxel size also leads to higher BOLD signals due to reduction of partial volume effects. Additionally, BOLD responses are increased for fMRI at ultrahigh magnetic field strength, for example, 7 T. These advances may further exacerbate the problem of spurious head motion as a result of the misclassification of stimulus‐related changes in brain images as motion‐related.

The introduction of ultra‐high‐field MRI systems has allowed neuroscientists to obtain submillimeter fMRI data with very high contrast‐to‐noise ratio. Current requirements regarding translational and rotational motion may no longer be acceptable at ultra‐high‐resolution fMRI. In a previously conducted pilot study, in which we included the acquisition of ultrahigh 0.65³ mm³ resolution data without prospective motion correction from six subjects, we have observed suspicious brain activation estimates outside the typical activation in the visual cortex, especially near the edges of the brain. In an attempt to find the cause, the fMRI data were analyzed after each intermediate preprocessing step, and it was determined that spurious brain activation appears after the very first preprocessing step—motion realignment. Remarkably, no systematic investigation of the effects of high‐resolution imaging at ultrahigh magnetic field strengths on motion correction procedures has previously been conducted with in vivo fMRI data. In this study, we therefore systematically evaluate the effect of retrospective motion‐correction performance of freely available fMRI analysis software packages (FSL, AFNI, and SPM) on activation maps. Importantly, we used fMRI data acquired with simultaneous prospective MPT‐based motion detection, which offers independent highly accurate motion information not affected by any changes in EPI images. The goal of this study is to identify the effect of retrospective motion correction using in vivo fMRI data, quantify it, evaluate its dependence on spatial resolution and retrospective motion correction algorithms used, and to finally suggest a solution for remaining motion effects.

METHODS

Participants

Two healthy participants (1 male, age 27, and 1 female, age 33) with normal vision (visual acuity ≥1) gave their written consent and took part in the study. The procedures followed the tenets of the declaration of Helsinki (World Medical Association, 2000) and the study was approved by the ethics committee of the Otto‐von‐Guericke‐University Magdeburg, Germany.

Visual Stimulation and Procedure

A black‐and‐white circular checkerboard [24 segments, 18 rings (ring width: 0.47°), width: 17.0°; height: 8.5°; mean luminance: 90 cd/m²; contrast 98%] with reverting contrast at 6 reversals per second was presented. In the center of the stimulus, a fixation dot (size: 0.3° diameter) was displayed, with colors changing briefly from red to green for 166 ms at random intervals to be reported by the subjects via button press.

For the functional scans blocks of “stimulation on,” checkerboard reversal and central fixation as detailed above, and “stimulation off,” central fixation on gray background (luminance: 90 cd/m²) were alternated. Each experimental run began with a 12 s “stimulation off” to be discarded to avoid transient onset artifacts, followed by six 36 s stimulation cycles comprising 18 s stimulus on and 18 s stimulus off, resulting in a total stimulation duration per scan of 228 s (3.8 min). The stimulus images were generated with Matlab (Mathworks Inc.), and presented using the software Presentation (Neurobehavioral Systems Inc.). The stimuli were projected with a video projector (DLA‐G150CL, JVC Ltd.) onto a screen mounted in the bore of the scanner superior to the head coil. Subjects were in supine position and viewed the projection through a surface mirror placed above their eyes and housed in the head coil. A specially molded foam pad was applied to restrict motion during experiments. The moiré pattern tracking system, which comprised a planar tracking marker attached to a custom‐made mouthpiece, a single camera, and software to process the camera images to compute pose in six degrees of freedom, was used for motion detection [Maclaren et al., 2012]. Subjects were instructed to minimize head movement, focus on the fixation dot, and report the color change of the fixation dot by button press during the experiment, to encourage subjects' vigilance and central fixation.

MRI Acquisition

For fMRI, T₂*‐weighted echo planar images (EPI) (TR/TE = 3000/22 ms, FA = 90°) of the occipital pole were acquired during visual stimulation using a 7 T whole‐body scanner (Siemens, Erlangen, Germany) and 32 receive channel head coil (Nova Medical, Wilmington, MA). The EPI sequence was modified to accept motion data from the motion‐detection system, convert it from camera to scanner coordinate system, and update the acquisition field of view (FOV) accordingly. This update was done for each acquired slice. The acquisition sequenced logged the motion parameters used for updating the FOV. Slices oriented perpendicular to the calcarine sulcus were acquired for four different scanning conditions, that is, with motion tracked and prospectively corrected by MPT and with motion tracked, but not corrected, and two isotropic spatial resolutions of 2.0³ mm³ (FOV = 180 mm, matrix size 90 × 117, 30 slices) and 0.65³ mm³ (FOV = 130 mm, matrix size 200 × 260, 40 slices). Two scans for each condition were acquired. The sequence in which data for the different conditions were acquired was counterbalanced to reduce sequential effects. Online reconstruction and geometric distortion correction [In and Speck, 2012] were applied to all scans of data.

DATA ANALYSIS

Preprocessing

The functional data were first converted to NIfTI format followed by retrospective realignment in FSL, AFNI, and SPM8. AFNI and SPM8 realignment algorithms use the method of least squares as a cost function. The method relies on finding an affine transformation that minimizes the sum of squares of intensity differences between corresponding voxels in two images. FSL allows users to pick one out of eight different cost functions, the default cost function being normalized mutual information. Therefore, to be consistent with general FSL use and other software packages used in this paper, both the default cost function, that is, normalized mutual information, and the method of least squares were used in FSL motion realignment. Other relevant parameters can be seen in Table 1. To evaluate if there are any effects produced by the retrospective realignment, the functional data were also analyzed without realignment. No slice timing correction and normalization were applied to avoid unnecessary data interpolation.

Table 1.

Information about the motion realignment procedure of the software packages used

Software	Version and/or year	Procedure or function	Reference image	Cost function	Interpolation method	Additional information
SPM	8, 2008	Realign	Mean	Least squares	2nd degree B‐spline	A two‐pass procedure is carried out, where after the first pass, a mean image is calculated and used as a reference image for the second pass.
FSL	5.0, 2012	MCFLIRT	Middle	Least squares	Trilinear	Several cost functions are available but the least squares method was selected for consistency with other packages. A three‐pass procedure is carried out with increasingly stricter tolerances.
AFNI	2012	3dvolreg	First	Weighted least squares	Fourier

Motion Data Analysis

Motion parameters were estimated using FSL (two cost function methods as described above), AFNI, and SPM8 for data which were acquired both with and without MPT motion‐correction. The gold standard motion was provided by the MPT motion tracking system. Six sets of parameters were obtained for each scan and method: three sets of translational and three sets of rotational motion parameters. All data from the different methods were ensured to be compatible with each other, that is, axes were aligned and values were converted to millimeters and radians accordingly. For scans where the MPT system only tracked subject motion without prospective motion‐correction (PMC), correlation coefficients between motion data acquired by MPT motion tracking and estimated retrospectively by above‐mentioned software packages were calculated for each motion parameter. After that, Fisher's z‐transformation was applied to the coefficients, and then they were averaged across resolutions, the two repeat scans at each resolution and three similar parameters, that is, translational and rotational motion, and z‐transformed back for statistical analysis. The z‐transformation was performed to convert the correlation coefficients into a normal distribution. This was performed to evaluate similarity between the reference motion measured by the MPT motion‐correction system and image‐based motion estimation. Also, for all scans, Fourier transformation was applied to the motion parameters to detect any periodic motion. As the activation paradigm had 6 blocks, or cycles, per scan, any motion correlated with the paradigm would also have this periodicity, that is, 6 cycles per scan, and therefore would appear as a peak at the value of 6 in the frequency domain of the Fourier transforms of motion parameters. To quantify it, a normalized Fourier frequency component (FFC) at the value of 6 was calculated as the magnitude of FFC at 6 divided by the square root of sum of squares of FFCs at all other values. These values were calculated for scans acquired with or without PMC applied, and for data retrospectively motion‐realigned by the selected software packaged. Then, the values were averaged across 2 scans and translation or rotational motion parameters.

EPI Data Time Series Analysis

The time series (TS) of the EPI data were analyzed using the Stanford VISTA Tools (VISTA). Each voxel's TS underwent the following analysis: (1) The first four temporal samples of each scan were discarded from the TS to avoid transient onset artifacts; (2) the TS were divided by the voxel's mean intensity; (3) the TS were filtered with a high‐pass cut‐off of 6 cycles/scan; (4) the TS of repeated experiments were averaged; (5) Fourier analysis was applied to the TS to obtain the amplitude and phase for each frequency; and (6) the coherence with a sinusoid of the fundamental frequency of the visual stimulation (1/36 Hz) was calculated [Engel et al., 1997]. The coherence measure is used to determine whether a significant response is obtained. The response phase serves to identify the delay between the signal and the stimulus onset.

ROI Definition and Quantitative Assessment

Using the SPM 8 Masking toolbox, masks were generated to confine the analysis of the echo planar images to the brain region by combining (logical OR) brain masks for each of the different conditions, that is, with or without PMC, and with or without retrospective realignment, manually in Matlab (Mathworks Inc.), for each resolution and subject. The mask creation algorithm is described in Ridgway et al. [2009]. Afterward, to ensure similar coverage of functional data at different spatial resolutions, masks of 22 adjacent slices of 0.65³ mm³ resolution, and 7 slices for 2.0³ mm³ resolution including the visual cortex were selected to be the final ROIs. Visual stimulation creates cortical activity in a specific phase range of the stimulation cycle. Therefore, to extract the brain activation related to the visual stimulation, a phase window was defined with respect to the mean phase of functional data without realignment, i.e., “phase window” (mean phase − π/2, mean phase + π/2) and “anti‐phase window” (mean phase + π/2, mean phase − π/2). For quantitative assessment, before averaging and calculating the standard error of the mean (SEM), the number of activated voxels in each ROI was calculated in the “phase window” and the “anti‐phase window,” as described above. Subsequently, results from different conditions were normalized by dividing the result in the condition with PMC and no retrospective motion realignment applied. Afterward, the normalized results of number of activated voxels, that is, relative activated voxels, were averaged across the subjects for each condition and spatial resolution.

Influence of Field of View and BOLD Signal Strength

The difference in stimulus‐correlated motion between the low‐ and high‐resolution data (Results) prompted further investigation of the influence of the two main differences between the data besides resolution: field of view and BOLD signal strength.

First, we matched the FOV of low‐resolution data to that of high‐resolution data. Brain masks for each resolution were created using the SPM Masking toolbox [Ridgway et al., 2009]. Then, anterior slices were removed one by one from low‐resolution data, until the remaining brain volume was equal to or less than that of the high‐resolution data. The new data were saved as image files, and SPM motion‐realignment was performed on this low‐resolution data with reduced FOV.

Second, we downsampled the high‐resolution data to several lower isotropic resolutions of 0.85³, 1.1³, 1.5³, and 2.0³ mm³ using the image resizing script from the SPM VBM toolbox. Then, SPM motion‐realignment was performed on the downsampled data. To investigate the dependence of BOLD signal strength on the downsampled resolution, the downsampled EPI data were analyzed using the Stanford VISTA Tools, and fMRI activation amplitudes were calculated for each downsampled resolution.

RESULTS

Figure 1 shows the correlation coefficient analysis results for all subjects. The correlation coefficients were calculated as described above: the true motion was measured by the MPT motion‐detection system and the estimated motion was calculated by selected software packages. In Figure 1, each bar represents the average over 2 resolutions, 2 scans, and 3 motion parameters for either translational or rotational motion for each of the 4 retrospective motion correction methods. The results show that both FSL cost‐function methods and AFNI‐evaluated motion parameters are in good agreement with each other and data measured by the MPT motion correction system. The AFNI motion data show slightly higher correlation with the reference motion data. However, motion data calculated by SPM8 consistently show noticeably lower correlation with the reference motion data.

Figure 1.

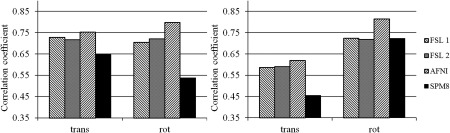
Correlation coefficients for subjects 1 (left) and 2 (right). The coefficients were calculated for correlation between motion parameters recorded by the prospective motion correction system and those estimated by retrospective motion correction from different software packages. Each bar is the average across 3 coefficients, that is, for translational motion parameters (left group) and rotational (right group), 2 scans, and 2 resolutions. Different colors correspond to different software packages used for motion realignment, with FSL 1 and 2 being FSL package using the default normalized mutual information and least squares methods, respectively.

At the time the data were collected, processed, and analyzed, we have not yet made the transition to SPM12 and used SPM8 for fMRI processing and analysis. When we decided that it was time to move on to SPM12, motion‐realignment was rerun using the newer version of SPM. Motion plots looked similar to those obtained by SPM8. More importantly, SPM12 motion realignment data exhibited the same behavior as SPM8, that is, correlation with the visual stimulus, as described below. Therefore, it was deemed unnecessary to redo all fMRI processing and analysis in SPM12.

Furthermore, Fourier transformed motion parameters show a peak at the value of 6 (corresponding to the frequency of 6/36 Hz) in the frequency domain, corresponding to the visual stimulus frequency of 6 cycles per scan, for SPM8. Figure 2 shows the Fourier‐transformed motion parameters in the frequency domain for high‐resolution scan of one of the subjects. The motion parameters were estimated by FSL, AFNI, and SPM8 (columns 1–3 correspondingly), and results for both translational and rotational motion are displayed (top and bottom rows correspondingly). To evaluate the significance of this finding, normalized FFCs were calculated for this value. Figures 3 and 4 show the results for one subject for resolutions of 0.65³ and 2.0³ mm³, respectively. Figure 3 demonstrates that motion parameters evaluated by SPM8 from data acquired at very high spatial resolution of 0.65³ mm³ exhibit significantly higher task‐related motion than motion parameters acquired with MPT motion tracking system or FSL and AFNI motion correction. This effect is independent of whether MPT motion‐correction was on, and therefore, data only had small residual motion, or MPT motion‐correction was not performed and data represented original subject motion. Figure 4 also shows that stimulus‐correlated motion is introduced only in motion realignment of very high‐resolution data.

Figure 2.

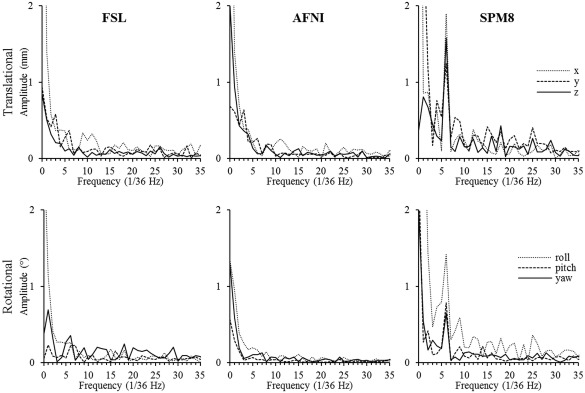
Fourier‐transformed motion parameters for one of the high‐resolution scans of one of the subjects. The parameters are estimated by FSL (left), AFNI (mid), and SPM8 (right), and both translational (top) and rotational (bottom) are shown. Note the peak at the stimulation frequency (6/36 Hz) for SPM8.

Figure 3.

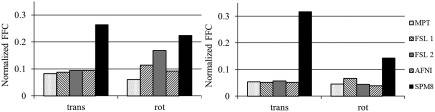
Normalized Fourier frequency components for one of the subjects. The data are from scans acquired at 0.65³ mm³ resolution with MPT‐based motion‐correction turned on (left graph) and off (right graph). The values were calculated as FFC at 6 (number of stimulation cycles per scan) divided by the square root of sum of squares of all FFCs, and averaged across 2 scans and translation or rotational parameters.

Figure 4.

Normalized Fourier frequency components for the same subject as in Figure 3. The data are from scans acquired at 2.0³ mm³ resolution with MPT motion‐correction turned on (left graph) and off (right graph). The values were calculated as FFC at 6 (number of stimulation cycles per scan) divided by the square root of sum of squares of all FFCs, and averaged across 2 scans and translation or rotational parameters.

To summarize, out of four different retrospective motion correction methods performed by FSL (two different cost function methods), AFNI, and SPM8, only motion parameters obtained by SPM8 showed significant periodic motion. Motion parameters obtained by FSL and AFNI corresponded to the reference motion, obtained by MPT tracking. Further Fourier analysis showed that only SPM8 motion parameters exhibited a prominent peak at the value of 6, which corresponds to the stimulation frequency. Therefore, it can be concluded that only SPM8 detects false task‐correlated motion. To scrutinize this effect, further fMRI analysis and quantifications were conducted for the data realigned in SPM8 and compared to those for the data acquired with MPT motion correction.

For a qualitative assessment of the effects of retrospective alignment in SPM8, the functional activation maps are overlaid onto the EPI planes in Figure 5 for different conditions, that is, for acquisitions with and without prospective motion correction by MPT and with and without retrospective realignment in SPM8. For this purpose, false‐color‐coded phase maps are overlaid onto EPI planes with spatial resolutions of 0.65³ mm³ (Rows 1 and 2) and 2.00³ mm³ (Rows 3 and 4), for a coherence threshold of 0.40, corresponding to a significance level of P ≤ 0.00025. The phase range comprises 0 to 2 π, that is, 360° (36 s). Response‐phases centered on 0.5 radians, that is, color‐coded red to yellow, indicate responses following stimulus onset. This phase range dominates for the data without retrospective realignment. In contrast, for retrospective realignment, additional responses were observed, that were, on average, 1 π (i.e., 180° = 16 s) shifted relative to the stimulus induced responses (color‐coded blue). To further emphasize the effect of motion realignment, the extent of activation in the phase and antiphase windows, as specified above, was quantified both for scans acquired with prospective MPT motion‐correction on and off before and after the retrospective motion realignment. Figure 6 shows the results for one of the subjects for both high‐ and low‐resolution data. The results show that motion realignment increases the number of activated voxels both in phase and antiphase windows. While some increase is expected due to unavoidable smoothing due to image reslicing interpolation, antiphase window gained considerably more activated voxels, than the phase window.

Figure 5.

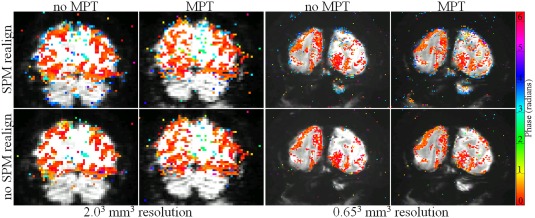
Comparison of phase maps overlaid on averaged EPIs. False‐color coded phase‐map‐overlays onto one EPI‐plane obtained at spatial resolutions of 2.00³ mm³ (left group of panels) and 0.65³ mm³ (right group of panels), for a coherence threshold of 0.40, corresponding to a significance level of P ≤ 0.00025. Data sets were preprocessed with or without retrospective realignment in SPM 8 (top and bottom rows correspondingly). The ones in the left column are without MPT‐based prospective motion correction; in the right with prospective motion correction. The color phase bar, phase of stimulation and driven response are encoded with orange–yellow. It should be noted that 1 π shifted (blue) responses are more evident after realignment, especially for 0.65³ mm³ resolution. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 6.

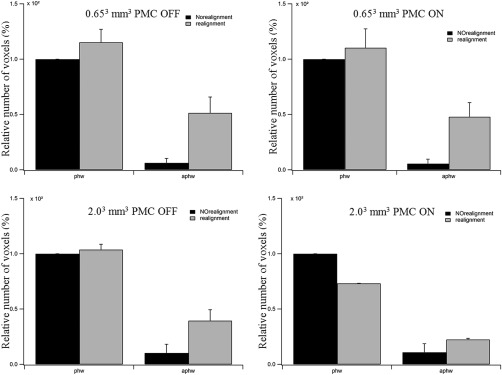
Number of relative activated voxels in phase and antiphase windows (left and right pair in each graph) for data acquired with prospective motion correction (PMC) off (1st row) and on (2nd row) for low (left) and high (right) resolutions before (black bars) and after (white bars) retrospective motion realignment.

The actual time courses of the responses are depicted in Figure 7. Here, parts of the activation maps with a spatial resolution of 0.65³ mm³ from Figure 5 are depicted. Two regions of interest (ROI) were defined on the phase map in Row 1: ROI 1 is a group of pixels, that are color coded blue and therefore do not reflect responses that follow the stimulus onset, and ROI 2 is a group of pixels, that are color coded red to yellow and therefore reflect responses that follow the stimulus onset. These two ROIs were applied to the other three conditions. Subsequently, the time series (TS) of these two ROIs were extracted and depicted in Figure 7. In ROI 2, time courses with six cycles of sizable signal modulation, that is, at the stimulation frequency, were obtained for all four conditions. In contrast, in ROI 2, time courses showed sizable signal modulation at the stimulation frequency only for the conditions with retrospective realignment. Importantly, their response phase is shifted with respect to the responses observed without realignment. This is further underlined by the time series obtained as the average across the six stimulation cycles. Retrospective realignment is thus demonstrated to introduce additional signal modulations. It should be noted that these are most obvious, but not restricted to response phases that are shifted by 180° to the response that follows stimulus onset. This is evident from the inspection of the response signatures in the cerebellum in Figure 7, which is expected to comprise no visually induced responses. Accordingly, superthreshold responses are mainly evident for the conditions with retrospective realignment. Importantly, these false‐positive activations are present in both response phase ranges.

Figure 7.

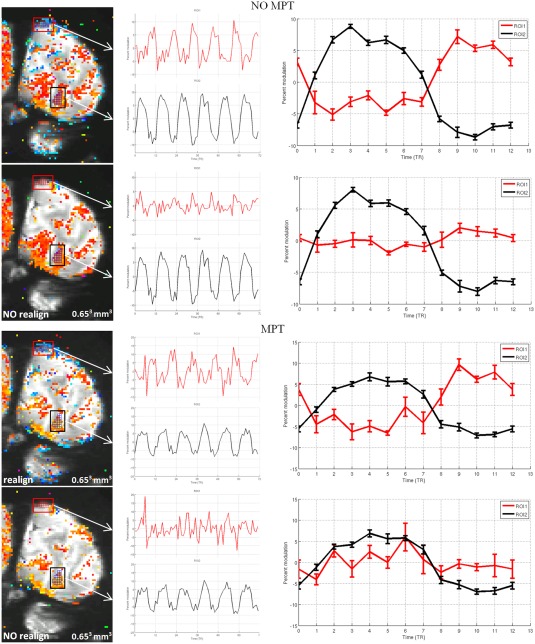
Time series (TS) comparison for high‐resolution data. In Rows 1 and 2, the phase maps generated from data without prospective motion correction by MPT were preprocessed with and without retrospective realignment by SPM 8, respectively; in Rows 3 and 4, the phase maps generated from functional data with prospective motion correction by MPT, preprocessed with and without realignment by SPM 8, respectively. Two regions of interest (ROI1 and ROI2) were defined on the activation map in Row 1. The TS of the two ROIs through cycles and average TS are plotted, respectively; threshold: 0.40, corresponding to a significance level of P ≤ 0.00025. [Color figure can be viewed at http://wileyonlinelibrary.com]

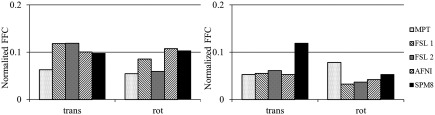
The results of the additional investigation into the influence of FOV and BOLD signal strength are as follows. After the reduction of FOV, low‐resolution data started exhibiting behavior similar to that of high‐resolution data, that is, motion plots, as estimated by SPM motion‐realignment procedure, showed periodic stimulus‐correlated motion. Figure 8 shows the motion‐realignment data for one of the low‐resolution scans of one of the subjects before and after the reduction of FOV. To quantify the results, motion data were Fourier transformed and normalized FFCs corresponding to the stimulus frequency were calculated as described above. Figure 9 shows the normalized FFCs for both subjects for data acquired with and without PMC. The values presented are averaged over 4 scans (2 with PMC and 2 without PMC) and 6 parameters (translational and rotational).

Figure 8.

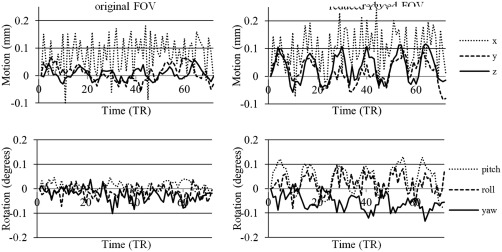
Motion‐realignment plots before (left) and after (right) reduction of FOV of low‐resolution 2³ mm³ data for one of the subjects (translational (top) and rotational (bottom) motion).

Figure 9.

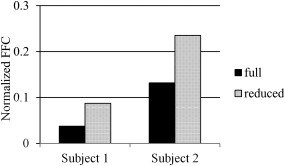
Fourier analysis results of motion‐realignment parameters for subject 1 (left) and 2 (right). Full (solid black) is the original low‐resolution data and reduced (dotted) is the low‐resolution data with reduced FOV to match that of high‐resolution data. Values are normalized Fourier frequency components corresponding to stimulus frequency averaged over 4 scans (2 with PMC and 2 without PMC) and 6 parameters (translational and rotational).

Downsampling the high‐resolution data had very little effect on motion‐realignment results. Figure 10 shows the motion plots for one of the subject's original high‐resolution data and most downsampled data, that is, 2.0³ mm³ data. All motion plots, both the original and all the downsampled data, showed very minor differences. This shows that resolution has little to no influence on the effect.

Figure 10.

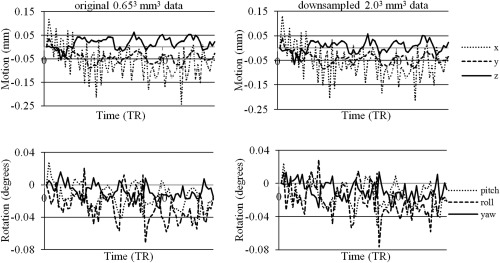
Motionz‐realignment plots before (left) and after (right) downsampling of high‐resolution 0.65³ mm³ data to the lowest resolution of 2.0³ mm³ for one of the subjects (translational (top) and rotational (bottom) motion).

To evaluate how downsampling affected BOLD signal strength, the downsampled data were analyzed with Stanford VISTA tools and average amplitudes were calculated. Figure 11 shows the average amplitude versus the number of voxels with highest amplitude for resolution from the original 0.65³ mm³ down to 2.0³ mm³. We can see that BOLD signal strength consistently decreases with decreasing resolution. This shows that even though high‐resolution data had stronger BOLD signal strength, it did not cause motion‐realignment corruption and introduction of stimulus‐correlated motion.

Figure 11.

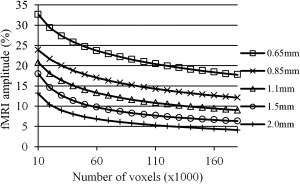
Activation amplitude calculation for the original high‐resolution 0.65³ mm³ and downsampled to 0.85³, 1.1³, 1.5³, and 2.0³ mm³ data. Amplitude is calculated by Stanford VISTA tools, and averages over varying number of maximum‐amplitude voxels are plotted for each resolution for one of the subjects.

DISCUSSION

In this study, three different software tools widely used for fMRI processing and analyses were tested with regards to motion realignment. Their results were compared with motion data obtained from an optical MPT motion‐correction system, which is independent of the acquired images and can be considered reference motion data. FSL—applied with two different cost function methods—and AFNI estimated motion parameters from the image data which correlated well with those obtained with the MPT system, and correlated better than those estimated by SPM8. Further Fourier analyses of motion parameters, calculated by SPM8, showed a large peak at the stimulus frequency of 6/36 Hz. Subsequent fMRI phase‐map analyses showed that more brain activity was detected at the edges of the brain after the data underwent motion‐realignment in SPM8. Also, brain activity was reduced after applying realignment to the images.

Even though we were not able to determine the reason why motion‐realignment performed by SPM8 produced results so drastically different from those by FSL and AFNI, we can speculate how such results occurred, based on the subsequent analyses. We have acquired data at two very different resolutions: 2.0³ and 0.65³ mm³ isotropic voxel sizes. However, the difference is not as simple as the voxel volume. First, smaller voxel size reduces partial volume effect due to more voxels containing homogeneous brain tissue, for example, gray matter only. It has been shown that decreasing voxel size increased BOLD signal changes as a result of reduced partial voluming in areas of interest [Frahm et al., 1993]. Another advantage of smaller voxel size comes from reducing the effect of physiological noise on time‐series SNR (tSNR), and therefore BOLD contrast. It was demonstrated that tSNR dependence on voxel size asymptotically reaches a limit at large voxel sizes, as physiological noise, rather than thermal noise, starts to dominate [Triantafyllou et al., 2005]. As a consequence, BOLD contrast scales nonlinearly with smaller voxel sizes, as increased BOLD signal—due to, for example, stronger magnetic field or less partial volume effect—becomes more prominent with decreased influence of physiological noise [Yakupov and Speck, 2011]. Second, the required TR imposed a strict limit on the maximum number of acquired slices. This, combined with thinner slices at the higher resolution, resulted in the reduction of acquired brain volume. The two above‐mentioned effects result in significant part of the acquired volume having changes in voxel intensity not caused by head motion. This violates the assumption that head motion can be described by 6‐degrees‐of‐freedom rigid‐body transformation with residual differences attributed to negligible noise. As has been shown previously in computer simulations [Freire et al., 2001] and as it was demonstrated in this study, violation of this assumption leads to motion‐realignment algorithms treating intensity changes due to brain activity as if they came from head motion. Increasing the size of the acquired volume might alleviate the problem, due to larger portion of the brain with no task‐related signal intensity changes counterbalancing the smaller activated areas. However, such limited brain coverage was not by choice, but rather due to strict TR limitations dictating the size of the area that can be imaged.

In our study, we attempted to separate these two effects, that is, increased BOLD effect (due to reduced partial volume effect and stronger signal at ultrahigh field strength of 7 T) and reduced brain coverage, and determine which one dominates the effect, if any. Reducing the FOV of low‐resolution data to match that of high‐resolution data introduced stimulus‐correlated spurious motion, as estimated by SPM8 motion‐realignment step. This shows that the brain volume scanned, or rather the relative volume of activated brain tissue, plays a significant role in the effect. Our attempt to produce data at different resolutions by downsampling high‐resolution data shows that even though activation amplitudes consistently decreased with lower resolution, they had very little effect on motion‐realignment parameters estimated by SPM8. This shows that acquisition resolution may have only limited effect on the fidelity of motion‐realignment. The downsampling approach has its advantages and disadvantages. The disadvantage is that actual low‐resolution data will have stronger influence of physiological noise and signal dephasing across the voxel, and therefore amplitude dependence on voxel size will be stronger than for downsampled data. The advantage is that for downsampled data, the subject motion is exactly the same for all data sets, while we have no control over subject motion if each data set at different resolution is acquired in a different scan. However, since downsampling the data—while noticeable reducing activation amplitudes—had little influence on motion‐realignment fidelity, we can speculate that actual data with even stronger dependence of amplitude on voxel size might still contribute little to the effect.

Recent development of various simultaneous multislice imaging techniques [Breuer et al., 2005; Moeller et al., 2010; Setsompop et al., 2012] can help resolve this issue. Using such techniques, it is possible to acquire whole‐brain EPI images at high resolution with reasonable repetition time. It will then be easy to separate the effect of small acquisition volume and high resolution by acquiring the data with whole‐brain and limited coverage at the same high resolution.

Different fMRI preprocessing and analysis software tools have been compared in previous studies with regards to their motion‐correction performance [Oakes et al., 2005]. The conclusion was that motion correction improves the results of fMRI analysis, and that the choice of the software package does not substantially affect this improvement. As evidenced by our study, however, this is not the case in some specific cases, for example, limited brain coverage acquired with ultrahigh resolution. The main conclusion of our study is that motion‐realignment, as performed by SPM8, can introduce spurious motion, which is highly correlated with the stimulus if the volume coverage is too small. As a result, “true” brain activity has lower significance due to increased temporal variation of the time course, as signal coming from the same voxel no longer corresponds to the same location in the brain, and false‐positive brain activity is determined in regions with high intensity gradients, for example, brain edges. SPM8 motion‐realignment offers several options that are adjustable to the user's preference. The motion‐realignment was tested with options aimed at improved motion‐realignment quality, namely quality parameter of 1, smaller separation between points sampled in the image, realigning to the first or the mean image of the series, bigger smoothing kernel size and higher degree B‐spline interpolation. However, changing those options did not change the result—estimated motion parameters still showed a periodic component correlated with the stimulus. The reason why only SPM8, but not FSL and AFNI, produces this effect was not determined and more investigation on this discrepancy is required in the future. Stronger signal changes in larger parts of acquired brain volumes violates the assumption of motion modeled as rigid‐body 6‐DOF transformation, and obviously the motion‐realignment procedure, as performed by SPM, is not as robust to this violation as FSL or AFNI. Maybe future versions of SPM will address this issue. As we tested all customizable settings of SPM8 motion‐realignment procedure, we can only speculate that the difference in the motion‐correction performance lies in the processing pipelines or implementation of algorithms. The main differences between the processing packages are interpolation methods, reference volume and the pipeline, that is, what and how many stages are performed. Smoothing of the data before estimation is performed by all three packages. While AFNI uses Fourier interpolation by default, SPM8 uses a more accurate higher degree (2^nd‐degree B‐spline) interpolation than FSL (trilinear, equivalent of 1^st‐degree B‐spline). Even tested higher degrees of interpolation did not affect the outcome; therefore, it is unlikely caused by the interpolation method. FSL by default registers to the mid volume, while AFNI to the first volume. SPM8 uses a mean volume as the reference. While it is unlikely that the choice of reference volume would change estimated motion parameters much, other than add a corresponding displacement to all estimated values, we tested SPM8 motion correction with the first volume as the reference with the same result. The most obvious difference between the software packages' processing pipelines at the default settings, the only ones tested for FSL and AFNI, is that FSL performs a three‐stage procedure with a first course estimation and then two finer estimations of the motion parameters, but SPM8 does two stages and AFNI just one. An additional stage may be configured for FSL or AFNI. We thus believe that the number of stages is unlikely the cause for the differences. It seems that a more in‐depth investigation examining and comparing the data after each intermediate calculation may provide further insight, but this is complicated by the fact that, even though SPM8 is a collection of Matlab scripts and it might be possible to save and examine the data after each intermediate step, FSL and AFNI only save the final result. As of this moment, therefore, we recommend to thoroughly examine the results of motion realignment performed by SPM on data acquired with limited brain coverage.

Investigating the fine structure of cortical activation has a long history. Human ocular dominance columns were successfully detected with fMRI more than a decade ago [Cheng et al., 2001; Menon et al., 1997]. However, it was not an easy task and required additional preparation, for example, custom‐designed and made surface coils [Cheng et al., 2001; Menon et al., 1997]. Recent developments in hardware and acquisition methods, wider availability of high‐field MRI systems, and broader application of ultra‐high‐resolution fMRI, for example, for detecting layer‐specific BOLD activation [Koopmans et al., 2010, 2011], will make the use of ultra‐high‐resolution fMRI more widespread. To date, a number of studies have been carried out using ultra‐high sub‐millimeter‐resolution fMRI [Menon et al., 1997; Cheng et al., 2001; Koopmans et al., 2010, 2011; Yacoub et al., 2003, 2007]. It has been demonstrated that motion‐realignment could considerably improve the magnitude and extent of detected activations [Oakes et al., 2005]. Even though in many studies varying steps were taken to address subject motion, for example, extrapadding or head‐fixation devices to minimize it [Cheng et al., 2001; Menon et al., 1997; Yacoub et al., 2003], or more careful approach to the problem of subject motion in general [Yacoub et al., 2003], it is impossible to completely avoid the subject motion. This leads to the need for retrospective motion correction in the absence of prospective non‐image‐based motion‐correction system. Not all studies have the conditions, that is, small fields of view and ultra‐high resolution, under which we have observed the problem of spurious brain activations caused by motion realignment, some studies will have these conditions due to acquisition sequence used, for example, 3D GRASE [De Martino et al., 2013; Kemper et al., 2015], in which case problems with retrospective motion‐correction may arise, and it should be approached carefully. As prospective motion correction methods are not yet wide‐spread, the need for accurate and robust methods for retrospective motion‐realignment of limited coverage and ultra‐high‐resolution data could become a new challenge for motion correction in fMRI.