Noise Effects in Various Quantitative Susceptibility Mapping Methods

Abstract

Various regularization methods have been proposed for single-orientation quantitative susceptibility mapping (QSM), which is an ill-posed magnetic field to susceptibility source inverse problem. Noise amplification, a major issue in inverse problems, manifests as streaking artifacts and quantification errors in QSM and has not been comparatively evaluated in these algorithms. In this paper, various QSM methods were systematically categorized for noise analysis. Six representative QSM methods were selected from four categories: two non-Bayesian methods with alteration or approximation of the dipole kernel to overcome the ill conditioning; four Bayesian methods using a general mathematical prior or a specific physical structure prior to select a unique solution, and using a data fidelity term with or without noise weighting. The effects of noise in these QSM methods were evaluated by reconstruction errors in simulation and image quality in 50 consecutive human subjects. Bayesian QSM methods with noise weighting consistently reduced root mean squared errors in numerical simulations and increased image quality scores in the human brain images, when compared to non-Bayesian methods and to corresponding Bayesian methods without noise weighting (p ≤ 0.001). In summary, noise effects in QSM can be reduced using Bayesian methods with proper noise weighting.

I. INTRODUCTION

QUANTITATIVE susceptibility mapping (QSM) has received a lot of scientific interest, as it can quantify a range of endogenous magnetic biomarkers and contrast agents such as iron, calcium, and gadolinium (Gd) [1]–[4]. It has been realized that QSM is a technically challenging ill-posed inverse problem because it is necessary to deconvolve the measured tissue magnetic field with the unit magnetic dipole field (dipole kernel) that has zeroes at the magic angle 54.7° in k-space [5]–[7]. While multiple orientations can be sampled by repositioning the subject to condition the inverse problem [8], the only clinically acceptable solution is to scan the patient in the neutral position. To develop a clinical QSM method using a single orientation, various regularization methods have been proposed to identify a unique bulk susceptibility map [1], [2], [9]–[16].

It should be noted that near the zeros of the k-space dipole kernel are infinitesimally small values, which cause noise amplification upon inversion, a major concern of an ill-conditioned inverse problem. This noise amplification should be an important consideration in developing QSM methods. However, noise effects in various QSM methods are often not analyzed.

In this study, we aim to methodically analyze QSM algorithms in terms of their treatment of noise in the data fidelity term and their choice of prior. We evaluate noise effects in representative QSM methods using a numerical phantom mimicking the human brain with a known susceptibility distribution and using in vivo human brain data with QSM image quality retrospectively assessed by the four experienced radiologists.

II. THEORY

A. Magnetic Resonance Imaging Signal Model for the Tissue Magnetism

The magnetic field controls the spin precession, which determines the magnetic resonance imaging (MRI) signal phase, permitting the estimation of the tissue magnetic field [17]–[20]. Notations used in the following derivation are summarized in Table I. The magnetic field perturbation due to the magnetic susceptibility distribution relative to the MRI main magnetic field B₀, δ_b(r) (r the spatial location) can be modeled as the convolution of the tissue magnetic susceptibility distribution χ(r) with the magnetic field of a unit dipole d(r) = (1/4π)(3cos²θ_r−1)/|r|³ (referred to as the dipole kernel, |r| > 0, θ_r is the azimuthal angle of r in the spherical coordinate) [21], plus noise n(r) in the estimated field.

$${\mathit{\delta }}_b=\mathit{d}\ast \mathit{\chi }+\mathit{n}$$ (1)

where r has been omitted for clarity and ∗ is the convolution symbol. This signal model for magnetic field and susceptibility can also be expressed in k-space as

$${\mathbf{\Delta }}_b=\mathit{D}X+\mathit{N}$$ (2)

where Δ_b = Fδ_b, F is the Fourier transform operator, X = Fχ, N = Fn, and $\mathit{D}=\mathit{F}\mathit{d}=\left(1/3-k_z^2/{\left|\mathbf{k}\right|}^2\right)$. Here, k_z denotes the Fourier space coordinate in the direction parallel to B₀ [5]–[7].

TABLE I.

Notations

Symbol	Meaning
r	spatial (r-space) location
k	spatial frequency (k-space) location
δb	δb(r), magnetic field in r-space
d	d(r), dipole kernel in r-space
χ	χ(r), susceptibility distribution in r-space
n	n(r), noise in r-space
F	Fourier transform operator
Δb	Δb(k), magnetic field in k-space
D	D(k), dipole kernel in k-space
X	X(k), susceptibility distribution in k-space
N	N(k), noise in k-space
E	data fidelity term
w	noise weighting
τ	predetermined k-space threshold
α,β	regularization parameter
R	regularization term
P	specific physical structure prior
m	edge mask

The dipole kernel (d or D) has a nontrivial null space where D = 0, which consists of a pair of opposing cone surfaces at the magic angle (54.7°) with respect to the B₀ direction. In addition, D has values that are infinitesimal in the vicinity of the cone surfaces, which will lead to large noise amplification upon inversion.

B. Noise Consideration

If the noise n had a uniform variance in space and could be modeled by independent and identically distributed Gaussian random variables, a statistically optimal solution is the maximum likelihood estimation, which can be found by minimizing a quadratic data fidelity term

$$E={\Vert \mathit{z}\Vert }_2^2,\text{with }\mathit{z}=\mathit{d}\ast \mathit{\chi }-{\mathit{\delta }}_b.$$ (3)

However, only noise in the real and imaginary parts of the MR signal can be modeled as zero mean Gaussian noise [22]–[26]. The noise n in the magnetic field δ_b in (1) estimated from the MRI signal phase has a complex probability distribution that can be approximated as Gaussian only when the SNR is much larger than 1 [22]–[24]. Moreover, this estimated Gaussian noise is not spatially uniform since its variance is equal to the square of the inverse of the SNR [22]–[24]. Accordingly, the data fidelity term in the Bayesian QSM methods should account for the Gaussian noise in the real and imaginary channels of the detected MR signal, which leads to a data fidelity term nonlinear in the estimated magnetic field δ_b and the unknown susceptibility χ [27].

$$E={\Vert \mathit{w}{\mathit{z}}_n\Vert }_2^2,\text{with }{\mathit{z}}_n=\text{exp}[-i(\mathit{d}\ast \mathit{\chi })]-\text{exp}(-i{\mathit{\delta }}_b)$$ (4)

which we refer to as the data fidelity term with noise weighting, w denoting the proper noise weighting, e.g., SNR at the voxel in a single echo acquisition, or calculated SNR [13]. In the following comparisons, the data fidelity term in (3) is referred to as without noise weighting, as it simply uses the standard least squares formula without considering the noise property of the data.

C. Algorithms for QSM Reconstruction

Here, we summarize various QSM algorithms according to the manner in which a unique susceptibility solution is identified.

1) Non-Bayesian Methods by Altering the Indeterminate Field-to-Kernel Ratio (Kernel Alteration)

In this category, the susceptibility map X in k-space is produced by dividing Δ_b by an altered kernel. An example is the k-space division method [9]–[11], [28] with truncation, referred to here as truncated k-space division (TKD) [9]. The altered kernel in TKD is set as sign(D)τ (τ is a small predetermined threshold) when |D| < τ and D as itself when |D| ≥ τ. The susceptibility solution of the TKD algorithm is

$$\mathit{X}=\mathit{H}{\mathbf{\Delta }}_b/\mathit{D}+(1-\mathit{H})\text{sign}(\mathit{D}){\mathbf{\Delta }}_b/\tau .$$ (5)

Here, H is equal to one in the |D| ≥ τ region and zero in the |D| < τ region in k-space.

2) Non-Bayesian Methods by Evaluating the Indeterminate Field-to-Kernel Ratio (Kernel Evaluation)

An example of this type of method is to take the partial derivative of both the susceptibility and the dipole kernel in a small neighborhood around the cone surface before division takes place. By applying L’Hospital’s rule, the indeterminate field-to-kernel ratio becomes determinate and can be evaluated around the cone surfaces, which is then used to solve for the susceptibility around the cone surfaces. This method is referred to as the weighted k-space derivative (WKD) [12]. WKD is formulated as a least-square fitting algorithm:

$$\mathit{X}=\mathit{H}\cdot \text{arg}min{\Vert \mathit{Z}\Vert }_2^2+(1-\mathit{H})\text{arg}min{\Vert {\mathit{M}}_{D3}{\mathit{Z}}^{\prime }\Vert }_2^2.$$ (6)

Here, Z = Δ_b − DX, and ${\mathit{Z}}^{\prime }={\mathbf{\Delta }}_b^{\prime }-{\mathit{D}}^{\prime }\mathit{X}-\mathit{D}{\mathit{X}}^{\prime }$; M_D3 is an empirical smooth weighting function that decays to zero at the k-space origin where D′ is ill defined [12].

3) Bayesian Methods Using a General Mathematical Prior

The Bayesian approach can be used to specify the input data (the likelihood) and for implementing the regularization term (the prior). Deconvolution of the input magnetic field as expressed in (1) and (2) bears similarity to those in super-resolution image reconstruction, where input image data are subsampled, warped, blurred, and noisy [29], [30]. Regularization methods using prior information, particularly those from the Bayesian stochastic approach, can be used to derive a unique estimate of the susceptibility.

General mathematical priors can be used to select a unique solution for the susceptibility map. Typically, the regularization prior is expressed as a cost function R that exponentially favors a solution with a desired property, and the degree to which it is favored is typically characterized by a regularization parameter α. Therefore, in the Bayesian approach, the maximum a posterior solution is

$$\mathit{\chi }=\text{arg}min(E+\alpha R).$$ (7)

Here, E is a data fidelity term such as in (3) and (4), which expresses the susceptibility source and magnetic field relationship with a specific noise distribution [13], [14], [16], [27], [31], [32]. Various regularization terms R have been explored for QSM, including 1) spatial smoothness expressed in the L2 norm of the gradient (G) (GL2) (Tikhonov regularization) [13], [16]; 2) sparsity expressed in the L1 norm of the gradient (GL1) [13]; 3) sparsity expressed in the total variation (TV) norm [14], [33]; 4) sparsity expressed in a wavelet domain such as a Daubechies wavelet(Φ) [14]; 5) a combination of two sparsity terms such as total variation and wavelet (TV&WA) [14].

$$\alpha R\to \alpha {\Vert {\mathbf{\Phi }}_{\mathit{\chi }}\Vert }_1+\beta \text{TV}(\mathit{\chi }).$$ (8)

4) Bayesian Methods Using Specific Physical Structure Prior

A prior specific to a physical situation P can be used in the regularization term. The solution is as follows:

$$\mathit{\chi }=\text{arg}min(E+\alpha P).$$ (9)

An example for incorporating specific anatomic information in QSM reconstruction is the morphology enabled dipole inversion (MEDI) algorithm [15]–[27], [31]. An edge mask m can be generated from the gradient of a known anatomical image, such as the gradient echo (GRE) magnitude image acquired with the phase data to weigh the edges in the susceptibility solution candidates [15], [27], [31], [32]. It has been proven that this formulation is able to exactly recover the susceptibility distribution given an accurate prior [34]. The L1 norm minimization of such a weighted gradient formulates the cost function of the MEDI algorithm [31]

$$P={\Vert \mathit{m}{\mathit{G}}_{\mathit{\chi }}\Vert }_1.$$ (10)

III. Material and Methods

A. Methods Performed in This Paper

As we cannot exhaustively evaluate all published QSM algorithms, we selected algorithms representing each of the categories. The TKD (5) and WKD (6) were selected as the representatives of categories I and II. The TKD was chosen because it is a widely adopted k-space QSM method. The WKD is currently the only kernel evaluation method.

In categories III and IV, the regularization terms in (8) and (10) were selected. Equation (8) was chosen because it bears a high degree of similarity to the formulation in compressed sensing, which is also an active research field, and (8) is easily extended to the other forms of regularization in category III. Equation (10) was chosen because it was the first L1-based QSM method utilizing structural consistency in category IV. The same regularization term in (8) or (10) in conjunction with the data fidelity term (4) with or (3) without noise weighting were selected to study any benefits of noise weighting. Accordingly, these four additional methods were selected: TVWA (TV and WA), NTVWA (nonlinear TVWA), MGL1 (Morphology enabled GL1), and NMEDI (nonlinear MEDI). The exact formulations of the methods are: $\text{TVWA}\left(\mathit{\chi }=\text{arg}min\left({\Vert \mathit{z}\Vert }_2^2+\alpha {\Vert \mathbf{\Phi }\mathit{\chi }\Vert }_1+\beta TV(\mathit{\chi })\right)\right)$, $\text{NTVWA}(\mathit{\chi }=\text{arg}min({\Vert \mathit{w}{\mathit{z}}_n\Vert }_2^2+\alpha {\Vert \mathbf{\Phi }\mathit{\chi }\Vert }_1+\beta TV(\mathit{\chi })))$, $\text{MGL}1(\mathit{\chi }=\text{arg}min({\Vert \mathit{z}\Vert }_2^2+\alpha {\Vert \mathit{m}\mathit{G}\chi \Vert }_1))$, and $\text{NMEDI}(\mathit{\chi }=\text{arg}min({\Vert \mathit{w}{\mathit{z}}_n\Vert }_2^2+\alpha {\Vert \mathit{m}\mathit{G}\chi \Vert }_1))$

Note that TKD, WKD, TVWA, and MGL1 do not use any noise weighting, while NTVWA and NMEDI account for Gaussian noise in complex MRI data. Here, MGL1 is not called MEDI, which is referred to as the algorithm accounting for Gaussian noise in phase data, $\mathit{\chi }=\text{arg}min({\Vert \mathit{w}\mathit{z}\Vert }_2^2+\alpha {\Vert \mathit{m}\mathit{G}\chi \Vert }_1)$.

B. Human Brain Simulation

A 256 × 256 × 128 Zubal-type [35] numerical phantom (see Fig. 1) was constructed with an additional “lesion.” The simulated susceptibility values were 0.08, 0.19, 0.10, 0.29, 0.06, −0.05, 0.04, 0.90, and 0.00 ppm for the caudate nucleus, globus pallidus, putamen, veins, thalamus, white matter, gray matter, lesion, and other parenchyma, respectively [12], [15], [27]. The field perturbation of the model was calculated by fast forward field computation [5]–[7] (B₀ = 3 T in superior–inferior direction) and converted to GRE phase values at TE = 20 ms. The noise standard deviation was set as one arbitrary unit (a.u.) and signal intensities were set to 1 a.u. in the lesion, and 68, 48, 71, 69, 78, 80, 92, 80 a.u. for the caudate nucleus, globus pallidus, putamen, veins, thalamus, white matter, gray matter, and other parenchyma, respectively. These values were empirically determined from in vivo human brain scans. The noise is simulated in real parts and imaginary parts independently [27], [31].

Fig. 1.

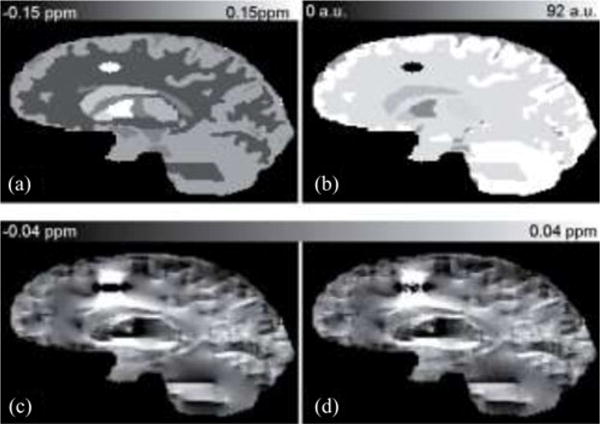
Human brain simulation. (a) True susceptibility map and (b) Magnitude image are shown in the top row. (c)Noiseless field map and (d) Noisy field map are shown in the bottom row.

The effect of noise was investigated by comparing reconstructions between noiseless and noisy data for methods without noise weighting: TKD, WKD, TVWA, and MGL1. The effect of noise weighting was investigated through comparisons between constructions of the noisy data with and without noise weighting in TVWA versus NTVWA and MGL1 versus NMEDI.

C. In Vivo Brain Imaging

The human study was approved by our Institutional Review Board. Thirty consecutive MR brain cases without hemorrhagic lesions (group 1, n = 30) and 20 consecutive MR brain cases with hemorrhages (group 2, n = 20) were used for this study. MR examinations were performed with a 3.0-T MR system (Signa HDxt, GE, USA), using an eight-channel head coil. A 3-D T2∗ weighted multiecho GRE sequence was used with the following parameters: FA = 20°; TR = 57 ms; number of TEs = 8; first TE = 5.7 ms; uniform TE spacing (ΔTE) = 6.7 ms; BW = ± 41.67 kHz; field of view = 24 cm; a range of resolutions were tested: 0.57 mm × 0.75 mm × 3 mm (n = 41), 0.57 mm × 0.75 mm × 2 mm (n = 7) and 0.7 mm × 0.7 mm 0.7 mm (n = 2). All methods were applied on the human subjects for evaluating reconstruction image quality.

D. Implementation Details for Various Algorithms

For the field map estimation, the same procedures as in previous studies [1], [13] were used. The noise weighting w was set equal to the local SNR in simulation and was estimated along with the field map estimation [13], [27] for in vivo imaging. For each subject, the weighting w was normalized by its mean value inside the ROI, so that the weighting w was comparable and consistent across subjects. The method of projection onto dipole fields [18] was used for removing the background field. Because the phase outside of the brain was corrupted by noise, the magnetic field outside the brain parenchyma was cropped by a mask, which was manually segmented in the numerical experiments and was obtained using a brain extraction tool for the in vivo brain data [36]. Voxels in the background region or within 3 mm to the background region were set to zero [18], [32].

For the WKD method, the LSQR [37] solver was used. The TVWA, NTVWA, MGL1, and NMEDI methods were solved using a lagged diffusivity fixed point method [15], [38]. In methods involving a structural prior, m was estimated by setting the gradients of magnitude image greater than a certain threshold to 0 and to 1 otherwise [31], [34].

E. Regularization Parameter Selections

In all QSM methods, the regularization parameter (α, β), if present, was searched from 10⁻⁵ to 10¹ (13 logarithmically spaced steps). The dipole kernel truncation level (τ) was searched from 0.0125 to 0.4 (32 equidistant steps) for methods requiring this parameter. From these ranges, the optimal parameters were determined in the following manner by exhaustively searching: The best parameter in noisy numerical reconstruction was chosen according to the least error with respect to the true susceptibility for TKD and WKD and the discrepancy principle [39], [40] for TVWA, NTVWA, MGL1, and NMEDI [27]–[31]. The same parameters were used in the noiseless simulation. The best parameters in the human brain reconstruction (true susceptibility not available) were selected according to the least number of artifacts and best contrast among brain components in one representative case determined by an experienced neuroradiologist (Weiwei Chen, ten years), and the chosen parameters were applied to all other cases.

F. Data Analysis

To assess the accuracy of the numerical phantom reconstruction, the root mean square error (RMSE) of the whole volume and in lesion was calculated for every method. To assess in vivo image quality, four neuroradiologists (Weiwei Chen, Wenzhen Zhu, Chu Pan, and Lingyun Zhao) reviewed all the reconstructed cases in a random order while being blinded to the reconstruction methods. In each case, all the QSM images were presented simultaneously to facilitate the scoring. Overall image quality was scored with a five-point scale based on radiological impression, where 1 = corrupted quality, undiagnosable, 2 = low quality, undiagnosable, 3 = moderate quality, low confidence to make any diagnosis, 4 = good quality providing useful information, and 5 = high quality, high confidence to make a diagnosis. The first radiologist (Weiwei Chen) repeated the image quality assessment five months later to assess intraobserver variability. Interobserver and intraobserver variabilities of image quality scores were assessed by using the intraclass correlation coefficient [41]. The following criteria for clinically relevant agreement were used to assess the calculated intraclass correlation coefficient: less than 0.40 was considered poor; 0.40–0.59, fair; 0.60–0.74, good; and greater than 0.74, excellent [42]. A Wilcoxon rank sum test was performed to assess the significance of image score differences between reconstructed susceptibility maps. Statistically significant with the higher image score was reported as an improvement when p < 0.05.

IV. Results

A. Numerical Simulation

The simulated maps are shown in Fig. 1. The influence of noise in the representative methods of the four categories is shown in Fig. 2. When noise was not taken into account in the QSM reconstruction, it generally led to more substantial streaking artifacts, as can be seen in column b in Fig. 2. The optimized parameters were τ = 0.1 for TKD and WKD, α = 10⁻³ and β = 10⁻³ for TVWA, α = 10⁻³ for MGL1. The RMSE over the entire volume was 0.045, 0.043, 0.041 and 0.040 ppm for TKD, WKD, TVWA, and MGL1, respectively. The RMSE in the lesion was 1.28, 1.25, 1.10, and 0.99 ppm, corresponding to 143%, 139%, 122%, and 110% for TKD, WKD, TVWA, and MGL1 relative to the lesion’s known susceptibility, respectively.

Fig. 2.

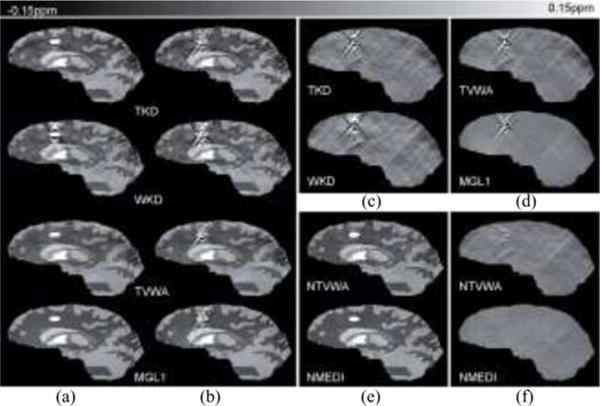
Noise and noise weighting effects in QSM methods. The result of the TKD, WKD, TVWA, and MGL1 (a) on the noiseless data and (b) on the noisy data. The TKD, WKD, TVWA, and MGL1 do not use noise weighting. Reconstructions in the noisy case that do not take into account the noise properties of the data clearly suffer from streaking artifacts as seen in (b) and difference images (c, d) between reconstruction and known susceptibility. Streaking artifacts were markedly reduced when noise weighting was incorporated in (e) NTVWA and NMEDI, comparing to the TVWA and MGL1 with same corresponding regularization term but without noise weighting (bottom two rows in b). The benefits of noise weighting were observed in reconstruction images (b, e) and difference images (d, f) between reconstruction and known susceptibility.

The influence of noise weighting is shown in Fig. 2(b), (c), (e), and (f). The optimized parameters are α = 10⁻³ and β = 10⁻³ for NTVWA, α = 10⁻³ for NMEDI. Noise weighting markedly suppressed the artifacts [see Fig. 2(b)] and improved the accuracy for NTVWA (RMSE = 0.018) versus TVWA and NMEDI (RMSE = 0.013) versus MGL1. The RMSEs in the lesion were 0.091 and 0.020 ppm, corresponding to 10% and 2% for NTVWA and NMEDI relative to lesion’s known susceptibility. The calculated mean susceptibility values of the lesion (assigned 0.90 ppm) were 0.78, 0.75, 0.84, 0.87, 0.85, and 0.89 ppm for TKD, WKD, TVWA, NTVWA, MGL1, and NMEDI, respectively.

B. In Vivo Brain Imaging

The optimal parameters were τ = 0.1 in TKD and WKD, α = 10⁻³ and β = 10⁻³ for TVWA and NTVWA, α = 10⁻³ for MGL1 and NMEDI.

The interobserver and intraobserver results are shown in Table II. These agreements ranged between good and excellent. The reconstructed images of QSM methods on one of the healthy subjects are shown in Fig. 3. For group 1, the overall image quality averaged from the four readers for TKD and WKD was 1.21 ± 0.37 (mean ± standard deviation) and 1.53 ± 0.43. The overall image quality for TVWA, NTVWA, MGL1, and NMEDI was 2.53 ± 0.51, 3.56 ± 0.55, 3.43 ± 0.73, and 4.18 ± 0.60. An increase in the image quality score was observed when noise weighting was included, and the differences were statistically significant (p = 3.59 × 10⁻⁶ for TVWA versus NTVWA and p = 0.001 for MGL1 versus NMEDI) between reconstructions with and without noise weighting.

TABLE II.

Inter- and Intraobserver Variabilities

Method	Interobserver variabilitya	Intraobserver variability
TKD	0.80 (0.72,0.87)	0.84 (0.73,0.90)
WKD	0.70 (0.59,0.80)	0.72 (0.56,0.83)
TVWA	0.68 (0.56,0.78)	0.73 (0.54,0.84)
NTVWA	0.69 (0.58,0.79)	0.75 (0.60,0.85)
MGL1	0.73 (0.63,0.82)	0.81 (0.68,0.89)
NMEDI	0.82 (0.74,0.88)	0.88 (0.79,0.93)

Data are intraclass correlation coefficients, with 95% confidence intervals in parentheses.

^aData are from the first reading of observer 1.

Fig. 3.

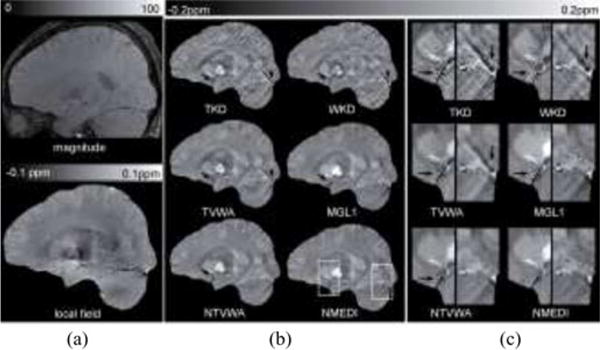
Noise weighting effect in QSM on a healthy subject shown in (a) magnitude, local field and (b) reconstructed QSM images in a sagittal section. The images in (c) correspond to the dashed boxes in (b). The average image quality scores were 1, 2, 3, 4.3, 4.5, and 5 for TKD, WKD, TVWA, MGL1, NTVWA, and NMEDI, respectively. Overall streaking artifacts were reduced in Bayesian methods. In the zoom-in images in (c), streaking artifacts were seen originating from vessels (black arrows) in TVWA and MGL1. This artifact was reduced to some extent in NTVWA and even further in NMEDI.

The reconstructed QSM images in one of the hemorrhage patients are shown in Fig. 4. For group 2, the average overall image quality was 1.05 ± 0.22 and 1.43 ± 0.47 for TKD and WKD, respectively. When noise weighting was included, improved image quality was also observed in group 2 with respect to the suppression of streaking artifacts (see Fig. 4). The overall image quality for TVWA, NTVWA, MGL1, and NMEDI was 1.95 ± 0.48, 3.26 ± 0.53, 3.00 ± 0.63, and 3.89 ± 0.63, respectively and the differences were statistically significant (p = 2.76 × 10⁻⁷, 9.73 × 10⁻⁵ for TVWA versus NTVWA and MGL1 versus NMEDI).

Fig. 4.

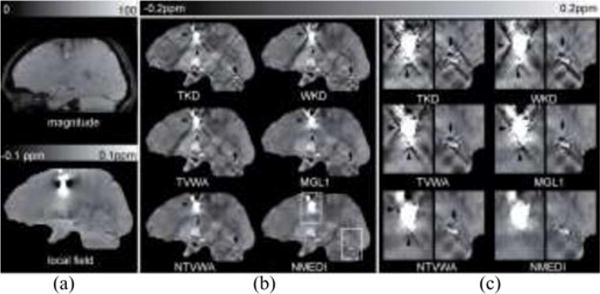
Noise weighting effects in QSM on a hemorrhage patient shown in (a) magnitude, local field and (b) reconstructed QSM images in a sagittal section. The zoom-in images in (c) correspond to the dashed boxes in (b). The average image quality scores were 1, 1, 2, 3, 3.5, and 4 for TKD, WKD, TVWA, MGL1, NTVWA, and NMEDI, respectively. Similar to volunteer images, overall streaking artifacts (black arrow heads and black arrows) were reduced in Bayesian methods. Streaking artifacts were seen originating mainly from the hemorrhage (black arrow heads) in TVWA and MGL1. This artifact was reduced in NTVWA and NMEDI.

The image scores’ difference was significant for TVWA versus NTVWA (p <10⁻⁵ for group 1 and p < 10⁻⁵ for group 2) and MGL1 versus NMEDI (p < 10⁻² for group 1 and p < 10⁻² for group 2) for each one of the four readers.

The average image quality according to the resolutions is shown in Table III. The image quality trend (sorted from worst to best: TKD, WKD, TVWA, MGL1, NTVWA, NMEDI) is same for the three resolutions.

TABLE III.

Average Image Quality According to the Resolutions

Method	Group1			Group2
	.57×.75×3a	.57×.75×2	.7×.7×.7	.57×.75×3	.57×.75×2
TKD	1.2±0.4	1.4±0.5	1.1±0.2	1.1±0.2	1.0±0.0
WKD	1.4±0.4	1.9±0.1	2.0±0.0	1.5±0.5	1.3±0.4
TVWA	2.5±0.5	2.6±0.5	3.4±0.2	2.0±0.5	1.8±0.3
NTVWA	3.5±0.5	3.6±0.5	4.5±0.0	3.2±0.6	3.4±0.1
MGL1	3.3±0.8	3.4±0.5	4.3±0.0	3.0±0.6	2.8±0.7
NMEDI	4.1±0.6	4.5±0.6	5.0±0.0	3.9±0.7	3.9±0.1

Data are shown in mean ± standard deviation.

^aIndicate the resolution (mm³).

V. Discussion

Our experimental results indicate that QSM quality is conspicuously improved when noise weighting is used, as in the Bayesian approaches, to properly account for the noise in measurements. Furthermore, QSM can be improved when a structural consistency prior is incorporated. Investigations with a numerical Zubal lesion phantom and 50 consecutive cases consistently corroborated these observations, which are concordant with the theoretical error analysis of QSM that the error in the reconstructed susceptibility comes from noise in the data and error in the prior [34].

Noise may cause severe streaking artifacts in QSM (see Figs. 2–4). We have noticed that the TKD has the most severe artifacts among the methods demonstrated (see Figs. 2–4). This may be explained by the truncation-related large noise amplification inherent in the k-space division in (5). The optimal truncated level τ is a tradeoff between fidelity to the model and suppression of artifacts, and the determined optimal τ in this study is consistent with previous studies [9], [10], [32]. The streaking artifacts and underestimation in the TKD reconstruction may be empirically reduced using some compensation strategies in images with high SNR [10], [43]. These compensations may influence the optimal τ (i.e., τ > 0.3 in [43]). We also noticed that the spatially varying noise of the input field data is not accounted for in (3) and (6), which also led to obvious streaking artifacts in the reconstructed susceptibility map.

Noise weighting is beneficial, as demonstrated in the Bayesian QSM methods (see Figs. 2–4). The incorporation of noise weighting in the data fidelity term, which is nonlinear with respect to the magnetic field as in (4), led to marked improvement in QSM image quality. Using the noise weighting consistently improved the image quality independent of resolution, group, and observers. The improvement was most pronounced in group 2 data, because hemorrhages generated low SNR regions. While Gaussian noise approximation for signal phase is a reasonable approximation in formulating the data fidelity term when the SNR is large, the Gaussian noise model for phase data becomes a poor approximation in low SNR regions. In the nonlinear formulation, the noise of the complex signal is Gaussian as is usually assumed in MRI. Since the L1 minimization problem is already nonlinear, this complex data fidelity term, which is nonlinear in the field, does not add any computation cost.

Low SNR lesions in clinical MRI include calcifications, hemorrhages, microbleeds, and other high iron deposits. Paramagnetic iron accumulation has been associated with Parkinson’s disease, multiple sclerosis, Alzheimer’s disease, Huntington’s chorea, and chronic hemorrhage [28], [44], [45]. Calcification, experimentally confirmed to be diamagnetic [1], [8], [46], [47], has been associated with oligodendrogliomas and craniopharyngiomas [48], [49]. In contrast to previous methods that assume a piece-wise constant model in low SNR regions (e.g., lesion or cortical bone), requiring an image segmentation [1], [2], susceptibility mapping may reveal spatial distribution of the hemosiderin deposits in a hematoma or allow the differentiation of calcification from hemorrhage when they are mixed together [50]. Noise weighting is essential for accurately reconstructing the susceptibility maps of these low SNR lesions with large negative or positive susceptibility.

A structural prior is useful to further suppress streaking artifacts, as observed in MGL1 versus TVWA and NMEDI versus NTVWA in image quality and Figs. 2–4. The structural matching between the magnitude image and susceptibility map by matching the locations of their gradients tends to improve the QSM image quality and accuracy. In the in vivo situation, the structural prior may not be as perfect as in simulation, so the improvement of the structural prior may not be so significant, as shown in Fig. 3(b) and (c) and Fig. 4(b) and (c). The gradient location consistency between the magnitude image and susceptibility map used in MEDI may be improved with more sophisticated identification and structural matching, such as incorporating edges derived from the magnetic field map [32], [51]. It is also theoretically shown that a comprehensive detection of all the edges in the true susceptibility distribution will reduce the error in the reconstructed QSM [32], [34].

Images from non-Bayesian TKD and WKD methods appeared to have more textures compared to the Bayesian methods. These perceived textures in non-Bayesian methods are likely streaking artifacts with low amplitudes in the numerical simulations. However, the simulated image is limited to a piece-wise constant model, lacking realistic variations. The perceived textures of non-Bayesian methods in human data are difficult to interpret due to the lack of ground truth. The prior in a Bayesian method can introduce artificial smoothness and patchiness, and there may be other artifacts. While QSM has advanced to reliably generate reasonable image quality, further algorithm optimization and experimental validation are needed to establish accurate and robust QSM.

VI. Conclusion

In summary, noise amplification is a major source of errors in QSM. Gaussian noise in the complex MR signal domain can be accounted for in the data fidelity term of a QSM algorithm formulated in the Bayesian approach. With proper noise weighting, noise effects in QSM can be reduced using Bayesian methods. Among the illustrated QSM methods, NMEDI using the Bayesian approach with a physical prior of structural consistency provided the best QSM image quality.