Abstract
Purpose
It is clinically important to accurately predict facial soft‐tissue changes prior to orthognathic surgery. However, the current simulation methods are problematic, especially in anatomic regions of clinical significance, e.g., the nose, lips, and chin. We developed a new 3‐stage finite element method (FEM) approach that incorporates realistic tissue sliding to improve such prediction.
Methods
In Stage One, soft‐tissue change was simulated, using FEM with patient‐specific mesh models generated from our previously developed eFace template. Postoperative bone movement was applied on the patient mesh model with standard FEM boundary conditions. In Stage Two, the simulation was improved by implementing sliding effects between gum tissue and teeth using a nodal force constraint scheme. In Stage Three, the result of the tissue sliding effect was further enhanced by reassigning the soft‐tissue‐bone mapping and boundary conditions using nodal spatial constraint. Finally, our methods have been quantitatively and qualitatively validated using 40 retrospectively evaluated patient cases by comparing it to the traditional FEM method and the FEM with sliding effect, using a nodal force constraint method.
Results
The results showed that our method was better than the other two methods. Using our method, the quantitative distance errors between predicted and actual patient surfaces for the entire face and any subregions thereof were below 1.5 mm. The overall soft‐tissue change prediction was accurate to within 1.1 ± 0.3 mm, with the accuracy around the upper and lower lip regions of 1.2 ± 0.7 mm and 1.5 ± 0.7 mm, respectively. The results of qualitative evaluation completed by clinical experts showed an improvement of 46% in acceptance rate compared to the traditional FEM simulation. More than 80% of the result of our approach was considered acceptable in comparison with 55% and 50% following the other two methods.
Conclusion
The FEM simulation method with improved sliding effect showed significant accuracy improvement in the whole face and the clinically significant regions (i.e., nose and lips) in comparison with the other published FEM methods, with or without sliding effect using a nodal force constraint. The qualitative validation also proved the clinical feasibility of the developed approach.
Keywords: facial soft‐tissue change prediction, finite element model, orthognathic surgery, soft‐tissue modeling, soft‐tissue sliding effect
1. Introduction
Human facial appearance plays an integral role in daily life. As such, dentofacial deformities may significantly impact esthetics and function of the human face with the probability of severe psychological impact. Orthognathic surgery is a surgical procedure to correct these dentofacial deformities. Due to the complex anatomy of the face and jaws, the success of orthognathic surgery depends on not only a good surgical technique, but also an accurate presurgical plan. Orthognathic surgery involves osteotomies that cut the jaws into pieces and then repositions them to desired (planned) positions. Facial soft tissues are “automatically” changed following the bone movement. However, to date, only virtual osteotomy can be accurately simulated.1, 2, 3 Facial soft‐tissue changes, as a result of the osteotomies, cannot be accurately predicted because facial soft tissue's anatomy is much more complex than that of the rigid bones.
Attempts have been made to predict facial soft‐tissue changes following the osteotomies. At the beginning, soft‐tissue change was predicted based on bone‐to‐soft‐tissue movement ratios, which has been proven to be clinically inaccurate.4 More recently, several reports have been published on three‐dimensional (3D) facial soft‐tissue prediction methods using finite element method (FEM),5, 6 mass‐spring model7 and mass tensor model.8, 9, 10 Among these, FEM is reported to be the most common, accurate and biomechanically relevant method.11 Nonetheless, the prediction of facial features following orthognathic surgery is still less than ideal, especially around the nose, lips and chin regions, which are critically important for facial esthetics and in evaluating surgical outcome. Reported absolute errors in the predicted lip were greater than 2 mm.12, 13 Although not officially documented, it is a consensus among clinicians that error between the planned and the actual soft tissue is acceptable if the error is below 2 mm (mean error) or 3 (maximum error). Therefore, there is an urgent clinical need to develop a reliable method that can provide accurate predictions of facial soft‐tissue changes, especially in those aforementioned critical regions.
In FEM simulation of facial soft‐tissue change in the orthognathic surgery, appropriate boundary conditions are required to simulate the interaction between bone and soft tissue. The most basic assumption for the orthognathic surgery simulation is that the nodes of the FEM mesh move together with the contacting bony surfaces as if they are attached to each other.6 The nodes in contact with the corresponding bony surfaces are first selected and then translated by the same amount as the bone movement. However, this assumption may lead to significant errors, especially when large amounts of bone movement and occlusal changes are involved. In addition, in contrast to human anatomy, cheek, and lip mucosa are falsely attached to the bone and teeth in this approach. More realistically, they need to slide over each other. It is the authors’ belief that applying realistic sliding effect can improve the inaccurate predictions around the critical regions.
There are many technical challenges in implementing realistic sliding movement of the mucosa in FEM simulations. First, high computational power and extensive time are required for the sliding effect simulation due to the dynamic sliding mechanism between the mucosa and the bone‐teeth surface. This may limit its incorporation as a clinical tool. In contrast, the force constraint technique has been proposed to reduce the complexity of implementing sliding effect.9, 10, 14 Secondly, even if the sliding movement with force constraint is implemented, the simulation results may still be inaccurate. This is because generally no strict nodal displacement boundary condition is applied to the sliding area. Since the soft tissues at sliding surfaces follow the buccal surface profile of the bones and teeth, it is necessary to consider the displacement boundary condition for sliding movement. Thirdly, mapping between the bony surface and FEM mesh nodes needs to be reestablished after repositioning the bony segments to their desired planned position. The translation and rotation of the osteotomized segments represent a discontinuity within the prior existing mesh, which needs to be corrected. This is critical because the initial relationship between the bone and soft‐tissue is not always preserved after the repositioning of the bony segments. In cases of double‐jaw surgery involving mandibular setback or advancement, the soft tissue's contact region to the bones may either decrease or increase. This mismatch may result in distortion of the resulting mesh. Fourthly, the occlusal changes (e.g., from preoperative Class III cross‐bite to postoperative normal Class I) may cause mesh distortion in the lip region, where the upper and lower teeth meet. Therefore, a simulation method with more advanced sliding effect is required to increase the prediction accuracy in critical regions such as the lips and chin.
We hypothesized that achieving a more realistic sliding effect is a key factor for increasing the prediction accuracy of facial soft‐tissue deformation in clinically critical anatomic regions. Therefore, we proposed a 3‐stage FEM simulation method that incorporates realistic sliding effects to increase the accuracy of facial soft‐tissue change prediction, especially in critical regions. Our three‐stage FEM prediction method was validated using 40 retrospectively analyzed patient datasets who underwent a double‐jaw orthognathic surgery. The prediction results achieved with our approach were quantitatively and qualitatively analyzed and compared to the results achieved with the other two methods: the traditional FEM method and the FEM with sliding effect, using a nodal force constraint method. A preliminary version of this approach was first reported at the 7th International Conference on Medical Imaging and Augmented Reality,15 then at 2016 Medical Image Computing and Computer‐assisted Intervention16 with an update in evaluation. In this manuscript, both methodology and clinical validation have been significantly improved.
2. Materials and methods
Our three‐stage approach of predicting facial soft‐tissue changes following the osteotomies is described below in detail. In the first stage, a patient‐specific FEM model is generated, using a previously developed template model.17 Then, the rough facial soft‐tissue changes are predicted as the consequence of the virtual osteotomies and repositioning of the bone segments in a patient specific numerical simulation with standard boundary condition. In the second stage, the simulation is improved by applying sliding effect of the mucosa around the teeth and partial maxillary and mandibular regions. Nodal force constraint was implemented to simulate the sliding effect by considering only the parallel nodal force on the sliding regions. In the third stage, nodal spatial boundary conditions are applied as a fine‐tuning technique to increase the prediction accuracy by exactly reflecting the bone surface geometry. During the simulation, the high‐quality photography acquired from a 3D surface camera (3dMD Inc, Atlanta, GA, USA) is mapped to the predicted result using texture mapping.
2.A. Stage one: FEM simulation with standard boundary condition
A uniform and homogeneous patient‐specific volume mesh (total of 38280 elements and 48593 nodes) was generated for FEM simulation using our previously developed and validated eFace template.17 The inner and outer surfaces of the template mesh were registered to the skeletal and facial surfaces of the patient, respectively, using the anatomical landmark‐based thin‐plate splines (TPS) technique. Then, the internal mesh volume was morphed to the patient data by interpolating surface registration results, using TPS.17
In our study, homogenous linear elastic material properties were utilized in the model for computational efficiency. Although prior bench tests and numerical studies have investigated optimal soft‐tissue properties for the replication of biomechanical effects, no significant differences in simulation results were found among varying linear elastic material properties.11, 18, 19 Furthermore, since the focus of our study is on shape deformation patterns due to surgery rather than on force requirements to move tissues, we can rely on a bulk modulus definition with nearly incompressible material properties. Consequently, when assuming minimal retained internal tissue stress 6 months after surgery, the current method is seeking information on soft‐tissue volume distortion whereby the material definition is essentially independent of Young's modulus and has a Poisson's ratio near incompressibility. In our simulation model, we assign a Young's modulus within physiological limits [3000 (Pa)] and 0.47 for Poisson's ratio.18, 19
Nodes of the FEM mesh are divided into boundary nodes and free nodes (Fig. 1). Free nodes are spatially unconstrained and their displacements [color coded in greenblue (or Gray in B&W) in Figs. 1(c) and 1(d)] are determined by the displacements of boundary nodes, using FEM. Boundary nodes are further divided into fixed, moving, and sliding nodes. Areas not affected by surgery are defined as fixed nodes (red (or dimgray in B&W) in Fig. 1), thus fixed nodes have zero nodal displacement relative to their counterpart, e.g., bone.
Figure 1.
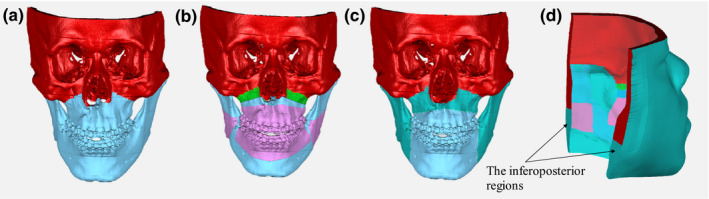
Mesh nodal boundary condition. (a) Mesh inner surface boundary condition (illustrated on the skull) for the first stage only; (b) Mesh inner surface boundary condition for the second stage only; (c) Mesh inner surface boundary condition (illustrated on the skull) for the third stage only. (d) Posterior and superior surface boundary condition for all stages. (Note that the inferoposterior regions are the fixed nodes in the first and third stage); Color coding of fixed nodes: red (or dimgray in B&W); Moving nodes: Blue (or lightgray in B&W); Sliding nodes: pink (or silver in B&W); Free nodes: GreenBlue (or gray in B&W); Tenting of periosteum: green (or gray in B&W). [Color figure can be viewed at wileyonlinelibrary.com]
In the first stage, moving nodes that are assumed to move in sync with the osteotomized bony segments are assigned on the mesh inner surface [blue (or lightgray in B&W) in Fig. 1(a)]. A search algorithm is used to determine the closest corresponding relationship between vertices on the surface mesh of the bony segments to the nodes of the mucosa mesh (moving nodes). The movement vector (magnitude and direction) of each bony segment in accordance to the surgical plan is then applied to the moving nodes as the nodal displacement boundary condition.
The movement of the free nodes was calculated by solving global FEM equation: Kδ = f, where K is a global stiffness matrix, δ is a global nodal displacement vector, and f is a global nodal force vector. This equation can be rewritten as follows:
| (1) |
where is the displacement of the moving and fixed nodes, is the to be determined displacement of the free nodes. Here f 1 is the nodal force on the moving and fixed nodes, and f 2 is the nodal force on the free nodes. During FEM calculation, because the free nodes are spatially unconstrained, its nodal force is assumed to be zero in all directions. With this assumption (f 2 = 0), the nodal displacement of the free nodes, , can be directly calculated: = [from Eq. (1)]. The resulting in this first‐stage simulation is the soft‐tissue change prediction result for the first stage.
2.B. Stage two: FEM simulation with sliding effect using nodal force constraint
In the second stage, the sliding effect is applied by adjusting boundary conditions to improve the prediction result. Sliding nodes [pink (or silver in B&W) in Fig. 1(b)] are assigned around the mouth, which include mucosa around the lips, inner cheeks, corresponding inner mesh surfaces of the partial maxilla and mandible, and teeth. Although widely used to simulate sliding movements in mechanical problems, the simple roller support boundary cannot be applied to the mucosa because of the complex surface geometry of the bone and teeth. Unlike sliding along articulating surfaces, the sliding movement of the mucosa is not congruent and varies along the bony surface geometry. Furthermore, the sliding mechanism of mucosa over bony surface is a dynamic process. Realistic simulation of dynamic sliding movement, using FEM is complex and computationally expensive. Therefore, a force constraint approach that mimics the sliding movement in a non‐dynamic fashion was adopted in this study to simulate sliding movement of the mucosa in an efficient way.9, 10, 14 In the force constraint mode, sliding nodes move along the bone surface and only the tangential component of sliding nodal force to the corresponding bone surface is assumed to be zero.9, 10, 14 In previous studies related to facial simulations, a limited area around the teeth was simulated to reflect sliding boundary conditions.9, 10 In our current study, a partial region of the inferior ramus was also included as part of the sliding area to reduce the effects of mesh distortion in the posterior region of the mandible [pink (or silver in B&W) in Fig. 1(b)].
The movement vector of each bony segment is applied to the moving nodes, as was done in the first stage. However, nodes in the areas, where two (proximal and distal) bony segments of the mandible collide with each other due to surgical movements, are not regarded as moving boundary nodes. Rather, nodes in these areas are designated as free nodes in order to prevent mesh distortion at the mandibular inferior border. Moreover, tenting of periosteum is considered as a moving boundary for the purpose of this approach [green (or gray in B&W) in Fig. 1(b)]. This is implemented because intraoperatively degloved soft tissue and displaced bony segments in these regions causes the tenting of the periosteum between the moved Le Fort segment and the unmoved midface, which subsequently affects the postoperative facial soft‐tissue geometry. The tenting of periosteum is added onto its corresponding moving nodes by shifting the nodes an additional 2 mm anteriorly, causing changes in nodal displacement boundary condition. Although not formally documented, the suggested 2 mm tenting adjustment is the best estimate based on the actual thickness of the titanium plate for rigid fixation and our clinical observations.
Note that in the second stage, free nodes are assigned to the inferoposterior regions of the soft‐tissue mesh. This is important because in conjunction with the sliding boundary condition at the ramus (explained above), these free nodes maintain the integrity of the soft tissue. In addition, these free nodes also protect the flexibility and smoothness of the posterior and inferior mandibular regions when excessive mandibular advancement or setback occur.
An iterative FEM implementation algorithm was developed to calculate the movement of the free and sliding nodes by solving the FEM equation [Eq. (1)]. In the second stage, is the displacement of the moving and fixed nodes, is the sought after displacement of the free and sliding nodes. The f 2 is the nodal force on the free and the sliding nodes. The nodal force of the free nodes is assumed to be zero, and only tangential nodal forces along the contacting bone surface are considered for the sliding nodes.9, 10, 14
The final value of δ 2 is calculated by iteratively updating δ 2 with Eq. (2) until the converging condition is satisfied. Through our preliminary studies, it was determined that the iteration will be halted if the delta change in between the two iterations converges below 0.01, which represents less than 1% of the expected peak displacement error of the mesh (details are described below).
| (2) |
is calculated as follows. First, f 2 is calculated by substituting current into Eq. (3), which is derived from Eq. (1). At the start of the iteration (k = 1), the initial is randomly assigned and substituted for to solve Eq. (3). The f 2 is composed of nodal forces of the sliding nodes () and the free nodes ().
| (3) |
Second, is calculated by transforming the nodal force that corresponds to the sliding nodes among f 2 to include only the tangential nodal force components.9, 10, 14 Now, is composed of the nodal force of the free nodes () and only a tangential component of the nodal force of the sliding nodes ().
In the final step of the iteration, is acquired to determine the required nodal displacement (. The nodal force is the required nodal force to make zero and is calculated by the difference between and f 2 (f 2−). is finally calculated as follows:
| (4) |
Equation (4) is derived from Eq. (1). Then, calculated using Eq. (2). The iteration continues until the maximal absolute value of converges below 0.01 (k = n). The final values of δ ( and ) represent the displacement of mesh nodes after applying bone movements and the sliding effect using nodal force constraint. The algorithm was implemented in MATLAB. The resulting δ in this second‐stage simulation is designated as .
2.C. Stage three: FEM simulation with sliding effect using nodal spatial constraint
According to human physiology, the mucosa (the inner side of the soft‐tissue volume mesh) contacts the teeth and buccal surface of the bone. However, calculations from the second stage only accounts for the nodal force constraint. Thus, the second‐stage results of the predicted facial soft‐tissue transformation may contain a mismatch between the simulated mesh inner surface and the bony outer surface (Fig. 2). The objective of the third stages to reduce this mismatch by applying nodal spatial constraint to refine the result of the nodal force constraint from the second stage.
Figure 2.
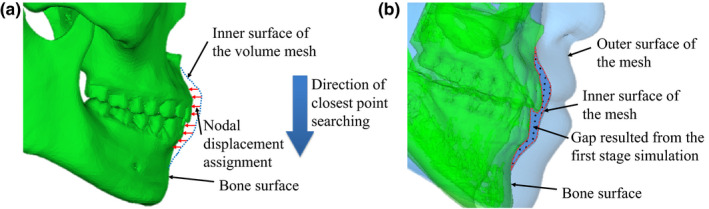
Assigning nodal spatial constraint. (a) Description of nodal displacement boundary condition assignment in the third stage. (b) Mismatch between the simulated mesh inner surface and the bone surface after sliding effect using nodal force constraint. [Color figure can be viewed at wileyonlinelibrary.com]
It is also necessary to redefine boundary mapping between the bone surface and mesh nodes in the sliding area. The relationship between the bone surface vertices and the mucosa mesh nodes has changed after bony segment movement (simulated in the first and second stage). To adjust for this change, the first step in the third stage is to assign the nodes of the inner mesh surface that correspond to the part of maxilla and mandible as moving nodes. Moving nodes in this stage are selected in the area where the mismatch between the simulated mesh inner surface and the bony outer surface may occur [blue (or lightgray in B&W) in Fig. 1(c)]. Therefore, the nodes correspond to the sliding nodes of the maxilla in the second stage and the distal segment of the mandible are assigned as moving nodes as shown in Fig. 1(c).
The nodal displacements of the moving nodes are then calculated by finding the closest point from each mesh node to the bone surface. This is in reverse order of the previous stages. The assignment is processed from the cranial to caudal direction, which ensures implementation of appropriate boundary condition (nodal spatial constraint) without mesh distortion (Fig. 2). This was decided because clinically the postoperative lower teeth are always inside of the upper teeth (as a normal bite) despite preoperative conditions. Care is taken to shift the vertical node displacement evenly between the superior and inferior nodes in order to prevent two vertical nodes from referring to the same point on the bone surface. This procedure prevents nodes with the same nodal displacement from being counted twice. The summation of previous steps solves the mismatch problem between the bone surface and its contacting surface on the inner side of the simulated soft‐tissue mesh. Once computed, the vector between each node and its closest corresponding vertex on the bone surface is assigned as the nodal displacement for the FEM simulation. The calculated nodal displacement serves as the nodal spatial constraint in the third stage that ensures the geometrical match between the simulated mesh inner surface and the bony outer surface.
Free nodes at the inferoposterior surface of the soft‐tissue mesh in the second stage [the inferoposterior regions of the soft‐tissue mesh in Fig. 1(d)] are now assigned as fixed nodes in this stage. In the second stage, due to mandibular movements from osteotomy, the inferoposterior surface of the soft‐tissue mesh is designated as free nodes to increase the degrees of freedom and to prevent mesh distortion in the inferior border of the mandible. In the third stage, since mandibular movements are already applied in the second stage, the total inferior surface of the mesh is designated as fixed nodes to prevent undesirable further deformation in the inferior border of the mandible. Note that the boundary condition for tenting of periosteum applied in the second stage remained the same. The remainder of the nodes are assigned as the free nodes [GreenBlue (or gray in B&W) in Figs. 1(c) and 1(d)]. Unlike the previous boundary assignment, there are no sliding nodes since the sliding translation has already occurred. The global stiffness matrix (K), the nodal displacement (δ) and the nodal force (f) are reorganized according to the new boundary conditions. The third‐stage results are calculated by solving Eq. (1). Based on the assumption that the nodal force of the free nodes, f 2, is zero (note no sliding nodes in the third stage), the nodal displacement of the free nodes, , can be directly calculated without iteration as follows: = (same as the first stage). Then, the final δ ( and ) is designated as . Lastly, the overall nodal displacement matrix is calculated by combining the resulting nodal displacements of the second () and the third () FEM simulations.
3. Experiments and results
3.A. Patient subjects
Our approach was evaluated quantitatively and qualitatively, using 40 sets of data of patients (22 females and 18 males) who were diagnosed with dentofacial deformity and had underwent double‐jaw surgery. Their mean age was 22.5 yr with a standard deviation of 3.2 yr. The study was approved by our Institutional Review Board (IRB# 0413‐0045). The inclusion criteria were: (a) patients who were diagnosed with dentofacial deformity; (b) patients who underwent double‐jaw surgery, either with or without a genioplasty; and (c) patients who had a complete record of preoperative and postoperative CT scans and 3D photographs of the face captured using a 3D surface camera (3dMD), in which the postoperative 3D photographs must be captured at least six months after the surgery in order to avoid the surgical swelling, while the postoperative CT scans were acquired within the first six weeks after the surgery based on our clinical routine20 (no long‐term CT scans were acquired because of unnecessary ionizing radiation exposure to the patients). The exclusion criteria were: (a) patients who were diagnosed with a syndromic deformity; and (b) patients who underwent a secondary revision, either bony or soft tissue, after the orthognathic surgery. The patient demographic data is listed in Table 1. The CT scans were acquired using our standardized scanning protocol: 512 × 512 of scanning matrix, 1.25 mm of slice thickness, and 25 cm of field of view. Please note: skeletal Class I indicates a correct relationship between the maxilla and the mandible, skeletal Class II dentofacial deformity indicates a retrusive mandible in relation to the maxilla, and skeletal Class III dentofacial deformity indicates a protrusive mandible in relation to the maxilla.
Table 1.
The classification of dentofacial deformity and the surgery
| Classification of deformity | Double‐Jaw surgery | Genioplasty | |
|---|---|---|---|
| Yes | Yes | No | |
| Skeletal class I | 5 | 1 | 4 |
| Skeletal class II | 7 | 4 | 3 |
| Skeletal class III | 28 | 10 | 18 |
| Subtotal | 40 | 15 | 25 |
3.B. Facial soft‐tissue change prediction using three different methods
The facial soft‐tissue change prediction was completed, using the following three methods. Method #1 is the traditional FEM simulation without employing the sliding effect.6 It is the algorithm used in the first stage of our approach. Method #2 is the traditional FEM simulation with sliding effect using nodal force constraint.9, 10 It is the algorithm used in the first and second stages in our approach. Method #3 is the FEM simulation with sliding effect using nodal spatial constraint. It is our complete three‐stage approach.
Prior to the prediction, the bony structures were segmented from the CT scan using thresholding (226 Hounsfield Unit) and manual editing. The movement vectors of each bony segment were computed using the preoperative and postoperative CT datasets (Fig. 3). Postoperative CT scans were first registered to preoperative CT scans using our previously proven surface‐best‐fit method (accuracy: 0.12 mm ± 0.19 mm).21 It was completed by matching both datasets at surgically unchanged regions, i.e., cranium and midface. Virtual osteotomies were then performed on the preoperative CT data according to the postoperative CT data. Next, to calculate bony segment movement vectors as performed on the patient, virtually osteotomized preoperative bony segments were moved and registered from its original preoperative position to the postoperative position. The translational and rotation movements were ranged from 0.0 to 7.0 mm and 0.0 to 9.6° for the maxillary Le Fort I segment, and from 0.0 to 8.8 mm to 0.0 to 9.4° for the mandibular distal segment. The registration was completed and cross‐verified by two experienced oral and maxillofacial surgeons (D.C.H. and H.M.).
Figure 3.
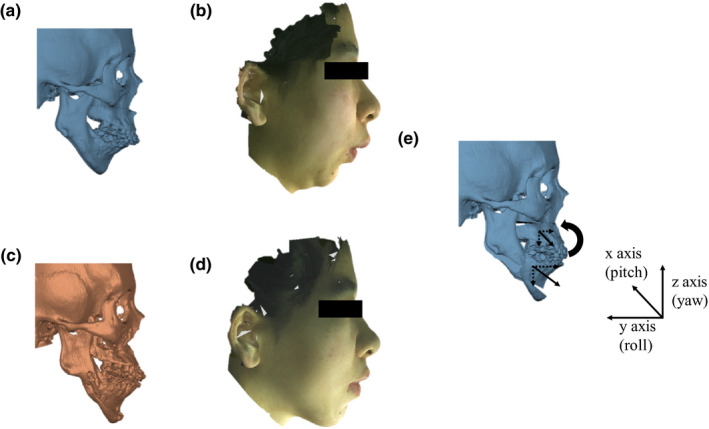
Computing bony segment movements for soft‐tissue change prediction. (a) Preoperative positions of maxillary, mandibular, and chin segments. (b) Corresponding preoperative facial 3D color photograph of the preoperative facial soft tissue. (c) Postoperative position of the maxillary, mandibular, and chin segments. (d) Corresponding postoperative facial 3D color photograph of the preoperative facial soft tissue. (e) Computed surgical movements of the bony segments by registering preoperative bony segments to postoperative ones. Computed movement vectors of bony segments by first registering the postoperative CT models to the preoperative CT models at surgically unchanged regions (i.e., cranium and midface), then registering each virtually osteotomized preoperative bony segment from its original position to the postoperative one. Arrows represent the movements of the bony segment relative to the surgically unaltered cranium and midface. The coordinate system follows the right‐hand rule. [Color figure can be viewed at wileyonlinelibrary.com]
Each patient's preoperative CT soft tissue was also replaced by his/her 3dMD 3D facial scan data prior to the prediction. This was done to correct operational and mechanical errors in the CT soft‐tissue model. During the CT scan, the patient was usually in the supine position, causing facial soft‐tissue sagging due to gravity. In addition, radiographic technologists usually lacked experience in relaxing patient's facial expression, causing unwanted strained lips, opened mouth, or unnatural facial expression. In contrast, 3dMD photographs (surface models) were taken in the medical office by experienced clinicians, thus to ensure the natural facial expression. To replace the CT soft tissue, the preoperative 3dMD facial surface was registered to the corresponding CT facial surface by superimposing rigid facial regions, i.e., forehead, nasal bridge and tragus.1, 22 For the purpose of evaluation, the postoperative 3dMD facial surface was also registered to the preoperative 3dMD facial surface using the same registration method. The registration was also completed and cross‐verified by the same two oral and maxillofacial surgeons.
Finally, the calculated bony segment movement vectors were applied to the preoperative models to simulate the soft‐tissue changes using the aforementioned three methods as a moving boundary condition. During the prediction, the postoperative models were not used.
3.C. Quantitative and qualitative evaluations for clinical validation
The prediction error was evaluated for the entire face and eight subregions, which were virtually divided using anatomical landmarks: palpebrale inferius, alar, subnasale, cheilion, and labrale inferius (Fig. 4). For the quantitative evaluation, mean and maximum displacement errors were computed using absolute mean Euclidean distances along the normal vectors between the predicted result and the actual postoperative outcome for the entire face and each of the eight subregions. In both computation, the direction of the vector was from the postoperative surface to the predicted surface. A repeated measures analysis of variance (ANOVA) and post hoc tests were used to detect any statistically significant difference among the simulated results using three methods. Since there was no published data on what the magnitude of an error is acceptable clinically, we defined the validation criteria based on the consensus among the oral surgeons. We considered the prediction accuracy was validated if the mean displacement error was less than 1.5 mm and the maximum displacement error was less than 3 mm. One‐tailed paired t‐test was used to check whether the errors satisfy the established validation criteria.
Figure 4.
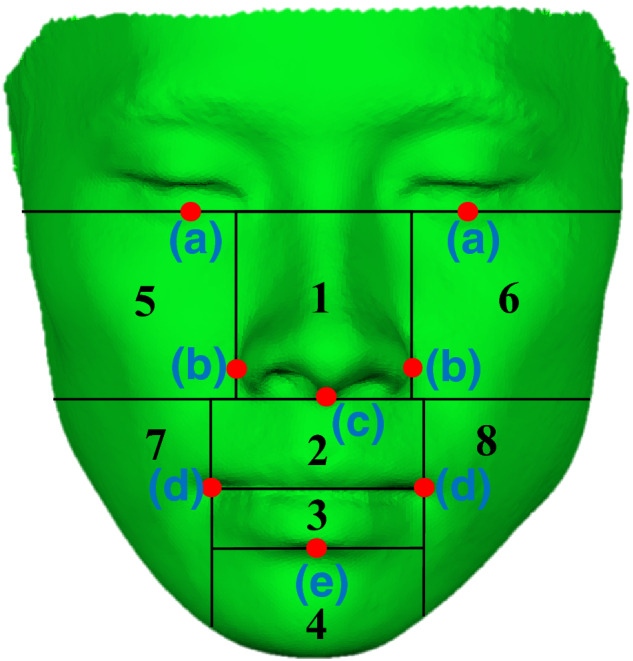
Sub‐regions (automatically divided using anatomical landmarks). The anatomical landmarks were: (a) palpebrale inferius, (b) alar, (c) subnasale, (d) cheilion, and (e) labrale inferius. [Color figure can be viewed at wileyonlinelibrary.com]
Qualitative validation was based on an equivalent test, i.e., the predicted result should be as good as the actual postoperative outcome. The same two oral and maxillofacial surgeons together completed the evaluation. The predicted results using aforementioned three methods were compared to actual postoperative images using a binary visual scoring scale (Unacceptable: the predicted result was not clinically realistic; Acceptable: the predicted result was clinically realistic and very similar to the postoperative outcome). The surgeons were unaware of the method behind each predicted result. They evaluated the predicted results based on their clinical judgment, consensus and the following correlated considerations: (a) whether we would show the predicted facial soft tissue to the patient – the predicted result was realistic; (b) whether the relationship of the upper and lower lips was correspondent to the actual surgical outcomes; (c) whether the symmetrical alignment of the lips were correct; (d) whether the projection and symmetrical alignment of the nose and chin were correct; and (e) whether the predicted facial mesh was smooth without distortion (the integrity of the mesh). The chi‐square test was used to detect the statistical significant differences.
3.D. Evaluation results
We successfully predicted facial soft‐tissue changes for all 40 patient subjects using three methods. Figure 5 shows two randomly selected examples of the predicted results with texture mapping. The results of each method were then compared with postoperative soft tissue quantitatively and qualitatively for the entire face and eight subregions (Fig. 6).
Figure 5.

Randomly selected two examples of simulated results with color texture mapped. The top row shows the frontal view while the bottom row shows the right view for each example patient. (a) Preoperative soft tissue. (b) Predicted soft‐tissue change using Method #1. (c) Predicted soft‐tissue change using Method #2. (d) Predicted soft‐tissue change using Method #3, our complete 3‐stage approach. (e) The actual postoperative soft tissue. For the Example Patient #1, the quantitative analysis showed 7.8 and 6.5 mm of maximum displacement error for Methods #1 and #2 in the chin region, respectively, while that of Method #3 was 1.0 mm. However, the upper and lower lip relationship resulted from the Method #3 was only getting similar to the actual postoperative lip relationship, even though the quantitative error was significantly improved. For the Example Patient #2, the quantitative analysis showed 3.6 and 5.3 mm of maximum displacement error for Methods #1 and #2 in the lower lip region, respectively, while that of Method #3 was 3.2 mm. The result achieved with Method #3 is the only one showing correct upper and lower lip relationship comparing to the actual postoperative soft tissue, even though the quantitative improvement was not significant. [Color figure can be viewed at wileyonlinelibrary.com]
Figure 6.
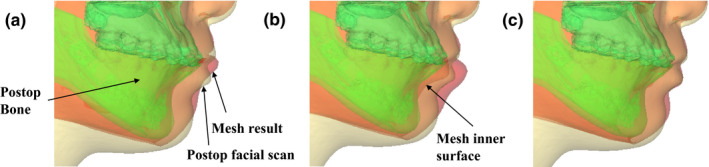
An example of quantitative and qualitative evaluation results. The predicted mesh (red (or gray in B&W)) is superimposed onto the postoperative bone (green (or dimgray in B&W)) and soft tissue (light yellow (or lightgray in B&W)). (a) The predicted result using Method #1. (b) The predicted result using Method #2. (c) The predicted result using Method #3. [Color figure can be viewed at wileyonlinelibrary.com]
The results of the quantitative evaluation are shown in Table 2. The accuracy of the facial soft‐tissue change prediction result achieved with our three‐stage method, the FEM simulation with sliding effect using nodal spatial condition, was statistically significant better than the ones achieved with either Method #1 or #2 (P < 0.05). In addition, the accuracies in critical regions, i.e., nose, lips, and malar, were also statistically significantly improved using our method (P < 0.05). Furthermore, the chin region predicted using our method also showed a trend of improvement (Table 2). Our three‐stage method also improved the cases with exceptionally large error for critical regions (Example Patient #1 in Fig. 5) compared to the current methods. Maximum value of mean displacement error for our complete 3‐stage method among 40 patient cases decreased from 6.6 mm to 3.2 mm and 6.7 mm to 3.5 mm for the lower lip and the chin region, respectively, compared to that of Method #1. Ultimately, among the three methods, only the results predicted using our complete 3‐stage method met the quantitative clinical criteria. All the averaged mean displacement errors were below 1.5 mm for the entire face and eight subregions (P < 0.05), and all the averaged maximum displacement errors were less than 3.0 mm for all subregions except the lower lip (P < 0.05).
Table 2.
Quantitative evaluation results. Accuracy improvement (%) of the results with sliding effect using nodal force constraint (Method #2) and sliding effect using nodal spatial constraint (our method) over the traditional FEM simulation result with standard boundary condition without sliding effect (Method #1) for 40 patients
| Mean error (mm) (Mean ± SD) | Maximum RMSD (mm) (Mean ± SD) | Improvement over Method #1 (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| Region | Method #1 | Method #2 | Our method | Method #1 | Method #2 | Our method | Method #2 | Our method |
| Entire face | 1.2 ± 0.4 | 1.3 ± 0.5 | 1.1 ± 0.3 | −4.9 | 8.6b | |||
| 1. Nose | 1.0 ± 0.4 | 0.9 ± 0.4 | 0.9 ± 0.3 | 3.2 ± 1.2a | 2.8 ± 1.1 | 2.8 ± 1.0 | 11.4 | 12.1b |
| 2. Upper lip | 1.4 ± 0.9 | 1.8 ± 1.1a | 1.2 ± 0.7 | 3.6 ± 2.2a | 3.3 ± 1.4 | 2.7 ± 0.9 | −25.0b | 16.8b |
| 3. Lower lip | 1.8 ± 1.2a | 2.4 ± 1.6a | 1.5 ± 0.7 | 4.5 ± 2.3a | 4.7 ± 2.4a | 3.5 ± 1.4a | −34.1b | 16.9b |
| 4. Chin | 1.4 ± 1.0 | 1.6 ± 1.1 | 1.3 ± 0.7 | 3.1 ± 1.4 | 3.9 ± 2.2a | 3.0 ± 1.2 | −14.5b | 4.6 |
| 5. Right malar | 0.9 ± 0.5 | 0.8 ± 0.4 | 0.9 ± 0.5 | 2.4 ± 0.8 | 2.1 ± 0.6 | 2.4 ± 1.5 | 12.8b | 6.7 |
| 6. Left malar | 0.9 ± 0.4 | 0.8 ± 0.3 | 0.8 ± 0.3 | 2.4 ± 0.8 | 2.3 ± 0.8 | 2.3 ± 0.8 | 3.1 | 8.1b |
| 7. Right cheek | 1.3 ± 0.7 | 1.2 ± 0.6 | 1.2 ± 0.6 | 3.5 ± 1.5a | 3.5 ± 1.5a | 3.0 ± 1.0 | 1.9 | 4.4 |
| 8. Left cheek | 1.4 ± 0.5 | 1.4 ± 0.6 | 1.3 ± 0.6 | 4.2 ± 3.1a | 3.6 ± 1.5a | 3.1 ± 1.0 | −1.0 | 8.0 |
Indicates that the result is significantly larger than the validation criteria (1.5 mm for average error and 3mm for average maximum error) (P < 0.05).
Indicates that the result is significantly different from the result achieved with Method #1 (P < 0.05).
Results of the qualitative evaluation showed that 80% (32/40) of the predicted results achieved with our method were clinically acceptable. It was significantly better than the other two methods (P < 0.05). In comparison, only 55% (22/40) and 50% (20/40) of the predicted results were acceptable for the results achieved with Methods #1 and #2, respectively.
4. Discussion
We have successfully developed and validated a 3‐stage FEM simulation method to predict the facial soft‐tissue changes following orthognathic surgery. This method has been proven better than the current methods. The patient‐specific soft‐tissue FEM model can efficiently be generated by deforming our eFace FEM template without the need to build a unique FEM model from raw data for each patient. This reduces processing time in MATLAB from > 20 h down to < 10 min, thus making our FEM simulation feasible for clinical use. The evaluation result showed our method increased the accuracy in clinically critical regions (i.e., nose and lips) and entire face compared to the traditional method without sliding effect. The result also improved limitation of the current sliding effect simulation method with nodal force constraint by adding nodal spatial constraint. Finally, our method was validated using 40 sets of data from actual patients with different types of dentofacial deformities (skeletal Class I, II and III) and who underwent double‐jaw orthognathic surgery. A third of them also underwent genioplasty. This further strengthened the clinical applicability of our method.
A major advantage of our method is an efficient sliding effect with spatial constraint simulation algorithm with improved boundary condition. First, sliding movement was simulated in a stepwise fashion without implementing complicated dynamic mechanism of sliding. Second, our complete three‐stage method solved the excessive errors in vertical and horizontal direction appeared in the result of current methods (method without sliding effect and method with nodal force constraint). The improved sliding effect solved substantial errors in critical regions that can occur without applying sliding effect with nodal spatial constraint. Third, the enhanced definition of the boundary condition clearly solved the mesh distortion problem in both the sliding regions and bone collision regions where the proximal and distal segments of mandible meet. The modifications to boundary conditions in Stage Two and Three contributed to protecting the flexibility and smoothness of the mandible when excessive mandibular advancements or setback occur. Additionally, the developed method can be easily integrated into the computer‐aided surgical simulation system in the future because it follows the same protocol of surgical simulation system.
Achieving accurate prediction of lip region is clinically important and a challenge.12, 18 Although our method showed significantly improvements on accurately predicting the lips over the other methods, preoperative strained lower lip was not considered in our 3‐stage method. During the orthognathic surgery, the strained lower lip can automatically be corrected to the reposed state by a simple horizontal surgical movement (either mandibular setback or advancement). However, the same is not true in virtual prediction. All eight clinically unacceptable results generated by our three‐stage FEM method were due to this particular reason. Additionally, lack of ability to simulate the interaction between the lips might have led to the inaccuracy in the lip region.12, 23 We are currently working on solutions for this clinically observed phenomenon considering aforementioned possible cause.
The quantitative results in this study did not necessarily reflect the qualitative results, and vice versa (Fig. 5). However, they are complementary to each other. The clinicians could quickly recognize geometrical features of the face, e.g., overall facial balance, the relationship between the upper and lower lips and clinical feasibility (whether the predicted correction was clinically achievable). This information could be sufficiently represented by quantitative analysis, even with the surface deviations calculated using the surface normal information. In addition, the unnatural shape and position of the lips, labiomental fold, and chin, and the mesh distortion in the cheek regions (mandibular inferior border) could only be recognized by qualitative analysis with the clinicians’ eyes. However, it was difficult for the clinicians to distinguish subtle regional differences. This is because the human eyes have tolerance in measuring size and position. Therefore, a more sophisticated evaluation method combing the strength of both the quantitative and qualitative evaluation is required in the future.
5. Conclusion
We developed a novel and now clinically validated three‐stage FEM approach to better predict facial soft‐tissue changes following orthognathic surgery. The main features of our approach included the enhanced sliding effect between mucosa and the teeth around the mouth area. Our overall goal was to improve predictability of facial features, and thereby clinical outcome, specifically around the upper lip and lower lip areas. The simulation result of the complete three‐stage method showed significant improved prediction accuracy in clinically critical region (i.e., nose and lips) compared to the current FEM simulation methods. However, the accuracy in the lip, especially the lower lip, still requires further improvement. The clinicians’ qualitative evaluation also proved that our approach is clinically acceptable. We found that the quantitative error evaluation doesn't necessarily correspond with the clinicians’ qualitative evaluation. Therefore, improved error evaluation method reflecting both the quantitative and qualitative evaluation result is necessary for more accurate and objective evaluation in the future.
Conflict of interest
The authors have no COI to report.
Acknowledgments
The author thank Chien‐Ming Chang, D.D.S., Yi‐Fang Lo, D.D.S., and Zhen Tang, D.D.S., M.S., Ph.D. for their contributions on this project. This work is funded in part by the United States NIH/NIDCR grants R01DE022676 and R01DE021863. Dr. Ho was sponsored by Taipei Municipal Wan Fang Hospital, Taiwan (ROC), and Dr. Mai was sponsored by Scholarship Fund of Guangxi Education Department, Guangxi, China, and, while working at the Surgical Planning Laboratory, Department of Oral and Maxillofacial Surgery, Houston Methodist Research Institute, Houston, TX, USA.
References
- 1. Xia JJ, Gateno J, Teichgraeber JF, et al. Algorithm for planning a double‐jaw orthognathic surgery using a computer‐aided surgical simulation (CASS) protocol. Part 1: planning sequence. Int J Oral Maxillofac Surg. 2015;44:1431–1440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. McCormick SU, Drew SJ. Virtual model surgery for efficient planning and surgical performance. J Oral Maxillofac Surg. 2011;69:638–644. [DOI] [PubMed] [Google Scholar]
- 3. Bobek S, Farrell B, Choi C, Farrell B, Weimer K, Tucker M. Virtual surgical planning for orthognathic surgery using digital data transfer and an intraoral fiducial marker: the charlotte method. J Oral Maxillofac Surg. 2015;73:1143–1158. [DOI] [PubMed] [Google Scholar]
- 4. Bell WH. Modern Practice in Orthognathic and Reconstructive Surgery: volume 3. Philadelphia, PA: W.B. Saunders company; 1993. [Google Scholar]
- 5. Chabanas M, Luboz V, Payan Y. Patient specific finite element model of the face soft tissues for computer‐assisted maxillofacial surgery. Med Image Anal. 2003;7:131–151. [DOI] [PubMed] [Google Scholar]
- 6. Koch RM, Gross MH, Carls FR, Büren DFV, Fankhauser G, Parish YIH. Simulating facial surgery using finite element models. In: Proc. of SIGGRAPH. New York, NY: ACM; 1996: 421–428. [Google Scholar]
- 7. Keeve E, Girod S, Kikinis R, Girod B. Deformable modeling of facial tissue for craniofacial surgery simulation. Comput Aided Surg. 1998;3:228–238. [DOI] [PubMed] [Google Scholar]
- 8. Cotin S, Delingette H, Ayache N. A hybrid elastic model for real‐time cutting, deformations, and force feedback for surgery training and simulation. The Visual Computer. 2000;16:437–452. [Google Scholar]
- 9. Kim H, Jürgens P, Nolte L‐P, Reyes M. Anatomically‐driven soft‐tissue simulation strategy for cranio‐maxillofacial surgery using facial muscle template model. In: Proc of MICCAI. New York, NY: Springer; 2010: 1361–1368. [DOI] [PubMed] [Google Scholar]
- 10. Kim H, Jürgens P, Weber S, Nolte L‐P, Reyes M. A new soft‐tissue simulation strategy for cranio‐maxillofacial surgery using facial muscle template model. Prog Biophys Mol Biol. 2010;103:284–291. [DOI] [PubMed] [Google Scholar]
- 11. Pan B, Xia JJ, Yuan P, et al. Incremental kernel ridge regression for the prediction of soft tissue deformations. In: Proc of MICCAI. New York, NY: Springer; 2012; 99–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Nadjmi N, Defrancq E, Mollemans W, Hemelen GV, Berge S. Quantitative validation of a computer‐aided maxillofacial planning system, focusing on soft tissue deformations. Ann Maxillofac Surg. 2014;4:171–175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Kaipatur NR, Flores‐Mir C. Accuracy of computer programs in predicting orthognathic surgery soft tissue response. J Oral Maxillofac Surg. 2009;67:751–759. [DOI] [PubMed] [Google Scholar]
- 14. Roose L, De Maerteleire W, Mollemans W, Maes F, Suetens P. Simulation of soft‐tissue deformations for breast augmentation planning. In: Proc of International Symposium on Biomedical Simulation. 2006; 197–205. [Google Scholar]
- 15. Kim D, Mai H, Chang C‐M, et al. FEM simulation with realistic sliding effect to improve facial‐soft‐tissue‐change prediction accuracy for orthognathic surgery. In: Proc of MIAR. New York, NY: Springer; 2016: 27–37. [Google Scholar]
- 16. Kim D, Chang C‐M, Ho DC‐Y, et al. Two‐stage simulation method to improve facial soft tissue prediction accuracy for orthognathic surgery. In: Proc of MICCAI. New York, NY: Springer; 2016: 559–567. [Google Scholar]
- 17. Zhang X, Tang Z, Liebschner MAK, et al. An eFace‐template method for efficiently generating patient‐specific anatomically‐detailed facial soft tissue FE models for craniomaxillofacial surgery simulation. Ann Biomed Eng. 2016;44:1656–1671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Mollemans W, Schutyser F, Nadjmi N, Maes F, Suetens P. Parameter optimisation of a linear tetrahedral mass tensor model for a maxillofacial soft tissue simulator. In: Proc of International Symposium on Biomedical Simulation. New York, NY: Springer; 2006: 159–168. [Google Scholar]
- 19. Zachow S, Hierl T, Erdmann B. A quantitative evaluation of 3D soft tissue prediction in maxillofacial surgery planning. In: Proc of CURAC. Stuttgart: CURAC; 2004: 75–79. [Google Scholar]
- 20. Hsu SS, Gateno J, Bell RB, et al. Accuracy of a computer‐aided surgical simulation protocol for orthognathic surgery: a prospective multicenter study. J Oral Maxillofac Surg. 2013;71:128–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Xia JJ, Gateno J, Teichgraeber JF, et al. Accuracy of the computer‐aided surgical simulation (CASS) system in the treatment of patients with complex craniomaxillofacial deformity: a pilot study. J Oral Maxillofac Surg. 2007;65:248–254. [DOI] [PubMed] [Google Scholar]
- 22. Xia JJ, Gateno J, Teichgraeber JF. New clinical protocol to evaluate craniomaxillofacial deformity and plan surgical correction. J Oral Maxillofac Surg. 2009;67:2093–2106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Smith JD, Thomas PM, Proffit WR. A comparison of current prediction imaging programs. Am J Orthod Dentofac Orthop. 2004;125:527–536. [DOI] [PMC free article] [PubMed] [Google Scholar]


