Large polarons in lead halide perovskites

Charge carriers in both hybrid and all-inorganic lead halide perovskites form large polarons.

Abstract

Lead halide perovskites show marked defect tolerance responsible for their excellent optoelectronic properties. These properties might be explained by the formation of large polarons, but how they are formed and whether organic cations are essential remain open questions. We provide a direct time domain view of large polaron formation in single-crystal lead bromide perovskites CH₃NH₃PbBr₃ and CsPbBr₃. We found that large polaron forms predominantly from the deformation of the PbBr₃⁻ frameworks, irrespective of the cation type. The difference lies in the polaron formation time, which, in CH₃NH₃PbBr₃ (0.3 ps), is less than half of that in CsPbBr₃ (0.7 ps). First-principles calculations confirm large polaron formation, identify the Pb-Br-Pb deformation modes as responsible, and explain quantitatively the rate difference between CH₃NH₃PbBr₃ and CsPbBr₃. The findings reveal the general advantage of the soft [PbX₃]⁻ sublattice in charge carrier protection and suggest that there is likely no mechanistic limitations in using all-inorganic or mixed-cation lead halide perovskites to overcome instability problems and to tune the balance between charge carrier protection and mobility.

INTRODUCTION

The exceptional rise in research activities on hybrid organic-inorganic lead halide perovskites (HOIPs) is a direct result of their marked optoelectronic properties that resemble defect-free semiconductors, despite static and dynamic disorder (1–3). Even with modest mobilities (4–8), they show long carrier lifetimes and diffusion lengths that are key to their successes in optoelectronic devices (9–11). An HOIP crystal consists of a lead halide sublattice (PbX₃⁻), which determines the band structure (12), and a disordered organic cation sublattice (A⁺), which modulates the electronic properties (13–17). This unique APbX₃ structure and associated dielectric responses (17, 18) have led to the large polaron proposal (19, 20) in which the dynamically screened coulomb potential minimizes charge carrier scattering with defects, with other charges, and with longitudinal optical (LO) phonons. Although this proposal may explain some of the carrier properties of HOIPs, there has been no direct observation or confirmation of (large) polaron formation. Whether A-site organic cations are essential (13–16, 21) or not (22–25) also remains an open question. Here, we provide a direct time domain view of phonon dynamics in the CH₃NH₃PbBr₃ HOIP in comparison to its all-inorganic counterpart, CsPbBr₃, using time-resolved optical Kerr effect (TR-OKE) spectroscopy (26, 27) in conjunction with hybrid density functional theory (DFT) calculations. We show the dominance of coupling between PbBr₃⁻ lattice motions to across-bandgap electronic transitions in both perovskites, but different polaron formation time constants of 0.3 and 0.7 ps for CH₃NH₃PbBr₃ and CsPbBr₃, respectively. DFT calculations reveal the major role of a subset of coupled Pb-Br stretching and Pb-Br-Pb bending modes in large polaron formation. Our calculations also suggest that the coupled motions of the organic cations to the PbBr₃⁻ lattice are responsible for faster polaron formation in CH₃NH₃PbBr₃ than that in its all-inorganic counterpart.

RESULTS AND DISCUSSION

We synthesized optically flat, single-crystal CH₃NH₃PbBr₃ and CsPbBr₃ samples (see Materials and Methods and fig. S1 for details) (6), with effective bandgaps of E_g = 2.28 and 2.35 eV, respectively (see fig. S2). In TR-OKE, the electric field of a linearly polarized pump laser pulse creates transient anisotropy, and the resulting birefringence is detected by the polarization rotation of a probe pulse, which allows us to measure the system’s response in a wide time range (femtosecond to nanosecond). We implement heterodyne-detected TR-OKE using homebuilt two-color pump-probe systems (see fig. S3). The photon energy of the pump was tunable (hν₁ = 1.85 to 2.45 eV), and that of the probe was fixed (hν₂ = 1.55 or 1.65 eV).

We examine structural flexibility and dynamic disorder in CH₃NH₃PbBr₃ coupled to carriers by varying the pump photon energy from nonresonant (1.85 eV) to preresonant (2.10 eV) regimes (Fig. 1A). We see that the broad and featureless nuclear response is distinctively different from that of a typical solid, where impulsively stimulated Raman excitation should appear as oscillatory features (28), and is instead characteristic of liquids (26, 27). The absence of oscillatory features suggests that we detect predominantly overdamped phonon modes that can be attributed to strong anharmonicity and dynamic disorder (29, 30). As hν₁ moves closer (2.03 to 2.18 eV) to E_g, we find enhanced slow responses (≥1 ps). This is attributed to the resonant Raman mechanism, where nuclear motions are coupled to electronic transitions (31). As seen in Fourier spectra of the OKE transients (Fig. 1B), approaching the E_g resonance enhances low-frequency (<100 cm⁻¹) motions corresponding to those of the PbBr₃⁻ lattice (32), particularly the coupled Pb-Br stretching and Pb-Br-Pb bending motions, as shown by the calculated phonon spectrum at the top of Fig. 1B.

Fig. 1. TR-OKE transients from a CH₃NH₃PbBr₃ crystal.

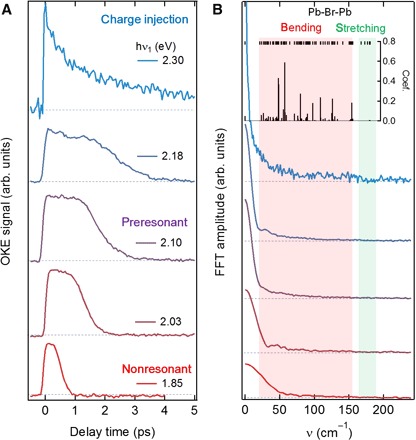
(A) OKE transients from CH₃NH₃PbBr₃ as a function of pump energy (1.85 to 2.30 eV). As it moves from nonresonant to preresonant condition, contribution from low-frequency motions coupled to electronic excitation is enhanced. As it reaches the carrier injection regime, additional subpicosecond dynamics manifest itself. (B) Fourier component of each OKE transient. The inset is the crystalline structure of CH₃NH₃PbBr₃. Black ticks at the top show calculated frequencies of normal modes, and sticks represent projections of the displacement vector on the normal modes upon large polaron formation (see fig. S4). FFT, fast Fourier transform.

By tuning hν₁ to 2.30 eV (≥E_g), we directly probe the OKE response upon charge injection (topmost transient in Fig. 1A). We observe qualitatively different structural dynamics: a subpicosecond component with a time constant of τ₁ = 0.29 ± 0.04 ps and longer-lived anisotropy that decays with τ₂ = 3.4 ± 0.5 ps. These features are absent in OKE transients for hν₁ < E_g and are thus associated with the dynamic response of nuclei to the photoinjection of carriers, that is, formation of (large) polarons. We show, at the top of Fig. 1B, projections (sticks) of the displacement vector following a positive charge injection onto the calculated normal modes and find that a subset of stretching and bending modes of the inorganic sublattice is mainly responsible for this structural relaxation, as detailed later.

We compare the OKE responses in CH₃NH₃PbBr₃ with those in a fully inorganic CsPbBr₃ single crystal (Fig. 2). When hν₁ (=1.83 or 2.00 eV) is far below E_g, the OKE signal consists of two responses: a broad feature within ~0.3 ps and an oscillatory response distributed over a few picoseconds (Fig. 2A); the former is liquid-like (26, 27), whereas the latter is Raman-active vibrations typical of solids (28). The corresponding Fourier spectra in Fig. 2B for hν₁ = 1.83 and 2.00 eV show a broad low-frequency peak (<100 cm⁻¹) in the region of coupled lead halide stretching and bending vibrations (see calculated frequencies in Fig. 2B and fig. S4). A few partially resolved phonon peaks are also present in the Fourier spectrum for hν₁ = 2.00 eV. The broad low-frequency peak, which agrees with the Raman spectra of Yaffe et al. (30), reflects the structural softness of CsPbBr₃, whose Young’s modulus is similar to that of CH₃NH₃PbBr₃; both are 10 times lower than those of Si and GaAs (33). As we increase hν₁ to the preresonant regime (2.21 to 2.25 eV), we see the resonance enhancement of slower picosecond-scale responses in CsPbBr₃. This is similar to the results from CH₃NH₃PbBr₃ and can again be attributed to PbBr₃⁻ motions. There is one important distinction: In CsPbBr₃, we see particularly long-lived oscillations, as well as a broad overdamped feature, whereas in CH₃NH₃PbBr₃ only the overdamped feature is observed. On the basis of the calculated vibrational frequencies, we assign the particularly prominent peaks at ~50 and ~85 cm⁻¹ to Pb-Br-Pb bending modes coupled with Pb-Br stretchings (see fig. S4) and the peak at ~130 cm⁻¹ to the pure Pb-Br stretching modes. When hν₁ (=2.43 eV) exceeds E_g, the TR-OKE response changes completely. All oscillatory features disappear upon carrier injection, suggesting that a large number of low-frequency modes could couple to photogenerated charge carriers and that there could be increased overdamping of the phonon oscillation due to their coulomb interaction with the charge carriers. Instead of oscillations, we see a subpicosecond component with a time constant of τ₁ = 0.7 ± 0.1 ps and longer-lived anisotropy that decays with τ₂ = 6.5 ± 0.3 ps. Notably, the phonon dynamics upon charge injection are similar in both CsPbBr₃ and CH₃NH₃PbBr₃, albeit the time constants are longer by about two times in the former. In CH₃NH₃PbBr₃, although there is negligible contribution of the high-frequency organic cation vibrations to polaron formation (see fig. S5), reorientational motions of these cations within the lead halide cage could couple to Pb-Br-Pb phonon modes, leading to faster polaron formation in CH₃NH₃PbBr₃ than that in CsPbBr₃, as we confirm below in first-principles calculations.

Fig. 2. TR-OKE transients from a CsPbBr₃ crystal.

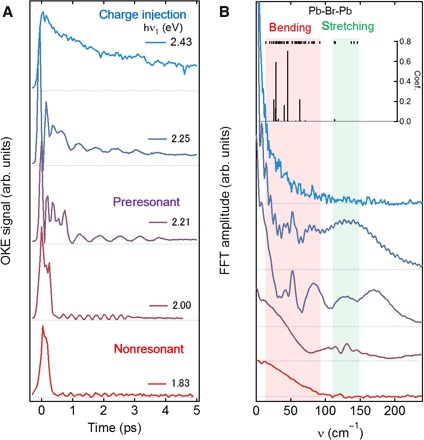
(A) OKE transients from CsPbBr₃ as a function of pump energy (1.83 to 2.43 eV). At the preresonant regime, low-frequency modes that are coupled to band-edge excitation are enhanced. At the carrier injection regime, additional subpicosecond dynamics, as well as long-lived polarization, manifest itself. (B) Fourier spectra of selected transients in nonresonant regime (1.83 and 2.00 eV), preresonant regime (2.21 and 2.25 eV), and carrier injection regime (2.43 eV). The inset is the crystalline structure of CsPbBr₃. Black ticks at the top show calculated frequencies of normal modes, and sticks represent projections of the displacement vector on the normal modes upon large polaron formation (see fig. S5).

The TR-OKE experiments with hν₁ ≥ E_g probe the injected charge dynamics from the phonon perspective. We now probe the same dynamics from the electronic degrees of freedom side using femtosecond transient reflectance. Figure 3A shows a two-dimensional pseudocolor plot of transient absorption coefficiency (Δα) of CH₃NH₃PbBr₃ as a function of probe photon energy and pump-probe delay (Δt) following the excitation at time 0 by hν₁ = 2.92 eV. Here, α is obtained by a Kramers-Kronig transformation from time-dependent reflectance, ΔR/R (see Materials and Methods and fig. S6 for details) (34). At Δt > 1 ps, the band-edge spectral region corresponds to simple bleaching of the excitonic resonance, but at shorter times, the spectrum features a derivative shape that corresponds to a red shift in the absorption peak. The red-shifted feature is attributed to band renormalization due to many-body coulomb interaction among photoexcited carriers, as is well known in inorganic semiconductors (35). Because the nanosecond lifetime of charge carriers (23) means that carrier population remains constant on the subpicosecond time scale, the disappearance of the red shift can thus be attributed to the reduction of the many-body coulomb potential, consistent with the dynamic screening of initially excited free carriers in polaron formation. A similar transient red shift has also been observed for CsPbBr₃ (fig. S6). The red shifts disappear with time constants of 0.28 ± 0.04 ps and 0.6 ± 0.1 ps for CH₃NH₃PbBr₃ and CsPbBr₃, respectively (Fig. 3B). These time constants agree with those of the ultrafast screening time in TR-OKE response at hν₁ ≥ E_g (Fig. 3C), where faster TR-OKE responses yield time constants of τ₁ = 0.29 ± 0.04 ps and 0.7 ± 0.1 ps for CH₃NH₃PbBr₃ and CsPbBr₃, respectively. The long time constants (τ₂ = 3.4 ± 0.5 ps and 6.5 ± 0.3 ps) in TR-OKE are not seen in transient reflectance, suggesting that the ultrafast screening and polaron formation processes are already completed on the subpicosecond time scale of τ₁. The longer time scales can be attributed to further depolarization due to the polaron motion possibly coupled to the slower dynamics of the A-site cations.

Fig. 3. Comparison of transient reflectance and TR-OKE with above-gap excitation.

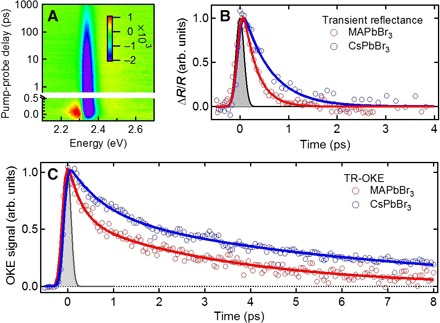
(A) Pseudocolor (Δα) representation of transient absorbance spectra of a CH₃NH₃PbBr₃ single crystal retrieved from transient reflectance (ΔR/R) pumped by 2.92 eV at 100 μW. (B) Dynamics of screening extracted from transient reflectance probed at 2.31 eV for CH₃NH₃PbBr₃ (blue) and at 2.38 eV for CsPbBr₃ (red) as a function of pump-probe delay. The lines are monoexponential fits convoluted with a Gaussian function, which describes the cross-correlation between pump and probe pulse [full width at half maximum (FWHM), 100 fs]. (C) The structural dynamics triggered by photo-carrier injection as a function of pump-probe delay observed by TR-OKE with across-gap excitation. CH₃NH₃PbBr₃ (blue) and at 2.38 eV for CsPbBr₃ (red) as a function of the pump-probe delay. The lines are double-exponential fits convoluted with a Gaussian function, which describes cross-correlation between the pump and probe pulse (FWHM, 70 fs).

Although the TR-OKE responses appear different between CH₃NH₃PbBr₃ and CsPbBr₃ when the pump photon energy is below the bandgap, as the Raman-active phonon modes are partially resolved (oscillatory features in the time domain) in the latter but not in the former, the responses become very similar for across-bandgap excitation (charge injection regime). To understand the seemingly similar origins of polaron formation in CH₃NH₃PbBr₃ and CsPbBr₃, and to reveal possible distinctive atomistic features underlying the different time response of the two perovskites, we carry out first-principles calculations on pseudocubic CH₃NH₃PbBr₃ and orthorhombic CsPbBr₃ 2 × 2 × 1 crystals (corresponding to the room temperature stable phases) in the absence and presence of positive/negative added charges using the hybrid PBE0 functional (36, 37) and the experimental cell parameters (38). In both CH₃NH₃PbBr₃ and CsPbBr₃ crystals, we find that a positive added charge induces a much larger structural relaxation than a negative charge, with the most significant variation associated to the average Pb-Br bond length and Pb-Br-Pb bond angle (θ) associated with the equatorial Br atoms (Fig. 4). Here, we are calculating the local relaxation, starting from the minimum energy structure in the absence of charges, likely representing the fast component of the relaxation process observed experimentally. A stabilization energy of 0.06 and 0.14 eV is calculated for a positive added charge to CH₃NH₃PbBr₃ and CsPbBr₃, respectively, whereas the negative charge is stabilized in both cases by only a few millielectron volts. For CH₃NH₃PbBr₃, θ increases from 162° to 167° in the positively charged structure (Fig. 4B). For CsPbBr₃, a correspondingly larger increase from θ = 153° to θ = 163° is calculated (Fig. 4D); the opposite holds for the negative charge, with θ decreasing by ~2° in both CH₃NH₃PbBr₃ and CsPbBr₃. The evident Pb-Br-Pb angle increase (decrease) is driven by the shortening (lengthening) of the Pb-Br average bond lengths [−0.04 Å versus +0.01 Å for positive (Fig. 4, B and D) and negative (Fig. 4, C and E) added charges, respectively]. The observed relaxation pattern is consistent with the dominant involvement of the coupled Pb-Br stretching and Pb-Br-Pb bending modes in polaron stabilization. This is most obvious in projected displacement vectors associated with a positive charge in CH₃NH₃PbBr₃ and CsPbBr₃ (inset in Figs. 1B and 2B and detailed in figs. S4 and S5). Associated with the Pb-Br-Pb angle increase due to the positive charge, the CH₃NH₃ and Cs cations also respond by progressively moving toward their cubic sites (Fig. 4, B to D); the opposite holds for negative charge. Thus, the overall atomic relaxation associated with positive (negative) charge leads to more cubic (tilted) crystal structures. We confirm this trend also in CH₃NH₃PbI₃, with similar stabilization energy and structural distortion as for CH₃NH₃PbBr₃ (fig. S7). This agrees with a two-dimensional electronic spectroscopy study of CH₃NH₃PbI₃ by Monahan et al. (39), who showed strong coupling of charge carriers to a 0.9-THz phonon mode attributed to Pb-I lattice distortions. Note that TR-OKE selectively detects nondiagonal terms of the Raman tensor, whereas a two-dimensional electronic spectroscopy detects all possible oscillation causing modulation in the band gap, which explains better resolved oscillation in the observation of Monahan et al. (39). The dominant coupling between an extra charge carrier and the distortions of the lead halide sublattice is consistent with the report of photostriction in CH₃NH₃PbI₃ single crystal (40) and with the suggestion of elongation of the [PbBr₆]²⁻ octahedra in CH₃NH₃PbBr₃ nanocrystals upon charge injection (41).

Fig. 4. Hybrid DFT calculations.

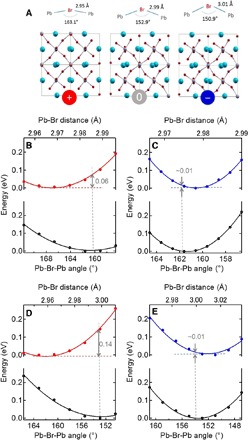
(A) Relaxed structures of CH₃NH₃PbBr₃ with positive and negative charge injection. Changes in Pb-Br-Pb bending and Pb-Br length are shown. (B to E) Potential energy surfaces for relaxation of the CH₃NH₃PbBr₃ (B and C) and CsPbBr₃ (D and E) unit cell (four formula units) upon positive (B and D; red curve) and negative (C and E; blue curve) charge injection. The neutral state energy (black) along the distortion coordinate is also shown.

The structural reorganization for an added hole is much larger than that caused by an added electron in either CH₃NH₃PbBr₃ or CsPbBr₃. This contrast between positive and negative charges can be understood by the different origins of valence and conduction bands. The valence band is composed of antibonding combinations of Pb 6s and Br 4p orbitals, whereas the conduction band is dominated by the Pb 6p orbital. As a result, the valence band should be much more sensitive than the conduction band is to the bending/stretching of Pb-Br-Pb. This implies that electrons experience less localization from the octahedral distortion than the holes do. To estimate the size of the polaron, we have carried out additional hybrid DFT calculations on a 2 × 2 × 8 CsPbBr₃ supercell, obtained by replicating the crystal unit cell along the c axis. The cubic cell parameter was first optimized for the neutral case, providing a value of 5.93 Å, matching the experimental value of 5.9 Å (38). By simultaneously shortening the Pb-Br bonds and, thus, the long supercell dimension, we find an increase in energy of the neutral system, but ~0.1-eV stabilization for the positive system (fig. S8). Upon geometrical relaxation by PBE0 of the distorted 2 × 2 × 8 supercell in the presence of a positive added charge, we obtain a distribution of Pb-Br distances along the long cell dimension (Fig. 5A), which correlates with the decay of density associated with the added hole away from a center of maximum distortion (Fig. 5B). This is the signature of the large polaron distortion, which slowly decays away from the point of maximally localized charge (set at the center) and approaching saturation for a radius of ρ_h ~ 2.5 nm. This polaron dimension is likely a lower bound approximation to the actual value due to the finite size of the used supercell. We are not able to similarly estimate the polaron size for an added electron due to the much smaller structural distortion requiring larger supercell sizes to observe a saturation behavior. However, our calculation suggests that the electron and the hole are localized in spatially distinct regions. By varying the Pb-Br distances in different crystal regions, we are able to localize the excess positive (negative) charge in regions of shorter (longer) Pb-Br distances (fig. S9). A similar behavior is observed when we modulate the octahedra tilting (fig. S10), with the positive charge mainly localized in the untilted region characterized by shorter Pb-Br bonds. The opposite structural distortion accompanying positive and negative excess charges suggests a spatially separated distribution of photogenerated electrons (more delocalized) and holes (more localized), consistent with a barrier to electron-hole recombination (42).

Fig. 5. Estimation of polaron size from first principle.

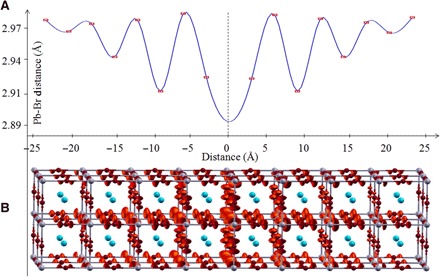
(A) Distribution of Pb-Br distances (Å; top) of the positive polaron state for a pseudocubic 2 × 2 × 8 CsPbBr₃ model made by 32 formula units. (B) Distribution of the excess positive charge (red isosurface) following the pattern of Pb-Br distances. The figure has been centered at the maximum of hole localization.

We point out that the present calculation focuses on PbBr₃⁻ lattice phonons that are most strongly coupled to the electronic degrees of freedom in APbBr₃. It may be necessary to use a much larger supercell, possibly coupled to long–time scale molecular dynamics simulations, to account for the reorientational motion of the CH₃NH₃⁺ cations in further localization. This approach is computationally beyond reach for the type of first-principles calculations used here but could be feasible with more approximate methods. By sampling randomly generated configurations of the CH₃NH₃⁺ cations in CH₃NH₃PbI₃, Ma and Wang (15) found localization of conduction and valence bands to spatially separate regions with radii of ρ_e ~ 8.3 nm and ρ_h ~ 5.6 nm for electrons and holes, with estimated stabilization energies as large as 100 meV. The larger screening exerted by the dipolar organic cations, as illustrated by Ma and Wang (15), may also explain the different polaron stabilization energies between CH₃NH₃PbBr₃ (60 meV) and CsPbBr₃ (140 meV) in our calculation. This was verified in separate calculations in which we removed the A-cations and recalculated the stabilization energy, considering the geometries for the full system. In this case, we calculate a similar positive charge relaxation energy of ~0.09 eV in both CH₃NH₃PbBr₃ and CsPbBr₃ (fig. S11), pointing to the A-cations as being responsible for the difference between the two perovskites beyond the different phases.

Our calculations not only reveal the essential role of the PbBr₃⁻ sublattice in polaron formation but also explain quantitatively the different polaron formation rates between CH₃NH₃PbBr₃ and CsPbBr₃. The projections of the displacement vector on the normal modes upon large polaron formation (black sticks in Figs. 1B and 2B) give mean frequencies of $\langle \overline{\mathrm{\nu }}\rangle$ = 92.4 and 40.8 cm⁻¹ in CH₃NH₃PbBr₃ and CsPbBr₃, respectively. These mean frequencies correspond to time constants of 0.36 and 0.82 ps, in excellent agreement with the corresponding time constants of τ_p = 0.3 and 0.7 ps in CH₃NH₃PbBr₃ and CsPbBr₃, respectively, observed in TR-OKE measurements. This difference can be attributed to the different coupling of cation motions to PbBr₃⁻ lattice phonon modes; the faster motion of CH₃NH₃⁺ (reorientation) than that of the heavier Cs⁺ (displacement) can account for the different $\langle \overline{\mathrm{\nu }}\rangle$ or τ_p between CH₃NH₃PbBr₃ and CsPbBr₃.

We can estimate charge carrier mobilities and large polaron sizes based on the formulism of Fröhlich (43) and Feynman (44). Because the low-frequency phonon modes (≤150 cm⁻¹; Figs. 1B and 2B) mainly responsible for polaron formation in CH₃NH₃PbBr₃ and CsPbBr₃ are highly populated at room temperature, the more general formula of Ōsaka is more appropriate (45). The strength of electron–LO phonon coupling is represented by the unitless Fröhlich coupling constant, α_e-ph, which can be calculated from the LO phonon frequency, carrier band mass, and dielectric constants (fig. S12 and table S2). On the basis of our calculated LO phonon frequencies, we obtain α_e-ph = 1.54 and 1.87 in CH₃NH₃PbBr₃ for the electron and the hole, respectively. The corresponding values in CsPbBr₃ are α_e-ph = 2.64 and 2.76 for the electron and the hole, respectively (see Materials and Methods and table S3). The weaker e-ph coupling in CH₃NH₃PbBr₃ than that in CsPbBr₃ and the weaker e-ph coupling for the electron than that for the hole both agree with the first-principles results in Fig. 4. These coupling constants are a bit smaller than those in the conventional inorganic perovskite materials, for example, α_e-ph = 3 to 4 in SrTiO₃ (46). We obtain from the Feynman-Ōsaka formula (44, 45) electron and hole polaron mobilities of μ_e = 149.8 cm² V⁻¹ s⁻¹ and μ_h = 79.2 cm² V⁻¹ s⁻¹ with corresponding polaron radii of ρ_e = 4.18 nm and ρ_h = 3.13 nm in CH₃NH₃PbBr₃. The corresponding values in CsPbBr₃ are μ_e = 48.2 cm² V⁻¹ s⁻¹, μ_h = 41.3 cm² V⁻¹ s⁻¹, ρ_e = 2.67 nm, and ρ_h = 2.49 nm (see Materials and Methods and table S3). The calculated ρ_h in CsPbBr₃ agrees with the estimation value from the first-principles calculation (Fig. 5). Our results also agree with similar treatments by Sendner et al. (47), who estimated an average electron/hole polaron mobility in CH₃NH₃PbBr₃ of μ_e-h ~ 158 cm² V⁻¹ s⁻¹ for a polaron radius of 4.3 nm and by Frost (48) who calculated electron and hole polaron mobilities in CH₃NH₃PbI₃ of 136 and 94 cm² V⁻¹ s⁻¹, respectively. These estimated polaron mobilities agree with the upper bounds in the range of experimental values from single crystals at room temperature (5, 6, 8, 23, 49, 50): 10 to 115 cm² V⁻¹ s⁻¹ for CH₃NH₃PbBr₃, 24 to 164 cm² V⁻¹ s⁻¹ for CH₃NH₃PbI₃, and 38 cm² V⁻¹ s⁻¹ for CsPbBr₃. Thus, it is mainly optical, not acoustic, phonons that limit the charge carrier mobility in lead halide perovskites. Note that although the experimentally determined temperature dependences in charge carrier mobility (42, 50, 51) agree with the μ ∝ T^{− 1.5} scaling law predicted from acoustic phonon scattering in nonpolar semiconductors (52), analysis based on this mechanism yields charge carrier mobilities of the order of 10³ cm² V⁻¹ s⁻¹ (53–56), which is one order of magnitude higher than the experimental values (5, 6, 8, 23, 49, 50). Note also that the weakly bound large polarons obtained here are responsible for coherent transport (19), in contrast to the more tightly bound small polarons that may function as minority trapped charges (57).

In summary, we provide a time domain experimental view and first-principles verification of large polaron formation in CH₃NH₃PbBr₃ and CsPbBr₃. The combined experiment and calculation establish the deformation of the PbBr₃⁻ sublattice as mainly responsible for the large polaron formation in both crystals. The large polaron model predicts modest charge carrier mobilities that agree with the experimental measurements. The lower frequencies of the PbBr₃⁻ sublattice motions (coupled to A-cation motion) in CsPbBr₃ than those in CH₃NH₃PbBr₃ also explain quantitatively the experimentally observed large polaron formation time constants. The difference in large polaron formation rate accounts for its competitiveness with hot carrier cooling in CH₃NH₃PbBr₃ and CH₃NH₃PbI₃ (20, 58), not in CsPbBr₃ (20), but the large polarons may otherwise show similar properties due to common deformations of the lead halide sublattice. The latter suggests a similar mechanism for the protection of band-edge carriers in HOIPs and their all-inorganic counterparts, thus accounting for similar solar cell performance and similar band-edge carrier properties obtained with purely organic, inorganic, and mixed-cation perovskites (22–25). Alloying different organic and inorganic A-cations, which was shown to be an effective strategy toward high-efficiency devices (59), could be a way of tuning the extent of polaron stabilization to balance charge carrier protection (screening) and mobility.

MATERIALS AND METHODS

Synthesis and structural characterizations of APbBr₃ (A = CH₃NH₃, or Cs) crystals

Millimeter-scale single-crystal samples of CH₃NH₃PbBr₃ and CsPbBr₃ were prepared under ambient conditions via a vapor diffusion method in which the vapor of an antisolvent slowly diffuses into a perovskite precursor solution (6). CH₃NH₃PbBr₃ crystals were grown by the slow diffusion of dichloromethane into a solution of PbBr₂ and CH₃NH₃Br (1:2 molar ratio, 0.5 M and 1.0 M) in N,N-dimethylformamide.

CsPbBr₃ crystals were grown by a modified vapor diffusion method in which a solution of PbBr₂ and CsBr (1:1 molar ratio, 0.4 M) in dimethyl sulfoxide was prepared. This solution was then titrated with MeOH. Once the saturation point was reached, the solution was left to stir for 24 hours. The resulting supernatant was filtered and used as the precursor solution for a similar vapor diffusion process. The antisolvent was MeOH (60).

The single-crystalline nature of the perovskite samples was confirmed by single-crystal x-ray diffraction. Optical images and reconstructed precession images are shown in fig. S1. Data were collected on an Agilent SuperNova single-crystal x-ray diffractometer at room temperature. The lattice constants are given in table S1. These were consistent with literature values and reflected the pseudocubic phase for CH₃NH₃PbBr₃ and the orthorhombic phase for CsPbBr₃ (61, 62).

TR-OKE measurements

We carried out femtosecond TR-OKE measurements using a homebuilt two-color pump-probe system described below. The outputs from two noncollinear optical parametric amplifiers (NOPAs) served as pump and probe laser pulse for the measurements for CH₃NH₃PbBr₃, except the one at hν₁ = 2.30 eV. The NOPAs were pumped by the second and third harmonic of a Yb-doped fiber laser (Clark-MXR Impulse) operated at 500 kHz. The center wavelengths of the visible pump and near-infrared probe pulses were in the range of 1.85 to 2.25 eV (tunable) and 1.61 to 1.66 eV, respectively. The bandwidths for both pulses were ~0.10 eV (FWHM). Pulse energies were 4 and 0.3 nJ for the pump and probe pulses with its spot sizes of about 600 and 120 μm, respectively. The pulses were focused on the sample with polarizations set to 45° with respect to each other, whereas a delay line was used to control the time delay between the pulses. The probe polarization was along the [110] crystal direction for CH₃NH₃PbBr₃ and along the [100] direction for CsPbBr₃ to minimize the polarization rotation from intrinsic anisotropy. The pump beam was blocked after the sample, whereas the probe beam was routed through a second polarizer, which was set at the crossed polarization against the first polarizer in front of the sample. To achieve heterodyne detection, a local oscillator was introduced by rotating the second polarizer by either +2 or −2° away from the homodyne orientation which gave maximum extinction of the probe beam. The Kerr signal was detected by a large-area amplified PIN photodiode (100A, Thorlabs), with 700-nm longpass filter to eliminate a scattered pump beam, and was recorded by a lock-in amplifier (SR830, Stanford Research Systems), synchronized with the modulation of the pump beam intensity by a mechanical chopper at 5 kHz. For the measurements for a CH₃NH₃PbBr₃ crystal at hν₁ = 2.30 eV and all the OKE measurements for a CsPbBr₃ crystal, the output pulses from NOPA pumped by the second harmonic of a Ti:sapphire laser (Wyvern1000-50, KMLabs) operated at 10 kHz were used as tunable pump pulses (1.83 to 2.48 eV) to gain higher-energy pulses, and its fundamental pulses (1.55 to 1.57 eV) were used as probe. Pulse energies were 100 and 3 nJ for the pump and probe pulses, respectively. The Kerr signal was detected by a homebuilt spectrometer equipped with a high-speed linear array detector (AVIIVA EM4, EV71YEM4CL1014-BA9, e2v) synchronized with the modulation of the pump beam intensity by a mechanical chopper at 5 kHz for shot-to-shot detection. Data collection was carried out via a homebuilt program based on LabVIEW. The typical temporal response measured by the cross-correlation between the pump and probe pulses from a 1-mm-thick glass plate was 70 ± 5 fs (FWHM).

Time-resolved reflectance measurements and Kramers-Kronig analysis

Transient reflection measurements made use of a 1-mJ Ti:sapphire femtosecond regenerative amplifier operating at a repetition rate of 1 kHz (Newport Spectra-Physics). The pump laser light (~100-fs pulse width) came from an optical parametric amplifier (TOPAS). The probe, a white-light supercontinuum (450 to 900 nm), was focused onto the sample with a small overlapped angle to the pump. The reflected probe light from a perovskite crystal was collected by a mirror and lenses. The detection consisted of a pair of high-resolution multichannel detector arrays coupled to a high-speed data acquisition system (Ultrafast Systems). We used a heat filter in the probe beam before the sample to remove the residual fundamental laser beam; the probe power over the entire spectrum was a few hundred nanowatts. The sample was mounted inside a quartz window cell containing inert gas to avoid sample degradation by absorbing oxygen and moisture. The complex refractive index is given by

$$\tilde{\mathit{n}}=\mathit{n}+\mathit{i}\mathit{k}$$ (1)

Here, the real part n is the refractive index, and the imaginary part k is the extinction coefficient.

The change of refractive index can be calculated from transient reflectance signal as (63)

$$\frac{\mathrm{\Delta }\mathit{R}}{\mathit{R}}(\mathrm{\hslash }\mathrm{\omega })=\frac{4\mathrm{\Delta }\mathit{n}(\mathrm{\hslash }\mathrm{\omega })}{\mathit{n}{(\mathrm{\hslash }\mathrm{\omega })}^2-1}$$ (2)

where n(ℏω) was adapted from Yang et al. (63).

The Kramers-Kronig relations are given by

$$\mathit{I}\mathit{m}[\tilde{\mathit{n}}(\mathrm{\omega })]=\frac{-2\mathrm{\omega }}{\mathrm{\pi }}\mathit{P}{\displaystyle {\int }_0^{\infty }}\frac{\mathit{R}\mathit{e}[\tilde{\mathit{n}}({\mathrm{\omega }}^{\prime })]}{{\mathrm{\omega }}^{\prime 2}-{\mathrm{\omega }}^2}\mathit{d}{\mathrm{\omega }}^{\prime }$$ (3)

$$\mathit{R}\mathit{e}[\tilde{\mathit{n}}(\mathrm{\omega })]=\frac{2}{\mathrm{\pi }}\mathit{P}{\displaystyle {\int }_0^{\infty }}\frac{{\mathrm{\omega }}^{\prime }\mathit{I}\mathit{m}[\tilde{\mathit{n}}({\mathrm{\omega }}^{\prime })]}{{\mathrm{\omega }}^{\prime 2}-{\mathrm{\omega }}^2}\mathit{d}{\mathrm{\omega }}^{\prime }$$ (4)

where P∫ is the Cauthy’s principal integral. We use Eq. 2 to calculate Δn(ℏω) and plug this value into Eq. 3 to calculate the change of imaginary part, Δk(ℏω). The change of absorption coefficient is then calculated by

$$\mathrm{\Delta }\mathrm{\alpha }(\mathrm{\hslash }\mathrm{\omega })=\frac{4\mathrm{\Delta }\mathit{k}(\mathrm{\hslash }\mathrm{\omega })}{\mathrm{\lambda }}$$ (5)

Theoretical calculations

DFT calculations were performed on the tetragonal phases of MAPbI₃ and MAPbBr₃ (48 atoms in unit cells) and on the orthorhombic phase of CsPbBr₃ (20 atoms in the unit cell), corresponding to four formula units in all cases. We used the experimental cell parameters throughout the work. We relaxed the geometries of both the neutral and positive and negative (+1 and −1 charge) systems in periodic boundary conditions by generalized gradient approximation (GGA)–DFT. This procedure is representative of the crystals being investigated at low temperature, where dynamic fluctuations due to thermal energy can be neglected. Thus, the results refer to the perfect crystals at zero temperature, although the phases are those corresponding to the room temperature stable phases for each system. The displacement vector was extracted as the difference of the geometrical coordinates in the neutral and charged states. This defines a global configurational coordinate that drives the system across the two minima, defined by the neutral and charged systems. Next, the energy was calculated as a function of the displacement along the identified distortion pathway, by performing both GGA (PBE) (64) and hybrid (PBE0) (36) DFT calculations. To quantify the displacement on the same scale for all the investigated systems, we calculated the mean square displacement of all atoms in the cell along the pathway, as well as the variations of the Pb-Br distances and of the Pb-Br-Pb angles.

Frequency calculations were performed by GGA-DFT at the experimental cell parameters for consistency with the relaxation and projection procedures. A 4 × 4 × 4 k-point mesh was used, which ensured converged results [see the study of Quarti et al. (21)].

PBE calculations (structural relaxations and phonon calculations) were performed by using ultrasoft pseudopotentials with a cutoff on the wavefunction of 25 Ry (200 Ry on the charge density) and uniform 4 × 4 × 4 grid of k-points in the Brillouin zone. Single-point PBE0 calculations were performed using norm-conserving pseudopotentials with a cutoff on the wavefunctions of 40 Ry and the same k-point grids used for the PBE calculations. The convergence of the cutoff in hybrid calculations, as well as the reliability of our approach in the determination of the minima and the relaxation energies of the charged systems, was checked by performing full PBE0 relaxation calculations on the charged and neutral orthorhombic phase of CsPbBr₃ with a cutoff of 70 Ry on the wavefunctions. The same setup was used to optimize the 2 × 2 × 8 CsPbBr₃ pseudocubic supercell. Relaxation of ions for the neutral and positive and negative charged systems showed relaxed geometries and relaxation energies in excellent agreement with the simulated pathways. All calculations in the work were carried out by using the QUANTUMESPRESSO simulation package (65).

Estimation of Fröhlich coupling and mobility

The behavior of polarons was analyzed by Fröhlich model, where a charge in polar medium was coupled to harmonic optical phonons. The strength of electron-phonon coupling is characterized by the so-called Fröhlich coupling, α_e-ph, defined by

$${\mathrm{\alpha }}_{\mathrm{e}-\text{ph}}\equiv \frac{{\mathit{e}}^2}{\mathrm{\hslash }}\frac{1}{4\mathrm{\pi }\mathrm{ϵ}}(\frac{1}{{\mathrm{\epsilon }}_{\infty }}-\frac{1}{{\mathrm{\epsilon }}_0})\sqrt{\frac{\mathit{m}}{2\mathrm{\hslash }\mathrm{\omega }}}$$

where e is the charge of carrier; $2\mathrm{\pi }\mathrm{\hslash }$ is the Planck’s constant; ϵ is the dielectric constant of vacuum; ε_∞ and ε₀ are optical and static dielectric constants, respectively; m is the effective mass of bare electron band; and ω is the angular frequency of a characteristic LO phonon mode. Parameters for the calculation of α_e-ph are shown in table S2. We estimated ω from the calculated Im[1/ε(ω)] spectra in far-infrared region (see fig. S12).

We figured out that the polaron in CH₃NH₃PbBr₃ and CsPbBr₃ was in the large-intermediate regime (α_e-ph = 1 to 3). The most successful model for describing the polaron in the regime at finite temperature is provided by Ōsaka based on the path integral calculation demonstrated by Feynman. In the model, the self free energy of polaron, F, with α_e-ph, under the phonon occupation factor $\mathrm{\beta }=\mathrm{\hslash }\mathrm{\omega }/{\mathit{k}}_{\mathrm{B}}\mathit{T}$ (where k_B is the Boltzman constant and T is the temperature) is calculated with two free parameters v and w (44, 45). To obtain the ground state of the polaron, we numerically find v and w that give the minimum F = − (A + B + C), where

$$\begin{array}{c}\mathit{A}=\frac{3}{\mathrm{\beta }}\left[\text{ln}\right(\frac{\mathit{v}}{\mathit{w}})-\frac{\text{ln}(2\mathrm{\pi }\mathrm{\beta })}{2}- \text{ln}\frac{\text{sinh}\left(\frac{\mathit{v}\mathrm{\beta }}{2}\right)}{\text{sinh}\left(\frac{\mathit{w}\mathrm{\beta }}{2}\right)}]\\ \mathit{B}=\frac{\mathrm{\alpha }\mathit{v}}{\sqrt{\mathrm{\pi }}[\text{exp}(\mathrm{\beta })-1]}{\displaystyle {\int }_0^{\frac{\mathrm{\beta }}{2}}}\frac{\text{exp}(\mathrm{\beta }-\mathit{x})+ \text{exp}(\mathit{x})}{\sqrt{{\mathit{w}}^2\mathit{x}(1-\frac{\mathit{x}}{\mathrm{\beta }})+\frac{\mathit{Y}(\mathit{x})({\mathit{v}}^2-{\mathit{w}}^2)}{\mathit{v}}}}\mathrm{d}\mathit{x}\\ \mathit{Y}(\mathit{x})=\frac{1}{1- \text{exp}(-\mathit{v}\mathrm{\beta })}[1+ \text{exp}(-\mathit{v}\mathrm{\beta })- \text{exp}(-\mathit{v}\mathit{x})- \text{exp}\{\mathit{v}(\mathit{x}-\mathrm{\beta })\}]\\ \mathit{C}=\frac{3({\mathit{v}}^2-{\mathit{w}}^2)}{4\mathit{v}}\left(\text{coth}\right(\frac{\mathit{v}\mathrm{\beta }}{2})-\frac{2}{\mathit{v}\mathrm{\beta }})\end{array}$$

v and w have a unit of ω, and, in particular, v is the frequency of relative motion between a charge and a coupled LO phonon. We can calculate the reduced mass (m_red) of the relative motion and the expectation value of the squared distance between the charge and the phonon, which defines Feynman large-polaron radius (ρ), as below (66)

$$\begin{array}{c}{\mathit{m}}_{\text{red}}=\mathit{m}\frac{{\mathit{v}}^2-{\mathit{w}}^2}{{\mathit{v}}^2}\\ \mathrm{\rho }=\sqrt{\frac{3\mathrm{\hslash }}{2{\mathit{m}}_{\text{red}}\times \mathit{v}\times 2\mathrm{\pi }\mathrm{\omega }}}\end{array}$$

In the theory, mobility μ is described by (67, 68)

$$\begin{array}{c}\mathrm{\mu }=\frac{3\sqrt{\mathrm{\pi }}\mathit{e}}{2\mathrm{\pi \omega }\mathit{m}{\mathrm{\alpha }}_{\text{e-ph}}}\frac{\text{sinh}(\mathrm{\beta }/2)}{{\mathrm{\beta }}^{5/2}}\frac{{\mathit{w}}^3}{{\mathit{v}}^3}\frac{1}{\mathit{K}}\\ \mathit{K}={\displaystyle {\int }_0^{\infty }}\frac{\text{cos}(\mathit{u})}{{({\mathit{u}}^2+{\mathit{a}}^2-\mathit{b} \text{cos}(\mathit{v}\cdot \mathit{u}))}^{3/2}}\mathrm{d}\mathit{u}\\ {\mathit{a}}^2={\left(\frac{\mathrm{\beta }}{2}\right)}^2+\left(\frac{{\mathit{v}}^2-{\mathit{w}}^2}{{\mathit{w}}^2\mathit{v}}\right)\mathrm{\beta } \text{coth}\left(\frac{\mathrm{\beta }\mathit{v}}{2}\right)\\ \mathit{b}=\left(\frac{{\mathit{v}}^2-{\mathit{w}}^2}{{\mathit{w}}^2\mathit{v}}\right)\frac{\mathrm{\beta }}{\text{sinh}\left(\frac{\mathrm{\beta }\mathit{v}}{2}\right)}\end{array}$$

The calculated parameters for the polarons—Fröhlich coupling constants (α_e-ph), phonon occupation factors (β), parameters at the lowest energy polaron in the Feynman-Ōsaka formula (v and w), Feynman polaron radii (ρ), and mobilities (μ)—are tabulated in table S3. Carrier effective masses of CsPbBr₃ for the calculations are taken from Yettapu et al. (69).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/8/e1701217/DC1

fig. S1. Optical images of single-crystalline CH₃NH₃PbBr₃ and CsPbBr₃.

fig. S2. The spectra of pump pulses in the TR-OKE measurement.

fig. S3. A schematic diagram of TR-OKE measurement and polarization-dependent OKE traces on the CH₃NH₃PbBr₃ crystal.

fig. S4. Calculated IR spectrum and the coefficients of the displacement vector associated with a positve charge injection in CsPbBr₃ projected to the normal modes.

fig. S5. Calculated IR spectrum and the coefficients of the displacement vector associated with a positive charge injection in CH₃NH₃PbBr₃ projected to the normal modes.

fig. S6. Details in transient reflectance measurements.

fig. S7. Hybrid DFT calculations of the relaxed structures of CH₃NH₃PbI₃.

fig. S8. Potential energy surface for the neutral and positive charged 2 × 2 × 8 cubic CsPbBr₃ supercells.

fig. S9. Pseudocubic 2 × 2 × 8 CsPbBr₃ model with elongated (shortened) Pb-Br bonds in the left (right) halves of the supercell.

fig. S10. Localization of the positive charge as a function of the octahedral tilting in 2 × 2 × 8 cubic CsPbBr₃ supercells.

fig. S11. Hybrid DFT calculations of stabilization energy of CH₃NH₃PbBr₃ and CsPbBr₃ with and without cations.

fig. S12. Calculated dielectric functions of CsPbBr₃ and MAPbBr₃.

table S1. Lattice constants for MAPbBr₃ and CsPbBr₃ single crystals.

table S2. The list of input parameters for the polaron calculations.

table S3. The list of the results of polaron calculations under the Feynman-Ōsaka model.