Benchmarking Density Functional Tight Binding Models for Barrier Heights and Reaction Energetics of Organic Molecules

Abstract

Density Functional Tight Binding (DFTB) models are two to three orders of magnitude faster than ab initio and Density Functional Theory (DFT) methods and therefore are particularly attractive in applications to large molecules and condensed phase systems. To establish the applicability of DFTB models to general chemical reactions, we conduct benchmark calculations for barrier heights and reaction energetics of organic molecules using existing databases and several new ones compiled in this study. Structures for the transition states and stable species have been fully optimized at the DFTB level, making it possible to characterize the reliability of DFTB models in a more thorough fashion compared to conducting single point energy calculations as done in previous benchmark studies. The encouraging results for the diverse sets of reactions studied here suggest that DFTB models, especially the most recent third-order version (DFTB3/3OB augmented with dispersion correction), in most cases provide satisfactory description of organic chemical reactions with accuracy almost comparable to popular DFT methods with large basis sets, although larger errors are also seen for certain cases. Therefore, DFTB models can be effective for mechanistic analysis (e.g., transition state search) of large (bio)molecules, especially when coupled with single point energy calculations at higher levels of theory.

Graphical Abstract

Is DFTB sufficiently reliable for predicting reaction energies and barrier heights for general organic reactions? The encouraging results for the diverse sets of reactions studied here suggest an affirmative answer to the question. DFTB models, especially DFTB3/3OB with dispersion corrections, provide generally satisfactory description of organic chemical reactions with an accuracy close to popular DFT methods with large basis sets, albeit being several orders of magnitude faster. Larger errors are observed in certain cases and can often be reduced via single point calculations at the DFT level.

Introduction

Computational studies play increasingly prominent roles in the analysis of a broad range of chemical, biochemical and materials problems. Various computational methods fall into one of two realms: methods based on the calculation of the many-electron wave function by the Ritz variational principle (or related principles), or methods based on the calculation of the electron density by the Hohenberg–Kohn variational principle, and force field methods (MM: “molecular mechanics”). Between them lie semi-empirical methods, which include Neglect-Diatomic-Differential-Overlap (NDDO) methods¹ such as AM1², PMx(x=3, 6, 7)^3–6 and OMx(x=2,3)^7–10, and Density Functional Tight Binding (DFTB).^11–13 Over the years, several DFTB approaches have been developed, starting from the first-order non-self-consistent DFTB1 (originally called DFTB),¹¹ to the second order DFTB2 (originally called SCC-DFTB)¹² and the latest extension to the third-order DFTB3,¹³ described in detail elsewhere.^14–18 Owing to its computational efficiency, DFTB has emerged in the past decade as a competitive quantum mechanical method for condensed phase applications, especially where an extensive sampling of the configurational space is important to the reactive process of interest.¹⁹ This is particularly the case for chemical reactions and charge transport processes in biological systems, aqueous solution and soft-materials, to which DFTB and DFTB/MM-based simulations have been applied and examined in recent studies.^{17–18, 20–25} The reliability of such simulations depends on the treatment of both non-covalent interactions, which govern the structural properties of the environment and stabilization of reactive species, and energetics of transition state (TS) structures that dictate the kinetic bottleneck of reactions. The description of non-covalent interactions by DFTB and popular semi-empirical methods has been discussed in a recent review article,¹⁸ while in this study we focus on the benchmark of DFTB on TS structures and energies. Validation studies for DFTB barrier heights have been previously reported,^26–27 but they were limited to single point DFTB energy calculations on structures optimized at the DFT level of theory. To the best of our knowledge, the current work is the first time that TS structures are fully optimized at the DFTB level in the context of a benchmark analysis that involves a broad range of chemical reactions.

Although the advantage of DFTB is particularly evident when applied in QM/MM simulations for chemical reactions in condensed phases,^{17, 25, 28} it is not straightforward to evaluate its accuracy for potential energy surfaces of very high dimensionality. Therefore, we focus on sets of smaller molecules for which high-level QM results are either available in the literature or possible to compute without excessive computational cost. Specifically, to evaluate the accuracy of DFTB for reaction energies, we focus on the ISO34,^29–31 DARC,^32–34 and ISOL22^35–36 datasets. Since conformational energy landscape is also important in biochemical applications, we have compiled a new dataset, CIT (Conformers, Isomers, Tautomers), to analyze the energy differences between conformers/tautomers. For barrier heights benchmark, we use the NHTBH38/08,^37–38 and BHPERI^39–41 databases. Finally, to further broaden the scope of chemical reactions, we have developed three datasets that target S_N2 reactions involving different small molecules (Sn2SM) or medium size molecules (Sn2MM) as leaving groups or nucleophiles, and the epoxidation of alkenes (PEREP). By comparing both DFTB2¹² and DFTB3¹³ (with and without an empirical dispersion correction⁴²) with higher level QM results or available experimental data, we are able to show that the DFTB methods generally yield encouraging results that are almost comparable to DFT methods with popular exchange-correlation functionals (e.g., B3LYP and PBE) and large basis sets, although larger errors are also observed in certain cases. Considering that DFTB is roughly two to three orders of magnitude faster, these models can be particularly well-suited for high-throughput type of applications where energetic evaluations for a large number of chemical reactions are needed.^43–46

Methods

We compute DFTB2¹² and DFTB3¹³ reaction energies for all structures in ISO34,^29–31 DARC,^32–34 ISOL22^35–36 and in our own dataset CIT, and barrier heights for the NHTBH38/08,^37–38 BHPERI,^39–41 PEREP, Sn2SM, and Sn2MM. The comparison with available experimental and/or high-level ab initio reference data is given in detail in Results and discussion section. CIT, PEREP, Sn2SM and Sn2MM structures were also optimized at the DFT level with the B3LYP^47–48 and PBE⁴⁹ functionals including D3-dispersion.⁴² To assess the energetic impact of structural differences between DFTB and DFT methods, B3LYP-D3/TZP single point energies were also computed at the DFTB3-D3 optimized structures. To evaluate DFTB for barrier heights, we performed geometry optimizations and transition state searches for species in NHTBH38/08,^37–38 BHPERI,^39–41 PEREP, Sn2SM, and Sn2MM databases. Stationary points were verified using normal mode calculations. DFT calculations were performed using an all-electron basis set consisting of triple-zeta Slater-type orbitals plus one polarization function (TZP) for all atoms. DFTB calculations were performed using the 3ob-3-1 set of parameters,^{26, 50–52} with and without dispersion (D3).^{42, 53}All the calculations were done with the ADF2013.01 software package.^54–55 DFTB2 results (with and without dispersion) for all sets are reported in the Supporting Information.

Results and Discussion

Reaction energies

We start with isomerization reactions since this allows comparisons on the performance for differences in bonding, conjugation, and steric effects.³⁰ Reaction energies for ISO34,^29–31 DARC^32–33 and ISOL22³⁵ databases are reported in Tables 1–3, respectively. DFTB values are compared to energies obtained either from experiment or from high-level ab initio calculations, and MSE (mean signed error) MAE (mean absolute error), RMSE (root-mean-square error) and LE (largest error in absolute value) are given in these Tables as well.

Table 1.

Computed isomerization energies (in kcal/mol) with DFTB3, with and without included dispersion, and single point DFT B3LYP energies on DFTB3-D3 geometries for the ISO34 database;^29–31 Comparison to previous DFT and reference values is also given. Previous DFT results are obtained on B3LYP/TZV(d,p)-optimized structures.⁵⁷

No.	Reaction	B3LYP- D3/ def2- QZVP58	PBE-D3/ def2- QZVP58	DFTB3	DFTB3- D3	B3LYP/TZP//DFTB3- D3	Ref. value31
1.		−1.8	−3.0	4.5	4.4	−1.5	1.6
2.		23.8	19.3	31.2	31.2	25.1	21.9
3.		9.2	5.4	6.3	6.4	10.2	7.2
4.		1.1	1.0	0.9	0.8	0.9	1.0
5.		0.8	0.7	0.5	0.7	1.1	0.9
6.		2.8	3.4	3.7	3.6	2.9	2.6
7.		15.3	10.4	7.8	7.8	15.0	11.2
8.		19.9	20.2	23.6	23.9	21.7	22.9
9.		7.8	8.7	8.0	7.8	7.7	6.9
10.		2.4	2.5	−0.3	0.4	2.8	3.6
11.		−2.5	−2.1	−5.5	−2.5	−0.9	1.9
12.		56.4	50.5	51.3	51.0	56.1	47.0
13.		38.1	38.3	42.4	42.0	38.3	36.0
14.		23.5	25.0	10.3	10.3	23.9	24.2
15.		7.6	7.8	9.6	9.6	7.4	7.3
16.		12.4	8.4	17.6	17.6	13.2	10.8
17.		26.5	26.1	40.9	41.1	26.5	27.0
18.		11.1	10.4	8.20	8.2	12.2	11.2
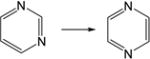
19.		4.1	3.8	4.47	4.5	4.2	4.6
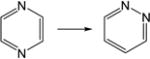
20.		18.2	17.0	27.0	26.9	17.8	20.2
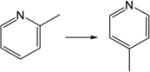
21.		1.1	1.0	1.0	0.9	1.1	0.9
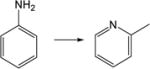
22.		3.9	4.7	3.3	3.4	3.0	3.2
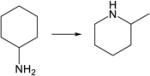
23.		4.9	5.1	7.5	7.5	4.8	5.3
24.		10.7	11.6	12.4	12.5	10.3	12.5
25.		28.0	24.7	31.9	32.0	28.5	26.5
26.		15.8	16.8	18.4	18.4	15.6	18.2
27.		61.7	59.6	66.5	66.8	60.8	64.2
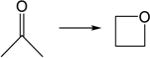
28.		33.6	31.1	29.4	29.5	33.5	31.2
29.		8.7	11.5	13.6	13.6	9.7	11.9
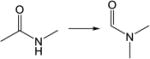
30.		9.5	9.2	11.4	11.2	9.1	9.5
31.		11.3	14.8	17.3	17.7	12.8	14.1
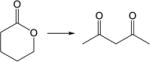
32.		3.0	5.3	3.6	3.8	3.3	7.1
33.		8.8	9.9	11.5	10.9	8.0	5.6
34.		6.9	8.6	11.3	11.4	6.9	7.3
	MSE	−0.1	−0.6	1.3	1.4	0.1
	MAE	1.9	1.6	3.6	3.4	1.8
	RMSE	2.6	2.1	5.0	4.9	2.5
	LE	9.4	4.6	13.9	14.1	9.1

Table 3.

Computed isomerization reaction energies (kcal/mol) with DFTB3, with and without included dispersion, and single point DFT B3LYP energies on DFTB3-D3 geometries for large organic molecules – the ISOL22 database;^35–36 Comparison to previous DFT and reference values is also given. Previous DFT results are obtained on B97-D/TZVP³⁵ geometries.

No.	Reaction	B3LYP- D3/ def2- QZVP58	PBE- D3/ def2- QZVP61	DFTB3	DFTB3- D3	B3LYP/TZP//DFTB3- D3	Ref. value36
1.		25.6	31.3	26.5	32.3	24.6	37.5
2.		6.9	7.0	8.3	8.1	6.4	9.8
3.		23.0	30.5	33.8	35.8	23.2	32.8
4.		23.0	25.7	28.2	27.7	22.8	25.5
5.		10.7	13.4	12.3	15.2	10.9	17.4
6.		42.5	38.8	46.6	40.6	44.7	22.3
7.		20.3	18.7	16.3	17.6	20.1	21.8
8.		3.4	5.9	3.4	4.2	2.8	6.8
9.		37.3	30.7	35.3	35.4	36.4	37.9
10.		0.6	0.0	−3.8	−4.0	1.9	0.2
11.		30.8	31.1	48.4	48.9	31.4	33.5
12.		4.6	7.0	5.3	5.9	5.9	5.3
13.		−1.0	1.5	23.7	24.8	3.3	3.1
14.		23.3	23.5	24.5	24.2	24.6	22.8
15.		−0.9	4.9	3.8	4.4	−1.2	10.3
16.		15.3	11.8	24.1	26.6	18.4	22.6
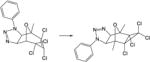
17.		20.3	17.2	17.3	17.5	21.7	18.3
18.		3.6	4.5	4.2	3.8	3.1	4.7
19		−2.1	2.7	−7.9	−6.8	−0.6	11.2
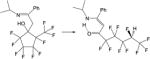
20.		−11.1	−9.3	−14.3	−13.8	−14.0	0.8
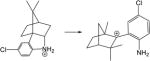
21.		14.3	15.1	5.4	6.4	14.4	23.4
	MSE	−3.7	−2.7	−1.3	−0.6	−3.2
	MAE	5.9	4.5	7.6	7.0	6.1
	RMSE	8.0	6.2	10.7	9.8	8.3
	LE	20.2	16.5	24.3	21.7	22.4

ISO34

The ISO34^29–31 is a compilation of 34 organic isomerization reactions including oxygen and nitrogen heteroatoms. DFTB results are tabulated in Table 1 and compared to experimental values,⁵⁶ excluding zero-point vibrational and thermal corrections,³¹ except for four cases (reactions 14, 19, 30 and 32) where the reference values are CCSD(T) calculations.³¹

The DFTB3-D3 structures are reliable and in a good agreement with reference values. This is also noted by the fact that B3LYP-D3 single points at those structures lead to a MAE of 1.8 kcal/mol, which is comparable to B3LYP-D3 with full geometry optimization (B3LYP-D3/def2-QZVP//B3LYP/TZVDP level of theory).^57–58 Overall, DFTB3-D3 performs rather well with a MAE of 3.4 kcal/mol, which is slightly larger than the values for B3LYP-D3 (1.9 kcal/mol) and PBE-D3 (1.6 kcal/mol) with large basis set.

A closer inspection of the results in Table 1 reveals that the exothermicity of reaction 11 is reversed. However, all applied methods suffer from the same deficiency. Shortcomings of DFT for the isomerization of branched alkanes to linear alkanes has been previously reported.^59–60 Hence, it is not surprising that DFTB also shows discrepancies for reactions 10, 11 and 33. Further, the energy for isomerization of propyne to propene (reaction 1) is challenging for DFT, while DFTB predicted the correct sign. For the nitrogen containing molecules, DFTB performs satisfactorily for aromatic nitrogen compounds. However, for molecules with sp³ hybridized nitrogen larger errors has been observed. Similarly, the isomerization of cyanide to isocyanide (reaction 14), where nitrogen is sp hybridized, DFTB underestimated isomerization energy. The inclusion of dispersion corrections did not improve DFTB results, as expected for these relatively small molecules.

DARC

The results for the 14 typical Diels-Alder reactions collected in the DARC dataset^32–34 are presented in Table 2. DFT is known to overestimate non-bonded repulsions of bridgehead carbons of the Diels–Alder reactions,³⁴ reflected by the large MAE (10.2 kcal/mol) for the B3LYP-D3 level of theory. However, DFTB shows an excellent agreement with the reference, high-level ab initio (CCSD(T)/CBS) reaction energies for cycloaddition of ethene and ethyne to a conjugated diene (reactions 1–6) and for reactions of cyclopentadiene with maleine and maleinimide (reactions 11–14).³⁴ The four reactions (reactions 7–10) with an oxygen bridge product exhibit largest errors for the DARC set. In general, the DFTB results are in good accordance with previous PBE-D3 results,⁶¹ as well as, with previous DFTB results²⁶ (MAE of 8.9 and 7.4 kcal/mol for DFTB and DFTB-D, respectively) which are improved by full geometry optimization (MAE of 8.7 and 5.8 kcal/mol, respectively). Here it is obvious that inclusion of dispersion corrections significantly improves the results. It should be noted that MSE is large and comparable to the MAE and RMSE. This implies that there is systematic error in DFTB reaction energies; therefore, mean absolute deviation (MAD) and root mean square deviation (RMSD), in which the systematic error is removed, are smaller in magnitude (3.1 and 4.1 kcal/mol, respectively, for DFTB3-D3; see Supporting Information for details). This implies that relative energetics are better described by the DFTB models.

Table 2.

Computed Diels–Alder reaction energies (in kcal/mol) with DFTB3, with and without included dispersion, and single point DFT B3LYP energies on DFTB3-D3 geometries for the DARC database;^32–34 Comparison to previous DFT and reference values is also given. Previous DFT results are obtained on B3LYP/6-31G (2df,p)- optimized structures.³⁴

No.	Reaction	B3LYP- D3/def2- QZVP58	PBE- D3/ def2- QZVP61	DFTB3	DFTB3- D3	B3LYP/TZP//DFTB3- D3	Ref. Value34
1.		−37.2	−44.5	−45.9	−48.2	−40.9	−43.8
2.		−55.1	−63.2	−57.1	−59.0	−59.6	−59.3
3.		−19.3	−27.0	−24.2	−26.8	−22.4	−30.0
4.		−24.3	−33.6	−24.9	−27.1	−27.6	−33.1
5.		−27.2	−34.9	−33.8	−36.9	−31.3	−36.5
6.		−40.1	−49.5	−40.8	−43.4	−44.2	−48.2
7.		−2.0	−7.5	−2.3	−6.2	−8.7	−14.4
8.		−4.1	−9.3	−2.9	−6.4	−10.2	−16.2
9.		−4.9	−10.3	−3.8	−7.9	−11.3	−17.2
10.		−7.2	−12.4	−4.7	−8.4	−13.2	−19.2
11.		−19.8	−26.2	−22.3	−26.5	−24.5	−31.6
12.		−20.5	−27.0	−22.7	−26.8	−25.0	−32.1
13.		−22.3	−28.7	−23.2	−27.7	−26.6	−34.1
14.		−22.9	−29.4	−23.6	−27.8	−26.9	−34.4
	MSE	10.2	3.3	8.4	5.1	5.6
	MAE	10.2	4.2	8.7	5.8	5.6
	RMSE	10.5	4.8	9.6	6.5	5.9
	LE	12.4	6.9	14.5	10.8	7.6

ISOL22

The molecules considered in the ISOL22 set represent a wide range of structures in the field of organic chemistry and are aimed for benchmarking chemical reactions for molecules of large size.^35–36 The performance of the DFTB models for these systems is compared to CCSD(T)-F12a/aug-cc-pVDZ and MCQCISD-MPW,³⁶ shown in Table 3. We find an overall good agreement, better with dispersion corrections, except for six (out of 21) reactions: reactions 6, 11, 13 and 19–21. However, these cases are also problematic for DFT. In some cases (particularly reactions 7, 10, 11, 13), but not all, B3LYP-D3 single point calculations on DFTB3-D3 optimized structures changes energetics to values closer to reference data.

CIT

Bearing in mind the importance of conformational energy landscape in biological systems, we have compiled a new set of reactions, CIT (Conformers, Isomers, Tautomers) which contains cyclohexane conformers, its substituted analogs, and heterocyclic derivatives. The CIT set evaluates the accuracy of DFTB in predicting the influence of intramolecular hydrogen bonding on conformational preferences, alkene isomerization reactions, and keto–enol and imine–enamine tautomerizations. We need to point out that high-level ab initio data are not available for this subset and we refer only to the comparison of DFTB3 to B3LYP-D3 and PBE-D3 DFT functionals (Table 4). DFTB is overall in a good agreement with DFT, with MAE relative to the B3LYP-D3/TZP level of theory of only 1.3 kcal/mol. Both DFT and DFTB follow expected chemical trends in this subset.

Table 4.

Computed reaction energies (kcal/mol) with DFTB3, with and without included dispersion, and DFT (PBE-D3 and B3LYP-D3) for the Conformers, Isomers, Tautomers – CIT database.

No.	Reaction	B3LYP-D3/ TZP	PBE-D3/ TZP	DFTB3	DFTB3- D3	B3LYP/TZP//DFTB3- D3
1.		6.3	6.2	4.3	4.3	6.3
2.		5.2	5.2	3.3	2.6	5.1
3.		1.9	1.9	1.0	0.7	1.8
4.		5.0	4.7	3.3	4.2	5.0
5.		4.7	4.4	4.0	3.2	4.8
6.		1.3	0.8	3.5	2.7	3.4
7.		8.9	10.7	6.0	6.1	8.4
8.		2.8	1.0	3.7	3.6	1.0
9.		1.0	3.2	0.9	0.8	2.7
10.		1.5	2.2	2.3	2.1	1.5
11.		2.1	2.6	2.9	2.9	2.1
12.		0.8	0.8	0.7	0.7	0.9
13.		13.5	12.9	11.5	11.5	12.4
14.		11.9	11.4	12.0	12.0	12.2
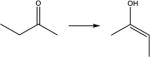
15.		13.8	12.0	13.2	13.3	13.0
16.		11.4	10.4	12.9	13.1	11.4
17.		10.0	7.7	5.8	5.8	9.9
18.		7.4	5.8	7.0	7.1	8.1
19.		3.9	3.6	5.0	5.0	3.9
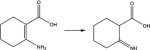
20.		5.5	9.4	4.3	4.2	6.7
	MSE[a]		−0.1	−0.6	−0.7	0.1
	MAE a]		1.0	1.3	1.3	0.5
	RMSE a]		1.4	1.6	1.6	0.9
	LE a]		3.9	4.2	4.2	2.1

^[a]Compared to B3LYP-D3/ TZP results

Barrier heights

In previous work,^26–27 DFTB models have been tested using single point energies on structures determined by high-level QM methods. In this work, we explicitly optimize transition state structures with DFTB, using the ADF program package.^54–55

For barrier heights benchmark, we use the NHTBH38/08,^37–38 and BHPERI^39–41 databases. Finally, to further broaden the scope of chemical reactions, we have developed three datasets that target S_N2 reactions involving different small molecules (Sn2SM) or medium size molecules (Sn2MM) as leaving groups or nucleophiles, containing C, H, O, N, S, Cl and F atoms, and the epoxidation of alkenes with peroxyacids (PEREP). All the results, together with error analysis are collected in Tables 5–9.

Table 5.

Computed barrier heights (kcal/mol) with DFTB3, with and without included dispersion for S_N2 reactions – subset of the NHTBH38/08 database;^37–38 Comparison to reference values is also given.

No.	Reaction (SN2)	B3LYP-D3/ TZP	PBE- D3/ TZP	DFTB3	DFTB3-D3	B3LYP/TZP//DFTB3- D3	Ref. value38
1.	F−…CH3F → FCH3…F−	5.7	5.8	8.6	8.6	8.8	13.4
2.	Cl−…CH3Cl → ClCH3…Cl−	7.8	6.0	3.5	3.5	7.5	13.4
3.	FCH3…Cl− → F−…CH3Cl	27.5	23.3	23.7	23.7	26.4	29.4
4.	HOCH3…F−→ OH−…CH3F	45.9	44.7	40.3	40.3	45.9	47.2
	MSE	−4.1	−5.9	−6.8	−6.8	−3.7
	MAE	4.1	5.9	6.8	6.8	3.7
	RMSE	4.9	6.2	7.1	7.1	4.1
	LE	7.7	7.6	9.9	9.9	5.9

Table 9.

Computed barrier heights (kcal/mol) with DFTB3, with and without included dispersion and DFT (PBE-D3 and B3LYP-D3) for the epoxidation of alkenes – PEREP database.

No.	Reaction	B3LYP-D3/ TZP	PBE-D3/ TZP	DFTB3	DFTB3- D3	B3LYP/TZP//DFTB3- D3
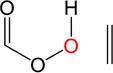
1.		13.3	4.0	8.2	7.0	16.0
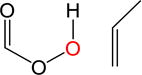
2.		10.5	1.9	7.1	5.2	10.0
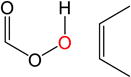
3.		7.8	−0.2	6.7	4.8	7.4
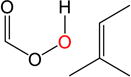
4.		5.8	−1.6	5.7	3.8	4.6
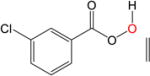
5.		14.1	5.0	9.4	8.1	17.0
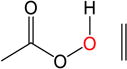
6.		15.2	5.7	9.1	7.8	17.0
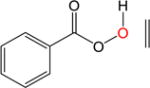
7.		14.8	5.6	9.7	8.4	18.3
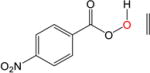
8.		12.9	4.1	8.6	7.3	13.4
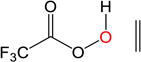
9.		8.9	1.0	6.4	5.2	8.8
	MSE[a]		−8.6	−3.6	−5.1	1.0
	MAE a]		8.6	3.6	5.1	1.5
	RMSE a]		8.7	4.1	5.3	1.9
	LE a]		9.5	6.1	7.4	3.5

^[a]Compared to B3LYP-D3/ TZP results

NHTBH38/08

The NHTBH38/08 database consists of a set of Non-Hydrogen Transfers reactions. Table 5 shows barriers for S_N2 reactions, a subset of the NHTBH38/08^37–38 database, obtained from DFTB optimized structures in comparison to QCISD/MG3 values.³⁸ DFTB3 underestimates barrier heights (MSE of −6.8 kcal/mol). The largest deviation is observed for the two reactions involving chloride ion, indicating that there may be a possibility for improvement when repulsive potentials are fitted more carefully including information from transition states. However, DFTB3 results are closer to the reference values than DFTB2 (Supplementary Information, Table S5). The inclusion of dispersion does not lead to any improvements. The optimized geometries of activated complexes and transition states are in good agreement with reference structures (Supplementary information, Table S6). Nevertheless, we note that the number of reactions included here is rather small and thus the uncertainty in the DFTB error is likely large.

BHPERI

The BHPERI set^39–41 compiles barrier heights of pericyclic reactions, including the ring opening reaction of cyclobutene, the intramolecular Diels-Alder reaction of cis-1,3,5-hexatriene, and the intermolecular Diels-Alder reaction of cis-butadiene with ethene. Reference values are based on the W1 method for the first eight reactions,⁴⁰ while the reference values for reactions 9 and 10 are obtained by CBS-QB3 calculations.³⁹ Moreover, 1,3-dipolar cycloadditions based on diazonium, azomethine, and nitrilium betaines were included and compared to CBS-QB3 level results.⁴¹ Six Diels-Alder reactions of different dienes with ethene were also considered with the reference to the CBS-QB3 values, Table 6.

Table 6.

Computed barrier heights (kcal/mol) with DFTB3, with and without included dispersion, and single point DFT B3LYP energies on DFTB3-D3 geometries for pericyclic reactions – the BHPERI database^39–41 (excluding reaction with Si as DFTB parameters for Si atom are currently not available); Comparison to previous DFT and reference values is also given. Previous DFT results are obtained on B3LYP/6-31G* and B3LYP/6-31G(2d,d,p) geometries.^62–64

No.	Reaction	B3LYP- D3/ def2- QZVP58	PBE-D3/ def2- QZVP58	DFTB3	DFTB3- D3	B3LYP/TZP//DFTB3- D3	Ref. value39–41
1.		33.0	32.1	41.5	41.4	33.0	35.3
2.		30.6	25.0	25.8	25.1	29.3	30.9
3.		28.4	23.2	34.4	34.3	27.7	28.3
4.		38.7	31.1	27.3	27.0	42.5	39.6
5.		27.4	22.9	42.4	42.6	34.5	28.2
6.		34.5	27.3	28.2	27.4	35.1	35.6
7.		21.6	13.7	14.9	12.0	18.9	22.1
8.		19.2	11.6	17.5	14.4	17.2	18.3
9.		16.4	8.9	19.8	15.1	16.4	9.8
10.		21.6	20.1	31.7	31.7	21.3	23.6
11.	N2O + C2H4	26.7	19.5	34.7	33.4	23.5	26.3
12.	N3H + C2H4	20.1	13.1	26.6	25.1	16.4	18.1
13.	N2CH2 + C2H4	15.3	9.2	15.1	17.1*	2.3	12.2
14.	HCNO + C2H4	12.7	6.2	13.8	12.4	8.5	11.1
15.	HCNNH + C2H4	7.5	2.5	13.1	11.3	3.7	5.3
16.	HCNCH2 + C2H4	6.5	1.5	8.3	6.4	3.3	4.0
17.	H2COHN + C2H4	13.0	7.4	10.5	8.7	11.2	11.5
18.	H2CNHNH + C2H4	6.5	1.2	6.1	3.9	4.9	4.0
19.	H2CNHCH2 + C2H4	0.9	−3.0	0.8	−1.4	−1.5	−1.4
20.	Furan + C2H4	25.4	17.2	20.7	18.2	22.2	19.8
21.	Pyrrole + C2H4	31.4	22.8	27.7	25.0	28.2	25.4
22.	C4H4PH + C2H4	24.4	15.9	22.8	19.7	20.7	18.1
23.	C4H4PH + C2H4	23.8	15.7	20.6	17.4	20.6	18.2
24.	Thiophene + C2H4	34.5	26.2	28.6	25.6	31.2	28.1
	MSE	2.0	−4.2	2.5	0.9	−0.1
	MAE	2.6	4.2	5.3	5.0	2.6
	RMSE	3.4	4.8	6.5	6.3	3.4
	LE	6.6	8.5	14.2	14.4	9.9

For the heterocyclic compounds (reactions 20–24) DFTB performs remarkably well. For all ethylene addition reactions to molecules including nitrogen, except for the two reactions with H₂CNHNH (18 and 19) and HCNO (reaction 14) the errors are larger. However, DFTB geometries are in excellent agreement with reference structures (Supporting Information, Table S8), which shows that DFTB is a good choice for transition state search of large molecules.

Sn2SM

This set of S_N2 reactions includes small nucleophiles and leaving groups and is used to further benchmark barrier heights, as shown in Table 7. For the present study, we performed DFT at B3LYP-D3 and PBE-D3 level and compared the DFTB results to DFT data. All reactions considered are formulated such that ΔE is positive. Sign errors (ΔE < 0) occur in two cases using DFTB2 methods, (Supplementary Information, Table S9), while DFTB3 methods result in a correct sign of barrier height.

Table 7.

Computed barrier heights (kcal/mol) with DFTB3, with and without included dispersion and DFT (PBE-D3 and B3LYP-D3) for S_N2 reactions involving different small molecules – Sn2SM database.

No.	Reaction	B3LYP-D3/ TZP	PBE- D3/ TZP	DFTB3	DFTB3- D3	B3LYP/TZP//DFTB3- D3
1.	OH−+ CH3OH → [HO…CH3…OH]‡−	4.8	−0.8	7.6	7.0	5.2
2.	CN−+ CH3OH → [NC…CH3…OH]‡−	23.1	16.9	21.7	20.9	22.7
3.	PhO−+ CH3OH → [PhO…CH3…OH]‡−	31.3	28.2	28.1	26.6	31.2
4.	NH2−+ CH3OH → [H2N…CH3…OH]‡−	2.8	−2.9	10.9	10.2	1.6
5.	CN−+ CH3CN → [NC…CH3…CN]‡−	21.5	17.8	28.9	28.1	21.5
6.	PhO−+ CH3CN → [PhO…CH3…CN]‡−	27.7	26.8	33.3	31.6	27.7
7.	CN−+ CH3NH2 → [NC…CH3…NH2]‡−	41.0	33.8	32.8	31.9	41.1
8.	PhO−+ CH3OPh →[PhO…CH3…OPh]‡−	10.1	5.9	8.7	6.8	9.8
9.	PhO−+ CH3NH2 → [PhO…CH3…NH2]‡−	49.8	46.2	39.6	37.9	50.3
10.	NH2−+ CH3NH2 → [H2N…CH3…NH2]‡−	18.9	12.4	21.2	20.4	18.3
	MSE[a]		−4.7	0.2	−1.0	−0.2
	MAE[a]		4.7	5.1	5.3	0.4
	RMSE[a]		5.0	5.9	6.2	0.5
	LE[a]		7.2	10.2	11.9	1.2

^[a]Compared to B3LYP-D3/TZP results

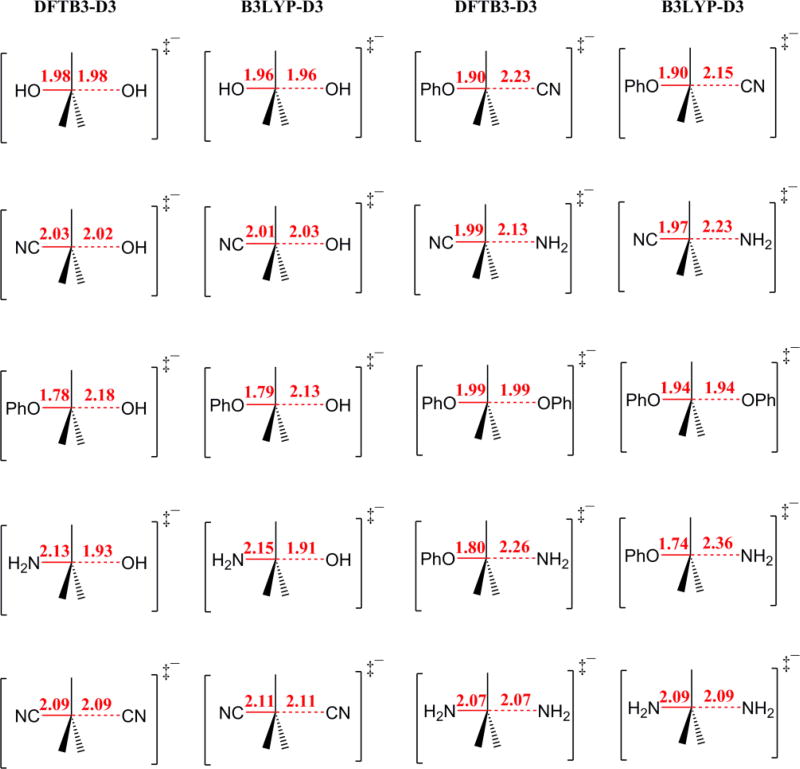
In Figure 1 comparison of TS geometries obtained at different levels of theory for Sn2SM subset are presented. The maximum deviation observed is 0.12 Å. Comparison with other DFTB formalisms is provided in Figure S1 in Supplementary information.

Figure 1.

Bond distances for transition states (Å) for Sn2SM DFTB3-D3 and B3LYP (DFT)-D3 levels of theory.

Sn2SM

The results for S_N2 reactions with NH₃ and CN⁻ as nucleophiles and ⁻OSO₂CH₃, ⁻OSO₂Ph as leaving groups are summarized in Table 8. This set of reactions was chosen to show the effect of different nucleophiles, leaving groups and the steric hindrance at the reaction center. From the inspection of Table 8, it is immediately clear that both DFT and DFTB show that CN⁻ is a better nucleophile than NH₃, as expected.^65–66 Further, the ⁻OSO₂CH₃ leaving group behaves comparably to ⁻OSO₂Ph. Table S11 presents a comparison of TS bond distances at different levels of theories.

Table 8.

Computed barrier heights (kcal/mol) with DFTB3, with and without included dispersion and DFT (PBE-D3 and B3LYP-D3) for S_N2 reactions involving different medium size molecules – Sn2MM database.

No.	React1	React2	B3LYP-D3/ TZP	PBE-D3/ TZP	DFTB3	DFTB3-D3	B3LYP/TZP//DFTB3- D3
1.	CN−	CH3- OSO2Ph	−10.4	−14.1	−8.3	−7.6	−9.9
2.	CN−	prim- OSO2Ph	−5.7	−9.8	−7.4	−9.7	−6.8
3.	CN−	sec- OSO2Ph	−7.5	−10.5	−7.1	−8.8	−6.0
4.	NH3	CH3- OSO2Ph	25.9	23.4	35.7	34.6	25.0
5.	NH3	prim- OSO2Ph	27.6	25.5	32.8	31.3	25.8
6.	NH3	sec- OSO2Ph	27.4	25.6	30.1	28.4	28.7
7.	CN−	CH3- OSO2CH3	−10.0	−13.2	−9.0	−10.4	−11.4
8.	CN−	prim- OSO2CH3	−5.5	−8.7	−7.1	−8.5	−5.0
9.	CN−	sec- OSO2CH3	−5.3	−8.1	−7.9	−9.6	−4.6
10.	NH3	CH3- OSO2CH3	25.9	23.6	34.7	33.6	24.6
11.	NH3	prim- OSO2CH3	27.6	25.8	32.0	30.5	25.9
12.	NH3	sec- OSO2CH3	27.1	25.6	29.3	27.6	28.3
	MSE[a]			−2.7	2.6	1.2	−0.2
	MAE[a]			2.7	3.5	3.4	1.2
	RMSE[a]			2.8	4.6	4.2	1.2
	LE[a]			4.1	9.8	8.7	1.8

^[a]Compared to B3LYP-D3/ TZP results

PEREP

The epoxydation of alkenes is a set of reactions with complicated mechanisms. An O-O bond cleavage is followed by the dissociation of the C-C π bond, while simultaneously forming two σ bonds with oxygen and hydrogen transfer between oxygen atoms.^65–66 Since it is an electrophilic addition to alkenes, the reaction proceeds faster with a more substituted, more electron-rich alkenes, and the peroxyacids with electron withdrawing groups.⁶⁷ To test the performance of DFTB, we used peroxyformic acid with ethene containing 0, 1, 2 and 3 methyl groups. We also compared six different peroxyacids for the reaction with ethene. Table 9 shows that the expected trends are well reproduced,^{65–66, 68} at all levels of theory, i.e. the barrier for the epoxydation with performic acid decreases as substitution increases, and the activity of peroxy acids can be summarized as follows: the most active is trifluoroacetic acid, followed by p-nitrobenzoic acid, performic acid, m-chloroperbenzoic acid, with peroxyacetic acid and peroxybenzoic acid at the end.

Conclusions

DFTB models have emerged in recent years as attractive methods for studying chemical reactions in large molecules and condensed phase systems. To establish the general applicability of these models to chemical reactions, it is essential to benchmark their performance for both reaction energies and barrier heights using available experimental data or highly accurate ab initio/DFT calculations.

We note that in the DFTB method, most of the parameters are computed based on DFT (PBE) calculations of atoms and diatomics, and the most empirical component of the method concerns the pair-wise repulsive potentials, which are fitted based on the comparison of a higher level DFT method and DFTB for a series of geometries that reflect different bonding situations for the relevant pair of atoms. Therefore, while it is true that parameterization of DFTB models has largely focused on equilibrium properties (e.g., equilibrium geometries, atomization energies and proton affinities), the formulation of the methodology and fitting protocol for the repulsive potential suggest that these models are not limited to the prediction of equilibrium properties. Such transferability is further supported by the barrier benchmark conducted in previous benchmark studies and the current work.

To evaluate the accuracy of DFTB for reaction energies, we studied isomerization reactions (ISO34,^29–31 ISOL22 datasets^35–36), Diels-Alder reactions (DARC^32–34), and newly compiled dataset CIT (Conformers, Isomers, Tautomers) bearing in mind the importance of conformational energy landscape in biological systems. Table 10 compares MAE to other available semiempirical¹⁰ and DFT methods^58,61 for reaction energies databases, including 69 reactions. Note that not all barrier benchmarks conducted here are included in this table; only those with published NDDO methods are included, and more complete error analyses for all tested datasets are summarized in Table S14 in the Supporting Information.

Table 10.

MAE (kcal/mol) and comparison to other available semiempirical¹⁰ and DFT methods;^{58, 61} N is a number of reactions herein considered.

	ISO34	DARC	ISOL22	NHTBH 38/08	BHPERI
N	34	14	21	4	24
DFTB2[a]	3.7	8.5	7.8	10.8	4.3
DFTB2-D3[a]	3.6	5.7	7.1	10.8	4.9
DFTB3[a]	3.6	8.7	7.6	6.1	5.3
DFTB3-D3[a]	3.4	5.4	7.0	6.1	5.0
PBE	1.8	6.8	7.1	6.2[a]	3.0
PBE-D3	1.6	4.3	5.8	4.4[a]	4.2
B3LYP	2.3	15.4	9.4	4.0[a]	5.5
B3LYP-D3	1.9	10.2	7.3	4.7[a]	2.6
MNDO	7.4	13.1	16.8	22.2	25.2
AM1	6.5	4.7	10.3	15.2	10.0
PM3	4.0	5.3	8.3	15.7	14.0
PM6	3.5	3.9	7.4	16.4	9.7
PM7	2.9	4.3	6.6	15.5	6.1
OM1	4.5	4.1	8.0	9.6	10.6
OM2	4.4	7.2	5.3	13.6	8.2
OM3	4.4	4.9	6.1	14.2	8.3

^[a]This work

The lowest MAE is observed for the ISO34 set. DFTB3-D3 is comparable to DFT-D3 methods in terms of the overall accuracy, for the sets of reactions analyzed here, although DFTB3 is a minimal basis approach and DFT calculations have been performed with the large def2-QZVP basis set. Furthermore, comparison to other available semi-empirical methods reveals that for ISO34 only PM7, and for ISOL22 OM2 and OM3, have lower MAEs, but the values are all in the similar range as DFTB. Closer inspection of Table 1 and Table 3 shows that DFT single point calculations at the DFTB3 structures give energies, for all cases, very close to the B3LYP-D3 values, reflecting the high quality of the DFTB3 structures. Even though Diels-Alder reactions (DARC) are challenging for DFT, DFTB3-D3 gives a MAE of 5.4 kcal/mol in accordance or better than other semi-empirical methods. Good performance of PM6 and PM7 is due to their extensive parameterization for common organic molecules.

For barrier heights benchmark, we use the NHTBH38/08,^37–38 and BHPERI^39–41 databases. Finally, to further broaden the scope of chemical reactions, we have developed three datasets that target S_N2 reactions involving different small molecules (Sn2SM) or medium size molecules (Sn2MM) as leaving groups or nucleophiles, and the epoxidation of alkenes (PEREP). MAE values for 28 barrier heights (NHTBH38/08 and BHPERI) are also shown in Table 10. It should be highlighted that barrier heights presented in this work are the result of the full geometry optimization of TS with DFTB, rather than single point energy calculations as done in previous benchmark studies. Geometries of resulted structures are in excellent agreement with DFT calculations. MAE values in comparison to B3LYP-D3/def2-QZVP⁵⁸ results are similar and represent major improvements over existing semi-empirical methods.

Overall, for both reaction energies and reaction barriers, DFTB3 is more accurate than DFTB2, and the inclusion of dispersion corrections, in general, improves results, especially for large molecules. Indeed, DFTB3-D3 results are generally in line with B3LYP-D3 for all reactions presented in this work, as summarized in Figure 2. Therefore, considering the high computational efficiency of DFTB models, they can be effective for mechanistic analysis (e.g., transition state search) of large (bio)molecules, especially when coupled with single point energy calculations at higher levels of theory. For example, one particularly interesting possibility for improving computed reaction energies is to adopt the connectivity-based hierarchy correction scheme developed by Raghavachari and co-workers.⁶⁹

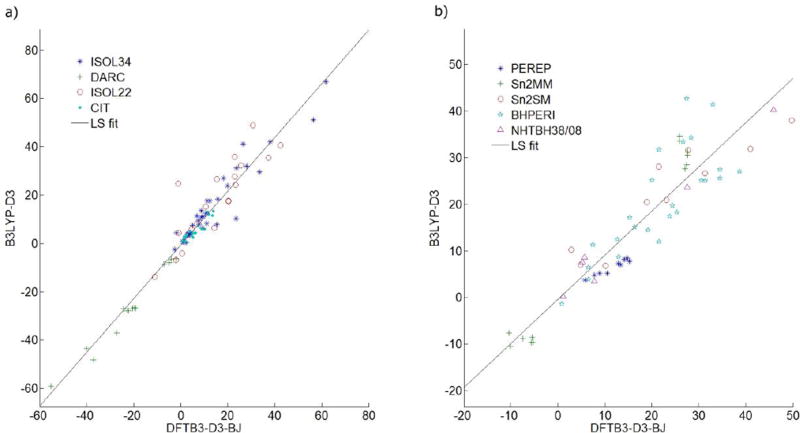
Figure 2.

Correlation plots of the reaction energies (a) and barrier heights (b), computed at DFTB3-D3 level vs. B3LYP-D3 (with different basis sets given in Tables 1–9) levels of theory.