Induced fit is a special case of conformational selection

Abstract

Conformational selection (CS) and induced fit (IF) are two widely used interpretations of ligand binding to biological macromolecules. Both mechanisms envision a two-step reaction where a conformational transition either precedes (CS) or follows (IF) the binding step. Under pseudo-first order conditions where the ligand is in excess to the macromolecule, both mechanisms produce two relaxations. A fast one, eventually increases linearly with the ligand concentration and reflects the binding interaction. A slow one saturates to a constant value after decreasing or increasing hyperbolically with the ligand concentration. This relaxation is the one most often accessible to experimental measurements and is potentially diagnostic of the mechanism involved. A relaxation that decreases unequivocally identifies CS, but a hyperbolic increase is compatible with both CS and IF. The potential ambiguity between the two mechanisms is more than qualitative. Here we show that the kinetic repertoire of IF is mathematically identical to CS under a simple transformation of the rate constants, which emphasizes the need for independent support of either mechanism from additional experimental evidence. We discuss a simple strategy to distinguish between IF and CS under the most common conditions encountered in practice, i.e., when the ligand is in excess to the macromolecule and a single relaxation is accessible to experimental measurements.

Graphical abstract

Induced fit is a special case of conformational selection Pradipta Chakraborty and Enrico Di Cera

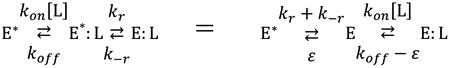
Introduction

Linkage between binding and conformational transitions is at the basis of any mechanism of recognition by a biological macromolecule. In its simplest formulation the linkage defines a two-step reaction scheme where conformational rearrangement either precedes or follows the binding interaction. The former case, first proposed by Eigen as pre-equilibrium (1) and later rebranded as conformational selection (CS) (2), assumes ligand binding to one of two pre-existing conformations in equilibrium. The latter case, first proposed by Koshland as induced fit (IF) (3), entails ligand binding followed by a conformational transition toward a more stable complex. For decades, IF and CS have dominated our interpretation of molecular recognition as irreducible mechanisms whose distinct kinetic signatures could easily be identified from analysis of experimental data (4, 5). Under the popular assumption that binding events take place on a time scale faster than conformational transitions, also known as the rapid equilibrium approximation, the two mechanisms make diametrically opposed predictions on how the system reaches equilibrium through a single relaxation. IF predicts this relaxation to increase hyperbolically with the ligand concentration, [L], whilst CS predicts the relaxation to decrease. The prevalence of systems displaying a relaxation increasing hyperbolically with [L] has then fostered the notion that IF should be considered a dominant mechanism of ligand binding, with CS applying only to a handful of cases (6, 7).

A recent analysis of the kinetic properties of IF and CS in the general case, without a priori assumptions on the time scales of binding and conformational transition, has led to quite different conclusions (8). Under pseudo-first order conditions where the ligand is in excess to the macromolecule, both mechanisms produce two relaxations to equilibrium: a fast one that eventually increases linearly with [L] and a slow one that saturates for large [L]. IF predicts this relaxation always to increase, as seen under the rapid equilibrium approximation. CS is more versatile and predicts this relaxation to increase with, decrease with or be independent of [L]. Hence, a relaxation that decreases with or is independent of [L] rules out IF and proves CS unequivocally. On the other hand, a relaxation that increases hyperbolically with [L] is compatible with either mechanism. CS is always sufficient and in some cases necessary as a mechanism of ligand binding. IF is in some cases sufficient but never necessary (9, 10).

The fact that a hyperbolic increase of the rate of relaxation to equilibrium as a function of [L] is compatible with both IF and CS calls into question the conclusions reached on many systems assumed to obey IF and the long assumed dominance of IF as a mechanism of ligand binding (6, 7). Here we report that the potential ambiguity between the two mechanisms is more than qualitative because IF is a mathematical special case of CS. The kinetic expressions of IF can be reproduced exactly by those of CS under a simple transformation of the rate constants. This stresses the need for distinguishing between the two mechanisms whenever the ambiguity is raised by experimental data and we discuss a simple strategy that accomplishes this task under conditions commonly encountered in practice.

Materials and Methods

Thrombin wild-type and its mutant W215A, with the active site Ser replaced by Ala to prevent hydrolysis, were expressed as prethrombin-2, purified and activated as previously described (11, 12). The chromogenic substrates H-D-Phe-Pro-Arg-p-nitroanilide (FPR) and H-D-Phe-Pro-Lys-p-nitroanilide (FPK) were purchased from Midwest Bio-Tech, Inc. Rapid kinetic experiments were conducted on an Applied Photophysics SX20 stopped-flow spectrometer under experimental conditions of 50 mM Tris, 0.1% PEG8000, 400 mM ChCl, pH 8.0, at 10 °C and 25 °C. The solution containing the protein was mixed 1:1 with 60 μL solutions of FPR or FPK in the same buffer. Both FPR and FPK are relevant probes of the active site of thrombin due to their similarity to the irreversible inhibitor H-D-Phe-Pro-Arg-CH₂Cl for which detailed structural information exists when bound to the enzyme (13, 14). FPK differs from FPR in the replacement of Arg at the P1 position that makes a strong double H-bonding interaction with D189 at the bottom of the primary specificity pocket. Both FPR and FPK interact similarly with residues of the 60-loop through Pro at the P2 position and with W215 through Phe in the D enantiomer at the P3 position. This interaction is specifically compromised when W215 is mutated to Ala or other residues (15-17). Rapid kinetics of FPR or FPK binding to thrombin wild-type and mutant W215A were studied using an excitation of 295 nm and a cutoff filter at 320 nm. Baselines were measured by mixing the protein into buffer in the absence of ligand. Each kinetic trace was taken as the average of at least ten determinations and fit to single or double exponentials based on the analysis of residuals using software supplied by Applied Photophysics. Values of the relaxations for single and double exponential fits were taken from the average of at least three independent titrations with errors calculated as the standard deviation between titrations.

Results

Consider the general reaction scheme

$$E_1\underset{k_{21}}{\overset{k_{12}}{\mathrm{\rightleftarrows }}}{E}_2\underset{k_{32}}{\overset{k_{23}}{\mathrm{\rightleftarrows }}}{E}_3$$ (Scheme 1)

where the independent transitions E₁ ⇄ E₂ and E₂ ⇄ E₃ may reflect ligand binding or a conformational transition. Because the system is closed, only two species are independent and relaxation to equilibrium obeys the two expressions (8)

$$2{\alpha }_{1,2}=k_{12}+k_{21}+k_{23}+k_{32}\pm \sqrt{{(k_{12}+k_{21}-k_{23}-k_{32})}^2+4k_{21}{k}_{23}}$$ (eq. 1)

It is straightforward to see that the sums k₁₂ + k₂₁ and k₂₃ + k₃₂, measuring the rates and time scales at which the independent transitions E₁ ⇄ E₂ and E₂ ⇄ E₃ reach equilibrium, make a symmetric contribution to eq. 1 and can be swapped without consequences. On the other hand, the term k₂₁k₂₃ makes a defining contribution to eq. 1 that depends on rates that selectively deplete the E₂ intermediate. The properties of Scheme 1 are dominated by this term.

Although long considered two mutually exclusive mechanisms of ligand binding (1, 3-5), IF and CS are closely related to each other and the connection is easily appreciated by rewriting Scheme 1 as

$$\mathrm{E}\ast \underset{k_{21}}{\overset{k_{12}}{\mathrm{\rightleftarrows }}}\mathrm{E}\underset{k_{\mathit{\text{off}}}^{\mathit{\text{CS}}}}{\overset{k_{\mathit{\text{on}}}^{\mathit{\text{CS}}}[\mathrm{L}]}{\mathrm{\rightleftarrows }}}\mathrm{E}:\mathrm{L}$$ (Scheme 2)

$$\mathrm{E}\ast \underset{k_{\mathit{\text{off}}}^{\mathit{\text{IF}}}}{\overset{k_{\mathit{\text{on}}}^{\mathit{\text{IF}}}[\mathrm{L}]}{\mathrm{\rightleftarrows }}}\mathrm{E}\ast :\mathrm{L}\underset{k_{32}}{\overset{k_{23}}{\mathrm{\rightleftarrows }}}\mathrm{E}:\mathrm{L}$$ (Scheme 3)

Two species, E* and E, pre-exist in equilibrium and only one of them binds the ligand in CS (Scheme 2). A single species, E*, interacts with ligand and then rearranges into a more stable E:L complex in IF (Scheme 3). Binding of ligand is quantified by a second order rate of association k_on, with all other rates being first order. The E₂ intermediate in Scheme 1 is defined by the free species E in CS and by the bound species E*: L in IF. The relevant expressions for the rates of relaxation to equilibrium in the two schemes are derived from eq. 1 under the pseudo-first order approximation where the ligand is in large excess over the macromolecule as (8)

$$2{\alpha }_{1,2}^{\mathit{\text{CS}}}=k_{12}+k_{21}+k_{\mathit{\text{on}}}^{\mathit{\text{CS}}}[\mathrm{L}]+k_{\mathit{\text{off}}}^{\mathit{\text{CS}}}\pm \sqrt{{(k_{\mathit{\text{on}}}^{\mathit{\text{CS}}}[\mathrm{L}]+k_{\mathit{\text{off}}}^{\mathit{\text{CS}}}-k_{12}-k_{21})}^2+4k_{21}{k}_{\mathit{\text{on}}}^{\mathit{\text{CS}}}[\mathrm{L}]}$$ (eq. 2)

$$2{\alpha }_{1,2}^{\mathit{\text{IF}}}=k_{23}+k_{32}+k_{\mathit{\text{on}}}^{\mathit{\text{IF}}}[\mathrm{L}]+k_{\mathit{\text{off}}}^{\mathit{\text{IF}}}\pm \sqrt{{(k_{\mathit{\text{on}}}^{\mathit{\text{IF}}}[\mathrm{L}]+k_{\mathit{\text{off}}}^{\mathit{\text{IF}}}-k_{32}-k_{32})}^2+4k_{23}{k}_{\mathit{\text{off}}}^{\mathit{\text{IF}}}}$$ (eq. 3)

The critical term k₂₁k₂₃ in eq. 1 depends on the ligand concentration [L] in CS (eq. 2), but is a constant in IF (eq. 3). We infer from analysis of eq. 1 that the difference between CS and IF resides in this term and must be significant. A richer repertoire of kinetic behaviors is expected for CS compared to IF as the rates of relaxation to equilibrium are studied as a function of [L].

Simple algebra shows that the fast relaxation, α₁, always increases and eventually grows linearly with [L] for both IF and CS (eqs. 2 and 3). The slow relaxation, α₂, grows hyperbolically with [L] in the case of IF (eq. 3) but has a more complex behavior in the case of CS (eq. 2). Depending on the sign of the expression $k_{\mathit{\text{off}}}^{\mathit{\text{CS}}}-k_{12}$, the value of ${\alpha }_2^{\mathit{\text{CS}}}$ hyperbolically decreases ( $k_{\mathit{\text{off}}}^{\mathit{\text{CS}}}>k_{12}$) or increases ( $k_{\mathit{\text{off}}}^{\mathit{\text{CS}}}<k_{12}$) with [L], and remains constant when $k_{\mathit{\text{off}}}^{\mathit{\text{CS}}}=k_{12}$ (8, 9). The fast relaxation that eventually grows linearly with [L] merely confirms the presence of a binding event in both mechanisms. The slow relaxation informs the nature of the conformational transition associated with binding. It is this relaxation the one most often detected experimentally, unless spectroscopically silent or itself too fast to measure. A decrease with [L] or a constant value provides unequivocal support for CS. A hyperbolic increase with [L] is consistent with both IF and CS and needs further scrutiny. The overlap is more than qualitative. Indeed, whenever $k_{\mathit{\text{off}}}^{\mathit{\text{CS}}}<k_{12}$, eq. 3 is identical to eq. 2 for any value of [L] under the transformations

$$k_{\mathit{\text{on}}}^{\mathit{\text{CS}}}=k_{\mathit{\text{on}}}^{\mathit{\text{IF}}}$$ (eq. 4a)

$$k_{12}=k_{23}+k_{32}$$ (eq. 4b)

$$k_{12}=\varepsilon$$ (eq. 4c)

$$k_{\mathit{\text{off}}}^{\mathit{\text{CS}}}=k_{\mathit{\text{off}}}^{\mathit{\text{IF}}}-\varepsilon$$ (eq. 4d)

$$2\varepsilon =k_{\mathit{\text{off}}}^{\mathit{\text{IF}}}-k_{23}-k_{32}+\sqrt{{(k_{\mathit{\text{off}}}^{\mathit{\text{IF}}}-k_{23}-k_{32})}^2+4k_{23}{k}_{\mathit{\text{off}}}^{\mathit{\text{IF}}}}$$ (eq. 4e)

As a result, IF and its relaxations (eq. 3) can be reproduced mathematically using CS and its relaxations (eq. 2) with rate constants defined by eqs. 4a-e. A data set consistent with IF can be fit to CS with identical accuracy by simply rearranging the kinetic rate constants defining IF (Scheme 4 below, left) into a mathematically equivalent mechanism based on CS (Scheme 4 below, right), i.e.,

$$\mathrm{E}\ast \underset{k_{\mathit{\text{off}}}}{\overset{k_{\mathit{\text{on}}}[\mathrm{L}]}{\mathrm{\rightleftarrows }}}\mathrm{E}\ast :\mathrm{L}\underset{k_{-r}}{\overset{k_r}{\mathrm{\rightleftarrows }}}\mathrm{E}:\mathrm{L}=\mathrm{E}\ast \underset{\varepsilon }{\overset{k_{\mathrm{r}}+k_{-r}}{\mathrm{\rightleftarrows }}}\mathrm{E}\underset{k_{\mathit{\text{off}}}-\varepsilon }{\overset{k_{\mathit{\text{on}}}[\mathrm{L}]}{\mathrm{\rightleftarrows }}}\mathrm{E}:\mathrm{L}$$ (Scheme 4)

where

$$2\varepsilon =k_{\mathit{\text{off}}}-k_r-k_{-r}\sqrt{{(k_{\mathit{\text{off}}}-k_r-k_{-r})}^2+4k_r{k}_{\mathit{\text{off}}}}$$ (eq. 5)

The result embodied by Scheme 4 shows that IF is a mathematical a special case of CS, even though the two mechanisms offer distinct physical interpretations of the binding interaction.

As an example, we address ligand binding to the active site of the clotting enzyme thrombin (Figure 1A). The two relaxations measured experimentally are compatible with both IF and CS and allow resolution of all independent parameters in the kinetic scheme. Interpretation of the data in terms of IF (red curves) yields best-fit parameter values: $k_{\mathit{\text{on}}}^{\mathit{\text{IF}}}=2.6\pm 0.1\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$, $k_{\mathit{\text{off}}}^{\mathit{\text{IF}}}=3.6\pm 0.1{\mathrm{s}}^{-1}$, k₂₃=12±1 s^-1, k₃₂=2.6±0.1 s^-1. The mathematically identical interpretation in terms of CS (black curves) returns the best-fit parameter values: $k_{\mathit{\text{on}}}^{\mathit{\text{CS}}}=2.6\pm 0.1{\mu \mathrm{M}}^{-1}{\mathrm{s}}^{-1}$, $k_{\mathit{\text{off}}}^{\mathit{\text{CS}}}=0.50\pm 0.02{\mathrm{s}}^{-1}$, k₁₂=14.6±0.5 s^-1, k₂₁=3.1±0.3 s¹. Application of Scheme 4 leads to the equivalence

Figure 1.

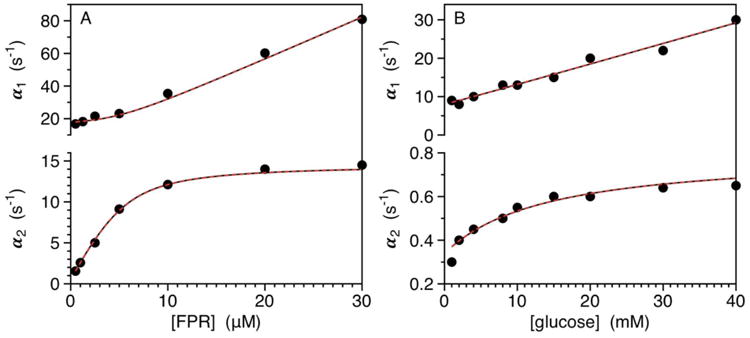
A-B. (A) Rates of relaxation measured for FPR binding to thrombin (50 nM) under experimental conditions of: 50 mM Tris, 200 mM ChCl, 0.1% PEG8000, pH 8 at 10 °C. FPR is in large excess (>10:1) even at the lowest concentration used, so the system is studied under pseudo-first order conditions of ligand. The fast relaxation (top panel) increases linearly with FPR at high concentrations reflecting the binding interaction. The slow relaxation (bottom panel) increases hyperbolically and monitors the conformational transition that either precedes (CS) or follows (IF) the binding step. Interpretation of the data in terms of IF (red curves) yields best-fit parameter values: $k_{\mathit{\text{on}}}^{\mathit{\text{IF}}}=2.6\pm 0.1\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$, $k_{\mathit{\text{off}}}^{\mathit{\text{IF}}}=3.6\pm 0.1s^{-1}$, k₂₃=12±1 s^-1, k₃₂=2.6±0.1 s^-1. The mathematically identical interpretation in terms of CS (black curves) returns the best-fit parameter values: $k_{\mathit{\text{on}}}^{\mathit{\text{CS}}}=2.6\pm 0.1\mu {\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$, $k_{\mathit{\text{off}}}^{\mathit{\text{CS}}}=0.50\pm 0.02{\mathrm{s}}^{-1}$, k₁₂=14.6±0.5 s^-1, k₂₁=3.1±0.3 s^-1. The fits are identical because of the complete equivalence of IF and CS according to eqs. 4a-e and Scheme 4 (see also Scheme 5). (B) Rates of relaxation for glucose binding to glucokinase (5-10 μM), taken from ref (20). As in the case of FPR binding to thrombin (panel A), the ligand is in large excess (>100:1) even at the lowest concentrations used and two relaxations monitor binding (top panel) and conformational transitions (bottom panel). The original report used the rapid equilibrium approximation to assign the mechanism as IF. Interpretation of the data in terms of IF (red curves) yields best-fit parameter values: $k_{\mathit{\text{on}}}^{\mathit{\text{IF}}}=0.54\pm 0.02{\text{mM}}^{-1}{\mathrm{s}}^{-1}$, $k_{\mathit{\text{off}}}^{\mathit{\text{IF}}}=7.54\pm 0.2{\mathrm{s}}^{-1}$, k₂₃=0.44±0.02 s^-1, k₃₂=0.36±0.01 s^-1. The mathematically equivalent interpretation in terms of CS (black curves) returns best-fit parameter values: $k_{\mathit{\text{on}}}^{\mathit{\text{CS}}}=0.54\pm 0.02{\text{mM}}^{-1}{\mathrm{s}}^{-1}$ $k_{\mathit{\text{off}}}^{\mathit{\text{CS}}}=0.34\pm 0.01{\mathrm{s}}^{-1}$, k₁₂=0.80±0.02 s^-1, k₂₁=7.2±0.2 s^-1. The equivalence between CS and IF is based on eqs. 4a-e and Scheme 4 (see also Scheme 6).

$$\mathrm{E}\ast \underset{3.6s^{-1}}{\overset{2.6[\mathrm{L}]s^{-1}}{\mathrm{\rightleftarrows }}}\mathrm{E}\ast :\mathrm{L}\underset{2.6s^{-1}}{\overset{12s^{-1}}{\mathrm{\rightleftarrows }}}\mathrm{E}:\mathrm{L}=\mathrm{E}\ast \underset{3.1s^{-1}}{\overset{14.6s^{-1}}{\mathrm{\rightleftarrows }}}\mathrm{E}\underset{0.50s^{-1}}{\overset{2.6[\mathrm{L}]s^{-1}}{\mathrm{\rightleftarrows }}}\mathrm{E}:\mathrm{L}$$ (Scheme 5)

where [L] is measured in μM units. Which one of the two mechanisms offering an identical fit of experimental data applies to ligand binding to thrombin? If IF is at play, thrombin binds the ligand with an association rate that approaches diffusion control in solution (18) and a dissociation rate of 3.6 s^-1. Binding is then followed by a conformational transition that optimizes the complex and takes place over a time scale τ = (k₂₃ + k₃₂)⁻¹ = 68 ms. If CS is invoked, thrombin exists in equilibrium between two conformations that exchange over a time scale τ = (k₁₂ + k₁₂)⁻¹= 56 ms. The ligand binds selectively to one of these conformations with a rate of association that approaches the diffusion limit and a rate of dissociation of 0.50 s^-1. The two mathematically equivalent interpretations involve a conformational transition that takes place over a relatively fast (56-68 ms) time scale that either precedes (CS) or follows (IF) a very rapid binding step. The only difference between the two interpretations is that the rate of ligand dissociation is much faster in IF than CS. This is a significantly different prediction that can be tested experimentally by measuring the rate independently. An elegant application of this strategy has been presented recently for sugar binding to LacY (19) and has helped assign CS as the mechanism of recognition. A similar scenario is observed for glucose binding to glucokinase (Figure 1B). The two relaxations resolved experimentally (20) can be interpreted in terms of IF (red curves) with best-fit parameter values: $k_{\mathit{\text{on}}}^{\mathit{\text{IF}}}=0.54\pm 0.02{\text{mM}}^{-1}{\mathrm{s}}^{-1}$, $k_{\mathit{\text{off}}}^{\mathit{\text{IF}}}=7.54\pm 0.2{\mathrm{s}}^{-1}$, k₂₃=0.44±0.02 s^-1, k₃₂=0.36±0.01 s^-1. The mathematically equivalent interpretation in terms of CS (black curves) returns best-fit parameter values: $k_{\mathit{\text{on}}}^{\mathit{\text{CS}}}=0.54\pm 0.02{\text{mM}}^{-1}{\mathrm{s}}^{-1}$, $k_{\mathit{\text{off}}}^{\mathit{\text{CS}}}=0.34\pm 0.01{\mathrm{s}}^{-1}$, k₁₂=0.80±0.02 s^-1, k₂₁=7.2±0.2 s^-1. Application of Scheme 4 yields the equivalence

$$\mathrm{E}\ast \underset{7.54s^{-1}}{\overset{0.54[\mathrm{L}]s^{-1}}{\mathrm{\rightleftarrows }}}\mathrm{E}\ast :\mathrm{L}\underset{0.36s^{-1}}{\overset{0.44s^{-1}}{\mathrm{\rightleftarrows }}}\mathrm{E}:\mathrm{L}=\mathrm{E}\ast \underset{7.2s^{-1}}{\overset{0.80s^{-1}}{\mathrm{\rightleftarrows }}}\mathrm{E}\underset{0.34s^{-1}}{\overset{0.54[\mathrm{L}]s^{-1}}{\mathrm{\rightleftarrows }}}\mathrm{E}:\mathrm{L}$$ (Scheme 6)

where [L] is measured in mM units. In this case, the same interaction can be interpreted with IF as a relatively slow conformational transition with τ = (k₂₃ + k₃₂)⁻¹ = 1.3 s that follows a binding step with relatively fast dissociation rate, or with CS as a relatively fast conformational transition with τ = (k₁₂ + k₂₁)⁻¹= 130 ms that precedes a binding step with a relatively slow dissociation rate. The two mathematically equivalent interpretations offer quite distinct physical scenarios for the time scales of conformational exchange and ligand dissociation that can again be tested by independent measurements.

Another instructive example where the mathematical equivalence between IF and CS becomes relevant is when the ligand dissociation rate is negligibly small. The pharmacology literature is particularly rich in such examples entailing inhibitors that bind tightly or irreversibly to their target (21). Serine protease inhibitors provide physiological regulation of enzyme activity (22) and also fall into this category. A widely accepted mechanism of action for such inhibitors is a rapid binding step followed by a slow and irreversible conformational rearrangement of the complex (21), which is basically IF in Scheme 3 with k₃₂ = 0. Scheme 4 offers a mathematically equivalent interpretation where the inhibitor binds selectively and irreversibly to only one of two pre-existing conformations of the macromolecule, i.e.,

$$\mathrm{E}\ast \underset{k_{\mathit{\text{off}}}}{\overset{k_{\mathit{\text{on}}}[\mathrm{L}]}{\mathrm{\rightleftarrows }}}\mathrm{E}\ast :\mathrm{L}\stackrel{k_r}{\to }\mathrm{E}:\mathrm{L}=\mathrm{E}\ast \underset{k_{\mathit{\text{off}}}}{\overset{k_r}{\mathrm{\rightleftarrows }}}\mathrm{E}\stackrel{k_{\mathit{\text{on}}}[\mathrm{L}]}{\to }\mathrm{E}:\mathrm{L}$$ (Scheme 7)

The second order association rate constant is the same for both schemes and the difference stems from the step assumed to be irreversible. In the case of IF (Scheme 7, left), the inhibitor binds reversibly and the complex rearranges irreversibly. In the case of CS (Scheme 7, right), the ligand binds irreversibly to one of two possible conformations of the macromolecule. What is interpreted as k_off in the IF mechanism is instead a rate of conformational transition in the CS mechanism. Assignment of the mechanism requires additional independent information on one or more steps of the kinetic scheme.

Discussion

The recent demonstration that a relaxation increasing hyperbolically with [L] cannot be used as unequivocal proof of IF (8) calls into question previous assignments of kinetic mechanisms based on the rapid equilibrium approximation (6) and creates a need for strategies that distinguish between IF and CS from analysis of experimental data. The need is made even more urgent by the complete mathematical equivalence between IF and CS reported in this study. Rapid kinetics carried out under conditions where the first-order approximation is no longer valid for either the ligand or the macromolecule have long been advocated in the assignment of mechanisms of ligand binding (23, 24) and their mathematical underpinnings have been detailed recently (25, 26). The kinetic equations of IF, or of a single step binding reaction, depend on the sum of the total concentrations of ligand and macromolecule (23) and are therefore invariant to conditions that alter the relative proportion of these components but not their total balance. That is not the case for CS, where the pre-existing equilibrium of the macromolecule is perturbed only when the ligand is in excess (23). Consequently, a comparison of rapid kinetics with excess macromolecule versus excess ligand is expected to produce no differences for IF, but should turn the hyperbolic increase with excess ligand into a straight line or constant value with excess macromolecule for CS (26). This test has been used to validate IF or CS in various systems (23, 25, 27-29). Measurements with excess thrombin over FPR prove that the relaxations in Figure 1A are due to CS and not IF (28). Similar measurements with excess antithrombin over heparin prove that heparin binding to antithrombin obeys IF and not CS (29). In the case of glucokinase the verdict is still out. The original suggestion that the data in Figure 1B are consistent with IF in the rapid equilibrium approximation (20) has been challenged by more recent kinetic measurements (30, 31) and structural data (32) in support of CS. The case for IF has been re-affirmed recently on the basis of the hysteretic behavior of glucokinase (33), but rapid kinetics with excess macromolecule would have been more persuasive.

Although the strategy of comparing measurements with excess ligand and excess macromolecule is informative (25, 26), it may find little application in practice. Large concentrations of macromolecule may be limited by availability or often produce aggregation and loss of stability. Increasing the ratio of macromolecule over ligand also weakens the amplitude of spectroscopic signal and adds significant error to the kinetic traces. Alternative approaches to resolve the ambiguity between IF and CS have been proposed in terms of global fit analysis (34), or detection of fluxes in extended kinetic mechanisms that encompass IF and CS as special cases (33, 35, 36). Although potentially valuable, these approaches and the analysis based on excess macromolecule cannot deal effectively with the case of a single relaxation obtained with excess ligand, which is by far the most common scenario encountered in practice. Understanding the properties of eqs. 3 and 4 under these conditions helps devising a strategy of general applicability.

When the slow relaxation increases hyperbolically with [L], the asymptotic values in the plot assume different meaning for IF and CS (8, 9). In the case of CS, the plot offers a straightforward interpretation of the two asymptotic values as the dissociation rate of the ligand, ${\alpha }_2^{\mathit{\text{CS}}}(0)=k_{\mathit{\text{off}}}^{\mathit{\text{CS}}}$, and the rate for the E* → E transition, ${\alpha }_2^{\mathit{\text{CS}}}(\infty )=k_{12}$, thereby enabling derivation of two important parameters of the kinetic scheme directly from experimental data. IF does not provide such convenience because the upper asymptote measures the sum of kinetic rates for the conformational rearrangement following the binding step, ${\alpha }_2^{\mathit{\text{IF}}}(\infty )=k_{23}+k_{32}$, and the lower asymptote, $2{\alpha }_2^{\mathit{\text{IF}}}(0)=k_{23}+k_{32}+k_{\mathit{\text{off}}}^{\mathit{\text{IF}}}-\sqrt{{(k_{\mathit{\text{off}}}^{\mathit{\text{IF}}}-k_{23}-k_{32})}^2+4k_{23}{k}_{\mathit{\text{off}}}^{\mathit{\text{IF}}}}$, is a convoluted expression of individual rate constants. Assignment of the lower asymptote for IF as ${\alpha }_2^{\mathit{\text{IF}}}(0)=k_{32}$ is only valid under the rapid equilibrium approximation where binding and dissociation are fast compared to conformational rearrangement. In general, the lower asymptote α₂(0) will measure either a convoluted expression of the rate constants for IF, or k_off for CS. In both cases, however, the value depends on properties of the bound complex and is expected to change with different ligands. Interestingly, the value of the upper asymptote α₂(∞) measures a property of the free macromolecule for CS or a property of the bound complex for IF. This value is expected to change with different ligands for IF but not for CS. Therefore, rapid kinetics measurements carried out with different ligands and under identical solution conditions may easily discriminate between IF and CS, without requiring excess macromolecule or more than a single relaxation.

Figure 2 shows application of this approach to the study of ligand binding to the thrombin mutant W215A. Residue W215 is assumed to play a major role in the pre-existing E* ⇄ E equilibrium of the trypsin fold by relocating its indole group in the active site during the E → E* transition (37, 38). X-ray crystallography documents a shift of the entire backbone of the 215-217 segment linked to movement of the indole of W215, thereby raising the interesting mechanistic question of which structural event is the trigger for the E → E* transition. Recent NMR measurements have reported assignments for the bound forms of thrombin and have been inconclusive on the conformational plasticity of the 215-217 segment in the free form (39, 40). Rapid kinetics carried out with excess ligand offer a possible solution. Binding of FPR to the W215A mutant produces a single relaxation that increases hyperbolically with [L] (Figure 2A) and suggests that the side chain of W215 is responsible for the functional differences between the two conformations in solution. Once steric hindrance of this side chain is removed with the Ala substitution, binding of FPR would occur with similar affinity to both conformations and through IF. Replacement of the Arg residue of FPR with Lys in FPK weakens binding to the primary specificity site without compromising interaction with W215 (16) and offers a valuable alternative probe of the active site region. As for FPR, binding of FPK produces a single relaxation that increases hyperbolically with [L] (Figure 2A). The two ligands produce distinct values of α₂(0) but the same value of α₂(∞). Although this behavior does not rule out IF, it is highly supportive of CS where ${\alpha }_2^{\mathit{\text{CS}}}(0)=k_{\mathit{\text{off}}}^{\mathit{\text{CS}}}$ measures the distinct dissociation rates of the two ligands and ${\alpha }_2^{\mathit{\text{CS}}}(\infty )=k_{12}$ measures the rate for the E* → E transition which is obviously ligand independent. A significantly different value of this upper asymptote for FPR and FPK would disprove CS automatically. Decisive support for CS comes from measurements carried out at 25 °C (Figure 2B) where FPK produces a relaxation that decreases with [L] and saturates at the same value as that measured for FPR. The drastic switch in kinetic profile for FPK at higher temperature is simply a consequence of the rate of dissociation of this ligand becoming faster than the rate for the E → E* transition. Rapid kinetics involving different ligands and experimental conditions prove that occlusion of the active site in the E → E* transition is caused by a shift in the backbone of the 215-217 segment. Relocation of the indole ring of W215 within the active site is a consequence and not the trigger of the E → E* transition. This advances our mechanistic understanding of the pre-existing equilibrium of the trypsin fold and offers a testable hypothesis for future X-ray and NMR studies.

Figure 2.

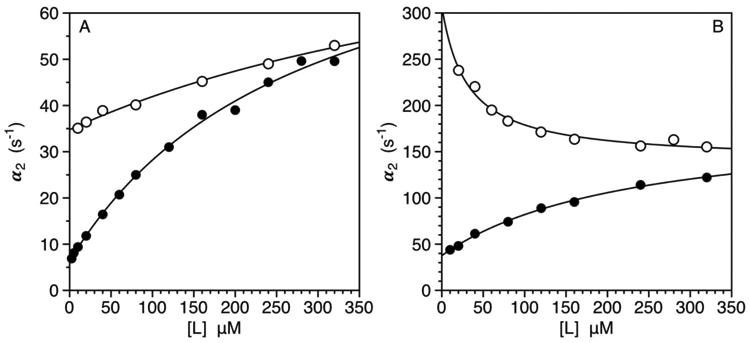
A-B. Rates of relaxation for FPR (filled circles) or FPK (open circles) binding to the thrombin mutant W215A (300 nM at 10 °C, 1 μM at 25 °C) under experimental conditions of: 50 mM Tris, 200 mM ChCl, 0.1% PEG8000, pH 8 at 10 °C (A) or 25 °C (B). FPR and FPK are in large excess (>10:1 at 10 °C, >300:1 at 25 °C) even at the lowest concentrations used, so the system is studied under pseudo-first order conditions of ligand. A single saturable relaxation could be measured for the two ligands, precluding unequivocal resolution of all four independent rate constants in eqs. 2 and 3. The data at 10 °C show the two ligands converging toward the same asymptotic value α₂(∞) = 90 s^-1 and distinct values of α₂(0). The profile does not rule out IF but is highly supportive of CS. Direct confirmation of CS is obtained from the data at 25 °C where the dependence of the relaxation on FPK switches to a hyperbolic decrease under the same experimental conditions where FPR binding obeys a hyperbolic increase. Again, both ligands converge to the same asymptotic value α₂(∞) = 145 s^-1 as expected for CS. Distinct values of α₂(0) reflect the different rates of dissociation, k_off, for the two ligands. Continuous lines were drawn with the empirical expression ${\alpha }_2={\alpha }_2(0)+\frac{{\alpha }_2(\infty )-{\alpha }_2(0)}{\beta +[\mathrm{L}]}[\mathrm{L}]$, where β gives an estimate of the apparent equilibrium dissociation constant.

Proof that IF is a mathematical special case of CS is somewhat counterintuitive because both mechanisms involve two elementary steps and the same number of independent species. Functional complexity therefore depends on how elementary transitions are arranged topologically. Pre-existing conformational equilibria influence complexity the most and likely provide the foundation of any kinetic mechanism. This feature fits well with the conformational plasticity of proteins in the free form (2, 41, 42) and invites a more realistic interpretation of Scheme 2 with E* and E as individual ensembles of rapidly interconverting conformations rather than individual species (10, 28). Our analysis by no means negates the relevance of IF, especially as a component of more complex kinetic mechanisms (1-7, 21, 23, 25, 41, 43-46). Rather, it motivates increased scrutiny of facile intepretations of rapid kinetics and the need for direct monitoring of the contribution of individual components of a kinetic mechanism by alternative techniques, as recently offered by single molecule detection (47) or analysis of NMR dispersions (48).

Abbreviations used

CS

conformational selection

IF

induced fit

FPK

H-D-Phe-Pro-Lys-p-nitroanilide

FPR

H-D-Phe-Pro-Arg-p-nitroanilide