Force production by depolymerizing microtubules: A theoretical study

Abstract

Chromosome movement during mitosis is powered in part by energy released through the depolymerization of kinetochore microtubules (MTs). Strong but indirect evidence suggests the existence of a specialized coupling between kinetochores and MT plus ends that enables this transduction of chemical energy into mechanical work. Analysis of this phenomenon is important for learning how energy is stored within the MT lattice, how it is transduced, and how efficient the process can be, given coupling devices of different designs. Here we use a recently developed molecular-mechanical model of MTs to examine the mechanism of disassembly dependent force generation. Our approach is based on changes in tubulin dimer conformation that occur during MT disassembly. We find that all of the energy of polymerization-associated GTP hydrolysis can be stored as deformations of the longitudinal bonds between tubulin dimers, and its optimal use does not require the weakening of lateral bonds between dimers. Maximum utilization of this stored energy and, hence, the generation of the strongest possible force, is achieved by a protofilament power-stroke mechanism, so long as the coupling device does not restrict full dissociation of the lateral bonds between tubulin dimers.

Microtubules (MTs) are the primary structural elements of mitotic spindles, where they are intimately involved in the processes of chromosome segregation. These thin, polar fibers grow by polymerization of αβ-tubulin dimers and can undergo rapid shrinking as a result of their dynamic instability (reviewed in refs. 1 and 2). It is now well established that this behavior is related to structural changes in the tubulin dimers that occur soon after polymerization and are tightly linked with the hydrolysis of tubulin-bound GTP (reviewed in refs. 3 and 4). The minimum energy conformation of GDP-bound dimers is more bent than that of the polymerization-competent, GTP-bound protein (5, 6). Tubulin dimers, therefore, display a nucleotide hydrolysis-dependent conformational change that is likely to be the driving force behind rapid MT shrinking (reviewed in ref. 7). Once tubulin depolymerization has been triggered, the lateral bonds between dimers dissociate quickly, beginning at MT ends. As a result, individual tubulin protofilaments (PFs) curl outward, which can be observed directly under conditions that preserve the subtleties of MT structure (8).

Both the polymerization of tubulin and the shortening of MTs can be viewed as molecular machines that generate force and can accomplish mechanical work by pushing or pulling, respectively, on appropriately attached objects (9). The polymerization motor is thought to use a Brownian ratchet mechanism, in which a newly added dimer rectifies movements that occurred through thermal fluctuations (reviewed in ref. 10). Growing MTs have been shown to generate pushing forces in vitro, and with a lesser certainty, in vivo; theoretical descriptions of the underlying mechanism are quite advanced (reviewed in ref. 11). In contrast, the mechanism by which MT depolymerization generates a pulling force remains relatively unknown, in part, because of the conceptual difficulty of specifying the device that would allow an object to follow the end of a depolymerizing MT without losing its mechanical connection. In the best characterized example of a depolymerization-driven motion in vitro, a microbead covered with certain motor proteins followed the plus end of a depolymerizing MT, even in the absence of ATP (12). Two theories describing this phenomenon were also based on a ratchet: one considered biased one-dimensional diffusion (12), and the other, rotational diffusion of the bead along the MT lattice, where a hypothetical free energy gradient near the depolymerizing end prevented the bead's detachment (13, 14). A rotation mechanism is, however, unlikely to be relevant for chromosome movement in mitosis, because neither the chromosome nor its parts are known to rotate as they move toward the poles. Instead, the butts of MT plus ends attach directly to kinetochores and, in a majority of cell types, tubulin depolymerization from this MT end accompanies pole-directed chromosome movements (reviewed in refs. 15 and 16).

There is substantial evidence that chromosome motions in mitosis can be driven primarily by MT depolymerization (reviewed in refs. 17 and 18). For example, anaphase movements can occur in very low concentrations of ATP, both in permeabilized cells (19, 20) and in vitro (21–23). Chromosome-to-pole motion in yeast cells appears to occur in strains that are deleted for all known kinetochore-associated motor enzymes (24, 25).

The coupling device that enables force production through the depolymerization of MTs attached to a chromosome is frequently referred to as a lateral tip attachment complex (26; reviewed in refs. 17 and 27). It is thought to form multiple weak bonds between the MT wall and some attachment proteins that form a cylindrical coat around the MT wall near its end. The most detailed theoretical description of such a mechanism was formulated by Hill and Kirschner (28, 29). MT movement inside this coat, or “sleeve,” occurs through thermal fluctuations and is biased by the free energy of a MT's binding to its inner surface. In this model, the plus end of the MT can exchange subunits with a pool of free tubulin inside the sleeve. Because the free energy of the system is a minimum when some optimal number of the binding sites is occupied, both shortening and elongation of the MT end are compensated by polymer sliding. Thus, if the kinetochore MT depolymerizes from its sleeve-associated plus end, the chromosome will follow without detachment.

A second hypothesis takes direct advantage of a more recently discovered pathway for MT depolymerization and is frequently called the “conformational wave model” (27, 30). In this model, force is produced by a “power-stroke” mechanism in which the curling PFs of the disassembling MT push directly on a cylindrical collar and drive its sliding toward the MT minus end. Such movement is powered by the release of strain stored in the MT lattice. In this work, we analyze force production by depolymerizing MTs and examine the effectiveness of the above coupling devices by applying a mathematical model that describes mechanical changes associated with MT depolymerization.

Mathematical Model

General Description. Our recently described molecular-mechanical model of MTs (31) has been modified to include interactions between an MT end and a hypothetical coupling device (described below). Briefly, the model used in the current study assumes that dimers are positioned in a helix with zero pitch (a 13_0 lattice), so all of the PFs are identical. The MT space is divided into 13 half planes, each originating at the MT's central axis and separated from its neighbors by 2π /13 rad. The bending of an individual PF during MT shortening occurs only in its respective plane (Fig. 1). Within the MT wall, each dimer interacts with its neighbors at six points: two “head-to-tail” points that provide longitudinal interactions and four points that define the sites of lateral attachment. The interactions at these points are characterized by two different functions. The longitudinal interactions are described by the potential g(χ) (Eq. 1), according to which dimer pair tends to assume a characteristic equilibrium angle χ_o. The model assumes that these longitudinal bonds are not extensible, and they do not break. These assumptions simplify the calculations but do not interfere with a study of the work produced by bending PFs.

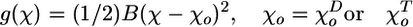[1]

where B is a parameter characterizing stiffness of the longitudinal bond; χ is the angle between two adjacent head-to-tail dimers in the plane of their PF; 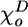and 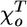are the equilibrium angles for GDP-associated dimer (D) and GTP-associated dimer (T). In this paper, their values are assumed to be 0.4 and 0.2 rad, respectively.

Fig. 1.

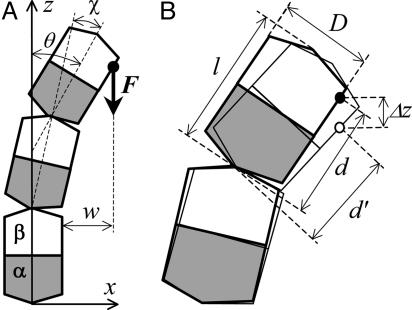
Side view of a bending PF and its interaction with a coupling device. (A) Schematic diagram of a PF; its head-to-tail attached dimers consist of lower α-(gray) and upper β-tubulin (white) monomers. Arrow on z axis points toward the MT's plus end; higher positioned dimers are referred to as more distal. Dimers are numbered from bottom to top (i = 1,..., N). Bending of the PF (exaggerated) occurs in a plane (x, z), where it is described by the angles χ_i between each pair of adjacent dimers and θ_i between the ith dimer and the z axis. During bending, the PF can exert force with a vertical component F (thick black arrow) by pushing against the hypothetical ring positioned at an arbitrary distance w from the outer surface of a straight PF. The ring is represented here by the fulcrum point (dark circle). (B) The bending PF accomplishes work if the ring moves a distance Δz downward parallel to the MT's axis (open circle). During this process, the PF's configuration changes (open contours with thinner solid borders), and it can accomplish biologically useful work (see Mathematical Model for other details).

The lateral forces, described by the potential v(r) (Eq. 2 and Fig. 4), depend only on the lateral distance r between the points of interaction on adjacent dimers. For simplicity, the strength of the lateral bond between two α-tubulins is assumed to be independent of GTP hydrolysis and equal to the strength of the GTP-bound β-β bond. Because the strength of the latter bond is unlikely to decrease significantly after GTP hydrolysis (31), we have also assumed the same strength for the GDP β-β bond.

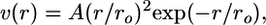[2]

where r_o characterizes bond length and A characterizes its stiffness. This equation has been modified compared to (31) so A is measured in energy units, which simplifies its utilization here.

Fig. 4.

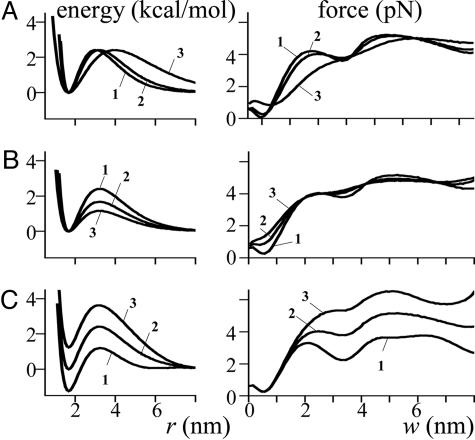
Role of energy potential for lateral interactions between dimers in force production. The energy potentials (kcal/mol) as a function of distance r between lateral interaction points (A–C Left) and the corresponding force (pN, numbered accordingly) developed by a PF as a function of w (A–C Right). (A) The potentials with different bond lengths (i.e., the half distance between the energy maximum and the bottom of the well). A = 4.43 kcal/mol, B = 93.8 kcal/(mol·rad²); r_o = 2.1 Å (curve 1), 2.4 Å (curve 2), and 3.6 Å (curve 3). (B) Potentials with different barrier heights (i.e., difference between the energy at its maximum and at the bottom of the well); B = 93.8 kcal/(mol·rad²), r_o = 2.4 Å; A = 4.43 (curve 1), 3.08 (curve 2) and 2.14 (curve 3) kcal/mol. C. The potentials with different depths of well. B = 93.8 kcal/(mol·rad²), r_o = 2.4 Å, A = 4.43 kcal/mol. Curve 1 is given by v(r) = (A/r²_o)(r²·exp(–r/r_o) – 0.001·exp(–4.7r⁴/r_o)), curve 2 by Eq. 2, curve 3 by v(r) = (A/r²_o)(r²·exp(–r/r_o) + 0.001·exp(–4.7r⁴/r_o)).

The total potential energy of the MT, U, is the sum of the interaction energies at all points in the lattice. The steady-state MT configuration has been determined by using matlab 6.5 (Mathworks, Natick, MA) to identify a local minimum of U for initial conditions that correspond to a straight MT configuration (31).

Estimating the Stiffness of Lateral and Longitudinal Bonds and the Value of r_o. Although exact values for these parameters are not known, they can be estimated with reasonable certainty from indirect evidence. During MT depolymerization, the PFs peel back from the shortening end(s), so the lateral bonds between dimers in neighboring PFs dissociate while the longitudinal bonds within a PF are still intact. Thus, the rate of MT shortening is determined mostly by the rate of dissociation of lateral bonds. The activation energy E_a for lateral bond dissociation and, hence, A can therefore be estimated from the temperature dependence of the rates of MT depolymerization by using an expression derived from the Arrhenius equation:

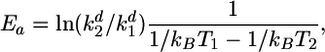[3]

where k_B is a Boltsman constant and k^d_n is the dimer dissociation rate constant at temperature T_n.

We used experimental data from refs. 32–37 and data for >20°C from ref. 38 to calculate the average activation energy over a temperature range of 21–39°C: E_a = 4.8 ± 0.6 kcal/mol. This value is a relatively large energy barrier that is comparable with the energy of hydrolysis of GTP under standard conditions, ≈7.3 kcal/mol (39). Parameter A can then be calculated from Eq. 2: E_a = v_max = v(2r_o), so for two bonds A = 1/8 E_ae² ≈ 4.4 kcal/mol.

The value of B, which describes the stiffness of the longitudinal bond, can be estimated from the above value for A and a given r_o by using our molecular-mechanical model of the MT, in which a MT's stability is determined by the ratio of lateral and longitudinal bond stiffness: a = A/B (31). It is easy to see that when the longitudinal bonds are very strong (smaller a), the capped MT will undergo a catastrophe regardless of the size of the GTP-cap. Correspondingly, when the longitudinal bonds are weak (larger a), the MT will be stable even if there is no GTP-cap. Thus, a = A/B is limited by a^T_cr < a < a_cr, where a^T_cr and a_cr are two critical values that limit the range of values for a over which only a capped MT is stable. For such a range of a (which depends on the value of r_o), one can determine the corresponding plausible ranges for B and the bending energy g_o, where g_o = 1/2B(χ^D_o)². Using this approach, we estimate r_o in the range of 2–3 Å. (For smaller r_o, the bending energy g_o exceeds the maximum that is thermodynamically possible, given the free energy of GTP hydrolysis.) In ref. 31, we have used r_o = 1.2 Å, but our analysis here suggests that this value may have been an underestimate. Unless stated otherwise, all calculations here were done for r_o = 2.4 Å, for which the range of plausible g_o is 6.7–7.3 kcal/mol.

Calculating the Equilibrium Force Produced by a Depolymerizing MT. PF bending energy can be put to work. For example, the MT can be inserted into a coupling device, such as a ring that can slide along the polymer (30). For a 13_0 MT enclosed by a symmetrical ring, all PFs are identical, and one can simply calculate the force produced by a single PF interacting with a ring at one point of contact, which we call a fulcrum (Fig. 1 A). We first examine a PF pushing at a fulcrum that does not slide and is positioned at an arbitrary distance w from the MT's outer surface. Thus, bending of the PF is restricted, and the site of its contact with the fulcrum cannot deviate farther than w. The equilibrium configuration of such a PF is found by minimizing its total potential energy over all variables with one additional condition:

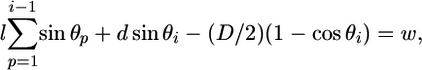[4]

where i is the number of the dimer that comes in contact with the fulcrum, the angle θ describes this dimer's tilt relative to the PF's axis, and l and D are the dimer's length (8 nm) and width (6.5 nm), respectively (40) (Fig. 1B). Thus, the left part of Eq. 4 describes the coordinates of the contact site on the surface of the ith-dimer, which is located a distance d away from the dimer's lower surface.

To calculate the work that can be accomplished by a PF pushing on a fulcrum, its position is moved slightly downward. We assume that the PF achieves the new minimum of its potential energy promptly, i.e., changes in the PF configuration occur significantly faster than any movement of the fulcrum. Also, the fulcrum's movement is assumed to be slow, so any forces that depend on the rate of movement are negligible. During the fulcrum's sliding from z into z′, its contact site with a PF moves along the PF's surface. If the new contact site is situated on the dimer's surface at d′ < d (Fig. 1B), the corresponding potential energy can be calculated with Eq. 4 simply by substituting d with d′. The maximal work that can be accomplished during this transition is given by the difference between the potential energies at the initial and final configurations. If all this energy is transformed into work, the average maximal force F with which the PF pushes against the ring in the direction parallel to MT's axis is

[5]

Choosing a small Δz, one can calculate force production as a function of different parameters, such as the size of the ring and parameters that describe the tubulin-tubulin bonds.

All graphs in this paper depict the vertical component of the force that is produced by a single PF, because it is the more relevant component biologically. For a complete MT, the force is 13 times larger. Note that for a symmetrical coupling device, the components perpendicular to the MT axis cancel. For obvious reasons, we refer to this force as “pushing,” although if the ring were attached to a load, e.g., a chromosome, the depolymerizing MT would be pulling that object. All calculations are carried out for the MT plus end, but all of the same principles apply to disassembly at the minus end.

Results

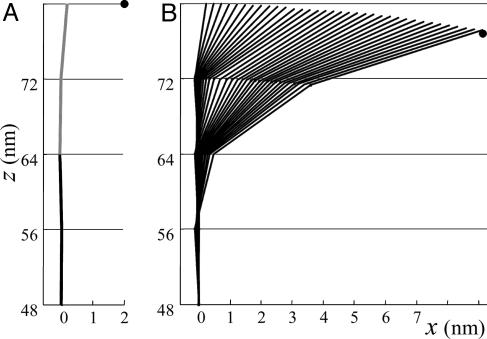
Lateral Bonds Break During PF Bending in a Highly Sequential Manner. We first used our molecular-mechanical model to calculate the shape of a MT that was capped with two layers of GTP-tubulin subunits and enclosed by a motionless ring whose inner rim was positioned at distance w = 2 nm from the MT outer surface (Fig. 2A). As described in Mathematical Model, such a MT is stable and all dimers except the most terminal are oriented highly parallel to the MT axis with radial deformations <0.005 Å (31). As expected, this configuration is unaffected by the presence of the ring, so long as the ring's diameter is larger than that of the MT and there is no interaction between them.

Fig. 2.

Steady-state configurations of a PF pushing at fixed fulcrums. Each contour is the result of a calculation that used a 13_0 MT consisting of N = 10 dimers, A = 4.43 kcal/mol, B = 93.8 kcal/(mol·rad²). Note the difference in scale between vertical and horizontal axes, both in nanometers. This difference makes a dimer look longer as it changes orientation. (A) Side view of last four dimers in a PF from the 2T-capped MT calculated for the fulcrum (inner side of the ring in the plane of this PF, •) positioned at w = 2 nm to the right from the uppermost point of the terminal dimer. Obviously, the PF shape is unaffected if the fulcrum is positioned at lower z. Area to the left of the contour corresponds to inner side of MT wall; black and gray segments represent G and T dimers, respectively. (B) The series of contours depicting side views of the PF as in A except from a homogeneous, GDP-containing MT. Each contour corresponds to a PF bent to its steady-state position while pushing against a fulcrum positioned at a different distance from the MT surface (w = 0–9 nm, 0.24 nm increment). For consistency, the PF always contacts the fulcrum at the uppermost site on its terminal dimer (Eq. 4). The • shows fulcrum's position corresponding to the most bent PF.

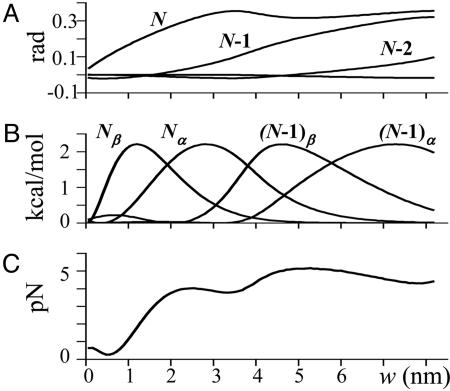
When similar calculations are carried out for MTs without a cap, i.e., consisting entirely of the D dimers, the PFs curl outward and come into contact with the ring's inner surface (Fig. 2B). The resulting equilibrium shape of the bent PF depends on the ring's size in a complex way. With increasing ring diameter, the bonds between the terminal, plus-end dimer N and its two lateral neighbors must stretch for the subunit to touch the ring. Thus, the tilting angle χ of the terminal dimer gradually increases, whereas its more proximal neighbors remain straight (Figs. 2B and 3A). With wider rings, the lateral bonds between terminal subunits will ultimately break (Fig. 3, compare A and B), leading to an abrupt change in the shape of the MT plus end (visualized as unevenness in the distribution of PF profiles on Fig. 2B). Note that because the lateral bond between β-monomers is located approximately three times farther away from the rotation point (i.e., the head-to-tail attachment site with the lower neighbor) than the bond between α-monomers, its contribution to adhesion between PFs is approximately three times greater than that of the α-monomers, and the overall bending of the dimer is determined mostly by the behavior of the β-β bond. Just as the terminal dimer separates from its lateral neighbors and reaches its equilibrium bend, the lateral bonds in its lower neighbor (N – 1) become stretched. Similarly, the third dimer from the top will begin to bend when its upper neighbor has almost achieved the equilibrium bend and lost its contacts with the neighboring PFs. Therefore, dimer bending and the accompanying breaking of lateral bonds occur in a domino-like fashion: significant stretching of a lateral bond begins when all more distal bonds have already separated.

Fig. 3.

Tilt, energy potential, and equilibrium force with which a PF pushes as a function of the ring's size. (A) Tilting angle χ for the three terminal dimers as a function of w. (B) Energy for lateral bonds engaged in force production as a function of w (only the last two dimers are shown). Symbols α and β refer to the tubulin subunits. With increasing w, every bond gets stretched, but the changes are smaller for less distal dimers. (C) Equilibrium pushing force exerted by a bending PF for different values of w.

Maximal Force Is Developed as the Lateral Bonds Between the Dimers Dissociate Completely. Although the above conclusions are intuitively clear in the context of our model, understanding the pathway of dimer bending is essential for explaining the accompanying generation of force. As shown on Fig. 3C, the equilibrium force production during this process depends on the size of the ring in a complex, nonlinear way. When w ≤ 0.5 nm, the paraxial force developed by bending PFs is very small. In part, this result is a simple consequence of the system's geometry. However, a more significant role in limiting the force at small w, as well as in creating its nonmonotonic behavior at larger w, is played by the sequential breakage of the lateral bonds. The underlying mechanism is best understood by considering the shape of the energy potential for lateral interactions between tubulin monomers (Eq. 2). When the longitudinal bond between adjacent dimers is only slightly bent, the lateral bonds in the upper dimer are stretched but remain shorter than the distance from the center of the potential well to the barrier's maximum (i.e., the system remains within the potential well of the lateral bonds). Thus, there are strong attraction forces between this dimer and its two lateral neighbors that counteract the tendency of GDP dimers to tilt. Once the lateral bond is stretched beyond the maximum of the potential barrier, the attractive lateral force changes into a repelling one. Therefore, depending on the ring's size, the lateral interactions can either counteract the bending or promote it (Fig. 3, compare B and C).

Accordingly, when w is very small, the force that can be developed is negligible because the energy stored in the lattice is mostly used to overcome the potential barrier in the lateral interactions of the most terminal dimer. This force increases with increasing w and reaches its local maximum when the lateral bonds between terminal dimers break, and this dimer begins to experience repulsion from its neighbors (Fig. 3C). With further increase in w, the pushing force begins to decline, because it is now used in part to stretch the lateral bonds of the next dimer, which still interacts with its lateral neighbors. Depressions in the curve for developed force appear periodically, but their amplitude decreases with w, because the dimers more distant from the fulcrum have less impact on force development. When w > 10 nm, the developed force decreases gradually because of the increase in lever arm at the fulcrum, i.e., the distance between the fulcrum and the dimer whose lateral bonds are stretched at this w. We conclude that the optimal size of a ring-shaped device for coupling MT depolymerization to force generation is one that positions its inner edge 5–7 nm from the MT's surface.

Strong Lateral Forces Between Dimers Do Not Impede Efficient Force Production if the Ring Is Appropriately Wide. To further analyze the role of lateral interactions between tubulin monomers, we examined directly how reasonable variations in the shape of their energy potential would affect force production. With increasing r_o (the length of this bond), the fluctuations in the force produced diminish visibly (Fig. 4A). The impact of lateral bond strength decreases because the walls of the potential well become less steep, weakening the force that counteracts bending. Similarly, with decreasing barrier height, E_a, the maximum strength of the dimer interactions also decreases, and the force curve becomes more monotonic while tending smoothly to a virtually unchanged maximum (Fig. 4B). With a narrow ring (w ≤ 0.5 nm, which is comparable to the bond's length) the force produced is relatively small regardless of r_o and E_a. It is also smaller for shorter bonds and larger barriers, consistent with the notion that strong lateral forces impede force production in a narrow sleeve. Importantly, these graphs demonstrate that the maximal force that can be developed by PF pushing on a wider ring is independent of the strength of lateral interactions between dimers in the MT lattice.

The above analysis was carried out for bonds that neither produce nor consume energy when broken, i.e., ones whose potential well has a minimum value of 0. Although r_o and E_a can be estimated with reasonable accuracy (see Mathematical Model), the depth of the potential well for lateral tubulin interactions is unknown. To investigate the role of this bond feature, we varied the potential minimum while keeping the energy level at an infinite distance and the barrier's height essentially unchanged (Fig. 4C). Unlike other parameters, the depth of the well is unimportant for small w, and the force produced in the narrow ring is always small. After the first bond is broken, however, there is a noticeable difference in the maximum pushing force because the energy difference between a dimer within the lattice and a dimer that is free contributes directly to the work produced. If energy is released during the breaking of bonds, the maximal force increases (Fig. 4C, curve 3), but if energy is consumed, the force gets smaller (Fig. 4C, curve 1). Regardless of the size of this contribution, however, it is independent of GTP hydrolysis: the same energy potential is used to describe lateral interactions between all tubulins, regardless of their associated nucleotide.

Estimating the Maximal Force That Can Be Produced by Depolymerizing MT Pushing on an Appropriately Wide Ring. We have considered the case of a ring whose diameter is enough greater than that of the MT to let it experience a strong force from bending PFs. One can then solve for the equilibrium force acting on a fulcrum that is constrained to a constant value of w but is allowed to move in z as the PF bends. Many of the features of the variation in force with z resemble those presented in Fig. 3, but the exact solutions at certain values of z depend on assumptions about the shape of the dimer. For example, if dimers are modeled as cylinders and z is such that the fulcrum encounters their longitudinal junction, the curve of force vs. z displays a singularity. To overcome this difficulty and to obtain a reliable value for the average maximum force predicted by our model, we have therefore taken an alternative approach.

We have considered a ring that maintains a constant w but allows variable z to examine the energy of the system at two states: when the fulcrum is touching an arbitrary point on the Nth dimer and when it is touching the same point on the (N – 1)th dimer (Supporting Appendix 1, which is published as supporting information on the PNAS web site). When the ring has a sufficient diameter, the developed force is directly proportional to the stiffness of longitudinal bonds, B, and the equilibrium bend of the GDP dimer χ^D_o (Eq. 7 in Supporting Appendix 1). Using the estimated values of parameters A and B (Mathematical Model), one can calculate the force produced by a PF pushing on an optimally sized ring. For an activation energy barrier in the lateral bond of 4.8 kcal/mol (corresponds to A = 4.43 kcal/mol), the minimal value of the bending energy that can overcome this barrier is 6.7 kcal/mol, which corresponds to 5.8 pN per dimer. Thus, the force that our model predicts for the entire MT during disassembly of one subunit layer is ≈75 pN. Note that the maximal force for this process is necessarily limited by the energy of GTP hydrolysis at ≈82 pN (Supporting Appendix 2, which is published as supporting information on the PNAS web site). For a comparison, the maximal force that can be produced by a MT depolymerizing in Hill's sleeve is ≈15 or ≈9 pN as interpreted by either Joglekar and Hunt (41) or us (Appendix 2). These values are significantly less than the prediction from the power-stroke mechanism.

Our estimated maximal force per MT is a significant fraction of the 700 pN that will stall a grasshopper meiotic chromosome in anaphase (42), suggesting that only ≈10 MTs are required for chromosome movement in this species. The number of MTs at the kinetochore in a related species is ≈40 (43), but it is not clear how many of these polymers extend to the pole and/or develop force at any one time. The anaphase mechanism may be designed to depend on only some of the kinetochore MTs at any one time, or it may not be optimized for force production. Perhaps some other consideration, like processivity, is more important; a larger number of MTs may increase the chances that a chromosome continues to move all of the way to the spindle pole.

Discussion

Although it is well known that the energy of GTP-hydrolysis during MT polymerization is captured by the MT lattice, a detailed understanding of the impact of this storage on tubulin interactions within the MT is still lacking. A priori, this energy could be used to decrease the strength of lateral bonds, to increase the bending moment of longitudinal bonds, or some combination of the two. Previous modeling has demonstrated that any of these options is compatible with destabilization of the capless MT because polymer stability is determined by the ratio of lateral and longitudinal bond stiffness, rather than by their absolute values (31). However, the similarity of disassembly rates for the plus and minus MT ends argues strongly against a weakening of the lateral bonds (31). From the temperature dependence of the rate of MT disassembly, we have estimated that the potential energy barrier for the lateral bond is relatively high (4.8 kcal/mol). The results reported here help to explain why the breakage of strong lateral bonds during disassembly does not necessarily lead to a reduction in the useful work that can be accomplished during this process. Eq. 7 (Supporting Appendix 1) shows that for a given lateral bond energy, the force that can be developed during PF bending, which is defined by the change in the MT's free energy, depends exclusively on the stiffness of longitudinal bond and the equilibrium GDP dimer configuration. This conclusion is consistent with the notion that the energy available from GTP-hydrolysis is stored as an increased bending moment for the longitudinal interdimer bond. When disassembly is triggered, some bending energy is first spent to stretch the lateral bonds between dimers in neighboring PFs. This expenditure continues to increase until the length of a lateral bond reaches 2r_o, which corresponds to the position of the maximum of the potential energy barrier. With a further increase in distance between lateral contacts, the bonds no longer resist the dissociation but instead promote it. The energy that was spent to disrupt the lateral bonds is now released, and if the coupling device is optimal, all of the energy can be used as mechanical work. Thus, the amount of work a disassembling MT can do is independent of the height of the lateral bond's potential barrier; it is affected only by the depth of this potential well, which may either increase or decrease the force produced (Fig. 4).

By satisfying the condition that MTs show a cap-dependent stability, we have estimated the range of plausible values for the bending energy, g_o. Although the unknown length of the lateral bond prevents our determining the value of g_o more accurately, it is noteworthy that for reasonable values of r_o, the predicted range includes 7.3 kcal/mol, the standard free energy of GTP hydrolysis (39). In other words, if the interdimer bond parameters are optimal, virtually all of the energy of GTP hydrolysis can be captured as stress in the longitudinal bonds. As described above, the entire bending energy can then be used to produce useful work. Thus, it is theoretically possible that during disassembly, MTs can work as molecular machines with up to 100% efficiency. The single most important parameter in determining the maximum possible work efficiency, regardless of the amount of energy captured from GTP hydrolysis, is the design of the coupling device. If it is a cylinder or ring, its inner radius must be at least 1–2 nm more than the outer radius of the MT.

The above conclusions contrast with the design of the coupling device in Hill's model (29) because its mechanism requires that the sleeve be very narrow. Indeed, in that model the sleeve is assumed to interact directly with the MT wall, suggesting an approach distance of only a few angstroms (44). It is easy to see from Fig. 3 that such narrowness does not allow enough dimer bending to produce significant force, so force generation by the power-stroke mechanism in such a sleeve would be <10% of the maximum possible. If, on the other hand, the force is interpreted with a biased diffusion mechanism (29, 41), maximal force is again significantly smaller than that predicted by our power-stroke mechanism working with an optimally sized ring. Furthermore, the principal feature of Hill's coupling device is that it requires dimers to dissociate without significant reorientation by using movements that are highly parallel to the MT and sleeve axes. On the basis of these considerations and more recently acquired knowledge about the structural changes in tubulin dimers that accompany MT depolymerization, this mechanism is not only relatively inefficient, it seems unlikely.

According to the “conformational wave model” the PFs lean against the edge of a MT-surrounding sleeve (30); there is no interaction between the inner surface of the sleeve and the MT wall. Therefore, the length of the sleeve is unimportant, so it is essentially the ring discussed here. According to our model, when the ring's inside diameter is optimal (35–40 nm), such a coupling would allow maximal force production. It is noteworthy that the recently identified “DAM/DASH” protein complex, which associates with kinetochores of budding yeast (45), can form rings and helices whose inner diameters as seen by cryoelectron microscopy are ≈32 nm (46, 47). This size is close to the value we predict as optimal for force production. Given the evidence that this complex is important for spindle stability and accurate chromosome segregation, such a ring is an excellent candidate for a force coupler in yeast mitosis. Note, however, that the DAM rings can assemble around MTs spontaneously, which implies interaction between the ring's inner surface and the MT wall. The presence of such a linkage may have important and as yet unknown consequences for the force generation process. These issues should be addressed in future theoretical work.

An important conclusion of our model is that maximal force will be achieved by a ring coupler only after complete dissociation of the lateral bonds between the dimers that push on the ring (Fig. 3 A and C). For a realistic MT, this extent of PF bending may be accompanied by some dissociation of longitudinal bonds as well. Under these circumstances, the MT attachment of a ring-like coupling device may become compromised. Thus, although the ring is plausibly the best coupler for maximizing the magnitude of the disassembly force generated, its ability to sustain prolonged movements of a large object, like a chromosome, is in question. Perhaps neither a narrow sleeve nor a ring is the optimal force-transduction coupler for chromosome movement, and the device that really does this job in vivo remains to be discovered.