Resolution of a deep animal divergence by the pattern of intron conservation

Abstract

The relationship between three biologically important groups, arthropods, nematodes, and deuterostomes, remains unresolved. It is unknown whether arthropods are more closely related to nematodes (consistent with the “ecdysozoa” hypothesis) or to deuterostomes (consistent with “coelomata”). We present a method in which we use the pattern of spliceosomal intron conservation to develop a series of inequalities that characterize each possible relationship. We find that only the ecdysozoa grouping satisfies these predictions, with P < 10^–6. Simulations show that our method, unlike some previous methods, is largely insensitive to rate variation between branches.

The traditional “coelomata” phylogeny joining deuterostomes with arthropods to the exclusion of nematodes has been questioned by analyses of molecular data sets (1–6). The alternative “ecdysozoa” hypothesis joins arthropods and nematodes with deuterostomes as the outgroup. Morphological (7–10) and molecular (1–6, 11–14) analyses have lent support to both sides. Molecular many-taxa studies have tended to support ecdysozoa (2–6), whereas many-gene analyses have tended toward coelomata (11–13). The result has been a web of studies and reviews of opposite conclusions. At the heart of the uncertainty lies a dearth of characters slow-evolving enough to guide in reconstruction of such deep divergences and the potential failure of many phylogenetic methods in cases of rate variations between lineages (e.g., see discussion in refs. 15–17).

A promising class of elements for resolving such deep divergences is spliceosomal intron positions (18, 19). Introns have a very slow rate of insertion and loss with intron turnover estimates ranging from around 10^–9 per year for flies (20, 21) and worms (21, 22) to 10^–11 per year for mammals (23) and with a large fraction of introns persisting for very long periods (18, 24, 25), presumably allowing them to retain phylogenetic signal long after nucleic acid and many protein sequences have saturated. In addition, intron loss is presumably virtually irreversible (once lost, an intron is quite unlikely to be subsequently gained at the exact site), thus evading the problems of back mutation endemic to sequence-based methods.

Previous studies have used one or a few shared nuclear or mitochondrial introns to try to determine various groupings (18, 26–29). However, such anecdotal evidence ignores the possibility of (multiple) intron loss and must therefore be treated with caution except in groups with extremely low rates of intron loss [e.g., vertebrates (18)]. Other studies finding that the same intron has been lost multiple times independently along different lineages have led some to conclude that introns are not useful as phylogenetic characters. Cho et al. (30) found that the same intron had been lost multiple times in separate Caenorhabditis lineages and thus concluded that introns are not good phylogenetic criteria. Rogozin et al. (24) found that a parsimony tree constructed by using the same data used here gave untenable groupings (Plasmodium with yeast as well as Homo sapiens with plants) and thus concluded that intron positions are not good phylogenetic characters.

However, these findings do not demonstrate that introns are useless as phylogenetic characters but rather that they are not a simple phylogenetic panacea. The same nucleotide position will change multiple times in a phylogenetic tree, yet we do not conclude that DNA sequences are useless for phylogenetic analysis; a parsimony reconstruction using protein sequences may suffer from many well documented biases leading to strange groupings, yet we do not discard protein sequences as phylogenetically uninformative out of hand. Indeed the failure of Dollo parsimony to reconstruct reasonable relationships noted by Rogozin et al. is, in fact, no surprise, because this method is expected by its very nature to group taxa with similarly high (or low) rates of character loss. Certainly, a single intron cannot be used to resolve a node if (multiple) loss is possible, but so long as some ancestral introns are retained in multiple lineages, a residual phylogenetic signal should be detectable.

To our knowledge, no method harnessing the pattern of intron conservation from a large number of genes has ever been proposed. We here develop a method to analyze the pattern of shared intron positions for a trio of taxa for which the relationship is unknown, and a known outgroup. We apply this method to the pattern of intron conservation found in 684 sets of eukaryotic orthologs for fully sequenced genomes from arthropods, nematodes, deuterostomes, and plants. Ecdysozoa is much more strongly supported than coelomata, with P < 10^–6. Simulations show that our method is very robust to rate differences between lineages, potentially overcoming a dogged problem of sequence-based methods. Our method is reminiscent of the invariant method of Cavender and Felsenstein, and we provide a comparison between the two as well as an explanation of why the invariant is inappropriate in cases where the total number of possible sites is unknown. We suggest a modified invariant method and find that this method also supports ecdysozoa. Our method should be generally applicable and useful in resolving other deep eukaryotic nodes.

Methods

Data Set. Protein-level alignments, intron positions, and presence–absence matrices for each intron position were downloaded from the web site of the authors of ref. 24 at ftp://ftp.ncbi.nlm.nih.gov/pub/koonin/intron_evolution. The subsets of animal-specific multitaxa introns and introns shared between animals and plants were extracted from the data. Short scripts were written in the perl programming language to facilitate the calculations described.

For each position at which an intron is found in any of the species, a binary matrix indicates whether there is an intron at that exact position in each species. Assuming that introns present at the same position are homologous, this is a character matrix of shared introns. Although some intron positions may be mismarked, the effect of such errors on our analysis are greatly diminished by three factors: (i) introns near alignment gaps are excluded from the analysis (for details, see ref. 24), avoiding the cause of the majority of such errors observed in previous studies (23); (ii) the original authors found that there were very few cases in which intron positions from different taxa nearly but not exactly matched, suggesting that the effect of mispredictions of introns on the data set is small (24); and (iii) introns found in a single taxon are not used in the analysis. The chance of having two mispredicted introns fall at the exact same position is very small, thus eliminating another large source of error.

Estimation of Retention Rates. Assuming the coelomata phylogeny (Fig. 1), our model assumes that some number of introns are present at node 2, and an additional number are present at node 1 but not at node 2, because of insertion along internal branch i. Introns present at the same position in different species are assumed to be homologous (i.e., an intron may only be introduced at a given position in a gene once in the tree). All introns present in D as well as N and/or P are presumed to be present in ancestor 1. Of these, 281 of 1,137 (24.7%) are retained in A; thus, we estimate that r_a = 0.247. Of the introns present in A as well as N and/or P (thus present in ancestor 1), 281 of 351 (80.1%) are retained in D; thus, we estimate r_d = 0.801. Of the introns present in A and/or D as well as P (thus present in ancestor 2), 179 of 821 (21.8%) are retained in N; thus, we estimate r_n = 0.218. Estimating r_i is somewhat more involved. The chance of an intron present in ancestor 2 being retained in A and/or D is r_i multiplied by one minus the chance of loss along both a and d, or r_i [1 – (1 – r_a)(1 – r_d)]. Of the introns present in N and P (thus present in ancestor 2), 179 of 240 are present in A and/or D; thus, 179/240 = r_i[1 – (1 – r_a)(1 – r_d)] = r_i × (1 – 0.753 × 0.199), so r_i is estimated as 0.877.

Fig. 1.

Coelomata phylogeny. A, arthropods; D, deuterostomes; N, nematodes; P, plants; 1, ancestral coelomate (last common ancestor of A and D); 2, last common ancestor of A, N, and D. a, d, and n are terminal branches leading to A, D, and N, respectively; and i is the internal node connecting 1 and 2.

Simulations Using Estimated Retention Rates. Simulations were performed assuming the coelomata topology to determine the chance of observing a false signal supporting ecdysozoa. Given values for r_a, r_d, r_n, and r_i, an intron present in ancestor 2 has eight possible fates with respect to presence/absence in the three animal groups studied (regardless of presence/absence in P).

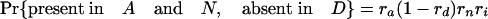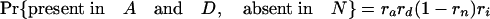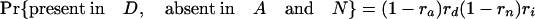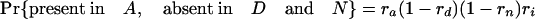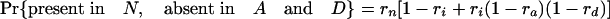The expression in brackets for the last two equations represents the probability of an intron present in ancestor 2 being absent in both A and D, either through loss along i (with probability 1 – r_i) or through retention along i followed by double loss along a and d [with probability r_i(1 – r_a)(1 – r_d)]. These probabilities hold regardless of presence/absence in plants (that is, for introns present at the plant–animal split and retained in plants, introns present at the plant–animal split and lost in plants, or introns inserted between the plant–animal split and ancestor 2). Based on the probabilities obtained by using the r values estimated above, we simulated two classes of introns: animal-specific and shared animal–plant introns.

For each simulated data set, we separately simulated 822 shared plant–animal introns and 630 animal-specific multitaxa introns (because single-taxa introns are uninformative), the same numbers as in the real set. For the simulations assuming “mild” intron insertion along i, we included among the 630 animal-specific introns 20 introns present in only both D and A (the results of insertion along i and retention along d and a) and simulated 610 additional multitaxa animal-specific introns. A positive result is defined as a data set for which at least one comparison gives a result significantly different from “=” (tested by using a Fisher's exact test), and all tests giving significant results support the same phylogeny, either coelomata (true positives) or ecdysozoa (false positives).

Robustness to Rate Variations. We varied r_a, r_d, r_n, and r_i independently from 0.2–0.9 in increments of 0.1 (8⁴ different sets of values). For each set of values, we simulated 1,000 data sets as above. In this case, data sets supporting either alternative topology (either ecdysozoa or the relationship joining nematodes and deuterostomes) were considered false positives. Combinations of r values giving specificity values near a critical value (0.85, 0.90, 0.95, 0.98, and 0.99) were resimulated with 10,000 data sets for each combination to yield more accurate specificity estimates (“near” defined as a specificity value not different from the critical value at the P < 0.01 level by a χ² test).

Results

A Method for Resolution of Deep Eukaryotic Nodes. We analyzed the pattern of shared intron positions for a set of 684 KOGs (eukaryotic orthologous groups), compiled by Rogozin and collaborators (24). Each KOG contains a set of orthologs, one each from eight fully sequenced eukaryotic genomes: Drosophila melanogaster, the mosquito Anopheles gambiae, Caenorhabditis elegans, human, the yeasts Schizosaccharomyces pombe and Saccharomyces cerevisiae, the flowering plant Arabidopsis thaliana, and the apicomplexan Plasmodium falciparum. In the data set, orthologs in each KOG are aligned and intron positions are marked, with introns found at identical positions (between the exact same pair of nucleotides) in multiple organisms assumed to be homologous and shared because of common descent (thus present in the ancestor). We extracted animal-specific multitaxa introns and shared animal–plant introns for the analysis. Only introns found in conserved, unambiguously aligned regions were considered (following ref. 24).

Fig. 1 shows a cartoon of the coelomata phylogeny, joining arthropods and deuterostomes. We use the plant A. thaliana as the known outgroup for the comparison, because it has many more data set introns than the other non-animals (Schizosaccharomyces pombe, Saccharomyces cerevisiae, and P. falciparum). For each branch x, there is some chance that an intron present at the beginning of that branch will be maintained along its entire length, which we call r_x (thus, an intron present in ancestor 1 will be retained in A with probability r_a). r values are <1 and likely to be different for each branch (if any r is equal to 1, the tree will be unresolvable). In our sample, arthropods are represented by D. melanogaster and A. gambiae, nematodes by C. elegans, and deuterostomes by humans. In the case of arthropods, presence in either D. melanogaster or A. gambiae is considered to be presence in arthropods. We use NP for the number of introns present in N and P (but absent in A or D) and ANDP for the number present in all four taxa. We use brackets to indicate that an intron may or may not be present in the bracketed taxon. Thus, NP[D] is the number of introns present in N and P, possibly present in D and absent in A (i.e., NP[D] = NP + NPD). The order of taxa does not matter, e.g., NPD = PDN.

We first generate a series of mathematical expectations given the phylogeny. Introns common to D and N are assumed present in ancestor 1. The chance that such an intron is present in A is just r_a, the chance that it is retained along branch a, and the chance it is absent in A is 1 – r_a. The ratio of such introns present-to-absent in A, ADN/DN, should therefore be r_a/(1 – r_a), the ratio of retainedto-lost along a. Among introns common to D and P (also present in ancestor 1), the ratio of introns present-to-absent in A, ADP[N]/DP[N], should also be r_a/(1 – r_a), the ratio of retained-to-lost along a. We therefore expect ADN/DN = ADP[N]/DP[N]. Identical reasoning predicts DAN/AN = DAP[N]/AP[N].

Introns common to P and N were present in ancestor 2. To be found in A, such an intron must be retained along both branches a and i with probability r_ar_i. The ratio of present-to-absent in A, ANP[D]/NP[D], should therefore be r_ar_i/(1 – r_ar_i). This value is less than r_a/(1–r_a), since r_i < 1, giving AND/ND > ANP[D]/NP[D]. Identical reasoning predicts DNA/NA > DNP[A]/NP[A].

Introns common to A and P were also present in ancestor 2. The chance of such an intron being present in N is r_n, giving NAP[D]/AP[D] = r_n/(1 – r_n). For introns shared between A and D, the case is more complicated. Each such intron was either (i) present in ancestor 2 or (ii) absent in ancestor 2 and inserted along branch i. Introns present in ancestor 2 may be present or absent in N, with relative probabilities r_n and (1 – r_n). By contrast, introns inserted along i were absent in ancestors of N and are thus absent in N. These introns increase AD but not NAD. The expected ratio of such introns present-to-absent in N, NAD/AD, is thus r_n/(1 – r_n + g) < r_n/(1 – r_n), where g is some unknown positive term representing the increase in AD due to introns inserted along branch i, giving NAD/AD < NAP[D]/AP[D]. Identical reasoning predicts NDA/DA < NDP[A]/DP[A].

Table 1 summarizes the six expectations predicted by the coelomata phylogeny and the reasoning underlying each. The equivalent predictions for each of the three phylogenies are easily derived and are given in Table 2. Note that some predictions of different phylogenies (shaded the same color) compare identical pairs of ratios (e.g., in each column, the yellow prediction compares ADN/DN and ADP[N]/DP[N]). For each pair of ratios compared (that is, for each color), one phylogeny predicts less than, one equal to, and one greater than. Thus, significant deviation from equal in one direction rejects two phylogenies and strongly supports the third. These predictions are reorganized in Table 3 so that comparisons between the same pairs of ratios are given in the same row.

Table 1. Predictions of the coelomata phylogeny.

The first column gives the two ratios to be compared, the second column gives the expected values, the third column gives the expected relationship, and the final column gives the reasoning that leads to each prediction, as explained in the text. gs in the fifth and sixth predictions are positive terms representing the contribution of intron insertions along branch i.

Table 2. Predictions of the three phylogenies.

Equivalent predictions for each phylogeny are given on the same line. Predictions that compare identical pairs of ratios are shaded the same color.

Table 3. Results for the three possible topologies for intron-position conservation among 684 KOGs.

The first column gives the ratios to be compared. The second through fourth columns give the predicted relationship between the two ratios under each of the three possible phylogenies. A circle around a prediction indicates the only prediction compatible with the data for that comparison. The Results column gives the values of the two ratios for numbers of introns in the 684 KOGs studied and the ratio of ratios. The P column gives the probability that the two ratios are equal as evaluated by Fisher's exact test.

The Data. The results for each comparison are given in Table 3. For each comparison we tested the deviation of the two ratios from equal with Fisher's exact test. Of the six comparisons, three give statistically significant results. All three significant comparisons fulfill predictions of ecdysozoa and disagree with the other two phylogenies. For two of the other three comparisons, ecdysozoa predicts “=” and the ratios are close to equal. This leaves only one comparison (the fourth line of Table 3), in which the ratios are nearly equal although ecdysozoa predicts “<,” as would be expected if there was little intron insertion between the deuterostome–ecdysozoa node and the arthropod–nematode node. Thus, all six results are easily explained by ecdysozoa, whereas three of six are incompatible with each of the other two alternatives. Notably, coelomata receives no more support than does the universally rejected phylogeny joining deuterostomes and nematodes.

Simulations. Could this be a false positive result? Assuming coelomata, we simulated data sets of the same size as the real set by using r values estimated from the data and assuming no insertions along branch i (this is a conservative assumption because such insertions are required for the fifth and sixth predictions in Table 2 to hold; lack of insertions along i thus reduces the number of comparisons expected to give a coelomata signal). Of one million simulated data sets, in zero did three comparisons support ecdysozoa (as in the real data set), in merely 0.024% did two support ecdysozoa [specificity (true positives/total positives) = 99.7%], and in only 2.8% did one support ecdysozoa (specificity = 94.9%). Assuming mild intron insertion along branch i, the respective numbers were zero, 0.0053% (specificity = 99.94%), and 2.2% (specificity = 96.0%). Thus, the chance of obtaining a false positive supported by three comparisons is <10^–6.

To test for sensitivity to rate variation, we simulated data sets over a range of values: 0.2–0.9 in increments of 0.1 for each of r_a, r_n, r_d, and r_i independently (8⁴ total combinations). For each combination of r values, we generated 1,000 data sets assuming coelomata and mild intron insertion along i and counted sets supporting coelomata (true positives) or either of the other two phylogenies (false positives). The results are summarized in Table 4. For most values, specificity was very high (for all sets with r from 0.2–0.7, >98%; for r from 0.2–0.8, >95%). Only when both r_i was very large (0.9) and r_d was very small (0.2–0.4) did specificity fall below 95%, although still never below 85%. This decrease in power is expected with near-complete intron stasis along branch i because changes along this branch, which is the period of shared history among the two more closely related taxa, are inherently necessary for resolution. Over the entire range, 972,278 of 4,096,000 total data sets gave true positives supported by three or four comparisons, whereas zero gave false positives so strongly supported.

Table 4. Summary of simulations.

r values	Specificity, %
ra = 0.25, rd = 0.80, rn = 0.22, ri = 0.88	94.9
(Estimated from data)
ra, rd, rn = 0.2-0.9
ri = 0.2-0.6	>99
ri = 0.7	>98
ri = 0.8	>95
ra, rd = 0.2-0.9, ri = 0.9
rn = 0.2	>85
rn = 0.3	>90
rn = 0.4-0.9	>95

Summary of specificity statistic (number of true positives/number of total positives) for 1,000 data sets each for combinations of r values from 0.2-0.9. For each combination of r values in the range given in the first column, the specificity exceeds the value given in the second column. For example, for every combination of r values with r_a, r_d, and r_n between 0.2 and 0.9 and r_i between 0.2 and 0.6, specificity exceeds 99%.

Introns and the Invariant. Our method is reminiscent of the Cavender–Felsenstein invariant method for distinguishing between the three possible unrooted phylogenies for four taxa by using identically evolving two-state characters, in that both rely on a set of values for which each phylogeny gives a qualitatively different prediction (31, 32). For taxa a, b, c, and d, the invariant method encompasses three values:

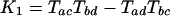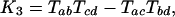where T_ij is the probability that taxa i and j are in the same state for a character minus the probability that they are not. For example, in our case, the number of characters that are not in the same state for arthropods and nematodes would be the number of introns present in arthropods but not in nematodes or vice versa, which is A[DP] + N[DP]. The number of characters in the same state for arthropods and nematodes is the number of introns that are present in both arthropods and nematodes, AN[DP], plus the number that are present in neither, [DP]. Importantly, this is an unknown quantity. We know that this quantity includes D, P, and DP, but it also includes the number of possible intron sites that are not occupied in any studied taxon, call it “[].” However, we do not have a good sense of how many possible intron sites there are; thus, we cannot calculate the T values. In general, T_AN = (AN[DP] + [DP] – A[DP] – N[DP])/([ANDP] + []); thus, the K values and our assessment of the phylogeny depend on an unknown quantity for which we have no clear estimate. For this important reason, direct application of the invariant is restricted to cases in which we know the total number of sites. In addition, other assumptions made by the Cavender–Felsenstein invariant, including a uniform stable state distribution and a symmetric mutation process, do not apply here (John Rhodes, personal communication).

If each character can only arise once on the tree, as we have assumed throughout for introns (so-called Dollo characters), we can develop a variation on the invariant that includes only cases of shared characters (introns) between pairs of taxa. For the unrooted topology in Fig. 2, we define M as the (unknown) number of characters that are of value 1 at node 1 and G as the number of characters that are of value 1 at node 2 but are of value 0 at node 1. We define c_x as the value of a general character at position x on the tree (e.g., c_a gives the value of a character in taxa a, either 0 or 1). We can further define

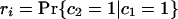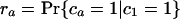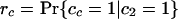The number of characters that are expected to be shared between pairs of taxa can then be written as

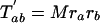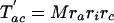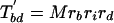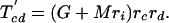We can now define K′ values analogous to the K values of Cavender and Felsenstein, as well as their expectations.

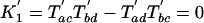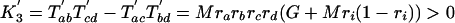The predictions for the other topologies are easy to derive, and we recover a situation analogous to the Cavender and Felsenstein predictions:

These values can be calculated from the data, giving an alternative method for distinguishing between topologies based on the pattern of intron conservation.

Fig. 2.

General four-taxa unrooted tree with ancestral nodes marked.

We performed this calculation, with topologies I, II, and III corresponding to coelomata, ecdysozoa, and the phylogeny joining deuterostomes and arthropods, respectively. The results are summarized in Table 5. All three results are as predicted by ecdysozoa (topology 2): 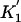is much greater than zero, is much less than zero, and is closest to zero. Thus, a modified invariant model also supports the ecdysozoa phylogeny. Because the T′ values are overlapping (for instance, all T′ values contain introns present in all four taxa), a Fisher's exact test is not appropriate nor is there another obvious statistic for calculating the significance for this result. We prefer our method for determining phylogenies based on shared intron positions both because it provides a straightforward statistic for each comparison and because the multiple comparisons test different predictions of a given phylogeny: constancy of the rate of loss for the terminal branches by predictions 1 and 2, loss along the internal branch by predictions 3 and 4, and insertion along the internal branch by predictions 5 and 6. By contrast, each of the modified invariant metrics combine all three of these factors.

Table 5. A modified invariant test for intron positions.

The first column defines the K′ metric being evaluated. The second through fourth columns give the predictions for the value of the metric under each of the three possible phylogenies. The Results column gives the values calculated from the data.

Discussion

We show here that spliceosomal intron positions are useful characters in resolving the relationship between deeply diverged eukaryotic taxa. Because of the depth of early metazoan divergences and the sparsity of taxa immediately basal to metazoans, it is difficult to confidently reconstruct protein sequences at the base of the metazoan radiation. Here, introns are useful. Introns shared between metazoans and non-metazoans are known to be present in the ancestor, allowing us to trace the subsequent pattern of intron loss for various phylogenies. We expect that introns will become increasingly useful as more and more metazoan genomes become available.

Although our method has proven to be very robust to variation in rates of intron loss along different branches, it does not incorporate possible differences in rates of loss between introns along the same branch. Future work should focus on incorporating this into a general phylogenetic method using intron-position conservation. This will require assessment of the shape of the distribution of loss rates for individual introns and implementation of a probabilistic model using this information. However, there is no reason to assume that such differences will be more extreme or difficult to correct for than for sequence data; thus, we expect such methods to offer a plausible molecular alternative to sequence-based methods as the number of fully characterized genomes increases.

The conservation of intron positions between genomes of well studied eukaryotes supports joining nematodes and arthropods to the exclusion of deuterostomes, consistent with the ecdysozoa hypothesis. These results directly contradict the findings of a very recent very large-scale protein sequence tree-building project, which supported the alternative coelomata hypothesis (13). However, whereas the previous results are complicated by the limitations of protein-sequence-based tree-building methods in cases of sparse taxonomic sampling and interlineage rate differences, our results are consistent and robust to such concerns. This method should prove useful in resolving other very deep eukaryotic nodes.