The effects of Achilles tendon compliance on triceps surae mechanics and energetics in walking

Abstract

Achilles tendon (AT) compliance can affect the generation and transmission of triceps surae muscle forces, and thus has important biomechanical consequences for walking performance. However, the uniarticular soleus (SOL) and the biarticular (GAS) function differently during walking, with in vivo evidence suggesting that their associated fascicles and tendinous structures exhibit unique kinematics during walking. Given the strong association between muscle fiber length, velocity and force production, we conjectured that SOL and GAS mechanics and energetic behavior would respond differently to altered AT compliance. To test this, we characterized GAS and SOL muscle and tendon mechanics and energetics due to systematic changes in tendon compliance using musculoskeletal simulations of walking. Increased tendon compliance enlarged GAS and SOL tendon excursions, shortened fiber operation lengths and affected muscle excitation patterns. For both muscles, an optimal tendon compliance (tendon strains of approximately 5% with maximum isometric force) existed that minimized metabolic energy consumption. However, GAS muscle-tendon mechanics and energetics were significantly more sensitive to changes in tendon compliance than were those for SOL. In addition, GAS was not able to return stored tendon energy during push-off as effectively as SOL, particularly for larger values of tendon compliance. These fundamental differences between GAS and SOL sensitivity to altered tendon compliance seem to arise from the biarticular nature of GAS. These insights are potentially important for understanding the functional consequences of altered Achilles tendon compliance due to aging, injury, or disease.

Introduction

The triceps surae muscles (i.e., gastrocnemius and soleus) generate the majority of the mechanical power during push-off in walking and contribute significantly to vertical support and forward propulsion (Neptune et al., 2001). A simulated reduction in triceps surae strength negatively affects ankle power generation during push-off and, compared to weakness in other leg muscles, can preferentially elicit uncharacteristic gait patterns (Goldberg and Neptune, 2007). Hence, preserving gastrocnemius (GAS) and soleus (SOL) muscle function is considered clinically important. However, triceps surae muscle behavior is governed, in part, by series elasticity provided by the Achilles tendon (AT). Hence, changes in AT compliance, independent of triceps surae muscle strength, could have important biomechanical consequences that emerge during walking. A better understanding of the effects of AT compliance is necessary given the important changes in tendon mechanical behavior seen with age (Franz and Thelen, 2015; Slane and Thelen, 2015; Stenroth et al., 2012), injury (Geremia et al., 2015) and disease (Arya and Kulig, 2010; Child et al., 2010).

Prior studies reveal that simulating altered AT compliance substantially affects GAS mechanical work and metabolic energy consumption (Lichtwark and Wilson, 2008, 2007), as well as the magnitude and timing of ankle power generation (Zelik et al., 2014). Indeed, tuning between muscle activation, muscle fascicle behavior, and in series tendon elasticity is an important factor underlying muscle-tendon unit (MTU) performance. However, the effects of tendon compliance on SOL performance may differ from those on GAS (Uchida et al., 2016) due to differences in their function and kinematics. The uniarticular SOL and biarticular GAS contribute differently to vertical support and forward propulsion (Francis et al., 2013; Neptune et al., 2001; Stewart et al., 2007), and their associated tendinous structures exhibit different elongations (Franz et al., 2015). Therefore, GAS and SOL may also respond differently to the presence of altered tendon compliance in walking, with potential for unique changes in mechanical power generation and metabolic energy consumption.

We investigated how AT compliance differentially modulates GAS and SOL muscle-tendon mechanics and energetics during walking. Our approach involved systematically varying AT compliance in a musculoskeletal model of walking and estimating triceps surae mechanics and muscle-specific metabolic energy consumption. We tested the hypotheses that: 1) increasing AT compliance would increase tendon excursions, alter excitations and muscle fiber operating lengths, and increase muscle metabolic energy consumption, and 2) these changes would differ between GAS and SOL.

Materials and Methods

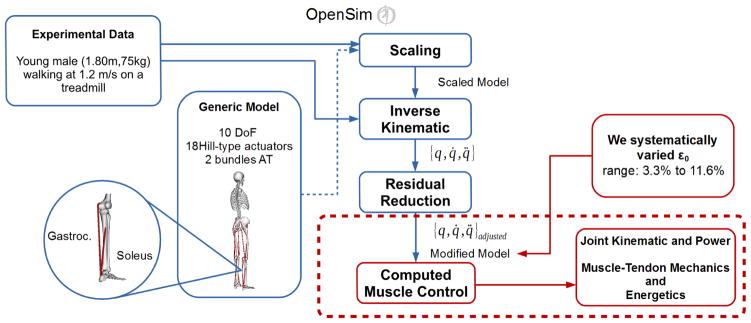
We used available (simtk.org) kinematic and ground reaction force data from one healthy adult male (height: 1.8 m, mass: 75 kg) walking at 1.2 m/s on an instrumented treadmill (John et al., 2012). We implemented a simplified version of the Gait2392 model, with 12 segments and 10 degrees of freedom describing flexion-extension of the lumbar spine, hips, knees and ankles, pelvis tilt and vertical and anterior-posterior translation. Eighteen Hill-type muscles (Delp et al., 1990; Thelen, 2003) representing the ankle, knee and hip flexors and extensors, and one torque generator at the lumbar spine actuated the model. We modeled the Achilles tendon as two independent bundles: a gastrocnemius tendon and a soleus tendon. The musculoskeletal model was scaled using marker trajectories from a static pose and an inverse kinematic procedure found the generalized coordinates that best matched experimental marker trajectories during walking. A Residual Reduction Algorithm (RRA) adjusted the generalized coordinate trajectories and ensured dynamic consistency with measured external forces and modelling assumptions (Delp et al., 2007). Finally, a Computed Muscle Control algorithm (CMC) (Thelen and Anderson, 2006) derived GAS and SOL excitations that drove the musculoskeletal model (with m = 18 muscles and n = 10 generalized coordinates) to match available kinematic and ground reaction force data while minimizing the sum of squared muscle activation (a_i), in accordance with the performance criterion J (eq. 1).

We simulated altered AT compliance by increasing peak strain of the GAS and SOL AT bundles at maximum isometric muscle force (ε₀, range: 3.3–11.6%) while maintaining the nominal value (i.e., 3.3%) for all other tendons (Fig. 1). We assessed sensitivity of model predictions to CMC simulation settings. To do this, we repeated CMC six times for each AT compliance, slightly modifying the instant in the gait cycle at which simulation was initiated (2 conditions) and the CMC generalized coordinate tracking weights (w_j; 3 sets), which allowed each model generalized coordinate (q̆_J) to match the prescribed kinematics (q̆_J^*) within a specific error tolerance. Ensemble mean of the six simulations were computed for GAS and SOL excitations and fiber, tendon, and MTU excursions and powers. We focused our analyses on periods corresponding to GAS and SOL stretch-shortening (SS) cycles during stance and their respective stretching (ST) and shortening (SH) sub-phases.

Figure 1.

Simulation workflow. In blue, the steps carried out before the data and model were made available for download via simtk.org; in red, the steps performed in order to modify the scaled model and run CMC algorithm.

$$J={\mathrm{\sum }}_{i=1}^m{a_i}^2+{\mathrm{\sum }}_{j=1}^n{w}_j{({{\ddot{q}}_J}^{\ast }-{\ddot{q}}_J)}^2$$

Positive, negative, and total work performed by GAS and SOL fiber, tendon, and MTU during the SS cycle and sub-phases were calculated by numerical integration of their respective power curves over the periods of interest. We also calculated the following quantities: the work performed on the tendon by external sources with respect to the MTU during the stretching phase ( ${{}^{ST}W}_T^{e-}$), i.e., tendon negative work ( ${{}^{ST}W}_T^{-}$) minus fiber positive work ( ${{}^{ST}W}_T^{+}$) during stretching; the work effectively performed by the tendon during the shortening phase ( ${{}^{SH}W}_T^{e+}$), i.e., tendon positive work ( ${{}^{SH}W}_T^{+}$) minus fiber negative work ( ${{}^{SH}W}_f^{-}$) during shortening.

GAS and SOL metabolic energy consumption were estimated using the OpenSim metabolic calculators, which predict mechanical work and thermal energy liberation according to the model from Umberger et al. (2003), which we normalized to body mass.

Regression analysis estimates the values of ε₀ that minimized GAS and SOL metabolic energy consumption. The values obtained for GAS and SOL were compared using Z-Scores, considering a significance level of 5%.

Results

Muscle-Tendon Mechanics

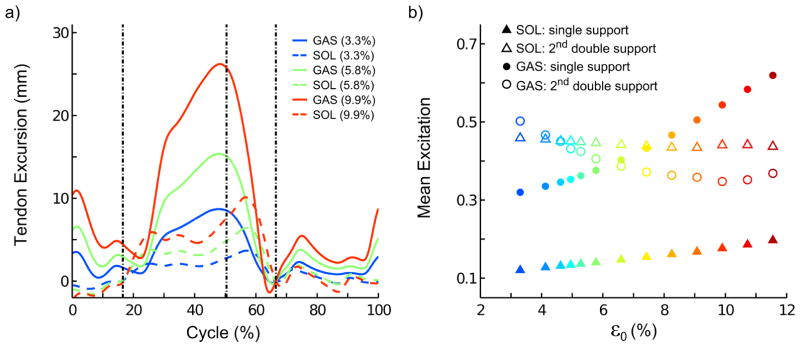
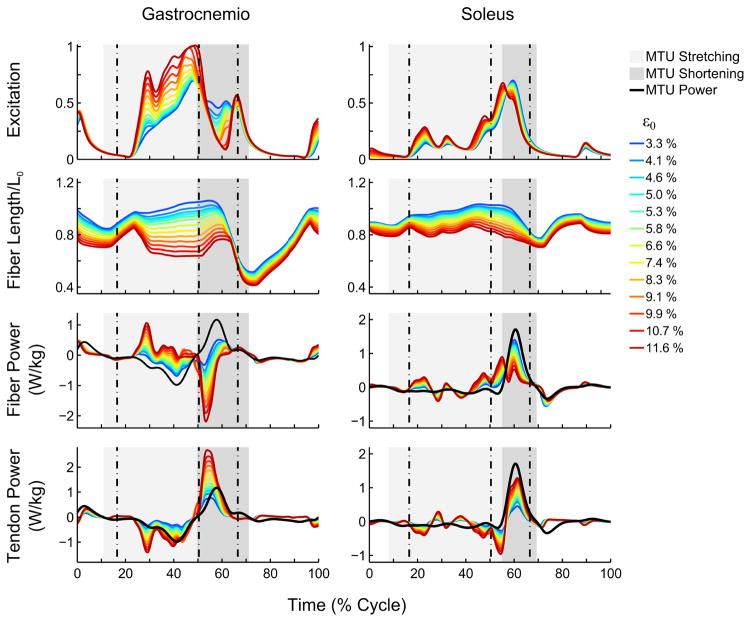
Increasing AT compliance increased GAS and SOL tendon excursions (Fig. 2a) and caused their fibers to operate at shorter fiber lengths (Fig. 3). GAS tendon excursions were greater than SOL for all conditions, and this differential behavior became larger with increasing AT compliance (Fig. 2a). These changes were accompanied by larger GAS and SOL excitations during single support and smaller excitations during push-off (Fig. 2b and Fig. 3).

Figure 2.

(a) Simulated gastrocnemius (GAS) and soleus (SOL) tendon excursion over a gait cycle (i.e., two consecutive heel strikes), referenced to tendon length at the ipsilateral toe-off and (b) mean muscle excitation during single support and late double support across the range tendon compliances. We increased tendon compliance by progressively increasing tendon peak strain at maximal isometric force (ε₀) from 3.3% to 11.6%. Vertical dashed lines in (a) indicate, respectively, the contralateral toe-off and heel strike and the ipsilateral toe-off.

Figure 3.

Simulated gastrocnemius (GAS) and soleus (SOL) mechanics over a gait cycle as a function of altered peak tendon strain at maximal isometric force (3.3 % – 11.6 %). Fiber and tendon powers were normalized to body mass and compared to the power developed in the whole muscle-tendon unit (MTU); fiber length was normalized to its optimal length (L_o). Vertical dashed lines indicate, respectively, the contralateral toe-off and heel strike and the ipsilateral toe-off, and shaded areas the stretching and shortening periods of each muscle during the stance phase.

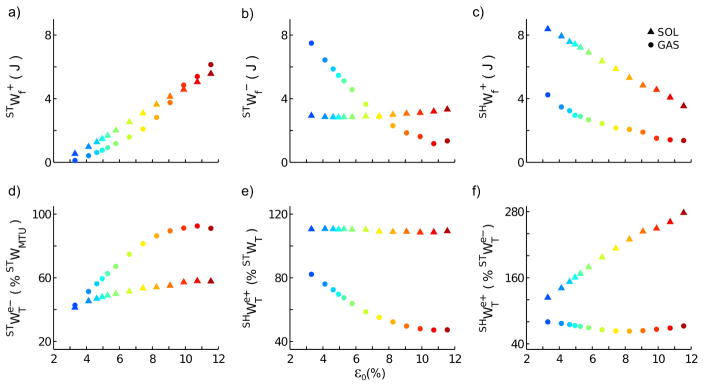
Several aspects of GAS and SOL tendon and fiber mechanics were affected differently by increasing AT compliance (Fig. 3). GAS fiber negative work during the stretching phase ( ${{}^{ST}W}_f^{-}$), decreased progressively with increasing AT compliance. In contrast, SOL ${{}^{ST}W}_f^{-}$ increased for ε₀ > 5% (Fig. 4b). Also during stretching, work performed on the tendon by the contractile element and by external sources with respect to the MTU increased with AT compliance for both GAS and SOL (Fig. 4a and Fig 4c). Consequently, increasing AT compliance reduced positive GAS and SOL fiber work performed during the shortening phase ( ${{}^{SH}W}_f^{+}$, Fig. 4d). With increasing AT compliance, the percentage of energy stored in the tendon during stretching that was effectively reused during shortening decreased significantly only for GAS (Fig. 4e). Finally, only for GAS was ${{}^{SH}W}_T^{e+}$ less than the amount of work stored in the tendon due to sources other than muscle fibers (i.e., ${{}^{SH}W}_T^{e+}/{{}^{ST}W}_T^{e-}<1$; see Fig. 4f).

Figure 4.

Mechanical work developed by gastrocnemius (GAS) and soleus (SOL) fiber and tendon as a function of peak tendon strain at maximal isometric force (ε₀). (a) Fiber positive and (b) negative work during stretching. (c) Fiber positive work during shortening. (d) Negative work stored in the tendon during stretching due to sources other than muscle fibers, given as percentage of the muscle-tendon unit (MTU) work performed over the same phase. The positive work performed by the tendon on sources other than muscle fibers during shortening is given as a percentage of the total work stored on the tendon during stretching in (f) and as percentage of the work stored on the tendon only due to the action of external sources with respect to the MTU in (g).

Metabolic Energy Consumption

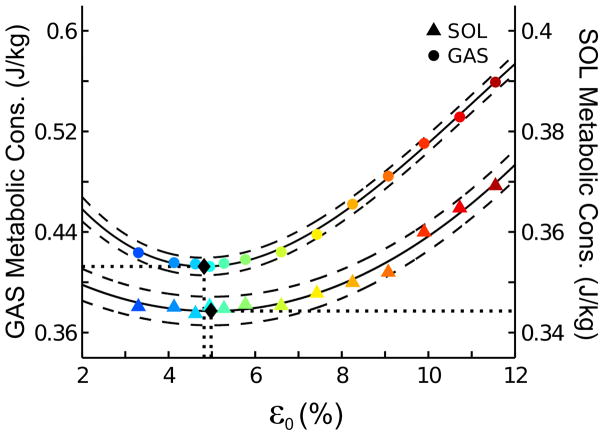
Mean metabolic energy consumption during the SS cycle was minimized at ε₀ = 4.8 ± 0.1% for GAS and at ε0 = 5.0 ± 0.1% for SOL (Fig. 5). The value of ε₀ that minimized metabolic energy consumption did not differ between GAS and SOL (z = 1.4, p = 0.15). However, mean metabolic consumption was significantly lower for SOL (0.34 ± 0.01 J/kg) than for GAS (0.41 ± 0.01 J/kg).

Figure 5.

Alterations in simulated gastrocnemius (GAS) and soleus (SOL) metabolic energy consumption per unit body mass as a function of altered tendon peak strain at maximal isometric force (ε₀). Solid and dashed lines are the polynomial fit to simulated data and respective 95% confidence intervals. Black diamonds indicate tendon strain at optimal metabolic energy consumption.

Discussion

We investigated differences between GAS and SOL muscle-tendon mechanics and energetics due to systematic changes in tendon compliance using a musculoskeletal model of walking. As hypothesized, our simulations showed that increased tendon compliance enhanced GAS and SOL tendon excursion, caused fibers to operate at shorter lengths, and increased GAS and SOL mean excitation during single support. Increasing tendon compliance also reduced mean excitations during push-off, presumably due to an increase in the tendon’s contribution to MTU power generation during this critical phase of the gait cycle (Roberts and Azizi, 2011). Consequently, optimal values of ε₀ emerged that minimized metabolic energy, though GAS exhibited larger sensitivity to changes in tendon compliance than SOL.

Our results corroborate the observations of Lichtwark and Wilson (2008, 2007) for GAS and extend them to SOL. We estimated optimal GAS and SOL metabolic energy consumption and efficiency to occur at physiological values of ε₀, which range from 4.0% to 7.0% (Arya and Kulig, 2010; Geremia et al., 2015; Stenroth et al., 2012). In contrast to observations from running simulations (Uchida et al., 2016), these values were similar for GAS and SOL, an interesting result given the considerable architectural differences between the muscle fibers and tendons of these two muscles (Szaro et al., 2009; Ward et al., 2009). However, independent of tendon compliance, metabolic energy consumption was significantly lower for SOL than GAS. This may arise from model predictions showing that SOL returned stored tendon energy during push-off more effectively than GAS (Fig. 4e). Particularly with increasing tendon compliance, the GAS tendon exhibited what Roberts and colleagues have described as elastic backfire (Astley and Roberts, 2012; Roberts and Azizi, 2011), dissipating a significant portion of its stored tendon energy to perform work on the lengthening muscle fibers during push-off (Fig. 3). Consequently, and again especially with increasing compliance, the GAS tendon returned less energy during push-off than it had stored in it during stretching by muscle fibers and external sources (Alexander, 2002). This greater sensitivity of GAS metabolic consumption to tendon compliance was also apparent in running (Uchida et al., 2016).

Differences in the mechanism by which GAS and SOL tendons store and release mechanical energy during stance may explain differences in their sensitivity to altered tendon compliance. Using ultrasound imaging, Ishikawa (Ishikawa et al., 2005) described muscle-tendon interaction in the GAS and SOL as a catapult, in which the tendon stretches slowly during stance before recoiling rapidly during push-off. This catapult action facilitates energy dissipation while subsequently amplifying power generated by the tendon (Roberts and Konow, 2013). However, consistent with our model predictions, those authors suspected that GAS and SOL exhibit different mechanical behaviors in this catapult action. Indeed, our findings suggest that while GAS muscle-tendon behavior clearly followed this catapult action, SOL exhibited more spring-like behavior during the late stance phase, with the tendon undergoing more rapid stretch prior to recoil. We suspect that, compared to SOL, the fundamental differences in GAS muscle-tendon behavior and thus its more pronounced sensitivity to altered tendon compliance arises from its biarticular nature. In particular, knee extension during single-support can enhance stretch of the gastrocnemius, and may promote energy storage and return in its tendon.

There are several limitations in this study many of which are common to other studies that used similar modeling approaches (e.g., Uchida et al., 2016). For example, muscle-tendon model parameters (maximal isometric strength, fiber length, tendon slack length) can affect model-predicted muscle-tendon behavior (Ackland et al., 2012; Delp et al., 1990; Thelen, 2003; Xiao and Higginson, 2010). The GAS and SOL in particular have relatively high tendon slack length to fiber length ratios, which affects the magnitude and rate of force development (Zajac, 1989). The model parameters assumed in this study were based on cadaveric studies and shown to predict in vivo measurements of joint moments (Arnold et al., 2010), such that further study is needed to fully understand the sensitivity to assumed muscle-tendon geometries. Nevertheless, our simulated results, especially those for ε₀ are near physiological values, correspond well to in vivo measurements of fiber (Ishikawa et al., 2005; Mian et al., 2007; Panizzolo et al., 2013) and tendon excursions (Franz et al., 2015). This includes in vivo evidence for larger GAS than SOL tendon excursions during walking. In this present study, we systematically adjusted GAS and SOL tendon compliances simultaneously in our simulations. We adopted this approach as more physiologically appropriate given the two muscles both attach to the Achilles tendon. However, the tendon in our model does reflect the lumped behavior of the free tendon and aponeuroses, such that it is conceivable the properties could adapt somewhat independently, which may affect the presumed load distribution between the muscles. We also based our model predictions on available experimental data from one participant. We address this in part by including a sensitivity analysis for model-predicted outcomes, and show that primary metabolic and mechanical efficiency trends were maintained across a range of simulation parameters. Finally, we assessed the influence of AT compliance when overall gait kinematics and kinetics are held constant. It is conceivable that one may adapt their gait to redistribute hip, knee and ankle kinetics to affect the overall metabolic demands of the triceps surae (Lewis and Ferris, 2008; Zelik et al., 2014). Further study is needed to assess such compensations.

In summary, increasing AT compliance during walking systematically altered GAS and SOL muscle excitations, fiber operating lengths and metabolic energy consumption. These effects are more pronounced in GAS than in SOL, which may arise from fundamental differences in their stance phase muscle-tendon behavior. These insights are important for understanding the consequences of altered tendon compliance due to aging, injury, or disease.