Abstract
Purpose
To inform quantification of MRI magnetization transfer contrast at high field by measuring the spectral characteristics of 1H protons in semi-solids in human brain at 7 T, while avoiding prohibitive RF tissue heating and confounding effects from chemical exchange.
Methods
Saturation-recovery type experiments were performed using brief, frequency-specific RF pulses that saturate semi-solid proton magnetization. Analysis of the subsequent recovery of water proton magnetization with a two-pool model of exchange allowed studying spectral characteristics of semi-solid protons.
Results
We show that in white matter, the semi-solid proton spectrum can be approximated with a symmetric, super-Lorentzian line at −2.58±0.05 ppm from the water resonance and an average transverse relaxation time constant (T2) of 9.6±0.6 µs.
Conclusion
These results are consistent with studies at lower field that have indicated a major contribution from methylene protons to magnetization transfer contrast and will facilitate the design and quantification of magnetization transfer studies at 7 T.
Keywords: white matter, magnetization transfer, macromolecular protons, lineshape, T2 relaxation
Introduction
In MRI of human brain, Magnetization Transfer (MT) contrast (1) has been used extensively to study tissue composition, specifically the fraction of hydrogen (1H) protons with restricted mobility, often referred to as semi-solid protons or macromolecular protons (MPs) (2–6). These protons, having a short T2, are generally not directly detectable by MRI but, through MT, exert an influence on 1H protons in water (WPs), the primary contributors to the MRI signal. Measures of the magnitude of this MT effect have been used to study MP content in brain tissue (4–6) and characterize alterations in brain myelin content in multiple sclerosis (7, 8) and other pathology (9–11).
The mechanisms underlying MT contrast are complex (12, 13), often rendering interpretation and quantification difficult. Generally, the strongest contributions to MT come from MPs such as proteins and lipids, whose protons can affect WP magnetization through dipolar coupling and chemical exchange (2, 12, 14, 15). However, chemical exchange effects of smaller molecules may contribute as well (16, 17). And chemical exchange effects can be enhanced by using long RF irradiation as is done in so called chemical exchange saturation transfer (CEST) techniques (18). While MT generally contributes to MRI contrast to some extent, this contribution is amplified by differentially perturbing WP and MP magnetization levels from their thermal equilibrium values (2). Because of this, MT contrast is not only dependent on dipolar coupling strength and exchange rate between WP and MP, but also on specifics of the MRI pulse sequence (2). It is the latter principle that has been exploited to highlight certain contributions to MT, rendering a contrast that emphasizes either MPs (4–6, 19, 20) or exchangeable protons (16, 18) with some chemical specificity (18). On the other hand, MP magnetization levels are often not well known and difficult to control, due to the short transverse relaxation time (T2) of MPs. Therefore, for proper quantification of MT, and avoid unintended contribution of MT in general (non-MT) MRI applications, MP magnetization levels need to be estimated.
Apart from the exchange rate between MPs and WPs, MT contrast is dependent on the characteristics of the radiofrequency (RF) irradiation, the spectral characteristics of MPs and WPs, and T1 relaxation. Of these factors, the MP spectrum may be the most critical and most difficult to measure, because of MPs extremely short transverse relaxation time constant (T2). Direct measurements with NMR spectrometers on ex-vivo brain tissue samples and various membrane model systems, including myelin extracts and lecithin, have shown that MPs have complex lineshapes with varying width and off-resonance frequency, dependent on the host molecules and strength of dipolar coupling with neighboring MPs (20–25). Typically, at field strengths up to 9.4 T, super-Lorentzian (SL) and Lorentzian lineshapes have been reported over a spectral range of about 6 ppm and T2 values of 20–100 µs (20–26). The general understanding is that in membrane-rich white matter, lipid methylene and methyl groups are the major contributors to these spectra (20, 24, 26, 27).
Because MP spectral characteristics may be quite different in-vivo, and at higher field strengths, various attempts have been made to infer the MP spectrum from their effect on the easier detectable WP signal using steady state MT experiments. Studies at clinical field strengths up to 3 T have reported a SL lineshape with a T2 of in the range of 9–15 µs for white matter (WM) in-vivo (5, 28, 29), similar to the range of 9–13 µs found for tissue samples using this approach (6, 14, 30, 31), but below the 20–100 µs range directly measured by NMR spectroscopy. In addition, several studies have found the MP spectrum to be shifted by about −3 ppm relative to the WP resonance (28, 32–34), consistent with the chemical shift of lipid methylene protons. However this has proven difficult to reproduce, in particular at high field, due to confounding CEST effects (35), and increased tissue heating associated with RF irradiation. Currently, most quantitative MT methods assume the MP spectrum to be centered on the water resonance.
To further investigate MP spectral characteristics, with the ultimate purpose of better quantifying MT contrast in MRI of brain tissue, we applied an indirect measurement approach based on transient MT effects after MP saturation with a brief, RF pulse (36). Using a range of specific RF frequencies allowed us to characterize MP spectral characteristics in human brain at 7 T in an efficient manner, while minimizing effects of CEST, tissue heating, and direct WP saturation.
Methods
MRI experiments were performed on eight human subjects (ages 20–49, average 30.6, 4 female), scanned under an IRB approval on a 7 T Siemens scanner using a 32-channel receive array. In order to study MT without CEST and direct MP saturation effects, we followed a recent approach based on monitoring the saturation of WP signal following a brief, 6–12 ms MP saturation pulse (3, 37). This saturation recovery (SR) approach resembles the selective inversion recovery (IR) approach (38, 39), but sacrifices some sensitivity to obtain an improved estimate of initial MP magnetization level, and render this level insensitive to B1 variation (3, 37). Like the IR approach, it allows sensitive determination of the parameters describing the MT process, by accounting for the direct water saturation effects (3, 37–39), and minimization of CEST effects and tissue heating. First, experiments were performed to determine parameters describing MT kinetics, assuming a two-pool model of exchange between MP and WP (defined as Experiment I), and subsequently, MP spectral characteristics were investigated by studying the magnitude of the MT effects as a function of the frequency of narrowband MP saturation pulse (defined as Experiment II).
Two-pool model
Following an initial RF pulse that differentially saturates the WP and MP pools, the fractional saturations of the two pools, FSWP and FSMP, experience bi-exponential evolutions as follows (3, 37, 40):
| [1] |
| [2] |
| [3] |
| [4] |
| [5] |
In these equations, MWP and MMP are the longitudinal magnetizations of the two pools, R1,WP and R1,MP are their relaxation rates, λ1 and λ2 are fast and slow rate constants of the saturation recovery, and a1 and a2 are the corresponding amplitudes. Parameters kWM and kMW represent the MT exchange rate constants relative to WP and MP pool sizes respectively.
Experiment I: Determination of MT parameters
To measure the parameters related to the two-pool exchange model, two types of preparation pulses, namely a WP IR pulse and a composite broadband MP SR pulse were used to saturate the two pools to different extents. After variable delay t, EPI image acquisition was performed to sample FSWP(t). The use of two different preparation pulses facilitated fitting λ1 and λ2, and furthermore allowed extraction of kMW, kWM, f, and R1,WP by assuming R1,MP = 2 s−1 and FSMP(0) = 0.93 for the broadband SR experiment as determined previously (3). The inversion pulse was adiabatic, with a hyperbolic secant envelope, duration of 5.12 ms, energy of 0.51 (µT)2s, maximum B1 (amplitude of the RF field) of 833 Hz (1 Hz equals 0.0235 µT) and β of 1400 s−1 (41). The broadband SR pulse had a duration of 6 ms and consisted of a train of 16 hard pulses with angles 60°, −120°, 120°, −120°, ….120°, −60°, with a B1 amplitude of 833 Hz (3).
Experiment II: Determination of MP spectral characteristics
To determine MP spectral characteristics, the broadband SR pulse was replaced by a frequency-specific SR pulse and applied at 12 different frequency offsets (F) with respect to the water resonance frequency, ranging from −16 kHz to 16 kHz (−16, −8, −4, −2, −1, −0.5, 0.5, 1, 2, 4, 8, 16 kHz). The order of scans for different values of F was randomized for each subject. The pulse had a duration of 12 ms, and a hyperbolic secant envelope for its amplitude, identical to that used for the inversion pulse described above, with a β of 600 s−1 (41). The full width at half maximum (FWHM) of its power spectral density is 119 Hz. A relatively low B1 amplitude of 200 Hz was used in order to avoid saturation and the non-linear relationship between FSMP(0) and the integral of squared B1 amplitude over the pulse duration for all values of F (42, 43). This simplified the derivation of the MP spectrum from the experimental data.
Image acquisition
For both IR and SR experiments, image data were acquired using single-shot EPI, sampling 5 slices consecutively after the preparation pulse; cycling the slice order over 5 repetitions thus resulted in acquisition of 5 delay times for each slice (44). Axial-oblique slices of 2 mm thickness were placed, with 3.4 mm inter-slice gap, parallel to AC-PC line and encompassed the central part of the corpus callosum. The delay times for the IR experiment were 6, 63, 144, 282 and 1200 ms (defined as the time from the center of the inversion pulse to the center of the EPI excitation pulse). The delay times for the broadband SR experiments were: 7, 127, 258, 401 and 559 ms and for the frequency-specific SR experiments were: 10, 130, 260, 402 and 559 ms. The IR and SR delay times were chosen to sample the signal recovery dynamics, within the constraint of the minimal slice repetition time (TR) set by the duration of the EPI readout. The image resolution was 144×108 with SENSE rate-2 acceleration, the field-of-view was 240×180 mm. The echo time (TE) was 24 ms, TRs were 6 and 3 s for IR and SR experiments respectively. In order to suppress signals from scalp lipids, the TE was increased by 0.49 ms on even numbered repetitions (3). A multi gradient echo (MGRE) sequence with TR of 0.2 s, TE of 2.5 ms, 7 echoes with echo spacing of 0.74 ms, the same resolution and field-of-view as the EPI scans and total scan time of 21.6 s, was scanned before all IR and SR experiments. This MGRE sequence served as reference to reconstruct the accelerated EPI scans and was also used to estimate the B0 (amplitude of the static field) inhomogeneity. For IR experiments, six repeat measurements were performed, the first two of which omitted the inversion pulse and were used to provide a reference signal to estimate MWP (∞) in Eq. [1], and allow conversion of the measured signals to FSWP(t). Similarly, ten repetitions (including two serving as reference) and six repetitions (including one reference) were acquired for the broadband and frequency-specific SR experiments respectively.
Data Analysis
Pre-processing
Pre-processing included motion correction, signal polarity correction, averaging, and calculation of FSWP(t). Prior to averaging repetitions, complex images were spatially registered to correct for motion. Only in-plane registration was performed, as the small number of slices did not support through-plane motion correction. Polarity correction was needed only for IR (magnitude) data, because of signal rectification during the complex-to-magnitude conversion. It was performed based on the phase difference between the IR images with the (un-inverted) reference image. The FSWP(t) level expressed in Eq. [1] was determined by dividing each IR image by the corresponding reference image (i.e. data acquired without inversion pulse). Analogous analysis was performed for the SR data, however without performing the signal polarity adjustment. All processing was done in IDL (Exelsis Visual Information Solutions, Boulder, CO, USA).
Voxel-wise determination of MP saturation
To determine λ1, λ2, kWM, kMW, and R1,WP, both the IR and the broadband SR data from Experiment I were analyzed on a voxel-wise basis. Defining FSMP(0, F) as the FSMP(0) created by a frequency-specific SR pulse applied at frequency F, FSMP(0,F) can be then calculated based on analysis of the frequency-specific SR data in Experiment II. The following steps were involved:
Fit Eq. [1] to the IR and broadband SR data jointly, yielding one pair of decay rates (λ1, λ2) and two pairs of amplitudes (a1, a2) for each voxel.
Assuming R1,MP=2 s−1 and FSMP(0) for the broadband SR experiment to be 0.93 as determined previously (3), calculate kWM, kMW, R1,WP, using Eq. [3–4], based on the decay rates and amplitudes found under Step (a).
Fit Eq. [1] to the frequency-specific SR data, to find a pair of amplitudes (a1(F), a2(F)) for every voxel at each F, using decay rates (λ1, λ2) found under Step (a). Then calculate FSMP(0,F) using these (a1(F), a2(F)) pairs, according to Eq. [2] by setting t=0 s, with all other parameters known from Steps (a) and (b), as shown in Eq. [6].
| [6] |
Calculation of B0 shift for frequency-specific SR scans
B0 inhomogeneity and its drift over the course of the experiments can potentially change the effective F for each of the frequency-specific SR pulses. B0 measurement with methods like WASSR (45) can be used to correct for these effects. Here, B0 inhomogeneity for each scan was calculated voxel-wise as follows:
The phase of even echoes of the MGRE scan was fitted to a linear model to estimate spatial variations (inhomogeneity) in B0.
The EPI (either IR or SR) scan following the MGRE was assumed to suffer from the same B0 inhomogeneity as the MGRE scan.
The relative B0 shift between successive EPI scans (temporal drift) was determined from their relative phase.
The absolute B0 shift, ΔB0, for a specific EPI scan was calculated by summing over all its previous relative B0 shifts and the B0 inhomogeneity of the first EPI scan, as determined in Step (c) and Step (b) respectively.
MP spectral characteristics in a WM region of interest
To infer MP spectral characteristics in WM in human brain, we performed region of interest (ROI) analysis. Since the total scan time for each subject took up to ~1.35 hours and only motion within the axial plane was corrected for by in-plane registration, care was taken to select the ROI well within WM. This was done from images of the MP fraction f thresholded at 0.2, and Gaussian smoothed over a kernel of 7 voxels. Fig. 1 shows an example of WM ROI’s on five slices for one of the 7 subjects studied.
FIG. 1.
Example of WM ROI selection. ROI location is shown superimposed on EPI scan (top row), together with corresponding f maps. Selection was based on thresholding f at 0.2, followed by Gaussian smoothing with a 7 voxel kernel.
The ROI averaged FSMP(0,F) was calculated for each subject. Following previous work (14, 30), a SL lineshape (Eq. [7]) and Lorentzian (L) lineshape (Eq. [8]) were fit to this data.
| [7] |
| [8] |
In Eqs. [7] and [8], A is a scaling factor, F is the frequency of the applied frequency-specific SR pulse as mentioned above, and ΔF is the resonance frequency of MPs. Δf0(F) is the WM ROI averaged frequency offset caused by the B0 shift for a frequency-specific SR scan applied at frequency F, and is equal to γΔB0/2π, with ΔB0 determined above and γ being the gyromagnetic ratio. The averages and standard deviations were calculated for T2 and ΔF over subjects for both lineshapes. Fitting using the sum of two Lorentzians to individual subject FSMP(0,F) was also performed, using a common ΔFL determined from the single Lorentzian fit for both Lorentzians, to account for the potential contribution of two MP pools with distinct spectral characteristics (31, 46–48). Finally, fitting SL, Lorentzian and sum of two Lorentzians to FSMP(0,F) data combined from all subjects was also performed.
Potential effects of B1 amplitude on the MP spectrum
The validity of our approach to infer the MP spectrum implicitly assumes a linear relationship between FSMP(0,F) and the power of off resonance MT pulses, which holds true only when the B1 amplitude is low enough to avoid substantial saturation (42, 43). To study the effect of B1 amplitude of the frequency-specific SR pulse on the inferred MP spectrum, we fitted a Lorentzian lineshape to simulated FSMP(0,F)’s using Bloch equation. First, FSMP(0,F) for the MPs with a T2,input of 65 µs is simulated, under the influence of frequency-specific hyperbolic secant SR pulse with a duration of 12 ms and a B1 of 200 Hz (matching the preparation pulses used in the frequency-specific SR experiments), applied at several different frequency offsets, ranging from −16 kHz to 16 kHz. A Lorentzian fit yielded a T2,output. Then, dependence of T2,output on T2,input and B1 were studied by varying T2,input while keeping B1 fixed as 200 Hz, and varying B1 while keeping T2,input fixed as 65 µs, respectively. A Lorentzian rather than a SL lineshape was used in all these simulations, due to the lack of a rigorous way to simulate Bloch equations incorporating a SL lineshape, under influence of a shaped MT pulse (49).
Potential effects of assumptions for the values of R1,MP and FSMP(0)
A potential source for inaccuracies in the extracted parameters are incorrect assumptions for the values of R1,MP and FSMP(0). For the broadband SR experiment (Experiment I), R1,MP=2.0 s−1 and FSMP(0)=0.93 were assumed, and these may not be entirely accurate. We investigated the effect of changes in these values on the MP T2 determined in Experiment II, based on subject and ROI averaged values of decay rates (λ1, λ2) and amplitudes (a1, a2) for all IR and SR experiments, which were fitted without using any assumption. By varying R1,MP from 1 to 3 s−1 and FSMP(0) from 0.8 to 1.0 respectively, and going through procedures described above, new T2 values were found for both SL and Lorentzian lineshapes, and these were compared with the original values.
Quantification of the symmetry of the MP spectrum
The effect of CEST on our spectrum measurements is expected to be small because of the short, 12 ms duration of the RF pulses used for the SR experiment. To investigate the presence of any remaining CEST effect, we analyzed spectral symmetry with the notion that any asymmetries would point to a potential CEST contribution (28, 33, 42, 43). Symmetry was shown by inspecting the residuals after subtracting the fits from ROI averaged FSMP(0,F) of all subject, done for all types of lineshapes, including SL, Lorentzian and sum of tow Lorentzians.
Results
Voxel-wise fitting of the 2-pool model (Eq. [1]) to the IR and broadband SR data allowed robust extraction of the model parameters. ROI averaged results are shown in Fig. 2 and Table 1. A single set of rate constants (λ1 and λ2) fitted both IR and SR data well, as judged from the close fit to the data apparent in Fig. 2. The ROI-averaged values for R1,WP, f, and kMW were similar to those found in a previous study based on IR and SR measurements at 7 T (37).
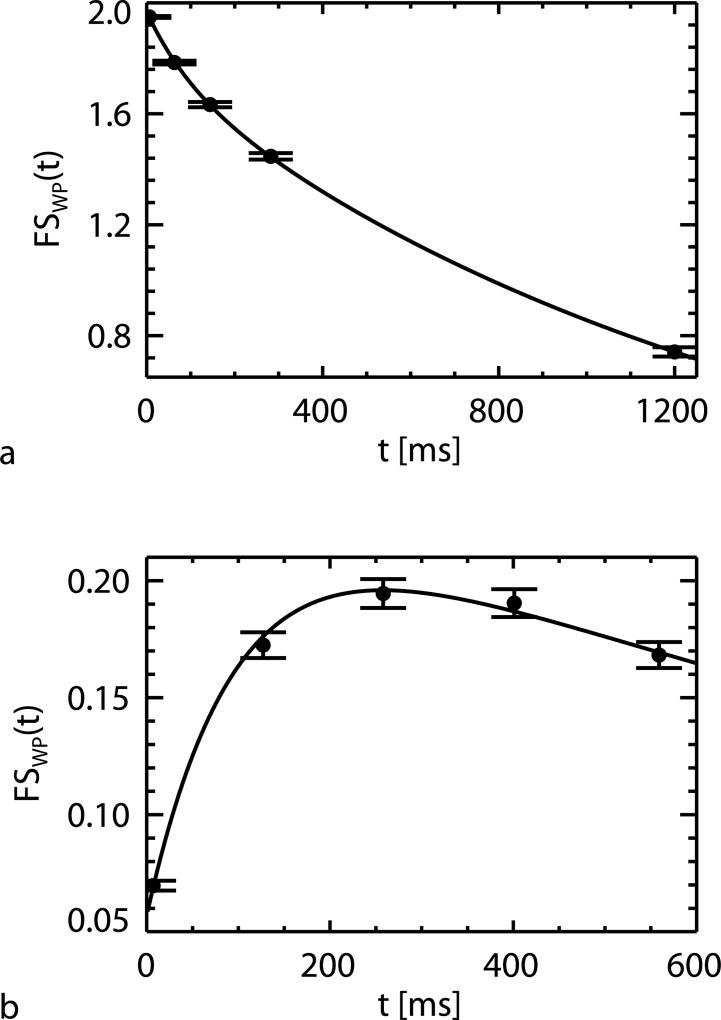
FIG. 2.
Two-pool model fitting (shown in lines) to subject and WM ROI averaged FSWP(t) (shown in dots) of IR (a) and broadband SR (b) experiments, with the error bars representing the standard deviations over subjects.
Table 1.
Average (standard deviation) of the extracted two-pool model parameters in WM ROI’s over subjects from Experiment I, with R1, MP assumed as 2.0 s−1 uniform across the brain for all subjects, as determined previously by van Gelderen et al (3, 37); all rates are reported in s−1; R2 was adjusted for degrees of freedoms.
| a1(IR) | a2(IR) | a1(SR) | a2(SR) | λ1 | λ2 | R1, WP | R1, MP | f | kWM | kMW | R2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.216 | 1.75 | −0.197 | 0.254 | 9.95 | 0.716 | 0.363 | 2.0 | 0.250 | 2.07 | 6.21 | 0.99996 |
| (0.009) | (0.01) | (0.010) | (0.010) | (0.32) | (0.015) | (0.010) | (0.012) | (0.13) | (0.25) | (1 × 10−5) |
With the voxel-wise fast (λ1) and slow (λ2) rate constants known, voxel-wise two-pool model fitting of FSWP(t) to the frequency-specific SR data yielded maps of coefficients a1(F) and a2(F), as exemplified in Fig. 3 (top two rows). Next, using Eq. [6], voxel-wise values for a1(F) and a2(F) were used to calculate FSMP(0,F), whose maps is shown as the bottom row of Fig. 3, and further ROI-averaged values for FSMP(0,F) were determined for each subject. Before proceeding with fitting line shapes to these data, small adjustments to the data were made to correct for potential shifts in F due to instrument drift. These correction values Δf0(F) were small relative to the spectral range.
FIG. 3.
Examples of maps of -a1(F) (first row) and a2(F) (second row), and FSMP(0,F) (third row), for the frequency-specific SR data fit, at different frequency F (from left to right: −16, −8, −4, −2, −1, −0.5, 0.5, 1, 2, 4, 8, 16 kHz)
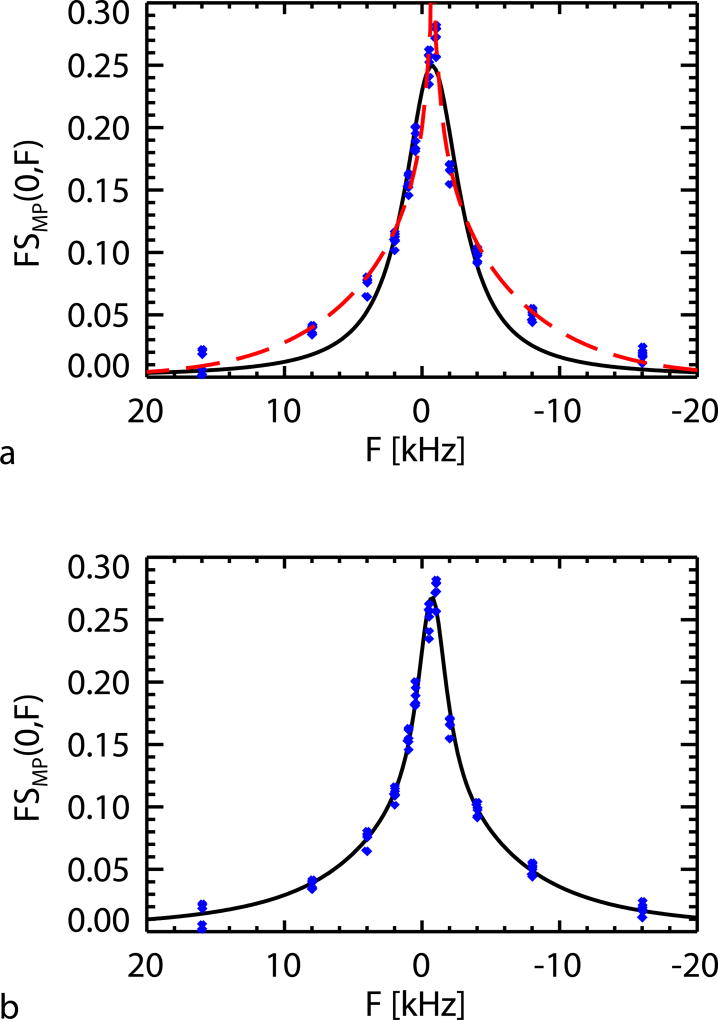
Table 2 summarizes the results of fitting a SL (Eq. [7]), Lorentzian (Eq. [8]), and sum of two Lorentzians to subject-wise ROI-averaged FSMP(0,F). T2,SL of 9.6±0.6 µs and ΔFSL of −773±14 Hz (−2.58±0.05 ppm), and T2,L of 65±2 µs and ΔFL of −727±28 Hz (−2.42±0.09 ppm) were found for SL and Lorentzian fitting respectively. For the two-Lorentzian fit, a common ΔFL of −727 Hz (−2.42 ppm) determined from the single Lorentzian fit was used. This fitting resulted in a 74±3% fraction of MPs with a T2 of 23±5 µs, and a 26±3% fraction with a T2 of 124±13 µs. Judging from the R2 (adjusted for degrees of freedoms) values, the SL and sum of two Lorentzians had similar performance in the fitting, and both provided better fit than Lorentzian.
Table 2.
Results of T2, ΔF and R2 (adjusted for degrees of freedoms) for fitting of SL, Lorentzian and sum of two Lorentzians lineshapes to FSMP(0,F) data, report in the form of subject average±(standard deviation over subjects); for sum of two Lorentzians fit, a common ΔFL for both Lorentzians was assumed to be −727 Hz (−2.42 ppm), identical to that obtained from the single Lorentzian fit. The component with T2 of 23±5µs, composes 74±3% of the total MPs, and the other component with T2 of 124±13 µs composing the rest.
| SL | Lorentzian | Sum of 2 Lorentzians | |
|---|---|---|---|
| T2 (µs) | 9.6±0.6 | 65±2 | 23±5/124±13 |
| ΔF (Hz) | −773±14 | −727±28 | −727 |
| R2 | 0.982±0.005 | 0.939±0.013 | 0.989±0.003 |
SL and Lorentzian fits to ROI averaged FSMP(0,F) data were also performed on all subjects jointly (but without averaging over subjects, since Δf0(F) is different across subjects). This is shown in Fig. 4a, yielding T2,SL of 9.5 µs and ΔFSL of −781 Hz (−2.60 ppm) for the former, and T2,L of 65 µs and ΔFL of −726 Hz (−2.42 ppm) for the later. Fitting to the same data using sum of two Lorentzians, resulted in T2,L ‘s of 23 µs (73%) and 122 µs (27%), as shown in Fig. 4b.
FIG. 4.
A SL lineshape (shown as the red dashed curve in a) and a Lorentzian lineshape (shown as the black solid curve in a) fitting to the WM ROI averaged FSMP(0,F) of all subjects jointly (shown in blue dots); sum of two Lorentzians (shown as the curve in b) fits to the same data (shown in blue dots).
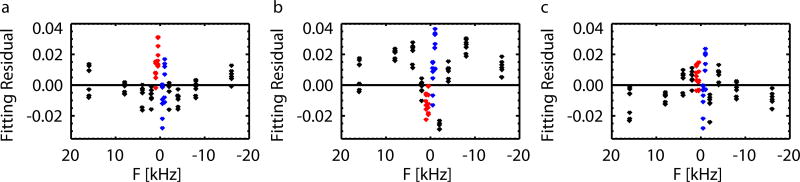
After subtraction of the fitted (symmetric) lineshapes from the spectral data, residual signal appears small for the SL fit (Fig. 5a), and the fit of two Lorentzians (Fig. 5c). The small residuals and the absence of any clear asymmetry in their distribution is consistent with expected suppression of CEST effects, and associated asymmetries, with the measurement approach followed here. However, deviation of the residuals from zero is obvious for the Lorentzian fit (Fig. 5b), confirming previous steady state MT studies (4–6, 19) where SL provided a fit superior over a Lorentzain lineshape.
FIG. 5.
Residuals for the SL fit (a), single Lorentzian fit (b), and sum of two Lorentzians fit (c) subtracted from the WM ROI averaged FSMP(0,F) of all subjects (shown in dots), with data in range of 0 Hz<F<1500 Hz marked in red and −1500 Hz<F<0 Hz marked in blue.
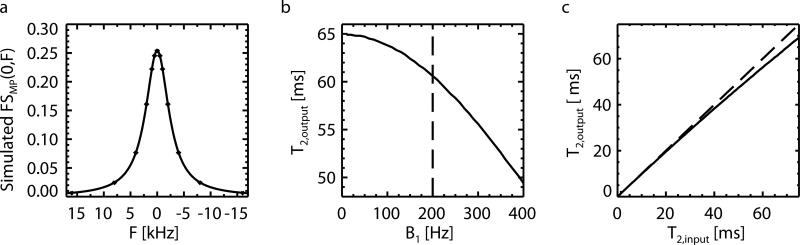
Results of the simulations performed to investigate the influence of the B1 amplitude on inferred T2 are shown in Fig. 6. As expected, for an actual MP T2 (T2,input) of 65 µs, the inferred T2 (T2,output) drops precipitously with RF power (Fig. 6b). However, at the experimental B1 amplitude of 200 Hz, this drop remains limited: the T2,output of 60 µs underestimates T2,input by 5 µs, i.e. less than 10%. According to Fig. 6b, variation of B1 by 25 Hz results in an error in the estimation of T2,output on the order of 1 µs, which suggest a low sensitivity to B1 inhomogeneity. Similarly, at other values of T2,input , and B1 =200 Hz, the difference between T2,input and T2,output remains modest (Fig. 6c).
FIG. 6.
Simulations of influence of B1 amplitude on inferred T2: (a) Lorentzian fit (the curve) to simulated FSMP(0,F) (the dots) of MP pool with T2,input of 65 µs, using Bloch equation, under the influence of frequency-specific hyperbolic secant pulses with B1 of 200 Hz, a common pulse duration of 12 ms, resulting in a T2,output of 60 µs; (b) B1 dependence of T2,output by varying B1 while keeping T2,input fixed as 65 µs; (c) T2,input dependence of T2,output by varying T2,input while keeping B1 fixed as 200 Hz.
The extracted MP T2 values proved robust against small changes in assumed values for R1,MP and FSMP(0). Changing R1,MP from 1 to 3 s−1 resulted in very little change in FSMP(0,F). For the SL lineshape, T2,SL changed from 9.4 to 9.3 µs, while for the Lorentzian, T2,L changed from 65 to 64 µs. Changes of FSMP(0) from 0.8 to 1.0 resulted in a similar T2,SL in the range of 9.3–9.4 µs, and T2,L remained at a constant value of 64 µs, although increasing FSMP(0) of the broadband SR experiment results in increased FSMP(0,F).
Discussion
In order to aid interpretation of MT contrast at high field, we investigated MP spectral characteristics in human brain WM at 7 T. For this purpose, we used a dedicated indirect measurement approach that minimized direct saturation of WPs, CEST effects, and tissue heating, problems often associated with the generation of MT contrast in-vivo. We found that at 7 T, the MP spectrum is well represented by a symmetric, SL lineshape with a time constant T2,SL of 9.6±0.6 µs, and shifted by −2.58±0.5 ppm relative to the water resonance. As will be discussed in the following, these results are consistent with previous findings and mechanistic interpretations of MT from studies at lower field and point to dipolar coupling between methylene protons as a major determinant of the MP spectral characteristics. We anticipate that these values for the MP spectral characteristics will help design and quantification of future MT studies at 7T.
As has been found with previous indirect measurement of MP spectral characteristics at 1.5 T and 3 T, (4–6, 14) the 7 T data could be reliably fit with a SL lineshape. This is consistent with a dipolar coupling mechanism in semi-solids such as membrane proteins and lipids (14, 25, 29, 50). In addition, it was found that the 9.6 µs T2,SL at 7 T was similar to the 9.2 µs – 13.1 µs range of values found in previous studies at lower fields between 0.5 T and 3 T (4–6, 28, 51). Like the SL lineshape, the field independence of the linewidth is suggestive of a dominant contribution of dipolar coupling, rather than width being determined by chemical shift differences between the 1H species contributing to MT (26). Previous direct measurements of MP spectral characteristics on fixed human WM tissue samples have found 50– 65 µs for T2,L (20, 23) at 7 T and 4.7 T. These values were based on Lorentzian lineshapes, and translate into T2,SL values of 16–21 µs for SL lines of the same FWHM. These ex-vivo Lorentzian linewidths therefore are quite consistent with the in-vivo values, especially when considering the differences in measurement conditions.
Our MT study at 7 T found that the center of the MPs spectrum is shifted upfield relative to the resonance frequency of WPs by −2.58 ppm. This result agrees well with values of −2.34 ppm previously reported at 3 T (28), and the −2.55 ppm reported in WM of cat brain at 4.7 T (32). Combined, these studies show that the absolute spectral frequency shift is proportional to field strength, an observation consistent with a chemically shifted proton species contributing to MT. The value of the shift is somewhat smaller than the range of −3.2 to −3.9 ppm measured for methylene protons, the dominant proton species in myelin (24). While methylene protons are most abundant in WM (20), a not insignificant contribution to our MT signal may have come from, more downfield shifted proton species (e.g. in proteins and smaller molecules). These protons, while measured together with the methylene protons, may shift the combined spectral line downfield from the −3.2 to −3.9 ppm range.
To the extent that MT is caused by methylene protons in myelin lipids, their substantial orientational order may introduce a dependence of spectral linewidth on the direction of white matter fibers relative to the magnetic field. In fact, a recent study found that T2,SL may vary between 12 and 15 µs, dependent on fiber orientation (29). Due to lack of information about fiber orientation, we could not confirm this dependence in our own data. Nevertheless, if confirmed, a fiber-orientation dependent MP T2 would further underscore the importance of the dipolar coupling mechanism for the apparent MP T2, and furthermore predict an orientation dependence of MT effects. Similarly, since the effect of an inversion RF pulse on MP magnetization depends on MP spectral characteristics (3), orientation dependence of MP T2 may also render apparent T1 (as measured from an IR experiment (3)) orientation dependent.
An advantage of the proposed method for the measurement of MP characteristic is the insensitivity to CEST effects, which can substantially contribute to so called “z-spectra” typically acquired to quantify MT effects (12, 28, 52), and thus confound interpretation. When generating MT contrast with seconds-long RF irradiation, MT from exchangeable protons can reduce the amplitude of the WP signal by as much of 2–4%, which is substantial when considering that typical asymmetry in z-spectra due to non-exchanging protons is only on the order of 1–2% (28). Although currently several approaches exist to distinguish CEST from other (non-exchange) MT effects (43, 52, 53), CEST effects were not explicitly excluded from z-spectrum asymmetry quantifications reported previously (28, 32). Nevertheless, it appears that the quantitative shifts characterizing this asymmetry are quite similar between the proposed and previous methods and amount to about −2.6 ppm.
A potential source for inaccurate quantification of MP spectral characteristics with the proposed method is the potential dependence on RF irradiation strength (B1 amplitude). Preliminary experimental study of effects of B1 on the spectrum measurement was performed on two subjects in a similar manner as described above. Experiment I was done in exactly the same way as described in Method for both subjects. In Experiment II, multiple B1’s were used for the frequency-specific SR experiment, to quantify the B1 dependence of ROI averaged FSMP(0,F). In lack of a rigorous way to do the simulation based on a SL lineshape (49) as mentioned above, attempts were made to simulate these data using single Lorentzian and a combination of multiple Lorentzians respectively, however no close fit was found. This may reflect the intrinsic insufficiency of a Lorentzian lineshape to represent the underlying interaction between the immobile MPs. The situation may be further complicated by the existence of multiple MP species, each with a SL lineshape centered on a different resonance frequency (24). Thus, while our spectral measurements provide a measure of linewidth and chemical shift, both of which provide insights into the molecular source of MT in white matter, uncertainty remains about the precise lineshape.
Conclusions
A novel approach was introduced to study MPs spectral characteristics while minimizing effects of RF-related tissue heating, direct saturation of WPs and CEST effects. Applied to WM in human brain at 7 T, MPs were found to have a symmetric, SL lineshape with a T2,SL of 9.6 µs and an resonance frequency ΔFSL of −773 Hz (−2.58 ppm), consistent with previous results at low field, and consistent with a previously suggested major contribution of dipolarly-coupled lipid methylene protons. These results, as well as the proposed measurement approach, are expected to facilitate the use and interpretation of quantitative MT approaches at high field.
References
- 1.Wolff SD, Balaban RS. Assessing contrast on MR images. Radiology. 1997;202:25–9. doi: 10.1148/radiology.202.1.8988186. [DOI] [PubMed] [Google Scholar]
- 2.Henkelman RM, Huang X, Xiang Q-SS, Stanisz GJ, Swanson SD, Bronskill MJ. Quantitative interpretation of magnetization transfer. Magn Reson Med [Internet] 1993;29:759–766. doi: 10.1002/mrm.1910290607. [DOI] [PubMed] [Google Scholar]
- 3.van Gelderen P, Jiang X, Duyn JH. Effects of magnetization transfer on T1 contrast in human brain white matter. Neuroimage [Internet] 2015;128:85–95. doi: 10.1016/j.neuroimage.2015.12.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yarnykh VL. Pulsed Z-spectroscopic imaging of cross-relaxation parameters in tissues for human MRI: Theory and clinical applications. Magn. Reson. Med. [Internet] 2002;47:929–939. doi: 10.1002/mrm.10120. [DOI] [PubMed] [Google Scholar]
- 5.Sled JG, Pike GB, Bruce Pike G. Quantitative imaging of magnetization transfer exchange and relaxation properties in vivo using MRI. Magn. Reson. Med. [Internet] 2001;46:923–931. doi: 10.1002/mrm.1278. [DOI] [PubMed] [Google Scholar]
- 6.Ramani A, Dalton C, Miller DH, Tofts PS, Barker GJ. Precise estimate of fundamental in-vivo MT parameters in human brain in clinically feasible times. Magn. Reson. Imaging [Internet] 2002;20:721–731. doi: 10.1016/S0730-725X(02)00598-2. [DOI] [PubMed] [Google Scholar]
- 7.Davies GR, Tozer DJ, Cercignani M, Ramani a, Dalton CM, Thompson aJ, Barker GJ, Tofts PS, Miller DH. Estimation of the macromolecular proton fraction and bound pool T2 in multiple sclerosis. Mult. Scler. [Internet] 2004;10:607–13. doi: 10.1191/1352458504ms1105oa. [DOI] [PubMed] [Google Scholar]
- 8.Levesque IR, Giacomini PS, Narayanan S, Ribeiro LT, Sled JG, Arnold DL, Pike GB. Quantitative magnetization transfer and myelin water imaging of the evolution of acute multiple sclerosis lesions. Magn. Reson. Med. 2010;63:633–640. doi: 10.1002/mrm.22244. [DOI] [PubMed] [Google Scholar]
- 9.Love S. Demyelinating diseases. J. Clin. Pathol. 2006;59:1151–1159. doi: 10.1136/jcp.2005.031195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Alizadeh A, Dyck SM, Karimi-Abdolrezaee S. Myelin damage and repair in pathologic CNS: challenges and prospects. Front. Mol. Neurosci. [Internet] 2015;8:35. doi: 10.3389/fnmol.2015.00035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Popescu BF, Lucchinetti CF. Pathology of demyelinating diseases. Annu Rev Pathol [Internet] 2012;7:185–217. doi: 10.1146/annurev-pathol-011811-132443. [DOI] [PubMed] [Google Scholar]
- 12.Van Zijl PCM, Zhou J, Mori N, Payen JF, Wilson D, Mori S. Mechanism of magnetization transfer during on-resonance water saturation. A new approach to detect mobile proteins, peptides, and lipids. Magn. Reson. Med. 2003;49:440–449. doi: 10.1002/mrm.10398. [DOI] [PubMed] [Google Scholar]
- 13.Chen JH, Sambol EB, DeCarolis P, O’Connor R, Geha RC, Wu YV, Singer S. High-resolution MAS NMR spectroscopy detection of the spin magnetization exchange by cross-relaxation and chemical exchange in intact cell lines and human tissue specimens. Magn. Reson. Med. 2006;55:1246–1256. doi: 10.1002/mrm.20889. [DOI] [PubMed] [Google Scholar]
- 14.Morrison C, Henkelman RM. A model for magnetization transfer in tissues. Magn. Reson. Med. [Internet] 1995;33:475–482. doi: 10.1002/mrm.1910330404. [DOI] [PubMed] [Google Scholar]
- 15.Liepinsh E, Otting G. Proton exchange rates from amino acid side chains--implications for image contrast. Magn. Reson. Med. 1996;35:30–42. doi: 10.1002/mrm.1910350106. [DOI] [PubMed] [Google Scholar]
- 16.Zhou J, Zijl PCM van. Chemical exchange saturation transfer imaging and spectroscopy. Prog. Nucl. Magn. Reson. Spectrosc. 2006;48:109–136. doi: 10.1016/j.pnmrs.2006.01.001. [DOI] [PubMed] [Google Scholar]
- 17.Liu G, Song X, Chan KWY, Mcmahon MT. Nuts and bolts of chemical exchange saturation transfer MRI. NMR Biomed. 2013;26:810–828. doi: 10.1002/nbm.2899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Van Zijl PCM, Yadav NN. Chemical exchange saturation transfer (CEST): What is in a name and what isn’t? Magn. Reson. Med. 2011;65:927–948. doi: 10.1002/mrm.22761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Morrison C, Stanisz G, Henkelman RM. Modeling magnetization transfer for biological-like systems using a semi-solid pool with a super-Lorentzian lineshape and dipolar reservoir. J Magn Reson B [Internet] 1995;108:103–113. doi: 10.1006/jmrb.1995.1111. [DOI] [PubMed] [Google Scholar]
- 20.Horch RA, Gore JC, Does MD. Origins of the ultrashort-T2 1H NMR signals in myelinated nerve: A direct measure of myelin content? Magn. Reson. Med. [Internet] 2011;66:24–31. doi: 10.1002/mrm.22980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chan SI, Feigenson GW, Serter CHA. Nuclear Relaxation Studies of Lecithin Bilayers. Nature [Internet] 1971;231:110–112. doi: 10.1038/231110a0. [DOI] [PubMed] [Google Scholar]
- 22.Finer EG, Darke A. Phospholipid hydration studied by deuteron magnetic resonance spectroscopy. Chem. Phys. Lipids. 1974;12:1–16. doi: 10.1016/0009-3084(74)90064-4. [DOI] [PubMed] [Google Scholar]
- 23.Ramani A, Aliev AE, Barkera GJ, Tofts PS. Another approach to protons with constricted mobility in white matter: Pilot studies using wideline and high-resolution NMR spectroscopy. Magn. Reson. Imaging. 2003;21:1039–1043. doi: 10.1016/S0730-725X(03)00207-8. [DOI] [PubMed] [Google Scholar]
- 24.Wilhelm MJ, Ong HH, Wehrli SL, Li C, Tsai P-H, Hackney DB, Wehrli FW. Direct magnetic resonance detection of myelin and prospects for quantitative imaging of myelin density. Proc. Natl. Acad. Sci. 2012;109:9605–9610. doi: 10.1073/pnas.1115107109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Malyarenko DI, Zimmermann EM, Adler J, Swanson SD. Magnetization transfer in lamellar liquid crystals. Magn. Reson. Med. [Internet] 2013;72:1427–1434. doi: 10.1002/mrm.25034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Feigenson GW, Chan SI. Nuclear magnetic relaxation behavior of lecithin multilayers. J. Am. Chem. Soc. [Internet] 1974;96:1312–1319. doi: 10.1021/ja00812a009. [DOI] [PubMed] [Google Scholar]
- 27.Koenig SH. Cholesterol of myelin is the determinant of gray-white contrast in MRI of brain. Magn. Reson. Med. [Internet] 1991;20:285–91. doi: 10.1002/mrm.1910200210. [DOI] [PubMed] [Google Scholar]
- 28.Hua J, Jones CK, Blakeley J, Smith SA, van Zijl PCM, Zhou J. Quantitative description of the asymmetry in magnetization transfer effects around the water resonance in the human brain. Magn. Reson. Med. [Internet] 2007;58:786–793. doi: 10.1002/mrm.21387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pampel A, Müller DK, Anwander A, Marschner H, Möller HE. Orientation dependence of magnetization transfer parameters in human white matter. Neuroimage. 2015;114:136–146. doi: 10.1016/j.neuroimage.2015.03.068. [DOI] [PubMed] [Google Scholar]
- 30.Li JG, Graham SJ, Henkelman RM. A flexible magnetization transfer line shape derived from tissue experimental data. Magn. Reson. Med. 1997;37:866–871. doi: 10.1002/mrm.1910370610. [DOI] [PubMed] [Google Scholar]
- 31.Stanisz GJ, Kecojevic A, Bronskill MJ, Henkelman RM. Characterizing white matter with magnetization transfer and T2. Magn. Reson. Med. 1999;42:1128–1136. doi: 10.1002/(SICI)1522-2594(199912)42:6<1128::AID-MRM18>3.0.CO;2-9. [DOI] [PubMed] [Google Scholar]
- 32.Pekar J, Jezzard P, Roberts DA, Leigh JS, Frank JA, McLaughlin AGC. Perfusion imaging with compensation for asymmetric magnetization transfer effects. Magn. Reson. Med. [Internet] 1996;35:70–79. doi: 10.1002/mrm.1910350110. [DOI] [PubMed] [Google Scholar]
- 33.Ng MC, Hua J, Hu Y, Luk KD, Lam EY. Magnetization transfer (MT) asymmetry around the water resonance in human cervical spinal cord. J. Magn. Reson. Imaging. 2009;29:523–528. doi: 10.1002/jmri.21610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Swanson SD, Pang Y. MT is Symmetric but Shifted with Respect to Water. Proc. Intl. Soc. Mag. Reson. Med. 2003;11:660. [Google Scholar]
- 35.Mougin OE, Coxon RC, Pitiot a, Gowland Pa. Magnetization transfer phenomenon in the human brain at 7 T. Neuroimage [Internet] 2010;49:272–81. doi: 10.1016/j.neuroimage.2009.08.022. [DOI] [PubMed] [Google Scholar]
- 36.Goldman M, Shen L. Spin-spin relaxation in LaF3. Phys. Rev. 1966;144:321–331. doi: 10.1103/PhysRev.144.321. [DOI] [Google Scholar]
- 37.van Gelderen P, Jiang X, Duyn JH. Rapid measurement of brain macromolecular proton fraction with transient saturation transfer MRI. Magn. Reson. Med. [Internet] 2016 doi: 10.1002/mrm.26304. n/a--n/a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gochberg DF, Gore JC. Quantitative magnetization transfer imaging via selective inversion recovery with short repetition times. Magn. Reson. Med. 2007;57:437–441. doi: 10.1002/mrm.21143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Dortch RD, Moore J, Li K, Jankiewicz M, Gochberg DF, Hirtle JA, Gore JC, Smith SA. Quantitative magnetization transfer imaging of human brain at 7T. Neuroimage. 2013;64:640–649. doi: 10.1016/j.neuroimage.2012.08.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Forsén S, Hoffman R. Study of moderately rapid chemical exchange reactions by means of nuclear magnetic double resonance. J. Chem. Phys. [Internet] 2004;39:2892–2901. doi: 10.1063/1.1734121. [DOI] [Google Scholar]
- 41.Tannús A, Garwood M, Tannus A, Garwood M. Adiabatic pulses. NMR in Biomedicine. 1997;10:423–434. doi: 10.1002/(SICI)1099-1492(199712)10:8<423::AID-NBM488>3.0.CO;2-X. [DOI] [PubMed] [Google Scholar]
- 42.Scheidegger R, Vinogradov E, Alsop DC. Amide proton transfer imaging with improved robustness to magnetic field inhomogeneity and magnetization transfer asymmetry using saturation with frequency alternating RF irradiation. Magn. Reson. Med. 2011;66:1275–1285. doi: 10.1002/mrm.22912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lee JS, Regatte RR, Jerschow A. Isolating chemical exchange saturation transfer contrast from magnetization transfer asymmetry under two-frequency rf irradiation. J. Magn. Reson. 2011;215:56–63. doi: 10.1016/j.jmr.2011.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ordidge RJ, Gibbs P, Chapman B, Stehling MK, Mansfield P. High-speed multislice T1 mapping using inversion-recovery echo-planar imaging. Magn. Reson. Med. 1990;16:238–245. doi: 10.1002/mrm.1910160205. [DOI] [PubMed] [Google Scholar]
- 45.Kim M, Gillen J, Landman BA, Zhou J, Van Zijl PCM. Water saturation shift referencing (WASSR) for chemical exchange saturation transfer (CEST) experiments. Magn. Reson. Med. 2009;61:1441–1450. doi: 10.1002/mrm.21873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Levesque IR, Pike GB. Characterizing healthy and diseased white matter using quantitative magnetization transfer and multicomponent T2 relaxometry: A unified view via a four-pool model. Magn. Reson. Med. 2009;62:1487–1496. doi: 10.1002/mrm.22131. [DOI] [PubMed] [Google Scholar]
- 47.Kalantari S, Laule C, Bjarnason TA, Vavasour IM, MacKay AL. Insight into in vivo magnetization exchange in human white matter regions. Magn. Reson. Med. [Internet] 2011;66:1142–1151. doi: 10.1002/mrm.22873. [DOI] [PubMed] [Google Scholar]
- 48.Charvolin J, Rigny P. Pulsed NMR in dynamically heterogeneous systems. J. Magn. Reson. 1971;4:40–46. doi: 10.1016/0022-2364(71)90022-9. [DOI] [Google Scholar]
- 49.Graham SJ, Henkelman RM. Understanding pulsed magnetization transfer. J. Magn. Reson. Imaging. 1997;7:903–912. doi: 10.1002/jmri.1880070520. [DOI] [PubMed] [Google Scholar]
- 50.Wennerstrom H. Proton nuclear magnetic resonance lineshapes in lamellar liquid crystals. Chem. Phys. Lett. 1973;18:41–44. doi: 10.1016/0009-2614(73)80333-1. [DOI] [Google Scholar]
- 51.Stanisz GJ, Odrobina EE, Pun J, Escaravage M, Graham SJ, Bronskill MJ, Henkelman RM. T1, T2 relaxation and magnetization transfer in tissue at 3T. Magn. Reson. Med. [Internet] 2005;54:507–512. doi: 10.1002/mrm.20605. [DOI] [PubMed] [Google Scholar]
- 52.Yadav NN, Chan KWY, Jones CK, McMahon MT, Van Zijl PCM. Time domain removal of irrelevant magnetization in chemical exchange saturation transfer Z-spectra. Magn. Reson. Med. 2013;70:547–555. doi: 10.1002/mrm.24812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Zaiss M, Schmitt B, Bachert P. Quantitative separation of CEST effect from magnetization transfer and spillover effects by Lorentzian-line-fit analysis of z-spectra. J. Magn. Reson. 2011;211:149–155. doi: 10.1016/j.jmr.2011.05.001. [DOI] [PubMed] [Google Scholar]