Abstract
Background
Large-scale Granger causality (lsGC) is a recently developed, resting-state functional MRI (fMRI) connectivity analysis approach that estimates multivariate voxel-resolution connectivity. Unlike most commonly used multivariate approaches, which establish coarse-resolution connectivity by aggregating voxel time-series avoiding an underdetermined problem, lsGC estimates voxel-resolution, fine-grained connectivity by incorporating an embedded dimension reduction.
New Method
We investigate application of lsGC on realistic fMRI simulations, modeling smoothing of neuronal activity by the hemodynamic response function and repetition time (TR), and empirical resting-state fMRI data. Subsequently, functional subnetworks are extracted from lsGC connectivity measures for both datasets and validated quantitatively. We also provide guidelines to select lsGC free parameters.
Results
Results indicate that lsGC reliably recovers underlying network structure with Area Under receiver operator characteristic Curve (AUC) of 0.93 at TR=1.5s for a 10-minute session of fMRI simulations. Furthermore, subnetworks of closely interacting modules are recovered from the aforementioned lsGC networks. Results on empirical resting-state fMRI data demonstrate recovery of visual and motor cortex in close agreement with spatial maps obtained from (i) visuo-motor fMRI stimulation task-sequence (Accuracy=0.76) and (ii) independent component analysis (ICA) of resting-state fMRI (Accuracy=0.86).
Comparison with Existing Method(s)
Compared with conventional Granger causality approach (AUC=0.75), lsGC produces better network recovery on fMRI simulations. Furthermore, it cannot recover functional subnetworks from empirical fMRI data, since quantifying voxel-resolution connectivity is not possible as consequence of encountering an underdetermined problem.
Conclusions
Functional network recovery from fMRI data suggests that lsGC gives useful insight into connectivity patterns from resting-state fMRI at a multivariate voxel-resolution.
Keywords: Resting-state fMRI, functional connectivity, network recovery, Granger causality, principal component analysis, independent component analysis, multivariate analysis, non-metric clustering, Louvain method, hemodynamic response, repetition time
1. Introduction
The resting human brain is a continuously communicating, dynamic network where functionally related components interact and process information, [1]. The study of such cognitive processes in the human brain using non-invasive modalities, such as EEG and fMRI, has gained significant momentum, e.g. [2, 3, 4] over the recent years, as it has potential to study intrinsic brain dynamics. Functional relatedness between fMRI voxel-time series is usually inferred by capturing associations between every pair of time-series. In commonly used methods, such as Pearson’s correlation, this is done in a bivariate sense, without taking into account the effects of confounding variables, thus resulting in an inability to distinguish between direct and indirect connections [5]. More recent approaches overcome these limitations and enable us to capture interactions in a multivariate sense [3, 6]. In [7], the authors have shown that a bivariate analysis could result in misleading information regarding propagation of influence, while multivariate analysis distinguishes direct from indirect influences. Although, a multivariate analysis would result in better estimates [8] of the effects of time-series on each other, the complexity of the model increases with increasing number of time-series in the system. Such a problem is particularly characteristic of multivariate fMRI analyses, as the number of temporal samples is usually much lower than the number of voxel time-series. This is often avoided by aggregating groups of similar voxels [3, 6, 9] to reduce the complexity of the mathematically ill-posed problem. Hence, bivariate approaches are able to provide an analysis of interactions at a fine-grained voxel level at the cost of establishing non-existent, indirect connections, while most conventional multivariate methods are limited to the analysis of coarse-scale regional level interactions. We have recently proposed an approach called large-scale Granger causality (lsGC) [10, 11, 12, 13] that quantifies directed information flow, in a multivariate sense at a fine-grained voxel level without encountering an underdetermined, complex problem. In this study, we extend the prior cited work on lsGC by a thorough quantitative investigation of its effectiveness for detecting directed functional connectivity. Specifically, 1) we perform a detailed analysis on realistic fMRI model simulations known from the literature [14], 2) quantitatively evaluate the effectiveness of lsGC in extracting brain networks by comparison with spatial maps from task-related fMRI experiments and ICA networks and 3) provide guidelines to help users select optimal parameters for lsGC.
Large-scale Granger Causality (lsGC) analysis is a data-driven approach to establish a voxel-wise, multivariate, measure of directed functional connectivity. The core concept of Granger causality (GC) is that if prediction quality of say time-series y improves in the presence of past values of time-series x, then it is said that x Granger causes y. Prediction is performed using multivariate auto-regression (MVAR) of time-series. The applicability of GC to study interactions in fMRI was demonstrated by [15] and since then, GC has emerged as a popular tool for such studies [6, 9, 16]. However, such analysis with conventional multivariate Granger causality are performed at a coarse, ROI (region of interest) level to avoid an underdetermined problem. Conventional multivariate Granger causality applied at a voxel level, conditions to all the time-series in the system, while the acquired time series are short. The combination of these two factors results in an ill posed underdetermined problem. Furthermore, the large number of time-series contain a lot of redundant information. Large-scale Granger causality analysis, makes a voxel level computation of interaction feasible by incorporating an invertible spatial dimension reduction, using Principal Component Analysis (PCA). It reduces redundancy in the system by conditioning on only the most meaningful information, using the most representative components in the system. The quantified interactions using lsGC, form edge weights in a directed network graph, hence representing the brain as a network, where each node in the graph corresponds to a voxel time-series [17]. Using this graph, we can identify the underlying modular network structure of functionally related regions by performing non-metric clustering methods to demonstrate the effectiveness of lsGC in recovering useful information in resting-state fMRI, which is in line with other approaches developed by our group [18, 19, 20, 21, 22] and others [23, 24].
In this paper, we investigate the robustness of lsGC to detect directed functional connectivity at a voxel level along with extracting functionally connected components in both realistic fMRI simulations [14] and empirical resting-state fMRI data, and also provide guidelines to select good parameters for lsGC. Furthermore, we study the effect of two important fMRI acquisition parameters, namely repetition time (TR) and session duration, on lsGC performance using fMRI simulations. As the simulation data are generated using a known ground truth of nodal connections, we evaluate the ability of lsGC to accurately quantify influence scores. Subsequently, these scores are represented as network graphs, from which modules or subnetworks are extracted. To this end, we use the Louvain method for community detection in order to recover modular structure from the simulated fMRI time-series and evaluate it with the known ground truth of modular structure. Using a similar approach on the empirical resting-state fMRI data, we can recover known functional sub-networks (or modules) in the brain. These are evaluated against networks obtained 1) from an fMRI visuo-motor task sequence and 2) using Independent Component Analysis (ICA) on the resting-state fMRI data. Since we do not have a ground truth of voxel-level connections, for the empirical resting-state fMRI data we cannot quantitatively evaluate the voxel-level connectivity established using lsGC.
The paper is organized as follows: In section 2 we discuss two data we use to evaluate lsGC, i.e. the realistic fMRI simulations and empirical resting-state fMRI. Section 3 describes Granger causality and lsGC methods to establish a measure of directed information flow between time-series in a multivariate sense. It also provides guidelines for good parameter selection using lsGC and discusses non-metric clustering methods for community detection from the lsGC network graphs. Section 4 presents the results obtained using lsGC to quantify causality scores between time-series, from which we extract the underlying modular network structure.
2. Materials
2.1. Simulated fMRI time-series
We tested the effectiveness of lsGC to reliably estimate influence scores for realistic fMRI simulation data designed by [14] using the NetSim software [14]. We analyzed the largest dataset (referred to as sim4 in [14]) whose network structure is shown here in Figure 1. Note that this network has 50 nodes with 10 different modules. NetSim takes as input the underlying network structure and generates fMRI simulations for every node by modeling the BOLD signals sampled at TR. We investigate lsGC for time-series at two TRs of 1.5 s and 3 s. Throughout the paper, we use T to refer to the number of temporal samples irrespective of the TR used. However, when referring to temporal samples at a specific TR, we use the notation TTR.
Figure 1.
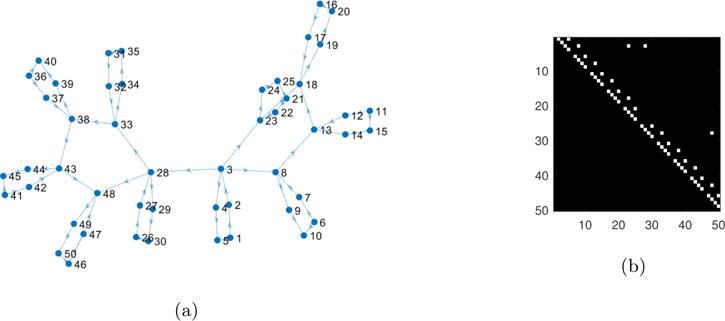
Network structure adopted from [14]. Figure (a) represents the connections as a network graph and Figure (b) represents the connections as a network matrix. We construct 50 different networks for each TR having the same structure as is seen in this figure but different connection strengths.
The simulation design used by [14] was based on the dynamic causal modelling [25] which modeled the neural network that was fed through a non-linear balloon model [26] for vascular dynamics. The neural signal simulation is given using the following equation by the DCM neural network model:
| (1) |
where z is the neural time-series and ż is the rate of change of the neural time-series z, A is the network matrix, which is the ground truth of neural connections in this model, C is the matrix defining external connections, u are external connections, and σ controls the temporal smoothing and neural lag within-node and between nodes. Further details on the simulation can be found in [14]. All parameters apart from the TR and session duration were adopted from [14]. A TR was incorporated by down-sampling the BOLD time-series such that the resulting fMRI simulations were generated at two repetition times, i.e. 1.5 s and 3 s. Figure 1 is the ground truth, i.e. the network matrix A that we use for our simulations. Fifty different trials of the simulation for different neural time-series, HRF delays, and random network weights were generated.
2.2. Empirical resting-state fMRI data
Functional MRI (fMRI) data from a healthy male, aged 44 years, was acquired using a 3.0 Tesla Siemens Magnetom TrioTim scanner at the Rochester Center for Brain Imaging (Rochester, NY, US). The study protocol included: (i) High resolution structural imaging using T1-weighted magnetization-prepared rapid gradient echo sequence (MPRAGE) (TE = 3.44 ms, TR = 2530 ms, isotropic voxel size 1mm, flip angle = 7). (ii) Resting-state fMRI scans using a gradient spin echo sequence (TE = 23 milliseconds, TR = 1650 milliseconds, 96 × 96 acquisition matrix, flip angle of 84). The acquisition lasted 6 minutes and 54 seconds, and 250 temporal scan volumes were obtained. A total of 25 slices, each 5 mm thick, were acquired for each volume. During acquisition, the subject was asked to lie down still with eyes closed. (iii) Task-based fMRI scans were acquired using similar parameters with the subject instructed to perform finger-tapping task on presentation of a visual stimulus on screen and lie down still in absence of the stimulus. A total of 110 volumes were acquired for this sequence. Imaging data were acquired as part of a NIH sponsored study (R01-DA-034977). The individual had given written consent as per IRB approved study protocol.
Standard preprocessing steps were applied to the data. The first 10 volumes were deleted to remove initial saturation effects [27]. Volumes were motion corrected, slice time corrected and the brain was extracted. To remove effects of signal drifts, linear detrending was performed by high pass filtering (0.01 Hz). Subsequently, the slices were registered to the standard MNI152 template (FSL, [28]). In addition, the ventricle mask based on the standard MNI152 template was used to eliminate time-series in the corresponding regions. All these steps were carried out using FMRI Expert Analysis Tool (FEAT) software which is a part of the FSL [28]. Finally, the time-series were normalized to zero mean and unit standard deviation to focus on signal dynamics rather than amplitude [18]. The motor task sequence was further processed using the standard (FEAT) boxcar design to test where the BOLD signal correlated with the stimulation. The z-statistic images obtained were thresholded at z > 4 with a corrected cluster significance threshold of p < 0.01. This results in a spatial map of the regions corresponding to the visual and motor cortex for each individual. The second spatial map was obtained after performing Independent Component Analysis (ICA) on the resting-state fMRI data. ICA was performed using FSL’s Multivariate Exploratory Linear Optimized Decomposition into Independent Components (MELODIC) toolbox [29]. The dimensionality of ICA components to be estimated was selected to be 32. We focused on specific resting-state networks (sensorimotor network/visual processing network) chosen through visual inspection based on previously defined maps [30] to validate results obtained from our approach.
3. Methods
3.1. Establishing multivariate connectivity scores between series
3.1.1. Granger causality analysis
The principle of Granger causality (GC) is based on the concept of precedence and predictability, where the improvement in prediction quality of a time-series in the presence of the past of another time-series is evaluated and quantified, revealing the directed influence between the two series [31]. As lsGC is an extension of traditional multivariate GC (mvGC), we briefly review the basic concepts of GC analysis.
Consider a system with N time-series, each with T temporal samples. Let the time-series ensemble X ∈ ℝN×T be X = (x1, x2,…, xN)T, where xn ∈ ℝT, n ∈ {1, 2,, N}, xn = (xn(1), xn(2), …, xn(T)) The time-series ensemble X can also be represented as X = (x(1), x(2), …, x(T)), where x(t) ∈ ℝ N×1, t ∈ {1, 2, …, T}, x(t) = (x1(t), x2(t), x3(t), …, xN (t))T.
We use multivariate vector auto-regression which is the most common prediction scheme used in GC analysis [32, 33].
| (2) |
Here, the matrices Aj are the model parameters obtained by minimizing the mean squared errors in the estimate of X, where Aj is an N × N matrix with j ∈ 1, 2, …, p, and p is the lag order. We define,
| (3) |
| (4) |
Granger causality analysis establishes a causal influence score between time-series xr influencing xs on the premise that, if the predictability of time-series xs improves in the presence of another time-series xr, then xr would have some influence on the predicted time-series xs. As we are looking at the full ensemble of time-series and establishing GC in a multivariate sense, we obtain the influence of xr on xs by quantifying the reduction in prediction quality of xs in the absence of time-series xr. Equations (2) and (3) obtain the prediction of all series when the full ensemble of time-series is used. Next, we obtain the prediction error when series xr is removed from the ensemble X:
| (5) |
Here, the are the values of the ensemble at time t without using the information of time-series xr(t). If the prediction quality of xs is higher when xr is used (2) rather that when it is not used (5) for predicting time-series xs, then it is said that xr Granger causes xs. The Granger Causality Index (GCI)
| (6) |
quantifies the influence of xr on xs, is the error in predicting xs when all the time-series are used, whereas is the error in predicting xs, when all the time-series other than xr are used. The quality of the prediction is determined by the variance σ of the error in the prediction. If the variance of the error in predicting xs is lower when xr is used, i.e. , then xr Granger causes xs.
3.1.2. Large-scale Granger causality analysis
We encounter an ill-posed, under-determined problem if we try to use the above approach to estimate influence scores for a high-dimensional system, like the brain, where the number N of time-series is high compared to the number T of temporal samples of these variables (N > T). In addition, the full ensemble of time-series N has redundant information, whose elimination does not result in substantial loss in quality of the analysis. To overcome these problems, we use a modification of the multivariate GC approach, as proposed by [10, 11, 12, 13], by first reducing the dimensionality of the space using Principal Component Analysis (PCA), thus obtaining the predictions in this low dimension, which are then projected back to the high-dimensional space. This method hence reveals a measure of Granger causality in a multivariate sense between every time-series pair in the system.
The large-scale Granger causality approach comprises of estimating a time point in the future, using multivariate vector auto-regressive (MVAR) modelling, in a dimension-reduced space defined by the first c high-variance principal components of the time-series. These predictions are then transformed back to the original ensemble space using the respective inverse PCA transformation. Let Z be the dimension-reduced system, when the whole ensemble Z is used, and the reduced system, when xr is removed from the ensemble. We quantify the change in prediction quality of a time-series xs, when Z is used for its prediction as compared to its prediction quality when is used. This quantity is a measure of the lsGC indices in a large-scale multivariate sense. We first perform PCA on all the time-series in X and retain the first c orthogonal components with the highest variance (c < T), which accounts for most of the variability in the data.
| (7) |
The matrix W is the c×N transformation matrix, which transforms the original N-dimensional time-series ensemble X ∈ ℝN×T to the dimension-reduced time-series ensemble Z ∈ ℝc×T. Z is an ensemble of the first c high variance components of X. We then perform the analysis in a similar manner as described in the previous section. MVAR modelling is performed on the dimension-reduced system:
| (8) |
| (9) |
Here, is the estimate of z(t) obtained after MVAR modelling, and r(t) is the estimation error. We then obtain the errors, i.e. residuals in the original space by inverting the PCA mapping:
| (10) |
Next, we obtain the prediction error , where the information of time-series xr is omitted. To do so, we calculate from and , where is obtained by eliminating the row in X that corresponds to xr, and is obtained by eliminating the column in W which corresponds to the transformation on xr. We then obtain in analogy to (9) and compute in analogy to (10). Thus, we obtain the lsGC indices according to equation (6).
The measure is stored in the affinity matrix S at position (S)s,r, where S is an N × N matrix of lsGC indices.
3.1.3. Selecting an appropriate number of principal components and lag order
An important preliminary step in lsGC analysis is the selection of the lag order p and the number c of principal components retained. We provide a few guidelines to selecting these parameters.
Select a suitable range of c for the problem: The explained variance (EV) of each principal component (PC) is indicative of the amount of information in the system retained by that component. The first PC contains the most information, i.e. it explains a large fraction of the variance in the system, while the last few components have a very low explained variance (corresponding mainly to noise in the system). Hence, for a system with N ≥ T, a plot of the amount of variance explained for increasing number of retained components c, has a steep increase, followed by a slow saturation to a complete representation of the system at 100% explained variance. The region at which this change to slow saturation occur is known as the knee of the curve. A good choice of c is towards the lower end of this knee (Figure 6).
Figure 6.
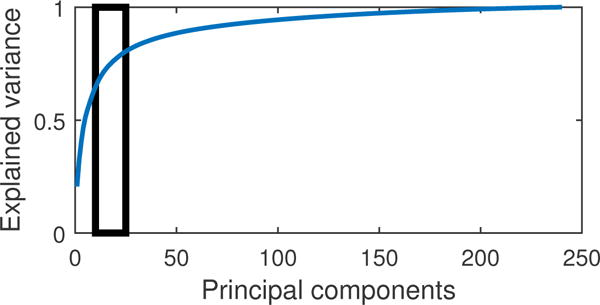
Plot showing the fraction of variance explained with increasing number of principal components c for the empirical fMRI data. We obsereve that the lower end of the knee is approaximately within 10 < c < 25. This range is useful to narrow down on an optimal order and c by minimizing the BIC.
To find the best order p: We determine an optimal order for the MVAR model by minimizing the Bayesian Information Criterion (BIC, [34]) over the range of c obtained above. The BIC can help narrow down the optimal c from the above range for the optimal order. We use the formula from the toolbox [35] and adapt it for lsGC as follows:
| (11) |
Here, Σ is the covariance matrix of the innovations obtained from MVAR modeling. Such an analysis can be subjective, as one may obtain a couple of orders and components at which the BIC is low. However, such guidelines are useful to follow as it limits the parameter space to be studied and ensures that equation 8 will not result in an underdetermined problem. Nevertheless, it is good practice to check if the inequality [13] is satisfied to verify that the parameters selected do not encounter such a problem. In GC analysis, BIC and methods similar to it have been commonly applied [36, 37, 38, 39], however, the Akaike’s Criterion [40] has also been used for order estimation [41, 42] and can be applied in lsGC analysis as well.
3.2. Modular structure recovery: the Louvain method
The affinity matrix S contains some information regarding the underlying dynamics and hence, the underlying modular community structure. This structure can be extracted using non-metric clustering approaches, such as the Louvain method [43, 44]. This community detection algorithm partitions the network into strongly connected modules, where nodes within a module are densely connected as compared to weakly connected nodes between modules. This approach does not require the pre-specification of number of modules in the network and obtains the best partition by optimizing the modularity [44] of the network. The modularity is a measure of the strength of the intra-module links as compared to the inter-modules links and is given by
| (12) |
where S is the affinity matrix obtained using lsGC, ki is the in-degree of node i given by Σi,j[Sij], and . The symbol δ is the Kronecker delta function, which is 0 when Ci ≠ Cj and 1 when Ci = Cj, where Ci is the community that node i belongs to. Exact modularity optimization is a computationally expensive problem. We use the method presented by [44] to approximately optimize the modularity and reveal closely interacting nodes as modules for large networks in short computation time. This optimization method results in a hierarchical community structure. The affinity matrix S contains N2 components, where N2 can reach orders of a million for systems such as the brain. Most of the connections in such a large network graph are weak. These dense network graphs need to be sparsened to avoid overestimation of module sizes by detecting weak patterns [45, 46] with the Louvain method. To counter this problem, we consider only the mutual k-nearest neighbors of the graph [47]. The size of the graph, the amount of noise in the system and the type of communities that one wishes to recover, weak or strong, determine the number of nearest neighbors used. Mutual nearest neighbors has been effective in other non-metric clustering approaches, such as spectral clustering [48] and agglomerative clustering [45]. By sparsening the graph using mutual nearest neighbors, we allow only stronger patterns to be detected hence producing multiple small clusters.
3.3. Model evaluation
With the simulations, we can perform a two-step evaluation since we have the ground truth of both, a) the existence of a connection between nodes b) the subnetwork a node belongs to, i.e. the modular structure of the full network. However, with empirical fMRI, we do not have a ground truth of voxel-level (nodal) connections. Nevertheless, we can still extract connections represented in a matrix of interaction of size N × N where N represents the number of nodes in empirical fMRI of order 103. From this matrix of interactions, we extract subnetworks from the empirical fMRI and the simulations. This gives us functionally connected subnetworks in resting-state fMRI. To test the validity of the subnetworks derived from the simulated data, we compare it to the inherent modular structure of the network. For the empirical fMRI data, the recovered modular structure is compared to spatial maps of the motor and visual cortex obtained with Independent Component Analysis (ICA) of resting-state data, and the motor and visual cortices obtained using a visuo-motor task sequence. Although the resting-state data and the task stimulation have inherently different underlying dynamics, there is a good correspondence of the functionally interacting subnetworks both at rest and under the presence of a stimuli [49]. As such, we were interested to see if the subnetworks detected from the lsGC connectivity matrix estimated functional subnetworks that correspond well to networks detected from both, a task sequence and from resting-state data, and agreed with the findings in [49].
To evaluate the effectiveness of lsGC in recovering network structure for the realistic simulated fMRI time-series data, we use the Area Under the Curve (AUC) in a Receiver Operating Characteristic (ROC) analysis. This curve is obtained by thresholding the recovered affinity matrix S at different values and comparing with the known ground truth of nodal connections. Additionally, we evaluate the subnetworks recovered with clustering using the Adjusted Rand Index (ARI) [50]. ARI ∈ [−1, 1], where 0 represents a random clustering result, 1 represents perfect clustering results and −1 represents no agreement between any pair of nodes. Furthermore, the accuracy of clustering, the Dice coefficient (DC) [51] and the average Dice coefficient (DC-II) are used to measure cluster quality for empirical fMRI data. The Dice coefficient takes a value of 0, when there is no agreement between the recovered clusters and spatial maps, and takes a value of 1, when the clusters agree perfectly with the spatial maps. Let SM be the spatial map and X be the clustering result obtained from the resting-state fMRI sequence. Then, we define:
| (13) |
| (14) |
| (15) |
| (16) |
Here, X′ and SM′ are the complements of sets X and SM. DC(X) is the Dice coefficient of the resulting clusters. DC(X′) is the Dice coefficient of the rest of brain that has been clustered as belonging to functional networks other than motor or visual cortex. DC-II(X) is the average of the two Dice coefficients.
4. Results
4.1. Simulated fMRI
4.1.1. Connectivity analysis
To understand the effect length T of time-series has on accurately estimating information flow between nodes in the network as lsGC indices, we use the simulated network described earlier and study how AUC changes as a function of T and c for two different TRs. The network connectivity graphs are represented as network matrices, as shown in Figure 1b. We adopt the 50 networks from [14], referred to as sim 4, but recreate the simulations for TR = 1.5 s and TR = 3 s and session duration of 10 minutes and 20 minutes respectively. Figure 2 shows the mean result of using mvGC and lsGC for different lengths of the simulated fMRI signal over 50 trials of the simulation. Figure 2a and 2b correspond to TR = 1.5 s and TR = 3 s. Note that a session duration of 10 minutes corresponds to T1.5 = 400 and T3 = 200. In many studies, resting-state fMRI data duration lasts for less than 10 minutes, which was shown to result in stable measures of functional connectivity [52]. Figure 3 is a representation of Figure 2a as a heat map, which aids in investigating the interplay between time-series length and dimensionality of input (c for lsGC and N for mvGC). The MVAR analysis was performed at model order p = 2 which was the optimal order as determined by BIC.
Figure 2.
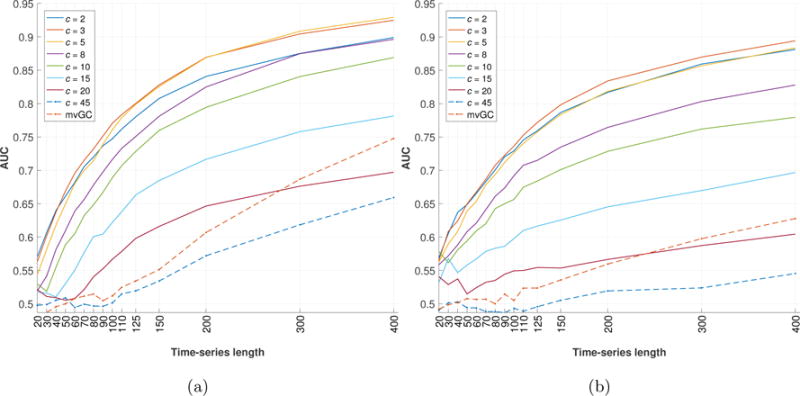
Plots showing the mean Area Under the Curve (AUC) for Reciever Operating Characterstics (ROC) analysis obtained when comparing the presence or absence of network connections in the recovered network structure with the known network ground truth depicted in Figure 1b. Note that the figures do not show individual ROC curves, but summarize the results of extensive ROC analysis using a wide range of parameter settings regarding number c of retained components and T of different time-series lengths. Figure a) is the result for simulations at TR = 1.5 s and b) is the result for simulations at TR = 3 s. For both TR settings, similar trends in AUC can be observed, where increasing T increases detection performance. Furthermore, increasing c increases detection performance initially, after which performance decreases. This is because the amount of information gained with higher c is small compared to the loss in performance due to increasing number of parameters to be estimated. Note that the scan duration is twice as much for simulations at TR = 3 s as compared with TR = 1.5 s.
Figure 3.
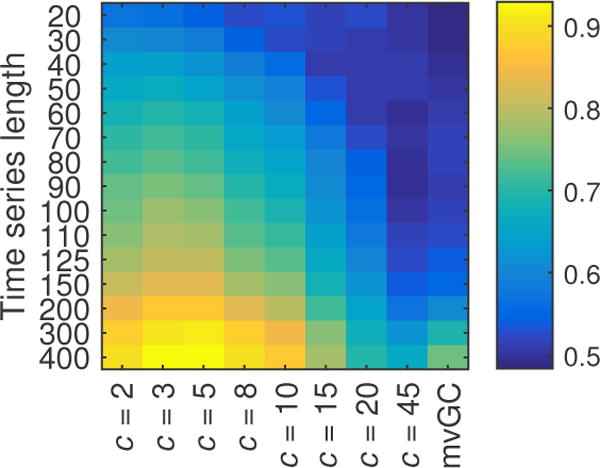
Heat map of the plot in Figure 2a. For T1.5 = 400, best results are at c = 3 and 5. However, at lower lengths, performance quality decreases with increasing number c of used principal components.
4.1.2. Clustering results
Connectivity analysis with lsGC and mvGC results in a set of network graphs for each of the 50 trials of the simulation whose ground truth network structure is shown in Figure 1. With clustering, we attempt to recover the modular structure of the network. Every node belongs to one module and the modular structure ground truth is shown in Figure 4. Note that the ground truth represents the clusters that each time-series (node) belongs to. It is not the network matrix as shown in Figure 1b, which contains the information regarding the influence of one time-series on another.
Figure 4.
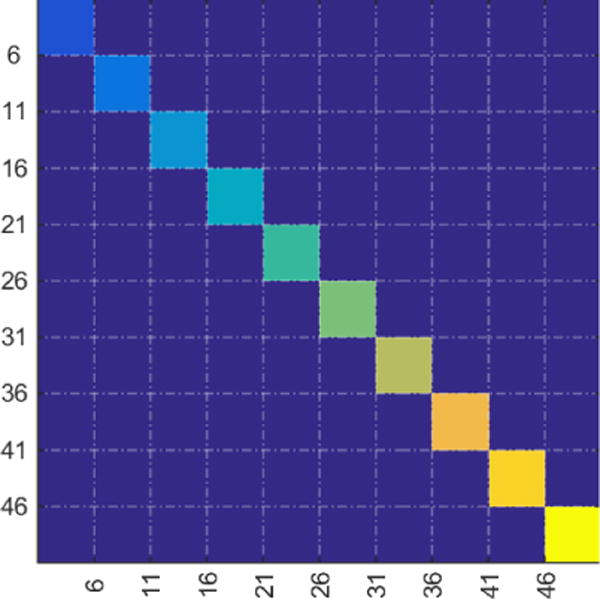
Module ground truth, i.e. the perfect cluster assignment matrix with ten modules containing 5 nodes each. Each unique color identifies a module where each module contains 5 nodes as indicated by the dotted lines.
We decompose the connectivity graph into modules using the Louvain method [44]. Results on clustering performed on the averaged connectivity graph are summarized in Figure 5. Figure 5 illustrates the effect of time-series length and number of lsGC principal components used on network recovery of the simulated time-series at TR = 1.5 s. Network recovery results for TR = 3 s follows a very similar trend as simulations at TR = 1.5 s. As can be expected from Figure 2, simulations generated with TR = 1.5 s yield better clustering results than those generated at TR = 3 s. In Figure 5, the numbers in blue represent the adjusted Rand index (ARI) which quantifies the degree of agreement between the module ground truth and the recovered modular structure.
Figure 5.

Cluster assignment matrices obtained for the simulated network model from Figure 1 at TR = 1.5 s using modularity-based community detection by the Louvain method. The figure shows how the clustering results are influenced by the time series length T and the number c of used principal components. Each ground truth node is represented as a specific color in the 2D plot, where the color is defined by the module it belongs to as seen in the ground truth, Figure 4. Incorrect placement of a node into a cluster results in an off-diagonal pattern. These structures are obtained after reorganizing the ground truth matrix in Figure 4 such that rows and columns belonging to a cluster assignment obtained by the Louvain method are grouped together. As the time-series length increases, the Adjusted Rand Index (ARI) improves as indicated below each plot.
Figure 5 is a visual aid to give an intuitive idea of what the recovered network looks like for the corresponding ARI. It is obtained in the following manner: From the averaged connectivity graph, we obtain the cluster labels using the Louvain method and rearrange the ground truth according to the cluster labels obtained. If all the time-series were assigned to the correct cluster, a block structure would exist around the diagonal. False assignment would result in structures away from the diagonal and a low ARI. The dotted vertical and horizontal lines show the cluster separation.
The best results are obtained for 3 < c < 10. Also, observe that as the length of the time-series increases, the best network recovery results are observed at a higher number c of principal components used for lsGC.
4.2. Resting-state fMRI
We carry out the analysis of the resting-state fMRI data in a similar manner. The preprocessed and atlas-registered fMRI data had over 150,000 voxels in a volume at one time instance. To demonstrate the usability of lsGC on fMRI data, we coarsen the spatial resolution of the imaging data by averaging the signal intensities in a cube of 3 × 3 × 3 adjacent voxels into a new, compound voxel, thus reducing the number of voxels to ~7000. Using all of the (~150, 000) voxels was not feasible because of computer memory and storage constraints. This reduced dataset, although not as large as the original, is still enough to demonstrate the effectiveness of lsGC for obtaining a measure of directed information flow and recover networks in resting-state fMRI.
To apply lsGC effectively, we first need to obtain a permissible range of values at which the order and the number of principal components will yield meaningful results. To do so, we apply the procedure described in section 3.1.3. First, we study the plot of the fraction of variance explained with increasing number of principal components Figure 6. A suitable range between 10 < c < 25 was obtained. Using this range, the optimal order with BIC was found to be 5, which is in line with the parameter settings in [13] and the minimum BIC at this order corresponds to c = 20. Many Granger causality studies on fMRI data have shown that a small lag order is good enough to capture relevant information with GC [16, 9, 38, 39]. The model order of local field potentials, capturing neuronal activity initially increases as a consequence of convolution with an HRF. However, heavy downsampling on account of the TR reduces the order close to 1 [53]
Figure 7 shows the result of performing non-metric clustering on the sparsened (mutual k-nearest neighbor approach, k = 5% of connections) affinity matrix obtained using lsGC with p = 5 in line with parameter settings in [13] and c = 20. We also evaluated the results for different number of components as seen in Table 1 and Table 2 corresponding to quantitive evaluation with the task sequence and the ICA spatial maps respectively. These results support our choice of c, although c = 15 produces better results than c = 20 by a very small margin.
Figure 7.
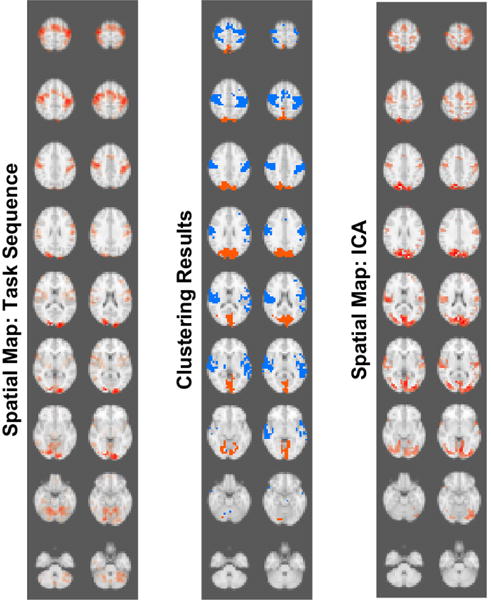
Visual comparison between two recovered clusters obtained using lsGC followed by non-metric clustering. We note the similarities between clustering results (middle panel) and the spatial maps provided by visual motor task stimulation (left panel) and independent component analysis (ICA, right panel).
Table 1.
Clustering results on fMRI data for different numbers of retained principal components compared with visual motor task sequence activation.
| Number of Principal components | ||||||
|---|---|---|---|---|---|---|
|
| ||||||
| Similarity measures | 10 | 15 | 20 | 25 | 30 | 35 |
| Accuracy | 0.71 | 0.76 | 0.76 | 0.74 | 0.73 | 0.73 |
| DC | 0.42 | 0.46 | 0.43 | 0.33 | 0.34 | 0.41 |
| DC-II | 0.61 | 0.65 | 0.64 | 0.58 | 0.59 | 0.62 |
Table 2.
Clustering results on fMRI data for different numbers of retained principal components compared with ICA based resting-state networks.
| Number of Principal components | ||||||
|---|---|---|---|---|---|---|
|
| ||||||
| Similarity measures | 10 | 15 | 20 | 25 | 30 | 35 |
| Accuracy | 0.81 | 0.86 | 0.86 | 0.83 | 0.85 | 0.82 |
| DC | 0.54 | 0.61 | 0.59 | 0.45 | 0.54 | 0.51 |
| DC-II | 0.71 | 0.765 | 0.754 | 0.676 | 0.726 | 0.697 |
Figure 8 shows the same result as a surface rendition. Visually comparing our result with the two spatial maps (Figure 7), we see that lsGC is able to recover functional networks that closely resemble the visual cortex and motor cortex. As the task sequence consisted of the subject tapping his/her fingers when presented with a checkerboard stimulus, the motor and visual cortices in the brain are stimulated, as seen in the task sequence spatial map. These two functionally connected regions are detected as two different modules in the resting-state fMRI data visualized as orange and blue clusters in Figure 7 (orange and blue clusters).
Figure 8.
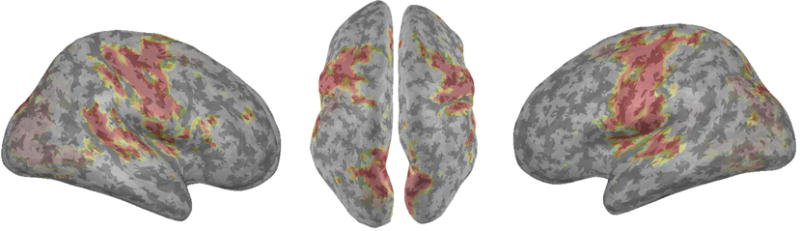
Surface rendering of functional segmentation results for the motor/visual cortex retrieved from resting-state fMRI data using lsGCI in conjunction with non-metric clustering for community detection using the Louvain method. The results of network recovery overlaid onto a standard brain atlas, MN152, are shown here. We see our approach recovers the cortical regions of the bilateral motor cortex (primary motor, premotor and also somatosensory regions encompassing Brodmann Areas 3 and 4 primarily) and also the regions of the occipital (primary and secondary visual) cortex, Brodmann Area 17 and 18. Both regions correspond to different modules in the clustering results and are combined here only for visual representation.
The recovery of the functionally connected regions is clearly demonstrated in Figures 7 and 8. We notice accurate representation of the bilateral motor cortex regions recovered by the clustering approach, identifying both the pre- and post-central gyrus and extending to portions of the frontal superior gyrus. In the central region, the cluster marginally covers paracentral lobules. Functionally, the detected regions cover the primary and pre-motor cortex and extend to the supplementary motor areas and the somatosensory cortex. Brodmann Areas (1, 3 and 4) are captured primarily in this cluster. Posteriorly, the cluster results cover the visual/occipital cortex and pole. Portions of the cuneal cortex and inter-calcarine cortex are also seen. This comprises of Brodmann Area 17 and 18, which cover the primary and secondary visual cortex.
Tables 1 and 2 evaluate the effect changing the number of principal components has on cluster recovery performance, compared with spatial maps defined by the task sequence and resting-state ICA, respectively. It is observed that the recoverability of the networks follows a similar trend as the simulated model does, where the clustering ability initially increases with an increasing number c of principal components followed by a subsequent decrease.
Figure 9a is the sparsened affinity matrix, Figure 9b is the corresponding affinity matrix, where rows and columns are rearranged such that each block (marked by dotted white lines) consists of nodes that were grouped together by the Louvain method. From Figure 9b we see a concentration of strong interactions along the diagonal and the formation of a block-diagonal structure, which indicates that the nodes of the modules detected strongly interact amongst themselves.
Figure 9.
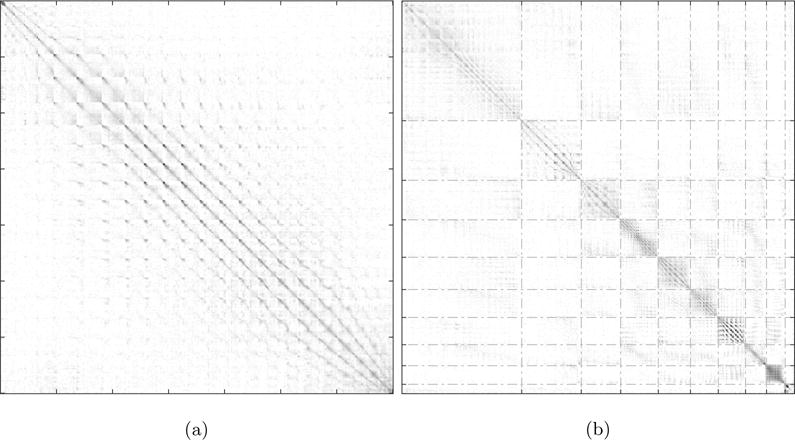
a) Sparsened affinity matrix obtained using c = 20 and p = 5 where each of the ~49 million matrix elements represents the lsGC index for every pair of interacting time-series. b) Matrix obtained as the result of rearranging matrix shown in a) according to cluster assignment obtained using the Louvain method. The lines correspond to the recovered modules. Note that prior to clustering no block-diagonal structure is seen. However, after clustering and corresponding reordering of rows and columns, strongly interacting voxels are grouped together and such a structure emerges. This image has been enhanced to improve visibility using spatial smoothening and applying a gamma correction of 0.5
5. Discussion
We explore large-scale Granger causality (lsGC) to establish a multivariate measure of information flow for every pair of time-series in both simulated and empirical resting-state fMRI time-series, where the computed lsGC indices represent a measure of interaction between time-series summarized as an affinity matrix. Subsequently, we recover the underlying modular structure of closely interacting nodes in the network using non-metric clustering. Our results suggest that lsGC recovers information relevant to extracting functionally connected networks. Large-scale GC analyzes information flow in a large number of time-series recorded at few temporal samples (N > T) and distinguishes direct from indirect connections in the presence of confounding variables using a multivariate approach. A purely multivariate GC (mvGC) approach using all the voxels in the brain presents an ill-posed, underdetermined problem, because the number of temporal samples is sub stantially lower than the number of time-series given the temporal and spatial resolution of current functional data acquisition.
Previous work by [10, 13] demonstrated the initial applicability of lsGC on a synthetic model and resting-state fMRI data [13]. However, the synthetic model used in these previous publications was linear and simplistic, because the time-series were generated by a linear MVAR process, which neither took into account the nonlinear hemodynamic response function (HRF) on the neural signal nor the repetition time TR. In contrast to the cited previous studies, this contribution addresses the need to quantitatively evaluate the performance of lsGC in more realistic simulations accounting for both the HRF and TR, as proposed by [14] and used extensively in the current literature [54, 55, 56], as well as provide a framework to select an optimal set of parameters for lsGC analysis. We thoroughly investigate the effects of TR and session duration on the performance of lsGC with respect to the number of retained principal components. Our results (Figures 2 and 3) quantitatively evaluate the effectiveness of lsGC in accurately identifying the presence of time-series interactions in complex networks, which provides the basis for recovering inherent modular network structure (Figure 5) even for high-dimensional situations, where the number N of time-series exceeds the number T of temporal samples (N > T). Furthermore, when applying lsGC to empirical resting-state fMRI data, we quantitatively show that recovered motor and visual cortices are in close agreement to the spatial maps, namely networks recovered from (i) visuo-motor fMRI stimulation task sequence brain activation and from (ii) independent component analysis (ICA) of resting-state fMRI data. In contrast to previous work on lsGC, we introduce a quantitative method validation scheme for both realistic computer simulations and empirical resting-state fMRI data. Furthermore, we provide a set of guidelines that outline a procedure to select the optimal set of parameters for lsGC analysis.
Effect of number of Principal Components used on connectivity analysis and network recovery on the simulated fMRI data
Large-scale GC performs GC analysis in a dimension-reduced space from which we obtain the lsGC indices after transforming the lower dimension to the original high-dimensional ensemble space. We quantitatively evaluate the performance of lsGC by first analyzing the results on simulated fMRI time-series created using the NetSim software [14], followed by analyzing fMRI data. From the AUC values in Figure 2, we can infer that lsGC is able to detect most of the connections correctly for the simulated time-series. For a given time-series length T, an increasing number c of retained principal components results in an increase of the observed AUC followed by a drop in AUC as c is increased further. A similar trend is observed for the recovered modules quantified by the Adjusted Rand Index (ARI, Figure 5). As c is increased, the initial rise in performance can be accounted to better representation of the N time-series resulting in improved estimation of connectivity. Subsequently, performance again drops with increasing c because of the increased number of parameters to be estimated in MVAR modelling while not providing a substantial increase in explained variance. This observation is complementary to the procedure described in section 3.1.3. The value of c close to the knee of the curve corresponds to the peak in lsGC performance. As c is increased beyond the first few high variance components, the additional components do not contribute relevant information for connectivity estimation. It should also be noted that for a given T, the maximum number of principal components that can be used to ensure that the problem is not underdetermined is [13], where p is the order used in the MVAR model.
Effect of TR and time-series length on affinity matrices and modular network recovery
For the simulated data, we also study the effects of repetition time (TR) and time-series length T. As seen in Figure 2, increasing T improves the performance of lsGC, irrespective of number c of retained principal components, as well as of mvGC. Increasing T allows for better estimation of MVAR model parameters, which in turn improves the estimation of network connections. Note that, for a given T, if the inequality T ≥ p(c + 1) [13] is not satisfied as a consequence of large c, AUC drops to around 0.5 (random connections). It is observed from Figure 2 that for the same time-series length T, lsGC performs better at estimating the network connections for a lower TR. For a constant session duration length, say 10 mins, which corresponds to T1.5 = 400 and T3 = 200, the best AUC was 0.93 and 0.83, respectively. This illustrates the effect of TR on the lsGC indices that are obtained. Hence, the best results can be obtained by lowering TR and increasing the session duration. However, with current state of the art fMRI systems, we cannot reduce TR to much below ~1.5 s, if whole brain coverage is desired. Our results suggest that the length of the scan should also be increased to achieve good performance if TR of the scanning protocol is large.
Work using linear, multivariate Granger causality have demonstrated the robustness of GC [53, 57, 58] on fMRI data. In the recent study [53] it was shown that Granger causality is invariant to HRF but not downsampling. As revealed in our study, large-scale GC performs well on the simulated fMRI data generated with a varying HRF function (standard deviation of ± 0.5 s). However, we observe a dependence of the recovered network with down-sampling as a consequence of TR. As seen from our results, decrease in TR of the simulated fMRI data improves the ability of lsGC to recover network structure.This is line with prior research [53], and confirms that lsGC behave similar to conventional GC.
For the modular network recovery, Figure 5, a trend similar to that followed by Figure 3 was observed, where the best recovery was for affinity matrices obtained from simulations with more temporal samples. Observe that at very low time-series length T = 40, for c = 2 the network module detection is very good with an ARI = 0.63, while results of mvGC are poor. This demonstrates that, even though the length T of the time-series is less than the number N of nodes in the network, i.e. N > T, which is generally the situation with fMRI data, lsGC is able to capture useful connections, which facilitates a good module recovery. In summary, our results suggest that lsGC captures enough relevant information for the modular structure to be reconstructed even for short time-series.
Network recovery: Resting-state fMRI analysis
Establishing that lsGC can work on realistic fMRI simulations which accounts for the hemodynamic response function and downsampling on account of TR was crucial to demonstrate its applicability on real fMRI data. Since with fMRI data we do not have a ground truth of voxel-wise connectivity, we evaluate the ability of lsGC to establish connectivity by investigating the functional networks recovered using non-metric clustering from lsGC connectivity profiles. The high values of accuracy and Dice coefficients for the recovered motor and visual cortices indicate that lsGC captures useful information about interactions at a voxel-level resolution scale in the human brain. The successful recovery of motor and visual cortices suggests the existence of local dynamic time-series interactions corresponding to these regions even in the resting state as shown in other studies [1, 29]. It should be noted here that, although we are computing and displaying the results of our study for both the motor and visual cortex simultaneously, these regions are segregated into different modules after clustering. Another interesting observation is that there is a slightly stronger agreement of lsGC recovered functional networks with the ICA spatial maps as compared to the spatial maps derived from the task sequence. This may be attributed to the fact that resting state activity is physiologically different from the activity during a task sequence stimulation of the corresponding regions. However, we choose to compare the resulting functional network structure with both, ICA spatial maps and motor visual task sequence spatial maps since studies have shown that there is strong correspondence between functional networks extracted at rest and during task activation [49]. In summary, our method is capable of extracting intrinsic information related to the resting state activity in the human brain. Besides the recovery of motor and visual regions, we aim to extend this analysis in future work to a full functional segmentation of the resting human brain, where the recovery of other functional regions will be studied as well.
In this analysis of empirical resting-state fMRI we showed that lsGC has the ability to work in a multivariate sense for systems with N > T and establish voxel-wise connectivity. Furthermore, it can also be used for systems that have N ~ T or N < T, since it provides flexibility in terms of lag order selection, while multivariate GC analyzing systems may not be able to use the optimal order since , where for multivariate GC, c = N.
6. Conclusion
In conclusion, this paper reveals that 1) Large-scale Granger causality (lsGC) analysis can capture the connectivity structure in complex networks, as evident from quantitative ROC analysis of realistic simulated fMRI time-series data. 2) Both shorter TR and longer scan duration improve lsGC connectivity estimation. If one of the two is the limiting factor in the study protocol, the other can be varied to improve brain connectivity analysis results. 3) The network structure captured by lsGC can reveal useful information on functionally connected modules in both simulated time-series and empirical resting-state fMRI data, as confirmed by both visual and quantitative analysis with different types of available spatial map comparisons. By analyzing realistically simulated fMRI time-series, we were able to show that lsGC can capture network connectivity patterns in a multivariate sense for situations, even when the number N of observed time-series significantly exceeds the number T of temporal samples. Functional MRI is a typical example, where such an N > T situation occurs naturally. Finally, we were able to demonstrate that lsGC can successfully recover functional brain networks at a voxel resolution scale, such as extracting visual and motor cortices from empirical resting state fMRI data of the human brain.
With this analysis, we hope to pave the path for large scale Granger causality to become more useable for investigators looking for a multivariate approach of establishing connectivity. To this end, we provide guidelines for selecting optimal lsGC parameters in this work and also make publically available the large scale Granger causality MATLAB software. LsGC can be used for other problems investigating functional connectivity as it describes the data in a more thorough manner by accounting for indirect connections in the presence of confounds, since it is multivariate, and establishes a measure of directional information as it adopts concepts from Granger causality. It can be applied in place of multivariate GC for problems that are ill-posed, underdetermined or even for problems where a more flexible lag order selection is required. In addition, lsGC can also be used to study differences in interaction patterns between healthy subjects and subjects with disorders affecting functional connectivity by investigating connection changes amongst different regions in the brain.
Highlights.
-
-
Resting-state connectivity with Large-scale Granger causality (lsGC) is studied
-
-
LsGC, a data-driven multivariate approach, estimates interactions in large systems
-
-
Effectiveness of lsGC tested with realistic simulated fMRI and empirical fMRI data
-
-
Network structure recovered in both datasets
-
-
Modular functional subnetworks corresponding to motor and visual cortices recovered
Acknowledgments
This work was funded by the National Institutes of Health (NIH) Award R01-DA-034977. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of Health. This work was conducted as a Practice Quality Improvement (PQI) project related to American Board of Radiology (ABR) Maintenance of Certificate (MOC) for Prof. Dr. Axel Wismüller. The authors would like to thank Dr. Stephen Smith and Dr. Mark Woolrich for providing us the NetSim simulation software [14]. The authors would also like to thank Prof. Dr. Herbert Witte of Bernstein Group from Computational Neuroscience Jena, Institute of Medical Statistics, Computer Science and Documentation, Jena University Hospital, Friedrich Schiller University, Jena, Germany, Dr. Oliver Lange and Prof. Dr. Maximilian F. Reiser of the Institute of Clinical Radiology, Ludwig Maximilian University, Munich, Germany for their support.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Biswal B, Yetkin F Zerrin, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magnetic resonance in medicine. 1995;34(4):537–541. doi: 10.1002/mrm.1910340409. URL http://maki.bme.ntu.edu.tw/{~}fhlin/courses/course{_}neuroimaging{_}fall10/materials/functional{_}connectivity{_}resting{_}motor{_}cortex{_}fmri{_}biswal{_}pdf. [DOI] [PubMed] [Google Scholar]
- 2.Fox MD, Raichle ME. Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat Rev Neurosci. 2007;8(9):700–711. doi: 10.1038/nrn2201. URL http://www.ncbi.nlm.nih.gov/pubmed/17704812. [DOI] [PubMed] [Google Scholar]
- 3.Lizier JT, Heinzle J, Horstmann A, Haynes JD, Prokopenko M. Multivariate information-theoretic measures reveal directed information structure and task relevant changes in fMRI connectivity. Journal of Computational Neuroscience. 2011;30(1):85–107. doi: 10.1007/s10827-010-0271-2. [DOI] [PubMed] [Google Scholar]
- 4.Wen X, Yao L, Liu Y, Ding M. Causal Interactions in Attention Networks Predict Behavioral Performance. Journal of Neuroscience. 2012;32(4):1284–1292. doi: 10.1523/JNEUROSCI.2817-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Stephan KE, Friston KJ. Analyzing effective connectivity with fMRI., Wiley interdisciplinary reviews. Cognitive science. 2010;1(3):446–459. doi: 10.1002/wcs.58. URL http://www.ncbi.nlm.nih.gov/pubmed/21209846$\delimiter“026E30F$nhttp://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=PMC3013343$\delimiter”026E30F$nhttp://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=3013343{&}tool=pmcentrez{&}rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dhamala M, Rangarajan G, Ding M. Analyzing information flow in brain networks with nonparametric Granger causality. NeuroImage. 2008;41(2):354–362. doi: 10.1016/j.neuroimage.2008.02.020. arXiv:arXiv:0711.2729v1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Blinowska KJ, Kuś R, Kamiński M. Granger causality and information flow in multivariate processes. Physical review E, Statistical, nonlinear, and soft matter physics. 2004;70(5 Pt 1):050902. doi: 10.1103/PhysRevE.70.050902. URL http://journals.aps.org/pre/abstract/10.1103/PhysRevE.70.050902. [DOI] [PubMed] [Google Scholar]
- 8.Geweke JF. Measures of conditional linear dependence and feedback between time series. Journal of the American Statistical Association. 1984;79(388):907–915. doi: 10.2307/2288723. URL http://www.jstor.org/stable/2288723. [DOI] [Google Scholar]
- 9.Deshpande G, LaConte S, James GA, Peltier S, Hu X. Multivariate granger causality analysis of fMRI data. Human Brain Mapping. 2009;30(4):1361–1373. doi: 10.1002/hbm.20606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wismüller A, Nagarajan MB, Witte H, Pester B, Leistritz L. Pair-wise clustering of large scale Granger causality index matrices for revealing communities. SPIE Medical Imaging. 2014;9038:90381R. doi: 10.1117/12.2044340. URL http://proceedings.spiedigitallibrary.org/proceeding.aspx?doi=10.1117/12.2044340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Schmidt C, Pester B, Nagarajan M, Witte H, Leistritz L, Wismueller A. Impact of multivariate Granger causality analyses with embedded dimension reduction on network modules, Engineering in Medicine and Biology Society (EMBC) 2014 36th Annual International Conference of the IEEE 2014. 2014:2797–2800. doi: 10.1109/EMBC.2014.6944204. [DOI] [PubMed] [Google Scholar]
- 12.Pester B, Leistritz L, Witte H, Wismueller A. Exploring effective connectivity by a granger causality approach with embedded dimension reduction. Biomed Tech. 2013;58(1):24–25. doi: 10.1515/bmt-2013-4172. [DOI] [PubMed] [Google Scholar]
- 13.Schmidt C, Pester B, Schmid-Hertel N, Witte H, Wismüller A, Leistritz L. A multivariate Granger Causality concept towards full brain functional connectivity. PLoS ONE. 11(4) doi: 10.1371/journal.pone.0153105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Smith SM, Miller KL, Salimi-Khorshidi G, Webster M, Beckmann CF, Nichols TE, Ramsey JD, Woolrich MW. Network modelling methods for FMRI. NeuroImage. 2011;54(2):875–891. doi: 10.1016/j.neuroimage.2010.08.063. URL http://dx.doi.org/10.1016/j.neuroimage.2010.08.063. [DOI] [PubMed] [Google Scholar]
- 15.Goebel R, Roebroeck A, Kim DS, Formisano E. Investigating directed cortical interactions in time-resolved fMRI data using vector autoregressive modeling and Granger causality mapping. Magnetic Resonance Imaging. 2003;21(10):1251–1261. doi: 10.1016/j.mri.2003.08.026. [DOI] [PubMed] [Google Scholar]
- 16.Roebroeck A, Formisano E, Goebel R. Mapping directed influence over the brain using Granger causality and fMRI. Neuroimage. 2005;25:230–242. doi: 10.1016/j.neuroimage.2004.11.017. [DOI] [PubMed] [Google Scholar]
- 17.Sporns O, Chialvo DR, Kaiser M, Hilgetag CC. Organization, development and function of complex brain networks. Trends in Cognitive Sciences. 2004;8(9):418–425. doi: 10.1016/j.tics.2004.07.008. [DOI] [PubMed] [Google Scholar]
- 18.Wismüller A, Lange O, Dersch DR, Leinsinger GL, Hahn K, Pütz B, Auer D. Cluster analysis of biomedical image time-series. International Journal of Computer Vision. 2002;46(2):103–128. doi: 10.1023/A:1013550313321. [DOI] [Google Scholar]
- 19.Wismüller A, Meyer-Bäse A, Lange O, Auer D, Reiser MF, Sumners D. Model-free functional MRI analysis based on unsupervised clustering. Journal of Biomedical Informatics. 2004;37(1):10–18. doi: 10.1016/j.jbi.2003.12.002. [DOI] [PubMed] [Google Scholar]
- 20.Wismüller A. International Workshop on Self-Organizing Maps. Springer; 2009. A computational framework for nonlinear dimensionality reduction and clustering; pp. 334–343. [Google Scholar]
- 21.Wismüller A, Abidin AZ, DSouza AM, Nagarajan MB. Advances in Self-Organizing Maps and Learning Vector Quantization. Springer; 2016. Mutual connectivity analysis (mca) for nonlinear functional connectivity network recovery in the human brain using convergent cross-mapping and non-metric clustering; pp. 217–226. [Google Scholar]
- 22.D’Souza AM, Abidin AZ, Nagarajan MB, Wismüller A. Mutual connectivity analysis (MCA) using generalized radial basis function neural networks for nonlinear functional connectivity network recovery in resting-state functional MRI. SPIE Medical Imaging. 2016;9788:97880K. doi: 10.1117/12.2216900. URL http://proceedings.spiedigitallibrary.org/proceeding.aspx?doi=10.1117/12.2216900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Liao TW. Clustering of time series dataa survey. Pattern Recognition. 2005;38:1857–1874. doi: 10.1016/j.patcog.2005.01.025. URL www.elsevier.com/locate/patcog. [DOI] [Google Scholar]
- 24.Margulies DS, Böttger J, Long X, Lv Y, Kelly C, Schäfer A, Goldhahn D, Abbushi A, Milham MP, Lohmann G, Villringer A. Resting developments: A review of fMRI post-processing methodologies for spontaneous brain activity. 2010 doi: 10.1007/s10334-010-0228-5. [DOI] [PubMed] [Google Scholar]
- 25.Friston KJ, Harrison L, Penny W. Dynamic causal modelling. NeuroImage. 2003;19(4):1273–1302. doi: 10.1016/S1053-8119(03)00202-7. [DOI] [PubMed] [Google Scholar]
- 26.Buxton RB, Wong EC, Frank LR. Dynamics of blood flow and oxygenation changes during brain activation: The balloon model. Magnetic Resonance in Medicine. 1998;39(6):855–864. doi: 10.1002/mrm.1910390602. [DOI] [PubMed] [Google Scholar]
- 27.Friston KJ. Functional and effective connectivity in neuroimaging: A synthesis. Human Brain Mapping. 1994;2(1–2):56–78. doi: 10.1002/hbm.460020107. URL http://doi.wiley.com/10.1002/hbm.460020107. [DOI] [Google Scholar]
- 28.Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, et al. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage. 2004;23(Suppl 1):S208–19. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- 29.Beckmann CF, DeLuca M, Devlin JT, Smith SM. Investigations into resting-state connectivity using independent component analysis. Philosophical transactions of the Royal Society of London Series B, Biological sciences. 2005;360(1457):1001–13. doi: 10.1098/rstb.2005.1634. URL http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=1854918{&}tool=pmcentrez{&}rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Beckmann CF, Mackay CE, Filippini N, Smith SM. Group comparison of resting-state FMRI data using multi-subject ICA and dual regression. NeuroImage. 2009;47(Suppl 1):S148. doi: 10.1073/pnas.0811879106. URL http://linkinghub.elsevier.com/retrieve/pii/S1053811909715113. [DOI] [Google Scholar]
- 31.Granger CWJ. Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica. 1969;37(3):424–438. doi: 10.2307/1912791. [DOI] [Google Scholar]
- 32.Ryali S, Supekar K, Chen T, Menon V. Multivariate dynamical systems models for estimating causal interactions in fMRI. NeuroImage. 2011;54(2):807–823. doi: 10.1016/j.neuroimage.2010.09.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Granger CWJ. Testing for causality. A personal viewpoint. Journal of Economic Dynamics and Control. 1980;2(C):329–352. doi: 10.1016/0165-1889(80)90069-X. [DOI] [Google Scholar]
- 34.Schwarz G, et al. Estimating the dimension of a model. The annals of statistics. 1978;6(2):461–464. [Google Scholar]
- 35.Seth AK. A matlab toolbox for granger causal connectivity analysis. Journal of neuroscience methods. 2010;186(2):262–273. doi: 10.1016/j.jneumeth.2009.11.020. [DOI] [PubMed] [Google Scholar]
- 36.Sysoeva MV, Sitnikova E, Sysoev IV, Bezruchko BP, van Luijtelaar G. Application of adaptive nonlinear granger causality: Disclosing network changes before and after absence seizure onset in a genetic rat model. Journal of neuroscience methods. 2014;226:33–41. doi: 10.1016/j.jneumeth.2014.01.028. [DOI] [PubMed] [Google Scholar]
- 37.Kornilov MV, Medvedeva TM, Bezruchko BP, Sysoev IV. Choosing the optimal model parameters for granger causality in application to time series with main timescale. Chaos, Solitons & Fractals. 2016;82:11–21. [Google Scholar]
- 38.Liao W, Marinazzo D, Pan Z, Gong Q, Chen H. Kernel granger causality mapping effective connectivity on fmri data. IEEE transactions on medical imaging. 2009;28(11):1825–1835. doi: 10.1109/TMI.2009.2025126. [DOI] [PubMed] [Google Scholar]
- 39.Marinazzo D, Liao W, Chen H, Stramaglia S. Nonlinear connectivity by granger causality. Neuroimage. 2011;58(2):330–338. doi: 10.1016/j.neuroimage.2010.01.099. [DOI] [PubMed] [Google Scholar]
- 40.Akaike H. A new look at the statistical model identification. IEEE transactions on automatic control. 1974;19(6):716–723. [Google Scholar]
- 41.Hesse W, Möller E, Arnold M, Schack B. The use of time-variant eeg granger causality for inspecting directed interdependencies of neural assemblies. Journal of neuroscience methods. 2003;124(1):27–44. doi: 10.1016/s0165-0270(02)00366-7. [DOI] [PubMed] [Google Scholar]
- 42.Chen Y, Rangarajan G, Feng J, Ding M. Analyzing multiple nonlinear time series with extended granger causality. Physics Letters A. 2004;324(1):26–35. [Google Scholar]
- 43.Clauset A, Newman MEJ, Moore C. Finding community structure in very large networks, Cond-Mat/0408187 70. 2004;066111 doi: 10.1103/PhysRevE.70.066111. arXiv:0408187v2. URL http://arxiv.org/abs/cond-mat/0408187. [DOI] [PubMed] [Google Scholar]
- 44.Blondel VD, Guillaume JL, Lambiotte R, Lefebvre E. Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment. 2008;10008(10):6. doi: 10.1088/1742-5468/2008/10/P10008. arXiv:0803.0476. URL http://arxiv.org/abs/0803.0476. [DOI] [Google Scholar]
- 45.Gowda KC, Krishna G. Agglomerative clustering using the concept of mutual nearest neighbourhood. Pattern Recognition. 1978;10(2):105–112. doi: 10.1016/0031-3203(78)90018-3. [DOI] [Google Scholar]
- 46.Brito MR, Chavez EL, Quiroz AJ, Yukich JE. Connectivity of the mutual k-nearest-neighbor graph in clustering and outlier detection. Statistics & Probability Letters. 1997;35(1):33–42. doi: 10.1016/S0167-7152(96)00213-1. URL http://www.sciencedirect.com/science/article/pii/S0167715296002131. [DOI] [Google Scholar]
- 47.Jarvis RA, Patrick EA. Clustering Using a Similarity Measure Based on Shared Near Neighbors. IEEE Transactions on Computers. 1973;C-22(11):1025–1034. doi: 10.1109/T-C.1973.223640. URL http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?arnumber=1672233. [DOI] [Google Scholar]
- 48.Luxburg UV. A Tutorial on Spectral Clustering A Tutorial on Spectral Clustering. Statistics and Computing. 2006 Mar;17:395–416. doi: 10.1007/s11222-007-9033-z. arXiv:arXiv:0711.0189v1. URL http://www.springerlink.com/index/10.1007/s11222-007-9033-z. [DOI] [Google Scholar]
- 49.Smith SM, Fox PT, Miller KL, Glahn DC, Fox PM, Mackay CE, Filippini N, Watkins KE, Toro R, Laird AR, et al. Correspondence of the brain’s functional architecture during activation and rest. Proceedings of the National Academy of Sciences. 2009;106(31):13040–13045. doi: 10.1073/pnas.0905267106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Yeung KY, Ruzzo WL. Principal component analysis for clustering gene expression data. Bioinformatics. 2001;17(9):763–774. doi: 10.1093/bioinformatics/bti465.Differential. URL http://www.cs.washington. [DOI] [PubMed] [Google Scholar]
- 51.Dice LR. Measures of the Amount of Ecologic Association Between Species Author (s): Lee R. Ecology. 1945;26(3):297–302. Dice Published by : Wiley Stable URL : http://www.jstor.org/stable/1932409 Accessed : 08-04-2016 13 : 33 UTC Your use of the JSTOR archive indicates your acceptance of th. [Google Scholar]
- 52.Van Dijk KRA, Hedden T, Venkataraman A, Evans KC, Lazar SW, Buckner RL. Intrinsic functional connectivity as a tool for human connectomics: theory, properties, and optimization. J Neurophysiol. 2010;103(1):297–321. doi: 10.1152/jn.00783.2009. URL http://www.ncbi.nlm.nih.gov/pubmed/19889849$\delimiter“026E30F$nhttp://jn.physiology.org/content/jn/103/1/297.full.pdf. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Seth AK, Chorley P, Barnett LC. Granger causality analysis of fMRI BOLD signals is invariant to hemodynamic convolution but not downsampling. NeuroImage. 2013;65:540–555. doi: 10.1016/j.neuroimage.2012.09.049. [DOI] [PubMed] [Google Scholar]
- 54.Iyer SP, Shafran I, Grayson D, Gates K, Nigg JT, Fair DA. Inferring functional connectivity in mri using bayesian network structure learning with a modified pc algorithm. Neuroimage. 2013;75:165–175. doi: 10.1016/j.neuroimage.2013.02.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Joshi AA, Salloum R, Bhushan C, Leahy RM. Measuring asymmetric interactions in resting state brain networks, in: International Conference on Information Processing in Medical Imaging. Springer. 2015:399–410. doi: 10.1007/978-3-319-19992-4_31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Eavani H, Satterthwaite TD, Filipovych R, Gur RE, Gur RC, Davatzikos C. Identifying sparse connectivity patterns in the brain using resting-state fmri. Neuroimage. 2015;105:286–299. doi: 10.1016/j.neuroimage.2014.09.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Deshpande G, Sathian K, Hu X. Effect of hemodynamic variability on granger causality analysis of fmri. Neuroimage. 2010;52(3):884–896. doi: 10.1016/j.neuroimage.2009.11.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Schippers MB, Renken R, Keysers C. The effect of intra-and inter-subject variability of hemodynamic responses on group level granger causality analyses. NeuroImage. 2011;57(1):22–36. doi: 10.1016/j.neuroimage.2011.02.008. [DOI] [PubMed] [Google Scholar]


