Using rapid-scan EPR to improve the detection limit of quantitative EPR by more than one order of magnitude

Abstract

X-band rapid-scan EPR was implemented on a commercially available Bruker ELEXSYS E580 spectrometer. Room temperature rapid-scan and continuous-wave EPR spectra were recorded for hydrogenated amorphous silicon powder samples. By comparing the resulting signal intensities the feasibility of performing quantitative rapid-scan EPR is demonstrated. For different hydrogenated amorphous silicon samples, rapid-scan EPR results in signal-to-noise improvements by factors between 10 and 50. Rapid-scan EPR is thus capable of improving the detection limit of quantitative EPR by at least one order of magnitude. In addition, we provide a recipe for setting up and calibrating a conventional pulsed and continuous-wave EPR spectrometer for rapid-scan EPR.

1. Introduction

For more than four decades, continuous-wave (CW) EPR has been utilized to quantitate the concentration of paramagnetic states in various branches of both science and industry. The most common application fields for quantitative EPR include radiation dosimetry [1–3], archaeological and geological dating [4–6], food analysis [7–9], environmental research [10, 11] and modern electronics, such as thin-film solar-cell materials [12–16]. Present X-band CWEPR spectrometers typically achieve spin sensitivities of about 10¹² spins per mT line width [17].¹ Despite this already high sensitivity, many examples exist where the number of spins present is close to or even below this detection limit.

A case in point are defect states in thin-film silicon (TFS) solar-cell materials, e. g., dangling Si-Si bonds (DBs) in hydrogenated amorphous silicon (a-Si:H). Such defects can act as recombination centers or trap states for charge carriers, thus impairing the electronic transport. Due to the paramagnetic nature of many of these defects, EPR is routinely employed to quantitate defect concentrations. Quantitative EPR experiments thereby contribute to reveal the impact of defect states on electronic device performance [12–16]. For typical TFS samples, an absolute spin sensitivity of 10¹² spins corresponds to a concentration sensitivity of about 10¹⁴ spins per cm³.² With increasing electronic quality, defect densities in state-of-the-art TFS materials are approaching this range [16].

The sensitivity of CWEPR is further limited in the presence of slow electron-spin relaxation: under these conditions, the spin system is readily saturated, which restricts the applicable incident microwave (MW) power—and hence the measurable signal intensity—to a low level. Especially spin species present at low concentrations frequently exhibit long relaxation times (as it is, e. g., the case for DB defects in a-Si:H), rendering quantitative CWEPR measurements substantially difficult. These challenges faced by CWEPR create a need for alternate EPR detection schemes, which both enable spin quantitation and improve the sensitivity.

This demand could potentially be met by the emerging rapid-scan (RS) technique, where resonance is passed on a time scale that is short with respect to the electron-spin relaxation times [18]. In particular, “rapid-scan” refers to the regime originally defined by Weger [19] in terms of the incident MW field B₁, the magnetic-field scan rate dB₀/dt (for field-swept RSEPR) and the relaxation times T₁ and T₂ [18, 19]:

$$\left|\frac{B_1}{\mathrm{d}{B}_0/\mathrm{d}t}\right|\ll \sqrt{T_1{T}_2}.$$ (1)

In this rapid-scan regime, B₁ and dB₀/dt can be selected to achieve improved signal-to-noise ratios (SNRs) relative to those attained by conventional CWEPR. This has been demonstrated for a variety of samples, such as nitroxides [20, 21], spin-trapped radicals [22], radiation-induced defects in tooth enamel [23] and defect states in solids, including DBs in a-Si:H [24]. Moreover, its applicability for quantitative intensity measurements has already been pointed out [25].

While RSEPR is still a relatively new EPR method, it refers to the regime of rapid-passage effects, which was explored already in the very early days of magnetic resonance [26–28]. Subsequently, rapid-passage experiments were repeatedly utilized to enhance the sensitivity of both EPR and NMR. For instance, Hyde demonstrated that out-of-phase detection under adiabatic rapid-passage conditions can be used to record the EPR absorption spectrum [29]. Adiabatic passage subsequently increased EPR signal intensities of ferric hemoglobin [30] and ferricytochrome c crystals [31], or natural diamond [32]. Another approach, which employed second-harmonic detection [33–35], was used to improve the sensitivity for defect states in silicon materials, such as the E′ center in amorphous SiO₂ [33], or conduction-band and valence-band tail states in a-Si:H, detected by light-induced EPR [35]. All these methods, however, required magnetic-field modulation and phase-sensitive detection, as in conventional CW magnetic resonance. By contrast, in 1974, a directly detected RSNMR technique was proposed [36, 37], which was based on non-adiabatic rapid passage. While RSNMR soon fell into oblivion due to the fast development of pulsed NMR, it was revived in 2004 in the field of EPR [38] and has been further developed since then by the Eaton group [18].

Herein, we implement RSEPR on a commercially available Bruker ELEXSYS E580 set-up and evaluate the feasibility of utilizing RSEPR for quantitative EPR. An initial foundation for quantitative RSEPR experiments has already been laid by Quine et al. [25]: they compared experimentally obtained SNRs to those calculated from first principles on a fully characterized spectrometer. We extend this by comparing CW and RSEPR signal intensities of a-Si:H samples with absolute spin numbers ranging from 10¹² to 10¹⁵, to have a routine procedure for quantitative RSEPR. By comparing SNRs of CW and RSEPR, we further show that, for a-Si:H, RSEPR is capable of improving the detection limit of quantitative EPR by at least one order of magnitude. In addition to these results, we provide a recipe for performing quantitative RSEPR experiments on a conventional CW and pulsed EPR (PEPR) spectrometer.

2. Materials and methods

2.1. Sample preparation

Undoped a-Si:H films were deposited on aluminum (Al) foil by plasma-enhanced chemical vapor deposition (PECVD). (Details on the deposition procedure can be found in refs. [39, 40].) To prepare powder samples, the Al substrate was chemically etched off in hydrochloride acid [40]. The remaining powders were weighed and sealed into EPR quartz tubes under helium atmosphere (Wilmad LabGlass, type 705-PQ-250M, with an inner diameter of 1.990(13) mm), with filling heights ranging from 2 mm to 5 mm. Seven samples were prepared, which are labeled with capital letters A to G, sorted in ascending order by their absolute number of spins (compare table 1).

Table 1.

Summary of electron-spin relaxation times (T₁, T₂) and absolute number of spins (N_S), determined by quantitative CWEPR, and the resulting spin concentration (ρ_S) of all a-Si:H samples under study.

Sample	NSa,b	ρS (cm−1)a,b	T1 (µs)b	T2 (µs)b
A	8 × 1012	2 × 1015	6.3	5.5
B	1 × 1013	2 × 1016	6.4	4.5
C	2 × 1013	2 × 1015	6.5	5.3
D	5 × 1013	2 × 1016	7.2	4.3
E	8 × 1013	3 × 1016	6.4	4.4
F	1 × 1014	3 × 1016	6.4	4.4
G	3 × 1015	9 × 1017	5.0	2.2

^aN_S and ρ_S were determined from the CWEPR signal intensity by comparison to a a-Si:H reference sample containing 1.4(4) × 10¹⁴ spins.

^bRelative errors are about 5% for T₁ and T₂, and about 30% for N_S and ρ_S.

2.2. EPR set-up

All EPR measurements were carried out at X-band (9.4 GHz to 9.8 GHz) and room temperature on a Bruker ELEXSYS E580 spectrometer. It is equipped with a lock-in amplifier for phase-sensitive detection of CWEPR, and with a quadrature mixer and a SpecJet-II fast digitizer for direct time-domain detection of RS and PEPR. For the PEPR experiments discussed in section 2.3, pulse sequences were generated by a PatternJet-II pulse programmer and amplified by a travelling-wave-tube (TWT) amplifier with a nominal power of 1 kW.

Different types of resonators were used for CW, RS and pulsed EPR: For CWEPR, a critically coupled Bruker ER 4122 super-high Q (SHQE) resonator was used. By featuring the highest quality factors (Q), the SHQE resonator is optimized for maximum sensitivity of CWEPR measurements. Rapid-scan EPR experiments were carried out using a critically coupled Bruker ER 4118X-MD5 dielectric resonator. It offers a larger detection bandwidth due to its lower Q, and, at the same time, a higher B₁ conversion than the SHQE resonator. In addition, using the MD5 resonator minimizes the effect of eddy currents induced by the rapidly changing magnetic field in the metallic parts of the resonator, as it was shown by Joshi et al. [41]. For PEPR, an overcoupled Bruker ER 4118 X-MS5 split-ring resonator was used due to its large bandwidth and high B₁ conversion. Typical Q-factors, bandwidths and B₁-conversion factors obtained for these three resonators are summarized in table 2.

Table 2.

Quality factors (Q), bandwidths (Δν_r) and B₁ conversion factors (C) of the resonators used for CW, RS and PEPR experiments.

Resonator	Qa	Δνr (MHz)b	$C(\text{mT}\sqrt{\text{MHz}}/\sqrt{\mathrm{W}})$ c
Bruker ER 4122 SHQE	9000	1.1	0.23
Bruker ER 4118 X-MD5	7000	1.4	0.65
Bruker ER 4118 X-MS5	1400	6.7	0.88

^aAverage loaded Q for a-Si:H powder samples.

^bResonator bandwidth, Δν_r = ν_r/Q, at the resonance frequency (ν_r) of each resonator (9.4 GHz to 9.8 GHz).

^cConversion of MW power (P) into B₁, such that $B_1=C\sqrt{P[\mathrm{W}]}/\sqrt{\mathrm{\Delta }{\nu }_{\mathrm{r}}[\text{MHz}]}$. Values are as specified by the manufacturer.

Resonator Q-factors were determined by recording the transient power ring-down after a 100 ns low-power MW pulse. The decay was fitted with a mono-exponential function using MAT-LAB. From the resulting time constant (τ) and the resonance frequency (ν_r), the resonator Q was calculated (Q = π τ ν_r).

2.3. Relaxation-time measurements

Rapid-scan EPR is based on increasing B₁ to maximize the undistorted signal amplitude while passing magnetic resonance on a time scale that is short with respect to the electron-spin relaxation times T₁ and T₂, as defined by eq. (1). To estimate the required magnetic-field scan rates, PEPR relaxation measurements where thus carried out: Transversal relaxation times (T₂) were determined from two-pulse primary electron-spin echo (ESE) decay (pulse sequence: π/2 – τ – π/2 – τ – echo, 8-step phase cycle); longitudinal relaxation times (T₁) were measured by three-pulse ESE-detected inversion recovery (pulse sequence: π – T – π/2 – τ – π/2 – τ – echo, 16-step phase cycle). The time constants T₁ and T₂ were extracted from the relaxation curves by mono-exponential³ fitting routines written in MATLAB.

2.4. Microwave-power saturation

To set the incident MW power (P) for both CW and RSEPR measurements, power-saturation curves were recorded by measuring the integrated signal intensity as a function of B₁.⁴ Saturation curves for sample C are exemplarily shown in fig. 1. To determine the regime where signal intensities increase linearly with B₁, a straight line was fitted to the intensity values obtained at the lowest B₁ values. For data acquisition, the highest B₁ values that resulted in an intensity within this linear regime were selected (compare fig. 1). B₁ values, together with resonator Q factors, used for all CW and RSEPR measurements are listed in table 3.

Figure 1.

Saturation curves for RS (red circles) and CWEPR (black triangles) on a-Si:H (sample C). Integrated signal intensities are plotted as a function of the MW field amplitude (B₁). The latter was calculated from P using the B₁ conversion factors (C) listed in table 2, according to $B_1=C\sqrt{P[\mathrm{W}]}/\sqrt{\mathrm{\Delta }{\nu }_{\mathrm{r}}[\text{MHz}]}$. Intensity values are normalized such that the slope in the linear regime (black dashed line) is equal for RS and CWEPR intensities. Circles mark the highest B₁ values within the linear regime, which were used for acquiring RS and CWEPR spectra, respectively. The inset magnifies the low-power region comprising the linear regime for CWEPR.

Table 3.

Summary of resonator quality factors (Q) and MW magnetic-field amplitudes (B₁) used for recording CW and RSEPR spectra for all samples under study.

Sample	QCWa	B1,CW (µT)b	QRSa	B1,RS (µT)b
A	9170	3.18	7010	22.9
B	9230	3.16	7520	23.6
C	9000	3.09	7910	24.3
D	9160	3.13	7120	23.0
E	9170	3.12	7140	23.0
F	9180	3.12	7270	23.2
G	9200	3.13	6770	22.3

^aResonator Q factors, as determined power-ring-down measurements (Q = π τ ν_r, where τ is the time constant of the mono-exponential fit to the ring-down curve, and ν_r is the MW frequency).

^bB₁ values were calculated from $B_1=C\sqrt{P[\mathrm{W}]}/\sqrt{\mathrm{\Delta }{\nu }_{\mathrm{r}}[\text{MHz}]}$, where P is the incident MW power, Δν_r = ν_r / Q the resonator bandwidth and C the resonator conversion efficiency as specified by the manufacturer (see table 2).

2.5. Continuous-wave EPR

For lock-in detection of CWEPR spectra, a sinusoidal magnetic-field modulation was applied with a modulation frequency (f_m) of 15 kHz and a peak-to-peak modulation amplitude (B_m) of 0.2 mT (≈ 30% of the peak-to-peak line width, ΔB_pp). The choice of f_m allows for a period > 5 T₁ between consecutive modulation half cycles, in order to prevent signal distortions by passage effects.

To obtain the signal intensity (I_CW) for quantitative EPR, the CWEPR derivative signal was numerically integrated twice. Polynomial baselines were fitted and subtracted prior to each integration step, i. e., for both the derivative and the absorption spectrum. The absolute number of spins (N_S) was then calculated from I_CW according to [44]

$$I_{\text{CW}}=c_{\text{CW}}·\left[G_{\mathrm{R}}\mathrm{\Delta }t{N}_{\text{scan}}\right]·\left[\frac{\sqrt{P}{B}_{\mathrm{m}}{\mathit{\text{Qn}}}_{\mathrm{B}}S(S+1)}{F(B_1,B_{\mathrm{m}})}\right]·N_S,$$ (2)

where the first bracket contains the acquisition parameters (G_R: receiver gain; Δt: sampling/“conversion” time; N_scan: number of scans) and the second bracket includes all experimental settings that influence the signal intensity (P: MW power; Q: resonator quality; n_B: temperature-dependent Boltzmann population of the spin states, n_B = ΔN_S/N_S ≈ ΔE/(2kT) for ΔE ≪ kT; S : total electron-spin quantum number, S = 1/2 for DBs in a-Si:H; F(B₁; B_m): correction factor for the spatial distribution of B₁ and B_m at the sample position). The calibration factor (c_CW) had been determined beforehand by measuring the signal intensity of an a-Si:H reference standard with an absolute number of spins of 1.4(4) × 10¹⁴. From N_S, the spin concentration (ρ_S) was calculated using the mass of each sample and the density of amorphous Si (2.285 g cm⁻¹ [45]).

2.6. Rapid-scan EPR

Rapid-scan EPR measurements were conducted by applying sinusoidal rapid magnetic-field scans and detecting the transient EPR signal directly in quadrature using the SpecJet-II transient recorder. Rapid magnetic-field scans were provided by the modulation coils integrated into the resonator assembly. To center the scan around the resonance position, a static magnetic field ( $B_0^{\text{const}}$) was applied and set to match resonance at the center of the scan. Accordingly, the total magnetic field is given by:

$$B_0(t)=B_0^{\text{const}}+\mathrm{\Delta }{B}_0(t)=B_0^{\text{const}}-\frac{B_{\mathrm{m}}}{2}\text{cos }(2\pi f_{\mathrm{m}}t).$$ (3)

During one scan period (T), resonance is passed twice: once in up-field direction at t = T/4, and a second time in down-field direction at t = 3T/4. At these resonance positions, the scan rate dB₀/dt is maximal and takes an approximately constant value α = dB₀/dt |_max = π f_mB_m.

2.6.1. Selection of the scan rate

To realize rapid-passage conditions, α must be sufficiently high to fulfill eq. (1). In this regime, maximizing α allows increased B₁ and thereby improves the SNR [18, 20, 24, 38, 46]. However, the maximum value for α is limited mainly by two factors [18]: First, using the Bruker modulation coils, the maximum scan frequency is 100 kHz at peak-to-peak amplitudes of up to 4 mT, resulting in a technically limited maximum α of 1.3 kT s⁻¹. Secondly, α determines the bandwidth of the RSEPR signal (Δν_s); the more rapidly resonance is passed, the larger Δν_s becomes. To avoid signal distortions by filtering out signal components, Δν_s must be kept below the available detection bandwidth.

An estimation for Δν_s in case of a pure Lorentzian line shape is given in ref. [18, p. 43]. A similar expression can be derived for a Gaussian line (see the supplemental material for a derivation and discussion of these expressions):

$$\mathrm{\Delta }{\nu }_{\mathrm{s}}=\frac{4\sqrt{N\text{ ln }2}}{\pi }\frac{\alpha }{\mathrm{\Delta }{B}_{1/2}}.$$ (4)

Herein, ΔB_1/2 denotes full width at half maximum (FWHM) of the EPR absorption line, and N determines the tolerable amount of signal distortion: a value N = 5 estimates Δν_s as comprising all frequency components with a relative amplitude larger than about 1% (see details in the supplemental material). The available detection bandwidth is limited by the resonator bandwidth, Δν_r = ν/Q. (The bandwidth of the detection system is 200 MHz for the E580 spectrometer, which is substantially higher than Δν_r.) For N = 5, the estimate for the maximum scan rate to ensure Δν_s < Δν_r is, based on eq. (4):

$$\alpha =\pi f_{\mathrm{m}}{B}_{\mathrm{m}}<\frac{\pi }{4\sqrt{N\text{ ln }2}}\frac{\nu \mathrm{\Delta }{B}_{1/2}}{Q}\approx 0.42\frac{\nu \mathrm{\Delta }{B}_{1/2}}{Q}.$$ (5)

For a-Si:H, typical Gaussian line widths are about 1 mT. For ν = 9.6 GHz and Q = 7000, eq. (5) yields a maximum scan rate of 0.58 kT s⁻¹. Based on this estimate, RSEPR spectra were recorded using f_m = 35 kHz and B_m = 4 mT, corresponding to α = 0.44 kT s⁻¹. This scan rate is sufficient to reach the rapid-passage regime for a-Si:H. For B₁ = 22 µT and the shortest measured relaxation times, T₁ = 5.0 µs and T₂ = 2.2 µs (sample G in table 1), rapid passage requires scan rates α ≫ 7 T s⁻¹, according to eq. (1).

2.6.2. Post-acquisition processing

Field-swept RSEPR spectra usually exhibit strong periodic background signals at the harmonics of the scan frequency. These can be attributed to the rapidly changing magnetic field that can cause eddy currents in the metallic parts of the resonator or mechanical vibrations in proximity to the modulation coils [18, 47, 48]. To remove these background signals, a numerical procedure based on the description of Tseitlin et al. [48] was used: Single scan cycles were extracted and averaged from the time-domain RSEPR raw data. Subsequently, the signal was split into up- and down-field half-cycles by separating the positive and negative components in the frequency domain. Sinusoidal baselines were then fitted and subtracted from both half-cycles individually. These half-cycle signals were finally averaged to yield the baseline-corrected RSEPR spectrum. The time axis was converted into magnetic-field units using the scan profile given in eq. (3). (Raw data and baseline fits are exemplarily shown for sample E in section 1 of the supplemental material). To determine the signal intensity, the baseline-corrected RSEPR absorption line was numerically integrated.

It is to be noted that we did not apply Fourier deconvolution as it was done in other RSEPR studies [20–24, 43, 46, 48, 51, 52]. By deconvolution, signal distortions by wiggles that are superimposed onto the RSEPR line can be removed to recover the undistorted slow-scan line shape. However, such wiggles may not be observed for inhomogeneously broadened lines, as is the case for a-Si:H (see discussion in section 4). Consequently, in this particular case of a-Si:H, RSEPR directly measures the the undistorted EPR absorption line shape; the deconvolution step is thus not required and can be replaced by a simple conversion from time to magnetic-field domain based on eq. (3).

2.7. Digital post-acquisition filtering

When recording CWEPR spectra, usually a low-pass RC filter is integrated into the lock-in amplifier to remove high-frequency noise and improve the SNR. The time constant τ = RC determines the cutoff frequency ν_c = 1/(2πτ) of the filter.⁵ To avoid signal distortions and filter artifacts, τ must be chosen such that ν_c is larger than the EPR signal bandwidth.

By contrast, RSEPR is detected directly and the signal is solely filtered by a video amplifier with a bandwidth of 200 MHz (apart from the fast averaging of the rapidly recorded scans). As a result, RSEPR spectra still contain high-frequency noise and the SNR can be improved by digital low-pass filtering. This was realized by a digital Butterworth low-pass filter implemented in MATLAB. To compare SNRs of CW and RSEPR spectra, not only RSEPR signals were digitally filtered, but also, for CWEPR, the hard-wired RC filter of the lock-in amplifier was replaced by digital filtering, in order to use the same type of filter for both methods. Accordingly, τ was set to a value such that ν_c was significantly above the estimated CWEPR signal bandwidth. Then, the same digital Butterworth low-pass filter was applied to CWEPR spectra.

The signal bandwidths (Δν_s) of RS and CWEPR could, in principle, be estimated by assuming Gaussian line shapes and using eq. (4). However, the DB signal is not a single Gaussian line, but comprises both Gaussian and Lorentzian line-shape contributions as well as g-value anisotropies [50]. Therefore, eq. (4) can merely provide a rough estimation of Δν_s. To assess Δν_s more precisely, simulated signals were fitted to the measured RS and CWEPR spectra using EasySpin [49]. The spin-Hamiltonian parameters of the DB defect in a-Si:H were taken from Fehr et al. [50]. Only the line-broadening parameters were varied to fit the experimental data. The bandwidths of these simulated signals were determined by numerical Fourier transformation: Δν_s was estimated as the spectral width of the Fourier transform enclosing all signal components with a relative amplitude larger than 1%. As an illustration, the Fourier-transformed experimental CW and RSEPR spectra of sample A are exemplarily shown in fig. 2, together with the Fourier transforms of the respective spectra after digital low-pass filtering and the Fourier transforms of the simulated signals. In fig. 2, the corresponding values for Δν_s are indicated by dotted vertical lines.⁶

Figure 2.

Fourier transforms of the CWEPR derivative (upper) and the RSEPR absorption spectrum (lower) of sample A. For the sake of comparability, the displayed spectra show the fast Fourier transformation (FFT) of the particular spectrum in the magnetic-field domain (in mT), yielding a representation in a magnetic-field-rate domain (in mT⁻¹). Both graphs show the FFTs of the raw experimental spectra (black lines) and of the spectra after digital low-pass filtering (blue lines). In addition, the FFTs of the simulated spectra (see section 2.7) are shown (red dashed lines). Amplitudes are normalized such that a value of one corresponds to the maximum amplitude of the FFT of the particular simulated spectrum. The indicated signal bandwidths (Δν_s) comprise those parts of the spectra where the relative amplitudes of the FFTs of the simulated spectra are larger than 1 %. The values Δν_s thus determined were used to set the cutoff frequencies for digital low-pass filtering.

2.8. Calculation of signal-to-noise ratios

Signal-to-noise ratios were determined from the absorption spectrum for RSEPR and the first derivative for CWEPR, respectively. Comparing SNRs of either both absorption or both derivatives spectra would change the noise spectrum of one or the other of the two methods: integration amplifies low-frequency noise, whereas differentiation enhances high-frequency noise. Accordingly, SNRs were calculated as the ratios of the RSEPR signal amplitude or the CWEPR peak-to-peak amplitude, respectively, to the root-mean-square (RMS) noise. For CWEPR, RMS noise was determined from baseline regions of the spectrum. For RSEPR, the limited scan width of 4 mT does not cover enough baseline. Therefore, an off-resonance noise spectrum was recorded by shifting the static center field ( $B_0^{\text{const}}$) by 10 mT. This RS noise signal was post-processed using the same procedure and parameters (e. g., filter cutoff frequency) as for the on-resonance spectrum, and then used for calculating the RMS noise.

The SNR increases linearly with the square root of acquisition time (T_acq). To compare SNRs of RS and CWEPR, the obtained values were thus normalized by division by $\sqrt{T_{\mathrm{a}\mathrm{c}\mathrm{q}}}$.

3. Results

3.1. Relaxation times

Electron-spin relaxation times obtained from PEPR measurements as described in section 2.3 are summarized in table 1. Longitudinal relaxation times (T₁) vary between 5 µs and 7 µs, while transversal relaxation times (T₂) range from 2 µs to 5 µs for the different a-Si:H samples under study. The values for T₂ increase with decreasing spin concentration (ρ_S).

3.2. Line shapes

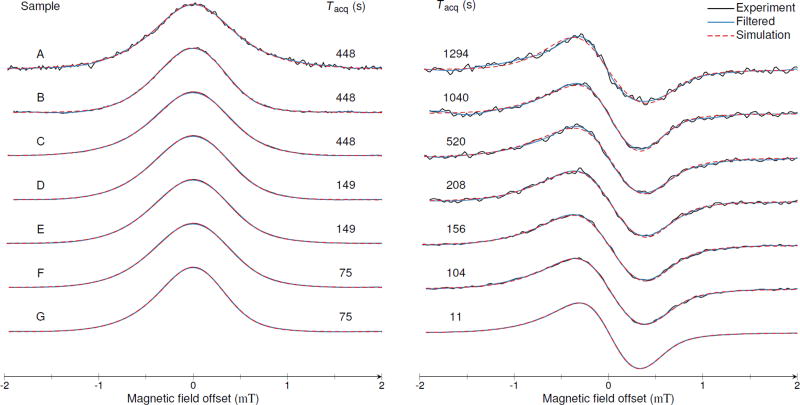
The resulting RS and CWEPR spectra are depicted in fig. 3. The RSEPR signals correspond to the absorption spectrum after baseline correction; for CWEPR, the first-derivative spectra are shown. The line widths range from 0.6 mT to 0.8 mT for CWEPR (peak-to-peak, ΔB_pp) and from 0.9 mT to 1.1 mT for RSEPR (FWHM, ΔB_1/2). The average ratio ΔB_pp/ΔB_1/2 between CW and RSEPR line widths is 0.69(4). For a purely Gaussian or a purely Lorentzian line shape, this ratio would be equal to $1/\sqrt{2\text{ ln }2}\approx 0.85$ or $1/\sqrt{3}\approx 0.58$, respectively. As already mentioned in section 2.7, the a-Si:H DB signal, however, exhibits both Gaussian and Lorentzian line-shape contributions, resulting in a Voigtian line shape [50]. The measured CW and RSEPR signals could be reproduced by simulations with EasySpin, using the spin-Hamiltonian parameters from ref. [50] (see also section 2.7). The resulting simulated spectra are included in fig. 3 (dashed red lines).

Figure 3.

RS (left) and CWEPR (right) spectra of the a-Si:H samples under study. The RSEPR absorption and the CWEPR derivative spectra after baseline subtraction are shown. Spectra were recorded using the listed acquisition times (T_acq). Both the raw experimental data (black) and the signals after applying a digital low-pass filter (blue) are included. In addition, simulated signals are shown (red dashed lines), which were obtained using EasySpin [49] and the spin-Hamiltonian parameters from ref. [50], with the line-broadening parameters left to fit the experimental data.

3.3. Signal-to-noise ratios

Signal-to-noise ratios of CW and RSEPR signals after digital low-pass filtering are summarized in table 4. Both the normalized SNR for the RSEPR absorption spectra (SNR_RS) and the CWEPR derivative (SNR_CW), respectively, are listed for all samples, as well as the ratio SNR_RS/SNR_CW. This ratio, expressing the SNR benefit of RS in comparison to CWEPR, varies between 11 to 47. For sample G, a ratio could not be determined, due to the high SNR_RS (> 20 000), which could not be measured accurately. The arithmetic mean amounts to a value of 26, with a standard deviation of 14.

Table 4.

Summary of the SNRs of RS (SNR_RS) and CWEPR (SNR_CW) spectra after digital low-pass filtering for all samples under study. The SNRs were computed as maximum signal amplitude for RSEPR, or peak-to-peak height for CWEPR, respectively, divided by RMS noise. Values are normalized to an acquisition time (T_acq) of 1 s by dividing by $\sqrt{T_{\text{acq}}}$.

Sample	${\text{SNR}}_{\text{RS}}(1/\sqrt{s})$	${\text{SNR}}_{\text{CW}}(1/\sqrt{s})$	SNRRS/SNRCW
A	19	1.7	11
B	56	2.6	22
C	170	4.4	38
D	590	13	47
E	570	16	36
F	540	28	19
G		230

The high standard deviation of SNR_RS/SNR_CW can be attributed to errors in the RMS noise values derived from the RSEPR signals after applying the numerical baseline-correction procedure described in section 2.6.2. Subtraction of the strong background signals that are superimposed onto the RSEPR signals by means of sinusoidal baseline fitting also affects the determination of RMS noise values and can thus lead to the significant fluctuation observed in the data presented in table 4. Nevertheless, all results for SNR_RS/SNR_CW are in the range of 10 to 50, which allows the conclusion that for all measurements compared in this study, SNRs of RSEPR are larger than those of CWEPR by at least one order of magnitude.

3.4. Signal intensities

The absolute numbers of spins (N_S) as well as the corresponding spin concentration (ρ_S) of all samples are shown in table 1. The values of N_S were calculated from I_CW using eq. (2). To estimate whether a similar relation holds for the intensity of RSEPR signals, the ratios of RS and CWEPR intensities (I_RS/I_CW) were calculated. Since I_CW ∝ N_S, these ratios must be constant in order to utilize RSEPR for determining N_S. To calculate I_RS/I_CW, both I_CW and I_RS were normalized for differences in B₁, the resonator Q, the number of averages and the gain (i. e., video amplifier gain G_VAMP and receiver gain G_R for RS and CWEPR, respectively). In addition, the integration of CWEPR signals was limited to the same field range covered by RSEPR measurements, i. e., to a width of 4 mT centered around resonance. The purpose of this limitation is to avoid introducing errors into the ratios I_RS/I_CW resulting from signal components not covered by the restricted scan width in RSEPR (see further discussion below). The resulting values for I_RS/I_CW are plotted as a function of N_S in fig. 4, normalized to the weighted arithmetic mean, which is indicated by the dashed line. Even though the resulting mean I_RS/I_CW has a standard deviation of about 20% (indicated by the shaded area in fig. 4), the obtained values for I_RS/I_CW exhibit a constant level and do not show any dependence on N_S.

Figure 4.

Ratio of signal intensities (I_RS/I_CW) obtained from integration of the RSEPR absorption spectrum and double integration of the CWEPR derivative, respectively, plotted as a function of the absolute number of spins (N_S) of each sample. The signal-intensity ratios are plotted on a relative axis, normalized to the weighted arithmetic mean. The N_S axis has a logarithmic scale. Capital letters A to G mark the particular sample. The shaded area indicates the standard deviation, which is about 20 %.

The rather high standard deviation of the values obtained for I_RS/I_CW can be attributed to the errors introduced by baseline corrections: For CWEPR, the signal is integrated twice, with baseline corrections before each integration step. Degrees of freedom in the choice of baseline region and polynomial order of the baseline fit significantly influences the result of the double integral, yielding estimated errors in the range of 10% to 20 %. For RSEPR, on the other hand, only one integration step is required, and sinusoidal background signals can be reduced to below noise level by using the procedure described in ref. [48]. Nevertheless, the limited scan width of 4 mT does not comprise the entire signal extent of the DB signal: a-Si:H has a natural abundance of ²⁹Si of about 4.7 at. % (nuclear spin I = 1/2), resulting in hyperfine sidebands that spread out more than 5 mT from the resonance position. After baseline subtraction, though, the RSEPR signal is set to zero at the edges of the field range. Thereby, an offset is introduced, which leads to an error in the resulting integrated intensity. To correct for this error, the RSEPR signals were shifted based on comparison with the simulated DB signals. This estimate is, however, prone to uncertainty, which contributes to the variation of I_RS/I_CW values shown in fig. 4.

4. Discussion

Summing up the results presented in section 3.4, we conclude that, due to the proportionality between the signal intensities I_RS and I_CW, quantitation of N_S by RSEPR is feasible. Furthermore, we found that SNRs of RSEPR are higher than those of CWEPR by up to factor of 50. Despite the considerable degree of variation in the calculated SNR_RS/SNR_CW ratios, the results imply that, for the particular case of a-Si:H, RSEPR is able to lower the detection limit of quantitative EPR by at least one order of magnitude. From another point of view, to attain the same SNRs by either CW or RSEPR measurements, the data-acquisition time can be decreased by a factor of up to 2500 by means of RSEPR.

For purely quantitative EPR, where line-shape preservation is not of critical interest, the SNR of CWEPR could still be improved by employing overmodulation: as I_CW is proportional to the modulation amplitude (independent of any modulation broadening), the latter could be increased to, e. g., about twice the peak-to-peak line width to maximize the signal amplitude. However, we found that the resulting gain in SNR is merely by a factor of about three to four, which is significantly below the enhancements obtained from RSEPR.

For the particular case of RSEPR on a-Si:H, an even higher SNR enhancement by more than a factor of 200 was reported by Mitchell et al. [24], using a dedicated laboratory-built RSEPR set-up. While the precise results of SNR comparisons between RS and CWEPR strongly depend on the experimental parameters (e. g., the criteria for selecting MW power, scan rate or filter bandwidths), it has become apparent from our results and from previous reports that RSEPR has the potential to significantly improve the sensitivity of EPR, not only for a-Si:H, but also for a variety of other samples [20–24].

An even higher benefit from RSEPR can be expected when operating at low temperatures: While the measurements in this study were conducted at room temperature, EPR experiments are often carried out at cryogenic temperature in order to improve sensitivity due to the increased spin polarization. However, relaxation times T₁ and T₂ also typically lengthen with decreasing temperature; this, for instance, holds true for a-Si:H [42]. In that case, unsaturated CWEPR measurements require to attenuate the incident MW powers. For RSEPR, on the other hand, the rapid-passage regime is readily met in case of slow relaxation processes (eq. (1)), where higher MW powers can be applied without saturating the spin system. The same argument applies to experiments at high frequencies/fields: increasing the MW frequency in many cases extends T₁, such that an additional benefit may be achieved from high-frequency/-field RSEPR applications.

To compare RSEPR not only to CWEPR, but also to PEPR techniques, a previous study of RSEPR on an a-Si:H sample by Mitchell et al. [24] compared the SNR of RSEPR also to SNRs obtained from field-swept echo (FSE) detected EPR and Fourier-transform (FT) EPR. While, in this study, the SNR for FSE-detected EPR was about a factor of two better than that for CWEPR, it was by about an order of magnitude lower than the SNR for RSEPR. A SNR comparison of RSEPR and FTEPR is not feasible for the case of a-Si:H. The large amount of inhomogeneous broadening, with peak-to-peak line widths ranging from 0.6 mT to 0.8 mT, leads to $T_2^{\ast }$ relaxation times on the order of a few nanoseconds, which is below the typical dead times of commercial PEPR resonators and thus inhibits FTEPR experiments on these samples. However, the authors of ref. [24] compared the SNRs of RSEPR and FTEPR for neutral single substitutional nitrogen centers ( ${\mathrm{N}}_{\mathrm{S}}^0$) in diamond and atomic nitrogen in C₆₀ (N@C₆₀), resulting in comparable SNRs for ${\mathrm{N}}_{\mathrm{S}}^0$ and a higher SNR for RSEPR by a factor of about five. These results illustrate that RSEPR is not only capable of improving the detection sensitivity in comparison to CWEPR, but also with respect to PEPR techniques.

Herein, we explored the feasibility of quantitative EPR by a signal intensity comparison between CW and RSEPR. The inferred proportionality of I_RS to N_S agrees with the findings of Quine et al. [25], who reported agreement between experimental and theoretically calculated SNRs of RSEPR, based on a study conducted on a fully characterized spectrometer. Moreover, our result is in agreement with theoretical predictions of the line shape in a RS experiment: Solving the Bloch equations in a first-order approximation for non-adiabatic rapid-passage conditions yields the following expression for the magnetic susceptibility (χ) [53, 54]:

$$\chi (t)\approx {\chi }_{\text{steady}}(t)+{\chi }_{\text{trans}}(t),$$ (6)

with

$${\chi }_{\text{steady}}(t)=-{\chi }_0·\frac{|\gamma |B_1{T}_2[1-i\mathrm{\Omega }(t)T_2]}{1+{[\mathrm{\Omega }(t)T_2]}^2}\text{and}$$

$${\chi }_{\text{trans}}(t)=-\text{const}·\text{exp}[-\frac{t}{T_2}-i{\int }_0^t\mathrm{\Omega }(t\prime )\mathrm{d}t\prime ],$$

where χ₀ denotes the thermal-equilibrium susceptibility and i the imaginary unit. The EPR signal under non-adiabatic rapid-passage conditions hence is a superposition of two components: The term χ_steady is the well-known steady-state solution of the Bloch equations in absence of saturation ( ${\gamma }^2{B}_1^2{T}_1{T}_2\ll 1$). The intensity of the corresponding signal component is proportional to N_S (χ₀ ∝ N_S) and can thus be used for spin quantitation. The term χ_trans expresses a transient damped free oscillation at frequency Ω(t). It causes a perturbation superimposed onto χ_steady, which can be understood as a free-induction decay (FID) at varying frequency Ω(t). It was shown by Jacobsohn and Wangsness [53] that these “wiggles” appear if $\sqrt{\mathrm{d}\mathrm{\Omega }/\mathrm{d}t}{T}_2^{\ast }\gtrsim 1$. This criterion is based on the effective transverse relaxation time ( $T_2^{\ast }$), which encompasses both T₂ relaxation and loss of coherence due to local field inhomogeneities. For a-Si:H, line broadening is inhomogeneous due to g-strain and unresolved hyperfine interactions with distant hydrogen nuclei. As a result, $T_2^{\ast }$ is of the order of a few nanoseconds. For $T_2^{\ast }=7.5\text{ ns}$ (corresponding to a FWHM of about 1 mT), a distortion by wiggles should not be present for scan rates ≲ 100 kT s⁻¹, which is well above the value of 0.65 kT s⁻¹ used for the experiments presented herein. The measured RSEPR signals can thus be solely described by the χ_steady term, such that a proportionality between I_RS and N_S is predicted.

In general, however, RSEPR signals are often distorted by wiggles, as is the case, for instance, with nitroxides [20, 21] or organic radicals [41, 52]. Nevertheless, it had been shown for RSNMR that the unperturbed line shape (χ_steady) can be restored by means of numerical Fourier deconvolution [36, 37]. A detailed description for RSEPR with either triangular or sinusoidal scan profiles can be found in refs. [43, 51]. After deconvolution, the signal is again described by χ_steady, and the resulting intensity is proportional to N_S.

The procedure to obtain the RSEPR signal intensity—and thus N_S—from the time-domain signal is schematically summarized in fig. 5: In a first step, full scan cycles are extracted and averaged, and a sinusoidal baseline is subtracted, as described in ref. [48]. Secondly, depending on the presence of wiggles, either Fourier deconvolution is applied or, in the case of inhomogeneous broadening, where no signal distortions occur, the time axis is converted into magnetic-field units by means of eq. (3). The resulting absorption spectrum is finally numerically integrated to yield I_RS, from which N_S can be determined. Considering all factors that influence the RSEPR signal intensity, we propose the following expression for I_RS (in similarity to eq. (2)):

$$I_{\text{RS}}=c_{\text{RS}}·\left[G_{\text{VAMP}}{N}_{\text{scan}}\right]·\left[\frac{\sqrt{P}{\mathit{\text{Qn}}}_{\mathrm{B}}S(S+1)}{F(B_1)}\right]·N_S.$$ (7)

In this equation, the acquisition parameters that influence I_RS are the video amplifier gain (G_VAMP) and the number of scans (N_scan), while the experimental settings affecting the directly detected EPR intensity are the MW power (P), the resonator Q, the Boltzmann population (n_B), the total electron spin (S) and the spatial distribution of B₁ (correction factor F(B₁)). The calibration factor c_RS can be obtained by measuring I_RS of a reference sample with a known number of spins. However, it must be noted that c_RS most certainly depends on the RS frequency (f_m) and width (B_m) since the scan rate determines the acquisition time at each point of the scan. After calibration with a reference sample at a given setting of f_m and B_m, eq. (7) can be used to determine N_S from the measured RSEPR signal intensity.

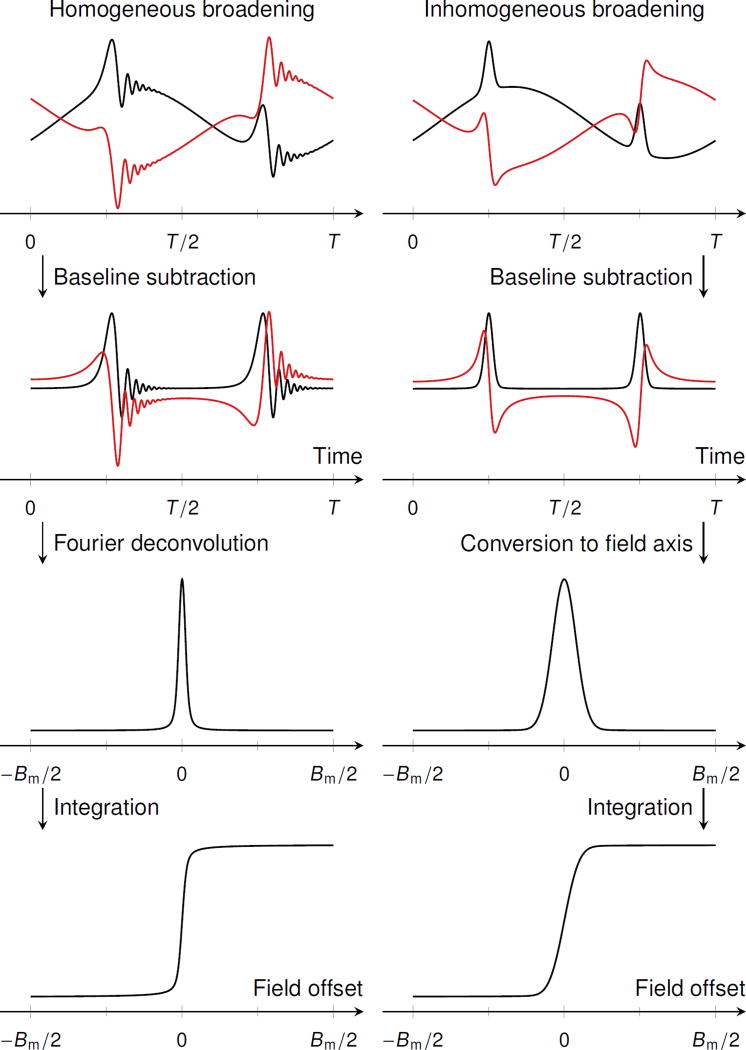
Figure 5.

Schematic illustration of the procedure to obtain the signal intensity from the transient RSEPR signal, separately displayed for the cases of homogeneously (left) and inhomogeneously (right) broadened lines. The upper row shows simulated time-domain EPR signals under non-adiabatic rapid-passage conditions for one sinusoidal scan cycle of period T and peak-to-peak amplitude B_m, with a sinusoidal background signal, oscillating at the rapid-scan frequency, added. Black lines mark the absorption and red lines the dispersion signals. Signals were simulated using the blochsteady and pepper functions of the EasySpin library [49]. The second row contains the signals after subtracting the sinusoidal baselines. The third row shows the EPR absorption line after applying Fourier deconvolution (for homogeneous broadening), or after converting the time axis to magnetic-field units (for inhomogeneous broadening). In the last row, the resulting integral of the absorption line is shown, from which the signal intensity and the absolute number of spins can be determined.

The results of this study show that field-swept RSEPR can be readily implemented on a commercially available spectrometer, using the standard modulation coils to provide the rapid field scans. A fast digitizer and a quadrature mixer are required to directly detect the transient RSEPR signal. Both are integrated into pulsed EPR spectrometers, such as the Bruker ELEXSYS systems. The scan rates that can be achieved with the Bruker modulation coils are up to 1.3 kT s⁻¹, which is sufficient to reach the rapid-passage regime (eq. (1)) for samples with relaxation times in the order of microseconds, as, e. g., in the case of a-Si:H. Nonetheless, a few limitations are to be mentioned: The major restriction resulting from employing the standard modulation coils for rapid field scans is the maximum scan width of 4 mT. For broad lines (as in the case of a-Si:H), signal components that spread out further from resonance may thereby be excluded. The signal intensity obtained from RSEPR in that case underestimated the actual number of spins in the sample. The standard modulation coils impose a second limitation, which is due to their small diameter of about 2.5 cm. For modulation coils of this size, the region where the magnetic field is homogeneous is confined to only a few millimeters. While this is not an issue for CWEPR, where the spatial distribution of B_m can be compensated by determining a correction factor from an EPR imaging experiment (F(B₁, B_m) in eq. (2)), the modulation coils provide the magnetic-field scan in RSEPR. Therefore, sample sizes for RSEPR experiments that are carried out using the Bruker modulation coils are limited to a few millimeters. Finally, the implementation of RSEPR in this study was based on prior knowledge of sample properties, such as line shape and relaxation times. T₁ and T₂ were measured to estimate the required scan rates for rapid-passage conditions, the simulated line shape of a-Si:H DBs was utilized to determine the signal bandwidth and, in addition, to correct for an offset error due to the restricted scan width. Nevertheless, within the given limitations, RSEPR experiments can be conducted on conventional CW and pulsed EPR set-ups without additional hardware requirements.

5. Conclusion

We have shown that quantitative RSEPR is feasible using a commercial Bruker ELEXSYS setup. Especially for samples with long relaxation times, RSEPR can improve the detection limit—or, alternatively, reduce the acquisition time required for quantitative EPR measurements. As this situation is frequently met in quantitative EPR applications, RSEPR has a large potential for these applications. In particular, for a-Si:H, we have found that RSEPR is capable of enhancing SNRs by up to a factor of 50 in comparison to conventional CWEPR. The dependence of acquisition parameters on sample-specific features, such as spectral width and relaxation times, renders RSEPR particularly useful for spin-quantitation routines on paramagnetic specimen with known properties. Once established for a particular sample (such as, e. g., a defect, polaron state or spin trap), RSEPR can be routinely repeated.

Furthermore, the present article provides criteria and data-processing strategies that can be readily utilized to assess the feasibility of RSEPR experiments for any given sample and spectrometer configuration. In addition, they allow for an evaluation of the potential sensitivity gain of RSEPR as compared to our experiments. This discussion may help to further exploit the benefits of RSEPR for a large variety of EPR samples and may assist potential users to optimize experimental settings.

Highlights.

• Rapid-scan EPR is implemented on a commercial Bruker ELEXSYS E580 pulse and continuous-wave EPR spectrometer without further hardware modifications.

• The feasibility of spin quantitation by rapid-scan EPR is demonstrated, using the example of dangling-bond defects in hydrogenated amorphous silicon.

• A sensitivity enhancement by more than one order of magnitude achieved by rapid-scan EPR in comparison to conventional continuous-wave EPR is demonstrated.

• Guidelines and criteria for carrying out routine quantitative rapid-scan EPR experiments are presented.