REVEALING THE ACTIVATION PATHWAY FOR TMEM16A CHLORIDE CHANNELS FROM MACROSCOPIC CURRENTS AND KINETIC MODELS

Abstract

TMEM16A (ANO1), the pore-forming subunit of calcium-activated chloride channels, regulates several physiological and pathophysiological processes such as smooth muscle contraction, cardiac and neuronal excitability, salivary secretion, tumour growth, and cancer progression. Gating of TMEM16A is complex because it involves the interplay between increases in intracellular calcium concentration ([Ca²⁺]_i), membrane depolarization, extracellular Cl⁻ or permeant anions, and intracellular protons. Our goal here was to understand how these variables regulate TMEM16A gating and to explain four observations. a) TMEM16A is activated by voltage in the absence of intracellular Ca²⁺. b) The Cl⁻ conductance is decreased after reducing extracellular Cl⁻ concentration ([Cl⁻]_o). c) I_Cl is regulated by physiological concentrations of [Cl⁻]_o. d) In cells dialyzed with 0.2 µM [Ca²⁺]_i, Cl⁻ has a bimodal effect: at [Cl⁻]_o < 30 mM TMEM16A current activates with a monoexponential time course, but above 30 mM [Cl⁻]_o I_Cl activation displays fast and slow kinetics. To explain the contribution of V_m, Ca²⁺ and Cl⁻ to gating, we developed a 12-state Markov chain model. This model explains TMEM16A activation as a sequential, direct, and V_m-dependent binding of two Ca²⁺ ions coupled to a V_m-dependent binding of an external Cl⁻ ion, with V_m-dependent transitions between states. Our model predicts that extracellular Cl⁻ does not alter the apparent Ca²⁺ affinity of TMEM16A, which we corroborated experimentally. Rather, extracellular Cl⁻ acts by stabilizing the open configuration induced by Ca²⁺ and by contributing to the V_m dependence of activation.

INTRODUCTION

Cl⁻ movements through Ca²⁺ activated chloride (Cl⁻) channels (CaCCs) play important roles in many cellular functions such as regulation of smooth muscle contraction, regulation of cardiac and neuronal excitability, salivary secretion, and tumour growth and progression in many types of cancer [13, 21, 29, 40]. TMEM16A (ANO1) and TMEM16B (ANO2) are the pore-forming subunits of CaCCs [6, 45, 50]. The gating mechanism of these channels is quite complex. Gating requires increases in intracellular calcium concentration ([Ca²⁺]_i), but also involves membrane depolarization, extracellular Cl⁻ or permeant anions, and intracellular protons. Ca²⁺-dependent activation is coupled to V_m [27, 35, 49] and is regulated by intracellular protons that compete for Ca²⁺ binding [1, 8]. When [Ca²⁺]_i is in the range of 0.1 – 0.8 µM, channel gating is strongly V_m-dependent, and the I–V_m relationships show outward rectification. Such V_m-dependence is lost when [Ca²⁺]_i >5 µM. Hence, the dose-response curve to [Ca²⁺]_i displays weak V_m-dependence [2, 49, 52]. This V_m-dependence is explained by a voltage-dependent Ca²⁺ dissociation [49]. We have shown that TMEM16A and TMEM16B exhibit fast and slow gating modes [11]. Both modes depend on intracellular Ca²⁺, membrane voltage (V_m) and the extracellular Cl⁻ concentration ([Cl⁻]_o). Apart from the Ca²⁺-dependent activation, TMEM16A can also be activated by strong depolarizations in the absence of intracellular Ca²⁺ [49].

We assume that direct binding of Ca²⁺ activates TMEM16A [2, 3, 27]. This idea is supported by the following observations: a) injection of Ca²⁺, Ba²⁺ or Sr²⁺ into Xenopus oocytes activates CaCC [32]; b) TMEM16A in excised patches or liposomes can be activated by Ca²⁺, Ba²⁺ or Sr²⁺ [34, 46, 49]; c) mutating residues E702, E705, E730 and D734 located in the Ca²⁺ binding pocket of TMEM16A decrease the Ca²⁺ sensitivity 100 – 1000-fold [47, 52]; d) the x-ray structure of the Nectria haematococca TMEM16 homolog (nhTMEM16) shows the presence of two Ca²⁺ ions bound to a site located within the membrane [5]; e) changing the nhTMEM16 Ca²⁺-coordinating residues significantly reduces the functional Ca²⁺ sensitivity, which strongly indicates these residues are part of a high-affinity Ca²⁺ binding site [5, 34, 47]; and f) vertebrate TMEM16A is activated in a cooperative manner by Ca²⁺ [49]. Also, other regions of TMEM16A including the N-terminus and the first intracellular loop have been shown to contribute to Ca²⁺ sensitivity [17, 49]. Thus, the existing evidence strongly suggests that TMEM16A is directly activated by binding at least two Ca²⁺ ions.

The role of permeant ions in channel gating has increasingly been recognized. Gating of Cl⁻ channels such as ClC-2, volume-sensitive channels, and CFTR are reported to be dependent on permeant anion [23, 25, 41, 51]. CaCCs are not the exception. Anions with a higher permeability than Cl⁻ such as SCN⁻, I⁻, and NO⁻₃ when applied from the extracellular side promote opening and accelerate the opening rate while slowing down the closing rate in CaCCs [4, 36, 38, 49]. In addition, these anions decrease the EC₅₀ for Ca²⁺ both in Xenopus oocyte CaCCs as well as heterologous-expressed TMEM16A and TMEM16B [4, 38, 39]. These observations suggest gating and ion permeation are coupled in TMEM16A channels.

The rather complex gating of TMEM16 channels cannot be understood without the help of a model. In this work, we developed a 12-state Markov chain model to explain the TMEM16A gating mechanism. The model reproduces the complex TMEM16A activation in response to V_m, Ca²⁺ and different [Cl⁻]_o. The model also predicts that extracellular Cl⁻ does not alter the channel’s affinity for Ca²⁺. Further experiments corroborated this prediction. We propose that TMEM16A is activated by sequential, direct, V_m-dependent binding of two Ca²⁺ ions coupled by a V_m-dependent binding of one external Cl⁻ ion.

MATERIALS AND METHODS

Culture of HEK 293 cells and expression of TMEM16A

Human embryonic kidney 293 cells (HEK293) were cultured in Dulbecco’s modified Eagle medium (DMEM, Gibco BRL, Carlsbad, CA, USA) supplemented with 10% heat-inactivated fetal bovine serum, 1% gentamicin and 1% L-glutamine at 37 C° in a 95% O₂/5% CO₂ atmosphere. Stable cell lines were developed by transfecting a cDNA encoding the mouse TMEM16A (ac variant) sub-cloned into the bi-cistronic expression vector pIRES2-EGFP (Clontech, Mountain View, CA, USA.). The PolyFect transfection reagent (Qiagen, Valencia, CA, USA) was used according to the manufacturer’s specification. After 24 h, the cells were transferred to 24-well plates at low density in DMEM medium supplemented with 1 mg/ml G418 (Sigma- Aldrich Co. St. Louis, MO, USA.). G418-resistant transformants were identified by EGFP fluorescence and expanded. Stable cell lines were maintained in medium supplemented with G418 at 500 µg/ml. Cells were seeded at low density on 5 mm circular coverslips before electrophysiological recordings.

Recording solutions

Table 1 lists the composition of external solutions (ES) and internal solutions (IS) used to record the Cl⁻ current activated by intracellular Ca²⁺ or V_m (I_Cl). IS with buffered Ca²⁺ was prepared using EGTA and Ca²⁺; the free [Ca²⁺]_i was estimated using MAXCHELATOR (maxchelator.stanford.edu). ES-140Cl and IS-40Cl/0.2Ca are control solutions. An IS with 5 µM [Ca²⁺]_i (IS-40Cl/5Ca) was used to activate fully TMEM16A and record I_Cl with long depolarizations in cells bathed with ES-140Cl. To analyse the activation of TMEM16A in zero [Ca²⁺]_i we used IS-40Cl/0Ca containing 25.2 mM EGTA and 50 mM HEPES. The Cl⁻ dependence of activation was studied using ES containing 140, 109, 70.5, 30, 10 or 1.5 mM [Cl⁻]_o. The pH of each solution was adjusted to 7.3 with TEA-OH or NaOH. ES was made hypertonic relative to the internal solutions to avoid activation of volume-sensitive Cl⁻ channels present in HEK293 cells [23]. Osmolarity was adjusted by adding D-mannitol and measured using the vapour pressure point method (VAPRO, Wescor Inc., South Logan, UT, USA). All chemicals were purchased from Sigma-Aldrich (Co. St. Louis, MO, USA.).

Table 1. Recording solutions.

External solutions with different [Cl⁻] were prepared by mixing solutions ES-136Cl⁻, ES-10Cl⁻ and ES-1.5Cl⁻ to obtain the required Cl⁻ concentration.

	External solutions (mM)
Compound	ES-140Cl	ES-140Na	ES-10Cl	ES-1.5Cl	ES-30Cl
TEA-Cl	139	-	9	0.5	29
NaCl		139	-	-
CaCl2	0.5	0.5	0.5	0.5	0.5
HEPES	20	20	20	20	20
D-Mannitol	100	100	300	320	330
Osmolarity (mosm/kg)	390	390	340	340	390
Total [Cl−]	140	140	10	1.5	30

	Internal solutions (mM)
Compound	IS-40Cl/0Ca	IS-40Cl/0.2Ca	IS-40Cl/0.8Ca	IS-40Cl/1.3Ca	IS-40Cl/5Ca	IS-40Cl/12Ca	IS-83Cl/0.2Ca
TEA-Cl	40	30	17	27.4	11.8	2	72.5
CaCl2	-	5.2	11.5	6.3	14.1	19	5.2
HEPES	50	50	50	50	50	50	50
D-Mannitol	90.2	85	150	154	85	85	-
EGTA-TEA	25.2	25.2	25	-	-		25.2
HEDTA	-	-	-	25	25	25	-
Osmolarity (mosm/kg)	290	290	290	290	290	290	288
Free [Ca2+] (µM)	0	0.2	0.8	1.3	5	12	0.2
Total [Cl−]	40	40	40	40	40	40	83

Electrophysiological recordings

We record I_Cl at room temperature using the whole cell configuration of the patch clamp technique. Cells were held at −60 mV and the V_m was changed stepwise from −100 mV to +160 mV or +180 mV in 20 mV increments, and then returned to −60 mV or −100 mV. Pulse duration varied between 0.5 to 20 s. I_Cl was recorded with an Axopatch 200B amplifier (Molecular Devices, Sunnyvale, CA, USA); currents were filtered at 5 kHz and digitized at 10 kHz for 0.5 s pulses. For 20 s pulses, the currents were filtered at 1 kHz and digitized at 2 kHz using pClamp software. Errors due to liquid junction potentials (−4.8 to −6.6 mV for our recording solutions) were minimized by using a 0.5 M KCl agar-bridge to ground the recording chamber and not corrected.

The effects of [Cl⁻]_o on TMEM16A activation were determined by measuring the magnitude of tail currents (I_tail) at −100 mV after a depolarising test pulse to +120 mV whose duration was varied from 0 to 3 s. The initial magnitude of I_tail after each pulse and each [Cl⁻]_o was used to calculate the tail conductance (Gt_ail) as a function of time and [Cl⁻]_o using Equation 1.

$$G_{\mathit{\text{tail}}}=\frac{I_{\mathit{\text{tail}}}}{V_m-V_{\mathit{\text{rev}}}}$$ Equation 1

where V_rev is the reversal potential of I_Cl. G(t,[Cl⁻]_o) was then normalized to the conductance obtained at the end of a 3 s test pulse with 140 mM Cl⁻. The resulting normalized G vs time curve represented the time course of TMEM16A activation at +120 mV at each [Cl⁻]_o. Dose-response curves were constructed using recordings obtained from patches excised from cells stably expressing TMEM16A. Patches were held at the desired V_m and exposed to increasing [Ca²⁺]_i ranging from 0 to 12 µM (Table 1) using a Fast-Step Perfusion System (VC-77SP Warner Instruments, Hamden, CT, USA). In between each [Ca²⁺]_i test solution, a control solution containing 0 Ca²⁺ and 25.2 mM EGTA was applied to check for changes in seal resistance. I_Cl was recorded with an Axopatch 200B amplifier, filtered at 1 kHz and digitized at 10 kHz.

Analysis and modelling

The magnitude of I_Cl at each V_m was converted to conductance using Equation 1. Normalization was carried out using either G_+120mV or G_max to obtain G_Norm (G/G_max or G/ G_+120mV), which is proportional to the apparent open probability of the channel. We extracted the time constants by fitting the data to a mono or bi-exponential function of the form:

$$y_0+a^{-t/\tau }\mathit{\text{ or }}{y}_0+a^{-t/{\tau }_f}+b^{-t/{\tau }_s}$$ Equation 2

where y₀ is the value of y when t→∞, t is the time, τ is a time constant, a and b are the contribution of fast and slow processes, and τ_f and τ_s are the fast and slow time constants [11], respectively. The dose-response curves were constructed using normalized currents; only patches with stable basal current obtained with 0 [Ca²⁺]_i were used. In each case the basal current was subtracted to obtain the magnitude of the current activated by a given [Ca²⁺]_i. The currents obtained from a particular patch were normalized to the maximum current estimated using equation:

$$\frac{{\mathrm{I}}_{\text{Cl}}}{{\mathrm{I}}_{\text{max}}}={\left[\frac{1}{1+\frac{{\text{EC}}_{50}}{{[{\text{Ca}}^{2+}]}_{\mathrm{i}}}}\right]}^{{\mathrm{n}}_{\mathrm{H}}}$$ Equation 3

where I_max is the estimated maximum current, EC₅₀ is the [Ca²⁺]_i needed to obtain I_max=0.5, and n_H is the Hill coefficient. To search for a kinetic scheme able to describe the time- and V_m-dependencies of I_Cl collected under a variety of experimental conditions we used Markov chain kinetic models [9] because they provide a good description of gating properties for different channels [24, 26, 28, 43, 48]. Different models with various discrete closed (C) and open (O) states were built using IChMASCOT software [10, 42]. Experimental and model I_Cl vs V_m, G_Norm vs [Ca²⁺]_i, and EC₅₀ were compared. Finally, by computing the probability of occupation of each of the kinetic states as a function of time we aimed to find the activation route(s) of TMEM16A. In the model, a given transition was controlled by forward and backward rate constants, which were V_m-dependent in most cases:

$${\mathrm{k}}_{\mathrm{f}}={\mathrm{k}}_{\mathrm{f},0}\ast {\mathrm{e}}^{\frac{z_{f}F{\mathrm{V}}_{\mathrm{m}}}{\mathit{\text{RT}}}}\text{ and }{\mathrm{k}}_{\mathrm{r}}={\mathrm{k}}_{\mathrm{r},0}\ast {\mathrm{e}}^{-\frac{z_{r}F{\mathrm{V}}_{\mathrm{m}}}{\mathit{\text{RT}}}}$$ Equation 4

where k_f and k_r are forward and backward rate constants, respectively, k_f,0 and k_r,0 are the values of k_f and k_r at V_m=0, z_f, z_r are the apparent gating charges associated with a given transition, F is the Faraday constant, R is gas constant, and T is the temperature. The most likely values of the rate constant parameters at V_m = 0 mV for a given model were obtained by best-fits as described in [12]. For that purpose, the squared differences between experimental and modelled values were minimized as follows:

$${\sum }_{i=1}^N{W}_i{\sum }_{j=1}^{M_i}{(E_{\mathit{\text{ij}}}-S_{\mathit{\text{iJ}}})}^2$$ Equation 5

and

$$W_i=\frac{w_i}{M_i{{\mathit{\text{WE}}}_{\mathit{\text{imax}}}}^2}$$ Equation 6

where N = number of different data sets included in the global fitting procedure; M_i = number of independent experimental observations in the dataset i; E_ij = experimental values of a given observation, S_ij = modelled values of a given observation; W_i = normalized weight factor for specific dataset; w_i = arbitrary weight factor for the measurement i; and E_imax = maximal experimental value for the dataset i. The global fit was repeated 15 times. The resulting values were averaged and then used for the final fit to obtain the values reported in Table 2. Subsequently, we simulated the steady-state activation properties of TMEM16A using the IonChannelLab software [44] along with the rate constants previously determined with IChMASCOT. The experimental conditions to be tested such as [Ca²⁺]_i, [Cl⁻]_o, [Cl⁻]_i, and V_m were included. To determine the most likely activation pathway, we calculated the probability (P) that TMEM16A stayed in a given state of a chosen gating kinetic model. For that purpose, the differential equations describing the time dependence of P (Equations 1 – 12 in Supplemental material) were numerically integrated using the Gear’s BDF method. P was calculated for 20 s depolarizations with 0.2 µM [Ca²⁺]_i, 140 mM and 30 mM [Cl⁻]_o and 40 mM [Cl⁻]_i and for 1 s depolarizations with 0 µM [Ca²⁺]_i, 140 mM and 30 mM [Cl⁻]_o and 40 mM [Cl⁻]_i using the rate constants listed in Table 2.

Table 2. Parameter values associated with the rate constants of Scheme IV.

(A) Figures listed were obtained from the global fit of TMEM16A data shown in Figures 5 and 6. z values are the apparent charge. (B) The relationship between forward and backward rate constants and weight factors l, L, h, H, m and M—which take into account the presence of Ca²⁺ in a given state. Grey boxes include weight factor values obtained from the global fit. Values shown in Italics and parenthesis (A and B) are averaged values obtained during the first 15 fit trials and were used as a seed for the final global fit. All listed parameter values were used for simulations of Scheme IV shown in Figures 7, 8 and 9.

A
Rate Constant	Expression	Parameter		Parameter Values At 0 mV
α1	${\alpha }_{1,0}{e}^{\frac{z_{\alpha }\mathit{\text{FVm}}}{\mathit{\text{RT}}}}$	α1,0 (s−1)		0.0077 (0.00803±0.00064)
		zα		0 (0±0)
β1	${\beta }_{1,0}{e}^{\frac{-z_{\beta }\mathit{\text{FVm}}}{\mathit{\text{RT}}}}$	β1,0 (s−1)		917.1288 (875.07±51.77)
		zβ		0.0064 (0.01133±0.0021)
kO1	$k_{O1,0}{e}^{\frac{z_1\mathit{\text{FVm}}}{\mathit{\text{RT}}}}$	kO1,0(s−1 µM−1)		597.9439 (583.58±14.41)
		z1		0 (0±0)
kO2	$k_{O2,0}{e}^{\frac{-z_2\mathit{\text{FVm}}}{\mathit{\text{RT}}}}$	kO2,0 (s−1)		2.8530 (2.8547±0.0189)
		z2		0.1684 (0.166±0.00118)
αCl1	$k_{1,0}{e}^{\frac{z_{l1}\mathit{\text{FVm}}}{\mathit{\text{RT}}}}$	k1,0 (s−1)		1.8872 (1.9349±0.0708)
		zl1		0.1111 (0.1141±0.00403)
βCl1	$k_{2,0}{e}^{\frac{-z_{l2}\mathit{\text{FVm}}}{\mathit{\text{RT}}}}$	k2,0 (s−1)		5955.783 (5769.96±207.83)
		zl2		0.3291 (0.3272±0.00346)
kCCl1	$k_{+\mathit{\text{Cl}},0}{e}^{\frac{z_{+\mathit{\text{Cl}}}\mathit{\text{FVm}}}{\mathit{\text{RT}}}}$	k+Cl,0(s−1 mM−1)		1.143×10−6 (1.14×10−6±9.17×10−8)
		z+Cl		0.1986 (0.2112±0.0238)
kCCl2	$k_{-\mathit{\text{Cl}},0}{e}^{\frac{-z_{-\mathit{\text{Cl}}}\mathit{\text{FVm}}}{\mathit{\text{RT}}}}$	k−Cl,0 (s−1)		0.0009 (8.52×10−4±1.28×10−5)
		z−Cl,0		0.0427 (0.04847±0.0098)
kOCl1	$k_{+\mathit{\text{Ol}},0}{e}^{\frac{z_{+\mathit{\text{Ol}}}\mathit{\text{FVm}}}{\mathit{\text{RT}}}}$	k+Ol,0 (s−1 mM−1)		1.1947 (1.1495±0.0459)
		z+Ol		0.6485 (0.65±0.0026)
kOCl2	$k_{-\mathit{\text{Ol}},0}{e}^{\frac{-z_{-\mathit{\text{Ol}}}\mathit{\text{FVm}}}{\mathit{\text{RT}}}}$	k−Ol,0		3.4987 (3.443±0.1096)
		z−Ol		0.0300 (0.0308±0.00054)
B
α2 = lα1	α3 = l2α1	β2 = Lβ1		β3 = L2β1
kCCl3 = hkCCl1	kCCl5 = h2kCCl1	kCCl4 = HkCCl2		kCCl6 = H2kCCl2
kOCl3 = mkOCl1	kOCl5 = m2kOCl1	kOCl4 = MkOCl2		kOCl6 = M2kOCl2
$k_{C1\mathit{\text{Cl}}}=\frac{h}{H}{k}_{O1}$	$k_{C2\mathit{\text{Cl}}}=\frac{l}{L}{k}_{O2}$	$k_{O1\mathit{\text{Cl}}}=\frac{m}{M}{k}_{O1}$		kO2Cl = kO2
${\alpha }_{\mathit{\text{Cl}}2}=\frac{\mathit{\text{Hml}}}{M}{\alpha }_{\mathit{\text{Cl}}1}$	${\alpha }_{\mathit{\text{Cl}}3}=\frac{{\mathit{\text{Hml}}}^2}{M^2}{\alpha }_{\mathit{\text{Cl}}1}$	βCl2 = hLβCl1		βCl3 = (hL)2βCl1
kC1 = kO1	$k_{C2}=\frac{l}{L}{k}_{O2}$	l = 41.6411 (42.04±1.7)	m= 0.0102 (0.010±0.00023)	h= 0.3367 (0.342±0.018)
		L= 0.1284 (0.134±0.004)	M= 0.0632 (0.064±0.001)	H= 14.2956 (14.2±0.70)

Figures and fits were constructed using Origin (Origin Lab, Northampton, MA). Data were plotted as mean ± SEM of n (number of independent experiments). Dashed black lines and arrows in each Figure indicate I_Cl=0. Where necessary, a Student t-test was used to evaluate statistically significant differences between data sets at P<0.05; as indicated by the * symbol.

RESULTS

Here we characterized the effects of V_m and [Cl⁻]_o on TMEM16A gating. We used these data to build a kinetic model to explain the contribution of V_m, Ca²⁺, and Cl⁻ to TMEM16A gating. Finally, using the model we predict the most likely pathway taken by the channel during activation.

Activation of TMEM16A in the absence of intracellular Ca²⁺

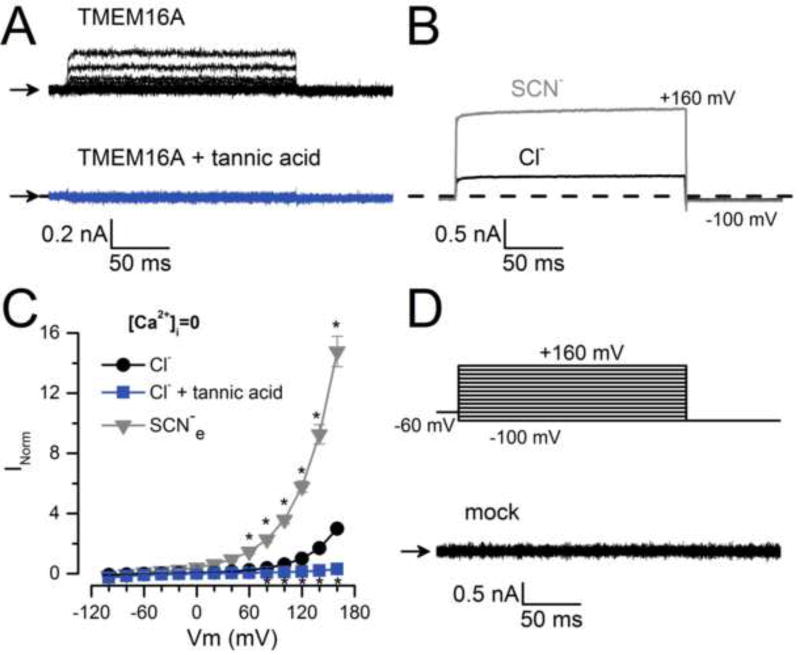
Under physiological conditions, CaCCs are activated by depolarization and increases in [Ca²⁺]_i [2, 27, 31, 35]. However, TMEM16A can be activated even when no Ca²⁺ is present on the cytosolic side [49]. Here we recorded whole cell Cl⁻ currents (I_Cl) in the absence of intracellular Ca²⁺ (with 25.2 mM EGTA). I_Cl displays fast onset kinetics and lacks an inward tail (I_tail) current upon repolarization to −100 mV (Figure 1A, black traces). The current is inhibited with 100 µM tannic acid, a TMEM16A blocker (Figure 1A, bottom panel). To strengthen the assertion that the current was carried through TMEM16A in the absence of intracellular Ca²⁺, we replaced external Cl⁻ with SCN⁻, a more permeable anion that accelerates opening and retards channel closing [36, 49]. Figure 1B shows representative current traces recorded at +160 mV from a cell bathed first with 140 mM Cl⁻ then 140 mM SCN⁻. This manoeuvre increased the current (Figures 1B and 1C, triangles), consistent with SCN⁻ permeating through TMEM16A. However, we could not determine a definite reversal potential of the current in zero [Ca²⁺]_i to calculate the permeability ratio P_SCN/P_Cl. In contrast, I_Cl was negligible at every V_m in cells transfected with an empty vector (Figure 1D). These results indicate that the I_Cl recorded in zero Ca²⁺ is flowing through TMEM16A activated by V_m and not through some other endogenous conductance.

Fig. 1. Activation of TMEM16A in zero intracellular Ca²⁺.

(A) Representative I_Cl recordings (n=5) obtained from HEK293 cells expressing TMEM16A, bathed in a solution containing 0 (black traces) or 100 µM tannic acid (grey traces). (B) Representative current traces (n=5) obtained from the same cell bathed in 140 mM Cl⁻ (black) or 140 mM SCN⁻ (grey). Currents evoked by pulses to +160 mV followed by repolarization to −100 mV. (C) I_Cl−V_m relationships from cells bathed in [Cl⁻]_o=140 mM (circles), [Cl⁻]_o=140 mM + 100 µM of tannic acid (squares), or 140 mM SCN⁻ (triangles). For each cell, whole cell currents were normalized to the current magnitude recorded at +120 mV from control cells bathed in [Cl⁻]_o=140 mM. Normalized currents from different cells were averaged and plotted. (D) Lack of I_Cl (n=6) in mock transfected cells dialyzed with a solution containing 40 mM [Cl⁻]_i. In A and D the [Cl⁻]_o was 140 mM and the I_Cl were generated using the protocol shown in D. In all experiments, cells were dialyzed with 0 µM [Ca²⁺]_i +40 mM [Cl⁻]_i (IS-40Cl/0Ca).

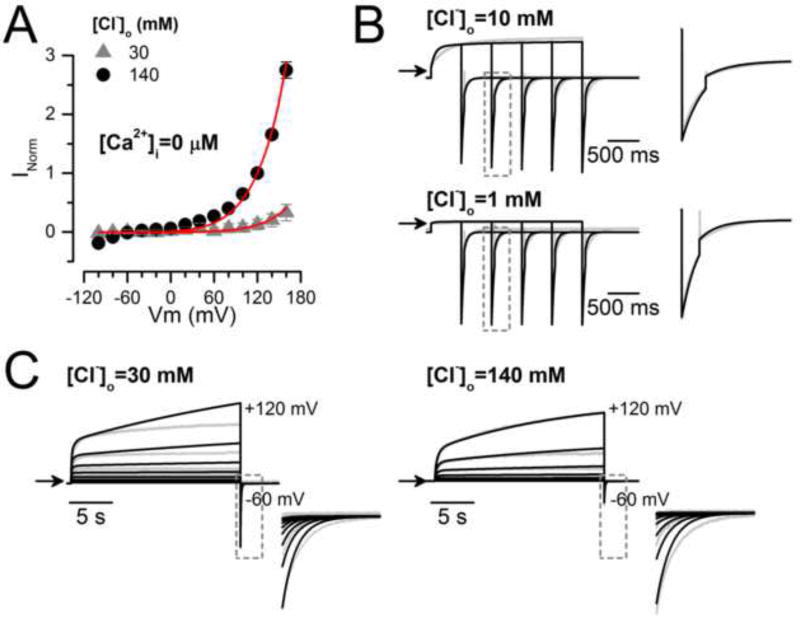
Cl⁻-dependence of TMEM16A gating

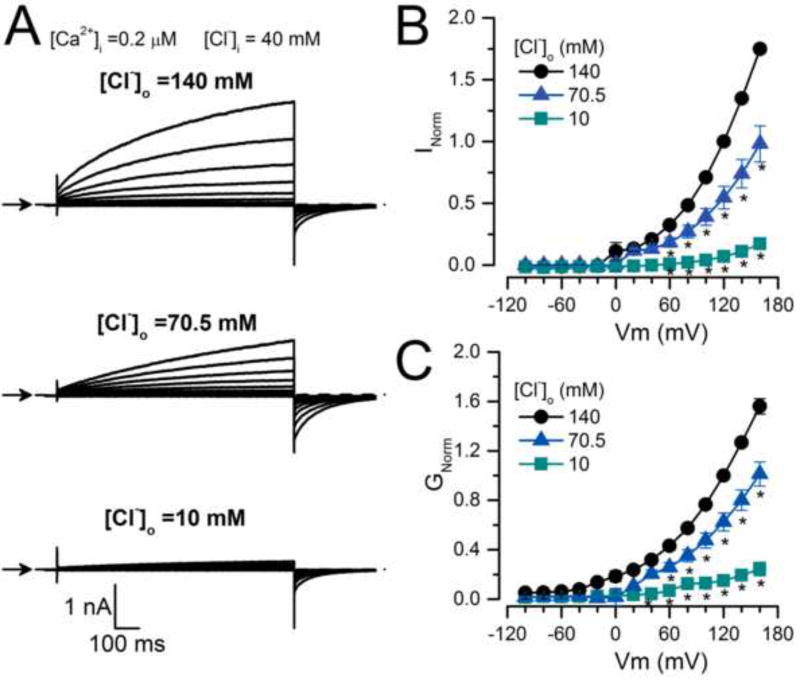
To analyse the effect of extracellular Cl⁻ we recorded I_Cl at different [Cl⁻]_o. Figure 2A shows examples of I_Cl recorded from the same cell dialyzed with an IS containing 0.2 µM [Ca²⁺]_i, 40 mM [Cl⁻]_i, that was sequentially exposed to 140 mM, 70 mM and 10 mM [Cl⁻]_o. The I_Cl magnitude decreased when [Cl⁻]_o was reduced. This is summarized in the I_Cl vs V_m curves in Figure 2B. Since reduction of [Cl⁻]_o from 140 mM to 10 mM increased the driving force (V_m−V_rev) from −92.6 ± 2.5 mV to −146.2 ± 4.6 mV, we expected a 1.6-fold increase in I_tail amplitude at −100 mV. However, I_tail in 10 mM Cl⁻ did not increase; instead it fell drastically; the mean I_{tail_10mM}/I_{tail_140mM} ratio was 0.78 ± 0.05 (n=7). The time constant values of I_tail at −100 mV after the pre-pulse to +160 mV were 47 ± 4 ms and 43.7 ± 3.1 ms with 140 mM and 10 mM [Cl⁻]_o, respectively, indicating no change in kinetics. When the conductance was calculated using the current magnitude at the end of each pulse and normalized using the value at +120mV (G_Norm), we observed a 5-fold conductance drop at each V_m (Figure 2C) when [Cl⁻]_o was reduced from 140 mM to 10 mM. Thus, at low external [Cl⁻]_o the apparent open probability of TMEM16A declines.

Fig. 2. TMEM16A chloride conductance depends on [Cl⁻]_o.

(A) Representative I_Cl recordings (n=7) obtained from the same cell sequentially bathed in ES containing 140, 70.5 and 10 mM [Cl⁻]_o and dialyzed with an IS containing 0.2 µM [Ca²⁺]_i + 40 mM [Cl⁻]_i (IS-40.5Cl/0.2Ca). Cells were held at −60 mV, then stepped for 0.5 s to voltages ranging from −100 mV to +160 mV in 20 mV increments and repolarised to −100 mV. Note that I_tail at −100 mV did not increase despite the increased driving force for Cl⁻ (i.e. driving force = −92.6 ± 2.5 mV with [Cl⁻]_o 140 mM and −146.2 ± 4.6 mV with 10 mM [Cl]_o). (B) I_Cl vs V_m relationships at the indicated [Cl⁻]_o. (C) G_Norm vs V_m curves at the indicated [Cl⁻]_o. I_Cl and G were normalized to either I_Cl or G obtained at +120 mV with [Cl⁻]_o=140 mM. External solutions with different [Cl⁻]_o were prepared by mixing ES-136Cl and ES-1.5Cl.

To determine the effects of [Cl⁻]_o on time-dependent activation we recorded I_tail from the same cell sequentially exposed to 140, 109, 70, 30, 10 and 1.5 mM. The cells were dialyzed with an IS containing 0.2 µM Ca²⁺ and 40 mM Cl⁻. Figure 3A shows representative recordings. Tail currents were obtained at −100 mV after a +120 mV depolarization as shown in the voltage protocol. In this case, we lengthened the depolarization from 0.5 s to 3 s in 0.5 s increments. At 140 mM [Cl⁻]_o the I_tail amplitude (indicated by arrows) increased with longer pulses. In contrast, with 10 mM [Cl⁻]_o the I_tail magnitude was smaller. This finding could be explained if gating is dependent on [Cl⁻]_o. In Figure 3B, G_Norm at the indicated [Cl⁻]_o is plotted as a function of pulse duration. The graph shows that decreasing the [Cl⁻]_o from 140 mM to 10 mM produces a 3- fold reduction in G_Norm. A 5-fold decrease in G_Norm is observed when comparing 140 mM with 1.5 mM [Cl]_o. At [Cl⁻]_o ≤ 30 mM, G_Norm levelled off and the G_Norm vs time curves were described by a single exponential function (solid lines) with τ = 293.7 ± 17 ms and 334 ± 19.6 ms for 1.5 mM and 10 mM [Cl⁻]_o, respectively. However, with [Cl⁻]_o >30 mM, only the initial part (time ≤ 0.5 s) of the curves was described by a single exponential because as pulse duration increased G_Norm rose in an almost linear fashion. τ = 368.2 ± 23 ms and 353.4 ± 23.1 ms for 109 mM and 140 mM [Cl⁻]_o, respectively.

Fig 3. Extracellular Cl⁻ regulates TMEM16A gating.

(A) I_Cl recordings from the same cell bathed in 140 mM (left) or 10 mM [Cl⁻]_o (right). I_Cl was recorded using the V_m protocol shown in the inset. The duration of the test pulse increased from 0 to 3 s in 0.5 s steps. Arrows indicate the peak current amplitudes at −100 mV. (B) The magnitude of I_tail recorded as in A was used to determine the conductance at each time and [Cl⁻]_o (n=5). G_Norm was calculated using the G obtained with [Cl⁻]_o=140 mM and a 3s depolarization. Note that a single exponential can not describe the entire time course (continuous lines) when [Cl⁻]_o ≥ 30 mM. (C) G_Norm(t) plots obtained from a cell stimulated with a 20 s depolarization to +140 mV and dialyzed with 0.2 µM Ca²⁺ (IS-40.5Cl/0.2Ca). The cell was exposed to 140 mM (left, ES-140Cl) and then to 30 mM (right, ES-30Cl) [Cl⁻]_o. I_Cl was converted to G(t) and then normalized using the G value at +140 mV to determine G_Norm(t) at each [Cl⁻]_o (n=4–8). G_Norm(t) plots were fit with a bi-exponential function (continuous lines) to obtain τ_s, τ_f and fractional contribution of each component. Note that the y-scale bar is 1 and 0.1 for 140 and 30 mM Cl⁻, respectively. (D) TMEM16A-I_Cl recorded from cells dialyzed with 5 µM [Ca²⁺]_i (IS-40Cl/5Ca) and depolarized to +100 mV. I_Cl from each cell was normalized to I_Cl obtained with a 20 s depolarization and then normalized values were averaged (n=8). The continuous line is the fit to a mono-exponential function.

In cells bathed with a solution containing 140 mM or 30 mM [Cl⁻]_o we extended the duration of the V_m pulses to 20 s and found that I_Cl displayed a second mode of gating, something we previously reported [11]. Figure 3C shows that the conductance was reduced nearly 22-fold upon switching from 140 mM to 30 mM [Cl]_o (note the scale bar is 10-times smaller for 30 mM [Cl]_o). At 140 mM [Cl⁻]_o (left) the G_Norm(t) at +140 mV continuously increased for the entire 20 s pulse duration. The time course had a fast (τ_f = 448.1 ± 26.3 ms) onset followed by a slower rise (τ_s = 19.1 ± 3.8 s). The contributions of the fast and slow components were 0.17 ± 0.04 and 0.83 ± 0.04, respectively. With 30 mM [Cl⁻]_o, G_Norm(t) was described by a τ_f of 368.6 ± 55.5 ms and τ_s of 6.2 ± 1.5 s; however, the fractional contribution of the fast and slow phases were reversed: 0.92 ± 0.1 and 0.08 ± 0.1, respectively. These observations reinforce the conclusion that TMEM16A gating depends on [Cl⁻]_o. We next asked if the Cl⁻ effect on gating would also occur in the presence of high [Ca²⁺]_i, a condition that maximally activates TMEM16A [49]. To test this, we recorded I_Cl from cells dialyzed with 5 µM [Ca²⁺]_i. Figure 3D shows a trace obtained by averaging the current from 8 cells that were bathed in 140 mM [Cl⁻]_o and depolarized to +100 mV for 20 s and then repolarizsed to −60 mV. Under these conditions, I_Cl did not display dual gating, instead the current had a monoexponential time course with τ of 3.7 ± 0.36 s. Taken together, our data demonstrate that TMEM16A gating is dependent on external Cl⁻ but the Cl⁻ effects are attenuated when high [Ca²⁺]_i activates the channel.

Kinetic analysis of TMEM16A gating

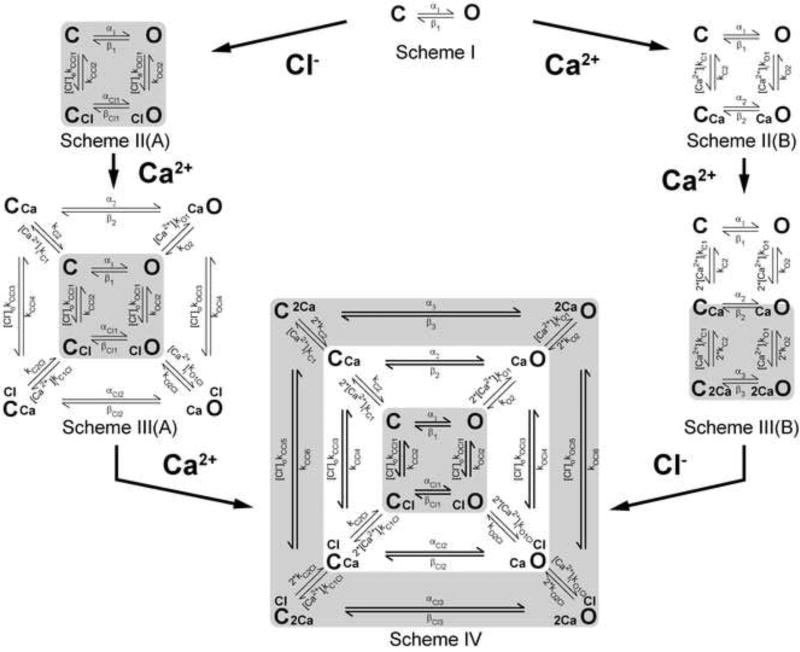
The data in Figures 1, 2 and 3 as well as evidence cited in the Introduction highlight the complexity of TMEM16A activation. In an effort to have an integrated view of the activation mechanism we constructed a kinetic model that takes into account the V_m, Ca²⁺, and [Cl⁻]_o dependencies of TMEM16A. Scheme IV in Figure 4 presents a 12-state model with 26 free parameters that satisfactorily reproduce the V_m, Ca²⁺ and Cl⁻ dependencies of channel activation. The model was built based on the following experimental data and assumptions:

1. TMEM16A can be activated by V_m in the absence of intracellular Ca²⁺ and the presence of extracellular Cl⁻ as shown in Figure 1 (see also [49]).

2. Intracellular Cl⁻ plays no role in TMEM16A activation. This observation is based on experiments where the V_m-dependence of TMEM16A was nearly identical in the presence of 40 and 88 mM [Cl⁻]_i (data not shown).

3. TMEM16A can be activated in a cooperative way by V_m, intracellular Ca²⁺, and Cl⁻ (Figures 2 and 3).

4. The interaction between intracellular Ca²⁺ and TMEM16A is a V_m-dependent process [49].

5. Binding of at least 2 Ca²⁺ ions activates TMEM16A as suggested by dose-response curves and structural data [5, 17, 35, 49, 52].

6. Binding of the two Ca²⁺ ions occurs in a sequential manner with the same single site-affinity.

Activation of TMEM16A by V_m in cells dialyzed with 0 µM [Ca²⁺]_i (Figure 1) was described as a simple closed-open (C ⇆ O) transition. This condition is represented by Scheme I in Figure 4 where α₁ and β₁ are forward and backward rate constants (Equation 4) that change exponentially with V_m [15, 16].

Fig 4. Kinetic model employed to explain the V_m, Ca²⁺, and Cl⁻ contributions to TMEM16A gating.

Scheme I represents V_m-dependent transitions in the absence of intracellular Ca²⁺ and external Cl⁻. C and O are closed and open states, and α₁ and β₁ are V_m-dependent rate constants. Scheme II(A) represents the transitions in the presence of one external Cl⁻ when [Ca²⁺]_i =0. [Cl⁻]_ok_CCl1 and [Cl⁻]_ok_OCl1 are rate constants controlling Cl⁻ association to C and O configurations, while k_CCl2, k_OCl2 rate constants control Cl⁻ dissociation. Scheme III(A) results after binding of one Ca²⁺ to states represented in Scheme II(A). The [Ca²⁺]_ik_O1, [Ca²⁺]_ik_O1Cl, [Ca²⁺]_ik_C1Cl and [Ca²⁺]_ik_C1 are Ca²⁺ association rate constants while k_O2, k_O2Cl, k_C2Cl and k_C1 are Ca²⁺ dissociation rate constants. The subscript Cl indicates rate constants associated with Cl⁻-occupied transitions. Scheme II(B) represents transitions resulting after binding of one intracellular Ca²⁺ to C and O states depicted in Scheme I. [Ca²⁺]_ik_C1, [Ca²⁺]_ik_O1 are rate constants controlling Ca²⁺ association to C and O configurations, while k_C2, k_O2 rate constants control Ca²⁺ dissociation. Scheme III(B) represents the transitions resulting after binding of an additional Ca²⁺ to states shown in Scheme II(B). Association and dissociation of the second Ca²⁺ was assumed to be same as for the first Ca²⁺ binding reaction. Scheme IV results after binding of an additional Ca²⁺ to states shown in Scheme III(A). The association and dissociation rate constants were the same as that for the first Ca²⁺ binding (left pathway). Alternatively, Scheme IV could be achieved after binding of one external Cl⁻ to states shown in Scheme III(B) with forward rate constants [Cl⁻]_ok_CCl5, [Cl⁻]_o k_CCl3, [Cl⁻]_ok_CCl1, [Cl⁻]_ok_OCl1, [Cl⁻]_ok_OCl3 and [Cl⁻]_ok_OCl5 and backward rate constants k_CCl6, k_CCl4, k_CCl2, k_OCl2, k_OCl4 and k_OCl6. Concentric kinetic cycles with states connected by wider arrows indicate cycles that did not satisfy microscopic reversibility. Table 2A shows the Equations for each rate constant.

In the presence of Cl⁻, a channel dwelling in C or O states can bind Cl⁻ and move into C_Cl and _ClO states (see Scheme II(A) in Figure 4). The rate constants [Cl⁻]_ok_CCl1, k_CCl2, [Cl⁻]_ok_OCl1, and k_OCl2 control the C ⇆ C_Cl and O ⇆ _ClO transitions in the presence of external Cl⁻, while α_Cl1 and β_Cl1 control the C_Cl ⇆ _ClO transitions. A subsequent increase in intracellular Ca²⁺ will drive the channel into one of the following states: C ⇆ C_Ca, O ⇆ _CaO, C_Cl ⇆ _ClC_Ca and _ClO ⇆ _ClO_Ca (see Scheme III(A), Figure 4). These transitions are controlled by forward rate constants [Ca²⁺]_ik_C1, [Ca²⁺]_ik_C1Cl, [Ca²⁺]_ik_O1Cl and [Ca²⁺]_ik_O1 and backward rate constants k_C2, k_C2Cl, k_O2Cl and k_O2 (described by Equation 4). Previous fast perfusion experiments show that upon Ca²⁺ removal the current deactivates in a V_m-dependent manner [49]. Therefore, only the rate constants controlling unbinding of Ca²⁺, k_O2, k_C2, k_C2Cl and k_O2Cl are V_m-dependent. The rate constants controlling Ca²⁺-binding are V_m-independent. Depending on their permeability anions can facilitate channel activation [36] and decrease the amount of Ca²⁺ needed to produce half-maximum activation [4, 39]. Based on this we introduced an effect of Ca²⁺ on the rate constants (k_CCl and k_OCl) controlling the C ⇆ C_Cl and O ⇆ _ClO transitions. This effect of Ca²⁺ is represented in the model by weight parameters l, L, h, H, m and M. Table 2B lists the relationship between rate constants and weight factors. Finally, the Ca²⁺ dose-response curves suggest that at least two Ca²⁺ are needed to activate TMEM16A [2, 27, 35, 47, 49, 52]. The binding of an additional Ca²⁺ to the channels leads to Scheme IV. In this new scheme we presuppose that: 1) the open and closed state can bind Ca²⁺ with different affinity, and 2) within each state both Ca²⁺ ions bind with the same single site affinity.

Alternatively, when both intracellular Ca²⁺ and Cl⁻ are present, a channel dwelling between C and O states (Scheme I) can bind two Ca²⁺ ions to move into Schemes II(B) and III(B), respectively. The transitions between C and O states are controlled by rate constants [Ca²⁺]_ik_C1, k_C2, [Ca²⁺]_ik_O1 and k_O2. Next binding of one external Cl⁻ to channels in Scheme III(B) leads to Scheme IV. Note that binding of just one Cl⁻ by channels represented in Scheme II(B) leads to Scheme III(A). Since Cl⁻ permeates through the channel, then we do not expect that all cycles of Scheme IV will satisfy microscopic reversibility. Cycles represented with states connected by wider arrows did not satisfy the reversibility principle.

The models depicted by Schemes III(A) and IV take into account the contribution of V_m, Ca²⁺, and Cl⁻ to gating and hence can be used to describe the properties of TMEM16A. To test them we performed a global fit of data describing the V_m, Ca²⁺, and Cl⁻ dependence of gating. The experimental data used in the global fits included:

1. I_Cl vs V_m curves obtained from cells dialyzed with 0 Ca²⁺ and 40 mM Cl⁻ and bathed in 140 mM or 30 mM Cl⁻.

2. Mean I_Cl traces obtained from cell dialyzed with [Ca²⁺]_i = 0, 0.2 and 1 µM and stepped to V_m ranging from −100 mV to 160 mV.

3. Representative I_Cl traces obtained by fast perfusion of 20 µM [Ca²⁺]_i to excised patches held at V_m from −100 mV to 100 mV in 20 mV increments.

4. Mean I_Cl recordings obtained from cells sequentially exposed to 1 mM, 10 mM and 140mM [Cl⁻]_o.

5. Mean I_Cl recordings obtained from cells dialyzed with 0.2 µM [Ca²⁺]_i and 40 mM [Cl⁻]_i while bathed in 140 mM or 30 mM [Cl⁻]_o and depolarized to −20 mV to +120 mM for 20 s.

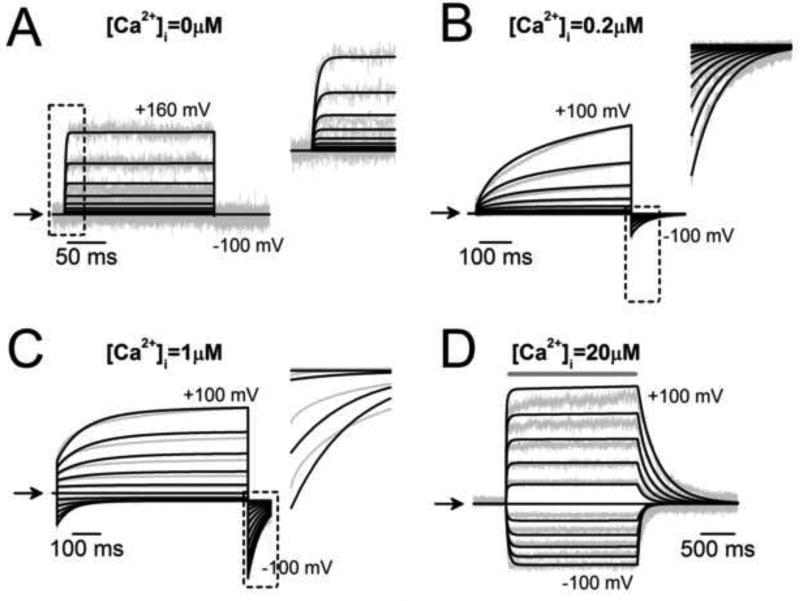
The inclusion of such a wide range of data in the global fit constrained the value for the rate constants and ensured the robustness of our model. The model depicted in Scheme III(A), which included only one Ca²⁺ bound, partially reproduced TMEM16A activation. It was not able to describe activation at very high [Ca²⁺]_i, the kinetics of tail currents in cells dialyzed with 1 µM Ca²⁺, or I_Cl generated with 20 s pulses from cells exposed to 30 mM Cl⁻ (Supplemental Figures 1 and 2). In contrast, Scheme IV, which included two Ca²⁺ ions bound, described the data reasonably well. The results are shown in Figures 5 and 6 as solid black traces (fits) superimposed on the experimental data (grey lines). Figures 5 A, B and C show fits of Scheme IV to I_Cl recorded from different cells dialyzed with 0, 0.2 and 1 µM [Ca²⁺]_i. Figure 5D displays the fits of I_Cl generated by rapid perfusion with 20 µM [Ca²⁺]_i to inside-out patches held from −100 mV to +100 mV. The model fit the entire traces nicely. The model was able to fit the fast onset of the currents recorded at 0 [Ca²⁺]_i (inset in A), the fast tail currents recorded with 0.2 µM Ca²⁺ (inset in B) and the fast on and off time courses of the current activated with 20 µM Ca²⁺. However, the model did not describe well the tail current recorded with 1 µM Ca²⁺ (inset in C). Similarly, Scheme IV was able to fit the I_Cl−V_m relationships obtained from cells exposed to 30 and then 140 mM [Cl⁻]_o in the absence of intracellular Ca²⁺ (Figure 6A, grey and black circles) and the I_tail recorded from different cells exposed to 10 and 1 mM [Cl⁻]_o, dialyzed with 0.2 µM [Ca²⁺]_i and 40 mM [Cl⁻]_i (Figure 6B). Scheme IV also fitted the mean I_Cl recorded with 20 s depolarizations from cells exposed to 30 mM and 140 mM [Cl⁻]_o and dialyzed with 0.2 µM [Ca²⁺]_i and 40 mM [Cl⁻]_i (Figure 6C). Here we can see that the model described quite well I_Cl recorded in the presence of 140 mM Cl⁻ but not 30 mM Cl⁻. Fast components, such as the tail currents (right insets in B and C) at both [Cl⁻] were well described. The overall global fit goodness of the model with the binding of Ca²⁺ to two sites with the same affinity (k_O2/ k_O1), given by the regression coefficient (R²) associated with the minimization process had a value of 0.98 (Equation 5). We also tested the alternative model that considers different Ca²⁺ affinities for the two Ca²⁺ binding sites: k_O2/ k_O1 for the first site and c* k_O2/ k_O1, for the second site, where c is a constant parameter. This model fits the data with the same R²=0.98 as that obtained with Scheme IV with two sites with the same affinity. However, the binding affinities only varied by a factor of 0.61and the V_m-dependence of EC₅₀ was indistinguishable from that obtained assuming the same affinity. Therefore, we consider that Scheme IV with two Ca²⁺ binding sites with the same affinity was a reasonable model of TMEM16A and can be used to obtain the rate constant parameters and the apparent charge (z) values for Scheme IV. Table 2 lists these values. The z values indicate that most of the V_m-dependence is conferred by: a) the charge transferred during the Ca²⁺ unbinding steps controlled by k_o2 (z=0.168), b) the transition C_Cl ⇆ O_Cl controlled by α_Cl1 (z=0.11) and β_Cl1 (z=0.32), and c) the Cl⁻ binding steps to C or O conformations controlled by k_CCl1 (z=0.2) and k_OCl (z=0.65), respectively.

Fig 5. Global fit using Scheme IV to TMEM16A recordings obtained at different V_m and [Ca²⁺]_i.

Best fits were performed with the IChMASCOT software; solid lines are fits and grey lines are data. (A–C) Fits to I_Cl recordings obtained between −100 mV to +100 mV (20 mV increments) from cells dialyzed with 0 (A), 0.2 (B), or 1 (C) µM [Ca²⁺]_i. D Best fits to data obtained by fast perfusion with 20 µM [Ca²⁺]_i to an inside-out patch held at V_m between −100 mV to +100 mV. The insets in A, B and C show magnified fits to fast phases of I_Cl enclosed in black squares. I_Cl shown in A and B were recorded from cells dialyzed with [Cl⁻]_i = 40 mM; C and D were from cells exposed to symmetrical 140 mM Cl⁻.

Fig 6. Global fit using Scheme IV to TMEM16A recordings obtained at different [Cl⁻]_o.

Grey lines are data and solid lines are best fits to: (A) I−V_m relationships obtained with 30 mM and 140 mM [Cl⁻]_o from cells dialyzed with a zero Ca²⁺ solution; (B) I_Cl recorded from the same cell exposed to 10 mM and 1 mM [Cl⁻]_o, dialyzed with 0.2 µM [Ca²⁺]_i and stimulated with the V_m protocol shown in Figure 3A; (C) I_Cl recorded from cells exposed to 30 mM and 140 mM [Cl⁻]_o, dialyzed with 0.2 µM [Ca²⁺]_i and stimulated with 20 s pulses from −20 mV to +120 mV. Data in B and C were obtained from cells dialyzed with [Cl⁻]_i = 40 mM. The right insets in B and C show magnified fits to fast phases of I_tail enclosed in grey squares. The R² value for the global fits shown in Figures 5 and 6 was 0.98.

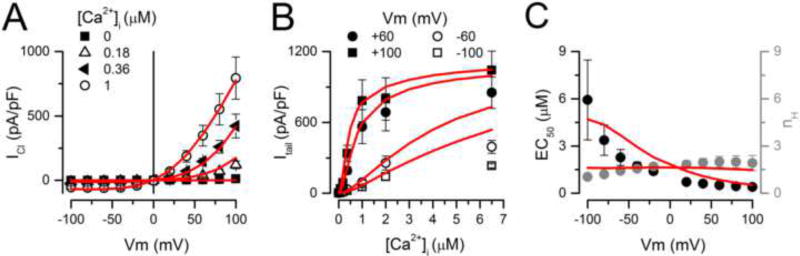
If these global fits are a realistic representation of TMEM16A gating, then Scheme IV plus the set of parameter values listed in Table 2 should be able to predict the quasi-steady-state properties of TMEM16A. These properties include I_Cl−V_m curves, Ca²⁺ dose-response curves, and the V_m-dependence of EC₅₀ and the Hill coefficient. We chose these fingerprint properties because they have been well characterized by different laboratories [2, 19, 27, 31, 32, 35]. Our approach consisted of simulating TMEM16A currents under different [Ca²⁺]_i and V_m using IonChannelLab software [44] as described in Methods. Then we used the simulated I_Cl to construct I_Cl−V_m curves and Ca²⁺ dose-response curves. To make a stringent comparison, we compared the simulated properties to previously published data [49]. Data was from cells dialyzed with [Ca²⁺]_i ranging from 0 to 6.5 µM, and stimulated with 0.7 s pulses from −100 mM to +100 mV. Figure 7 shows superimposed experimental data (black symbols) and model predictions (solid lines) for I_Cl vs V_m relationships at the indicated [Ca²⁺]_i (Figure 7A), dose-response curves to [Ca²⁺]_i at different V_m (Figure 7B), and V_m-dependence of EC₅₀ and the Hill coefficient n_H (Figure 7C). These properties of TMEM16A, except the EC₅₀, were adequately predicted by Scheme IV and its associated rate constants. Nevertheless, the EC₅₀ value predicted by the model at +60 mV/140 mM [Cl⁻]_o was 0.85 µM, which is within the range of values determined experimentally [2, 17, 22, 35, 49].

Fig 7. Scheme IV mimics the I_Cl vs V_m, dose-response curve to [Ca²⁺]_i and the EC₅₀/n_H vs V_m relationships for TMEM16A channels.

Black symbols correspond to experimental data. Solid lines are simulations using Scheme IV. (A) Current Density vs V_m relationships. (B) Current Density as a function of [Ca²⁺]_i at the indicated V_m. (C) EC₅₀ for TMEM16A Ca²⁺ activation and the Hill coefficient nH vs V_m. EC₅₀ and n_H values were obtained from B. The experimental data was collected using [Cl⁻]_i=[Cl⁻]_o= 140 mM and 0.7 s depolarizations. The same conditions were used in the simulations. All simulations were carried out using the IonChannelLab software and the rate constants listed in Table 2. R² = 0.95.

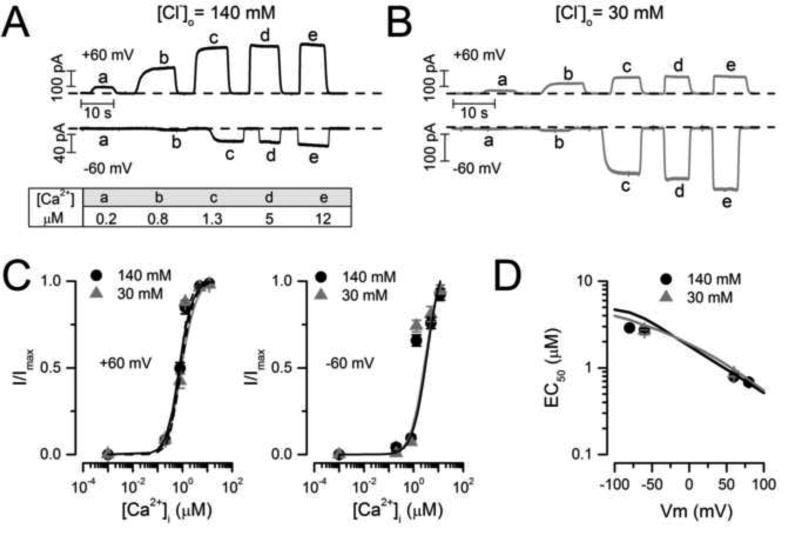
Finally, it has been shown that anions more permeable than Cl⁻ modify CaCC and TMEM16A gating [36, 49]. Importantly, anions more permeable than Cl⁻ increase the apparent Ca²⁺ sensitivity of TMEM16A and TMEM16B [4, 39]. In this work, we show that increasing [Cl⁻]_o facilitates gating, but whether or not this effect is due to an increased Ca²⁺ sensitivity is unknown. Therefore, we used the model to predict whether extracellular Cl⁻ regulates TMEM16A gating by altering its Ca²⁺ or voltage sensitivity. Dose-response curves to Ca²⁺ were calculated using Scheme IV with 140 mM or 30 mM [Cl⁻]_o and V_m = +60/−60 mV. The model predicts that neither the apparent Ca²⁺ sensitivity nor the V_m-dependence of EC₅₀ are altered by decreasing [Cl⁻]_o. To determine whether this prediction is true, we determined the dose-response curves to Ca²⁺ for TMEM16A using inside-out patches held at ± 60 and ± 80 mV in 140 mM or 30 mM [Cl⁻]_o. Figures 8A and 8B show typical raw I_Cl traces obtained from two different patches bathed in 140 mM (A) and 30 mM (B) Cl⁻ while the [Ca²⁺]_i was changed between zero and the concentrations indicated by the small letters. Upward deflections are records obtained at +60 mV while downward deflections are records obtained at −60 mV. Clearly I_Cl at +60 mV saturated when [Ca²⁺]_i was around 5–12 µM regardless of the [Cl⁻]_o present. At −60 mV, I_Cl nearly saturated with 12 µM [Ca²⁺]_i. Figure 8C shows the resulting dose-response curves at +60 mV (left) and at −60 mV (right). The data (black and grey circles) nicely matched the values predicted by Scheme IV (solid lines). Furthermore, the predicted V_m-dependence of EC₅₀ was also matched by the experimental data (continuous lines and symbols in Figure 8D). The EC₅₀ value of 0.85 µM predicted by the model at +60 mV and 140 mM [Cl⁻]_o was similar to those experimentally reported: 1.5, 1.3, 0.4, 1.5, and 0.79 ± 0.05 µM [27, 46, 48, 49, this work]. Taken together these results demonstrate that external Cl⁻ does not alter Ca²⁺-sensitivity in TMEM16A. The fact that our kinetic model predicted this result is a good indication of the model robustness and that the model includes critical information about the mechanism of TMEM16A gating.

Fig 8. The apparent Ca²⁺ sensitivity of TMEM16A was not altered by lowering the [Cl⁻]_o.

A–B Typical I_Cl recordings from inside-out patches held at ± 60 mV and exposed to 140 mM (A) or 30 mM [Cl⁻]_o (B). I_Cl were activated by applying 0, 0.2 (a), 0.8 (b), 1.3 (c), 5 (d) and 12 µM [Ca²⁺]_i (e). Dashed lines indicate I_Cl obtained with 0 [Ca²⁺]_i and 25.2 mM EGTA. (C–D) Dose-response and EC₅₀ vs V_m curves (symbols) obtained from experimental data like that shown in A and B were identical to the predictions made with Scheme IV at 30 (grey lines) and 140 (black lines) mM [Cl⁻]_o.

Activation pathways

Since Scheme IV was able to reproduce the activation properties of TMEM16A, we decided to apply the model to determine what would be the most likely pathway(s) followed by TMEM16A during the activation process. For this purpose, we calculated the probability (P) that TMEM16A visited each of the 12 states when intracellular Ca²⁺, external Cl⁻, and V_m were varied (Supplemental material). To obtain a gating pathway we determined the most likely state to be occupied once the channel visited a given state. For example, when the channel visits state C, it can go to O, C_Cl or C_Ca states. Our P value calculations indicated that state C_Ca was the most likely state to be occupied. We repeated this strategy to find the next most probable state to be visited until the channel reached _ClO_2Ca. First, we consider activation of TMEM16A by a 0.5 s depolarization to +120 mV followed by repolarization to −60 mV when [Ca²⁺]_i = 0, [Cl⁻]_i = 40 mM and [Cl⁻]_o changed between 140 mM and 30 mM. This condition is represented by the pink kinetic scheme box in Figure 9C. The time-dependent P values for states C, O, C_Cl, and _ClO are shown in Figure 9A. P_C, P_O, P_CCl and P_ClO values were 0.782, 0, 0.217 and 0.0008, when [Cl⁻]_o was 140 mM. After external Cl⁻ was decreased to 30 mM P_C increased to 0.941, while P_CCl and P_ClO fell to 0.057 and 0.0002, respectively. Thus, in the absence of intracellular Ca²⁺ the most likely gating route is C → C_Cl → _ClO (Figure 9C, blue and pink arrows).

Fig 9. TMEM16A activation pathways predicted by Scheme IV.

(A) Time dependent P_C, P_O, P_CCl and P_ClO when [Cl⁻]_o was 140 mM (blue lines) or 30 mM (red lines) while [Ca²⁺]_i and [Cl⁻]_i were 0 M and 40 mM, respectively. Note that P_O was ≈ 0 at both [Cl⁻]. (B) Time dependent P_C, P_CCl, P_CCa, P_ClCCa, P_ClOCa, P_C2Ca, P_O2Ca, and P_ClO2Ca are shown in rectangles coloured according to the colours of the layers of Scheme IV presented in panel C. Left column: [Ca²⁺]_i = 0.2 µM, [Cl⁻]_o/[Cl⁻]_i=140/40 mM. Right column: [Ca²⁺]_i = 0.2 µM, [Cl⁻]_o/[Cl⁻]_i=30/40 mM. P_O, P_ClO, P_OCa, and P_ClC2Ca are not shown for clarity, their values were ≈ 0. P values were calculated by numerically integrating the differential equations (supplemental material) under the following conditions: [Cl⁻]_o =140 mM or 30 mM, [Cl⁻]_i = 40 mM, [Ca²⁺]_i = 0 (A), 0.2 (B) µM, and 20 s pulse to +140 mV followed by repolarization to −60 mV. The set of rate constants listed in Table 2 was used to obtain the time dependence of occupation probability. (C) TMEM16A activation pathways according to probability of occupation. Blue and pink arrows indicate the pathway in the absence of intracellular Ca²⁺ while [Cl⁻]_o was 140 mM or 30 mM, respectively. Black, grey, green and light green arrows indicate the activation pathways when intracellular Ca²⁺ was 0.2 µM while [Cl⁻]_o was 140 mM (black and green lines) or 30 mM (grey and light green lines). [Cl⁻]_i was set at 40 mM. Red button = Ca²⁺, blue donut = Cl⁻.

Subsequently, P values were calculated when [Ca²⁺]_i was 0.2 µM, [Cl⁻]_o was either 140 or 30 mM, [Cl⁻]_i = 40 mM, and V_m was +120 mV during 20 s followed by repolarization to −60 mV. These experimental conditions are the same as the ones used for collecting data shown in Figure 3C (right) and data collected using short depolarizations. Figure 9B shows P values for states in the inner circle (pink), middle circle (white), and outer circle (grey), respectively. When [Cl⁻]_o was 140 mM (left column), the depolarization induced an abrupt decrease of P_C, followed by a further exponential decrease. Such decrease was mirrored by an abrupt increase and then exponential decrease in P_CCa. At the same time, P_ClOCa and P_C2Ca increased little, and P_O2Ca increased transiently. Notably, P_ClO2Ca increased steadily reaching 0.4 by the end of the 20 s depolarization. The same trend was observed when [Cl⁻]_o was 30 mM, albeit the magnitude of P for each state declined. Interestingly, during the first 2 s into the depolarization P_ClC decreased but then increased in a time-dependent manner. In summary, in the presence of 0.2 µM [Ca²⁺]_i and 140 mM or 30 mM [Cl⁻]_o, TMEM16A activation proceeded following two pathways. At early times (<2 s), the route C → C_Ca → C_2Ca → O_2Ca → _ClO_2Ca (black arrow) was preferred. However, as depolarization continued, the route C → _ClC → _ClC_Ca → _ClO_Ca → _ClO_2Ca (green arrow) also contributed to the total current. The effect of lowering [Cl⁻]_o to 30 mM was to decrease the contribution of both routes to the total current (grey and light green arrows). From these calculations, we observed that the greatest contribution to the total current is given by the active states _CaO_Cl, _2CaO and _2CaO_Cl. Therefore the net effect of increasing chloride from 30 to 140 mM was to increase P_CaOCl and P_2CaOCl.

DISCUSSION

CaCC gating is a complex process; it involves the combined action of V_m, Ca²⁺ and Cl⁻. Several kinetic models have been previously proposed to explain the V_m and Ca²⁺-dependence of CaCC gating [2, 20, 27]. However, these early models assumed an initial Ca²⁺-dependent C ⇆ C_Ca transition and did not consider a C ⇆ O transition in the absence of Ca²⁺ or the role of external Cl⁻ in gating. These models predict an open probability of zero at any V_m if [Ca²⁺]_i = 0, which is not the case for TMEM16A [49]. In this work, we present an alternative kinetic model that satisfactorily accounts for the V_m, Ca²⁺, and Cl⁻-dependent gating of TMEM16A channel. We propose that the gating of the TMEM16A Cl⁻ channel is caused by consecutive direct V_m-dependent binding of two intracellular Ca²⁺ ions, coupled to a V_m-dependent binding of external Cl⁻. External Cl⁻ facilitates gating by binding to a Ca²⁺-free closed state and favouring the transition to Ca²⁺-bound open states. By means of facilitating the _2CaO ⇆ _2CaO_Cl transition, external Cl⁻ induces the slow gating [11]. In our model (Scheme IV) the direct Ca²⁺-binding is controlled by forward rate constants that are independent of voltage and V_m-dependent backward rate constants. The off-rate constant measured from simulations with the model predicted that Ca²⁺ remains attached to the channel at depolarized voltages. This coincides with experimental data showing that at depolarized V_m the rate of current decay—due to Ca²⁺ washout—is very slow compared to that observed at negative V_m. Also, increasing the [Ca²⁺]_i decreases the off rate of whole cell currents at negative potentials [2, 27, 52]. Such data show that Ca²⁺ unbinding is a V_mdependent phenomenon [19, 27, 35, 49, 52]. Thus, the open state is stabilized when Ca²⁺ is high, and/or V_m is depolarized.

The model is not perfect. It cannot describe well I_tail recorded with 1 µM Ca²⁺ and I_Cl recorded in the presence of 30 mM Cl⁻ using 20 s depolarizations. Also, the EC₅₀ is not adequately predicted by Scheme IV. There are different possibilities to explain these discrepancies. The rate constants are relatively simple; they are exponential functions of V_m and depended linearly on [Cl⁻]_o. However, such dependence could be state dependent and/or be more complicated. The weight factors (l, L, h, H, m, and M) are assumed to be constant and we considered that only one Cl⁻ ion is needed affect channel gating without affecting the single channel conductance. These assumptions may not hold under all experimental conditions. Finally, for simplicity, we assumed that Ca²⁺ binds to two sites with a single binding affinity which we call single-site affinity. This may not be the case as suggested by mutagenesis experiments which show that mutations located in different parts of the protein alter Ca²⁺ sensitivity [17, 47, 49, 52]. Inadequacies of one or all these variables would hinder the ability of the model to reproduce the data. Refining the model to include the exact number of Ca²⁺ binding sites, their binding affinity and allosteric interactions with Cl⁻ would be more realistic as more structural data becomes available. In addition, our model ignores the permeation process. Including this property would be necessary to understand the effects of pore occupancy by permeant anions on channel gating [4, 36, 39]. Despite these limitations, Scheme IV predicted no change in the apparent Ca²⁺ affinity of TMEM16A when [Cl⁻]_o was lowered from 140 mM to 30 mM, and this prediction was successfully corroborated experimentally. The model also predicts that a small fraction of the charge (z₂ = 0.17) is transferred during the Ca²⁺ unbinding steps. This number agrees with the small V_m-dependence of the dose-response curves to [Ca²⁺]_i [2, 22, 35, 49]. We consider that Scheme IV was effective because a large data set was used to extract the rate constant parameters. This tactic largely constrained the possible values of the rate constant parameters and contributed to enhance the robustness of the model.

The effect of external Cl⁻ on CaCCs is maybe more complex than previously anticipated since our data show that varying external Cl⁻ alters both the fast and slow gating modes of TMEM16A and TMEM16B [11]. In addition, our model-dependent calculations using the rate constants listed in Table 2 revealed that external Cl⁻ ion plays a significant role on V_m-dependent activation in the absence of Ca²⁺. Under this condition, there is a substantial amount of charge transferred during the Cl⁻ binding steps to either C or O conformations as indicated by z_+Cl = 0.2 and z_+Ol = 0.65 (Table 2A). The binding of one Cl⁻ to the C conformation of the channel prompts its conversion into _ClC and subsequently the _ClO state. The later transition is also accompanied by charge transferred as indicated by z_l1 = 0.11 and z_l2 = 0.33 (Table 2). The _ClO state would enable Cl⁻ conductance in the absence of intracellular Ca²⁺. Furthermore, when Ca²⁺ is bound to the channel the external Cl⁻ favours the _2CaO ⇆ _2CaO_Cl transition and so the slow component of channel gating arises. In fact, by increasing [Cl⁻]_o from 30 mM to 140 mM in the presence of 0.2 µM [Ca²⁺]_i we observed an increase in P_2CaOCl + P_CaOCl from 0.08 to 0.22, suggesting that Ca²⁺ remains bound to the channel for a longer time. Also, an increased occupation of the _2CaO_Cl state implies a longer dwell time of the channel in this state. High [Cl⁻]_o shifted to negative values the V_m-dependence of occupation for the _2CaO_Cl state such that at a given V_m the probability of occupation is increased with high [Cl⁻]_o. Despite these changes, the overall apparent affinity of TMEM16A for Ca²⁺ was not altered. However, previous experimental observations suggest a coupling of the permeation and gating mechanisms. For example, highly permeant anions alter the kinetics and EC₅₀ as described for CaCC from mouse parotid acinar cells, Xenopus oocytes and TMEM16B [4, 36, 38, 39]. These data can be reconciled considering that TMEM16A may have two anion binding sites as previously suggested [38] and the external anions might alter TMEM16A gating by at least two mechanisms. One mechanism may involve permeation and gating, while another mechanism may affect only gating, similar to what we describe here. Our idea describes the effect of external Cl⁻ onTMEM16A based on what has been proposed for other Cl⁻ channels. For example, in CLC-0 and CLC-1 external anions have a profound facilitating effect on gating [7, 14, 37] and in CLC-2 V_m-dependence is conferred by permeant anions that occupy and then exit the pore [25, 41]. Thus, the role of permeant anions in gating the Cl⁻ channels may be more important that thought in the past. More research is needed to establish the connection between permeation and gating.

TMEM16A gating shares some similarities with BK channel gating. For example, both channels display coupling between V_m and Ca²⁺ binding, both channels are activated by V_m alone, and increments in [Ca²⁺]_i lead to a leftward shift of the G_Norm(V_m) curve. However, there are also differences: BK has an intrinsic V_m sensor and TMEM16A does not, Ba²⁺ activates BK channels by interacting with the Ca²⁺ binding site but Ba²⁺ also binds and blocks the conduction pathway of BK channels while Ba²⁺ only activates TMEM16A [24, 33, 34, 49, 52, 53]. Allosteric models have been successful in explaining the interaction between V_m and Ca²⁺ in the gating of BK channels [24]. Although TMEM16A gating is not exactly like the gating of BK channels, an allosteric model should be considered for TMEM16A channel.

Our findings could be relevant to TMEM16A function under physiological conditions. For example, the model could be helpful to understand the behaviour of TMEM16A during agonist-stimulated Ca²⁺-dependent fluid secretion. Secretory epithelial cells response to agonist include an oscillatory membrane potential accompanied by oscillations in the intracellular [Ca²⁺]_i [30]. Furthermore, during fluid and electrolyte secretion by acinar cells, [Cl⁻]_i decreases from about 61 to 29 mM [18] due to Cl⁻ exit through TMEM16A channels [40]. Under these conditions, Cl⁻ would transiently increase on the extracellular side which would favour activation of TMEM16A to sustain secretion. Although the TMEM16A activation pattern may very complex under physiological conditions, it can be understood using Scheme IV.

In summary, we propose a TMEM16A gating mechanism caused by consecutive direct V_m-dependent binding of two intracellular Ca²⁺ ions, coupled to a V_m-dependent binding of one external Cl⁻.