Perceptual learning in clear displays optimizes perceptual expertise: Learning the limiting process

Abstract

Human operators develop expertise in perceptual tasks by practice or perceptual learning. For noisy displays, practice improves performance by learned external-noise filtering. For clear displays, practice improves performance by improved amplification or enhancement of the stimulus. Can these two mechanisms of perceptual improvement be trained separately? In an orientation task, we found that training with clear displays generalized to performance in noisy displays, but we did not find the reverse to be true. In noisy displays, the noise in the stimulus limits performance. In clear displays, performance is limited by noisiness of internal representations and processes. Our results suggest that training in one display condition optimizes the limiting factor(s) in performance in that condition and that noise filtering is also improved by exposure to the stimulus in clear displays. The asymmetric pattern of transfer implies the existence of two independent mechanisms of perceptual learning, which may reflect channel reweighting in adult visual system. These results also suggest that training operators with clear stimuli may suffice to improve performance in a range of clear and noisy environments by simultaneous learning by two mechanisms.

Perceptual learning (1–4) can improve the performance of observers significantly, creating perceptual expertise (5, 6). Practice on a stimulus and task often results in very substantial improvements reflected in improved accuracy or in an ability to perform at a given threshold accuracy level with a more difficult (e.g., lower contrast) stimulus. Also, perceptual learning accrued by practice often exhibits specificities to stimulus characteristics such as retinal position (2, 7), orientation (8, 9), or scale (10, 11), demonstrating perceptual rather than strategic knowledge. Refs. 1 and 12 proposed the possible existence of three independent mechanisms of perceptual learning and empirically documented the existence of two of the mechanisms: external-noise filtering and stimulus amplification. The mechanisms are characterized and tested by a perceptual template model (PTM) of the human observer with titrated external-noise manipulations (12–14). The two mechanisms are important in different environments: external-noise filtering or exclusion in noisy environments and stimulus amplification in clear environments. Perceptual learning in these two mechanisms reflects the improvements in different kinds of limitations: improvements in the quality of the information in the stimulus by external-noise filtering and improvements in the intrinsic limitations in the processing of the human observer by stimulus enhancement.

In these investigations of perceptual learning in visual tasks (1, 12, 15), training in high and low noise have always been intermixed, so that the two documented mechanisms have often occurred together as mixtures (for exception, see ref. 16). Single-mechanism models have provided one explanation for simultaneous learning (15). However, improvements in performance for noisy stimuli and improvements in performance for clear stimuli in these designs could reflect improvements in quite distinct mechanisms; yet, because each mechanism receives an approximately equal amount of training in any interval because of the intermixed noise-training schedule, both are learned together. Here, we address the question of whether these two mechanisms can be trained independently. In other words, is specific practice or training in each noise condition necessary to optimize performance in that condition?

In this experiment, the training with clear and noisy stimuli is separated in time, and transfer to the other noise context is measured. This training protocol is designed to reveal the consequences of independent training of the two mechanisms, corresponding to clear and noisy stimuli. Training in a simple object orientation identification task exhibited an asymmetric pattern of transfer after training with low-noise or high-noise exemplars. Training with low-noise exemplars transferred to high-noise performance, whereas training with high-noise exemplars [in which target objects were embedded in white external noise (12, 17)] did not transfer to low-noise performance. Low-noise conditions required direct practice, independent of the experience in high-noise conditions. When external noise dominates any internal sources of noise or inefficiencies, only the external-noise-limited processes are improved. The internal noise or inefficiencies that are important in performance with clear stimuli cannot be trained in high noise, a result that is incompatible with single-mechanism theories. However, experience with clear stimuli trains amplification but also provides the experience with the stimulus that allows filtering to be trained. Training yielded improvements only in the limiting process(es). This result has practical as well as theoretical implications.

Materials and Methods

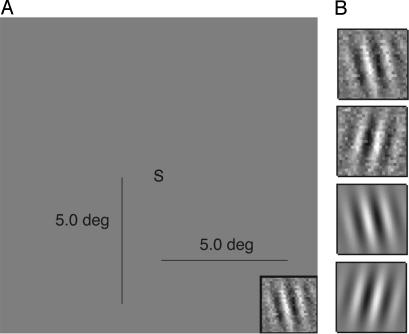
Observers performed a perceptual task in which they discriminated between two orientations (±8° from vertical) of a briefly presented Gabor stimulus 8° in the lower-right periphery (Fig. 1). The Gabor is a sine wave of 1.6 cycles per degree that is windowed by a Gaussian with of σ = 0.6° with peak contrast c (background luminance of 19.5 cd/m²). In the high-noise condition, the Gabor was combined with a random-noise mask (2 × 2°, Gaussian distributed pixel noise of σ = 0.33 × 19.5 cd/m²). A central task in which a target S or 5 appeared simultaneous with the Gabor encouraged fixation (2, 12). Improvements in contrast threshold c were measured at two criteria (70.7% correct or 1.087 d′ and 79.3% correct or 1.634 d′) with adaptive staircase methods (18) in which maximum Gabor contrast c was reduced by 10% after either two or three correct responses, respectively, and increased by 10% after each error. This task paradigm has shown substantial joint learning in both high and low noise in studies using intermixed training protocols (1, 12). Two pretest measurements in each noise condition were followed by successive blocks of practice/training in the high- or low-noise conditions. Each measurement (block) corresponds to 180 trials of practice. Error bars were generated by Monte Carlo bootstrap methods on individual trials.

Fig. 1.

Task display and sample stimuli. Observers identify the orientation (θ of ± 8°) of a Gabor patch with a digit/letter (5/S) task at fixation. (A) Layout of the stimulus display, with Gabor patches in the lower right quadrant and digit/letter task at fixation. (B) Sample Gabor patches in clear and noisy displays, in which the Gabor patch is combined with white, random Gaussian pixel noise. Observers identified the tilt (top left or right of vertical) of the Gabor patch.

Results

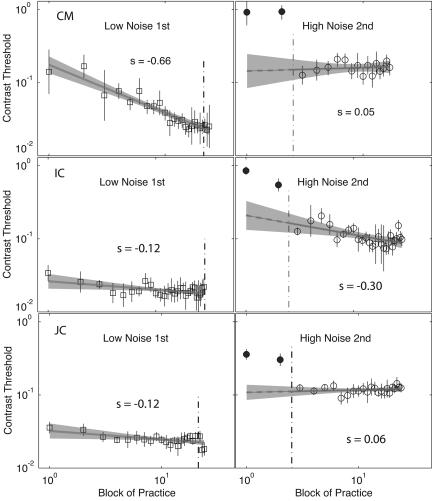
For the observers trained first in low noise (low→high) (Fig. 2), initial training (Left) showed substantial improvements in low-noise displays, described as a linear function of log₁₀ contrast threshold versus log₁₀ practice blocks, evaluated by regression analysis (see Table 1 for statistics). This pattern of improvement is generally consistent with a power-law function of practice (19, 20), with slopes of –0.12 log units for two observers. The third observer (C.M.), with a slope of –0.65, has unusually high initial thresholds for both low- and high-noise conditions but exhibited the same pattern. Subsequent performance in high noise (Fig. 2 Right) benefited noticeably from training in low noise. The transfer effect (estimated improvement between pretest thresholds and transfer in a two-intercept regression) averaged 0.51 (log units) of contrast threshold. Indeed, training in low noise was so effective that additional improvement from additional high-noise training was negligible (F <1) for two of the observers and modest for a third observer. Training with low-noise displays improved performance in both low- and high-noise environments.

Fig. 2.

Threshold training improvements and transfer for three observers trained first in low noise (low→high). The log₁₀ contrast threshold is shown, averaged over two adaptive staircases (75% accuracy), versus log₁₀ practice block for the initial training in low noise (Left) and the posttransfer training in high noise (Right), which includes two pretraining baseline threshold measures. Error bars indicate 95% confidence intervals for each threshold, and the 95% confidence region around the regression lines are shaded in gray. Filled circles to the left of the vertical line were collected in pretesting or in phase 1, and points to the right of the vertical line were collected in phase 2 or posttesting.

Table 1. Learning slopes for first and second training phases and transfer index.

	Low→high noise			High→low noise
Training/transfer statistics	CM	IC	JC	CD	KL	RW
Phase 1 slope	-0.65	-0.12	-0.12	-0.34	-0.24	-0.64
Phase 1 intercept	-0.73	-1.58	-1.49	-0.66	-0.62	-0.31
r2	0.81**	0.31**	0.36**	0.73**	0.63**	0.79**
Phase 2 slope	0.05	-0.30	0.03	-0.15	-0.14	-0.07
Phase 2 intercept	-0.85	-0.63	-0.96	-1.55	-1.54	-1.54
r2	0.04ns	0.40**	0.03ns	0.43**	0.45**	0.16ns
Transfer index	0.91*	0.10ns	0.52**	-0.16ns	0.03ns	0.31ns

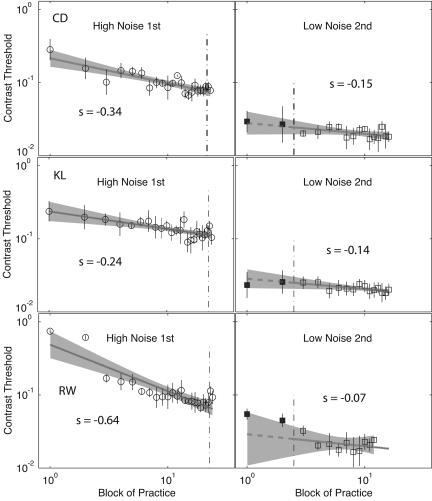
Learning slopes from regressions of (log₁₀) contrast threshold on (log₁₀) practice block, including the two pretest blocks in the first stage and excluding the two pretest blocks in the second stage. Transfer is tested as a nested F on regressions with and without an independent intercept for the pretest stimuli in the second stage, with df = 1,21. P < .1; *, P < .05; **, P < .01; ns, nonsignificant.

For the observers trained first in high noise (high→low) (Fig. 3), initial training (Left) resulted in performance improvements, with slopes of –0.24 to –0.64 log units per log practice block. Training in high-noise displays did not reliably transfer to low-noise performance. The baseline pretest measurements fall on or near (F < 1) the improvement line extrapolated from subsequent low-noise practice improvements. Subsequent training in low noise (Right) results in additional learning, with magnitudes (average, –0.12 log units) typical of initial low-noise training. We speculate that high-noise experience did not alter substantially the rate of learning in subsequent low-noise training (discounting unusual observer C.M.), but the current experiment does not provide a strong test of this hypothesis. The specificity of high-noise training here is unusually strong because the target stimuli and tasks are identical except for the noise context; other examples of specificity in the literature (21, 22) typically involve different stimuli or tasks.

Fig. 3.

Threshold training improvements and transfer for three observers trained first in high noise (high→low). The log₁₀ contrast threshold is shown, averaged over two adaptive staircases (75% accuracy), versus log₁₀ practice block for the initial training in high noise (Left) and the pretest baseline (two points) and the posttransfer training in low noise (Right). Error bars indicate 95% confidence intervals for each threshold, and the 95% confidence region around the regression lines are shaded in gray. Filled circles to the left of the vertical line were collected in pretesting or in phase 1, and points to the right of the vertical line were collected in phase 2 or posttesting.

Fits of an observer model (PTM) (12) to the thresholds estimated from the two criterion thresholds over training blocks (mean, r² = 0.95; range, 0.93–0.97) led to similar conclusions. This procedure provides stronger tests that estimate the transfer as the number of equivalent training blocks (see Appendix). The model (1, 12) characterizes performance improvements in terms of the following two mechanisms: improved external noise filtering and stimulus amplification, with separate power law improvements in these two mechanisms. Transfer from training in high noise to subsequent low-noise performance was negligible (F <1), estimated as 0–2 blocks of effective training from the 22 blocks of high-noise practice. Transfer from training in low noise to subsequent high-noise performance was substantial (all P < 0.01), estimated as 15–25 blocks of training from the 22 blocks of low-noise practice. Thus, this analysis directly estimates essentially no transfer from high-noise training to low-noise performance, and substantial (I.C.) to essentially full transfer (C.M. and J.C.) from low-noise training to high-noise performance.

In summary, initial training in either high or low noise exhibited improved performance, well approximated by a power function (19, 20) on contrast thresholds. Despite the existence of individual differences often exhibited in perceptual learning data, the overall pattern was quite consistent. Training in low-noise displays transferred, either completely or substantially, to high-noise displays. Indeed, low-noise training of high-noise performance was so effective for some subjects that little or no subsequent improvements occurred in the noisy condition with additional practice. In contrast, training with high-noise displays did not consistently improve subsequent performance in low-noise tests. This experiment was not designed to compare learning rates in low noise in the two groups explicitly, but we speculate that pretraining with high-noise displays had little effect on the learning rate. This asymmetry in transfer-result pattern appears to be robust because we have subsequently observed a similar pattern in a motion-perception task.

Discussion

This deceptively simple pattern of asymmetric transfer of training between clear and noisy conditions has wide-ranging consequences for models of the observer, perceptual learning, and perceptual expertise. The pattern rules out a single-mechanism account of perceptual learning. Two distinct mechanisms of perceptual learning (and attention), one mechanism that is effective only in low-noise displays and another mechanism that is effective only in high-noise displays, have been observed in numerous studies (16, 23, 24). The fact that one mechanism could be observed without the other mechanism implies that the two mechanisms are independent. This study further documents independence in a situation in which both mechanisms are generally expressed. Whether two independent mechanisms appear together in a particular situation depends on whether the training protocol trains both mechanisms simultaneously or is effective only in training one or the other. In this study, the high-noise training protocol impacted only the external-noise-filtering mechanism, whereas the low-noise training protocol impacted both external-noise filtering and stimulus-enhancement mechanisms.

Visual perception is always limited both by the quality of the information in the stimulus and by limitations in the processing of the human observer (14, 17). In high-noise conditions, the external noise in the stimulus is the important limiting factor in performance (14, 17). Learned optimization of performance for noisy tests works to reduce, or filter, the impact of external noise, equivalent to training the perceptual template. In high-noise displays, amplification of the stimulus would amplify signal and external noise alike, and reduction of nonlimiting internal noise would similarly be of no benefit. However, training in clear displays requires the system to work to reduce internal limitations (or equivalently amplify the stimulus) but also provides good information about the nature of the target stimulus or the perceptual template. Although an optimized template is far more critical in noisy displays, template tuning may nonetheless occur in low-noise training by optimization of information about the stimulus,¶ or possibly by repetitive task-relevant exposure to the signal stimuli (25, 26). Training the template in (low-contrast) low-noise displays may be sufficient to optimize the filtering of external noise substantially, especially when the external noise is white.

The human visual system represents the visual stimulus by activity in an ensemble of basic visual channels tuned to various scales and orientations. External noise may be excluded by focusing on the representations that most closely match the target (signal) stimulus, whereas minimizing input from representations that convey noise but not signal. In white noise, an ideal observer will use a template or templates approximately matched to the signal(s). In comparing performance at the beginning and the end of training, the pattern of performance changes is a natural consequence of optimization of weighting of the basic channels to reduce or eliminate inputs from irrelevant channels in favor of the small subset of channels best matched to the target stimuli (1). Low-noise training under some circumstances simultaneously trains both mechanisms. This study suggests that training in clear (low-noise) displays may suffice to optimize performance in a range of clear and noisy task environments. Here, white noise was used, and thus, the noise spectrum is flat. In situations in which noise is nonwhite, the noise environment cannot be known in advance. Training in clear displays should remain useful, but training in the nonwhite noise environment may also be necessary to further optimize performance for the particular qualities of the external noise.

From a practical perspective, perceptual expertise in certain tasks may be needed in noisy as well as in clear operating environments. Noisy stimuli occur in both natural viewing because of crowding or camouflage (27) and alternative sensor environments, such as night-vision, radar, and medical imaging displays (28, 29). Is specific practice or training in each given environment necessary to optimize performance? Our results indicate that training in clear displays of performance-relevant stimuli may have unique advantages.

Appendix

The PTM (1, 12, 13) predicts the performance accuracy of the observer, d′, based on the fundamental signal-to-noise (both internal and external) relations:

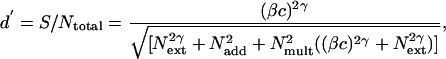where c is the contrast of the target (signal) stimulus, 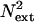is the power of the external noise in the stimulus, 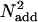is equivalent additive internal noise (the amount of internal noise necessary to account for limitations in performance associated with absolute threshold), 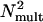is equivalent multiplicative internal noise (reflecting noise that increases with the base contrast of the stimulus), β is a scaling factor representing the strength of the response of the perceptual template to the signal stimulus, and γ incorporates nonlinearity in transduction (∥•∥^γ). Rearranging the contrast threshold required to achieve a particular accuracy level d_i is as follows:

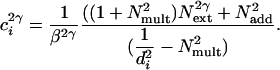Independent mechanisms (i) filter external noise 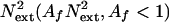noise or (ii) reduce internal additive noise 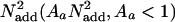These independent mechanisms of improvement may be trained independently. Here, we assume a power-law improvement in each mechanism with training (A_f(t) = 1.0t^{–α f} and A_a(t) = 1.0t^{–α a}). Values of practice, t, are counted here in blocks of trials. To assess transfer between the initial phase of learning and the second phase of learning, the number of blocks for observations after the first two (pretest) values was set at t = t + t*, where t* is an estimated parameter that captures the extent of transfer in units of practice blocks. If t* is estimated at 0, then there is no transfer. Increasing values of t* indicate larger amounts of transfer, and when t* is estimated at or near the number of training blocks in the first phase, then transfer is estimated as essentially full.

The PTM was fit to the 3:1 (d′= 1.6337) and 2:1 (d′= 1.0061) staircase contrast threshold data from the high-noise and low-noise conditions. The ratio of thresholds for the two staircases was 1.2–1.3 for all six observers, which is significantly smaller (P < 0.001) than the contrast threshold ratio of 1.623 predicted by a linear amplifier model (LAM) (15, 30) (P < 0.001), a reduced form of the PTM with 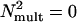and γ = 1, associated with a single-mechanism form of learning (30). This result is consistent with a wide range of prior results that also require the full PTM with two independent mechanisms of learning. Statistical comparisons occur by using nested F tests on nested models with eliminated or constrained parameters.