Arterial Input Functions Determined From MR Signal Magnitude and Phase for Quantitative Dynamic Contrast-Enhanced MRI in the Human Pelvis

Abstract

Dynamic contrast-enhanced (DCE) MRI is often used to measure the transfer constant (K^trans) and distribution volume (v_e) in pelvic tumors. For optimal accuracy and reproducibility, one must quantify the arterial input function (AIF). Unfortunately, this is challenging due to inflow and signal saturation. A potential solution is to use MR signal phase (ϕ), which is relatively unaffected by these factors. We hypothesized that phase-derived AIFs (AIF_ϕ) would provide more reproducible K^trans and v_e values than magnitude-derived AIFs (AIF_|S|). We tested this in 27 prostate dynamic contrast-enhanced MRI studies (echo time = 2.56 ms, temporal resolution = 13.5 s), using muscle as a standard. AIF_ϕ peak amplitude varied much less as a function of measurement location (inferior–superior) than AIF_|S| (5.6 ± 0.6 mM vs. 2.6 ± 1.5 mM), likely as a result of ϕ inflow insensitivity. However, our main hypothesis was not confirmed. The best AIF_|S| provided similar reproducibility versus AIF_ϕ (interpatient muscle K^trans = 0.039 ± 0.021 min⁻¹ vs. 0.037 ± 0.025 min⁻¹, v_e = 0.090 ± 0.041 vs. 0.062 ± 0.022, respectively).

Dynamic contrast-enhanced MRI (DCE-MRI) involves rapid, continuous imaging during and after the administration of a gadolinium (Gd)-based contrast agent (GdCA). The time series of images is analyzed to obtain physiological information about the microvasculature of the tissue such as K^trans, the volume transfer constant for exchange between blood plasma and the extravascular extracellular space, and v_e, the volume of the extravascular extracellular space per unit volume of tissue (1,2). This dynamic technique has many applications in the human pelvis, most importantly in characterizing tumors. DCE-MRI has been used for tumor staging, prediction of outcome, and detection of recurrence (3–7), as well as monitoring the response of tumors to treatment (8–10).

To maximize DCE-MRI accuracy and reproducibility, absolute quantification of GdCA concentration vs. time in tissue and arterial blood (arterial input function or AIF) is necessary (11–14). Unfortunately, as in other body regions, quantification of the AIF in the pelvis (using the aorta, iliac, or femoral arteries) is challenging due to saturation, inflow and nonuniformity of the B₁ field of the radiofrequency pulses across the volume of interest (2,12,13,15–19). Often the AIF is found to be so difficult to measure that a population-averaged AIF is used instead (1,3,7,8,10).

A potential solution for the AIF problem is the use of MR signal phase (ϕ), which is normally discarded once the magnitude MR images are reconstructed. ϕ is linear with GdCA concentration (i.e., no saturation), is less sensitive to B₁ variations, and can provide absolute measures of GdCA concentration (12,13,15–17). Moreover, ϕ is relatively unaffected by inflow, due to the fact that ϕ in blood is not biased by the inflow-related increase in the MR signal magnitude (|S|) (12). Furthermore, ϕ can be obtained from any gradient-echo-based DCE-MRI pulse sequence, without the need for additional measurements or specialized pulse sequences.

In this work, ϕ was saved for 27 routine prostate DCE-MRI exams. Using obturator internus muscle (OIM) as a reference (i.e., assuming that this muscle has the same K^trans and v_e values in all of our subjects), we hypothesized that individually measured phase-derived AIFs (AIF_ϕ) would provide more reproducible K^trans and v_e values than individually measured magnitude-derived AIFs (AIF_|S|).

MATERIALS AND METHODS

Imaging was performed on a 1.5 T Siemens Symphony MR scanner using a whole-body transmit coil with whole-body, “flex,” and spine receive coils. Conventional magnitude image data as well as raw data were saved from 27 DCE-MRI studies performed during routine, clinical, Gd-enhanced prostate examinations. DCE was performed using a 3D spoiled gradient echo sequence with TR = 5.8 ms, flip angle = 35°, echo time (TE) = 2.56 ms, 20 5-mm-thick axial slices, field of view = 250 × 220 mm², matrix = 256 × 224, temporal resolution = 13.5 s, total number of 3D data sets (number of time points) = 30, total acquisition time = 6.75 min. The CA was Gadovist® (Berlex, Inc., Canada) and 0.2 mmol per kg of body weight was injected intravenously via a power injector at a rate of 4 mL/s (followed by a saline flush) after four baseline time points were acquired. The double dose (0.2 mmol/kg) was used to obtain greater signal enhancement in tissue, to maximize tumor detection. Image analysis was performed offline using custom software written in IDL© (ITT Visual Information Solutions) to reconstruct the raw data and manipulate images.

For each patient, three contiguous slices were identified which encompassed the largest cross-section of OIM. On each of these three slices, an 86 mm² region of interest (ROI) was drawn on both left and right OIM. For each 3D image set (i.e. each time point), the magnitude signal of OIM was calculated as the average signal in all six of these ROIs (left and right × 3 slices). Circular ROIs were also drawn in the lumen of either the external iliac or femoral arteries in each of the 20 slices.

The OIM magnitude signal as a function of time, |S| (t), was converted to T₁ vs. time via standard spoiled gradient echo equations (20,21). The native (pre-GdCA) T₁(T_1,0) in muscle was assumed to be 1000 ms (20). GdCA concentration vs. time in OIM was computed from changes in 1/T₁ assuming a T₁ relaxivity of 4.3 mM⁻¹ s⁻¹. Tracer, kinetic modeling was performed on the OIM concentration vs. time curve to obtain K^trans and v_e, using the theory of Kety, assuming fast water exchange between all compartments (intra/extravascular, intra/extracellular), a negligible plasma compartment, and hematocrit of 0.45 (2).

For each patient, K^trans and v_e were computed in four separate analyses, with each analysis differing only in the AIF used. These four different AIFs were: (1) AIF_TK, a population-averaged AIF (i.e., identical AIF to be used for all 27 patients) developed in the early 1990s by Tofts and Kermode (22). This AIF is in the form of a biexponential decay which was fit to the data of Weinmann et al. (23) and has been used by a large number of researchers. (2) AIF_P, a high temporal resolution population-averaged AIF recently developed by Parker et Al. (1). Both AIF_TK and AIF_P were scaled to reflect the correct injection dose of 0.2 mmol/kg. (3) AIF_|S|, an MR signal magnitude-derived AIF. (4) AIF_ϕ, an MR signal phase-derived AIF. AIF_|S| and AIF_ϕ were calculated separately for each subject (calculation details given below).

For the calculation of AIF_|S|, |S| (t) data from the arterial ROI voxels (external iliac or femoral arteries) were averaged together for blocks of five contiguous slices. The slice blocks used were overlapped to form a total of seven slice blocks. For comparison purposes, the relative position of the center of each block (inferior–superior direction) was varied from 0.125 to 0.875, where zero represents the most inferior edge of the entire 3D block and one represents the most superior edge. The average |S| (t) was then converted to whole-blood GdCA concentration vs. time (C_a(t)) using the same procedure as for the OIM, assuming blood T_1,0 = 1250 ms (19).

AIF_ϕ was calculated in a similar way except that changes in ϕ(t) relative to the baseline phase ϕ₀ [i.e., Δϕ(t) = ϕ(t) = ϕ₀] were used. When necessary, “unwrapping” of Δϕ(t) was used to keep the ϕ difference for successive points between ±π radians (15,24). Voxels were rejected if there was a shape mismatch between the |S| (t) and Δϕ(t) curves, as determined by the cross-correlation following the work of van Osch et al. (24). The cross-correlation can range from −1 to +1, with a value of +1 meaning that both curves have identical shapes. A threshold value of +0.1 was determined empirically after testing values ranging from 0.0 to 1.0 in increments of 0.1, where it was found that all values above zero resulted in similar AIFs. Voxels were also rejected if Δϕ(t) exhibited a positive, instead of the expected negative, slope during the last 4.5 min of the curve (24). The average Δϕ(t) was converted to C_a(t) using the following equation (12,14,17,24):

$$\mathrm{\Delta }\mathrm{\varphi }=\text{TE}\mathrm{\pi }\mathrm{\gamma }{B}_0{\mathrm{\chi }}_{\mathrm{m}}\mathrm{\Delta }{C}_{\mathrm{a}}({cos}^2\mathrm{\theta }-1/3)$$ [1]

where γ is the proton gyromagnetic ratio (4.258 × 10⁷ Hz/T), B₀ is the magnitude of the main magnetic field in Tesla, χ_m is the molar susceptibility of the CA (3.4 × 10⁻⁷ mM⁻¹ for Gd, in MKS units), and θ is the angle of the vessel relative to the main magnetic field (θ = 0° being parallel with that field). θ was set to an average value of 15°, based on the observed orientations of the arteries (15° ± 6° for all 27 patients). An additional AIF_ϕ was also calculated using all 20 slices instead of just one block of five slices (rationale given in Results section).

These calculations resulted in four sets of K^trans and v_e distributions (one set per AIF type). For each distribution, outliers were defined as points lying more than five standard deviations away from the mean of the remaining distribution and were removed. Reproducibility of the distributions was measured using the coefficient of variation (COV), defined as the standard deviation divided by the mean, expressed as a percent. Reproducibility is inversely related to COV, assuming that K^trans and v_e in OIM are the same for all patients.

For each block of five contiguous slices used to compute the AIFs, the AIF curves and resulting K^trans and v_e parameters were each averaged (and standard deviations computed) over all 27 patients, to investigate dependencies on slice position (inferior–superior). The variation of the AIF_|S| and AIF_ϕ amplitudes with slice position were compared via the F test of equality of two variances. The variation of K^trans and v_e with slice position was analyzed using a one-way ANOVA. The K^trans and v_e values computed from the four AIFs tested in this work were compared via the Student’s t test (to compare means) and the F test of equality of two variances (to compare COVs).

For each of AIF_|S| and AIF_ϕ, the interpatient mean, standard deviation, and COV of the maximum amplitude, equilibrium amplitude (mean of last 1 min), and area under the curve were measured. To compare AIF_|S| and AIF_ϕ for these characteristics, the Student’s t test was used to compare means and the F test of equality of two variances was used to compare COVs.

Tracer kinetic parameters were also measured in right versus left OIM, to check for any systematic differences between the two. All calculations were repeated with T_1,0 for OIM = 850 and 1150 ms, to test the sensitivity of the results to the T_1,0 used.

RESULTS

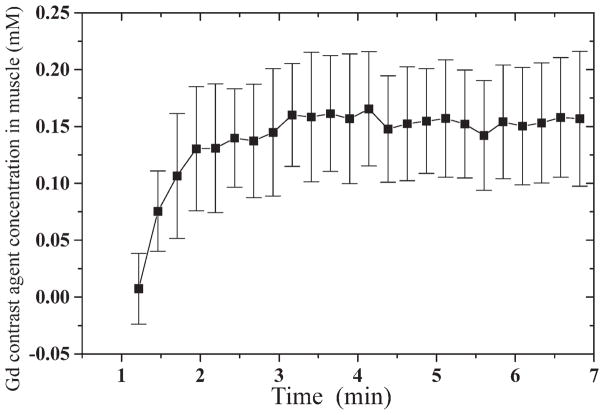
The measured GdCA concentration vs. time in OIM, averaged over all 27 patients, exhibited a plateau of 0.15 ± 0.05 mmol/kg (Fig. 1).

FIG. 1.

Gd contrast agent concentration vs. time in obturator internus muscle, averaged over all 27 patients, for a 0.2 mmol/kg intravenous bolus injection of Gadovist. Error bars show inter-patient standard deviations.

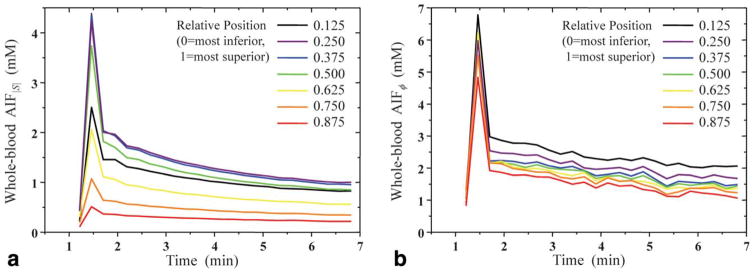
AIF_|S| varied significantly with measurement position, with decreasing amplitude towards the superior slices. The peak amplitude of these AIFs ranged from 0.5 to 4.3 mM, whereas the washout amplitude (defined as the average of the last 1 min of data) ranged from 0.2 to 1.0 mM (Fig. 2a). For AIF_ϕ, the peak and washout amplitudes ranged from 4.7 to 6.7 mM and from 1.3 to 2.2 mM, respectively, (Fig. 2b). The AIF_ϕ’s peak amplitudes varied considerably less with measurement position than that of AIF_|S| (F test, P < 0.001).

FIG. 2.

Effect of the position (inferior–superior) within the 3D imaging slab on the measured arterial input function (AIF), derived from (a) MR signal magnitude (|S|) and (b) MR signal phase (ϕ). Each AIF shown is the average over all 27 patients. The temporal resolution of the AIFs is approximately 13.5 s. Data points as a function of time are connected with straight lines with no interpolation. Note the smaller dependence on position of AIF_ϕ relative to AIF_|S|.

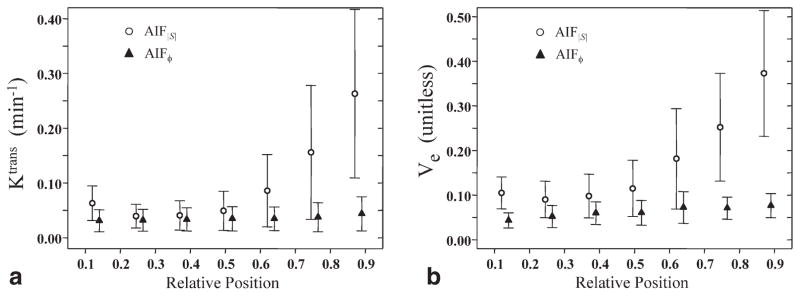
For AIF_|S|, K^trans and v_e both varied significantly with the position used to measure the AIF. Interpatient mean values of K^trans ranged from 0.039 to 0.263 min⁻¹, whereas those for v_e ranged from 0.090 to 0.373 (Fig. 3). Both K^trans and v_e varied smoothly with the position used to measure the AIF, reaching minimum values at a relative position (defined in Methods section) of 0.25. For all further analyses employing AIF_|S|, it was assumed that the most accurate AIF measurements would be found at the relative position of 0.25, where both inflow and slab profile effects are presumably minimal (25). Thus, the artery data at that position only were used for further analyses involving AIF_|S| (i.e., Fig. 4 and Table 1).

FIG. 3.

Effect of the position (inferior–superior) used for measuring the AIF within the 3D imaging slab on calculated values of (a) K^trans and (b) v_e in obturator internus muscle. Each data point shows the interpatient mean and standard deviation. Open circles show results obtained using AIFs derived from MR signal magnitude (|S|), whereas filled triangles show results using AIFs derived from MR signal phase (ϕ). The relative position changes from 0 to 1 as position in the 3D slab changes from the most inferior slice to the most superior slice. Note the considerably smaller dependence on AIF measurement position of parameters computed from AIF_ϕ relative to AIF_|S|.

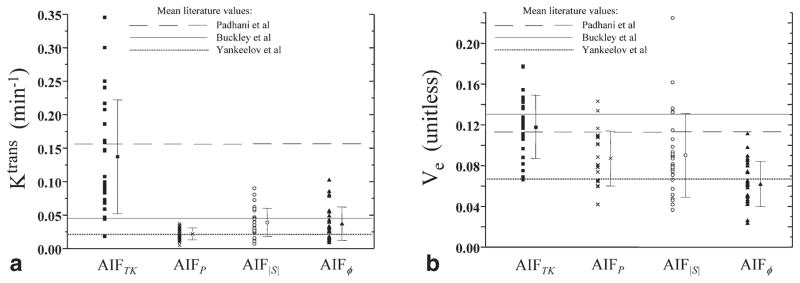
FIG. 4.

Interpatient distribution of calculated K^trans and v_e values in obturator internus muscle, for tracer kinetic analysis performed with four different AIF types: (1) AIF_TK, a population-averaged AIF originally reported by Tofts and Kermode and subsequently used by many other researchers; (2) AIF_P, a high temporal resolution population-averaged AIF recently developed by Parker et al. (1); (3) AIF_|S|, AIFs derived separately for each patient from the MR signal magnitude in the external iliac or femoral arteries at relative position = 0.25 (half-way between the center slice of the 3D imaging slab and the most inferior slice); and (4) AIF_ϕ, AIFs derived separately for each patient from the MR signal phase in the external iliac or femoral arteries for all slices. Horizontal lines through the graphs show mean literature values from Padhani et al. (8), Buckley et al. (20), and Yankeelov et al. (2).

Table 1.

Interpatient Mean and Standard Deviation (SD) of K^trans and v_e in Muscle

Study	AIF	Ktrans (min−1)			ve (unitless)
		Mean	SD	COVa	Mean	SD	COVa
Currentb	Tofts/Kermode	0.137	0.085	62	0.118	0.031	26
Current	Parker	0.022	0.009	41	0.087	0.027	31
Current	|S|	0.039	0.021	54	0.090	0.041	46
Current	ϕ	0.037	0.025	68	0.062	0.022	35
Padhani et al.c	Tofts/Kermode	0.156	0.095	61	0.113	0.021	19
Buckley et al.b	|S|	0.045	0.025	56	0.130	0.040	31
Yankeelov et al.d	Blood samplinge	0.021	0.002	10	0.067	0.010	15

^aCoefficient of variation = 100 × SD/mean. Smaller COV = better reproducibility.

^bHuman OIM, both sides (20).

^cLeft human OIM (8).

^dRat perivertebral muscle (2).

^eFirst-pass blood sampling with temporal resolution = 2.5 s.

For AIF_ϕ, interpatient mean values of K^trans did not vary significantly as a function of the position used for the AIF (one-way ANOVA, F = 0.89, P = 0.5). The interpatient mean values of v_e did vary significantly with the position used to measure the AIF (range 0.043–0.076), although this variation was much less than that for AIF_|S| (range 0.090–0.373). However, for relative positions >0.25, v_e values obtained using AIF_ϕ did not show a statistically significant dependence on the position used to measure the AIF (one-way ANOVA, F = 1.7, P = 0.15). As a result of this generally small dependence on slice position, all further analyses employing AIF_ϕ were performed with AIFs measured using all slice positions (i.e., Fig. 4 and Table 1).

The general effect of switching from one AIF to another was a statistically significant change in the mean of the K^trans or v_e distributions with no significant change in reproducibility (COV) (Fig. 4, Table 1). However, there were some exceptions to this general trend: the mean K^trans was the same for AIF_|S| and AIF_ϕ (Student’s t test, P = 0.7); the mean v_e was the same for AIF_P and AIF_|S| (Student’s t test, P = 0.8); AIF_P provided better K^trans reproducibility than AIF_TK (F test, P = 0.02) and AIF_ϕ (F test, P = 0.006); finally, AIF_TK provided better v_e reproducibility than AIF_|S| (F test, P = 0.008).

For the K^trans and v_e distributions measured in this study, outliers were rare (typically zero or one per 27 patients, maximum of three). Moreover, no statistically significant difference in enhancement or tracer kinetic parameters was observed between right and left OIM. T_1,0 for OIM had no major effect on the relationships between the different K^trans and v_e distributions. On average, 12% of the pixels in the AIF ROIs were rejected for having a cross-correlation between |S|(t) and Δϕ(t) of less than 0.1, and 24% of the pixels in the AIF ROIs were rejected for having a positive slope in Δϕ(t) during the last 4.5 min.

For the optimal AIF_|S|, computed for relative slice position 0.25, the interpatient maximum amplitude, equilibrium amplitude (mean of last 1 min), and area under the curve were 4.1 ± 1.3 mM (COV = 32%), 1.0 ± 0.27 mM (COV = 27%), and 460 ± 115 mM s (COV = 25%), respectively. For AIF_ϕ, the interpatient maximum amplitude, equilibrium amplitude, and area under the curve were 5.7 ± 2.4 mM (COV = 41%), 1.4 ± 0.56 mM (COV = 39%), and 620 ± 140 mM (COV = 23%), respectively. The mean values of maximum and equilibrium amplitude were significantly different for AIF_|S| and AIF_ϕ (Student’s t test, P ≤ 0.001). COVs were not significantly different; however, except for equilibrium amplitude which was nearly significant (F test, P = 0.051). The intrapatient COVs for AIF_|S| averaged over all slice positions were much higher than those reported above.

DISCUSSION

In this work, phase-derived AIFs (AIF_ϕ) were compared with magnitude-derived AIFs (AIF_|S|) for 27 routine prostate DCE-MRI exams, with the hypothesis that the AIF_ϕs would provide more reproducible K^trans and v_e values in OIM. It is important to note that the AIF_ϕ’s are available “for free”, requiring only that one save the raw data from any gradient-echo pulse sequence used for DCE-MRI. No additional image acquisitions or specialized pulse sequences are necessary.

AIF_ϕ varied much less in amplitude as a function of measurement location (inferior–superior) than AIF_|S|. This result is not surprising, given that ϕ is much less sensitive to inflow effects. Measuring the AIF with ϕ can therefore potentially offer more flexibility in terms of where the AIF may be sampled.

K^trans and v_e values determined using the AIF_|S|’s exhibited a strong, undesirable dependence on AIF measurement position. However, with the particular imaging protocol used in this work, and with the AIF_|S| measured at its optimal position (halfway between the center slice of the 3D slab and the most inferior slice), AIF_ϕ, averaged over all slices, provided approximately equal, although not improved, reproducibility in K^trans and v_e compared to AIF_|S| and population-averaged AIFs. This may be due to the relatively poor temporal resolution (13.5 s) and short, single TE (2.56 ms) of the DCE MRI pulse sequence used (13,21). We have shown previously that, for temporal resolution = 2.2 s and TE = 5.5 ms, both the accuracy and precision of vascular function measurements in the brain are significantly improved by using ϕ (26). Further work is thus needed to evaluate whether improved temporal resolution and longer TE could provide an overall precision advantage using ϕ for pelvic AIFs. For a fixed temporal resolution, given that Δϕ does not saturate with GdCA concentration, the signal-to-noise ratio (SNR) for AIF_ϕ is expected to be proportional to TE and to the dose of GdCA used. One possibility for improving AIF_ϕ would therefore be simply to employ a double-echo pulse sequence where the second, longer TE would provide more phase accrual and therefore increased phase SNR (13). It also follows that using a standard GdCA dose (0.1 mmol/kg) instead of a double dose (0.2 mmol/kg) would be expected to worsen the SNR for AIF_ϕ by a factor of two, unless the TE was doubled. On the other hand, |S| begins to experience saturation effects for GdCA >2–3 mM; therefore, using a standard GdCA dose instead of a double dose would be expected to reduce saturation effects in |S| and improve AIF_|S| measurements. Using a standard GdCA dose would decrease GdCA enhancement in tissue, however, which would reduce the overall precision of the tracer kinetic parameters. One advantage of using AIF_ϕ is that double GdCA doses can be used to improve tissue enhancement, without saturating the AIF measurements.

The choice of AIF type strongly affected the mean K^trans and v_e values in OIM. This shows that interinstitution comparisons of K^trans and v_e values may be difficult without careful consideration of the AIF techniques used to measure the AIF. The results reported here and elsewhere show that the Tofts and Kermode population AIF produces K^trans values which are much greater than those produced by the other AIFs (see Fig. 4 and Table 1). This is due to the fact that AIF_TK does not have sufficient temporal resolution to represent accurately the rapid first pass of GdCA, resulting in a peak amplitude which is at least four times smaller than those of the other AIFs, ultimately leading to much larger K^trans values. It should also be noted that the choice of AIF type affected v_e (mean values ranging from 0.062 to 0.118) much less than K^trans (mean values ranging from 0.037 to 0.137 min⁻¹), which is consistent with the literature (11).

The average estimated GdCA concentration vs. time in OIM, averaged over all 27 patients, was consistent with the results of Padhani et al. (8), who reported a maximum GdCA accumulation in the left OIM of 0.086 ± 0.020 mmol/kg for a GdCA dose of 0.1 mmol/kg of body weight.

The decrease in the calculated AIF_|S| amplitude toward superior slices (Fig. 2) may be attributed to reduced GdCA contrast in arterial blood of superior slices due to inflow, as has been observed by other investigators (25,27). This effect was not seen with AIF_ϕ

For the equilibrium portion of the AIF curves (Fig. 2, time > 2 min), AIF_ϕ showed about the same spread in values compared to AIF_|S|. This is likely, in part, because the magnitude curves are less error-prone for that part of the AIF than they are at the peak. The equilibrium portion involves much lower GdCA concentrations, resulting in reduced errors in the magnitude signal due to saturation. For this portion, the AIF_ϕ were also significantly noiser (in time) than the AIF_|S|. This is not surprising, given that the ratio of phase SNR to magnitude SNR is approximately equal to the phase angle in radians (28): for this work, the phase angle on the equilibrium portion of the AIF curve (relative to baseline) was only about 0.13 radians. The amplitudes of the equilibrium portion of AIF_ϕ also appear to have a small dependence on slice position, although the reasons for this are not clear.

The values of K^trans and v_e calculated for this study using AIF_TK were consistent with those found by Padhani et al. (8), who also used AIF_TK (Fig. 4, Table 1). The values of K^trans calculated for this study using the other three AIFs (Parker, |S|, ϕ) were more consistent with K^trans values found in recent studies performed by Buckley et al. (20) and Yankeelov et al. (2). The similarity of K^trans values between the current study, the Buckley study, and the Yankeelov study is not surprising, considering that the Buckley and Yankeelov studies employed high-temporal resolution (1.5–2.5 s) individually measured AIFs similar in amplitude to those of the Parker, |S|, and ϕ AIFs of this study. The values of v_e calculated for this study using the Parker, |S|, and ϕ AIFs tended to lie between those found by Padhani and Yankeelov.

The study reported here had several limitations. T_1,0 was not measured in blood, which may have adversely affected the reproducibility of AIF_|S| and the values of K^trans and v_e computed from it. T_1,0 was also not measured in OIM. Although this will have affected the K^trans and v_e measurements, it has no fundamental impact on the comparison between results obtained from AIF_|S| and AIF_ϕ. This work assumed that all patients have the same K^trans and v_e values in OIM. True variations between patients would, therefore, worsen the observed measurement precision and could potentially mask any differences in fundamental measurement precision between the analyses performed with AIF_|S| and AIF_ϕ. Correction for blood vessel orientation (θ in Eq. 1) was not performed for each patient, although the relatively small variation of observed angles (standard deviation = 6°) indicates that this should not have affected the AIF_ϕ’s by more than 10%. The temporal resolution used in this particular study (13.5 s) was not sufficient to achieve complete characterization of the first pass peak of the AIF (29). Such undersampling can introduce large errors into the tracer kinetic parameters. For a temporal resolution of 13.5 s, simulations reported by Roberts et al. indicate that K^trans may suffer errors in the range of 15–60% due to undersampling of the AIF (29).

CONCLUSION

For quantitative DCE-MRI of the human pelvis performed using a 3D spoiled gradient echo pulse sequence with a single short TE (2.56 ms) and modest temporal resolution (13.5 s), MR signal phase-derived AIFs measured in the external iliac or femoral arteries vary much less in amplitude, as a function of measurement location (inferior–superior), than magnitude-derived AIFs. This is likely due to the fact that phase is much less sensitive to inflow effects than magnitude. The phase-derived AIFs did not, however, improve reproducibility in K^trans and v_e measured in OIM compared to “optimal” magnitude-derived and population-averaged AIFs. Thus, although the phase technique shows promise, further work using improved acquisition protocols is warranted.