Molecular crowding enhances native state stability and refolding rates of globular proteins

Abstract

The presence of macromolecules in cells geometrically restricts the available space for poplypeptide chains. To study the effects of macromolecular crowding on folding thermodynamics and kinetics, we used an off-lattice model of the all-β-sheet WW domain in the presence of large spherical particles whose interaction with the polypeptide chain is purely repulsive. At all volume fractions, ϕ_c, of the crowding agents the stability of the native state is enhanced. Remarkably, the refolding rates, which are larger than the value at ϕ_c = 0, increase nonmonotonically as ϕ_c increases, reaching a maximum at 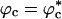. At high values of ϕ_c, the depletion-induced intramolecular attraction produces compact structures with considerable structure in the denatured state. Changes in native state stability and folding kinetics at ϕ_c can be quantitatively mapped onto confinement in a volume-fraction-dependent spherical pore with radius R_s ≈ (4π/3ϕ_c)^1/3 R_c (R_c is the radius of the crowding particles) as long as 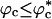. We show that the extent of native state stabilization at finite ϕ_c is comparable with that in a spherical pore. In both situations, rate enhancement is due to destabilization of the denatured states with respect to ϕ_c = 0.

The interior of cells contains several kinds of macromolecules like lipids, sugars, nucleic acids, and proteins, along with large organized macromolecular arrays, such as cytoskeleton fibers. The volume fraction ϕ_c, occupied by the macromolecular crowding agents in Escherichia coli, can be as large as 0.4 (1, 2). The large volume occupied by crowding agents can have profound effect on a number of processes of biological importance. For example, biochemical reactions, stability of actin, and amyloid formation are profoundly altered in a crowded environment (3, 4). Folding of globular proteins, which is the focus of this study, in such a crowded environment can be significantly different from that at ϕ_c = 0. Although systematic studies of the effect of crowding on folding kinetics of well characterized proteins are lacking, several experiments have shown that refolding at finite ϕ_c is greatly affected. The oxidative refolding of hen lysozyme is changed when crowding agents are present (5). The rate for the molecules that reach the native basin of attraction (NBA) rapidly increases by a factor of ≈2-5, whereas the rate for the slow track molecules (i.e., those that are trapped in misfolded states) increases only by ≈80% (5). These studies and the need to systematically assess crowding effects on folding of proteins have motivated this work.

Because of the complexity of interactions, E_pc, between the crowding agents and the protein of interest, it is difficult to predict the effect of macromolecular crowding on refolding of proteins. If E_pc is short-ranged and repulsive, then excluded volume interactions, which prevent the polypeptide chain from accessing regions occupied by the crowding particles, are the most important. Typically, the range of the site-site excluded interactions between amino acid residues and small molecules (water, urea, GdmHCl, etc.) is on the order of a few angstroms. In contrast, the range of macromolecular excluded volume interactions can be on the order of 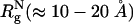, where 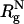is the size of the protein in the native state. As a result, even inert macromolecules alter folding of proteins, especially at large volume fractions of the crowding agents.

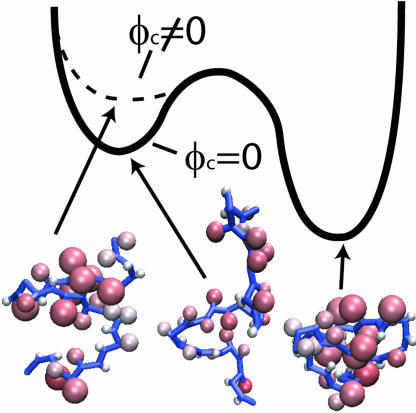
By modeling the crowding particles as hard spheres, we can predict the changes in the folding of two-state folders at finite ϕ_c by using arguments that have been used (6) to describe collapse of homopolymers in random media. The polypeptide chain would prefer to be localized in a region that is free of the macromolecular objects. Because the probability of finding such regions decreases as exp(-3ϕ_cR_g³/4πR_c³), where R_g is the typical dimension of the protein and R_c is the size of the crowding agent, we expect the polypeptide chain to be a compact globule at high values of ϕ_c. If the polypeptide is compact at large ϕ_c values, then the entropy change ΔS = S(ϕ_c) - S(0) < 0 because conformations with large R_g are suppressed. Thus, the stability of the native state, provided that it is not dramatically altered, is predicted to increase as ϕ_c increases (Fig. 1). Because of the loss in conformational entropy of the denatured states at finite ϕ_c values, the effective free-energy barrier to folding decreases (Fig. 1). As a result, the ratio k_f(ϕ_c)/k_f(0) must exceed unity, where k_f(ϕ_c) is the refolding rate at ϕ_c.

Fig. 1.

Schematic free-energy profile for WW (PDB ID code 1PIN; sequence, KLPPGWEKRMSRSSGRVYYFNHITNASQWERPSG) domain folding. The simulated structures corresponding to the NBA and representative structures in the unfolded states are shown. The enhanced stability at ϕ_c ≠ 0 is due to destabilization of the unfolded states.

Similar arguments were used to rationalize the observed enhancement in stability (7-9) and increase in folding rates (8-11) for proteins encapsulated in nanopores (8). Indeed, it has been advocated that folding in a crowded environment can be mimicked by confinement. In this study, we studied the effects of crowding as a function of ϕ_c as well as confinement in spherical pores of different radii to probe the effects on the stability and kinetics of folding of WW domain. We show that for 0 < ϕ_c ≤ 0.25, the stability of the native state is enhanced. Surprisingly, whereas k_f(ϕ_c) > k_f(0) at all ϕ_c, the dependence of k_f(ϕ_c) on ϕ_c is nonmonotonic. The rates k_f(ϕ_c) increase until a critical value 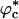and decrease for 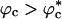. Crowding effects can be quantitatively mimicked by confinement of the protein in a volume fraction-dependent spherical pore as long as 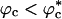. The differences between the two situations, at high volume fractions, arise because of variations in the initial compact structures. In the crowded environment, density fluctuations can lead to expanded structures in the denatured state ensemble (DSE), whereas for proteins encapsulated in pores, poplypeptide conformations with R_g > R_s, the pore radius, are strictly forbidden. This difference results in variations in the nature of DSE, which in turn affect the folding kinetics at .

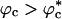Methods

Model for the WW Domain. We used a coarse-grained C_α side-chain model (SCM) of the all-β-sheet WW domain (PDB ID code 1PIN) in which only the positions of the α-carbon and the centers of mass of side chains are retained (12, 13). Numerous experimental (14, 15) and computational (16) studies at ϕ_c = 0 of the WW domain make it an attractive system for our purposes. If E_p and E_c are the potential energies of the protein and the crowding agents, respectively, then the energy of the combined system is 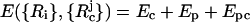, where {R_i} refers to the coordinates of the polypeptide chain, {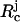; j = 1, 2,..., N} are the coordinates of the N spherical crowding agents, and E_pc is the interaction energy between the crowding agents and the protein. Following earlier studies (12, 13), we assume that E_p is the sum of bond-length potential, side chain-backbone connectivity potential, bond-angle potential, dihedral potential, hydrogen bond (HB), and nonbonded interactions. A simple energetic bias is used to favor the l-form of the side chains (13). The nonbonded (residues that are separated by at least one residue along the sequence) potential between two side chains at a distance r is as follows:

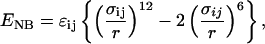[1]

where σ_ij = f(σ_i + σ_j), and σ_i and σ_j are the van der Waals radii of the side chains. To avoid clashes between bulky side chains, we use f = 0.9. For the native contact energies ε_ij, we use the Betancourt-Thirumalai statistical interactions potential (17). Because we are mainly interested in the physical consequences of crowding as a function of ϕ_c, we use a modified Go-like (18) model in which only the native interactions are retained and nonbonded interactions depend on the residue type. The repulsive nonnative interactions depend explicitly on the size of the side chains.

The purely repulsive interactions between the C_α atoms, side chain, and the spherical crowding agents with radius R_c are assumed to be pairwise additive. The repulsive potential energy between two particles i and j at a distance r is as follows:

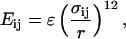[2]

where σ_ij = σ_i + σ_j, σ_i and σ_j are the sizes of the interaction sites, and ε is 0.6 kcal/mol (1 cal = 4.18 J).

Simulation Details. The radius of the macromolecular crowding agents is 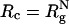, where 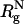is the radius of gyration of the folded protein at infinite dilution. To minimize finite size effects, we use periodic boundary conditions (PBC), which take into account interactions between images of the crowding agents with themselves and the protein of interest (19). To carry out the simulations, we use the topology files and the PBC implementations in the amber6 program (20). The size of the cubic simulation box is >2L, where L = (N - 1) σ is the maximum length of the polypeptide chain. The unit of length σ ≈ 3.8 Å is the typical distance between α-carbon atoms. To ensure that there are no errors due to truncation of the interactions, we choose L = 75σ, which not only can accommodate an expanded polypeptide chain but also allows us to explore a range of volume fractions

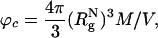where M is the number of crowding agents, and V = L³. The simulations, for ϕ_c in the range 0 ≤ ϕ_c ≤ 0.25, are performed by initially equilibrating only the system of spherical crowding agents at the desired ϕ_c. Subsequently, the polypeptide chain is inserted and the interactions between the protein and the crowding agents are increased incrementally to avoid generating sudden changes in forces.

Calculations of Thermodynamic and Kinetic Properties. To compute the thermodynamic quantities, we integrated the Langevin equation of motion in the low-friction limit by using a Verlet-like algorithm (21, 22). The integration time step is 10^-4τ_L, where τ_L = (mσ²/ε)^1/2. To achieve efficient sampling of the allowed conformational space, we used the replica exchange method (REM) (23-25), covering a wide temperature range (245-425 K). The initial structures were equilibrated from independent molecular dynamics simulations. At certain times (e.g., 4τ_L), configurations with “neighboring” temperatures are exchanged simultaneously with the probability that is determined by the Metropolis criterion. Only pairs of replicas with temperatures that are close to each other are exchanged, and they are alternatively switched from one of two possible choices: (T1, T2), (T3, T4),....and (T2, T3), (T4, T5)..., given that T1 < T2 < T3 < T4 < T5... We used the weighted-histogram-analysis method (WHAM) (26) to compute the temperature dependence of the thermodynamic properties. The density of states was calculated by using only the energy of the protein. The ϕ_c-dependent folding temperature T_f(ϕ_c) are calculated from the fluctuations of the structural overlap function χ (27).

To probe crowding-dependent folding kinetics, we used Brownian dynamics by choosing the friction coefficient that is appropriate for water (27), for which the natural unit of time, τ_H, is 4.2 ns. The initial denatured configurations of the protein and crowders are prepared at 1.18T_f(ϕ_c = 0) (T_f(0) = 342 K). Folding kinetics is obtained at a fixed T = 0.83T_f(0). For each ϕ_c, we obtained 200 folding trajectories. The folding rates are computed from the distribution of first passage times. For the ith trajectory, the first passage time corresponds to the first time a molecule reaches a conformation with overlap 〈χ〉 ≈ 0.19, where the angular brackets indicate equilibrium averages.

Results and Discussions

Native State Is Not Significantly Perturbed in the Range of 0 ≤ ϕ_c ≤ 0.25. To assess the effects of crowding agents on the folding of the WW domain, it is necessary to ensure that the native state is not greatly altered. The number of native contacts and χ do not vary much as ϕ_c is increased from 0 to 0.25. For example, χ measured with respect to the coarse-grained version of the PDB structure, changes from 0.06 at ϕ_c = 0 to 0.04 at ϕ_c = 0.25. The repulsive interactions with the crowding agents make only a minor contribution to the total energy of the WW domain in the native state. The average repulsive energy of interaction between the crowding agents and the WW domain, 〈E_pc〉, varies from 0.03 <〈E_pc〉/ε < 0.6 (ε = 0.6 Kcal/mol) as ϕ_c changes from 0.02 to 0.25. Thus, the native structure of the WW domain does not change significantly, even at ϕ_c = 0.25.

Crowding Enhances the Stability of the Native State. The WW domain folds in an all-or-none manner as the temperature is changed from high temperature to T < T_f(ϕ_c) for 0 < ϕ_c ≤ 0.25 (M.S.C. and D.T., unpublished data). The collapse temperature T_θ at ϕ_c = 0 is nearly coincident with T_f(ϕ_c = 0), which is also a characteristic of sequences that fold in an apparent two-state manner (28, 29).

Because only excluded volume interactions between the polypeptide chain and the crowding particles are taken into account, it is clear the WW domain would prefer to be localized in a region that is free of the crowding agents (6, 30). Such regions, which arise because of density fluctuations in the crowding particles, can easily be found with high probability, especially when ϕ_c is low. Given that the native state is not greatly perturbed, it follows that localization of the polypeptide chain results in the destabilization of the ensemble of unfolded states with respect to the case when ϕ_c = 0. If F_u(ϕ_c) - F_u(0) > 0[F_u(ϕ_c) and F_u(0) are the unfolded state free energies at ϕ_c and ϕ_c = 0, respectively], then the change in the folding temperature ΔT_f = T_f(ϕ_c) - T_f(0) > 0. These arguments suggest that crowding should increase the folding temperature and, hence, promote the stability of the native state as long as interactions between the crowding agents and the polypeptide chain are repulsive.

The folding-transition temperatures calculated from the temperature dependence of Δχ (Fig. 2A), T_f(ϕ_c), at all values of ϕ_c, are >T_f(0). The change in ΔT_f is ≈7% as ϕ_c is increased from 0 to 0.25. This shift, which is significant, compares well with recent measurements of folding temperature changes of proteins in nanopores (31, 32). The dependence of ΔT_f on ϕ_c can be rationalized by using changes in the free energy due to localization in a volume (33). By assuming that the native state energy is not altered because of crowding, we expect that ΔT_f ≈ C ϕ_c^α, where α ≈ 3ν [where ν (≈0.6) is the Flory exponent for the random coil]. A plot of lnΔT_f as a function of ln(Cϕ_c) (Fig. 2B) indeed shows that α = 1.8. The nonlinear dependence of ΔT_f on ϕ_c is in accord with experiments (34).

Fig. 2.

Crowding effect on folding thermodynamics. (A) Fluctuations in the overlap function (Δχ = 〈χ²〉 - 〈χ〉²) as a function of temperature at different values of ϕ_c. The fraction of conformations in the NBA (f_NBA) at ϕ_c = 0 (□) and ϕ_c = 0.15 (•) as a function of temperature. (B) Crowding-dependent change in the folding temperature ΔT(ϕ_c) = T_f(ϕ_c) - T_f(0) as a function of ϕ_c. The solid line is a theoretical fit using ΔT(ϕ_c) = Cϕ_c^3ν, with ν = 0.6. (C) Radius of gyration (R_g), at various volume fractions of the crowding particles, as a function of temperature.

The entropically stabilized native state due to crowding is also reflected in the free energy of stability ΔF(ϕ_c) = -k_BT_sln (P_NBA(ϕ_c)/1 - P_NBA(ϕ_c)), where P_NBA(ϕ_c) is the thermal probability of occupying the NBA at ϕ = ϕ_c and T_s is the simulation temperature. The NBA is the set of conformations for which χ ≤ 〈χ (T_f)〉 = 0.19. In infinite dilution, ΔF(0) = -2.8 Kcal/mol. The value of ΔF(ϕ_c) increases with ϕ_c and at ϕ_c = 0.25, ΔF(0.25) is -3.9 Kcal/mol. The increases in stability of the native state and ΔT_f are in accord with the Minton argument that the enhanced stability of the native state is due to crowding-induced, entropic destabilization of the DSE.

Collapse of the WW Domain Is Driven by the Depletion Effect. When ϕ_c = 0, the denatured poplypeptide d chains are expanded random coils with mean dimension 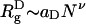, with ν ≈ 0.6 (35), whereas in the folded states, they are near by maximally compact (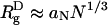) (36). Upon reducing T from high temperatures, proteins undergo coil-to-globule transition at the Flory θ temperature, T_θ. Thus, the global characterization of the DSE at ϕ_c = 0 are in accord with the expectations from polymer theory (33). As ϕ_c increases, we expect WW to become compact even at high temperatures (T > T_θ at ϕ_c = 0). The temperature dependence of R_g (T) (Fig. 2C) shows that, at ϕ_c = 0.25, the WW domain is only ≈25% larger than its value in the native state at T ≈ 375 K.

The substantial reduction in R_g at large values of ϕ_c at high temperature is due to a coil-to-globule transition in the WW domain at a critical value of 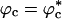because of volume excluded by the crowding agents. The collapse of WW domain at 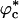is due to two opposing contributions to the free energy (30). The protein prefers to be in a crowding-free region, which is difficult to find at high ϕ_c. However, localization in a confined volume decreases chain entropy. As a result, at a critical volume fraction 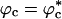, the WW domain becomes compact even at relatively high temperatures. From this physical reasoning, which was made precise by Shaw and D.T. (ST) (37), it follows that when the mean spacing between the crowding agents, 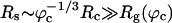, then the crowding agents do not perturb the folding of the polypeptide chain. In the opposite limit, the probability of finding a region free of the crowding agents in which the polypeptide chain can be accommodated becomes small. The localization results in the reduction of the conformational entropy of the chain. As a result, there is an entropically generated intramolecular effective attractive interaction that drives the collapse transition even when T > T_θ (ϕ_c = 0). This interaction is the depletion-induced attraction between colloidal particles in polymer solution (38).

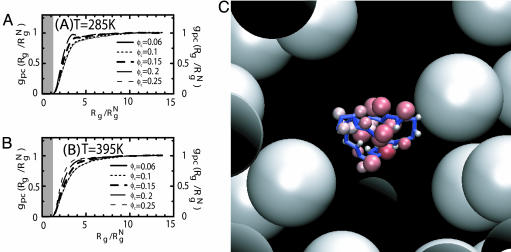
The depletion effect is most clearly evident in the radial distribution functions between the crowding agents and the polypeptide chain g_pc(r) (Fig. 3 A and B). At all values of ϕ_c, there is clear depletion in the density of crowding particles near the WW domain. In particular, for 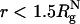, the probability of finding the crowding agents is zero, which shows that the WW domain is localized in a region that is essentially devoid of the crowding particles. Because large conformational fluctuations are not probable because of the volume occupied by crowding agents, the WW chain adopts a compact conformation even at relatively high temperatures (Fig. 3C). The striking similarity between the g_pc(r) shown here and the ST theory for homopolymer (see figure 1 in ref. 37) in a colloidal solution further reinforces the importance of depletion-induced collapse for proteins because of macromolecular crowding.

Fig. 3.

Depletion-induced attraction. (A and B) Radial distribution functions between the protein residues and crowding particles as a function of ϕ_c at two temperatures. At both temperatures, there is a depletion layer (shaded area) surrounding the protein, which effectively excludes the crowding agents (see also C). (C) A snapshot of the WW protein and crowding particles in the simulation. There is a rim of depletion layer surrounding the protein in which the crowding particles are absent. Sizes of side chains are highlighted in red.

Folding Rates Vary Nonmonotonically with ϕ_c. The refolding rates at various ϕ_c values were calculated by a temperature quench from T = 1.18T_f(0) to T_s = 0.83 T_f(0). The distributions of first passage times, from which k_f(ϕ) were computed, were obtained for 200 folding trajectories.

Based on the entropic destabilization of the DSE, we expect that k_f(ϕ_c) should increase as ϕ_c increases, provided that the free-energy barrier does not change (Fig. 1). When ϕ_c exceeds 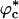, the volume fraction above which the WW chain adopts a globular conformation even at high temperatures, we expect k_f(ϕ_c) to decrease. For 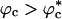, the polypeptide chain is localized in a small enough volume that the conformational fluctuations that may be required to cross the free-energy barrier are restricted. The expected nonmonotonic dependence of k_f(ϕ_c) on ϕ_c is borne out in the simulations (Fig. 4). The rate initially increases as ϕ_c increases. At ϕ_c ≈ 0.1, k_f(ϕ_c) is nearly three times as large as in ϕ_c = 0. Surprisingly, k_f(0.15) is nearly 80% larger than k_f(0), which shows that the search among compact conformations is faster than transitions to the NBA from the expanded random coil conformations. Thus, even high density of crowding can lead to modest increases in folding rates.

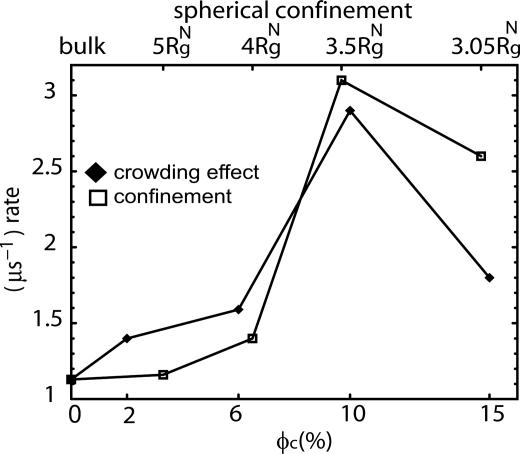
Fig. 4.

Dependence of the folding rates as a function of ϕ_c and the radius of the volume-fraction-dependent confining sphere, . This figure shows that crowding effects can be mimicked by encapsulation in a spherical pore with radius R_s.

Crowding Can Be Mimicked by Confinement. Encapsulation of polypeptide chains in nanopores has been used to mimic macromolecular crowding. The ST arguments suggest that, at a volume fraction ϕ_c, the polypeptide chain should be localized in a spherical region with the most probable radius

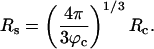If this mapping between crowding and effective confinement is qualitatively correct, then we expect thermodynamic and kinetic properties at ϕ_c and an encapsulated protein in a spherical pore with radius R_s to be similar. To validate this proposal, we computed changes in T_f and folding rates for the WW chain confined to spherical pores by using the procedures described in ref. 8.

As shown in refs. 8 and 10, ΔT_f(R_s) = T_f(R_s) - T_f(R_s → ∞) [T_f(R_s → ∞) ≡ T_f(ϕ_c = 0)] increases as R_s increases. The ST mapping between confinement and crowding is quantitatively accurate for ϕ_c ≤ 0.1. For example, when 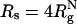, ϕ_c ≈ 0.065, for which 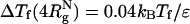, whereas ΔT_f(ϕ_c = 0.06) = 0.03k_BT_f/ε. Similarly, we find that ΔΔG = (ΔG(ϕ_c) - ΔG(R_s))/k_BT_s is small, ranging from 0.16 to 0.32 in the range of 0 < ϕ_c ≤ 0.1. As ϕ_c exceeds 0.1, encapsulation in an equivalent nanopore results in marginally greater stability. At higher volume fraction, the optimal cavity in which the WW domain is localized is likely to be cylindrical. Thus, the mapping onto an equivalent spherical pore is only qualitatively valid. These results and a recent analysis (39) show that crowding and confinement affect the stability of the native state to the same extent.

Strikingly, the folding rates k_f(R_s) and k_f(ϕ_c) exhibit similar behavior. By the proposed mapping, the folding rates k_f(ϕ_c) can be quantitatively predicted by using k_f(R_s) as long as 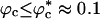(Fig. 4). When 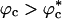, decrease in k_f(ϕ_c) is somewhat greater than k_f(R_s) (Fig. 4). This difference arises because of destabilization of the DSE due to crowding does not occur to the same extent as it does in nanopores in which conformations with R > R_s are strictly disallowed. Even at high volume fractions, density fluctuations in the crowding particles can accommodate polypeptide conformations with R_g > R_s. These conformational fluctuations may be required in the transition from compact nonnative states to the folded structure.

Confinement Suppresses Large-Scale Shape Fluctuations. In the transition from denatured to folded states, the WW domain undergoes substantial changes in the overall shape, which we characterize as Δ (Δ = 0 for spheres), the asphericity parameter, and S, the shape parameter (S > 0 for prolate ellipsoid, and S < 0 for oblate ellipsoid) (36). Both Δ and S are calculated by using the inertia tensor (36). From the 200 folding trajectories, we computed the profiles of Δ and S under various conditions (Fig. 5). Although on an average WW domain is compact (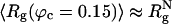) at ϕ_c ≈ 0.15, the distribution of Δ and S are qualitatively similar to what is found at ϕ_c = 0 (Fig. 5 A and B). In going from the unfolded states to the NBA, S changes substantially from ≈1.5 to the native value of 0.07, which shows large fluctuations in the shape. Similarly, substantial changes in Δ also occur in the transition from the DSE to the NBA (Fig. 5 A and B).

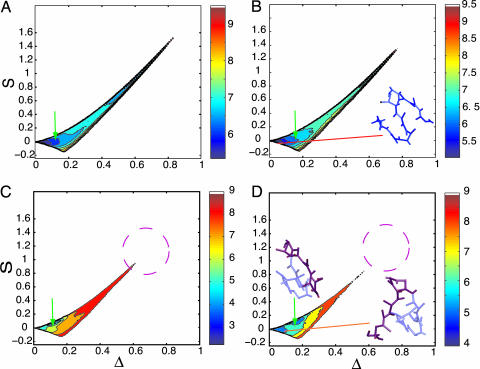
Fig. 5.

Crowding effects and confinement on folding kinetics. Histograms of 200 folding kinetic trajectories are plotted at T_s as a function of shape parameters, Δ and S, at several different conditions: ϕ_c = 0 (A); ϕ_c = 0.15 (B); 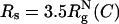; and 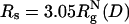. The color bar is scaled by k_BT_s. The green arrows indicate the NBA. The dashed circle in C and D is a visual guide to highlight the suppression of the extended configurations as the radius of the spherical pore decreases. In contrast, both at ϕ_c = 0 (A) and ϕ_c = 0.15 (B), density fluctuations of the crowding agents allow large fluctuations in Δ and S. When the spherical pore is small enough, 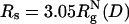, which mapped to ϕ_c ≈ 0.15, folding occurs by a kinetic partitioning mechanism as a result of being trapped in a structure with an inaccurate turn (highlighted in a purple β-strand in D). There is no such barrier caused at ϕ_c = 0.15 (B).

In contrast to crowding, encapsulation greatly restricts fluctuations in Δ and S (Fig. 5 C and D). Regions with S > 1 and Δ > 0.6 are strictly forbidden when 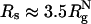, and the are allowed conformations further restricted when R_s is decreased to 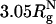. When 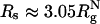, a maximally compact state with both Δ≈ 0 and S ≈ 0 is populated (dark blue in Fig. 5D). The structure in this region has a nonnative turn (purple in Fig. 5D). The formation of this low-energy kinetic trap results in a decrease in k_f(R_s) when 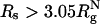. Because density fluctuations in the crowding agents can always allow polypeptide chains to sample different R_g values, we find that at high-volume fractions, highly spherical structures (Δ≈ 0 and S ≈ 0) are also explored. However, these structures are more mobile and can rearrange readily, which prevents them from being kinetic traps. The differences in the nature of DSE as ϕ_c increases and R_s decreases lead to variations in the folding mechanisms between the two situations.

Confinement-Induced Unfolded States Are Highly Structured. To assess the nature of the structures in the denatured states, we generated an ensemble of conformations at T = 1.18T_f(0). The clustering procedure (40) shows that the DSE ensemble can be classified into two dominant clusters at ϕ_c = 0 and ϕ_c = 0.15, and in the spherical pore with 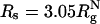(Fig. 6). The structures in the two clusters are remarkably similar at both volume fractions (compare Fig. 6 B and C). Structures in DSI are expanded, whereas in DSII there is evidence for formation of native fold (Fig. 6 B and C). However, at ϕ_c = 0.15, there is a suppression of chain conformations with large R_g, which leads to destabilization of the DSE. In contrast to the behavior at ϕ_c = 0.15, the DSE structures in the spherical pore are dramatically different (compare Fig. 6 C and D). In the nanopore, the DSE is more compact and highly structured, which shows that confinement leads to substantial long-range interactions even at elevated temperature. The structures in DSII in the encapsulated WW domain can have incorrect topologies (Fig. 6D) that serve as kinetic traps.

Fig. 6.

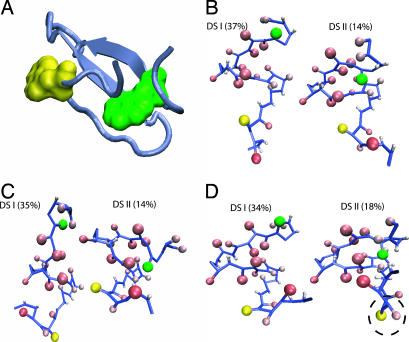
Distributions of denatured states at 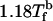under high volume fractions of crowding agents and in spherical pore with encapsulation 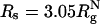. (A) The native structure of WW domain (PDB ID code 1P1N) in ribbon representation as a reference to show the relative positions of Trp-11 (green) and Trp-34 (yellow) along the backbone. (B)ϕ_c = 0. (C)ϕ_c = 0.15. (D) 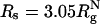. The dominant cluster, at ϕ_c = 0 (B) in the DSE (DSI) corresponds to expanded structures. DSI has few contacts between side chains and between backbone α-carbon atoms. DSII contain a significant amount of side-chain contacts, but backbone structures are not aligned properly for hydrogen bonding. A DSE structure represents an averaged conformation over a given cluster. Percentages of DSI decrease as ϕ_c increases (C), whereas those of DSII increase, implying that compact structures are favored at high volume fraction. Interestingly, under stringent spherical encapsulation (D), there are trapped structures in DSII because the bulky Trp side chain (dashed circle) is unable to flip over to form correct contacts as a result of a hindrance by the spherical boundary condition.

Conclusions

We have made experimentally testable predictions for crowding-induced changes in the native stability and kinetics (1). Excluded volume effects due to macromolecular crowding enhance native state stability at all values of ϕ_c. The stabilization is linked directly to crowding-induced destabilization of the unfolded states (39). This interpretation is reaffirmed further by comparing unfolding rates at ϕ_c = 0 and ϕ_c ≠ 0. If the free energy landscape changes, as indicated in Fig. 1 at ϕ_c ≠ 0, then we expect that unfolding rates k_u(ϕ_c) should not vary much with ϕ_c. Indeed, unfolding simulations show that k_u(0) and k_u(0.15) at T = 395 K are nearly identical (M.S.C. and D.T., unpublished data) (2). Surprisingly, we find that the refolding rates change nonmonotonically with ϕ_c. Even at relatively high ϕ_c, k_f(ϕ_c) > k_u(0) (3). Crowding effects can be mimicked quantitatively by confinement in a spherical pore with a ϕ_c-dependent pore size for 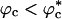. Even when 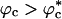, we find that the rates in the two cases do not differ significantly. Although calculations have been done for the WW domain, the general results should be applicable to other proteins as well.

There are two factors that were not considered in our model that could potentially affect our conclusions. (i) It could be argued that, in the presence of crowding agents, the neglected nonnative interactions could be enhanced, thus increasing the roughness of the energy landscape. However, because of the repulsive nature of the interactions between the crowding agents and the polypeptide chain, such an interaction is unlikely. Thus, the sole effect of the crowding particles is to create a large depletion zone around the polypeptide chain. (ii) It is possible that the intrapeptide interactions are modified by the interstitial water. Because the WW domain is localized in a region whose volume, at the highest volume fraction, is nearly 27 times as large as that of the folded protein (see Fig. 3), we suspect that interactions between the amino acids are the same as in the bulk. Thus, we expect the qualitative nature of the predicted results to be valid even for more realistic models.

We have only considered only one value for the size of the crowding particles, namely, 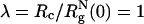. Besides temperature, the effective binary system of proteins and molecular crowding effects is described by three variables (namely, λ, ϕ_c, and ϕ_p, the volume fraction of the proteins). At a fixed temperature, variations of the three variables can produce a complex phase diagram. Several scenarios can be anticipated by using results familiar in the colloid literature (see ST for an example) and by modeling the poplypeptide chains as approximately spherical particles. When λ < 1, the smaller crowding agents promote protein-protein association because of a depletion effect. In this limit, we propose that folding would be unaffected as long as 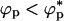, the overlap concentration. However, if , crowding particles should promote aggregation of proteins. In the limit λ > 1, attractive interactions between the crowding agents is enhanced by the polypeptide chains. This attraction would lead to a microphase separation containing protein-rich phase and crowding agent rich phase. In this limit, folding would be unaffected when ϕ_p → 0 and aggregation would result if 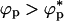. Thus, in both limits (λ < 1 or λ > 1) and 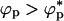, we predict that crowding agents enhance protein aggregation.