Partitions with short sequences and mock theta functions

Abstract

P. A. MacMahon was the first to examine integer partitions in which consecutive integers were not allowed as parts. Such partitions may be described as having sequences of length 1. Recently it was shown that partitions containing no sequences of consecutive integers of length k are of interest in seemingly unrelated problems concerning threshold growth models. The object now is to develop the subject intrinsically to both provide deeper understanding of the theory and application of partitions and reveal the surprising role of Ramanujan's mock theta functions.

1. Preliminaries

In MacMahon's monumental work on combinatorial analysis (1), we find the first study of partitions without sequences. For example, there are eight partitions of 7 without sequences: 7, 6 + 1, 5 + 2, 5 + 1 + 1, 4 + 1 + 1 + 1, 3 + 3 + 1, 3 + 1 + 1 + 1 + 1, and 1 + 1 + 1 + 1 + 1 + 1 + 1. MacMahon was able to obtain the generating function for such partitions as a q series. He concluded his chapter on the subject by showing that the number of partitions of n without sequences and without ones equals the number of partitions of n into parts not congruent to 1 or 5 modulo 6.

Subsequently, in the 20th century, there were a few additional papers (2-4) devoted to furthering the study of such partitions.

Recently, however, Holroyd et al. (5) made an ingenious study of several definite integrals with widespread applications. The main integral in question is

[1.1]

where 0 < a < b and f = f_a,b is the unique decreasing function mapping the unit interval into itself and satisfying

[1.2]

This result has wide application. Holroyd et al. (5) prove an asymptotic theorem in probability. Let 0 < s < 1, and let C₁, C₂,... be independent events with probabilities

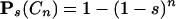under a probability measure P_s. (We can think of C_n as the event that at least one occurs of a further set of n independent events, each of probability s.) Let k be a positive integer, and let A_k be the event

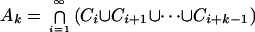that there is no sequence of k consecutive C_i values that do not occur.

Theorem 1 (5). For every positive integer k,

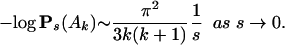Holroyd et al. apply this theorem directly to a central probability question regarding threshold growth models. They also consider the application of Eq. 1.1 to partitions with short sequences and speculate that it might be possible to base many of their discoveries on the combinatorial aspects of the theory of partitions.

Indeed, in ref. 5, the more general partition function p_k(n) is considered; p_k(n) is the number of partitions of n that do not contain any sequence of consecutive integers of length k. Thus, from our previous calculation we see that p₂ (7) = 8. Holroyd et al. also study the related generating function:

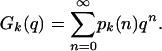[1.3]

Using the close connection of G_k(q) to the probability function P_s(A_k), they then prove that

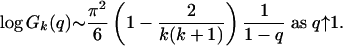[1.4]

From this result they deduce the asymptotic behavior of log p_k(n) as n → ∞.

In the final section of ref. 5, the authors show for the case k = 2 how to deduce their results from MacMahon's theorem. Section 4 of ref. 5 concludes with the observation that if Eq. 1.4 could be partition-theoretically proved for general k, then it would allow a reversal of their arguments and by analytic continuation provide an independent proof of Eq. 1.1.

We shall prove the following results:

Theorem 2. For |q| < 1,

[1.5]

where

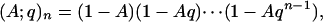[1.6]

and

[1.7]

To make our second result clear, we introduce further notation:

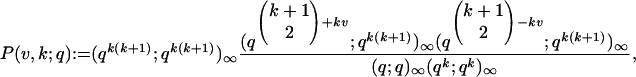[1.8]

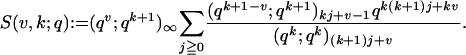[1.9]

Theorem 3. For |q| < 1,

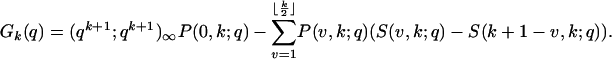[1.10]

Now the results in Theorems 1 and 2 are true for all k. In light of the fact that P(v, k; q) is a quotient of three theta functions, we can easily obtain asymptotic results on it of great accuracy as q ↑ 1. On the other hand, we do not yet have enough information about S(v, k; q) to handle its asymptotics as q ↑ 1 in general. However, we shall provide a full treatment when k = 2 with the hope that it may point the way to understanding G_k(q) fully as q ↑ 1.

It is surprising that the key to the k = 2 case lies in one of Ramanujan's mock theta functions (6, 7):

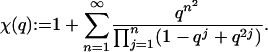Theorem 4. For |q| < 1,

From here we are led directly to the full asymptotics of P_s(A₂). Namely:

Theorem 5. .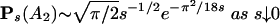

Note that this is a much stronger result than the k = 2 instance of theorem 2 of ref. 5.

We hope that these initial successes will lead to an effort to understand the many implications of Theorems 1 and 2. In particular, it would be very appealing to obtain the asymptotics of P_s(A_k) not just for k = 2.

Numerical calculations of the series arising in Theorem 2 lead us to the following:

Conjecture. For each k ≥ 2, there is a positive constant C_k such that

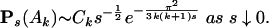2. Proof of Theorem 1

To accomplish our argument, we must refine P_k(n) to P_k(m, n), the number of partitions of n into m parts containing no sequences of consecutive integers of length k or longer. We then define

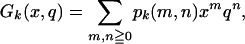[2.1]

and we note that

[2.2]

We begin by noting that G_k(0, q) = 1, and

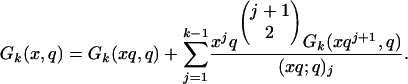[2.3]

The proof of the functional Eq. 2.3 is quite straight forward. We split the partitions enumerated by G_k(x) into k classes, where the jth class contains those partitions in which 1 occurs in a maximal sequence of precisely j consecutive integers. If j = 0 (i.e., 1 is not a part), then the relevant partitions are clearly generated by G_k(xq, q). If 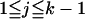, the relevant generating function is easily seen to be

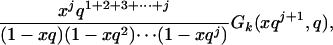[2.4]

and adding up the generating functions for these k exhaustive classes, we obtain Eq. 2.3.

To prove Eq. 1.5 and consequently Theorem 1, we shall prove more generally

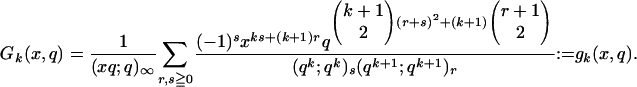[2.5]

Once Eq. 2.5 is proved, we may deduce Theorem 1 by setting x = 1 therein and applying Eq. 2.2.

To prove Eq. 2.5, we proceed by denoting the right side of Eq. 2.5 by g_k(x, q); we need only show that g_k(0, q) = 1 (which is obvious by inspection) and that g_k(x, q) satisfies the functional Eq. 2.3, which together with g_k(0, q) = 1 uniquely defines G_k(x, q).

Apart from the right side of Eq. 2.5, there are two other useful representations of g_k(x, q). First,

[2.6]

by Eq. 2.5.

Second, we may start with the top line of Eq. 2.6, and noting 1 - q^ks+(k+1)r = 1 - q^ks + q^ks(1 - q^(k+1)r), we see that also

[2.7]

We take the representation of g_k(x, q) given by Eq. 2.6 and insert it in the right side of the required functional equation

by Eq. 2.5, and thus we obtain the desired defining functional equation.

Hence,

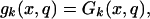and thus Theorem 1 follows.

3. Proof of Theorem 2

The object in this second result is to obtain a representation of G_k(q) that will yield the asymptotics promised in Theorem 3. To this end, we require several results from the literature. First is Euler's identity (see p. 490, corollary 10.2.2.b, in ref. 8),

[3.1]

next is Jacobi's triple product identity (see p. 497, theorem 1.4.1., in ref. 8; with q → q^2a, x = q^a+h),

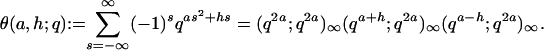[3.2]

We proceed with the proof of Theorem 2 starting from Eq. 1.5. Hence,

[3.3]

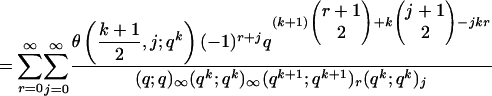(byEq.3.1)

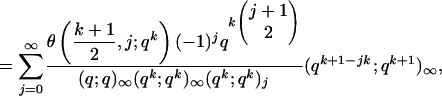(byEq.3.2)

by Eq. 3.1.

Now we note several things about this last expression. First, if j is a positive multiple of (k + 1), then the infinite product in the summand vanishes. Next, we observe that θ(a, - h; q) = θ(a, h; q); also,

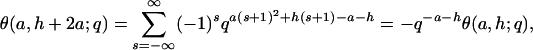[3.4]

and thus,

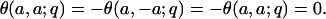This last identity means that if j ≡ k + 1/2(mod k + 1), the sum in Eq. 3.4 also vanishes. Finally, we note that the j = 0 term in Eq. 3.3 is in fact (q^k+1; q^k+1)_∞P (0, k; q) by Eqs. 1.8 and 3.2.

Hence, separating the terms of the sum in Eq. 3.2 according to the residue of j modulo k + 1, we see that

This last expression simplifies term by term into the formulation in Theorem 2; in the simplification one must invoke Eq. 3.2 and the fact that

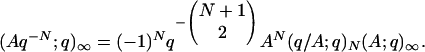[3.5]

4. Proof of Theorem 3

It is surprising that half the proof of Theorem 3 relies on an identity of MacMahon (1), and half relies on an identity of Fine (7). Thus, we shall refer to the result as the MacMahon-Fine identity. We begin with MacMahon, (ref. 1, p. 52) who proved

[4.1]

which may be algebraically simplified term by term to

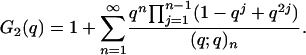[4.2]

Next, in his study of Ramanujan's mock theta functions, Fine (7) showed that

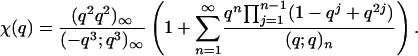[4.3]

Combining Eqs. 4.2 and 4.3, we obtain the assertion of Theorem 3.

5. Proof of Theorem 4

Here we rely principally on one of Ramanujan's mock theta function identifies (6), which we write as

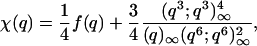[5.1]

where

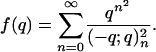[5.2]

In light of the fact that q/(1 + q)² is increasing for 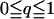, one may easily deduce that

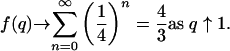[5.3]

Finally, we require (see theorem 1.12.8 in ref. 8)

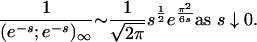[5.4]

Combining these results with Theorem 3, we see that as s ↓ 0 and q = e^-s,

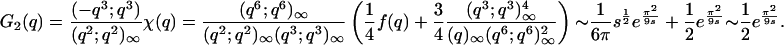[5.5]

Finally, then, from the identity of Holroyd et al. (5),

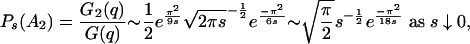[5.6]

which is the assertion in Theorem 4.

6. Conclusions

Several themes have been brought together in this article. First, the partition function, G_k(q), of Holroyd et al. (5) has been represented in explicit q series. In Theorem 1, G_k(q) is represented as an infinite product times a double series, and Theorem 2, G_k(q) is represented by less than k single-fold series multiplied by infinite products.

Empirical studies of the functions appearing on the right side in Theorem 2 suggest that (q^k+1; q^k+1)_∞P(0, k; q) is the dominant term. This observation is what led to Conjecture.

We hope that Theorem 3 provides a hint of further discoveries for G_k(q) in general. The fact that G₂(q) is an infinite product (in fact, a modular form) times the mock theta function, χ(q), suggests that the analytic nature of G_k(q) for k > 2 may be very interesting. Indeed, additional discoveries may well lead to the extension of Theorem 4 to results such as those stated in Conjecture.

The striking applications of such results pioneered by Holroyd et al. (5) make clear the potential significance of additional discoveries.