An Ensemble-Based Protocol for the Computational Prediction of Helix–Helix Interactions in G Protein-Coupled Receptors using Coarse-Grained Molecular Dynamics

Abstract

The accurate identification of the specific points of interaction between G protein-coupled receptor (GPCR) oligomers is essential for the design of receptor ligands targeting oligomeric receptor targets. A coarse-grained molecular dynamics computer simulation approach would provide a compelling means of identifying these specific protein–protein interactions and could be applied both for known oligomers of interest and as a high-throughput screen to identify novel oligomeric targets. However, to be effective, this in silico modeling must provide accurate, precise, and reproducible information. This has been achieved recently in numerous biological systems using an ensemble-based all-atom molecular dynamics approach. In this study, we describe an equivalent methodology for ensemble-based coarse-grained simulations. We report the performance of this method when applied to four different GPCRs known to oligomerize using error analysis to determine the ensemble size and individual replica simulation time required. Our measurements of distance between residues shown to be involved in oligomerization of the fifth transmembrane domain from the adenosine A_2A receptor are in very good agreement with the existing biophysical data and provide information about the nature of the contact interface that cannot be determined experimentally. Calculations of distance between rhodopsin, CXCR4, and β₁AR transmembrane domains reported to form contact points in homodimers correlate well with the corresponding measurements obtained from experimental structural data, providing an ability to predict contact interfaces computationally. Interestingly, error analysis enables identification of noninteracting regions. Our results confirm that GPCR interactions can be reliably predicted using this novel methodology.

1. Introduction

We need to understand how proteins behave in order to manipulate them successfully. The means by which to achieve accurate, precise, and reproducible predictions of the key properties of therapeutically relevant proteins is a fundamental question in computational biology. Molecular dynamics (MD) simulations have been used to study complex biomolecular systems, but it is not possible to define how a system behaves from a single trajectory; single trajectory systems behave as Gaussian random processes, making the attainment of accurate predictions from a single run not a realistic proposition. Accurate predictions that correlate well with experimental data have been achieved with the use of multiple short MD simulations to enhance the sampling of conformational space and hence the convergence of observable properties.¹⁻⁷ These ensemble-based fully atomistic MD studies have primarily focused on ligand-protein binding free energies, where there exists a wealth of experimental data with which to compare computational findings. In this paper, we take our first steps to assess the reliability and reproducibility of analogous CG-MD simulations. For this work, we have elected to examine the molecular nature of protein–protein interactions between G protein-coupled receptors (GPCRs). This is a biological system with which we are familiar experimentally.⁸⁻¹⁴

GPCRs are a particularly well-studied family of membrane proteins. Not only are they a large and important group of signaling proteins, they are also the targets for approximately 40% of all therapeutic compounds in clinical use. Although over 800 human proteins are classified as GPCRs, drugs have been developed against fewer than 10% of these targets.¹⁵ Thus, there is huge potential to expand the number of targets for which new therapies can be designed. Novel therapeutic design is also important if one of the goals of personalized medicine, to develop new drugs for patient-specific variations of GPCRs, is to be achieved. Inclusion of functional GPCR homomers and heteromers in drug discovery programs also provides a means of expanding the range of novel targets for the development of therapeutic agents.¹⁶ Originally believed to function as monomeric proteins, many functional GPCR oligomers have now been identified. Early examples include the obligate heteromeric assembly of GABA_BR1 and GABA_BR2 required to form a functional GABA_B receptor¹⁷ and heterodimerization of the delta and kappa opioid receptor subtypes to form an opioid receptor with the κ₂ receptor subtype pharmacology.¹⁸ The archetypal class A GPCR rhodopsin forms structural dimers organized in paracrystalline arrays in membranes¹⁹ and in the model crystal structure of this GPCR (1N3M).²⁰ For the design of cost-effective “designer” drugs for individuals that target receptor oligomers, it will be necessary to develop a powerful and sophisticated computational method for understanding the interactions involved in the formation of GPCR oligomers.

Biological methods for studying GPCR oligomers in native cells and tissues or in recombinant mammalian expression systems include coimmunoprecipitation, Western blot analyses, cross-linking studies, yeast two hybrid experiments, bimolecular fluorescence complementation via GFP reconstitution (BiFC), energy transfer-based methods (FRET and BRET), functional cross-talk, and activation by dimeric/bivalent ligands.²¹ Unfortunately, these methods frequently allow for alternative interpretations of the results and therefore do not provide unequivocal answers regarding multimerization occurrence between candidate pairs of GPCRs nor do they yield specific details of the interface(s) between interacting GPCRs. Structural methods such as X-ray crystallography and atomic force microscopy could provide some of this information, but only three Class A GPCR dimer structures have been solved²²⁻²⁴ and tend to describe “contact areas” rather than specific molecular interfaces. For the development of an accurate computational model for analyzing GPCR interfaces, it is essential to have good experimental data with which to validate the model. Such data are made available for the A_2A adenosine receptor subtype, which has been shown to participate in the formation of both heteromeric²⁵ and homomeric GPCRs.²⁶ The identification of homomeric A_2A receptors provided an opportunity to identify the transmembrane domain (TM5) involved in self-association by far-UV CD spectroscopy and SDS-PAGE using synthetic peptides corresponding to the different transmembrane domains.²⁷ A subsequent study²⁸ mapped TM helix interactions in the A_2A receptor for 31 different peptide pairs. We have previously worked with the A_2A receptor gene²⁹ and are interested in identifying patient-specific variations within this and related nucleoside and nucleotide receptor subtypes.

There have been many computational studies of GPCR interactions (see Table 1). The methodologies for modeling these have, in general, adopted one of two approaches: (i) molecular dynamics simulations using models based on homology with the nearest related GPCR for which structural data exist or (ii) docking.^30,31 Initial GPCR MD studies were performed using CHARMM and AMBER, which were subsequently integrated into NAMD^32,33 and GROMACS.^34,35 Although there is no established standard protocol for MD simulations of GPCRs, a number have used GROMACS with the Martini force field,³⁶⁻⁴¹ which is designed specifically for lipids and membranes and allows the lipid composition most suited to the receptor in question to be incorporated into the simulation. The more recent of the GPCR dimer modeling studies have been conducted using coarse-grained simulations, which take less compute time and therefore provide an opportunity to perform a substantial number of replicas for each set of simulation conditions.

Table 1. Computational Methods Used for Modeling Mammalian GPCR Dimers.

type	GPCR dimers	method	force field	interface	number of replicas	time scale	ref
homodimers	Rho/Rho	docking	CVFF	TM4,5/TM4,5		100 ps	Filipek et al., 200463
						NDa	Han et al., 200964
				TM1,2/TM1,2		ND	Kaczor et al., 201365
		MD	Gromos-87	TM4,5/TM4,5	1	45 ns	Filizola et al., 200666
			OPLSAA		1	0.1 μs	Cordomí and Perez, 200967
			Amber/parm99		2	300 ns	Neri et al., 201068
		CG-MD	Martini	TM1,2, H8	1b	8 μs	Periole et al., 200736
				TM4,5	10	100 μs	Periole et al., 201269
				TM6,7
	β2-/β2-adrenergic	CG-MD	Martini	H8/H8	2	5 μs	Ghosh et al., 201441
				TM1/TM1	4	∼200 μs	Prasanna et al., 201440
				TM4,5/TM4,5	1c	∼18 μs	Mondal et al., 201339
				TM5/TM5
				TM6/TM6
				TM3/TM3
	β1-/β1-adrenergic	CG-MD	Martini	TM1/TM1	3d (2 runs; different starting point)	2 μs	Mondal et al., 201339
				TM5/TM5
	α1B-/α1B-adrenergic	docking		TM5/TM5		ND	Fanelli et al., 199970
				TM6/TM6
				TM7/TM7
	5-HT4/5-HT4	docking		TM2,4/TM2,4		ND	Soulier et al., 200571
				TM4,6/TM4,6			Russo et al., 200772
							Berthouze et al., 200773
	5-HT1A/5-HT1A	docking	CHARMM	TM4,5/TM4,5		15 ns	Gorinski et al., 201274
	CXCR4/CXCR4	docking		TM4,5,IL2/TM4,5		ND	Kaczor et al., 201365
		MD	OPLSAA	TM3/TM4,5	1	50 ns	Rodriguez et al., 201275
				TM5/TM5
	NTSR1/NTSR1	docking	CHARMM	TM1/TM4		ND	Casciari et al., 200876
				TM4/TM4
	δ-OR/δ-OR	CG-MD	Martini	TM2,3,4/TM2,3,4	1e	250 ns	Provasi et al., 201037
				TM4/TM4 favored over TM4,5/TM4,5	2	1.5 μs	Johnston et al., 201177
	κ-OR/κ-OR	docking		TM1/TM2		ND	Kaczor et al., 201365
	A2AR/A2AR	docking	CHARMM	TM1,2,3/TM1,2,3 TM1/TM1		ND	Fanelli and Felline, 201178
				TM1,4/TM1,4
				TM2,3/TM2,3
				TM6,7/TM6,7
				H8,I3/TM6
	A3R/A3R	MD	Amber7 FF99	TM4,5/TM4,5	1	500 ps	Kim and Jacobson, 200679
	TXA2/TXA2	docking		TM1/TM1		ND	Fanelli et al., 201180
				TM1/TM2,EL2
				H8/H8
	D2R/D2R	Monte Carlo		ND		ND	Woolf and Linderman, 200481
	SSTR1/SSTR1	Monte Carlo		ND		ND	Woolf and Linderman, 200481
	LHR-LHR	docking		TM4/TM6,7		ND	Fanelli 200780
		MD	CHARMM	TM4/TM4	1	1 ns	Fanelli 200780
				TM4/TM6
				TM5/TM6
				TM4/TM1,3
heterodimers	A2AR/D2R	docking		TTM3,4/TM5,6		ND	Canals et al., 200325
				TM3,4,5/TM4,5
				TM4,5/TM3,4,5
	mGluR2/5-HT2A	docking		TM4,5/TM4,5		ND	Bruno et al., 200933
		MD	CHARMM22/27	TM4,5/TM4,5	1	40 ns	Bruno et al., 200933
	μ-OR/δ-OR	docking		TM6,7/TM4,5		ND	Liu et al., 200982
				TM1,7/TM4,7
		MD	GROMOS87	TM1,7/TM4,5	1	5 ns	Liu et al., 200982
				TM4,7/TM4,5
homotetramer	(V2R)4	MD	CHARMM22/27	TM3,4/TM4,7	1	5 ns	Witt et al., 200732
				TM4,5/TM4,5

^aND: not defined, IL: intracellular loop, EL: extracellular loop.

^bFour different structures.

^cNine different structures.

^dTwo runs; different starting point.

^eUmbrella sampling of 43 different starting points.

When we began our studies, approximately 30 computational GPCR dimer models had been published (Table 1). Of these, two are Monte Carlo-derived, 15 are based on docking, and nine have been generated using atomistic MD simulations. The rest are CG-MD models. Historically, docking was the earliest method to be employed and has been used regularly; its current use is widespread. Alternative methods of modeling began with Monte Carlo methods, moving to fully atomistic MD and a subsequent shift to CG-MD, which is the predominant MD method currently in use for GPCRs. CG-MD is popular as it is cheaper and faster and has been shown, when CG models are subsequently converted to atomistic representations, to produce similar results to models generated by atomistic MD.^38,42,43 CG-MD simulations have also been used to study TM helix–helix dimers for non-GPCR types of cell surface receptors such as Glyphorin A and ErbB dimers.^44,45

GPCRs exhibit thermodynamic equilibrium states and therefore are “mixing” in the language of ergodic dynamical systems theory.⁵ Neighboring trajectories diverge exponentially, and only probabilistic descriptions are meaningful. For these intrinsic reasons, collections of trajectories differing only in their initial conditions, known as ensembles, are the best means of studying the properties of such systems. Each individual system in the ensemble is referred to as a replica. As an additional benefit, performing such ensemble-based molecular dynamics simulations provides close control of errors and uncertainties in predictions. In this paper, we present the development of a robust and rapid method of this kind for identifying helix–helix interactions in GPCRs.

2. Methods

Here, we aim to develop a consistent, rapid, reproducible CG-MD methodology for the study of interacting helices. This method involves placing two GPCR transmembrane helices (a simulation set) in a membrane and running simulations with the hope of identifying interactions between the helices. In these simulations, we will be using distance as a means of identifying two different types of interactions: interactions between helices and interactions between amino acid residues on each helix. For the successful identification of both types of interactions, it is necessary to specify the number of replicas (identical independent simulations other than for the initial velocity seeds assigned to the particles) and the run time needed to achieve converged results and see how well they reproduce experimental results. The number of replicas must be sufficient to achieve a reproducible result as evidenced by a sufficiently small error estimate.

We will use the terms “stable dimer” and “dimerization” to refer to interactions between helices. A 10 Å truncation cutoff (backbone to backbone) has been set for dimerization, as it has been shown experimentally that a unique FRET signal is generated when two labeled peptides are located within 10 Å of each other and form an excited stated dimer.⁴⁶ The term “specific interactions” will be used to refer to interactions between amino acid side chains on the dimerized helices. Specific interactions will be identified from contact matrices (heat maps). Although a 12 Å truncation cutoff had previously been used to analyze these interactions,⁴⁷ we will set our interaction cutoff to 10 Å because the existence of hydrogen bond (C_α-H^......O) contacts as a function of the interhelical axial distance is between 6 and 12 Å. Side chain to side chain distances consistent with this are used to identify specific interactions with distances of 5–7 Å reflecting stronger interactions.

From Table 1, it can be seen that the longest total simulation time for atomistic MD is 0.1 μs and for CG simulations is 200 μs. The formation of a long-lasting helix dimer was identified within a few hundred nanoseconds in CG-MD studies of Glocophorin A, a non-GPCR model for studying TM membrane protein structure.²³ The number of replicas performed in these different studies varies tremendously but is never greater than 10. Excellent agreement has been obtained between computed binding free energies and experimental data when ensembles of up to 50 replicas are used.¹ We therefore selected 500 ns for the run time and 50 replicas as starting parameters for these studies. These calculations were run on Legion and Grace, two high-performance Research Computing clusters at University College London (UCL) (details of the machines used can be found at https://wiki.rc.ucl.ac.uk/wiki/RC_Systems#Legion_technical_specs and https://wiki.rc.ucl.ac.uk/wiki/RC_Systems#Grace_technical_specs). Our preliminary tests showed that CG simulations (one ensemble) of 500 ns run on Legion completed within approximately 150 h. CG simulations (one ensemble) of 500 ns run on Grace completed within approximately 72 h.

2.1. CG Simulations

All CG-MD simulations were performed in GROMACS (version 4.6.4) (www.gromacs.org). The temperature was equilibrated for all three groups: protein, lipid bilayer, and solvent (water) with ions to remove the center of mass motion relative to the bilayer and protein. The thermalization run was carried out for 100 ps. The simulations were then run at 310 K (the human physiological temperature), which is below the phase transition temperature of pure DPPC (315 K). The system output of the temperature was evaluated to ensure that it stabilized at the required temperature (310 K) before continuing until pressure equilibration was attained. An ensemble of 50 replicas for each simulation box (see Tables 2 and 4) was performed. Each simulation was run for 500 ns. CG atom velocities were drawn from a Maxwell–Boltzmann distribution at T = 310 K, but all other variables were kept constant; standard deviation was used to compare differences in mean distance outputs. Each simulation was run independently with the initial configurations differing by only the starting velocity; they were performed under the NPT ensemble (i.e., constant temperature, pressure, and particle number) using the Martini 2.2 force field.⁴⁸ The temperatures of the protein and lipid were coupled using the velocity-rescaling (modified Berendsen) thermostat at 310 K (human physiological body temperature) with a coupling constant of T_t = 1 ps. The system pressure was semi-isotropic using the Berendsen algorithm at 1 bar with a coupling constant of T_p = 1 ps and a compressibility of 1 × 10^–4 bar^–1. An integration time step of 30 fs was chosen, and the coordinates were saved every 10000 subsequent steps for further analysis. The electrostatic interactions were shifted to zero between 1.0 nm. The Lennard-Jones (LJ) potential was shifted to zero between 0.9 and 1.2 nm to reduce the cutoff noise. The neighbor list for pairwise nonbonded interactions was determined by the Verlet cutoff scheme at 1.4 nm and updated every 10 steps.

Table 2. Sequences of the A_2AR Helices Used in Ensemble Simulation Sets.

A2AR helices	sequencea
TM2-wild-type	FVVSLAAAD522.50IAVGVLAIPFAITI
TM5-wild-type	MNYMVYFNFFACVLVP1895.50LLLMLGVYLRI
TM5-M1775.38A	MNYAVYFNFFACVLVP1895.50LLLMLGVYLRI
TM5-M1935.54A	MNYMVYFNFFACVLVP1895.50LLLALGVYLRI
TM5-M1935.54I	MNYMVYFNFFACVLVP1895.50LLLILGVYLRI

^aResidues suggested to play a key role in the dimerization of the A_2AR TM5 helix²⁷ are indicated in bold; mutated residues are underlined and italicized. The conserved amino acid for each TM helix is italicized and is numbered using both the Ballesteros and Weinstein nomenclature (superscript) and by residue number.

Table 4. Sequences of the Rhodopsin, CXCR4, and β₁AR Receptor Helices Used in Ensemble Simulation Sets.

receptor	helices	sequencesa
rhodopsin	TM1	QFSMLAAYMFLLIMLGFPIN1.50(55)FLTLYVTVQ
	TM2	NYILLNLAVAD2.50(83)LFMVFGGFTTTLYTSLH
	TM4	ENHAIMGVAFTW4.50(161)VMALACAAPPL
	TM5	NESFVIYMFVVHFIIP5.50(215)LIVIFFCYGQ
CXCR4	TM5	VVVFQFQHIMVGLILP5.50(211)GIVIL
	TM6	VILILAFFACWLP6.50(254)YYIGISI
β1AR	TM1	QWEAGMSLLMALVVLLIVAGN1.50(59)VLVIAAIG
	TM2	NLFITSLACAD2.50(87)LVMGLLVVPFGATLVV
	TM4	ARAKVIICTVW4.50(166)AISALVSFLPIMM
	TM5	AYAIASSIISFYIP5.50(219)LLIMIFVYLRVY

^aThe conserved amino acid for each TM helix is shown in italics and is numbered using both the Ballesteros and Weinstein nomenclature (superscript) and by residue number.

2.2. Dimer Analysis

Interhelix distance matrices were calculated for the helix–helix dimer formation and contact maps used to identify specific interactions between residues were generated using the GROMACS tool g_mdmat. The individual helix–helix contacts from each replica were examined by calculating the resulting interhelix distance matrices from the initial simulation starting distance of 4 nm (40 Å) to assess the reproducibility, number of replicas, and run time needed to achieve convergence through a locally written code. In those runs where dimerization was observed, the trajectories were combined and examined in greater depth by calculating the averaged interhelix distance matrices with three different truncation distances of 10, 12, and 15 Å to determine the dimerization properties between the helices. A cutoff distance of 10 Å was then applied to identify residues involved in helix–helix interactions. To investigate the influence of the number of replica simulations on the reliability of our results, we calculated mean interaction distances for ensembles of varying size. For evaluations of run length, mean distance output for the entire ensemble was calculated at 100 ns increments.

Representative atomistic structures of the different CG dimers were generated through use of the “backward” Python script⁴⁹ and the g_cluster tool in GROMACS using the gromos algorithm at a cutoff of 2.5 nm.⁵⁰ Visualization was performed using VMD.⁵¹ Approximate distances between the atomistic residues in interacting helices were measured using Jmol (www.jmol.org). Amino acid positions have been described using amino acid number in conjunction with the Ballasteros–Weinstein nomenclature⁵² (in superscript). Pairwise combinations used in the analyses were obtained from a matrix of the number of amino acid residues in helix 1 multiplied by the number of amino acid residues in helix 2. In the A_2A receptor, there are 729 possible pair combinations between the two 27 residue long TM5 helices; for example, combination 552 specifies the combination of residue 23 (helix 1) with residue 24 (helix 2), representing the V196^5.57–Y197^5.58 interaction.

2.3. Construction of A_2AR TM Helices and Preparation of the Simulation Box

Initial simulations were performed using TM5 of the human A_2A adenosine receptor, which has been shown experimentally to form a homodimer.²⁸ TM2 of the A_2A receptor was used as a negative control as it was unable to form a homodimer under the same experimental conditions. M193^5.54, identified experimentally as being involved in the helical interface and located within a PXXXM motif, and M177^5.38, which we identified as residing in a previously unidentified upstream PXXXM motif, were mutated in silico (M177^5.38A, M193^5.54A, and M193^5.54I), to permit simulation of the experimental condition in which M193^5.54 had been mutated and the biological properties of the mutated protein compared with wild type.

The five A_2A TM helices shown in Table 2 were generated using MODELLER 9.12 following the procedure detailed^53,54 using the crystal structure of the A_2A receptor (PDB accession number 3EML; GI: 209447557).⁵⁵ The atomistic helices were subsequently converted to CG models using the “martinize” Python script.⁴³ A simulation box of dimensions 8 nm × 8 nm × 8 nm was constructed containing two wild-type TM5 helices (Figure 1). The helices were placed 4 nm apart and aligned in a parallel orientation mimicking the natural positioning of the helix in the membrane (see Figure 1a) with their long axes parallel to the z-axis of the box (see Figure 1b). The TM helices were separated by 4 nm at the beginning of the simulation to rule out any initial interhelix interactions. Water and lipids were then added. Approximately 190 molecules of the 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) lipid bilayer and additional water molecules (∼2660–2690) were added in coarse-grained form in a 3-dimensional cuboid box with periodic boundary conditions using the “insane” Python script.⁵⁶ For neutralization of the net charge on the protein, water molecules were replaced by counterions (either Na⁺ or Cl^–, as appropriate, depending on the amino acid composition of the helices).

Figure 1.

Experimental system showing (a) a schematic representation of the A_2A receptor structure indicating the directionality of the TM helices within the lipid bilayer and (b) placement of the TMs within the simulation box prior to the addition of lipid and water.

3. Results

Our aim is to investigate the computational parameters required to obtain converged results, to identify whether these results match the experimentally obtained data for the self-association of the TM5 helices of the A_2A adenosine receptor, and if they do, to further validate these parameters using structural biology data from class A GPCRs that have been experimentally shown to form a dimeric biological unit.

3.1. Internal Sampling, Convergence, and Reproducibility

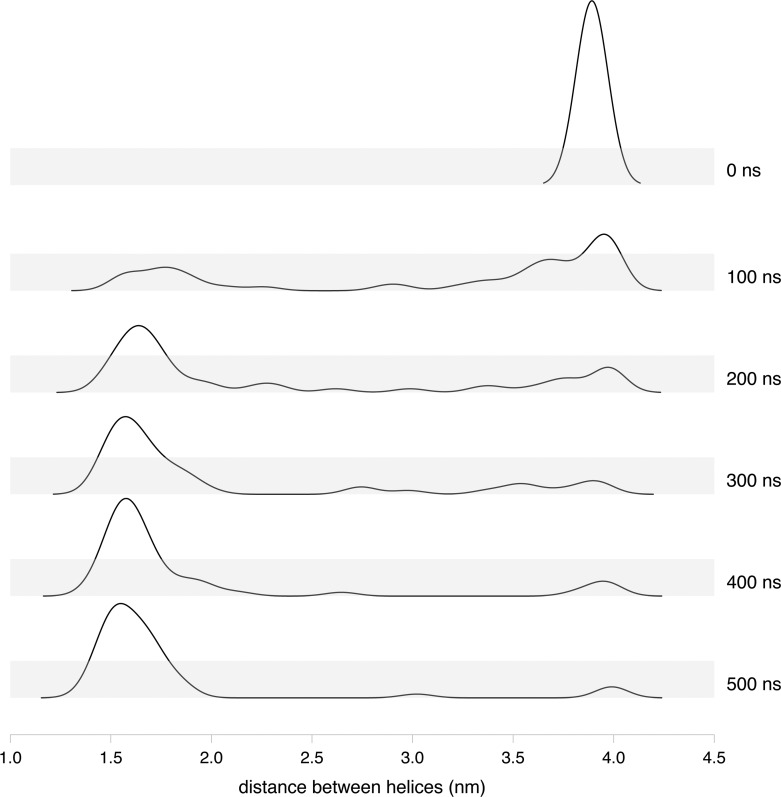
In our simulations, the TM helices were observed to diffuse freely in the lipid bilayer. The kernel density estimation of the mean distance between the two wild type TM5 helices at t = 0 and at increments of 100 ns up to completion of the simulation at 500 ns across the 50 replica ensemble is shown in Figure 2. At t = 0, the two helices are at their starting positions 40 Å (4.0 nm) apart. At t = 500 ns, the mean distance between the helices has adopted a normal distribution with a mean distance of ∼16 Å between them. The intermediate time points show the redistribution of the distance from the starting point at t = 0 to the final mean distance between the helices at 500 ns. A graphical representation of the number and timing of interactions observed in each replica within the ensemble of 50 replicas for the wild-type TM5–TM5 simulation is shown in Figure 3. Four of the 50 replicas showed no contact between the helices, which gives rise to the small peak at 40 Å in Figure 2. Three of the replicas began to show contact toward the end of the run, which corresponds to the smaller peak seen at 30 Å in Figure 2.

Figure 2.

Distribution of the mean distance between the two TM5–TM5 wild type helices at 0, 100, 200, 300, 400, and 500 ns in all 50 replicas.

Figure 3.

Number and timing of pairwise interactions for each of the 50 replicas within the wild-type TM5–TM5 dimer ensemble are shown. The x and y axes are linear and represent run length from 0 to 500 ns and the number of interaction events from 0 to 250 counts, respectively.

3.1.1. Optimal Replica Number Required

Five different ensembles, one for each A_2A receptor simulation set, were run independently in CG-MD simulations for the total run time of 500 ns. These data, which included both wild type and mutated helix sequences, were used to investigate whether variations in the optimal replica number required would occur between different simulation sets. This information was used to identify the minimum replica number required to achieve convergence for any given simulation set.

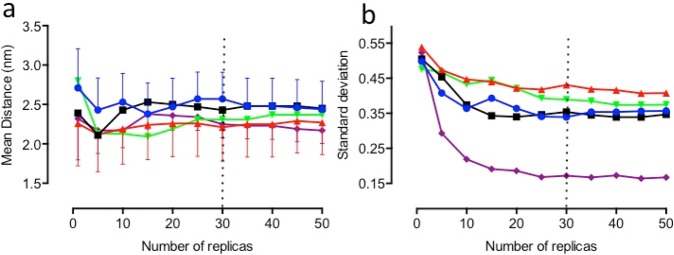
Figure 4a reveals that there is no statistically significant difference in the mean distance as a function of replica number. However, a decrease in the error of the mean is observed with increasing ensemble size. From Figure 4b it can be seen that the rate of decrease in the error slows after approximately 15 replicas are included in the ensemble. For each of the five sets, larger ensembles provide less variation in the error of the mean, and an ensemble of 30 replicas represents a good compromise between computational effort and minimization of the error in the mean distance calculated. We conclude that an ensemble of 30 replicas is sufficient to achieve convergence.

Figure 4.

Variation in (a) the mean distance between TM helices and (b) the error (standard deviation) is shown as a function of the number of replicas performed for the following simulation sets: (blue circle) wild-type TM5–TM5 helices, (black square) M177A-mutated TM5–TM5 helices, (red triangle) M193A-mutated TM5–TM5 helices, (green inverted triangle) M193I-mutated TM5–TM5 helices, and (purple diamond) wild-type TM2–TM2 helices.

3.1.2. Minimum Run Length Required

The effect of run time on the average distance between the helices was examined by calculating the mean distance and the standard deviation within the 50 replicas for simulations of varying duration (0, 100, 200, 300, 400, and 500 ns). Figure 5a shows a significant effect of run length on both mean distance and standard deviation, confirming the results of Figure 3 and reflecting the time required for interactions to take place. For four of the five simulation sets, the standard deviation increases as a function of time with the rate of increase slowing as the run length becomes longer. In contrast, no change in the standard deviation over time is seen in the TM2–TM2 set (Figure 5b). Interestingly, TM2 homodimers could not be detected experimentally.⁵⁷ The absence of an increase in error in the mean distance as a function of time may serve as an indicator of an absence of interaction between two helices within an ensemble. We conclude that an ensemble run for a simulation time of 300 ns is sufficient to achieve convergence.

Figure 5.

Variation in (a) the mean distance between TM helices and (b) the error (standard deviation) is shown as a function of the run length for the following simulation sets: (blue circle) wild-type TM5–TM5 helices, (black square) M177A-mutated TM5–TM5 helices, (red triangle) M193A-mutated TM5–TM5 helices, (green inverted triangle) M193I-mutated TM5–TM5 helices, and (purple diamond) wild-type TM2–TM2 helices.

3.2. Interacting Interfaces

The final mean distance between the two helices in the ensemble of 50 replicas was used to identify the specific interactions between the A_2A homodimers for each simulation set tested. Following application of the 10 Å cutoff, 26% of the ensemble formed stable dimers in the wild-type TM5–TM5 simulations. In the mutated TM5-M177^5.38A and TM5-M193^5.54I simulation sets, 16% of the ensemble formed stable dimers, whereas in TM5-M193^5.54A, dimers were detected in 28% of the ensemble. For all four of the TM5 simulation sets, the detected interactions took place at the same position within the helices, indicating that a defined orientation is needed to establish a specific interaction. In the negative control (the TM2–TM2 simulation set), 24% of the ensemble resulted in the formation of stable dimers, but there were no specific interactions identified between residues. For all simulations, we combined the trajectories of those pairwise combinations in which dimerization was identified after the cutoff of 10 Å had been applied and compared the results with heat maps of interactions observed at 12 and 15 Å (see Figure 6). The location of the contact interface was then mapped by comparison with the crystal structure of A_2AR (3EML).

Figure 6.

Contact matrices (heat maps) showing specific interactions between residues, as measured by distance, between two A_2A helices (“helix 1” and “helix 2”) for the wild-type TM5–TM5 simulation (a–c) and the TM2–TM2 negative control (d–f). Results shown are the average for each ensemble. Interhelical distances at the 15 Å cutoff are shown in the top left quarter of panels (a) and (d). Interhelical distances at the 12 Å cutoff are shown in the top left corner of (b) and (e) and in the lower right quarter of panels (a) and (d). Interhelical distances at the 10 Å cutoff are shown in the lower right quarter of panels (b) and (e). The region shown in the black rectangle in (a) and (d) is magnified in (c) and (f), respectively. The five numbered interactions shown in (c) are identified in Table 3. The color scale indicates distance between helices: blue corresponds to 0 Å (superposition of the two helical backbones at all cutoffs); green corresponds to 5 Å (10 Å cutoff), 6 Å (12 Å cutoff), and 7.5 Å (15 Å cutoff); yellow corresponds to 7 Å (10 Å cutoff), 8 Å (12 Å cutoff), and 12 Å (15 Å cutoff); red corresponds to the cutoff distances applied (10, 12, or 15 Å).

3.2.1. Identification of Contact Interface for the Wild-Type TM5–TM5 Homodimer

Figure 6 shows the average interhelical contact distance between the two wild-type TM5–TM5 helices (Figure 6a–c) or between the negative control TM2–TM2 helices (Figure 6d–f). The proximity of the wild-type helices is best visualized at 15 Å (Figure 6a and c). The interacting residues in the wild-type TM5–TM5 simulation are found in the bottom third of the C terminal end of TM5. From the averaged interhelix contact matrices, the specific interactions were found to be within the experimentally identified M193^5.54xxVY197^5.58 motif at an interhelical distance of ∼8–9 Å. The methionine at position 193^5.54 of helix 1 interacts with the methionine at the same position on helix 2, reinforcing the suggestion²⁷ of its importance in the formation of the TM5 homodimer. From Figure 6d it can be seen that the distance between TM2–TM2 is close enough to form potential specific interactions; however, none were detected in the combined trajectories for this negative control. Results obtained at the 15 Å cutoff (Figure 6f) were random and nonspecific, supporting the selection of a minimum cutoff distance of 12 Å. It should also be noted that there was no increase in the standard deviation over time for the TM2–TM2 simulation (Figure 5b), whereas there was an increase in this quantity for all simulation sets in which specific interactions occurred, indicating that the change in error over time may be a useful indicator of helix–helix interactions. The frequency of specific interactions identified in the wild-type TM5–TM5 ensemble was determined by calculating the mean distance for each frame of every replica individually. Table 3 shows that the five most prominently occurring interactions were between M193^5.54–M193^5.54_, V196^5.57–Y197^5.58, Y197^5.58–R199^5.60, R199^5.60–R199^5.60, and R199^5.60–I200^5.61.

Table 3. Number of Interactions (Hits) for Specific Interacting Residues Identified in the Contact Matrices for the Wild-Type TM5–TM5 Simulation at the 10 Å Cutoff.

		replica number
figure label	interacting residues	1	5	10	15	20	25	30	35	40	45	50	mean distance ± standard deviation (in Å)
1	M1935.54–M1935.54	0	0	1	1	1	2	2	3	5	6	6	7.59 ± 2.89
2	V1965.57–Y1975.58	0	1	2	2	2	4	4	6	9	12	13	9.16 ± 2.5
3	Y1975.58–Y1975.58	0	1	1	1	1	1	2	4	6	7	8	9.11 ± 2.85
4	Y1975.58–R1995.60	0	1	1	1	1	1	1	3	5	6	6	9.83 ± 3.57
5	R1995.60–R1995.60	0	1	1	1	1	1	1	3	4	5	5	8.06 ± 2.99

These findings are consistent with the experimental results²⁷ identifying that the interaction between two wild-type A_2A TM5 peptide sequences involved amino acid residue M193^5.54. Our findings are also consistent with experimental data showing the formation of A_2A receptor homodimers using bioluminescence resonance energy transfer (BRET)²⁶ and bimolecular fluorescence complementation (BiFC).⁵⁸ The presence of specific interactions between TM2 helices was experimentally investigated, and none were detected.^27,57 Our CG-MD simulations produced the same results as the experimentally obtained findings with the formation of wild-type TM5–TM5 dimers involving the M193^5.54 residue, and no specific interaction was detected between TM2–TM2 helices in silico.

3.2.2. Mutated TM5 Interacting Interfaces

Identification of the presence of M193^5.54 in the contact interface suggested that this residue may play a significant role in how the two TM5 helices interact. To investigate this possibility, we introduced sets of ensemble simulations that included mutated helices (see Table 2). Two types of point mutations were used: substitution of (i) methionine to alanine and (ii) methionine to isoleucine. Investigation of the TM5 peptide sequence revealed that two separate PxxxM motifs existed within the same helix with a methionine residue present at M177^5.38 as well the methionine residue identified at M193^5.54. Each of these methionine residues was mutated to alanine. We also mutated M193^5.54 to isoleucine because a conserved PxxxI motif is found in the related family of P2Y receptors at the same location as the originally identified PxxxM motif in A_2AR.

Specifically interacting residues in the TM5-M177A simulation set were identical to those identified in wild type TM5–TM5 dimers (Figure 7a) and included the M193^5.54xxxVY197^5.58 motif. M177^5.38 was not directly involved in the dimerization between the two helices in any simulation. The specific interactions observed in the TM5-M193I^5.54 simulation set were almost identical to those found in the wild-type but included I193^5.54 in the interaction despite the loss of the methionine at position 193 (Figure 7b). In contrast, the TM5-M193A^5.54 mutation completely changed the contact interface of the helices (Figure 7c), and the key interacting residues were identified at a similar distance but contained within a novel V196^5.57YxR199^5.60 motif. This provides a molecular explanation for the finding that mutation of the full-length A_2AR at position M193^5.54 noticeably alters the monomer:dimer ratio as observed with SDS-PAGE.²⁷ Mutation of M193A^5.54 causes a change in the way in which the two helices come together that prevents formation of TM5 homodimers, emphasizing the importance of the M193^5.54 residue in the specificity of TM5–TM5 dimer formation in vivo.

Figure 7.

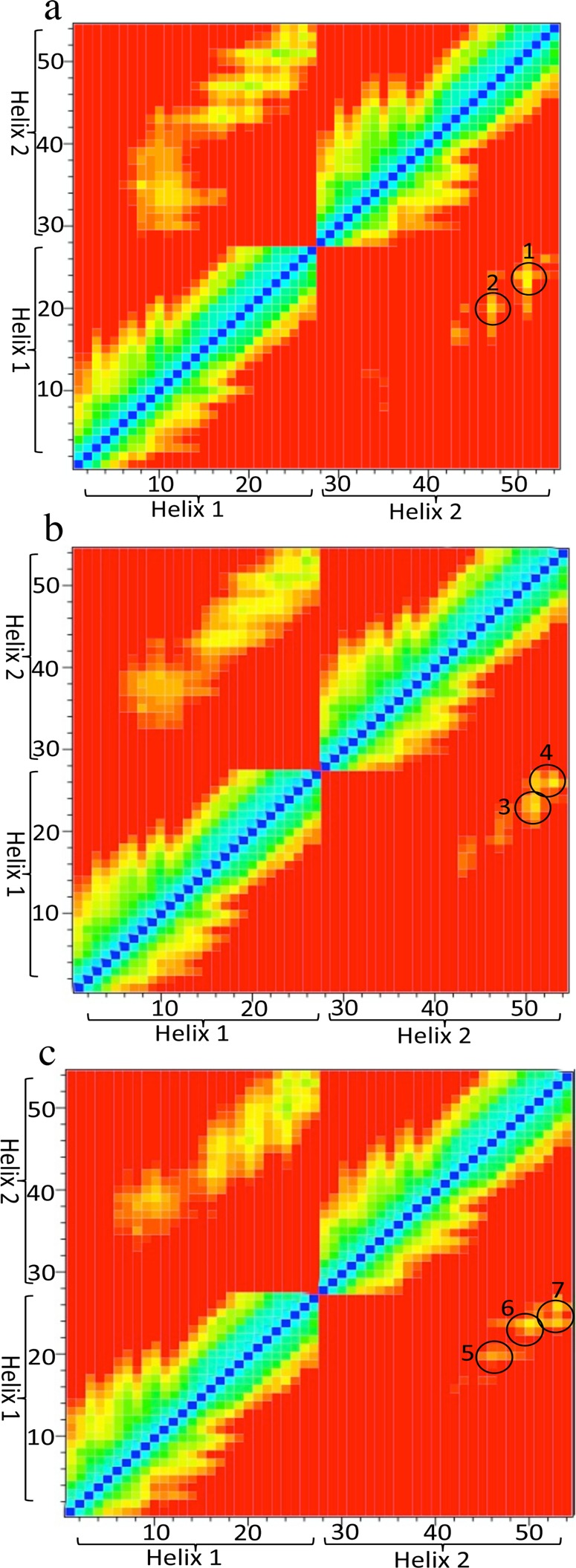
Contact matrices (heat maps) showing specific interactions between two mutated A_2A TM5 helices (“helix 1” and “helix 2”) with the following residues mutated: M177A (a), M193^5.54A (b), and M193^5.54I (c). Results shown are the average for each ensemble. Interhelical distances at the 15 and 12 Å cutoff distances are shown in the top left and lower right quarter of panels (a–c), respectively. The color scale is as indicated in Figure 6. Circles indicate areas with key interhelical contacts. The identified amino acid interactions are numbered as follows: (1) M193^5.54 with M193^5.54; (2, 3) V196^5.57 with Y197^5.58 and Y197^5.58 with Y197^5.58; (4) Y197^5.58 with I200^5.61 and R199^5.60 with R199^5.60; (5) L192^5.53 with I193^5.54, V196^5.57 with Y197^5.58, and Y197^5.58 with R199^5.60, (6) Y197^5.58 with I200^5.61 and Y197^5.58 with R199^5.60; and (7) R199^5.60 with R199^5.60.

3.3. Comparison with Experimental Structural Data

For assessing the validity of our method, it is necessary to compare our results with experimental values. Our computational results closely match the experimental biophysical data of A_2A receptor homodimers and provide information regrading the nature of the contact interface between the two helices that cannot be determined experimentally. We then wished to determine if we could obtain findings in agreement with experimentally obtained structural data. Dimerization in Class A GPCRs involves the transmembrane domains, as opposed to Class C GPCRs, where dimerization is mediated by the large N terminal domain of the protein.⁵⁹ We identified three additional dimeric Class A GPCRs in the PDB database that fulfilled the following criteria: (1) the crystallographic asymmetric unit is a dimer; (2) the software-determined (PISA) quaternary structure is a dimer; and (3) the dimeric quaternary structure has been confirmed functionally. Rhodopsin, the CXCR4 chemokine receptor, and the β₁ adrenergic receptor were chosen for further study; their corresponding TM helices (listed in Table 4) were constructed as described in section 2.3 and used in ensemble-based simulations.

3.3.1. Rhodopsin (1N3M)

Rhodopsin has been shown to exist in a native oligomeric form,²⁰ and an atomic model of the rhodopsin dimer has been proposed as a working model for G protein-coupled receptors.¹⁹ Three contact points between the rhodopsin monomers have been reported. The first is considered to be the strongest with the largest contact area (578 Ų) and is located between TM4 and TM5. The second exhibits a contact area of 333 Ų and is located between TM1 and TM2. The third contact point is considered the weakest interaction and is found between rows of dimers at the extracellular ends of TM1 with a contact area of 146 Ų.^19,22 We ran two heterologous simulations between rhodopsin helices TM1 and TM2 and between rhodopsin helices TM4 and TM5 (see Table 4) to identify whether contact interfaces could be identified for either. Figure 8 shows that, for both simulation sets, stable dimers were established, confirming that our computational method is able to produce results in agreement with structural data. In each case, the mean distance between helices was ∼7.6–8 Å. The mean distance between specific interacting residues in the TM1–TM2 simulation (Figure 8a) is further apart than the mean distance between specific interacting residues in the TM4–TM5 simulation (Figure 8b).

Figure 8.

Contact matrices (heat maps) between two rhodopsin helices, showing specific interactions between TM1 (helix 1) and TM2 (helix 2) (a) and between TM4 (helix 1) and TM5 (helix 2) (b). Results shown are the average for each ensemble. The color scale is as indicated in Figure 6. Circles indicate areas with key interhelical contacts. The identified amino acid interactions are numbered as follows: (1) F127^1.47 with L218^2.44; (2) L122^1.42 with L220^2.46, I123^1.43 with L218^2.44, and N219^2.45 with L220^2.46; (3) Y118^1.38 with D224^2.50, M119^1.39 with D224^2.50, F120^1.40 with D224^2.50, and F120^1.40 with L225^2.51; (4) F418^4.48 with L521^5.51 and T419^4.49 with L521^5.51; (5) F418^4.48 with F525^5.55; (6) M414^4.44 with F525^5.55, G415^4.45 with F525^5.55, and V416^4.46 with F525^5.55; (7) H411^4.41 with Y528^5.58, H411^4.41 with G529^5.59, and H411^4.41 with Q530^5.60.

3.3.2. CXCR4 (3ODU)

The crystal structure of the CXCR4 chemokine receptor bound to an antagonist small molecule IT1t has been reported and reveals a homodimer with an interface involving TM helices 5 and 6.²³ We investigated interactions between helices in the CXCR4 receptor and identified the formation of stable dimers with specific interactions (Figure 9). We first ran a heterologous simulation between TM5 and TM6 and were unable to identify any interactions. CXCR4 is able to form homodimers in the absence of ligand⁶⁰ that are unable to be dissociated by a peptide derived from TM6,⁶¹ suggesting that in unliganded CXCR4, the dimer interface may reside between TM5 and TM5 in a manner analogous to the A_2A receptor. We then ran a CXCR4 TM5–TM5 simulation and identified, from the averaged interhelix contact matrices, the formation of dimers with specific interactions between F201^5.40 and the following six residues: V198^5.37, Q200^5.39, F201^5.40, Q202^5.41, I204^5.43, and M205^5.44.

Figure 9.

Contact matrices (heat maps) between two CXCR4 helices, showing specific interactions (a) between TM5 (Helix 1) and TM6 (Helix 2) and (b) between TM5 (Helix 1) and TM5 (Helix 2). The identified amino acid interactions are numbered as follows: 1) F201^5.40 with V198^5.37, Q200^5.39, F201^5.40, Q202^5.41, I204^5.43 and M205^5.44. Table 5 shows a comparison of the distances between specific atoms in interacting residues of the representative structures and the distances between the same atoms in the model structure.

3.3.3. β₁-Adrenergic Receptor (4GPO)

Two alternating dimer interfaces have been proposed from the crystal structure of the ligand-free basal state of the β₁ adrenergic receptor (β₁AR). The first involves TM1, TM2, extracellular loop 1, and the C-terminal H8; the second involves TM4 and TM5.²⁴ We ran two heterologous simulations between β₁AR helices TM1 and TM2 and between β₁AR helices TM4 and TM5 (see Table 4) to identify whether contact interfaces could be identified for either. No stable dimers were formed in the TM1–TM2 simulation (Figure 10a). We investigated the possibility that the contact interface was formed between the two TM1 helices. We ran a TM1–TM1 simulation and identified a stable dimer in only one replica in the ensemble (Figure 10b). Stable dimers were formed between TM4 and TM5 with specific interactions identified between L159^4.43 and Y231^5.58 and between W166^4.50 and Y277^5.62 (Figure 10c).

Figure 10.

Contact matrices (heat maps) between two β₁AR helices showing specific interactions between (a) TM1 (helix 1) and TM2 (helix 2), (b) TM1 (helix 1) and TM1 (helix 2), and (c) between TM4 (helix 1) and TM5 (helix 2) (c). Results shown are the average for each ensemble. The color scale is as indicated in Figure 6. Circles indicate areas with key interhelical contacts. The identified amino acid interactions are numbered as follows: in (a) (1) W40^1.31 with A42^1.33, S45^1.36, and L46^1.37; (2) M44^1.35 with L46^1.37; (3) A49^1.39 with M48^1.38; (4) L53^1.44 with M48^1.38; (5) L53^1.44 with M48^1.38, V51^1.40, and V52^1.41; (6) L54^1.45 with V51^1.40; (b) (1) K159^4.43 with Y231^5.58 and (2) W166^4.50 with Y227^5.62. Table 5 shows a comparison of the distances between specific atoms in interacting residues of the representative structures and the distances between the same atoms in the model structure.

3.4. Atomistic Representation and Proposed Nature of Interactions

In CG simulations, a small group of atoms is treated as a single particle (in a 4:1 ratio), a representation that lacks the specific details needed to describe the nature and type of interactions that might take place when the two TM helices are within 10 Å of each other. Representative atomistic structures were generated from CG models to enable a measurement of distance between atoms,⁴⁹ allowing hypotheses to be drawn regarding the molecular nature and possible role of the interactions between dimeric helices.

Figure 11 shows a representation of the converted atomistic wild-type A_2A TM5 dimer. Using this atomistic representation, the presence of possible electrostatic interactions or hydrogen bonding was investigated by measuring the distance between the specific interacting residues. The interaction between the two methionine residues (M193^5.54–M193^5.54) and between valine and tyrosine (V196^5.57–Y197^5.58) is likely to correspond to van der Waals interactions. Y197^5.58 in helix 1 and Y197^5.58 in helix 2 each interact as hydrogen donor and acceptor in the dimer, forming bonds between the peptide backbone and the tyrosine side chain (see Figure 11). As the measurement of these distances is longer than the optimal hydrogen bond distance, 2.7 Å, such hydrogen bonds are more likely to be formed backbone-to-side-chain because their interhelical distance of 8 Å is above the 7.6 Å limit of backbone-to-backbone interactions.⁴⁷

Figure 11.

Atomistic representation of the pairwise interactions identified from the wild-type TM5–TM5 ensemble. The representative mean distance is shown in the figure, and the mean distance ± SD for all hits detected per pair is shown in Table 3. All distances between interacting amino acids are calculated from side chain to side chain.

The rhodopsin dimer model (1N3M), shown in Figure 12a, reveals that there is a greater interface area between TM4 and TM5 than between TM1 and TM2. The specific interacting residues identified from the atomistic representation obtained using our computational method are distributed throughout the length of TM1 and TM2 but restricted to the bottom third of TM4 and TM5 with respect to the intracellular face of the receptor (Figure 12b–e). A comparison of our results with the TM1 and TM2 contact interface of 1N3M is shown in Figure 12b and c, respectively. The measured distance between the hydrogen on the COOH group of M119^1.39 and the double-bonded oxygen of the COOH group on the side chain of D224^2.50 is 10.32 ± 3.21 Å in our model (Figure 12b), similar to 9.01 Å in 1N3M (Figure 12c). Measurement of the distance between F127^1.47 and L218^2.44 is 14.20 ± 4.07 Å in our model and 15.28 Å in 1N3M. F127^1.47 and L218^2.44 are located toward the bottom of their respective helices, a position that is constrained by the first intracellular loop of rhodopsin in 1N3M but not in our model. Similar conservation of distance was identified between interacting residues in TM4 and TM5 (see Table 5).

Figure 12.

(a) Atomistic structure of the rhodopsin dimer model (1N3M) viewed from above with the TMs used for simulations identified by color as follows: TM1 (blue), TM2 (red), TM4 (purple), and TM5 (orange). Representative TM structures were obtained from the means of all replicas in which interactions were detected. The representative and model structures of TM1–TM2 are shown in (b) and (c), respectively. The representative and model structures of TM4–TM5 are shown in (d) and (e), respectively. Specific interactions were identified in TM1–TM2 simulations (M119^1.39 with D224^2.50 and F127^1.47 with L218^2.44) and in TM4–TM5 simulations (H411^4.41 with Q530^5.60, G415^4.45 with F525^5.55, F418^4.48 with L521^5.51, and T419^4.49 with L521^5.51). Table 5 shows a comparison of the distances between specific atoms in interacting residues of the representative structures and the distances between the same atoms in the model structure.

Table 5. Comparison of Distance of the Identified Interacting Residues^a from Contact Matrix Graphs of the Rhodopsin, CXCR4, and β₁AR Helices and the Crystal Rhodopsin Dimer (1N3M), CXCR4 Dimer (4GPO), and the β₁AR Dimer (3ODU).

receptor	helices	interacting residues	crystal structure distance (Å)	mean distance (Å) ± standard deviation
rhodopsin	TM1–TM2	F1271.47–L2182.44	15.28	14.2  ±  4.07
		M1191.39–D2242.50	9.01	10.32  ±  3.1
	TM4–TM5	F4184.48–L5215.51	12.07	9.18 ± 3.24
		T4194.49–L5215.51	14.77	8.13 ± 1.96
		G4154.45–F5255.55	16.44	7.5 ± 2.3
		H4114.41–Q5305.60	17.64	9.06 ± 3.34
CXCR4	TM5–TM5	F2015.40–V1985.37	7.37	15.55 ± 3.34
		F2015.40–Q2005.39	11.03	13.7 ± 1.46
		F2015.40–F2015.40	7.91	13.6 ± 2.89
		F2015.40–Q2025.41	8.72	14.93 ± 3.13
		F2015.40–I2045.43	12.14	13.11 ± 3.37
		F2015.40–M2055.44	10.6	12.6 ± 4.96
β1AR	TM1–TM1	W401.31–A421.33	12.21	15.28b
		W401.31–S451.36	12.41	17.5b
		W401.31–L461.37	13.84	18.3b
		M441.35–L461.37	9.8	13.46b
		A491.39–M481.38	8.86	5.39b
		L531.44–M481.38	12.19	5.01b
		L531.44–V511.40	10.75	4.9b
		L531.44–V521.41	11.13	5.2b
		L541.45–V511.40	13.9	5.09b
	TM4–TM5	K1594.43–Y2315.58	NDc	9.01 ± 2.22
		W1664.50–Y2275.62	NDc	7.9 ± 1.99

^aDistances are measured from backbone to backbone.

^bInteractions were detected in only one replica in the ensemble.

^cNot determined (ND): The distances between TM4 and TM5 could not be measured due to the orientation of the dimer in the 4GPO crystal structure, which is submitted showing the TM1–TM2 dimer interface.

Our studies of CXCR4 identified novel interactions in the homodimer between TM5 and TM5 (Figure 13). This is similar to what was seen for A_2A, but the interacting residues in CXCR4 are closer to the extracellular side of the membrane than in A_2A. A comparison of the mean distance between interacting residues obtained from the simulations with the distance measured between the same residues in the crystal structure shows a similar conservation of distance, particularly between interacting residues further down the helix. This suggests a contribution of the loops for influencing interactions toward the ends of the helices, as was seen for rhodopsin.

Figure 13.

(a) Atomistic structure of the CXCR4 dimer model (3ODU) with the TMs used for simulations identified by color where TM5 is pink. Representative TM structures were obtained from the means of all replicas in which interactions were detected. The representative and model structures of TM5–TM5 are shown in (a) and (b), respectively. Specific interactions were identified in TM5–TM5 simulations (F201^5.40 with V198^5.37, Q200^5.39, F201^5.40, Q202^5.41, I204^5.43, and M205^5.44). Table 5 shows a comparison of the distances between specific atoms in interacting residues of the representative structures and the distances between the same atoms in the model structure.

Like rhodopsin, contact interfaces between between TM1 and TM2 (Figure 14a,b) and between TM4 and TM5 had been proposed for the β₁ adrenergic receptor. However, using our method it is possible to identify a contact interface between TM1 and TM1 rather than between TM1 and TM2. Our measurements of distance are in agreement with those of the crystal structure. Our data suggest that the TM4–TM5 contact interface, and the four specific amino acids identified within it, may constitute the principal dimer interface in β₁AR homodimers (Figure 14c). It was not possible to compare the distances obtained in the TM4–TM5 simulation with those measured in the crystal structure 4GPO, which had been submitted with the orientation of the dimer showing the proposed TM1–TM2 interface.

Figure 14.

(a) Atomistic structure of the β₁AR dimer model (4GPO) with the TMs used for simulations identified by color as follows: TM1 (pink), TM4 (red), and TM5 (blue). Representative TM structures were obtained from the means of all replicas in which interactions were detected. The representative and model structures of TM1–TM1 are shown in (a) and (b), respectively. The representative and model structures of TM4–TM5 are shown in (c). Specific interactions were identified in TM1–TM1 simulations (W40^1.31 with A42^1.33, S45^1.36, and L46^1.37; M44^1.35 with L46^1.37; A49^1.39 with M48^1.38; L53^1.44 with M48^1.38; L53^1.44 with M48^1.38, V51^1.40, and V52^1.41; L54^1.45 with V51^1.40) and in TM4–TM5 simulations (K159^4.43 with Y231^5.58; W166^4.50 with Y227^5.62.). Table 5 shows a comparison of the distances between specific atoms in interacting residues of the representative structures and the distances between the same atoms in the model structure.

4. Conclusions

In the present study, we have developed and assessed a method of ensemble-based coarse-grained classical molecular dynamics that we have used to predict protein–protein interactions between TM helices of dimeric GPCRs. We applied our method to four different homomeric GPCRs for which experimental data exist and compared our predicted results with published experimental data. We have found that, in each case, the ensemble-based CG-MD methodology provides a reproducible measurement of the distance between interacting helices that corresponds well with the experimental data and is within the range of distances at which protein–protein interactions occur.

The first case was that of the A_2A adenosine receptor, which had been shown experimentally to form homodimeric receptors through interactions between the TM5 helices of the two monomers. Our results identified specific interactions involving the PxxxM motif of TM5 and, specifically, at the M193^5.54 residue within that motif. Our method accurately identified residues shown experimentally to be involved in TM5 homodimerization. In parallel with work done experimentally, we investigated the role of M193^5.54 by characterizing the M193^5.54A mutation. From this, we identified that the contact interface of the helices was completely changed and that the key interacting residues identified in the wild-type conformation had moved to a new position, preventing the formation of TM5 homodimers. Our results provide a molecular explanation for the experimental finding that the M193^5.54A mutation alters the monomer:dimer ratio at a level of detail that could not be determined biophysically and would require structural biology studies to confirm experimentally. The second case we examined was that of the rhodopsin dimer for which crystallographic data had identified contact interfaces between TM1 and TM2 and between TM4 and TM5. Ensemble CG-MD confirmed dimerization and the identification of specific interactions within each of these heterologous TM pairs. There is a striking convergence between the distances predicted computationally and those calculated from 1N3M, particularly for specific interactions between TMs 1 and 2, showing that our method is able to provide accurate and precise predictions in agreement with experimental findings. Our method is also able to identify novel interfaces as seen in the third (CXCR4) and fourth (β₁AR) cases we studied, where we identified a novel interface in CXCR4 between TM5 and TM5 and a novel interface in β₁AR between TM1 and TM1, in addition to confirming the previously identified contact interface between TM4 and TM5 in β₁AR. The β₁AR has been shown to form transient interactions, whereas the β₂ adrenergic receptor can form stable oligomers.⁶² Our ability to detect a stable dimer of TM1–TM1 in the β₁AR shows the value of ensemble-based simulations for the identification of transient interactions.

We note that, in the four cases we studied, there appears to be a pattern emerging of the nature and location of the contact interfaces. We observe either a single interface, at TM5 in both A_2A and CXCR4, or two contact interfaces, as seen in rhodopsin and β₁AR, one of which involves TM1 and the other which is between TM4 and TM5. Interestingly, interactions in TM5 are observed in both cases. As a greater number of dimeric GPCR crystal structures with corresponding biophysical and functional data become available, the conservation of the pattern we have detected should become clearer.

Our results unequivocally demonstrate that sufficient conformational sampling is required in coarse-grained MD to obtain reproducible and reliable results. In our simulations, we identified that several of the replicas within the ensemble failed to show any interactions and that a number of others began to interact late in the simulation at a point when accurate estimates of distance could no longer be achieved. A single trajectory simulation, particularly if either of these circumstances were to occur, would give inaccurate and potentially misleading results. Indeed, as we have repeatedly emphasized, ensembles are required to obtain accurate and precise results. We used error analysis to determine appropriate choices for ensemble size and run length. For ensemble size, we observed that the rate of change in the standard deviation of the mean distance between helices decreased with increasing replica size and found that approximately 30 replicas were sufficient per ensemble to obtain reproducible results. For run length, we observed that the rate of increase in the standard deviation of the mean distance between helices increased with increasing run length, but that the rate of increase slowed substantially after approximately 300 ns. Interestingly, the negative control we included in our simulations showed no variation in the standard deviation of the mean distance between helices as a function of run length and a low standard deviation with a very rapid decrease to a constant value at an ensemble size of ∼15 replicas. This behavior was notably different from simulations in which interactions were identified and provides a means of confirming the absence of interaction.

In conclusion, we have provided a systematic, reproducible, and reliable protocol for determining the specific points of interaction between GPCR dimers. Our method discriminates between residues in TM helices that form specific interactions and residues that are in close proximity but do not interact. Our work extends the recent findings of ensemble-based fully atomistic MD studies, which have shown that an ensemble-based approach is required to generate predictions of protein properties that correlate well with experimental data.⁸³ Our method, which is similar in spirit to a recent publication by Wassenaar et al.,⁸⁴ is of great utility in further understanding GPCR function and also has broad applicability to many different types of membrane proteins, including receptor tyrosine kinases, ion channels, transporters, and oligomeric complexes of their various combinations.

The authors declare no competing financial interest.