Determining conformational order and crystallinity in polycaprolactone via Raman spectroscopy

Abstract

Raman spectroscopy is a popular method for non-invasive analysis of biomaterials containing polycaprolactone in applications such as tissue engineering and drug delivery. However there remain fundamental challenges in interpretation of such spectra in the context of existing dielectric spectroscopy and differential scanning calorimetry results in both the melt and semi-crystalline states. In this work, we develop a thermodynamically informed analysis method which utilizes basis spectra – ideal spectra of the polymer chain conformers comprising the measured Raman spectrum. In polycaprolactone we identify three basis spectra in the carbonyl region; measurement of their temperature dependence shows that one is linearly proportional to crystallinity, a second correlates with dipole-dipole interactions that are observed in dielectric spectroscopy and a third which correlates with amorphous chain behavior. For other spectral regions, e.g. C-COO stretch, a comparison of the basis spectra to those from density functional theory calculations in the all-trans configuration allows us to indicate whether sharp spectral peaks can be attributed to single chain modes in the all-trans state or to crystalline order. Our analysis method is general and should provide important insights to other polymeric materials.

I. INTRODUCTION

Polycaprolactone (PCL) is employed in a variety of applications including additive manufacturing,[1] tissue engineering,[2, 3] and drug delivery.[4] The ease of blending PCL with other polymers or composite fillers allow for enhanced control over physical properties, including the structural stability of components during degradation processes.[5] Often, non-destructive optical techniques are employed to characterize the degree of crystallinity and chain morphology in polymeric biomaterials,[6] which are key parameters that dictate the mechanical response of these systems.

Raman spectroscopy is a powerful technique for characterizing chain conformation and crystallinity in semicrystalline polymers. Much of this work has been done on the characterization of alkanes and polyethylenes to understand the possible ordered chain sequences that occur prior to crystallization.[7, 8] Raman measurements of PCL have primarily focused on identifying peaks that occur in the semicrystalline state versus the melt to give qualitative indicators of crystallinity.[9] However, more quantitative measures of crystallinity are required for developing structure-property relationships. Potential crystallinity indicators have been identified for vibrational modes corresponding to C-COO stretch, C-C stretch, CH₂ twist, CH₂ bend, and carbonyl (C=O) stretch modes.[9] Peak height ratios in the CH₂ twist region[10] and peak deconvolution of the carbonyl stretch region[11–13] have been used to qualitatively assess crystallinity without quantitative verification.

A challenge in identifying crystalline peaks in Raman spectroscopy is determining whether the peaks observed in the semicrystalline state can be explained via the vibrational modes of isolated perfectly regular chains or the factor group modes of chains packed in a crystalline lattice.[14] The modes of conformationally-ordered single chains are well-explained by coupled oscillator theory,[15] but additional space group modes can appear in the spectrum due to interchain interactions and the symmetry of the crystal subcell. These additional modes include low wavenumber lattice modes, degenerate modes made active due to the distorting forces of surrounding chains (crystal field splitting), and single-chain modes correlated between chains in the unit cell (correlation splitting). [14] In some cases, Raman spectra are sensitive to the conformational ordering of single chains separate from crystalline packing, as in the case of polyethylene,[7] polypropylene,[16] polyethylene terephthalate,[17] and polystyrene.[18] Although crystallinity and single-chain order are correlated, the use of interchain vibrational modes is critical to assessing the crystallinity of polymers like PCL.

The primary method used to separate single-chain modes from crystalline peaks relies on theoretical calculations of the Raman spectrum of single polymer chains and chains in the crystalline packing determined via X-ray scattering. Comparison of these calculations with experimental spectra provides an identification of crystalline bands, but the quantitative correlations between peak shapes requires costly all-atom simulations. Purely experimental identification of single-chain order occurs when chains undergo non-crystalline structural transitions, as with the crystal-rotator transition in alkanes. This transition can be observed and quantified via standard peak fitting techniques,[8] but multivariate analysis techniques such as principal component analysis (PCA) have also been identified as a way to identify peaks sensitive to conformational changes in melting alkanes.[19] PCA has also been used to identify potential hydrogen-bonded chain conformers in poly(acrylic acid) based on subtle changes in the carbonyl stretch region of the Raman spectrum.[20] We thus expect that multivariate analysis techniques like PCA can also separate single-chain effects from crystalline bands in the Raman spectrum of PCL.

Along with crystallinity, dipole-dipole effects in PCL are also important in understanding properties such as polymer miscibility[21] and processability via electrospinning.[22] The carbonyl stretch region of the Raman spectrum indicates dipole-dipole interactions in esters and polyesters when C=O groups are of the order (4 to 5) Å apart.[23] Dielectric spectroscopy measurements of PCL during melting indicates the presence of a non-crystalline chain conformer that is evident in dipole ordering.[24] Identification of such dipole ordering in PCL via Raman spectroscopy would provide further evidence of these ordered non-crystalline conformers.

In this work, we identify the specific indicators of crystallinity and dipolar interactions in the Raman spectrum of PCL. To separate the single-chain and crystalline ordered peaks, we perform PCA on Raman spectra in two temperature ranges: one in the melt state and one in the semicrystalline state. Linear combinations of the principal components are used to generate what we term basis spectra – ideal spectra of the polymer chain conformers comprising the measured Raman spectrum – based on physical arguments. The basis spectra in the melt state indicate an increase in more ordered conformers at lower temperatures which are specifically not due to crystalline order. A comparison of these basis spectra with those in the semicrystalline state allows for identification of purely crystalline contributions to the Raman spectrum of PCL. We describe our methodology in detail using the carbonyl stretch region of the spectrum to identify features of the spectrum due to dipole-dipole ordering separate from a purely crystalline peak. Applying this methodology to other regions of the spectrum indicates that many, if not all, of the sharp peaks in the C-COO stretch, C-C stretch, CH₂ twist, and CH₂ bend regions of the spectrum can be identified as single-chain effects. The crystalline peak in the carbonyl stretch region is shown by comparison to differential scanning calorimetry to be a reliable indicator of crystallinity in PCL over a wide range of crystallinities and temperatures.

II. EXPERIMENTAL

The poly-ε-caprolactone (PCL) samples used in this work are shown in Table I (see Disclaimer). All polymers are used as received. The crystallinity α_D is calculated via differential scanning calorimetry (DSC), which is measured on a TA Instruments Q1000 DSC. Temperature calibration is performed at the same heating rate as the samples with adamantane, benzophenone, indium, tin, and lead standards. Enthalpy calibration is performed with indium. A 10 mg sample of each polymer is heated at a rate of 10 °C/min from room temperature to temperatures above the equilibrium melting temperature T_m⁰ of PCL (69.2 °C).[25] The measured heat of fusion ΔH_f for each sample is used to calculate the mass fraction crystallinity based on the heat of fusion for a 100% crystalline sample ( $\mathrm{\Delta }{H}_f^0=139.5\mathrm{J}/\mathrm{g}$)[26] and employing the finite crystal size correction described by Crist and Mirabella as[27]

$${\alpha }_D=\frac{\mathrm{\Delta }{H}_f}{\mathrm{\Delta }{H}_f^0}\left(\frac{T_m^0}{T_m}\right),$$ (1)

where T_m is the melting temperature of the sample of interest. For calculation of crystallinity as a function of temperature, the finite size correction is performed by multiplying the heat flow by T_m⁰/T prior to integration. Proton nuclear magnetic resonance (¹H NMR) measurements of samples in CDCl₃ on a Bruker AVANCE 600 MHz spectrometer confirm that the polycaprolactones are free from configurational defects. The purity of each PCL is estimated from the ratio of the areas of the NMR peaks attributed to PCL[28] relative to the total peak area in the region of (0.15 to 7.0) ppm and is reported in Table I. With the exception of the 33K molar mass sample, all the polymers used are of a purity exceeding 96%.

Table I.

Number average molar mass M_n, supplier, crystallinity (from DSC), and purity (from NMR) for the polymers used.

Mn (g/mol)	Supplier	Crystallinity αD (%)	Purity (%)
4700	Polymer Source	84	97.6
10,000	Aldrich	76	96.2
33,000	Polymer Source	71	81.6
50,000	Perstorp	55	99.3
80,000	Aldrich	67	99.9
80,000	Perstorp	51	99.9
92,000	Polymer Source	80	96.9

The experimental results and analysis are based on the Raman spectra of the 80,000 g/mol PCL from Perstorp unless otherwise noted due to the high chemical purity of the sample and minimal background in the measured Raman spectra. The melting temperature of this polymer measured from the peak in the DSC trace is 59.7 °C.

Raman spectra measurements are performed using a rheo-Raman microscope, which provides an accurate temperature-controlled environment for performing Raman measurements.[29] Each sample is loaded into a parallel plate geometry at 20 °C, and the sample is either kept at temperature or heated at a rate of 1 °C/min to 160 °C. Raman measurements are performed in 180° backscattering mode using a 532 nm laser at a power of 10 mW at the sample. Spectra are collected using total exposure times of 5 s to 2000 s to ensure that the signal-to-noise ratio measured from the carbonyl peak in the (1720 to 1740) cm⁻¹ range is greater than 100-to-1. At least two exposures are averaged together within the OMNIC software (Thermo Fisher Scientific) to remove cosmic rays using a spike filter. During the temperature ramp, experimental spectra are collected every 31 s.

All spectra are analyzed in MATLAB (MathWorks). A linear baseline subtraction is independently performed on each region of the spectrum by performing a linear-least squares fit on a background region at least 15 cm⁻¹ wide at the high and low frequency ends of the fitting region (indicated in Table II). The baseline-subtracted spectra are then analyzed using the built-in pca function for principal component analysis. The analysis uses singular-value decomposition to generate the principal components p_n, eigenvalues (or variances), and scores s_ni for component n and experimental spectrum i.[30] To determine the number of eigenvectors to retain in our analysis, we stipulate the criterion that the variance of each principal component must exceed a critical value (0.01%), which is a common method.

Table II.

Number of principal components needed to explain the variance in the spectra of the different vibrational modes for various temperature ranges.

Vibrational Mode	Wavenumber range (cm−1)	20 °C to 160 °C	20 °C to 62 °C	62 °C to 160 °C
C-COO stretch	685 to 1018	4	3	2
C-C stretch	997 to 1150	4	3	2
CH2 twist	1200 to 1362	3	2	2
CH2 bend	1362 to 1540	3	2	2
C=O stretch	1600 to 1850	3	2	2

When k = 2 principal components are retained, we use self modeling curve resolution to generate the basis spectra. [31] The basis spectra are generated from linear combinations of the principal components using physical constraints: 1) the intensity of the basis spectra must be positive, 2) only nonnegative linear combinations of the basis spectra are used to fit the experimental spectrum, and 3) the total integrated intensity of the basis spectra must equal 1.[31] The k^th basis spectrum c_k is then a band of solutions defined by a linear interpolation between a maximum spectrum $c_k^{\ast }=s_{1k}^{\ast }{p}_1+s_{2k}^{\ast }{p}_2$ and minimum spectrum $c_k^{\ast \ast }=s_{1k}^{\ast \ast }{p}_1+s_{2k}^{\ast \ast }{p}_2$, or

$$c_k=a_k{c}_k^{\ast }+\left(1-a_k\right)c_k^{\ast \ast }$$ (2)

where 0 ≤ a_k ≤ 1 and $s_{nk}^{\ast }\left(s_{nk}^{\ast \ast }\right)$ is a constant coefficient on the n^th principal component to generate the k^th maximum (minimum) basis spectrum. The properties of self modeling curve resolution on two component Raman spectra generate one basis spectrum with $\left(s_{2k}^{\ast },s_{2k}^{\ast \ast }\right)<0$ and a second basis spectrum with $\left(s_{2k}^{\ast },s_{2k}^{\ast \ast }\right)>0$; we define the k = 1 basis spectrum as having $\left(s_{21}^{\ast },s_{21}^{\ast \ast }\right)<0$.

The resulting basis spectra are a table of intensities for a given Raman shift ν. These are fit to the experimental spectrum h(ν) using the lsqcurvefit function assuming that the experimental spectrum is represented by

$$h\left(\nu \right)={\displaystyle \sum _{j=1}^k{b}_j{c}_j\left(\nu +\delta \nu \right)}$$ (3)

where b_j are scaling factors and δν is a horizontal shift factor common to all basis spectra. The horizontal shift factor is used to account for accuracy in the measured Raman shift and has values δν < 1 cm⁻¹.

Density functional theory (DFT) calculations of the Raman spectrum of an all-trans PCL oligomer with seven repeat units are performed using the Gaussian 09 (Gaussian, Inc.) suite of programs.[32] Geometry optimization and frequency calculations are performed using the B3LYP functional and the 6-31G(d,p) basis set. The Raman scattering intensity is calculated based on the calculated Raman cross section and an assumed Lorentzian peak shape with 4 cm⁻¹ peak width for each vibrational mode. The calculated Raman shift values are scaled by 0.961 to more closely match experimental values.

III. RESULTS

The Raman spectra of PCL at temperatures above and below the melt temperature are shown in Figure 1. We follow the work of Holland-Moritz and Hummel[33] in the assignment of the CH₂ twist, CH₂ bend, and C=O stretch regions of the spectrum. Measurements on a number of aliphatic polyesters indicate that the 850 cm⁻¹ to 1110 cm⁻¹ region of the spectrum consists of a mixture of skeletal modes including C-C stretch, C-O stretch, and C-COO stretch.[9, 34, 35] We separate the skeletal stretch region into a primarily C-COO stretch region at 850 cm⁻¹ to 950 cm⁻¹ and a primarily C-C and C-O stretch region (which we refer to as C-C stretch for brevity) at 1030 cm⁻¹ to 1110 cm⁻¹ as indicated in Figure 1 based on assignments for polyesters of similar configuration.[34] In the semicrystalline state the spectrum shows sharp peaks in the regions corresponding to specific vibrational modes that are specific to either the alkyl chain segment or the ester group.[36] The presence of these sharp peaks are often associated with crystallinity in the sample.[9] The spectrum of PCL in the melt state shows broader peaks in the same regions of the semicrystalline Raman spectrum, which indicates that the polymer is in a conformationally disordered state at higher temperatures.

Figure 1.

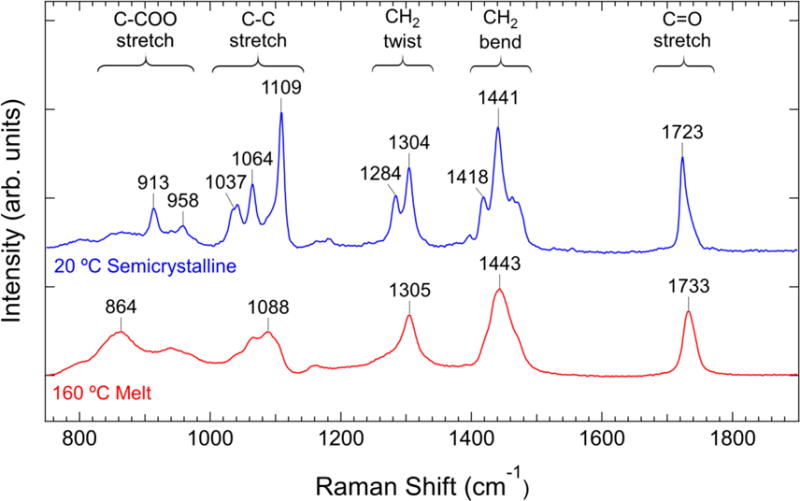
Raman spectrum of PCL at two temperatures. The peak positions and spectral regions corresponding to specific vibrational modes are indicated. The spectra have been normalized to the integrated intensity of the peak in the C=O stretch region.

The spectrum of the semicrystalline PCL qualitatively indicates that the system is more conformationally ordered than in the melt state. However, a challenge in analyzing vibrational spectra is determining what spectral features are due to chains in a crystalline packing versus those due to single chains. The individual measurement of single chain and crystalline peaks allows for the identification of non-crystalline precursors during polyethylene crystallization.[7] To identify peaks associated with single-chain ordering we utilize the fact that conformational changes occur in the melt state: as the temperature decreases towards the equilibrium melting point, the probability of finding a dihedral angle with a low free energy increases. Since these lower energy states are more conformationally ordered, we can expect a corresponding increase in Raman peaks corresponding to single-chain ordered conformers. When the polymer is semicrystalline, the single-chain ordered conformers and the crystalline peaks will both have a high intensity. Therefore, a systematic temperature variation in the melt state should allow for identification of ordered single chain effects.

The Raman spectrum at two temperatures in the melt state is shown in Figure 2a. The peaks in the spectra show small peak shifts with temperature in the C-COO stretch, C-C stretch, and C=O stretch regions of the spectrum, but the general features of the spectra remain largely unchanged. Subtle differences in Raman spectra can often be enhanced via spectral subtraction techniques, where two spectra are scaled and subtracted so that the resulting difference spectrum has no feature with an intensity less than the experimental background. From the two measurements we generate two difference spectra: a spectrum where the high temperature spectrum is subtracted from the lower one (T_lh = T_l – ξ_hT_h), and a second spectrum where the opposite subtraction occurs (T_hl = T_h – ξ_lT_l). The coefficients ξ_h and ξ_l are constant scaling factors that generate difference spectra with non-negative peaks. The T_lh spectrum shows sharper features compared to the experimental melt spectra, whereas the T_hl spectrum indicates much broader features in the regions corresponding to the different vibrational modes.

Figure 2.

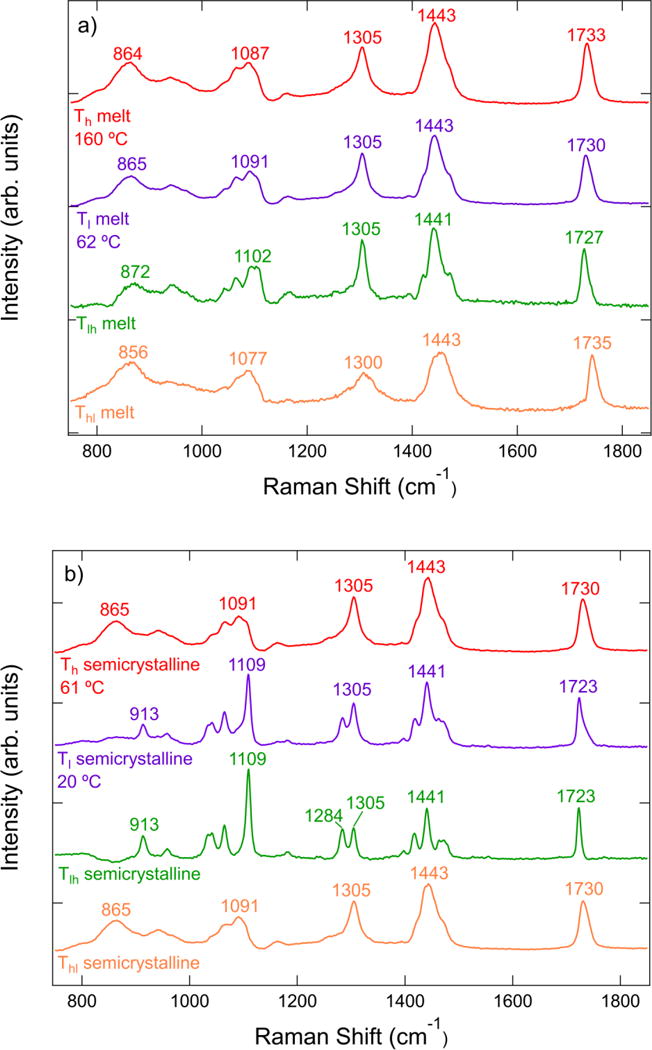
a) Raman spectra of PCL at high (T_h) and low (T_l) temperatures in the melt state. Also shown are the two difference spectra T_lh and T_hl. b) Raman spectra and difference spectra at temperatures in the semicrystalline state. The positions of peak maxima are indicated.

The difference spectra indicate changes in the chain conformer distribution with temperature. The T_lh spectrum emulates the spectrum of more ordered conformers in the melt state, since the more disordered spectrum T_h has been removed, whereas the T_hl spectrum indicates the broad distribution of vibrational modes for more disordered conformers. Although the difference spectra indicate conformational changes, the signal-to-noise ratio is decreased compared to the experimental spectra. The difference spectra also provide no information on whether the features in the difference spectra are due to multiple conformational changes, or the evolution of the chain conformer distribution with temperature.

We can address the number of independently-evolving conformer distributions by performing principal component analysis in regions of the Raman spectrum over various temperature ranges. Although PCA on the entire spectrum would be ideal, this requires that background effects are subtracted from the Raman spectrum prior to analysis. Methods of background subtraction are numerous and can change the loadings and scores of the principal components.[37] Also, our intent is to differentiate between regular ordered single-chain bands and those bands of chains in a crystalline packing. We therefore focus on separate frequency regions of the spectrum that have potential crystallinity bands so that small changes in each region of the spectrum can be identified, and we can use a simple linear background subtraction method.

The number of components that contribute more than 0.01% of the variance in the measured spectra is shown in Table 2 for three temperature ranges: the entire experimental temperature range from semicrystalline to melt, the semicrystalline temperature range, and the melt temperature range. Over the entire temperature range the vibrational modes can be explained using either 3 or 4 principal component spectra. In the semicrystalline temperature range from 20 °C to 62 °C, 2 or 3 components are necessary, but in the melt state only 2 components are required. We note that the sum of the components required separately in the melt and semicrystalline states are more than the number of components required over the entire temperature range. This inequality indicates that either one of the melt or semicrystalline components is redundant.

Table II indicates that different vibrational modes can require a different number of principal components to describe the spectra over the temperature range. This discrepancy appears in the semicrystalline state, where two components are necessary to explain the CH₂ twist, CH₂ bend, and C=O stretch regions of the semicrystalline spectra, whereas three components are required for the C-COO stretch and C-C stretch regions. In the melt state, all vibrational modes require two principal components. The number of melt components for the vibrational modes associated with the alkyl chain segment (C-C stretch, CH₂ twist, and CH₂ bend) is equivalent to the number of states (trans and gauche) that are expected for aliphatic ester chains.[38] These states are also expected to change the vibrational spectrum of the C-COO stretch modes, since the dihedral bond between the methylene group and the carbonyl group has a probability of being trans or gauche that is of similar magnitude to the alkyl chain segment.[26] In contrast, the carbonyl stretch mode is localized, and the ester group is expected to exist in the melt in a rigid trans conformation.[38] Therefore, we expect that the principal components in the carbonyl stretch region of the spectrum is due to other interchain interactions.

To gain further insight into the conformers described by the principal component analysis, we can use the calculated principal components to determine basis spectra by self-modeling curve resolution. To demonstrate how the analysis is performed we focus on the carbonyl stretch region of the spectrum, which has been used as a crystallinity indicator in previous studies with a single component in the melt state. [11–13]

The principal components of the carbonyl stretch region in the temperature range of 62 °C to 160 °C are shown in Figure 3a. The first principal component p_1m comprises over 99 % of the total variance and consists of a broad peak positioned at 1731 cm⁻¹. The second principal component p_2m in the melt resembles a first derivative spectrum of a peak indicating a shift in the Raman peak position over the temperature range. The remaining principal components comprise 0.02 % of the variance in the Raman spectra; the next largest component p_3m is noisy and contributes a negligible amount to the total variance. The carbonyl stretch region of the spectrum is therefore comprised of two principal components in the melt state, which account for the spectral features observed in the melt state. Semicrystalline PCL also exhibits variation in the carbonyl stretch region over a temperature range from room temperature to 62 °C. Figure 3b shows that two principal components p_1c and p_2c again comprise the majority of the variance in the Raman spectra, with the third component p_3c contributing less than 0.01%. The positions of peak extrema are shifted towards lower Raman shift values compared to the melt principal components. The principal component magnitudes (scores) for the principal components shown in Figure 3 as a function of temperature are included in the Supplementary Material. The scores of the first principal component are large and always positive, but the scores of the second component range from positive to negative values. The third component has negligible scores over both the melt and semicrystalline temperature ranges, which further indicates that the third component is negligible.

Figure 3.

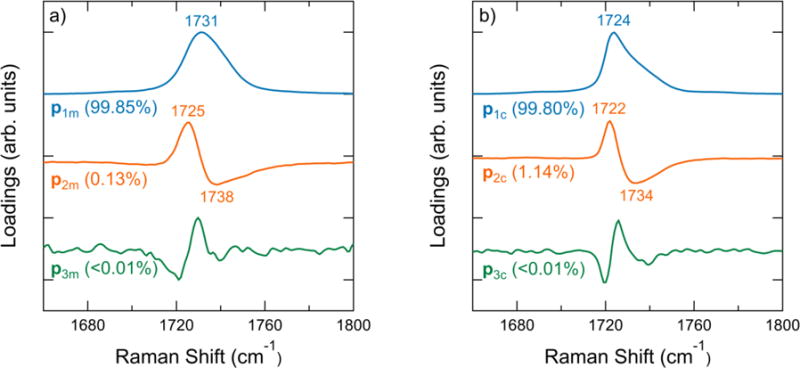
a) Principal components of PCL spectra in the melt from 62 °C to 160 °C. b) Principal components of spectra during crystal melting from 20 °C to 62 °C. The position in cm⁻¹ is labeled near peak extrema. The percentage of the total variance explained by each principal component is indicated in parentheses. See Supplementary Material for the variance of additional principal components.

The principal components do not have direct physical meaning but are linear combinations of basis spectra. It is impossible to completely isolate different chain conformers and structures within a polymer melt to directly measure these basis spectra, but we can approximate their shape by choosing linear combinations of the principal components to generate basis spectra with positive intensities and prefactors. Self modeling curve resolution produces the basis spectra ranges shown in Figure 4a and b for the melt and semicrystalline temperatures, respectively. The c₂ ranges in the melt and semicrystalline state indicate narrow peaks when a₂ = 1, which agree well with the T_lh spectra. The melt and semicrystalline T_hl difference spectra fall between the bounds generated by the c₁ basis component range. In cases where two components are expected, the difference spectra provide a useful approximation for the basis spectra.[14] Further evidence of this comes from the fact that the difference spectra occur within the feasible region of the basis spectra range. We generate basis spectra c_k for each range by varying each a_k to determine the least-squares best fit to the difference spectra, which occurs in the melt spectra for a₂ = 1 and a₁ = 0.57. In the semicrystalline spectra, we find the best fit occurs for a₂ = 1 and a₁ = 0.17.

Figure 4.

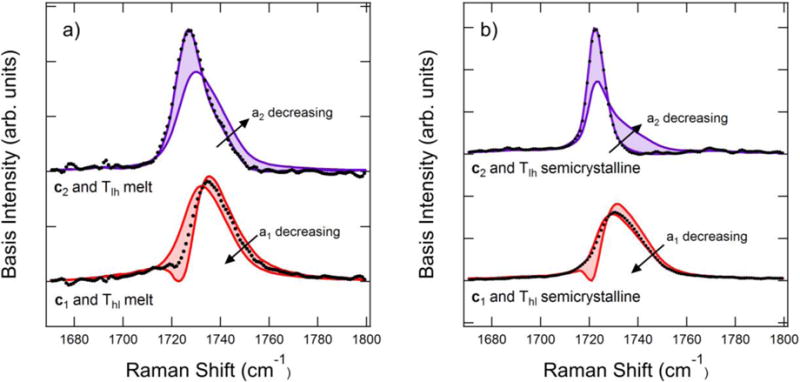
Basis spectra ranges and difference spectra in the C=O stretch region for a) the melt temperature range and b) the crystalline temperature range. The bold lines indicate $c_k^{\ast }$ and $c_k^{\ast \ast }$, and the shaded region indicates where the basis spectra are possible. The points indicate the difference spectra shown in Figure 2.

Our analysis generates two basis spectra in the melt and two in the semicrystalline state. However, the total of only three components expected over the entire melt and semicrystalline temperature range in Table II suggests that one of the basis spectra is redundant. Linear least squares fitting of the basis spectra indicates that the semicrystalline c₁ basis spectrum can be represented by a combination of the two melt components (see Supplementary Material). The resulting basis spectra are shown in Figure 5a.

Figure 5.

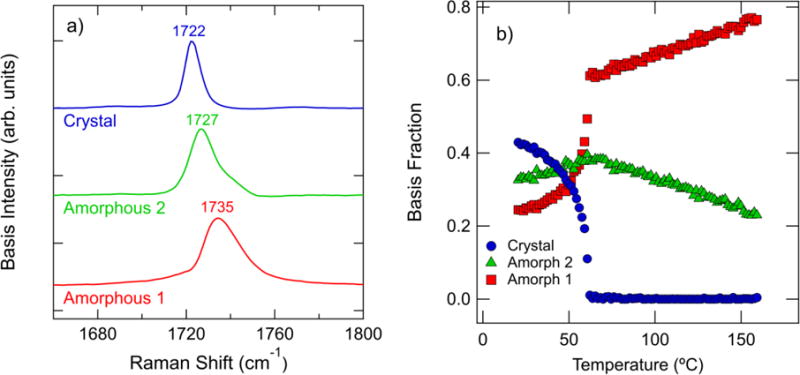
a) Estimated basis spectra of the Raman spectra in the carbonyl stretch region. b) Integrated intensity of the components in (a) plotted versus temperature. The intensities are normalized by the total integrated area in the carbonyl stretch region. The results of every 3^rd spectra are plotted for clarity in (b).

The temperature dependence of the basis spectra is key to relating these spectral features to physical phenomena. The basis spectra intensities are shown in Figure 5b to change dramatically with temperature over the entire temperature range. The “crystal” basis spectrum consists of a single peak centered at 1722 cm⁻¹. This basis intensity decreases with increasing temperature until the melting point, above which the peak comprises a negligible fraction of the experimental spectra. Above the melting point, the basis spectra labeled “amorphous 1” and “amorphous 2” comprise the experimental spectrum. The amorphous 1 component comprises the majority of the spectrum above 62 °C and increases with increasing temperature. The amorphous 1 and amorphous 2 spectra are asymmetric about the peak maximum, with the amorphous 2 component exhibiting a shoulder near 1740 cm⁻¹. Neither of the amorphous basis spectra could be fit by a single peak.

The increase in the amorphous 1 component fraction with increasing temperature suggests that these features are associated with a more disordered state in the melt. We note that although the amorphous 2 spectrum increases with temperature from room temperature to 62 °C, then shows an opposite trend with temperature in the melt state. The decrease in the amorphous 2 fraction as temperature increases in the melt state indicates that this basis spectrum is likely to indicate chain conformers that are somehow ordered but non-crystalline. Since the ester group exists primarily in a trans state,[39] the changes in basis fraction in the melt are not due to variation in conformer distribution. The carbonyl stretch region of the Raman spectrum is also sensitive to dipole-dipole interactions.[23] Raman measurements of syndiotactic poly(methyl methacrylate) (s-PMMA) in various solvents indicate that the carbonyl stretch region is sensitive to structural transitions.[40] The carbonyl stretch peak is observed to shift from 1734 cm⁻¹ to 1728 cm⁻¹ when s-PMMA in solution goes from a random coil structure to an aggregated structure. This peak shift to lower values is attributed to increased dipole-dipole interactions between neighboring extended chain segments and can be reversed by heating.[40] Our amorphous basis spectra are similar in peak position and qualitative temperature dependence to the measurements performed on s-PMMA.

Classical perturbation theory predicts that interchain interactions of carbonyl-containing chains can shift the observed C=O stretch peak to higher or lower frequencies depending on the phase angle, distance, and interaction constant between adjacent oscillators.[41] The shift to lower frequencies with increased dipole-dipole interactions is directly explained by the work of Galbati et al: dipole-dipole interactions lengthen the C=O bond length, increase the charge on the oxygen atom, and decrease the vibrational frequency when dipoles are within a distance of (4 to 5) Å.[23] We therefore attribute the amorphous 2 spectrum to extended chain segments with increased dipole-dipole interactions and the amorphous 1 spectrum to a random coil conformation.

To gain further insight into the properties of the amorphous spectra, we perform a van ‘t Hoff analysis of the basis fractions as a function of temperature in the melt state (Supplementary Material), which indicates a transition enthalpy of (9.5 ± 0.1) kJ/mol. This transition enthalpy is significantly less than the enthalpy associated with ester torsion (54.8 kJ/mol)[42] but greater than the (2 to 4) kJ/mol trans-gauche transition enthalpy of dihedral bonds along the chain.[38] Ab initio calculations on interacting acetone molecules predict that carbonyl-carbonyl interaction energies in the range of approximately (8 to 22) kJ/mol,[43] which falls in the range of our calculated transition enthalpy in the melt.

The temperature dependence of the crystal basis spectrum suggests that this peak is indicative of crystalline conformational order. The crystal basis spectrum decreases to negligible intensities above the melt temperature, which suggests that the basis spectrum peak at 1722 cm⁻¹ captures an interchain interaction between chains in the PCL crystal. Furthermore, the distinct narrow crystal peak compared to the amorphous peaks in Figure 5a indicate a more ordered chain conformer than that observed in the melt state. At temperatures in the semicrystalline state, we note that the crystalline component fraction dominates at temperatures below 40 °C. Decreasing crystalline order is expected as we increase temperature towards the melting point, which is evident in the increase in the amorphous basis fractions as temperature increases to 62 °C.

A similar analysis used to generate the basis spectra for the carbonyl stretch region of the spectrum can be applied to other regions of the spectrum when two components are observed in the semicrystalline state. Three components are necessary to describe the semicrystalline temperature range for the C-COO and C-C stretch regions of the spectrum, which means that their difference spectra shown in Figure 2b include a combination of three basis spectra. Although self-modeling curve resolution has been developed for three-component systems,[44] we find that a conceptually easier method is to perform principal component analysis on smaller temperature ranges in the semicrystalline state until only two components are needed to describe each region. We then proceed in a manner identical to melt and semicrystalline ranges for the carbonyl stretch region: the basis spectra ranges are fit to the difference spectra in those temperature ranges to determine the basis spectra, and the resulting basis spectra are checked for redundancy. The major principal components for each region of the PCL Raman spectrum are shown in the Supplementary Material. The resulting basis spectra are shown in Figure 6 for the C-COO stretch, C-C stretch, CH₂ twist, and CH₂ bend vibrational regions. Comparing the crystal 1 and crystal 2 components in Figure 6 indicates similar strong spectral features with shifted peak positions for both the C-COO stretch and C-C stretch modes. The CH₂ twist and CH₂ bend modes are well-described using a single crystalline component.

Figure 6.

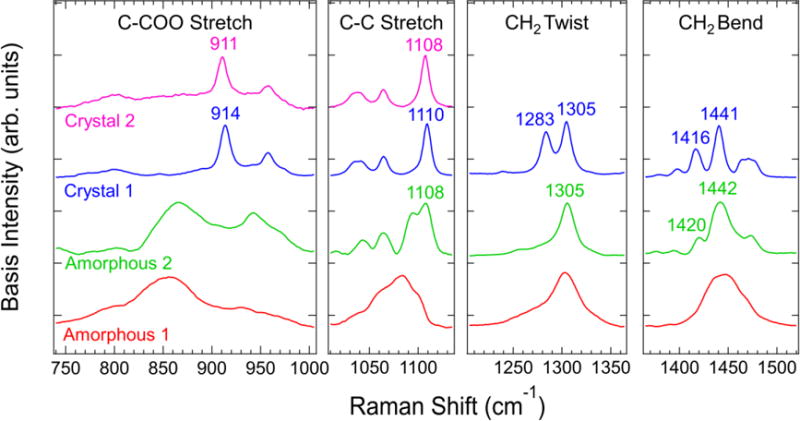
From left to right: estimated basis spectra in the indicated C-COO stretch, C-C stretch, CH₂ twist, and CH₂ bend region.

A comparison of the crystal and amorphous components indicates that many of the peaks that are associated with crystallinity in these regions appear in the melt state. In the C-C stretch region, the peak in the crystal spectra located in the range of (1108 to 1110) cm⁻¹ appears in the amorphous 2 spectrum. The 1305 cm⁻¹ peak in the CH₂ twist region is also present in the melt state.

Of particular interest are the peaks in the (1416 to 1420) cm⁻¹ range, which appear in a similar position of the spectrum as the peak commonly associated with crystallinity in alkanes and polyethylenes.[7] However, our analysis in the melt temperature range indicates that the amorphous 2 component of the CH₂ bend region contains a shoulder at 1419 cm⁻¹ prior to any crystallinity in the material. We attribute this peak to the CH₂ bend vibrational mode adjacent the carbonyl group based on the Raman measurements of Holland-Moritz.[34] The amorphous 2 peak and band assignments of Holland-Moritz are close to the 1416 cm⁻¹ peak observed in the crystal 1 basis spectrum. Additionally, Fermi resonance in the CH₂ bend region of the spectrum is expected due to the presence of alkyl chain segments.[45] The temperature dependence of this effect will be convoluted with the changes in the spectra due to a varying conformer distribution. Based on these observations we cannot assign a peak in the CH₂ bend region to crystallinity with absolute certainty.

The C-COO stretch crystal basis spectra have a peak in the range of (911 to 914) cm⁻¹ that arises in the same region as the broad C-COO amorphous 2 feature. It is therefore difficult to distinguish whether it arises from single-chain or interchain vibrational modes. A similar effect is observed in the CH₂ twist region where the peak at 1283 cm⁻¹ in the crystalline component spectrum occurs in the same region as the asymmetric 1305 cm⁻¹ peak in the amorphous 2 component.

Although we use the names “amorphous 1” and “amorphous 2” in Figures 5 and 6, we do not mean to imply that these are two separate phases. Neither do we mean to imply that the “crystal 1” and “crystal 2” basis spectra correspond to two different crystalline forms. We designate two amorphous basis spectra because two principal components are necessary to account for the gradual changes in the experimental Raman spectra in the melt state. These are not separate phases that undergo a liquid-liquid phase transition[46] or the formation of an ordered fringed micelle-type structure postulated by Yeh.[47] Instead, we attribute the amorphous 1 and amorphous 2 components generally as the two components necessary to explain variation in the melt Raman spectrum due to changes in the distribution of polymer chain conformations with temperature as expected in rotational isomeric state theory.[48] In the case of the C=O stretch, the amorphous 1 and amorphous 2 components can be used to explain the subtle shift in the experimental Raman spectrum due to changes in dipole-dipole interactions.

We also advise against combining the different regions of the spectrum shown in Figure 6 to indicate the full spectrum of a chain conformer population. We instead treat each vibrational mode as a separate region, with the amorphous 1 peaks more prevalent at higher temperatures in the melt state and the amorphous 2 peaks increasing with decreasing temperature in the melt state (see Supplementary Material). In the C-COO stretch and C-C stretch regions of the spectrum, the crystal 2 basis spectrum exceeds the crystal 1 spectrum at lower temperatures.

The sharp peaks of the crystal spectra of Figure 6 that also appear in the amorphous spectra can be immediately eliminated as indicators of crystallinity, since no crystals are present in the melt state. Crystal spectra peaks that arise out of broad amorphous spectra are difficult to identify as crystalline or non-crystalline indicators. To confirm our assignment of single-chain ordered peaks in the crystalline spectra, we perform single-chain DFT calculations of the Raman spectrum of a PCL oligomer with seven repeat units which is shown in Figure 7. The highest intensity peaks in the C-COO stretch, C-C stretch, and CH₂ twist regions of the calculated spectrum correspond to the basis spectra peaks at 911 cm⁻¹, 1108 cm⁻¹, and 1283 cm⁻¹, which confirms that these peaks are due to vibrational modes of single chains. The peak near 1420 cm⁻¹ is identified as the bending vibration of the methylene unit adjacent to the carbonyl in the ester group and is also due to single chain effects.

Figure 7.

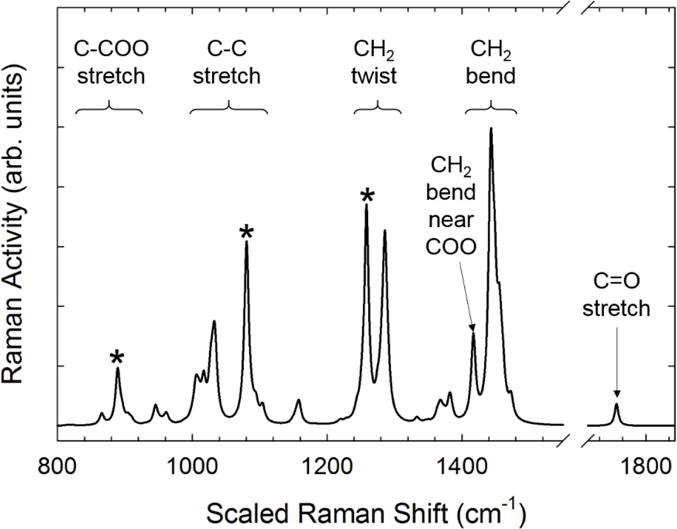
Calculated spectrum of a PCL oligomer in the all trans configuration. Specific peaks that are commonly associated with crystallinity are denoted with the * symbol.

The calculated Raman spectrum in the carbonyl stretch region compares poorly with the experimental spectrum in Figure 1 or the basis spectra shown in Figure 5a. This comparison further indicates that the changes in the carbonyl stretch region are not due to single chain effects but are more likely due to dipole-dipole interactions of adjacent chains, which is expected to increase the carbonyl bond length and shift the vibration to lower frequencies.[23]

The temperature dependence of the crystalline component of the carbonyl stretch region suggests that a quantitative correlation between crystallinity and the basis spectra can be developed. We fit the three basis spectra shown in Figure 5a to the Raman spectra of the polymers shown in Table I at room temperature. Each spectrum is normalized by the total integrated intensity in the carbonyl stretch region I_T = I_C = I_A1 = I_A2, where the subscripts indicate the crystalline (C), amorphous 1 (A1), and amorphous 2 (A2) basis spectra. The crystallinity measured by DSC α_c is then assumed to be a linear function of the relative integrated intensity of the crystalline peak

$${\alpha }_c=\beta \frac{I_{\mathrm{C}}}{I_{\mathrm{T}}}+\gamma$$ (4)

where β is a proportionality constant and γ is a linear offset. A linear least-squares fit indicates β = 1.26 ± 0.09 and γ = 0.00 ± 0.05. The zero offset indicates that the intensity ratio is directly proportional to the crystallinity, which furthers our assignment of the crystalline basis spectra to interchain vibrational modes only present in the crystalline structure of PCL. Attempts to find a linear correlation between the modes shown in Figure 6 and the DSC crystallinity yield a nonzero offset, which indicates a poor quantitative correlation at low crystallinities. The agreement between eq (4) for the C=O stretch region and the DSC measured values of crystallinity is excellent, as shown in Figure 8 for all polymers listed in Table I. The maximum relative error between the Raman-predicted value of crystallinity and the crystallinity reported from DSC measurements is 2 %.

Figure 8.

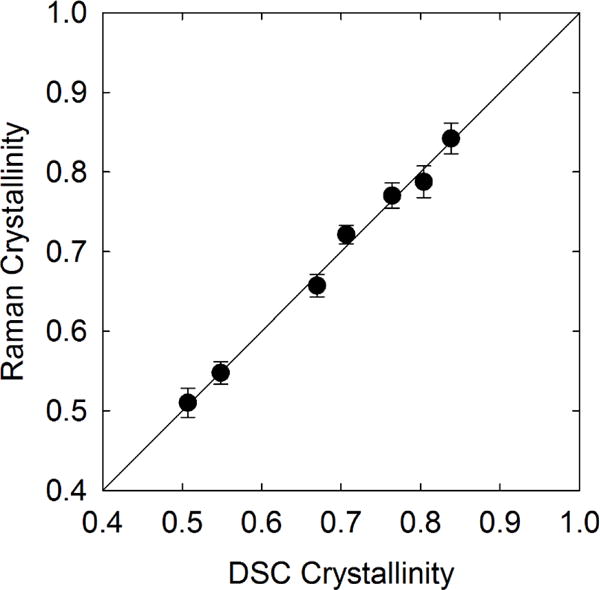
Comparison of the calculated Raman crystallinity versus the crystallinity measured from DSC for the PCLs listed in Table I. The uncertainty in the Raman crystallinity is less than the symbol size.

The Raman-based measurement of crystallinity also works well over a temperature range from room temperature to melting, as shown in Figure 9. The Raman measurement of crystallinity closely follows the DSC measurement, with complete melting occurring slightly above 60 °C. There is a slight discrepancy between the Raman and DSC measurements in the temperature range of approximately (35 to 55) °C where the Raman-measured value falls below the DSC value. The relative difference between crystallinity measurements is approximately 7%. Temperature-modulated DSC measurements of PCL in this temperature range indicate the chain sliding of molecules within crystals. [49] This chain motion would disrupt the crystal structure, which is orthorhombic with the chains slightly twisted along the chain backbone,[50, 51] and cause a corresponding decrease in the intensity of this specific vibrational mode. We can approximate the melting temperature as the temperature at which the relative crystallinity is less than 1 %. For the Raman-based measurement the melting temperature is 61.2 °C, whereas the DSC-based melting temperature is 60.4 °C. The difference in melting temperatures is attributed to the large thermal mass used in the Raman measurement.

Figure 9.

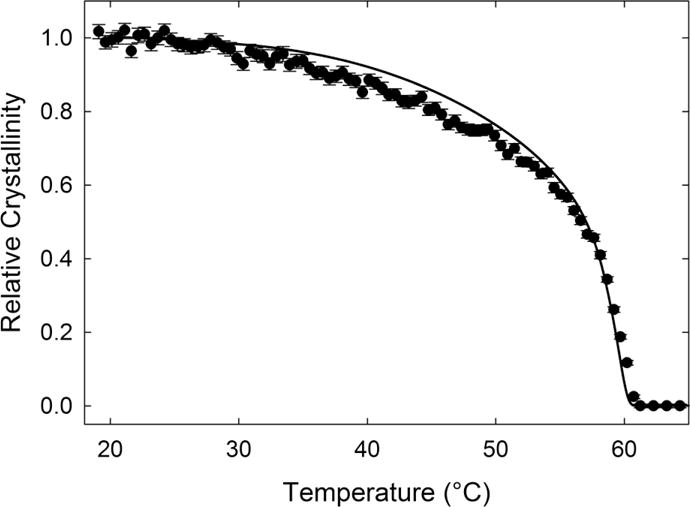
Comparison of relative crystallinity versus temperature for PCL. The solid points indicate Raman measurements and the line indicates the DSC measurement. The temperature ramp is 1 °C/min.

V. DISCUSSION

We use the principal component analysis to generate basis spectra using two pieces of information: experimental constraints on the Raman spectrum and the knowledge of a phase transition between the melt and semicrystalline states. By analyzing a series of Raman spectra in the melt state separate from the semicrystalline state, we can develop multiple basis spectra to account for changes in spectral features that occur in different regions of the Raman spectrum. Some limitations of this method stem from the statistical procedure to generate principal components. Peaks cannot be separated if their motion is correlated, which is evident in the multiple peaks apparent in the amorphous and crystalline components developed in Figure 6. Our ability to distinguish crystalline peaks from single chain effects is thermodynamically informed: it relies on prior knowledge of the melting temperature and the temperature-dependent equilibrium of more ordered and less ordered conformers in the melt state. An analysis of spectra over temperature ranges encompassing both the melt and semicrystalline states would generate multiple principal components that would need to be combined in a linear fashion to generate basis spectra. The resulting basis spectra are developed by assuming a minimum peak resolution that is set by instrument limitations, therefore the exact peak widths in the basis spectra will be instrument-dependent. Background subtraction is also an important preprocessing step in PCA; if temperature-dependent background effects are not minimized they can dominate the principal components, scores, and variances. We have attempted to minimize background effects that might occur with higher-order polynomial (or more complicated) subtraction techniques by performing a linear background subtraction in the Raman shift ranges of interest.

We have provided two separate validations of our basis spectra via DFT calculations and the quantitative correlation with crystallinity for various samples of varying molecular weight and purity. The peaks that appear in both the crystalline basis spectra and the amorphous 2 basis spectra in Figure 6 are confirmed as single-chain ordered peaks from the calculated DFT spectrum in Figure 7. The agreement between these peaks validate the basis spectra as a way to differentiate single-chain order from crystalline bands. The fact that the crystal basis spectrum in the C=O stretch region is linearly proportional to the crystallinity (with a zero offset in eq 4) as determined by DSC further indicates that our method can be used to separate crystalline bands from single-chain ordered bands. Further validation studies on other polymers are beyond the scope of this work.

The benefits of using basis spectra versus standard peak deconvolution methods in determining crystallinity is especially apparent when the experimental spectra show significant overlap of multiple crystalline and amorphous peaks, which is the case for the carbonyl stretch region of PCL. Whereas common peak fitting requires variation in spectral line shape, height, width, and position for an assumed number of peaks in a spectral region, the fitting procedure for the basis spectra only require the component intensities and a shift factor common to all basis spectra to account for instrument accuracy in the reported Raman shift. Additionally, the sample used to determine the basis spectra was not highly crystalline, yet the resulting crystallinity indicator performs well at higher crystallinities. The adequate extrapolation of the model in eq 4 to higher crystallinities indicates the adequacy of the carbonyl stretch region for crystallinity analysis as well as our method for generating basis spectra.

The results show that many of the peaks that are assumed to be crystalline indicators in PCL appear in the melt state and are therefore not true indicators of crystallinity, but instead indicate an increased degree of order along individual chains. Specifically, the sharp peaks that appear in the C-COO stretch, C-C stretch, CH₂ twist, and CH₂ bend regions indicate a chain with the methylene groups in primarily trans sequences. The identification and separation of single-chain and crystalline effects is critical in determining the presence of ordered precursors during crystallization, as in the case of polyethylenes.

In addition to the crystallinity indicator in the carbonyl stretch region, the appearance of a more ordered peak in the melt can help to explain changes in dipole mobility observed in other measurements. Dielectric spectroscopy measurements have shown a change in dipole mobility prior to crystallization which is attributed to pre-ordered structures growing within the melt.[52] This change in mobility, indicated by a peak in the dielectric permittivity at a frequency of 20 Hz, also occurs during melting.[24] Our basis spectra indicate an increase in the melt 2 component prior to the melting point, which we attribute to increased dipole-dipole interactions for chains that are non-crystalline.

VI. CONCLUSIONS

Analysis of the Raman spectrum of polycaprolactone indicates that the carbonyl stretch region indicates three different chain conformers: amorphous chains, more ordered chains with dipole-dipole ordering, and ordered chain segments in a crystalline packing. In contrast, the other vibrational modes in the C-COO stretch, C-C stretch, CH₂ twist, and CH₂ bend regions of the spectrum indicate single-chain order that can be observed in the melt state. A simple linear scale factor between the normalized intensity of the crystalline carbonyl stretch peak and DSC measurements allows for quantitative measures of crystallinity via Raman spectroscopy. This quantitative relationship allows for non-destructive on-line measurements of PCL crystallization during processing. In addition, the ability to observe dipole-dipole ordering separate from crystallization is potentially useful in understanding the crystallization pathway of polycaprolactone.

More generally, we have developed a methodology for analyzing the Raman spectra of polymers to experimentally identify crystalline indicators in vibrational spectrum that are separate from single-chain conformational order. The basis spectra require no curve fitting and are readily correlated with crystallinity measurements from DSC. We expect that this technique will be beneficial in further characterizing the spectral features that accompany non-crystalline conformational order during the crystallization process, such as in the helical non-crystalline chains in isotactic polypropylene[16] and the pre-crystalline trans-rich conformers identified in polyethylene.[7]

Supplementary Material

Figure S1. Plot of the percent variance that is explained by each principal component versus the principal component number. This analysis is based on the C=O stretch region in the melt and semicrystalline temperature ranges. The dotted line indicates the cutoff criterion of a percent variance contribution of 0.01%.

Figure S2. Scores of the principal components as a function of temperature in the C=O stretch region of the spectrum in a) the melt state and b) the semicrystalline state.

Figure S3. Basis spectra developed from principal components in the carbonyl stretch region. The melt basis spectra are labelled as c₁ and c₂ melt, the crystalline basis spectra are labeled as c₁ and c₂ semicrystalline.

Table S1. Linear dependence analysis assuming a linear combination of three basis spectra (“Independent spectra”) fit the remaining basis spectrum (“Dependent spectrum”). The values in the independent spectra columns indicate the best-fit coefficients to the dependent spectrum, normalized to a total intensity of 1.

Figure S4. Plot of ln(I₂/I₁) versus 1/T for the component melt peaks in the carbonyl stretch region of the spectrum. The error bars indicate uncertainty in the coefficients used to fit the components to the experimental spectra.

Figure S5. a) Principal components of the CCOO stretch region from 62 °C to 160 °C. b) Principal components of spectra during crystal melting from 20 °C to 62 °C. The position in cm⁻¹ is labeled near peak extrema. The percentage of the total variance explained by each principal component is indicated in parentheses.

Figure S6. a) Principal components of the C-C stretch region from 62 °C to 160 °C. b) Principal components of spectra during crystal melting from 20 °C to 62 °C. The position in cm⁻¹ is labeled near peak extrema. The percentage of the total variance explained by each principal component is indicated in parentheses.

Figure S7. a) Principal components of the CH2 twist region from 62 °C to 160 °C. b) Principal components of spectra during crystal melting from 20 °C to 62 °C. The position in cm⁻¹ is labeled near peak extrema. The percentage of the total variance explained by each principal component is indicated in parentheses.

Figure S8. a) Principal components of the CH2 bend region from 62 °C to 160 °C. b) Principal components of spectra during crystal melting from 20 °C to 62 °C. The position in cm⁻¹ is labeled near peak extrema. The percentage of the total variance explained by each principal component is indicated in parentheses.

Figure S9. Integrated intensity of the components in Figure 6 of the main text plotted versus temperature for the a) CCOO stretch, b) C-C stretch, c) CH₂ twist, and d) CH₂ bend regions. The intensities are normalized by the total integrated area of each region. The results of every 3^rd spectra are plotted for clarity.