Functional genomic analysis of the rates of protein evolution

Abstract

The evolutionary rates of proteins vary over several orders of magnitude. Recent work suggests that analysis of large data sets of evolutionary rates in conjunction with the results from high-throughput functional genomic experiments can identify the factors that cause proteins to evolve at such dramatically different rates. To this end, we estimated the evolutionary rates of >3,000 proteins in four species of the yeast genus Saccharomyces and investigated their relationship with levels of expression and protein dispensability. Each protein's dispensability was estimated by the growth rate of mutants deficient for the protein. Our analyses of these improved evolutionary and functional genomic data sets yield three main results. First, dispensability and expression have independent, significant effects on the rate of protein evolution. Second, measurements of expression levels in the laboratory can be used to filter data sets of dispensability estimates, removing variates that are unlikely to reflect real biological effects. Third, structural equation models show that although we may reasonably infer that dispensability and expression have significant effects on protein evolutionary rate, we cannot yet accurately estimate the relative strengths of these effects.

Soon after Kimura (1), Ohta (2), and King and Jukes (3) proposed that much evolutionary change at the molecular level may be caused by drift and fixation of mutations that have little impact on the organism, a number of authors (4, 5) offered a prediction that seemed to follow fairly directly from this view of molecular evolution. They reasoned that the strength of selection against a deleterious mutation must depend, at least in part, on the dispensability of the entire protein to the organism. Specifically, in proteins that make a smaller contribution to organismal fitness, a larger fraction of mutations would fall within the range that could be considered nearly neutral. (In this range, the product of effective population size and selection coefficient is at most 1, and the dynamics of allele frequencies are largely controlled by stochastic sampling effects.) Therefore, if protein evolution was caused in part by the drift of nearly neutral mutations, then the rate of evolution should be higher in proteins that are less important to the organism.

This prediction has been difficult to test because the variables are difficult to measure. As a proxy for estimates of protein dispensability, Hirsh and Fraser (6) used the growth rates of yeast strains in which individual genes were deleted. Although the laboratory conditions under which these strains were grown probably differed considerably from the environment relevant to the organism's evolutionary history, Hirsh and Fraser suggested that the growth rate of a deletion mutant in the laboratory might at least correlate with protein dispensability in the wild, such that estimates from a large number of proteins would reveal a statistically significant trend. To estimate the rate of evolution of a large number of proteins, they required a fully sequenced genome for comparison with yeast and therefore resorted to the evolutionarily distant nematode Caenorhabditis elegans. They observed a weak but highly significant correlation between their estimators of dispensability and evolutionary rate, corroborating the early prediction of nearly neutral theory. However, when proteins were separated into two categories, those that were deemed “essential,” meaning that the gene deletion effect is lethal, and those that were deemed “nonessential,” meaning that the gene deletion effect is not lethal, they did not observe a significant difference in evolutionary rate between categories. They attributed this finding to the functional form of the relationship between dispensability and evolutionary rate, suggesting that a protein whose deletion causes a substantial growth defect is, in evolutionary terms, no more dispensable than a protein that is essential for viability.

Several studies have offered important extensions or revisions of these findings. Jordan et al. (7) suggested that the unexpected absence of a significant difference in evolutionary rate between essential and nonessential categories may have been a result of Hirsh and Fraser's relatively small sample size (n = 287) and distant evolutionary comparisons. To obtain closer comparisons and a larger sample, they analyzed Escherichia coli proteins, and the predicted difference between essential and nonessential proteins was in fact observed. Yang et al. (8) used yeast deletion mutant growth rates and a Saccharomyces cerevisiae–Candida albicans comparison to argue that the relationship between dispensability and evolutionary rate holds among proteins with close paralogs, but not among the yeast genome's singletons. Krylov et al. (9) offered a measure of the evolutionary conservation of a gene that showed a strong association with the lethality of the deletion mutant. They used the phylogenetic distribution of orthologous sequences among seven eukaryotes to estimate a propensity for gene loss (PGL) for each sequence. PGL may function partly as an integral of sequence evolutionary rate over time, effectively reducing statistical noise and revealing clear patterns of association with functional genomic variables.

Each of these studies is consistent with the view that some molecular evolutionary change is caused by drift, and that this process operates more rapidly in more dispensable proteins because the efficacy of purifying selection is reduced. A more fundamental reinterpretation of the relationship between protein dispensability and evolutionary rate was offered by Pal et al. (10). Building on their previous demonstration (11) that highly expressed yeast genes evolve slowly, Pal et al. argued that dispensable proteins evolve more rapidly only because they are weakly expressed, not because there is a direct effect of dispensability on evolutionary rate. [One possible mechanistic explanation for the association between expression level and evolutionary rate is provided by the suggestion that selection favors the use of metabolically cheap and rapidly translated amino acids in highly expressed proteins (12, 13).] Such translational selection would subject more highly expressed proteins to a set of constraints that are less important for weakly expressed proteins.) Using the set of yeast growth rates analyzed by Fraser et al. (14), but somewhat closer evolutionary comparisons of S. cerevisiae with Saccharomyces pombe and C. albicans, Pal et al. (10) showed that when they statistically controlled for expression level, the effect of dispensability on evolutionary rate completely disappeared. Rocha and Danchin (15) reached the same conclusion when they used functional genomic and evolutionary data from E. coli in a multiple regression. They showed that when the effects of expression and functional category were regressed out first, very little residual variance was explained by each gene's designation as essential or nonessential. Although their procedure is likely to reduce the apparent effect of dispensability by first removing the effect of functional category, a strong correlate of a gene's essential/nonessential designation, they concluded that protein dispensability has almost no impact on protein evolutionary rate.

In all of these studies, the difficulty of measuring the relevant variables without overwhelming noise or inaccuracy has remained an important obstacle. Arguably the most elusive quantity is the dispensability of a protein over the evolutionary time scales sampled by relatively distant comparisons. For example, in Pal et al.'s study (10), the complete genome closest to S. cerevisiae was C. albicans. However, recent high-throughput gene deletion studies of this species (16) have revealed that many genes that are essential in S. cerevisiae have nonessential orthologs in C. albicans (and vice versa), suggesting that estimates of dispensability from S. cerevisiae are only rough correlates of the actual level of dispensability over the sampled evolutionary period. Among prokaryotes, closer evolutionary comparisons are possible, but growth rates of deletion mutants have not been systematically measured, so studies must use exclusively binary fitness data.

In the present study, we address these obstacles to obtain accurate measurements of functional genomic and molecular evolutionary variables. Specifically, we address the problem in three ways. First, we analyze a substantially expanded and improved functional genomic database. Our estimates of evolutionary rate are based on four fully sequenced genomes in the genus Saccharomyces. In addition to improving the accuracy of ortholog designation and divergence estimation, the proximity of these comparisons should improve the reliability of dispensability measurements performed only in S. cerevisiae. In addition, the dispensability estimates we analyze are based on a larger number of growth replicates and an improved method of growth rate estimation. Second, we show that distinct functional genomic data sets can be cross-referenced to remove estimates that are unlikely to be accurate or biologically meaningful. Third, we use structural equation models to investigate what kinds of conclusions can be supported, given the accuracy with which variables are currently measured.

Materials and Methods

Functional Genomic Data. For one data set of dispensability estimates, labeled SGTC for Stanford Genome Technology Center, growth rates were measured by the array-based method described in ref. 17. Six replicate growth experiments were conducted for each of two independently constructed pools of all viable homozygous yeast deletion strains. All 12 growth experiments were conducted in rich glucose medium. Data were collected at five time points for each replicate. Each deletion strain is typically represented by four hybridization signals, corresponding to tags on the array. If a tag failed to exhibit fluorescence intensity that was 4-fold higher than the mean array background at time 0, or if a tag was found to contain sequence errors (17), the tag was removed from the analysis. With a linear multiple regression model that allowed for time effects, replicate series effects, and series-time interactions, relative growth rate was estimated from changes in the logarithm of each tag's fluorescence over the time course of each replicate. Estimates were averaged across tags and across replicates to obtain a relative growth rate for each deletion strain. These data are available at http://chemogenomics.stanford.edu/supplements/01yfh/files/orfgenedata.txt.

As a second data set of dispensability estimates, labeled Warringer et al., we used deletion mutant growth rates in basal synthetic medium (a standard glucose medium) reported in ref. 18. A list of putatively essential genes was obtained from The Saccharomyces Genome Database (www.yeastgenome.org) and was added to both dispensability data sets. We assigned these genes a deletion mutant growth rate of zero, unless the dispensability data set indicated a nonzero value.

As measurements of expression, we used mRNA abundance (19) and the Codon Adaptation Index (CAI) (20). Total mRNA abundance reported in ref. 19 was determined by the method described in ref. 19. CAI values were for S. cerevisiae, as reported (20). Use of other codon reference tables and average CAI values across all four Saccharomyces species did not alter the conclusions presented here. Alternate tables were based on the following gene sets: the top 20 most highly expressed genes in S. cerevisiae from ref. 19, the top 50 most highly expressed genes in S. cerevisiae from ref. 19, and Schizosaccharomyces pombe orthologs of 20 highly expressed genes in S. cerevisiae.

Evolutionary Rate Estimation. We obtained whole genomic sequence data, as well as ORF annotation and synteny-based orthology designation (as described in ref. 21), for Saccharomyces bayanus, Saccharomyces mikatae, Saccharomyces paradoxus, and S. cerevisiae (22). Of 5,538 putatively orthologous sets of ORFs, 1,418 did not contain sequence from one or more of the species; these ORFs were excluded from further analyses to allow use of nonsynonymous divergence (dN) in the four species phylogeny as a measure of evolutionary rate (see below). Each of the remaining 4,120 ORF sets was aligned with clustalw 1.83, using amino acid sequences as a template for nucleotide sequences and reverse-complementing when necessary. Because the method we used to estimate evolutionary distances is based on a model of point substitutions, it was important to exclude frame shifts, whether they were caused by authentic indel mutations or sequencing errors. We therefore implemented the following filter. A majority-rule consensus amino acid sequence was constructed for each alignment. In the event that an individual sequence disagreed with the consensus at five consecutive sites in which the consensus was defined, this ortholog set was dropped from the data set. This filter resulted in the exclusion of 417 ORF sets. An additional 237 ORFs known to contain introns were also dropped, because some splice sites are uncertain and introns may result in distinctive evolutionary processes that could obscure the relationships we hoped to detect here.

phylip's dnaml (23) was used to construct a maximum-likelihood tree for each of the remaining alignments. Ortholog sets that did not exhibit the consensus phylogeny ((S. paradoxus, S. cerevisiae), S. mikatae, and S. bayanus) were dropped. paml's codeml was then used to estimate the dN, synonymous substitutions per synonymous site (synonymous divergence, dS), and their ratio (dN/dS). Two models of protein evolution were used: codeml model 0 allows for a single dN/dS value throughout the genealogy, whereas codeml model 1 allows for a different dN/dS value for each branch. The results presented below did not differ between the two models, so only model 0 results will be presented. dN/dS′, a measure of the rate of protein evolution that corrects dN/dS for selection on synonymous sites (24), was also estimated for the final collection of ortholog sets (8).

Statistical Analyses. Correlations and partial correlations were estimated by using nonparametric (Spearman's rank correlation coefficients) and parametric (Pearson's product-moment correlation coefficients) statistics. For calculation of Pearson's coefficients, measures of evolutionary rate, k, were first transformed according to the function f(k) = Log[k + 0.001]. [Addition of a small number was necessary because some variates of k are 0. The number 0.001 was chosen because it results in a smooth distribution of f(k) values without outliers and a linear relationship between f(k) and other variables.] P values were estimated by using the asymptotic approximation 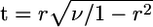, where r is the observed correlation coefficient, and ν is the number of degrees of freedom (n – 2 for a correlation coefficient and n – 3 for a partial correlation coefficient) (25). Estimation of P values by randomization, rather than asymptotic approximation, would require a prohibitively large number of permutations of the data, as P values were generally «10^–6. We therefore used the asymptotic approximation, but also performed 10⁶ permutations to confirm that P values were indeed <10^–6. Randomization was performed according to the method prescribed in ref. 25.

Results and Discussion

Relationship Between Functional Genomic Variables and Evolutionary Rate. Comparative analysis of the genomes of S. cerevisiae, S. mikatae, S. paradoxus, and S. bayanus yielded 5,538 putatively orthologous sets of ORFs (22). These sets were realigned and subjected to filters to remove ORFs exhibiting frame shifts or atypical phylogenies (see Materials and Methods). These filters yielded a final set of 3,038 high-quality, four-taxa alignments, for which the following quantities were estimated by maximum likelihood: dN, dS, dS′ (see Materials and Methods and ref. 24), and the ratios dN/dS and dN/dS′. These estimates of evolutionary rate are available in Table 4, which is published as supporting information on the PNAS web site.

To determine whether protein dispensability is correlated with evolutionary rate, independent of the level of expression, we calculated the partial correlation of deletion mutant growth rate with protein evolutionary rate, controlling for level of expression. (Partial correlation measures the association between two variables, statistically controlling for the effects of a third variable that could be related to each of the other two.) To ensure that results were robust to the methods by which dispensability, expression, and evolutionary rate were measured, we used two distinct measures of expression, two independent data sets of growth rate, and three measures of protein evolutionary rate. Abundance of mRNA and the CAI both have been used previously as measures of expression level (10, 12). Codon bias is more likely to reflect the level of expression that is relevant to protein evolution, as it estimates expression over the recent evolutionary history of the gene, rather than at a single time point in the laboratory. Although a comparable measure of dispensability is not available, data sets of growth rates analyzed here do represent improvements over previous generations of dispensability measurements, both in terms of the number of replicates performed and the regression method used in analysis of raw data (see Materials and Methods).

Because different measures of the rate of protein evolution reflect slightly different processes, we analyzed three distinct quantities: dN in all four species of Saccharomyces, dN/dS, and dN/dS′. Comparison of dN across proteins with equal divergence times has been used in a number of studies (6, 9, 10). Because this measure does not involve synonymous sites, it can be informative in relatively distant comparisons; however, it does not control for differences in mutation rate across the genome, so rates of evolution measured in this way confound mutational and selective processes. The ratio dN/dS is commonly used to control for differences in mutation rate or divergence time, revealing the degree of constraint or positive selection on proteins. However, in many species, dS is also subject to selection, making dS an inaccurate measure of mutation rate and divergence time (26). Furthermore, the inverse relationship between the rate of dS and expression level might weaken the relationship between expression and dN/dS, partly obscuring the relationship between expression and protein evolutionary rate. Therefore, to correct for selection on synonymous sites, we here use a measure of dS adjusted according to the gene's level of codon bias (24).

The correlations and partial correlations estimating the relationship between dispensability and evolutionary rate, and between expression and evolutionary rate, are shown in Table 1; additional correlations are provided in Table 5, which is published as supporting information on the PNAS web site. In addition to nonparametric statistics, parametric linear statistics were calculated to confirm robustness to statistical method, and because the structural equation models investigated below are based on normally distributed variables involved in linear relationships. Irrespective of our measures of dispensability, expression, and evolutionary rate, the growth rates of homozygous deletion mutants exhibit a highly significant correlation with rates of protein evolution, and this correlation remains highly significant when expression is partialed out. The correlation between our estimates of dispensability and evolutionary rate ranges from r_dk = 0.219 (n = 2931, P = 3 × 10^–33, Spearman rank correlation between SGTC dispensability estimates and dN/dS) to r_dk = 0.274 (n = 2914, P = 2 × 10^–51, Pearson correlation between Warringer et al. dispensability estimates and dN). The partial correlation between dispensability and evolutionary rate, controlling for level of expression, ranges from r_dk|x = 0.163 (n = 2768, P = 5 × 10^–18, Spearman partial rank correlation between SGTC dispensability estimates and dN, controlling for mRNA abundance) to r_dk|x = 0.259 (n = 2754, P = 3 × 10^–43, Pearson partial correlation between Warringer et al. dispensability estimates and dN or dN/dS′, controlling for mRNA abundance).

Table 1. Correlation and partial correlation coefficients estimating the association between protein dispensability (d) and evolutionary rate (k), and between expression level (x) and k.

Evolution rate	Dispensability	rdk	Expression	rxk	rdk|x	xk|d
dN/dS′	Warringer et al.	0.239 np	mRNA abundance	-0.368 np	0.183 np	-0.328 np
			CAI	-0.528 np	0.190 np	-0.513 np
dN	Warringer et al.	0.237 np	mRNA abundance	-0.363 np	0.181 np	-0.324 np
			CAI	-0.493 np	0.189 np	-0.478 np
dN/dS′	SGTC	0.230 np	mRNA abundance	-0.368 np	0.166 np	-0.330 np
			CAI	-0.528 np	0.187 np	-0.516 np
dN	SGTC	0.227 np	mRNA abundance	-0.363 np	0.163 np	-0.325 np
			CAI	-0.493 np	0.185 np	-0.479 np
dN/dS′	Warringer et al.	0.274	mRNA abundance	-0.279	0.259	-0.256
			CAI	-0.522	0.241	-0.505
dN	Warringer et al.	0.274	mRNA abundance	-0.282	0.259	-0.259
			CAI	-0.509	0.241	-0.491
dN/dS′	SGTC	0.264	mRNA abundance	-0.279	0.252	-0.258
			CAI	-0.522	0.232	-0.505
dN	SGTC	0.264	mRNA abundance	-0.282	0.251	-0.262
			CAI	-0.509	0.232	-0.491

r_AB denotes the correlation coefficient between any two variables A and B, while r_AB|C denotes the partial correlation coefficient between any two variables, while controlling for a third, C. For description of dispensability data sets (SGTC and Warringer et al.), expression data sets (mRNA abundance and CAI), and evolutionary rate estimates (dN, dN/dS, and dN/dS′) see Materials and Methods. See Results for discussion of statistical significance. np denotes nonparametric correlation, all other correlation coefficients are parametric.

As one would expect in view of the relationship between expression and dS, the ratio dN/dS shows a weaker correlation with expression level than do the other measures of evolutionary rate. Excluding dN/dS from consideration, the correlation between expression and evolutionary rate is generally highly significant and larger in magnitude than the correlation between dispensability and evolutionary rate. The ratio r_xk/r_dk ranges in magnitude from 1.02 to 1.60 (Table 1). The ratio r_xk|d/r_dk|x ranges in magnitude from 1.00 to 2.59 (Table 1). Whether this ratio can be interpreted as an indicator of the relative importance of different determinants of protein evolutionary rate, or of different processes in protein evolution, is discussed below.

Two further questions recently raised in the literature can be addressed with the data analyzed here. Observing a significant difference in evolutionary rate between essential and nonessential categories of prokaryotic proteins, Jordan et al. (7) suggested the absence of such a difference (6) was caused by their relatively small sample size and distant evolutionary comparison. This suggestion is borne out by the data analyzed here, as we do now find that nonessential proteins evolve significantly faster than essential ones. (Mean dN of 612 essential proteins = 0.122; mean dN of 2,285 nonessential proteins = 0.179; Mann–Whitney U test, P = 8 × 10^–33. This result does not depend substantially on the measure of evolutionary rate used.) Yang et al. (8) argued that only proteins that have close paralogs exhibit a significant relationship between dispensability and evolutionary rate. As shown in Table 2, this argument is not borne out by the data analyzed here: When we separate genes into three categories according to Yang et al.'s criteria (those with close paralogs, those without paralogs, and all genes) we find a significant correlation between dispensability and evolutionary rate in all three categories. The correlation, however, does appear to be particularly strong among genes with close paralogs.

Table 2.

Pearson's correlation (r) between dispensability (d, from ref. 18) and evolutionary rate (k, estimated by dN) among all genes and genes with (duplicates) or without (singletons) close paralogs (as defined in ref. 8), and with or without controlling for expression (x, estimated by CAI)

	All genes n = 2,914		Singletons n = 1,298		Duplicates n = 691
r	r	P	r	P	r	P
rdk	0.274	2 × 10-51	0.252	4 × 10-20	0.397	2 × 10-27
rdk|x	0.241	9 × 10-40	0.162	4 × 10-9	0.387	5 × 10-26

Cross-Referencing Functional Genomic Data Sets. An important source of inaccuracy in our estimates of dispensability is that many proteins are likely to perform functions that are important in the environment relevant to yeast evolution, but superfluous in the laboratory conditions in which growth rates are measured. If such proteins are under regulatory control that allows induction under conditions in which they are useful, measurements of the dispensability of proteins that are weakly expressed in the laboratory would be more likely to reflect only experimental noise, whereas measurements of the dispensability of proteins that are strongly expressed in the laboratory would be more likely to reflect a real effect of removing a biological function.

An example may serve to clarify this point. Knocking out the genes specifically responsible for galactose utilization (the GAL genes) has little effect in the glucose medium in which fitness effects were measured. However, for cells growing in galactose, these genes are highly expressed and indispensable for maximal growth. If yeasts have had to metabolize galactose fairly often in their evolutionary history, then these genes would be expected to show a relatively slow rate of evolution. Thus their dispensabilities in glucose medium, where they are not expressed, are not indicative of their importance to yeast. (We note that this argument requires only that deletion of genes that are not expressed in a certain growth environment has no effect on fitness in that environment; it does not require that most genes up-regulated in a certain condition be required for growth in that condition.)

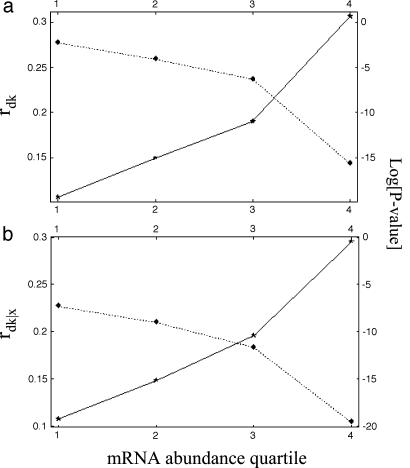
This consideration of the relationship between dispensability and expression in a given environment raises the prospect of using laboratory measurements of expression to improve the quality of dispensability data. Specifically, the accuracy of dispensability data would be expected to increase with the level of expression in the laboratory. We can test this prediction in two ways. First, we divide genes into quartiles according to microarray measurements of mRNA abundance (19). For each quartile, we calculate the correlation between our two independent data sets of dispensability. (We exclude genes required for laboratory viability, as the list of essential genes between the two data sets is virtually identical.) As expected, we find that the correlation between independent measurements of knockout mutant growth rates increases as a function of expression quartile, suggesting that the signal-to-noise ratio of dispensability data does indeed improve among higher quartiles of expression in the laboratory (Fig. 3, which is published as supporting information on the PNAS web site). Second, using the same division of genes into quartiles, we plot the correlation coefficient between dispensability and evolutionary rate, as a function of expression quartile. The strength of the correlation between dispensability and evolutionary rate increases with expression quartile, again suggesting that the accuracy of dispensability estimates increases among genes that are observed to be highly expressed in the laboratory (Fig. 1a). This analysis also serves to confirm that the relationship between dispensability and evolutionary rate is not entirely mediated by expression level. The partial correlation between dispensability and evolutionary rate, controlling for level of expression, is strongest among genes for which dispensability estimates appear to be most accurate, namely, those genes that are highly expressed in the laboratory (Fig. 1b). For additional arguments see Supporting Text, which is published as supporting information on the PNAS web site.

Fig. 1.

The Spearman rank correlation coefficient, r_dk (a), and partial correlation coefficient, r_dk|x (b), between protein dispensability d (Warringer et al. data set; see Materials and Methods), and evolutionary rate, k, as a function of mRNA abundance quartile. Expression quartile is shown on the x axis. Correlation coefficient values are indicated by stars, and P values are indicated by diamonds. The points are joined only for visual clarity.

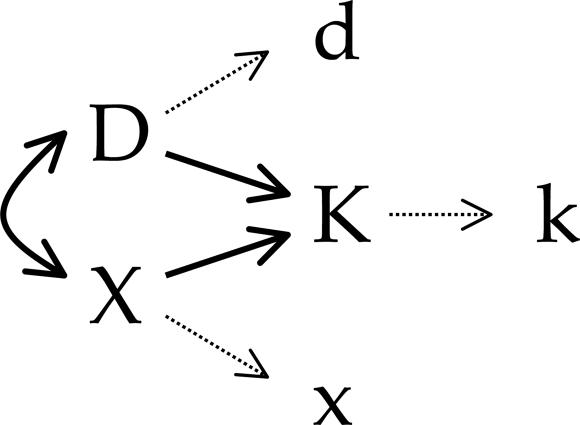
Statistical Models. In a number of recent studies, the relative magnitudes of partial correlation coefficients or standard partial regression coefficients have been interpreted as indicators of the relative importance of different functional variables, or even different evolutionary processes, in determining the rates of protein evolution (9, 10, 15, 27). However, because different functional genomic variables are almost certainly measured with very different levels of accuracy, it is important to consider the potential impact of inaccurate measurement on the relative magnitudes of statistical measures of association. To this end, it is instructive to analyze a structural equation model in which statistical variation caused by uncertain measurement is partitioned from variation caused by the stochastic biological process of sequence evolution. Such a model is diagramed in Fig. 2. We use capital letters to represent true values of protein dispensability (D), expression (X), and evolutionary rate (K). The causal relationships among these variables are shown as solid arrows in Fig. 2. Dashed arrows in Fig. 2 represent the introduction of variance caused by inaccurate measurement, leading to observed values of dispensability (d), expression (x), and evolutionary rate (k). Assuming variation is normally distributed and relationships are linear, the statistical relationships shown in Fig. 2 are described by the following structural equations.

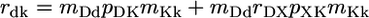[1a]

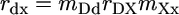[1b]

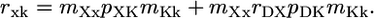[1c]

The correlation coefficients r_ab (a ≠ b; a, b ∈ {d, x, k}; –1 ≤ r_ab ≤ 1) are the observed associations between variables. The coefficients m_Dd, m_Xx, and m_Kk are associations between true and observed values of dispensability, expression, and evolutionary rate. We assume (hopefully not too optimistically) that 0 ≤ m_Aa ≤ 1; that is, our observed values are positively correlated with true values. The correlation coefficient r_DX (–1 ≤ r_DX ≤ 1) is the true association (unaffected by imperfect measurement) between protein dispensability and expression level, and the path coefficients, p_XK and p_DK, measure the true effects of expression, X, and dispensability, D, on evolutionary rate, K.

Fig. 2.

Structural equation model partitioning statistical variation caused by uncertain measurement from variation caused by the stochastic biological process of sequence evolution. Capital letters represent true values of protein dispensability (D), expression (X), and evolutionary rate (K). The causal relationships among these variables are shown as solid arrows. Dashed arrows represent the introduction of variance caused by inaccurate measurement, leading to observed values of dispensability (d), expression (x), and evolutionary rate (k). The inaccuracy of measurement may be the result of several variables, including differences between laboratory and wild conditions, variance brought on by technical errors, etc.

We would like to use this model to address the following question. If we assume a certain level of inaccuracy in our measurements, what are the magnitudes of the true associations among dispensability, expression, and evolutionary rate that are compatible with our observed associations among these variables? Here, we will use the Pearson correlation coefficients among variables transformed to achieve linearity, as the assumptions underlying these coefficients match those of the model. For functional data, we will use the dispensability and expression data sets that show the strongest associations with evolutionary rate. The relationship between the Warringer et al. data set and evolutionary rate is marginally stronger than the relationship between the SGTC data set and evolutionary rate. More importantly, CAI is twice as strongly associated with evolutionary rate as is mRNA abundance. This finding is consistent with the hypothesis that CAI reflects historical expression levels relevant to protein evolution, rather than expression levels in the laboratory.

Our observed associations among variables are r_dk = 0.274, r_dx =–0.086, and r_xk =–0.509. We substitute these values into Eq. 1, and then solve for p_DK, p_XK, and r_DX. Because the accuracy of measurement is unknown, or known only very roughly, we consider a range of values for m_Dd and m_Xx, the correlations between actual and observed values of dispensability and expression. Specifically, we allow measurement accuracy to range from a lower bound approximately equal to the observed association between each variable and evolutionary rate, to an upper bound of 0.9, which is likely to exceed the accuracy of measurement for expression as well as dispensability. For simplicity, we set m_Kk = 0.8; although we do not know the accuracy of our estimates of dN, it is reasonable to assume that with high-quality alignments of four species, it is fairly high.

In Table 3, the values of p_DK, p_XK, and r_DX are shown for various measurement accuracies. For the range of accuracy levels shown, p_DK/p_XK, the ratio of the true effect of dispensability to that of expression on evolutionary rate, ranges in magnitude from 0.11 (for m_Dd = 0.9 and m_Xx = 0.5) to 2.7 (for m_Dd = 0.3 and m_Xx = 0.9). Thus, when we explicitly consider a plausible range of measurement error, we see that the observed associations among dispensability, expression, and evolutionary rate, are consistent with a very wide range of true impacts of dispensability and expression on evolutionary rate. Without a better understanding of the accuracy of our estimates of dispensability and expression, attempts to estimate the relative importance of dispensability and expression in determining the rate of protein evolution are premature. At this point, the best available functional genomic and evolutionary data suggest that each of these variables has an effect on protein evolution (Table 1), but we cannot determine their relative importance.

Table 3. True path (p) and correlation (r) coefficients among true values of dispensability (D), expression (X), and evolutionary rate (K), for a range of measurement accuracy (m).

	mDd
mXx	0.3	0.5	0.7	0.9
0.5	pDK = 0.61	pDK = 0.28	pDK = 0.19	pDK = 0.14
	pXK = -0.92	pXK = -1.18	pXK = -1.23	pXK = -1.24
	rDX = -0.57	rDX = -0.34	rDX = -0.25	rDX = -0.19
0.7	pDK = 0.92	pDK = 0.49	pDK = 0.34	pDK = 0.26
	pXK = -0.53	pXK = -0.79	pXK = -0.85	pXK = -0.87
	rDX = -0.41	rDX = -0.25	rDX = -0.18	rDX = -0.14
0.9	pDK = 1.02	pDK = 0.57	pDK = 0.40	pDK = -0.31
	pXK = -0.38	pXK = -0.60	pXK = -0.65	pXK = -0.67
	rDX = -0.32	rDX = -0.19	rDX = -0.14	rDX = -0.11

m is the association between real (uppercase) and observed (lowercase) values of the three genomic variables.

An additional analysis of evolutionary rates, motivated by our simple model (Eq. 1), also suggests that expression and dispensability have separate effects on evolutionary rate. In view of the importance of the unknown coefficients of measurement error, m_Dd and m_Xx, we use the model to derive a testable null hypothesis that is expected to be independent of m_Dd and m_Xx. Eq. 1 was written for dN. An analogous set of equations could be written for dS. To distinguish between the two models, we append the subscript N or S to the variables k (observed evolutionary rate) and K (true evolutionary rate). Dividing Eq. 1a by Eq. 1c, we obtain

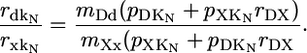If the effect of dispensability on the rate of protein evolution is entirely mediated by level of expression, as has been suggested (10, 15), then p_DKN, in which case

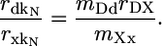There are no evolutionary rate variables on the right side of the equation. Therefore, when we take precisely the same steps with the equations for dS, we find that

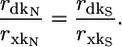Thus, if dispensability has no independent effect on dN, then the ratio of the correlation observed between dispensability and evolutionary rate to that observed between expression and evolutionary rate should be the same for dN and dS, regardless of the values of the measurement accuracy coefficients, m_Dd and m_Xx. The data show that this is not the case. Using the growth rate data of Warringer et al. (18), codon bias as a measure of expression, and transformed values of dN and dS (see Materials and Methods), we find that r_dkN/r_xkN =–0.54, whereas r_dkS/r_xkS =–0.18 (r_dkN = 0.274, r_xkN = –0.509, r_dkS = 0.13, and r_xkS = –0.71. Thus, if the effect of dispensability on protein evolution was mediated entirely by expression, we would expect the association between dispensability and synonymous evolution to be much stronger than is actually observed.

Concluding Remarks

This article provides three main results. First, we have shown that with the best available estimates of protein dispensability, expression, and evolutionary rate in the yeast genus Saccharomyces, dispensability and expression have independent, significant effects on the rate of protein evolution. Second, we have shown that measurements of expression levels in the laboratory can be used to filter data sets of dispensability estimates, removing variates that are unlikely to reflect real biological effects. This result may be useful in a variety of analyses of dispensability data, including many that are not concerned with evolutionary questions (17, 28, 29). Third, we have shown that in view of the relatively low accuracy with which functional genomic variables are currently measured, recent estimates of the relative importance of different functional variables as determinants of evolutionary rate should be treated very cautiously. Much of the data remain only rough estimates of evolutionarily relevant quantities. If a gene serves an important function in yeast's natural environment, but plays little role in rapid growth in glucose medium, measurement of a deletion mutant's growth rate will not provide an accurate estimate of the gene's dispensability, even if such measurement is highly precise.

A potentially important source of unexplained variance in evolutionary rate that we have not investigated here is variation in the “functional density” of proteins (14, 30). An essential protein in which only 10% of sites must contain specific amino acids for proper protein function is likely to evolve faster than a protein of much smaller fitness effect in which 90% of sites are similarly constrained. It will be intriguing to investigate the relationship between the rate of evolution at individual amino acid sites and estimates of the mean fitness effect of mutations at those sites.

Although recent work has focused on simply characterizing the relationships between functional genomic variables and evolutionary rate, the deeper interest of these relationships lies in the possibility that they might shed light on the evolutionary process. The correlation between dispensability and evolutionary rate was offered as an early prediction of the nearly neutral theory, and its corroboration could be viewed as an indication that at least some protein evolution is caused by drift. However, although the prediction was made with purifying selection in mind, it remains a possibility that the correlation between evolutionary rate and dispensability is partly caused by positive selection. For example, an hypothesis compatible with propensity for gene loss results (9) is that relatively dispensable proteins are more likely to be enlisted in dramatic functional changes. Polymorphism data for a large number of genes in the yeast genome will permit estimation of the frequency of positive selection for proteins of various levels of conservation, dispensability, and expression and will thus allow us to disentangle the processes of adaptive and nearly neutral evolution.