Abstract
Coordinated interactions between cytokine signaling and morphological dynamics of microglial cells regulate neuroinflammation in CNS injury and disease. We found that pro-inflammatory cytokine gene expression in vivo showed a pronounced recovery following systemic LPS. We performed a novel multivariate analysis of microglial morphology and identified changes in specific morphological properties of microglia that matched the expression dynamics of pro-inflammatory cytokine TNFα. The adaptive recovery kinetics of TNFα expression and microglial soma size showed comparable profiles and dependence on anti-inflammatory cytokine IL-10 expression. The recovery of cytokine variations and microglial morphology responses to inflammation were negatively regulated by IL-10. Our novel morphological analysis of microglia is able to detect subtle changes and can be used widely. We implemented in silico simulations of cytokine network dynamics which showed—counter-intuitively, but in line with our experimental observations—that negative feedback from IL-10 was sufficient to impede the adaptive recovery of TNFα-mediated inflammation. Our integrative approach is a powerful tool to study changes in specific components of microglial morphology for insights into their functional states, in relation to cytokine network dynamics, during CNS injury and disease.
Keywords: CNS inflammation, microglia morphology, TNFα, IL-10, cytokine adaptation
Introduction
The interplay between pro and anti-inflammatory cytokines in the central nervous system (CNS) determines the outcome of inflammation after CNS injury and in disease (DiSabato et al., 2016). Neuroinflammation is regulated by cytokines that interact through complex signaling networks (Benveniste, 1992; Codarri et al., 2010; Crotti and Ransohoff, 2016), and functions related to morphological properties of microglia (Kettenmann et al., 2013). While microglia-mediated neuroinflammation is a signature of infection, neurotrauma, and many neurological, neurodegenerative, and psychiatric diseases (David et al., 2015; Witcher et al., 2015; Hong et al., 2016; Vasek et al., 2016), microglia have homeostatic roles which are important for neural development and synaptic function (Tremblay et al., 2010; Schafer et al., 2012; Sipe et al., 2016). The complexity of the neuroinflammatory response is such that it can be both detrimental and beneficial to CNS injury and recovery, depending on the timing of inflammation and context of the injury (Sierra et al., 2013; David et al., 2015; Gadani et al., 2015). The pro-inflammatory cytokine TNFα and the anti-inflammatory cytokine interleukin-10 (IL-10) are known to play key roles in the balance of inflammation and are mediators in many CNS injuries and diseases (Ishii et al., 2013; Montgomery et al., 2013; Kroner et al., 2014; Chakrabarty et al., 2015; Guillot-Sestier et al., 2015; Madsen et al., 2016). However, a basic understanding of the kinetics of the TNFα response in relation to the anti-inflammatory control by IL-10 is lacking.
In our previous work, we performed an extensive literature search and formulated a microglia-specific cytokine network (Anderson et al., 2015). Based on this network, we developed a mathematical model of cytokine regulatory dynamics. Our microglia model predicted counter-intuitively that the anti-inflammatory cytokine intereukin-10 (IL-10) impedes adaptation or recovery of pro-inflammatory TNFα levels to baseline under conditions of inflammatory stimulation. This prediction was supported by in vitro evidence using bone marrow-derived macrophages (Anderson et al., 2015). However, this has yet to be validated in cultures of adult microglia or in vivo.
In addition to the production and response to cytokines, microglia exhibit a range of morphologies that reflect changes in function, their response to injury and disease, and their ability to shape the neuroinflammatory microenvironment (Walker et al., 2014). In response to injury, microglia alter their morphology within minutes (Davalos et al., 2005; Hines et al., 2009) and long-term changes in microglial morphology have been related to impairments in their immune function (Erny et al., 2015). Morphological changes in microglia are essential for processes such as phagocytosis (Tremblay et al., 2010; Abiega et al., 2016); however, it is not known if, and how, changes in cytokine networks during inflammation induce changes in microglial morphology.
In the present work, we investigated whether IL-10 controls TNFα expression dynamics and changes in microglial morphology in response to inflammation. To assess microglial morphology, we developed a novel unsupervised, multivariate analysis that is capable of detecting subtle changes in morphological parameters. We show here that IL-10-mediated feedback inhibition of TNFα in vivo after LPS stimulation influences adaptation of both TNFα expression and microglial morphology. We developed a novel mathematical model of multi-cellular cytokine networks in vivo which illuminated potential feedback interactions that could explain our CNS data in response to systemic LPS stimulation.
This combined analysis of cytokine networks and morphological changes in microglia could serve as a powerful approach to examine pathological CNS states and responses to interventions.
Materials and methods
Animals
All procedures were approved by the Animal Care Committee of the Research Institute of the McGill University Health Centre and followed the guidelines of the Canadian Council on Animal Care and the ARRIVE guidelines for reporting animal research (Kilkenny et al., 2010). Male C57BL/6 (WT) mice or IL-10−/− mice on the same background (age 8–12 weeks) (Siqueira Mietto et al., 2015) were kept under a 12 h light/dark cycle with ad libitum access to food and water.
Model of CNS inflammation
Mice were injected intraperitoneally with saline or Escherichia coli lipopolysaccharide (LPS; 0.33 mg/kg; serotype 0111:B4, Sigma; n = 3–4 per group) and sacrificed at 24 h, 3 and 5 days after injection.
Cytokine profiling
We performed quantitative real time polymerase chain reactions (RT-qPCR) to assay for the expression levels of multiple cytokines. Mice were deeply anesthetized by intraperitoneal injection of ketamine (50 mg/kg), xylazine (5 mg/kg), and acepromazine (1 mg/kg), cardiac perfused (0.1 M PBS, pH 7.4) 6, 24 h, 3, or 5 days after injection, and brains or spinal cords snap-frozen for analysis. Tissue was homogenized and total RNA was extracted using the RNeasy Lipid Tissue Kit (Qiagen, CA). Reverse-transcription was performed with the Omniscript Reverse Transcription Kit (Qiagen, CA), and qPCR was performed using 1 mL of cDNA with Fast SYBR Green Master Mix (Applied Biosystems, CA) on a Step-One Plus qPCR machine (Applied Biosystems). Peptidylprolyl isomerase A (PPIA) was used as an internal control gene. The 2−ΔΔCt method was used to calculate the cDNA expression fold change following standardization relative to PPIA (Schmittgen and Livak, 2008). All primers had a Tm of 60° C. Primer sequences were as follows: Tnf —fwd: 5′ TTG CTC TGT GAA GGG AAT GG 3′, rev 5′ GGC TCT GAG GAG TAG ACA ATA AAG 3′; Il6—fwd 5′ CTT CCA TCC AGT TGC CTT CT 3′, rev 5′ CTC CGA CTT GTG AAG TGG TAT AG 3′; Il1b—fwd 5′ ATG GGC AAC CAC TTA CCT ATT T 3′, rev 5′ GTT CTA GAG AGT GCT GCC TAA TG 3′; Tgfb1—fwd 5′ CTG AAC CAA GGA GAC GGA ATA C 3′, rev 5′ GGG CTG ATC CCG TTG ATT T 3′.
Tissue processing and morphological image analysis
Animals were deeply anesthetized as mentioned above and perfused via the heart with 4% paraformaldehyde in 0.1 M PBS, pH 7.4. Thoracic spinal cords segments were removed and processed for cryostat sectioning (30 μm-thick coronal sections). Immunofluorescence was performed using rabbit anti-Iba1 (1:1,000; Wako) and detected using secondary antibody anti-rabbit Alexa Fluor 488 (1:500; Invitrogen). Sections were visualized using a confocal laser scanning microscope (FluoView FV1000; Olympus) and 30 μm z-stacks were prepared using FV10-ASW 3.0 software (Olympus). Iba1-positive microglia were imaged from the dorsal horn gray matter of the spinal cord. A total of 218 microglia from 28 mice were reconstructed with semi-automated procedures using IMARIS software (Oxford Instruments). Every complete microglia (full cell body and processes within the 30 μ m z-stack) within the field of view was reconstructed. The IMARIS software facilitates a semi-automated, interactive filament tracing method to reconstruct cells contained within confocal image stacks. Selected cells were subjected to the FilamentTracer algorithms that estimate the numeric values of features including geometric properties of the somata and processes. The FilamentTracer processed one channel (color) at a time, extracted objects corresponding to somata and process segments, and quantified lengths, areas, volumes, and between-segment angles. Following the automatic extraction of geometric features, manual editing was performed to delete erroneous process segments. Importantly, all analyses were completed in an unbiased manner, with respect to cell selection, by an individual blinded to the experimental conditions.
Time-series analysis
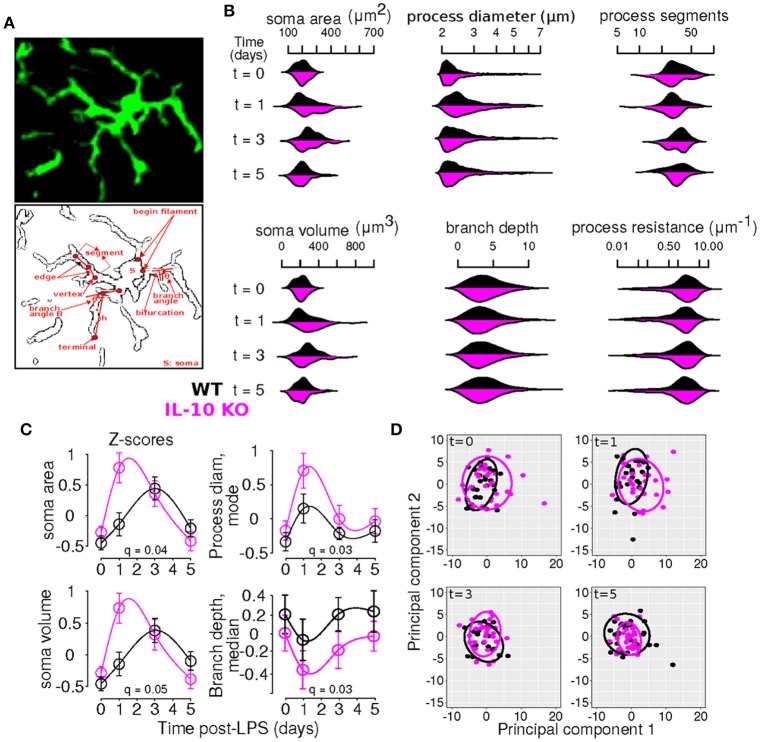
Our general approach to statistically evaluating differences between the WT and KO conditions entailed comparing temporal profiles rather than individual data points (Storey et al., 2005; Anderson et al., 2017). We used kernel density plots visualize the distributions of morphological variables using the beanplot package in R (Kampstra, 2008). To determine whether particular morphological features exhibited differential dynamic profiles in WT versus IL-10 KO microglia, we implemented the optimal discovery procedure (Storey et al., 2007), as documented in our recent work (Anderson et al., 2017). According to this method, we fitted natural cubic splines to a given feature's temporal profile for each genotype and compared the computed error (i.e., sum of squared error, SS) to the error obtained if a single spline was fitted to the entire data set without regard for genotype. The latter error is termed SS0 and the former is SSA, corresponding to the null and alternative hypotheses, respectively. For a given feature i, a statistic was computed to describe the relative increase in goodness of fit achieved by including genotype-specific spline models: . The distribution of this statistic was estimated using bootstrap re-sampling and the resulting p-values were computed and corrected for multiple testing (Storey et al., 2005, 2007). This analysis was implemented using the EDGE package for the statistical programming language R (Storey et al., 2015; R-Core-Team, 2016). In particular, because we were comparing overall temporal profiles defined by spline fits, rather than individual data points, post-hoc analyses of genotype differences at specific time points were not applicable. Rather, our analyses provided information as to whether the general dynamic profiles differed as a function of genotype. For instance, consider the plot for soma area in Figure 3C. Our ODP analyses showed that fitting two spline curves, one for each genotype (black and magenta), resulted in a superior fit compared to fitting a single curve to the entire data set, based on the F statistic and associated corrected p-value (i.e., q-value) generated by our analysis (q = 0.04, see Table 2). This finding suggests that the dynamic responses of the soma area following an inflammatory trigger were distinct with respect to genotype.
Principal component analysis (PCA)
PCA was utilized to illuminate inter-cellular relationships defined by multivariate measures that can be visualized in two or three dimensions. This is accomplished by projecting the multivariate data set onto a basis defined by coordinates aligned with vectors through highly variable regions of feature space. Importantly, groups of cells with distinguishable phenotypes can often be categorized by spatially separated projections in PC space. The respective projections of the cellular data in the principal component subspace are known as “scores” that are determined by “loadings” which indicate the relative contributions of each variable to the separation of cellular score data. Hence, variables or features with higher absolute loadings, corresponding to the PCs utilized for the data reduction, have a greater influence on the representation of the data in the PC space. Further details regarding the theoretical background and implementation details of our PC analysis are available in our previous work (Anderson et al., 2016).
Feature selection
We identified features for NMF analysis as follows. We considered morphological features, or their distribution statistics, with ODP P < 0.05 or PCA loading magnitude > 0.2 (computed across the first four PCs (Anderson et al., 2016)) as the most significant features (n = 65) for further analysis (Table 2). Note that in some cases either the loadings or the ODP p-values did not meet our criteria. This “inclusive” feature selection approach allowed us to include features that showed substantial variation without significant differences in temporal profiles (based on α = 0.05), or significant genotype-specific temporal dynamics without substantial contributions to the variance (based on the loading magnitude cutoff of 0.2).
Non-negative matrix factorization (NMF)
The NMF analysis incorporates elements of both dimensionality reduction and clustering to determine groups of features that are associated with varying degrees of expression in distinct clusters of cells (Brunet et al., 2004). Our NMF analysis was applied to decompose a data matrix D, with morphological features corresponding to rows and samples representing each column, into two non-negative matrices—the basis matrix W and the coefficient matrix H—such that the data matrix D is proportional to the product of the basis and coefficient matrices (D ≃ WH) (Lee and Seung, 1999). W provided basis vectors for the projection of coefficients H for each sample. The rows of W correspond to the features, and each column of W represents a meta-feature. Each meta-feature is a basis vector with a weight for each feature. Because NMF algorithms are generally designed to optimize sparsity of W and H (Gaujoux and Seoighe, 2010), most elements in each meta-feature are close to zero and all other elements compose a feature set that defines the meta-feature. The coefficient matrix H has a column for each sample and a row for each meta-feature. Hence, element (i, j) of H (i.e., Hi,j) represents the contribution of meta-feature i to the morphological profile of sample j.
In implementing NMF, there are a number of ways to initialize W,H and to algorithmically refine the final matrices (Gaujoux and Seoighe, 2010). Further, the fidelity of the resulting factorization can be determined based on the likelihood that samples will cluster together across multiple iterations of the NMF algorithm, the degree of W,H sparsity, and/or the degree of agreement between the factorization product and the original data matrix (Brunet et al., 2004; Gao and Church, 2005; Cieślik and Bekiranov, 2014). We employed a plethora of methods to initialize the matrices (Brunet et al., 2004; Boutsidis and Gallopoulos, 2008; Marchini et al., 2013) and implement the refinement algorithm (Lee and Seung, 2001; Brunet et al., 2004; Badea, 2008; Gaujoux and Seoighe, 2010) and evaluated the results based on all aforementioned criteria. We found that singular value decomposition-based initialization (Boutsidis and Gallopoulos, 2008) coupled with optimization using a modified version of the original NMF algorithm (Lee and Seung, 1999), in which the objective function contains an offset term that accounts for features expressed at constant levels across samples (Badea, 2008), provided a viable approach when considering all fidelity criteria. Our implementation of NMF established a number of morphological cell states based on a predefined “rank” term. We implemented the NMF analysis with ranks spanning the range 1–12. We settled on rank = 6 as this setting facilitated interpretability of the resulting factorization at minimal expense of error and sparsity, consistent with previous approaches (Brunet et al., 2004).
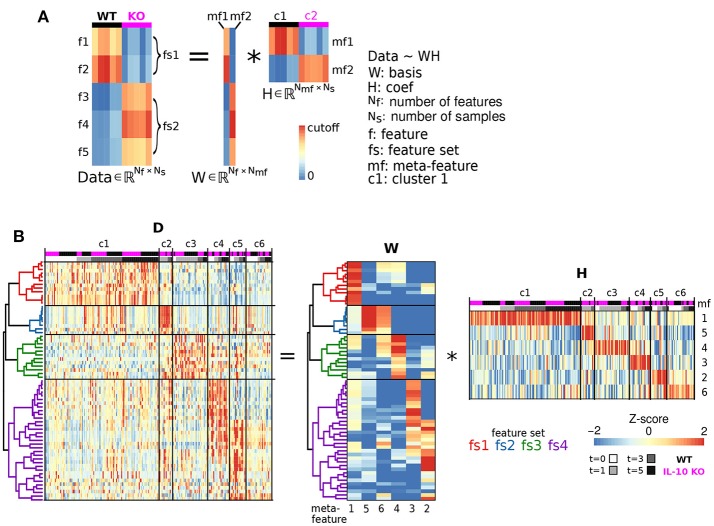
The basic computations underlying NMF are illustrated in Figure 4A. In matrix computation, the element of the Data matrix in the top left corner (1,1) is computed by taking every element in the first row of W, multiplying each of these values by the corresponding values in first column of H, and taking the sum of these products. To compute the value of the Data matrix in the second row of the first column (2,1), take the sum of multiples of the second row of W and the first column of H. To compute the value in the second row of the second column (2,2), take the sum of multiples of the second row of W and the second column of H. Thus, the Data heatmap is organized based on the organization of both W and H.
Multidemensional scaling (MDS)
MDS is a commonly employed method for dimensionality reduction (Park et al., 2014). This analysis was based on distances di,j computed using the Spearman rank correlation coefficients ρi,j between two cells i and j where the correlation was computed across all features: di,j = 1 − ρi,j. The MDS algorithm was used to plot cellular data in 3D by minimizing the difference between Euclidean distance and distance in MDS space, where inter-cellular distance was defined by the correlation based distance metric d. In contrast to PCA, MDS facilitates the distinction of cell classes based on nonlinear relationships between features. We employed nonmetric MDS as described in detail previously (Park et al., 2014).
The MDS analysis was based on the correlation data from Figure 5D and provides a simplified representation of each sample as a point in 3D space such that the distances between points were scaled by the correlation between the respective samples. Samples with high correlations were represented by points that were close together. Samples with negative correlations are represented by points that were farther apart (Figure 5E). Both the correlation data and its transformation into MDS coordinates—when organized or colored based on the NFM clusters—showed that within a given NMF cluster, the global morphological profiles were similar. This analysis provides an independent way to view the similarities/differences within and between NMF-based clusters. The generally high correlations within clusters, and close cluster groupings in MDS-space, independently support the specificity of the NMF-based cluster/class identification.
Morphological adaptation analysis
The adaptive recovery of individual morphological properties was assessed as follows. We first computed Z-score averages at each time point, and scaled these values to the interval [0,1]. We implemented this scaling transformation because our main interest was in evaluating the relative extent of recovery to baseline following the peak response to LPS. Because some temporal profiles of morphological variables decreased (as opposed to increased) following LPS application, we evaluated whether adaptation should be considered based on recovery to baseline following an increase or decrease in each morphological feature (see Figure 3C). We evaluated the maximal deviation from baseline by computing the following quantities:
where is the maximal averaged scaled Z-score, is the minimal averaged scaled Z-score, is the averaged scaled Z-score under baseline conditions (t = 0 days), and |.| is the absolute value of the argument. For cases in which Δmin > Δmax was obtained, consistent with an LPS-mediated decrease in the corresponding morphological variable, we set the respective Z-score to for our assessment of adaptation:
| (1) |
where is the mean peak Z-score and is the mean Z-score at time t = 5 d. Note that we did not compare adaptation indices between WT and IL-10 KO in instances where one genotype showed an LPS-mediated increase whereas the other genotype showed an LPS-mediated decrease in a given morphological feature. The standard deviation of the adaptation metric A was estimated as follows using propagation of error (Anderson et al., 2015):
| (2) |
where all refers to Zpeak and Zfinal, SEM refers to the estimated standard deviation of the mean (), and was treated as a constant. Note that the SEM terms were computed using individual Z-score values transformed with the same scaling factors used to establish [0,1], that is, the min and max terms applied for Zscaled = (Z − min(Z)) / (max(Z) − min(Z)), as described above for the computation of A.
We compared adaptation between WT and IL-10 KO when the following conditions were met: min(AWT, AKO) > 0.5, AWT > −0.2, AWT < 1.2, AKO > −0.2, and AKO < 1.2. To evaluate the degree to which adaptation differed between WT and IL-10 KO, we estimated p-values as follows (Ogunnaike, 2011). We first defined the following T-statistic:
where nmin is the minimal number of samples across all time points and both genotypes, considered for a given feature set. This choice of nmin tends to reduce the value of the T-statistic and therefore provides a more conservative estimate of its probability. We then used the t-distribution defined according to df degrees of freedom to estimate two-tailed p-values associated with T to test the null hypothesis that AKO − AWT = 0 against the alternative hypothesis that AKO − AWT ≠ 0. For each feature set, we adjusted the p-values for multiple testing by applying the Benjamini-Hochberg procedure with the qvalue package in R (Dabney et al., 2010). For our analyses of computed adaptation indices, we plotted errors associated with our adaptation indices based on estimates of 95 confidence intervals defined as follows:
Statistical analysis
Statistical methods included the analysis of variance (ANOVA) with subsequent multiple comparison tests using the Fisher least significant difference (LSD) test with the Sidak correction (Figures 6A,B) and the hypergeometric test (using phyper in R). For the TNFα gene expression analysis depicted in Figure 6A, we performed a two-way ANOVA and then we compared the WT genotype to the IL-10 KO genotype at all time points. This analysis was motivated by our interest in investigating differences in the peak response between the WT and KO conditions. Similarly, for the analysis presented in Figure 6B, we utilized a two-way ANOVA. To specifically assess whether there were cases in which differences occurred relative to baseline for means computed across all features within given feature sets, we performed post hoc tests comparing feature set means to the mean at time = t0 within each genotype. In addition, we performed post hoc tests to compare the WT and IL10 KO means at each time point (see Figure 6C).
Computational modeling
We developed a novel computational model to account for the dynamics of cytokine interactions between microglia and the CNS environment. Our model builds on a previous modeling formalism that we have successfully utilized to study cytokine interaction network dynamics in microglia in vitro (Anderson et al., 2015). The microglial compartment was formulated as follows to simulate cytokine expression dynamics:
| (3) |
| (4) |
Cytokine expression Cx = Cx(t) was modeled for the following cytokines: x = TNFα, IL-1β, IL-6, TGFβ, IL-10, and CCL5. Cytokine x could be produced at a maximal rate of 1+kx. The time-dependent production rate was modulated by activation from cytokines Ci and inhibition from cytokines Cj. Activation and inhibition were modeled with sigmoidal functions characterized by half-maximal activation constant Kix and cooperativity coefficient nix. The degradation of Cx was modeled with both concentration-dependent and concentration-independent rate constants: γx and γss,x. The initial value of cytokine x was set to Css,x = 0.1 for all cytokines, and the concentration-independent degradation constant that was set to maintain a constant steady state (Equation 4) in the absence of stimulation. Based on available data, LPS stimulation was applied to all microglial species other than TGFβ as explained previously (Anderson et al., 2015). We set the stimulus duration to 16 h, but the qualitative characteristics of our simulation were robust to LPS stimulus duration.
We expanded our microglial model to incorporate the inflammatory influences of the CNS microenvironment. We formulated a CNS compartment of the model in which we assumed that astrocytes were the primary source of TGFβ–mediated feedback regulation of microglia (Norden et al., 2014). We simulated the delay between microglial IL-10 production and subsequent TGFβ production from the CNS environment (Norden et al., 2014) based on a series of coupled first-order systems (Ogunnaike and Ray, 1994):
| (5) |
| (6) |
where MIL10 represents microglial IL-10, represents the i-th element in the cascade of terms leading up to CNS environment TGFβ . The rate constants for the activation and degradation of the ATGF terms are kA and γA, respectively, and τA is the time constant governing the interaction dynamics. This formulation has been utilized extensively in engineering applications involving time delays between the activation of process control components (Liu et al., 2013). We note that this representation of CNS neuroinflammation by a restricted repertoire of cytokines in only microglia and the CNS microenvironment is an oversimplification of the biological complexity. We address this issue in the discussion.
Results
In vivo analysis of cytokine expression and microglial morphology dynamics
To assess the in vivo expression of cytokines described as important by our previous in silico modeling, based on published data, we investigated the temporal responses to systemic LPS (0.33 mg/kg i.p) which elicits a pro-inflammatory cytokine response in the brain in adult mice (Henry et al., 2009; Fenn et al., 2012). The inflammatory responses of the CNS spinal cord in vivo were distinct from in vitro data (Anderson et al., 2015): (i) Tnf and Il6 were rapidly expressed with fast recovery to the baseline level, (ii) Il1b showed rapid decay toward the baseline, and (iii) Tgfb1 showed partial recovery of expression with sustained upregulation for 5 days (Figure 1). The prominent adaptive responses observed for Tnf and Il6 suggest that these cytokines are regulated by robust negative feedback in vivo.
Figure 1.
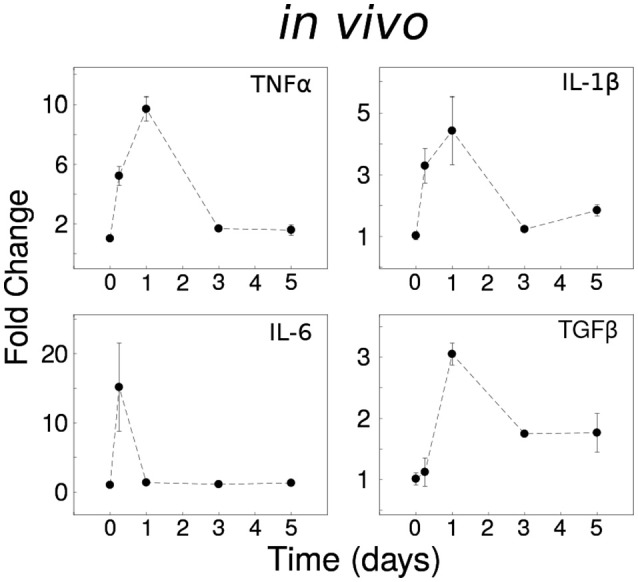
Dynamical analyses of cytokine network behavior in vivo. Spinal cord tissue cytokine gene expression data following systemic LPS (0.33 mg/kg i.p) at time = 0 (n = 3–4 mice per group).
Microglial morphology is critical for both the chemical and physical functions of microglia (Kettenmann et al., 2013; Morrison and Filosa, 2013; Šišková and Tremblay, 2013; Yamada and Jinno, 2013; Erny et al., 2015; Schafer and Stevens, 2015). Because previous studies have not compared the dynamic profiles of cytokine expression with the temporal responses of microglial morphology, we assessed microglial morphology over time following systemic LPS (Figure 2A). Based on our previous work, we hypothesized that IL-10 could regulate neuroinflammation through negative feedback, and we examined both wildtype (WT) and IL-10 knockout mice (IL-10−/−; Figure 2B). We reconstructed the morphological properties of 218 spinal cord microglia from WT and IL-10−/−. We analyzed an expansive set of geometrical features related to microglial soma and processes (Figure 3A, Table 1). Kernel density plots show the distributions of morphological variables as a function of time for WT and IL-10−/− (black and magenta, respectively) (Figure 3B). These analyses illustrate the relative influence of LPS on morphological properties in WT and IL-10−/− microglia over time. Note the non-Gaussian forms of the distributions, many of which exhibit long tails. In many cases, LPS (dosed IP at time = 0, t0) resulted in an apparent expansion of the distributions. These complexities highlight the utility of sensitive analytic methods for deciphering the temporal properties of microglial responses to neuroinflammation.
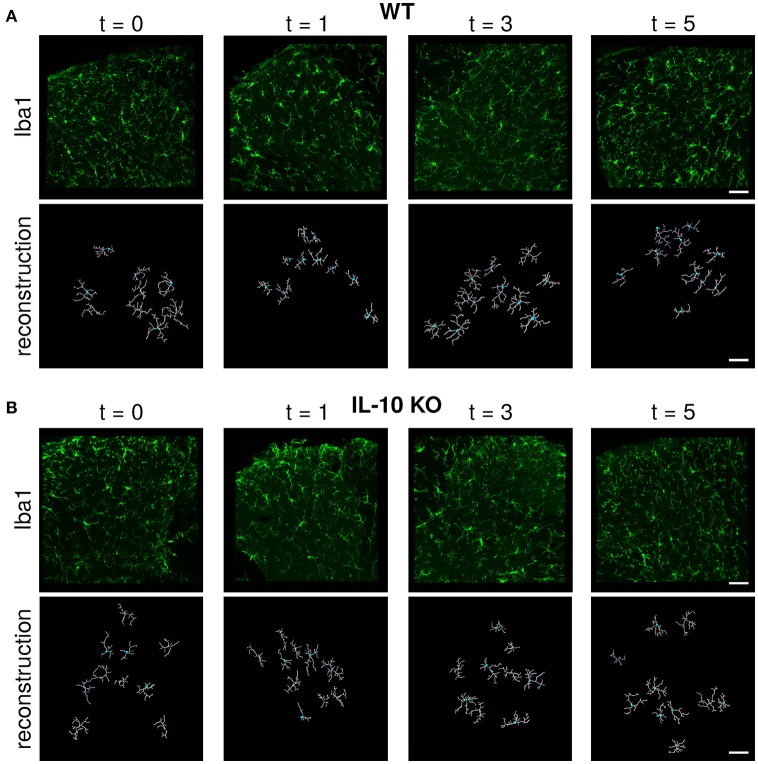
Figure 2.
Immunofluorescent labeling and IMARIS reconstruction of microglial morphology in the spinal cord dorsal gray matter over time after LPS injection in WT and IL-10 KO mice. Representative examples of Iba-1 labeled microglial morphology (green) in naive mice or 24 h, 3, and 5 days after systemic LPS (0.33 mg/kg i.p) in (A) WT and (B) IL-10−/− mice. Below each Iba-1 image is the respective IMARIS reconstruction of microglial morphology (white). Dorsal horn gray matter was imaged, as shown. Scale bar = 50 μm.
Figure 3.
Time-series and multivariate statistical analyses reveal that IL-10 modulates the dynamics of microglial morphology. (A) Panels show an Iba1 stained microglia (top) and a line sketch showing some of the main morphological features analyzed (bottom). (B) Kernel density plots show the distributions of various morphological variables as a function of time for WT and IL-10−/− (black and magenta, respectively). These analyses illustrate the relative influence of LPS on morphological properties in WT and IL-10−/− microglia. (C) Morphological features with statistically different dynamic profiles between genotypes were analyzed using the optimal discovery procedure (ODP). Several features showed genotype-specific significant differences. As described in the methods, we used the ODP to compare the temporal profiles of WT and IL-10−/− microglial features and we indicated the false discovery rate adjusted p-values (i.e., q-values) in the four panels; see Table 2 for documentation of all q-values. (D) Principal component analysis of differences in morphological features at various times after LPS administration. Note the difference between the two groups at t = 1 day.
Table 1.
IMARIS labels and descriptors.
| IMARIS label—features | Renamed label—features | Compartment | Units | Distributed | Feature set | Primary cluster | Description |
|---|---|---|---|---|---|---|---|
| Area | Soma area | Soma | um2 | No | fs2 | c2 | Surface area of the soma |
| Ellipsoid.Axis.Length.A | Soma ellipsoid length A | Soma | um | No | fs2 | c2 | Refers to parameters associated with ellipsoidal fits to somata |
| Ellipsoid.Axis.Length.B | Soma ellipsoid length B | Soma | um | No | fs2 | c2 | Refers to parameters associated with ellipsoidal fits to somata |
| Ellipsoid.Axis.Length.C | Soma ellipsoid length C | Soma | um | No | fs2 | c2 | Refers to parameters associated with ellipsoidal fits to somata |
| Ellipticity.oblate. | Ellipticity oblate | Soma | NA | No | NA | NA | Shape parameter of the soma |
| Ellipticity.prolate. | Ellipticity prolate | Soma | NA | No | fs2 | c2 | Shape parameter of the soma |
| Number.of.Triangles | Number triangles | Soma | Count | No | fs2 | c2 | Number of triangles, associated with resolution required for analysis |
| Number.of.Vertices | Number vertices | Soma | Count | No | fs2 | c2 | Number of vertices in a filament (a filament is a process emanating from the soma, along with all associated branches) |
| Number.of.Voxels | Number voxels | Soma | Count | No | fs2 | c2 | Number of voxels in the contour surface of the soma |
| Sphericity | Soma sphericity | Soma | NA | No | NA | NA | Shape parameter of the soma |
| Volume | Soma volume | Soma | um3 | No | fs2 | c2 | Volume of the soma |
| Filament.No.Dendrite.Branc.28 | Process branches | Process | Count | No | fs1 | c1 | The number of process branch points |
| Filament.No.Dendrite.Segments | Process segments | Process | Count | No | fs1 | c1 | Number of process segments in a filament |
| Filament.No.Dendrite.Termi.31 | Process terminals | Process | Count | No | fs1 | c1 | Number of process terminals in a filament |
| Filament.No.Edges | Filament edges | Process | Count | No | fs1 | c1 | Number of connections between vertices in a filament |
| Filament.Volume.sum. | Filament volume | Process | um3 | No | fs1 | c1 | Total volume of all processes of the cell |
| Dendrite.Area | Process area | Process | um2 | Yes | fs4 | c4-6 | Surface area of a process segment (sum of areas encompassing edges) |
| Dendrite.Branch.Depth | Branch depth | Process | Count | Yes | fs1 | c1 | Number of process bifurcations along the shortest path from the soma to a given coordinate |
| Dendrite.Branch.Level | Branch level | Process | NA | Yes | fs1 | c1 | Metric of incremental decrease in dendrite diameter at each bifurcation point |
| Dendrite.Branching.Angle | Branch angle | Process | Degrees | Yes | fs3 | c3 | Angle between branches at a bifurcation point |
| Dendrite.Branching.Angle.B | Branch angle B | Process | Degrees | Yes | fs3 | c3 | Angle between the line from the beginning of a filament to a bifurcation and between a bifurcation and terminal |
| Dendrite.Length | Process length | Process | um | Yes | fs4 | c4-6 | Sum of edge lengths between bifurcation points |
| Dendrite.Mean.Diameter | Process diameter | Process | um | Yes | fs3 | c3 | Diameter of a process |
| Dendrite.Orientation.Angle | Process orientation angle | Process | Degrees | Yes | fs3,4 | c3-6 | Angle between image plane and line connecting the start to end of a branch |
| Dendrite.Position | Process position | Process | um | Yes | fs1,4 | c1,4-6 | Positional coordinate of a process |
| Dendrite.Resistance | Process resistance | Process | um−1 | Yes | fs4 | c4-6 | Proxy for electrical length based on process length and cross-sectional area |
| Dendrite.Straightness | Process straightness | Process | NA | Yes | fs3,4 | c3-6 | Sum of edge lengths divided by distance from start to end of a segment (h) |
| Dendrite.Volume | Process volume | Process | um3 | Yes | fs4 | c4-6 | Total filament volume including all segments |
Unsupervised, multivariate analysis of microglial morphology reveals distinct cell states characterized by functionally defined sets of morphological properties
To comprehensively analyze the features of microglia, such as number of branch points and branch point angles, which are distributed variables in single cells, we assessed distributional statistics related to center (mean, median, mode), spread (standard deviation, variance, coefficient of variation), and shape (skewness, and kurtosis), yielding 110 total features (Table 2). To elucidate the morphological features with statistically distinguishable dynamic profiles between WT and IL-10−/−, we employed the optimal discovery procedure (ODP) (Storey et al., 2005, 2007). This analysis facilitated the direct comparison of temporal profiles (smooth curves in Figure 3C), as opposed to individual data points, which is optimal for time-series analysis (Storey et al., 2005). Several features showed genotype-specific significant differences in the respective temporal dynamics (P < 0.05; Figure 3C; Table 2–q-values). For distributed features of microglial processes, we directly compared the underlying distributions using the Kolmogorov-Smirnov (K-S) test and observed several time- and genotype-specific differences (data not shown). To determine whether the temporal dynamics of global cell state variations were sensitive to IL-10, we applied principal components analysis (PCA) to our multivariate morphology data. This analyses revealed subtle but distinct quantitative morphological differences between WT and IL-10−/− microglia, particularly in the initial phase of the response to LPS (t = 1 day; Figure 3D). Furthermore, our PCA data facilitated the identification morphological features with high variability that we utilized in downstream analysis (Table 2, see Methods–Feature selection).
Table 2.
Genotype-specific differences in the temporal dynamics of features.
| Feature | Compartment | Feature set | Dist property | Loading | q-value |
|---|---|---|---|---|---|
| Process branches | Process | fs1 | NA | 0.24 | 0.023 |
| Process segments | Process | fs1 | NA | 0.238 | 0.023 |
| Process terminals | Process | fs1 | NA | 0.233 | 0.023 |
| Filament edges | Process | fs1 | NA | 0.237 | 0.04 |
| Filament volume | Process | fs1 | NA | 0.229 | 0.042 |
| Branch depth_mean | Process | fs1 | Center | 0.213 | 0.028 |
| Branch depth_median | Process | fs1 | Center | 0.203 | 0.03 |
| Branch level_mean | Process | fs1 | Center | 0.189 | 0.015 |
| Branch level_median | Process | fs1 | Center | 0.178 | 0.015 |
| Branch level_mode | Process | fs1 | Center | 0.175 | 0.015 |
| Process position_sdev | Process | fs1 | Spread | 0.206 | 0.078 |
| Branch depth_sdev | Process | fs1 | Spread | 0.179 | 0.03 |
| Soma area | Soma | fs2 | NA | 0.286 | 0.04 |
| Soma ellipsoid length A | Soma | fs2 | NA | 0.216 | 0.113 |
| Soma ellipsoid length C | Soma | fs2 | NA | 0.243 | 0.015 |
| Number triangles | Soma | fs2 | NA | 0.29 | 0.041 |
| Number vertices | Soma | fs2 | NA | 0.29 | 0.041 |
| Number voxels | Soma | fs2 | NA | 0.288 | 0.052 |
| Soma volume | Soma | fs2 | NA | 0.288 | 0.054 |
| Ellipticity prolate | Soma | fs2 | NA | 0.136 | 0.04 |
| Process diameter_mean | Process | fs3 | Center | 0.258 | 0.078 |
| Process diameter_median | Process | fs3 | Center | 0.225 | 0.042 |
| Process straightness_mean | Process | fs3 | Center | 0.205 | 0.113 |
| Branch angle_mean | Process | fs3 | Center | 0.12 | 0.03 |
| Process diameter_mode | Process | fs3 | Center | 0.139 | 0.03 |
| Branch angle_95ci | Process | fs3 | Spread | 0.232 | 0.106 |
| Branch angle B_95ci | Process | fs3 | Spread | 0.238 | 0.09 |
| Process diameter_95ci | Process | fs3 | Spread | 0.226 | 0.148 |
| Branch angle B_sdev | Process | fs3 | Spread | 0.197 | 0.04 |
| Process orientation angle_95ci | Process | fs3 | Spread | 0.188 | 0.03 |
| Branch angle B_skew | Process | fs3 | Shape | 0.248 | 0.03 |
| Branch angle B_kurt | Process | fs3 | Shape | 0.217 | 0.099 |
| Process area_mean | Process | fs4 | Center | 0.239 | 0.033 |
| Process area_median | Process | fs4 | Center | 0.236 | 0.04 |
| Process area_sdev | Process | fs4 | Center | 0.251 | 0.063 |
| Process length_mean | Process | fs4 | Center | 0.245 | 0.04 |
| Process length_median | Process | fs4 | Center | 0.221 | 0.066 |
| Process resistance_mean | Process | fs4 | Center | 0.246 | 0.077 |
| Process resistance_median | Process | fs4 | Center | 0.212 | 0.075 |
| Process volume_mean | Process | fs4 | Center | 0.238 | 0.03 |
| Process volume_median | Process | fs4 | Center | 0.238 | 0.03 |
| Process area_mode | Process | fs4 | Center | 0.159 | 0.03 |
| Process volume_mode | Process | fs4 | Center | 0.173 | 0.03 |
| Process area_95ci | Process | fs4 | Spread | 0.242 | 0.023 |
| Process area_cv | Process | fs4 | Spread | 0.283 | 0.125 |
| Process length_sdev | Process | fs4 | Spread | 0.259 | 0.091 |
| Process length_95ci | Process | fs4 | Spread | 0.25 | 0.03 |
| Process length_cv | Process | fs4 | Spread | 0.281 | 0.115 |
| Process resistance_sdev | Process | fs4 | Spread | 0.239 | 0.13 |
| Process resistance_95ci | Process | fs4 | Spread | 0.245 | 0.042 |
| Process resistance_cv | Process | fs4 | Spread | 0.245 | 0.1 |
| Process volume_sdev | Process | fs4 | Spread | 0.228 | 0.04 |
| Process volume_95ci | Process | fs4 | Spread | 0.228 | 0.015 |
| Process volume_cv | Process | fs4 | Spread | 0.245 | 0.11 |
| Process position_95ci | Process | fs4 | Spread | 0.174 | 0.015 |
| Process area_skew | Process | fs4 | Shape | 0.27 | 0.115 |
| Process area_kurt | Process | fs4 | Shape | 0.241 | 0.09 |
| Process length_skew | Process | fs4 | Shape | 0.271 | 0.13 |
| Process length_kurt | Process | fs4 | Shape | 0.239 | 0.106 |
| Process resistance_skew | Process | fs4 | Shape | 0.238 | 0.13 |
| Process resistance_kurt | Process | fs4 | Shape | 0.201 | 0.078 |
| Process volume_skew | Process | fs4 | Shape | 0.205 | 0.109 |
| Process orientation angle_kurt | Process | fs4 | Shape | 0.09 | 0.04 |
| Process straightness_skew | Process | fs4 | Shape | 0.056 | 0.023 |
We next examined whether genotype-specific microglial cell states could be segregated into distinct classes based on specific groups of morphological features. We employed non-negative matrix factorization (NMF), a highly effective technique to define groups of features that are associated with varying degrees of representation in distinct clusters of cells (Lee and Seung, 1999), which involves factorization of a data matrix D (Nf morphological features measured in Ns cells) into a basis matrix W of meta-features (a combination of individual features), and a coefficient matrix H with entries corresponding to the non-negative weight of each meta-feature in each sample (Figure 4A). We utilized NMF to test whether particular combinations of morphological features were overrepresented in specific subsets of the microglial population. Because the interpretability of multivariate analysis results is sensitive to the information content of the variables included in the analysis, we implemented a novel step-wise approach in which we initially identified informative features based on independent ODP and PC analyses. Figure 4B shows Z-score feature data with microglial cells (columns of the heatmap) organized based on the clustering of the coefficient matrix H, and rows organized based on the clustering of the basis matrix W. The clarity of the Z-score groupings, as indicated by the lines and diagonal pattern of ‘reddish blocks’, suggest that the WH decomposition (an estimate of two matrices whose product approximates but is not identical to the data set) provides a useful representation of the data that facilitates its interpretation. Thus, the Z-score data matrix (D) can be approximated by multiplying W and H (Figure 4B). This analysis identified four clusters of features (“feature sets,” fs1-4) and six clusters of discrete microglial cell states, each characterized by a specific profile of feature-set representation (c1-6; Figure 4B).
Figure 4.
Morphological cell states characterized by distinct sets of morphological features. (A) Illustrative example of Non-negative matrix factorization (NMF) to show representations of a Data matrix, Basis matrix, and Coefficient matrix. (B) Microglial morphology data set organized according to feature sets. The Z-score matrix of morphological data D is organized based on the NMF analysis. The Basis matrix W of morphological meta-features is defined by four sets of features (fs1-4) from 218 reconstructed microglia, and the Coefficient matrix H shows a representation of meta-features in clusters of microglia (c1-6). *Denotes multiplication.
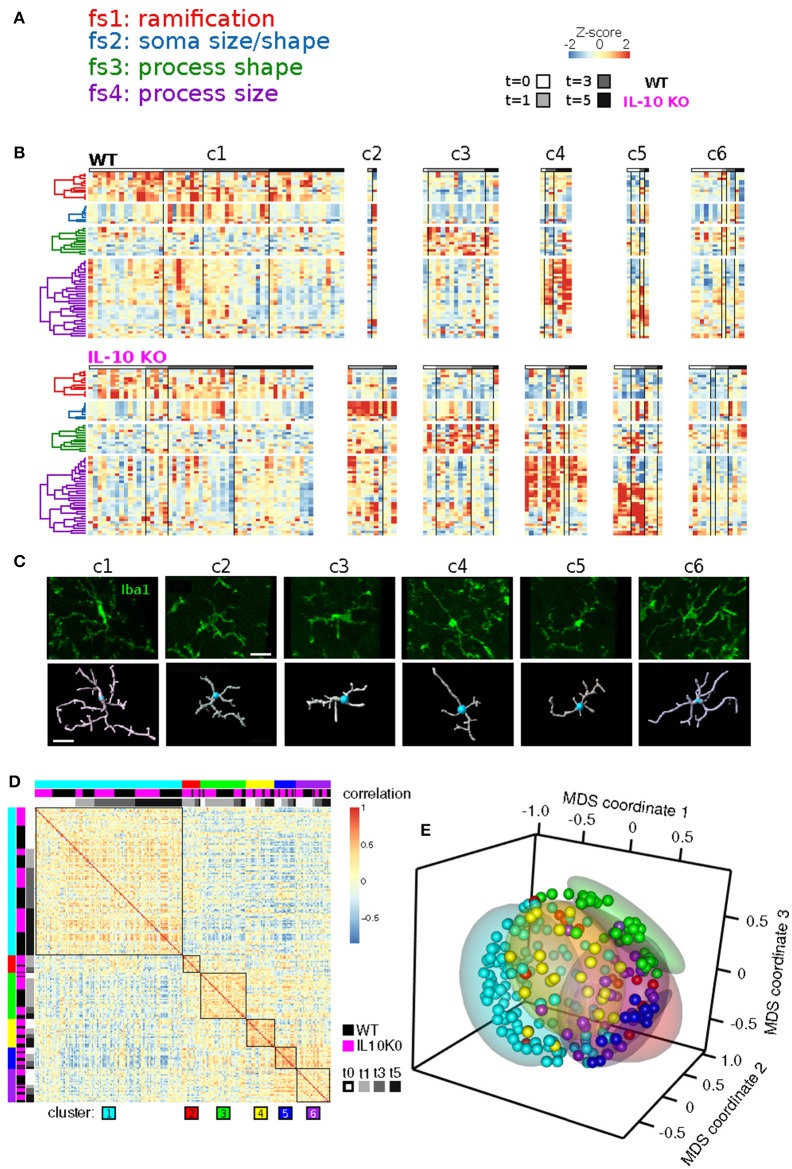
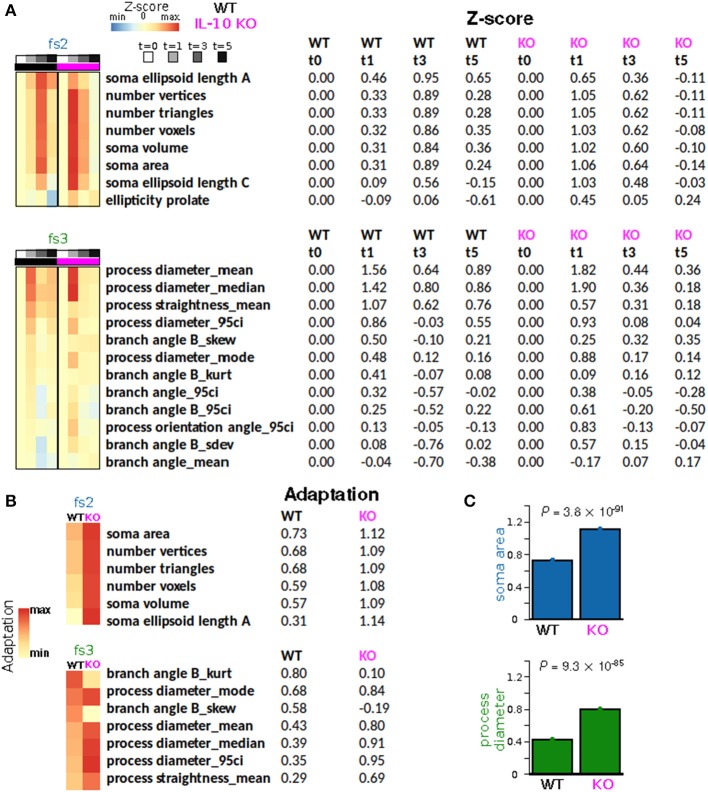
Our analysis revealed four clusters of morphological features involving process ramification (fs1), soma size/shape (fs2), process shape (fs3), and process size (fs4) (Figure 5A; Table 2). There was considerable agreement between the features included in each feature-set and previously identified feature relationships (Yamada and Jinno, 2013; Kongsui et al., 2014). Feature set 1 (fs1) was associated with large branch arbors with numerous branch bifurcations and progressive decrements in thickness from soma to terminal (Table 2). This feature set was highly represented in both WT and IL-10−/− microglia from cluster 1 (Figure 5B), with features indicative of the ramified morphology of healthy microglia. Fs2 was associated with larger soma size, consistent with microglial activation following LPS application (Kozlowski and Weimer, 2012). Interestingly, cluster 2 microglia with relatively high fs2 levels were observed primarily in IL-10−/− (P = 0.019, hypergeometric test), indicating that this cell state may be associated with pro-inflammatory up-regulation associated with the absence of IL-10. Fs3 was associated with the complexity of branch shape, including features related to the angularity of branching, the functional significance of which is not clear (Karperien et al., 2013) and was represented equally in cluster 3 WT and IL-10−/− microglia. Fs4 was associated with the size of the branches, indicated by features such as branch length. Cluster 4-5 microglia showed relatively high levels of fs4 morphological features and a trend toward predominant representation in IL-10−/− microglia (P = 0.15). Cluster 6 microglia were characterized by moderate expression of all feature sets. Overall, the morphological feature sets could be summarized respectively to indicate the extent of ramification, soma size/shape, process shape, and process size (Figure 5A, Table 2).
Figure 5.
Temporal analysis of IL-10 influences on feature set dynamics. (A) List of morphological signatures of the 4 feature sets (see Table 2): ramification, soma size/shape, process shape, and process size. (B) Morphological cell state clusters (c1-6) are displayed for WT (top) and IL-10−/− microglia (bottom). Note the 6 classes of microglia based on differences in feature set distribution, and differences in the population size of the different classes (c1-c6) between genotypes. (C) Representative confocal images of the six classes of cells and their confocal image-based reconstructions. Scale bar = 20 μm. (D) The Spearman rank correlation matrix shows that samples are highly correlated within the six clusters defined by NMF. (E) The Multidimensional scaling (MDS) analysis shows that samples of NMF-defined clusters are grouped together in a 3-dimensional projection according to MDS. These results independently support the findings from the NMF analysis.
When sample images of reconstructed microglia representative of each NMF-based cluster were examined, the six clusters were not easily or unambiguously identifiable by visual inspection (Figure 5C). The heterogeneity seen within and across microglial clusters highlights the need for detailed morphological analyses across a range of experimental contexts, based on large sample sizes of microglia, in an unbiased manner (Walker et al., 2014). To confirm that our NMF results could not be attributed to a spurious product of algorithmic processing, we implemented an independent analysis using sample-by-sample correlations and multidimensional scaling (Figures 5D,E; also see Methods). We found that clusters of samples, based on the NMF analysis, exhibited high correlations and relative proximity within MDS coordinates. Overall, our analyses revealed subtle differences in microglial morphology mediated by IL-10 in this model of CNS inflammation.
IL-10 impedes adaptation of TNFα and microglial morphology
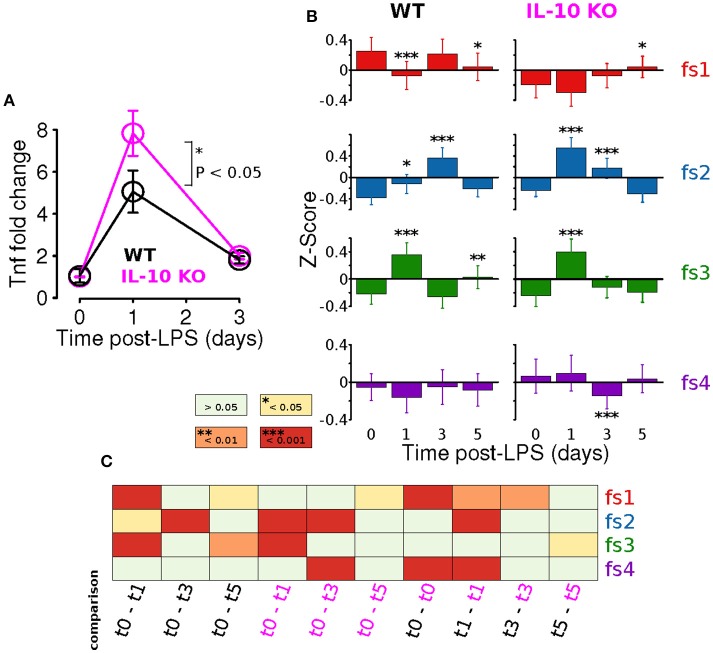
Adaptation is an important emergent property of engineered feedback control systems and components of the immune system operating inside and out of the CNS (Brudecki et al., 2013; Anderson et al., 2015; Montefusco et al., 2016). Our previous study showed that IL-10 restrained the adaptation of the TNFα response to LPS in vitro. We directly tested the hypothesis that IL-10 represses adaptation of CNS TNFα expression in response to systemic LPS in vivo at peak (24 h) and recovery (3 days) of expression. We assessed the TNFα response to LPS (i.p.) in brain tissue. Despite reported microglial heterogeneity in the healthy CNS (Grabert et al., 2016), or during plasticity, we found no difference in TNFα expression the brain and spinal cord 24 h after LPS injection (Supplementary Figure 1). Our experimental results with IL-10−/− mice showed, as predicted, a larger fold change in TNFα gene expression in the CNS following LPS (P < 0.05, two-way ANOVA with with Sidak's multiple comparisons P = 0.0147, Figure 6A). However, TNFα expression showed complete recovery to WT levels 3 days after LPS injection (Figure 6A). Thus, the absence of IL-10 resulted in enhanced adaptive recovery of the TNFα inflammatory response to LPS in vivo. These results suggest a novel hypothesis that the anti-inflammatory cytokine IL-10 restrains the degree of adaptive recovery following in vivo inflammation in the CNS.
Figure 6.
IL-10 restrains TNFα adaptation and regulates specific morphological features. (A) In vivo CNS gene expression of TNFα in WT and IL-10−/− LPS-treated mice show that the absence of IL-10 is associated with an enhanced LPS response and corresponding enhanced adaptive recovery to baseline (two-way ANOVA with with Sidak's multiple comparisons P = 0.0147, n = 4 mice per group, brain tissue). (B) For both WT and IL-10−/−, the arithmetic means across each feature set (fs1-4) was computed at the four time points (t = 0, 1, 3, and 5 days). Temporal dynamics of each feature set was analyzed using a two-way ANOVA and p-values based on a Fisher LSD post-hoc test with a Sidak correction. (C) The heatmap depicts corrected p-values for a focused set of post hoc comparisons (columns) applied for each feature set (rows). For instance, the first column shows results for the comparison of the WT means at time 0 and time 1 day, the third column shows the comparison of the IL-10−/− means at time 0 and time 1 day, and the last column shows the comparison of the WT and IL-10−/− means at time 5 days.
We next assessed whether IL-10−/− influences the adaptation of morphological properties in response to LPS stimulation, as was observed for TNFα gene expression in vivo (Figure 6A). For this analysis, the arithmetic mean levels of each feature-set were evaluated at each time-point. For all feature sets, we observed significant main effects for time [P < 0.001; F(3, 2608) = 9.5, F(3, 1736) = 56.1, F(3, 2608) = 63.8, and F(3, 5878) = 5.6 for fs1-4, respectively], and we observed significant main effects of genotype (P < 0.001) for every feature set other than fs3 [P = 0.85; F(1, 2608) = 48.1, F(1, 1736) = 18.0, F(1, 2608) = 0.04, and F(1, 5878) = 24.0]. Likewise, significant time-genotype interaction terms were observed for all feature sets (F > 5, P < 0.001), thus indicating that the occlusion of Il10 modifies the temporal dynamics of the morphological response the systemic inflammation, consistent with our time series analysis. When the temporal dynamics of feature set averages were compared across genotypes, the mean response profiles for fs2 and fs3 appeared to be consistent with enhanced morphological adaptation in IL-10−/−, as compared to WT (Figure 6B). It is noteworthy that WT microglia showed peak fs2 responses at t = 3 d whereas IL-10−/− microglial expression of fs2 features were maximal at t = 1 d following LPS. In contrast, the fs3 peak responses of both genotypes were observed at t = 1 day post-LPS (Figure 6B). See Figure 6C for a complete summary of our post hoc analysis results. These data indicate that genetic ablation of IL-10 has selective influences on the kinetics of morphological responses to TLR-4 stimulation. Furthermore, the IL-10−/− responses appeared to show a more complete recovery to the pre-stimulus (t = 0) levels in comparison to the findings for the WT microglia for fs2 and fs3 (Figure 6B).
To quantify morphological adaptation between WT and IL-10 KO, we computed adaptation indices and estimated the standard errors corresponding to these adaptation indices (Figures 7A,B; see Methods). For morphological features that met our criteria for adaptation analysis, all fs2 features showed greater adaptation for the IL-10 KO genotype, and 5/7 fs3 features showed greater adaptation for IL-10 KO (Figures 7B,C). When we considered all morphological features, the majority showed significantly greater adaptation for IL-10 KO (all P < 1.4 × 10−15, Figure 7B; the p-values were computed as described in the Methods section “Morphological adaptation analysis” based on the t-distribution corresponding to an estimate of the T-statistic). Strikingly, these data indicate that the adaptive recovery of morphological features and cytokine responses to infiammatory insult are enhanced by the absence of IL-10 in the cytokine regulatory network.
Figure 7.
IL-10 restrains morphological adaptation. (A) Average Z-scores represented as a function of time for individual features from feature sets fs2 (soma size/shape) and fs3 (process shape). Rows (features) were sorted according to the peak WT average Z-scores. (B) Adaptation indices were computed and displayed for a subset of features that met certain criteria (Methods). IL-10−/− microglia exhibit enhanced adaptation of key features associated with the shape of somata and processes. (C) Specific examples of adaptation indices illustrate the enhancement of morphological adaptation associated with IL-10−/−. The data were analyzed using two-tailed t-test with corrected p-values using the Bengamini-Hoshberg procedure.
In silico modeling analysis of IL-10 feedback regulation of TNFα adaptation
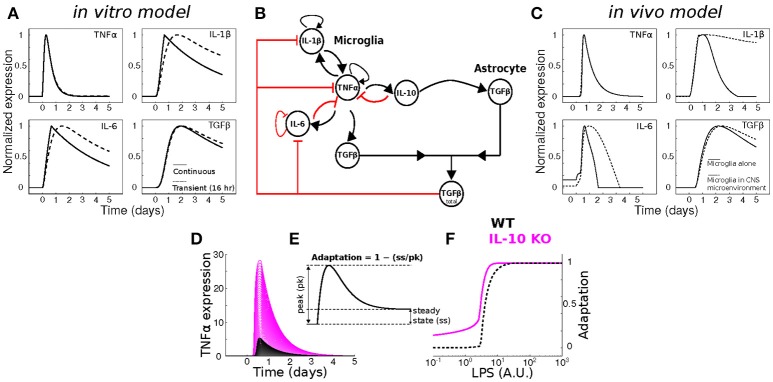
To assess whether our previous model of in vitro microglial cytokine dynamics (Anderson et al., 2015) agreed with our in vivo cytokine expression measurements, we compared the model simulations (Figure 8A) to our data (Figure 1). Our original model was designed to simulate the microglial response to a continuous LPS stimulus (Figure 8A, dashed traces). To match our in vivo experiment, we re-simulated the model with a transient stimulus (Figure 8A, solid traces). Regardless of the LPS stimulus duration, our in vitro model did not capture the expression dynamics observed in vivo (note that we show data for a 16 h stimulus). In particular, the pronounced degree of adaptation observed for Il1b and Il6 in vivo suggested that additional negative feedback constraints may enforce adaptive recovery to infection or insult in the CNS.
Figure 8.
Dynamical modeling analyses of cytokine network regulation. (A) Simulation of our in vitro cytokine model cannot account for in vivo dynamics under conditions of either continuous (dashed) or transient (solid) LPS stimulation. (B) Literature-based data-driven cytokine interaction network based on in vivo data. (C) In silico model simulations of in vivo cytokine network dynamics (see Methods and Discussion for further explanation of this model). (D) Simulations of wildtype (WT; black) and IL-10 KO; magenta) model TNFα response to a range of LPS stimulus magnitudes (arbitrary units). (E) Analytic framework for computing adaptive recovery of the TNFα response to LPS. (F) LPS concentration response profiles for adaptation of WT and IL-10 KO phenotypes in silico show that the IL-10 KO enhances adaptation to LPS (left-shifted curve).
To quantitatively evaluate network influences on cytokine expression dynamics in vivo, we developed a new multi-cellular computational model in which IL-10 from microglia stimulates TGFβ up-regulation by in the surrounding microenvironment (most likely derived from astrocytes) and TGFβ inhibits microglial IL-1β and IL-6 expression (Norden et al., 2014) (Figure 8B). The inclusion of microglia interactions with the CNS environment was critical to account for the in vivo cytokine expression dynamics in the simulations (Figure 8C; compare with Figure 1). Simulation of our new neuroinflammation model yielded temporal patterns of cytokine expression that were in qualitative agreement with our experimental data (Figure 1). To examine the implications of negative feedback on the cytokine network, we simulated the effects of IL-10 KO on the TNFα response to LPS by removing the IL-10 node from the network (Anderson et al., 2015). As expected, removal of IL-10 resulted in enhanced TNFα responses to LPS over a range of doses (Figure 8D). This model prediction is consistent with a wealth of data demonstrating that IL-10 provides feedback inhibition on TNFα expression in glia (Sheng et al., 1995). In agreement with our previous in vitro results (Anderson et al., 2015), simulating IL-10 KO in our new model enhanced adaptive recovery of TNFα response to LPS, particularly at lower stimulus intensities (Figures 8E,F). Thus, our simulations and analysis derived from the present in vivo data supported the counter-intuitive prediction that IL-10, a feedback inhibitor of TNFα expression, impedes the recovery of TNFα expression toward the baseline level following an LPS stimulus.
Discussion
This work presents a new approach to investigate microglia by integrating measurements of inflammatory cytokines with novel, unbiased, multivariate analyses to assess microglial morphology and dynamics in vivo. Our analyses detected subtle changes in microglial morphology that are missed by conventional qualitative analysis. We also quantitatively characterized adaptation processes based on negative feedback regulation in a novel computational model of CNS inflammation.
It is assumed that microglial morphology affects cell function, and assessments of microglial morphology as a readout of the cell's activation state have been employed for many years (Streit et al., 1999, 2014). Stratifying microglia into classes along a continuum of ramified/hyper-ramified/reactive/ameboid states serves as a useful descriptor of gross changes in morphology. However, such changes (ramified to amoeboid) are rarely seen outside of overt injury sites, such as in traumatic/ischemic lesions. Furthermore, assessment of microglial cell morphology in such lesions has been confounded by the presence of infiltrating monocyte derived macrophages (Mawhinney et al., 2012; Greenhalgh and David, 2014; Bennett et al., 2016; Greenhalgh et al., 2016). As microglial functions are now implicated in the onset of Alzheimer's disease, schizophrenia, epilepsy and intellectual disability (Frick et al., 2013; Abiega et al., 2016; Hong et al., 2016), appropriate assessment of subtle changes in microglial morphology may illuminate their homeostatic and pathophysiological functions. Our current approach circumvents the shortcomings associated with conventionally applied qualitative morphology analyses. For example, when sample images of reconstructed microglia most representative of each cluster were examined, the six clusters were not easily or unambiguously identifiable by visual inspection. Many studies have used 3-D reconstruction software, such as IMARIS, to advance the study of microglia by providing quantitative measures of their morphology (Madore et al., 2013; Erny et al., 2015; Lewitus Gil et al., 2016). Our results show that over one-hundred measurable parameters can be quantified using such analyses. The caveat with these large data sets is that it is difficult to identify significantly different morphological features while controlling for the type I error rate. We have attempted to avoid such errors by incorporating the entire dataset and using appropriate statistical measures such as the optimal discovery procedure (ODP) (Storey et al., 2005, 2007) instead of ANOVA, which is sub-optimal for analyzing temporal dynamics across many features (Storey et al., 2005). Furthermore, for the first time in the assessment of microglial morphology, we employed non-negative matrix factorization (NMF), which is a highly effective technique to define groups of features that are associated with varying degrees of representation in distinct clusters of cells (Lee and Seung, 1999). Spatiotemporal monitoring of microglia morphology in relation to brain injury has been investigated (Morrison and Filosa, 2013) and hierarchical cluster analysis of the morphometric features was used to objectively describe and classify morphological changes under homeostatic and neuropathological conditions (Yamada and Jinno, 2013; Diniz et al., 2016). Our present data build on these hierarchical clustering techniques and provide an approach that is unbiased, sensitive, and can be widely used to study subtle changes in microglial morphology.
After predicting and validating the counter-intuitive notion that IL-10 limits the recovery of TNFα in vivo, we sought to investigate whether certain aspects of microglial morphology were also regulated similarly. Using the sensitive, unbiased approaches to assess morphology, we found that adaptation of feature sets associated with soma size/shape (fs2) and process shape (fs3) showed significantly increased adaptation in the absence of IL-10. These findings indicate that IL-10 impedes the recovery of these features of microglial morphology to homeostatic levels in a similar time-course as IL-10 impedes the return of TNFα to baseline. We also considered groups of individual morphological features, the majority of which showed significantly greater adaptation in IL-10−/− mice, especially those associated with larger soma size, consistent with microglial activation following LPS application (Kozlowski and Weimer, 2012). Interestingly, features associated with the complexity of branch shape, including features related to the angularity of branching, also showed significantly greater adaptation, consistent with the notion that ramified microglia represent a surveying, non-activated state (Karperien et al., 2013).
We developed a novel computational model to account for the dynamics of cytokine interactions between microglia and the CNS environment based on the in vivo cytokine data collected in the current study. In the present two-compartment model, we improved our previously established model of cytokine dynamics which represented a single compartment of microglial cells, regulated through autocrine/paracrine signaling, based on data obtained from primary microglial cell cultures (Anderson et al., 2015). To incorporate the interactions of microglial cells with their in vivo microenvironment, we added a second compartment to the model. This compartment was proposed to be dominated by astrocyte-mediated feedback influences on microglia based on astrocyte TGFβ release and consequent feedback inhibition of microglial IL-1β and IL-6 (Norden et al., 2014). CNS neuroinflammation involves an expansive repertoire of cytokines secreted by cell types including neurons, endothelial cells, pericytes, astrocytes, and microglia. Our simplified modeling approach was driven by (a) the dearth of data regarding the cellular sources, temporal expression dynamics, and relative functional influences of the multitude of cytokines, and (b) the motivation to develop a parsimonious model that could capture the complex dynamics of multivariate cytokine expression—as regulated by feedback control of microglial inflammation—without the unnecessary inclusion of unknown molecular interaction parameters. Such simplified models are often considered to be desirable from the perspective of model analysis because model simplification facilitates the identification of critical regulators of the system's function (Huang et al., 2010; Transtrum and Qiu, 2014). While we have not undertaken focused experimental analyses to verify the proposed components of astrocyte-mediated feedback of microglia via TGFβ, our data are consistent with our model analyses. Even if astrocyte-mediated feedback regulation of microglial inflammation were not exclusively controlled by TGFβ, our model illustrates a plausible mechanism from the perspective of the observed process dynamics. Furthermore, we have argued that computational modeling can be utilized for numerous purposes other than accurately recapitulating or predicting the precise mechanisms of function (Anderson and Vadigepalli, in press). Alternatively, as in our study, modeling can be used to show that negative feedback processes—regardless of their precise molecular mechanisms—are sufficient to explain the effect of IL-10 occlusion on the adaptive response to CNS insult. Our model of in vivo neuroinflammation captures the dynamics of two glial cell types with distinct regulatory interactions. Based on model simulations, we predicted that the anti-inflammatory cytokine IL-10 would impede the adaptation of TNFα. Our experimental data confirmed this prediction, highlighting the utility of mathematically modeling of complex cytokine networks to investigate neuroinflammation.
Morphological analyses were performed on microglial cells of the spinal cord. This is a particularly relevant region of the CNS to study neuroinflammatory mechanisms, as understanding its effect on neuronal degeneration and regeneration are key to recovery in spinal cord injury. An interesting avenue for further investigation will be to understand if there are region-specific responses during neuroinflammation. It has been demonstrated that there is microglial diversity between different brain regions (Grabert et al., 2016). This is more pronounced in the healthy brain as, in perturbed CNS states, such as aging and pathological conditions, microglial diversity and the homeostatic signature of microglia is lost (Grabert et al., 2016; Keren-Shaul et al., 2017).
Transcriptional analyses of microglia in their various states of activation have contributed greatly to our understanding of these cells (Butovsky et al., 2014; Healy et al., in press). As microglia morphology also reflects their function (Walker et al., 2014), the coupling of morphological data-sets, such as in the present study, with transcriptional profiles of these individual cells, could provide a tool kit to the exact functions of distinct morphologies.
Future extensions of our study include identifying disease or injury-specific dynamic profiles of cytokine networks and correlations with changes in particular aspects of microglial morphology that can reveal functional states, and lead to the identification of molecular mechanisms underlying the coupling between cytokine regulation and microglial morphology. Our results depict a hitherto unrecognized association between the dynamics of cytokine gene expression and microglial morphology in the CNS, and the counter-intuitive role of IL-10 in regulating these dynamics in vivo. The combination of mathematical modeling of cytokine networks, in vivo validation, and sensitive morphological analysis will be a valuable tool to study changes in microglial responses in CNS injury and disease.
Author contributions
WA and AG designed experiments, analyzed data, and wrote manuscript. AG performed experiments and WA performed statistical analysis and mathematical modeling. AT performed experiments. SD and RV supervised studies and wrote manuscript.
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by grants from the National Institutes of Health, National Heart, Lung, and Blood Institute R01 HL111621 RV; and the Canadian Institutes of Health Research (CIHR; MOP-14828) and MS Society of Canada to SD. AG was supported by a postdoctoral fellowship from the CIHR.
Supplementary material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fncel.2017.00233/full#supplementary-material
TNFα expression increases to the same extent in both brain and spinal cord tissue after systemic LPS (0.33 mg/kg i.p) at 24 h (n = 3–4 mice per group).
References
- Abiega O., Beccari S., Diaz-Aparicio I., Nadjar A., Layé S., Leyrolle Q., et al. (2016). Neuronal hyperactivity disturbs ATP microgradients, impairs microglial motility, and reduces phagocytic receptor expression triggering apoptosis/microglial phagocytosis uncoupling. PLoS Biol. 14:e1002466 10.1371/journal.pbio.1002466 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson W. D., DeCicco D., Schwaber J. S., Vadigepalli R. (2017). A data-driven modeling approach to identify disease-specific multi-organ networks driving physiological dysregulation. PLoS Comput. Biol. 13:e1005627. 10.1371/journal.pcbi.1005627 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson W. D., Makadia H. K., Greenhalgh A. D., Schwaber J. S., David S., Vadigepalli R. (2015). Computational modeling of cytokine signaling in microglia. Mol. Biosyst. 11, 3332–3346. 10.1039/C5MB00488H [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson W. D., Makadia H. K., Vadigepalli R. (2016). Molecular variability elicits a tunable switch with discrete neuromodulatory response phenotypes. J. Comput. Neurosci. 40, 65–82. 10.1007/s10827-015-0584-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson W. D., Vadigepalli R. (in press). Modeling cytokine regulatory network dynamics driving neuroinflammation in central nervous system disorders. Drug Dis. Today. 10.1016/j.ddmod.2017.01.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badea L. (2008). Extracting gene expression profiles common to colon and pancreatic adenocarcinoma using simultaneous nonnegative matrix factorization, in Pacific Symposium on Biocomputing (Bucharest: Citeseer; ), 279–290. [PubMed] [Google Scholar]
- Bennett M. L., Bennett F. C., Liddelow S. A., Ajami B., Zamanian J. L., Fernhoff N. B., et al. (2016). New tools for studying microglia in the mouse and human CNS. Proc. Natl. Acad. Sci. U.S.A. 113, E1738–E1746. 10.1073/pnas.1525528113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benveniste E. N. (1992). Inflammatory cytokines within the central nervous system: sources, function, and mechanism of action. Am. J. Physiol. Cell Physiol. 263, C1–C16. [DOI] [PubMed] [Google Scholar]
- Boutsidis C., Gallopoulos E. (2008). SVD based initialization: a head start for nonnegative matrix factorization. Pattern Recognit. 41, 1350–1362. 10.1016/j.patcog.2007.09.010 [DOI] [Google Scholar]
- Brudecki L., Ferguson D. A., McCall C. E., El Gazzar M. (2013). MicroRNA-146a and RBM4 form a negative feed-forward loop that disrupts cytokine mRNA translation following TLR4 responses in human THP-1 monocytes. Immunol. Cell Biol. 91, 532–540. 10.1038/icb.2013.37 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunet J.-P., Tamayo P., Golub T. R., Mesirov J. P. (2004). Metagenes and molecular pattern discovery using matrix factorization. Proc. Natl. Acad. Sci. U.S.A. 101, 4164–4169. 10.1073/pnas.0308531101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butovsky O., Jedrychowski M. P., Moore C. S., Cialic R., Lanser A. J., Gabriely G., et al. (2014). Identification of a unique TGF-β-dependent molecular and functional signature in microglia. Nat. Neurosci. 17, 131–143. 10.1038/nn.3599 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chakrabarty P., Li A., Ceballos-Diaz C., Eddy James A., Funk Cory C., Moore B., et al. (2015). IL-10 Alters immunoproteostasis in APP mice, increasing plaque burden and worsening cognitive behavior. Neuron 85, 519–533. 10.1016/j.neuron.2014.11.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cieślik M., Bekiranov S. (2014). Combinatorial epigenetic patterns as quantitative predictors of chromatin biology. BMC Genomics 15:76. 10.1186/1471-2164-15-76 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Codarri L., Fontana A., Becher B. (2010). Cytokine networks in multiple sclerosis, lost in translation. Curr. Opin. Neurol. 23, 205–211. 10.1097/WCO.0b013e3283391feb [DOI] [PubMed] [Google Scholar]
- Crotti A., Ransohoff R. M. (2016). Microglial physiology and pathophysiology: insights from genome-wide transcriptional profiling. Immunity 44, 505–515. 10.1016/j.immuni.2016.02.013 [DOI] [PubMed] [Google Scholar]
- Dabney A., Storey J. D., Warnes G. (2010). qvalue: Q-Value Estimation for False Discovery Rate Control. R package version 1.
- Davalos D., Grutzendler J., Yang G., Kim J., Zuo Y., Jung S., et al. (2005). ATP mediates rapid microglial response to local brain injury in vivo. Nat. Neurosci. 6, 752–758. 10.1038/nn1472 [DOI] [PubMed] [Google Scholar]
- David S., Greenhalgh A. D., Kroner A. (2015). Macrophage and microglial plasticity in the injured spinal cord. Neuroscience 307, 311–318. 10.1016/j.neuroscience.2015.08.064 [DOI] [PubMed] [Google Scholar]
- Diniz D. G., Silva G. O., Naves T. B., Fernandes T. N., Araújo S. C., Diniz J. A. P., et al. (2016). Hierarchical cluster analysis of three-dimensional reconstructions of unbiased sampled microglia shows not continuous morphological changes from stage 1 to 2 after multiple dengue infections in callithrix penicillata. Front. Neuroanat. 10:23 10.3389/fnana.2016.00023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DiSabato D. J., Quan N., Godbout J. P. (2016). Neuroinflammation: the devil is in the details. J. Neurochem. 139, 136–153. 10.1111/jnc.13607 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erny D., Hrabe de Angelis A. L., Jaitin D., Wieghofer P., Staszewski O., David E., et al. (2015). Host microbiota constantly control maturation and function of microglia in the CNS. Nat. Neurosci. 18, 965–977. 10.1038/nn.4030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fenn A. M., Henry C. J., Huang Y., Dugan A., Godbout J. P. (2012). Lipopolysaccharide-induced interleukin (IL)-4 receptor-α expression and corresponding sensitivity to the M2 promoting effects of IL-4 are impaired in microglia of aged mice. Brain Behav. Immun. 26, 766–777. 10.1016/j.bbi.2011.10.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frick L. R., Williams K., Pittenger C. (2013). Microglial dysregulation in psychiatric disease. Clin. Dev. Immunol. 2013, 10. 10.1155/2013/608654 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gadani S. P., Walsh J. T., Lukens J. R., Kipnis J. (2015). Dealing with danger in the CNS: the response of the immune system to injury. Neuron 87, 47–62. 10.1016/j.neuron.2015.05.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao Y., Church G. (2005). Improving molecular cancer class discovery through sparse non-negative matrix factorization. Bioinformatics 21, 3970–3975. 10.1093/bioinformatics/bti653 [DOI] [PubMed] [Google Scholar]
- Gaujoux R., Seoighe C. (2010). A flexible R package for nonnegative matrix factorization. BMC Bioinformatics 11:367. 10.1186/1471-2105-11-367 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grabert K., Michoel T., Karavolos M. H., Clohisey S., Baillie J. K., Stevens M. P., et al. (2016). Microglial brain region-dependent diversity and selective regional sensitivities to aging. Nat. Neurosci. 19, 504–516. 10.1038/nn.4222 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenhalgh A. D., David S. (2014). Differences in the phagocytic response of microglia and peripheral macrophages after spinal cord injury and its effects on cell death. J. Neurosci. 34, 6316–6322. 10.1523/JNEUROSCI.4912-13.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenhalgh A. D., Passos dos Santos R., Zarruk J. G., Salmon C. K., Kroner A., David S. (2016). Arginase-1 is expressed exclusively by infiltrating myeloid cells in CNS injury and disease. Brain Behav. Immun. 56, 61–67. 10.1016/j.bbi.2016.04.013 [DOI] [PubMed] [Google Scholar]
- Guillot-Sestier M.-V., Doty Kevin R., Gate D., Rodriguez J., Jr., Leung Brian P., Rezai-Zadeh K., et al. (2015). Il10 Deficiency rebalances innate immunity to mitigate alzheimer-like pathology. Neuron 85, 534–548. 10.1016/j.neuron.2014.12.068 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Healy L. M., Perron G., Won S.-Y., Rao V. T. S., Guiot M.-C., Moore C., et al. (in press). Differential transcriptional response profiles in human myeloid cell populations. Clin. Immunol. 10.1016/j.clim.2016.04.006 [DOI] [PubMed] [Google Scholar]
- Henry C. J., Huang Y., Wynne A. M., Godbout J. P. (2009). Peripheral Lipopolysaccharide (LPS) challenge promotes microglial hyperactivity in aged mice that is associated with exaggerated induction of both pro-inflammatory IL-1β and anti-inflammatory IL-10 cytokines. Brain Behav. Immun. 23, 309–317. 10.1016/j.bbi.2008.09.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hines D. J., Hines R. M., Mulligan S. J., Macvicar B. A. (2009). Microglia processes block the spread of damage in the brain and require functional chloride channels. Glia 57, 1610–1618. 10.1002/glia.20874 [DOI] [PubMed] [Google Scholar]
- Hong S., Beja-Glasser V. F., Nfonoyim B. M., Frouin A., Li S., Ramakrishnan S., et al. (2016). Complement and microglia mediate early synapse loss in Alzheimer mouse models. Science 352, 712–716. 10.1126/science.aad8373 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Z., Chu Y., Hahn J. (2010). Model simplification procedure for signal transduction pathway models: an application to IL-6 signaling. Chem. Eng. Sci. 65, 1964–1975. 10.1016/j.ces.2009.11.035 [DOI] [Google Scholar]
- Ishii H., Tanabe S., Ueno M., Kubo T., Kayama H., Serada S., et al. (2013). ifn-γ-dependent secretion of IL-10 from Th1 cells and microglia/macrophages contributes to functional recovery after spinal cord injury. Cell Death Dis. 4:e710. 10.1038/cddis.2013.234 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kampstra P. (2008). Beanplot: a boxplot alternative for visual comparison of distributions. J. Stat. Softw. 28, 1–9. 10.18637/jss.v028.c0127774042 [DOI] [Google Scholar]
- Karperien A., Ahammer H., Jelinek H. F. (2013). Quantitating the subtleties of microglial morphology with fractal analysis. Front. Cell. Neurosci. 7:3. 10.3389/fncel.2013.00003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keren-Shaul H., Spinrad A., Weiner A., Matcovitch-Natan O., Dvir-Szternfeld R., Ulland T. K., et al. (2017). A unique microglia type associated with restricting development of Alzheimer's disease. Cell 169, 1276–1290. 10.1016/j.cell.2017.05.018 [DOI] [PubMed] [Google Scholar]
- Kettenmann H., Kirchhoff F., Verkhratsky A. (2013). Microglia: new roles for the synaptic stripper. Neuron 77, 10–18. 10.1016/j.neuron.2012.12.023 [DOI] [PubMed] [Google Scholar]
- Kilkenny C., Browne W. J., Cuthill I. C., Emerson M., Altman D. G. (2010). Improving bioscience research reporting: the ARRIVE guidelines for reporting animal research. PLoS Biol. 8:e1000412. 10.1371/journal.pbio.1000412 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kongsui R., Beynon S. B., Johnson S. J., Walker F. R. (2014). Quantitative assessment of microglial morphology and density reveals remarkable consistency in the distribution and morphology of cells within the healthy prefrontal cortex of the rat. J. Neuroinflammation 11:182 10.1186/s12974-014-0182-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozlowski C., Weimer R. M. (2012). An automated method to quantify microglia morphology and application to monitor activation state longitudinally in vivo. PLoS ONE 7:e31814. 10.1371/journal.pone.0031814 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kroner A., Greenhalgh Andrew D., Zarruk Juan G., Passos dos Santos R., Gaestel M., David S. (2014). TNF and increased intracellular iron alter macrophage polarization to a detrimental M1 phenotype in the injured spinal cord. Neuron 83, 1098–1116. 10.1016/j.neuron.2014.07.027 [DOI] [PubMed] [Google Scholar]
- Lee D. D., Seung H. S. (1999). Learning the parts of objects by non-negative matrix factorization. Nature 401, 788–791. 10.1038/44565 [DOI] [PubMed] [Google Scholar]
- Lee D. D., Seung H. S. (2001). Algorithms for non-negative matrix factorization, in Advances in Neural Information Processing Systems (Cambridge: The MIT Press; ), 556–562. [Google Scholar]
- Lewitus Gil M., Konefal Sarah C., Greenhalgh Andrew D., Pribiag H., Augereau K., Stellwagen D. (2016). Microglial TNF-α suppresses cocaine-induced plasticity and behavioral sensitization. Neuron 90, 483–491. 10.1016/j.neuron.2016.03.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu T., Wang Q.-G., Huang H.-P. (2013). A tutorial review on process identification from step or relay feedback test. J. Process Control 23, 1597–1623. 10.1016/j.jprocont.2013.08.00321777915 [DOI] [Google Scholar]
- Madore C., Joffre C., Delpech J. C., De Smedt-Peyrusse V., Aubert A., Coste L., et al. (2013). Early morphofunctional plasticity of microglia in response to acute lipopolysaccharide. Brain Behav. Immun. 34, 151–158. 10.1016/j.bbi.2013.08.008 [DOI] [PubMed] [Google Scholar]
- Madsen P. M., Motti D., Karmally S., Szymkowski D. E., Lambertsen K. L., Bethea J. R., et al. (2016). Oligodendroglial TNFR2 mediates membrane TNF-dependent repair in experimental autoimmune encephalomyelitis by promoting oligodendrocyte differentiation and remyelination. J. Neurosci. 36, 5128–5143. 10.1523/JNEUROSCI.0211-16.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchini J. L., Heaton C., Ripley B. D. (2013). Fastica: Fastica Algorithms to Perform ICA and Projection Pursuit, R Package Version 1. Oxford: Oxford University Press; Available online at: http://cran.r-project.org/web/packages/fastICA/index.html [Google Scholar]
- Mawhinney L. A., Thawer S. G., Lu W.-Y., Rooijen N. V., Weaver L. C., Brown A., et al. (2012). Differential detection and distribution of microglial and hematogenous macrophage populations in the injured spinal cord of lys-EGFP-ki transgenic mice. J. Neuropathol. Exp. Neurol. 71, 180–197. 10.1097/NEN.0b013e3182479b41 [DOI] [PubMed] [Google Scholar]
- Montefusco F., Akman O. E., Soyer O. S., Bates D. G. (2016). Ultrasensitive negative feedback control: a natural approach for the design of synthetic controllers. PLoS ONE 11:e0161605. 10.1371/journal.pone.0161605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montgomery S. L., Narrow W. C., Mastrangelo M. A., Olschowka J. A., O'Banion M. K., Bowers W. J. (2013). Chronic neuron- and age-selective down-regulation of TNF receptor expression in triple-transgenic alzheimer disease mice leads to significant modulation of amyloid- and tau-related pathologies. Am. J. Pathol. 182, 2285–2297. 10.1016/j.ajpath.2013.02.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrison H., Filosa J. (2013). A quantitative spatiotemporal analysis of microglia morphology during ischemic stroke and reperfusion. J. Neuroinflammation 10:4 10.1186/1742-2094-10-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norden D. M., Fenn A. M., Dugan A., Godbout J. P. (2014). TGFβ produced by IL-10 redirected astrocytes attenuates microglial activation. Glia 62, 881–895. 10.1002/glia.22647 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogunnaike B. A. (2011). Random Phenomena: Fundamentals of Probability and Statistics for Engineers. Boca Raton, FL: CRC Press. [Google Scholar]
- Ogunnaike B. A., Ray W. H. (1994). Process Dynamics, Modeling, and Control. New York, NY: Oxford University Press. [Google Scholar]
- Park J., Brureau A., Kernan K., Starks A., Gulati S., Ogunnaike B., et al. (2014). Inputs drive cell phenotype variability. Genome Res. 24, 930–941. 10.1101/gr.161802.113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- R-Core-Team (2016) R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Schafer D. P., Lehrman E. K., Kautzman A. G., Koyama R., Mardinly A. R., Yamasaki R., et al. (2012). Microglia sculpt postnatal neural circuits in an activity and complement-dependent manner. Neuron 74, 691–705. 10.1016/j.neuron.2012.03.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schafer D. P., Stevens B. (2015). Microglia function in central nervous system development and plasticity. Cold Spring Harb. Perspect. Biol. 7:a020545. 10.1101/cshperspect.a020545 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmittgen T. D., Livak K. J. (2008). Analyzing real-time PCR data by the comparative C(T) method. Nat. Protoc. 3, 1101–1108. 10.1038/nprot.2008.73 [DOI] [PubMed] [Google Scholar]
- Sheng W. S., Hu S., Kravitz F. H., Peterson P. K., Chao C. C. (1995). Tumor necrosis factor alpha upregulates human microglial cell production of interleukin-10 in vitro. Clin. Diagn. Lab. Immunol. 2, 604–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sierra A., Abiega O., Shahraz A., Neumann H. (2013). Janus-faced microglia: beneficial and detrimental consequences of microglial phagocytosis. Front. Cell. Neurosci. 7:6. 10.3389/fncel.2013.00006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sipe G. O., Lowery R. L., Tremblay M. È., Kelly E. A., Lamantia C. E., Majewska A. K. (2016). Microglial P2Y12 is necessary for synaptic plasticity in mouse visual cortex. Nat. Commun. 7:10905. 10.1038/ncomms10905 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siqueira Mietto B., Kroner A., Girolami E. I., Santos-Nogueira E., Zhang J., David S. (2015). Role of IL-10 in resolution of inflammation and functional recovery after peripheral nerve injury. J. Neurosci. 35, 16431–16442. 10.1523/JNEUROSCI.2119-15.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Šišková Z., Tremblay M-. È. (2013). Microglia and synapse: interactions in health and neurodegeneration. Neural Plast. 2013:425845 10.1155/2013/425845 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storey J. D., Dai J. Y., Leek J. T. (2007). The optimal discovery procedure for large-scale significance testing, with applications to comparative microarray experiments. Biostatistics 8, 414–432. 10.1093/biostatistics/kxl019 [DOI] [PubMed] [Google Scholar]
- Storey J. D., Xiao W., Leek J. T., Tompkins R. G., Davis R. W. (2005). Significance analysis of time course microarray experiments. Proc. Natl. Acad. Sci. U.S.A. 102, 12837–12842. 10.1073/pnas.0504609102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storey J., Leek J., Bass A. (2015). edge: Extraction of Differential Gene Expression. R package version 2.6.0. 16357033
- Streit W. J., Walter S. A., Pennell N. A. (1999). Reactive microgliosis. Prog. Neurobiol. 57, 563–581. 10.1016/S0301-0082(98)00069-0 [DOI] [PubMed] [Google Scholar]
- Streit W. J., Xue Q.-S., Tischer J., Bechmann I. (2014). Microglial pathology. Acta Neuropathol. Commun. 2:142. 10.1186/s40478-014-0142-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Transtrum M. K., Qiu P. (2014). Model reduction by manifold boundaries. Phys. Rev. Lett. 113:098701 10.1103/PhysRevLett.113.098701 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tremblay M.-È., Lowery R. L., Majewska A. K. (2010). Microglial interactions with synapses are modulated by visual experience. PLoS Biol. 8:e1000527. 10.1371/journal.pbio.1000527 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vasek M. J., Garber C., Dorsey D., Durrant D. M., Bollman B. P., Soung A., et al. (2016). A complement–microglial axis drives synapse loss during virus-induced memory impairment. Nature 534, 538–543. 10.1038/nature18283 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker F. R., Beynon S. B., Jones K. A., Zhao Z., Kongsui R., Cairns M., et al. (2014). Dynamic structural remodelling of microglia in health and disease: a review of the models, the signals and the mechanisms. Brain Behav. Immun. 37, 1–14. 10.1016/j.bbi.2013.12.010 [DOI] [PubMed] [Google Scholar]
- Witcher K. G., Eiferman D. S., Godbout J. P. (2015). Priming the inflammatory pump of the CNS after traumatic brain injury. Trends Neurosci. 38, 609–620. 10.1016/j.tins.2015.08.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamada J., Jinno S. (2013). Novel objective classification of reactive microglia following hypoglossal axotomy using hierarchical cluster analysis. J. Comp. Neurol. 521, 1184–1201. 10.1002/cne.23228 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
TNFα expression increases to the same extent in both brain and spinal cord tissue after systemic LPS (0.33 mg/kg i.p) at 24 h (n = 3–4 mice per group).