Poisson Statistics of Combinatorial Library Sampling Predict False Discovery Rates of Screening

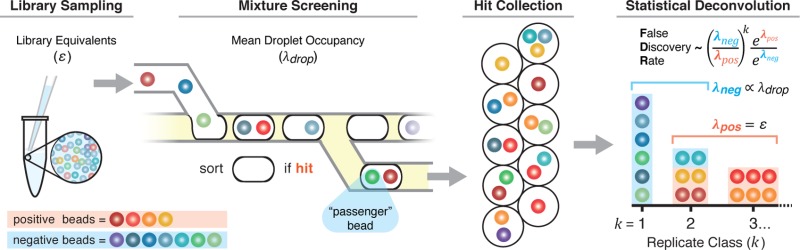
Abstract

Microfluidic droplet-based screening of DNA-encoded one-bead-one-compound combinatorial libraries is a miniaturized, potentially widely distributable approach to small molecule discovery. In these screens, a microfluidic circuit distributes library beads into droplets of activity assay reagent, photochemically cleaves the compound from the bead, then incubates and sorts the droplets based on assay result for subsequent DNA sequencing-based hit compound structure elucidation. Pilot experimental studies revealed that Poisson statistics describe nearly all aspects of such screens, prompting the development of simulations to understand system behavior. Monte Carlo screening simulation data showed that increasing mean library sampling (ε), mean droplet occupancy, or library hit rate all increase the false discovery rate (FDR). Compounds identified as hits on k > 1 beads (the replicate k class) were much more likely to be authentic hits than singletons (k = 1), in agreement with previous findings. Here, we explain this observation by deriving an equation for authenticity, which reduces to the product of a library sampling bias term (exponential in k) and a sampling saturation term (exponential in ε) setting a threshold that the k-dependent bias must overcome. The equation thus quantitatively describes why each hit structure’s FDR is based on its k class, and further predicts the feasibility of intentionally populating droplets with multiple library beads, assaying the micromixtures for function, and identifying the active members by statistical deconvolution.

Introduction

Combinatorial chemistry is fundamentally a massive, statistical undertaking. The binomial distribution and its limiting form in the Poisson discrete probability distribution function variously describe the number of each compound type that a split-and-pool library synthesis yields, the scale required to guarantee the synthesis of all possible compounds,¹⁻³ and even the number of library members to analyze during quality control.⁴ Library screening is also a numbers game; it is a process designed to generate a systematically biased subsample of the library whose members meet defined experimental criteria. As statistical processes, sampling and confidence are linked: larger sample sizes more accurately reflect the population and give the experimentalist greater confidence in hypothesis testing. For combinatorial library screening, each “sample” requires the elucidation of one screening hit’s molecular structure, thus structure elucidation throughput directly impacts the statistical confidence of library screening outcomes.

In this regard, the “structure elucidation problem” of combinatorial library synthesis and screening was a bit of a red herring. It spurred the development of numerous, ingenious strategies for gleaning the structures of combinatorial library screening hits (e.g., positional scanning, recursive deconvolution, single-bead analysis, encoding),⁵⁻¹² while the root problem, throughput, remained concealed. The low-throughput of structure elucidation constituted a prohibitive barrier to the rigorous determination of which screening hits reject the null hypothesis (i.e., statistically significantly deviate from a random subsample of the library), a principle that now dominates high-throughput screening (HTS) assay development (Z′-factor).^13,14 Until recently it has not been tractable to acquire the number of hit structures (let alone bona fide negative structures) required to perform the same analysis for combinatorial library screens.

DNA-encoded library (DEL) technology has been a game changer for combinatorial library synthesis and screening, largely by solving the structure elucidation throughput problem. DELs contain millions to billions of members, each comprising a DNA molecule whose sequence encodes an associated small molecule.^7,15−17 Using DNA, it is possible to prepare large and structurally complex compound collections, encoding myriad structures and thereby accessing diverse chemical space.¹⁸⁻²⁰ Importantly, DEL screening output can be analyzed by highly parallel next-generation DNA sequencing (NGS),^17,21 revealing hit homology²²⁻²⁴ and guiding selection of structural families for lower throughput synthesis and validation. Adaptation of DEL to solid-phase libraries²⁵ provides additional certainty to hit prioritization via reproducibility. Hit compounds observed on multiple beads as “replicates” have long been known to exhibit higher rates of authenticity,^4,26,27 prompting the development of bead-specific barcoding to enumerate replicate hits directly by NGS.^28,29 These studies showed that the hit collection contains higher sampling rate of authentic, active compounds compared to inactive compounds (false positives), suggesting the existence of a quantitative method for evaluating hit authenticity. Here we provide the theoretical framework for such an argument, demonstrate the theory’s agreement with experimental findings, and discuss ramifications for activity-based screening of DNA-encoded one-bead-one-compound combinatorial libraries.

Results and Discussion

An aliquot of a combinatorial bead library, S, is a random sample of the library’s diversity, L, the set of distinct library compounds, or elements. A convenient measurement of an aliquot’s size is the library equivalent, ε:³⁰

1

where |S| is the number of elements in S and |L| is the number of unique library elements. Assuming that library synthesis scale is sufficiently large such that sampling does not influence library content,^1,2 the general form of the Poisson distribution describes the probability, P, of observing a given member of L:

2

where λ is the mean library sampling and integer k is the number of copies of a given bead library member, or replicate class (Figure 1A). For example, in an ε = 2 library aliquot (λ = 2), the fraction of L observed k = 1 time in S is 27% according to the model. Likewise, the fractions of L observed in S at k = 2, 3, 4, and 5 times are approximately 27%, 18%, 9%, and 4%, respectively. The expected fraction of Lnot observed in S, k = 0, is 13.5%. The fractional representation of L in S, f, is given by a modified form of the Poisson cumulative distribution function:

3

Plotting Equation 3 as a function of ε and k visualizes the fraction of elements in L observed at least k times in S, or library coverage (Figure 1B). Using the ε = 2 library aliquot as an example, 86.5% of L is present k ≥ 1 time, 59.4% of L is present k ≥ 2 times, and 32.3% of L is present k ≥ 3 times.

Figure 1.

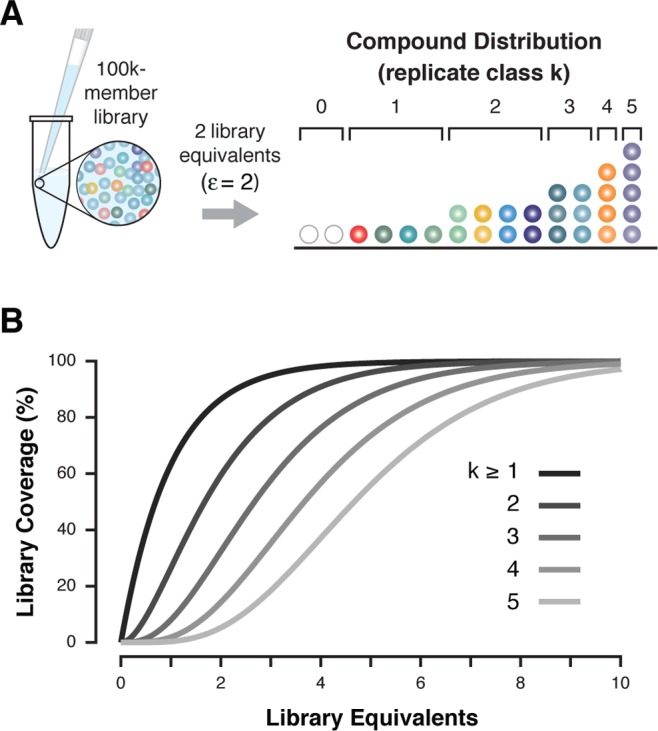
Combinatorial library sampling schematic and statistics. (A) An example of a random 200k-bead aliquot of a theoretical 100k-member bead library stock is used to illustrate the predicted compound distribution. The Poisson distribution describes the probability of observing any given library member with replicate class, k. Some compounds are not present in the aliquot, having a replicate class k = 0. (B) Library coverage, the fraction of the library observed ≥ k times, is plotted as a function of library equivalents sampled (ε).

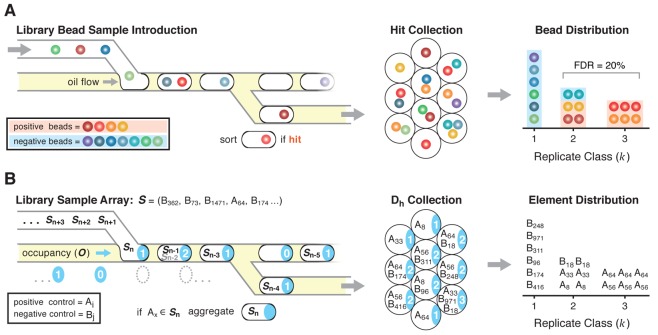
Screening a library aliquot, S, is accomplished by examining each element of S and systematically segregating those members that satisfy a defined activity assay threshold. Common screening strategies include directly examining target binding to the library member or by arraying members in microtiter plate wells and assaying target activity in solution.^5,15,31−33 Our group has miniaturized and automated these processes with the development of DNA-encoded one-bead-one-compound library synthesis²⁵ and microfluidic screening circuitry that loads individual beads into activity assay droplets, then sorts “hit” droplets containing functional library members into a hit collection (Figure 2A).²⁹ Library bead loading into droplets is also a Poisson process; droplets contain 0, 1, 2, or more beads as a function of the mean droplet occupancy, λ_drop.³⁴ Droplets in the hit collection each contain at least one bead that is active in the assay (positive beads); some droplets also contain one or more inactive “passenger” beads (negative beads) according to the Poisson distribution. It is possible to simulate this process using Monte Carlo methods to understand system performance. We define the library, L, as the union of two enumerated sets:

4

5

6

where A is the set of i positive elements and B is the set of j negative elements. The library hit rate, r

7

is an independent variable used to define the population of A and B. The library sample aliquot, S, is filled by selecting random elements from L, with replacement. An occupancy vector, O, is filled with k values selected according to the Poisson occurrence probabilities of eq 3 with λ = λ_drop. For example, for λ_drop = 1 bead/droplet, we expect the probability of observing k_drop beads within a droplet to be P(k_drop = 0) = 36.7%, P(k_drop = 1) = 36.7%, P(k_drop = 2) = 13.5%. A droplet set, D, is populated using O to specify the sampling of S without replacement to simulate the stochastic loading of beads into droplets. For example if the first value of O is 1, then the first entry of D is filled with one element from S; if the next value of O is 3, the following entry of D is filled with three elements from S. Once S is empty, entries of D containing at least one A element are used to populate a hit collection subset, D_h. The elements within D_h are then aggregated by replicate class k (Figure 2B).

Figure 2.

Experimental and theoretical bead library sampling schematic. (A) Library beads in a microfluidic channel are introduced in an aqueous stream and stochastically encapsulated in water-in-oil droplets. Compounds are photochemically cleaved from the bead into the assay droplet, then droplets are incubated, interrogated, and sorted to the hit collection output based on assay threshold. Each droplet in the hit collection contains at least one positive bead (orange-red hues), and any coencapsulated negative passenger beads (blue-green hues). The hit bead collection can be displayed as a distribution where positive beads are expected to be observed in higher replicate k classes. (B) Monte Carlo simulations of stochastic compound bead library sampling and encapsulation generated a library sample vector, S, filled with elements from positive set A = (A₁, A₂, A₃, ..., A_i) and negative set B = (B₁, B₂, B₃, ..., B_j), an occupancy vector of integers (cyan indices) calculated using the Poisson distribution, and a simulated “droplet” set loaded from S with the number of elements specified by the occupancy vector. The set of “droplets” containing positive elements (A_i) is aggregated, yielding the D_h collection. The elements of D_h are distributed into k classes.

The Monte Carlo simulation results were in close agreement with experimental observations. In a previous study,²⁹ we screened an 18 009-member model DNA-encoded library at ε = 1.89. The library contained 729 distinctly encoded positive library members (authentic hits), and 17 280 distinctly encoded negative library members (r = 4.05%). After screening, the encoding DNA was amplified, sequenced, and decoded. The hit collection contained 1377 positive beads and 486 negative beads. If all positive beads were sorted, the count of positive beads in the hit collection defines library sampling (ε = 1377/729 = 1.89). The experimentally observed hit droplet occupancy was best approximated with λ_drop = 0.37. Simulations were performed (100 iterations) using these values (|L| = 18,009, r = 0.0405, ε = 1.89, λ_drop = 0.37). Observed hit droplet occupancy agreed well with simulated droplet occupancy (Figure 3A), differing slightly from the model in that λ_drop varies with bead sedimentation, which drives bead introduction. This results in a larger singly occupied droplet population during the later stages of the experiment when mean droplet occupancy is low. The hit collection bead distribution among replicate classes again agreed closely with the simulation (Figure 3B). Experimental counts were compared to the distribution of element counts produced from simulations (N = 100) within their respective k class bins. Outlier analysis returned all experimental counts (A, k = 0–6; B, k = 0–3) falling within the inner fence of simulations, indicating that our experimental results could be expected to be contained within the simulation set. The simulation results also recapitulate experimental findings that compound library members residing in higher k classes are more likely to be authentic, which is measured by the false discovery rate (FDR), or fraction of known negative elements in the hit collection. While crudely dividing the library into positives and negatives (A and B) would seem on the surface an overly simplified model of a true library, which is expected to contain compounds with a spectrum of activities, the binary nature of droplet sorting digitizes library members into “hit” or “not-hit” collections only by virtue of activity assay measurement and comparison to a threshold for decision. Modest hits from library screens with activity near the threshold may not be reproducibly detected as a hit and sorted, reducing their k into a k-class that may not be deemed worthwhile for secondary validation.

Figure 3.

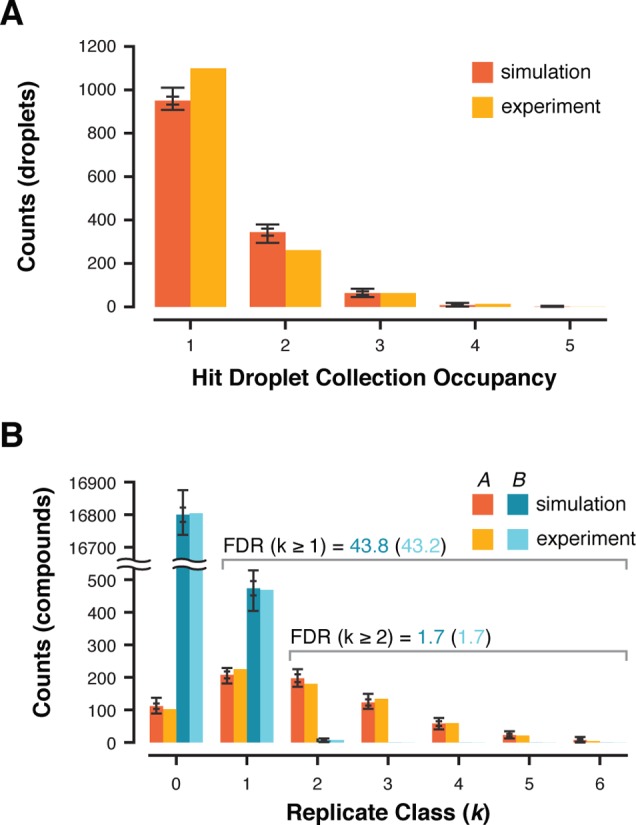
Comparison of simulation results and experimental data. Experimentally derived parameters were used for 100 simulations. (A) Hit collection droplet occupancy for the experiment is plotted and compared to simulation average (λ_drop = 0.37). (B) Positive A compounds and negative B compounds identified in the hit collection were distributed into replicate k classes and compared to the simulation distribution of A and B elements. The cumulative false discovery rate (FDR) for all hit collection elements in k ≥ 1 class and k ≥ 2 class as observed experimentally and by simulation are displayed above the chart. Standard deviation and value range are displayed as nested error bars for all simulation data.

It is gratifying to observe the hit collection bead k class distribution recapitulating Poisson statistics, however the k classes themselves are intrinsically significant for their ability to predict a hit collection bead’s authenticity. Early combinatorial library screening experiments demonstrated that isolated hit beads in higher k classes (more replicates) tended to validate during followup assays more reliably, however this was only appreciated as a qualitative property relating to reproducibility.^26,27 These analyses were the result of elucidating the structures contained in small hit pools (∼20–100 hits) by low-throughput methods. DNA-encoded library screens have enabled the use of high-throughput structure elucidation via NGS, revealing the contents and k class distributions of very large hit collections (>1000 beads). By screening a model library containing only known positive and negative beads, it was possible to determine the FDR, which indeed decreased for higher k classes. Ensuring that FDR remains as low as possible is critical because hit validation (synthesis, purification, secondary assay) is more time-consuming and expensive than screening. Investigating false positive hits rapidly negates the efficiency of combinatorial library synthesis and screening, thus quantitative prediction of FDR as a function of experimental parameters is of central importance.

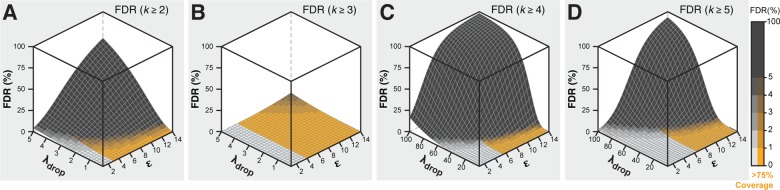
With the validated simulation strategy in hand, we investigated the influence of experimental parameters ε, r, and λ_drop on hit collection composition. |L| and r were held constant at 100 000 members and 1.5%, respectively. Monte Carlo simulations were conducted for several ε (1–10) and droplet occupancies (λ_drop = 0.3–3). The results of 100 simulations were averaged for each condition. The FDR

8

was calculated for each cumulative k class (k ≥ 1, k ≥ 2,... k ≥ 4) as the percent of negative elements observed at least k times in D_h. The observed positive coverage:

9

is calculated for each cumulative k class as the percent of all possible positive elements that were observed in D_h. Simulations for each ε were averaged and the positive coverage assigned based on the lowest cumulative k class with FDR ≤ 5% (an arbitrary, empirically acceptable level of error). Cumulative k class FDR (teal hues) and the positive coverage at FDR ≤ 5% (bold trace) were plotted as a function of ε and λ_drop (Figure 4andSupporting Information). For example, simulation results at λ_drop = 0.30 and ε = 2 predict 86.5% positive coverage at k ≥ 1, similar to the experimental observation (86%, 627 of 729, Figure 3B). The simulations also predict 40.5% FDR for k ≥ 1 class, in agreement with experimental data (43.2%). The FDR drops to 0.46% for k ≥ 2 class with concomitant decrease in positive coverage to 59.3%. A second screen could be executed, increasing ε to 4, and thereby increasing the k ≥ 2 class positive coverage to >90% while maintaining low FDR (∼1%). Increasing λ_drop in two 3-fold steps results in much higher FDR for a given cumulative k class, but it is still quite feasible to achieve acceptable FDR and positive coverage by examining higher k classes. For example, a screen at ε = 2 and λ_drop = 0.3 gives an expected positive coverage of 59.3% and an FDR of 0.5% when examining the k ≥ 2 classes. To improve positive coverage, one could triple screening throughput by conducting the experiment at λ_drop = 1 and ε = 6 over the same duration, which would result in 94% positive coverage and FDR = 0.7% in k ≥ 3 classes.

Figure 4.

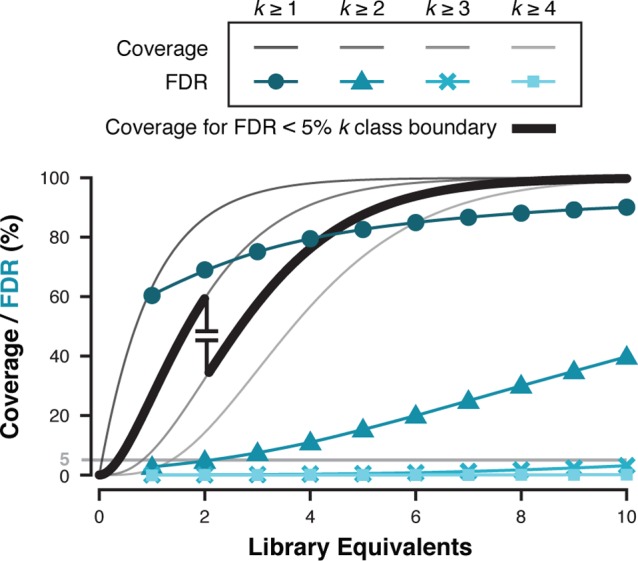
Library coverage as a function of FDR and library equivalents (ε) screened. Screening simulations were run for a 100k-member library with a 1.5% hit rate. Screening aliquot sizes ranged from 1−10 library equivalents (100 simulations). Library coverage curves for each cumulative replicate class (k ≥ 1–5, gray) are based on a Poisson cumulative distribution function. FDR (%) was plotted as a function of ε for each cumulative replicate class (k ≥ 1–4, teal). Coverage (bold trace) constrained by FDR (<5%, gray horizontal) is calculated for each simulation iteration and the average is plotted (standard deviation markers are smaller than the data points). Simulation results are shown for average droplet occupancy λ_drop = 1.

The FDR and positive coverage simulation data illustrate the quantitative dependence of FDR on k class. Assuming the system identifies and sorts all droplets containing at least one positive bead, positive coverage exactly tracks with library coverage because ε defines the hit element k class distribution just as it defines the broader k class distribution of S. Screening larger S samples a larger swath of the positives, however, this increases the FDR of each cumulative k class because the number of elements entering the hit collection scales linearly with ε. Redundantly sampling any given negative element then becomes more probable, populating higher k classes with negatives and thereby increasing that class’s FDR. Intuition suggests that higher k classes will more strongly resist such contamination because they increasingly diminish the odds that randomly sampled negatives exist as replicates. Under the constraint of FDR ≤ 5%, as one screens larger library aliquots and the negatives begin to populate the lower cumulative k classes unacceptably, one is forced to migrate up to the next lowest cumulative k-class to remain below 5% FDR but sacrifice positive coverage.

The FDR and positive coverage simulation data also predict unanticipated robustness to higher droplet occupancy. We had previously conducted experiments at λ_drop < 1 to minimize frequency of encapsulating multiple library beads in single droplets, which we hypothesized would be the largest source of negative beads in the hit collection. While this hypothesis experimentally bears out, the simulation results show that increasing λ_drop does not compromise a screen’s ability to identify authentic hits. Simulations at λ_drop > 1 clearly indicated that the k class analysis can effectively discriminate the larger number of negatives collected due to higher frequency of multibead droplets. In fact, from an experimental design perspective, screening such “micro-mixtures” is attractive because it is a straightforward means of increasing screening throughput, and would only be limited by parameters that affect the number of beads collected. One such parameter is clearly ε; higher ε inherently results in the collection of more negative beads, and the simulation data reflect this trend. Another yet unstudied parameter that would profoundly affect the number of sort events (and therefore number of beads collected) is r itself.

We next explored whether r appreciably influenced the k class-dependent FDR. Simulations (100 iterations for each variable set) across three values of r (0.5%, 1.5%, 4.5%) examined FDR as a function of ε within the different cumulative k classes (k ≥ 1, k ≥ 2, ..., k ≥ 4). Library size (|L| = 100 000) and mean droplet occupancy (λ_drop = 1) were held constant. FDR was calculated for each r and cumulative k class and plotted as a function of ε (Figure 5). FDR increases with library sampling within a given cumulative k class as before, and does so regardless of r. Screens of lower r libraries result in markedly lower FDR. For example, in the same configuration of screen (ε = 6) but r = 4.5% (purple trace), FDR = 5.4% for k ≥ 3 class. At r = 0.5% (yellow trace), FDR = 0.1% for the same k class.

Figure 5.

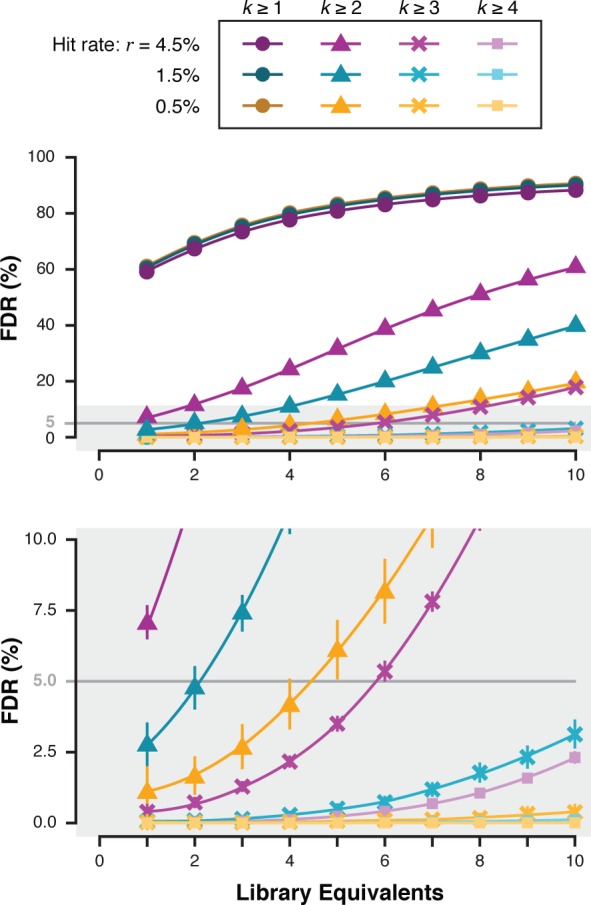
FDR as a function of library equivalents (ε) screened. Screening simulations (100 iterations) were run for three 100k-member libraries with λ_drop = 1, and hit rates set at 0.5% (yellow), 1.5% (teal), or 4.5% (purple). FDR = 5% is shown as a gray line. Error bars display standard deviation, which are smaller than the point size in the top plot. The low FDR portion of the graph (gray highlighting) was magnified and replotted (bottom).

Library screens with higher r result in higher FDRs, demanding examination of higher cumulative k class hits to maintain an acceptable FDR for validation studies. This makes intuitive sense because a screen containing fewer positive library members results in fewer total sorted droplets and thereby fewer passenger bead negative elements. In consideration of the potential for this system to screen mixtures of compounds in droplets (discussed above), it is important to note that both λ_drop and r negatively and differentially impact FDR, thus an expression that integrates the effects of all parameters is necessary in proposing the feasibility of such a combinatorial screening experiment.

Given that the Poisson distribution governs library sampling and droplet encapsulation, we can derive an integrated statistical expression describing the impact of all combinatorial library screening experimental parameters. The Poisson distribution (P) of elements in the hit collection (H), is defined by the mean number of times a given element is observed (λ). The hit collection contains a population of positive elements (H_pos) and negative elements (H_neg), defining the mean sampling of each respective population, λ_pos, and λ_neg

10

11

Assuming reasonably low hit rates, the library size approximates the number of negative elements. A perfect system identifies and sorts all positive elements within S

12

such that λ_pos simplifies to library sampling, ε. In this limit, replicate k class distribution of positive elements is identical to that of the library sample distribution. If negative element collection only occurs due to passenger bead collection, then a Poisson distribution relating to droplet occupancy and the total number of droplets sorted defines H_neg. First, we assume that every droplet in D_h contains only one positive element

13

This is a reasonable assumption given that simulations (|L| = 100 000, r = 1.5%, ε = 1, and λ_drop = 1) produced an average of 11 droplets containing ≥2 positive elements, out of 1489 total hit droplets, or just 0.7% of the hit droplet population using a relatively high r and λ_drop. Equation 2 defines the droplet occupancy probability distribution

14

where k_drop is the number of elements in a droplet or the droplet occupancy class. The total number of elements contained within the hit droplet collection is H_tot

15

We define the number of negative elements inside a droplet, k_neg

16

recalling the previous assumption that k_pos = 1. Substituting k_neg for k_drop and then expanding with eqs 13 and 16 gives the full expression for H_neg

17

Substituting H_neg into eq 11 gives us an expression for the mean sampling of the negative elements, λ_neg

18

With mean sampling of the positive and negative elements in hand, the Poisson distribution describes the hit collection, P_pos and P_neg

19

20

where k is the replicate k class. In the context of the simulation, the FDR of eq 8 was defined for each cumulative k class as the percent of negative elements in D_h observed ≥ k times. The above Poisson expressions define the fraction of elements in each k class. Scaling by the total number of positive (|L|r) or negative (∼|L|) elements, respectively, yields the k class-dependent populations and FDR

21

The scaling factor, |L|, cancels, giving an expression dependent only on r, ε, and λ_drop. Given the simplification that each sorted hit droplet contains at most one positive element, eq 21 less accurately reflects simulation results at higher r and λ_drop, though not to an appreciable extent under experimentally relevant conditions (see Table T1). The statistical model of eqs 18−21 describes the expected k class-dependent FDR over a range of droplet occupancies (λ_drop = 0.1−5, Figure 6A−B; λ_drop = 0.1−100, Figure 6C–D) and library sampling (ε = 1−14), at a constant library hit rate (r = 0.1%). The surfaces can be used to discover conditions of library and bead sampling that yield screening output at a desired FDR and library coverage. Lower droplet occupancy and library sampling conditions are directly relevant to current droplet-based screening, and the model predicts the expected FDR in this parameter space (see Table T2). At higher occupancy (λ_drop = 10–50) and sampling (ε = 7), simulation data confirmed that the model retains accuracy, even as some approximations, such as the assumption of eq 16, become increasingly inaccurate (see Table T3).

Figure 6.

FDR calculated as a function of droplet occupancy and library equivalents screened. Library hit rate (r = 0.1%) was held constant. FDR is plotted across library equivalents (ε = 1–14), and (A) λ_drop = 0.1–5, at k ≥ 2, (B) λ_drop = 0.1–5, k ≥ 3, (C) λ_drop = 0.1–100, k ≥ 4, (D) λ_drop= 0.1–100, k ≥ 5. The surface elevation contrast is scaled to highlight 0–5% FDR. Orange hues indicate >75% library coverage. FDR is calculated using eqs 18–21.

The model can be simplified to a more intuitive form by substituting eqs 19 and 20 into eq 21 and rearrangement to yield an explicit expression for FDR

22

23

Both eqs 22 and 23 contain the term 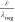, which is the k class-dependent “sampling bias.” The higher the library sampling relative to the mean negative sampling as a result of screening, the more likely the hit’s authenticity. Importantly, this sampling bias is exponential in k, explaining why higher k classes exhibit markedly diminished FDR. Triplicate hits are not just a little more trustworthy than duplicates! The equations also contain a “sampling saturation” term, e^λ_neg–ε, which consistently increases FDR across all k classes as library sampling increases. One would expect that screening more equivalents of a library is functionally analogous to performing replicate experiments, and therefore engender the benefits of enhanced confidence in hit validity. This is true, but, the statistics describe the more nuanced relationship, which includes noise as a factor. With nonzero stochastic noise, screening more equivalents always decreases each k class’s authenticity. However, sampling saturation is independent of k, thus it is always possible to counteract the impact of this term by examining higher k classes. It is noteworthy that this proposition is now uniquely possible due to the throughput of NGS-based hit decoding, which reveals both the structural content and k class distribution of each hit collection, or “statistical deconvolution”.

If negative population sampling is purely random noise as has been shown for the case of passenger beads, then these same expressions broadly govern screening hit authenticity as a function of k class. For example, in FACS-based target-binding screens of DNA-encoded combinatorial library beads,²⁸ operating the FACS instrument in full sort yield mode will include false positive elements due to passenger effects. The present theory could be used in the design of those types of screening experiments. As another example, consider DEL selections, which result in enrichment of sequences encoding ligands of the target or “counts” parlance.^17,21,35,36 Authentic positive ligands are identified as being present with more counts than noise sequences (the false positives), although recent studies implicate low selection yield (giving rise to high false negative rates) as a potentially limiting source of error for DEL technology.³⁷ Both screening modalities entail random, nonspecific interactions that influence screening outcome and k class analysis could be used to reject platform-specific noise. However, statistical deconvolution is powerless to discriminate systematically false positive compounds (“pan-assay interference compounds,” PAINs), which are detected as hits in primary screens, but fail to validate due to a variety of nonselective behaviors.³⁸ It may be possible to reject PAINs by triaging compounds that do not exhibit dose–response behavior during light-induced and -graduated high-throughput screening after bead release (hνSABR).^39,40hνSABR and statistical deconvolution could thus address most false positive hits from combinatorial library screens.

In conclusion, the simulations and statistical modeling presented here completely parametrizes the design of experiments for combinatorial library screening in microfluidic droplets. Experimental system performance is closely in line with Monte Carlo simulation results, highlighting sampling and sampling bias as central features of a statistical framework for describing hit bead authenticity. The extent to which authentic hit sampling eclipses negative sampling dictates the k classes containing hits with acceptably low FDR and optimal library screening experimental configurations. These findings are essential in guiding the design of experiments and interpretation of the screening output, and may find use in other compartmentalized combinatorial library screening strategies where shot noise is limiting.

Experimental Procedures

Microfluidic DNA-Encoded Library Screen

DNA-encoded library beads were loaded into a microfluidic device via suspension hopper and encapsulated into droplets of homogeneous fluorescence-based cathepsin D (catD) activity assay. Subsequently, compound was photochemically cleaved from the bead to dose the droplets,³⁹ and dosed droplets were incubated (∼20 min) in Frenz-type delay lines.⁴¹ Assay results were detected in flow by laser-induced fluorescence and used for high-speed droplet sorting.⁴²⁻⁴⁴ The device was used to screen a model library containing positive control beads (displaying pepstatin A, a potent inhibitor of catD), and negative control beads. Both bead types were DNA encoded. Positive control beads were additionally labeled with a fluorophore for visual identification. The model library was prepared by mixing positive control beads (∼1500 beads, 729 encoding sequences) into a background of negative control beads (>30 000 beads, 17 280 encoding sequences). Epifluorescence microscopy was used for visual bead type analysis of the hit droplet collection to determine the droplet occupancy. The DNA encoding tags of the entire hit collection were amplified in a bulk PCR, gel purified, and sequenced (Ion Proton, Thermo Fisher Scientific).^28,29 Sequence analysis of the hit collection revealed a population of positive control beads (1,377) and negative control beads (486).

Monte Carlo Simulation of DNA-Encoded Library Bead Screening

Simulations were run using the statistical analysis programming language R.⁴⁵ The library was defined as a vector, L, with hit rate, r, the fraction of positive elements. A positive bead vector, A, with defined length (|A| = |L| × r) and containing elements A_i (i = 1: |A|) and a negative bead vector, B, with defined length (|B| = |L|× (1 – r)) and containing elements B_j (j = 1: |B|) were sampled to generate L = A ∪ B. Library equivalents, ε, defines the number of elements (|L| × ε) to sample randomly from L with replacement to generate a library sample vector, S. Given a mean droplet occupancy, λ_drop, a droplet occupancy vector, O, was created with a length in excess of the expected average number of droplets required to encapsulate all beads (|O| = (|S|/λ_drop) × 1.2). O was filled with values according to a Poisson-defined probability distribution (λ = λ_drop).⁴⁶ Each element of a droplet encapsulation vector, D, is filled by the number of elements defined by occupancy vector O, from library sample vector S. Vector D is the simulated droplet population, and a subset hit droplet vector, D_h, was created using entries in D containing at least one element of A. The instances for each individual element (A_i, B_j) found within vector D_h were aggregated into replicate classes.

Monte Carlo Simulation Comparison with Experimental Screening

The NGS analysis of the model library screen’s hit bead collection revealed a population of positive control hit beads (1377) and negative beads (486). The positive control bead encoding diversity (|A| = 729) defined the average library equivalents screened (ε = 1377/729 = 1.89). A model library was prepared by mixing an aliquot of A with an aliquot of B (|B| = 17 280), giving the model library size (|L| = |A| + |B| = 18 009) simulation value. The hit rate for the experiment was defined as the number of possible hit compounds divided by the library size (r = |A|/|L| = 729/18 009 = 0.0405). Mean droplet occupancy (λ_drop = 0.37) was defined to fit the occupancy distribution observed from visual analysis of the hit droplet collection from experiment. Simulations (100) were executed using the input variable values based on the model DNA-encoded bead library screening experiment defined above (|L| = 18,009; r = 0.0405; ε = 1.89; λ_drop = 0.37). Simulation results for hit collection droplet occupancy were based on the number of elements in each entry of D_h. Simulation results for hit element distributions were obtained by aggregating all elements from D_h into a replicate class histogram for both positive compounds (A_i) and negative compounds (B_j). Average, standard deviation, maximum value, and minimum value were determined.

Monte Carlo Simulations of Library Coverage and FDR Analysis

Simulations (100) were executed for each set of input variables: |L| = 100 000; r = 0.005, 0.015, 0.045; ε = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10; λ_drop = 0.15, 0.3, 0.6, 1, 2, 3. Positive coverage was calculated for each simulation set as the average fraction of positive elements contained in the hit collection (|A ∩ D_h|/|A|). The FDR was calculated for each cumulative k class (elements observed ≥ k times) as the fraction of negative elements in the hit droplet vector (|B ∩ D_h|/|D_h|). For each set of input variables, the positive coverage and FDR were calculated for each simulation iteration, then the average and standard deviation were plotted.

Glossary

Abbreviations

NGS

next-generation sequencing

HTS

high-throughput screening

DEL

DNA-encoded library

hνSABR

light-induced and -graduated high-throughput screening after bead release

catD

cathepsin D

|L|

number of unique library elements

ε

mean bead library sampling

k

number of copies (replicate beads) of a given library member

k_drop

number of elements in a droplet

λ

mean library sampling

λ_drop

mean droplet occupancy

r

library hit rate

i

number of negative elements, equal to r × |L|

j

number of negative elements, equal to |L| – r × |L|

A

set of hit elements, {A₁, A₂,...A_i}, in L

B

set of negative elements, {B₁, B₂,...B_j}, in L

L

set of distinct library elements, created as the union of A and B

S

set of random elements sampled with replacement from library L

O

droplet occupancy vector, filled with a distribution of k_drop values defined by Poisson

D

simulated droplet vector populated based on O to sample k_drop elements from S without replacement

D_h

hit collection subset of D containing at least one A element

FDR

false discovery rate

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscombsci.7b00061.

• Comparison of FDR from simulation and statistical model, example of predicted optimal experimental parameters for compartmentalized activity-based library screening, comparison of FDR from simulation and statistical model at high occupancy, and library coverage as a function of FDR and library equivalents screened (PDF)

The authors declare no competing financial interest.