Conformational dynamics of the frameshift stimulatory structure in HIV-1

Abstract

Programmed ribosomal frameshifting (PRF) in HIV-1 is thought to be stimulated by a hairpin in the mRNA, although a pseudoknot-like triplex has also been proposed. Because the conformational dynamics of the stimulatory structure under tension applied by the ribosomal helicase during translation may play an important role in PRF, we used optical tweezers to apply tension to the HIV stimulatory structure and monitor its unfolding and refolding dynamics. The folding and unfolding kinetics and energy landscape of the hairpin were measured by ramping the force on the hairpin up and down, providing a detailed biophysical characterization. Unexpectedly, whereas unfolding reflected the simple two-state behavior typical of many hairpins, refolding was more complex, displaying significant heterogeneity. Evidence was found for multiple refolding pathways as well as previously unsuspected, partially folded intermediates. Measuring a variant mRNA containing only the sequence required to form the proposed triplex, it behaved largely in the same way. Nonetheless, very rarely, high-force unfolding events characteristic of pseudoknot-like structures were observed. The rare occurrence of the triplex suggests that the hairpin is the functional stimulatory structure. The unusual heterogeneity of the hairpin dynamics under tension suggests a possible functional role in PRF similar to the dynamics of other stimulatory structures.

INTRODUCTION

In programmed ribosomal frameshifting (PRF), the ribosome is induced to shift into a different reading frame by specific signals in the messenger RNA (mRNA), typically bypassing the original stop codon and continuing protein synthesis in the new reading frame (Giedroc and Cornish 2009; Brierley et al. 2010). PRF into the −1 reading frame is used by many viruses, including HIV, West Nile Virus, and SARS coronavirus as well as plant viruses and certain bacteriophages, to produce multiple protein products from a single mRNA. Despite decades of research, PRF mechanisms are still incompletely understood (Giedroc and Cornish 2009; Brierley et al. 2010; Dinman 2012; Caliskan et al. 2015). PRF is stimulated by a stable structure formed by the viral mRNA downstream from a “slippery sequence” where the frameshift actually occurs. Together, these elements of the frameshift signal achieve a stringent regulation of −1 PRF levels, which is essential for virus propagation (Dinman and Wickner 1992; Dulude et al. 2006; Plant et al. 2010). However, the details of how PRF is induced and its level regulated by frameshift signals remain controversial, and many different models have been proposed (Brierley et al. 2010). A feature common to several of these models is that the mRNA is under tension while the ribosome attempts to resolve the stimulatory structure during the critical step for frameshifting, suggesting that the properties of the stimulatory structure under mechanical tension may play an important role.

This view has motivated the study of the mechanical properties of stimulatory structures, using force probes like optical tweezers to perform single-molecule force spectroscopy (SMFS). SMFS, wherein force is applied to a molecule and the molecular extension measured as the structure changes in response, is a powerful tool for probing the conformational dynamics of single molecules (Ritchie and Woodside 2015), exploring questions like the role of intermediate states and competing pathways (Onoa et al. 2003; Chen et al. 2007; Li et al. 2007; Greenleaf et al. 2008; Stigler et al. 2011; Frieda and Block 2012; Gao et al. 2012; Ritchie et al. 2012; Yu et al. 2012, 2015) and measuring the energy landscape underlying the behavior (Woodside and Block 2014). Pseudoknots, formed when nucleotides within a hairpin loop base pair with complementary nucleotides outside of that loop (Dam et al. 1992), are the most common PRF stimulatory structure. Initial suggestions that −1 PRF levels are determined by the resistance of the pseudoknot to mechanical unfolding (Hansen et al. 2007; Chen et al. 2009) were found not to hold true when surveying a wider range of pseudoknots (Ritchie et al. 2012). Instead, the conformational plasticity of the pseudoknot under tension has been suggested to play an important role (Ritchie et al. 2012, 2014; de Messieres et al. 2014). Such studies have not yet been extended to other types of stimulatory structure, however, to test whether conformational plasticity plays a similar role.

HIV-1 is unusual among eukaryotic viruses in that the stimulatory structure is thought to be a simple hairpin, as opposed to a pseudoknot. A structure for this hairpin has been solved by NMR (Fig. 1A), featuring a two-stem helix containing a 3-purine bulge separating an 11-bp stable upper stem and a weak, U-rich lower stem (Dulude et al. 2002; Gaudin et al. 2005; Staple and Butcher 2005). However, the lower stem of the hairpin must be unwound and its 5′ end sequestered inside the ribosome during frameshifting in order to position the slippery site properly. The notion that the upper stem alone is the stimulatory structure (Jacks et al. 1988; Wilson et al. 1988; Parkin et al. 1992; Kollmus et al. 1996; Bidou et al. 1997) is supported by the observation that it can indeed induce significant PRF levels (Wilson et al. 1988; Parkin et al. 1992; Bidou et al. 1997). An alternative model has been proposed, however, whereby a pseudoknot-like triplex composed of interactions between the upper stem and the 3′ arm of the lower stem forms upon lower-stem unwinding by the ribosome (Dinman et al. 2002; Hong et al. 2010; Huang et al. 2014).

FIGURE 1.

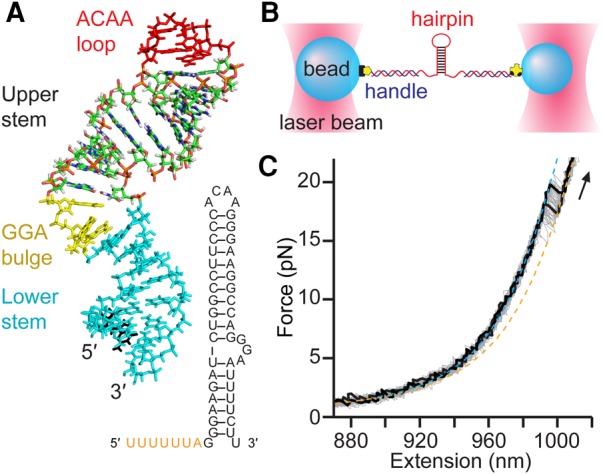
Structure and force spectroscopy of the full-length HIV-1 frameshift-stimulating hairpin. (A) The three-dimensional NMR structure of the full-length HIV-1 frameshift-stimulating hairpin (Staple and Butcher 2005) is shown with key structural features indicated. The secondary structure is shown with the slippery sequence (orange). (B) Experimental setup consisting of a single RNA hairpin molecule tethered between two beads held in optical traps. (C) Individual unfolding FECs (black) are plotted above the aggregated data from 50 FECs (gray). The FECs show a monotonic rise of force with extension until the RNA contour length changes abruptly upon unfolding, causing a “rip” in the FEC. Worm-like chain (WLC) fits to the folded (cyan) and unfolded (orange) branches of the FECs yield the contour length change upon unfolding. Arrow denotes direction of force ramp.

Previous work on the mechanical unfolding of the HIV-1 stimulatory hairpin using optical tweezers found that the upper stem was mechanically stable but not the lower stem (Mazauric et al. 2009). Neither the heterogeneity of the dynamics nor the energy landscape was investigated, however. We revisited the HIV-1 frameshift signal to explore its properties under tension in more detail, finding that the upper stem hairpin displayed heterogeneous refolding dynamics unlike those typically observed for simple stem–loop structures, suggesting possible parallels with the conformational plasticity seen in stimulatory pseudoknots. We also tested whether the proposed pseudoknot-like triplex occurs by using a truncated version of the full-length hairpin sequence, finding that although the triplex can form, it does so sufficiently rarely that it is unlikely to be the functional stimulatory structure.

RESULTS

We first investigated the mechanical unfolding of the full-length HIV-1 frameshifting hairpin, containing both the stable upper stem and U-rich lower stem (Fig. 1A). Constructs containing the mRNA hairpin flanked on each side by kb-long DNA–RNA duplex handles were attached to beads held in optical traps (Fig. 1B). The traps were held close together for 3 sec to permit zero-force folding of the RNA, then separated at constant velocity to ramp up the force applied to the RNA while the molecular extension was measured, generating force-extension curves (FECs). Single molecules were unfolded and refolded repeatedly by increasing and decreasing the force, resulting in a distribution of FECs displaying the range of possible behaviors. FECs for unfolding the full-length hairpin (Fig. 1C) showed a characteristic nonlinear rise of force with extension as the handles were stretched, interrupted by an abrupt extension increase and concomitant force decrease as the hairpin unfolded cooperatively (Liphardt et al. 2001; Woodside et al. 2008). A single discrete unfolding transition was typically observed in the range 14–21 pN (122 FECs), although sometimes multiple transitions were seen. Fitting the FECs to extensible worm-like chain (WLC) models (Fig. 1C, dotted lines), the contour length change upon unfolding, ΔL_c, was found to be consistent with unfolding only the upper stem: ΔL_c = 13 ± 1 nm (all errors represent S.E.M.), in agreement with previous work (Mazauric et al. 2009) and the expectation from the NMR structure (ΔL_c = 13.5 nm). The lower stem unfolding occurred at very low force, as found previously (Mazauric et al. 2009), making it difficult to observe directly.

Because the lower stem is almost certainly unfolded during PRF in order to satisfy spacer-length requirements (Léger et al. 2004; Staple and Butcher 2005), we focused primarily on the behavior of the upper stem alone. Unfolding FEC measurements were repeated for a construct consisting of the upper stem alone (Fig. 2A, inset). Discrete unfolding events in the FECs (Fig. 2A) were observed in the same force range as for the full construct, 14–20 pN, and with the same ΔL_c from WLC fits (Fig. 2A, dashed lines), 12.5 ± 0.5 nm, confirming that the discrete unfolding transition seen for the full-length hairpin did indeed involve only the upper stem. Such two-state behavior is very typical for simple stem–loop structures under tension (Liphardt et al. 2001; Manosas et al. 2006; Woodside et al. 2006a,b). Investigating the unfolding of the upper stem in more detail, we examined the distribution of unfolding forces in the FECs (Fig. 2B, black), p(F), to quantify the resistance of the hairpin to mechanical unfolding. The average unfolding force from 3280 FECs, here 17 ± 1 pN, provided the simplest measure of the mechanical stability. Other parameters, describing the unfolding rate and the shape of the underlying energy landscape, were obtained by fitting p(F) to Equation 2 (Fig. 2B, red). As seen, p(F) was exactly the shape expected for a two-state system with a single barrier (Dudko et al. 2006) and was well-fit by Equation 2. A complementary analysis of the kinetics based on the cumulative probability of unfolding (Dudko et al. 2008) was also used to obtain the unfolding rate as a function of force, k(F) (Fig. 2B, inset), which was again well fit by the same type of landscape model using Equation 3. These fits yielded log k_off [s⁻¹] = −9.9 ± 0.7, Δx^‡ = 8.2 ± 0.8 nm, and ΔG^‡ = 38 ± 4 k_BT.

FIGURE 2.

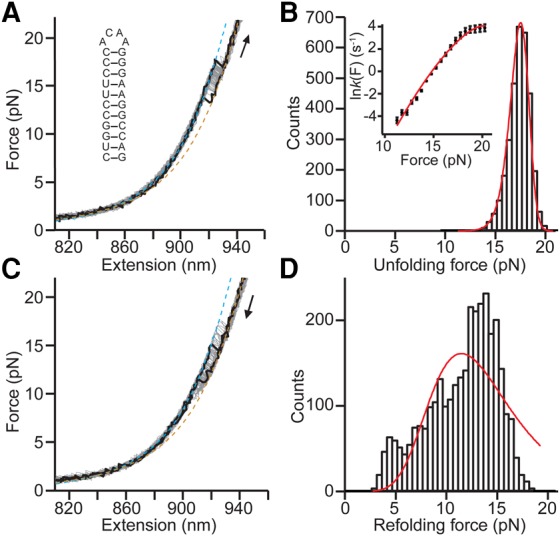
Force spectroscopy of the HIV-1 upper stem alone. (A) Individual unfolding FECs (black) are plotted above the aggregated data from 100 FECs (gray). WLC fits are shown for the folded (cyan) and unfolded (orange) branches of the FECs. (Inset) Secondary structure of the HIV-1 upper stem alone. (B) The distribution of unfolding forces for HIV-1 upper stem alone FECs (black) is fit well by Equation 2 (red), yielding parameters describing the mechanical resistance to unfolding. (Inset) Force-dependent unfolding rate (black) is fit well by Equation 3 (red). (C) Individual refolding FECs (black) are plotted along with the aggregated data from 100 FECs (gray). WLC fits are shown for the unfolded (orange) and folded (cyan) branches of the FECs. (D) The distribution of refolding forces for HIV-1 upper stem alone FECs (black) is poorly fit by Equation 2 (red), a consequence of heterogeneous refolding that is more complicated than the single-barrier two-state behavior observed for unfolding.

Turning to the refolding FECs (Fig. 2C), discrete refolding events were observed that looked qualitatively similar to the unfolding events but occurred over a lower force range (3–18 pN). WLC fitting revealed that ΔL_c during refolding, 13.0 ± 0.7 nm, was the same (within error) as for unfolding, indicating that the hairpin was switching between the same two states. However, the refolding force distribution (Fig. 2D) was qualitatively different: Where one would normally expect to see a smooth rise to the most probable unfolding force followed by a swift fall to zero as the force was reduced (the mirror image of the distribution for the unfolding forces), there was instead a fat tail in the distribution at low forces, and possibly several discrete peaks. Proceeding nevertheless to fit the refolding p(F) (Fig. 2D, red) from 3277 refolding FECs to the analog of Equation 2 for refolding force distributions (Pierse and Dudko 2013), we found log k_on [s⁻¹] = 3.3 ± 0.5, Δx^‡ = 1.3 ± 0.3 nm, ΔG^‡ = 5 ± 3 k_BT. However, the fit was not particularly good and thus these results are likely not reliable—indeed the shape of p(F) for refolding suggests that refolding is more complex than a single-barrier, two-state system. Fat tails or multiple peaks in the force distribution have been shown to be a consequence of heterogeneity in the folding behavior (Hyeon et al. 2014; Pierse and Dudko 2017).

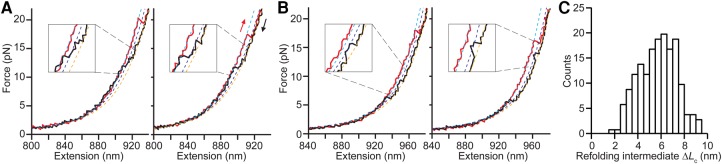
Examining the refolding curves in more detail provided additional support for the view that refolding was more complex than unfolding. Roughly 5% of curves showed evidence of partially folded intermediate states. In some cases, the intermediate state was on-pathway between the unfolded and folded states, as seen by the progression from unfolded to intermediate to folded (Fig. 3A). Notably, such intermediates were never seen in the unfolding curves, indicating that new pathways between the unfolded and folded states were being observed during refolding that were not observed during unfolding. In other cases, the intermediates appeared as transient excursions out of the unfolded state that returned to the unfolded state before the folded structure was attained (Fig. 3B), suggesting that they may be off-pathway states that represent yet another behavior not seen during unfolding. The distribution of contour length changes for the intermediates, measured relative to the unfolded state via WLC fits (Fig. 3A,B insets, dotted lines), was quite broad (Fig. 3C), indicating the presence of several different intermediate structures.

FIGURE 3.

Refolding intermediates in FECs for the upper stem alone. (A) Representative FECs with on-pathway refolding intermediates showing individual unfolding (red) and refolding (black) FECs with WLC fits to the folded (cyan) and unfolded (orange) branches and the intermediate state (blue). The folding progresses from unfolded to folded through the intermediate, indicating the latter is on-pathway. (B) Representative FECs with off-pathway refolding intermediates showing individual unfolding (red) and refolding (black) FECs with WLC fits to the folded (cyan) and unfolded (orange) branches and the intermediate state (blue). The intermediate state appears as a transient excursion out of the unfolded state that returns to the unfolded state before the folded structure is attained, indicating that it is likely off-pathway. (C) Distribution of contour length changes from the intermediate states to the unfolded state. The broad range indicates the presence of several different intermediate structures.

In order to explore the possible formation of the proposed pseudoknot-like triplex, we next investigated a construct, denoted Δ5′FL, in which the 5′ arm of the lower stem in the full-length hairpin was deleted to mimic the mRNA sequence that would be free to fold after unwinding of the lower stem by the ribosome (Fig. 4A, inset). Based on 2714 FECs, the unfolding of Δ5′FL was almost always identical to that of the upper stem alone (Fig. 4A, black). WLC fits of the unfolding FECs found ΔL_c = 13 ± 1 nm, and the average unfolding force was 18 ± 1 pN, the same in each case (within error) as for upper-stem unfolding. The distribution of unfolding forces (Fig. 4B) was well fit by Equation 2, and the parameters found from fitting p(F) to Equation 2 (Fig. 4B, red) and k(F) to Equation 3 (Fig. 4B, inset) were in excellent agreement with those obtained for the upper stem alone: log k_off [s⁻¹] = −9.7 ± 0.9, Δx^‡ = 7.4 ± 0.7 nm, and ΔG^‡ = 39 ± 6 k_BT.

FIGURE 4.

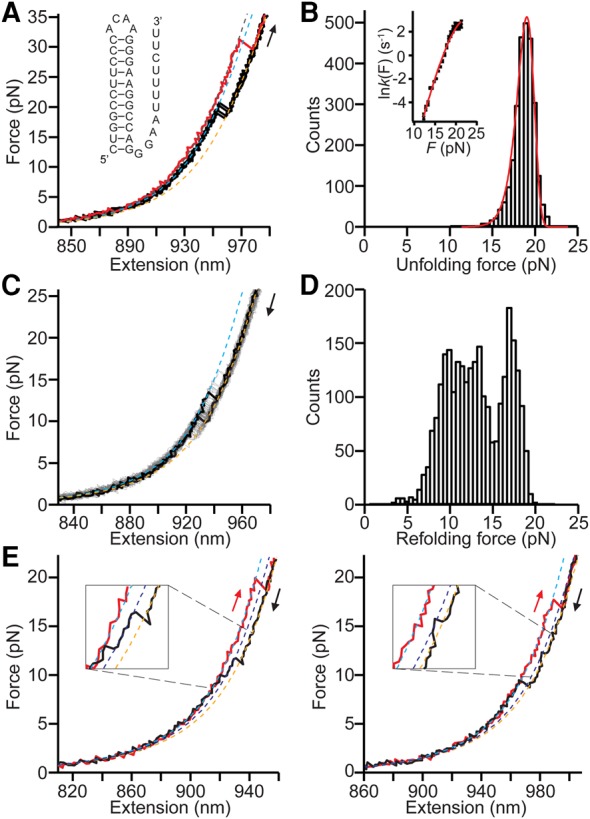
Force spectroscopy of the Δ5′FL construct. (A) Most FECs show length changes and unfolding forces corresponding to those expected for unfolding the upper stem alone (black). A few FECs show a longer length and a higher unfolding force, indicating the presence of a larger structure containing tertiary contacts (red). (Dotted lines) WLC fits to the unfolded state (orange), folded upper stem (cyan), and folded triplex state (blue). (Inset) Secondary structure of the Δ5′FL construct. (B) The unfolding force distribution for the events with shorter ΔL_c (black) is well fit by Equation 2 (red), yielding the same fitting parameters as for the upper stem alone. (Inset) Force-dependent unfolding rate (black) fit by Equation 3 (red). (C) Refolding FECs (black, gray) all have ΔL_c consistent with the upper stem only. (Dotted lines) WLC fits to the unfolded state (orange) and folded upper stem (cyan). (D) The refolding force distribution is again broad, a consequence of heterogeneous refolding, similar to that for the upper stem alone. (E) Some refolding FECs (black) contain intermediate states not observed in unfolding FECs (red). A broad range of intermediate-state ΔL_c values from WLC fits (orange: unfolded, blue: intermediate, cyan: folded) indicates the presence of multiple intermediate states, as for the upper stem only.

Turning to the refolding of Δ5′FL, we found that refolding FECs, too, were very similar to those for upper stem only (Fig. 4C). The same ΔL_c (within error) was found as for the upper stem, 13 ± 1 nm from 2713 FECs. Furthermore, a similarly broad distribution of refolding forces was observed (Fig. 4D), and intermediates were again detected in a small subset of refolding FECs (Fig. 4E), with a range of contour lengths similar to that for the upper stem, again reflective of extensive heterogeneity in the refolding dynamics. The qualitative and quantitative similarities between the unfolding and refolding of the upper stem only and the Δ5′FL construct lead us to conclude that the Δ5′FL sequence must form the upper-stem hairpin structure almost all the time.

In a handful of cases (∼0.1% of the pulls), however, we saw unfolding FECs that did not fit this pattern (Fig. 4A, red). These curves displayed a much higher unfolding force, roughly 30 pN as opposed to 18 pN, in conjunction with noticeably larger contour length change, 16 ± 1 nm versus 13 ± 1 nm. These differences are both significant and revealing. A larger ΔL_c than for the upper stem is only possible if nucleotides that are not part of the upper-stem hairpin (i.e., those in the 3′ arm of the lower stem) are participating in this new structure. Based on the proposed triplex structure (Fig. 4A; Dinman et al. 2002), we would expect ΔL_c ∼ 17 ± 1 nm, in good agreement with the observed value. The high unfolding force can only be explained by the presence of tertiary structure: It is much higher than the unfolding forces observed previously for nucleic acid secondary structure (Liphardt et al. 2001; Li et al. 2006; Manosas et al. 2006; Woodside et al. 2006b; Chen et al. 2007; Green et al. 2008; Greenleaf et al. 2008; Mazauric et al. 2009; Neupane et al. 2011; Bercy and Bockelmann 2015). Instead, it is similar to the typical unfolding force of about 30–40 pN observed for most pseudoknots (Chen et al. 2007; Green et al. 2008; Ritchie et al. 2012, 2014; de Messieres et al. 2014; Zhong et al. 2016), suggesting that the Δ5′FL mRNA can indeed form a pseudoknot-like structure as proposed, although it does so only very rarely.

DISCUSSION

These results provide insight into how the frameshift signal may stimulate −1 PRF in HIV-1. Addressing first the question of whether frameshifting may be stimulated by a putative triplex structure, we found that a structure consistent with this pseudoknot-like triplex can indeed form when the 5′ strand of the lower stem is removed, mimicking the situation when this strand is sequestered under the ribosome footprint just before the frameshift occurs. However, the notion that the frameshift signal partitions into a triplex structure that actively triggers −1 PRF and a hairpin that is inactive in PRF is contradicted by the observation that the triplex structure formed roughly two orders of magnitude less frequently than would be needed to account for the typical 5% PRF efficiency in HIV-1 (at least under our measurement conditions). Instead, the similarity between the behavior of the 5′ΔFL and upper-stem constructs across all the characteristics examined (length changes and forces for unfolding and refolding, intermediates and heterogeneity during refolding) supports the view that the upper-stem hairpin alone is the stimulatory structure.

Given that most stimulatory structures are pseudoknots, not hairpins (Giedroc and Cornish 2009), a key question is what property of this hairpin accounts for its unusual ability to trigger −1 PRF efficiently, in contrast to other hairpins that are poor PRF stimulators. The unfolding force, barrier height and compliance, and unfolding rate are all different from pseudoknots, but these properties have previously been shown to be unrelated to PRF stimulation efficiency (Ritchie et al. 2012). More intriguing as an explanation is the heterogeneity in the refolding: The HIV-1 stimulatory hairpin has folding dynamics that are unusually complex for a simple duplex stem–loop, which typically unfold and refold as two-state systems (Liphardt et al. 2001; Woodside et al. 2006a,b) along a single pathway (Neupane et al. 2015, 2016) in a way that can be predicted from the sequence (Manosas et al. 2006; Woodside et al. 2006b; Neupane et al. 2015). The HIV-1 hairpin, in contrast, shows evidence of multiple refolding pathways likely involving both on- and off-pathway intermediates, behavior typically associated with more complex structures including bulges or helix junctions as in molecules like the HIV-1 transactivation response (TAR) hairpin (Li et al. 2006) or purine riboswitch aptamers (Neupane et al. 2011). Such heterogeneity is not unheard-of in simple stem–loops, as both temperature-jump measurements (Ma et al. 2006) and computational simulations (Bowman et al. 2008) suggested the presence of multiple folding pathways in the folding of hairpins with highly structured tetraloops similar to the loop in the HIV-1 hairpin, but it has not previously been suggested to play a functional role.

We note that the broad refolding force distributions are consistent with the presence of both static and dynamic heterogeneity, arising from conformational fluctuations that occur on timescales that are, respectively, much slower than or similar to the timescale for refolding (Hyeon et al. 2014). Static heterogeneity would result in a distribution containing multiple peaks (Pierse and Dudko 2017), each the characteristic shape for a single refolding transition (Pierse and Dudko 2013), whereas dynamic heterogeneity produces a distinct tail at low forces (Hyeon et al. 2014). The observed distributions provide evidence for both types of heterogeneity: Multiple peaks may be discerned, but there is also a low-force tail. Because it is difficult to separate the static and dynamic components reliably, however, we are unable to quantify the heterogeneity by fitting the distributions. Nevertheless, we can test the picture we propose to account for our observations, involving refolding via native or nonnative loops and on- or off-pathway intermediates (Fig. 5A), by modeling the intermediates. The existence of an on-pathway intermediate is supported by modeling of the energy landscape expected from the sequence (Woodside et al. 2006a), which shows a shallow well halfway between the folded and unfolded states (Fig. 5B). Structure-prediction tools like mfold (Zuker 2003) also reveal several possible off-pathway intermediates having native or nonnative loops (Fig. 5, insets). The range of length changes associated with these intermediates, ΔL_c ∼ 3–7.5 nm, is fully consistent with the values observed in the refolding FECs (Fig. 5C), supporting the picture in Figure 5A.

FIGURE 5.

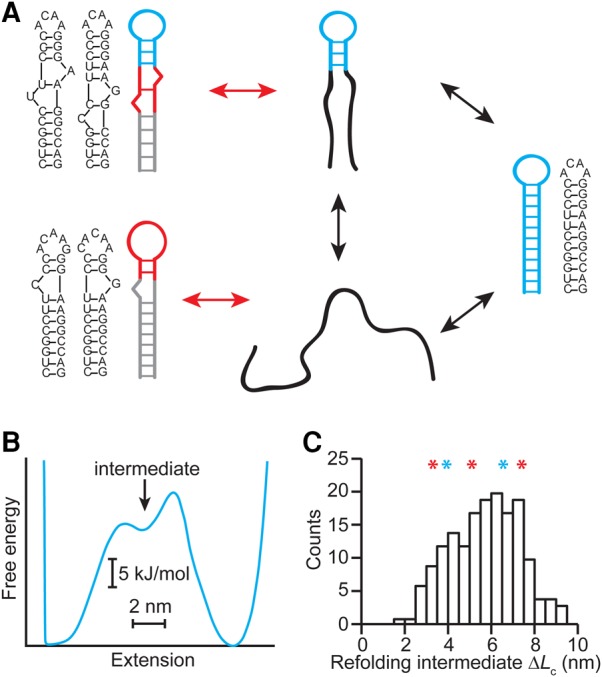
Model of heterogeneous folding for HIV-1 upper stem alone. (A) The folding is proposed to include two-state folding between the unfolded (black) and native (cyan) states, as well as on-pathway intermediates containing a native loop (cyan) but an incomplete stem, and off-pathway intermediates having nonnative stems or loops (red) that must be resolved before the native structure can form (all suboptimal structure predictions from mfold). (B) A model of the energy landscape for native folding under tension (Woodside et al. 2006a) shows a shallow well that could support an intermediate state. (C) The ΔL_c values expected from the proposed intermediate states (asterisks: red—off-pathway, cyan—on-pathway) match the range of values in the measured histogram (black).

The heterogeneity observed in the refolding of the HIV stimulatory hairpin evokes a key feature of pseudoknot folding that has been linked to efficient PRF—the fact that PRF efficiency correlates well with the conformational plasticity of the stimulatory structure (Ritchie et al. 2012, 2014). This connection may help to explain how this hairpin can act as a stimulatory structure in −1 PRF in lieu of a more typical pseudoknot: Similar to the way that frameshift-inducing pseudoknots differ from other pseudoknots in having more heterogeneous dynamics (reflected in a greater tendency to form alternate structures when refolding), so too does the HIV frameshifting hairpin display more heterogeneous dynamics than expected for a simple hairpin structure. We speculated previously that such heterogeneity might play a role via fluctuations in the tension in the mRNA generated by structural fluctuations in the stimulatory structure induced by the mechanical tension applied by the ribosome, fluctuations that are then communicated to the tRNA binding sites to induce −1 PRF (Ritchie et al. 2012). Our results for the HIV stimulatory hairpin are consistent with this picture, suggesting that it extends beyond pseudoknots and may be a general feature of structures that are efficient at stimulating PRF. A role for structural fluctuations in triggering −1 PRF has also been suggested for a hairpin-based stimulatory structure in an alphavirus (Kendra et al. 2017).

It is important to note that hairpin-stimulated frameshifting has not been studied as extensively as PRF stimulated by pseudoknots, and diverse stimulatory structures may not necessarily induce frameshifting via identical mechanisms. Some studies of hairpin-induced frameshifting have led to the proposal that hairpins stimulate PRF by acting as a simple roadblock, but robust quantitative correlations remain elusive (Bidou et al. 1997; Yu et al. 2011; Mouzakis et al. 2013) and such a picture is inconsistent with the properties of pseudoknots (Ritchie et al. 2012, 2014). It remains unclear precisely how dynamics in the stimulatory structure (not to mention other elements like interactions between the stimulatory structure and the ribosome) lead to −1 PRF, and much work remains to be done before a complete mechanistic model of −1 PRF can be built. Nevertheless, identifying features like conformational heterogeneity that are shared between diverse frameshift signals provide important clues that may help clarify this long-standing problem.

MATERIALS AND METHODS

Sample preparation and measurement

Sequences encoding the full-length hairpin, the upper stem only, or the full-length hairpin with 5′ strand of the lower stem deleted were inserted into the pMLuc-1 plasmid between the SpeI and BamHI restriction sites. The resulting transcription template, containing a hairpin flanked by linker regions on either side, was amplified by PCR and transcribed in vitro using T7 RNA polymerase. Two ssDNA handles (one complementary to 840 nt on the 3′ end of the transcript and labeled with biotin, the other complementary to 2280 nt on the 5′ end of the transcript and labeled with digoxigenin) were produced by asymmetric PCR from double-stranded DNA PCR products corresponding to the flanking handle sequences (Neupane et al. 2011). The handles were annealed with the RNA transcript, then incubated with 600 and 820 nm diameter polystyrene beads labeled with avidin DN (Vector Labs) and anti-digoxigenin (Roche), respectively, to create dumbbells. Dumbbells were placed in measuring buffer (50 mM MOPS, pH 7.0, 130 mM KCl, 4 mM MgCl₂, 50 U/mL Superase•In RNase inhibitor [Ambion] and oxygen scavenging system: 40 U/mL glucose oxidase, 185 U/mL catalase, and 8.3 mg/mL glucose) and inserted into a sample chamber on a clean microscope slide in the optical trap.

Force-extension curves (FECs) were measured with a custom-built, dual-beam optical trap similar to one described previously (Neupane et al. 2011). Briefly, two orthogonally polarized beams from a single 1064-nm laser were steered independently with acousto-optic deflectors to create two traps. The motion of beads held in the traps was detected by collecting the light from two orthogonally polarized 830-nm laser beams aligned on the traps that was scattered by the beads onto position-sensitive diodes. Trap stiffnesses were 0.58 and 0.37 pN/nm, calibrated as described previously (Svoboda and Block 1994); each RNA construct was measured using a different stiffness calibration, possibly giving rise to systematic differences of up to 5%–10%. The traps were moved apart at a constant speed of 110–270 nm/sec, sampling data at 20 kHz and filtering online at 10 kHz with an 8-pole Bessel filter.

FEC analysis

To determine the contour length change during unfolding and refolding transitions, ΔL_c, FECs were aligned to correct for small amounts of drift in the measurement and fit to extensible worm-like chains (WLCs) (Wang et al. 1997):

$$F(x)=\frac{k_{\mathrm{B}}T}{L_{\mathrm{p}}}\left[\frac{1}{4}{\left(1-\frac{x}{L_{\mathrm{c}}}+\frac{F}{K}\right)}^{-2}-\frac{1}{4}+\frac{x}{L_{\mathrm{c}}}-\frac{F}{K}\right],$$ (1)

where L_c is the contour length of the polymer, L_p the persistence length, K the enthalpic elasticity, and k_BT the thermal energy. Two WLCs in series were used, one for the duplex handle (L_c ∼ 1100 nm, L_p ∼ 35 nm, K ∼ 1200 pN) and the other for the unfolded mRNA (L_c = 0.59 nm/nt, L_p = 1 nm, K = 2000 pN). The change in RNA contour length was found by fitting the two branches of the FECs on either side of a transition. The contour length change expected from the NMR structure of the HIV-1 frameshift hairpin (Staple and Butcher 2003) was calculated using ΔL_c = n_nt · L_c^nt – d_T, where d_T is the distance between the termini of the folded hairpin as measured from the NMR structure (1.8 nm), n_nt is the number of nucleotides in the hairpin, and L_c^nt = 0.59 nm/nt is the contour length per nucleotide (Saenger 1984). For the proposed HIV triplex structure, d_T was estimated from pseudoknots of similar size as 5 nm, yielding an expected ΔL_c of 17 ± 1 nm.

The distribution of unfolding forces was analyzed using the kinetic theory of Dudko et al. (2006) to determine the parameters characterizing the energy landscape underlying the unfolding behavior:

$$p(F)\propto \frac{k(F)}{r}\exp \left\{\frac{k_{\mathrm{off}}}{\beta \mathrm{\Delta }{x}^{‡}r}-\frac{k(F)}{\beta \mathrm{\Delta }{x}^{‡}r}{\left(1-\frac{\mathrm{\Delta }{x}^{‡}F}{\mathrm{\Delta }{G}^{‡}}\nu \right)}^{1-1/\phantom{1\nu }\nu }\right\},$$ (2)

where

$$k(F)=k_{\mathrm{off}}{\left(1-\frac{\mathrm{\Delta }{x}^{‡}F}{\mathrm{\Delta }{G}^{‡}}\nu \right)}^{1/\phantom{1\nu }\nu -1}\exp \left\{\frac{\mathrm{\Delta }{G}^{‡}}{k_{B}T}\left[1-{\left(1-\frac{\mathrm{\Delta }{x}^{‡}F}{\mathrm{\Delta }{G}^{‡}}\nu \right)}^{1/\phantom{1\nu }\nu }\right]\right\},$$ (3)

k_off is the unfolding rate at zero force, Δx^‡ is the distance to the transition state from the folded state, ΔG^‡ is the height of the energy barrier, r is the loading rate, β is the inverse thermal energy, and ν is a parameter characterizing the shape of the energy barrier (ν = 1/2 for a sharp cusp-like barrier, 2/3 for a softer linear-cubic potential). We averaged the results obtained under these two limiting cases for the shape of the energy barrier, since this shape was unknown.

The free energy change between the folded and unfolded states of the HIV upper stem was determined from the FECs using the Crooks fluctuation theorem (Crooks 1999; Collin et al. 2005). The work distributions for unfolding and refolding, respectively P_U(W) and P_F(W), were calculated from integrals of the pulling curves, and the free-energy change was found from

$$\frac{P_{\mathrm{U}}(W)}{P_{\mathrm{F}}(-W)}=\exp (\beta [W-\mathrm{\Delta }G]),$$ (4)

using the Bennett acceptance ratio to determine the intersection of P_U(W) and P_F(W) (Collin et al. 2005). The result, ΔG = 23 ± 1 k_BT, was compared with previous ensemble measurements of the upper stem using UV absorbance, which found ΔG = 25 ± 1 k_BT (Mouzakis et al. 2013), in reasonable agreement given the systematic uncertainty in the force calibration.

No significant changes in any of the properties of the RNA constructs were observed over time during repeated unfolding–refolding cycles. Molecule-to-molecule variations were small, with the average unfolding force varying by ∼10%, similar to the amount expected from calibration errors. Different numbers of pulling cycles were measured on different molecules, but this did not affect the qualitative analysis of the refolding heterogeneity: Resampling the refolding force distributions to ensure equal weighting from each molecule produced histograms in which the range of forces and overall shape were not materially changed.