Detection and quantification of inbreeding depression for complex traits from SNP data

Significance

Inbreeding depression (ID) is the reduction of fitness in offspring of related parents. This phenomenon can be quantified from SNP data through a number of measures of inbreeding. Our study addresses two key questions. How accurate are the different methods to estimate ID? And how and why should investigators choose among the multiple inbreeding measures to detect and quantify ID? Here, we compare the behaviors of ID estimates from three commonly used SNP-based measures of inbreeding and provide both theoretical and empirical arguments to answer these questions. Our work illustrates how to analyze SNP data efficiently to detect and quantify ID, across species and traits.

Abstract

Quantifying the effects of inbreeding is critical to characterizing the genetic architecture of complex traits. This study highlights through theory and simulations the strengths and shortcomings of three SNP-based inbreeding measures commonly used to estimate inbreeding depression (ID). We demonstrate that heterogeneity in linkage disequilibrium (LD) between causal variants and SNPs biases ID estimates, and we develop an approach to correct this bias using LD and minor allele frequency stratified inference (LDMS). We quantified ID in 25 traits measured in $\sim 140,000$ participants of the UK Biobank, using LDMS, and confirmed previously published ID for 4 traits. We find unique evidence of ID for handgrip strength, waist/hip ratio, and visual and auditory acuity (ID between −2.3 and −5.2 phenotypic SDs for complete inbreeding; $P<0.001$). Our results illustrate that a careful choice of the measure of inbreeding combined with LDMS stratification improves both detection and quantification of ID using SNP data.

Mating between close relatives has detrimental consequences on the survival and fertility of resulting offspring (1). This overall reduction of fitness, referred to as inbreeding depression (ID), is observable in a wide range of organisms, including plants (2), animals (3, 4), and humans (5). In humans, major abnormalities are more frequent in children from consanguineous marriages (6) and genes causing rare diseases can be mapped by ascertaining children from such matings (7). To date, although the genetic basis of ID is not completely elucidated, two main hypotheses are proposed to explain this phenomenon: homozygosity for partially recessive deleterious mutations and heterozygous advantage (overdominance) (1, 8). More generally, ID can be estimated for any complex trait, even if the trait is not an obvious component of fitness. For polygenic traits, ID can be detected if there is directional dominance (DD) across loci, which means that the phenotype of individuals who are heterozygous deviates from the average phenotypes of homozygous individuals in a consistent direction. For fitness components, DD is negative; i.e., on average homozygosity reduces fitness.

In practice, ID can be estimated from pedigree studies when the relationships between parents are known (6, 9). However, given the limited number and the small sizes of such studies in humans, contemporary efforts (5, 10) to quantify ID have instead used SNP genotyping platforms to directly estimate inbreeding coefficients (F). SNP data may allow a more accurate evaluation of inbreeding (11), in particular for distant and cryptic inbreeding, and allow inference to be drawn from large population data (10). Conceptually, once a measure of F is derived from SNP data, ID can subsequently be estimated by correlating phenotype with the estimated F.

Genome-wide estimators of F fall in two categories: average homozygosity measures across loci (irrespective of position) and measures of continuous runs of homozygosity (ROH). Using ROH, ID has been reported for diseases (12, 13), height (5), and cognition (10). ROH-based estimates of F (${\text{F}}_{\text{ROH}}$) have been previously shown to better correlate with the unobserved pedigree-inbreeding coefficient compared with other measures of inbreeding (14, 15), which has made them a gold standard. However, the sampling variance of these estimates is large, and consequently large sample sizes (10) are required to detect ID with ${\text{F}}_{\text{ROH}}$ measures. In addition, ${\text{F}}_{\text{ROH}}$ estimation depends on arbitrary (although optimized) choices of multiple parameters like the minimum number of SNPs covered by a ROH, the distance between two consecutive ROHs, and the number of heterozygous genotypes allowed in each ROH. Setting ROH length cutoffs ignores the contribution to ID of smaller identity by descent segments due to distant ancestors.

Therefore, quantifying the theoretical properties (bias and variance) of ID estimates derived from ${\text{F}}_{\text{ROH}}$ is challenging. These two critical limitations led us to consider two other commonly used measures of inbreeding (3, 15), namely the excess of homozygosity inbreeding coefficient (hereafter denoted ${\text{F}}_{\text{HOM}}$) as estimated in PLINK (16) and the correlation between uniting gametes (hereafter denoted ${\text{F}}_{\text{UNI}}$) previously introduced as ${\widehat{F}}^{III}$ in Yang et al. (17), as potential efficient measures for detecting and quantifying ID. We present the theory underlying unbiased estimation of ID and compare through simulations the performances of these three measures of inbreeding. We then quantify ID in 25 quantitative traits measured in a large dataset of $\sim \mathrm{140,000}$ individuals from the UK Biobank, using an approach that is robust to different assumptions on the distribution of effect sizes, to possible directional effects of minor alleles and to population stratification.

Results

Theoretical Determinants of Unbiased Estimation of ID.

We assume that the phenotype of interest is a quantitative trait y with genetic component that is underlain by random additive and dominance effects of m independent causal variants. We denote $\text{b}=-{\sum }_{j=1}^{m}2p_j(1-p_j){\delta }_j$ as the expected depression in y resulting from complete inbreeding, where $p_j$ is the minor allele frequency (MAF) of the jth causal variant and ${\delta }_j$ the expectation of its dominance effect. In the absence of epistasis, fitness-related phenotypes linearly decrease with increasing inbreeding (Eq. S2). This well-established linear relationship naturally implies the use of linear regression methods to estimate ID.

Least-squares estimates of ID obtained with ${\text{F}}_{\text{UNI}}$ converge with increasing sample size toward ${\text{b}}_{\text{UNI}}=\text{cov}[\text{𝒚},{\text{F}}_{\text{UNI}}]/\text{var}[{\text{F}}_{\text{UNI}}]$. When explicitly calculating $\text{cov}[\mathit{\text{y}},{\text{F}}_{\text{UNI}}]$ and $\text{var}[{\text{F}}_{\text{UNI}}]$ with respect to the genotypes and the effect size distributions, we found under classical assumptions (Eq. S4 and Table S1) that ${\text{b}}_{\text{UNI}}$ is unbiased when the average linkage disequilibrium (LD) among observed SNPs equals the weighted (by effect sizes) average LD between causal variants and observed SNPs. Although influenced by the effect size distribution, the consistency of ${\text{b}}_{\text{UNI}}$ toward b is mainly driven by differences in LD between causal variants and observed SNPs. Therefore, a simple condition under which ${\text{b}}_{\text{UNI}}$ is unbiased is if the causal variants are a random subset of the observed SNPs. However, if the causal variants are enriched in high-LD regions of the genome, ${\text{b}}_{\text{UNI}}$ will overestimate the actual inbreeding depression. In contrast, if the causal variants are enriched in a low-LD region like DNAse-I hypersensitive sites or enhancers (18), or if they are enriched among low-frequency variants, ${\text{b}}_{\text{UNI}}$ is expected to underestimate the true effect. This is further illustrated in our first simulation (Fig. 1).

Table S1.

Joint distribution of allele frequencies as a function of the LD

Alleles	aj	Aj	Allele frequency
ak	pjpk + Djk	(1 − pj) pk − Djk	pk
Ak	(1 − pk) pj − Djk	(1 − pj) (1 − pk) + Djk	1 − pk
	pj	1 − pj	1

a_j and a_k are the minor alleles of SNP j and SNP k, and A_j and A_k are their major alleles, respectively The MAFs of SNP j and SNP k are p_j and p_k, respectively. D_jk is the LD parameter.

Fig. 1.

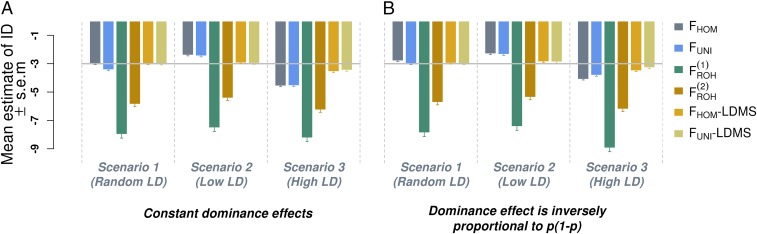
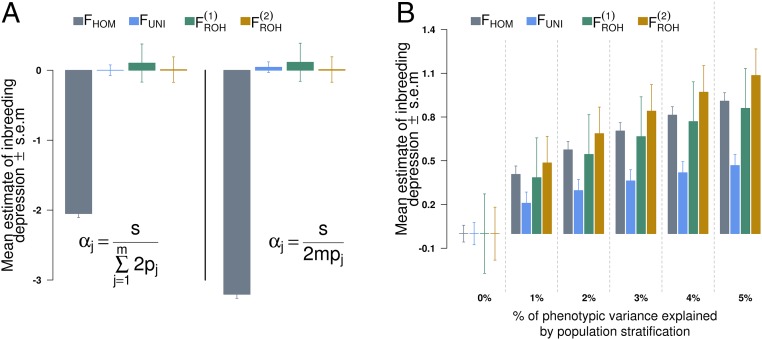
Averaged estimates of inbreeding depression (ID) from 1,000 simulated datasets. Datasets were simulated assuming a true ID parameter b = −3 (horizontal gray line) phenotypic SD for complete inbreeding. In scenario 1 the $m=1,000$ causal variants were randomly sampled from all observed SNPs, whereas in scenarios 2 and 3 they were respectively sampled from low- and high-LD regions of the genome. In A the expectation of the dominance effects (${\delta }_{\text{j}}$ for the jth causal variant) is constant (neutral model) whereas in panel B ${\delta }_{\text{j}}$ is inversely proportional to the variance of the minor allele count at each causal variant. ${\text{F}}_{\text{HOM}}$, excess homozygosity inbreeding measure; ${\text{F}}_{\text{ROH}}$, runs of homozygosity-based inbreeding measures; ${\text{F}}_{\text{UNI}}$, measure of inbreeding based on correlation between uniting gametes; LDMS, LD and minor allele frequency stratified inference; SEM, SE of the mean.

LD heterogeneity between causal variants and SNPs used for inference has been previously shown to determine the consistency of heritability estimates (19–21). We leveraged this estimation problem to propose a strategy to correct the differential LD bias when estimating ID. Following a previous approach (19), we explored how stratifying SNPs according to their LD score (22) and their MAFs before analyses (details given in Supporting Information) could correct or at least reduce these biases. We illustrate in our first simulation that LD score and MAF (LDMS) stratification performs well in correcting these biases (Fig. 1).

Similar to that shown with ${\text{F}}_{\text{UNI}}$, we prove that the consistency of ID estimates obtained with ${\text{F}}_{\text{HOM}}$ (hereafter denoted ${\text{b}}_{\text{HOM}}$) is also determined by LD differences between SNPs and causal variants (Eq. S5). However, the bias of ${\text{b}}_{\text{HOM}}$ cannot simply be predicted by the ratio of the mean LD score in causal variants over the mean LD score in SNPs (Supporting Information). Nevertheless, our derivations predict that ${\text{b}}_{\text{HOM}}$ behaves similarly to ${\text{b}}_{\text{UNI}}$ with respect to LD differences between causal variants and SNPs. Importantly, we also prove that possible directional effects of minor alleles (DEMA) could confound ${\text{b}}_{\text{HOM}}$ because of the correlation between minor allele counts and ${\text{F}}_{\text{HOM}}$ (Supporting Information). Such directional effects could arise as a consequence of directional selection (when the minor allele is also the derived allele) as previously reported in human height (23) or simply because of population stratification (PS).

Simulation Study.

The complete description of the simulation study is given in Supporting Information.

Influence of differential MAF and LD between causal variants and SNPs.

We first considered three scenarios to illustrate the influence of LD and MAF heterogeneity between causal variants and SNPs. In all these scenarios, we assumed no DEMA, i.e., parameter $\text{s}=0$ in Eq. S3, and that b = −3 phenotypic SDs. Moreover, we assumed the expectation of the dominance effects to be either constant, i.e., ${\delta }_j=-b/{\sum }_{j=1}^{m}2p_j(1-p_j)$, or inversely proportional to the variance of the minor allele count, i.e., ${\delta }_j=-b/2m{p}_j(1-p_j)$. The first assumption corresponds to neutral traits, whereas the second one assigns a larger effect to SNPs with lower MAF and therefore corresponds more to traits under directional selection. Unbiasedness is defined below as when the average estimate of ID over multiple simulation replicates does not significantly differ from the value of b used for simulation.

Scenario 1.

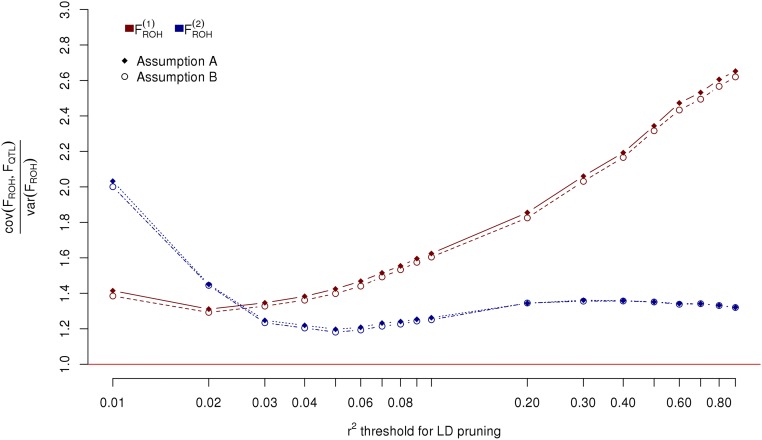
In this scenario the causal variants were randomly sampled from the 3,857,369 autosomal SNPs that passed the genotypes quality control (Supporting Information). As predicted by our derivations, we observed that ${\text{F}}_{\text{UNI}}$-based estimates of b were unbiased when dominance effects are assumed inversely proportional to the variances of allele counts, whereas an overestimation of $\sim 14\%$ of b was observed when dominance effects are assumed constant (Fig. 1A). This overestimation is explained by the fact that assuming a constant dominance effect, regardless of allele frequencies, creates an apparent MAF and LD heterogeneity between SNPs and causal variants by relatively up-weighting common SNPs compared with rarer SNPs (Eq. S3). We observed that LDMS stratification, which accounts for that heterogeneity, completely corrected this upward bias as presented in Fig. 1A. In addition, we found that ${\text{F}}_{\text{HOM}}$ produced unbiased estimates of b when dominance effects are assumed constant as for a neutral trait (Fig. 1A), but was biased downward ($-7\%$ of b) when dominance effects are inversely proportional to the variances of allele counts (Fig. 1B). This downward bias can be explained using the same reasoning presented above because in that case assuming dominance effects inversely proportional to the variances of allele counts relatively up-weights rarer SNPs compared with common ones. This downward bias could similarly be corrected using LDMS stratification. We also found that estimates of b obtained with ROH-based measures of inbreeding were strongly biased: $+162\%$ of b using the definition of ROH from Joshi et al. (10) [hereafter denoted $F_{\text{ROH}}^{(1)}$] and $+91\%$ of b using an alternative definition from Gazal et al. (15) or Howrigan et al. (24) [hereafter denoted as $F_{\text{ROH}}^{(2)}$]. The main difference between those two definitions of ROH is that $F_{\text{ROH}}^{(2)}$ requires LD pruning of the SNPs before calling the ROHs, whereas $F_{\text{ROH}}^{(1)}$ explicitly imposes a constraint on the ROH lengths (here $>1.5$ Mb). This result highlights that LD pruning improves ID estimation using ROH-based inbreeding measures but still remains insufficient to produce unbiased estimates. Indeed, using more stringent LD pruning thresholds did not change our conclusion (Fig. S1). Overall, we found that LDMS stratified estimates for ${\text{F}}_{\text{UNI}}$ and ${\text{F}}_{\text{HOM}}$ were unbiased in all cases (Fig. 1 A and B), which emphasizes that this strategy can be safely used even when causal variants are perfectly tagged by SNPs.

Fig. S1.

Bias of the ROH-based inbreeding measures ($F_{\mathrm{ROH}}$) expressed as the linear regression of the inbreeding coefficient at causal variants ($F_{QTL}$) over $F_{\mathrm{ROH}}$. Unbiasedness is equivalent to a regression coefficient of 1 (red horizontal line). All 3,857,369 SNPs were considered as causal variants. Assumption A: The expectations of dominance effects are equal for all SNPs. Assumption B: The expectation of the dominance effect of each SNP is inversely proportional to the variance of the minor allele count for that SNP.

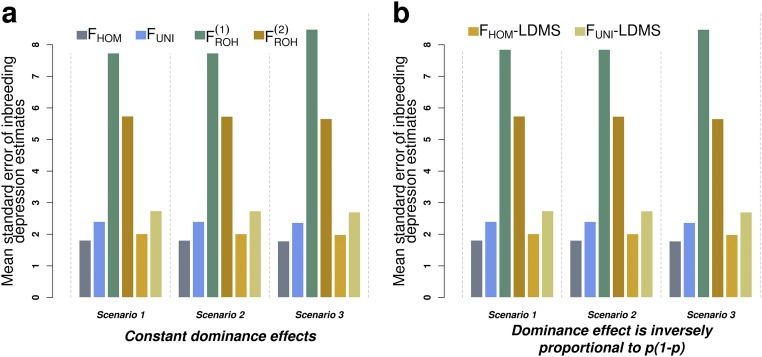
On average over 1,000 simulation replicates we found that ${\text{F}}_{\text{HOM}}$-associated estimates had smaller standard errors (SE) compared with ${\text{F}}_{\text{UNI}}$ or ${\text{F}}_{\text{ROH}}$ ($F_{\text{ROH}}^{(1)}$ and $F_{\text{ROH}}^{(2)}$) (Fig. S2 A and B). ${\text{F}}_{\text{HOM}}$ consequently yielded the largest statistical power whereas ${\text{F}}_{\text{UNI}}$ was second best with a power on average $10\%$ below that of ${\text{F}}_{\text{HOM}}$. On the other hand, because of their large SEs, $F_{\text{ROH}}^{(1)}$ and $F_{\text{ROH}}^{(2)}$ yielded the smallest statistical power to detect ID. Finally, we found that LDMS stratified estimates had $\sim 13\%$ larger SEs compared with nonstratified estimates. This increase in SE corresponds on average over all inbreeding measures to an $\sim 8\%$ loss of statistical power and is explained by the larger underlying effective dimensionality (4 LD score strata $\times$ 6 MAF strata = 24 parameters actually estimated; Supporting Information) of the LDMS approach compared with the nonstratified inference.

Fig. S2.

Averaged SEs of ID estimates from 1,000 simulated datasets. Datasets were simulated assuming a true ID parameter $b=-3$ (horizontal gray line) phenotypic SD for complete inbreeding. In scenario 1 the $m$ = 1,000 causal variants were randomly sampled from all observed SNPs, whereas in scenarios 2 and 3 they were respectively sampled from low- and high-LD regions of the genome. In A the expectation of the dominance effects (${\delta }_j$ for the $j$th causal variant) is constant (neutral model) whereas in B ${\delta }_j$ is inversely proportional to the variance of the minor allele count at each causal variant. $F_{\mathrm{HOM}}$, excess homozygosity inbreeding measure; $F_{\mathrm{ROH}}^{(1)}$ and $F_{\mathrm{ROH}}^{(2)}$, runs of homozygosity-based inbreeding measures; $F_{\mathrm{UNI}}$, measure of inbreeding based on correlation between uniting gametes; LDMS, LD and MAF stratified inference.

Scenarios 2 and 3.

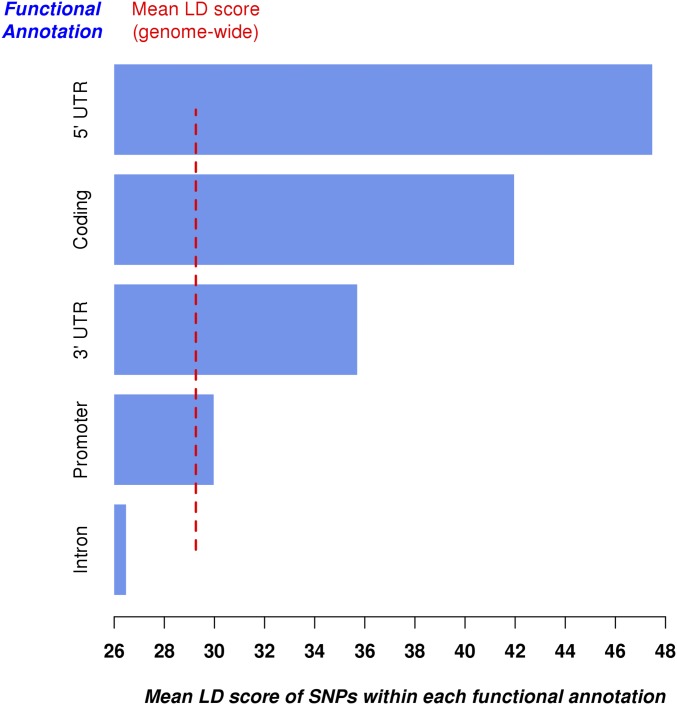
For the two other scenarios we used 1,358,699 SNPs within exons, introns, 3’-UTRs, 5’-UTRs, and promoter regions ±500 bp (SI Materials and Methods, URLs). SNPs within these five genomic (sets of) regions have distinct MAF and LD distributions as shown in Figs. S3 and S4. In scenario 2, we sampled the causal variants among 542,379 intronic SNPs with MAF $<5\%$ whereas in scenario 3 causal variants were sampled among 28,341 SNPs within exons, 3’-UTRs, and 5’-UTRs. Our theoretical derivations predict that ${\text{F}}_{\text{UNI}}$ and ${\text{F}}_{\text{HOM}}$ would underestimate the true ID in scenario 2 because causal variants in that scenario had on average lower LD scores (Fig. S3). Accordingly, we found over 1,000 simulation replicates an underestimation of $\sim 19\%$ of the true ID for ${\text{F}}_{\text{UNI}}$ and ${\text{F}}_{\text{HOM}}$ (Fig. 1). These downward biases could be reduced below $1\%$ of b using LDMS stratification (Fig. 1 A and B) and were not significantly different from 0 $(P>0.5)$. In scenario 3 causal variants had on average larger LD scores and MAF (Figs. S3 and S4). We therefore expected an overestimation of ID estimates in that scenario according to our theoretical derivations. This predicted upward bias was indeed more noticeable in our simulations ($\sim 40\%$ on average over all inbreeding measures) compared with scenario 2. Still, using LDMS stratification we were able to reduce these biases down to $<15\%$ of b on average over all inbreeding measures (Fig. 1) and more specifically $<10\%$ of b for ${\text{F}}_{\text{UNI}}$. Overall, LDMS stratification using ${\text{F}}_{\text{UNI}}$ yielded the smallest biases compared with all other strategies.

Fig. S3.

Mean LD score for SNPs within exons (coding), introns, 3’- and 5’-UTRs, and promoter regions. LD scores were calculated using $\sim$3.8 million genotyped and imputed SNPs that passed our quality control.

Fig. S4.

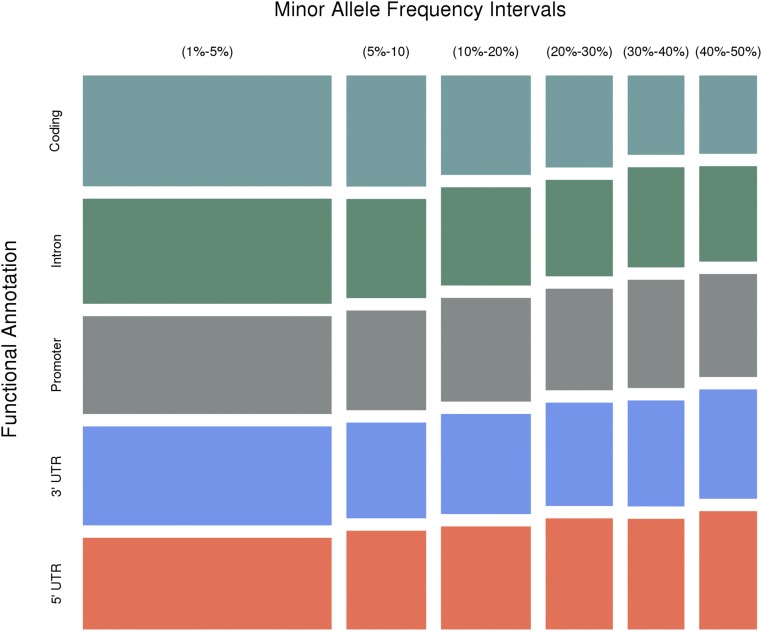
MAF distribution for $\sim$3.8 million SNPs within exons (coding), introns, 3’- and 5’-UTRs, and promoter regions. The height of each rectangle is proportional to the fraction of SNPs within the functional category and the width is proportional to the fraction of SNPs within the MAF interval.

Influence of DEMA.

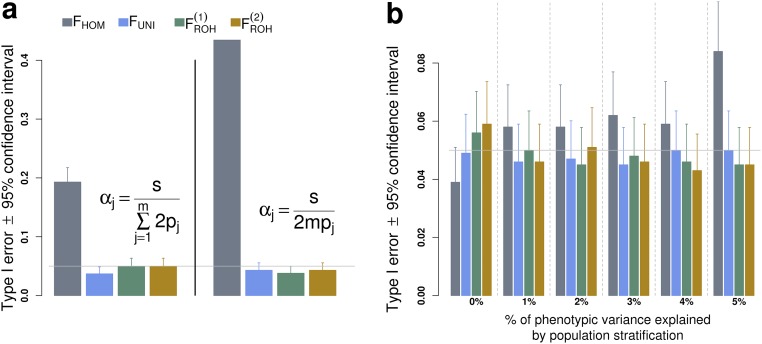
Let ${\alpha }_j$ denote the expectation of the additive effect of the minor allele at the jth causal variant. We define $\text{s}={\sum }_{j=1}^{m}2p_j{\alpha }_j$ as an overall measure of DEMA. Under this assumption we prove that estimates of ID obtained with ${\text{F}}_{\text{HOM}}$ are confounded because of the correlation between ${\text{F}}_{\text{HOM}}$ and minor allele counts (Supporting Information). We illustrate and quantify here that confounding bias. The parameters of this simulation are similar to scenario 1 of the first simulation, except that data are now simulated assuming no ID, i.e., $\text{b}=0$ and using $\text{s}=10$. With $\text{s}=10$, DEMA (which contributes to the additive genetic variance) accounts in our simulations for $\sim 0.3\%$ of the total phenotypic variance (Supporting Information). We considered two alternatives for the expectation of the additive effects ${\alpha }_j$: (i) ${\alpha }_j=s/{\sum }_{j=1}^{m}2p_j$ is constant and (ii) ${\alpha }_j=s/2m{p}_j$ is inversely proportional to the MAF $p_j$. Under both alternatives, we found that estimates of ID obtained with ${\text{F}}_{\text{HOM}}$ were severely biased (between −2 and −3 phenotypic SDs whereas the true value is 0; Fig. 2A) unlike those derived from other inbreeding measures. Whether this bias can be corrected is a difficult question in practice. Indeed, under the simplistic scenario considered here where causal variants are well tagged, adjusting for a genetic score summing all minor alleles should completely correct this bias. However, in more realistic situations where causal variants are only partially tagged, this would remain insufficient. In contrast, theory shows that ${\text{F}}_{\text{UNI}}$ is orthogonal to minor allele counts and consequently would not be influenced by such directional effects if these exist. This result has motivated our decision to restrict real data analyses to ${\text{F}}_{\text{UNI}}$ only even if ${\text{F}}_{\text{HOM}}$ had better statistical power in our previous simulations.

Fig. 2.

Averaged estimates of ID from 1,000 simulated datasets. In A datasets were simulated assuming no ID, i.e., $\text{b}=0$ and nonnegative expectation for the additive effects (i.e., ${\alpha }_{\text{j}}>0$, for the jth causal variant). In B datasets were simulated assuming no ID $(\text{b}=0)$ and no directional effect of minor alleles $(\text{s}=0)$ but including the contribution of the first 10 genotypic PCs to model the effect of population stratification. ${\text{F}}_{\text{HOM}}$, excess homozygosity inbreeding measure; ${\text{F}}_{\text{ROH}}$, runs of homozygosity-based inbreeding measures; ${\text{F}}_{\text{UNI}}$, measure of inbreeding based on correlation between uniting gametes; SEM, SE of the mean.

DEMA could also arise as a consequence of PS. To illustrate that second aspect, we performed another simulation with settings similar to scenario 1 of the first simulation (with $\text{b}=0$ and $\text{s}=0$) but now include the effect of 10 genotypic principal components (PC) as a proxy for PS (Supporting information). When varying the contribution of PS to the phenotypic variance from 0 to $5\%$, we observed that PS had a larger influence on estimates derived from ${\text{F}}_{\text{HOM}}$ and ${\text{F}}_{\text{ROH}}$. These observations are consistent with our theoretical results (at least for ${\text{F}}_{\text{HOM}}$) as they directly derive from the correlation between ${\text{F}}_{\text{HOM}}$ and minor allele counts, the weighted sum of which constitutes the PC. The biases of ${\text{F}}_{\text{HOM}}$- and ${\text{F}}_{\text{ROH}}$-associated ID estimates were on average $\sim 1$ phenotypic SD (Fig. 2B) when PS explained $5\%$ of the phenotypic variance but were significant only for ${\text{F}}_{\text{HOM}}$ (Fig. S5B). On the contrary, the biases observed when using ${\text{F}}_{\text{UNI}}$ never exceeded 0.5 phenotypic SD (Fig. 2B) and were not statistically different from 0 (Fig. S5B). In conclusion, orthogonality between ${\text{F}}_{\text{UNI}}$ and minor allele counts (25) (Supporting Information) guarantees that confounding by DEMA or PS is negligible for ID estimates obtained with this measure.

Fig. S5.

Type I error rate associated with the detection of ID. Type I error rate is measured as the fraction of P values $<5\%$ from 1,000 simulated datasets. In A datasets were simulated assuming no ID; i.e., $b=0$ and nonnegative expectation for the additive effects (i.e., ${\alpha }_j>0$, for the $j$th causal variant). In B datasets were simulated assuming no ID ($b=0$) and no directional effect of minor alleles ($s=0$), but including the contribution of the first 10 genotypic PCs to model the effect of PS. Abbreviations are as defined in Fig. S2.

To summarize this section, we show in our simulations that biases in ID estimates induced by MAF and LD heterogeneity between SNPs and causal variants can be corrected using LDMS stratification. Moreover, we show on average that LDMS correction performs better when applied to ${\text{F}}_{\text{UNI}}$ and that ${\text{F}}_{\text{UNI}}$-based ID estimates are robust to DEMA and PS. Overall, ${\text{F}}_{\text{UNI}}$ offers the best trade-off between statistical efficiency and unbiasedness in the situations covered in this simulation study. We therefore recommend its use and focus hereafter our analyses on real data to ${\text{F}}_{\text{UNI}}$.

Analysis of UK Biobank Data.

We quantified ID in 25 quantitative traits measured in $\sim \mathrm{140,000}$ (Table 1) participants from the UK Biobank (Supporting Information). These traits can be grouped into three categories including physical measures (standing height, weight, body mass index, waist and hip circumferences, waist/hip ratio, bone mineral density, body fat percentage, hand grip strength, systolic blood pressure, diastolic blood pressure, heart pulse rate, peak expiratory flow, visual acuity measured on log minimum angle of resolution (MAR) scale, and auditory acuity measured as the speech reception threshold), cognitive traits and educational attainment (fluid intelligence score, mean time to identify matches, maximum number of digits remembered, and age when completed full education), and sex-specific reproductive traits (number of children fathered, number of live births, age at menarche, and age at menopause) (Table S2). Some of these traits like standing height, peak expiratory flow (strongly correlated with forced expiratory volume in 1 s: $r=0.79$, $P<{10}^{-10}$), educational attainment, and cognitive ability were previously reported to be associated with inbreeding (10). Beyond quantifying the effect of inbreeding on these traits, we also aimed to evaluate whether differential LD and MAF distribution in causal variants influenced classical least-squares estimates and if so to correct these biases using our LDMS inference. The analyses were performed using linear regression adjusted for age, sex (for traits not specific to males or females), recruitment center, Townsend deprivation index (26) as a proxy for socio-economical status, and the first 10 genotypic PCs. The last three adjustments were considered to account for geographical and socio-economic structures in the UK population, which we found to correlate with levels of inbreeding (Table S3).

Table 1.

Statistically significant estimates of inbreeding depression for eight quantitative traits measured in the UK Biobank

		${\text{F}}_{\text{UNI}}$			${\text{F}}_{\text{UNI}}(\text{LDMS})$
Traits	N	Estimate	SE	P value	Estimate	SE	P value	PHET
PEF	117,575 (103,781)	−4.1 (−4.1)	0.62 (0.74)	4.57 $\times {10}^{-11}$ (3.48 $\times {10}^{-8}$)	−4.12 (−4.19)	0.69 (0.84)	2.25 $\times {10}^{-9}$ (6.35 $\times {10}^{-7}$)	0.941 (0.81)
AA, speech reception threshold	43,175 (38,449)	5.23 (4.44)	1.04 (1.26)	5.55 $\times {10}^{-7}$ (4.45 $\times {10}^{-4}$)	5.34 (4.39)	1.16 (1.45)	4.6 $\times {10}^{-6}$ (2.51 $\times {10}^{-3}$)	0.828 (0.94)
FIS	45,043 (40,089)	−3.9 (−3.14)	0.97 (1.23)	5.36 $\times {10}^{-5}$ (1.08 $\times {10}^{-2}$)	−4.72 (−4.32)	1.06 (1.42)	8.52 $\times {10}^{-6}$ (2.25 $\times {10}^{-3}$)	0.061 (0.07)
HGS, average of left and right hands	139,623 (122,950)	−2.36 (−2.72)	0.54 (0.68)	1.38 $\times {10}^{-5}$ (5.79 $\times {10}^{-5}$)	−2.43 (−3.31)	0.6 (0.76)	4.64 $\times {10}^{-5}$ (1.51 $\times {10}^{-5}$)	0.771 (0.1)
NCF	51,494 (45,483)	−3.09 (−3.69)	0.96 (1.16)	1.27 $\times {10}^{-3}$ (1.44 $\times {10}^{-3}$)	−4.01 (−4.58)	1.07 (1.32)	1.79 $\times {10}^{-4}$ (5.17 $\times {10}^{-4}$)	0.039 (0.14)
MTCIM	138,902 (122,334)	1.94 (1.7)	0.54 (0.68)	3.66 $\times {10}^{-4}$ (1.21 $\times {10}^{-2}$)	2.05 (2.1)	0.6 (0.77)	6.14 $\times {10}^{-4}$ (6.24 $\times {10}^{-3}$)	0.647 (0.26)
WHR	140,295 (123,540)	2.35 (3.03)	0.53 (0.67)	1.12 $\times {10}^{-5}$ (6.18 $\times {10}^{-6}$)	1.97 (2.89)	0.6 (0.76)	7.85 $\times {10}^{-4}$ (1.37 $\times {10}^{-4}$)	0.121 (0.69)
VA, log MAR scale	29,616 (26,596)	4.04 (5.77)	1.20 (1.51)	7.42 $\times {10}^{-4}$ (1.37 $\times {10}^{-4}$)	4.39 (6.68)	1.32 (1.73)	9.04 $\times {10}^{-4}$ (1.14 $\times {10}^{-4}$)	0.518 (0.26)

Effect sizes and standard errors are expressed in phenotypic SD of the trait. Results presented in parentheses were obtained after removing 16,781 related individuals and 19 extreme cases of inbreeding (F_UNI >0.15). N: sample size in the analysis. P_HET is the P value from the LDMS heterogeneity test comparing nonstratified and LDMS-stratified estimates.

Table S2.

Estimates of inbreeding depression for 25 quantitative traits measured in the UK Biobank

		FUNI		FHOM		$F_{\mathrm{ROH}}^{(1)}$		$F_{\mathrm{ROH}}^{(2)}$
Traits	N	Estimate (SE)	P value	Estimate (SE)	P value	Estimate (SE)	P value	Estimate (SE)	P value
PEF	117,575	−4.1 (0.6)	4.6 $\mathrm{\times }$ 10−11	−2.7 (0.5)	2.1 $\mathrm{\times }$ 10−8	−7.6 (1.4)	1.3 $\mathrm{\times }$ 10−7	−8.5 (1.5)	3.9 $\mathrm{\times }$ 10−8
AA	43,175	5.2 (1.0)	5.5 $\mathrm{\times }$ 10−7	3.2 (0.8)	7.5 $\mathrm{\times }$ 10−5	9.4 (2.4)	1.1 $\mathrm{\times }$ 10−4	11 (2.6)	1.3 $\mathrm{\times }$ 10−5
WHR	140,295	2.3 (0.5)	1.1 $\mathrm{\times }$ 10−5	1.8 (0.4)	3.2 $\mathrm{\times }$ 10−5	2.7 (1.2)	0.02	4.5 (1.3)	5.5 $\mathrm{\times }$ 10−4
HGS	139,623	−2.4 (0.5)	1.4 $\mathrm{\times }$ 10−5	−1.6 (0.4)	1.5 $\mathrm{\times }$ 10−4	−3.8 (1.2)	1.8 $\mathrm{\times }$ 10−3	−4.3 (1.3)	1.1 $\mathrm{\times }$ 10−3
FIS	45,043	−3.9 (1.0)	5.4 $\mathrm{\times }$ 10−5	−2 (0.8)	8.2 $\times$ 10−3	−7.9 (2.2)	3.9 $\mathrm{\times }$ 10−4	−7.9 (2.4)	9 $\mathrm{\times }$ 10−4
MTCIM	138,902	1.9 (0.5)	3.7 $\mathrm{\times }$ 10−4	1.3 (0.4)	2.4 $\times$ 10−3	3.7 (1.2)	2.5 $\times$ 10−3	3.6 (1.3)	6.2 $\times$ 10−3
Height	140,302	−1.9 (0.5)	4.8 $\mathrm{\times }$ 10−4	−1.1 (0.4)	0.01	−2.7 (1.2)	0.03	−3.5 (1.3)	7.3 $\times$ 10−3
VA	29,616	4 (1.2)	7.4 $\mathrm{\times }$ 10−4	2 (0.9)	0.04	7.7 (2.7)	4.9 $\times$ 10−3	7.9 (2.9)	7.3 $\times$ 10−3
NCF	51,494	−3.1 (1.0)	1.3 $\mathrm{\times }$ 10−3	−2.4 (0.7)	1.4 $\mathrm{\times }$ 10−3	−5.4 (2.2)	0.01	−7.7 (2.4)	1.3 $\mathrm{\times }$ 10−3
WC	140,233	1.4 (0.5)	7.2 $\times$ 10−3	0.91 (0.4)	0.03	1.9 (1.2)	0.12	2.7 (1.3)	0.04
BFat	138,055	1.1 (0.4)	0.05	0.71 (0.4)	0.09	1.6 (1.2)	0.19	1.9 (1.3)	0.14
HR	130,694	1.1 (0.6)	0.05	1.2 (0.4)	5.7 $\times$ 10−3	2.6 (1.3)	0.04	3.2 (1.4)	0.02
MNDR	145,75	−3.4 (1.8)	0.06	−2.7 (1.4)	0.06	−6.7 (4.3)	0.19	−8.3 (4.5)	0.07
A-Mena	72,196	1.3 (0.8)	0.08	0.29 (0.6)	0.63	1.4 (1.7)	0.42	1.9 (1.9)	0.3
BMI	139,686	0.94 (0.5)	0.08	0.54 (0.4)	0.21	0.86 (1.2)	0.48	1.3 (1.3)	0.3
BMR	138,047	−0.83 (0.5)	0.12	−0.61 (0.4)	0.16	−2.3 (1.2)	0.05	−2.5 (1.3)	0.05
A-Edu	95,540	−0.6 (0.6)	0.34	−0.36 (0.5)	0.48	0.19 (1.4)	0.89	−0.07 (1.5)	0.96
NLB	59,943	0.8 (0.9)	0.36	0.26 (0.7)	0.71	1.1 (2)	0.57	0.77 (2.1)	0.72
NIM	138,543	−0.45 (0.5)	0.41	−0.79 (0.4)	0.07	−2.9 (1.2)	0.02	−3.1 (1.3)	0.02
A-Meno	42,782	−0.82 (1.0)	0.43	−0.2 (0.9)	0.82	−1.8 (2.5)	0.46	−2 (2.7)	0.44
SBP	130,787	0.32 (0.6)	0.57	0.01 (0.4)	0.99	0.24 (1.3)	0.85	0.79 (1.4)	0.56
BMD	80,698	−0.31 (0.7)	0.65	−0.26 (0.5)	0.64	0.69 (1.5)	0.65	0.08 (1.6)	0.96
DBP	130,831	0.17 (0.56)	0.75	−0.21 (0.4)	0.63	0.8 (1.3)	0.52	1.1 (1.4)	0.39
HC	139,694	0.11 (0.54)	0.83	−0.1 (0.4)	0.81	0.5 (1.2)	0.68	0.17 (1.3)	0.89
Weight	139,916	−0.07 (0.5)	0.89	−0.096 (0.4)	0.82	−0.71 (1.2)	0.56	−0.68 (1.3)	0.59

AA, auditory acuity measured as the speech reception threshold; A-Edu, age when completed full education; A-mena, age at menarche; A-Meno, age at menopause; BFat, body fat percentage; BMD, bone mineral density; BMI, body mass index; BMR, basal metabolic rate; DBP, diastolic blood pressure; FIS, fluid intelligence score; HC, hip circumference and weight; HGS, hand grip strength; HR, heart pulse rate; MNDR, maximum number of digits remembered; MTCIM, mean time to correctly identify matches during cognitive test; NCF, number of children fathered; NIM, number of incorrect matches during cognitive test; NLB, number of live births; PEF, peak expiratory flow; SBP, systolic blood pressure; VA, visual acuity in log MAR scale; WC, waist circumference; WHR, ratio of waist circumference over hip circumference. Effect sizes and SEs are expressed in phenotypic SD. N: sample size in the analysis. Other abbreviations are defined in Fig. S2. P values <0.05/25 = 0.002 are highlighted in boldface type.

Table S3.

Statistical association between the inbreeding measures F_UNI (correlation between uniting gametes) and different measures of geographical and socio-economic structure in the UK Biobank

Measure of population structure	F statistic	Degrees of freedom	P value
Age at recruitment	6.84	1, N	8.9 $\times$ 10−3
Sex	0.32	1, N	0.57
Recruitment center	2.68	21, N	4.5 $\times$ 10−5
Townsend deprivation index Genotypic PCs	47.6	1, N	5.4 $\times$ 10−12
PC1	94.6	1, N	2.4 $\times$ 10−22
PC2	202	1, N	7.9 $\times$ 10−46
PC3	19.4	1, N	1.1 $\times$ 10−5
PC4	6.53	1, N	0.01
PC5	1.66	1, N	0.19
PC6	3.15	1, N	0.07
PC7	0.71	1, N	0.40
PC8	>3.35	1, N	0.07
PC9	0.03	1, N	0.86
PC10	1.63	1, N	0.20

Statistical association was measured analysis of variances. N = 140,720.

After Bonferroni correction ($P<0.05/25$ traits = $2\times {10}^{-3}$), we detected significant ID in eight traits (Table 1), using LDMS stratified inference based on ${\text{F}}_{\text{UNI}}$. Ranked by decreasing magnitude of depression, these traits are auditory acuity (AA), fluid intelligence score (FIS), visual acuity (VA), peak expiratory flow (PEF), number of children fathered (NCF), hand grip strength (HGS), mean time to correctly identify matches (MTCIM), and waist/hip ratio (WHR). This analysis included 16,781 related individuals (estimated to be first, second, or third degree) and 19 participants with extreme inbreeding $({\text{F}}_{\text{UNI}}>0.15)$. As a sensitivity analysis we reran all analyses without related and inbreeding outliers, which reduced the number of traits passing the significance threshold to five. The three traits dropped in this secondary analysis were AA ($P=2.51\times {10}^{-3}$ in secondary analysis), FIS ($P=2.25\times {10}^{-3}$ in secondary analysis), and MTCIM ($P=6.24\times {10}^{-3}$ in secondary analysis). To test whether the differences in ID estimates between full and reduced analyses are significant, we used a jackknife procedure to compare the observed differences with differences generated when randomly excluding 16,800 participants. Over 1,000 resampling events, we found that the observed differences in ID estimates for the eight traits highlighted above were not significantly different from those obtained when excluding random subsets (empirical $P>0.14$; Fig. S6). We consequently believe that the drop of significance between those two analyses is mainly explained by the reduced statistical power and not by confounding. In addition, we explored how much of ID could be captured at genome-wide significant (GWS) SNPs. We therefore selected trait-specific GWS SNPs from the genome-wide association studies (GWAS) catalog (SI Materials and Methods, URLs) and assessed inbreeding depression for the same traits using ${\text{F}}_{\text{UNI}}$ at those loci. We could not, however, detect any significant association with the traits analyzed in our study. Even for height, for which $\sim 700$ common GWSs are now reported (27), the estimate of inbreeding depression at GWS was only −0.08 SD for complete inbreeding $(P=0.072)$.

Fig. S6.

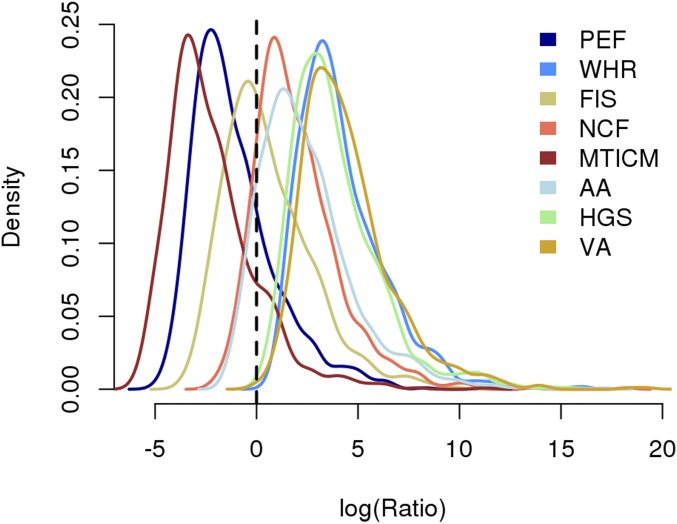
Distribution of the log ratio of absolute differences in ID estimates observed when excluding from our main analysis 16,800 (19 inbreeding outliers and 16,781 first-degree related) participants over differences generated by randomly excluding the same number of participants. These log ratios were $>0$ (ratio $>1$) in more than 14% of the 1,000 sampling replicates, suggesting that excluding the 16,800 participants from our main analysis has the same effect as excluding a random subset. AA, auditory acuity measured as the speech reception threshold; FIS, fluid intelligence score; HGS, hand grip strength; MTCIM, mean time to correctly identify matches during cognitive test; NCF, number of children fathered; PEF, peak expiratory flow; VA, visual acuity in log MAR scale; WHR, ratio of waist circumference over hip circumference.

We observed for all traits that ID estimates derived from ${\text{F}}_{\text{ROH}}$ were systematically larger than those obtained with ${\text{F}}_{\text{UNI}}$ (Table S3). As expected, their SEs were also larger. In particular, only four and six traits (of eight detected with ${\text{F}}_{\text{UNI}}$) passed the Bonferroni threshold when using ${\text{F}}_{\text{ROH}}^{\left(1\right)}$ and ${\text{F}}_{\text{ROH}}^{\left(2\right)}$, respectively. On the other hand, ID estimates obtained with ${\text{F}}_{\text{HOM}}$ were systematically smaller than those obtained using ${\text{F}}_{\text{UNI}}$ (Table S3), with an average over the eight traits significantly associated with ${\text{F}}_{\text{UNI}},{\text{b}}_{\text{HOM}}\approx 0.64\times {\text{b}}_{\text{UNI}}$. The latter observation would be expected if the traits analyzed are under directional selection as observed in our simulations when rarer variants were assumed to have larger effects.

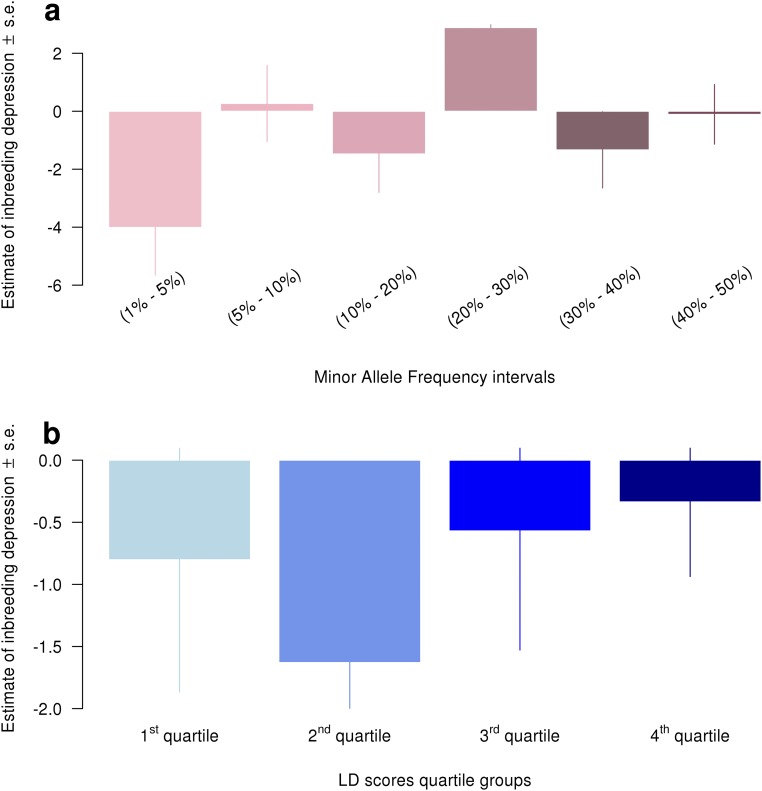
We observed for most traits that LDMS stratified and nonstratified ${\text{F}}_{\text{UNI}}$ estimates were similar (Table 1), suggesting weak differential LD and MAF distributions in SNPs tagging causal variants. Nonetheless, a marginally significant (LDMS heterogeneity test $P<0.05$; Table 1 and Fig. S7) difference could be observed in NCF for which the LDMS ID estimate was $\sim 1$ SE larger than the nonstratified one (Table 1). This also translated into an improvement of the association P value from $1.27\times {10}^{-3}$ to $1.79\times {10}^{-4}$ (Table 1). We subsequently assessed which component(s) in the LDMS stratification contributed the most to NCF (Fig. S8). We therefore fitted a first multivariate regression model adjusted for four inbreeding coefficients specific to each LD score strata component and then another multivariate regression model adjusted for six inbreeding coefficients specific to each MAF stratum. We chose to fit two different models (for MAF and LD separately) instead of one including 24 covariates to minimize the effects of colinearity between inbreeding measures in each LDMS stratum. We found a nominally significant contribution of SNPs with minor alleles $<5\%$ (${\text{b}}_{\text{FUNI}}$ = −4.01 phenotypic SD; $P=0.01$) but no significant enrichment in LD strata despite a large contribution of the second-lowest LD score stratum (${\text{b}}_{\text{FUNI}}$ = −1.62 phenotypic SD; $P=0.12$). According to our derivations, this enrichment of ID in lower-frequency SNPs and more generally in low-LD regions explains why nonstratified analyses produced smaller estimates compared with the LDMS approach. These results imply a disproportionate contribution of low-frequency SNPs to ID in NCF.

Fig. S7.

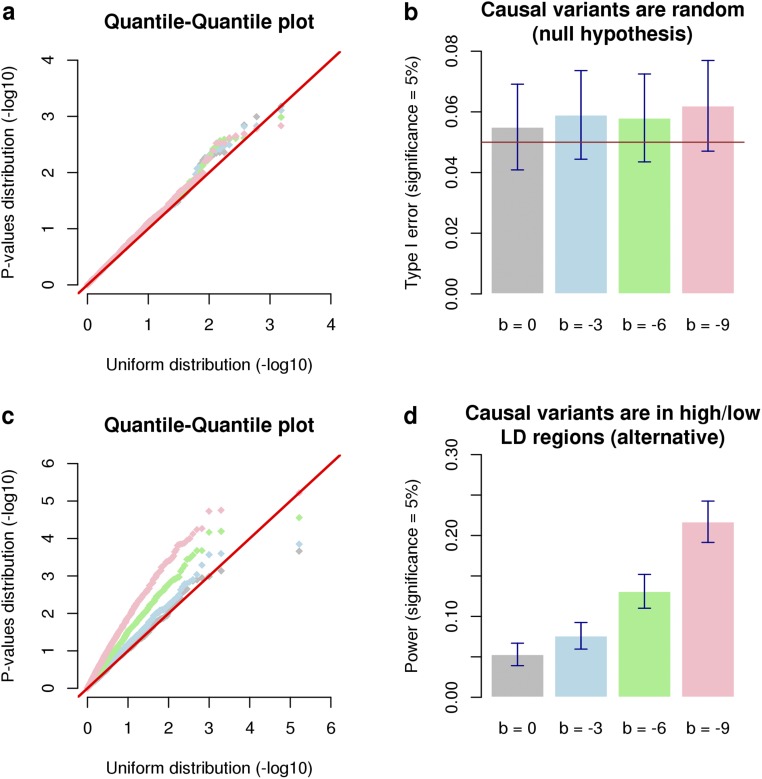
P-values distribution of the LD and MAF heterogeneity test. P values were calculated on data generated in simulation 1. A and B correspond to the null hypothesis ($H_0$) of no LD or MAF heterogeneity between SNPs and causal variants. C and D correspond to the alternative hypothesis ($H_1$) of LD and MAF heterogeneity between causal variants and SNPs. A and C compare via a quantile–quantile plot the P-value distribution to the uniform distribution between 0 and 1. B and D represent, for different values of the true inbreeding depression used to simulate the data ($b=0$, −3, −6, and −9), the proportion of those P values smaller than 0.05.

Fig. S8.

Estimates of ID in the NCF from the MAF and LD score stratified analysis (LDMS), using the F_UNI (correlation between uniting gametes) inbreeding measure. A corresponds to stratification into six MAF strata, whereas B corresponds to stratification into LD score segments. First LD score quartile corresponds to low LD.

SI Materials and Methods

Statistical Models and Notations.

We consider the following model:

$$y_i=\mu +\sum _{j=1}^m{a}_j{x}_{ij}+\sum _{j=1}^m{d}_j{H}_{ij}+{\epsilon }_i.$$ [S1]

For individual $i$, $y_i$ is the observed value of the fitness component of interest, and $x_{ij}$ is the minor allele count at the $j$th causal SNP ($x_{ij}\in \{\mathrm{0,1,2}\}$). $p_j$ is the MAF of the $j$th causal SNP, $H_{ij}=x_{ij}\left(2-x_{ij}\right)$ is the indicator of heterozygosity, and ${\epsilon }_i$ is a residual term capturing nongenetic effects on the observed phenotype. The additive and dominance effect sizes of the minor allele at the $j$th causal SNP are denoted $a_j$ and $d_j$, respectively. For the sake of simplicity, we assume that SNP interactions are negligible and consequently do not appear in Eq. S1. We also assume independence between the $m$ causal variants, between the genotypes and the effect sizes, and between the genetic and the nongenetic effects. Finally we assume the effect sizes to be random and such that $𝔼[a_j]={\alpha }_j$ and $𝔼[d_j]={\delta }_j$. We denote $f_i$ individual $i$s inbreeding coefficient. From Eq. S1 the expectation of $y_i$ with respect to the genotypes and the effect sizes can be written as

$$𝔼[y_i|f_i]=\underset{\text{Constant for all individuals}}{\underbrace{\mu +\sum _{j=1}^{m}2p_j{\alpha }_j+2p_j(1-p_j){\delta }_j}}+\underset{b:\hspace{0.17em}\text{reduction for complete inbreeding}}{\underbrace{\left(-\sum _{j=1}^{m}2p_j(1-p_j){\delta }_j\right)}}{f}_i,$$ [S2]

which translates a linear and often negative relationship between the average fitness component and the inbreeding coefficient $f_i$. The slope $b=-{\sum }_{j=1}^{m}2p_j(1-p_j){\delta }_j$ in this linear relationship is the expected depression in the fitness component due to complete inbreeding ($f_i=1$). Eq. S1 can also be written as

$$y_i=\mu +s{X}_i^{\text{QTL}}+b{F}_i^{\text{QTL}}+g_i^A+g_i^D+{\epsilon }_i,$$ [S3]

where $g_i^A={\sum }_{j=1}^m(a_j-𝔼[a_j])x_{ij}$ and $g_i^D={\sum }_{j=1}^m(d_j-𝔼[d_j])H_{ij}$ are the nondirectional additive and dominance breeding values of individual $i$, respectively. $X_i^{\text{QTL}}$ and $F_i^{\text{QTL}}$ are defined as

$$X_i^{\text{QTL}}=\frac{{\sum }_{j=1}^m{\alpha }_j{x}_{ij}}{{\sum }_{j=1}^{m}2p_j{\alpha }_j}\hspace{0.17em}\text{and}\hspace{0.17em}{F}_i^{\text{QTL}}=1-\frac{{\sum }_{j=1}^m{\delta }_j{H}_{ij}}{{\sum }_{j=1}^{m}2p_j(1-p_j){\delta }_j},$$

and $s$ and $b$ are defined as

$$s=\sum _{j=1}^{m}2p_j{\alpha }_j\hspace{0.17em}\text{and}\hspace{0.17em}b=-\sum _{j=1}^{m}2p_j(1-p_j){\delta }_j.$$

Measures of Inbreeding.

We studied three measures of inbreeding. All these measures of inbreeding require individual SNP genotypes and can be used in the absence of any pedigree information. The first inbreeding measure is the excess of homozygosity measure defined here as

$$F_{\mathrm{HOM}}=1-\frac{{\sum }_{k=1}^p{x}_k(2-x_k)}{{\sum }_{k=1}^{p}2p_k(1-p_k)},$$

where $x_k$ is the minor allele count of SNP $k$, $p_k$ is the MAF, and $p$ is the number of genotyped or imputed SNPs available. $F_{\mathrm{HOM}}$ is implemented in PLINK2 (command: –het).

The second measure ($F_{\mathrm{UNI}}$) is based on the correlation between uniting gametes. This measure was defined in Yang et al. (17) as

$$F_{\mathrm{UNI}}=\frac{1}{p}\sum _{k=1}^p\frac{x_k^2-(1+2p_k)x_k+2p_k^2}{2p_k(1-p_k)}.$$

$F_{\mathrm{UNI}}$ is implemented in PLINK2 and GCTA software (command: –ibc). The last measure is defined as the proportion of the genome within ROH. More specifically, the inbreeding measure $F_{\mathrm{ROH}}$ was calculated as the cumulated length (in base pairs) of one individual’s genome within ROHs divided by $3\times {10}^9$ (the approximate length of the autosomal genome in base pairs). We used two definitions of ROHs corresponding to those proposed in Joshi et al. (10) (definition 1) and Gazal et al. (15) (definition 2). Inbreeding measures calculated using definition 1 and definition 2 are respectively denoted as $F_{\mathrm{ROH}}^{(1)}$ and $F_{\mathrm{ROH}}^{(2)}$. Both definitions used SNPs with MAF $>5$% as previously reported in Joshi et al. (10) and Gazal et al. (15).

Definition 1 requires ROHs to be at least 1.5 Mb long, to cover at least 50 SNPs, and to be located at least 1 Mb away from one another. This corresponds to the following PLINK2 command: –homozyg –homozyg-density 50 –homozyg-gap 1000 –homozyg-kb 1500 –homozyg-snp 50 –homozyg-window-het 1 –homozyg-window-missing 5 –homo- zyg-window-snp 50. Definition 2 requires only LD pruning the SNPs (PLINK2 command –indep 50 5 2), but does not impose additional explicit constraint on ROHs besides not allowing any heterozygote in the ROHs. The following PLINK1 command was used to call ROHs under definition 2: –homozyg –homozyg-window-het 0 –homozyg-snp 50 –homozyg-kb 0 –homozyg-density 5000 –homozyg-gap 5000. As explained in Gazal et al. (15), the options –homozyg-density 5000 and –homozyg-gap 5000 are set for PLINK1 to ignore those constraints.

Theoretical Determinants of Unbiased Estimation.

The linear relationship in Eq. S2 naturally implies the use of linear regression to estimate ID. Least-squares estimates of ID derived from the inbreeding measure F asymptotically converge toward ${\widehat{b}}_F=\mathrm{cov}[F,y]/𝕍[F]$.

For F = $F_{\mathrm{UNI}}$, ${\widehat{b}}_F$ can be written as (proof in SI Appendix)

$$b_{\text{UNI}}=b\times \left(\frac{{\sum }_{j=1}^p{w}_j{L}_j^C}{1/p{\sum }_{k=1}^p{L}_k^{\text{SNP}}}\right),\text{where}\hspace{0.17em}{w}_j=\frac{2p_j(1-p_j){\delta }_j}{{\sum }_{j=1}^{m}2p_j(1-p_j){\delta }_j}.$$ [S4]

In Eq. S4, $L_j^C$ is the average LD between the $j$th causal variants and the $p$ observed SNPs, whereas $L_k^{\text{SNP}}$ is the average LD between the $k$th observed SNPs and the $p$ observed SNPs. To better understand Eq. S4, we note that when ${\delta }_j$ is inversely proportional to $2p_j(1-p_j)$, $w_j$ simplifies into $1/m$ and therefore $b_{\text{UNI}}/b$ is simply the ratio of mean LD score in causal variants over the mean LD score in SNPs. More generally, if $L_j^C\approx 1/p{\sum }_{k=1}^p{L}_k^{\text{SNP}}$ (which would hold when causal variants are a subset of SNPs), then Eq. S4 simplifies as $b_{\text{UNI}}=b({\sum }_{j=1}^m{w}_j)=b$.

For F = $F_{\mathrm{HOM}}$ we can derive a somewhat similar expression (proof in SI Appendix),

$$b_{\text{HOM}}=-s\times \left(\frac{{\sum }_{j=1}^p{w}_j^{(a)}{R}_j^C}{1/S_p{\sum }_{k=1}^p{S}_k}\right)+b\times \left(\frac{{\sum }_{j=1}^p{w}_j^{(d)}{S}_j^C}{1/S_p{\sum }_{k=1}^p{S}_k}\right).$$ [S5]

In Eq. S5, $R_j^C$ and $S_j^C$ measure the LD between causal variant and SNPs, whereas $S_k$ measures the LD among SNPs. Detailed derivations of these quantities are given in SI Appendix as well as the proof of unbiasedness when causal variants are randomly sampled from SNPs.

LD Score and MAF (LDMS) Stratified Inference.

We defined the LD score (22) of SNP j as the sum of pairwise $r^2$ between SNP $j$ and all SNPs located within 10 Mb around SNP $j$’s physical position. To correct potential biases induced by uneven LD (and MAF) distribution between causal variants and SNPs, we used a LD and MAF stratified inference as previously described (19). This approach is summarized below in five steps.

(i) The first step consists of identifying segments of the genome with uniform LD patterns. For this we used a sliding-window approach where each segment contains $2m_s$ SNPs with overlap of $m_s$ SNPs with adjacent segments. The number $m_s$ was chosen as in Yang et al. (19) to be the average number of SNPs per 100 kb of a chromosome: $m_s=100\times n_{SNP}/L_{SNP}$, with $n_{SNP}$ and $L_{SNP}$ being respectively the number of SNPs and the length (in kilobases) of the chromosome. We then calculated the mean LD score of the variants in each segment and took the average of the mean LD scores of two adjacent segments for overlapped regions. This process partitioned the genome into a large number of segments. (ii) The second step consists of stratifying the SNPs into K groups $(G_1\mathrm{\dots }{G}_K)$ according to the mean LD score of the segments ($m_{LDS}$) and the MAF interval they belong to. We used here four classes of LD [$m_{LDS}<$first quartile (low LD), first quartile$<m_{LDS}<$median, median $<$ $m_{LDS}$ $<$ 3rd quartile, and $m_{LDS}>$third quartile) and six MAF intervals [(1–5%), (5–10%), (10–20%), (20–30%), (30–40%), and (40–50%)], i.e., $4\times 6=24$ strata in total. (iii) For each group $G_k$, the third step consists of calculating a measure of inbreeding $F_k$ (could be any of the three measures presented in this study) specific to that group. (iv) In the fourth step we fitted a multivariate linear regression model using all of the $F_k$s as covariates to obtain ${𝐛}_{𝐊}=({\widehat{b}}_1,\mathrm{\dots },{\widehat{b}}_K)$, a vector of $K$ regression coefficients corresponding to each group. (v) The fifth and last step comprises collapsing these $K$ estimates into a single genome-wide estimate ${\widehat{b}}^{(LDMS)}$: ${\widehat{b}}^{(LDMS)}={\widehat{b}}_1+\mathrm{\dots }+{\widehat{b}}_K$, where ${\mathrm{𝟏}}_K$ is a $K$-dimensional vector with all entries equal to 1. The SE of ${\widehat{b}}^{(LDMS)}$) can be obtained from the asymptotic variance–covariance matrix of ${𝐛}_{𝐊}$, using the following relationship:

$$𝕍[{\widehat{b}}^{(LDMS)}]={\mathrm{𝟏}}_K𝕍[{𝐛}_{𝐊}]{\mathrm{𝟏}}_K^{\prime }.$$

We developed and applied a Wald test to assess the statistical significance of differences between nonstratified and LDMS stratified ID estimates. The test statistic is defined as the squared difference between the two estimates divided by the variance of that difference. The details of that derivation and some additional simulations showing that this test is not inflated in the absence of LD or MAF heterogeneity are presented in SI Appendix and Fig. S7. The LDMS procedure is implemented in GCTA as part of the GCTA-GREML-LDMS analysis (SI Materials and Methods, URLs).

UK Biobank Data.

Inclusion criteria.

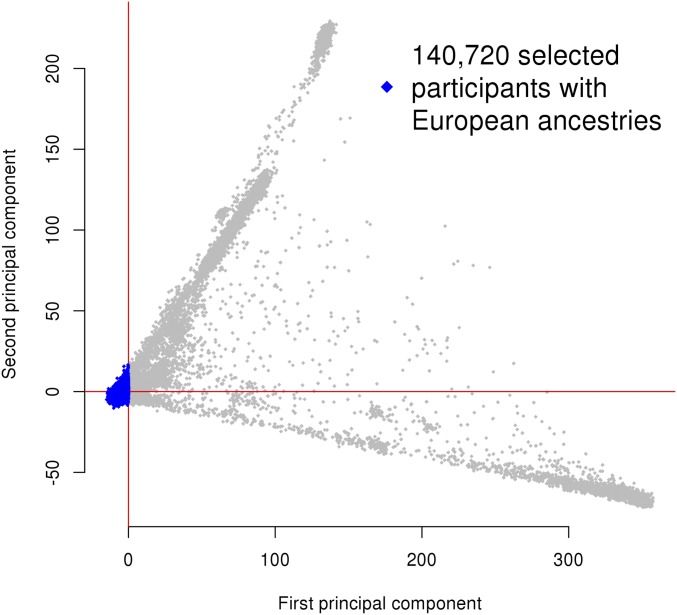
We used baseline data from 152,729 participants from the UK Biobank (34). To ensure ancestry homogeneity, we selected individuals who reported to be British, Irish, white, or of any other white background and whose coordinates on the first genetic PC were below 0 (Fig. S9). In total, we included 140,720 participants in this analysis. All participants in the UK Biobank study provided written informed consent.

Fig. S9.

First two PCs used to infer ethnicity in the UK Biobank participants. Principal components were calculated using $\sim$150,000 independent SNPs.

Phenotyping.

We analyzed 25 traits: standing height, weight, body mass index, waist and hip circumferences, ratio between waist circumference and hip circumference (referred to as WHR), bone mineral density, body fat percentage, HGS, systolic blood pressure, diastolic blood pressure, heart pulse rate, PEF, VA (measured on log MAR scale) and AA (measured as the speech reception threshold), cognitive traits and EA (FIS, MTCIM, maximum number of digits remembered, and age when completed full education), and sex-specific reproductive traits (NCF, number of live births, age at menarche, and age at menopause). For each trait, we excluded values $>4$ SD away from the mean. The sample sizes specific to each trait are given in Table S2. Finally, all traits were adjusted for age, sex (for traits not specific to males or females), recruitment center, 10 genotypic PCs, and Townsend deprivation index (26) as a proxy for the socio-economic status. After adjustment, we used inverse normal transformed residuals as the traits to be correlated with inbreeding measures. Although focused on $F_{\mathrm{UNI}}$, we also provide ID estimates from other inbreeding measures, in particular from $F_{\mathrm{ROH}}$ for comparison with previous and future studies using those measures (Table S2).

Genotyping.

We used data from 152,729 participants (including 140,720 analyzed in this study; SI Materials and Methods, Inclusion criteria) genotyped in the first phase of genotyping of the UK Biobank. The first steps of the quality control have been previously described (SI Materials and Methods, URLs). Phasing and imputation were performed using SHAPEIT and IMPUTE2 (SI Materials and Methods, URLs), respectively, as previously described (35). After imputation, we selected 9,493,148 autosomal SNPs with imputation quality $r^2>0.3$, MAF$>$1%, and Hardy–Weinberg equilibrium test P value $>{10}^{-6}$. Imputed SNPs were then called to the genotypes having the largest posterior probability. Finally, we removed redundancy by LD pruning SNPs with a squared genotype correlation $r^2>0.9$. In total we used 3,857,369 SNPs in this analysis.

Simulation Study.

In all simulations we used 10,000 unrelated (pairwise genetic relationship $<0.05$) individuals randomly sampled from the 140,720 individuals selected for analysis.

Simulation 1: Influence of MAF and LD distribution in causal variants.

To illustrate the importance of LD and MAF distribution in causal variants, we considered three scenarios. In the first scenario (scenario 1) we sampled the causal variants at random among the 3,857,369 observed SNPs. For the two other scenarios we used 1,358,699 SNPs within exons, introns, 3$\prime$-UTR, 5$\prime$-UTR, and promoter regions $\pm$500 bp (SI Materials and Methods, URLs). The LD score and MAF distributions of SNPs within these functional annotations are presented in Figs. S3 and S4. In scenario 2, we sampled the causal variants among 542,379 intronic SNPs with MAF $<5$% (low-LD scenario) whereas in scenario 3 causal variants were sampled among 28,341 SNPs within exons and 3$\prime$- and 5$\prime$-UTRs (high-LD scenario). In all simulations, we sampled 1,000 sets of $m=1,000$ causal variants each and simulated a phenotype (1 replicate per set of causal variants), using the following modified version of Eq. S3:

$$y_i=\mu +s{X}_i^{\text{QTL}}+b{F}_i^{\text{QTL}}+g_i^{A\prime }+g_i^{D\prime }+{\epsilon }_i.$$ [S6]

In Eq. S6, $g_i^{A\prime }$ and $g_i^{D\prime }$ are respectively defined as in ref. 25 as the scaled additive and orthogonal dominance values:

$$g_i^{A\prime }=\sum _{j=1}^m(a_j-{\alpha }_j)\left[\frac{x_{ij}-2p_j}{\sqrt{2p_j(1-p_j)}}\right]\text{and}\hspace{0.17em}{g}_i^{D\prime }=\sum _{j=1}^m(d_j-{\delta }_j)\left[\frac{x_{ij}(1+2p_j-x_{i}j)-2p_j^2}{2p_j(1-p_j)}\right].$$

Under Eq. S1 and assuming that $a_j\sim \mathcal{N}({\alpha }_j,{\sigma }_a^2)$ and $d_j\sim \mathcal{N}({\delta }_j,{\sigma }_d^2)$, the phenotypic variance can be expressed as

$$𝕍[y]=𝕍[s{X}^{\text{QTL}}+b{F}^{\text{QTL}}]+m({\sigma }_a^2+{\sigma }_d^2)+{\sigma }_e^2\approx m({\sigma }_a^2+{\sigma }_d^2)+{\sigma }_e^2,$$ [S7]

where ${\sigma }_e^2=𝕍[{\epsilon }_i]$ is the variance of the nongenetic effects [derivation of Eq. S7 in SI Appendix]. Zhu et al. (25) found on average across multiple traits that additive variance was about fivefold larger than dominance variance. Following their findings, we fixed in our simulations ${\sigma }_a^2=5{\sigma }_d^2=5H^2/6m$, ${\sigma }_e^2=1-H^2$, and $H^2=0.8$, where $H^2$ denotes the heritability of the trait. We observed in our simulations that $𝕍[s{X}^{\text{QTL}}+b{F}^{\text{QTL}}]$ was negligible and consequently $𝕍[y]\approx 1$. We used two values of $b$, $b=0$ and $b=-3$ SD of the trait, to study statistical power to detect ID. In all simulations, the statistical significance threshold for P values is 5%. The ID parameter $b$ was estimated for each measure of inbreeding by fitting a linear regression model with the phenotype as the response variable and the corresponding measure as the primary covariate.

Simulation 2: Influence of directional effects of minor alleles.

In this simulation we illustrated how directional effects of minor alleles may confound estimates of ID. The settings of this simulation are similar to scenario 1 in the first simulation. We simulated data assuming no inbreeding depression, i.e., $b=0$ and fixed $s=10$. We considered two alternatives for the expectation of the additive effects ${\alpha }_j$: (i) ${\alpha }_j=s/{\sum }_{j=1}^{m}2p_j$ is constant and (ii) ${\alpha }_j=s/(2m{p}_j)$ is inversely proportional to the MAF $p_j$.

We further quantified the effect of PS on ID estimates by running another simulation (also similar to scenario 1 in the first simulation) with $b=0$, $s=0$, and now including the effect of the first 10 genotypic PCs $(P{C}_1,P{C}_2,\mathrm{\dots },P{C}_{10})$ as a proxy for PS:

$$y_i=\mu +\theta \left(\sum _{k=1}^{10}P{C}_k\right)+g_i^{A\prime }+g_i^{D\prime }+{\epsilon }_i.$$ [S8]

In Eq. S8 $\theta$ was chosen so that PS accounts for 1%, 2%, 3%, 4%, and 5% of the total phenotypic variance. PCs were calculated using genotypes from the 10,000 unrelated participants selected for the simulations. Type I error in this simulation was calculated as the fraction of P values (testing for the significance of ID) below 0.05.

Selection of Genome-Wide Significant SNPs from the GWAS Catalog.

To assess how much ID could be captured at GWS SNPs, we assessed inbreeding using $F_{\mathrm{UNI}}$ at GWS SNPs from the GWAS catalog (SI Materials and Methods, URLs). We downloaded version 1.0 of the GWAS catalog and selected SNPs so that their associated “DISEASE/TRAIT” field exactly matched “height,” “weight,” “body mass index,” “waist circumference,” “waist-hip ratio,” “bone mineral density,” “body fat percentage,” “systolic blood pressure,” “diastolic blood pressure,” “intelligence” [or “intelligence (childhood)”], “cognitive test performance,” “cognitive function,” “cognitive performance,” “general cognitive ability,” “educational attainment,” “educational attainment (years of education),” “educational attainment (college completion),” “age at first birth,” “menarche (age at onset),” “menopause (age at onset),” “forced expiratory volume in 1 s,” and “lung function (forced expiratory flow between 25% and 75% of forced vital capacity).” In total we selected 2,069 unique SNPs.

URLs.

• i)UK Biobank quality control: www.ukbiobank.ac.uk/wp-content/uploads/2014/04/UKBiobank_genotyping_QC_documentation-web.pdf.
• ii)UK Biobank imputation: www.ukbiobank.ac.uk/wp-content/uploads/2014/04/imputation_documentation_May2015.pdf.
• iii)SHAPEIT3, IMPUTE2: https://jmarchini.wordpress.com/software/.
• iv)Genomic annotations from UCSC website: https://genome.ucsc.edu/cgi-bin/hgTables.
• v)GCTA LDMS: gcta.freeforums.net/thread/194/gcta-ldms-estimating-heritability-sequencing.
• vi)GWAS catalog: https://www.ebi.ac.uk/gwas/.

SI Appendix

Derivation of Equation S2.

Starting with the following equation (Eq. 1 in the main text),

$$y_i=\mu +\sum _{j=1}^m{a}_j{x}_{ij}+\sum _{j=1}^m{d}_j{H}_{ij}+{\epsilon }_i,$$

and assuming independence between the effect sizes and the genotypes and $𝔼[a_j]={\alpha }_j$ and $𝔼[d_j]={\delta }_j$, then we can write that

$$𝔼[y_i|f_i]=\mu +\sum _{j=1}^m{\alpha }_j𝔼[x_{ij}|f_i]+\sum _{j=1}^m{\delta }_j𝔼[H_{ij}|f_i],$$

where $f_i$ is individual $i$’s inbreeding coefficient. We know that $𝔼[x_{ij}|f_i]=2p_j$ and $𝔼[H_{ij}|f_i]=2p_j(1-p_j)(1-f_i)$. Hence follows Eq. S2:

$$𝔼[y_i|f_i]=\mu +\sum _{j=1}^{m}2p_j{\alpha }_j+\sum _{j=1}^{m}2p_j(1-p_j)(1-f_i){\delta }_j=\mu +\sum _{j=1}^{m}2p_j{\alpha }_j+2p_j(1-p_j){\delta }_j+(-\sum _{j=1}^{m}2p_j(1-p_j){\delta }_j)f_i.$$

Derivation of Eqs. S4 and S5.

Additional notations and useful formulas.

We introduce now new notations. Let $x_j^{(f)}$ and $x_j^{(m)}$ be the number of minor alleles (0 or 1) inherited from the father and the mother, respectively. Then the minor allele count $x_j$ is defined as $x_j=x_j^{(f)}+x_j^{(m)}$. We introduce $D_{jk}$ as the LD parameter between minor alleles of SNP $j$ and SNP $k$. We assume that the LD between paternal and maternal alleles is the same, i.e., that $(x_j^{(f)},x_k^{(f)})$ and $(x_j^{(m)},x_k^{(m)})$ have the same probability distribution. The latter distribution is presented in Table S1.

Let $I_i$ be the indicator of complete inbreeding; i.e., $I_i=1$ with probability $f_i$ if individual $i$ is completely inbred and $I_i=0$ if its parents are completely independent. We note $f=𝔼[f_i]$. We have now that

$$\mathrm{cov}[x_{ij}^{(f)},x_{ij}^{(m)}]=𝔼\left[𝔼[x_{ij}^{(f)}{x}_{ij}^{(m)}]\right]-𝔼[x_{ij}^{(f)}]𝔼[x_{ij}^{(m)}]=𝔼\left[\mathbb{P}[x_{ij}^{(f)}{x}_{ij}^{(m)}=1]\right]-p_j^2=𝔼\left[\mathbb{P}[x_{ij}^{(f)}{x}_{ij}^{(m)}=1|I_i=1]\mathbb{P}[I_i=1]\right]+𝔼[\mathbb{P}[x_{ij}^{(f)}{x}_{ij}^{(m)}=1|I_i=0](1-\mathbb{P}[I_i=1])-p_j^2]=𝔼[f_i{p}_j+(1-f_i)p_j^2-p_j^2]=p_j(1-p_j)𝔼[f_i]\mathrm{cov}[x_{ij}^{(f)},x_{ij}^{(m)}]=p_j(1-p_j)f.$$

Moreover, because we assume that LD between the father’s alleles is the same as between the mother’s alleles, then we have that $\mathrm{cov}[x_j^{(f)},x_k^{(f)}]=\mathrm{cov}[x_j^{(m)},x_k^{(m)}]=D_{jk}$.

Another important formula is

$$\mathrm{cov}[x_{ij}^{(f)},x_{ik}^{(m)}]=𝔼\left[𝔼[x_{ij}^{(f)}{x}_{ik}^{(m)}]\right]-𝔼[x_{ij}^{(f)}]𝔼[x_{ik}^{(m)}]=𝔼\left[\mathbb{P}[x_{ij}^{(f)}{x}_{ik}^{(m)}=1]\right]-p_j{p}_k=𝔼\left[\mathbb{P}[x_{ij}^{(f)}{x}_{ik}^{(m)}=1|I_i=1]\mathbb{P}[I_i=1]\right]+𝔼[\mathbb{P}[x_{ij}^{(f)}{x}_{ik}^{(m)}=1|I_i=0]\times (1-\mathbb{P}[I_i,=1])-p_j{p}_k]=𝔼[\mathbb{P}[x_{ij}^{(f)}{x}_{ik}^{(f)}=1|I_i=1]f_i+p_j{p}_k(1-f_i)-p_j{p}_k]=𝔼[f_i(p_j{p}_k+D_{jk})+p_j{p}_k(1-f_i)-p_j{p}_k]\mathrm{cov}[x_{ij}^{(f)},x_{ik}^{(m)}]=D_{jk}f.$$

Following the same reasoning, we can prove that

$$\mathrm{cov}[F_{\mathrm{UNI}}^{(j)},F_{\mathrm{UNI}}^{(k)}]=r_{jk}^2+\left(1-r_{jk}^2+\frac{D_{jk}(1-2p_j)(1-2p_k)}{p_j{p}_k(1-p_j)(1-p_k)}\right)f-f^2,\mathrm{cov}[H_j,F_{\text{UNI}}^{(k)}]=-2p_j(1-p_j)\left[r_{jk}^2+f(1-r_{jk}^2)\right],\mathrm{cov}[x_j,F_{\text{UNI}}^{(k)}]=\frac{4D_{jk}(1-2p_k)f}{2p_k(1-p_k)},\mathrm{cov}[H_j,H_k]=4p_j{p}_k(1-p_j)(1-p_k)f(1-f)+(1-f)\left[4D_{jk}^2+2D_{jk}(1-2p_k)(1-2p_j)\right]\mathrm{cov}[H_k,x_j]=2D_{jk}(1-2p_k)(1-f),$$ [S9]

where $F_{\text{UNI}}^{(j)}$ is defined as

$$F_{\text{UNI}}^{(j)}=\frac{x_j^2-(1+2p_j)x_j-2p_j^2}{2p_j(1-p_j)}.$$

Getting back to Eqs. S4 and S5.

Eq. S4.

Using the results above we have that

$$\frac{\mathrm{cov}[F_{\mathrm{UNI}},y]}{𝕍[F_{\mathrm{UNI}}]}=\frac{A^{(I)}f+A^{(R)}(1-f)}{B^{(I)}f+B^{(R)}(1-f)-f^2},$$ [S10]

where

$$A^{(I)}=\sum _{j=1}^m\sum _{k=1}^p\left\{\frac{4D_{jk}(1-2p_k)}{2p_k(1-p_k)}{\alpha }_j-2p_j(1-p_j){\delta }_j\right\}{A}^{(R)}=\sum _{j=1}^m\sum _{k=1}^p\left\{-\frac{4D_{jk}^2}{2p_k(1-p_k)}{\delta }_j\right\}=-\sum _{j=1}^{m}2p_j(1-p_j){\delta }_j\underset{L_j^C}{\underbrace{\left(\sum _{k=1}^p{r}_{jk}^2\right)}}$$

$$B^{(I)}=\frac{1}{p}\sum _{l=1}^p\sum _{k=1}^p\left(1+\frac{D_{lk}(1-2p_l)(1-2p_k)}{p_l{p}_k(1-p_l)(1-p_k)}\right)B^{(R)}=\frac{1}{p}\sum _{l=1}^p\underset{L_k^{\text{SNP}}}{\underbrace{\left(\sum _{k=1}^p{r}_{lk}^2\right)}}.$$

Given that $f\ll 1$, we may assume that $f\approx 0$ and therefore simplify Eq. S10 into Eq. S4.

Eq. S5.

For $F_{\mathrm{HOM}}$ we have that

$$\frac{\mathrm{cov}[F_{\mathrm{HOM}},y]}{𝕍[F_{\mathrm{HOM}}]}=S_p\times \frac{C^{(I)}f(1-f)+C^{(R)}(1-f)}{D^{(I)}f(1-f)+D^{(R)}(1-f)},$$ [S11]

where

$$S_p=\sum _{k=p}^{p}2p_k(1-p_k)C^{(I)}=\sum _{j=1}^m\sum _{k=1}^p\left\{4p_j{p}_k(1-p_j)(1-p_k)\times {\delta }_j\right\}{C}^{(R)}=\sum _{j=1}^m\sum _{k=1}^p\left\{-2{\alpha }_j{D}_{jk}(1-2p_k)+\left[4D_{jk}^2+2D_{jk}(1-2p_k)\times (1-2p_j)\right]\times {\delta }_j\right\}{D}^{(I)}=\sum _{l=1}^p\sum _{k=1}^p\left\{4p_l{p}_k(1-p_l)(1-p_k)\right\}=S_p^2{D}^{(R)}=\sum _{l=1}^p\sum _{k=1}^p\left\{4D_{lk}^2+2D_{lk}(1-2p_k)(1-2p_l)\right\}.$$

Therefore, with $f=0$, we have that

$$\frac{\mathrm{cov}[F_{\text{HOM}},y]}{𝕍[F_{\text{HOM}}]}=-s\left(\frac{{\sum }_{j=1}^m{\omega }_j^{(a)}{R}_j^{(C)}}{\frac{1}{S_p}{\sum }_{k=1}^p{S}_k}\right)+b\left(\frac{{\sum }_{j=1}^m{\omega }_j^{(d)}{S}_j^{(C)}}{\frac{1}{S_p}{\sum }_{k=1}^p{S}_k}\right),$$ [S12]

where

$${\omega }_j^{(a)}=\frac{{\alpha }_j}{{\sum }_{j=1}^{m}2{\alpha }_j{p}_j},{\omega }_j^{(d)}=\frac{{\delta }_j}{{\sum }_{j=1}^{m}2p_j(1-p_j){\delta }_j},R_j^{(C)}=\sum _{k=1}^{p}2D_{jk}\left(1-2p_k\right)S_k=\sum _{l=1}^p\left\{4D_{lk}^2+2D_{lk}(1-2p_k)(1-2p_l)\right\},$$

and

$$S_j^{(C)}=\sum _{k=1}^p\left\{4D_{jk}^2+2D_{jk}(1-2p_j)(1-2p_k)\right\}.$$

$R_j^{(C)}$ and $S_j^{(C)}$ both measure LD between the $j$th causal variant and the $p$ SNPs used for inference, and $S_k$ measures LD between SNP $k$ and all observed SNPs. To better understand the relationship described in Eq. S12, let us consider a special case. When $s=0$ and ${\delta }_j$ is constant, Eq. S12 can be written

$$\frac{\mathrm{cov}[F_{\text{HOM}},y]}{𝕍[F_{\text{HOM}}]}=b\left(\frac{\frac{1}{S_m^{(C)}}{\sum }_{j=1}^m{S}_j^{(C)}}{\frac{1}{S_p}{\sum }_{k=1}^p{S}_k}\right)=b\times \frac{\frac{1}{p}{S}_p}{\frac{1}{m}{S}_m^{(C)}}\times \frac{\frac{1}{m}{\sum }_{j=1}^m{S}_j^{(C)}}{\frac{1}{p}{\sum }_{k=1}^p{S}_k},$$ [S13]

where $S_m^{(C)}={\sum }_{j=p}^{m}2p_j(1-p_j)$. Therefore, when causal variants are randomly sampled from observed SNPs, $\frac{1}{m}{S}_m^{(C)}\approx \frac{1}{p}{S}_p$ and $\frac{1}{m}{\sum }_{j=1}^m{S}_j^{(C)}\approx \frac{1}{p}{\sum }_{k=1}^p{S}_k$, which guarantees unbiasedness.

Derivation of Eq. S7.

To derive Eq. S7, we assumed the following modified version of Eq. S3:

$$y_i=\mu +s{X}_i^{\text{QTL}}+b{F}_i^{\text{QTL}}+g_i^{A\prime }+g_i^{D\prime }+{\epsilon }_i.$$ [S14]

In Eq. S14 $g_i^{A\prime }$ and $g_i^{D\prime }$ are respectively defined as the scaled additive and orthogonal dominance values (25):

$$g_i^{A\prime }=\sum _{j=1}^m(a_j-{\alpha }_j)\times \left[\frac{x_{ij}-2p_j}{\sqrt{2p_j(1-p_j)}}\right]\text{and}\hspace{0.17em}{g}_i^{D\prime }=\sum _{j=1}^m(d_j-{\delta }_j)\times \left[\frac{x_{ij}(1+2p_j-x_{ij})-2p_j^2}{2p_j(1-p_j)}\right].$$

Because of the independence between effect sizes and genotypes, we have that

$$\mathrm{cov}[X_i^{\text{QTL}},g_i^{A\prime }]=𝔼[X_i^{\text{QTL}}{g}_i^{A\prime }]-𝔼[X_i^{\text{QTL}}]\underset{=0}{\underbrace{𝔼[g_i^{A\prime }]}}=\sum _{j,l}^m𝔼[a_j-{\alpha }_j]𝔼[a_l-{\alpha }_l]\times 𝔼\left(X_{il}^{\text{QTL}}\left[\frac{x_{ij}-2p_j}{\sqrt{2p_j(1-p_j)}}\right]\right)=0.$$

Similarly, we have that $\mathrm{cov}[X_i^{\text{QTL}},g_i^{D\prime }]=\mathrm{cov}[F_i^{\text{QTL}},g_i^{A\prime }]=\mathrm{cov}[F_i^{\text{QTL}},g_i^{D\prime }]=0$. Therefore,

$$𝕍[y_i]=𝕍[s{X}_i^{\text{QTL}}+b{F}_i^{\text{QTL}}]+𝕍[g_i^{A\prime }+g_i^{D\prime }+{\epsilon }_i].$$

Let us now derive the expression of $𝕍[s{X}_i^{\text{QTL}}+b{F}_i^{\text{QTL}}]$. We note that $h_j=2p_j(1-p_j)$:

$$𝕍[s{X}_i^{\text{QTL}}+b{F}_i^{\text{QTL}}]=𝕍\left[\sum _{j=1}^m{\alpha }_j{x}_{ij}+b-\sum _{j=1}^m{\delta }_j{H}_{ij}\right]=\sum _{j=1}^m{\alpha }_j^2𝕍[x_{ij}]+{\delta }_j^2𝕍[H_{ij}]-2{\alpha }_j{\delta }_j\mathrm{cov}[x_{ij},H_{ij}]=\sum _{j=1}^m{h}_j\left[{\alpha }_j^2+{\delta }_j^2(1-h_j)-2{\alpha }_j{\delta }_j(1-2p_j)\right].$$

We consider two cases corresponding to the different configurations presented in this paper:

$i)$ ${\alpha }_j=0$.

$$𝕍[s{X}_i^{\text{QTL}}+b{F}_i^{\text{QTL}}]=𝕍[b{F}_i^{\text{QTL}}]=\sum _{j=1}^m{h}_j\left[{\delta }_j^2(1-h_j)\right].$$

When ${\delta }_j=-b/2m{p}_j(1-p_j)$, we have that

$$𝕍[b{F}_i^{\text{QTL}}]=\frac{b^2}{m^2}\sum _{j=1}^m\frac{(1-h_j)}{h_j}=\frac{b^2}{m}\left(\frac{1}{m}\sum _{j=1}^m\frac{1}{h_j}-1\right).$$

If we assume for example the causal variants to be a random subset of HapMap 3 (HM3) SNPs ($\sim$1.1 million SNPs), we can therefore use their allele frequencies to approximate $\frac{1}{m}{\sum }_{j=1}^m\frac{1}{h_j}$. Using allele frequencies of HM3 SNPs in the UK Biobank, we found that $\frac{1}{m}{\sum }_{j=1}^m\frac{1}{h_j}\approx 5$ and therefore that

$$𝕍[b{F}_i^{\text{QTL}}]\approx \frac{4b^2}{m}.$$

A different set of SNPs could have been used instead of HM3 SNPs. However, we argue here that in any case, $\frac{1}{m}{\sum }_{j=1}^m\frac{1}{h_j}$ is constant with respect to the number of causal variants $m$ and therefore $𝕍[b{F}_i^{\text{QTL}}]$ would be negligible for a trait with a large number of causal variants. When ${\delta }_j=-b/{\sum }_{j=1}^m{h}_j$, we have that

$$𝕍[b{F}_i^{\text{QTL}}]=b^2\left(\frac{{\sum }_{j=1}^m{h}_j(1-h_j)}{{\left({\sum }_{j=1}^m{h}_j\right)}^2}\right)=\frac{b^2}{m}\left(\frac{\frac{1}{m}{\sum }_{j=1}^m{h}_j(1-h_j)}{{\left(\frac{1}{m}{\sum }_{j=1}^m{h}_j\right)}^2}\right).$$

Using HM3 SNPs, we can similarly approximate $\frac{1}{m}{\sum }_{j=1}^m{h}_j(1-h_j)\approx 0.198$ and $\frac{1}{m}{\sum }_{j=1}^m{h}_j=0.325$, which gives

$$𝕍[b{F}_i^{\text{QTL}}]\approx \frac{1.88\times b^2}{m}.$$

In conclusion, we show here that $𝕍[b{F}_i^{\text{QTL}}]$ is of order $1/m$ and therefore contributes little to the phenotypic variance of traits with large numbers of causal variants.

$\mathrm{𝑖𝑖})$ ${\delta }_j=0$.

$$𝕍[s{X}_i^{\text{QTL}}+b{F}_i^{\text{QTL}}]=𝕍[s{X}_i^{\text{QTL}}]=\sum _{j=1}^m{h}_j{\alpha }_j^2.$$

When ${\alpha }_j=s/2m{p}_j$, we have (still using HM3 SNPs) that

$$𝕍[s{X}_i^{\text{QTL}}]=\frac{s^2}{m^2}\sum _{j=1}^m\frac{h_j}{4p_j^2}=\frac{s^2}{2m^2}\sum _{j=1}^m\frac{1-p_j}{p_j}=\frac{s^2}{2m}\left(\frac{1}{m}\sum _{j=1}^m\frac{1}{p_j}-1\right)\approx \frac{4.32\times s^2}{m}.$$

and similarly, when ${\alpha }_j=s/{\sum }_{j=1}^{m}2p_j$, we can write that

$$𝕍[s{X}_i^{\text{QTL}}]=\frac{s^2}{m}\left(\frac{\frac{1}{m}{\sum }_{j=1}^m{h}_j}{{\left(\frac{1}{m}{\sum }_{j=1}^{m}2p_j\right)}^2}\right)\approx \frac{1.41\times s^2}{m}.$$

Just like $𝕍[b{F}_i^{\text{QTL}}]$, $𝕍[s{X}_i^{\text{QTL}}]$ is also of order $1/m$ and hence contributes little to the phenotypic variance.

We now denote $a_j^{\prime }$ and $d_j^{\prime }$ as

$$a_j^{\prime }=a_j-{\alpha }_j\sim \mathcal{N}(0,{\sigma }_a^2)\text{and}\hspace{0.17em}{d}_j^{\prime }=d_j-{\delta }_j\sim \mathcal{N}(0,{\sigma }_d^2).$$

Let $x_j^{(s)}$ and $x_j^{(D,s)}$ be defined as

$$x_j^{(s)}=\frac{x_{ij}-2p_j}{\sqrt{2p_j(1-p_j)}}\hspace{0.17em}\text{and}\hspace{0.17em}{x}_j^{(D,s)}=\frac{x_{ij}^D-2p_j^2}{2p_j(1-p_j)}$$

with $x_{ij}^{D,s}=x_{ij}\left(1+2p_j-x_{ij}\right)$. Hence,

$$𝕍[a_j^{\prime }{x}_j^{(s)}+d_j^{\prime }{x}_j^{(D,s)}]=𝕍\left[a_j^{\prime }{x}_j^{(s)}\right]+𝕍\left[d_j^{\prime }{x}_j^{(D,s)}\right]+2\mathrm{c}\mathrm{o}\mathrm{v}[a_j^{\prime }{x}_j^{(s)},d_j^{\prime }{x}_j^{(D,s)}]=𝔼\left[a_j^{\mathrm{\prime }2}{\left(x_j^{(s)}\right)}^2\right]-𝔼{\left[a_j^{\prime }{x}_j^{(s)}\right]}^2+𝔼\left[d_j^{\mathrm{\prime }2}{\left(x_j^{(D,s)}\right)}^2\right]-𝔼{\left[d_j^{\prime }{x}_j^{(D,s)}\right]}^2+2\mathrm{c}\mathrm{o}\mathrm{v}[a_j^{\prime }{x}_j^{(s)},d_j^{\prime }{x}_j^{(D,s)}]=𝔼\left[a_j^{\mathrm{\prime }2}\right]𝔼\left[{\left(x_j^{(s)}\right)}^2\right]-𝔼{\left[a_j^{\prime }\right]}^2𝔼{\left[x_j^{(s)}\right]}^2+𝔼\left[d_j^{\mathrm{\prime }2}\right]𝔼\left[{\left(x_j^{(D,s)}\right)}^2\right]-𝔼{\left[d_j^{\prime }\right]}^2𝔼{\left[x_j^{(D,s)}\right]}^2+2\mathrm{c}\mathrm{o}\mathrm{v}[a_j^{\prime }{x}_j^{(s)},d_j^{\prime }{x}_j^{(D,s)}]={\sigma }_a^2+{\sigma }_d^2+2\mathrm{c}\mathrm{o}\mathrm{v}[a_j{x}_j^{(s)},d_j{x}_j^{(D,s)}]={\sigma }_a^2+{\sigma }_d^2+2𝔼[(a_j{x}_j^{(s)}).(d_j{x}_j^{(D,s)})]-2𝔼\left[(a_j{x}_j^{(s)})\right]𝔼\left[(d_j{x}_j^{(D,s)})\right]={\sigma }_a^2+{\sigma }_d^2+2𝔼[(a_j{x}_j^{(s)}).(d_j{x}_j^{(D,s)})]={\sigma }_a^2+{\sigma }_d^2+2𝔼\left[a_j{d}_j\underset{=0,\left[\text{Zhu et al.}\left(\text{25}\right)\right]}{\underbrace{𝔼[x_j^{(s)},x_j^{(D,s)}]}}\right]𝕍[a_j{x}_j+d_j{H}_j]={\sigma }_a^2+{\sigma }_d^2.$$

Now assuming independence between the $m$ causal variants we can derive Eq. S7,

$$𝕍[y]=𝕍[s{X}_{\text{QTL}}+b{F}_{\text{QTL}}]+m\left({\sigma }_a^2+{\sigma }_d^2\right)+{\sigma }_e^2\approx m\left({\sigma }_a^2+{\sigma }_d^2\right)+{\sigma }_e^2+\frac{K}{m},$$

where $K$ is constant with respect to the number of causal variants. For large $m$, $𝕍[y]\approx m\left({\sigma }_a^2+{\sigma }_d^2\right)+{\sigma }_e^2$.

Effect of Strong PS.

The contribution of PS reported in this study needs, however, to be put in perspective as our simulations and real data analyses were based upon a relatively homogeneous population within the United Kingdom. For stronger PS (e.g., between European and Asian populations) $F_{\mathrm{UNI}}$-based ID estimates can also be biased. This extreme situation would in general be handled as part of quality control. Still, we quantify below in a simulation study the bias of $F_{\mathrm{UNI}}$-based estimates in such a context.

Description of the simulation study.

Model and notations.

We assume that the data are collected from two populations: population 1 and population 2. For the sake of simplicity, we assume that all $m=\mathrm{1,000}$ causal variants are observed and have the same allele frequency $p_1$ in population 1 and $p_2$ in population 2. We denote $F_{st}$ as $F_{st}=p_1-p_2$ and $\pi$ as the proportion of samples from population 2 in the data used for inference.

For individual $i$ in population $k$ ($k=1$ or $2$), we simulated a trait $y_i^{(k)}$ from the model

$$y_i^{(k)}=\underset{g_i^{(k)}}{\underbrace{\sum _{j=1}^m\left(\frac{x_{ij}^{(k)}-2p_j^{(k)}}{\sqrt{h_j^{(k)}}}\right)a_j+\sum _{j=1}^m\left(\frac{H_{ij}^{(k)}-h_j^{(k)}}{h_j^{(k)}}\right)d_j}}+e_i^{(k)},$$

where $h_j^{(k)}=2p_j^{(k)}(1-p_j^{(k)})$ and $p_j^{(k)}$ is the MAF of SNP $j$ in population $k$; i.e., $p_j^{(1)}=p_1$ and $p_j^{(2)}=p_2$. We defined $a_j$ as $a_j=a\times {(-1)}^j$ so that the additive genetic variance equals $m{a}^2$ without directional effect because the sum of all $a_j$ is 0. We also defined $d_j=-b$, where $b$ is the depression for complete inbreeding. The residual term $e_i^{(k)}$ was simulated from a normal distribution with mean 0 and variance equal to $\mathrm{var}[g_i^{(k)}]/\left(\frac{1}{H^2}-1\right)$, where $H^2$ is the heritability of the trait.

Simulation parameters.

In this simulation we fixed $H^2=0.8$, $p_1=0.3$, $m=1,000$, and the total sample size $N=10,000$. We varied $F_{st}=p_1-p_2$ between $-0.1$ and $+0.1$ and the proportion $\pi$ of samples from population 2 between 0.1 and 0.5.

Simulation results.

Table S4 reports the averaged estimates (over 10 simulation replicates) of inbreeding depression for the different combinations of $F_{st}$ and $\pi$. We observed for large values of $F_{st}$ that ${\text{F}}_{\text{UNI}}$ produced biased estimates of inbreeding depression, but that bias was at most $12\%$ of the true effect. On the contrary, ${\text{F}}_{\text{HOM}}$ shows larger biases (on average 50% of $b$), which is in line with our results presented in the main text.

Table S4.

Averaged estimates (over 10 simulation replicates) of inbreeding depression under different scenarios of strong population stratification

	$\pi$ = 10%		$\pi$ = 25%		$\pi$ = 50%
Fst	FUNI $\widehat{b}$ (SE)	FHOM $\widehat{b}$ (SE)	FUNI $\widehat{b}$ (SE)	FHOM $\widehat{b}$ (SE)	FUNI $\widehat{b}$ (SE)	FHOM $\widehat{b}$ (SE)
−0.10	−0.88 (0.01)	−0.23 (0.005)	−0.87 (0.009)	−0.13 (0.003)	−0.93 (0.01)	−0.09 (0.004)
−0.05	−0.99 (0.01)	−0.59 (0.005)	−0.99 (0.006)	−0.43 (0.005)	−0.99 (0.01)	−0.35 (0.005)
0.0	−1.00 (0.01)	−1.00 (0.006)	−1.00 (0.008)	−1.00 (0.007)	−1.00 (0.01)	−1.00 (0.004)
+0.05	−0.98 (0.01)	−0.71 (0.007)	−0.99 (0.008)	−0.56 (0.006)	−0.99 (0.01)	−0.47 (0.004)
+0.10	−0.89 (0.01)	−0.45 (0.005)	−0.89 (0.01)	−0.30 (0.004)	−0.95 (0.01)	−0.24 (0.003)

The true inbreeding depression parameter used to simulate the data is b ⁼ −1. Datasets are simulated as mixtures of two populations with mixture proportions π and 1 − π and allele frequency difference equal to F_st.

LDMS Heterogeneity Test.

Derivation of the test statistic.

We developed and applied a Wald test to assess the statistical significance of a difference between nonstratified ID estimation and LDMS stratified ID estimation.

Let us denote $𝐅$ the $n\times p$ matrix of inbreeding measure for each individual ($1$–$n$) and each SNP ($1$–$p$). The nonstratified measure of inbreeding ${𝐅}_g$ (subscript $g$ means genome) is defined as the mean inbreeding across all SNPs. Therefore, ${𝐅}_g=\frac{1}{p}𝐅1_p$, where ${\mathrm{𝟏}}_p$ is the $p$-dimensional vector with all entries equal to 1.

Stratifying the SNPs into $K$ LD and MAF categories defines a linear map of the $p$ individual SNP inbreeding measures into $K$ aggregated inbreeding measures for each of the strata. The matrix of these strata-specific inbreeding measures can be written

$${𝐅}_s=\mathrm{𝐅𝐙},$$

where $𝐙$ is a $p\times K$ matrix with entries $z_{jk}$ so that $z_{jk}$ equals the proportion of SNPs in the $k$th category if SNP $j$ belongs to that category or equals 0 otherwise.

Without loss of generality, we assume that the sample means of $F_g$ and the columns of ${𝐅}_s$ are 0. Using least-squares estimation theory, we can write the closed-form expressions of the the nonstratified ($\widehat{b_g}$) and the LDMS stratified ($\widehat{b_s}$) estimators. Assuming $𝐲$ is the vector of the phenotypes (with sample mean 0), we have that

$$\widehat{b_g}=\frac{1}{{𝐅}_g^{\prime }{𝐅}_g}{𝐅}_g^{\prime }𝐲\hspace{0.17em}\text{and}\hspace{0.17em}\widehat{b_s}={\mathrm{𝟏}}_K^{\prime }{[{𝐅}_s^{\prime }{𝐅}_s]}^{-1}{𝐅}_s^{\prime }𝐲.$$

We note that both $b_g$ and $b_s$ are linear functions of $𝐲$. We can therefore use the following matrix relationship:

$$\left[\begin{array}{c}\hfill \widehat{b_g}\hfill \\ \hfill \widehat{b_s}\hfill \end{array}\right]=\underset{𝐀}{\underbrace{\left[\begin{array}{c}\hfill \frac{1}{{𝐅}_g^{\prime }{𝐅}_g}{𝐅}_g^{\prime }\hfill \\ \hfill {\mathrm{𝟏}}_K^{\prime }{[{𝐅}_s^{\prime }{𝐅}_s]}^{-1}{𝐅}_s^{\prime }\hfill \end{array}\right]}}𝐲⟹𝕍\left[\begin{array}{c}\hfill \widehat{b_g}\hfill \\ \hfill \widehat{b_s}\hfill \end{array}\right]=𝐀𝕍[𝐲]{𝐀}^{\prime }.$$ [S15]

When the individuals in the study are independent and when assuming homoscedasticity of the residuals, we have that $𝕍[𝐲]={\sigma }^2{\mathrm{I}}_n$. We therefore deduce that the correlation between $\widehat{b_g}$ and $\widehat{b_s}$ is

$${\widehat{r}}_{gs}=\mathrm{corr}(\widehat{b_g},\widehat{b_s})=\frac{{\mathrm{𝟏}}_K^{\prime }{[{𝐅}_s^{\prime }{𝐅}_s]}^{-1}{𝐅}_s^{\prime }{𝐅}_g}{({𝐅}_g^{\prime }{𝐅}_g)\sqrt{\frac{1}{{𝐅}_g^{\prime }{𝐅}_g}\times ({\mathrm{𝟏}}_K^{\prime }{[{𝐅}_s^{\prime }{𝐅}_s]}^{-1}{\mathrm{𝟏}}_K)}}=\frac{{\mathrm{𝟏}}_K^{\prime }{[{𝐅}_s^{\prime }{𝐅}_s]}^{-1}{𝐅}_s^{\prime }{𝐅}_g}{\sqrt{({𝐅}_g^{\prime }{𝐅}_g)\times ({\mathrm{𝟏}}_K^{\prime }{[{𝐅}_s^{\prime }{𝐅}_s]}^{-1}{\mathrm{𝟏}}_K)}}.$$ [S16]

Therefore, to test the hypothesis $H_0:b_g=b_s$ vs. $H_1:b_g\ne b_s$, we can use the test statistic

$$\frac{{\left(\widehat{b_g}-\widehat{b_s}\right)}^2}{𝕍\left(\widehat{b_g}-\widehat{b_s}\right)}=\frac{{\left(\widehat{b_g}-\widehat{b_s}\right)}^2}{\sigma {(\widehat{b_g})}^2-2{\widehat{r}}_{gs}\sigma (\widehat{b_g})\sigma (\widehat{b_s})+\sigma {(\widehat{b_g})}^2}\stackrel{H_0}{\sim }{\chi }_1^2,$$ [S17]

where $\sigma (\widehat{b_g})$ and $\sigma (\widehat{b_s})$ are respectively the standard errors of $\widehat{b_g}$ and $\widehat{b_s}$.

Control of type I error and statistical power.

To check that type I error is well controlled under the null hypothesis, we analyzed the distribution of P values from the comparison of $\widehat{b_g}$ with $\widehat{b_s}$ when the causal variants are a random sample of the SNPs. Under this scenario, we expect $\widehat{b_g}$ and $\widehat{b_s}$ to coincide as illustrated in our first simulation study (simulation 1, scenario 1). We reused data generated in our first simulation study but simply varied the value of the true ID parameters $b$ between 0, –3, –6, and –9 SDs of the simulated trait. The results presented in Fig. S7 correspond to the comparison of $F_{\text{UNI}}$ with $F_{\text{UNI}}-\text{LDMS}$ under the assumption that the dominance effect at each SNP is inversely proportional to the variance of allele counts.

As expected, the P-values distribution in this scenario was indistinguishable from the uniform distribution (Kolmogov–Smirnov test $P>0.26$ for all values of $b$). In particular, the observed proportion of P values below 5% does not deviate from its expectation of 5% (Fig. S7B). This result confirms that this test can be used safely to detect LD and MAF heterogeneity.

When we simulated LD and MAF heterogeneity by sampling causal variants from high or LD regions of the genome (simulation 1, scenarios 2 and 3), we noticed a deviation from the uniform distribution as illustrated in Fig. S7C. The power calculations presented in Fig. S7D are based on the fixed sample size of $n=\mathrm{10,000}$ used in our simulations.

Dataset S1 (PDF)

Discussion

We comprehensively quantified the behavior of ID estimators based on three commonly used measures of inbreeding. Our study illustrated some of the shortcomings of the most commonly used ROH-based estimates of ID, which not only are biased but also have large SE (approximately three times larger compared with ${\text{F}}_{\text{UNI}}$). This, along with the arbitrary choices underlying the definition of ROHs, leads us to recommend the use of ${\text{F}}_{\text{UNI}}$ over ${\text{F}}_{\text{ROH}}$. Overall, our results suggest that ${\text{F}}_{\text{UNI}}$-based ID estimates are robust to different assumptions about the distribution of effect sizes, to possible directional effects of minor alleles, and also to population stratification. The contribution of population stratification reported in this study needs, however, to be put in perspective as our simulations and real data analyses were based upon a relatively homogeneous population within the United Kingdom. For stronger population stratification (e.g., between European and Asian populations) ${\text{F}}_{\text{UNI}}$-based ID estimates can also be biased. This somewhat extreme situation, which would in general be handled as part of quality control, is discussed in Supporting Information (Table S4 and Dataset S1).

This study also highlights that differential LD distribution between causal variants and SNPs could bias ID estimates. As previously reported for genomic-relatedness-based restricted maximum-likelihood (GREML) (28) heritability estimates (19–21), we demonstrate through simulations that an LDMS approach successfully corrects these biases when estimating ID. More generally, the flexibility of the LDMS approach in terms of numbers and types of MAF/LD strata allows adaptation to any effect size distribution. Indeed, all SNP-based inbreeding measures are defined upon an underlying assumption on the distribution of dominance effects (e.g., when assuming constant dominance effects, the underlying inbreeding measure is ${\text{F}}_{\text{HOM}}$), which, when not verified, creates biases in ID estimates even when causal variants are randomly distributed among observed SNPs. We showed in our simulations using two distributions of dominance effects that such biases are explained by MAF and LD heterogeneity between causal variants and SNPs and therefore can be corrected using the LDMS approach. This result is important as it guarantees an unbiased estimation of ID regardless of the distribution of dominance effects.

Beyond methodological considerations, we confirmed in this study known associations between increased inbreeding and reduced lung function (PEF), cognitive ability (FIS and MTCIM), and fertility (NCF), which were previously reported, however, using different proxy traits (10, 29–31). We also replicated the association between inbreeding and decreased height (${\text{𝐛}}_{\text{UNI}}-\text{LDMS}$: −1.71 phenotypic SD for complete inbreeding; $P=0.003$) even though it was below the Bonferroni threshold. We did not replicate the association with educational attainment (EA) measured, as the “age when completed full education.” However, when measuring EA as whether or not participants went to college or university as in Joshi et al. (10), we found a strong although nominally significant negative association (odds ratio of 0.04, $P=0.02$).

We report evidence of ID for HGS, VA, AA and WHR. Although HGS, VA, and AA seem obvious fitness-related traits, these results still require replication. The association with WHR is particularly interesting as it illustrates on real data that one may benefit from using a less variable measure of inbreeding. Joshi et al. (10) reported a positive effect of inbreeding on WHR using ${\text{F}}_{\text{ROH}}$; however, even with $\sim \mathrm{200,000}$ individuals the effect did not reach statistical significance $(P=0.09)$. Although heterogeneity between the cohorts involved in that meta-analysis may explain that apparent lack of statistical power, our theoretical and simulation results predict that if the authors had used a different metric [${\text{F}}_{\text{UNI}}$ instead of $F_{\text{ROH}}^{(1)}$ to reduce the SE] combined with a LD and MAF stratified inference, then such an effect would have been easily detected. We have not considered in this study the detection and estimation of nonlinear effects of inbreeding because of a lack of statistical power to detect such effects. Nonlinearity is predicted by theory in the presence of epistasis involving dominance (32) and was implied by Szpiech et al. (33), who showed that long runs of homozygosity were enriched for coding variants that are predicted to be deleterious. In conclusion, we have demonstrated that LD and MAF stratified inference based on ${\text{F}}_{\text{UNI}}$ as a measure of inbreeding minimizes bias relative to the other ID estimation strategies compared in this study. As illustrated here on real data, we believe that our approach will lead to more discoveries in forthcoming and larger studies.

Materials and Methods

Statistical Models and Notations.

We consider the following model:

$$y_i=\mu +\sum _{j=1}^m{a}_j{x}_{ij}+\sum _{j=1}^m{d}_j{H}_{ij}+{\epsilon }_i,$$ [1]

For individual i, $y_i$ is the observed value of the phenotype of interest, and $x_{ij}$ is the minor allele count at the jth causal SNP ($x_{ij}\in \{0,1,2\}$). We denote $p_j$ the minor allele frequency of the jth causal SNP, $H_{ij}=x_{ij}(2-x_{ij})$ is the indicator of heterozygosity, and ${\epsilon }_i$ is a residual term capturing nongenetic effects on the observed phenotype. The additive and dominance effect sizes of the minor allele at the jth causal SNP are respectively denoted $a_j$ and $d_j$. We assume independence between the m causal variants, between the genotypes and the effect sizes, and between the genetic and the nongenetic effects. Finally, we assume the effect sizes to be random and such that $E[a_j]={\alpha }_j$ and $E[d_j]={\delta }_j$.

Measures of Inbreeding.

We studied three measures of inbreeding. All these measures of inbreeding require individual SNP genotypes and can be used in the absence of any pedigree information. The first inbreeding measure is the excess of homozygosity measure defined here as

$${\text{F}}_{\text{HOM}}=1-\frac{{\sum }_{k=1}^p{x}_k(2-x_k)}{{\sum }_{k=1}^{p}2p_k(1-p_k)},$$

where $x_k$ is the minor allele count of SNP k, $p_k$ is the minor allele frequency, and p is the number of genotyped or imputed SNPs available. ${\text{F}}_{\text{HOM}}$ is implemented in PLINK2 (command: –het).

The second measure (${\text{F}}_{\text{UNI}}$) is based on the correlation between uniting gametes. This measure was defined in Yang et al. (17) as

$${\text{F}}_{\text{UNI}}=\frac{1}{p}\sum _{k=1}^p\frac{x_k^2-\left(1+2p_k\right)x_k+2p_k^2}{2p_k(1-p_k)}.$$

${\text{F}}_{\text{UNI}}$ is implemented in PLINK2 and GCTA software (command: –ibc).

The last measure is defined as the proportion of the genome within ROH. More specifically, the inbreeding measure ${\text{F}}_{\text{ROH}}$ was calculated as the cumulated length (in base pairs) of one individual’s genome within ROHs divided by $3\times {10}^9$ (the approximate length of the autosomal genome in base pairs). We used two definitions of ROHs corresponding to those proposed in Joshi et al. (10) (definition 1) and Gazal et al. (15) (definition 2). Inbreeding measures calculated using definition 1 and definition 2 are respectively denoted as $F_{\text{ROH}}^{(1)}$ and $F_{\text{ROH}}^{(2)}$. Both definitions used SNPs with $\text{MAF}>5\%$ as previously reported in Joshi et al. (10) and Gazal et al. (15) (Supporting Information).

UK Biobank Data.

We used baseline data from 152,729 men and women who were genotyped in the first phase of genotyping of the UK Biobank (34). To ensure ancestry homogeneity, we selected individuals who reported to be “British,” “Irish,” “white,” or of “any other white background” and whose coordinates on the first genetic PC were below 0 (Fig. S9). In total, we included 140,720 participants in this analysis. The Northwest Multicentre Research Ethics Committee (MREC) approved the study and all participants in the UK Biobank study provided written informed consent. The first steps of the quality control have been previously described (SI Materials and Methods, URLs). Phasing and imputation were performed using SHAPEIT and IMPUTE2 (SI Materials and Methods, URLs), respectively, as previously described (35). After imputation, we selected 9,493,148 autosomal SNPs with imputation quality ${\text{r}}^2>0.3$, $\text{MAF}>1\%$, and Hardy–Weinberg equilibrium test P value $>{10}^{-6}$. Imputed SNPs were then called to the genotypes having the largest posterior probability. Finally, we removed redundancy by LD pruning SNPs with a squared genotype correlation ${\text{r}}^2>0.9$. In total we used 3,857,369 SNPs in this analysis.