Neural basis for hand muscle synergies in the primate spinal cord

Significance

How the CNS coordinates complex movements, each comprising a large number of muscles and joints, to attain a behavioral goal remains a fundamental question. Previous studies in phylogenetically older animals indicate that functional modules in the spinal cord (“muscle synergies”) construct motor behaviors. However, whether similar mechanisms exist in primates is unknown. For example, hand movements are believed to depend on direct inputs from the corticomotoneuronal pathway, which bypass spinal interneuron circuits. Here we demonstrate that spinal premotor interneurons underlie the spatiotemporal patterns of muscle synergies in primates during a precision grip task. Our results suggest that the phylogenetically older premotor interneuron system provides synergistic control of hand movements upon which the newer corticomotoneuronal system superimposes more fractionated control.

Abstract

Grasping is a highly complex movement that requires the coordination of multiple hand joints and muscles. Muscle synergies have been proposed to be the functional building blocks that coordinate such complex motor behaviors, but little is known about how they are implemented in the central nervous system. Here we demonstrate that premotor interneurons (PreM-INs) in the primate cervical spinal cord underlie the spatiotemporal patterns of hand muscle synergies during a voluntary grasping task. Using spike-triggered averaging of hand muscle activity, we found that the muscle fields of PreM-INs were not uniformly distributed across hand muscles but rather distributed as clusters corresponding to muscle synergies. Moreover, although individual PreM-INs have divergent activation patterns, the population activity of PreM-INs reflects the temporal activation of muscle synergies. These findings demonstrate that spinal PreM-INs underlie the muscle coordination required for voluntary hand movements in primates. Given the evolution of neural control of primate hand functions, we suggest that spinal premotor circuits provide the fundamental coordination of multiple joints and muscles upon which more fractionated control is achieved by superimposed, phylogenetically newer, pathways.

Following the pioneering work of Sherrington early in the 20th century, it has been proposed that the central nervous system (CNS) coordinates complex body movements by combining sets of simpler movements, such as simple reflexes (1). This hypothesis is phenomenologically supported by experimental observations that a wide range of behaviors can be decomposed into basic patterns of muscle activity, namely “muscle synergies” (2–5). However, there remains heated debate regarding whether these observations reflect a neurophysiological basis or are an epiphenomenon of task constraints and biomechanics (6–8). This controversy stems from a lack of direct evidence for (or against) the neural implementations of muscle synergies in the CNS (9–11). Previous studies have suggested that output projections of spinal premotor interneurons (PreM-INs) to motoneuron pools are the neural basis of coordinated muscle activity (10, 11). For example, Hart and Giszter demonstrated in spinalized frogs that PreM-INs have divergent output projections to motoneurons that match the pattern of muscle synergies extracted during spinal motor behaviors (e.g., wiping reflexes) (10). Recent optogenetic approaches also revealed that selective stimulation of a small population of PreM-INs in isolated mouse spinal cords evokes coordinated muscle activity of the hindlimb (11). However, whether these outcomes reflect the situation in the intact, phylogenetically newer spinal cord of primates is unknown.

We previously showed that PreM-INs in monkey cervical cords have divergent postspike effects on a group of hand muscles during a precision grip task, termed the neuron’s “muscle field” (12). This finding suggests that PreM-INs contribute to the synergistic control of primate hand movements (9, 13–15), but this question has not been examined directly. We hypothesize that if PreM-INs underlie the generation of muscle synergies, then (i) the distribution of muscle fields will exhibit significant clustering corresponding to extant muscle synergies, rather than being uniform, and (ii) the activities of PreM-INs will be temporally associated with the muscle synergies. To test these hypotheses, we examined (i) how the muscle fields of PreM-INs correlate with muscle synergies extracted during voluntary hand movements, and (ii) how the firing of PreM-INs correlates with the temporal activity of muscle synergies.

Results

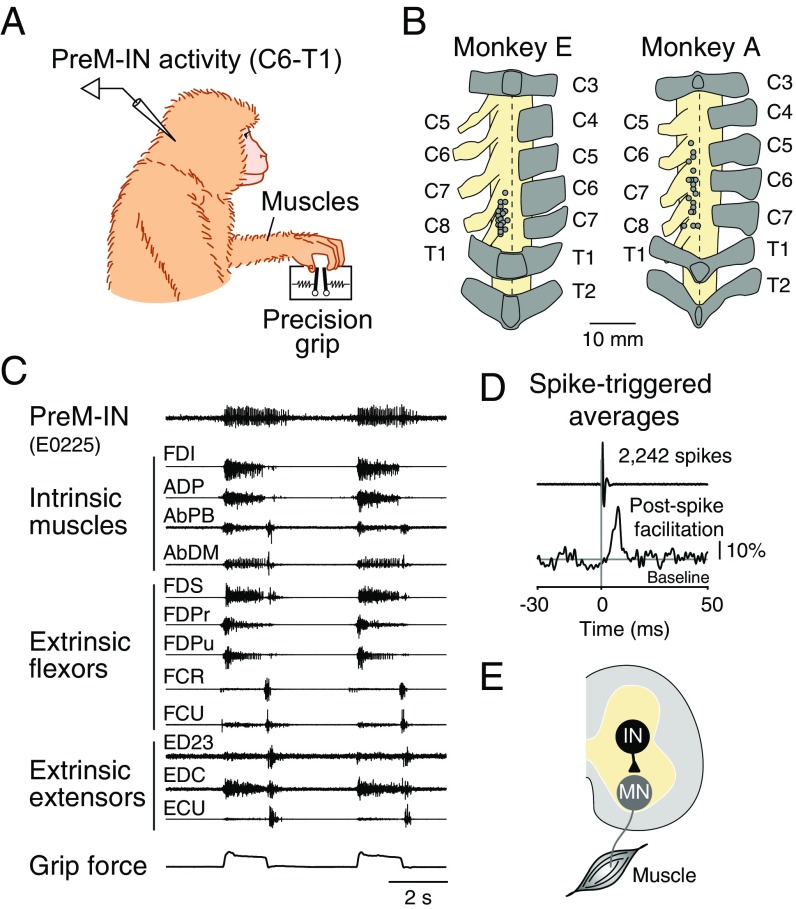
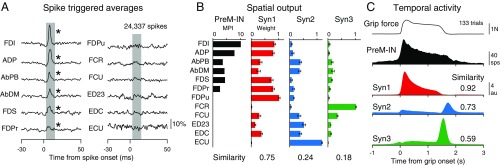
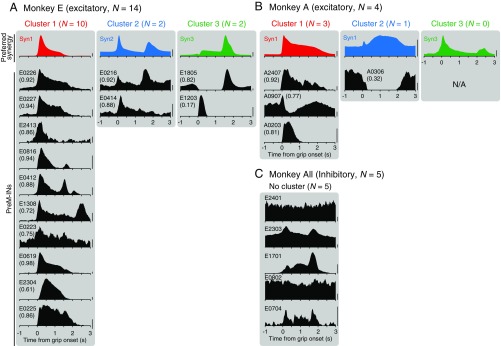
Two macaque monkeys were trained to perform a precision grip task, in which they were required to grip and release two spring-loaded levers with their index finger and thumb to target positions (12, 16). During the task, we recorded single-unit activity from cervical spinal neurons and electromyographic (EMG) activity from 12 hand muscles (Fig. S1). Using spike-triggered averaging of rectified EMGs, we identified 23 PreM-INs that produced postspike effects in the recorded muscles (18 excitatory and 5 inhibitory PreM-INs). About half of the neurons displayed postspike effects on multiple muscles (9/18 excitatory and 2/5 inhibitory PreM-INs; for complete data, see Table S1). For example, Fig. 1A illustrates the muscle field of an excitatory PreM-IN. This PreM-IN has a muscle field encompassing six muscles, including intrinsic hand muscles (first dorsal interosseous, adductor pollicis, abductor pollicis brevis, and abductor digiti minimi) and digit flexors (flexor digitorum superficialis and radial part of the flexor digitorum profundus) but not digit or wrist extensors (extensor digitorum-2,3, extensor digitorum communis, and extensor carpi ulnaris). Importantly, these muscles in the muscle field are synergistically activated during a precision grip task (17).

Fig. S1.

Experimental procedures. (A) Recording setup. We recorded spinal neuron activity as well as muscle activity of hand and arm muscles while the monkey was performing a precision grip task. (B) Spinal recording sites in each monkey. Dots indicate the locations where we recorded the spinal neurons. Letters on the left indicate the number of spinal segments, and those on the right indicate the number of vertebrae. Dorsal views are shown. (C) Example recordings of neural and muscle activity during two successive trials. (C, Top to Bottom) PreM-IN activity, muscle activity (n = 12), and grip force. (D) Example of spike-triggered averaging. Rectified EMG (FDS muscle) was aligned to the spikes of a single spinal neuron (shown in C) and averaged (2,242 spikes). Significant postspike effects are detected by comparing with baseline (Materials and Methods). Scale bar, 10% increase from the baseline amplitude. (E) Schematic illustration of the PreM-IN output. Postspike effects reflect the synaptic connections of the PreM-IN (IN) to the target motoneurons (MN).

Table S1.

Summary of PreM-IN characteristics

Cell ID	Animal ID	Excitatory/inhibitory	Muscle field	Cluster	Spatial similarity			Temporal similarity
					Syn1	Syn2	Syn3	Syn1	Syn2	Syn3
A0203	A	Excitatory	AbDM	1	0.30	0.19	0.11	0.81	0.45	0.77
A0306	A	Excitatory	ED45, EDC	2	0.01	0.70	0.08	0.28	0.32	0.53
A0907	A	Excitatory	FDPr	1	0.49	0.04	0.02	0.77	0.95	0.86
A2407	A	Excitatory	FCR, FCU, FDPr	1	0.66	0.17	0.14	0.92	0.70	0.88
E0216	E	Excitatory	ECU	2	0.01	0.78	0.01	0.49	0.92	0.81
E0223	E	Excitatory	2DI, AbPB, ADP	1	0.42	0.22	0.12	0.75	0.80	0.66
E0225	E	Excitatory	2DI, FDS	1	0.37	0.05	0.13	0.86	0.68	0.64
E0226	E	Excitatory	2DI, 3DI, AbDM, AbPB, ADP, FDI, FDPr, FDS	1	0.75	0.24	0.18	0.92	0.73	0.59
E0227	E	Excitatory	2DI, 3DI, AbDM, AbPB, ADP, FDI, FDPr, FDS	1	0.73	0.25	0.18	0.94	0.66	0.50
E0412	E	Excitatory	FDPu	1	0.51	0.10	0.03	0.88	0.80	0.72
E0414	E	Excitatory	2DI, 3DI, ED23	2	0.07	0.35	0.09	0.90	0.88	0.61
E0619	E	Excitatory	ADP	1	0.40	0.08	0.04	0.98	0.54	0.58
E0816	E	Excitatory	AbPB, ADP, FDI	1	0.55	0.24	0.14	0.94	0.58	0.43
E1203	E	Excitatory	AbPL, ED23, EDC, FCR	3	0.13	0.34	0.71	0.90	0.44	0.17
E1308	E	Excitatory	2DI, AbDM, ADP	1	0.42	0.16	0.10	0.72	0.82	0.54
E1805	E	Excitatory	FCR	3	0.01	0.03	0.90	0.06	0.67	0.82
E2304	E	Excitatory	FCU, FDPr	1	0.40	0.23	0.25	0.61	0.50	0.46
E2413	E	Excitatory	AbPB, AbPL, FDPr, FDPu	1	0.65	0.18	0.09	0.86	0.91	0.42
E0704	E	Inhibitory	ECU	N/A	−0.01	−0.78	−0.01	0.73	0.76	0.88
E0802	E	Inhibitory	FCU, FDPr	N/A	−0.41	−0.22	−0.24	0.59	0.81	0.72
E1701	E	Inhibitory	AbPL, EDC	N/A	−0.19	−0.26	−0.10	0.50	0.67	0.94
E2303	E	Inhibitory	AbPL, BRD, ECU, FCU, FDPu, FDS	N/A	−0.55	−0.54	−0.18	0.60	0.94	0.71
E2401	E	Inhibitory	ECU	N/A	−0.01	−0.78	−0.01	0.55	0.74	0.55

N/A, no cluster was identified for the inhibitory PreM-INs.

Fig. 1.

Spatial and temporal similarity between PreM-IN output effects and muscle synergies. (A) Spike-triggered averages of rectified EMGs triggered on spikes of an excitatory PreM-IN (24,337 spikes). Gray rectangles indicate the test windows for the postspike effects (3 to 15 ms after the spike). Asterisks indicate significant postspike facilitation (P < 0.05). (B) Similarity of spatial outputs between the PreM-IN (shown in A) and muscle synergies (Syn1 to 3). The amplitude of postspike facilitation was quantified as a mean percentage increase (black bars) and compared with muscle synergy weights. The similarity was quantified as the cosine of the angle between the two vectors in the muscle dimension. Error bars indicate SEMs. (C) Similarity of temporal activities between the PreM-IN (shown in A) and muscle synergies. The profile was aligned to grip onset and averaged across trials (133 trials). (C, Top to Bottom) Grip force, PreM-IN activity, and synergy activities (Syn1 to 3). The similarity was quantified in the same way as in B but in the time dimension. AbDM, abductor digiti minimi; AbPB, abductor pollicis brevis; ADP, adductor pollicis; ECU, extensor carpi ulnaris; ED23, extensor digitorum-2,3; EDC, extensor digitorum communis; FCR, flexor carpi radialis; FCU, flexor carpi ulnaris; FDI, first dorsal interosseous; FDPr and FDPu, radial and ulnar parts of the flexor digitorum profundus; FDS, flexor digitorum superficialis. au, arbitrary unit; sps, spikes per second.

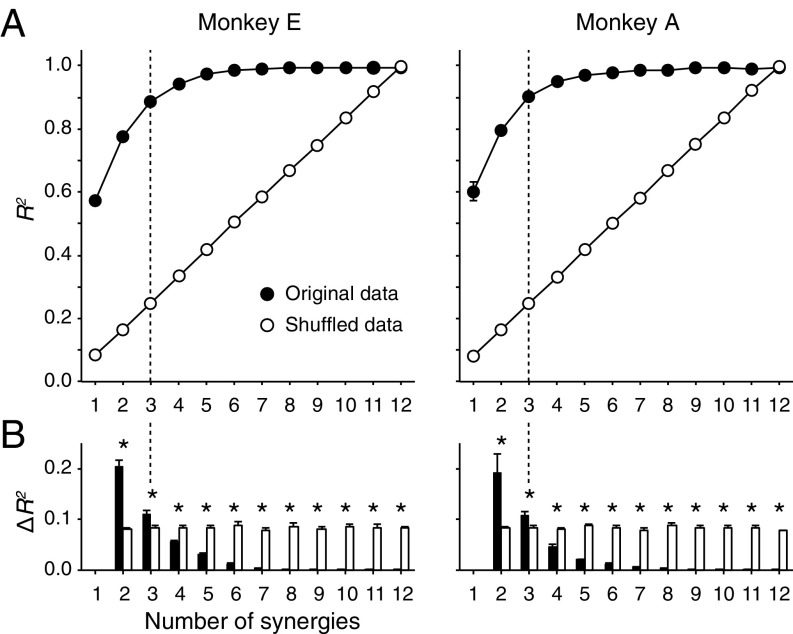
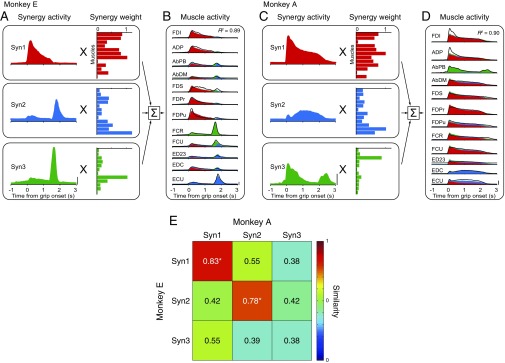
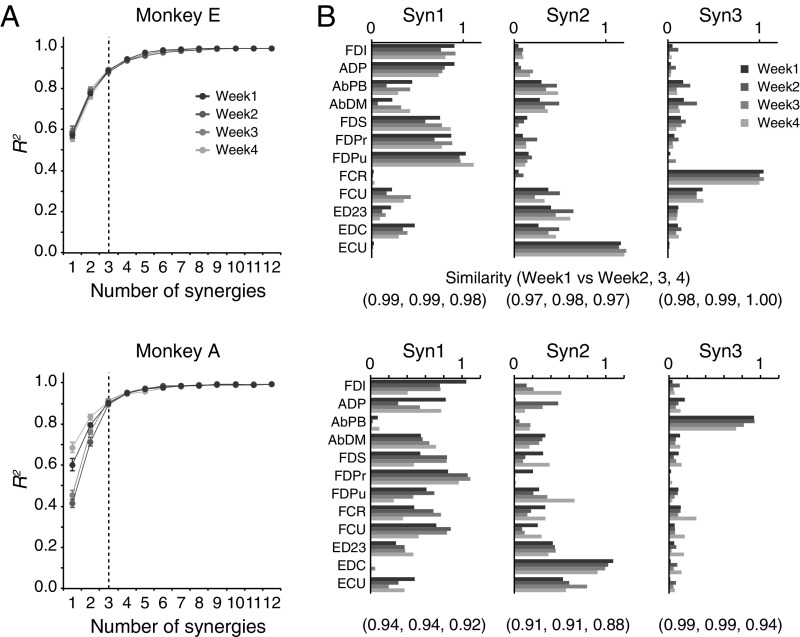
We next quantified the basic patterns of coordinated muscle activity by applying a standard decomposition analysis (nonnegative matrix factorization) (18). Each outcome component is referred to as a muscle synergy. We found that a linear combination of three muscle synergies (Syn1 to 3) accounted for 89% (monkey E) and 91% (monkey A) of the original EMG variance (Figs. S2 and S3). We confirmed that these three muscle synergies were consistent over the experimental period of neural recordings (4 wk; Fig. S4; see also SI Text and Fig. S5). We also found that most of the muscle synergies were similar between monkeys but that some were specific to each monkey (e.g., Syn3 in Fig. S3E). Therefore, we only compared muscle synergies to PreM-INs recorded in the same monkey.

Fig. S2.

Selection of the number of muscle synergies. (A) Variance accounted for (R²) as a function of the number of extracted synergies (R² curve) for week 1 EMG data of monkeys E (Left) and A (Right). The R² curve was obtained by the fourfold cross-validation of the original EMG data (filled circles). To evaluate the chance level of the R² curve, we repeated the same procedure for the shuffled EMGs (open circles). Error bars indicate SDs. (B) Increment of the R² curves (∆R²) for each monkey. The number of muscle synergies (vertical dotted line) was defined by a saturation point, where the ∆R² of the original data (filled bars) became significantly smaller than the ∆R² of the shuffled data (open bars). *P < 0.05, t test. Error bars indicate SDs.

Fig. S3.

Muscle synergies during a precision grip task. (A) Muscle activities were reconstructed by a weighted sum of muscle synergy activities. Week 1 data for monkey E. The activities were aligned to grip onset and averaged across trials. (B) Muscle activity in the same session. Solid lines indicate the original EMG profile, and shaded areas indicate the reconstruction by muscle synergies (Syn1 to 3). (C and D) Same format as A and B but of data from week 1 for monkey A. Scale bars, 2 normalized units. (E) Similarity of weights of muscle synergies (Syn1 to 3) between monkeys E (vertical axis) and A (horizontal axis). Color indicates the similarity between each pair of muscle synergies, which was quantified using the cosines of the angles between the muscle synergy vectors. Asterisks denote that the similarity exceeded the chance level obtained by shuffling (P < 0.05).

Fig. S4.

Consistency of muscle synergies across different sessions. (A) R² curves for EMG data of weeks 1, 2, 3, and 4 from monkeys E (Top) and A (Bottom). The muscle synergy number of 3 was consistently selected in both monkeys and all different sessions (vertical dashed lines). Error bars indicate SDs. (B) Comparison of weights of muscle synergies across different experimental days (weeks 1 to 4). The numbers below indicate the similarity (the cosine of the angle) of synergy weights compared with week 1.

Fig. S5.

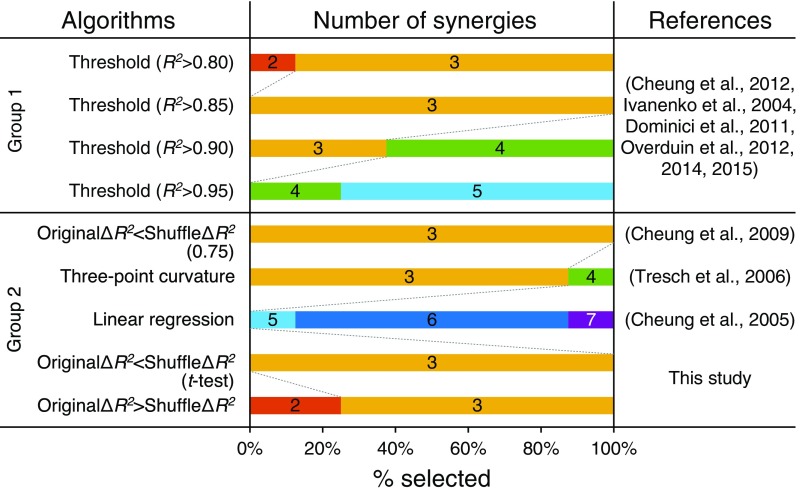
Number of muscle synergies selected using different algorithms. This plot compares how many muscle synergies were selected using different algorithms proposed by previous studies and the present study. Each algorithm was applied to eight different datasets (4 wk of two monkeys), and each horizontal bar indicates the probability of a given number of muscle synergies being selected by each algorithm. The algorithms are classified into two groups (groups 1 and 2). Group 1 uses the R² value [the threshold method (5, 9, 13, 41–43)] and group 2 uses the difference between R² values [the ΔR², original ΔR² < shuffle ΔR² (0.75) (40), three-point curvature (18), linear regression (44), original ΔR² < shuffle ΔR² (t test), and original ΔR² > shuffle ΔR² methods].

Spatial Similarity Between PreM-INs and Muscle Synergies.

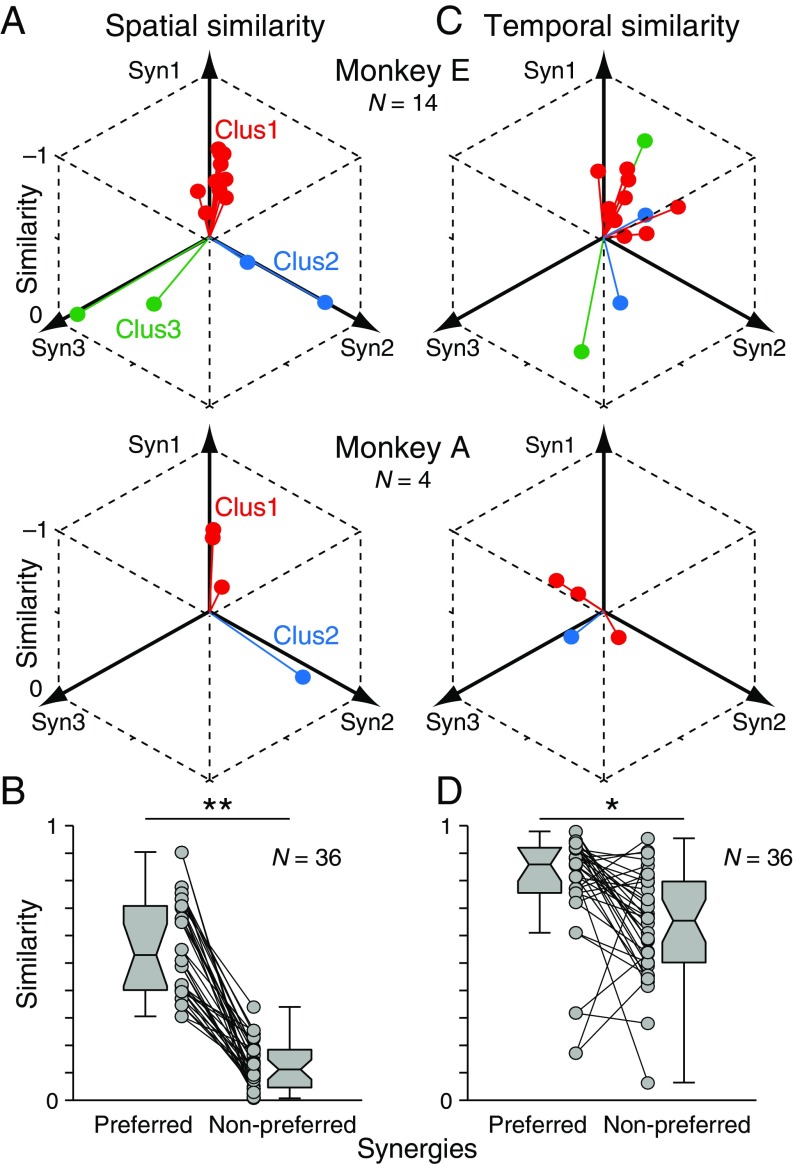
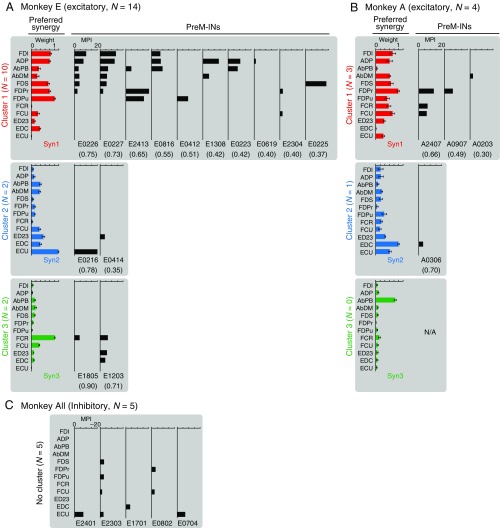
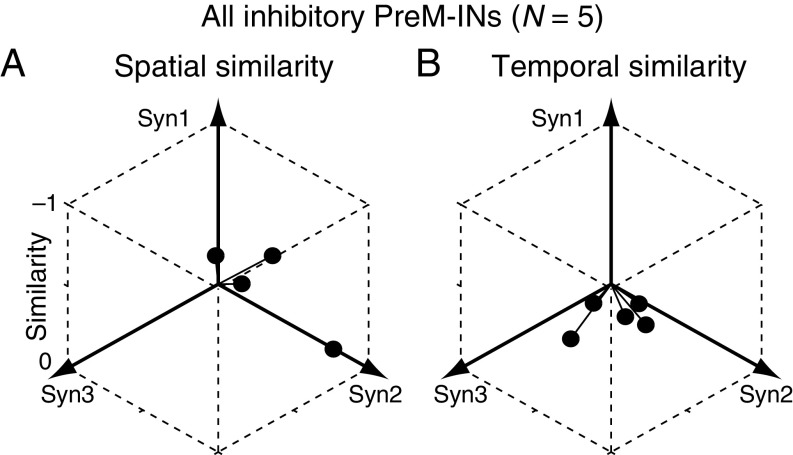
We examined how PreM-IN muscle fields correlated with the spatial weights of muscle synergies. Fig. 1B illustrates a muscle field of the sample PreM-IN, which is expressed as the amplitude of postspike facilitations (Fig. 1B, Left) and the weights of extracted muscle synergies (Syn1 to 3; Fig. 1B, Right). We quantified the similarity as the cosine of the angle between the two weight vectors, and refer to this as the “spatial similarity” (2). The sample muscle field showed the highest similarity with Syn1, which was also weighted toward intrinsic hand and digit flexors. This similarity suggests that the muscle field of PreM-INs underlies the generation of the spatial pattern of the muscle synergy. We calculated the spatial similarity of all neuron–synergy pairs and plotted them in a 3D muscle synergy space (Fig. 2A), in which each axis represents the similarity with each muscle synergy (Syn1 to 3). We expected that if the muscle fields of PreM-INs contributed to the generation of the muscle synergies, they should show clustered distributions in the muscle synergy space. Fig. 2A illustrates such a distribution of excitatory PreM-INs from each monkey (Top: monkey E, n = 14; Bottom: monkey A, n = 4). These plots demonstrate that PreM-INs systematically cluster in the muscle synergy space. In monkey E (Fig. 2A, Top), the data were separated into three clusters (Clus1 to 3; k-means clustering, silhouette value 0.79, P < 0.05, permutation test; Materials and Methods). Note that each cluster distributes along each axis; that is, Clus1, 2, and 3 distribute along the axes of Syn1, 2, and 3, respectively. Therefore, we defined the axis that each cluster corresponds to as the “preferred synergy” of each cluster. Similar separation was observed in the excitatory PreM-INs of monkey A (Fig. 2A, Bottom). The clustering analysis showed that there were two clusters in the muscle synergy space (Clus1 and 2; k-means clustering), although their index of separation (silhouette value) did not reach statistical significance (silhouette value 0.87, P = 0.14, permutation test). This is probably due to an inappropriate estimation of the chance level by using the smaller sampling of PreM-INs in monkey A (n = 4), as the silhouette value itself is as high as in monkey E. Therefore, we kept this clustering for the following analyses. Importantly, we confirmed that all individual PreM-INs from both monkeys had a greater similarity with the preferred synergies than the nonpreferred synergies (Fig. 2B). These results indicate that the muscle fields of PreM-INs are not randomly distributed across hand muscles but distributed as clusters that correspond to the component muscle synergies. Please note that, although the PreM-INs exhibited clear clustering in the muscle synergy space, their muscle fields exhibited substantial variability within each cluster (Fig. S6). This kind of clustering was not observed in inhibitory PreM-INs (Fig. S7A).

Fig. 2.

Spatial and temporal similarity between excitatory PreM-INs and muscle synergies. (A) Spatial similarity of excitatory PreM-INs with muscle synergies (Syn1 to 3) in monkey E (Top; n = 14) and monkey A (Bottom; n = 4). Colors indicate the result of the unsupervised clustering of spatial similarity (k-means clustering; silhouette value 0.79, P = 0.021 and silhouette value 0.87, P = 0.138 for monkeys E and A, respectively). (B) Comparison of spatial similarity between the preferred and nonpreferred synergies. The preferred synergy was defined as the closest axis to each cluster in A, and the two nonpreferred synergies were defined as the other axes. Connected circles indicate the spatial similarities of the individual PreM-IN with the preferred or nonpreferred synergy. Each PreM-IN yields two pairs of preferred and nonpreferred synergies, and are counted individually. Data from both monkeys were pooled (n = 36). Boxplots indicate the median and interquartile range. Whiskers and notches indicate the max–min values, except outliers, and the 95% confidence intervals of the medians. (C) Temporal similarity of the same PreM-INs with muscle synergies (Syn1 to 3) in each monkey. The colors indicate the clusters obtained in A. (D) Comparison of temporal similarity between the preferred and nonpreferred synergies. Same format as B. **P < 0.01, *P < 0.05, Wilcoxon signed-rank test.

Fig. S6.

Muscle fields of each PreM-IN and their preferred muscle synergy. The muscle fields of all PreM-INs (n = 23) are displayed with their preferred muscle synergy (Syn1, Syn2, and Syn3). (A) Excitatory PreM-INs of monkey E, (B) excitatory PreM-INs of monkey A, and (C) inhibitory PreM-INs of all monkeys. The figure format is the same as in Fig. 1B, and muscle synergies are color-coded as in Fig. S3. The PreM-INs are grouped according to the results of clustering (clusters 1 to 3 for monkey E, and clusters 1 and 2 for monkey A; Fig. 2A) and displayed according to the spatial similarity to the preferred synergy (numbers in parentheses). Note that for the inhibitory PreM-INs (C), the preferred synergy and similarity to it are not shown because the clustering was not significant for this population. In addition, the horizontal axis is inverted to display their negative MPI values for the inhibitory PreM-INs (C). The spatial similarity of all PreM-IN and muscle synergy pairs is summarized in Table S1. N/A, data not available.

Fig. S7.

Spatial (A) and temporal (B) similarities between inhibitory PreM-INs and muscle synergies. Same format as in Fig. 2 A and C but for the inhibitory PreM-INs (n = 5). Note that the clustering failed for the inhibitory PreM-INs and therefore the plots are not grouped.

Temporal Similarity Between PreM-INs and Muscle Synergies.

Given the clear clustering of PreM-INs in muscle synergy space, we hypothesized that the firing activity of each excitatory PreM-IN would mediate a temporal profile of its preferred muscle synergy. To test this hypothesis, we examined the similarity between the temporal profiles of each PreM-IN and muscle synergy, which we refer to as the “temporal similarity.” Fig. 2C illustrates the temporal activity of a sample PreM-IN and the three muscle synergies (Syn1 to 3). This neuron shows a phasic burst at grip onset followed by tonic firing activity. When we calculated the temporal similarity of this firing profile with the temporal profiles of Syn1 to 3, the similarity was highest with Syn1, which was the neuron’s preferred synergy as defined by spatial similarity analysis. Such a correspondence between spatial and temporal similarities suggests that the activity of this sample PreM-IN mediates the temporal profile of the preferred synergy. However, contrary to our expectations, when we plotted the temporal similarities of all excitatory PreM-INs, we did not find any clear separations of clusters within muscle synergy space (Fig. 2C; silhouette value 0.46 and 0.79 for monkeys E and A, respectively, P > 0.20). This suggests that individual PreM-INs do not directly represent the temporal profile of their preferred synergy but that they have diverse temporal patterns. This diversity is also evident when we plot the temporal profiles of all PreM-INs aligned with the temporal profiles of their preferred synergy (Fig. S8). Despite this diversity of temporal profiles, when we compared the temporal similarities of preferred and nonpreferred synergies defined by spatial similarities, the preferred synergies had significantly higher temporal similarity than the nonpreferred (Fig. 2D; Wilcoxon signed-rank test, P < 0.05). These results suggest that although individual neurons have diverse temporal profiles, the population of PreM-INs reflects the temporal features of the preferred synergy. Again, inhibitory PreM-INs did not display a prominent clustering of temporal similarities in muscle synergy space (Fig. S7B).

Fig. S8.

Temporal profiles for each PreM-IN and their preferred muscle synergies. The temporal activity of all PreM-INs (n = 23) is displayed with the temporal activity of their preferred synergy (Top; Syn1 to 3) using the same format as in Fig. 1C. (A) Excitatory PreM-INs of monkey E, (B) excitatory PreM-INs of monkey A, and (C) inhibitory PreM-INs for all monkeys. The muscle synergies are color-coded as in Fig. S3. The PreM-INs are grouped according to the result of clustering (Clus1 to 3) and displayed according to the spatial similarity (not temporal similarity) with the preferred synergy as in Fig. S6. Numbers in parentheses indicate temporal similarity with their preferred synergy. Note that for the inhibitory PreM-INs (C), the preferred synergy and similarity to it are not shown, as the clustering was not significant. The temporal similarity of all PreM-IN and muscle synergy pairs is summarized in Table S1. Scale bars, 1 normalized unit for muscle synergies and 10 spikes per s for PreM-INs.

Population Coding of Muscle Synergies by PreM-INs.

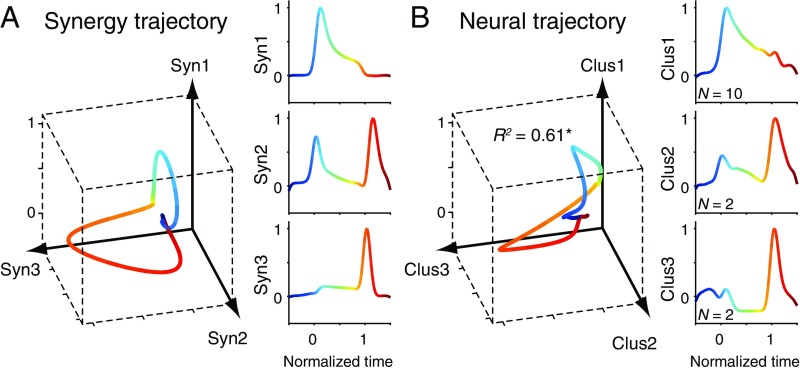
Our conclusion regarding the population coding of muscle synergies was further supported by a direct comparison of the population activity of PreM-INs and the activity of muscle synergies (Fig. 3). This comparison was performed only in monkey E, which had a sufficient number of sampled PreM-INs. Fig. 3A (Right) shows the temporal profile of three muscle synergies (Syn1 to 3) normalized to grip onset (time 0) and release onset (time 1). The 3D plot (Fig. 3A, Left) illustrates an averaged trajectory of grip movement expressed by the activity of muscle synergies (“synergy trajectory”). This trajectory displays the relative temporal relationship of synergy activities. First, at the beginning of the grip (blue-green), the trajectory moves mostly in the Syn1–2 plane. Then, at the end of the grip (orange-red), it moves in the Syn2–3 plane. This temporal relationship of muscle synergies was reproduced by the population activity of PreM-INs (Fig. 3B). Population activities were calculated for each PreM-IN cluster (Clus1 to 3; Fig. 3B, Right), and the temporal relationship is expressed as a 3D trajectory of the population activities (“neural trajectory”; Fig. 3B, Left). The neural trajectory showed a similar temporal profile to that of the synergy trajectory, first moving mainly in the Clus1–2 plane at grip onset and then in the Clus2–3 plane at the end of the grip. The goodness of fit (R²) between the neural and synergy trajectories was 0.61, indicating that ∼60% of the temporal profile of the muscle synergy can be explained by the population activity of PreM-INs. This R² significantly exceeded the chance level that would be expected if the PreM-INs were randomly assigned to one of three clusters (P < 0.01, permutation test). This result supports the idea that the population activity of PreM-INs represents the temporal activity of muscle synergies.

Fig. 3.

Similarity between muscle synergy activity and PreM-IN population activity. (A) Synergy trajectory during a mean grip movement by monkey E. Axes indicate the activity of muscle synergy (Syn1 to 3). Colors indicate the time course of the grip: 0, grip onset; 1, release onset. (A, Right) The activity of each muscle synergy (Syn1 to 3). (B) Neural trajectory during the same movement of the same monkey. Axes indicate the population activity of the PreM-IN cluster (Clus1 to 3) as defined in Fig. 2A. (B, Right) The activity of each cluster (Clus1 to 3). Same format as A. *P < 0.01, permutation test.

SI Text

Muscle synergy analysis using NMF requires the number of muscle synergies to be determined a priori (39). To determine the optimal number of muscle synergies, various algorithms have been used in previous papers (5, 9, 13, 18, 40–44). Here we summarize them and compare their performance on the datasets of this study.

The various algorithms can be classified into two groups: those using the R² value itself, and those using the difference between them (ΔR²). The first group simply detects the point where the R² curve exceeds or becomes closest to a certain threshold value as the optimal number of synergies (the threshold method). Using this method, a single threshold value is arbitrarily selected from study to study and ranges from 0.8 to 0.95 [R² > 0.8 (41), > 0.9 (5, 42), > 0.95 (9, 13, 43)]. Therefore, the determined number of synergies is susceptive to the arbitrary selection of the threshold.

The second group of algorithms focuses on the change of the R² curve (ΔR²), instead of absolute R² values. In contrast to the first method, the number of synergies is determined from a geometric feature of the R² curve rather than the absolute value of R². Using this method, the determined number of synergies should be more robust for the selection of the threshold. In these methods, the number of synergies is defined by the cusp of the R² curve, which is a point beyond which additional synergies capture only noise and/or a small additional fraction of data variation (18, 40, 44).

Several algorithms are proposed to detect the cusp: Cheung et al. used shuffling of EMG signals to estimate the chance level of ΔR² (shuffle ΔR²) (40). They defined the number of synergies as the point beyond which the original ΔR² is smaller than 75% of the shuffle ΔR² [the original ΔR² < shuffle ΔR² (0.75) method]. Tresch et al. proposed a method to detect the point at which the ΔR² curve steeply changes its slope (18). To do so, they first normalized the range of the R² curve from 0 to 1 and then calculated the curvature for every three adjacent points on the curve (e.g., points 1, 2, 3; points 2, 3, 4; points 3, 4, 5; etc.). They traced the curvatures starting from the last points and proceeded to smaller numbers to find the point exceeding 0.075 (the three-point curvature method). Cheung et al. proposed a stricter algorithm for defining the cusp (44). They defined the number of synergies as the point beyond which the R² curve converges to a straight line. They fitted a straight line to a portion of the R² curve, first including all data points on the curve. Then, they reduced the points included as the second to last, third to last, and so on. In each step, they calculated the mean squared error (MSE) of the fit. It was expected that the MSE would decrease as it progresses because the R² curve approaches a straight line as the number of muscle synergies increases. They selected the first point for which the MSE drops below 10⁻⁵ (the linear regression method). In summary, this second group of methods uses objective criteria to determine the number of synergies, but the algorithms are variable and not standardized.

We investigated two other algorithms of our own to compare their performance. The first algorithm is described in the main text (Materials and Methods). In short, this method is based on the method developed by Cheung et al. [the original ΔR² < shuffle ΔR² (0.75) method] (40). To detect the point at which the original ΔR² is smaller than the shuffle ΔR², they used an arbitrary threshold (i.e., 75% of shuffle ΔR²) (40). To exclude the arbitrariness, we instead used a t test between the original ΔR² and shuffle ΔR² and determined when the original ΔR² is significantly smaller than the shuffle ΔR² [P < 0.05, the original ΔR² < shuffle ΔR² (t test) method]. The second algorithm is also derived from Cheung et al. (40), but this algorithm determines the maximum point at which the original ΔR² is significantly greater than the shuffle ΔR² [t test, P < 0.05, the original ΔR² > shuffle ΔR² method]. In other words, this method determines the point at which increments in the number of synergies significantly improves the quality of EMG reconstruction to better than expected from shuffled EMG data.

We applied each of these methods to our eight datasets used for the muscle synergy analysis (4 wk of two monkeys) and compared the number of synergies selected by each algorithm. Fig. S5 shows the results of the comparison. This comparison provides several important insights into the methods for the selection of the number of synergies. First, the number of synergies determined by the threshold method (group 1) is quite susceptible to the threshold value. For example, when the threshold was set to R² > 0.8, almost all of the datasets had three synergies but one had two synergies. Then, when it was increased to R² > 0.85, all datasets had three synergies. After that, the probability of selecting a larger number of synergies steeply increased, as the threshold increased (R² > 0.9 and 0.95). This clearly demonstrates the instability of the number of muscle synergies determined by the simple threshold methods.

Contrary to the first group, the second group (including ours) yielded a relatively consistent result, except for the linear regression method. These algorithms [the original ΔR² < shuffle ΔR² (0.75), three-point curvature, original ΔR² < shuffle ΔR² (t test), and original ΔR² > shuffle ΔR² methods] revealed three muscle synergies in most cases (8/8, 7/8, 8/8, and 6/8, respectively). The linear regression method yielded a larger number of muscle synergies (5, 6, and 7 synergies) because this method is based on an additional assumption that the R² curve converges to a straight line as the number of muscle synergies increases. This assumption might cause idiosyncratic results. Together, most of the algorithms consistently indicated three synergies as the optimal number of synergies for our datasets, and therefore we used this value in our analyses.

Discussion

In this study, we demonstrate that the muscle fields of excitatory PreM-INs in awake behaving primates are not randomly distributed across hand muscles but distributed as clusters corresponding to muscle synergies. Furthermore, the population activity of excitatory PreM-INs correlates with the temporal profiles of muscle synergies during voluntary hand movements. These findings are consistent with previous hypotheses derived from observations of the lumbar spinal cord of reduced animal preparations [e.g., spinalized frogs (10) and isolated mouse spinal cords (11)] that PreM-INs underlie the generation of muscle synergies. Our study provides direct evidence that the activity of PreM-INs underlies coordination of muscle activity during dexterous hand movements in primates.

Neural Control of Voluntary Hand Movements in Primates.

It is generally believed that the direct corticomotoneuronal (CM) pathway, which is a phylogenetically newer pathway in higher primates, plays a critical role in the fractionation of muscle activity during dexterous hand movements (19–21). However, the present study demonstrated that PreM-INs, which are phylogenetically older, have spatiotemporal properties that correlate with muscle synergies during voluntary hand movements. Therefore, it is likely that these two systems have specialized functions for the control of primate hand movements, namely “fractionated control” and “synergistic control,” respectively.

The interaction of these two putative control systems might be the source of the exceptional versatility of primate hand movements. For example, a power grip (e.g., gripping a hammer) is characterized by the predominant coactivation of hand muscles (22). It is known that power grip requires less involvement of the CM system (19), and therefore might result more from the PreM-IN system. Conversely, fine control of individual finger movements (e.g., control of a fingertip force of a single digit) (23, 24) requires higher fractionation of individual muscles and probably depends more on the CM system. Indeed, muscle synergies are not active during fine individual finger movements in some cases (23, 24). Precision grip requires the fractionation of hand muscles as well as their coactivation (17, 21), and thus might depend on cooperation of both the CM and PreM-IN systems. These examples suggest that the optimal balance of the two control systems may vary according to task requirements. Optimization of balanced control may be an important factor also for the acquisition of new motor skills. For example, Berger et al. demonstrated that learning a new movement that is compatible with existing muscle synergies occurs much more quickly than learning a movement requiring new muscle synergies (25). This implies that establishing, modifying, or masking muscle synergies requires more training. This might explain our everyday experience that highly fractionated movements require extensive practice (e.g., using chopsticks requires more extensive training than using spoons). This conceptual framework of balanced control systems may help future studies to clarify how our nervous system controls and acquires versatile hand functions.

Neural Implementation of Hand Muscle Synergies with PreM-INs.

Despite our findings that PreM-INs underlie the generation of muscle synergies, we also found that individual PreM-INs associated with a given muscle synergy exhibit substantial spatiotemporal diversity with respect to that muscle synergy’s activation (Fig. 2C and Figs. S6 and S8). This was a surprising result because previous studies have often modeled each muscle synergy as a single functional unit, or “module,” in which constituent spinal INs were assumed to be synchronously recruited (for reviews, see refs. 6 and 26). Our finding demonstrates that this is not the case, at least for the control of primate hand movements. Why are the individual PreM-INs so heterogeneous? One possible explanation is that the modules are not organized such that CNS inputs are simply distributed to target motoneurons. Instead, the CNS may organize the modules as active pattern generators, as proposed for locomotor circuits (26, 27), which would intrinsically generate spatiotemporal patterns of target muscle activity. In such dynamic modules, PreM-INs may be individually activated to create the desired muscle synergy activity. Alternatively, it is possible that the CNS does not organize muscle synergies as explicit modules. Sussillo et al. demonstrated that a chaotic recurrent network could be trained to imitate complex animal behaviors by adjusting network connections as well as “readout” weights to muscles (28). In such networks, individual elements (i.e., neurons) show heterogeneous activities similar to actual neural recordings in primate motor cortices (29, 30). From this perspective, the clustering muscle field of PreM-INs identified in the present study might reflect the outcome of the optimization to effectively read out significant motor commands from complex neural networks to coordinate complex hand movements. Whatever the organization of the entire network, the present findings require the revision of previous hypotheses on the neural implementation of muscle synergies that assume synchronous modules for the control of voluntary hand movements.

In this study, we tested the correlation between the spatiotemporal properties of PreM-IN and muscle synergies during a single type of behavior (i.e., precision grip). Of course, primates exhibit a much wider variety of hand movements, so futures studies should combine spinal recordings with different movements. These should aim to elucidate (i) how the clusters of PreM-INs identified in the present study are generalized to the other types of hand movements, (ii) how many and what variety of clusters can be identified when a wider variety of hand movements are tested, and (iii) the long-term plasticity of clusters required to acquire new motor skills.

In summary, this study shows that the population activity of spinal PreM-INs is spatially and temporally correlated with hand muscle synergies during voluntary hand movements in primates. These findings suggest that spinal PreM-INs underlie the generation of hand muscle synergies, and thus contribute to the coordination of dexterous hand movements in primates.

Materials and Methods

Dataset.

The dataset analyzed for the present study was the subject of previous reports (12, 31, 32). We analyzed the data of two monkeys (monkey A: Macaca fuscata, 6.8 kg; monkey E: Macaca mulatta, 5.6 kg). All procedures were approved by the Animal Research Committee at the National Institute for Physiological Sciences.

Behavioral Task.

The monkeys were trained to grip spring-loaded levers with their index finger and thumb (precision grip task; Fig. S1A) (12, 16). Lever positions were displayed on a computer screen as cursors, and monkeys were required to track targets in a step-tracking task. Each trial consisted of a rest period (1.0 to 2.0 s), lever grip, lever hold (1.0 to 2.0 s), and lever release. Successful completion of a trial was rewarded with a drop of applesauce. The force required to reach the target positions was adjusted individually for the index finger and thumb (monkey E: 0.6 to 1.1 N for index, 0.1 to 0.3 N for thumb; monkey A: 0.4 to 2.0 N for index, 1.0 to 3.0 N for thumb).

Data Recordings.

Unilateral laminectomy of vertebrae cervical (C)4 to C7 was performed under isoflurane or sevoflurane anesthesia and aseptic conditions, and a spinal recording chamber was implanted over the laminectomy (33). Single-unit activity from C6 to thoracic (T)1 was recorded with a tungsten or Elgiloy microelectrode using standard techniques (Fig. S1B) (12, 31, 32). Action potential timing was detected online using a spike-sorting device (MSD; Alpha Omega Engineering).

EMGs from 12 hand and arm muscles were recorded simultaneously. EMGs were recorded by pairs of stainless steel wires (AS 631; Cooner Wire) implanted s.c. in the forelimb muscles (Fig. S1C), including the intrinsic hand muscles (first dorsal interosseous, adductor pollicis, abductor pollicis brevis, and abductor digiti minimi), extrinsic digit flexors (flexor digitorum superficialis and the radial and ulnar parts of the flexor digitorum profundus), wrist flexors (flexor carpi radialis and flexor carpi ulnaris), extrinsic digit extensors (extensor digitorum-2,3 and extensor digitorum communis), and a wrist extensor (extensor carpi ulnaris). Neural signals and spike timings were sampled at 25 kHz. EMGs were band pass-filtered (5 Hz to 3 kHz) and sampled at 5 kHz. We also sampled grip force and timing of behavioral events at 1 kHz simultaneous with the neural and EMG signals.

Identification of Postspike Effects of Spinal Interneurons.

The spike-triggered average of the rectified EMG was calculated to identify the postspike effects of individual spinal interneurons on the recorded EMGs (12, 31, 32). We analyzed only neurons with ≥2,000 recorded spikes (range, 2,138 to 67,946 spikes; mean ± SD, 12,583 ± 15,201 spikes). Spike-triggered averages were compiled by averaging segments of rectified EMG activity from 30 ms before to 50 ms after each trigger (Fig. S1D). Spikes were accepted as triggers only if the root mean square (RMS) of the EMG from 30 ms before to 50 ms after the spike was greater than 1.25 times the RMS noise level in that EMG channel. The spike-triggered average was smoothed with a flat five-point finite impulse response filter. The baseline trend was subtracted using the increment-shifted averages method (34), and significant spike-triggered average effects were identified with multiple-fragment statistical analysis (35). The test window was set to 12 ms at 3 to 15 ms after the spinal neuron spike.

Potential cross-talk between simultaneously recorded EMGs was evaluated by combining a cross-correlation method (20) and the third-order differentiation of EMG signals (36). Spike-triggered average effects, potentially resulting from cross-talk between EMG recordings, were eliminated from the dataset. To distinguish postspike effects from synchrony effects (37), we measured the onset latency and peak width at half-maximum (PWHM); effects with onset latency >3.5 ms and PWHM <7 ms were identified as postspike effects (12). Neurons that showed postspike effects on at least one muscle were identified as PreM-INs (Fig. S1E). If neurons showed a large “motor-unit” signature in the spike-triggered average of the unrectified EMG with only 50 spikes (38), they were identified as putative motoneurons and excluded from the dataset.

Extraction of Muscle Synergies.

Muscle synergies were extracted from the EMGs using nonnegative matrix factorization (NMF) (39). First, we removed electrical cross-talk between EMG signals using a blind-signal separation for the third-order differentiated EMG signals (36). Then, the NMF was applied to the processed EMG signals. The separated EMGs were high pass-filtered (cutoff 50 Hz), rectified, low pass-filtered (20 Hz), linearly smoothed (100 time points), and down-sampled to 100 Hz. The EMG amplitudes were normalized to their mean value and the mean amplitude was set as unitary (=1). The NMF algorithm was initialized with random weight and activity matrices, the elements of which were drawn from a uniform distribution between 0 and 1; the values of these matrices were iteratively updated using the multiplicative rule until convergence, defined as having 20 consecutive iterations that resulted in a change of EMG-reconstruction variance, accounted for (R²) < 0.01%. Because the solutions for the synergies and their coefficients could fall into a local minimum, we repeated the synergy extraction 10 times from different initial values and selected the synergies that showed the highest R² for further analyses. The synergy weights and activities were normalized to set the mean amplitude of synergy activity to unitary (=1).

We extracted muscle synergies from 480-s-long continuously recorded EMG signals from four different weeks in each monkey (days 1, 9, 13, and 20 for monkey E and days 1, 6, 14, and 19 for monkey A after the start of spinal recording) that cover an entire experimental period for each monkey (31 and 27 d for monkey E and A, respectively). Then, we made a grand average of each muscle synergy by averaging it across the dataset. These grand averaged muscle synergies were applied to individual datasets to estimate the temporal activity of muscle synergies (SI Materials and Methods).

Number of Muscle Synergies.

We identified the number of muscle synergies based on the method proposed by Cheung et al. (40). The NMF algorithm requires the number of muscle synergies to be determined a priori. Therefore, we successively increased the number of synergies extracted from 1 to the number of muscles recorded (Fig. S2). The R² values for each number of muscle synergies (i.e., n = 1 to 12) were obtained with fourfold cross-validation by first extracting synergies from three out of four 120-s datasets (the training sets) and then fitting the extracted synergies to the other unused quarter (the testing set). R² was calculated as R² = 1 − SSE/SST, where SSE is the sum of the squared residuals and SST is the sum of the squared difference of each EMG data point from the overall mean EMG. We averaged the R² values in the testing set and plotted them against the number of synergies extracted (R² curve; Fig. S2A, original data). We also drew a similar R² curve for the shuffled (i.e., uncorrelated) EMG data, which were obtained by randomly shuffling data across times and muscles (Fig. S2A, shuffled data). The R² curve for the shuffled data increased almost linearly, such that the increment of R² (ΔR²) was similar over the different number of muscle synergies (Fig. S2B). We used the shuffle ΔR² values as an estimate of chance. The basic premise of Cheung et al.’s method is that the number of muscle synergies can be defined by the cusp of the R² curve—or the number beyond which any further increase in the number of muscle synergies yields an R² increase smaller than expected by chance (40). In the original study, they used 75% of shuffle ΔR² as the threshold to detect the smaller original ΔR². Here we used a more statistically based method to detect the significant decrease of original ΔR² by applying t tests between the original and shuffled data. We defined the number of muscle synergies at the point just before the ΔR² of the original data dropped significantly below the ΔR² of the shuffled data (Fig. S2B). We also comprehensively tested other algorithms proposed by other studies (5, 9, 13, 18, 40–44) to compare how the algorithm used affects the estimation of the number of muscle synergies (SI Text and Fig. S5).

Consistency of Muscle Synergies Between Different Experimental Days.

To confirm the long-term consistency of the extracted muscle synergies, we compared the number of muscle synergies and the similarity of the extracted synergies between the different experimental weeks (Fig. S4). Similarity between the muscle synergies was quantified by calculating the cosine of the angle between the weighting vectors. The order of muscle synergy is arbitrary in the NMF algorithm, so the muscle synergies in weeks 2 to 4 were matched to the muscle synergy with the highest similarity in week 1.

Similarity of Muscle Synergies Between Monkeys.

We quantified the similarity of muscle synergies between monkeys E and A by calculating the cosine of the angle (similarity) between two vectors of muscle synergies from the two monkeys (Fig. S3E). To find the significant limits of this similarity, we obtained the chance level of the similarity by randomizing the muscle synergy weights of the muscles in each synergy, and then calculated the similarity in all synergy pairs to obtain the median. We repeated this procedure 10,000 times and set the 95th percentile of this distribution, 0.64, as the significance limit. Therefore, if the muscle synergy similarity was higher than this, we concluded that the muscle synergy pair was more closely related than expected by chance.

Spatial and Temporal Similarities Between PreM-INs and Muscle Synergies.

Similarities between PreM-INs and muscle synergy were examined for their spatial and temporal aspects. Similarity in the PreM-IN muscle field and synergy weight was quantified as the cosine of the angle between two vectors in the muscle dimension (spatial similarity). The muscle field was quantified as a vector of the postspike effect size. The size of the postspike effect was measured as the mean percent increase (MPI) by averaging the spike-triggered average amplitude from the onset to the offset, subtracting the baseline mean, and then dividing the result by the baseline mean and multiplying by 100. Muscle synergy was expressed as a vector of weighting factors. The index of similarity ranged from 1 to −1, where 1 (or −1) indicates that the vectors are parallel in the same (or opposite) direction, and 0 indicates that the vectors are orthogonal (no correlation).

The similarity between PreM-IN activity and muscle synergy was quantified as the cosine of the angle between vectors of temporal profiles of activities in the time dimension (temporal similarity). We compiled the response profiles by aligning each signal to grip onset (from 1 s before to 3 s after grip onset) and averaging across trials. Grip onset was defined as the time at which the rate of change of the total grip force exceeded 2 N/s. Again, the index of similarity ranges from 1 to −1, where 1 (or −1) indicates that the vectors are parallel in the same (or opposite) direction, and 0 indicates that the vectors are orthogonal (no correlation).

Cluster Analysis of Spatial and Temporal Similarities.

Cluster analysis was applied independently for the spatial and temporal similarities in 3D muscle synergy space (Fig. 2 A and C). First, we explored the cluster size by iteratively clustering the PreM-INs into the number of clusters ranging from 1 to 10. For each cluster, we used the k-means algorithm with the squared Euclidean distance calculation. We evaluated the clustering performance by calculating the average silhouette value (45). If the silhouette value showed local maxima, we defined the first local maximum as the cluster size of the PreM-INs.

We validated the clustering performance with a permutation test. We randomly assigned original spatial or temporal similarity values to one of three muscle synergies. This procedure removed any correlations between PreM-IN and muscle synergies. We then calculated the silhouette value for the shuffled data. We repeated this procedure 10,000 times and obtained the baseline distribution of the silhouette values. For the k-means clustering, we fixed the cluster size to the same as that of the original dataset, namely three clusters for the excitatory PreM-INs of monkey E and two clusters for the excitatory PreM-INs of monkey A (Fig. 2A). We set the 95th percentile of this distribution as the significance limit of the silhouette value. Because no cluster was identified for the inhibitory PreM-INs (Fig. S7), no significance test was applied to these data.

Synergy and Neural Trajectories.

We examined how the population activity of the PreM-IN clusters reproduced the muscle synergy activities. This analysis was performed only for monkey E because insufficient data were obtained from monkey A (Table S1). First, we averaged the temporal profile of the synergy activity. To correct the trial-to-trial variation of the grip interval, that is, the interval between grip onset and release onset, we segmented the interval into 100 bins and averaged the signals within each bin. Grip and release onset were defined as the time at which the rate of change of the total grip force exceeded 2 N/s and fell below −2 N/s, respectively. Using this procedure, the time was normalized from 0 (grip onset) to 1 (release onset). We used the same scaling factor to extend the normalization from −0.5 before grip onset to 0.5 after release onset. We performed this normalization for each trial and averaged them across the trials. After the time normalization, we smoothed the profile with a Gaussian kernel (SD 5 time points) and then averaged the profiles from different data recordings. To focus the comparison on the temporal characteristics, we also normalized the amplitudes of the profile: We linearly scaled the amplitude from the baseline activity (mean amplitude between 0.5 and 0.4 time units before grip onset; =0) to the maximum (=1) amplitude.

We calculated the population activity of PreM-INs independently for each cluster. The population averages of PreM-INs were obtained by weighting the individual activity profile (in spikes per s) by the norm of the postspike facilitation size (in units of MPI, ranging from 1.4 to 26.1%), that is, PreM-INs with larger postspike effects were weighted more heavily. Time and amplitude were normalized, and Gaussian smoothing was applied in the same way as to the muscle synergies.

To compare the temporal modulations of muscle synergy activity and PreM-IN cluster activity, we plotted the two trajectories in 3D space, which we termed synergy and neural trajectories. The goodness of fit between the trajectories was calculated by concatenating the three individual temporal profiles into single vectors. The significance of the similarity was tested with a permutation test. We randomly assigned the PreM-INs to one of the clusters, computed the population activity, and then calculated the similarity with the synergy trajectory. We repeated this procedure 10,000 times and obtained the baseline distribution of the R². The significance limit was set to the 95th percentile of this distribution.

SI Materials and Methods

Dataset.

We analyzed the data of two (monkeys A and E) out of three monkeys of original reports (12, 31, 32) because, in the third monkey (U), we recorded only two muscles (FDI and AbDM) and therefore synergy analysis could not be applied. In addition, in the original dataset, different sets of muscles were recorded from the two monkeys (19 and 20 muscles in monkeys A and E, respectively). To ensure consistency between animals, we selected 12 muscles that we consistently recorded from both monkeys.

Extraction of Muscle Synergies.

To extract the muscle synergies, we used the same EMG data used to test the postspike effect. We found, however, that data length varied depending on the stability of the single-unit recordings and ranged from 127 to 3,899 s (mean ± SD, 573 ± 468 s). This length of data is not ideal for muscle synergy analyses because, for example, 127 s is likely to be too short to obtain reliable muscle synergy, even though it is sufficient to collect enough spikes to test postspike effects (>2,000 spikes, ranging from 2,014 to 67,649 spikes; mean ± SD, 9,233 ± 9,526 spikes from all datasets). This indicated that it is not appropriate to calculate muscle synergies from every dataset.

Consequently, we designed our analysis to obtain representative muscle synergies for each monkey. The underlying assumption of this is that muscle synergies are consistent throughout the recording period for each monkey. To confirm this assumption, we compared the representative EMG recordings for each recording week in each monkey (1 to 4 wk after the start of spinal recording). We selected the representative EMG data using the following criteria: (i) the monkey steadily performed the task (typically at the beginning of each recording day), (ii) the datasets were chosen approximately evenly separated in time to represent each week (i.e., 1 to 4 wk), and (iii) the longest EMG length satisfying criteria (i) and (ii). As a result, we obtained more than 480 s of data on days 1, 9, 13, and 20 for monkey E (546, 1,499, 649, and 1,324 s, respectively) and on days 1, 6, 14, and 19 for monkey A (3,889, 875, 496, and 616 s, respectively). We then used the first 480-s-long period of these eight datasets for the muscle synergy analysis. These datasets contained 52 to 88 precision grip trials (mean ± SD, 70 ± 13 trials).

We confirmed the consistency of the resulting muscle synergies across the datasets in a different week by testing the similarity of muscle synergies (Consistency of Muscle Synergies Between Different Experimental Days). Furthermore, fourfold cross-validation of nonnegative matrix factorization (NMF) results indicated that a data length of 480 s was sufficient to extract robust muscle synergies from the EMG data (Number of Muscle Synergies). After confirming this consistency and robustness, we averaged the weight of muscle synergies to obtain the grand averages of each muscle synergy for each monkey. Finally, we applied these averaged muscle synergies to each dataset with the NMF algorithm to estimate the temporal activity of muscle synergies during each recording session.