Interactions between feedback and lateral connections in the primary visual cortex

Significance

One of the fundamental tasks of vision is to group the image elements that belong to one object and to segregate them from other objects and the background. Such a process, known as contour integration, is thought of as involving both long-range horizontal connections in the primary visual cortex (V1) and feedback influences from higher cortical areas such as V4. Using conditional Granger causality analysis of simultaneously recorded neurons in monkey visual cortical areas V1 and V4, we are able to dissect the respective contributions of intraareal and interareal interactions during contour integration, indicating that feedback and lateral connections work synergistically to group and segment visual image components.

Abstract

Perceptual grouping of line segments into object contours has been thought to be mediated, in part, by long-range horizontal connectivity intrinsic to the primary visual cortex (V1), with a contribution by top-down feedback projections. To dissect the contributions of intraareal and interareal connections during contour integration, we applied conditional Granger causality analysis to assess directional influences among neural signals simultaneously recorded from visual cortical areas V1 and V4 of monkeys performing a contour detection task. Our results showed that discounting the influences from V4 markedly reduced V1 lateral interactions, indicating dependence on feedback signals of the effective connectivity within V1. On the other hand, the feedback influences were reciprocally dependent on V1 lateral interactions because the modulation strengths from V4 to V1 were greatly reduced after discounting the influences from other V1 neurons. Our findings suggest that feedback and lateral connections closely interact to mediate image grouping and segmentation.

A key step in the visual system’s analysis of object shape is to group line segments into global contours and segregate these contours from background features. This process is critical to identifying object boundaries in complex visual scenes, and thus particularly important for performing shape discrimination; image segmentation; and, ultimately, object recognition.

Contour integration follows the Gestalt principle of good continuation (1). The underlying neural underpinnings have been characterized as an association field (2), which links contour elements that are part of smooth contours. Neurophysiological studies in monkeys have identified that the primary visual cortex (V1) makes a fundamental contribution to contour integration (3–6), and anatomical studies have shown that the topology of horizontal connections in V1 is well suited for mediating interactions between neurons with a similar orientation preference (7–10). Such intracortical circuitry in V1 has been implemented in many computational models to account for the successful process of contour integration (11–13). Although many lines of converging evidence suggest that V1 is intimately involved in contour integration, circuit-based models have to take into account the findings that contour grouping is more than a bottom-up or hard-wired process, but that it is strongly dependent on top-down feedback influences (5, 14–17). Surface segmentation, another important intermediate stage in processing of visual images, is also mediated by interactions between feedforward and feedback connections (18).

We have proposed a model whereby cortical feedback contributes to the effective connectivity of horizontal connections within V1 (13, 19). A possible role of higher cortical areas in this process is to disambiguate local image components by creating a template that is fed back to V1, which then can selectively enhance object components and suppress interfering background (20–22). This notion is exemplified in one of our recent studies through simultaneous recordings from monkey visual cortical areas V1 and V4 implanted with microelectrode arrays (23). We have shown that in the presence of a complex background, information about global contours emerges initially in V4 and then rapidly builds up in both cortical areas. Bidirectional interareal interactions not only facilitate V1 neurons encoding the contour elements but also suppress V1 neurons responding to the background. Because the onset of contour-related signals in V1 is much delayed relative to the onset of contour-related signals in V4, an unsolved important question is whether the contour signals in V1 are derived from feedback inputs alone, or whether they are mediated by an intimate interaction between feedback signals and horizontal connections within V1.

In the current study, we used conditional Granger causality (GC) to tease apart the contributions of horizontal interactions within V1 and top-down feedback from V4 to V1. Although conventional GC provides a statistical measure of the influences of one recording site on another, conditional GC provides a further measure of whether such influences are dependent on other simultaneously recorded sites. It also has the ability to remove confounding influences that result from common inputs to a pair of recording sites, thus allowing us to dissect the respective contributions of horizontal connections and feedback influences during contour integration.

Results

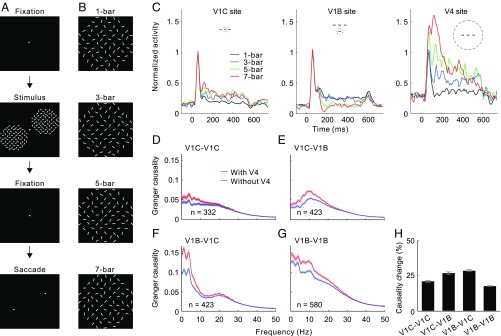
To look at the interplay between feedback and intrinsic cortical connections, we recorded neural activities from V1 and V4 of awake monkeys performing a contour detection task (23). In this task, two identical background patterns of randomly oriented bars were presented in two visual field quadrants (Fig. 1A). A contour was formed by collinearly aligning one, three, five, or seven bars in either of these two patterns (Fig. 1B). The monkeys were rewarded for choosing the pattern containing the contour by making a saccade to it. When the number of collinear bars was one, the two simultaneously displayed patterns were identical and the animals were randomly rewarded for choosing either of the two stimuli.

Fig. 1.

GC analysis of V1 lateral interactions based on spike trains. (A) Contour detection task. (B) Sample contour patterns with embedded contours formed by different numbers of collinear bars. (C) Sample recording sites showing normalized neuronal responses to contours of different lengths for a V1 recording site on the contour (V1C site), a V1 site on the background (V1B site), and a V4 site. (Insets) Cartoons illustrate the spatial relationship between the collinear contour and the examined RFs. (D–G) GC value as a function of frequency in the seven-bar contour condition, showing the directional interactions in V1 between contour sites (V1C–V1C), from contour sites to background sites (V1C–V1B), from background sites to contour sites (V1B–V1C), and between background sites (V1B–V1B) before (red) and after (blue) discounting V4 influences. Shaded areas represent ±SEM. (H) Data shown in D–G are replotted here, showing percentage reductions in overall GC (summed over 0–50 Hz) after removing V4 influences. Error bars represent ±SEM. A similar analysis based on LFP data is shown in Fig. S2.

Feedback Modulation from V4 Strengthens V1 Lateral Interactions.

We analyzed multiunit spiking activity recorded by microelectrode arrays implanted in V1 and V4 from neurons with preferred orientations close to the contour orientation and with overlapping receptive fields (RFs) in these two cortical areas. The simultaneously recorded V1 sites were further separated into two groups: the contour sites with RFs lying on the contour and the background sites with RFs on the complex background. Analysis of spiking activity (Fig. 1C) confirmed the previous observations (23) of both contour facilitation (increasing responses for V1 contour sites with increasing contour length) and background suppression (decreasing responses for V1 background sites with increasing contour length). V4 sites, similar to V1 contour sites, showed progressively enhanced responses as the number of collinear bars increased.

To dissect the respective contributions of V1 horizontal connections and V4 feedback influences during contour integration, we performed conditional GC analysis on spike trains collected in the seven-bar condition. Specifically, we compared the interactions between V1 neurons, as measured by GC, with and without taking into account V4 influences. We observed that after discounting V4 influences using conditional GC analysis, V1 horizontal connectivity along the contour path significantly decreased in the frequency range of 0–30 Hz compared with horizontal connectivity calculated using conventional GC analysis (Fig. 1D). Similar reductions were observed in V1 effective connectivity between two recording sites representing the contour and the background, respectively (Fig. 1 E and F), and between two sites on the background (Fig. 1G), with significant percentage changes across all types of paired recording sites in V1 (Fig. 1H; Friedman test for repeated-measures: ${\chi }^2\left[332\right]=69.61$, P < 10⁻¹⁴; four categories with different sample sizes were randomly down-sampled to the smallest number, which was 332). Interestingly, the directional interactions were asymmetrical between V1 contour and background sites when the same recording sites were analyzed (compare Fig. 1 E with F), suggesting asymmetrical figure–ground interactions within V1 in the presence of a global contour.

We repeated the above analyses by shuffling V4 spike trains across trials. The changes in GC for paired V1 sites were negligible after discounting the influences from trial-shuffled V4 data (compare Fig. S1 A–D with Fig. 1 D–G), further confirming that the effective connectivities between V1 sites are subject to feedback modulation.

Fig. S1.

Control analysis of GC of V1 lateral interactions with trial-shuffled V4 spike trains. GC of spiking activities are shown between V1 contour-contour sites (A), contour-background sites (B), background-contour sites (C), and background-background sites (D), respectively, before (red) and after (blue) discounting V4 influences. Shaded areas represent ±SEM.

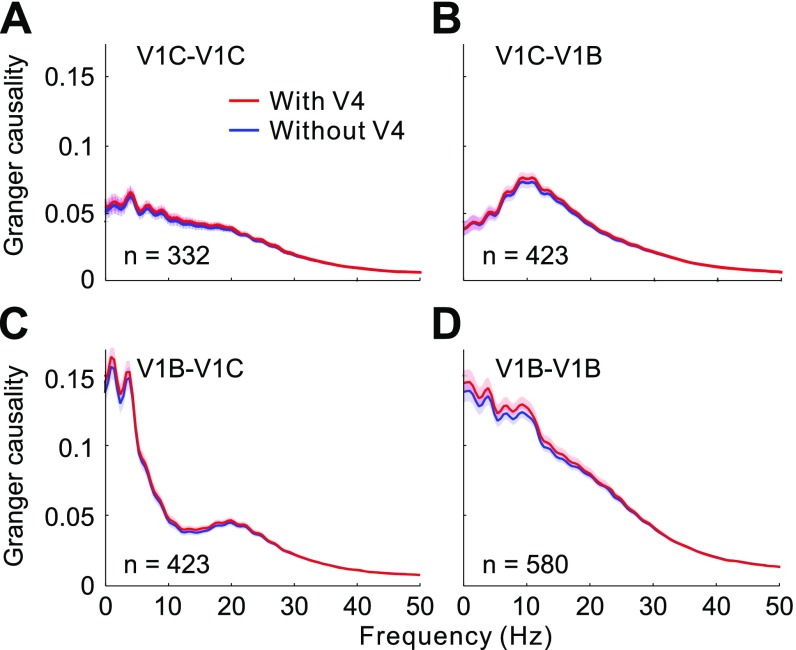
In addition to multiunit spiking data, we performed conditional GC analyses on simultaneously recorded local field potentials (LFPs), which reflect aggregate activity over a large population of neurons. We observed similar feedback modulatory effects from V4 on lateral interactions within V1 along the contour, between the contour and background, and within the background (compare Fig. S2 A–E with Fig. 1 D–H).

Fig. S2.

GC analysis of V1 lateral interactions based on LFP data. GC between V1 contour-contour sites (A), contour-background sites (B), background-contour sites (C), and background-background sites (D), respectively, before (red) and after (blue) discounting V4 influences. (E) Data shown in A–D are replotted here, showing percentage reductions in overall GC (summed over 0–50 Hz) after removing V4 influences. Shaded areas and error bars represent ±SEM.

The analyses of both spike-train and LFP data using conditional GC strongly support the notion that feedback from V4 strengthens V1 lateral interactions.

Feedback Modulation from V4 Is Amplified by V1 Lateral Interactions.

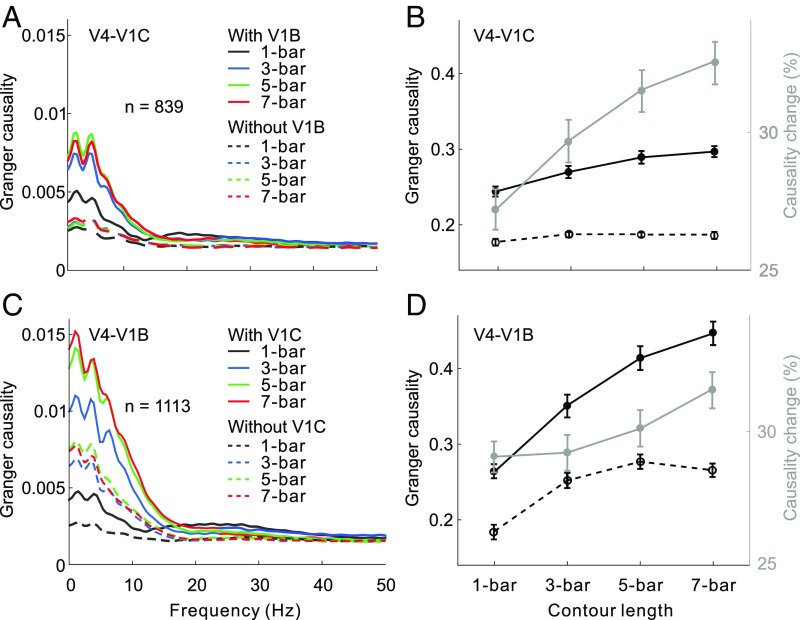
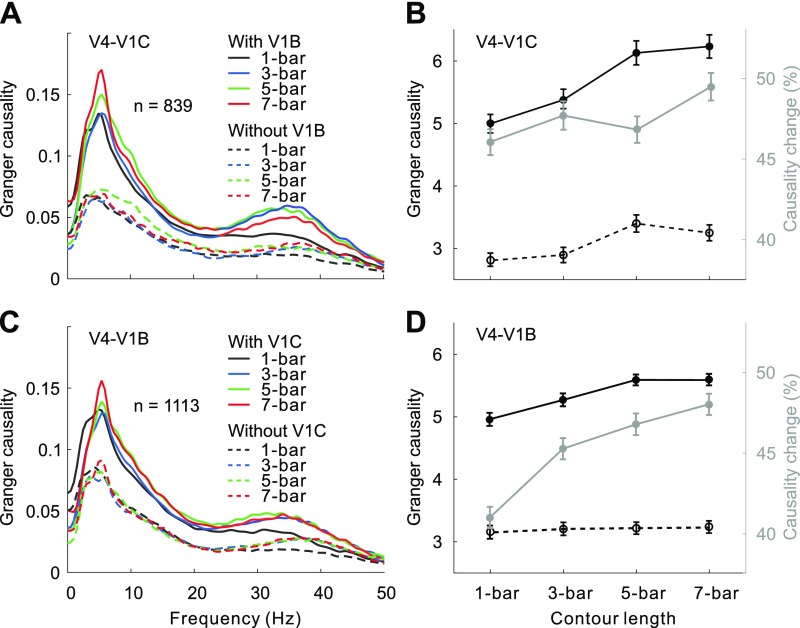
In the detection task, contour saliency was signaled by the number of collinear bars embedded in the complex background. Previous studies have shown that V1 neurons encode perceptual saliency of contours, with more salient contours inducing stronger facilitatory effects on neurons with RFs lying on the contour (5, 23, 24) and stronger inhibitory effects on neurons with RFs lying on the background (23, 24). Our GC analysis using spike-train data showed that the strength of feedback influence from V4 to V1 contour sites (Fig. 2 A, solid lines and B, dark solid line) and to V1 background sites (Fig. 2 C, solid lines and D, dark solid line) also progressively increased as the visual contour became longer. This result suggests the involvement of feedback from V4 in generating the contour signals as well as in suppressing the background noise within V1.

Fig. 2.

GC analysis of V4 feedback modulations based on spike trains. (A) Influences of V4 on V1 contour sites with (solid lines) and without (dashed lines) the influences from V1 background sites for different contour lengths. (B) Data shown in A are replotted here, showing the overall GC (summed over 0–50 Hz, left y axis) as a function of contour length with (solid black curve) and without (dashed back curve) the influences from V1 background sites. The gray curve (associated with the right y axis) represents percentage reductions (Friedman test, all Ps < 0.001) in GC after discounting the influences from V1 background sites. Error bars represent ±SEM. (C and D) Similar to A and B, but showing the influences of V4 on V1 background sites with and without the influences from V1 contour sites (Friedman test, all Ps < 0.001). A similar analysis based on LFP data is shown in Fig. S3.

We next used the conditional GC to examine whether the lateral interactions in V1 are required for the feedback signals to take effect. After discounting the influences from V1 background sites, we found a substantial reduction in influence from V4 to V1 contour sites (Fig. 2 A and B, dashed line versus solid line of the same color). The amount of reduction was larger for longer contours (Fig. 2B, gray line). The feedback influences from V4 to V1 background sites also showed a similar pattern of dependency on the influences from V1 contour sites (Fig. 2 C and D).

In agreement with the results from spike-train data analysis, GC analysis using LFPs showed similar effects (compare Fig. S3 with Fig. 2). Together, these results indicate the contributions of V1 lateral interactions to mediating and strengthening the feedback modulatory effects, which could play an important role in amplifying the contour signals and suppressing the background noise.

Fig. S3.

GC analysis of V4 feedback modulations based on LFP data. (A) Influences of V4 on V1 contour sites with (solid lines) and without (dashed lines) the influences from V1 background sites for different contour lengths. (B) Data shown in A are replotted here, showing the overall GC (summed over 0–50 Hz, left y axis) as a function of contour length with (solid black curve) and without (dashed black curve) the influences from V1 background sites. The gray curve (associated with the right y axis) represents percentage reductions (Friedman test, all Ps < 0.001) in GC after discounting the influences from V1 background sites. (C and D) Similar to A and B, but showing the influences of V4 on V1 background sites with and without the influences from V1 contour sites (Friedman test, all Ps < 0.001). Error bars represent ±SEM.

The Relative Contribute of Feedback Modulation and Lateral Interactions to Contour Integration in V1.

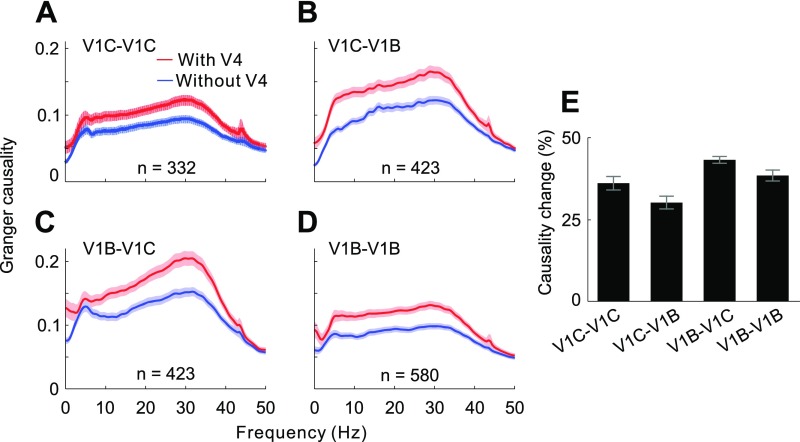
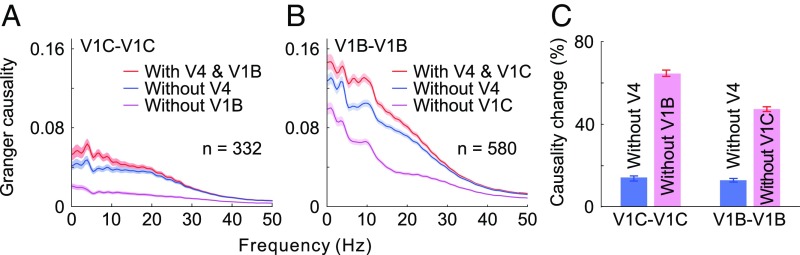
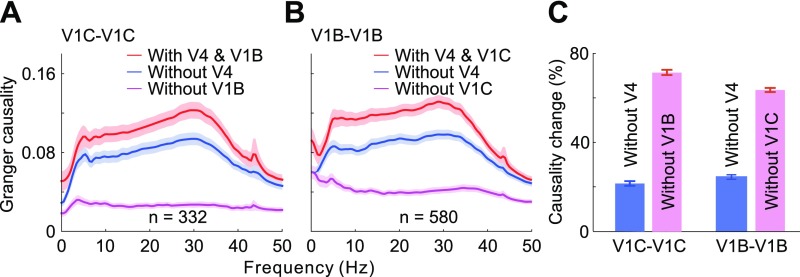
Figs. 1 and 2 showed interdependence between feedback modulation and horizontal interactions in generating contour signals in V1. We next set out to examine the relative contributions of V1 lateral interactions and V4 feedback influences during this process. We first compared the influences from V4 recording sites and from V1 background sites, respectively, on the interactions between two V1 contour sites lying on a seven-bar contour. We observed, by means of conditional GC, that the interactions between V1 contour sites showed a significantly larger reduction in strength when the influence of V1 background sites was removed than when V4 influence was removed (Fig. 3 A and C, two left bars in C; unpaired t test: t₆₆₂ = 23.24, P < 10⁻⁸⁷).

Fig. 3.

Relative contributions of V4 feedback modulations and V1 lateral interactions to the contour integration process in V1. (A) GC of spiking interactions between V1 contour sites (red) compared with GC without the influences from V4 sites (blue) or V1 background sites (magenta). (B) GC of spiking interactions between V1 background sites (red) compared with GC without the influences from V4 sites (blue) or V1 contour sites (magenta). (C) Same data as in A and B are replotted to show percentage reductions in GC after discounting V4 feedback or V1 lateral influences. Shaded areas and error bars represent ±SEM. A similar analysis of LFP data is shown in Fig. S4.

We then repeated the same analysis to examine the interactions between two V1 background sites influenced by V4 sites and by V1 contour sites, respectively. We also found a significantly larger decrease in lateral interactions between V1 background sites after discounting V1 contour sites than after discounting the influences from V4 (Fig. 3 B and C, two right bars in C; unpaired t test: t₁₁₅₈ = 38.3, P < 10⁻²⁰⁷).

Consonant with the results from analysis of spiking data, conditional GC analyses on LFPs also showed that the lateral interactions among V1 neurons contribute more to the contour integration process in V1 than feedback modulation from V4 (compare Fig. S4 with Fig. 3).

Fig. S4.

Relative contributions of V4 feedback modulations and V1 lateral interactions based on GC analysis of LFP data. (A) Interactions between V1 contour sites (red) compared with interactions without the influences from V4 sites (blue) or V1 background sites (magenta). (B) Interactions between V1 background sites (red) compared with interactions without the influences from V4 sites (blue) or V1 contour sites (magenta). (C) Same data in A and B are replotted to show percentage of reductions in GC after discounting V4 feedback or V1 lateral influences. Shaded areas and error bars represent ±SEM.

Both Feedback Modulation and Lateral Interactions Reflect Behavior.

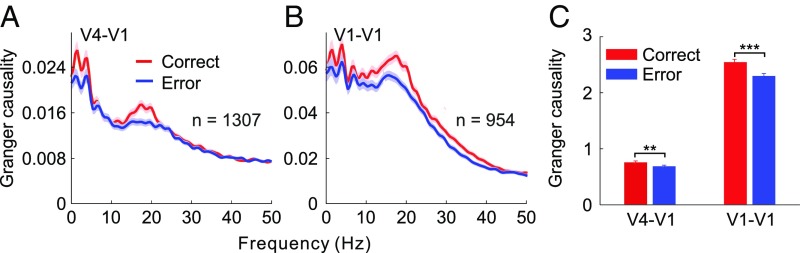
To examine whether V4 feedback influences and V1 lateral interactions were related to behavior, we measured the GC separately for trials in which the animals made correct and erroneous responses. Because there were only a small number of error trials in the five- or seven-bar contour condition, we instead used the three-bar condition for this comparison. The numbers of the correct and error trials were equated to avoid potential confounds due to a difference in sample size.

We found overall decreases of GC in the error trials compared with the correct trials for both V4 feedback influences (Fig. 4A) and V1 lateral interactions (Fig. 4B). These changes were statistically significant (Fig. 4C, two left bars: unpaired t test: t₂₆₁₂ = 3.16, P < 0.01; two right bars: t₁₉₀₆ = 5.61, P < 10⁻⁶), showing that both feedback influences and V1 lateral interactions are behaviorally relevant.

Fig. 4.

Behavioral relevance of feedback influences and lateral interactions. The feedback influences of V4 on V1 (A) and the lateral interactions within V1 (B), measured by GC analysis of spike trains, were weaker in trials with erroneous behavioral choice (blue) compared with the correct trials (red). (C) GC values summed over 0–50 Hz for data shown in A and B (**P < 0.01, ***P < 0.001). Shaded areas and error bars represent ±SEM.

Discussion

Despite the prevalence of feedback projections throughout the visual cortex, it remains unclear what role the cortical feedback plays in contour integration. We showed that feedback influences from V4 remarkably promote the lateral interactions within V1 (Fig. 1 and Fig. S2). This result supports a neural network model involving gating of V1 lateral interactions through feedback modulation (11–13).

It is intriguing to observe that intrinsic V1 interactions substantially strengthen V4-to-V1 feedback modulatory effects, especially in the presence of a global contour (Fig. 2 and Fig. S3). This observation is somewhat surprising, but it can be explained within the theoretical framework of countercurrent processing between cortical areas (20–23): The intrinsic V1 connections provide a substrate on which the feedback operates, and the interactions between feedback and horizontal connections may, in turn, reinforce the feedback modulatory effects for effectively analyzing and disambiguating complex visual scenes. The consequence is to augment the contour signals and suppress the background noise, resulting in a parallel increment of global contour information in both V1 and V4 (23).

We also showed that although both feedback influences and lateral interactions were behaviorally relevant and tightly coupled in contour grouping, the lateral interactions seemed to contribute more to the integration process in V1 (Fig. 3 and Fig. S4). This result is in agreement with the structure of long-range horizontal connections, which tend to link neurons with nonoverlapping RFs and similar orientation preferences (7–10).

GC is a statistical measure of directional influence of one time series on another (25). For two simultaneously measured time series, one is called causal to the other if the predictability of the second process at a given time point is improved by including measurements from the immediate past of the first. GC has been shown to be suitable for probing directionality in neuronal interactions for both continuous signals (26–29) and spike trains (30–32). However, the pairwise approach to GC analysis may not clearly distinguish causal influences from different sources. Conditional GC is instrumental in disambiguating such a situation (33), yet it has not been available for spike-train data. The development of such a measure allows us to perform multivariate analyses of spike-train data collected by electrode arrays, which is particularly important, given the common use of spikes in neuroscience research. In the contour detection process examined in the current study, results from analyses of both spiking and LFP data were largely in agreement, but only the spiking data can be used to differentiate V1 neurons reliably on the contour and background.

There are several important methodological issues when interpreting the results obtained by GC analysis of spike-train data. First, the data under analysis are assumed to be stationary, which can usually be reduced with a sliding window approach (32). Second, the noise contained in the data can bias the GC estimation. Previous work has shown that GC estimation of continuous time series can be strongly affected by noise, whereas spike trains are less affected (32, 34). In addition, our simulations (Figs. S5 and S6) have demonstrated that the noise-contaminated spike trains usually lead to reduced absolute GC values, yet the reduction does not change the GC directionality (relative GC). Third, the difference in firing rates between neurons can confound the GC estimation. One way to correct for this issue is the so-called thinning procedure (27), whereby the spikes of the more active recording site are randomly removed to equate the firing rates of the paired sites. Fourth, the directional influence revealed by GC analysis is statistical in nature; thus, the observation of a Granger causal influence in the cortex does not necessarily imply the existence of direct anatomical connections between the corresponding neurons. Although GC analysis has proven informative in dissecting neuronal interactions (26, 27, 32, 33), we note that it is difficult to exclude possible influences from hidden variables or unrecorded neurons. Although this problem has motivated several modeling studies (e.g., ref. 35), future work to account for the common, yet hidden, inputs is needed to address this issue. Functional influences between V4 and V1 can be mediated by a number of anatomical routes, including direct connections between V4 and V1 and indirect connections passing through V2 or even pulvinar (33, 36). Nonetheless, the interactions within V1 are likely mediated by a plexus of horizontal connections that run between columns of similar orientation preference (7–10, 37). The columnar specificity of these horizontal connections, as well as their extent, is consonant with the functional and perceptual characteristics of the putative association field that links contour elements belonging to a smooth contour (2, 38, 39). The task-dependent nature of contour-related responses in V1 suggests the involvement of higher order feedback influences on the expression of the association field (14). The results presented here from the conditional Granger analysis support the idea of such an interaction.

Fig. S5.

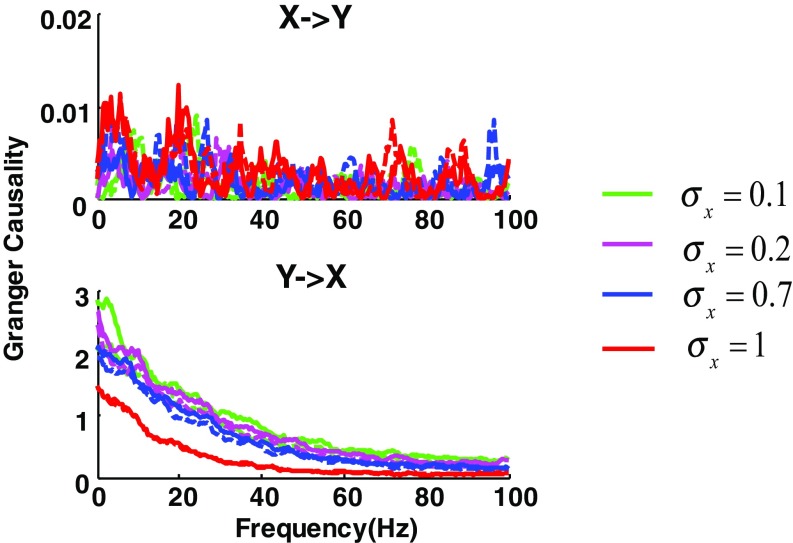
Effect of signal power on GC estimation assessed by a computer simulation. A two-channel model is used, where GC is from y to x: $\{\begin{array}{c}x\left(t\right)=0.4x(t-1)+0.6y(t-1)+{\epsilon }_x\left(t\right)\\ y\left(t\right)=0.9y(t-1)+{\epsilon }_y\left(t\right)\end{array}$, where ${\epsilon }_x$ and ${\epsilon }_y$ are independently generated white noise of variances ${\sigma }_x^2$ and ${\sigma }_y^2.$ Gaussian random noise of variances ${\delta }_{noise1}^2$ and ${\delta }_{noise2}^2$ are added to x and y, respectively, to generate the noise-contaminated data, which are then thresholded to produce spike trains. In the simulation, the additive noise is fixed by setting ${\delta }_{noise1}={\delta }_{noise2}=0.2,$ and the power of x is changed by systematically varying ${\sigma }_x$ at different values of 0.1, 0.2, 0.7, and 1 while fixing y at ${\sigma }_y=1.$ Several results can be obtained: (i) In agreement with the model setup, GC from y → x (Lower) is generally observed compared with the model setup in the opposite direction, GC from x → y (Upper; note the much smaller scale); (ii) when the signal power of x is increased (${\sigma }_x$ from 0.1 to 1; the relative power of y is decreased accordingly), the estimation of GC from y → x is also reduced; and (iii) the stronger the power of x, the weaker is the noise effect on GC (solid lines, without noise; dashed line, with noise).

Fig. S6.

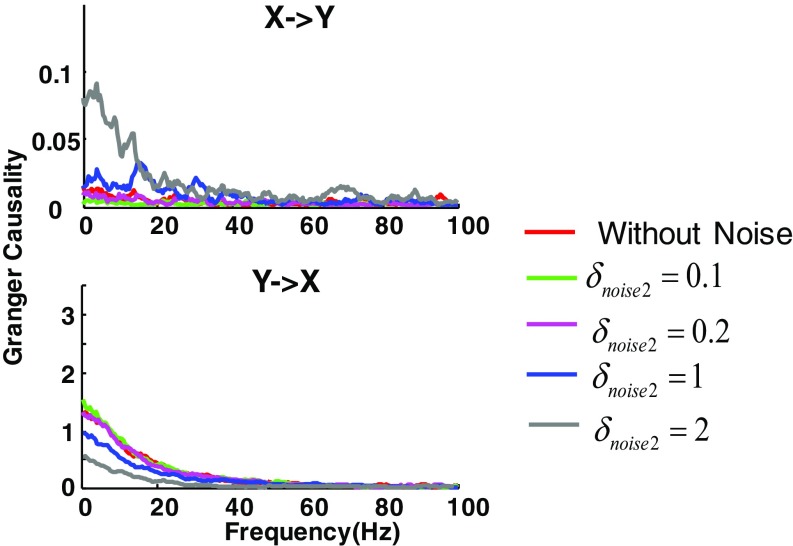
Effect of noise on GC estimation. Spike trains are generated by the same model as shown in Fig. S5, yet with different model parameters. Keeping the signal power constant (${\sigma }_x={\sigma }_y=1$), we changed the noise added to y (${\delta }_{noise2}$ = 0.1, 0.2, 1, and 2) while fixing the noise added to x (${\delta }_{noise1}=0.2$). In general, GC from y → x (Lower) is observed, as opposed to GC in the opposite direction (Upper, note the small scale), which is consistent with the model setup. Moreover, although the additive noise can reduce the absolute GC values, the reduction does not alter the GC directionality (relative GC).

In summary, by distinguishing whether the intraareal and interareal interactions between cortical neurons have components of different origins, the current study dissected the respective contributions of V1 horizontal connections and V4 feedback to contour grouping, and revealed an interactive role between feedback and intrinsic circuits in parsing visual images.

Materials and Methods

Ethical approval was granted by the Institutional Animal Care and Use Committee of Beijing Normal University, with all experimental procedures in compliance with the NIH Guide for the Care and Use of Laboratory Animals (40).

Behavioral Paradigm and Electrophysiological Recordings.

Details of the experimental design are available elsewhere (23). In brief, two adult monkeys (Macaca mulatta, male, weighing 6.5 and 10.5 kg) were trained to detect a visual contour formed by collinear bars embedded in either of two stimulus patches displayed simultaneously (Fig. 1A). Each component bar was 0.25° by 0.05° in size and distributed in a circular area 4.5° in diameter divided by 0.5° by 0.5° grids. The number of collinear bars forming the contour was randomly set to one, three, five, or seven in a trial (Fig. 1B). The task started with an initial fixation period of 300 ms, followed by a 500-ms stimulus presentation. After a 300-ms blank delay period, the monkey was rewarded for making a saccade within 800 ms to the location of the contour pattern. When the monkeys were performing the contour detection task, multiunit activities (waveforms sampled at 30 kHz) and LFPs (sampled at 2 kHz) were recorded from two microelectrode arrays (Blackrock Microsystems; six by eight electrodes, each ∼0.5 mm in length and spaced 0.4 mm apart) implanted in V1 and V4, respectively, at corresponding retinotopic locations.

Data Analysis.

All data analyses were performed using MATLAB (The MathWorks). Spike trains and LFPs within 0–500 ms after stimulus onset were used. The orientation tuning curves and RFs of V1 and V4 recording sites were measured using grating patches and were fitted with Gaussian functions. The recorded V1 and V4 RFs had mean eccentricities of 5.08 ± 0.92° (mean ± SD) and 4.07 ± 1.77°, respectively, and mean sizes of 0.67 ± 0.19° and 5.23 ± 2.35°, respectively. Only recording sites with preferred orientations deviated from the global contour by less than 35° were selected. Based on the distance of a neuron’s RF center to the contour path, the selected V1 sites were further divided into contour sites (RF contour distance ≤ 0.35°) and the background sites (RF contour distance ≥ 0.55° and ≤ 1.50°). Among the selected V4 sites, only those sites with central RF regions (±1.17 SD of the Gaussian envelope) intersecting the axis of the contour and covering the RF centers of selected V1 sites were used (more details are provided in ref. 23).

Conditional GC Analysis.

Conditional GC analysis was performed to evaluate the influence of one recording site (Y) on another (X), after taking into account the influence of other recorded sites (Z). It allowed us to dissect contributions of different sources to neuronal interactions. Within the multivariate regression framework, the frequency domain representation of the conditional GC measure from Y to X, conditional on Z, is given by $I_{\mathrm{Y}\to \mathrm{X}|\mathrm{Z}}\left(f\right)=\ln \left[{\displaystyle {\sum }_{\mathrm{XX}}\left(\mathrm{X,Z}\right)}/\left|{\stackrel{\sim }{H}}_{\mathrm{XX}}\left(f\right){\stackrel{\sim }{\mathrm{\Sigma }}}_{\mathrm{XX}}\left(\mathrm{X,Y,Z}\right){\stackrel{\sim }{H}}_{\mathrm{XX}}^{\ast }\left(f\right)\right|\right],$ where ${\displaystyle {\sum }_{\mathrm{XX}}\left(\mathrm{X,Z}\right)}$ is the residual variance of X that is not explained by the joint regression of X and Z; ${\stackrel{\sim }{\mathrm{\Sigma }}}_{\mathrm{XX}}\left(\mathrm{X,Y,Z}\right)$ and ${\stackrel{\sim }{H}}_{\mathrm{XX}}\left(f\right)$ are, respectively, the noise covariance matrix in the joint regression of X, Y, and Z and the normalized transfer function, and the asterisk denotes complex conjugate (41, 42).

To make the conditional GC directly applicable to spike trains, we took a nonparametric approach (43). In our implementation, to construct the spectral density matrix, the spectral estimate of spike trains was directly applied to the neural point process itself (i.e., sequences of spike times rather than the spike counts), using the multitaper technique (44). To calculate the spectral estimates of spike trains that were down-sampled to 1 kHz, five orthogonal Slepian tapers were applied to the spiking activity within the 500-ms stimulus presentation period. The obtained spectral matrix, $\mathbf{S}\left(f\right)$, was then factorized into the product of transfer functions and the noise matrix (45), $\mathbf{S}\left(f\right)=\mathbf{H}\left(f\right)\mathrm{\Sigma }{\mathbf{H}}^{\ast }\left(f\right)$, from which the conditional GC was finally computed.

For the analysis of LFP time series, LFPs were first down-sampled to 200 Hz, followed by prewhitening with a first-order autoregressive model to reduce the dynamic range of the data. This preprocessing helps reduce bias of the final spectral estimate. Similar to the above analysis procedures of spike data, conditional GC was obtained based on the prewhitened LFP data.

The strength of the directional influence from one recording site to another was defined as the total GC values that were integrated over the frequency range of 0–50 Hz. To rule out the possibility that changes in GC could be due to different neuronal firing rates at different contour lengths, a thinning procedure (27) was performed to correct the spiking rate differences by randomly removing the spikes of the more active recording site until the average firing rates of the paired sites were equal.