Conspectus
Solid state nuclear magnetic resonance (NMR) measurements at low temperatures have been common in physical sciences for many years, and are becoming increasingly important in studies of biomolecular systems. This article reviews a diverse set of projects from my laboratory, dating back to the early 1990s, that illustrate the motivations for low-temperature solid state NMR, the types of information that are available from the measurements, and likely directions for future research. These projects include NMR studies of both physical and biological systems, performed at low (cooled with nitrogen, down to 77 K) and very low (cooled with helium, below 77 K) temperatures, and performed with and without magic-angle spinning (MAS).
In NMR studies of physical systems, the main motivation is to study phenomena that occur only at low temperatures. Two examples from my laboratory are studies of molecular rotation and an orientational ordering in solid C60 at low temperatures and studies of unusual electronic states, called skyrmions, in two-dimensionally confined electron systems within semiconductor quantum wells. NMR measurements on quantum wells were facilitated by optical pumping of nuclear spin polarizations, a signal enhancement phenomenon that exists at very low temperatures.
In studies of biomolecular systems, motivations for low-temperature NMR include suppression of molecular tumbling (thereby permitting solid state NMR measurements on soluble proteins), suppression of conformational exchange (thereby permitting quantitation of conformational distributions), and trapping of transient intermediate states in a non-equilibrium kinetic process (by rapid freeze-quenching). Solid state NMR measurements on AIDS-related peptide/antibody complexes, chemically denatured states of the model protein HP35, and a transient intermediate in the rapid folding pathway of HP35 illustrate these motivations.
NMR sensitivity generally increases with decreasing sample temperature. It is therefore advantageous to go as cold as possible, particularly in studies of biomolecular systems in frozen solutions. However, solid state NMR studies of biomolecular systems generally require rapid MAS. A novel MAS NMR probe design that uses nitrogen gas for sample spinning and cold helium only for sample cooling allows a wide variety of solid state NMR measurements to be performed on biomolecular systems at 20-25 K, where signals are enhanced by factors of 12-15 relative to measurements at room temperature.
MAS NMR at very low temperatures also facilitates dynamic nuclear polarization (DNP), allowing sizeable additional signal enhancements and large absolute NMR signal amplitudes to be achieved with relatively low microwave powers. Current research in my laboratory seeks to develop and exploit DNP-enhanced MAS NMR at very low temperatures, for example in studies of transient intermediates in protein folding and aggregation processes and studies of peptide/protein complexes that can be prepared only at low concentrations.
Introduction
There are several motivations for performing nuclear magnetic resonance (NMR) measurements at low temperatures, including: (1) to study phenomena that occur only at low temperatures; (2) to immobilize molecules in frozen solutions, thereby permitting solid state NMR measurements on soluble systems; (3) to trap transient states that would quickly disappear at higher temperatures; (4) to enhance the signal-to-noise of the NMR measurements; (5) to facilitate dynamic nuclear polarization and other hyperpolarization methods. This article reviews research projects in my laboratory that have involved both low temperatures (defined as sample temperatures that can be achieved with liquid nitrogen) and ultra-low temperatures (defined as sample temperatures that require liquid helium) and that illustrate these five motivations. Of course, many other laboratories have pursued low-temperature NMR measurements for various purposes and continue to do so. This article does not include a review of work from other laboratories, although results from other laboratories are mentioned at appropriate points.
Low-temperature NMR to study temperature-dependent phenomena
Molecular motions in solid C60
Since biological processes do not ordinarily occur at low temperatures, the phenomena that are studied by low-temperature NMR (and other low-temperature techniques) are generally drawn from the fields of physics, physical chemistry, and materials science. In physics, phenomena such as superconductivity,1 antiferromagnetism,2 and charge density waves3 have been the subjects of numerous low-temperature NMR studies.
When simple methods for producing macroscopic quantities of the all-carbon molecules called fullerenes were invented in 1990,4 my colleagues at AT&T Bell Laboratories and I became interested in the dynamics of fullerenes in the solid state, originally with the idea that the soccer-ball shape proposed for the “buckminsterfullerene” C60 molecule might lead to isotropic molecular rotation within solid C60. This idea was born out by the natural-abundance 13C NMR spectra of C60 powder shown in Fig. 1a, which show the broad chemical shift anisotropy (CSA) powder pattern lineshape expected for static molecules at temperatures below 140 K, but a single line at the isotropic chemical shift position at higher temperatures.5 The temperature-dependent change in the 13C NMR spectrum is due to averaging of the CSA to zero at the higher temperatures by rapid molecular reorientiation, together with the fact that all carbon sites in C60 are related by rotational symmetry, making their isotropic chemical shifts equal.
Figure 1.
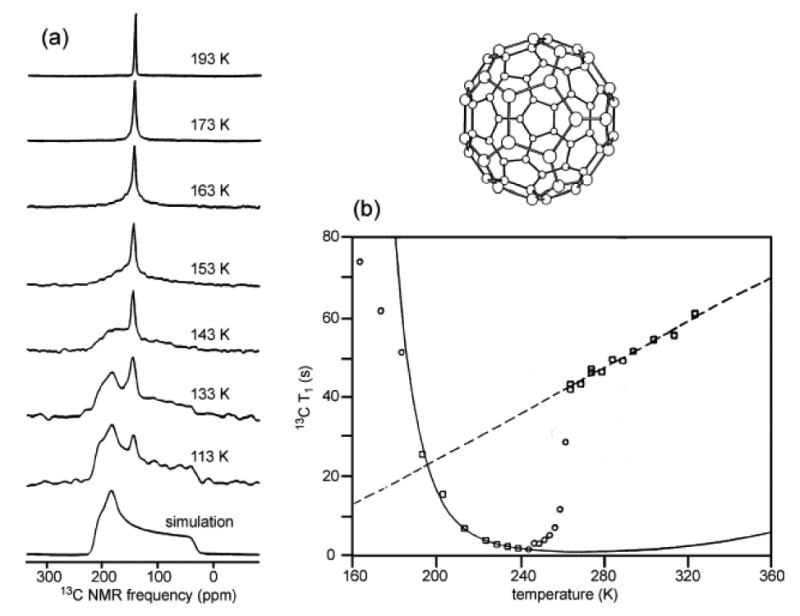
(a) 13C NMR spectra of polycrystalline C60 at the indicated temperatures and 9.39 T, compared with the simulated chemical shift anisotropy powder pattern line shape for immobilized molecules. (b) Experimental temperature dependence of the spin-lattice relaxation time (squares and circles) and best-fit theoretical curves for low-temperature and high-temperature phases (solid and dashed lines, respectively) with different activation energies for molecular reorientation. [reprinted from Phys. Rev. Lett. 67, 1886 (1991)].
On the other hand, diffraction measurements on C60 powder by Heiney et al.6 seemed to show that molecular motion stopped at an orientational order-disorder phase transition at Tc ≈ 250 K. More precisely, C60 molecules appeared as nearly featureless spheres in diffraction data above Tc, but as objects with the expected icosahedral symmetry below Tc. Yet the solid state NMR spectra in Fig. 1a showed that rotational motion on the microsecond time scale continued down to 150 K.
The apparent contradiction between NMR and diffraction results for solid C60 was resolved by the temperature-dependent 13C spin-lattice relaxation time (T1) measurements shown in Fig. 1b. These measurements show that the nature of molecular motions changes qualitatively at the phase transition identified by diffraction, from reorientation on the ∼20 ps time scale immediately above Tc (which we found to be 260 K) to reorientation on the ∼3 ns time scale immediately below Tc.5 Above the phase transition, C60 molecules reorient by rotational diffusion, assuming all possible orientations with nearly equal probabilities and therefore appearing as spheres in diffraction data. Below the phase transition, C60 molecules reorient by thermally activated jumps among symmetry-related orientations and therefore appear as icosahedrally symmetry objects in diffraction data.
Skyrmions in two-dimensional electron systems
Technologically important devices often depend on thin-film materials, which are difficult to study by NMR due to the low sensitivity of conventional NMR measurements. For this reason, while still at Bell Labs, Sean Barrett and I became interested in optical pumping of nuclear spin polarizations in III-V semiconductors, a phenomenon in which excitation of electron-hole pairs by light tuned near the semiconductor band gap energy leads to the creation of large nuclear spin polarizations through hyperfine couplings between photo-excited electrons and nuclei.7 Optical pumping can generate nuclear spin polarizations on the order of 10%,8 but requires low temperatures where electron spin-lattice relaxation times (T1e) and excited-state lifetimes are relatively long.
We decided to study GaAs/AlGaAs quantum well samples, i.e., samples produced by molecular beam epitaxy in which thin GaAs layers were separated by thicker AlGaAs layers. Due to the lower band gap energy in GaAs than in AlGaAs, the GaAs layers act as potential energy wells for conduction electrons, confining the conduction electrons to states that are essentially two-dimensional (2D) at sufficiently low temperatures.9 Strong optical pumping effects in GaAs had already been demonstrated,10,11 interesting phenomena such as the integral and fractional quantum Hall effects were known to occur in GaAs/AlGaAs quantum wells,12 and our colleagues Loren Pfeiffer and Ken West were willing to supply us with high-quality samples. Initially, we did not know precisely what we would learn from optically pumped NMR measurements on quantum wells. However, we thought we might find something new, simply because similar measurements on similar samples had not been attempted before.
Fig. 2a shows 71Ga NMR spectra of a quantum well sample at 1.6 K after various optical pumping times.13,14 At short times, the spectrum contains one relatively broad line, arising from the GaAs layers where optical pumping occurs. At longer times, a second, sharper line grows in due to 71Ga-71Ga spin diffusion that transports optically pumped nuclear spin polarization to the AlGaAs layers. The frequency shift K between GaAs and AlGaAs lines is due to contact hyperfine couplings between 71Ga nuclei and electrons in the wells.
Figure 2.
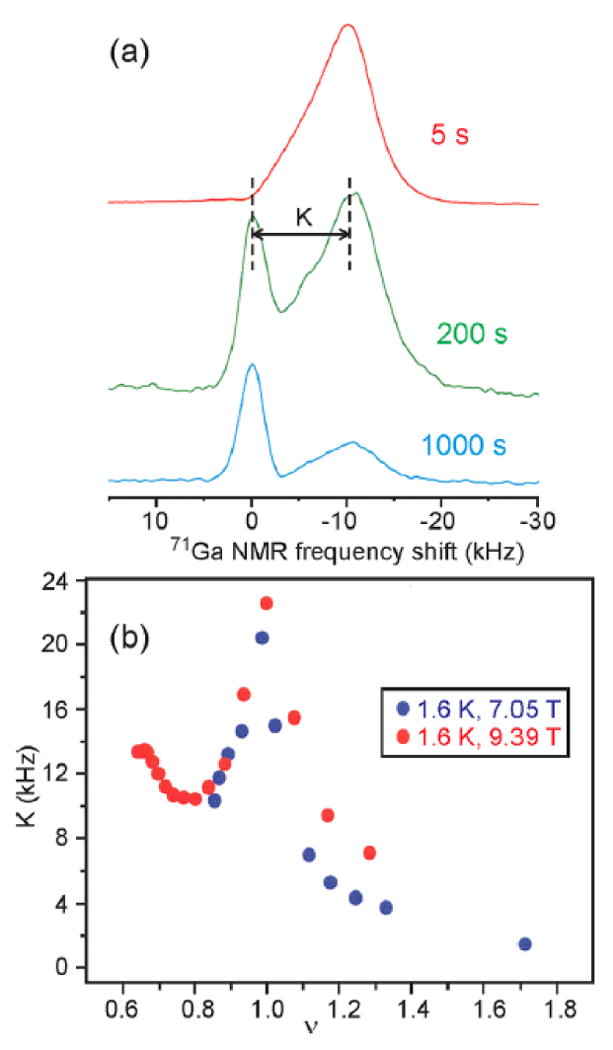
(a) 71Ga NMR spectra of a GaAs/AlGaAs quantum well (40 n-doped GaAs layers, 30 nm thick, separated by 180 nm AlGaAs layers, ∼0.3 cm2 area) at 1.6 K at 7.05 T, with optical pumping at 806 nm wavelength for the indicated times after saturation of 71Ga spin polarization. (b) Dependence of the hyperfine shift K between GaAs and AlGaAs signals on Landau-level filling factor ν, varied by tilting the sample relative to the external magnetic field, at 7.05 T and 9.39 T.
Fig. 2b shows that K has a surprising dependence on a quantity called the Landau-level filling factor, or ν, which is the ratio between the actual number of electrons per unit area in a quantum well and the maximum number per unit area that can accommodated in a single “particle-in-a-box” state with the same spin direction.9 At ν = 1, K has its maximum value, indicating that all 2D electrons are fully polarized (i.e., have the same spin direction). But as ν becomes either slightly greater than or slightly less than one, K drops rapidly, indicating that many electrons flip their spins when a single extra electron is added or subtracted from the 2D electron system. In effect, each extra electron carries a spin substantially greater than 1/2. These unusual electron states arise from electron-electron interactions within the 2D electron system, and are called “skyrmions”. Data in Fig. 2b constitute the first experimental evidence that skyrmions exist in 2D electron systems at low temperatures and in strong magnetic fields.13,14 These data stimulated a surge of subsequent experimental and theoretical studies of skyrmions in the quantum well research community.15-17
Low-temperature NMR to immobilize proteins
In studies of proteins and other biopolymers, multidimensional solution NMR measurements constitute a powerful approach to full structure determination and detailed dynamical characterization of proteins and other biopolymers. However, these measurements become less informative as molecular weight increases and rotational diffusion slows down. In contrast, solid state NMR methods are applicable to biopolymers of arbitrarily high molecular weight (provided that some form of selective isotopic labeling is used, that natural-abundance 13C signals are not overwhelming, and that sufficiently high concentrations can be achieved). Thus, even for soluble proteins, it can be advantageous to freeze the sample and apply solid state NMR methods.
Fig. 3 shows one example, taken from our efforts to determine the conformations of peptides derived from the third variable (V3) loop of the HIV-1 gp120 protein when bound to anti-gp120 antibodies.18,19 The V3 loop is of particular interest both because it is a primary target of antibodies that neutralize HIV-1 and because it interacts with chemokine receptors on host cell surfaces during the infection process. In Fig. 3a, the 2D 13C-13C spectrum of a free V3 peptide, uniformly 15N,13C-labeled at seven successive residues, shows relatively broad crosspeak signals in frozen glycerol/water at 153 K under magic-angle spinning (MAS), indicating substantial conformational disorder. In Fig. 3b, the 2D spectrum of the antibody-bound peptide shows much sharper signals, about 1.8 ppm wide (full width at half maximum), indicating a well-defined conformation in the peptide/antibody complex. From 13C chemical shifts and 13C-13C distance measurements, it was possible to develop a structural model for the epitope region of the antibody-bound V3 loop.19
Figure 3.
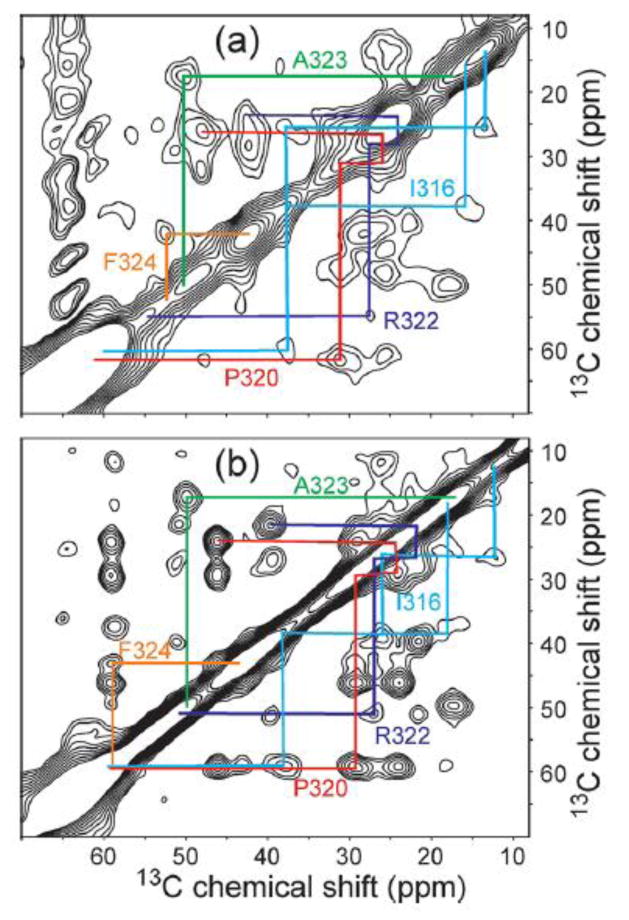
Aliphatic regions of 2D 13C-13C NMR spectra of a 20-residue peptide from the V3 loop of HIV-1 gp120 in the free (a) and antibody-bound (b) states, recorded in frozen solutions at 153 K and 9.39 T with MAS. The peptide is uniformly 15N,13C-labeled in seven consecutive residues, including the five non-glycine residues whose crosspeak signals are indicated by color-coded assignment paths.
Measurements in Fig. 3 were performed at 9.39 T, with 6 mm diameter MAS rotors and a 240 μl sample volume. The sample was cooled with cold N2 gas, supplied to the sample space within the MAS module from the top of the magnet. To reduce the 1H T1 value to ∼1 s and thereby accelerate data acquisition, paramagnetic Cu2+ (20 mM CuNa2EDTA) was added to the frozen solutions, as originally demonstrated by Weliky et al.18 With a 1.0 mM peptide/antibody concentration, the 2D spectrum in Fig. 3b was acquired in about 90 hr.
Similar measurement conditions were used to acquire the data in Fig. 4. In these experiments on the 35-residue villin headpiece subdomain (HP35), a popular model protein for folding studies,20-23 we investigated the dependence of site-specific conformational distributions on the extent of unfolding induced by the denaturant guanidine hydrochloride (GdnHCl). In its fully folded state, HP35 is a three-helix bundle.24 For solid state NMR measurements, HP35 samples were 13C-labeled at sequential pairs of backbone carbonyl sites; quantitative structural techniques developed in my laboratory25-27 were used to place constraints on the backbone φ and ψ torsion angles between the labeled sites. The solid state NMR data revealed the specific conformational pathway shown in Fig. 4, in which helical segments present at [GdnHCl] = 0 convert first to mixtures of helical and extended conformations near the unfolding midpoint at [GdnHCl] = 4.5 M, then to mixtures of extended and polyproline II conformations in the fully unfolded state at [GdnHCl] = 7.0 M.28 Identification of this conformational pathway was purely a consequence of the solid state NMR data, with no reliance on structural databases, prior expectations, or other measurements.
Figure 4.
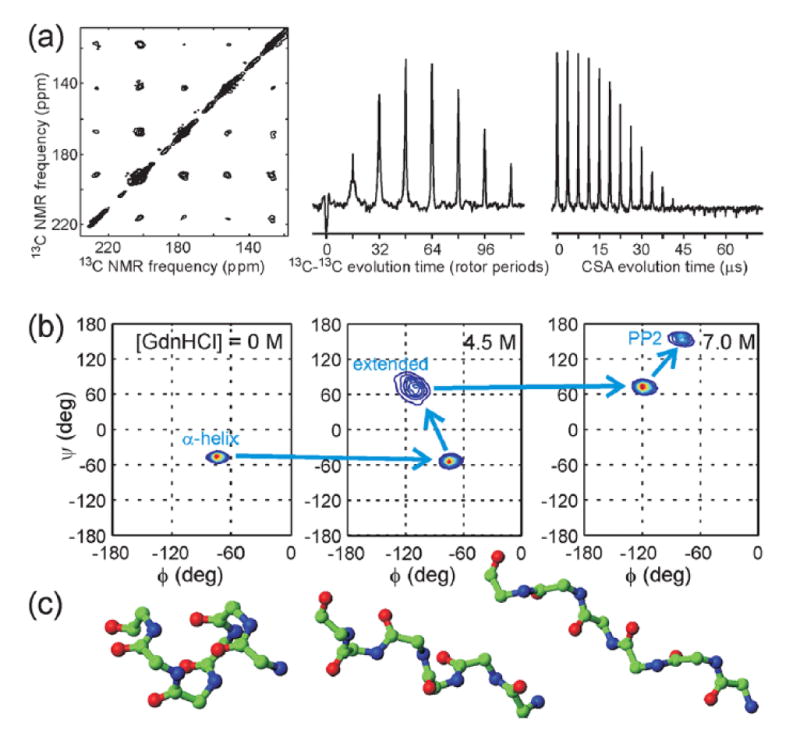
(a) 2D MAS exchange spectrum (left), constant-time double-quantum-filtered dipolar evolution data (center), and double-quantum CSA data (right) for HP35 in glycerol/water at 153 K. The protein is 13C-labeled at carbonyl sites of A49 and V50; the data place constraints on the backbone ϕ and ψ angles of V50. (b) Backbone conformational distributions at V50 for HP35 in frozen solution with indicated denaturant concentrations, derived from data as in panel a. (c) Models of a polypeptide backbone with the α-helical, extended, and polyproline II (PP2) conformations that are predominant components of the distributions in panel b.
These experiments on HP35 show how detailed structural information about unfolded states of proteins can be obtained from solid state NMR, information that is difficult to obtain from other experimental techniques. These experiments also illustrate how low-temperature NMR can be used to suppress conformational exchange in unfolded states (in addition to rotational diffusion), allowing conformational distributions to be characterized at a quantitative and site-specific level.
Low-temperature NMR to trap transient states
Partially and fully unfolded states created by addition of a chemical denaturant are equilibrium states. Transient, non-equilibrium states can also be created if solvent conditions, such as temperature, pH, ionic strength, or denaturant concentration, are changed rapidly from conditions that favor the unfolded state to conditions that favor the folded state. If a protein solution can be frozen on a time scale less than the structural equilibration time, then solid state NMR measurements can be used to characterize the protein structure in a transient intermediate state.
Fig. 5 shows examples of data from our initial demonstration of solid state NMR as a structural probe of transient states in a non-equilibrium protein folding process.29 In these experiments, a glycerol/water solution of HP35 was heated to 363 K, creating a thermally unfolded state, then frozen by spraying a fine jet of the solution into a bath of isopentane at 128 K. Under our conditions, the time to cool from above 80° C to 0° C was 10-20 μs. Comparison of 2D 13C-13C NMR spectra of HP35 solutions that were frozen slowly from room temperature (Fig. 5a) with spectra of solutions that were frozen rapidly from 363 K (Fig. 5b) showed that the 10-20 μs freeze-quenching time was sufficient to trap an intermediate state. Distributions of crosspeak intensity in the 2D spectra showed that this intermediate state has about 60% of the helical secondary structure but not the full tertiary structure (i.e., ordered packing of the hydrophobic core) of fully folded HP35. In fact, no fully folded HP35 molecules were detected in spectra of the freeze-quenched intermediate state. This result is particularly interesting because previous studies of HP35 folding by optical spectroscopy20 and recent computational studies23 suggest a time scale less than 5 μs for folding (although under somewhat different conditions).
Figure 5.
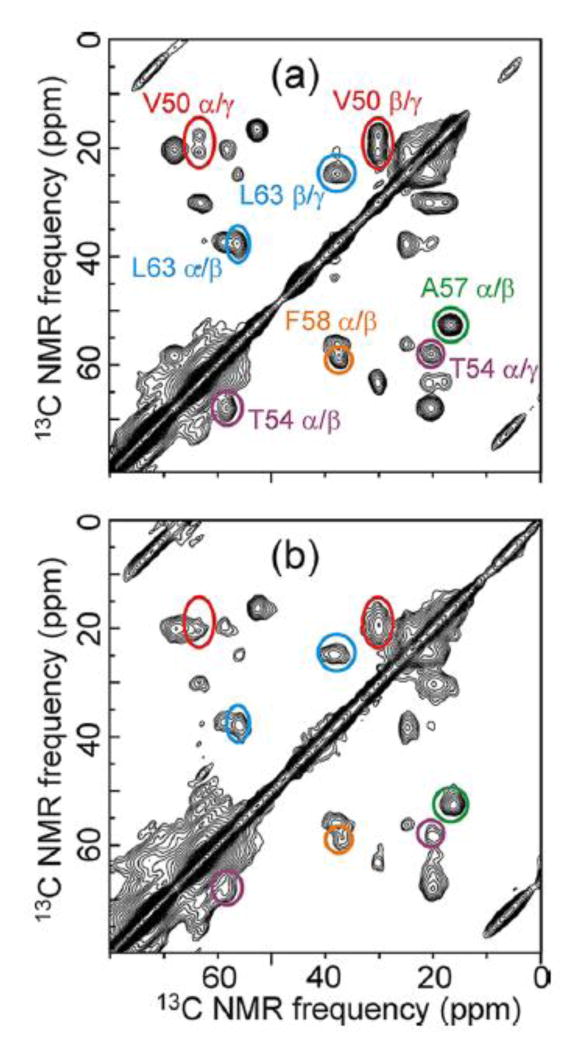
Aliphatic regions of 2D 13C-13C NMR spectra of HP35 in fully folded (a) and freeze-trapped intermediate (b) states, recorded in glycerol/water at 153 K and 9.39 T with MAS. Color-coded lines indicate signals that are unchanged (solid lines) or significantly shifted or broadened (dashed lines) in the partially folded intermediate state, for the uniformly 13C-labeled residues V50 (red), T54 (purple), A57 (green), F58 (yellow), and L63 (blue).
Even with Cu+2 doping, a 200 μl sample volume, a 153 K sample temperature, and a 4 mM protein concentration, 2D spectra as in Fig. 5b required 100-240 hr of data acquisition. To make experiments of this sort more practical, further sensitivity enhancements are clearly needed.
Low-temperature NMR to enhance sensitivity
Nuclear spin polarizations at thermal equilibrium are proportional to 1/T, where T is the sample temperature. The noise amplitude from radio-frequency (rf) circuitry in the NMR probe is proportional to T-1/2, if all circuit elements are at temperature T. The quality factor (Q) of the rf circuit generally increases with decreasing temperature. Therefore, the signal-to-noise ratio in an NMR spectrum, acquired with a given number of scans and a given sample size, is expected to increase by a factor of at least 15-60 if T is reduced from 300 K to 20 K. The main difficulty is that cooling to 20 K requires liquid helium, and most studies of biomolecular systems require MAS. MAS probe designs in which helium is used both to cool the sample and to supply gas to the MAS drive and bearing components suffer from high liquid helium consumption rates and relatively low MAS frequencies30 unless MAS rotor volumes are small.31 We therefore chose to pursue an ultra-low-temperature MAS design in which nitrogen is used as the MAS drive and bearing gas, while helium is used only for sample cooling.
Fig. 6a shows the MAS system.32 We use zirconia MAS rotors with 4 mm outer diameter, 45.7 mm length, and a maximum sample volume of 82 μl. The low thermal conductivity of zirconia and the large rotor length allow the sample to be cooled to 20-25 K with helium, while the bearing and drive areas are well above 77 K. A teflon insert within the MAS module limits the helium-cooled volume to a minimal space around the rf coil. Cold helium from a liquid helium transfer line enters the MAS module from above and exits the sample area by flowing toward the bearings through the narrow gap between the rotor sleeve and the teflon insert. Vent holes near the bearings ensure that nitrogen bearing gas does not enter the helium-cooled volume. With this design, stable spinning at MAS frequencies up to 7.0 kHz is achieved with 20-25 K sample temperatures and liquid helium consumption rates of 2-4 l/hr. Rf performance is quite comparable to conventional MAS NMR probes. Rf arcing is not a serious problem, even during measurements that involve cross-polarization and 1H decoupling at high powers, provided that helium gas is not allowed to escape from the sample space along the leads of the rf coil.
Figure 6.
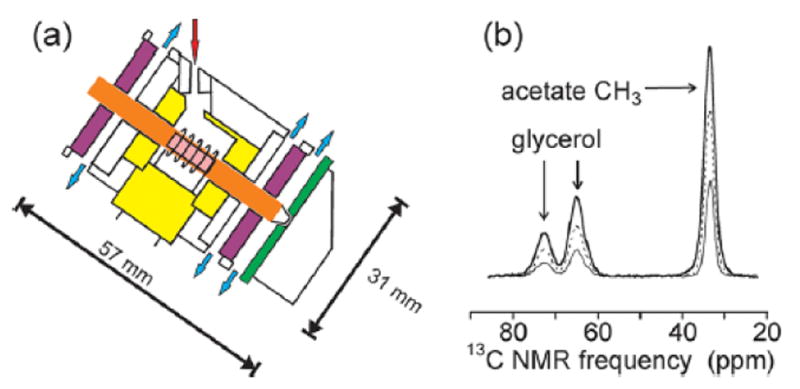
(a) Diagram of MAS module for ultra-low-temperature solid state NMR experiments. The rotor (orange) is supported by bearings (purple) and spun by a stator (green) that are driven by nitrogen gas, which exits as indicated by blue arrows. Cold helium (red arrow) enters the space around the rf coil and sample (pink) that is defined by the teflon insert (yellow) and exits along the outer surface of the rotor, toward the bearings. (b) 13C MAS spectra of 13CH3-labeled sodium acetate in glycerol/water at 25 K (heavy solid line), 40 K (dashed line), and 79 K (thin solid line), recorded at 9.39 T with 7.00 kHz MAS.
Fig. 6b shows 13C MAS NMR spectra obtained at temperatures between 40 K and 79 K, demonstrating the 1/T dependence of signal amplitudes on sample temperature.32 In practice, only minor reductions in noise and increases in Q with decreasing temperature are observed, because only the rf coil (and not the rest of the rf circuitry) is cooled in our current probe design. Sample temperatures in Fig. 6b were determined from measurements of the T1 of 79Br in KBr powder, which can be measured quickly in a probe that tunes near the 13C NMR frequency and which decreases monotonically from 140 s to 2.6 s in the temperature range from 20 K to 60 K.33 A less accurate, but nonetheless useful, assessment of sample temperature can be obtained from a fiber optic temperature sensor that is inserted into the helium-cooled volume within the MAS module.
1H T1 values for biomolecular samples near 20 K can be substantially greater than 10 s, especially for soluble, monomeric proteins in frozen glycerol/water solutions, where the effective 1H T1 is dominated by the T1 of the solvent. Slow 1H spin-lattice relaxation at low temperatures limits the rate at which data can be acquired, reducing the sensitivity advantage of low-temperature measurements. Near 20 K, the T1e of Cu2+ becomes too long for Cu2+ to be an effective paramagnetic relaxation agent. As an alternative, we have found that Dy3+ in the form of DyH-EDTA at concentrations near 0.2 mM works well as a relaxation agent for monomeric proteins.32 On the other hand, even without paramagnetic doping, certain macromolecular assemblies such as amyloid fibrils may exhibit 1H T1 values of approximately 5 s near 20 K, presumably due to a large local concentration of methyl groups (or perhaps other chemical groups) with motional correlation times around 1 ns.
Dynamic nuclear polarization at ultra-low temperatures
Dynamic nuclear polarization is a phenomenon in which irradiation of electron paramagnetic resonance (EPR) transitions at microwave frequencies leads to enhancements of nuclear spin polarizations, and hence NMR signals, through cross-relaxation processes driven by electron-nucleus hyperfine couplings.34,35 While my laboratory was developing the ultra-low-temperature MAS probe design described above, the M.I.T. group led by R.G. Griffin began to obtain quite promising results from their efforts to apply DNP to biomolecular solid state NMR with MAS at high magnetic fields.36 Among their many contributions to DNP methods, the M.I.T. group showed that nitroxide radicals could be used as paramagnetic dopants in frozen solutions, leading to large enhancements of 1H spin polarizations relative to thermal equilibrium values (i.e., DNP enhancement factors, εDNP) through the “cross effect” mechanism, especially when pairs of nitroxide moieties were combined within biradical dopants.37,38 In addition, they showed that continuous-wave gyrotrons are effective sources of high-power microwaves at the EPR frequencies in high-field NMR magnets.39
DNP generally requires that electron spin polarizations be perturbed from thermal equilibrium (i.e., partially saturated) by the applied microwaves, implying that the microwave fields must be strong enough to produce electron spin Rabi frequencies comparable to electron spin-lattice relaxation rates (1/T1e). DNP experiments with MAS at M.I.T. were performed at 80 K or higher temperatures, where T1e values for nitroxides are 0.1-1 ms.40,41 Since we had constructed a MAS NMR probe that could operate in the 20-25 K range, we decided to explore the possibility of performing DNP experiments at ultra-low temperatures, where nitroxide T1e values can be much greater than 1 ms.42 With longer T1e, lower-power microwave sources could be used. In addition, intrinsic nuclear T1 values (i.e., T1 values in the absence of paramagnetic doping) are expected to be longer, at least in certain classes of samples, possibly leading to larger values of εDNP in cases where intrinsic nuclear spin-lattice relaxation competes with DNP processes. Finally, since εDNP represents polarization enhancement relative to thermal equilibrium, a given value of εDNP corresponds to larger NMR signals at 20-25 K than at 80-100 K.
Our initial DNP experiments were performed without MAS, at 9.39 T and temperatures in the 7-80 K range, using a tunable microwave source with a 30 mW maximum output.43 Measurements on frozen glycerol/water solutions of various nitroxide compounds yielded values of εDNP for 1H spins as large as 80 at 7 K. The largest values of εDNP and shortest DNP build-up times (TDNP) were obtained with a tri-radical compound, called DOTOPA-TEMPO.43 In our hands, the absolute DNP-enhanced 1H NMR sensitivity at 20 K with 30 mW microwave power was comparable to the absolute sensitivity expected hypothetically at 80 K with εDNP ≈ 130 and TDNP ≈ 1.4 s. Similar enhancements of cross-polarized 13C NMR sensitivity were observed in double-resonance DNP experiments at ultra-low temperatures.44 These results encouraged us to construct a version of the ultra-low-temperature MAS probe that includes provisions for microwave irradiation for DNP.
Fig. 7 shows 13C MAS NMR spectra obtained recently with DNP at temperatures in the 20-25 K range, again at 9.39 T with a 30 mW microwave source.45 One-dimensional spectra of 13C3-L-alanine, dissolved in glycerol/water and doped with DOTOPA-TEMPO, show εDNP ≈ ±25 at 20 K (Fig. 7a). As predicted by theory and numerical calculations of cross-effect DNP under MAS,46 the sign of the DNP-enhanced signal depends on the microwave frequency. The 2D 13C-13C spectrum of a model peptide (Fig. 7b) shows that high-quality 2D data can be obtained in about 2 hr from 82 μl of isotopically labeled peptides or proteins at 1.9 mM concentration.45 Compared with the experimental conditions in Fig. 5, this represents a six-fold reduction in quantity of labeled sample and a 50-to-120-fold reduction in measurement time.
Figure 7.
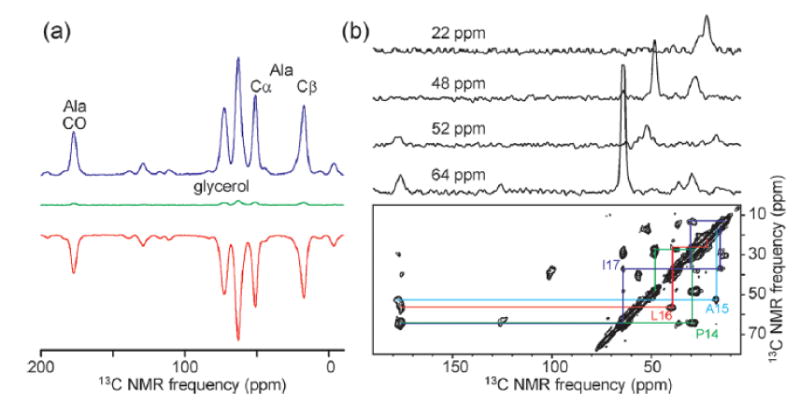
(a) 13C NMR spectra of 50 mM uniformly 13C-labeled L-alanine in partially deuterated glycerol/water with 10 mM DOTOPA-TEMPO, recorded at 20 K and 9.39 T with 6.7 kHz MAS. Spectra are shown with 30 mW microwave irradiation at 264.05 GHz (blue) and 264.65 GHz (red), and without microwave irradiation (green). (b) 2D 13C-13C spectrum of the 26-residue peptide melittin in partially deuterated glycerol/water with 9.9 mM DOTOPA-TEMPO, recorded at 25 K and 9.39 T with 6.4 kHz MAS. The peptide is uniformly 13C-labeled at P14, A15, L16, and I17. The peptide concentration is 1.9 mM, the sample volume is 82 μl, the recycle delay is 10 s, and the total measurement time is 2.2 hr.
Concluding remarks
Experimental examples discussed above illustrate some of the important motivations for pursuing NMR measurements at low and ultra-low temperatures, some of the techniques and technology that are associated with low-temperature experiments, and some of the likely directions for future research. In my laboratory, we are currently planning to apply ultra-low-temperature DNP with MAS to several structural problems in biomolecular systems, including freeze-trapped intermediate states in protein folding and peptide aggregation processes and membrane-associated peptide/protein complexes. The success of these specific efforts may depend on factors that are now under investigation, such as intrinsic 1H T1 values and 13C NMR linewidths under ultra-low-temperature DNP conditions. Further optimization of paramagnetic dopants and other aspects of sample preparation may be required. Modifications of our DNP apparatus to increase the available microwave power and to reach lower sample temperatures while reducing liquid helium consumption are also in progress. Through this combination of exploratory applications to biomolecular systems and ongoing technological developments, it seems likely that ultra-low-temperature NMR measurements will soon make important contributions to our understanding of systems that are of widespread interest outside the community of solid state NMR spectroscopists.
Acknowledgments
Work described in this article was supported by the Intramural Research Program of the National Institute of Diabetes and Digestive and Kidney Diseases, National Institutes of Health, and by the NIH Intramural AIDS Targeted Antiviral Program. I thank current and past members of my laboratory for their many contributions to this work. Data shown in the figures were acquired by Gary Dabbagh, Sean Barrett, Simon Sharpe, Kan-Nian Hu, and Kent Thurber.
Footnotes
Biographical information: Robert Tycko is a Senior Investigator in the NIH Intramural Research Program, where he has been since 1994. His educational background includes A.B. and Ph.D. degrees in chemistry, and eight years as a Member of Technical Staff at AT&T Bell Laboratories. His research centers on solid state NMR and its applications in biophysics and biophysical chemistry.
References
- 1.Hebel LC, Slichter CP. Nuclear Spin Relaxation in Normal and Superconducting Aluminum. Phys Rev. 1959;113:1504–1519. [Google Scholar]
- 2.Jaccarino V, Shulman RG. Observation of Nuclear Magnetic Resonance in Antiferromagnetic Mn(F-19)2. Phys Rev. 1957;107:1196–1197. [Google Scholar]
- 3.Kramer S, Mehring M. Low-temperature charge ordering in the superconducting state of YBa2Cu3O7-delta. Phys Rev Lett. 1999;83:396–399. doi: 10.1103/PhysRevLett.84.1636. [DOI] [PubMed] [Google Scholar]
- 4.Kratschmer W, Lamb LD, Fostiropoulos K, Huffman DR. Solid C-60 - a New Form of Carbon. Nature. 1990;347:354–358. [Google Scholar]
- 5.Tycko R, Dabbagh G, Fleming RM, Haddon RC, Makhija AV, Zahurak SM. Molecular-Dynamics and the Phase-Transition in Solid C60. Phys Rev Lett. 1991;67:1886–1889. doi: 10.1103/PhysRevLett.67.1886. [DOI] [PubMed] [Google Scholar]
- 6.Heiney PA, Fischer JE, McGhie AR, Romanow WJ, Denenstein AM, McCauley JP, Smith AB, Cox DE. Orientational Ordering Transition in Solid C60. Phys Rev Lett. 1991;66:2911–2914. doi: 10.1103/PhysRevLett.66.2911. [DOI] [PubMed] [Google Scholar]
- 7.Lampel G. Nuclear Dynamic Polarization by Optical Electronic Saturation and Optical Pumping in Semiconductors. Phys Rev Lett. 1968;20:491. -&. [Google Scholar]
- 8.Michal CA, Tycko R. Stray-field NMR imaging and wavelength dependence of optically pumped nuclear spin polarization in InP. Phys Rev B. 1999;60:8672–8679. [Google Scholar]
- 9.Weisbuch C, Vinter B. Quantum Semiconductor Structures: Fundamentals and Applications. Academic Press; New York: 1991. [Google Scholar]
- 10.Paget D. Optical-Detection of Nmr in High-Purity Gaas under Optical-Pumping - Efficient Spin-Exchange Averaging between Electronic States. Phys Rev B. 1981;24:3776–3793. [Google Scholar]
- 11.Buratto SK, Shykind DN, Weitekamp DP. Time-Sequenced Optical Nuclear-Magnetic-Resonance of Gallium-Arsenide. Phys Rev B. 1991;44:9035–9038. doi: 10.1103/physrevb.44.9035. [DOI] [PubMed] [Google Scholar]
- 12.Willett R, Eisenstein JP, Stormer HL, Tsui DC, Gossard AC, English JH. Observation of an Even-Denominator Quantum Number in the Fractional Quantum Hall-Effect. Phys Rev Lett. 1987;59:1776–1779. doi: 10.1103/PhysRevLett.59.1776. [DOI] [PubMed] [Google Scholar]
- 13.Barrett SE, Dabbagh G, Pfeiffer LN, West KW, Tycko R. Optically Pumped Nmr Evidence for Finite-Size Skyrmions in Gaas Quantum-Wells near Landau-Level Filling Nu=1. Phys Rev Lett. 1995;74:5112–5115. doi: 10.1103/PhysRevLett.74.5112. [DOI] [PubMed] [Google Scholar]
- 14.Tycko R, Barrett SE, Dabbagh G, Pfeiffer LN, West KW. Electronic States in Gallium-Arsenide Quantum-Wells Probed by Optically Pumped Nmr. Science. 1995;268:1460–1463. doi: 10.1126/science.7539550. [DOI] [PubMed] [Google Scholar]
- 15.Aifer EH, Goldberg BB, Broido DA. Evidence of Skyrmion excitations about nu=1 in n-modulation-doped single quantum wells by interband optical transmission. Phys Rev Lett. 1996;76:680–683. doi: 10.1103/PhysRevLett.76.680. [DOI] [PubMed] [Google Scholar]
- 16.Bayot V, Grivei E, Melinte S, Santos MB, Shayegan M. Giant low temperature heat capacity of GaAs quantum wells near Landau level filling nu=1. Phys Rev Lett. 1996;76:4584–4587. doi: 10.1103/PhysRevLett.76.4584. [DOI] [PubMed] [Google Scholar]
- 17.Fertig HA, Brey L, Cote R, MacDonald AH, Karlhede A, Sondhi SL. Hartree-Fock theory of skyrmions in quantum Hall ferromagnets. Phys Rev B. 1997;55:10671–10680. [Google Scholar]
- 18.Weliky DP, Bennett AE, Zvi A, Anglister J, Steinbach PJ, Tycko R. Solid-state NMR evidence for an antibody-dependent conformation of the V3 loop of HIV-1 gp120. Nature Struct Biol. 1999;6:141–145. doi: 10.1038/5827. [DOI] [PubMed] [Google Scholar]
- 19.Sharpe S, Kessler N, Anglister JA, Yau WM, Tycko R. Solid-state NMR yields structural constraints on the V3 loop from HIV-1 Gp120 bound to the 447-52D antibody Fv fragment. J Am Chem Soc. 2004;126:4979–4990. doi: 10.1021/ja0392162. [DOI] [PubMed] [Google Scholar]
- 20.Kubelka J, Eaton WA, Hofrichter J. Experimental tests of villin subdomain folding simulations. J Mol Biol. 2003;329:625–630. doi: 10.1016/s0022-2836(03)00519-9. [DOI] [PubMed] [Google Scholar]
- 21.Wang MH, Tang YF, Sato SS, Vugmeyster L, McKnight CJ, Raleigh DP. Dynamic NMR line-shape analysis demonstrates that the villin headpiece subdomain folds on the microsecond time scale. J Am Chem Soc. 2003;125:6032–6033. doi: 10.1021/ja028752b. [DOI] [PubMed] [Google Scholar]
- 22.Freddolino PL, Schulten K. Common Structural Transitions in Explicit-Solvent Simulations of Villin Headpiece Folding. Biophys J. 2009;97:2338–2347. doi: 10.1016/j.bpj.2009.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Piana S, Lindorff-Larsen K, Shaw DE. Protein folding kinetics and thermodynamics from atomistic simulation. Proc Natl Acad Sci USA. 2012;109:17845–17850. doi: 10.1073/pnas.1201811109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.McKnight CJ, Matsudaira PT, Kim PS. NMR structure of the 35-residue villin headpiece subdomain. Nature Struct Biol. 1997;4:180–184. doi: 10.1038/nsb0397-180. [DOI] [PubMed] [Google Scholar]
- 25.Weliky DP, Tycko R. Determination of peptide conformations by two-dimensional magic angle spinning NMR exchange spectroscopy with rotor synchronization. J Am Chem Soc. 1996;118:8487–8488. [Google Scholar]
- 26.Bennett AE, Weliky DP, Tycko R. Quantitative conformational measurements in solid state NMR by constant-time homonuclear dipolar recoupling. J Am Chem Soc. 1998;120:4897–4898. [Google Scholar]
- 27.Blanco FJ, Tycko R. Determination of polypeptide backbone dihedral angles in solid state NMR by double quantum C-13 chemical shift anisotropy measurements. J Magn Reson. 2001;149:131–138. [Google Scholar]
- 28.Hu KN, Havlin RH, Yau WM, Tycko R. Quantitative Determination of Site-Specific Conformational Distributions in an Unfolded Protein by Solid-State Nuclear Magnetic Resonance. J Mol Biol. 2009;392:1055–1073. doi: 10.1016/j.jmb.2009.07.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hu KN, Yau WM, Tycko R. Detection of a Transient Intermediate in a Rapid Protein Folding Process by Solid-State Nuclear Magnetic Resonance. J Am Chem Soc. 2010;132:24. doi: 10.1021/ja908471n. -+ [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hackmann A, Seidel H, Kendrick RD, Myhre PC, Yannoni CS. Magic-Angle Spinning Nmr at near-Liquid-Helium Temperatures. J Magn Reson. 1988;79:148–153. [Google Scholar]
- 31.Carravetta M, Johannessen OG, Levitt MH, Heinmaa I, Stern R, Samoson A, Horsewill AJ, Murata Y, Komatsu K. Cryogenic NMR spectroscopy of endohedral hydrogen-fullerene complexes. J Chem Phys. 2006;124 doi: 10.1063/1.2174012. [DOI] [PubMed] [Google Scholar]
- 32.Thurber KR, Tycko R. Biomolecular solid state NMR with magic-angle spinning at 25 K. J Magn Reson. 2008;195:179–186. doi: 10.1016/j.jmr.2008.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Thurber KR, Tycko R. Measurement of sample temperatures under magic-angle spinning from the chemical shift and spin-lattice relaxation rate of Br-79 in KBr powder. J Magn Reson. 2009;196:84–87. doi: 10.1016/j.jmr.2008.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Carver TR, Slichter CP. Polarization of Nuclear Spins in Metals. Phys Rev. 1953;92:212–213. [Google Scholar]
- 35.Overhauser AW. Polarization of Nuclei in Metals. Phys Rev. 1953;91:476–476. [Google Scholar]
- 36.Maly T, Debelouchina GT, Bajaj VS, Hu KN, Joo CG, Mak-Jurkauskas ML, Sirigiri JR, van der Wel PCA, Herzfeld J, Temkin RJ, Griffin RG. Dynamic nuclear polarization at high magnetic fields. J Chem Phys. 2008;128 doi: 10.1063/1.2833582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hu KN, Yu HH, Swager TM, Griffin RG. Dynamic nuclear polarization with biradicals. J Am Chem Soc. 2004;126:10844–10845. doi: 10.1021/ja039749a. [DOI] [PubMed] [Google Scholar]
- 38.Hu KN, Debelouchina GT, Smith AA, Griffin RG. Quantum mechanical theory of dynamic nuclear polarization in solid dielectrics. J Chem Phys. 2011;134 doi: 10.1063/1.3564920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bajaj VS, Farrar CT, Hornstein MK, Mastovsky I, Vieregg J, Bryant J, Elena B, Kreischer KE, Temkin RJ, Griffin RG. Dynamic nuclear polarization at 9T using a novel 250 GHz gyrotron microwave source. J Magn Reson. 2003;160:85–90. doi: 10.1016/j.jmr.2011.09.010. [DOI] [PubMed] [Google Scholar]
- 40.Sato H, Kathirvelu V, Spagnol G, Rajca S, Rajca A, Eaton SS, Eaton GR. Impact of electron-electron spin interaction on electron spin relaxation of nitroxide diradicals and tetraradical in glassy solvents between 10 and 300 K. J Phys Chem B. 2008;112:2818–2828. doi: 10.1021/jp073600u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Zagdoun A, Casano G, Ouari O, Lapadula G, Rossini AJ, Lelli M, Baffert M, Gajan D, Veyre L, Maas WE, Rosay M, Weber RT, Thieuleux C, Coperet C, Lesage A, Tordo P, Emsley L. A Slowly Relaxing Rigid Biradical for Efficient Dynamic Nuclear Polarization Surface-Enhanced NMR Spectroscopy: Expeditious Characterization of Functional Group Manipulation in Hybrid Materials. J Am Chem Soc. 2012;134:2284–2291. doi: 10.1021/ja210177v. [DOI] [PubMed] [Google Scholar]
- 42.Farrar CT, Hall DA, Gerfen GJ, Inati SJ, Griffin RG. Mechanism of dynamic nuclear polarization in high magnetic fields. J Chem Phys. 2001;114:4922–4933. [Google Scholar]
- 43.Thurber KR, Yau WM, Tycko R. Low-temperature dynamic nuclear polarization at 9.4 T with a 30 mW microwave source. J Magn Reson. 2010;204:303–313. doi: 10.1016/j.jmr.2010.03.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Potapov A, Thurber KR, Yau WM, Tycko R. Dynamic nuclear polarization-enhanced H-1-C-13 double resonance NMR in static samples below 20 K. J Magn Reson. 2012;221:32–40. doi: 10.1016/j.jmr.2012.05.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Thurber KR, Potapov A, Yau WM, Tycko R. Solid state nuclear magnetic resonance with magic-angle spinning and dynamic nuclear polarization below 25 K. J Magn Reson. 2013;226:100–106. doi: 10.1016/j.jmr.2012.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Thurber KR, Tycko R. Theory for cross effect dynamic nuclear polarization under magic-angle spinning in solid state nuclear magnetic resonance: The importance of level crossings. J Chem Phys. 2012;137 doi: 10.1063/1.4747449. [DOI] [PMC free article] [PubMed] [Google Scholar]


