Continuous Representations of Brain Connectivity using Spatial Point Processes

Abstract

We present a continuous model for structural brain connectivity based on the Poisson point process. The model treats each streamline curve in a tractography as an observed event in connectome space, here the product space of the gray matter/white matter interfaces. We approximate the model parameter via kernel density estimation. To deal with the heavy computational burden, we develop a fast parameter estimation method by pre-computing associated Legendre products of the data, leveraging properties of the spherical heat kernel. We show how our approach can be used to assess the quality of cortical parcellations with respect to connectivity. We further present empirical results that suggest that “discrete” connectomes derived from our model have substantially higher test-retest reliability compared to standard methods. In this, the expanded form of this paper for journal publication, we also explore parcellation free analysis techniques that avoid the use of explicit partitions of the cortical surface altogether. We provide an analysis of sex effects on our proposed continuous representation, demonstrating the utility of this approach.

Graphical Abstract

1. Introduction

In recent years the study of structural and functional brain connectivity has expanded rapidly. Following the rise of diffusion and functional MRI, connectomics has unlocked a wealth of knowledge to be explored. Almost synonymous with the connectome is the network-theory based representation of the brain [1]. In much of the recent literature the quantitative analysis of connectomes has focused on region-to-region connectivity. This paradigm equates physical brain regions with nodes in a graph, and uses observed structural measurements or functional correlations as a proxy for edge strengths between nodes.

Critical to this representation of connectivity is the delineation of brain regions, the parcellation. Multiple studies have shown that the choice of parcellation influences the graph statistics of both structural and functional networks [2, 3, 4, 5]. It remains an open question which of the proposed parcellations is the optimal representation, or even if such a parcellation exists [6].

It is thus useful to construct a more general framework for cortical connectivity, one in which any particular parcellation of the cortex may be expressed and its connectivity matrix derived, and one in which the variability of connectivity measures can be modeled and assessed statistically. It is also important that this framework allow comparisons between parcellations, and representations in this framework must be both analytically and computationally tractable. Since several brain parcellations at the macroscopic scale are plausible, a representation of connectivity that is independent of parcellation is particularly appealing.

In this paper, we develop such a general framework for a parcellation independent connectivity representation, building on the work of [7]. We describe a continuous point process model for the generation of observed tract¹ (streamline) intersections with the cortical surface, from which we may recover a distribution of edge strengths for any pair of cortical regions, as measured by the inter-region tract count. Our model is an intensity function over the product space of the cortical surface with itself, assigning to every pair of points on the surface a connectivity density, opposed to the usual connectivity mass assigned in discrete models. We describe an efficient method to estimate the parameter of the model, as well as a method to recover the region-to-region edge strength. We then demonstrate the estimation of the model on a test-retest dataset. We provide reproducibility estimates for our method and the standard direct count method [8] for comparison. We also compare the representational power of common cortical parcellations with respect to a variety of measures.

In this, the extended journal form of the conference publication [9], we explore possible methods for direct analysis of the continuous connective object. We present an exemplar analysis of group differences in continuous summary measures (regressing a connectivity measure on sex, with age and ICV covariates), showing significant differences in regions also identified using parcellation-based representations. We use this analysis to demonstrate a practical analysis of the proposed model.

2. Continuous Connectivity Model

The key theoretical component of our work is the use of point process theory to describe estimated cortical tract projections. A point process is a random process where any realization consists of a collection of discrete points on a measurable space. The most basic of these processes is the Poisson process, in which events occur independently at a specific asymptotic intensity (rate) λ over the chosen domain [10]. λ completely characterizes each particular process, and is often defined as a non-negative function λ : Domain → ℝ⁺, which allows the process to vary in intensity by location. This is functionally similar to a probability density, except that realizations of the Poisson process can consist of zero, one, or many points, the points are independent by assumption, and λ need not integrate to one.

The expected count of any sub-region (subset) of the domain is its total intensity, the integral of λ over the sub-region. In this paper, our domain is the connectivity space of the cortex, the set of all pairs of points on the surface, and the events are estimated tract intersections with the cortical surface.

2.1. Model Definition and Properties

Let Ω be union of two disjoint subspaces each diffeomorphic to the 2-sphere representing the white matter boundaries in each hemisphere. Further consider the space Ω × Ω, which here represents all possible endpoint pairs for tracts that reach the white matter boundary. We denote the set of observed tract endpoint pairs as D. We treat the observation of such tracts as events generated by an inhomogeneous (symmetric) Poisson process on Ω × Ω; in our case, for every event (x, y) we have a symmetric event (y, x).

Assuming that each event is independent of all other events except for its symmetric event (i.e., each tract in D is recovered independently), we model connectivity as a intensity function λ : Ω × Ω → ℝ⁺, such that for any regions E₁,E₂ ⊂ Ω, the number of events is Poisson distributed with parameter

$$\mathcal{C}(E_1,E_2)=\int {\int }_{E_1,E_2}\lambda (x,y)\mathit{dxdy}.$$ (1)

Due to properties of the Poisson distribution, the expected number of tracts is exactly 𝒞(E₁,E₂). For any collection of regions ${\{E_i\}}_{i=1}^N=P$, we can compute a weighted graph 𝒢(P, λ) by computing each 𝒞(E_i,E_j) for pairs (E_i,E_j) ∈ P × P. Each node in this graph is an element of P (a subset of Ω, a region of the cortical surface), and the edges between them are the rate at which we observe streamlines between the regions.

We call P a parcellation of Ω if ∪_i E_i = Ω and ∩_i E_i has measure zero ({E_i} is almost disjoint). If P is a parcellation, then 𝒢(P, λ) has Poisson rate parameters as edges. For any realization of endpoints, the count matrices that form traditional connectomes are independent draws from Poisson distributions with elements of 𝒢(P, λ) as parameters. The independence of the observations is conditional on λ and the fact that P is a parcellation, and does not imply an independence of the rates of the different regions—in other words, the observed counts are independent given the parameters, but this model does not speak to the generation of the parameters themselves.

It is immediately clear that λ is one such parcellation independent representation of connectivity that we desired in Section 1. λ is defined without reference to any particular parcellation; moreover, for any choice of parcellation P or even more general sets of subsets of Ω (e.g. overlapping sets) we can recover the parameters of a random network 𝒢(P, λ). While λ is a representation of cortical connectivity, we posit that λ itself is not a weighted graph as it no longer has a countable set of nodes. However, it does retain several graph-like constructions, namely a function analogous to weighted-degree (“strength”).

Define the marginal connectivity over a region E ⊂ Ω as M(·;E) : Ω → ℝ⁺ as:

$$M(x;E)={\int }_E\lambda (x,y)dy.$$ (2)

This is the aggregate connectivity to any point in region E_i from any point x–the pointwise intensity of observing a tract incident on x for which the other endpoint is contained in E_i. Further define

$$M(x)=M(x;\mathrm{\Omega })={\int }_{\mathrm{\Omega }}\lambda (x,y)dy.$$ (3)

This is the direct analogue of the sum of the edge weights for a given node x, i.e. the weighted degree. It is equal to the pointwise rate at which tracts are incident on x, connecting to any other point. If λ is continuous, then it can be shown that M(x) is also continuous.

2.2. Selection of a Parcellation

𝒢(P, λ) is a summary statistic for the intensity function λ, in that it summarizes information about the rate of tract observation into a finite set of scalars. It is clearly dependent on the parcellation P. Thus, given λ and two or more parcellations P₁, P₂, . . . , we would like to know which parcellation and associated summary statistic (graph) 𝒢(P, λ) best represents the underlying connectivity function. This requires a definition of the goodness of a representation; in practical terms, this means we need to choose a loss function in order to quantify how well 𝒢(P, λ) represents λ. There are at least two perspectives to consider, one in which 𝒢(P, λ) is viewed as an approximation to the function λ, and another in which 𝒢(P, λ) is viewed as an approximation to the parameter of the point process model.

L₂ Approximation Error

Because each P_i covers Ω (and P_i×P_i = Ω×Ω), each 𝒢(P₁, λ) can be viewed as a piece-wise function g : Ω × Ω → ℝ⁺, where $g(x,y)=\frac{1}{\mid E_i\mid \mid E_j\mid }\mathcal{C}(E_i,E_j)$ such that x ∈ E_i and y ∈ E_j. In other words, g is the constant approximation to λ over every pair of regions. A natural measure of error is another form of Integrated Squared Error:

$$\mathit{Err}(\lambda ,\mathcal{G}(P_1,\lambda ))=\int {\int }_{\mathrm{\Omega }\times \mathrm{\Omega }}{(g(x,y)-\lambda (x,y))}^2\mathit{dxdy}.$$ (4)

This is analogous to squared loss (ℓ₂-loss).

Likelihood

An alternative viewpoint leverages the point process model to measure the likelihood of the observed endpoint count in each region:

$$log\mathcal{L}(P)=\sum _{E_i,E_j}log\text{Pois}(\underset{\text{Number}\text{of}\text{Tracts}\text{in}{E}_i\times E_j}{\underbrace{\mid {\{x,y\}}_i\in D:(x,y)\in E_i\times E_j\}\mid }};\underset{\text{Regional}\text{Rate}}{\underbrace{\mathcal{C}(E_i,E_j)}}).$$ (5)

This uses the Poisson assumption on the tract endpoints, that the number of endpoints in any region E_i ×E_j is Poisson distributed with rate parameter equal to the integral of the intensity function over the region 𝒞(E_i,E_j). Here, the independence assumption plays a critical role, allowing pairs of regions to be evaluated separately. Unfortunately this is biased toward parcellations with more, smaller regions, as the Poisson distribution has tied variance and mean in one parameter. A popular likelihood-based option that somewhat counterbalances this is Akaike’s Information Criterion (AIC) [11],

$$\mathit{AIC}(P)=-2log\mathcal{L}(P)+\left(\begin{array}{c}\mid P\mid \\ 2\end{array}\right)log\mid D\mid .$$ (6)

AIC balances accuracy with parsimony, penalizing overly parameterized models— in our case, parcellations with too many regions.

2.3. Recovery of the Intensity Function

A sufficient statistic for Poisson process models is the intensity function λ(x, y). Estimates of this function, denoted λ̂, represent a non-trivial learning task, and have been the subject of much study in the spatial statistics community [12]. We choose to use non-parametric Kernel Density Estimation (KDE), and we present an efficient method for tuning the bandwidth parameter (up to a choice of desiderata). We first inflate each surface to a sphere and register them using a spherical registration (See Section 3); recovery of λ can be undertaken without group registration, but for later analysis such a registration is useful. We treat each hemisphere as disjoint from the other, allowing us to treat Ω×Ω as the product of spheres (S₁ ∪ S₂) × (S₁ ∪ S₂).

The unit normalized spherical heat kernel is a natural choice of kernel for 𝕊². We use its truncated spherical harmonic representation [13], which is defined as the following for any two unit vectors p and q on the 2-sphere:

$$K_{\sigma }(p,q)=\sum _h^H\frac{2h+1}{4\pi }exp\{-h(h+1)\sigma \}{P}_h^0(p·q)$$ (7)

Here, $P_h^0$ is the h^th degree associated Legendre polynomial of order 0. Note that the non-zero order polynomials have coefficient zero due to the radial symmetry of the spherical heat kernel [13]. We extend this kernel to our context trivially: since Ω is actually the union of two spheres, S₁ ∪ S₂ (each the inflation of the anatomic hemispheres), we define K_σ(p, q) to be zero if (p, q) are not on both on S₁ or both on S₂. Since we are estimating a function on Ω × Ω, we use the product of two heat kernels as our KDE kernel κ. For any test point (p, q), the kernel value associated to an endpoint pair (x_i, y_i) is κ_σ((p, q)|(x_i, y_i)) = K_σ(x_i, p)K_σ(y_i, q). It is easy to show that ∫_Ω×Ω K_σ(x_i, p)K_σ(y_i, q)dpdq = 1.

As is standard KDE practice, we evaluate

$$\begin{array}{l}\widehat{\lambda }(x,y)=\sum _{(x_i,y_i)\in D}{\kappa }_{\sigma }((x,y)\mid (x_i,y_i))\\ =\sum _{(x_i,y_i)\in D}[\sum _h^H\frac{2h+1}{4\pi }exp\{-h(h+1)\sigma \}{P}_h^0(x·x_i)\times \sum _k^H\frac{2k+1}{4\pi }exp\{-k(k+1)\sigma \}{P}_k^0(y·y_i)]\end{array}$$ (8)

on a discrete grid of Ω × Ω. The surface mesh itself provides a convenient choice for such a grid, though various remeshing schema can also be used. We rewrite the estimator into a more computationally efficient form for estimating σ in the next section.

2.3.1. Bandwidth Selection

The spherical heat kernel has a single shape parameter σ which corresponds to its bandwidth. The practitioner may either set this parameter manually or select a tuning criterion and then optimize the parameter for the given criterion. We provide an efficient method for the latter case; a discussion on the advantages and disadvantages of the former is provided in Section 5.2.

In general, automated tuning of kernel hyper-parameters requires the re-estimation of the density estimate λ̂ at every iteration; most procedures would, at each step, propose a parameter value, measure some criterion and/or its derivative with respect to the parameter value, and then propose a next parameter value. Assuming the chosen criterion requires numerical integration, this usually has of order O(NMS) operations, where N is the number of observations (tracts), M is the number of mesh points, and S is the number of tuning steps/sigma grid points. For our particular context we are able to reduce this to O(NM +MS) operations. This is achieved by rewriting our kernel in the following form:

$$\widehat{\lambda }(x,y)=\sum _h^H\sum _k^H[\underset{\text{Independent}\text{of}D,\text{evaluated}\text{every}\text{iteration}}{\underbrace{\left(\frac{2h+1}{4\pi }\right)\left(\frac{2k+1}{4\pi }\right)exp\{-\sigma (h^2+h+k^2+k)\}}}\times \underset{\text{Independent}\text{of}\sigma ,\text{evaluated}\mathbf{once}}{\underbrace{\sum _{(x_i,y_i)\in D}{P}_h^0(x_i·x)P_k^0(y_i·y)}}]$$ (9)

The right hand side is clearly separable into two functions, one of which is independent of the bandwidth and the other of which is independent of the data. This allows the memoization of part of the computation so that we only need to store the sum of the outer products of the harmonics. Evaluations of the kernel can then be done quickly computed for sequences of values of σ.

We then are left with the choice of loss function. Denoting the true intensity function λ, the estimated intensity λ̂, and the leave-one-out estimate λ̂_i (leaving out observation i), Integrated Squared Error (ISE) is defined:

$$\mathit{ISE}(\sigma \mid D)={\int }_{\mathrm{\Omega }\times \mathrm{\Omega }}{(\widehat{\lambda }(x,y\mid \sigma )-\lambda (x,y))}^2\mathit{dxdy}$$ (10)

$$\approx \int \widehat{\lambda }{(x,y\mid \sigma )}^2\mathit{dxdy}-\frac{2}{\mid D\mid }\sum _{(x_i,y_i)\in D}{\widehat{\lambda }}_i(x_i,y_i\mid \sigma )+\mathit{Constant}.$$ (11)

Hall and Marron [14] suggest tuning bandwidth parameters using estimated ISE. In practice, we find that replacing each leave-one-out estimate with its logarithm log λ̂_i(x_i, y_i|σ) yields more consistent and stable results.

3. Preprocessing and Procedure

We demonstrate the use of our framework in two separate analyses. The first is a test-retest reliability analysis using a subset of the Consortium for Reliability and Reproducibility (CoRR) dataset [15]; we compare the reliability of our method versus the standard counting method. We also compare three parcellations using the criteria defined in Equations 4, 5, and 6. Our second analysis is a demonstration of groupwise tests of parcellation free measures. This was performed on data from the Human Connectome Project, and tests sex differences in marginal connectivity (Eq. 3), a derived statistic of the proposed representation. In the first analysis we use the self-tuning bandwidth parameter, while in the second we use a pre-specified bandwidth. This was done to avoid conditioning results on the bandwidth parameter itself (avoiding the possibility of a group-wise effect on bandwidth selection).

3.1. IPCAS (Test-Retest Reliability)

Our first dataset is comprised of 29 subjects from the Institute of Psychology, Chinese Academy of Sciences (IPCAS) sub-dataset of the larger Consortium for Reliability and Reproducibility (CoRR) dataset [15]. T1-weighted (T1w) and diffusion weighted (DWI) images were obtained on 3T Siemens TrioTim using an 8-channel head coil and 60 directions. Each subject was scanned twice, roughly two weeks apart. T1w acquisition parameters were as follows: flip angle: 7 degrees; TI: 1100 ms; TE: 2.51 ms; TR: 2530 ms; voxel: 1×1×1.3 mm³. DWI acquisition parameters were as follows: flip angle: 90 degrees; TE: 30; TR: 200; 60 directions; voxel: 1.8×1.8×2.5 mm³.

T1w images were processed with FreeSurfer’s [16] recon-all pipeline to obtain a triangle mesh of the gray-white matter boundary registered to a shared spherical space [17], as well as corresponding vertex labels per subject for three atlas-based cortical parcellations, the Destrieux atlas [18], the Desikan-Killiany (DK) atlas [19], and the Desikan-Killiany-Tourville (DKT31) atlas [20]. Probabilistic streamline tractography was conducted using the DWI in 2 mm isotropic MNI 152 space, using Dipy’s LocalTracking module [21], as well as its implementation of constrained spherical deconvolution (CSD) [22] with a harmonic order of 6. Tractography streamlines were seeded at 2 random locations in each voxel labeled as likely white matter via the segmentation maps generated by FMRIB’s Automated Segmentation Tool [23], also known as FSL FAST. Streamline tracking followed directions randomly in proportion to the orientation function at each sample point at 0.5 mm steps, starting bidirectionaly from each seed point. As per Dipy’s Anatomically Constrained Tractography (ACT) criteria [24], we retained only tracts longer than 5mm with endpoints in likely gray matter.

We estimate λ̂ (the continuous connectivity representation) on each scan using the self-tuning kernel given in Section 2, and the vertices of a equi-areal triangular mesh (geodesic grid) as our sample points. This, along with the convention of unit surface area instead of unit radius (thereby eliminating an unnecessary division), simplifies computation. We threshold each of the sample points for λ̂ at 10⁻⁵, which is approximately one half of one unit tract density. We then numerically integrate λ̂ to compute regional connectivity graphs as in Eq. 1, and compare these to traditional count-based connectivity graphs. As a measure of reliability we provide the mean Intraclass Correlation (ICC) score [25] computed both with and without entries that are zero for all subjects, for both count and integrated-intensity connectivity matrices, for each element (each edge of the connectome). We also compute three measures of parcellation representation accuracy, namely ISE, Negative Log Likelihood, and AIC scores.

3.2. HCP (Demonstration Analysis of Marginal Connectivity)

Our second dataset is comprised of 731 subjects from the Human Connectome Project² S900 release [26]. We used the minimally preprocessed T1-weighted (T1w) and diffusion weighted (DWI) images rigidly aligned to MNI 152 space. T1w acquisition parameters were as follows: flip angle: 8 degrees; TI: 1000 ms; TE: 2.14 ms; TR: 2400 ms; voxel: 0.7×0.7×0.7 mm³. DWI acquisition parameters were as follows: flip angle: 78 degrees; TE: 89.5 ms; TR: 5520 ms; 90 directions at each b-value; b-values: 1000, 2000, and 3000 s/mm²; voxel: 1.25×1.25×1.25 mm³.

The preprocessing of these images included gradient nonlinearity correction (T1w, DWI), motion correction (DWI), eddy current correction (DWI), and linear alignment (T1w, DWI). We use the HCP Pipeline (version 3.13.1) FreeSurfer [17] protocol to run an optimized version of the recon-all pipeline in order to extract registered surfaces and region labels. We remesh subjects in the FreeSurfer shared spherical space in order to construct registered meshes with a dense correspondence between the vertices [27]. Tractography was conducted using the DWI in 1.25mm isotropic MNI 152 space. Probabilistic streamline tractography was again performed using Dipy’s implementation of constrained spherical deconvolution (CSD) [22], here using a harmonic order of 8. The same seeding and tracking procedures were used as the above IPCAS dataset processing, as well as pruning short tracts, or those that did not end in likely gray matter (again as specified by Dipy’s ACT).

We again estimate λ̂ (the continuous connectivity representation) on each scan. In the HCP data, we use a fixed kernel bandwidth of σ = 0.005. While using a self-tuning kernel on each subject does not invalidate the proceeding analysis, it may be advantageous to instead fix a kernel bandwidth across the group (See Section 5). We then numerically integrate each λ̂ function to form the marginal connectivity defined in Eq. 3, sampled at every mesh vertex. We then conduct a linear regression on the marginal connectivity values at each vertex, using HCP subject data for Sex, with covariates of Age (in years), and intercranial volume. We exclude any vertex identified as part of the medial wall in more than 95% of the subjects (~ 700 subjects), since labels are not fixed in the registered space. We correct the parametric p-values for each regression coefficient using the the Benjamini–Hochberg [28] False Discovery Rate correction for multiple comparisons.

4. Results

4.1. IPCAS Test–Retest

Table 1 and Figure 1 show that networks derived from the continuous connectivity estimates are preferable to regular count networks with respect to reliability as measured by ICC in the IPCAS dataset. Table 1 shows surprisingly low mean ICC scores for regular count matrices. This may be because ICC normalizes each measure by its s² statistic, meaning that entries in the adjacency matrices that should be zero but that are subject to a small amount of noise—a few erroneous tracts—have very low ICC. Our method in effect smooths tract endpoints into a density; end points near the region boundaries are in effect shared with the adjacent regions. Thus, even without thresholding we dampen noise effects as measured by ICC. With thresholding, our method’s performance is further improved, handily beating the counting method with respect to ICC score. It is important to note that for many graph statistics, changing graph topology can greatly affect the measured value [3]. While it is important to have consistent non-zero measurements, the difference between zero and small but non-zero edge values in the graph context is also non-trivial [29]. The consistency of zero-valued measurements is thus very important in connectomics.

Table 1.

This table shows mean ICC scores for each connectome generation method. The count method - the standard approach - defines edge strength by the fiber endpoint count. The integrated intensity method is our proposed method; in general it returns a dense matrix. However, many of the values are extremely low, and so we include results both with and without thresholding. Highest ICC scores for each atlas are bolded.

Atlas	DK	Destrieux	DKT31
Number of Regions	68	148	62
Count ICC	0.2093	0.1722	0.2266
Intensity ICC (Full)	0.4868	0.4535	0.4388
Intensity ICC (w/Threshold)	0.5613	0.6481	0.4645

Figure 1.

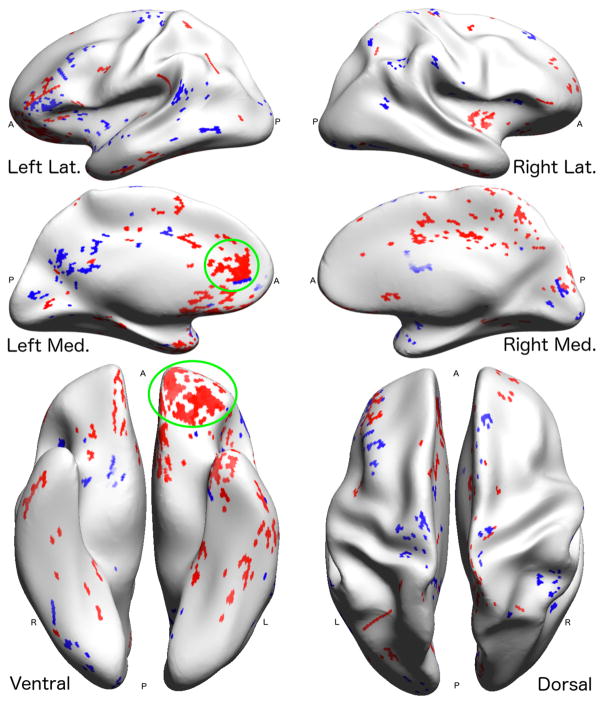
A visualization of the test-retest ICC scores for connectivity to Brodmann Area 45 (Destrieux region 14) for the Count connectomes (left) and the proposed Integrated Intensity connectomes (right). denotes a higher score.

Table 2 suggests that all three measures, while clearly different, are consistent in their parcellation selection at least with respect to these three parcellations. It is somewhat surprising that the Destrieux atlas has quite low likelihood criteria, but this may be due to the (quadratically) larger number of region pairs. It should be noted that these results must be conditioned on the use of a probabilistic CSD tractography model. Different models may lead to different intensity functions and resulting matrices. The biases and merits the different models and methods (e.g. gray matter dilation for fiber counting vs streamline projection) remain important open questions.

Table 2.

This table shows the means over all subjects of three parcellation selection criteria (Eq. 4, 5, and 6) for three different parcellations. In each case, lower is better. Values were rounded to three significant figures.

Type	DK	Destrieux	DKT31
ISE	1.85 × 10−5	2.10 × 10−5	2.13 × 10−5
Negative LogLik	85000	355000	88000
AIC Score	174000	733000	185000

4.2. HCP Sex Differences

Figure 3 shows a map of the areas in which significant differences of marginal connectivity were discovered between males and females in the HCP dataset, given the pointwise correspondence of the surfaces and under the fixed σ parameter. The marginal connectivity M(x) defined in Eq. 3 is the rate at which we observe tracts which have one endpoint at x as estimated by λ̂. Thus, estimated differences in marginal connectivity have a simple interpretation: in regions of significant difference, observed tracts are more likely to be incident on those regions in one group over the other. That is, the relative tract density per unit area is higher.

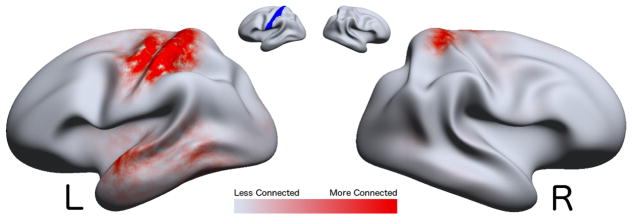
Figure 3.

A visualization of the significant differences of marginal connectivity (Eq. 3) values by mesh vertex between healthy normal human males and human females, controlled for age and inter-cranial volume, taking a critical value of α = 0.05, using the Benjamini–Hochberg [28] False Discovery Rate (FDR) correction for multiple comparisons. The marginal connectivity M(x) is the rate at which we observe tracts which have one endpoint at x. Regions of significant difference are thus interpreted as areas in which observed tracts are more likely to be incident in one group than in another. Note that the medial wall was removed and not tested. The results have been projected from registered space to a smoothed exemplar subject. denotes significantly higher marginal connectivity in females, denotes significantly higher marginal connectivity in males. Annotations in denote the anterior cingulate (top) and the inferior pre-frontal cortex (bottom), regions with large areas of significance.

There is a clear region of difference in the left pre-frontal cortex. We also identify another significant region as the left anterior cingulate. Outside of these regions, there are areas suggestive of significant changes, but no large contiguous groups of significant vertices. Even though the FDR correction is conservative in its adjustment of positively correlated p-values, we encourage researchers to take caution in the more scattered significant regions.

5. Discussion

In this paper we have proposed a continuous representation for cortical connectivity. While we believe our particular formulation to be novel, graph-like objects defined over continuums are by no means new. In particular, the continuum limits of graphs [30], also known as graphons, appear similar to the proposed framework, and have been used in the analysis of large random networks. Point process forms of graphons also exist [31], though in both these and the more general context the analysis is usually conducted with the assumption of exchangeability (i.e. the random function is invariant under measure preserving transformations of the domain). Our proposed structure is precisely the opposite, imposing the surface metric (or its proxy, a metric on S²); it is unreasonable to assume that phenomena of neurological interest on the cortical surface are exchangeable. Further, due to the surface metric the proposed object is not the graph limit of a parcellation-based graph.

Several dense connectome representations have been proposed [32, 26]. These representations use parcellations on the voxel or mesh-face level. Sampled continuous connectivity on mesh vertices and dense connectomes [26] have, at surface level, the same representation. They are both large arrays of connective values, with each element representing the connectivity to a very small physical feature; in the representation proposed here, however, each of these scalar values is a point density of an underlying function defined over the continuum of the cortical surface, with an imposed smoothness constraint. The former requires integration over an area to have matching units to traditional connectomes (tracts), while the latter is exactly that count, not a count per unit area. The former is equipped with a surface topology that is separate from the network topology; the latter abstracts away this surface. In the dense connectome case a joint analysis could surely be undertaken with the mesh vertices; indeed, we believe our proposed framework could be construed as one such analysis.

Another alternative to atlas-based parcellations are stochastic parcellations [33, 34], such as those generated by Poisson disk-sampling. While the resulting representations may have a large number regions approaching that of the dense connectomes, the regions are usually sampled at the time of processing, and may not have correspondence between studies. The normalization of network measures across these random network configurations is still possible [35] using a resampling scheme. This still ignores the underlying surface, and does not provide insight into the nature of parcellation differences, but appears empirically useful.

The proposed framework can also be put in the context of tractographic probability spaces. Ours is a reduction of a tract to its endpoints since traditional connectivity analyses are mostly concerted with the gray matter intersections, but more general spaces have been proposed. In particular O’Donnell and Westin [36] and the later Wassermann et al. [37] both propose implicit spaces via an inner product definition (a kernel trick). More recently, Parisot et al. [38] and Gallardo et al. [39] both propose implicit spaces based on similarity measures (scalar functions on Ω × Ω), both for the purpose of connectivity based parcellation. In their contexts the connective profiles (or transformations thereof) generate the similarity measures, whereas we seek to define connectivity as a (non-negative) scalar function.

5.1. HCP Analysis

The objective of our analysis of the HCP data is the demonstration of a simple analysis based on our proposed parcellation free model. The use of mass univariate regression with FDR correction is a compromise; in the best possible case we would prefer a spatial regression. However, accounting for spatial covariance is a non-trivial task (especially considering the manifold under consideration is not truly S²), and so we leave this challenge for later work. Though such a method is desirable, the results recovered from the naïve method remain promising.

The identification of changes in the left pre-frontal cortex and anterior cingulate is encouraging for simple analyses such as these. The left pre-frontal cortex was identified in Ingalhalikar et al. [40] as well as Duarte-Carvajalino et al. [41] as having significant connectivity differences between the sexes. The anterior cingulate was also identified in Duarte-Carvajalino et al. as a region of significant change. Both of these studies used other, more complex measures of network changes, and of course used parcellation based network representations. The qualitative result remains similar, that females have “higher connectivity” in left pre-frontal cortex, and in the second case, the anterior cingulate. It should be noted, however, that these regions are also quite large, and the effects documented need not be co-localized.

While in network analysis the degree statistic taken locally is somewhat heavy-handed, here its simplicity makes it easily interpretable. The lack of pre-defined parcels also removes the need for areal regularization. In a traditional connectome, it might be advisable to regularize by region size in order to make the units into tracts per unit area. This is implicit under the proposed representation.

We fail to identify other large contiguous regions outside of the left prefrontal cortex; this may, of course, be related to the underlying signal, but there are several confounding factors that should be considered. The identified small areas of significance may be artifacts of pre-processing or tractography biases. In particular, it may be the case that one sex or another is more easily registered (or that a correlated trait, such as head-size, adds or detracts from such a registration). A similar case may be made for tractography. It may also be the case that the use of a stationary kernel (i.e. a kernel that does not change by general cortical region) biases our analyses towards regions with matching scale as our chosen bandwidth.

Sex differences in the brain have been studied in a number of other papers, especially with respect to connectivity. Alongside Ingalhalikar et al. [40] and Duarte-Carvajalino et al. [41], Rymen et al. [42] also measure sex differences in structural connectomes, using a proxy measure of creativity to explore phenotypic correlations with estimated connectivity. Of the three, only Rymen et al. directly use the degree statistic (in their paper referred to as Connectivity, or S^weighted), while both of the other studies use more complex topological measures.

As with almost all group difference statistical analyses, we do not make the assertion that all males or females exhibit the characteristics we found to be significantly different between the groups. These differences are found on average, are necessarily a generalization and not the rule, and then only given our model assumptions and procedural choices. Some of these differences are probably due to latent factors such as the aforementioned registration bias.

5.2. Kernel Bandwidth Selection

ISE is a global measure, and bandwidth parameters chosen using this criterion will thus be set globally. Other forms of bandwidth estimation are actively being researched in the literature [43], including local methods which allow σ to vary as function of the location. It is not clear as of yet which method or loss function serves best the overall desiderata of brain connectivity analysis.

An alternative to the self-tuned kernel is one with specified bandwidth, as demonstrated in the previous analysis. While clearly any subsequent results must be conditioned on this choice, in our opinion this option simplifies interpretation across multiple subjects, and opens up a wealth of theoretical results. Furthermore, it has been suggested, albeit on Euclidean spaces, that the estimation of a smoothed form of the underlying density still retains its qualitative value.

A general kernel estimate of some general density p with the form

$$\widehat{p}(x)=\frac{1}{\mid D\mid Z(h)}\sum _{x^{\prime }\in D}K\left(\frac{d(x,x^{\prime })}{h}\right)$$

can be shown to be asymptotically consistent, unbiased, and has known variance in the limit as h → 0 (see [44]). Here Z(h) chosen so that λ̂ integrates to 1. More recent work suggests the use of fixed h may also be of use [45], i.e. eschewing the asymptotic result in favor of estimating a mollified (smoothed or blurred) form of λ. Fixing h, the estimate can be rewritten as the convolution of the empirical data function (a sum of delta functions) with the kernel K_h. This work was performed on ℝⁿ for a density P estimated with a slightly different kernel than the one given above, but we may transport the general concept by using spherical convolution [46]. In more general settings outside of density estimation, the value of mollified signals has long been accepted [47].

6. Conclusion

We have presented a general framework for structural brain connectivity. This framework provides a representation for cortical connectivity that is independent of the choice of regions, and thus may be used to compare the accuracy of a given set of regions’ connectivity matrix. We provide one possible estimation method for this representation, leveraging spherical harmonics for fast parameter estimation. We have demonstrated this framework’s viability, as well as provided a preliminary comparison of regions using several measures of accuracy. We further have provided an example analysis of the continuous connective object.

The results presented here lead us to conjecture that our connectome estimates are more reliable compared to standard fiber counting, though we stress that a much larger study is required for strong conclusions to be made. However, we believe that it is important to explore connectomics beyond the confines of the graph-theoretic abstraction. This particular instantiation of continuous connectivity is fairly general, and could be made more nuanced with a variety of existing statistical technologies, including regressions accounting for spatial auto-correlations, marked processes, and inter-subject hierarchical models of tract generation.

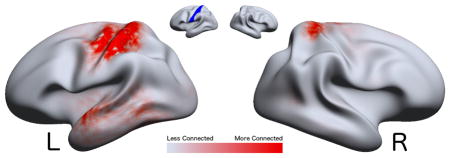
Figure 2.

A visualization of the marginal connectivity M(x;E) = ∫_Eλ̂ (x, y)dy for the Left Post-central Gyrus region of the DK atlas (Region 57). The region is shown in on the inset. denotes higher connectivity regions with the region.

Highlights.

• Generalizes traditional connectome count matrices to spatial process of tracts

• Provides fast estimator, with efficient hyper parameter tuning

• Provides results showing improved reliability (as measured by ICC score)

• Includes demonstration analysis using analogous “degree” function

• Significant differences in example analysis between sexes

Appendix: Implementation Notes

We optimize σ using grid search using a large linear grid. Using Equation 9 makes the marginal time cost of additional grid points low, so we can densely sample any reasonable interval quickly (σ is one dimensional). The boundary and spacing of the interval can be determined heuristically, and overcautious estimates are, again, relatively cheap.

Both the leave-one-out estimation and the quadrature can be done in parallel. In practice we find that caching calls to exp and the Legendre polynomials (i.e. computing a look-up table beforehand, or constructing one at run-time), reduces the computational costs of bandwidth estimation. The truncation error introduced by using a lookup table is minimal with a sufficiently dense table; since this is a one-time cost and can be completely computed in parallel, we choose a table optimal for our physical memory constraints. Note that we will only be computing exp and the Legendre polynomials for either fixed numbers known a priori, fixed grids, or (in the latter case) arguments in on the interval [−1, 1]. After σ has been computed or specified by the user, the estimation of λ̂ is relatively fast, as it is a sub-problem of the bandwidth estimation.

Because these operations are taking place on a mesh and significant mesh pre-processing steps are undertaken (e.g. re-meshing), we implemented our method in C++ using a half-edge structure. We take full advantage of compile time optimization. For repeated loops over constant sets (e.g. the spherical harmonic coefficients), loop unrolling and the appropriate use of const declared variables in tandem with standard optimizations speed up processing by an order of magnitude. (This is usually at the cost of code size, which is, practically speaking, almost free.)