Depth perception: the need to report ocean biogeochemical rates as functions of temperature, not depth

Abstract

For over 50 years, ocean scientists have oddly represented ocean oxygen consumption rates as a function of depth but not temperature in most biogeochemical models. This unique tradition or tactic inhibits useful discussion of climate change impacts, where specific and fundamental temperature-dependent terms are required. Tracer-based determinations of oxygen consumption rates in the deep sea are nearly universally reported as a function of depth in spite of their well-known microbial basis. In recent work, we have shown that a carefully determined profile of oxygen consumption rates in the Sargasso Sea can be well represented by a classical Arrhenius function with an activation energy of 86.5 kJ mol⁻¹, leading to a Q₁₀ of 3.63. This indicates that for 2°C warming, we will have a 29% increase in ocean oxygen consumption rates, and for 3°C warming, a 47% increase, potentially leading to large-scale ocean hypoxia should a sufficient amount of organic matter be available to microbes. Here, we show that the same principles apply to a worldwide collation of tracer-based oxygen consumption rate data and that some 95% of ocean oxygen consumption is driven by temperature, not depth, and thus will have a strong climate dependence. The Arrhenius/Eyring equations are no simple panacea and they require a non-equilibrium steady state to exist. Where transient events are in progress, this stricture is not obeyed and we show one such possible example.

This article is part of the themed issue ‘Ocean ventilation and deoxygenation in a warming world’.

1. Introduction

Old habits die hard—so goes the adage, and quite possibly no better expression of this truism can be found than within the ranks of ocean scientists addressing some of the challenges posed by rapidly evolving climate change impacts on biogeochemical cycles and the ocean. The specific example addressed here is the now more than 50-year-old tradition of ocean chemists reporting deep ocean microbial consumption rates of O₂ solely as a function of depth rather than primarily as an Arrhenius function of temperature. We have recently [1] tackled this problem and have shown that, for an exemplary Sargasso Sea rate profile, originally reported by Stanley et al. [2] as an exponential function of depth, the data can be better represented as a classical Arrhenius function with an activation energy for the microbial oxidation of marine organic matter of 86.5 kJ mol⁻¹. From this, we derive a Q₁₀ of 3.63 (Q₁₀ is a measure of rate increase per 10°C temperature rise) for the temperature interval 16°C–6°C, broadly consistent with the temperature-dependent decay of organic matter in soils [3,4].

This result was derived from only a single rate profile obtained from meticulous use of the ³H–³He tracer clock via the He ingrowth technique, and no other datasets of comparable quality are available. There are, however, other tracer-derived rate estimates, primarily from observations of the time history of penetration of chlorofluorocarbons (CFCs) and SF₆ into the ocean, and these span a far wider range of oceanic conditions. In this paper, we examine reported O₂ consumption rates derived from the ³H–³He, CFC and SF₆ tracer fields in an effort to assess the range of values of the activation energy to be found in different ocean regions spanning a far wider range of temperature and production of organic matter.

We extend the analysis by use of the related Eyring equation [5] to include estimation of Δ^‡G and Δ^‡S. We also note that conversion of the decades-old use of depth-dependent rates as a quasi-substitute for temperature is no simple matter. There are situations where the requirement of a non-equilibrium steady state will not hold, as when the ocean is in transition and where the use of the simple Arrhenius equation is therefore ill-advised.

The requirement for this assessment lies in the problem of understanding the climate link for rapidly unfolding evidence of large-scale deoxygenation at mid-water depths associated with ocean warming [6–9]. Should large increases in hypoxic waters occur, the outcome could be devastating for marine life over very large regions. The possible impacts range from complete loss of O₂ with emergence of H₂S in regions that are already sub-oxic [10] to more frequent damaging intrusions of low-O₂/high-CO₂ water onto continental shelves with important fisheries [10]. The organic matter consumed is in finite supply, and thus we will probably see rapidly declining O₂ at shallower depths, compensated to some extent by slightly higher O₂ levels in the abyss with reduced organic matter supply to the deep sea. The earlier derived Q₁₀ of 3.63 is quite high and would result in an increase in microbial rates of 29.2% for only 2°C warming.

The problem is not easy because, as is well recognized, the reported rates are from the ensemble of processes affecting a water parcel during transit from initial formation to the observation point. While temperature is largely conserved along this trajectory, large depth changes occur, and so too does the exposure to varying quantities of organic matter, both dissolved as carried in the flow, and in particulate form raining from above. At this time, there is no easy way of normalizing for these effects and the derived rates must be viewed with caution.

It is a puzzle as to why the tradition of reporting observed O₂ consumption rates as an exponential function of depth has persisted for so very long; the pattern was initiated by Riley 65 years ago [11]. Ocean biologists have always dealt with the fundamentals of temperature-dependent rates, and elegant arguments giving the big picture of this are readily available [12]. But ocean chemical and physical oceanographers have persisted with depth-based reporting of rates, largely it seems from simple familiarity of use, with no specific example of an alternative approach at hand to guide them.

2. Background

The problem of global warming from fossil fuel CO₂ build-up in the atmosphere identified by Callendar [13] and Revelle & Suess [14] clearly predicted the enormous uptake of heat by the ‘great flywheel’ of the ocean, so that a projected doubling of atmospheric CO₂ would lead to warming of the air and ocean by about 2°C. There are three obvious oceanic consequences of this—the increased thermal stratification of the ocean surface layers, thereby inhibiting vertical mixing of both the downward transport of heat and the upward mixing of nutrients, the reduced solubility of gases in warmer water and the increase in microbial decomposition rates of organic matter in the deep sea directly tied to rising temperature. It is this latter point that is the focus of this paper and it is familiar to every household with a refrigerator; the chemical physics basis for this was laid down in classic papers by van't Hoff and Arrhenius in the late nineteenth century [15,16].

Yet, when early papers noting oxygen declines related to ocean warming were first published, the emphasis was almost entirely on the association with stratification and the reduced ventilation with new atmospheric O₂. The century-old well-known increase in chemical and microbial reaction rates with temperature was scarcely mentioned as a contributing cause.

The 2007 report by Nakanowatari et al. [6] on oxygen declines associated with ocean warming at intermediate depths in the North Pacific over a 49-year period can be simply analysed—the decline in O₂ that can be attributed solely to the reduced solubility can account for only about 15% of the observed signal. The remaining 85% must be attributed to other causes. As the impact of 2°C warming leads to a solubility loss of O₂ of approximately 14 µmol kg⁻¹, if the present trend in this ratio holds, loss of some 84 µmol kg⁻¹ O₂ could be possible in some regions. This seems extreme and the comment is included here only to illustrate the potential seriousness of the problem and why some better understanding of the forces at work is important.

Persistently declining oxygen levels in the eastern North Pacific were also noted by Whitney et al. [7] from the time series at Ocean Station Papa (50° N, 145° W). Rates of oxygen loss in the depth range 100–400 m of −0.39 to −0.70 µmol kg⁻¹ yr⁻¹ were associated with warming of 0.005–0.012°C yr⁻¹. Here, the explanation offered was ‘hypoxia may increase in the subarctic Pacific due to global warming as upper ocean stratification strengthens’ and no mention of warming directly increasing microbial oxygen consumption rates was made.

Widespread expansion of the oxygen minimum zones in the tropical oceans was later noted by Stramma et al. [8] but no specific mechanism was attributed, nor model predictions cited. The status of observable oceanic oxygen declines was examined by Helm et al. [9] who also concluded that ‘Approximately 15% of global oxygen decrease can be explained by a warmer mixed-layer reducing the capacity of water to store oxygen, while the remainder is consistent with an overall decrease in the exchange between surface waters and the ocean interior.’ Again, no mention of the temperature dependence of microbial decomposition rates was made.

There is clear evidence of rapid expansion of oxygen minimum zones in the recent geologic past [17] with ‘extreme compression of upper-ocean oxygenated ecosystems' associated with the warming at the end of the last glacial period, and occurring in synchrony across all ocean basins. But the mechanisms invoked were ‘processes associated with a warm surface ocean, including gas solubility reduction and physical stratification’ with, yet again, no mention of increased microbial decomposition rates of the organic matter accumulated during the cold period.

From the above, it is clear that the primary cause of a very large fraction, some 85%, of the observed present-day declines in oceanic oxygen levels just beneath the critical twilight zone is under debate and that the tendency in the literature is to attribute upper ocean stratification as the primary, or even sole, cause. The major 2010 review article by Keeling et al. [18] on ‘Ocean deoxygenation in a warming world’ addressed only the physical mechanisms of solubility and stratification—concepts of chemical physics involving fundamental microbial rate dependences on temperature were notably absent.

Why the fundamental increase in microbial decomposition rates, and thus oxygen consumption, with increasing temperature has suffered relative neglect in these discussions is not well known. Yet, over 20 years ago [19] the IPCC 1995 report noted the ‘profound effect on growth and metabolic processes' of temperature and suggested a typical Q₁₀ of 2. But derivations of the actual activation energy, and from this a Q₁₀, for deep-sea processes were not attempted and these are the focus of this paper.

3. Derivations from tracer-based estimates of ocean O₂ consumption rates

In earlier work [1], we showed that the traditional representation of oceanic consumption rates of oxygen as a logarithmic function of depth could be better described as a classical Arrhenius function of temperature. We used a single Sargasso Sea profile from the Bermuda Atlantic Time-series Study (BATS: 31.7° N, 64.2° W, with samples taken in the period 2003–2006) site reported by Stanley et al. [2] with oxygen consumption rates derived from careful use of the ³H–³He pair via the ³He ingrowth technique. The particular success here lies not only in the measurement skill but in the attention to detail in estimation of the water ages (τ) at different depths calculated from the transit time distributions [20].

The derivation of ocean O₂ consumption rates from the ³H–³He tracer pair has the advantage that the input function, originating from nuclear bomb tests in the mid-twentieth century, is quite well defined [21]. By contrast, the input function of both CFC-11 and SF₆ is far more broadly spread in time [22] and the reduction in atmospheric growth rates of the CFCs since 1990 has a significant complicating effect.

All such tracer-based ‘ages’ suffer from biases associated with mixing processes in the ocean interior; this problem is now well recognized, and appropriate corrections for transit time distributions are normally made [21,22]. In spite of these challenges, the tracer-based estimates of O₂ consumption rates are the best resource available because the ensemble rates are so slow that direct experimental attack is not useful. We say ‘ensemble rates’ to reflect the net result observed in the ocean water column. Within localized small-particle assemblages, attached microbes ‘see’ a very different environment from that in dilute bulk fluid. In localized particles, there is high organic carbon availability with strong local chemical gradients, lower local O₂ levels driven by microbial consortia maximizing their energy gain, and thus far faster rates on the micro-scale [23] than in the bulk fluid.

Here, we examine seven case studies of net water column apparent oxygen consumption rates from tracer observations in widely different oceanic regions spanning a large range of temperature. In earlier work [1], we derived the apparent Arrhenius activation energy, and thus a Q₁₀, from a Sargasso Sea dataset; here, we extend the analysis to include application of the Eyring [5] equation, developed from transition state theory, which is typically more useful for condensed-phase reactions in that it does not depend strictly on the collision model. The more familiar Arrhenius equation takes the form

where a plot of ln(K) versus 1/T yields the Arrhenius activation energy as E_a = −slope × R, where R is the ideal gas constant of 8.314 J K⁻¹ mol⁻¹.

The Eyring equation, less familiar to ocean scientists, yields the Gibbs free energy of activation, which is the difference between the transition state of a reaction (for either an elementary reaction or a stepwise reaction) and the ground state of the reactants. It is calculated from the experimental rate constant k via the conventional form of the absolute rate equation:

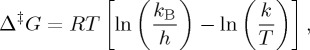where k_B is the Boltzmann constant and h is the Planck constant (k_B/h = 2.08358 × 10¹⁰ K⁻¹ s⁻¹). The values of the rate constants, and hence Gibbs energies of activation, depend upon the choice of concentration units (or of the thermodynamic standard state).

The form of the Eyring equation used here is

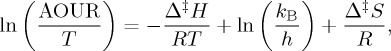where AOUR is the apparent oxygen utilization rate, R is the gas constant, h is the Planck constant (6.626 × 10⁻³⁴ J s) and k_B is the Boltzmann constant (1.381 × 10⁻²³ J K⁻¹). From this, we derive the Gibbs energy of activation Δ^‡G, the enthalpy of activation Δ^‡H and the entropy of activation Δ^‡S: the enthalpy of activation is derived from the slope of the model-2 regression line when ln(AOUR/T) is plotted versus 1/T, and the entropy of activation comes from the y-intercept of the same line:

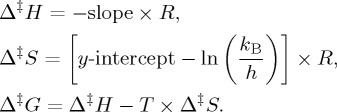Again, we note that these are ‘apparent’ properties, not pure thermodynamic properties, due to the multiplicity of processes simultaneously at work. Nonetheless, they provide essential information for assessing changes in the ocean biogeochemical state under climate warming.

4. Ocean observations used

(a). Sargasso Sea

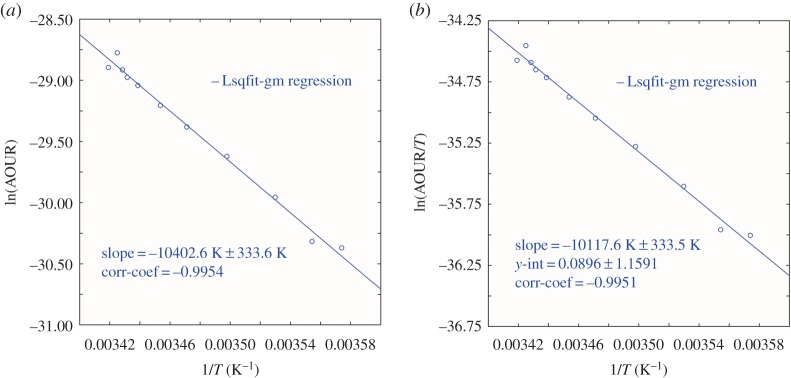
For the Sargasso Sea we re-examine AOUR data from Stanley et al. [2] derived from observed ³H–³He distributions. We earlier reported derivation of an Arrhenius activation energy of 86.5 kJ mol⁻¹, with a Q₁₀ of 3.63 for the temperature interval of 16°C to 6°C. Here (figure 1) we derive in addition an enthalpy of activation of 84.1 kJ mol⁻¹, an entropy of activation of −196.8 J mol⁻¹ K⁻¹ and a Gibbs activation energy in the range 139.2–141.7 kJ mol⁻¹ depending on the temperature used for the calculation.

Figure 1.

Sargasso Sea (a) Arrhenius activation energy plot (from [1]) and (b) Eyring–Gibbs free energy of activation equation plot. Data from Stanley et al. [2]. (Online version in colour.)

(b). Northeast Pacific

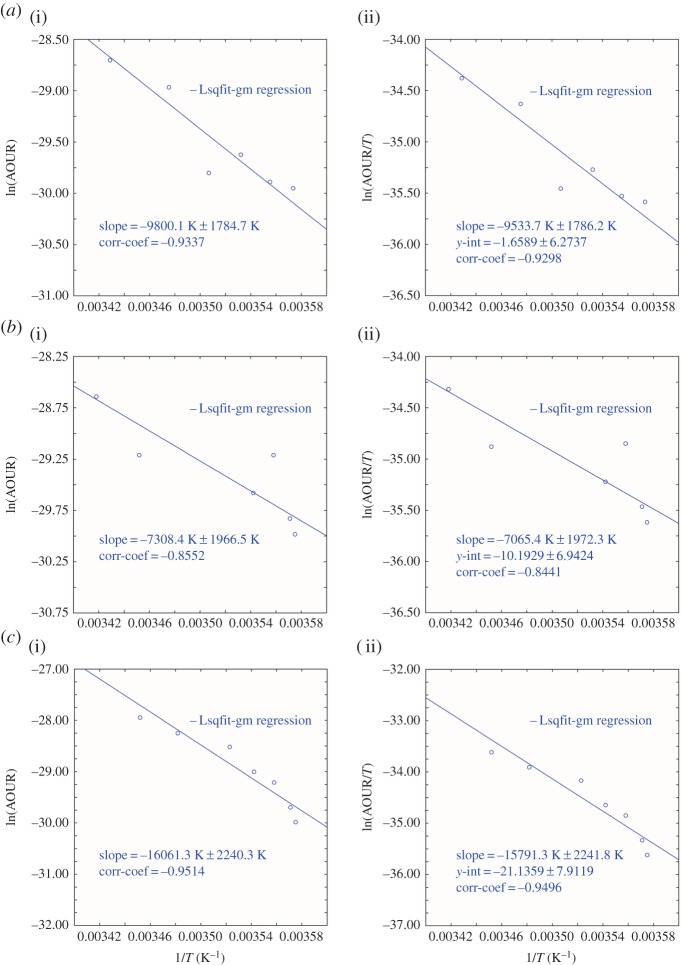
For a North Pacific example, we take data on transit time distributions and AOURs derived from CFC and SF₆ observations by Sonnerup et al. [22] from a September 2008 northeast Pacific transect spanning the range 20°–37° N along 152° W. The original individual data points are not available to us. For figure 2a, we have extracted information from their table 2, which reports the average AOURs on seven density surfaces from σ_θ 25.0 to 27.0, but did not report the associated temperatures. We estimated the temperature associated with those density surfaces from the NODC database at the appropriate latitude and longitude. Data for figure 2b,c were extracted from their fig. 9 [22] where the data from their ‘gradient’ calculations were used for figure 2b and data from their ‘path’ calculations were plotted in figure 2c.

Figure 2.

(a) Northeast Pacific along 152° W (i) Arrhenius activation energy plot and (ii) Eyring–Gibbs free energy of activation equation plot. Data are from table 2 in Sonnerup et al. [22]. (b) Northeast Pacific 20° N, 152° W (i) Arrhenius activation energy plot and (ii) Eyring–Gibbs free energy of activation equation plot. Data are from fig. 9 (gradient calculation) in Sonnerup et al. [22]. (c) Northeast Pacific 20° N, 152° W (i) Arrhenius activation energy plot and (ii) Eyring–Gibbs free energy of activation equation plot. Data are from fig. 9 (path calculation) in Sonnerup et al. [22]. (Online version in colour.)

In figure 2, we show plots of the data in the form required for determination of both the Arrhenius activation energy and the related Eyring functions. The analysis is necessarily less precise than for the ³H–³He determined rates for the Sargasso Sea due both to the challenges posed by the tracer input functions and to the need to estimate mean temperatures for the density surfaces reported. The results from these calculations are given in tables 1 and 2, respectively.

Table 1.

Properties of the estimated slope and standard deviation derived from Arrhenius equation calculations of the oxygen consumption rate data reported in the references listed. The actual AOUR data and temperature for each station or transect are reported in the electronic supplementary material. The form of the Arrhenius equation is ln(AOUR) = ln(A) − E_a/RT where R = 8.314 J mol⁻¹ K⁻¹ and T is 273.15 + T°C. The slope and standard deviations are in kelvin.

location	slope (K)	s.d. (K)	correlation coefficient	activation energy Ea (kJ mol−1)	refs
BATS	−10 402	333.6	−0.9954	86.5	[2]
Sargasso Sea
North Pacific	−9800	1784.7	−0.9337	81.5	[22]
152° W
North Pacific	−7308	1966.5	−0.8552	60.8	[22]
20° N (grad)
North Pacific	−16 061	2240.3	−0.9514	133.5	[22]
20° N (path)
Southeast Pacific	−15 021	2290.5	−0.9419	124.9	[24]
30° S–42° S
Southeast Pacific	−91 180	18 020.6	−0.9609	758.1	[24]
43° S–54° S
Mediterranean	−20 002	8825	−0.9903	1662.9	[25]
Red Sea	−47 207	4922	−0.7717	392.5	[26]

Table 2.

Application of the Eyring equation to the AOUR dataset reported in table 1. The Eyring equation has the form ln(AOUR/T) = −Δ^‡H/RT + ln(k_B/h) + Δ^‡S/R, which yields the Gibbs energy of activation Δ^‡G and the entropy of activation Δ^‡S, where R = 8.314 J mol⁻¹ K⁻¹, h = 6.626 × 10⁻³⁴ J s, k_B = 1.3807 × 10⁻²³ J K⁻¹ and T is 273.15 + T°C. From this equation, the slope = −Δ^‡H/R and the y-intercept = ln(k_B/h) + Δ^‡S/R. The mean Δ^‡G is remarkably constant at 140.0 ± 2.8 kJ mol⁻¹.

location	slope (K)	s.d. (K)	y-int	s.d.	r	Δ‡H (kJ mol−1)	Δ‡S (J mol K−1	T range (°C)	Δ‡G (kJ mol−1)	refs
BATS	−10 117.6	333.5	0.0896	1.1591	−0.9951	84.1	−196.8	19.33–6.64	141.7–139.2	[2]
Sargasso Sea
North Pacific	−9533.7	1786.2	−1.6589	6.2737	−0.9298	79.3	−211.3	18.50–5.98	140.9–138.3	[22]
152° W
North Pacific	−7065.4	1972.3	−10.193	6.9424	−0.8441	58.7	−282.3	19.41–5.84	141.3–137.5	[22]
20° N (grad)
North Pacific	−15 791.3	2241.8	21.136	7.9119	−0.9496	131.3	−21.8	16.54–5.84	137.6–137.4	[22]
20° N (path)
Southeast Pacific	−14 755.7	2292.2	16.504	8.1496	−0.9397	122.7	−60.3	14.80–4.65	140.0–139.4	[24]
30° S–42° S
Southeast Pacific	−90 910.9	18 021.7	289.05	64.3783	−0.9607	755.8	2205.6	8.42–4.74	134.8–142.9	[25]
43° S–54° S
Mediterranean	−199 731	8825	658.98	30.71	−0.9902	1660.6	5281.2	15.01–13.59	138.7–146.2	[25]
Red Sea	−46 980	4925	124.72	16.70	−0.7692	390.6	839.4	24.55–20.99	140.7–143.7	[26]

(c). Southeast Pacific

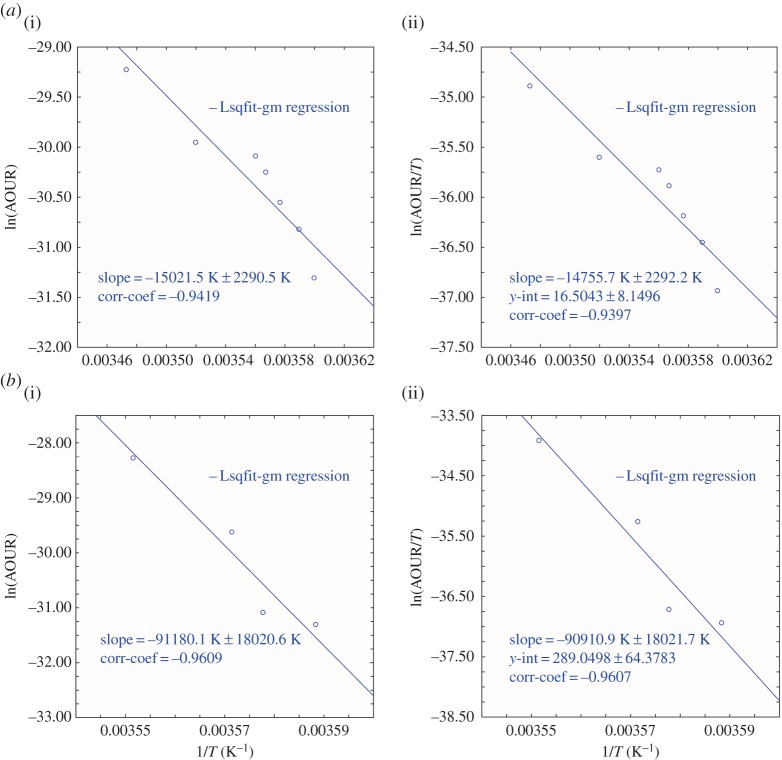
Observations of oxygen utilization rates along an N–S section at 105° W (spanning the range 40°–64° S) have recently been reported by Sonnerup et al. [24] with rates based upon pCFC and pSF₆ ages again reported (their table 2) as average AOURs on six potential density surfaces in the range 26.5–27.4 σ_θ. The actual temperature values were not reported, and again we have obtained estimated values of the temperature associated with the density intervals from known databases. The results (figure 3), and the limitations, are very much as given for the companion North Pacific dataset above. Activation energies are reported in tables 1 and 2.

Figure 3.

(a) Southeast Pacific 32°–42° S (i) Arrhenius activation energy plot and (ii) Eyring–Gibbs free energy of activation equation plot. Data are from Sonnerup et al. [24]. (b) Southeast Pacific 43°–54° S (i) Arrhenius activation energy plot and (ii) Eyring–Gibbs free energy of activation equation plot. Data are from Sonnerup et al. [24]. (Online version in colour.)

(d). Red Sea

The Red Sea is the warmest of the major semi-enclosed seas and thus offers a high-temperature case study where deep water temperatures are around 22°C. CFC and SF₆ tracer data have recently been reported by Zhai et al. [26] together with dissolved oxygen data. The authors did not present AOURs from the combined transit time distributions and AOU data in this publication. We are indebted to lead author P. Zhai for kindly carrying out this calculation and forwarding the results to us. The dataset is limited, with only five stations reported and transit times calculated from pSF₆ data. The results from these analyses are given as before in tables 1 and 2.

(e). Other data

Our literature survey indicates that, while there are additional AOUR estimates available, these are less suitable for inclusion here. The Sargasso Sea estimates of Kadko [27] based on ⁷Be isotopic data yield values significantly higher than those from ³H–³He rate estimates. They may be idiosyncratic and cannot be independently verified. AOUR values for the Japan/East Sea are reported by Jenkins [28], but these are given in such widely separated depth bands (200–600 m, 600–1500 m) that they do not provide useful constraints for our purpose.

(f). Non-steady-state events

A so far unspoken assumption in the above cases is that the system has had time to come to an apparent steady state where the observed microbial consumption rates approximate the rate of supply of organic matter. But transient episodic events do occur in the ocean such as from deep mixing events or from rapid pulses of sinking organic matter. A very different case can also arise from deep sea methane eruptions or from oil releases from the sea floor that rapidly inject large quantities of readily oxidizable material at depth, and these too provide insights into processes at work.

The Mediterranean Sea presents a well-known example of warm deep waters, but also of rapid dense water formation events where non-steady-state conditions may occur, and we examine this case here.

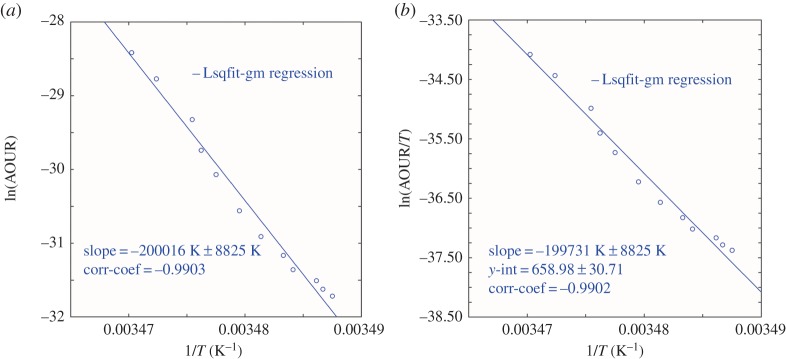
Observations of AOURs have been reported for the Eastern Mediterranean Sea by Roether & Well [25] by using a combination of CFC-12 observations, and ³H–³He data on samples obtained from a 1987 cruise. They reported consumption rates (R) as an exponential function of depth of the form

For z < 1000 m, and for depths greater than 1000 m, a constant value of R (z = 1000 m) was applied. We have derived rates from this equation and plotted the results in figure 4. We present estimated values of the activation energies from both the Arrhenius and Eyring equations, based on literature values of in situ temperatures, in tables 1 and 2.

Figure 4.

Eastern Mediterranean Sea (a) Arrhenius activation energy plot and (b) Eyring–Gibbs free energy of activation equation plot. Data are from Roether & Well [25]. (Online version in colour.)

The oceanographic context for these observations is important and the Mediterranean is well known as a site for rapid deep water formation events. One extreme event took place from the particularly strong winters of 1991–1992 and 1992–1993. This is 3 years after the Roether & Well cruise, and while it cannot have influenced their data, descriptions of the event are revealing and may have some bearing on the observed rates. Klein et al. [29] reported observations directed at understanding the consequences of this large-scale perturbation of the Eastern Mediterranean Deep water newly created from an Aegean Sea source. Termed the Eastern Mediterranean Transient (EMT), this event ‘massively transferred oxygen-rich near-surface waters into the deep layers'. This ‘made available large amounts of dissolved organic carbon with an unusually high fraction of labile material which in turn enhanced oxygen consumption’ [30]. We note here that the resident microbial population of the shallow waters of the Aegean Sea was also transferred to depth along with its chemical components.

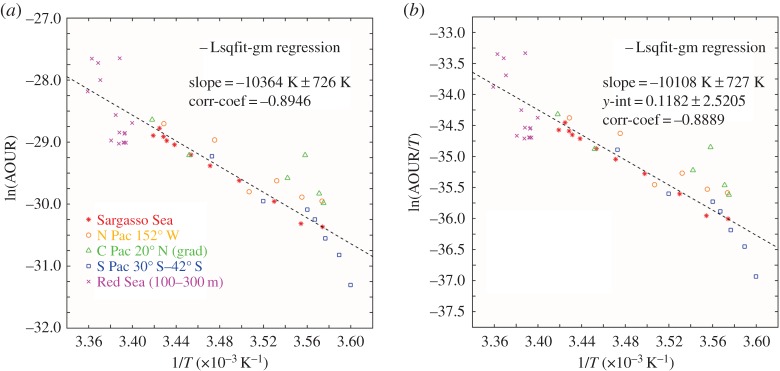
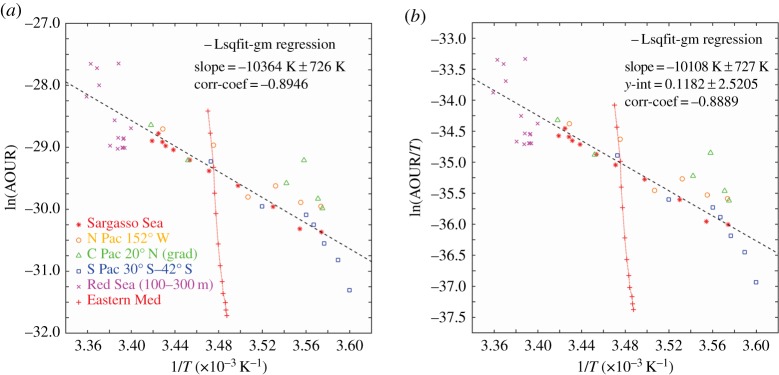
In figure 5, we plot the ensemble results from the five mutually consistent datasets. This plot demonstrates in remarkable fashion the global consistency of the effect of temperature upon the bacterial respiration-dominated AOURs. In figure 6, we show the Arrhenius plot derived from the tracer age and oxygen consumption rate data of Roether & Well [25] overlaid on the ensemble results in figure 5; this is startlingly different from the other oceanic observations. Temperature gradients from surface to depth are small, and a quite large range in rates as a function of depth—more akin to the traditional view—is found. The slope of the line is far steeper than elsewhere, with a calculated activation energy of 1663 kJ mol⁻¹—almost 20× higher than the activation energy calculated for the Sargasso Sea dataset. The enthalpy calculated too is unusually high at 1661 kJ mol⁻¹.

Figure 5.

(a) All qualified datasets as indicated in the text plotted as an Arrhenius function. From this ensemble data, we calculate the Arrhenius activation energy of 86.3 kJ mol⁻¹. This is almost identical to the activation energy calculated earlier [1] for a single Sargasso Sea station dataset, probably indicating a remarkably robust value for the temperature dependence of the microbial oxidation of marine organic matter across all ocean basins. (b) The same dataset plotted as an Eyring function. Again the thermodynamic properties are consistent across a very wide geographical and temperature range. (Online version in colour.)

Figure 6.

(a) The identical dataset as in figure 4 with the Eastern Mediterranean dataset of Roether & Well [25] included. The remarkable difference is clear evidence of the consequences of the massive water mass overturning reported as the Eastern Mediterranean Transient [29,30], which negates the steady-state requirement for application of the Arrhenius equation. (b) The same data shown as an Eyring plot. The strictures on the use of this equation apply equally and the remarkable ongoing Eastern Mediterranean Transient is again clearly seen. (Online version in colour.)

The calculated rates appear oddly distributed: the Arrhenius plot shows that the deeper water rates in the ln(AOUR) range between −30 and −31.5 are more akin to the far colder water rates reported for the South Pacific region; and the upper layers with ln(AOUR) between −29 and −28.3 are more consistent with warmer waters in the upper layers of the Sargasso Sea.

The unusually high activation energy might be taken as an indication that the organic matter is extremely hard to oxidize, but that flies in the face of the observations reported above where a large supply of fresh dissolved organic carbon from deep water formation events is cited. An alternative hypothesis is that there is a significant mismatch between the microbial enzymes and their optimal temperature. The line indicates apparent high temperature sensitivity—as though the microbes present would function better with even a small increase in temperature.

Direct pressure effects too cannot be fully discounted and may be compounding. The review by Barlett [31] notes that ‘when the model mesophilic (atmospheric pressure-adapted) bacterium Escherichia coli is grown at a low temperature or a more acidic pH its growth is markedly more pressure-sensitive’, possibly reflecting the case given here.

One possible alternative explanation is simply that the observations here are characteristic of the Mediterranean being in a non-steady-state condition and that the microbial adjustments to numerous water mass transitions are still occurring. Thus, the strictures on the use of the Arrhenius equation will not hold. But we have no evidence for this, and a simple misprint in the form of the published rate equation might also be considered.

What is remarkable is the startling clarity with which this observation of what is probably associated with transient events stands out from the ‘normal’ open ocean cases. There is also the hint here of a possible testable hypothesis—if no further large-scale transient events occur, then over time the Eastern Mediterranean signal should relax back to the ‘normal’ line represented in figure 5.

Hints of a similar situation can be seen in the data from the Southeast Pacific transect reported by Sonnerup et al. [24]. Here, data from the northern segment of the line (approx. 30°–42° S) show an Arrhenius relationship consistent with other regions of the world's oceans. But from 43° to 54° S, the data show a trend towards much higher activation energy (tables 1 and 2). This region is close to the formation latitude of the Antarctic Intermediate Water, where again surface waters are rapidly subducted to depth.

A very different case of a rapid perturbation has been reported from the deep injection of massive amounts of methane from the tragic 2010 Deepwater Horizon oil spill. There, some 2 × 10¹¹ g of hydrocarbon gases (primarily methane) was rapidly injected into the deep waters of the Gulf of Mexico [32]. The rate of hydrocarbon oxidation was carefully tracked by Kessler et al. [33] by following and modelling the resulting oxygen anomaly created by ‘a vigorous deep-water bacterial bloom’ which rose and fell over a period of some 80 days. Clearly, such rapid changes would not be describable in terms of a steady-state rate constant.

In these cases where transients are observed, it is unlikely that the strictures on the use of the Arrhenius equation hold true, and these instances reveal the need for caution in applying these rules.

5. Discussion

There is no theoretical basis for the traditional representation of oceanic oxygen consumption rates solely as a function of depth [1], but there is also, as noted above, a well-known need for caution in applying the van't Hoff/Arrhenius/Eyring equations for ‘while it is futile to search for a “better” equation than that of Arrhenius, it becomes all the more necessary to understand the precise meaning of the Arrhenius parameters' [34]. Ocean scientists are as yet quite far from this goal and thus a brief history of the development of this field may be helpful.

The original thermodynamic concepts of van't Hoff [15] were extended by Arrhenius [16] to include the concept of an activated molecule. Eyring [5] made the advance of considering the reaction process to proceed through a transition state of an activated complex at which point the normal internal translational degrees of freedom of the molecule are at a minimum, and one added degree of translational energy (that required for crossing the potential energy barrier) is at a maximum. The Eyring formulation is particularly suitable for reactions at high pressures or in condensed phases, and this is the reason for its inclusion here. It is an early form of the mechanism used by enzymes which create an activated complex that serves to lower energy barriers for reaction and thus is equally appropriate for the microbial oxidation of organic matter.

In this early examination of the datasets above, we are well aware of the challenges in deriving and interpreting the ensemble activation energies in terms of specific processes. For example, we have not yet been able to normalize the rates to the quantity of organic carbon, or to that at a standard temperature. Both normalizations will be helpful for future progress.

Rate estimates are only usefully available in the upper 1 km or so of the ocean where reliable tracer data can be found—and rates in the abyssal ocean are far too slow for direct measurement. The difficulty in obtaining future tracer-based rate measurements is clear due to the continued decline of the valuable ³H signal, and the broad smearing of the ongoing invasion of CFC-11 and SF₆ rendering precise estimates difficult. Nonetheless, these are at this time the prime tools available.

Of all properties estimated, the Gibbs energy of activation (Δ^‡G) derived from the Eyring equation appears remarkably robust at 140.0 ± 2.8 kJ mol⁻¹ for all datasets. It is not known why this particular function should be so well defined and the ocean science community has little experience with this formulation. We do note the remarkable constancy of the Redfield ratio worldwide, suggesting that marine organic matter in the upper 1 km of the ocean has equally constant thermodynamic properties with respect to microbial oxidation.

The earlier, and more commonly used, Arrhenius activation energy (E_a) varies more widely; the best defined dataset from the Bermuda BATS location [1,2] yields an E_a of 86.5 kJ mol⁻¹. This is broadly consistent with the activation energy range for the temperature-dependent decay of organic matter in soils [4], which falls within the range of 110.0 kJ mol⁻¹ (Q₁₀ = 4.44) for the lowest observed rates, to as low as 57.7 kJ mol⁻¹ (Q₁₀ = 2.17) for the highest observed rates; that is, in soils E_a decreases as the respiration rate increases. We cannot yet report such a trend in oceanic data although it may well exist.

It is not yet known why such a large range of estimates is found for the entropy of activation Δ^‡S—but errors in deriving O₂ consumption rates from the CFC–SF₆ datasets may account for some of this, and in particular where we were forced to make estimates of the mean temperature associated with the average values given in published work only as within isopycnal bands [22,24]. As an alternative hypothesis, noted by one reviewer of this paper, a negative entropy of activation indicates a system with more order (for example, two reactants coming together in the transition state), whereas a positive entropy of activation indicates a system with increasing disorder (for example, a reactant dissociates into two or more compounds in the transition state). It is possible that the microbial processes responsible for these AOUR data in different ocean regimes are thus different. A possible interpretation for a positive entropy of activation is that, during microbial processing of organic matter, enzymes break up that organic matter into smaller molecules that are then degraded eventually to carbon dioxide.

We are not yet able to evaluate this interesting hypothesis using the existing datasets.

6. Conclusion

The sine qua non of describing climate change impacts on the ocean is that correct temperature-dependent terms are included. But in preparing this paper, we are forcibly struck as to how little consideration has been given by ocean chemists to the most basic property of the temperature dependence of microbial decomposition rates of organic matter in climate change predictions. It is difficult to escape the impression that the vast majority of ocean field programmes have over many decades been executed and reported with only a depth-dependent model in mind.

We have been able to make use, but with some difficulty, of tracer-based estimates of the required properties for the calculation of activation energies from which the more familiar Q₁₀ values can be derived. We have not been able to make use of more informally observed ocean deoxygenation rates from accumulated time-series data such as those reported by Nakanowatari et al. [6] and Whitney et al. [7]. Compelling though this evidence of the changing state of the ocean may be, these estimates are not formal rates such as those derived from fully qualified tracer-based ages.

It is difficult to tell how well these concepts are integrated into present-day ocean climate biogeochemical models. The CMIP5 model projections reported by Bopp et al. [35] contain forms of the Arrhenius equation, yet the model description by Dunne et al. [36] gives no indication of temperature-dependent microbial terms. A form of temperature-dependent terms was included in the model examination of Taucher & Oschlies [37] in their investigation of the direction of marine primary productivity change under global warming. For guidance they took the estimate of Eppley [38] of 1.88 for the average Q₁₀ of marine photosynthetic production of organic matter in the warm surface ocean, and, lacking evidence otherwise, applied this to microbial decomposition rates in the colder deep sea. Our derived Q₁₀ values are about a factor of 2 greater than this. In figure 7, we show the effects of climate change-related increases in T on the AOUR for a Q₁₀ of 1.88, and for a Q₁₀ of 3.63, for different warming scenarios. The effect is quite large.

Figure 7.

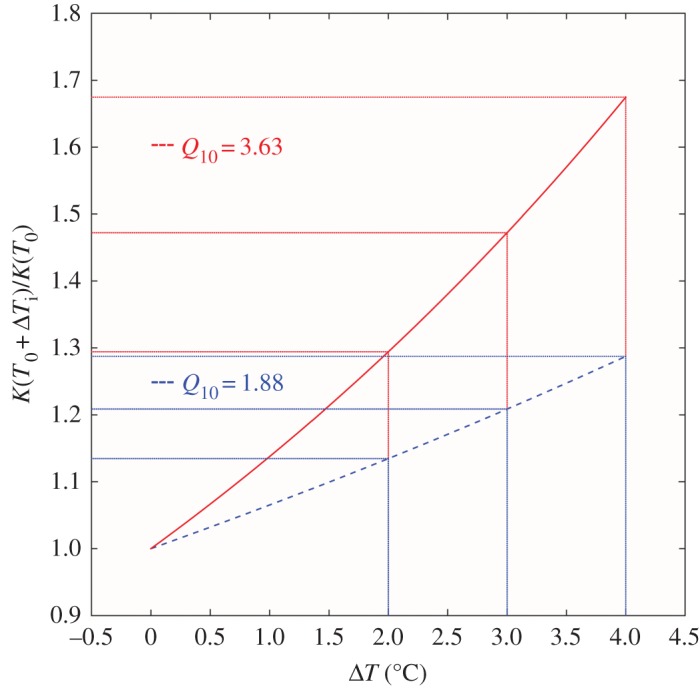
Sample calculation of the effect of warming on estimated AOURs for comparison of a Q₁₀ of 1.88 [39,40] (lower, blue dashed lines) and a Q₁₀ of 3.63 [1] (upper, red lines) for warming scenarios of 2°C, 3°C and 4°C. (Online version in colour.)

Taucher & Oschlies [37] reported separate model runs described as ‘TEMP’ and ‘NOTEMP’ and concluded that the model runs with, and without, temperature terms were little different with the caution that ‘temperature sensitivities of recycling processes and especially the microbial loop … are not considered in most other global models.’ The difficulty with this approach is that there really is no such thing as a ‘NOTEMP’ system in the physical world—temperature is omnipresent and is the primary driver of microbial rates. Models that rely on a depth-dependent set of functions simply masquerade temperature within a complex of depth-dependent terms and it is thus latently present; and separate climate warming functions cannot reliably be added on top of this.

One striking finding in this work has been the clear anomaly represented by the Mediterranean data of Roether & Well [25]. We have no reason to doubt the data obtained, but our interpretation that this may represent an oceanic transient event needs to be tested; a simple misprint is also possible. One clear observation is that essentially all of the AOUR datasets reported here and listed in tables 1 and 2 are from stable mid-ocean basin waters where the conditions for applying the Arrhenius equation can reasonably be met. But upwelling regimes are of great interest and they drive intense low-oxygen systems. There, non-steady-state conditions frequently occur and transient events are commonplace and thus water mass AOUR and age determination will be difficult. Nonetheless, the principle that higher temperatures will drive faster rates remains—although the net result may be offset by other factors.

The effort made in this paper to move beyond the unfortunate depth-based formulations of oceanic microbial rates that have persisted for so very long has at this moment a very simple classical look reaching back to the late nineteenth and early twentieth centuries for the basic rules; these are well established and cannot be challenged. But we should now ask if it is possible to fast forward to the modern world in linking chemical physics and molecular biology with climate change science. One recent review by Mock et al. [41] addressed this point and specifically noted the temperature dependence of metabolic rates.

The challenge faced by molecular biologists is that, although a very large number of genes can be detected in marine samples, it is difficult to know which ones are active at any one time. But in the big picture, this may not matter for microbial populations that can rapidly change as chemical opportunity arises.

For a specific example of microbial complexity within localized microenvironments, consider the report by Canfield et al. [42] of cryptic sulfur cycling within the intense oxygen minimum waters off the Chilean coast. This is consistent with the broad description of intense local chemical gradients created by microbial consortia reviewed by Wright et al. [23]. From a chemical physics perspective, the matter of bacterial decision-making is consistent with maximizing local chemical energy gains where microbes constantly ‘taste’ their immediate microenvironment, computing the benefits, and switching on/off states; a useful review of this was recently given by Kondev [43].

We have focused here on the temperature dependence of rates derived from ocean water column measurements. The corollary is the effect of temperature on the ‘remineralization rates' of sinking particles or organic matter. There too the focus on purely depth-dependent models with no temperature terms is astonishing. The early work by Martin et al. [44] described a particle flux decreasing exponentially with depth, and forms of that equation have persisted ever since. For example, the recent particle flux model by DeVries et al. [45] contains no temperature terms whatsoever.

For the subject matter here, it is clear that marine microbial populations have abundant armamentaria to cope with changing oxygen conditions and are capable of driving chemical reactions far below zero O₂ levels, and that all of these microbial reactions have a basic T dependence consistent with Arrhenius/Eyring rules that is largely independent of depth. The future of ocean oxygen losses under climate change will be controlled by a combination of physical stratification, thermally enhanced microbial oxidation rates and solubility changes. Most disturbingly, these impacts appear to be additive. We do note that the longevity of these effects may differ—for example, the stratification caused by the meltwater pulse at the end of the last ice age has long since dissipated, but the thermally enhanced oxidation rates and solubility reductions remain. Purely depth-dependent biogeochemical processes as are frequently modelled today are not a significant factor.

We note that although the subject matter here is the observable decline in oceanic oxygen levels, this is simply the end effect. The controlling process is the increased rate of consumption of marine organic matter with temperature. In the deep-ocean competition between microbes and higher life forms for accessing this chemical energy, microbes will gain an advantage in warmer waters, and thus even in quite well-oxygenated waters there will be less chemical energy available in the deep sea for the animal food chain. It is disturbing to realize that after decades of work we are still far from understanding this problem.

Finally, we have been asked if there is likely to be experimental ‘proof’ of this approach. There is no need to ‘prove’ the basic Arrhenius/Eyring functions for they have been established as fundamental science for decades; but their applicability in any one situation can be questioned. Direct incubation experiments all run into problems that local concentration effects appear to conflict with results obtained from the bulk fluid state [39,46], and thus the tracer-based approach gives invaluable insights today. Unfortunately, the continued availability of useful tracer-based rates from the ocean is no sure thing due to the passage of time, the decay of tritium, the uncertainties of the input function and the broadening with time of tracers. Thus, novel approaches that are based on sound science would be welcome indeed.

We should note that while this paper draws attention to the relative lack of formal temperature-dependent rate terms in describing contemporary oceanic oxygen declines, we readily acknowledge that there have been specific examples of the use of the Arrhenius function in paleoceanographic [40,47] examinations of past climate change.

Data accessibility

All data used in this paper were derived from published literature. We include a full data table in electronic supplementary material in support of the figures provided.

Authors' contributions

The authors contributed equally to the production of this paper. Both authors gave their final approval for publication.

Competing interests

The authors declare no competing interests.

Funding

We gratefully acknowledge the support to MBARI from the David and Lucile Packard Foundation in producing this work.