Protein adsorption on nanoparticles: model development using computer simulation

Abstract

The adsorption of proteins on nanoparticles results in the formation of the protein corona, the composition of which determines how nanoparticles influence their biological surroundings. We seek to better understand corona formation by developing models that describe protein adsorption on nanoparticles using computer simulation results as data. Using a coarse-grained protein model, discontinuous molecular dynamics simulations are conducted to investigate the adsorption of two small proteins (Trp-cage and WW domain) on a model nanoparticle of diameter 10.0 nm at protein concentrations ranging from 0.5 to 5 mM. The resulting adsorption isotherms are well described by the Langmuir, Freundlich, Temkin and Kiselev models, but not by the Elovich, Fowler–Guggenheim and Hill–de Boer models. We also try to develop a generalized model that can describe protein adsorption equilibrium on nanoparticles of different diameters in terms of dimensionless size parameters. The simulation results for three proteins (Trp-cage, WW domain, and GB3) on four nanoparticles (diameter = 5.0, 10.0, 15.0, and 20.0 nm) illustrate both the promise and the challenge associated with developing generalized models of protein adsorption on nanoparticles.

1. Introduction

We investigate models that can be used to describe protein adsorption on nanoparticles via computer simulation. Nanoparticles are used widely for a variety of biological and medical applications such as drug delivery [1], sensors [2] and disease diagnostics [3, 4]. When a nanoparticle enters a biological fluid such as blood, proteins adsorb on it spontaneously, forming a layer called the protein corona [5]. In essence, it is the protein corona, instead of the nanoparticle, that interacts with the biological surroundings and determines the nanoparticle’s biological impact and fate [6, 7]. We seek to develop models that can describe protein adsorption on nanoparticles so as to better understand the mechanisms that govern formation of the protein corona and predict its composition.

Several experimental studies have been conducted on the adsorption of specific proteins on nanoparticles in an effort to develop empirical models of protein adsorption on nanoparticles. Calzolai et al [8] investigated the interactions between human ubiquitin and a gold nanoparticle using a combination of NMR, chemical shift perturbation analysis, and dynamic light scattering. They proposed an empirical expression that estimates the maximum number of ubiquitin molecules on a gold nanoparticle based on the radii of the ubiquitin molecule, the nanoparticle, and the ubiquitin-nanoparticle complex. Wang et al [9] investigated the adsorption of six types of proteins on a gold nanoparticle with a diameter of 15.0 nm using NMR spectroscopy. They correlated the number of proteins adsorbed on the gold nanoparticle with the radius of gyration of the proteins and the size of the nanoparticle. Though focusing on a single type of protein and/or certain nanoparticles, these experimental efforts set up a basis for us to develop universal models that can be used to predict protein adsorption on nanoparticles.

Theoretical and simulation studies have also been conducted with the aim of explaining and predicting protein adsorption on nanoparticles or other substrates. The Szleifer group [10, 11] developed a theoretical approach based on mean field theory to describe protein adsorption on surfaces with grafted polymers. More recently, Oberle et al [12] developed a cooperative binding model for competitive adsorption of proteins on a soft polymeric layer. Despite the fact that the protein representation had to be simplified significantly, the models developed by these two groups describe some systems quite well and can be used to guide the engineering of surfaces to tune protein adsorption. Although most computer simulation studies of protein adsorption have focused on how a single protein interacts with the substrate [13–16], several simulation-based investigations of the adsorption of multiple proteins on nanoparticles have been conducted. For instance, Tavanti et al [17] investigated the formation of a ubiquitin corona on nanoparticles of size 10–26 nm using Go-type coarse-grained modeling. They also investigated the adsorption of insulin on the same type of nanoparticle with or without the presence of fibrinogen [18]. Li et al [19] used coarse-grained modeling to characterize the apolipoprotein corona on silver nanoparticles. Ding et al [20] simulated the interactions between human serum albumin and nanoparticles using dissipative particle dynamics simulations. Lopez et al [21] investigated the adsorption of single α1-antitrypsin, human serum albumin, transferrin, immunoglobulin G, fibrinogen and α2-macroglobulin on a model nanoparticle using coarse-grained modeling. Ding et al [22] explored the ubiquitin corona on silver nanoparticles using multiscale modeling. These simulations provide useful insights that help us to understand the adsorption of proteins on nanoparticles.

The development of adsorption models has been a quest in chemical physics for over a century [23, 24]. Quite a few theoretical and empirical models have been developed to describe the adsorption of molecules on a variety of substrates such as active carbon [25], metal-organic frameworks [26], zeolites [27] and carbon nanotubes [28]. The adsorbates in these models are generally small molecules and the adsorbents are usually flat surfaces or porous materials. Proteins possess much more complex chemical and physical features than small molecules, and nanoparticles have curvature and finite surface area, making protein adsorption on nanoparticles fundamentally different from small molecule adsorption on flat substrates or in nanoporous materials. It would be interesting to examine how well these classical adsorption models describe the adsorption behavior of proteins on nanoparticles.

It is also interesting to ask if it is possible to develop generalized adsorption models that can describe the adsorption of proteins on nanoparticles of varying chemical and physical features. Generalized models can help us distinguish features that are common in a wide spectrum of protein-nanoparticle systems from those that are unique to a specific protein/nanoparticle system. Generalized adsorption models could be constructed in terms of dimensionless variables that characterize the physical properties of the proteins and the nanoparticles with some adjustable parameters that describe the chemical features of each system. There are two challenges associated with developing such generalized models: (1) choosing parameters that characterize the most important chemical and physical features of protein-nanoparticle systems, and (2) obtaining sufficient quantitative protein adsorption data on a wide spectrum of protein-nanoparticle systems. Our use of computer simulation data on model protein-nanoparticle systems is one way of attempting to meet the second challenge.

Here we present our efforts to develop models of protein adsorption on nanoparticles using data obtained from computer simulation of model protein-nanoparticle systems. We analyze the adsorption of three types of proteins, Trp-Cage miniprotein (Trp PDB ID 1L2Y), Pin1 WW domain (WW PDB ID 2M8I) and histidine-containing phospho-transfer protein (GB3 PDB ID: 1PTF) on model nanoparticles with diameters from 5 to 20 nm at protein concentrations 0.5–10 mM using discontinuous molecular dynamics simulations and a coarse-grained protein model developed by us [29]. The model proteins in this work are constrained to be close to their native state conformation. Using our simulation data, we first investigate how well seven known isothermal adsorption models (Langmuir, Freundlich, Temkin, Kiselev, Elovich, Fowler–Guggenheirm and Hill–de Boer) describe the adsorption of two proteins (Trp and WW) on a model nanoparticle with a diameter of 10.0 nm. Then we attempt to develop a generalized model of protein adsorption in terms of dimensionless variables that describe the adsorption equilibrium of three proteins (Trp, WW and GB3) on four model nanoparticles with diameters 5.0, 10.0, 15.0 and 20.0 nm. Section 2 presents the details of the coarse-grained model and simulation process; section 3 lists the expressions for seven known adsorption isotherm models for the equilibrium adsorption coverage in term of the equilibrium concentrations and describes them briefly, section 4 presents the results and discussion, and section 5 describes our conclusions.

2. Simulation model and method

We use an implicit-solvent two-bead-per-residue model developed in our group [29] to represent proteins. The two-bead-per-residue representation is a good compromise between describing the full chemical heterogeneity of individual amino-acid residues and minimizing the number of beads in the system. Each amino-acid residue is represented by one bead (C_α) at the position of the Cα atom and another bead (C_β) at the center of mass of the sidechain. Glycine and pro-line are represented by a bead at the position of the Cα atom. The nanoparticle is modeled as a single sphere.

The potential energy of the simulation system accounts for the intermolecular bead–bead interactions, and the intramolecular bead–bead bond/virtual bond and non-bonded interactions. The intramolecular virtual bond interactions are used to maintain the protein near its native state configuration. A detailed description about these virtual bonds in the proteins will be given later.

The intermolecular bead–bead interactions between proteins and between proteins and the nanoparticle are described by a square well/shoulder or hard sphere potential

$$\{\begin{array}{l}{U}_{\text{inter}}(r)=\infty ,r\le {\sigma }_1\hfill \\ U_{\text{inter}}(r)=\epsilon ,{\sigma }_1<r<{\sigma }_2\hfill \\ U_{\text{inter}}(r)=0,r\ge {\sigma }_2\hfill \end{array}$$ (1)

where r is the distance between the bead centers, σ₁ is a geometric parameter that represents the inner boundary of the square well/shoulder, σ₂ is a geometric parameter that represents the outer boundary of the square well/shoulder, and ε is an energetic parameter that represents the shoulder height or well depth of the potential. A hard sphere potential only has the parameter σ₁, which represents the position of the hard wall. The values of parameters σ₁, σ₂ and ε are obtained from atomistic molecular dynamics simulations of 210 amino acid pairs in explicit solvent [29]. We calibrated the energetic parameter using the experimental value of the second virial coefficient of lysozyme; the details are described in our previous paper [29]. Tables S1–S3 (stacks.iop.org/JPhysCM/28/414019/mmedia) list their values after the calibration.

The intramolecular interactions between beads that do not have a bond or virtual bond between them are described by a hard-sphere potential to prevent overlap,

$$\{\begin{array}{ll}{U}_{\text{intra}}(r)=\infty ,\hfill & r\le 0.8{\sigma }_1\hfill \\ U_{\text{intra}}(r)=0,\hfill & r>0.8{\sigma }_1.\hfill \end{array}$$ (2)

The intramolecular bead–bead bond/virtual bond interactions are described by a double-wall potential

$$\{\begin{array}{ll}{U}_{\text{bond}}(r)=\infty ,\hfill & r\le (1-\delta )\sigma \hfill \\ U_{\text{bond}}(r)=0,\hfill & (1-\delta )\sigma <r<(1+\delta )\sigma \hfill \\ U_{\text{bond}}(r)=\infty ,\hfill & r\ge (1+\delta )\sigma \hfill \end{array}$$ (3)

Where σ is the equilibrated distance between the bead centers when the protein is in its native state, and δ is a parameter that adjusts the fluctuation of the bond length. The bonds connect adjacent Cα beads, and Cα and Cβ beads on the same amino acid residue. The virtual bonds can be divided into local and non-local ones, depending on the difference between the indexes of the two beads on the residue sequence: the local virtual bonds connect beads whose index difference is less than four, and the non-local ones connect beads far away from each other along the amino-acid sequence. The bonds and local virtual bonds are used to maintain the secondary structure, and the non-local virtual bonds are used to maintain the tertiary and quaternary structures of a protein. Our previous study discussed how to determine the value of parameter δ for the bonds, and local and non-local virtual bonds [29]. Table 1 lists the PDB ID, numbers of residues, beads and bonds/virtual bonds, and the radius of gyration for the three model proteins. Table 2 lists the values of δ for the local and non-local virtual bonds and the types of virtual bonds considered in these two categories, where C_α[i] and C_β[i] refer to the backbone and side-chain bead of the ith residue.

Table 1.

The protein models for Trp, WW and GB3.

Protein	PDB ID	Number of residues	Number of beads	Number of bonds/virtual bonds	Radius of gyration (nm)a
Trp	1L2Y	20	33	98	0.75
WW	2M8I	43	79	262	1.08
GB3	1PTF	87	164	572	1.15

^aThe radius of gyration was calculated using the PDB utility servers provided by the Bax group at NIH [30].

Table 2.

Bonds/virtual bonds considered in the models for the three proteins.

	Bonds & local virtual bonds (δ = 0.05)	Non-local virtual bonds(δ = 0.10)
Trp	Cα[i] − Cα[i + 1]	Cα[i] − Cα[i + 10] (i = i + 2)
	Cα[i] − Cα[i + 2]	Cα[i] − Cα[i + 20] (i = 2, i = i + 4)
	Cα[i] − Cα[i + 3]	Cβ[i] − Cβ[i + 10] (i = i + 4)
	Cβ[i] − Cα[i]	Cβ[i] − Cβ[i + 20] (i = 2, i = i + 4)
	Cβ[i] − Cα[i − 1]
	Cβ[i] − Cα[i + 1]
WW	The same as for Trp	Cα[i] − Cα[i + 10] (i = i + 2)
		Cα[i] − Cα[i + 20] (i = 2, i = i + 4)
		Cα[i] − Cα[i + 40] (i = 2, i = i + 16)
		Cβ[i] − Cβ[i + 10] (i = i + 4)
		Cβ[i] − Cβ[i + 20] (i = 2, i = i + 4)
GB3	The same as for Trp	Cα[i] − Cα[i + 10] (i = i + 2)
		Cα[i] − Cα[i + 20] (i = 2, i = i + 4)
		Cα[i] − Cα[i + 40] (i = 2, i = i + 16)
		Cα[i] − Cα[i + 60] (i = 2, i = i + 32)
		Cβ[i] − Cβ[i + 10] (i = i + 4)
		Cβ[i] − Cβ[i + 20] (i = 2, i = i + 4)

As stated above, the interactions between the nanoparticle bead and C_α/C_β beads are described as a square well/shoulder potential with geometric parameters σ₁, σ₂, and energetic parameter ε, as explained in equation (1). The geometric parameter σ₁ for all nanoparticle- C_α/C_β bead interactions should be the sum of the nanoparticle radius r_NP and the bead hard sphere radius r_bead. Since r_NP ≫ r_bead, here we set σ₁ equal to the nanoparticle radius r_NP. Our ongoing study about the binding of amino acids on gold nanoparticles with different sizes showed that the interaction energy between the amino acid backbone/sidechains and gold nanoparticles becomes negligible around 0.5 nm, independent of the nanoparticle size. Thus the well/shoulder width for all nanoparticle- C_α/C_β bead interactions is set equal to 0.5 nm. That is to say, σ₂ = σ₁ + 0.5. The model nanoparticle is assumed to be nonpolar, the well depth/shoulder height ε for the nanoparticle and C_α/C_β beads interactions is set equal to five times the well depth/shoulder height ε between the alanine side-chain bead and the same type of bead, which can be found in table S3.

The initial configuration in the system is established by placing a nanoparticle at the center of a cubic box and adding the desired number of proteins at random positions. The size of the cubic box is calculated based on the required protein concentration and the number of proteins in the system. The initial distance between beads belonging to different entities must be at least 4.0 nm to avoid any artificial aggregation. The system’s initial configuration was generated using Packmol [31]. Table 3 lists the number of proteins in the simulation systems in this work. Figure 1 shows the initial configuration in a simulation of 800 Trp-cage proteins and a nanoparticle with a diameter 10.0 nm.

Table 3.

Nanoparticle size r_NP, number of proteins N, box size L, initial protein concentration C_initial, and protein volume faction η = V_protein/V_total.

Protein	rNP (nm)	N	L (nm)	Cinitial (mM)	η
Trp	5.0	100	31	5.0	0.030
	10.0	40	49	0.5	0.003
	10.0	80	49	1.0	0.006
	10.0	120	49	1.5	0.009
	10.0	160	49	2.0	0.012
	10.0	200	49	2.5	0.015
	10.0	240	49	3.0	0.018
	10.0	280	49	3.5	0.021
	10.0	320	49	4.0	0.024
	10.0	360	49	4.5	0.027
	10.0	400	49	5	0.030
	10.0	800	49	10	0.060
	15.0	825	63	5	0.030
	20.0	1600	79	5	0.030
GB3	5.0	100	31	5	0.120
	10.0	400	49	5	0.120
	15.0	825	63	5	0.120
	20.0	1600	79	5	0.120
WW	5.0	100	31	5.0	0.0720
	10.0	40	49	0.5	0.0072
	10.0	80	49	1.0	0.0144
	10.0	120	49	1.5	0.0216
	10.0	160	49	2.0	0.0288
	10.0	200	49	2.5	0.0360
	10.0	240	49	3.0	0.0432
	10.0	280	49	3.5	0.0504
	10.0	320	49	4.0	0.0576
	10.0	360	49	4.5	0.0648
	10.0	400	49	5	0.0720
	15.0	825	63	5	0.0720
	20.0	1600	79	5	0.0720

Note: Here $V_{\text{protein}}=N\frac{4}{3}\pi r_{Pr}^3$, where N is the number of proteins in the system, r_Pr is the radius of gyration of a protein, and V_total = L³, where L is the simulation box length.

Figure 1.

Snapshot of an initial configuration containing 800 Trp-cage proteins (C_α beads in blue and C_β beads in red) and a nanoparticle (in green, diameter = 10.0 nm).

Discontinuous molecular dynamics (DMD) simulations were conducted in the canonical (NVT) ensemble using a code developed in our group. Details of the DMD simulation procedure can be found in the literature [32]. The systems in this work were simulated using reduced units (energy unit ε* = 2.5 kJ mol⁻¹, length unit σ* = 1.0 nm, mass unit m* is 1.0 Da). The reduced temperature was defined as k_BT/ε*, the reduced time was defined as ${\sigma }^{\ast }\sqrt{m^{\ast }/{\epsilon }^{\ast }}$, and the other properties were also converted to reduced units. The reduced temperature of the system was maintained at 1.0, which is equivalent to 298 K, using the Andersen thermostat [33]. The simulation was run for 10–600 billion collisions, depending on the number of steps needed for the proteins to adsorb on the nanoparticle and reach equilibrium. The trajectory was saved every 50, 100 or 200 million steps, depending on the average time between successive collisions. The simulations of systems containing the Trp or WW proteins and a nanoparticle (diameter = 10.0 nm) with initial concentrations ranging from 0.5 to 5.0 mM were repeated twice.

3. Adsorption isotherm models

Seven adsorption isotherm models are considered in this work. They are the Langmuir [34], Freundlich [35], Temkin [36], Kiselev [37], Elovich [38], Fowler–Guggenheim [39] and Hill–de Boer [40] models. Here we list each model’s expression for the equilibrium adsorption coverage θ_eq of proteins in term of the equilibrium protein concentrations C_eq and describe them briefly.

3.1. Langmuir model

The Langmuir model can be written as

$${\theta }_{\text{eq}}=\frac{k{C}_{\text{eq}}}{1+k{C}_{\text{eq}}}$$ (4)

where θ_equation is the equilibrium adsorption coverage, C_eq is the equilibrium concentration of adsorbate in bulk phase, and k is the Langmuir equilibrium constant. In this work we slightly modify this expression to become

$${\theta }_{\text{eq}}=\frac{k{C}_{\text{eq}}}{1+\alpha k{C}_{\text{eq}}}$$ (5)

Where α is an adjustable parameter. This will be explained later when we deploy the model to describe the adsorption of Trp and WW on the nanoparticle with a diameter of 10.0 nm. A linearized version of the expression for the revised Langmuir term is shown in Table 4.

Table 4.

Linear forms for the seven isothermal adsorption models.

Name	Linear-form expression
Langmuir	$\frac{1}{{\theta }_{\text{eq}}}=\frac{1}{k{C}_{\text{eq}}}+\frac{1}{\alpha }$
Freundlich,	ln θeq = ln KF + α ln Ceq
Temkin,	${\theta }_{\text{eq}}=\frac{RT}{\mathrm{\Delta }Q}ln{K}_0+\frac{RT}{\mathrm{\Delta }Q}ln{C}_{\mathrm{e}}$
Kiselev,	$\frac{1}{C_{\text{eq}}(1-{\theta }_{\text{eq}})}=\frac{k_1}{{\theta }_{\text{eq}}}+k_1{k}_n$
Elovich,	$ln\frac{{\theta }_{\text{eq}}}{C_{\text{eq}}}=ln{K}_{\mathrm{E}}-{\theta }_{\text{eq}}$
Fowler–Guggenheim	$ln\frac{C_{\text{eq}}(1-{\theta }_{\text{eq}})}{{\theta }_{\text{eq}}}=-ln{K}_{\text{FG}}+\frac{2{\theta }_{\text{eq}}W}{RT}$
Hill–de Boer	$ln\frac{C_{\text{eq}}(1-{\theta }_{\text{eq}})}{{\theta }_{\text{eq}}}-\frac{{\theta }_{\text{eq}}}{1-{\theta }_{\text{eq}}}=-ln{K}_1-\frac{K_2{\theta }_{\text{eq}}}{RT}$

3.2. Freundlich model

$${\theta }_{\text{eq}}=K_{\mathrm{F}}{C}_{\text{eq}}^{\alpha }$$ (6)

Where K_F is a constant that indicates the adsorption capacity of the substrate, and α is a constant that indicates the adsorption intensity. The linearized expression for the Freundlich model is shown in Table 4.

3.3. Temkin model

$${\theta }_{\text{eq}}=\frac{RT}{\mathrm{\Delta }Q}ln{K}_0{C}_{\mathrm{e}}$$ (7)

where R is the universal gas constant, T is the temperature, ΔQ is the desorption energy, and K₀ is the Temkin equilibrium constant. The linearized expression for the Temkin model is shown in Table 4.

3.4. Kiselev model

$$k_1{C}_{\text{eq}}=\frac{{\theta }_{\text{eq}}}{(1-{\theta }_{\text{eq}})(1+k_n{\theta }_{\text{eq}})}$$ (8)

where k₁ is the Kiselev equilibrium constant, and k_n is a constant representing complex formation between adsorbed molecules. The linearized expression for the Kiselev model is shown in Table 4.

3.5. Elovich model

$${\theta }_{\text{eq}}=K_{\mathrm{E}}{C}_{\text{eq}}exp(-{\theta }_{\text{eq}})$$ (9)

where K_E is the Elovich equilibrium constant. The linearized expression for the Elovich model is shown in Table 4.

3.6. Fowler–Guggenheim model

$$K_{\text{FG}}{C}_{\text{eq}}=\frac{{\theta }_{\text{eq}}}{1-{\theta }_{\text{eq}}}exp\left(\frac{2{\theta }_{\text{eq}}W}{RT}\right)$$ (10)

where K_FG is the Fowler–Guggenheim equilibrium constant, and W is the interaction energy between adsorbed molecules. The linearized expression for the Fowler–Guggenheim model is shown in Table 4.

3.7. Hill–de Boer model

$$K_1{C}_{\text{eq}}=\frac{{\theta }_{\text{eq}}}{1-{\theta }_{\text{eq}}}exp\left(\frac{{\theta }_{\text{eq}}}{1-{\theta }_{\text{eq}}}-\frac{K_2{\theta }_{\text{eq}}}{RT}\right)$$ (11)

Where K₁ is the Hill–de Boer constant and K₂ is a constant representing the interaction energy between adsorbed molecules. The linearized expression for the Hill–de Boer model is shown in Table 4.

4. Results and discussion

4.1. Adsorption isotherm model for Trp and WW proteins

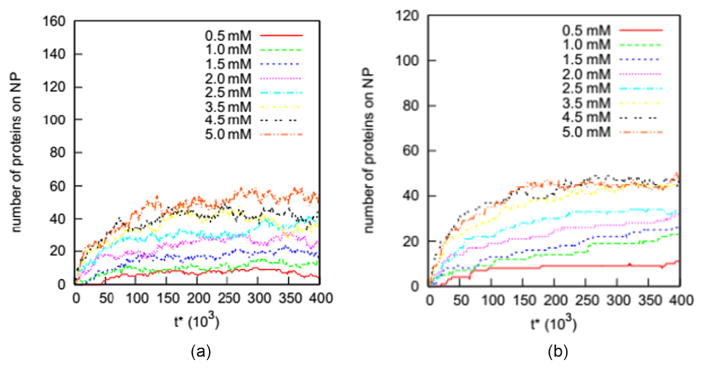
In this section we examine how well the seven adsorption isotherm models (Langmuir [34], Freundlich [35], Temkin [36], Kiselev [37], Elovich [38], Fowler–Guggenheim [39] and Hill–de Boer [40]) describe the adsorption of proteins on a nanoparticles. As described earlier, we conducted two independent sets of simulations for the Trp and WW proteins on the nanoparticle (diameter = 10.0 nm) at initial concentrations ranging from 0.5 to 5 mM. These two simulation sets are named Case 1 and Case 2. Figure 2 shows the number of Trp and WW proteins on the nanoparticle (diameter = 10.0 nm) versus simulation time for solutions with initial concentrations ranging from 0.5 to 5.0 mM in Case 1. A protein is defined to be adsorbed on the nanoparticle if any of its beads are within 0.5 nm of the nanoparticle surface. This distance criterion, 0.5 nm, is equal to the well width of the potential energy between the nanoparticle and any protein bead. The flat regions on all these curves indicate that the adsorption of proteins on the nanoparticle has reached its equilibrium state.

Figure 2.

Number of (a) Trp and (b) WW proteins on the nanoparticle (diameter = 10.0 nm) versus reduced time (t*) for systems with initial concentrations ranging from 0.5 to 5.0 mM.

Tables 5 and 6 list the number of adsorbed proteins in the equilibrium state N_eq for the Trp-10.0 nm nanoparticle and WW-10.0 nm nanoparticle cases at initial concentrations C_initial ranging from 0.5 to 5.0 mM for both Case 1 and Case 2. In general, N_eq increases as the protein concentration increases, consistent with the adsorption behavior of small molecules on flat substrates [23]. This suggests the possibility of describing the adsorption of proteins using classical adsorption models. Tables 5 and 6 indicate that while Trp does not seem to reach its maximal adsorption capacity even at 4.0 mM concentration, WW reaches its maximal adsorption amount on the nanoparticle at a concentration around 3.0 mM. The higher saturation concentration for Trp could be due to its smaller size. As shown in Table 1, the radius of gyration of Trp is 0.75 nm, while that of WW is 1.08 nm. A WW protein then could occupy more surface area of the nanoparticle than a Trp. Another possible reason is that Trp-nanoparticle interactions are weaker than WW-nanoparticle interactions. However, the analysis of fitted parameters in the seven isotherm models indicates that the Trp-nanoparticle interactions may be stronger than that of WW-nanoparticle interactions. We will discuss this in detail when we analyze the fitted values for the parameters in the seven adsorption isotherm models.

Table 5.

Equilibrium state of Trp protein adsorbed on the nanoparticle (diameter = 10.0 nm).

Cini (mM)	Case 1			Case 2
	Ceq (mM)	Neq	θeq	Ceq (mM)	Neq	θeq
0.5	0.39	9	0.051	0.39	9	0.051
1.0	0.83	14	0.079	0.74	21	0.12
1.5	1.2	24	0.14	1.19	25	0.14
2.0	1.69	25	0.14	1.63	30	0.17
2.5	2.08	34	0.19	2.03	38	0.21
3.0	2.54	37	0.21	2.51	39	0.22
3.5	3	40	0.23	2.96	43	0.24
4.0	3.44	45	0.25	3.46	43	0.24
4.5	4.01	49	0.28	3.9	48	0.27
5.0	4.3	58	0.33	4.35	52	0.29
10.0	9.25	60	0.34

Table 6.

Equilibrium state of WW proteins adsorbed on the nanoparticle (diameter = 10.0 nm).

Cini (mM)	Case 1			Case 2
	Ceq (mM)	Neq	θeq	Ceq (mM)	Neq	θeq
0.5	0.38	10	0.12	0.36	11	0.13
1.0	0.76	19	0.22	0.71	23	0.27
1.5	1.12	26	0.31	1.12	26	0.31
2.0	1.64	29	0.34	1.6	32	0.38
2.5	2.06	35	0.41	2.1	32	0.38
3.0	2.61	31	0.36	2.5	40	0.47
3.5	3	40	0.47	2.95	44	0.52
4.0	3.44	45	0.53	3.45	44	0.52
4.5	4	40	0.47	3.93	46	0.54
5.0	4.44	45	0.53	4.44	45	0.53

We also investigate the adsorption of Trp on the nanoparticle with a diameter of 10.0 nm in a solution at 10.0 mM to try to find out the solution concentration at which the adsorption of Trp reaches its maximal amount. The number of Trp proteins adsorbed on the 10.0 nm nanoparticle at 10.0 mM is also shown in Table 5. We can see that the number of proteins adsorbed at 10.0 mM is similar to that at 5.0 mM, suggesting that the coverage at 5.0 mM could be the maximal coverage for Trp on the 10.0 nm nanoparticle.

We calculate C_eq and θ_equation for the systems listed in tables 5 and 6 in order to test how well the seven classical adsorption models describe the adsorption of Trp and WW proteins on the nanoparticle with a diameter of 10.0 nm. The value of C_eq is calculated as C_initial(N − N_eq)/N. The value of θ_equation is calculated as N_eq/N_max, where N_max is the maximal allowed number of proteins on the nanoparticle.

$$N_{max}=\frac{4r_{\text{NP}}^2}{r_{\text{Pr}}^2}.$$ (12)

Here N_max is the number of proteins we need to cover 100% of the nanoparticle surface if we assume both the proteins and the nanoparticles are hard spheres. Tables 5 and 6 list the values of θ_equation and C_eq for the Trp and WW systems.

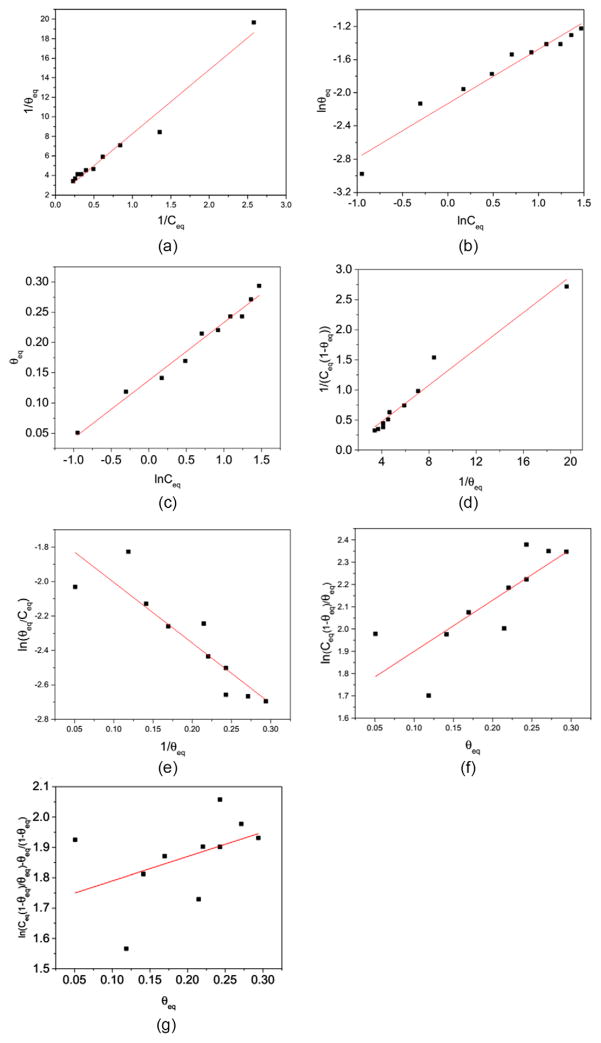
We examine how well the seven adsorption isotherm models fit the simulation data on θ_equation and C_eq for Trp and WW on the nanoparticle with a diameter of 10.0 nm. Figure 3 shows how well the linearized forms for the seven models fit the simulation results for the number of Trp proteins adsorbed on the 10.0 nm nanoparticle in the Case 2 simulations. The values for the coefficients of determination (R²) are 0.96, 0.94, 0.98, 0.96, 0.78, 0.61 and 0.09 for the Langmuir, Freundlich, Temkin, Kiselev, Elovich, Fowler–Guggenheim and Hill–de Boer models. Similar values for R² are found for the Case 1 simulations for Trp and Case 1 and Case 2 simulations for WW. The R² values indicate that the Langmuir, Freundlich, Temkin and Kiselev models fit the simulation results for Trp and WW well, while the models with an exponential term, including the Elovich, Fowler–Guggenheim and Hill–de Boer models, do not fit the results well.

Figure 3.

The fitting of the adsorption data for Trp in Case 2 with the linearized forms of the seven adsorption models (a) Langmuir, (b) Freundlich, (c) Temkin, (d) Kiselev, (e) Elovich, (f) Fowler–Guggenheim and (g) Hill–de Boer. The small circles are the data derived from simulation results and the lines are calculated using the linearized expressions with fitted parameters.

Table 7 lists the fitted values of the various model parameters from the intercept and slope for the Langmuir, Freundlich, Temkin and Kiselev models. Comparison between the values of the parameters for Trp and WW provide some insights into the adsorption behavior of Trp and WW on the nanoparticle with a diameter of 10.0 nm. For instance, in the Langmuir model, WW has a larger k than Trp. In the Freundlich model, the K_F parameter for WW is two times that for Trp. In the Temkin model, the value of K₀ for WW is larger than that for Trp. In the Kiselev model, the value of the k₁ parameter for WW is also larger than that for Trp. The comparison of these parameters in the four models indicates that the equilibrated coverage of WW on the 10.0 nm nanoparticle grows with the protein concentration at a higher rate than that for Trp. The higher coverage to concentration ratio for WW may be due to its larger size, which makes a WW protein able to cover more nanoparticle surface area than a Trp. The higher coverage to concentration ratio of WW also partially explains why WW reaches its maximal adsorption amount on the 10.0 nm nanoparticle at a concentration lower than Trp.

Table 7.

Values of fitted parameters of Trp and WW.

	Trp	WW
Langmuir	α = 1.71 ±0.23, k = 0.15 ± 0.01	α = 1.28 ± 0.02, k = 0.45 ±0.05
Freundlich	α = 0.71 ± 0.06, KF = 0.11 ± 0.01	α = 0.64 ± 0.16, KF = 0.26 ± 0.02
Temkin	ln K0 = 1.43 ±0.24, $\frac{RT}{\mathrm{\Delta }Q}=0.10\pm 0.01$	ln K0 = 1.72 ± 0.04, $\frac{RT}{\mathrm{\Delta }Q}=0.16\pm 0.0$
Kiselev	k1 = 0.14 ± 0.01, kn = −1.0 ± 0.3	k1 = 0.46 ± 0.05, kn = −0.52 ± 0.01

The values of the parameter ΔQ in the Temkin model also indicate that desorption of a Trp from the nanoparticle with a diameter of 10.0 nm may be harder than that for a WW. The parameter ΔQ is the desorption energy and should reflect the level of the adsorbate–adsorbate interactions, as mentioned in section 3. From Table 7, we see that the value of ΔQ for Trp is larger than that for WW, which indicates that the desorption energy for Trp is higher than that for WW. In other words, the adsorption of Trp proteins on the 10.0 nm nanoparticle is more stable than that of WW proteins. This could be because the Trp-nanoparticle interaction is stronger than the WW-nanoparticle interaction, or because the Trp–Trp interactions are stronger than the WW–WW interactions in the vicinity of the nanoparticle.

4.2. Generalized adsorption model

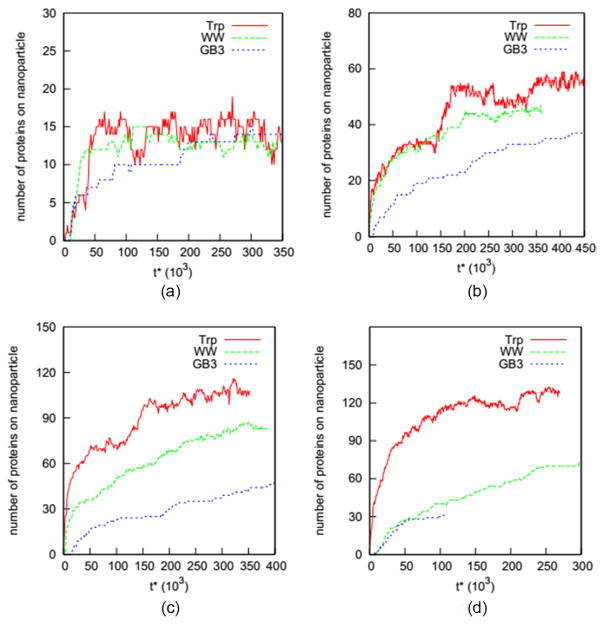
We explore the possibility of developing a generalized adsorption model for proteins on nanoparticles. To enable the exploration, we conducted simulations of three proteins (Trp, WW and GB3) on four nanoparticles with diameters 5.0, 10.0, 15.0, and 20.0 nm with C_initial at 5.0 mM. Figure 4 shows how the number of proteins on a nanoparticle vary as a function of reduced time for these 12 systems. Eight of these systems reach the equilibrium state in the simulations, as indicated by the flat curves in figure 4 for Trp and WW proteins on the nanoparticles (diameter = 5.0, 10.0 and 15.0 nm), and GB3 proteins on the nanoparticles with diameters of 5.0 and 10.0 nm. We thus use the data on these eight systems to explore the possibility of developing a generalized function for the adsorption of proteins on nanoparticles.

Figure 4.

Number of Trp, WW and GB3 adsorbed versus reduced time for nanoparticles of diameter (a) 5.0 nm, (b) 10.0 nm, (c) 15.0 nm, and (d) 20.0 nm during simulations with an initial concentration of 5.0 mM.

The analysis in the previous section has shown that the modified Langmuir model can well represent the adsorption isotherm of proteins on nanoparticles. Here we explore the possibility of developing a generalized function for the adsorption equilibrium constant k in the Langmuir model in terms of the parameter r_Pr/r_NP. The parameter k can be expressed in terms of C_eq, θ_eq, as:

$$k=\frac{{\theta }_{\text{eq}}}{C_{\text{eq}}(1-\alpha {\theta }_{\text{eq}})}$$ (13)

where α is an adjustable parameter. The values of α for Trp and WW on the nanoparticle with a diameter of 10.0 nm fitted from the simulation data are 1.7 and 1.2. The value of α for GB3 is set equal to that for WW due to their similar radii of gyration. Reference to Table 8, which shows the values of r_Pr/r_NP, C_eq, θ_eq, and k for the eight systems studied, shows that the value of k increases as r_Pr/r_NP, increases. This suggests that k may be represented by a polynomial function of the dimensionless parameter r_Pr/r_NP.

Table 8.

Protein radius of gyration/nanoparticle size ratio, equilibrium protein concentration and adsorption coverage and value of parameter k at a 5.0 mM initial protein concentration.

Case	rPr/rNP	Ceq	θeq	k
Trp
5.0 nm	0.30	4.3	0.34	0.19
10.0 nm	0.15	4.3	0.33	0.17
15.0 nm	0.10	4.4	0.28	0.12
WW
5.0 nm	0.43	4.4	0.67	0.77
10.0 nm	0.22	4.4	0.54	0.35
15.0 nm	0.14	4.5	0.39	0.16
GB3
5.0 nm	0.46	4.4	0.63	0.59
10.0 nm	0.23	4.5	0.50	0.28

$$k=a_0+a_1\left(\frac{r_{Pr}}{r_{\text{NP}}}\right)+a_2{\left(\frac{r_{Pr}}{r_{\text{NP}}}\right)}^2+a_3{\left(\frac{r_{Pr}}{r_{\text{NP}}}\right)}^3+\dots$$ (14)

where a₀, a₁, a₂,… are parameters that depend on the properties of the proteins and nanoparticles, such as the hydrophobicity, charge distribution and dipole moment. As the radius of gyration of a protein r_Pr is usually much smaller than the radius for a nanoparticle r_NP, we can truncate equation (14) at terms (r_Pr/r_NP)ⁿ where n is large enough so that (r_Pr/r_NP)ⁿ ≪ 1.

Here we try to fit the simulation data on the eight systems in Table 8 using the linear, 2nd order and 3rd order functions. There are only eight k versus (r_Pr/r_NP) data points, the values of r_Pr/r_NP range from 0.10 to 0.46. We assume that k is zero when r_Pr/r_NP is equal to zero. The particles become infinitely small when r_Pr/r_NP = 0. Since a finite number of particles cannot cover any surface on the nanoparticle, this is equivalent to θ_eq = 0, which according to equation (13), yields k = 0. Table 9 lists the fitted values for the parameters in the linear, 2nd and 3rd order functions, as well as the coefficients of determination R². The values of R² for the three functions are 0.72, 0.77 and 0.81, indicating that these functions can qualitatively predict how k should change with r_Pr/r_NP but present relatively poor quantitative agreement between the simulation data. This poor quantitative agreement illustrates the complexity and challenge of modeling the adsorption of proteins of different sizes and chemistries on nanoparticles of different curvatures all within a single function.

Table 9.

Fitted values for parameters in equation (13).

Function	a0	a1	a2	a3	R2
1st	−0.06	1.55			0.75
2nd	0.12	−0.03	2.75		0.73
3rd	−0.055	2.42	−7.40	12.40	0.67

There are, however, two encouraging signs in tables 8 and 9 concerning the development of generalized models for protein adsorption on nanoparticles. The first is that different proteins have the same k versus r_Pr/r_NP trend. The second is that the systems with similar r_Pr/r_NP have close values of k. For instance, the Trp-10.0 nm nanoparticle system and the WW-15.0 nm nanoparticle system have their r_Pr/r_NP as 0.15 and 0.14, and their k have similar values. These two signs indicate a possibility to develop a generalized model for protein adsorption on nanoparticles for a variety of protein-nanoparticle systems by correlating the equilibrium constant k of adsorption isotherm models to the chemical and physical properties of proteins and nanoparticle. This is an area that we are currently investigating.

5. Conclusion

The adsorption of proteins on nanoparticles is a determining factor in predicting the impact of nanoparticles on biological systems. Here we attempted to answer two questions regarding protein adsorption on nanoparticles: (1) how well do the known adsorption models describe protein adsorption on nanoparticles, and (2) is there a generalized model that describes the adsorption equilibrium of proteins on nanoparticles with different diameters? To answer these two questions, we investigated the adsorption of Trp, WW and GB3 proteins on model nanoparticles with diameters ranging from 5–20 nm in protein solutions at concentrations from 0.5 to 5 mM using data obtained from discontinuous molecular dynamics simulations of coarse-grained protein models.

The simulation results showed that four adsorption models (Langmuir, Freundlich, Temkin, and Kiselev) can describe the adsorption of two proteins (Trp and WW) on the nanoparticle with a diameter of 10.0 nm quite well, while three others (Elovich, Fowler–Guggenheirm and Hill–de Boer) did not perform very well. The analysis of the fitting parameters indicates that the adsorption of WW is more sensitive to its concentration than that of Trp.

We also attempted to develop a generalized model that can correlate the Langmuir model equilibrium constant k with the ratio of the protein radius of gyration and the nanoparticle radius r_Pr/r_NP using linear, 2nd and 3rd order expressions. The low values of the coefficient of determination imply that more effort is needed to meet the challenge of developing generalized models for protein adsorption on nanoparticles. However, two positive signs indicate the possibility of developing a generalized adsorption model for a wide spectrum of protein-nanoparticle systems: (1) different proteins show the same k versus r_Pr/r_NP trend; and (2) systems with similar r_Pr/r_NP present close values of k.