Hierarchically Organized Medial Frontal Cortex-Basal Ganglia Loops Selectively Control Task- and Response-Selection

Abstract

Adaptive behavior requires context-sensitive configuration of task-sets that specify time-varying stimulus–response mappings. Intriguingly, response time costs associated with changing task-sets and motor responses are known to be strongly interactive: switch costs at the task level are small in the presence of a response-switch but large when accompanied by a response-repetition, and vice versa for response-switch costs. The reasons behind this well known interdependence between task- and response-level control processes are currently not well understood. Here, we formalized and tested a model assuming a hierarchical organization of superordinate task-set and subordinate response-set selection processes to account for this effect. The model was found to successfully explain the full range of behavioral task- and response-switch costs across first and second order trial transitions. Using functional magnetic resonance imaging (fMRI) in healthy humans, we then characterized the neural circuitry mediating these effects. We found that presupplementary motor area (preSMA) activity tracked task-set control costs, SMA activity tracked response-set control costs, and basal ganglia (BG) activity mirrored the interaction between task- and response-set regulation processes that characterized participants' response times. A subsequent fMRI-guided transcranial magnetic stimulation experiment confirmed dissociable roles of the preSMA and SMA in determining response costs. Together, these data provide evidence for a hierarchical organization of posterior medial frontal cortex and its interaction with the BG, where a superordinate preSMA-BG loop establishes task-set selection, which imposes a (unidirectional) constraint on a subordinate SMA-BG loop that determines response-selection, resulting in the characteristic interdependence in task- and response-switch costs in behavior.

SIGNIFICANCE STATEMENT The ability to use context-sensitive task-sets to guide our responses is central to human adaptive behavior. Task and response selection are strongly interactive: it is more difficult to repeat a response in the context of a changing task-set, and vice versa. However, the neurocognitive architecture giving rise to this interdependence is currently not understood. Here we use modeling, neuroimaging, and noninvasive neurostimulation to show that this phenomenon derives from a hierarchical organization of posterior medial frontal cortex and its interaction with the basal ganglia, where a more anterior corticostriatal loop establishes task-set selection, which constrains a more posterior loop responsible for response-selection. These data provide a neural explanation for a key behavioral signature of human cognitive control.

Introduction

Imagine working in quality-control on a fast-paced assembly line, having to produce quick “accept” or “reject” responses while monitoring a particular product. Psychological research has shown that your responses will be faster when they are repeated (e.g., two “accepts” in a row) than when they have to be alternated (Bertelson, 1963; Kirby, 1976; Soetens et al., 1985). Intriguingly, however, response repetitions are actually slower than response alternations if they are accompanied by a change in task-set (Rogers and Monsell, 1995; Meiran, 1996, 2000; Hübner and Druey, 2006; Altmann, 2011): if you had to judge the quality of two different products that are intermixed on the assembly line, it would take you longer to produce consecutive “accept” responses when moving from one product to the other than it would take you to change your response. Similarly, the typical performance benefit obtained under conditions of task repetitions as compared with task switches (Allport et al., 1994; Monsell, 2003) is reduced or abolished if task repetition is accompanied by a change in motor response (Rogers and Monsell, 1995; Kleinsorge and Heuer, 1999). This interaction between task- and response-switch costs has long been considered a key signature of cognitive control (Rogers and Monsell, 1995), but the neurocognitive architecture producing this effect is presently uncertain.

Kleinsorge and Heuer (1999) advanced a plausible cognitive account of the interdependence between task- and response-selection, involving three basic assumptions: first, task-sets comprise distinct “levels”, a task-level that specifies the stimulus categorization (e.g., “is this a male or female face?”), and a response-level that specifies the mapping between categories and motor responses (e.g., “female face → left button press”). Second, these levels are organized hierarchically, such that a switch at the superordinate (task) level primes a switch at the subordinate (response) level, but not vice versa. Third, by default, task- and response-level settings are carried over from the previous trial; switching either one relative to the previous trial incurs a processing cost (switch cost). It follows that a full task- and response-repetition incurs no switch costs. A task-repetition accompanied by a response-switch incurs a response-level switch cost only. Similarly, if both the task and the response switch, only a task-level switch cost arises, because the subordinate response-switch is already primed by the superordinate task-switch. Critically, however, if the task-set switches but the response is repeated, both task and response switch costs are incurred. This is because the task-level switch primes a corresponding response-level switch and the latter has to be “switched back” for the correct (repeated) response to be selected.

Beyond providing an accurate qualitative description of response times, this account is also concordant with the general view that actions are organized in a hierarchical manner (Cooper and Shallice, 2006; Fuster, 2008) and with contemporary models suggesting a hierarchical neural organization of control processes in prefrontal cortex (Koechlin and Summerfield, 2007; Badre, 2008). However, experiments supporting the latter models have not examined the interaction between task- and response-switching processes (Koechlin, et al., 2003; Badre and D'Esposito, 2007). Moreover, the hierarchical task-switching model has remained untested beyond its original remit of accounting for first-oder task- and response-transition effects; no novel predictions have been derived to test the model's general validity. Finally, the implied hierarchical neural architecture giving rise to the behavioral interaction effect is currently unknown.

To address these questions, we first formalized the hierarchical switch model in mathematical terms. This allowed us to generate and test novel behavioral predictions regarding second-order task- and response-transition effects, which are known to strongly modulate first-order transition effects (Brown et al., 2007). Second, we acquired functional magnetic resonance imaging (fMRI) data to determine the neural mechanisms giving rise to the hierarchical behavioral effects. Finally, the causal role of the brain regions identified as potential mediators of these effects was tested through fMRI-guided repetitive transcranial magnetic stimulation (rTMS).

Materials and Methods

fMRI experiment

Participants.

Twenty-five healthy volunteers with no history of or current neurological or psychiatric illness participated in the fMRI study after signing informed consent approved by Duke University's Institutional Review Board. Two participants were excluded from further analysis due to poor task performance (>2 SD below the group mean) and one participant's data could not be analyzed because of technical difficulties during the scan. The remaining 22 participants (11 female; age: M = 23 years, SD = 3.75 years) had normal or corrected to normal vision and were all right-handed as assessed by the Edinburgh Handedness Inventory (Oldfield, 1971). A monetary compensation of USD 20.00 per hour was awarded for time and effort.

Stimuli.

The task stimuli consisted of greyscale photographs of male or female faces, semitransparently overlaid on greyscale photographs of interior and exterior views of houses. Face photographs with neutral expression were selected from the Cohn–Kanade Facial Expression Database (Kanade et al., 2000) and cropped to remove hair. Pictures of indoor scenes (unfurnished rooms) and houses were selected from online real estate databases. To match the amount of detail between indoor and outdoor scenes, photographs of houses were cropped to show only part of the house, e.g., entrance door and one window (Fig. 1A). All face and scene images were resized to 328 × 421 pixels, which corresponded to approximate visual angles of height = 8.4° and width = 6.6°. An initial set of pictures (34 per category: female, male, indoor scene, outdoor scene) was analyzed with respect to gray value distribution as an index of contrast. Subsequently, 10 images per category with closely matched contrast distribution (within and across categories) were selected and multiplied with the mean gray value per pixel across all 40 pictures using MATLAB (version 7.10.0/2010a) to achieve isoluminance. Subsequently, each face picture was overlaid semitransparently with each scene picture using Adobe Photoshop CS4 (version 11.0.2), resulting in 400 unique stimuli (20 faces × 20 scenes). Task cue stimuli consisted of the words “FACE” and “SCENE”, which were presented in light gray, R/G/B = 136/136/136 at a visual angle of approximate height = 0.8° and width = 2.7°/ 3.6°, respectively.

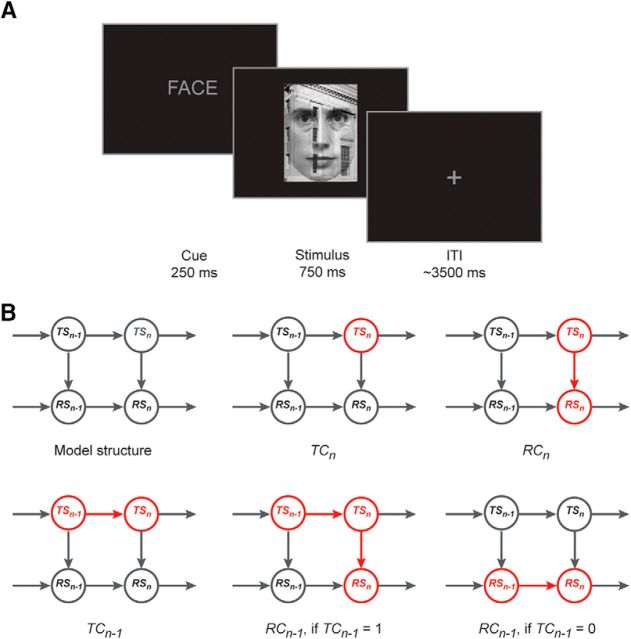
Figure 1.

Task and model. A, Example trial of the cued switch task. For illustration purposes, the relative size of the items on the screen is inflated. B, A graphical representation of the sequential hierarchical switch model. Nodes represent task switch states (TS) and response switch states (RS) on trial N − 1 and trial n, and their modulatory relationships are indicated by arrow connectors. Top, Left, The basic model structure, whereas each of the other five panels highlights (in red) the manner in which TC and RC are produced by the model (see main text for details).

Procedure.

Participants performed a cued task-switching paradigm (Fig. 1A): a gender classification task and a scene classification task. Following the verbal cue “FACE”, participants had to categorize the gender of the face (female vs male) in the subsequent stimulus, whereas if the cue word “SCENE” was shown, they had to indicate the location of the scene (inside vs outside) in the subsequent stimulus. Stimuli were presented on a black background via a projector, which was viewed by participants through a coil-mounted mirror, simulating a viewing distance of 80 cm. On each trial, the task cue was displayed for 200 ms in the center of the screen, followed by a 50 ms of blank black screen, followed by the task stimulus, presented centrally for 750 ms (see Fig. 1A). Responses were given by pressing one of two buttons on a MRI-compatible button box (Current Designs) with the index or middle finger of the right hand, with stimulus category-to-response mappings counterbalanced across subjects. Stimulus presentation was followed by an intertrial-interval with an average length of 3465 ms (durations were randomly drawn from a pseudo-exponential distribution ranging from 3000 to 5000 ms in increments of 500 ms: 50% 3000 ms, 25% 3500 ms, 12% 4000 ms, 8% 4500 ms, 5% 5000 ms) during which a central fixation cross (height/width: 0.4°) was shown. Presentation software (Neurobehavioral Systems) was used for task programming, stimulus presentation, and response recording.

Trials were presented in a pseudo-randomized manner, controlling the factors of task (face vs scene), task transition (task switch vs non-switch), response (left vs right), and response transition (response alternation vs repetition) to occur with equal probability. Note that for clarity, we refer to switches/non-switches when describing task transitions, and to repetitions/alternations when describing response transitions. Although each stimulus was unique, its constituent parts (face and scene) occurred 20 times during the experiment (each face was combined with each of the 20 scenes and vice versa). Each face and scene picture was presented an equal number of times as relevant stimulus part (i.e., target) and as irrelevant part (i.e., distracter). There were no direct repetitions of the same picture, regardless of whether it was displayed as the target or distracter of the stimulus. Each unique stimulus was presented once during the main experiment, in five blocks of 80 trials each, resulting in a duration of 6 min and 20 s per block. Before scanning, all participants underwent a training session for both tasks on a laptop computer outside the scanner. To ensure high performance, participants were first trained on univalent pictures (i.e., faces or scenes only) to a criterion of 100% discrimination accuracy before undergoing a practice for the switching condition with overlaid face–scene stimuli. For the main experiment subjects were instructed to respond as quickly and accurately as possibly. On average, the entire testing procedure took 90 min.

Behavioral data analysis.

To assess first-order and second-order task- and response-transition effects, response time data were analyzed according to the factors trial N − 1 task transition (N − 1 non-switch/switch), trial N task transition (N non-switch/switch), trial N − 1 response transition (N − 1 repetition/alternation) and trial N response transition (N repetition/alternation). Only those trials were sorted into these 2 × 2 × 2 × 2 design bins for which both the trial N−1 and the trial N response had been correct and reaction times (RTs) were within 3 SD above and below the mean (calculation based on all correct responses per subject). After excluding these trials, as well as the first two trials of each run, an average of 88.5% of trials was submitted to the analyses (ranging from 67.5–97% across subjects and 84.1–93.4% across conditions). Analyses of RTs were based on 2 × 2 × 2 × 2 repeated-measures ANOVA (rmANOVA) with the factors described above. Significant interactions from this four-way rmANOVA were followed up using paired-sample Student's t-tests. Levels of significance were Bonferroni-corrected based on the number of possible comparisons. The equivalent method was applied to the percentage of erroneous responses, i.e., errors were sorted into the same 2 × 2 × 2 × 2 rmANOVA design bins, and subsequent Bonferroni-corrected paired-sample Student's t-tests were conducted, if applicable.

Behavioral data modeling.

To generate and test quantitative predictions based on the hierarchical switch model (Kleinsorge and Heuer, 1999), we defined two binary variables, TS_n and RS_n, as follows:

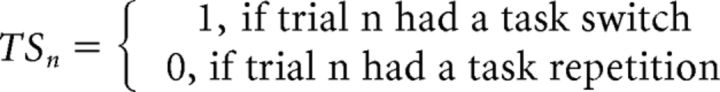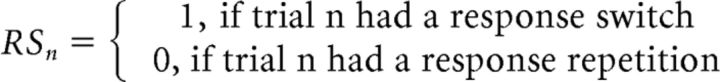We denote the task-switch cost and the response-switch cost of trial N as TC_n and RC_n, respectively. These cost variables are also binary, representing the absence (0) or presence (1) of such costs. The cost variables were defined as follows (Fig. 1B):

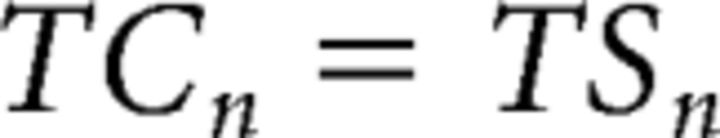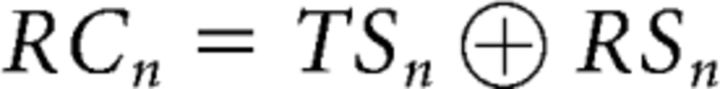Where ⊕ represents an “exclusive or” operation, defined as follows:

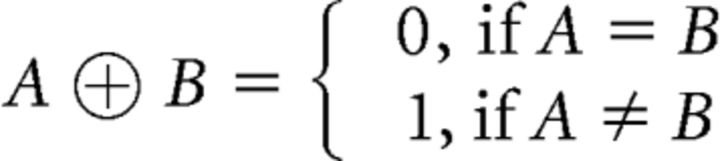This operation accounts for the modulation of A on B, given that A sits at a higher hierarchical level or precedes B. For example, consider RC_n = TS_n ⊕ RS_n: there is a response cost when either task-set or response-set changes (that is, either TS_n or RS_n is 1) but no response cost when both task- and response-sets change or both of them repeat (both TS_n and RS_n are 0 or 1).

Following Kleinsorge and Heuer (1999), we assume that: (1) the task-switch cost of trial N (TC_n) is solely determined by the state of the task-switch (TS_n), and is not modulated by the response-switch state. (2) The response-switch cost of trial N (RC_n), however, is determined by both the response and task transition states, because the task-set primes the response-set when a task-switch occurs. Together, these assumptions portray a hierarchical control scheme in which the task-set level modulates the response-set level. Note that the model is agnostic as to whether switch costs primarily reflect operations associated with the top-down reconfiguration of sets (Rogers and Monsell, 1995) or with overcoming inertia of previous sets (Allport et al., 1994; Wylie and Allport, 2000).

To further model the higher-order sequential effects of task-switch and response-switch costs (Brown et al., 2007), we expanded the model by Kleinsorge and Heuer (1999) to create the sequential hierarchical switch model (Fig. 1B). The extension of the model to predict higher-order effects is grounded in two assumptions, both of which follow the spirit of the original model. First, we expand the idea of a default carry-over of task- and response-settings from trial N − 1 to trial N to second-order transitions, such that, for instance, a task-switch on the previous trial implies a task-switch on the current trial. Second, we assume that these second-order sequential effects follow the same hierarchical organization as the first-order transition effects addressed by the original model, such that changes in task-set transitions lead to changes in response-set, but not the other way around. This necessitates 2 additional binary variables, TS_n−1 and RS_n−1, to represent the previous trial task and response transitions. Specifically, the task-switch cost (TC_n−1) and the response-switch cost (RC_n−1) of trial N − 1 on trial N were defined as follows:

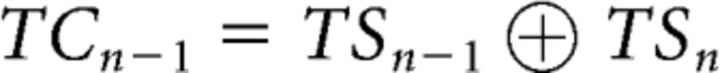These definitions assume that: (1) TC_n−1 is determined only by task-switch states. Specifically, this cost is present only when there is a change of task-switch state from trial N − 1 to trial N (e.g., from task-switch to task-repetition, or vice versa). Thus the formula of TC_n−1 modeled a second-order sequential effect on task-switch cost (TC_n) emerging from the task-switch state at the previous trial. (2) Similarly, if successive task transitions are identical (e.g., two switches in a row, which would lead to TC_n−1 = 0), then the response-switch cost (RC_n) is modulated by the response-switch state at the previous trial (RC_n−1), reflecting a second-order sequential effect. Notably, however, this sequential effect can be overridden by the task-set if there is a change in the task-switch state (i.e., when TC_n−1 = 1). Thus, akin to the trial N level, we also assume a hierarchical architecture for sequential trial effects, in which the task-set level unidirectionally modulates the response-set level. In other words, our added assumptions are that a task-switch (repetition) on the previous trial primes a task-switch (repetition) on the current trial, and the same is true for responses, but the latter is overridden in case the higher-order task-transition changes (e.g., from a task-switch to a task-repeat trial). The way in which each of these costs would be expected to affect each of the 16 trial types in our design is depicted in Table 1, with each cost term forming a vector consisting of the 16 trial types. Note that the vectors were mean centered (with 1, −1, and 0 indicating the presence, absence, and unavailability of a given cost term, respectively) to ensure orthogonality between vectors, and hence guarantee that the model estimates can be uniquely attributed to the corresponding cost term (see below).

Table 1.

Task- and response-set transition costs derived from the sequential hierarchical switch model

Trial type		Trial N − 1 cost			Trial N cost		Constant C
N-1	N	TCn−1 (TCn)	TCn−1 (RCn)	RCn−1 (RCn)	TCn	RCn
nsw rep	nsw rep	−1	0	−1	−1	−1	1
nsw rep	nsw alt	−1	0	1	−1	1	1
nsw rep	sw rep	1	1	0	1	1	1
nsw rep	sw alt	1	−1	0	1	−1	1
nsw alt	nsw rep	−1	0	1	−1	−1	1
nsw alt	nsw alt	−1	0	−1	−1	1	1
nsw alt	sw rep	1	1	0	1	1	1
nsw alt	sw alt	1	−1	0	1	−1	1
sw rep	nsw rep	1	1	0	−1	−1	1
sw rep	nsw alt	1	−1	0	−1	1	1
sw rep	sw rep	−1	0	−1	1	1	1
sw rep	sw alt	−1	0	1	1	−1	1
sw alt	nsw rep	1	1	0	−1	−1	1
sw alt	nsw alt	1	−1	0	−1	1	1
sw alt	sw rep	−1	0	1	1	1	1
sw alt	sw alt	−1	0	−1	1	−1	1

nsw, Task non-switch; sw, task switch; rep, response repetition; alt, response alternation.

With the definitions above, RT can be simulated using a linear model:

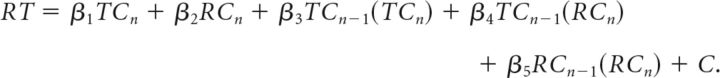The parameters β₁, β₂, β₂, β₄, and β₅, model the contribution of TC_n, RC_n, TC_n−1 (on both TC_n and RC_n) and TC_n−1 (on RC_n only), respectively, and C is a constant that represents the condition-independent information processing time. The group mean RTs for each condition were used to fit the data to a general linear model and estimate the parameters (β₁ − β₅ and C). The quality of fit was assessed through a linear correlation between simulated and measured data, thus determining the variance in behavior accounted for by the model (Table 2).

Table 2.

Fitted model parameters (mean and SEM in ms) for each of the behavioral datasets (fMRI study and TMS study, the latter calculated separately for preSMA and SMA stimulation)

Dataset	Trial N − 1 cost			Trial N cost		Constant C
	TCn−1 (TCn)	TCn−1 (RCn)	RCn−1 (RCn)	TCn	RCn
fMRI	4.38	4.70	14.31	1.59	4.02	749.08
	(2.49)	(3.19)	(2.65)	(2.73)	(2.01)	(23.43)
preSMA-TMS	5.10	4.15	4.14	14.97	6.87	696.87
	(2.81)	(3.88)	(4.39)	(3.78)	(3.70)	(26.68)
SMA-TMS	11.50	16.77	14.4	12.80	10.34	709.47
	(4.27)	(7.17)	(5.11)	(4.06)	(2.16)	(29.76)

For detailed model parameter description, see Materials and Methods, Behavioral data modeling.

Imaging data acquisition and preprocessing.

All MRI data were obtained on a GE MR750 3.0 tesla scanner. The scanning session started with the acquisition of a T1-weighted sagittal localizer scan, which was followed by a high resolution anatomical scan (T1-weighted fast inverse-recovery-prepared SPGR sequence; 120 axial slices parallel to AC/PC of 1 mm thickness and an in-plane resolution of 1 mm²). Functional MRI were collected using a T2*-weighted single-shot gradient EPI sequence (TR = 2 s; TE = 28 ms; 90° flip angle). Thirty-six axial slices, parallel to the AC-PC-plane (3 mm slice thickness, 3 × 3 mm in-plane resolution; 19.2 cm FOV) were scanned in an ascending interleaved manner. Participants completed five experimental runs, each lasting 190 TRs. Functional MRI data were analyzed using SPM8 (http://www.fil.ion.ucl.ac.uk/spm/software/spm8/). Each subject's functional images were slice-time corrected, realigned, and coregistered to their anatomical scan. Spatial transformation parameters for normalizing the anatomical image to the standard MNI brain were calculated and subsequently applied to the functional images. Normalized functional images with an interpolated resolution of 2 mm³ isotropic voxels were spatially smoothed with a Gaussian filter of 8 mm full-width at half-maximum.

Imaging data statistical analysis.

All five experimental runs were modeled in a concatenated fashion with an additional regressor coding for the factor of experimental run. A high-pass filter of 128 s was applied to the time series to control for low-frequency signal drift. Each stimulus event was convolved with a canonical hemodynamic response function. Onsets were locked to the cue presentation time and sorted according to trial N − 1 task transition (N − 1 non-switch/switch), trial N task transition (N non-switch/switch), trial N − 1 response transition (N − 1 repetition/alternation) and trial N response transition (N repetition/alternation). Only correct trials following a correct trial were placed in one of these 16 regressors. All other onsets, including the first two trials of each run and error and post-error trials, were modeled separately as a nuisance regressor. Linear contrasts were computed for the main effects of each of the four factors and all possible interactions at the individual subject level.

The contrast images of each subject were then submitted to one-sample random effects t-tests at the group level. Group statistics were corrected at p < 0.05 by applying a combined voxel- and cluster-level threshold using the program 3dClustSim (http://afni.nimh.nih.gov/afni; “fixed” version, downloaded Sept., 2016), which performs α probability simulations (based on Monte Carlo simulations) that take into account the search volume and the inherent smoothness of the data along all three axes. The output results matrix contains the minimum required cluster size at a given (uncorrected) threshold to obtain a desired corrected significance level. We chose cluster-size values that would combine with a voxelwise threshold of p < 0.01 to represent a combined corrected threshold at p < 0.05, within a search volume confined to a gray matter voxel mask using the WFU Pick Atlas tool (Maldjian, Laurienti et al., 2003).

Note that this represents a relatively lenient cluster-forming threshold. Combined with using parametric statistical tests, this increases the likelihood of obtaining false-positive activations (Eklund et al., 2016; but see Cox et al., 2017a,b). Nonparametric tests that can mitigate the false-positive detection risk are not applicable to the type of complex task design of the current study (Cox et al., 2017b). However, more stringent cluster-forming thresholds will naturally increase the likelihood of rejecting true activations (false-negatives), which also poses a considerable problem in studies with typical fMRI sample sizes of the kind we used here (Lohmann et al., 2017). The current thresholding approach thus errs on the side of false-positive (rather than false-negative) findings, but we counter the risk of our fMRI results representing false-positives by validating the implied functions of the main implicated cortical regions via an fMRI-guided TMS follow-up experiment. Note also that although cluster-based thresholding can lead to ambiguous anatomical conclusions when large voxel clusters span several anatomical regions (Woo et al., 2014), all regions we report were robust to changes in the height/extent trade-off (i.e., each anatomical region displayed significant effects in their own right when using more stringent voxelwise thresholds combined with smaller cluster sizes). Finally, unthresholded statistical maps of the main contrasts can be inspected at http://neurovault.org/collections/QBLMMVAV/.

To elucidate any high-level interaction effects observed in whole-brain corrected analyses, we extracted β parameter estimates from the identified clusters using MarsBaR (Brett et al., 2002) and submitted them to follow-up rmANOVAs. Note that these analyses only serve to clarify the interaction effect that was established through whole-brain analysis, rather than to recapitulate that finding at the ROI level. Finally, to test whether the sequential hierarchical switch model could explain significant variance in activation, the same linear model fitting approach as applied to the behavioral data (see Behavioral data modeling) was applied to the extracted β parameters.

fMRI-guided rTMS experiment

Participants.

For the TMS study, the 22 participants of the fMRI cohort were reinvited, 10 of whom volunteered to undergo TMS and perform the task again. To achieve a sufficient sample size, data of 16 additional healthy volunteers were collected who were naive to the experimental task. Anatomical T1-weighted MRI scans of participants who had not been part of the prior fMRI participant sample were acquired through the imaging facilities' data base after receiving individual written consent. None of the subjects had a history of or current neurological or psychiatric illness. All were screened for TMS eligibility, following conventional guidelines (Rossi et al., 2009), and signed informed consent approved by Duke University's Institutional Review Board. Due to elevated mean reaction times (>2 SD above the group mean) one participant was excluded from further analysis. As there was no difference in the behavioral measures between the groups with and without prior task experience, all reported analyses are based on the combined sample of 25 participants (16 female; age: M = 24.9 years, SD = 5.1 years). All participants had normal or corrected-to-normal vision. Three subjects were classified as ambidextrous, all others were right-handed as assessed by the Edinburgh Handedness Inventory (Oldfield, 1971). A monetary compensation of USD 20.00 per hour was awarded for time and effort.

Procedure, stimuli, and task.

Stimuli were presented on a Dell Latitude D630 laptop with a screen resolution of 1280 × 800 pixels (32 bit, 60 Hz; NVIDIA Quadro NVS 135M graphics card). Both stimulus material and task were identical to the fMRI task. The 400 experimental trials were presented in two sessions of 200 trials, each following 15 min rTMS over one cortical target. Responses were given using a standard two-button mouse. The absolute size of the stimuli was adjusted for the screen to achieve identical angular sizes across experiments. Like in the fMRI study, participants were first trained on the univalent pictures (i.e., faces or scenes only) to a criterion of 100% discrimination accuracy, before undergoing a practice for the switching condition with overlaid face–scene stimuli. Subsequently, we assessed their individual resting motor threshold (rMT) to determine the stimulation intensity for the rTMS protocol using a two-channel EMG device (Rogue Research). Each participant received 15 min of 1 Hz rTMS over the presupplementary motor area (preSMA) and the SMA (for details, see below). Pulses were delivered using a Magstim Rapid2 stimulator with a Magstim Double 70 mm Air Film Coil. Stimulation targets were localized using Brainsight Neuronavigation Software (Rogue Research). The order of target stimulation sites was counterbalanced across participants. Each rTMS session was followed by immediate performance of 200 experimental trials presented in one block (≈16 min). Taking into account the duration of the experimental block, the transfer from TMS chair to testing computer and back, as well as the coregistration of the participants' heads to their T1-weighted MR-image before each block, there was an approximate time window of 30 min between the stimulation sessions.

Motor threshold.

The rMT was determined through recordings of motor-evoked potentials (MEPs) from the first dorsal interosseous muscle of the right hand. Surface electrodes were placed in a belly-tendon montage on the muscle with the reference electrode placed on the forearm of the same side. The coil was positioned tangentially on the skull over the contralateral primary hand area (M1) in a 45° angle to the parasagittal plane and with the magnetic current flowing in an anterior–posterior direction (i.e., the coil handle pointing toward the left ear and neck). The rMT was defined as the lowest percentage of maximum stimulator output that was required to evoke at least 5 of 10 MEPs with peak-to-peak amplitude of at least 100 μV (Rossini et al., 1994).

Target identification.

Stimulation targets in preSMA and SMA were chosen based on results from the fMRI study. As rTMS was in part performed on participants who had not been part of the fMRI sample, the fMRI MNI group results coordinates rather than individual peak activations were used for all subjects (Sack et al., 2009). Because of the relative proximity of the two target sites, and to achieve maximal stimulation comparability, we selected the two local maxima (one per contrast) that had similar cortical depths and the greatest possible Euclidean distance (Table 3). A transformation matrix mapped to MNI space was estimated for each individual brain, resulting in a stereotactic coordinate system for each brain in native space. Thus, individual brain sizes were accounted for despite using the same coordinates for each participant. Virtual markers and trajectories were placed on the chosen coordinates (preSMA: −2/4/54, SMA: −8/−12/56). The trajectory allowed for determination of pitch, roll, and yaw of the coil, so that it could be placed tangentially on the scull directly over the targets.

Table 3.

Activation clusters (with documentation of local maxima) revealed by whole-brain analyses

Anatomical area	Hemisphere	Voxels	x	y	z	Tmax
Task-set control
(sw(N) > nsw(N))nsw(N−1) > (sw(N) > nsw(N))nsw(N−1)
SMA cluster	L/R	745
SMA (extending to middle frontal gyrus)	R		8	10	48	3.82
SMA (extending to middle frontal gyrus)	L		−4	−4	52	3.18
Superior frontal gyrus	L		−2	4	54	3.05
Response-set control
(alt(N) > rep(N))rep(N−1) > (alt(N) > rep(N))alt(N−1)
preSMA cluster	L	851
Precentral gyrus	L		−38	−18	68	3.45
Paracentral lobule	L		−12	−20	62	3.20
Medial frontal gyrus (BA6)	L		−8	−12	56	3.08
Task-set control × Response-set control interaction
Basal ganglia cluster	L/R	688
Pallidum	R		16	0	−6	3.38
Thalamus	L		−4	−4	−10	2.87
Pallidum	L		−6	0	2	2.86

nsw(n)/nsw(n−1), Task non-switch in trial N/N−1; sw(n)/sw(n−1), task switch in trial N/N−1; rep(N)/rep(N−1), response repetition in trial N/N-1; alt(N)/alt(N−1), response alternation in trial N/N−1).

rTMS.

Participants' head location was registered to align their position in the TMS chair (Rogue Research) with their anatomical brain scan using Brainsight's frameless stereotactic navigation system in combination with anatomical landmarks that had been specified on each subject's structural scan. This method allowed for exact navigation of the coil with respect to the stimulation targets. Stimulation was delivered at a frequency of 1 Hz, which has been shown to temporarily disrupt poststimulation cortical processing in the underlying brain area (Chen et al., 1997; Muellbacher et al., 2000) for approximately the same duration as the stimulation period (for reviews, see Walsh and Cowey, 2000; Pascual-Leone et al., 2000). rTMS was delivered at an intensity of 110% rMT for a total of 900 pulses, resulting in 15 min of stimulation per target. After each stimulation session, participants transitioned immediately from the TMS chair to a nearby desk and chair to start the task-switching experiment. Before the second target was stimulated, participants' head location was registered again. However, rMT was only assessed once (at the beginning of the session). The entire procedure lasted approximately 2.5 h.

Behavioral data analysis and modeling.

RT data were analyzed analogously to those of the fMRI study, with the addition of the factor of stimulation site (preSMA/SMA) to the rmANOVA. Behavioral data from each TMS condition were also subjected to the same modeling approach as described above for the fMRI study, such that best-fitting task- and response-cost parameter values could be compared between preSMA and SMA stimulation conditions.

Results

Data were analyzed according to first-order (trial N) and second-order (trial N − 1) task- and response-transitions (see Materials and Methods). Note that for clarity, we refer to switches/non-switches when describing task transitions, and to repetitions/alternations when describing response transitions.

Behavioral data and model fit

The rmANOVA of RT data revealed that our protocol replicated the typical task by response transition interaction effect that is the focus of the hierarchical switch model (Kleinsorge and Heuer, 1999) and the present paper (Fig. 2A); namely, reduced task switch costs in the presence of response alternations (12.6 ms) compared with response repetitions (42.7 ms, p < 0.001 corrected; F_(1,21) = 9.741, p < 0.01). However, as also observed in prior studies (Brown et al., 2007), this interaction was qualified by higher-order task and response transition effects, as indicated by a four-way interaction effect (F_(1,21) = 15.334, p < 0.005; Fig. 2B). Specifically, the reduction in task switch costs with a concurrent response alternation was evident when the previous task and response transitions either both changed (i.e., trial N − 1 task switch/response alternation; post hoc 2 × 2 rmANOVA for trial N task by response transition interaction: F_(1,21) = 18.674, p < 0.001) or both remained the same (i.e., trial N − 1 task non-switch/response repetition; post hoc 2 × 2 rmANOVA for trial N task by response transition interaction: F_(1,21) = 15.240, p < 0.005; Fig. 2B, outer panels), but it was abolished when the task and response transitions on the previous trial mismatched (i.e., trial N − 1 task non-switch/response alternation and task switch/response repetition; Fig. 2B, inner panels). Specifically, when a task non-switch and a response alternation co-occurred on the previous trial, current trial task switch cost did not vary with response transition (post hoc 2 × 2 rmANOVA, trial N task transition: F_(1,21) = 18.674, p < 0.001; trial N task by response transition interaction: p > 0.1; Fig. 2B, second panel), whereas when a task switch and a response repetition co-occurred on the previous trial, no task or response switch costs were observed on the current trial (post hoc 2 × 2 rmANOVA: all p values > 0.1; Fig. 2B, third panel).

Figure 2.

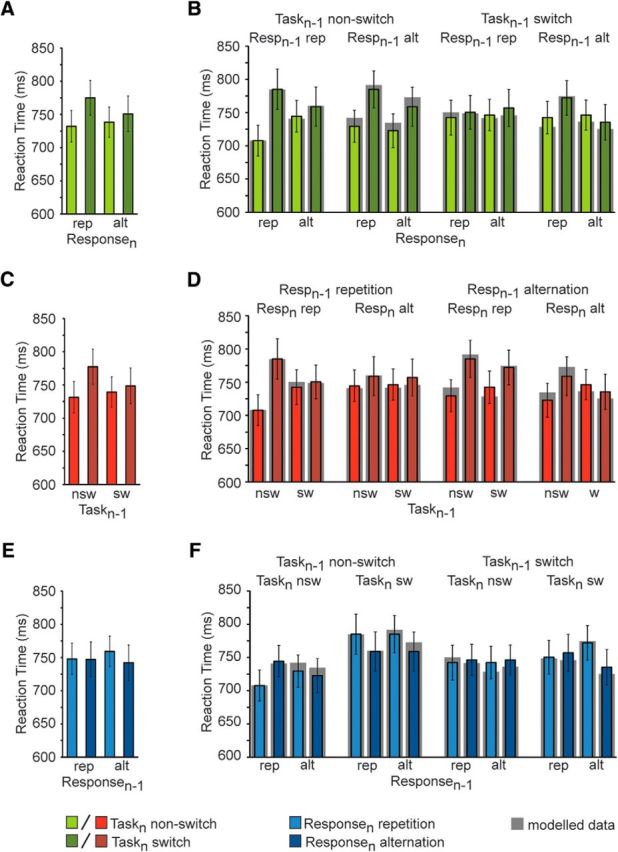
Empirical behavior and model fits. A, Mean response time (±SEM) is plotted as a function of trial N response (rep, repetition; alt, alternation) and task transitions (lighter shading, non-switch; darker shading, switch). B, The interaction effect in RT (±SEM) between response and task transitions in A is displayed as a function of trial N − 1 response and task transitions. C, Mean response time (±SEM) is plotted as a function of trial N − 1 (nsw, non-switch; sw, switch) and trial N task transitions (lighter shading, non-switch; darker shading, switch). D, The interaction effect in response time (±SEM) between previous and current trial task transitions in B is here displayed as a function of trial N − 1 and trial N response transitions. E, Mean response time (±SEM) is plotted as a function of trial N − 1 (rep, alt) and trial N response transitions (lighter shading, repetition; darker shading, alternation). F, The interaction effect in response time (±SEM) between previous and current trials response transitions in E is here displayed as a function of trial N − 1 and trial N task transitions. For all panels, gray shading around the bars corresponds to best-fit model values. Resp, response; nsw, non-switch; sw, switch.

This data pattern is predicted by the sequential hierarchical switch model (compare Table 1 and Fig. 2B,D,F, gray shading): first, under conditions where there are no changes in task transitions, a current response repetition incurs a cost if the response alternated during the previous transition. This leads to a relatively high RT in trials where a trial N − 1 response alternation is accompanied by a trial N response repetition in the absence of any task switches, thus removing the typical trial N task by response transition interaction effect (Fig. 2B, second panel). Second, if a task switch occurred on trial N − 1, current switch trials will incur no trial N-1 task switch costs (leading to relatively fast trial N switches) but current task non-switch trials will incur such costs (leading to relatively slow non-switch trials), thus abolishing current-trial task switch costs (Fig. 2B, third panel).

Accordingly, as can be seen in Figure 2B, the model (gray shading around the bars) was able to provide an excellent fit to the behavioral data (best-fit parameter values: TC_n = 13.8 ms, RC_n = 7.5 ms, TC_n−1 (TC_n) = 9.1 ms, TC_n−1 (RC_n) = 5.5 ms, RC_n−1 (RC_n) = 10.8 ms, C = 749 ms). Using six free parameters, the model accounted for ∼85% of the variance across the 16 conditions (correlation between simulated and observed data, r = 0.92, p < 1e−6), with no simulated data point falling outside of one SE of the empirical data. To further assess each cost variable's ability to account for behavior across subjects, the model was fit to condition-mean RTs of each subject. Group-level one-sample t-tests (against null) on each cost variable indicated that each of the (orthogonal) model cost terms contributed significantly to explaining RT across subjects (TC_n: t₍₂₁₎ = 3.761, p = 0.001; RC_n: t₍₂₁₎ = 3.121, p = 0.005; TC_n−1 (TC_n): t₍₂₁₎ = 3.645, p < 0.005; TC_n−1 (RC_n): t₍₂₁₎ = 2.315, p < 0.05; RC_n−1(TC_n): t₍₂₁₎ = 4.346, p < 0.001).

Given that our model assumes that this data pattern arises from the hierarchically organized workings of two distinct (though interacting) task-selection and response-selection mechanisms, a functionally more intuitive way of approaching the four-way interaction reported above may be to consider task and response transitions separately. Figure 2, D and F, replot the data from Figure 2B according to a focus on task transitions (Fig. 2D) and response transitions (Fig. 2F), respectively. Here, we observe main effects for the factors of previous trial (N − 1) task transition, due to faster responses following task switches (743.8 ms) than non-switches (754.3 ms; F_(1,21) = 4.782, p < 0.05), and current trial (N) task transition, reflecting slower RTs on task switches (762.9 ms) than on non-switch trials (735.3 ms; F_(1,21) = 14.149, p < 0.005). Importantly, these two factors interacted (F_(1,21) = 13.284, p < 0.005), as task switch costs were reduced following a task switch on trial N − 1 compared with N − 1 non-switch trials (9.4 vs 45.9 ms, p < 0.001 corrected; Fig. 2C).

A similar trend was evident in the response transitions interaction between trial N − 1 and N, due to a response repetition cost on trial N if it followed a response alternation on trial N − 1, but no such cost when the previous trial was a response repetition (trial N response alternation–repetition difference after N − 1 response alternation: 17 ms, p < 0.05 corrected vs after trial N − 1 response repetition: 0.9 ms; interaction: F_(1,21) = 3.684, p = 0.069; Fig. 2E). In other words, current trial task (response) transitions were facilitated if they matched previous trial task (response) transitions compared with when higher-order transitions were violated. Moreover, these two-way interactions between previous and current trial task (response) transition effects were of course qualified by the four-way interaction, because the data patterns described above were only present when the previous task and response transitions either both changed or both remained the same, but it was abolished when the task and response transitions on the previous trial mismatched (Fig. 2C,D). From this perspective, one can view the four-way interaction as reflecting two interdependent sequential (task- and response-set) regulatory mechanisms that become engaged (and thus produce RT costs) whenever higher-order transition patterns are violated, that is, when moving from a switch to a non-switch (or vice versa) and from a repetition to an alternation trial (or vice versa).

Performance accuracy was generally very high in the current study (fMRI session: M = 94.5%, SEM = 1.0; rTMS session: M = 94.8%, SEM = 0.8) and thus did not represent a primary dependent measure of interest as in other targeted investigations of hierarchical switch effects (Ranti et al., 2015). Nonetheless, largely mirroring the RT data and Kleinsorge and Heuer (1999), task switch effects (fMRI session: F_(1,21) = 24.418, p < 0.001; TMS sessions: F_(1,24) = 8.240, p < 0.01), response switch effects (fMRI session: F_(1,21) = 5.123, p < 0.05; TMS sessions: F_(1,24) = 9.070, p < 0.01), and the critical task switch × response switch interaction (fMRI session: F_(1,21) = 4.811, p < 0.05; TMS sessions: F_(1,24) = 9.912, p < 0.01) were significant in both sessions.

Model comparison

To further validate the proposed model, it was compared with 17 alternative models. Two of the 17 models were non-hierarchical, including: (1) a model where behavior is only modulated by the main effects of the 4 factors (TC_n−1, RC_n−1, etc.); and (2) a model where experimental conditions are independent to each other (e.g., the model is a 16 × 16 identity matrix). The remaining models were hierarchical models, including one model assuming RC_n−1 does not depend on the state of TC_n−1, and 14 reduced versions of the proposed model (i.e., where only a subset of the task and response costs, TC_n−1, RC_n−1, TC_n, and RC_n, are contributing to behavior). To minimize possible bias introduced by overfitting due to having more free parameters, model comparison analysis used a cross-validation approach (cf., Chiu et al., 2017). Specifically, the 22 subjects were randomly divided into two folds of 11 subjects each. Each model was fit to the experimental condition-specific mean RTs of the first fold. The resulting fitting parameters were then applied to the other fold to predict the mean RTs for each of the 16 experimental conditions in the remaining fold. This procedure was repeated 1000 times to ensure stable estimation of prediction errors for each experimental condition, based on which the likelihood of observing the behavioral data based on each model was calculated. For each model, its likelihood was then divided by the sum of likelihood estimates over all models to produce the probability that this model accounted for variance in behavioral data better than all other models. We found that, out of all models entered into the model comparison analyses, the sequential hierarchical switch model yielded the highest probability of 0.876. Compared with the chance level of 0.0556 and the second highest probability of 0.0601, these results strongly support the proposed model as offering the most appropriate account for the behavioral data. We therefore use that model to guide the subsequent fMRI data analyses.

In sum, the behavioral data analyses have shown that a model of hierarchically organized task- and response-set regulation processes can successfully predict the full range of first and second order sequential effects in task-switching response times. We next set out to identify the neural mechanisms giving rise to these hierarchical effects.

fMRI data

The behavioral data and simulation results indicate that the interaction between task and response transitions can be accounted for by two hierarchically organized task- and response-set regulatory mechanisms. To determine the neural substrates of these mechanisms, we pursued an identical analysis strategy in the neuroimaging data as in the behavioral data. Specifically, we first searched for neural correlates of trial N task × response transition effects in isolation (Fig. 2A); we then examined the data from the perspective of separate (but interacting) task- and response-set control mechanisms, each defined on the basis of the interaction between previous and current trial task (Fig. 2C) or response (Fig. 2E) transitions; finally, we then considered these two-way interaction effects in the context of the complete four-way interaction between previous and current trial transitions (Fig. 2, compare B, D, F). All fMRI data we report are whole-brain corrected (p < 0.05) with cluster size thresholds ranging from 649–662 voxels, depending on the exact contrast in question (for an overview of activation clusters with local maxima >8 mm apart and their extent, see Table 3).

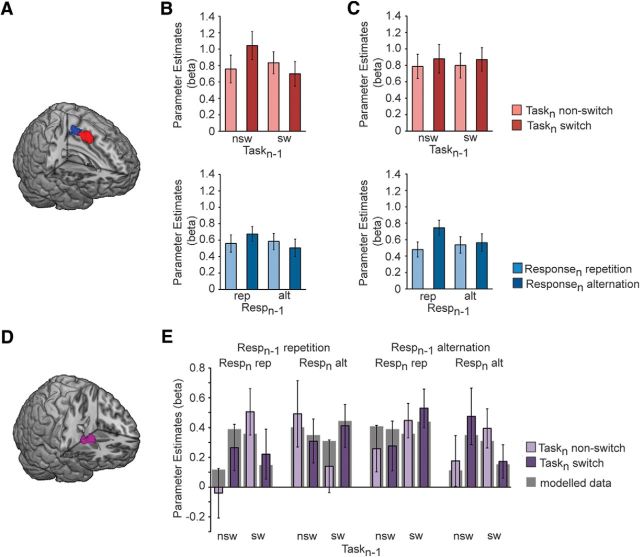
When exploring the neural substrate of the interaction between trial N task and response transition factors (Fig. 2A), we observed no significant activation clusters. A possible explanation for the absence of a significant task by response transition interaction in the fMRI data is of course that the behavioral effect may be driven by interactions between two distinct task- and response-set control mechanisms, as envisaged by the hierarchical model. Therefore, analogous to the analyses of the RT data, we examined the interaction contrasts of trial N − 1 × trial N both for task and response transitions (Fig. 2, compare C, E). At the task level, a cluster spanning bilateral preSMA exhibited higher activation for task switch compared with non-switch trials following a non-switch compared with a switch trial (F_(1,21) = 11.226, p < 0.005; Fig. 3A, red overlay, B, top). The response-level analysis revealed a similar pattern in left-lateralized motor areas, comprising primary motor cortex, middle frontal gyrus and SMA, yielding elevated activation for response alternations relative to repetitions, only if the response on the previous trial also repeated (F_(1,21) = 11.226, p < 0.005; Fig. 3A, blue overlay, C, bottom).

Figure 3.

fMRI Results. A, Voxel clusters showing effects of task- and response- transitions were detected in the preSMA (red) and SMA (blue), respectively (p < 0.05, whole-brain corrected). B, Mean cluster β values (±SEM) in the preSMA, plotted as a function of task-transitions (top) and response-transitions (bottom). C, Mean cluster β values (±SEM) in the SMA, plotted as a function of task transitions (top) and response transitions (bottom). D, A voxel cluster reflecting a four-way interaction effect between task- and response-transition factors was detected in the basal ganglia (p < 0.05, whole-brain corrected). E, Mean cluster β values (±SEM) in the BG; the interaction effect between previous and current trial task transitions is displayed as a function of trial N − 1 and trial N response transitions (compare with Fig. 2D). E, Gray shading around the bars corresponds to best-fit model values. Note that although the model simulations do not provide a perfect fit with the data, they fall within 1 SD of the BG activation in all conditions, and are therefore within the margin of measurement noise for all conditions. Resp, response; rep, repetition; alt, alternation; nsw, non-switch; sw, switch.

Given the close proximity of these activation clusters we sought to ascertain that the preSMA and SMA displayed sequence effects that were truly selective to task and response transitions, respectively. Strikingly, there were indeed no effects of the transition of the other hierarchical level at either site (all p values >0.1; Fig. 3B, bottom, C, top): higher activation in trial N for task switches compared with non-switches following non-switch rather than switch trials was only evident in the preSMA, but not in the SMA (interaction effect: F_(1,21) = 12.675, p < 0.01), whereas the equivalent pattern of higher activation for response alternations relative to repetitions following previous-trial response repetitions could only be found for the SMA, but not the preSMA (interaction effect: F_(1,21) = 5.068, p < 0.05). In sum, the preSMA displayed precisely the type of activation pattern one would expect from a region involved in invoking task-level control when the current task-set transition differs from the preceding one. By the same token, the neighboring SMA displayed the type of activation pattern expected from a region involved in implementing response-level control when the current response-set transition diverges from the preceding one.

Given that our behavioral analysis had shown the task- and response-level transitions to be interactive, we focused next on the four-way interaction contrast involving both types of transition factors. In a whole-brain search, we obtained an activation cluster centered on the basal ganglia (BG), mostly comprising the head of the caudate and pallidum, as well as the thalamus (Fig. 3D). In Figure 3E, the BG activity pattern across all conditions is displayed (four-way interaction: F_(1,21) = 10.193, p < 0.005), with a focus on task transitions (Fig. 2D shows the corresponding plotting of behavioral results). Similar to the RT data (Fig. 2D), activity in the BG was characterized by task switch costs that were reduced following a task switch on trial N − 1 compared with N − 1 non-switch trials (Fig. 3E, outer panels), but this two-way interaction between previous and current trial task transition effects was modulated by response transitions, because the data patterns described above were only present when the previous task and response transitions either both changed (F_(1,21) = 6.930, p < 0.05) or both remained the same (F_(1,21) = 3.547, p = 0.074), but it was abolished when the task and response transitions on the previous trial mismatched (Fig. 3E, inner panels; both p values >0.1).

The fact that BG activation qualitatively tracked RT costs (with higher activation for slower RTs) in this protocol is commensurate with a role for the BG as representing a final response selection pathway (Mink, 1996; Grillner et al., 2005; Redgrave et al., 2010), and as being involved in delaying responding under conditions of decision conflict (Frank et al., 2007), here under conditions where higher-order task- and response-level transitions were violated, and accordingly when putative control processes in the preSMA and SMA were recruited to resolve these violations. Given the similarity between the BG activation data and the behavioral performance pattern, we ran an equivalent model fitting procedure on the mean BG cluster activation estimates. As shown in Figure 3E (gray shading around the bars), the BG activity pattern was captured well by the model (r = 0.72, p = 0.002). Note that the BG cluster shown was detected in a corrected whole-brain analyses. To test whether anatomically defined subregions within the greater subcortical cluster centered in the BG might reveal different activation patterns, we created anatomical masks using the WFU Pick Atlas tool (Maldjian et al., 2003), and subsequently submitted parameter estimates a post hoc 2 × 2 × 2 × 2 rmANOVA. However, all of the investigated subregions, including the caudate, pallidum, thalamus, amygdala, and hippocampus, displayed equivalent response patterns to the overall cluster (significant four-way interactions all F_(1,21) between 7.266 and 11.017, all p values <0.05). Accordingly, a supplemental rmANOVA with these five anatomical ROIs as additional factor did not reveal any interaction with ROI.

In sum, we have first shown that the full range of behavioral effects for first-and second-order task and response transitions can be closely captured by a model that assumes a hierarchical relationship between task and response selection processes. Second, at the neural level these sequential hierarchical dependencies appear to arise from task-set control processes in the preSMA and response-set control processes in the SMA, and their respective interactions with the basal ganglia in driving final response selection. Neuroanatomically, the preSMA and SMA are known to project to, and receive projections from, distinct zones of the BG, with the preSMA implicated in a more anterior, cognitive “associational” frontostriatal loop and the SMA in a more posterior “sensorimotor” frontostriatal circuit (Inase et al., 1999; Akkal et al., 2007). In light of these anatomical considerations, we interpret the present results as indicating that the preSMA interacts with the BG in establishing task-set selection, which in turn imposes a (hierarchical) constraint on the interaction between the BG and SMA in determining response-selection.

To provide a robust test of this interpretation of the respective roles of the preSMA and SMA within the hierarchical switch model, especially considering current concerns about false-positive fMRI results (Eklund et al., 2016), we conducted a follow-up, fMRI-guided rTMS experiment. This allowed us to gauge the effect of temporarily disturbing function in the preSMA versus SMA on task performance, particularly as captured by the task- and response-switch cost parameter values of our statistical model.

rTMS data

The above results foster the hypothesis that preSMA-BG interactions implement control processes at the task-set level, and SMA-BG interactions implement control at the hierarchically subordinate response-set level. Specifically, the SMA's response profile (Fig. 3C) suggests that this structure is involved in counter-acting a tendency for repeating the previous response-set transition. Moreover, the four-way interaction observed in the BG (Fig. 3E), in combination with neuroanatomical considerations, suggests that the hierarchical relationship of task- and response-level costs in behavior may arise from interdependent preSMA-BG and SMA-BG corticostriatal loops. Thus, within the framework of our statistical model, we can derive the hypothesis that response costs [RC_n, TC_n−1(RC_n), RC_n−1(RC_n)] arise from the influence of the preSMA-BG loop on the hierarchically subordinate SMA-BG loop.

To test this proposal, we used the preSMA and SMA sites identified in the fMRI analyses as target sites for repetitive TMS at 1 Hz (see Materials and Methods), which has been shown to have sustained disruptive effects on processing in stimulated cortex (for reviews, see (Pascual-Leone et al., 2000, Walsh and Cowey, 2000). Specifically, subjects performed the identical task-switching protocol as above, once following preSMA-TMS, and once following SMA-TMS. Importantly, we could then use our model to derive best-fit values for task- and response-cost parameters for each of these two datasets and compare them against each other, thus enabling us to directly assess differential effects of TMS site on the latent variables underlying task performance. Our main hypothesis was that preSMA-TMS should significantly reduce response costs when compared with SMA-TMS (or, equivalently, that SMA-TMS should result in enhanced response costs compared with preSMA-TMS).

As shown in Figure 4A,B, the behavior in the TMS experiment replicated the basic overall RT pattern we had obtained in the fMRI experiment (Fig. 2D), as indicated by a qualitatively equivalent four-way interaction effect (F_(1,24) = 6.112, p < 0.05) that did not interact with stimulation site (F_(1,24) = 2.301, p = 14.2). Moreover, our model again provided an excellent account of the observed data (Fig. 4A,B, shaded areas), which was true both for the preSMA-TMS condition (correlation between simulated and observed data: r = 0.93, p < 1e−6; best-fit parameter values: TC_n = 15.0 ms, RC_n = 6.9 ms, TC_n−1(TC_n) = 5.1 ms, TC_n−1(RC_n) = 4.2 ms, RC_n−1(RC_n) = 4.1 ms, C = 697 ms), as well as for the SMA-TMS condition (correlation between simulated and observed data: r = 0.95, p < 1e-7; best-fit parameter values: TC_n = 12.8 ms, RC_n = 10.3 ms, TC_n−1(TC_n) = 11.5 ms, TC_n−1(RC_n) = 16.8 ms, RC_n−1(RC_n) = 14.4 ms, C = 709 ms).

Figure 4.

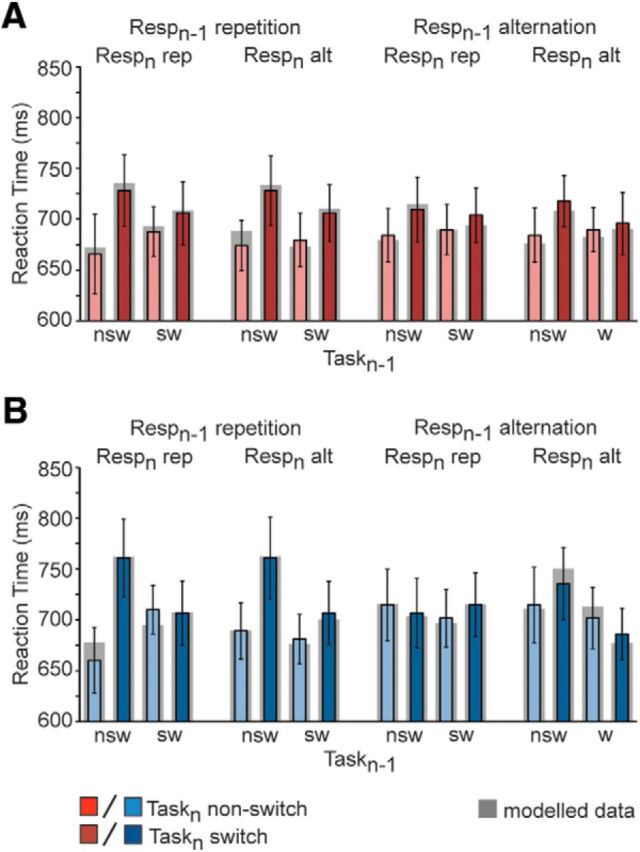
TMS experiment behavioral results. Mean RT (±SEM) interaction effect between previous and current trial task transitions as a function of trial N − 1 and trial N response transitions following 1 Hz rTMS stimulation of (A) the preSMA and (B) the SMA. Gray shading around the bars corresponds to best-fit model values. Resp, response; rep, repetition; alt, alternation; nsw, non-switch; sw, switch.

Most importantly, however, when comparing the effects of preSMA versus SMA stimulation, we found that the combined total response cost [RC_n, TC_n−1(RC_n), RC_n−1(RC_n); Table 2] was significantly increased following SMA stimulation compared with preSMA stimulation (t₍₂₄₎ = 2.81, p < 0.01). Task-level costs, on the other hand, were unaffected by the TMS conditions (t₍₂₄₎ = 0.48, p = 0.63). To elucidate in which direction response costs were effected after rTMS, i.e., whether they were relatively increased or decreased, we further assessed differential effects between preSMA and SMA stimulation (as revealed via paired-sample t-tests) by comparisons with the fMRI study-derived model parameters (via independent sample t-tests). Results clarified that although the combined response cost was driven on the one hand by increased costs after SMA stimulation (t₍₄₅₎ = 2.060, p < 0.05), it was also accentuated by a trend for a reduction in response costs after preSMA stimulation (t₍₄₅₎ = 1.755, p = 0.083), albeit limited to response costs that are driven by N − 1 trial transition. In summary, the fMRI-guided rTMS experiment supported the hierarchical organization in medial frontal cortex that we had predicted on the basis of the behavioral and fMRI data, in that a temporary disturbance of processing in the preSMA, relative to SMA, resulted in a selective reductions of response-switch costs, while temporary disruption of the SMA led to an increase in response-switch costs.

Discussion

The mutual constraints that task- and response-selection processes impose on each other have long been considered to reflect some important (yet unknown) organizing principle of cognitive control (Rogers and Monsell, 1995). We here formalized, extended, and tested a prominent account for task- by response-cost interactions based on the assumption of a hierarchical relationship between superordinate task-set and subordinate response-set representations (Kleinsorge and Heuer, 1999). A hierarchical sequential switch model implementation provided excellent fits for the entire range of first- and second-order sequence RT (and BG fMRI) data and outperformed alternative models. The behavioral task- and response-cost data were furthermore systematically related to neural activity in key regions of premotor cortex and BG circuitry, whereby preSMA activation tracked putative task-set control costs, the SMA tracked putative response-set control costs, and BG and thalamus activity mirrored the interaction between task- and response-set regulation processes that characterized participants' response times. A subsequent fMRI-guided TMS experiment confirmed dissociable roles of the preSMA and SMA in determining response costs, as implied by their hypothesized roles. Together, these data provide novel evidence for a hierarchical functional gradient in the organization of posterior medial frontal cortex and its interaction with the BG, where a superordinate preSMA-BG loop establishes task-set selection that imposes a (hierarchical) constraint on a subordinate SMA-BG loop that determines response-selection.

To characterize the neurocognitive mechanisms underlying the well known interaction effect between task- and response switching processes, we first formalized Kleinsorge and Heuer's (1999) hierarchical switch model and then expanded the model to generate new predictions for higher-order sequential effects. This allowed us to put the model to a novel test, but it also necessitated additional assumptions. These were based closely on the logic of the original model, however. First, the assumption that, by default, a previous-trial task-set and response is “carried over” to the present trial was extrapolated to the assumption that the higher-order task sequence (i.e., whether the previous trial transition constituted a task repetition or a task switch) would also impose a carry-over effect, whereby subjects enjoy a performance benefit from regular higher-order sequences (i.e., two or more task alternations or task repetitions in a row) relative to irregular ones. Second, the task level also supersedes the response level in the expression of this higher-order sequence effect. Apart from representing a straightforward extrapolation of the original model tenets, the assumption of subjects' performance being susceptible to regularities in higher-order sequences is grounded in previous behavioral (Bertelson, 1963; Kirby, 1976; Soetens et al., 1985; Cho et al., 2002; Brown et al., 2007) and neural findings (Squires et al., 1976; Huettel et al., 2002). These model assumptions produced excellent fits of RT data across two datasets, accounting for ∼85% of the variance, and thus providing strong support for the underlying assumption of hierarchically organized task- and response-sets.

The current model proved superior in explaining the data than a large set of other model variants. However, one alternative account holds that the basic (first-order) task- by response-switch interaction effect reflects a mix of response inhibition and category priming processes. Specifically, this account assumes that (1) responses are by default (self-) inhibited after they have been executed, and (2) that the task-relevant stimulus category produces some form of cross-trial priming effects, such that priming due to the repeated relevant stimulus category on task repetition trials (over-) compensates for the default response inhibition, thus turning a repetition cost into a repetition benefit in RT (Hübner and Druey, 2006; Druey, 2014). However, without adding assumptions to this theory that are not implied by these two basic tenets, it is difficult to see how this model could account for the higher-order effects obtained in the present study. For instance, it does not seem to follow from the assumptions of category priming and self-inhibiting responses that a change in higher-order task transition would abolish these first-order effects, as is the case in the empirical data. However, it would be valuable if this or other alternative accounts of the first-order effects could be similarly expanded to generate predictions for higher-order sequence effects and then formally pitted against the model described here.

Our imaging results suggest a key role in task selection for the preSMA. This fits closely with a prominent view of this structure as mediating proactive (cued) switching of behavioral strategies (Hikosaka and Isoda, 2010), which takes support from electrophysiological studies in the monkey showing that preSMA houses neurons that are activated when switching between target stimuli (Matsuzaka and Tanji, 1996) or procedural rules (Nakamura et al., 1998), and whose functions appear to include the suppression of a previous, now irrelevant task-set, and the facilitation of the newly relevant task-set (Isoda and Hikosaka, 2007). Moreover, a prominent role for preSMA in task-switching has also been highlighted in the human literature, where this regions is reliably activated in fMRI studies of switching (Derrfuss et al., 2005; Ruge et al., 2013), and disruptive TMS to preSMA selectively impairs switch trial performance (Rushworth et al., 2002). Together with a large literature indicating that lateral prefrontal and posterior parietal cortex are involved in representing task rules and implementing them in terms of biasing of perceptual processing and stimulus-response linkages (Brass and von Cramon, 2004; Woolgar et al., 2011; Waskom et al., 2014), the role of preSMA is likely one of controlling the motor output end of the task-regulation process by suppressing irrelevant and facilitating relevant S–R mappings (cf. Nachev, 2006; Hikosaka and Isoda, 2010). Because the preSMA has no direct anatomical connections with primary motor cortex (Luppino et al., 1993), its influence on action selection would have to be mediated through its connections to the SMA, which connects densely with M1 (Luppino et al., 1990), and/or its projections to the striatum/BG (Inase et al., 1999), given the latter's well established role in inhibiting and facilitating response selection (Mink and Thach, 1993; Mink, 1996; Grillner et al., 2005; Redgrave et al., 2010).

Based on the current data and a large literature suggesting that selecting an action among competing alternatives relies on cortico-BG-cortico loops (for review, see Redgrave et al., 2010), we therefore argue that the influence of preSMA on appropriate response selection likely plays out via a preSMA-BG task-selection loop that constrains a hierarchically subordinate SMA-BG response-selection loop. These differential roles for the preSMA and SMA are congruent with a large literature. As noted above, the preSMA (but not the SMA) receives direct input from dorsolateral prefrontal cortex, whereas the SMA, but not the preSMA, projects directly to primary motor cortex (for review, see Nachev et al., 2008). Moreover, the preSMA and SMA are thought to form part of a more anterior, cognitive associational and a more posterior sensorimotor cortico-BG loop, respectively (Inase et al., 1999; Akkal et al., 2007). Accordingly, preSMA neurons are activated by cues that signal task shifting before the implementation of the implied responses, whereas SMA neurons are activated in relation to the actual motor responses (Matsuzaka and Tanji, 1996). In line with a hierarchical relationship of these regions, however, our TMS findings show that disrupting preSMA processing will nevertheless have predictable knock-on effects on SMA response selection processes. Finally, our proposal of a hierarchical rostrocaudal gradient of task- and response-selection processes in the posterior medial frontal cortex has close conceptual correspondence with similar proposals concerning an abstract-to-concrete rostrocaudal organization of cognitive control functions in lateral PFC (Koechlin et al., 2003; Badre and D'Esposito, 2007; Koechlin and Summerfield, 2007). Empirical data and computational modeling suggest, congruent with our current proposal, that the hierarchical interactions between adjacent levels of these processing structures play out via rostrocaudally arranged corticostriatal loops (Badre and Frank, 2012; Frank and Badre, 2012).

In summary, we used modeling, fMRI, and TMS to investigate the neurocognitive mechanisms underlying a key behavioral signature of human cognitive control, namely interdependent task- and response-selection costs. We found strong evidence that this behavioral phenomenon reflects a hierarchical organization of premotor regions in posterior medial frontal cortex and their interactions with the BG. Specifically, our data suggest that a superordinate preSMA-BG loop establishes task-set selection, which consequently constrains a subordinate SMA-BG loop that determines response-selection, which produces the characteristic interdependence in task- and response-switch costs in behavior.