Defining the role of active-site loop fluctuations in dihydrofolate reductase catalysis

Abstract

Dynamic processes are implicit in the catalytic function of all enzymes. To obtain insights into the relationship between the dynamics and thermodynamics of protein fluctuations and catalysis, we have measured millisecond time scale motions in the enzyme dihydrofolate reductase using NMR relaxation methods. Studies of a ternary complex formed from the substrate analog folate and oxidized NADP⁺ cofactor revealed conformational exchange between a ground state, in which the active site loops adopt a closed conformation, and a weakly populated (4.2% at 30°C) excited state with the loops in the occluded conformation. Fluctuations between these states, which involve motions of the nicotinamide ring of the cofactor into and out of the active site, occur on a time scale that is directly relevant to the structural transitions involved in progression through the catalytic cycle.

Proteins are dynamic molecular machines, and conformational fluctuations on a wide range of time scales are intimately associated with protein function. It has long been recognized that dynamic processes play an important role in the catalytic function of enzymes (1, 2). Protein motion is implicated in events such as binding of substrate or cofactor, allosteric regulation, and product release, and the catalyzed reaction itself is inherently dynamic, with changes in atomic positions occurring along the reaction coordinate (3). Despite mounting experimental evidence that the active sites of enzymes are inherently flexible (4–6), a detailed understanding of the relationship between the dynamics and thermodynamics of protein fluctuations and the catalytic process is currently lacking.

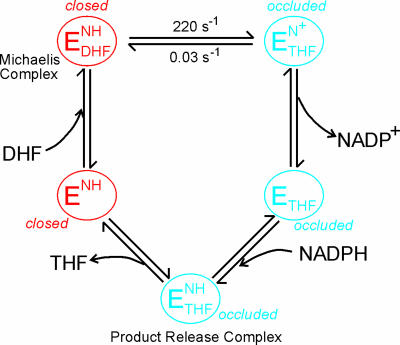
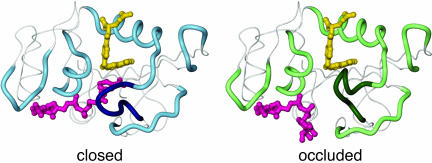
A number of experimental and theoretical investigations have suggested that protein motions play an important role in catalysis by the enzyme dihydrofolate reductase (DHFR) (see refs. 7 and 8 for recent reviews). DHFR catalyzes the reduction of 7,8-dihydrofolate (DHF) through stereo-specific hydride transfer from reduced nicotinamide-adenine dinucleotide phosphate (NADPH) cofactor. The enzyme is essential for tetrahydrofolate (THF) biosynthesis, plays a central role in promoting cell growth and proliferation, and is the target of several anticancer and antibiotic drugs. Escherichia coli DHFR has been subjected to extensive kinetic and structural studies that have defined the complete kinetic mechanism (9) and the structural transitions involved in the catalytic cycle (10, 11). During the reaction cycle (Fig. 1), the enzyme progresses through conformations in which the active site loops are in a closed state, in the holoenzyme and the Michaelis complex, and a series of product complexes in which the loops adopt an occluded conformation. In the closed state, the Met-20 loop (residues 9–24) packs against the nicotinamide ring of the cofactor and seals the active site (10). In the occluded state, Met-16 and Glu-17 in the Met-20 loop project into the active site and sterically occlude the binding site for the nicotinamide-ribose moiety. The closed conformation is stabilized by a network of hydrogen bonds between the Met-20 loop and the FG loop (residues 116–132), whereas the occluded state is stabilized by hydrogen bonding interactions with the GH loop (residues 142–150) (10).

Fig. 1.

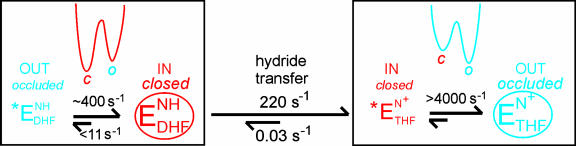
Schematic representation of the catalytic cycle of E. coli DHFR for steady-state turnover under saturating substrate conditions (9). The active site loops in the holoenzyme (E^NH) and Michaelis complex (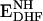) are in the closed conformation. The ternary (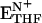) and binary (E_THF) product complexes and the product release complex (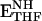) all adopt the occluded conformation (10, 11). NH and N⁺ refer to reduced and oxidized cofactor, NADPH and NADP⁺, respectively.

Kinetic analysis of Met-20, FG, and GH loop mutants has confirmed their functional role in catalysis and in binding and release of cofactor, substrate, and products (12–14). The active site loops must cycle between the closed and occluded conformations at two steps in the reaction pathway, immediately after hydride transfer and again after product release; mutations that destabilize the closed conformation impair hydride transfer (13). These conformational transitions require large-scale reorganization of the Met-20 loop, with atoms moving as much as 10 Å in the backbone and nearly twice that for certain side chains (10). Molecular dynamics simulations of the closed Michaelis complex have revealed strong motional coupling between the FG and Met-20 loops that is lost in the product complexes (15). More recent simulations have suggested the presence of a network of dynamically coupled residues in DHFR whose thermal motions promote catalysis by helping to direct the nicotinamide ring of the cofactor toward the pterin ring of the substrate (16).

To advance our understanding of the link between protein dynamics and DHFR catalysis, we have undertaken detailed NMR studies of the E. coli enzyme. Previous spin relaxation studies revealed large-amplitude picosecond-to-nanosecond time scale motions of the Met-20 loop in the occluded states of the enzyme that are abrogated upon loop closure (4, 17, 18). These studies also hinted at changes in microsecond-to-millisecond time scale motions that are potentially relevant to catalysis. Here, we describe the application of recently introduced relaxation dispersion experiments to analyze quantitatively the dynamics and thermodynamics of slow conformational fluctuations of the active site loops, in a ternary complex that is a model for the Michaelis complex (10, 11, 19). By measuring the dependence of transverse ¹⁵N relaxation rate (R₂) on the temporal separation (τ_cp) between pulses in the NMR experiment, information is obtained on the differences in chemical shift (Δω) between the exchanging conformers and on the kinetics and thermodynamics of the exchange process. For DHFR, these measurements reveal conformational exchange between a closed ground state and an occluded excited state on a millisecond time scale that is directly relevant to the structural transitions involved in progression through the catalytic cycle.

Materials and Methods

Sample Preparation. Uniformly ¹⁵N, ²H-labeled DHFR was expressed in BL21-DE3 cells in M9 minimal medium and purified as described in ref. 20. MALDI mass spectrometry was used to check the purity and extent of deuteration (≈80%). The protein was exchanged into argon-saturated NMR buffer [50 mM potassium phosphate (pH 6.8), containing 0.1 M KCl, 1 mM EDTA, and 1 mM DTT] by using a NAP5 column. The ternary complex with folate and NADP⁺ was formed by addition of a 10-fold excess of NADP⁺ to the DHFR solution, followed by immediate titration with 1 M sodium hydroxide to maintain the pH at 6.8 (4). A 6-fold excess (over DHFR) of folate was then added, and the DHFR:folate:NADP⁺ complex was split into two samples (each ≈1.2 mM) and placed in amberized NMR tubes to avoid degradation of folate from exposure to light.

¹⁵NR₂ Dispersion Experiments. ¹⁵N R₂ relaxation rates were measured by using a relaxation-compensated–Purcell–Meiboom–Gill (CPMG) pulse sequence as described in refs. 21 and 22. The CPMG period was implemented in a constant time manner, with T = 40 ms. Relaxation dispersion profiles were generated by measuring R₂ relaxation rates as a function of τ_cp, the time between successive 180° pulses in the CPMG sequence. Spectra were acquired as two-dimensional data sets at τ_cp intervals of 10, 5, 3.33, 2.5, 2, 1.66, 1.43, 1.25, 1, 0.83, 0.71, 0.63, 0.56, and 0.5 ms (data points 3.33, 1, and 0.5 are duplicated). A reference spectrum with the CPMG blocks omitted was also acquired in duplicate. Spectra were acquired by using (1,536 × 128) complex points in the (t₂ × t₁) dimensions for both 500- and 800-MHz fields with eight scans per t₁ increment and 3-s recycle delays. Spectral widths used at 500 MHz were (8,012 × 1,852) Hz and (12,019 × 3,333) Hz at 800 MHz. Data were recorded on Bruker Avance spectrometers operating at ¹H frequencies of 500 and 800 MHz. The probe temperature was calibrated with methanol, and data were acquired at temperatures of 303.4, 306.4, 309.4, and 312.4 K. Spectra were processed by using nmrpipe (23), and peak intensities were measured as the sum of the intensities for a 3 × 3 grid centered on the peak maxima by using an in-house computer program. Effective R₂ relaxation rates (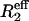) were determined from the relation 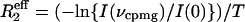(24), where T (= 40 ms) is the total relaxation period during CPMG pulsing, I(ν_cpmg) represents peak intensities with CPMG pulsing at a particular radio frequency field, and I(0) is the intensity in the reference spectrum obtained without the CPMG pulse train or the associated delay.

Data Fitting. The dispersion data from each residue were initially tested to determine whether a significant amount of relaxation dispersion was present. Data for which R₂ changed by <2 s^–1 over the entire range of τ_cp were excluded from further analysis. The remaining residues were tested to determine whether the variation in R₂ was statistically significant by fitting each to a horizontal line and to a simplified two-site expression valid for fast exchange (25):

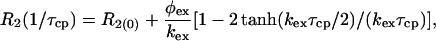[1]

where φ_ex = p_ap_bΔω² and R₂₍₀₎ is the R₂ relaxation rate in the absence of exchange. Residues for which an F test at the 99.9% confidence limit indicated that the dispersion was not significant were also excluded from further analysis.

For each residue that displays statistically significant dispersion, the R₂ relaxation dispersion data at the two fields were fit simultaneously to the general equation for exchange between two sites, A and B (21, 26):

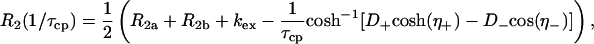[2]

where

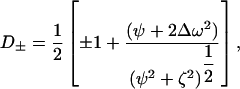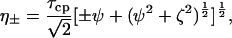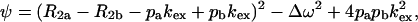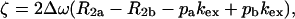τ_cp is the delay between CPMG 180° pulses, p_a and p_b are the populations of sites A and B, R_2a and R_2b are the R₂ relaxation rates in sites A and B in the absence of exchange (it is assumed that R_2a = R_2b = R₂₍₀₎ in the present work), k_ex is the rate of exchange, and Δω is the chemical shift difference between the two sites.

Initially, the data for each residue were fitted individually to Eq. 2 by using the in-house program glove (by J.C.L.), resulting in a reduced χ² value for each residue, 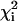. Upon examination of the individual fits for all residues, it was evident that, at any given temperature, the exchange rates were clustered in two distinct sets characterized by small or large values of k_ex. Consequently, the dispersion data for the residues in each set were then refitted with a global value of k_ex and of p_b while allowing Δω and R₂₍₀₎ for the individual residues to float. The global reduced χ² value, 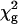, for each residue was compared with 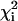. A global fit for each residue in the set was considered justified 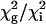was <2. Uncertainties the parameters were estimated by Monte in Carlo simulations. The majority of dispersion curves at each temperature could be adequately fit by using a global rate constant (k_ex = 477, 555, 595, and 651 s^–1 at 303.4, 306.4, 309.4, and 312.4 K, respectively). The dispersion curves for a small cluster of residues near the C terminus and in a neighboring loop could not be fit satisfactorily by these exchange rates (i.e., 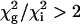) and were fit better by k_ex values of 1,010, 1,280, 2,040,2,100 s^–1 at 303.4, 306.4, 309.4, and 312.4 K, respectively. Thermodynamic parameters for the slowly exchanging residues were determined by using transition-state theory (27) with uncertainties estimated by jackknife simulations.

Results

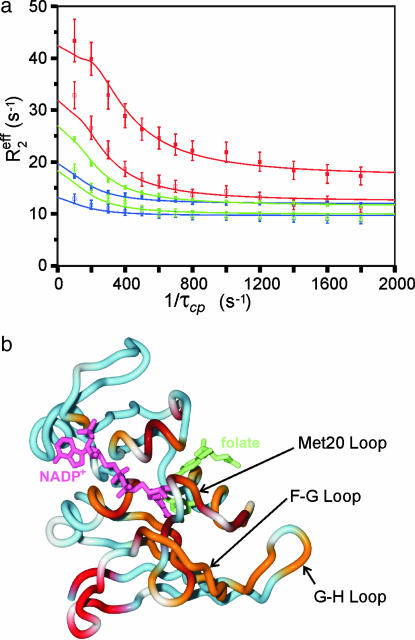
Relaxation Dispersion Measurements. NMR experiments were performed on E. coli DHFR bound to the substrate analog folate and the oxidized NADP⁺ cofactor. This complex adopts the closed conformation with both the nicotinamide and pterin rings occupying the active site, and is a model for the reactive Michaelis complex (10, 19). To probe backbone motional processes occurring on a microsecond-to-millisecond time scale, effective transverse ¹⁵N relaxation rates (R^eff₂) were recorded at two magnetic field strengths as a function of the pulse spacing τ_cp in CPMG relaxation experiments (21). Representative relaxation dispersion profiles as a function of 1/τ_cp are shown in Fig. 2a. Of the resolved backbone amide resonances in the ¹H-¹⁵N correlated spectra, those of 41 residues exhibit well defined ¹⁵N R₂ dispersion profiles; a further 80 residues display no dispersive behavior. All of the dispersion curves could be fit well by using a two-site exchange model,

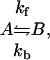where the measured exchange rate, k_ex, is k_f + k_b, and the populations of the ground state and excited state are p_a and p_b, respectively. The dispersion data were initially fit independently for individual residues. However, inspection of the k_ex values revealed clustering about slow and fast rates, and the data were therefore subjected to a global fitting procedure for each cluster (see Materials and Methods).

Fig. 2.

Relaxation dispersion measurements for the ternary complex of DHFR with folate and NADP⁺.(a) ¹⁵N relaxation dispersion profiles for representative residues from the Met-20 (Ala-19, blue lines and symbols), FG (Glu-120, green), and GH (His-149, red) loops. The data were acquired at 306.4 K at spectrometer frequencies of 500 (open symbols) and 800 (filled symbols) MHz. The solid lines show the fits to the general exchange equation (Eq. 2) with k_ex = 555 s^–1 and p_b = 5.5%. (b) Structure of the ternary complex of E. coli DHFR with bound folate and NADP⁺ (10) showing the location of residues that exhibit exchange broadening. Residues that exhibit ¹⁵N relaxation dispersion due to conformational fluctuations with k_ex = 555 s^–1 (at 306.4 K) are colored orange; residues fit to k_ex = 1,280 s^–1 are colored red. Residues that exhibit severe exchange broadening at all temperatures are colored brown, and those that show no dispersive behavior are colored blue. Proline and residues with missing or overlapped ¹⁵N resonances are white. The bound NADP⁺ is pink and folate is shown in green.

Slow Backbone Dynamics in the Active Site. The residues affected by conformational exchange processes are mapped onto the DHFR backbone structure in Fig. 2b. The dispersion curves for most residues were best fit by a global exchange rate of k_ex = 555 ± 24 s^–1 at 306.4 K, describing the overall rate of fluctuations between the ground state, A, and a small population (p_b = 5.5 ± 0.2%) of an excited state, B. These residues are located in the immediate vicinity of the substrate and cofactor binding sites and in the Met-20, FG, and GH loops. The ¹H-¹⁵N cross peaks of an additional 13 residues, all located in the same regions around the active site, are severely broadened at all temperatures studied and are clearly subject to microsecond-to-millisecond time scale exchange processes. A cluster of residues near the C terminus and in the neighboring region of the FG loop (residues 127–134) experience a faster exchange process, with k_ex = 1,280 ± 90 s^–1 at 306.4 K and an excited state population, p_b = 3.5%.

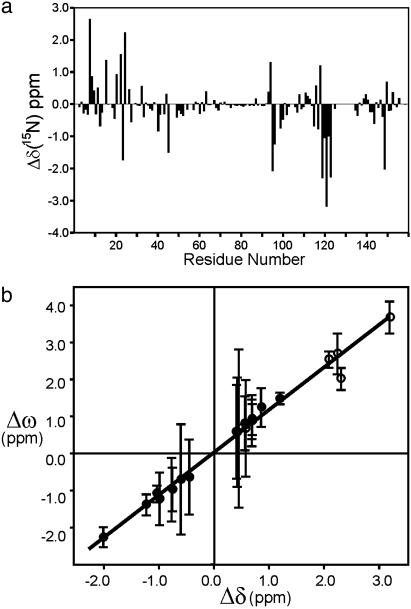
Identification of the Excited State. Previous NMR studies of DHFR have identified a subset of resonances that report on the conformation, closed or occluded, of the active site loops (28). Most of these marker resonances are exchange broadened and exhibit dispersive behavior in the CPMG experiments reported here. To obtain insights into the nature of the 555-s^–1 exchange process, we determined the magnitude of Δω, the difference in ¹⁵N chemical shift between the ground and excited states, by analysis of the ¹⁵N R₂ relaxation dispersion profiles. The CPMG dispersion experiments can give only an absolute value for Δω, but the sign can be determined for many resonances from exchange-induced shifts of ¹⁵N frequencies in heteronuclear single quantum correlation and heteronuclear multiple quantum correlation spectra (29). For the subset of residues that are sensitive to the 555-s^–1 exchange process, the Δω values calculated from the relaxation data correspond very closely in both magnitude and sign (where known) to the ¹⁵N chemical shift differences associated with the transition between the closed and occluded conformations (Fig. 3). The equilibrium chemical shift differences (Fig. 3a) were measured between the closed ternary complex with folate and NADP⁺ and the occluded complex formed by folate and the reduced cofactor analog, 5,6-dihydro-NADPH (28). These complexes differ only in the conformation of the active site loops and in the occupancy of the nicotinamideribose binding site, which is empty in the occluded form; the adenosine moiety of the cofactor remains bound to the enzyme in both complexes. The remarkable correlation between the dynamic and equilibrium chemical shifts (Fig. 3b) shows unequivocally that the exchange process in the model Michaelis complex involves fluctuations between a closed ground state and an occluded excited state. The rate constants for the transition from the closed ground state to the occluded excited state (k_f = 31 ± 1.7 s^–1 at 306.4 K) and for the reverse process (k_b = 524 ± 30 s^–1) were determined from the global k_ex and the population p_b.

Fig. 3.

Correlation of chemical shift differences observed between closed and occluded ternary complexes of DHFR and the chemical shift differences determined from the relaxation dispersion measurements. (a) Difference in ¹⁵N chemical shift (Δδ) between the closed DHFR:folate:NADP⁺ complex and the occluded DHFR:folate:DHNADPH complex (28). (b) Scatter plot showing correlation (R = 0.99) between Δω, determined from ¹⁵N relaxation dispersion curves fit with k_ex = 555 s^–1 (at 306.4 K), and the equilibrium ¹⁵N chemical shift difference, Δδ. Residues for which the sign of Δω can be determined experimentally (see text) are indicate by filled circles. Absolute values of both Δω and Δδ are plotted (open circles) when the sign of Δω is unknown. The line of best fit is shown (slope = 1.12 ± 0.05). Residues for which Δδ is <0.4 ppm, and which are therefore relatively insensitive to the closed–occluded conformational transition, are omitted from the correlation plot.

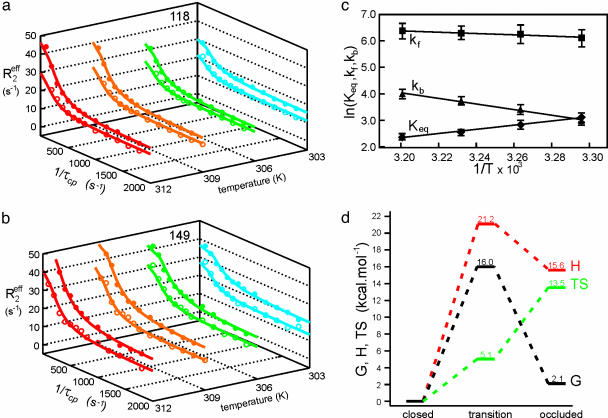
Thermodynamics of Backbone Fluctuations. To obtain information on the thermodynamics of the exchange process, ¹⁵N relaxation dispersion measurements were performed at additional temperatures ranging from 303.4 to 312.4 K. The temperature range was limited by instability of the protein complex at higher temperatures and by excessive broadening of resonances at lower temperatures. Nevertheless, substantial changes in the dispersive behavior of many resonances occurred even within this temperature range (Fig. 4 a and b). The temperature dependencies of the rate constants k_f and k_b and the equilibrium constant K_eq = k_b/k_f were determined from fits of the dispersion curves and values of the underlying thermodynamic parameters were calculated (Fig. 4c). For the closed to occluded transition, ΔG = 2.1 ± 0.3 kcal·mol^–1, ΔH = 15.6 ± 2.1 kcal·mol^–1, and TΔS = 13.5 ± 2.1 kcal·mol^–1 at 298 K. The large increase in entropy is consistent with the significantly enhanced backbone flexibility of the Met-20 and FG loops in the occluded state (4). Indeed, using the method of Yang and Kay (30) to calculate entropy from backbone order parameters, we estimate that differences in picosecond-to-nanosecond time scale backbone motions contribute ≈75% of the measured TΔS. The activation thermodynamic parameters for the forward and backward processes were determined (Fig. 4d) by applying conventional transition state theory with Arrhenius-type temperature dependence of the rates (27). The entropy of the transition state, and hence the flexibility of the active site loops, is intermediate between that of the closed and occluded states.

Fig. 4.

Determination of thermodynamic parameters for the closed–occluded exchange process. Relaxation dispersion profiles for Glu-118 (a) and His-149 (b) at 303.4 (blue), 306.4 (green), 309.4 (orange), and 312.4 (red) K. The data were acquired at spectrometer frequencies of 500 (open symbols) and 800 (filled symbols) MHz. The solid lines show the fits to the general exchange equation (Eq. 2). (c) Arrhenius and van't Hoff plots for the forward (k_f) and backward (k_b) rate constants and the equilibrium constant (K_eq = k_b/k_f) obtained from global fits of k_ex and p_b for the exchange process affecting the active site loops. (d) Schematic energy level diagram showing enthalpy (H), free energy (G), and entropy (TS) at 298 K of the occluded excited state and the transition state relative to the closed ground state.

Discussion

Relaxation dispersion measurements provide a powerful method for probing the energy landscape of proteins, identifying small populations of excited states, and mapping the kinetics of conformational transitions (27, 31, 32). Application of these methods to a number of enzymes has revealed motions of active site loops on the time scale of catalysis (33–36). However, it has generally proved difficult to characterize structurally the excited state that is involved in the conformational averaging. In the present work, ¹⁵N relaxation dispersion measurements have not only provided a detailed description of the kinetics and thermodynamics of active site loop fluctuations in a complex of DHFR, but have allowed identification of the conformational states involved.

Millisecond time scale fluctuations have been observed between the closed ground state of the ternary complex of DHFR with folate and NADP⁺ and an occluded excited state. The extent of the conformational changes involved is illustrated in Fig. 5. The experiments on the DHFR:folate:NADP⁺ complex provide valuable insights into the dynamics of loop conformational changes that occur before and during the transition from the closed Michaelis complex to the occluded DHFR:THF:NADP⁺ product complex (Fig. 1). For the closed ground state of the DHFR:folate:NADP⁺ complex (and by inference, the Michaelis complex), the rate of spontaneous fluctuations to the occluded excited state [estimated from the Arrhenius plot (Fig. 4c) to be 11 s^–1 at 25°C], with concomitant expulsion of the nicotinamide ring from the active site, is >10-fold slower than the chemistry [the rate of hydride transfer is 220 s^–1 at 25°C and pH 7.0 (9)]. Thus, the nicotinamide ring is confined within the active site, in close proximity to the substrate, for long enough to facilitate hydride transfer. The active site loops must remain closed during the chemical step to protect the reactants from solvent and to correctly position the nicotinamide and pterin rings for hydride transfer; deletion of the central region of the Met-20 loop and replacement by a single glycine residue leads to a 500-fold decrease in the rate of hydride transfer and an increase in the rate of NADPH dissociation (12).

Fig. 5.

Structural changes associated with the closed-to-occluded transition. The polypeptide backbone surrounding the active site and the adenosine binding site is shown as a thick tube, with the central region of the Met-20 loop emphasized in darker colors. The substrate and cofactor are colored yellow and pink, respectively. The closed conformation is represented by the x-ray structure of the DHFR:folate:NADP⁺ complex (PDB ID code 1RX2) (10). The nicotinamide ring occupies the active site, with the Met-20 loop packed against it. The occluded conformer is represented by the structure of the ternary complex of DHFR with 5,10-dideazatetrahydrofolate and NADPH (PDB ID code 1RX6) (10); the nicotinamide-ribose moiety is absent from the crystal structure and has been modeled with the nicotinamide ring projecting into solution. In the occluded conformation, the Met-20 loop blocks the nicotinamide-ribose binding pocket.

After hydride transfer, the increased pterin ring pucker of the THF product and resulting steric conflict with the nicotinamide ring of the oxidized cofactor destabilizes the closed state, leading to a transition to the occluded conformation and expulsion of the nicotinamide-ribose moiety from its binding pocket (10, 11). The relative energies of the closed and occluded states are therefore inverted immediately after hydride transfer: The occluded state is the ground state in the product ternary complex, and the closed state becomes the higher-energy excited state (Fig. 6). We assume that the energies of the transition state and the occluded state remain approximately the same and that the population of the newly formed closed excited state is <10% [based on the absence of observable resonances for the closed conformer in HSQC spectra of the DHFR:THF:NADP⁺ complex (11)]. Then, from the kinetics measured for the DHFR:folate:NADP⁺ complex, we can estimate a lower limit (k > 4,000 s^–1 at 25°C) on the rate of the loop conformational change after the chemical step. Thus, active site loop motion to the occluded conformation and loss of the oxidized nicotinamide ring from the binding pocket are expected to occur very rapidly after hydride transfer is complete.

Fig. 6.

Schematic diagram showing the additional steps (in boxes) implicated in the transitions from the closed Michaelis complex to the occluded product ternary complex. The experimentally observed kinetic intermediates (9) are enclosed in circles, and closed and occluded conformations are indicated in red and blue, respectively. Schematic free energy diagrams indicating the relative energies of the closed and occluded states, deduced from the present relaxation dispersion studies of the DHFR:folate:NADP⁺ model of the Michaelis complex, are shown. Excited states associated with the closed–occluded equilibria are marked with an asterisk. “IN” and “OUT” denote whether the nicotinamide ring of the cofactor occupies the active site or is displaced by the Met-20 loop. The estimated rates, extrapolated to 25°C, for the conformational transitions are indicated.

Previous kinetic studies of DHFR have revealed the important role played by the Met-20, FG, and GH loops in stabilization of the transition state and in control of substrate, product, and cofactor binding affinity and turnover (12–14). Our present relaxation dispersion measurements provide new insights into the mechanism by which millisecond time scale fluctuations of the active site loops, modulated by ligand-dependent changes in the relative stabilities of the major Met-20 loop conformations, are coupled to progression through the catalytic cycle. The enzyme is revealed as a finely tuned molecular machine, in which large-scale fluctuations in the protein structure are integral to its catalytic function. It seems unlikely that the slow loop fluctuations observed in the present experiments are linked directly to the chemistry. Recent experiments have shown that protein motions are coupled directly to hydrogen tunneling in the hydride transfer step (37), but these motions probably involve local fluctuations within the closed ground state of the Michaelis complex, and not the large scale conformational transitions involving restructuring of the active site loops. Rather, the flexibility in the active site loops appears to be harnessed by the enzyme to control the flux of substrate, product, and cofactor, and to correctly position the reactants in the active site before the hydride transfer step.