Contentious relationships in phylogenomic studies can be driven by a handful of genes

Abstract

Phylogenomic studies have resolved countless branches of the tree of life (ToL), but remain strongly contradictory on certain, contentious relationships. Here, we employ a maximum likelihood framework to quantify the distribution of phylogenetic signal among genes and sites for 17 contentious branches and 6 well-established control branches in plant, animal, and fungal phylogenomic data matrices. We find that resolution in some of these 17 branches rests on a single gene or a few sites, and that removal of a single gene in concatenation analyses or a single site from every gene in coalescence-based analyses diminishes support and can alter the inferred topology. These results suggest that tiny subsets of very large data matrices drive the resolution of specific internodes, providing a dissection of the distribution of support and observed incongruence in phylogenomic analyses. We submit that quantifying the distribution of phylogenetic signal in phylogenomic data is essential for evaluating whether branches, especially contentious ones, are truly resolved. Finally, we offer one detailed example of such an evaluation for the controversy regarding the earliest-branching metazoan phylum, where examination of the distributions of gene-wise and site-wise phylogenetic signal across 8 data matrices consistently supports ctenophores as sister group to all other metazoans.

A well-resolved tree of life (ToL) is essential for understanding life’s history and the evolution of phenotypic diversity. The genomics revolution has enabled the assembly of many taxon-rich genome-scale data matrices for reconstructing the phylogenies of a wide diversity of lineages across the ToL^1–4. One important consequence of the large number of loci or genes included in these phylogenomic data matrices is that the internal branches (internodes) in the inferred topologies typically receive very high support values^5–9, leading to the perception that such branches are definitive and unlikely to change.

However, different phylogenomic analyses can sometimes strongly support branches that contradict one another. For example, concatenation analysis of a 1,233-gene, 96-taxon phylogenomic data matrix (609,899 amino acid sites) provided absolute clade support for the family Ascoideaceae as the closest relative of the families Phaffomycetaceae + Saccharomycodaceae + Saccharomycetaceae⁴; in contrast, concatenation analysis of a 1,559-gene, 38-taxon phylogenomic data matrix (364,126 amino acid sites) robustly placed the family Ascoideaceae as sister to a broader clade composed of the family Pichiaceae, the CUG-Ser clade, the family Phaffomycetaceae, the family Saccharomycodaceae, and the family Saccharomycetaceae¹⁰. Contradictory branches can even be observed when different analytical approaches are used on the same data matrix. Case in point, a phylogenomic analysis (maximum likelihood, homogeneous model, Opisthokonta as outgroup) of 406 genes from 70 taxa (88,384 amino acid sites) recovered ctenophores as sister to all other metazoan phyla¹¹, whereas another analysis (Bayesian inference, heterogeneous model, Choanoflagellata as outgroup) of the same data matrix supported sponges, rather than ctenophores, as the sister to the rest of the metazoan phyla¹².

While both biological and analytical factors influence phylogenetic inference^13–17, the first step to understanding why different phylogenomic data matrices (or different analyses of the same data matrix) yield two contradictory topologies is the precise quantification of the phylogenetic signal and identification of the genes or sites that gave rise to such conflict. To address this critical, yet poorly understood, question, we examined the distribution of phylogenetic signal in 17 contentious branches and 6 well-established branches (used as controls), in three large phylogenomic data matrices from plants, animals, and fungi (Table 1). Finally, we applied our approach of dissecting the distribution of phylogenetic signal in eight different phylogenomic data matrices aimed to resolve the controversy regarding the earliest-branching phylum of the Metazoa.

Table 1.

The 17 contentious branches and 6 well-established branches (controls) as well as their alternative hypotheses in three phylogenomic data matrices from plants, animals, and fungi.

Kingdom	Branch	Maximum likelihood tree (T1)	Alternative hypothesis (T2)	P-value of AU& test
Plants	Amborella	Amborella as sister to all other flowering plants	Amborella + Nuphar as sister to all other flowering plants	0.001*
	Angiosperm	Magnoliids as sister to Eudicots + Chloranthales	Magnoliids + Chloranthales as sister to Eudicots	0.030*
	Bryophyte	Hornworts as sister to all other land plants	Hornworts as sister to mosses + liverworts	0.012*
	Gymnosperm	Gnetales as sister to the Pinaceae, nested within the Coniferales	Gnetales as sister to the Coniferales	2e-06*
	Land plant	Zygnematophyceae as sister to all land plants	Charales as sister to all land plants	0.003*
	Control: Seed plant	Seed plants are monophyletic	Seed plants are paraphyletic	3e-99*
	Control: Moss	Mosses are monophyletic	Mosses are paraphyletic	1e-43*
Animals	Amphibian	Gymnophiona as sister to all other amphibians	Anura as sister to all other amphibians	6e-13*
	Eutherian	Xenarthra + Afrotheria as sister to all other placental mammals	Afrotheria as sister to all other placental mammals	0.036*
	Lungfish	Lungfishes as sister to all tetrapods	Lungfishes + coelacanths as sister to all tetrapods	7e-41*
	Neoavian	Pigeons as sister to all other Neoaves	Falcons as sister to all other Neoaves	0.322
	Teleost	Elopomorpha + Osteoglossomorpha as sister to all other teleosts	Osteoglossomorpha alone as sister to all other teleosts	2e-05*
	Turtle	Turtles as sister to archosaurs (birds + crocodiles)	Turtles as sister to crocodiles	1e-29*
	Control: Amniote	Amniotes are monophyletic	Amniotes are paraphyletic	2e-05*
	Control: Mammal	Mammals are monophyletic	Mammals are paraphyletic	1e-06*
Fungi	Ascoideaceae	Ascoideaceae as sister to Phaffomycetaceae + Saccharomycodaceae + Saccharomycetaceae	Ascoideaceae as sister to Pichiaceae + CUG-Ser clade + Phaffomycetaceae + Saccharomycodaceae + Saccharomycetaceae	0.005*
	Candida glabrata	Candida glabrata + Nakaseomyces as sister to Saccharomyces	Kazachstania + Naumovozyma as sister to Saccharomyces	1e-07*
	Candida tanzawaensis	Candida tanzawaensis as sister to Scheffersomyces stipitis + Candida	Candida tanzawaensis + Scheffersomyces stipiti as sister to Candida	0.012*
	Candida tenuis	Candida tenuis as sister to all other CUG-Ser yeasts	Candida tenuis as sister to Debaryomyces +Meyerozyma + Candida	2e-59*
	Hyphopichia	Hyphopichia burtonii as sister to Candida auris + Metschnikowia	Hyphopichia burtonii as sister to Debaryomyces + Meyerozyma	1e-53*
	WGD clade	Yeasts of the WGD clade are monophyletic	Yeasts of the WGD clade are paraphyletic	0.002*
	Control: Saccharomycetaceae	Yeasts of the family Saccharomycetaceae are monophyletic	Yeasts of the family Saccharomycetaceae are paraphyletic	2e-05*
	Control: Pichiaceae	Yeasts of the family Pichiaceae are paraphyletic	Yeasts of the family Pichiaceae are monophyletic	7e-05*

^&For each branch, the topological test between T1 and T2 was conducted using the approximately unbiased (AU)¹⁹ test, as implemented in the CONSEL software, version 2.0²⁰, with 1000 bootstrap replicates. Star symbols (*) indicate cases where T1 is significantly better than T2 (P-value < 0.05).

Results

Measuring phylogenetic signal

We defined phylogenetic signal as the difference in the log-likelihood scores between two alternative resolutions, T1 and T2, of a given branch (or internode or bipartition) in a phylogenetic tree¹⁸. For a given data matrix and branch in question, we defined T1 as the bipartition recovered by the phylogenetic tree obtained by maximum likelihood (ML) when the full data matrix is analyzed by concatenation analysis; we defined T2 as a bipartition in the phylogenetic tree that shows substantial topological conflict with T1 (e.g., in most cases, T2 was the most prevalent bipartition conflicting with T1) (Fig. 1a).

Figure 1. A schematic representation of our approach for quantifying and visualizing phylogenetic signal in a phylogenomic data matrix.

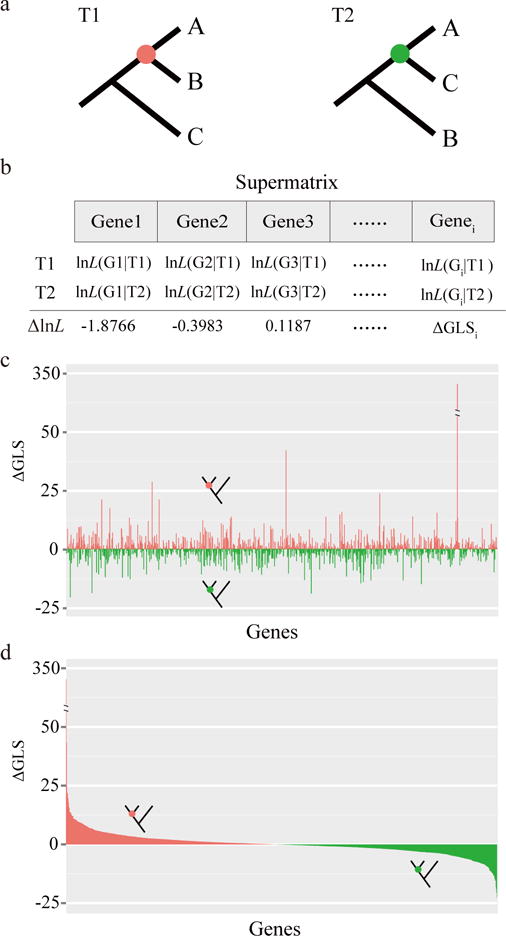
a, Two alternative phylogenetic hypotheses (T1, the unconstrained ML tree under concatenation; T2, the ML tree constrained to recover the T2 branch). b, Calculation of the difference in the gene-wise log-likelihood scores (ΔGLS) of T1 versus T2 for each gene in the data matrix. The difference in the site-wise log-likelihood scores, ΔSLS, of T1 versus T2 for each site in the data matrix is also calculated but is not shown here. The gene-wise phylogenetic signal (ΔGLS) for T1 versus T2 can be visualized either by arranging genes in the order of their placements in the data matrix (c) or in descending order of their ΔGLS values (d). Red bars denote genes supporting T1, whereas green bars denote genes supporting T2. The data for panels c and d are the actual values from the analysis of the Ascoideaceae branch in the fungal phylogenomic data matrix (Table 1). The schematic representation of our approach for quantifying and visualizing phylogenetic signal among three alternative phylogenetic hypotheses (T1, T2, and T3) is shown in Supplementary Fig. 1.

To calculate phylogenetic signal, we first calculated the site-wise log-likelihood scores for the unconstrained ML tree under concatenation (by definition, this topology contained the T1 branch and will be hereafter abbreviated T1) as well as for the ML tree constrained to recover the T2 branch (hereafter called T2) under the same substitution model and partitioning strategy (Fig. 1a). Next, we calculated the difference in site-wise log-likelihood scores (ΔSLS) between T1 and T2 for every site in a given data matrix. By summing the ΔSLS scores of all sites for every gene in a given data matrix, we then obtained the difference in gene-wise log-likelihood scores (ΔGLS) between T1 and T2 (Fig. 1b). By doing so, we were able to quantify the distribution of phylogenetic signal for T1 and T2 at the site and gene levels (Fig. 1c), as well as visualize the proportions of sites’ or genes’ support for T1 and T2 (Fig. 1d). This quantification and visualization of phylogenetic signal can be extended to the comparison of three alternative phylogenetic hypotheses (T1, T2, and T3), as shown in Supplementary Fig. 1.

A tiny amount of data can drive phylogenetic inference

For each of the 17 contentious branches and the 6 well-established branches (used as controls) in plants, animals, and fungi, we first examined whether the unconstrained ML tree under concatenation (T1) had a significantly different log-likelihood score than the ML tree constrained to recover the T2 branch (T2) using the approximately unbiased (AU) test^19,20. We found that T2 was significantly worse (P-value < 0.05) than T1 in 22/23 internodes (Table 1); the only exception was the neoavian branch in animals.

Examination of the distribution of ΔGLS values (i.e., difference in gene-wise log-likelihood scores between T1 and T2) in the 17 contentious and 6 control branches showed that the proportion of genes supporting T1 was generally greater than that of genes supporting T2 (Fig. 2; Supplementary Figs. 2 and 3a; Supplementary Tables 1–3). The only exceptions were the angiosperm (plants), eutherian (animals), and Ascoideaceae (fungi) branches, where the proportions of genes supporting T1 were slightly smaller than those supporting T2.

Figure 2. Distributions of phylogenetic signal for 17 contentious branches in plant, animal, and fungal phylogenomic data matrices.

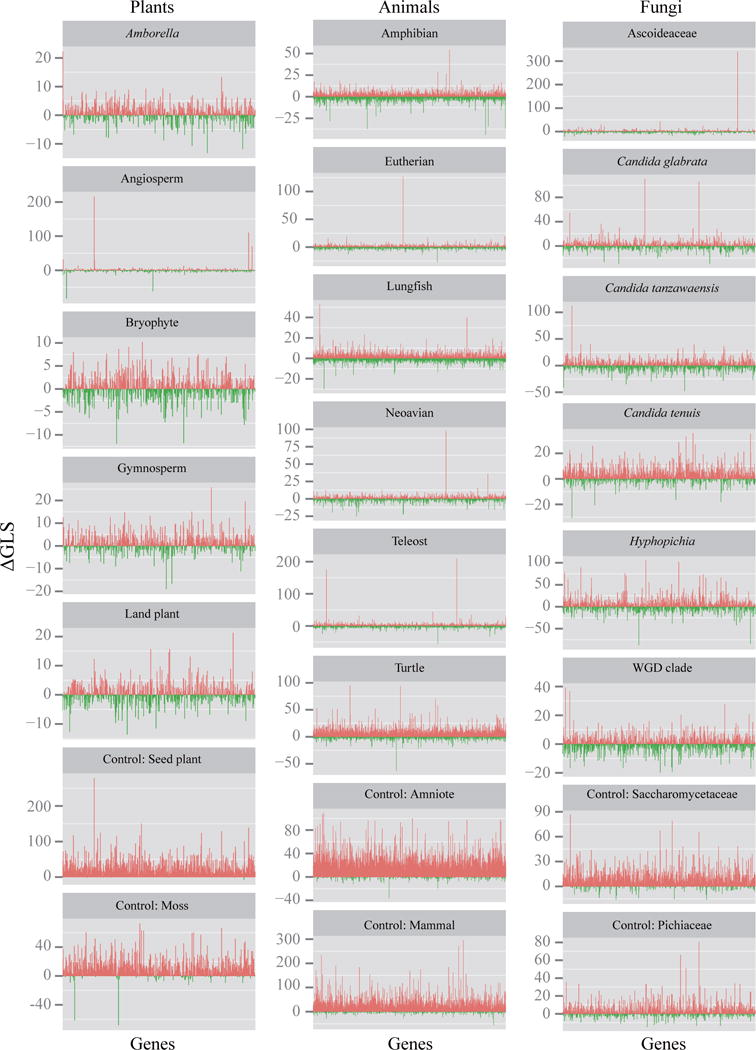
For each branch, ΔGLS values (Y-axis) were calculated by measuring the difference in gene-wise log-likelihood scores for T1 versus T2. The distribution of ΔGLS values was visualized by displaying their values for all genes in the phylogenetic data matrix in the order of their placement in the matrix (X-axis; see Supplementary Table 1–3). As a control, we also examined the distribution of ΔGLS values for two well-established branches for each of the three data matrices (Plants, monophyly of seed plants and monophyly of mosses; Animals, monophyly of amniotes and monophyly of mammals; Fungi, monophyly of the family Saccharomycetaceae and paraphyly of the family Pichiaceae; Table 1). Red bars denote genes supporting T1, whereas green bars denote genes supporting T2. The distributions of ranked ΔGLS values for these 23 branches are provided in Supplementary Fig. 2. The specific T1 and T2 topologies compared in each of the branches examined are provided in Table 1.

Examination of the distribution of ΔSLS values (i.e., difference in site-wise log-likelihood scores between T1 and T2) showed that the proportion of sites supporting T1 was greater than that of sites supporting T2 for 18 of the 23 branches (Supplementary Fig. 3b); the remaining 5 branches (eutherian, lungfish, and neoavian in animals, Ascoideaceae and WGD clade in fungi) had lower proportions of sites supporting T1 than T2 (Supplementary Fig. 3b). We observed the same pattern (Supplementary Fig. 4) when we considered only “weak” sites, whose absolute ΔSLS values were smaller or equal to 0.5¹⁷; as more than 95% of sites in each branch were weak ones (Supplementary Table 4), the similarity in results when considering all sites versus only weak sites is not surprising. Comparison of “strong” sites¹⁷, whose absolute ΔSLS values were >0.5, with all sites for each branch, showed that there was a higher proportion of strong (relative to all) sites favoring T1 in 13 branches and a lower proportion in the other 10 branches. Finally, 3 branches (eutherian and neoavian in animals, Ascoideaceae in fungi) had fewer strong sites supporting T1 than T2 (Supplementary Fig. 4).

Examination of the distribution of ΔGLS values also revealed that, in 6/17 contentious branches, a single or a handful of genes displayed very high ΔGLS values (Fig. 2 and Supplementary Figs. 2, 5–30). Remarkably, we found that removal of the gene with the highest absolute ΔGLS value switched the ML tree’s support from T1 to T2 in 3 branches (angiosperm in plants, neoavian in animals, and Ascoideaceae in fungi) (Figs. 2 and 3; Supplementary Figs. 7, 17, and 23). In contrast, random exclusion of a single gene did not change support in any analysis (Fig. 4 and Supplementary Figs. 5, 13, and 22); Similarly, removal of the gene with the highest ΔGLS value in our 6 control branches (Table 1) favored T1 over T2 (Figs. 2–4; Supplementary Figs. 11, 12, 20, 21, 29, and 30).

Figure 3. Quantification of the effect of the removal of tiny amounts of data on the branch’s topology for 17 contentious branches in plant, animal, and fungal phylogenomic data matrices.

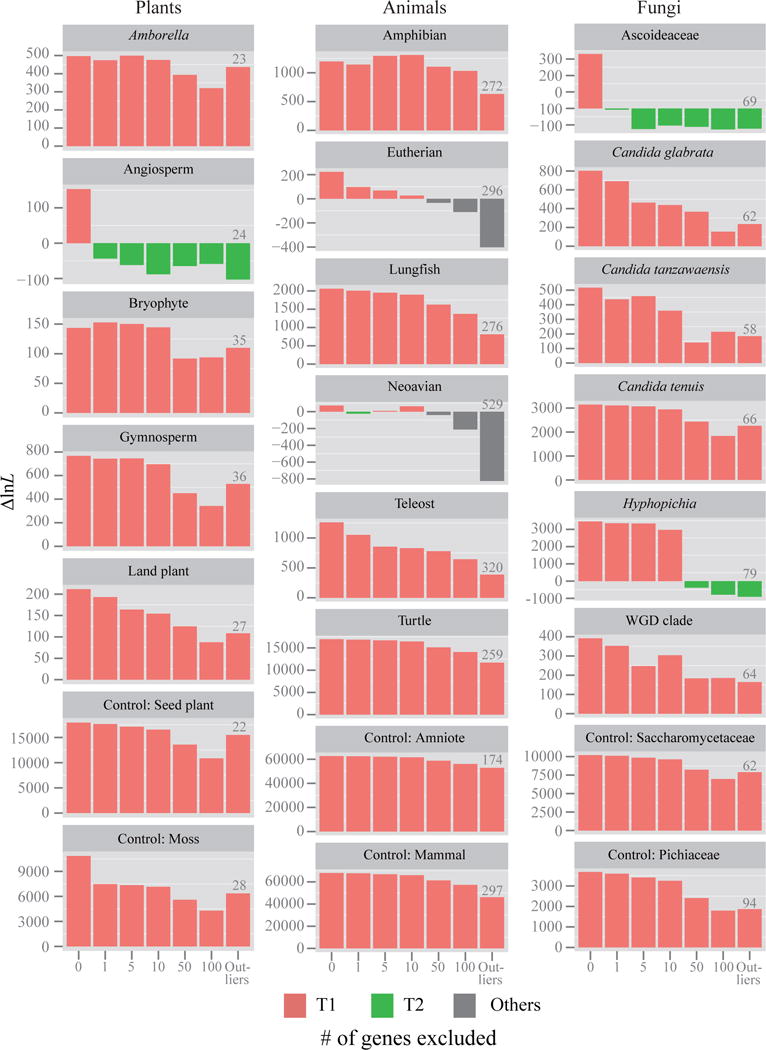
For each branch, the 1, 5, 10, 50, and 100 genes with the highest absolute ΔGLS values were excluded; we also excluded the genes with outlier ΔGLS values (the number of outlier genes is given above the corresponding bar for each branch). The Y-axis shows the difference in log-likelihood scores (ΔlnL) for the favored topological hypothesis. The different hypotheses favored are indicated by different bar colors; red bars denotes that ML trees inferred from their corresponding data matrices support T1; green bars denote ML trees supporting T2; gray bars denote ML trees supporting hypotheses other than T1 and T2. The ΔlnL values displayed on the Y-axis corresponds to the difference in log-likelihood values for T1 against either T2 or “others”. If ΔlnL is > 0, then the ML tree supports T1, whereas if ΔlnL is < 0, then ML tree supports T2 or “others”.

Figure 4. Tiny amounts of data exert decisive influence in the resolution of certain contentious branches in phylogenomic studies.

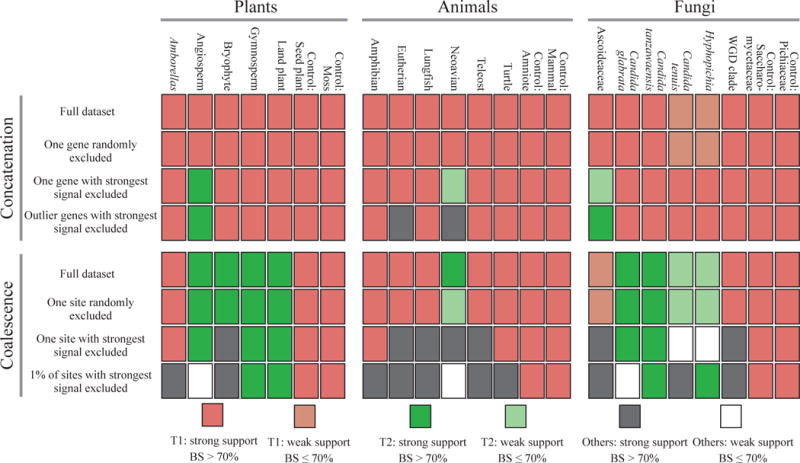
The effect of the removal of tiny amounts of data on the branch’s topology and bootstrap support (BS) was quantified for 17 contentious branches and 6 well-established branches (controls) in plant, animal, and fungal phylogenomic data matrices. Different colors indicate different branch topologies and levels of BS. Topologies other than T1 and T2 are collectively referred to as “Others”. (Top panel: Concatenation) The first row depicts the results of the concatenation analysis when the full data matrix is used, the second row when a single random gene is excluded, the third row when the gene with the highest absolute ΔGLS value is excluded, and the fourth row when the genes with outlier ΔGLS values are excluded. (Bottom panel: Coalescence) The first row depicts the results of the coalescence-based analysis when the full data matrix is used, the second row when one random site from every gene’s alignment is excluded, the third row when the site with the highest absolute ΔSLS value from every gene is excluded, and the fourth row when the 1% of sites with the highest absolute ΔSLS values from every gene are excluded. All topologies summarized in this figure are provided in Supplementary Figs. 5–56.

The single genes whose removal caused the switch of the phylogenomic data matrices’ support from T1 to T2 in the angiosperm, neoavian, and Ascoideaceae branches were orthologs of the Arabidopsis thaliana AT3G46220 gene (alignment id: 6040_C12), the Homo sapiens AUTS2 gene (alignment id: Pro_ENSG00000158321), and the Saccharomyces cerevisiae DPM1 gene (alignment id: BUSCOfEOG7W9S51), respectively. Plotting of the ΔSLS values (i.e., difference in gene-wise log-likelihood scores between T1 and T2) for the three gene alignments showed that 14.4% of the 6040_C12 gene alignment, 11.0% of Pro_ENSG00000158321, and 47.9% of BUSCOfEOG7W9S51 had high ΔSLS values (>0.5); moreover, these strong sites were unevenly distributed in the 6040_C12 and Pro_ENSG00000158321 gene alignments (Supplementary Fig. 57). Further examination of the sequence alignments of these three genes did not identify apparently unusual sequences or columns (Supplementary Figs. 58–60), while topological distances (measured by the normalized Robinson–Foulds tree distance, RFD, using RAxML with the option “-f r”) of their ML gene trees from the concatenation-based ML phylogenies (T1) inferred from the full data matrices were slightly higher than the corresponding means of topological distances of all individual gene trees from the concatenation-based ML phylogenies (Supplementary Tables 6–8). Finally, none of the three genes’ properties²¹ (e.g., alignment length, alignment quality, compositional heterogeneity or disparity index, rate of evolution, single-gene tree resolution [e.g., average bootstrap support]; see Supplementary Table 5) could consistently explain why they exhibited such high ΔGLS values (Supplementary Tables 6–8).

To investigate the impact of model of sequence evolution in the proportions of sites supporting T1 versus T2, we used Seq-Gen v1.3.3²² to simulate alignments of the plant (290,718 sites), animal (1,806,035 sites) and fungal (609,772 sites) phylogenies using exactly the same ML trees and model parameters (i.e., state frequency, rates, and alpha parameter: the shape for the gamma rate heterogeneity among sites) used in the original three phylogenomic studies as well as in our analyses. Comparison of the differences in the proportions of strong, weak, and all sites supporting T1 between biological and simulated data showed that differences were small for the 6 control branches but much larger for the 17 contentious branches (Supplementary Fig. 61); this trend was especially noticeable when only the strong sites were considered. Furthermore, the differences in the proportion of sites supporting T1 between biological and simulated data were especially pronounced in the angiosperm, neoavian, and Ascoideaceae branches (Supplementary Fig. 61), suggesting that the site- and gene-specific patterns of support for T1 or T2 are a poor fit to those predicted by the employed models of sequence evolution.

To quantify the effect of gene removal, we next investigated the effects of excluding 5, 10, 50, and 100 genes with the highest absolute ΔGLS values, as well as of excluding the genes with outlier ΔGLS values (see equations (3) and (4) in the Methods section). Our results showed that these gradual removals of genes had the same effect as single gene removal (a switch from T1 to T2) for the angiosperm and Ascoideaceae branches, whereas the neoavian branch was unstable, switching between T1, T2, and other topologies (Fig. 3). Interestingly, the results on single or few gene removals were very similar to the results obtained when outlier genes were removed (Fig. 3). Furthermore, when the number of removed genes was equal or greater than 50, a switch from T1 to T2 or other hypotheses was also observed for the eutherian and neoavian branches in animals and the Hyphopichia branch in fungi (Fig. 3).

Coalescence-based species tree approaches^23,24, by taking into account each gene tree’s history, are less likely to be influenced by a single or handful of genes in a phylogenomic data matrix. However, these approaches can be sensitive to errors and biases in estimating individual gene trees^25–27. To test whether the support for the 17 contentious branches from coalescence-based approaches was, like concatenation, sensitive to the presence of a very small subset of data, we examined the effect of removing the site with the highest absolute ΔSLS value from every gene. We found that this removal of a single site per gene altered the topology supported in 9/17 contentious branches (Fig. 4 and Supplementary Figs. 31–56). In contrast, exclusion of a randomly selected single site from every gene did not change support in any analysis (Fig. 4 and Supplementary Figs. 31, 39, and 48); similarly, removal of the single site with the highest absolute ΔSLS value per gene in the 6 control branches did not result in a switch of support from T1 to another topology (Fig. 4 and Supplementary Figs. 37, 38, 46, 47, 55, and 56).

Among the branches strongly influenced by the removal of the single site with the highest absolute ΔSLS value from every gene were the bryophyte branch in plants, the eutherian, lungfish, neoavian, and teleost branches in animals, and the Ascoideaceae and WGD clade branches in fungi. Interestingly, the neoavian and Ascoideaceae branches were sensitive to both the removal of the gene with the highest absolute ΔGLS value and to that of the site with the highest absolute ΔSLS value from every gene. Exclusion of the 1% of sites with the highest absolute ΔSLS values²⁸, from every gene showed that the coalescence-based topology based on the full data matrix was no longer supported for 13/17 contentious branches (Fig. 4 and Supplementary Figs. 31–56).

While some of these 17 contentious relationships appear to be driven by a tiny subset of data and should effectively be considered unresolved, the quantification of ΔGLS and ΔSLS values for a specific branch of a phylogeny can also augment the support for one of the alternative hypotheses. For example, similar to the well-established branch associated with the monophyly of amniotes on the vertebrate phylogeny that we used as a control (Figs. 2–4), examination of the evolutionary placement of turtles (Table 1 and Figs. 2–4) showed very strong support for the hypothesis that turtles are the sister group to archosaurs (birds + crocodiles). Specifically, the ΔGLS values of 74% (3,466 / 4,682) of the genes in the data matrix favor this hypothesis over the second best alternative (turtles as sister group to crocodiles) (Supplementary Fig. 2a); the same is true for ΔSLS values (88% or 1,588,738 / 1,806,035 sites favor turtles as the sister group to archosaurs than to just crocodiles; Supplementary Fig. 3b).

What is the earliest branch of the metazoan phylogeny?

To further illustrate how the quantification of phylogenetic signal for a specific branch of a phylogeny can augment the resolution of contentious branches, we next examined the support for three alternative hypotheses regarding the earliest-branching lineage of the Metazoa (T1: Ctenophora-sister, T2: Porifera-sister, and T3: Porifera+Ctenophora-sister)^11,12,29 (Fig. 5a). Specifically, we collected 8 phylogenomic data matrices from three recent studies^11,29,30, comprised of different data types (genomic data or “transcriptomic + genomic data”) and different outgroups (Opisthokonta or Choanoflagellata).

Figure 5. The distribution of phylogenetic signal for three alternative topological hypotheses on the earliest-branching metazoan lineage.

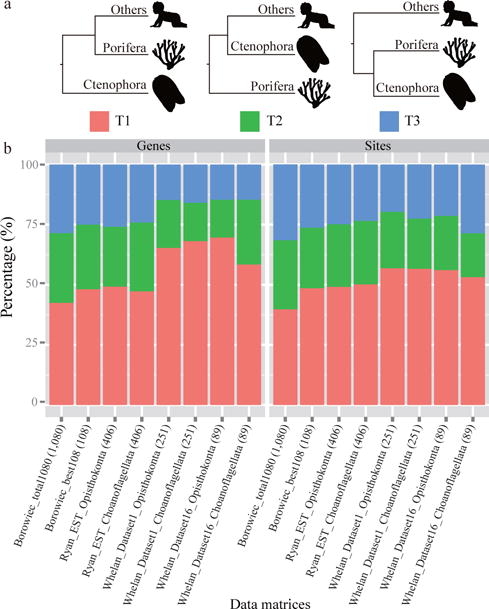
a, The three alternative topological hypotheses are: ctenophores as the sister group to all other metazoan phyla (Ctenophora-sister) (T1), sponges as the sister group to all other metazoans (Porifera-sister) (T2), or a clade composed of ctenophores and sponges as the sister group to all other metazoans (Porifera+Ctenophora-sister) (T3). All silhouettes come from http://phylopic.org. Human image by Andrew Farke, ctenophore and sponge images by Mali’o Kodis, adapted from photograph by Derek Keats (http://www.flickr.com/photos/dkeats/). b, Proportions of genes or sites supporting each of three alternative hypotheses for each of eight data matrices from three phylogenomic studies^11,29,30. Note that two different non-animal outgroup sets are used in the studies by Ryan et al.¹¹ and by Whelan et al.²⁹: datasets whose labels include the word “Choanoflagellata” use only choanoflagellate taxa as outgroups, whereas datasets labeled with “Opisthokonta” use fungal, holozoan taxa, including choanoflagellates, as outgroups. Values in parentheses next to data matrices’ names indicate the number of genes present in each phylogenomic data matrix. The ΔGLS values for the genes across each data matrix are provided in Supplementary Table 9 and their distributions are shown in Supplementary Figs. 62 and 63. The phylograms of all concatenation ML analyses following the removal of the gene with the highest ΔGLS value as well as those following the removal of the genes with outlier ΔGLS values in the eight data matrices can be found in Supplementary Figs. 65a–65h.

Examination of ΔGLS values between T1, T2, and T3 (see Methods for full details) showed that T1 had the highest proportions of supporting genes, ranging from 42.5% to 69.7%, across the 8 data matrices (Fig. 5a and Supplementary Table 9). In addition, the ΔGLS values of genes favoring T1 were higher than those favoring either T2 or T3 across all 8 data matrices (Supplementary Table 9 and Supplementary Fig. 62). This is most easily observed by examining the distribution of ranked ΔGLS values for each data matrix (Supplementary Fig. 63). Moreover, all concatenation ML analyses of the removal of one single gene and the genes with outlier ΔGLS values still supported Ctenophora-sister hypothesis (T1) (Supplementary Figs. 65a–65h).

Examination of ΔSLS values between T1, T2, and T3 (see Methods for full details) showed that T1 also had the highest proportions of supporting sites, ranging from 39.8% to 56.9% (Fig. 5b). Importantly, comparison of the proportions of strong, weak, and all sites supporting T1 showed that this hypothesis received its highest support in all 8 data matrices by the strong sites; their proportions in favor of T1 ranged from 52.2% to 85.3% (Supplementary Fig. 64). Thus, examination of ΔGLS and ΔSLS values in 8 phylogenomic data matrices shows robust support for the Ctenophora-sister hypothesis.

Discussion

In this study, we examined the distribution and strength of phylogenetic signal on contentious branches of the ToL. For some contentious branches, our approach clarified the nature of the phylogenetic incongruence and, by quantifying the support for alternative hypotheses at the site and gene levels, illuminated their resolution. For other contentious branches, however, we found that tiny amounts of data – in what are otherwise very large phylogenomic data matrices – exerted decisive influence in their resolution.

There are two potential explanations for why this is so. One explanation is that the evolution of these genes may have been shaped by positive selection³¹, which can give rise to convergent evolution that misleads phylogenetic inference^17,32–35, or by evolutionary processes such as incomplete lineage sorting, horizontal gene transfer, and hybridization, which can give rise to gene histories that differ from each other and from the species history^13,14. Another, not mutually exclusive, explanation is that the evolutionary history of these genes may have been incorrectly inferred due to the influence of analytical factors, such as taxon choice³⁶, taxon sampling³⁷, and misspecification of the model of sequence evolution^15,38 (see also Supplementary Fig. 61). Irrespective of the underlying biological or analytical factors at play, our results on branches sensitive to tiny amounts of data raise doubts about whether these branches are truly resolved.

Our proposed framework for quantifying and visualizing phylogenetic signal could be used to analyze any branch of the tree of life, irrespective of how contentious they are; our examination of 6 control branches (Figs. 2 and 3) is a good case in point. However, our approach is most likely to useful in cases of branches showing a high degree of conflict (e.g., low scores of internode certainty-related measures^39–41), or in cases of branches shown to conflict between topologies inferred by different phylogenomic data matrices. For such contentious branches, we would argue that dissecting the distribution of support for each of the main alternative hypotheses is essential for understanding the extent to which they are (or are not) supported by the phylogenomic data^42,43. Finally, the same analytical approach could be employed to examine the influence of different analytical models (e.g., homogeneous model versus mixture model) on the distribution of phylogenetic signal and the resolution of contentious branches.

Quantifying and visualizing the distribution of phylogenetic signal at the level of sites or genes would also be helpful for the identification of any sites or genes that might be exerting a disproportionate amount of influence on the resolution of a given contentious branch. The undue influence of one or a few genes or a few sites on phylogenetic inference has been previously observed in smaller data matrices^{17,28,44–47}. Our results show that this undue influence of one gene or a few sites can, in some cases, be the main reason for the generation of very high support values on a given branch in phylogenomic data matrices that contain several hundreds or thousands of genes. Moreover, both concatenation- and coalescence-based approaches are susceptible to this behavior.

How are we then to interpret inferred relationships that rest on the presence of tiny amounts of data in phylogenomic studies? The history of life abounds with examples of ancient evolutionary radiations. Previous theoretical as well as empirical studies^6,14,48,49 suggest that the resolution of relationships within such series of closely spaced species divergences in deep time can be extremely challenging. It is our view that the branches of the ToL that exhibit this behavior (i.e., their resolution rests on the presence of a tiny subset of genome-scale data) should effectively be considered unresolved. Of course, this does not mean that these branches will never be fully resolved, but rather that we are unable to do with our current methodology and sampling of genes and taxa. Clear demarcation of such unresolved branches would provide a more accurate account of the phylogenetic hypotheses supported by the available data.

Methods

Data matrices

We used three taxon- and gene-rich phylogenomic data matrices representing three eukaryotic kingdoms of the tree of life: plants (103 plant species × 620 nuclear genes; Figure 2 in original study)¹, animals (58 jawed vertebrate species × 4,682 nuclear genes; Figure 1 in original study)⁵⁰, and fungi (86 yeast species × 1,233 nuclear genes; Figure 3 in original study)⁴. Although these studies constructed several different data matrices, we used only the full data matrix in each study.

Topological hypothesis testing

We investigated a total of 17 contentious branches present in three phylogenomic data matrices from plants, animals, and fungi (Table 1). These branches were deemed contentious either because they were considered as such in the original papers^1,50 or because they were incongruent between the concatenation- and coalescence-based phylogenies⁴. As a control, we also investigated two well-established branches from each of the three phylogenomic data matrices (see Table 1 for full details). For each branch, the unconstrained ML tree under concatenation (T1) and the ML tree constrained to recover the T2 branch were examined (Table 1). In most cases, T2 was the most prevalent bipartition conflicting with T1. The ML tree constrained to recover the T2 branch was obtained by enforcing the topological constraint option (option -g) in RAxML⁵¹, version 8.2.3. All ML searches were performed by using the same models and partitioning strategies as the original studies; the ML phylogeny was obtained by conducting 5 separate tree searches using 5 different random seeds (option -p). To test whether the T2 topology was statistically worse than the T1 topology for each of the 17 branches, we applied the approximately unbiased (AU)¹⁹ test in the software package CONSEL²⁰, version 0.20. The AU test was conducted using the multi-scale bootstrap technique based on the site-wise log-likelihood scores, which were calculated in RAxML (option –f G). Notably, the difference between the RAxML software⁵¹, version 8.2.3, and the IQ-TREE software⁵², version 1.5.1, in calculating log-likelihood scores for our 17 contentious branches was very small (Supplementary Table 10).

Phylogenetic signal

A schematic workflow for the calculation and visualization of phylogenetic signal is shown in Fig. 1. For a given data matrix and branch in question, we defined T1 as the bipartition recovered by the phylogenetic tree obtained by maximum likelihood (ML) when the full data matrix is analyzed by concatenation analysis; we defined T2 as a bipartition in the phylogenetic tree that shows substantial topological conflict with T1 (e.g., in most cases, T2 was the most prevalent bipartition conflicting with T1) (Fig. 1a). For a given data matrix and branch in question, using the maximum likelihood framework¹⁸, we here defined phylogenetic signal as the difference in the log-likelihood scores for the unconstrained ML tree under concatenation (by definition, this tree contained the T1 branch) against the ML tree constrained to recover the T2 branch (T2). Briefly, we first estimated the site-wise log-likelihood values for both T1 and T2 based on the concatenation data matrix and the same models using RAxML (option -f G). We then calculated the difference in site-wise log-likelihood scores (ΔSLS) between T1 and T2 using the equation:

$${\mathrm{\Delta }\mathrm{SLS}}_{\mathrm{i}}=\ln L({\mathrm{S}}_{\mathrm{i}}|\mathrm{T}1)-\ln L({\mathrm{S}}_{\mathrm{i}}|\mathrm{T}2)$$ (1)

where T1 is the unconstrained ML tree obtained by concatenation analysis of the full data matrix and T2 the ML tree constrained to recover the T2 branch. ΔSLS_i is the difference in site-wise log-likelihood scores under T1 and T2 for the ith site (S_i) in the full data matrix. Similarly, we also calculated the difference in gene-wise log-likelihood scores (ΔGLS) for T1 versus T2 for every gene according to:

$${\mathrm{\Delta }\mathrm{GLS}}_{\mathrm{j}}=\ln L({\mathrm{G}}_{\mathrm{j}}|\mathrm{T}1)-\ln L({\mathrm{G}}_{\mathrm{j}}|\mathrm{T}2)$$ (2)

where T1 is the unconstrained ML tree obtained by concatenation analysis of the full data matrix and T2 the ML tree constrained to recover the T2 branch. ΔGLS_j is difference in gene-wise log-likelihood scores under T1 and T2 and can be calculated as the sum of ΔSLS values of all sites within the jth gene (G_j).

Effect of removing a tiny amount of data on phylogenetic inference

To examine the influence of tiny amounts of data on phylogenetic inference, we generated 6 reduced data matrices by excluding 1, 5, 10, 50, and 100 genes with the highest absolute ΔGLS values (i.e., difference in gene-wise log-likelihood scores between T1 and T2), as well as all genes whose ΔGLS values were outliers, from the full data matrix for each of the 17 contentious branches and 6 well-established control branches. Outlier genes were defined as those whose absolute ΔGLS values were greater than the upper whisker or smaller than the lower whisker of a boxplot in R⁵³,

$$\mathrm{Upper}\mathrm{whisker}=\min (\max (\mathrm{x}),\mathrm{Q}3+1.5\ast \mathrm{IQR})$$ (3)

$$\mathrm{Lower}\mathrm{whisker}=\max (\mathrm{mix}(\mathrm{x}),\mathrm{Q}1-1.5\ast \mathrm{IQR})$$ (4)

where max(x) and mix(x) are the maximum value and minimum value for a set of absolute ΔGLS values, respectively. Q1 and Q3 are the first quartile and the third quartile, respectively. IQR (interquartile range) is difference in value between Q3 and Q1 (Q3 - Q1).

As a control, we also randomly excluded a single gene from the full data matrix and repeated this process 5 times in each of the three data matrices. For each reduced data matrix (we examined a total of 153 data matrices), the ML tree was inferred, as implemented in the IQ-TREE software⁵² using the same substitution models (plant: GTR+GAMMA; animal: LG+GAMMA+F; fungi: LG+GAMMA) and partitioning strategies (plant: 8 partitions; animal: 1 partition; fungi: 1 partition) as described in the original papers. Branch support for each internode was evaluated with 100 rapid bootstrapping replicates⁵⁴ using RAxML⁵¹ (option -x). Since the bootstrapping analysis of such large data matrices in RAxML is computationally very expensive (each plant data matrix takes ~150 CPU hours; each animal data matrix takes ~4,200 CPU hours; each fungal data matrix takes ~2,900 CPU hours), we performed bootstrapping on only two (those associated with removal of a single gene and removal of all outlier genes) of the 6 reduced data matrices for each of the 17 contentious branches and 6 well-established branches.

Similarly, we excluded the site with the highest absolute ΔSLS value (i.e., the difference in site-wise log-likelihood scores between T1 and T2) from every gene for each branch. As a control, we also created reduced individual gene alignments where one site was randomly excluded for each data matrix. Maximum likelihood analysis of each reduced individual gene alignment was performed in RAxML by conducting 100 rapid bootstrapping replicates and 10 separate ML searches. Finally, the resulting RAxML ML trees and their 100 rapid bootstrapping trees were used to infer the coalescence-based species phylogeny with the ASTRAL software⁵⁵, version 2.4.7.7. In addition to removal of a single site with the highest absolute ΔSLS value, we also excluded the 1% of sites with the highest absolute ΔGLS values from every gene for each branch, as implemented in Shavit Grievink et al.²⁸.

The root of the Metazoan phylogeny

To investigate the distribution of phylogenetic signal in studies aiming to elucidate which was the first-branching metazoan phylum^{11,12,29,30,56–61}, we considered 8 data matrices from three recent studies that were constructed from either EST and genomic data¹¹, transcriptomic and genomic data²⁹, or genomic data alone³⁰. Because different choices of outgroups could influence phylogenetic inference^9,12, we investigated the distribution of phylogenetic signal in data matrices that used two different types of outgroups: Choanoflagellata, the closest relative of the metazoan phyla, and non-metazoan Opisthokonta, which included fungi and non-metazoan holozoans, such as choanoflagellates.

We examined 3 hypotheses: Ctenophora-sister (T1; Fig. 5a), Porifera-sister (T2; Fig. 5a), and Porifera + Ctenophora-sister (T3; Fig. 5a). For each hypothesis, its corresponding constraint ML phylogeny and its site-wise log-likelihood scores were estimated for each of 8 data matrices using RAxML, as described above. We then calculated the mean of all pairwise absolute differences in site-wise log-likelihood scores (ΔSLS_i) between T1, T2, and T3 for the ith site (S_i) in the full data matrix using the equation (5):

$${\mathrm{\Delta }\mathrm{SLS}}_{\mathrm{i}}=\frac{|\ln L({\mathrm{S}}_{\mathrm{i}}|\mathrm{T}1)-\ln L({\mathrm{S}}_{\mathrm{i}}|\mathrm{T}2)|+|\ln L({\mathrm{S}}_{\mathrm{i}}|\mathrm{T}1)-\ln L({\mathrm{S}}_{\mathrm{i}}|\mathrm{T}3)|+|\ln L({\mathrm{S}}_{\mathrm{i}}|\mathrm{T}2)-\ln L({\mathrm{S}}_{\mathrm{i}}|\mathrm{T}3)}{3}$$ (5)

Similarly, we calculated the mean of all pairwise absolute differences in gene-wise log-likelihood scores (ΔGLS_j) between T1, T2, and T3 (see Supplementary Fig. 1 for full schematic representation) using the equation (6):

$${\mathrm{\Delta }\mathrm{GLS}}_{\mathrm{j}}=\frac{|\ln L({\mathrm{G}}_{\mathrm{j}}|\mathrm{T}1)-\ln L({\mathrm{G}}_{\mathrm{j}}|\mathrm{T}2)|+|\ln L({\mathrm{G}}_{\mathrm{j}}|\mathrm{T}1)-\ln L({\mathrm{G}}_{\mathrm{j}}|\mathrm{T}3)+|\ln L({\mathrm{G}}_{\mathrm{j}}|\mathrm{T}2)-\ln L({\mathrm{G}}_{\mathrm{j}}|\mathrm{T}3)|}{3}$$ (6)

Last, we examined whether removal of a single gene with the highest absolute ΔGLS value or removal of the genes with outlier ΔGLS values [see equations (3) and (4)] altered the hypothesis favored by concatenation analysis.