Abstract
Purpose
A breast cancer risk prediction rule previously developed by Rosner and Colditz has reasonable predictive ability. We developed a re-fitted version of this model, based on more than twice as many cases now including women up to age 85, and further extended it to a model that distinguished risk factor prediction of tumors with different estrogen/progesterone receptor status.
Methods
We compared the calibration and discriminatory ability of the original, the re-fitted, and the type-specific models. Evaluation used data from the Nurses’ Health Study during the period 1980–2008, when 4,384 incident invasive breast cancers occurred over 1.5 million person-years. Model development used two thirds of study subjects and validation used one third.
Results
Predicted risks in the validation sample from the original and re-fitted models were highly correlated (Rho=0.93), but several parameters, notably those related to use of menopausal hormone therapy and age, had different estimates. The re-fitted model was well-calibrated and had an overall C-statistic of 0.65. The extended, type-specific model identified several risk factors with varying associations with occurrence of tumors of different receptor status. However, this extended model relative to the prediction of any breast cancer, did not meaningfully reclassify women who developed breast cancer to higher risk categories, nor women remaining cancer free to lower risk categories.
Conclusions
The re-fitted Rosner-Colditz model has applicability to risk prediction in women up to age 85, and its discrimination is not improved by consideration of varying associations across tumor subtypes.
Keywords: prediction, models, statistical, calibration, discrimination, reclassification
Although breast cancer is the most common cancer occurring in women, and many risk factors have been identified, the ability to predict who in a general population will develop breast cancer is limited [1–18]. In general, limited discriminatory ability of available models that are easily assessed in a large population arises because risk factors with large associations such as mutations in the BRCA1 or BRCA2 genes have low prevalence, and common risk factors such as early age at menarche or late age at first birth have only modest associations with risk. Enhancement of discriminatory models can be obtained through additional testing such as measures of mammographic density and testing for relevant genetic variation [11–16]. However, this additional information can be costly and may be available only in populations of limited size, or after eligibility for mammographic screening. Further, the available risk prediction rules have been judged sufficient to help direct treatment such as the decision to initiate tamoxifen therapy [19].
In this paper, we compare the original version of the Rosner-Colditz model [6–9] developed in women up to age 70 with a refitted version that includes data from women up to age 85 years, as well as additional information on women with more contemporaneous patterns of menopausal hormone therapy (MHT). We provide an in-depth evaluation of whether extension of the Rosner-Colditz model to predict rates of tumors of different estrogen receptor (ER) and progesterone receptor (PR) status, in a competing risks framework, would improve prediction. This includes more cases, and alternative methods compared to the earlier report on the topic [8]. We base comparisons on several criteria: calibration, discrimination, and ability of a more complex model to re-classify both cases and non-cases more accurately.
METHODS
Study population
The Nurses’ Health Study cohort was established in 1976 when 121,701 female US registered nurses aged 30–55 years responded to a mailed questionnaire that inquired about risk factors for breast cancer, including reproductive factors, hormone use, anthropometric variables, benign breast disease, and family history of breast cancer. The risk factor data have been updated by means of repeat questionnaires sent every 2 years up to the present time [20]. Alcohol consumption, both current and at age 18 years, was ascertained in 1980, with information updated in 1984 and then every 4 years from 1986 onwards. Building upon previous descriptions of the Rosner-Colditz model to predict incident breast cancer (6–9), we considered time-varying measures, beginning in 1980, of all variables included in that model, updated through 2006. For every 2-year interval with updated risk factor information, we estimated a woman’s Rosner-Colditz risk of breast cancer, as long as she remained alive and free of breast cancer, and continued to report her updated risk factor information.
Measures
The 22 time-varying variables included in the Rosner-Colditz model [6–8] are: duration of premenopause (t*=minimum [of current age and age at menopause] minus age at menarche in years); duration of natural menopause (years since menopause if natural menopause, 0 otherwise); duration of menopause if bilateral oophorectomy (years since menopause if bilateral oophorectomy, 0 otherwise); gynecological age at first birth (age at first birth minus age at menarche in years if parous, 0 if nulliparous); birth index (sum over all births of years from age at that birth to t*, 0 for nulliparous women); benign breast disease (1=yes, 0=no); benign breast disease times age at menarche; benign breast disease times duration of premenopause; benign breast disease times duration of menopause; duration of use of oral estrogen alone (years); duration of use of oral estrogen plus progesterone (years); duration of use of other MHT types (years); current MHT use (1=yes, 0=no); past MHT use (1=yes, 0=no); (average body mass index [BMI] during premenopause minus 21.8 kg/m2) times the duration of premenopause in years plus (average BMI after menopause while on MHT minus 24.4 kg/m2) times duration of menopausal years while taking MHT; (average BMI after menopause minus 24.4 kg/m2) times duration of menopausal years while not taking MHT; (height in inches minus 64.5) times duration of premenopause plus (height in inches minus 64.4) times duration of menopausal years while taking MHT; (height in inches minus 64.4) times duration of menopausal years while not taking MHT; (average alcohol consumption in grams while premenopausal) times duration of premenopause; (average alcohol consumption in grams while postmenopausal and taking MHT) times duration of menopausal years while taking MHT; and (average alcohol consumption in grams while postmenopausal and not taking MHT) times duration of menopausal years while not taking MHT therapy.
On each questionnaire, women were asked whether breast cancer had been diagnosed and, if so, the date of diagnosis. All women (or their next of kin, if deceased) were contacted for permission to review their medical records so as to confirm the diagnosis. Pathology reports were reviewed to obtain information on estrogen receptor (ER) and progesterone receptor (PR) status. In addition, we excluded women with types of menopause other than natural menopause or bilateral oophorectomy because of the inability to determine the true age at menopause and menopausal status, prevalent cancer (other than nonmelanoma skin cancer) in 1980, or missing data for weight at age 18 years, age at first birth, parity, age at menarche, age at menopause, or type and duration of hormone use. We censored women who developed another type of cancer (except non-melanoma skin cancer) at their diagnosis date.
Cases of invasive breast cancer from 1980 to 2008 for which we had a pathology report were included in these analyses. During follow-up of 76,922 (768,948 2-year intervals) women with complete data on baseline risk factors from 1980 to 2006, 4,384 women developed invasive breast cancer. In the analyses that considered occurrence of breast cancers of specified ER and PR status, 991 breast cancer cases with missing data on ER and/or PR status were censored at the time of diagnosis. Also, the small number of women (n=106) with breast cancer classified as ER−/PR+ were censored at their date of diagnosis, as in previous analyses [21], because a validation study based on tumor tissue microarray found a low confirmation rate for this type [22].
Analysis
We used the variables previously determined for inclusion in the Rosner-Colditz model, and assumed the published functional form of the model, but re-estimated the parameters in this updated dataset. Importantly, the published parameter estimates for the model [7] were based on data from women up to age 70, while our analyses included data from women up to age 85 years and also reflected the more current patterns of MHT use. Specifically, we randomly assigned two-thirds of the women in this study to the development sample (51,437 women with 514,181 2-year intervals who accrued 2,966 incident breast cancers), used to estimate coefficients in the Rosner-Colditz model, and one-third of women (25,485 women with 254,767 2-year intervals who accrued 1,418 incident breast cancers) to be included in the validation sample, used to evaluate the performance of the model.
Units of analysis were 2-year risk windows with updated information at the beginning of each interval in women who survived and remained free of cancer, following previously described perspectives on time-varying risk prediction [23–25]. Preliminary analyses indicated very good agreement between parameter estimates obtained from logistic regression, compared with those obtained from Poisson regression, or the proportional hazards model. Use of logistic regression models allowed for implementation of readily interpretable measures of discrimination, calibration, and net reclassification, and facilitated comparisons with models that distinguished estrogen receptor status of cases.
We used the Hosmer-Lemeshow test, with deciles of risk based on the development sample, to evaluate calibration of the predictions from both the model with the original parameter estimates and the re-fitted model in the validation sample. We compared discrimination in the original and re-estimated models in the overall validation sample and separately within each of four age groups: <50, 50–59, 60–69, and 70 years or older.
We extended the Rosner-Colditz model to consider prediction of ER/PR type of breast cancer, with the goal of evaluating whether this extension would improve overall prediction. This analysis was initially carried out in the entire dataset (i.e. both development and validation samples) with women with unknown ER/PR status and those with breast cancer classified as ER−/PR+ censored at the time of diagnosis. Specifically, we fitted a polytomous logistic regression model, with all independent variables in the Rosner-Colditz model for each 2-year interval, and an unordered four-category outcome: no breast cancer (referent group), ER+/PR+ breast cancer (occurring in 2,123 women), ER+/PR− breast cancer (occurring in 542 women), and ER−/PR− breast cancer (occurring in 622 women). We fitted the polytomous logistic model using Proc Logistic in version 9.3 of SAS Statistical Software, and, for each variable, performed a 2 degree of freedom Chi square test of the null hypothesis that the variable had a uniform effect on each of the three ER/PR types, allowing the coefficients for the other variables to differ in their relationships with the ER/PR types. To evaluate possible improvement in prediction associated with this extended model, we considered the variance explained by the simpler model assuming common effects of each risk factor on each ER/PR type (i.e. the nested logistic regression model), as described by Glynn and Rosner [26].
To evaluate risk re-classification based on alternative models, we used four a priori chosen absolute 2-year risk categories suggested by Tice et al (14): 0–<.4%; .4–<.67%; .67–<1.0%; and ≥1.0%. Following recommendations of Kerr et al [27], we report reclassification percentages separately for breast cancer cases and non-cases.
Specifically, we evaluated percent reclassification of cases and non-cases, based on a polytomous logistic model that included separate effects for the relationship of each risk factor with each receptor status type. For consistency with our previous approach to model development, we fitted the polytomous model to the development dataset, and evaluated predictions in the evaluation set. Also, to include all cases, we added a separate indicator variable for cases of breast cancer of unknown ER/PR status, and also included cases classified as ER−/PR+ in this category. Based on this polytomous model, we obtained the predicted probability of breast cancer in a 2-year interval as the sum of predicted probabilities of each of ER+/PR+, ER−/PR−, ER+/PR−, and unknown type. Predictions from this model could then be compared with predictions from the previously developed Rosner-Colditz model, fitted in the development sample but applied to the evaluation set with cases of unknown ER/PR status censored at event time. Reclassification was again compared between the original Rosner-Colditz model and its extended version accounting for ER/PR status with reference to the four absolute risk categories (0–<.4%; .4–<.67%; .67–<1.0%; and ≥1.0%) considered above.
Results
Several parameters, notably those related to use of menopausal hormone therapy and age, had somewhat attenuated estimates (Table 1) in the Rosner-Colditz model re-fitted to more current data with older women. Specific variables with parameter estimates decreased by more than two standard errors from the original estimates were duration of premenopause, duration of postmenopausal estrogen alone use, duration of postmenopausal estrogen plus progesterone use, and postmenopausal body mass index times years menopausal. Conversely, the parameter estimates for current MHT use and cumulative alcohol ounces before menopause were increased in the re-fitted model. However, 2-year predicted risks in the validation sample from the two models were highly correlated (Spearman correlation 0.93).
Table 1.
Comparison of parameter estimates between originally published and newly estimated parameters of the Rosner-Colditz model for 2-year risk prediction
| Nurses’ Health Study, 1980–1994 | Nurses’ Health Study, 1980–2008 | |
|---|---|---|
| Parameter | Estimated beta (SE) | Estimated beta (SE) |
| Duration of premenopause (years) | 0.085 (0.007) | 0.070 (0.006) |
| Duration of menopause (natural, years) | 0.025 (0.006) | 0.016 (0.004) |
| Duration after bilateral oophorectomy (years) | 0.009 (0.009) | 0.013 (0.005) |
| Age at first birth – age at menarche (years) | 0.010 (0.005) | 0.008 (0.004) |
| Birth index | −0.0042 (0.0008) | −0.0034 (0.0006) |
| BBD (yes/no) | 0.190 (0.525) | 0.663 (0.417) |
| BBD x age at menarche | 0.067 (0.026) | 0.022 (0.020) |
| BBD x duration of premenopause | −0.014 (0.010) | −0.013 (0.078) |
| BBD x duration of menopause | −0.015 (0.007) | −0.015 (0.004) |
| Duration of postmenopausal E alone use | 0.049 (0.011) | 0.019 (0.006) |
| Duration of postmenopausal E +P use | 0.097 (0.026) | 0.033 (0.008) |
| Duration of postmenopausal other HT | 0.038 (0.017) | 0.008 (0.008) |
| Current postmenopausal hormone use | −0.129 (0.088) | 0.254 (0.056) |
| Past postmenopausal hormone use | −0.195 (0.081) | −0.227 (0.058) |
| (Average premenopausal BMI-21.8) x yrs premenopause | −0.0013 (0.00027) | −0.0010 |
| (Average postmenopausal BMI-24.4) x yrs menopausal | 0.0049 (0.0008) | 0.0025 (0.0004) |
| (Height-64.5) x yrs premenopause | 0.00096 (0.00033) | 0.00049 |
| (Height-64.4) x yrs menopausal | −0.0018 (0.0018) | −0.00002 |
| Cumulative alcohol ounces premenopause | 0.00017 (0.00008) | 0.00044 |
| Cumulative alcohol ounces with HT after menopause | 0.00031 (0.0002) | −0.0001 |
| Cumulative alcohol ounces without HT after menopause | 0.00022 (0.0004) | 0.00028 |
| Family history (yes/no) | 0.40 (0.07) | 0.45 (0.05) |
| Intercept | −8.703* (0.25) | −8.115 (0.21) |
Adjusted from published coefficient for 2-year risk prediction
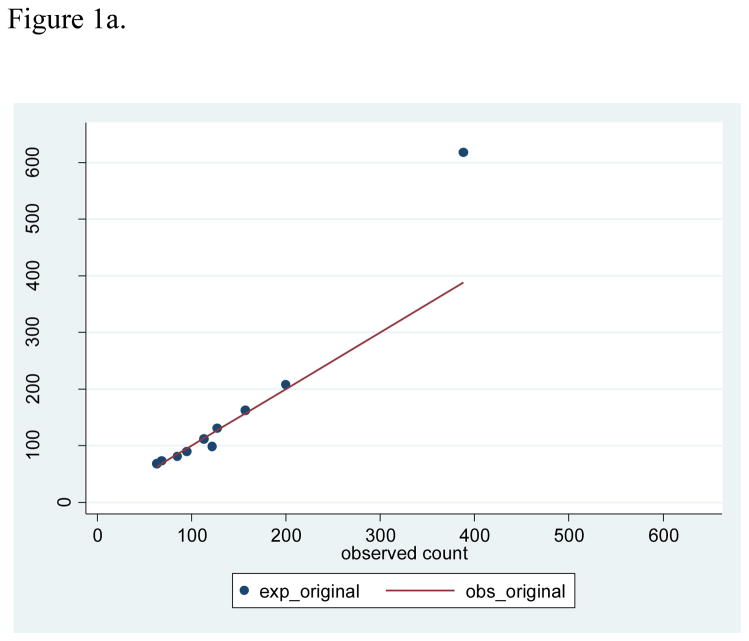
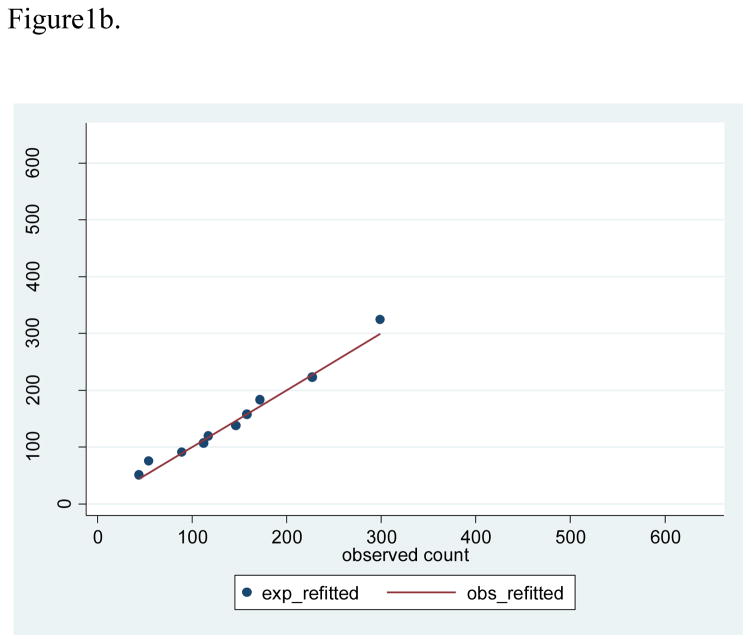
Based on the development sample, the lowest predicted 2-year risk was 0.05%, the cutpoint for the lowest decile was 0.25%, the cutpoint for the top decile was 0.98%, and the highest predicted risk was 5.36% (Table 2). These deciles of risk observed in the development sample were used to evaluate calibration in the validation sample. With 1,418 breast cancer cases observed in the validation sample, the observed 2-year risk was 0.56%, compared with average predicted 2-year risks of 0.58% (SD 0.32) from the re-fitted Rosner-Colditz model, and a larger average predicted risk of 0.64% (SD 0.53) from the original model. The Rosner-Colditz model with original estimates had generally good agreement between observed and predicted numbers of events in lower risk women, but this model substantially over-estimated the number of events in the highest risk women (Figure 1a). The likely explanation for the poor fit of the original model in the highest risk women is that 41.2% of the two year intervals in this highest risk decile accrued from women age 70 or older who were not represented in the original model estimation. For the re-estimated Rosner-Colditz model applied to the validation sample, 2-year intervals in the top decile of risk had more than 6 times as many cases as the bottom decile, and calibration, based on comparison of observed and predicted risks in deciles with accompanying Hosmer-Lemeshow tests, was generally good (Figure 1b).
Table 2.
Calibration in the validation sample for the Rosner-Colditz model with risk deciles from the development sample
| Rosner-Colditz model | Original Rosner-Colditz model | Re-fitted Rosner-Colditz model | ||||
|---|---|---|---|---|---|---|
| Development sample risk deciles | Validation sample: 254,767 2-yr intervals | Validation sample: 254,767 2-yr intervals | ||||
| Predicted risk (%)* | N | O/E (ratio) | (O-E)2/E | N | O/E (ratio) | (O-E)2/E |
| .0519–.2501 | 37,044 | 63/68.5 (.92) | 0.44 | 25,434 | 44/50.8 (.87) | 0.91 |
| .2502–.3226 | 25,447 | 68/73.1 (.93) | 0.36 | 26,021 | 54/74.9 (.72) | 5.83 |
| .3227–.3855 | 22,837 | 85/80.9 (1.05) | 0.21 | 25,706 | 89/91.1 (.98) | 0.05 |
| .3856–.4466 | 21,514 | 95/89.5 (1.06) | 0.34 | 25,692 | 112/106.9 (1,05) | 0.24 |
| .4467–.5100 | 20,607 | 122/98.4 (1.24) | 5.66 | 24,971 | 117/119.4 (.98) | 0.05 |
| .5101–.5811 | 20,582 | 113/112.1 (1.01) | 0.01 | 25,216 | 146/137.4 (1.06) | 0.54 |
| .5812–.6664 | 20,955 | 127/130.4 (.97) | 0.09 | 25,348 | 158/157.7 (1.00) | 0.00 |
| .6665–.7844 | 22,524 | 157/162.7 (.96) | 0.20 | 25,432 | 172/183.5 (.94) | 0.72 |
| .7845–.9824 | 23,703 | 200/207.1 (.97) | 0.24 | 25,589 | 227/223.4 (1.02) | 0.06 |
| .9825–5.3633 | 39,554 | 388/617.4 ((.63) | 85.24 | 25,358 | 299/324.2 (.92) | 1.96 |
| Overall | 254,767 | 1,418/1,640.0 (.86) | 254,767 | 1,418/1,469.3 (.97) | ||
| Average (SD), min-max predicted risk (%) | 0.644 (.53), .03–16.22 | 0.577 (.32), .06–5.93 | ||||
| Hosmer-Lemeshow Chi square=92.78, d.f.=8, P<0.001 | Hosmer-Lemeshow Chi square =10.36, d.f.=8, P=0.24; | |||||
O/E denotes observed number of breast cancer cases/expected number of cases
Predicted 2-year risk from the re-fitted Rosner-Colditz model
Figure 1.
Figure 1a. Scatterplot of observed versus expected counts based on original model with 45 degree line
Figure 1b. Scatterplot of observed versus expected counts based on refitted model with 45 degree line
The discriminatory ability of the re-fitted Rosner-Colditz prediction rule when applied to the validation sample was comparable, but slightly higher than overall discrimination based on the original prediction rule (.649 versus .640, Table 3). Discrimination by either prediction rule was slightly weaker when comparisons were made among women in the same age-group (ranging from 0.63 to 0.59, with age-adjusted C-statistic of 0.63) and tended to be lower in older women (Table 3). Not surprisingly, the largest age-specific difference between the original and re-fitted model in discrimination occurred among women age 70 or older.
Table 3.
Comparison of age-specific, and weighted averages of age-specific C-statistics for the original and re-scored Rosner-Colditz models in the validation sample
| Cases | Original Rosner-Colditz model | Re-scored Rosner-Colditz model | |
|---|---|---|---|
| Age group | N | C ±SE | C ±SE |
| <50 years | 196 | .634±.020 | .626±.020 |
| 50–59 years | 469 | .632±.013 | .636±.013 |
| 60–69 years | 503 | .617±.012 | .630±.012 |
| ≥70 years | 250 | .572±.018 | .594±.018 |
| Weighted average† | 1418 | .617±.0074 | .625 ± .0074 |
| Overall‡ | 1418 | .640±.0073 | .649±.0073 |
Weighted average of the age-group specific C-statistic
Based on prediction in the entire evaluation dataset without age adjustment
From a polytomous logistic regression model that considered breast cancer of different ER/PR types separately, some differences in the effects of risk factors for different types were noted (Table 4). Overall, findings were similar to those seen for specific ER/PR types in an alternative analysis (21). Specifically, duration of premenopause had a weaker effect on the risk of ER−/PR− cancers, relative to its association with ER+/PR+ and ER+/PR− cancers, years from menarche to first birth had no association with ER+/PR+ cancer, but a significant positive association with the other types, the birth index had little association with risk of ER−/PR− breast cancer, and postmenopausal BMI had a stronger effect on risk of ER+/PR+ cancers relative to other types. Overall, prediction of ER+/PR+ and ER+/PR− cancers attained higher C-statistics than prediction of ER−/PR− cancers. However, the simpler logistic model assuming common effects of all risk factors on each type of breast cancer explained 91% of the variance accounted for by the more complicated polytomous model.
Table 4.
Comparison of parameter estimates for different breast cancer ER/PR types based on the Rosner-Colditz model extended via multinomial logistic regression
| ER+/PR+ (n=2123) | ER+/PR− (n=542) | ER−/PR− (n=622) | Heterogeneity P-value | |
|---|---|---|---|---|
| Parameter | Estimate (SE) | Estimate (SE) | Estimate (SE) | |
| Duration of premenopause (years) | 0.086 (0.007) | 0.091 (0.015) | 0.038 (0.013) | 0.003 |
| Duration of menopause (natural, years) | 0.030 (0.004) | 0.035 (0.008) | 0.016 (0.007) | 0.15 |
| Duration after bilateral oophorectomy (years) | 0.025 (0.006) | 0.027 (0.011) | 0.023 (0.010) | 0.97 |
| Age at first birth – age at menarche (years) | −0.002 (0.005) | 0.023 (0.009) | 0.019 (0.009) | 0.013 |
| Birth index | −0.0037 (0.0007) | −0.0033 (0.0014) | 0.00045 (0.0013) | 0.014 |
| BBD (yes/no) | 0.79 (0.50) | 0.96 (0.99) | 0.47 (0.88) | 0.92 |
| BBD x age at menarche | 0.040 (0.023) | 0.042 (0.045) | −0.0082 (0.043) | 0.60 |
| BBD x duration of premenopause | −0.018 (0.0094) | −0.023 (0.019) | 0.0011 (0.016) | 0.52 |
| BBD x duration of menopause | −0.024 (0.0048) | −0.015 (0.0093) | −0.0024 (0.0086) | 0.078 |
| Duration of postmenopausal E alone use | 0.018 (0.007) | 0.011 (0.014) | −0.001 (0.014) | 0.46 |
| Duration of postmenopausal E + P use | 0.050 (0.008) | 0.008 (0.018) | 0.017 (0.018) | 0.045 |
| Duration of postmenopausal other HT | 0.015 (0.009) | −0.014 (0.018) | 0.005 (0.017) | 0.34 |
| Current postmenopausal hormone use | 0.40 (0.065) | 0.42 (0.13) | 0.21 (0.12) | 0.36 |
| Past postmenopausal hormone use | −0.25 (0.068) | −0.017 (0.13) | −0.26 (0.13) | 0.26 |
| (Average premenopausal BMI-21.8) x yrs premenopause | −0.00057 (0.00021) | −0.0016 (0.00047) | −0.00079 (0.00042) | 0.12 |
| (Average postmenopausal BMI-24.4) x yrs menopausal | 0.0033 (0.00047) | 0.0013 (0.0010) | −0.00005 (0.0010) | 0.004 |
| (Height-64.5) x yrs premenopause | 0.0011 (0.00028) | 0.00002 (0.00057) | −0.00012 (0.00053) | 0.063 |
| (Height-64.4) x yrs menopausal | −0.00013 (0.00011) | −0.00081 (0.0021) | 0.0033 (0.0020) | 0.26 |
| Cumulative alcohol ounces premenopause | 0.00044 (0.00012) | 0.00055 (0.00023) | 0.00044 (0.00024) | 0.91 |
| Cumulative alcohol ounces with HT after menopause | −0.000001 (0.0003) | −0.00004 (0.0006) | −0.0016 (0.00083) | 0.19 |
| Cumulative alcohol ounces without HT after menopause | 0.00039 (0.00023) | 0.00018 (0.00043) | −0.00007 (0.00047 | 0.66 |
| Family history (yes/no) | 0.41 (0.057) | 0.50 (0.11) | 0.35 (0.11) | 0.65 |
| C-statistic (SE) | 0.683 (0.0056) | 0.688 (0.011) | 0.622 (0.011) |
Variance explained by the model assuming uniform effects: 1173.89/1284.67 = .914
When we compared reclassification of overall breast cancer risk (based on the four absolute risk categories previously defined) between the refitted Rosner-Colditz model and the extended Rosner-Colditz model allowing for different associations of risk factors with ER/PR types, and including an indicator for missing ER/PR status, we saw little change in overall prediction between the two models (Table 5). Specifically, each model, relative to the other, reclassified between one and two percent of cases to a higher risk category, and between one and two percent of non-cases to a lower risk category. Further, if we estimated a woman’s probability of breast cancer as the sum of her predicted probabilities of each ER/PR type, the C-statistic for this prediction was 0.648 (95% CI: 0.634 – 0.661), in close agreement with the simpler model assuming common effects of all risk factors summarized in Table 1.
Table 5.
Cross-classification of predicted and observed risk by the type-specific Rosner-Colditz model* and the overall Rosner-Colditz model with models estimated in the development sample and evaluated in the validation sample
| Rosner-Colditz model 2-yr risk | |||||
|---|---|---|---|---|---|
| Type-specific R-C model 2-yr risk | 0–<.4% | .4–<.67% | .67–<1.0% | ≥1.0% | Total |
| 0–<.4%, n | 81,969 | 2,279 | 0 | 0 | 84,248 |
| Cases (risk*) | 199 (2.4) | 8 (3.5) | 0 (-) | 0 (-) | 207 (2.5) |
| .4−<.67%, n | 1,275 | 92,571 | 1,969 | 0 | 95,815 |
| Cases (risk*) | 10 (7.8) | 505 (5.5) | 15 (7.6) | 0 (-) | 530 (5.5) |
| .67−<1.0%, n | 0 | 1,181 | 48,871 | 681 | 50,733 |
| Cases (risk*) | 0 (-) | 5 (4.2) | 381 (7.8) | 6 (8.8) | 392 (7.7) |
| ≥1.0%, n | 0 | 3 | 839 | 23,129 | 23,971 |
| Cases (risk*) | 0 (-) | 0 (-) | 8 (9.5) | 281 (12.1) | 289 (12.1) |
| Total | 83,244 | 96,034 | 51,679 | 23,810 | 254,767 |
| Cases (risk*) | 209 (2.5) | 518 (5.4) | 404 (7.8) | 287 (12.1) | 1,418 (5.6) |
2-year risk x 1,000
Rosner-Colditz NRIe†= (8+0+0+15+0+6)/1,418 = 2.0%
Type-specific R-C NRIe†= (10+0+0+5+0+8)/1,418 = 1.6%
Rosner-Colditz NRIne†= (1,265+0+0+1,176+3+831)/253,349 = 1.3%
Type-specific R-C NRIne†= (2,271+0+1,954+0+0+675)/253,349 = 1.9%
The multinomial extension of the Rosner-Colditz model (labeled type-specific R-C) considers all variables included in the Rosner-Colditz model with separate effect estimates for ER+/PR+, ER+/PR−, ER−/PR−, and other incident breast cancers of unknown ER/PR status. Both models developed in the training set and evaluated in the validation set.
NRIe denotes net reclassification index among events of breast cancer, while NRIne denotes net reclassification index among non-events
Discussion
We used data from 26 years of experience in the Nurses’ Health Study to re-fit and evaluate the performance of a previously described risk prediction model, now extended to include more recent data with information from women up to age 85 years. The Rosner-Colditz model is one of several risk prediction rules, including popular alternatives such as the Gail model, and the IBIS model developed by Tyrer and Cuzick, that base predictions solely on information from self-reported risk factor information without biomarkers. As previously noted [10–12], these models have only modest ability to predict breast cancer; although consideration of biomarkers such as a genetic risk score [28, 29] or plasma hormones can improve predictive performance (at least modestly), this additional information is costly and thus the cost-benefit is unclear. For example, recent evidence finds that addition of measures of several endogenous hormone levels improves prediction (measured by the C-statistic) in the Rosner-Colditz model by about 5%, but in analyses restricted to postmenopausal women not using postmenopausal hormones [30]. Further, while these models are probably not sensitive enough to excuse a woman from screening on the basis of a low predicted risk, they have been judged to be suitable for directing clinical decisions [19].
When we updated the estimated parameters in the Rosner-Colditz model by inclusion of information from women up to age 85 years, we found some changes in estimated associations, notably for age and variables that characterize use of postmenopausal hormones. These changes likely reflect the wider age distribution of the study population, and the marked changes in use of postmenopausal hormones during the past decade [31]. Predicted risks based on the originally published model markedly over-estimated observed risk among higher risk women. However, overall predictions from the updated model strongly correlated with predictions from the originally published model, and the discriminatory ability of the original model was quite similar to that based on the re-fitted Rosner-Colditz model. A recent external evaluation of the validity of the Rosner-Colditz model in data from the California Teachers’ Study found that the model performed equally well in that study [32].
Our finding of significant heterogeneity of the relationships of some breast cancer risk factors with different ER/PR types of breast cancer is consistent with previous studies [21]. However, the observed heterogeneity did not contribute substantially to prediction of the overall endpoint of any breast cancer. Our result in this setting is similar to a previous investigation of the separate and joint prediction of myocardial infarction, stroke, and cardiovascular death in the Physicians’ Health Study [26]. We found that prediction of the first occurrence of any major cardiovascular event was not substantially improved by separate consideration of relationships of risk factors with components of this outcome, although specific risk factors had substantially different relationships with individual components.
In summary, we found that fitting the Rosner-Colditz model to include women up to age 85 years old, yielded a well-calibrated model with somewhat different coefficients relative to the original model. Levels of discrimination for the re-fitted model were modest relative to criteria proposed by Hosmer and Lemeshow [33], but slightly higher than those seen for commonly used models such as the Gail model [1] and the Tyrer-Cuzick model [11]. Discrimination was somewhat better for younger women. An advantage of the Rosner-Colditz model is that it includes information obtained only from questionnaires, but does involve some complexity, including interactions involving menopausal factors. Also, while some risk factors have different relationships with different ER/PR types of breast cancer, consideration of these differences in an extended model did not enhance prediction.
Acknowledgments
Funding
This project was finded by a cohort infrastructure Grant (UM1 CA186107), and a program project Grant (P01 CA87969) from the National Cancer Institute. The authors declare that they have no conflict of interest.
References
- 1.Gail MH, Brinton LA, Byar DP, Corle DK, Green SB, Shairer C, Mulvihill JJ. Projecting individualized probabilities of developing breast cancer for white females who are being examined annually. J Natl Cancer Inst. 1989;81:1879–86. doi: 10.1093/jnci/81.24.1879. [DOI] [PubMed] [Google Scholar]
- 2.Costantino JP, Gail MH, Pee D, Anderson S, Redmond CK, Benichou J, Wieand HS. Validation studies for models projecting the risk of invasive and total breast cancer incidence. J Natl Cancer Inst. 1999;91:1541–8. doi: 10.1093/jnci/91.18.1541. [DOI] [PubMed] [Google Scholar]
- 3.Gail MH, Costantino JP, Pee D, Bondy M, Newman L, Selvan M, Anderson GL, Malone KE, Marchbanks PA, McCaskill-Stevens W, Norman SA, Simon MS, Spirtas R, Ursin G, Bernstein L. Projecting Individualized Absolute Invasive Breast Cancer Risk in African American Women. J Natl Cancer Inst. 2007;99(23):1782–1792. doi: 10.1093/jnci/djm223. [DOI] [PubMed] [Google Scholar]
- 4.Matsuno RK, Costantino JP, Ziegler RG, Anderson GL, Li H, Pee D, Gail MH. Projecting individualized absolute invasive breast cancer risk in asian and pacific islander american women. JNCI. 2011;103:951–61. doi: 10.1093/jnci/djr154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Division of Cancer Epidemiology and Genetics. Breast cancer risk assessment macro BrCa_RAM.sas. Downloaded from http://dceg.cancer.gov/tools/risk-assessment/bcrasasmacro.
- 6.Rosner B, Colditz GA. Nurses’ health study: log-incidence mathematical model of breast cancer incidence. J Natl Cancer Inst. 1996;88:359–364. doi: 10.1093/jnci/88.6.359. [DOI] [PubMed] [Google Scholar]
- 7.Colditz GA, Rosner B. Cumulative risk of breast cancer to age 70 years according to risk factor status: data from the Nurses’ Health Study. Am J Epidemiol. 2000;152:950–964. doi: 10.1093/aje/152.10.950. [DOI] [PubMed] [Google Scholar]
- 8.Colditz GA, Rosner BA, Chen WY, Holmes MD, Hankinson SE. Risk factors for breast cancer according to estrogen and progesterone receptor status. J Natl Cancer Inst. 2004;96:218–228. doi: 10.1093/jnci/djh025. [DOI] [PubMed] [Google Scholar]
- 9.Rockhill B, Spiegelman D, Byrne C, Hunter DJ, Colditz GA. Validation of the Gail et al. model of breast cancer risk prediction and implications for chemoprevention. J Natl Cancer Inst. 2001;93(5):358–66. doi: 10.1093/jnci/93.5.358. [DOI] [PubMed] [Google Scholar]
- 10.Boyle P, Mezzetti M, La Vecchia C, Franceschi S, Decarli A, Robertson C. Contribution of three components to individual cancer risk predicting breast cancer risk in Italy. Eur J Cancer Prev. 2004;13:183–91. doi: 10.1097/01.cej.0000130014.83901.53. [DOI] [PubMed] [Google Scholar]
- 11.Tyrer J, Duffy SW, Cuzick J. A breast cancer prediction model incorporating familial and personal risk factors. Stat Med. 2004;23:1111–30. doi: 10.1002/sim.1668. [DOI] [PubMed] [Google Scholar]
- 12.Boyd NF, Guo H, Martin LJ, Sun L, Stone J, Fishell E, Jong RA, Hislop G, Chiarelli A, Minkin S, Yaffe MJ. Mammographic density and the risk and detection of breast cancer. N Engl J Med. 2007;356:227–36. doi: 10.1056/NEJMoa062790. [DOI] [PubMed] [Google Scholar]
- 13.Barlow WE, White E, Ballard-Barbash R, Vacek PM, Titus-Ernstoff L, Carney PA, Tice JA, Buist DS, Geller BM, Rosenberg R, Yankaskas BC, Kerlikowske K. Prospective breast cancer risk prediction model for women undergoing screening mammography. J Natl Cancer Inst. 2006;98:1204–14. doi: 10.1093/jnci/djj331. [DOI] [PubMed] [Google Scholar]
- 14.Tice JA, Cummings SR, Smith-Bindman R, Ichikawa L, Barlow WE, Kerlikowske K. Using clinical factors and mammographic breast density to estimate breast cancer risk: development and validation of a new predictive model. Ann Intern Med. 2008;148:337–47. doi: 10.7326/0003-4819-148-5-200803040-00004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mavaddat N, Pharoah PD, Michailidou K, et al. Prediction of breast cancer risk based on profiling with common genetic variants. J Natl Cancer Inst. 2015;107(5) doi: 10.1093/jnci/djv036. pii: djv036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Pharoah PD, Antoniou AC, Easton DF, Ponder BA. Polygenes, risk prediction, and targeted prevention of breast cancer. N Engl J Med. 2008;358:2796–803. doi: 10.1056/NEJMsa0708739. [DOI] [PubMed] [Google Scholar]
- 17.Tamimi RM, Rosner B, Colditz GA. Evaluation of a breast cancer risk prediction model expanded to include category of prior benign breast disease lesion. Cancer. 2010;116:4944–53. doi: 10.1002/cncr.25386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Meads C, Ahmed I, Riley RD. A systematic review of breast cancer incidence risk prediction models with meta-analysis of their performance. Breast Cancer Res Treat. 2012;132:365–77. doi: 10.1007/s10549-011-1818-2. [DOI] [PubMed] [Google Scholar]
- 19.Visvanathan K, Hurley P, Bantug E, Brown P, Col NF, Cuzick J, Davidson NE, Decensi A, Fabian C, Ford L, Garber J, Katapodi M, Kramer B, Morrow M, Parker B, Runowicz C, Vogel VG, 3rd, Wade JL, Lippman SM. Breast cancer follow-up and management after primary treatment: American Society of Clinical Oncology clinical practice guideline update. J Clin Oncol. 2013;31:2942–62. doi: 10.1200/JCO.2013.49.3122. [DOI] [PubMed] [Google Scholar]
- 20.Colditz GA, Hankinson SE. The Nurses’ Health Study: lifestyle and health among women. Nat Rev Cancer. 2005;5:388–396. doi: 10.1038/nrc1608. [DOI] [PubMed] [Google Scholar]
- 21.Rosner B, Glynn RJ, Tamimi RM, Chen WY, Colditz GA, Willett WC, Hankinson SE. Breast cancer risk prediction with heterogeneous risk profiles according to breast cancer tumor markers. Am J Epidemiol. 2013;178:296–308. doi: 10.1093/aje/kws457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hefti MM, Hu R, Knoblauch NW, Collins LC, Haibe-Kains B, Tamimi RM, Beck AH. Estrogen receptor negative/progesterone receptor positive breast cancer is not a reproducible subtype. Breast Cancer Res. 2013;15:R68. doi: 10.1186/bcr3462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Prentice RL, Gloeckler LA. Regression analysis of grouped survival data with application to breast cancer data. Biometrics. 1978;34(1):57–67. [PubMed] [Google Scholar]
- 24.Wu M, Ware JH. On the use of repeated measurements in regression analysis with dichotomous responses. Biometrics. 1979;35(2):513–21. [PubMed] [Google Scholar]
- 25.D'Agostino RB, Lee ML, Belanger AJ, Cupples LA, Anderson K, Kannel WB. Relation of pooled logistic regression to time dependent Cox regression analysis: the Framingham Heart Study. Stat Med. 1990;9(12):1501–15. doi: 10.1002/sim.4780091214. [DOI] [PubMed] [Google Scholar]
- 26.Glynn RJ, Rosner B. Methods to evaluate risks for composite end points and their individual components. J Clin Epidemiol. 2004;57:113–22. doi: 10.1016/j.jclinepi.2003.02.001. [DOI] [PubMed] [Google Scholar]
- 27.Kerr KF, Wang Z, Janes H, McClelland RL, Psaty BM, Pepe MS. Net reclassification indices for evaluating risk prediction instruments: a critical review. Epidemiology. 2014;25:114–21. doi: 10.1097/EDE.0000000000000018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Shieh Y, Hu D, Ma L, Huntsman S, Gard CC, Leung JW, Tice JA, Vachon CM, Cummings SR, Kerlikowske K, Ziv E. Breast cancer risk prediction using a clinical risk model and polygenic risk score. Breast Cancer Res Treat. 2016;159:513–25. doi: 10.1007/s10549-016-3953-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Vachon CM, Pankratz VS, Scott CG, Haeberle L, Ziv E, Jensen MR, Brandt KR, Whaley DH, Olson JE, Heusinger K, Hack CC, Jud SM, Beckmann MW, Schulz-Wendtland R, Tice JA, Norman AD, Cunningham JM, Purrington KS, Easton DF, Sellers TA, Kerlikowske K, Fasching PA, Couch FJ. The contributions of breast density and common genetic variation to breast cancer risk. J Natl Cancer Inst. 2015;107(5) doi: 10.1093/jnci/dju397. pii: dju397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Tworoger SS, Zhang X, Eliassen AH, Qian J, Colditz GA, Willett WC, Rosner BA, Kraft P, Hankinson SE. Inclusion of endogenous hormone levels in risk prediction models of postmenopausal breast cancer. J Clin Oncol. 2014;32:3111–7. doi: 10.1200/JCO.2014.56.1068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Steinkellner AR, Denison SE, Eldridge SL, Lenzi LL, Chen W, Bowlin SJ. A decade of postmenopausal hormone therapy prescribing in the United States: long-term effects of the Women's Health Initiative. Menopause. 2012;19:616–21. doi: 10.1097/gme.0b013e31824bb039. [DOI] [PubMed] [Google Scholar]
- 32.Rosner BA, Colditz GA, Hankinson SE, Sullivan-Halley J, Lacey JV, Jr, Bernstein L. Validation of Rosner-Colditz breast cancer incidence model using an independent data set, the California Teachers Study. Breast Cancer Res Treat. 2013;142:187–202.33. doi: 10.1007/s10549-013-2719-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hosmer DW, Lemeshow S. Applied Logistic Regression. 2. John Wiley and Sons; New York: 2000. [Google Scholar]