Effect of Stimulus Level on the Temporal Response Properties of the Auditory Nerve in Cochlear Implants

Abstract

Electrically evoked compound action potentials (ECAPs) have been used to examine temporal response patterns of the auditory nerve in cochlear implant (CI) recipients. ECAP responses to individual pulses in a pulse train vary across stimulation rates for individual CI users. For very slow rates, auditory neurons have ample time to discharge, recover, and respond to each pulse in the train. As the pulse rate increases, an alternating ECAP-amplitude pattern occurs. As the stimulation rate increases further, the alternating pattern eventually ceases and the overall ECAP amplitudes are diminished, yielding a relatively stochastic state that presumably reflects a combination of adaptation, desynchronization, and facilitation across fibers. Because CIs operate over a range of current levels in everyday use, it is important to understand auditory-nerve responses to pulse trains over a range of levels. The effect of stimulus level on ECAP temporal response patterns in human CI users has not been well studied. The first goal of this study was to examine the effect of stimulus level on various aspects of ECAP temporal responses to pulse-train stimuli. Because higher stimulus levels yield more synchronous responses and faster recovery, it was hypothesized that: (1) the maximum alternation would occur at slower rates for lower levels and faster rates at higher levels, (2) the alternation depth at its maximum would be smaller for lower levels, (3) the rate that produces a stochastic state (‘stochastic rate’) would decrease with level, (4) adaptation would be greater for lower levels as a result of slower recovery, and (5) refractory-recovery time constants would be longer (slower) for lower levels, consistent with earlier studies. The second goal of this study was to examine how refractory-recovery time constants relate specifically to maximum alternation and stochastic rate. Data were collected for 12 ears in 10 CI recipients. ECAPs were recorded in response to each of 13 pulses in an equal-amplitude pulse train ranging in rate from 900–3500 pps for three levels (low, medium, high). The results generally supported hypotheses 1–4; there were no significant effects of level on the refractory-recovery time constants (hypothesis 5). When data were pooled across level, there was a significant negative correlation between alternation depth and refractory recovery time. Understanding the effects of stimulus level on auditory-nerve responses may provide further insight into improving the use of objective measures for potentially optimizing speech-processing strategies.

1. Introduction

Individuals with cochlear implants (CIs) have demonstrated differences in performance for different stimulation rates, with no single rate being optimal for all recipients (e.g., Arora et al., 2009; Friesen et al., 2005; Holden et al., 2002; Kiefer et al., 2000; Loizou et al., 2000; Plant et al., 2007; Vandali et al., 2000). Differences in neural survival patterns and the temporal response properties of the underlying auditory neural population likely contribute to differences in performance as a function of stimulation rate. The electrically evoked compound action potential (ECAP) is a whole-nerve response that has been used to study auditory-nerve responses to equal-amplitude pulse trains in human CI recipients (Finley et al., 1997; Hay-McCutcheon et al., 2005; He et al., 2016; Hughes et al., 2012, 2014; McKay et al., 2013; Rubinstein et al., 1999; Wilson et al., 1997; Zhang et al., 2013). Only three of these studies have reported data for different stimulus levels within individuals (Finley et al., 1997; Hughes et al., 2012; McKay et al., 2013); however, none of these studies reported aggregate data for which stimulus level was the primary variable of interest. Because the stimuli that CI recipients listen to in daily life represent a range of input levels, it is worthwhile to examine auditory neural responses to pulse trains at different stimulus levels in greater detail to better characterize the range of responses across individuals.

Earlier research in animals and humans has described the basic temporal aspects of auditory-nerve responses to electrical stimulation using equal-amplitude pulse trains (e.g., Finley et al., 1997; Hughes et al., 2012; Matsuoka et al., 2000; Rubinstein et al., 1999). These results show that for stimulation rates up to approximately 200 pps, the ECAP amplitudes for each pulse in the train are relatively equivalent, consistent with complete recovery from depolarization to each pulse. As the stimulation rate increases, an alternating-amplitude pattern emerges, in which the amplitudes in response to the odd-numbered pulses are larger than those in response to the even-numbered pulses, presumably reflecting a common range of relative refractory periods across individual auditory nerve fibers (e.g., Matsuoka et al., 2000; Ramekers et al., 2015). In humans, this alternating pattern can typically be observed for rates ranging from approximately 400—2400 pps (Hughes et al., 2012; Wilson et al., 1997). Hughes et al. (2012) showed that the maximum alternation depth occurred most often between 1200–1800 pps for stimulus levels at the upper level of participants’ dynamic ranges, which coincides with time constants that are within the early portion of the relative refractory period for humans. Further increases in stimulation rate result in a flattening of the pattern (lack of alternation) and an overall decrease in ECAP amplitude, which has typically been referred to as adaptation. It should be noted that the term ‘adaptation’ is used in this study in concert with the literature (e.g., Masuoka et al., 2000; McKay et al., 2013; He et al., 2016) to describe an overall decrease in the ECAP response amplitude across the pulse train, even though the underlying mechanisms contributing to that decrease (e.g., non-overlapping refractory-recovery times, neural fatigue) are unclear for human CI recipients. Collectively, the patterns described here reflect a combination of refractory effects, adaptation, accommodation, and desynchronization of the responses of individual auditory neurons that contribute to the aggregate ECAP response (see Boulet et al., 2016 for a review). The rate at which the alternating pattern ceases has been referred to as the “stochastic rate,” and has been shown to occur most often between 2400–3500 pps (Hughes et al., 2012).

As noted above, fewer studies have reported stimulus level effects on ECAP responses to equal-amplitude pulse trains in human CI users. Finley et al. (1997) showed an individual example of ECAP responses for pulse-train rates of 100, 604, and 1016 pps at four different stimulus levels. That individual demonstrated an increase in adaptation over the course of the pulse train for the higher stimulus levels than for the lower levels. In other words, the alternating pattern for high levels demonstrated an overall continuous decline in amplitude over the course of the pulse train, whereas the alternating pattern for lower levels remained relatively steady across the duration of the 30-ms pulse train. For the lower current levels, their data also showed a larger overall reduction in ECAP amplitude relative to the amplitude for the first pulse. That is, lower current levels produced more adaptation than higher current levels. In a group of five subjects, McKay et al. (2013) also reported more adaptation for lower stimulus levels than for higher levels. In an across-subjects comparison (29 ears), Hughes et al. (2012) found that subjects who were tested at higher current levels demonstrated faster stochastic rates, consistent with evidence that higher levels yield greater synchrony and faster recovery from the refractory period (Finley et al., 1997; Matsuoka et al., 2000; Miller et al., 2001). Consequently, as the stimulus level increases, faster pulse-train rates are likely necessary to produce an alternating pattern, and even faster rates would be required to produce a stochastic state. To date, no study has systematically evaluated the effects of stimulus level on ECAP responses to pulse trains at different rates for a larger group of human CI recipients.

The first aim of this study was to evaluate within-subjects effects of stimulus level across rates for the following measures: (1) the rate at which the maximum alternation occurs, (2) the alternation depth at its maximum, (3) the rate at which the alternating pattern ceases (stochastic rate), (4) the overall degree of adaptation at each stimulation rate, and (5) refractory-recovery time constants (tau) for a standard two-pulse forward-masking paradigm. For the first four outcome measures, ECAPs were obtained in response to each of 13 pulses in an equal-amplitude pulse train for rates of 900, 1200, 1800, 2400, and 3500 pps at three levels (high, medium, and low) within the ECAP dynamic range. For refractory-recovery functions, ECAPs were obtained in response to a forward-masked probe (using a single masker) with a gradually increasing masker-probe interval (MPI). Because lower stimulus levels have been shown to yield less synchrony and slower recovery (e.g., Battmer et al., 2004; Finley et al., 1997; Matsuoka et al., 2000; Miller et al., 2008), we hypothesized that (1) the maximum alternation would occur at slower rates for lower levels; (2) the alternation depth at its maximum would be smaller for lower levels; (3) the stochastic rate would decrease for lower levels; (4) adaptation would be greater for lower levels (in accordance with Finley et al., 1997 and McKay et al., 2013), due to slower recovery observed at lower stimulus levels (e.g., Finley et al., 1997; Matsuoka et al., 2000; Miller et al., 2001); and (5) refractory-recovery time constants would be longer (slower) for lower levels.

The second aim of this study was to examine how refractory-recovery time constants relate to the maximum alternation and stochastic rate. Although the time course of recovery from the refractory period is not the only mechanism that contributes to ECAP responses to individual pulses in the train (e.g., Boulet et al., 2016), we anticipated that single-pulse recovery time constants should, at a minimum, reflect the underlying temporal characteristics that contribute to the alternation depth and the rate at which the maximum alternation occurs. Matsuoka et al. (2000) suggested that the alternating pattern depends on a “resonance” between the refractory-recovery time period and the pulse rate. If the period of the pulse train coincides with the refractory-recovery period of the majority of neurons, we would expect a correlation between recovery time and the rate that yields the maximum alternation. Regarding the depth of alternation, we would expect smaller alternation depths for larger, more heterogeneous neural populations because of greater variance in recovery times across fibers. Auditory nerve-fiber loss likely limits the heterogeneity of temporal response properties across the population, likely leading to overall shorter recovery times. Indeed, modeling data by Botros and Psarros (2010) showed shorter recovery times for smaller neural populations. More homogeneous temporal responses might divide neural responses more clearly into ‘response’ or ‘no-response’ categories for subsequent pulses, thereby producing larger alternation depths (Finley et al., 1997). In guinea pigs, Ramekers et al. (2015) found faster recovery times and larger alternation depths for animals with poorer spiral ganglion cell survival, which supports this theory. The relation between single-pulse recovery time and the stochastic rate, however, could be more complicated. For faster rates that produce a stochastic state, the loss of alternation could simply be due to a loss of synchrony secondary to the variance in refractory-recovery times across individual fibers that contribute to the whole-nerve response. Or, the interplay between more complex temporal aspects of individual neurons (refractory effects, adaptation, accommodation, desynchronization; see Boulet et al., 2016) might obscure any clear relation between single-pulse recovery time constants and the stochastic state. For the second aim of the study, we therefore hypothesized that (1) faster refractory-recovery time constants would be correlated with (i) a faster rate at which the maximum alternation occurs, and (ii) larger alternation depth; and (2) single-pulse refractory-recovery time constants would not be correlated with the stochastic rate because at these faster rates, there likely will be more interactions between refractory recovery, adaptation, and facilitation.

2. Materials and Methods

2.1. Participants

Fourteen participants were initially enrolled in this study. Data collection could not be completed for two participants because ECAP amplitudes were too small (< 30 μV) at the highest stimulus level; one additional participant did not have measurable ECAPs at the lowest stimulus level tested. Data for a fourth participant (FS21), who also had very small ECAPs (<34 μV), demonstrated an increasing amplitude pattern across the duration of the pulse trains (i.e., ECAP responses were progressively larger for each pulse in the train), consistent with artifact contamination as reported by He et al. (2016). As a result, the data presented here represent the remaining 10 CI recipients (12 ears) implanted with Cochlear devices (Cochlear Ltd., Sydney, Australia). Relevant demographic information is detailed in Table 1. Nine recipients were adults at the time of testing; one was an adolescent (14.9 years old; subject F10). The mean duration of deafness prior to implantation was 8.5 years (range, 1.8–22.8); the mean age at implantation was 49.9 years (range, 8.3–82.0); and the average duration of CI use at the time of participation was 5.3 years (range, 0.5–10.7). Three recipients (F10, N1, and N6) had undergone re-implantation prior to participation in this study. For these participants, the duration of CI use was calculated using the date of the original activation. This study was approved by the Boys Town National Research Hospital (protocol 03-07-XP) Institutional Review Board. All participants signed an informed consent and were paid for their time.

Table 1.

Demographic information for study participants. Asterisks indicate the three subjects that were explanted and re-implanted; age at implant and duration of CI use were calculated relative to the time of the initial implant. Paired symbols in the Ear column indicate the left and right ears for the two participants with bilateral implants. CI, cochlear implant; CL, current level units.

Subject	Internal Device	Ear	Duration Deafness (yrs)	Age at CI (yrs)	Dur. CI Use (yrs)	Onset	Probe Levels (CL) Used (low, medium, high)
R2	24R(CS)	R^	3.5	51.8	9.9	progressive	200, 205, 210
R3	24R(CS)	R†	6.0	56.2	10.7	progressive	205, 210, 215
R7	24R(CS)	R	5.0	62.2	8.7	progressive	190, 200, 210
F1	24RE(CA)	L†	11.0	60.7	6.2	progressive	205, 210, 215
F2	24RE(CA)	R	10.0	60.3	5.7	progressive	185, 195, 205
F4	24RE(CA)	L	17.5	17.5	4.8	sudden	200, 210, 220
F10*	24RE(CA)	R	8.3	8.3	6.5	congenital	185, 195, 205
F15	24RE(CA)	L	22.8	22.8	2.9	congenital	185, 195, 205
FS20	CI422	R	3.0	67.3	0.5	progressive	185, 195, 205
N1*	CI512	L^	9.0	58.3	3.4	progressive	200, 205, 210
N5	CI512	R	1.8	50.8	1.7	sudden	185, 190, 195
N6*	CI512	R	4.0	82.0	3.0	progressive	185, 200, 215

2.2. Equipment and Stimuli

ECAP measurements were made using the Advanced Neural Response Telemetry (NRT) feature within Custom Sound EP (Cochlear Ltd., Sydney, Australia). Stimuli were presented through a laboratory Freedom speech processor interfaced with a programming pod. For all but two subjects (F2 and FS20), electrode 11 (middle of the array) was used for the masker and probe stimuli. For F2, electrode 9 was used and for FS20, electrode 17 was used because the ECAPs were larger than for other mid-array electrodes. The recording electrode was two positions apical to the stimulating electrode (software default). Stimulation and recording modes were monopolar (re: MP1 and MP2, respectively). All stimuli consisted of the standard cathodic-leading, symmetrical, biphasic current pulses that were 25 μsec in duration with an interphase gap [25 μsec for the older-generation 24R(CS) devices and 7 μsec for all newer-generation devices; these were software defaults]. Recordings were made using 100 sweeps with 60 dB gain for recipients with 24R(CS) devices and 50 dB gain for all other devices (respective software defaults). The probe rate was reduced to 35 Hz to allow enough time for presentation of the masker pulse-train stimuli. The recording delay was optimized on an individual basis to reduce artifact.

2.3. Procedures

Impedances were measured using Custom Sound EP (v. 2.0) at the beginning of the study visit to ensure that the stimulus and recording electrodes were functioning within normal limits as defined in the clinical software. Next, initial loudness judgments were obtained via the “stimulate only” mode of NRT using a 3500-pps train of 12 masker pulses and a single probe, for a total of 13 pulses¹. This stimulus represented the longest duration of the fastest rate, and was therefore expected to be the loudest for a given current-level (CL) unit. The MPI was set to 286 μsec (period of the 3500-pps pulse train) so that all 13 pulses were equally spaced in time. The probe level was set to equal that of the maskers to achieve a 13-pulse train with equal amplitudes. Stimulation began below threshold and masker/probe levels were increased in 5-CL steps. Participants used a visual loudness-rating scale that ranged from 1 to 10 to indicate when the stimulus was just noticeable (1), loud but comfortable (7), loud (8), and when the sound had reached the upper comfort level (9).

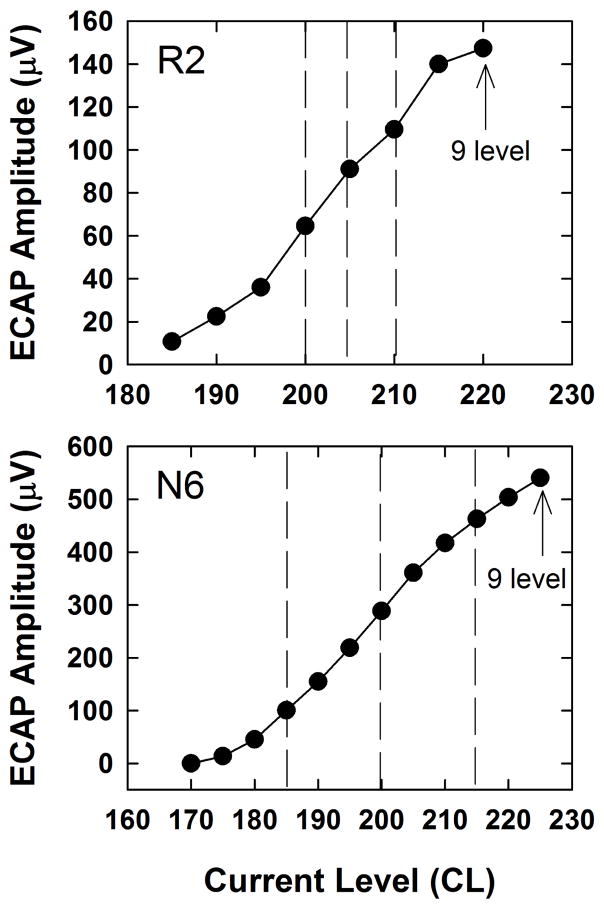
An ECAP amplitude growth function was then obtained using the standard two-pulse (masker-probe) forward-masking paradigm (Abbas et al., 1999) to determine the three stimulus levels that could be used for the main experiment. For the growth function, the masker was fixed at the 9 loudness level obtained with the pulse train while the probe, which also started at the 9 level, was reduced in 5-CL steps until no measurable ECAP remained (0 μV). Three CLs within each subject’s ECAP dynamic range (defined as the range of CLs that spanned the ECAP growth function) were chosen for the high, medium, and low stimulus levels used in the main experiment. Two examples are shown in Fig. 1, where the vertical dashed lines represent the three experimental stimulus levels for each subject. The highest level used for the experiment was typically 10 CL below the 9 level (highest point on the growth function) to allow headroom for the masker to be 10 CL higher than the probe in the template subtraction condition (described further in the following paragraph). The medium and low CLs were chosen to be equally spaced across the ECAP dynamic range, with the goal of having the lowest CL yield an ECAP amplitude of at least 40–50 μV in the single-pulse condition. This criterion was adopted because ECAP amplitudes generally decrease in response to pulse trains, so it was necessary for ECAP responses to single pulses to be sufficiently large to accommodate potential adaptation and desynchronization effects. In two cases (F2 and F4), the device exceeded voltage compliance limits before an 8 level was reached. In these cases, the highest point on the growth function represented the highest CL that remained within compliance. On average, the high, medium, and low CLs were at 83%, 65%, and 46% of the range of CLs used for the ECAP amplitude growth function.

Fig. 1.

Representative ECAP amplitude growth functions obtained using the standard two-pulse forward-masking subtraction paradigm. Data are shown for two subjects; subject number is indicated in each panel. The vertical dashed lines represent the three stimulus levels (low, medium, and high) used for the main experiment.

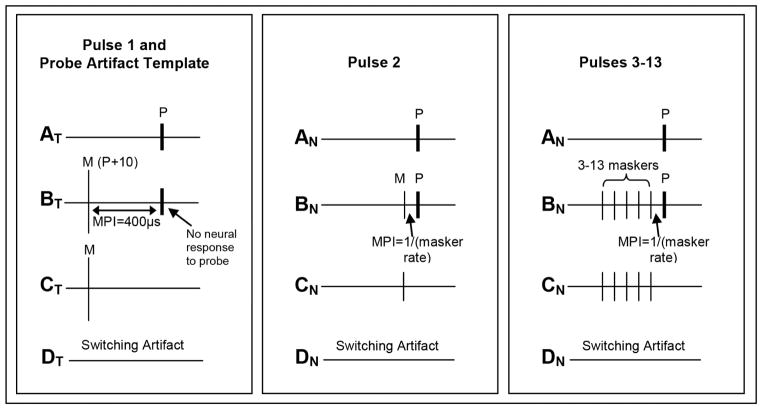
Next, ECAPs were obtained in response to each of 13 equal-amplitude pulses in a pulse train for rates of 900, 1200, 1800, 2400, and 3500 pps for each of the three stimulus levels. Each rate was tested in pseudorandom order, with all three levels tested within that rate before testing the next rate. The response to the first pulse was obtained using the standard forward-masking subtraction method (Abbas et al., 1999). A schematic of this method is shown in the left panel of Fig. 2. This method is comprised of four frames: (A_T) probe alone, which yields stimulus artifact and a neural response to the probe; (B_T) a masker followed by a probe using a short masker-probe interval of 400 μsec, which should result in only artifact in response to the probe (no neural response); (C_T) the response to the masker measured in isolation, and (D_T) the system signature, which is artifact associated with switching on the recording amplifier. The equation, A_T – B_T + C_T – D_T, is then applied to resolve the neural response to a single probe.

Fig. 2.

Schematic illustrating the modified forward-masking subtraction method used to resolve ECAP responses to each pulse in the pulse train. In all panels, probe pulses are labeled “P” and masker pulses are labeled “M.” MPI is the masker-probe interval. Left: the standard forward- masking technique is applied to obtain the response to the first pulse in the train (A_T) and to derive a template of the probe artifact (B_T - C_T) to be applied to pulses 2–13. A_T is the probe alone, B_T is the forward-masked condition with the standard MPI of 400 μsec, C_T is the masker alone, and D_T is a recording of the switching artifact. The masker is set 10 CL above the probe to ensure adequate masking. Middle: the modified forward-masking technique [(B_N-C_N)-(B_T-C_T)] is used to resolve the response to the second pulse in the train. In this case, the masker and probe are equal in amplitude and the MPI is equal to the period of the pulse train. Right: the modified forward-masking technique [(B_N-C_N)-(B_T-C_T)] is used to resolve the response to pulses 3–13. In B_N and C_N, the masker and probe amplitudes are equal, and the number of maskers is systematically increased, keeping the MPI equal to the period of the masker pulse train.

For pulses 2–13, stimulus artifact reduction was accomplished using a modified version of the standard forward-masking technique (Miller et al., 2000; also described in Hay-McCutcheon et al., 2005; He et al., 2016; and Hughes et al., 2012, 2014). First, traces B_T and C_T were extracted from the frames used to obtain the response to the first pulse (described above). The C_T trace was subtracted from the B_T trace to obtain a template of the probe artifact. In contrast to our earlier studies (Hughes et al. 2012, 2014), which used the same CL for the masker and probe, this study used a masker that was 10 CL above the probe to ensure no neural response to the probe was recorded in the forward-masked condition (frame B_T in the left panel of Fig. 2). To resolve the ECAP in response to the second pulse in the train, the masker level was reduced to equal that of the probe, and the MPI was set to be the inverse of the pulse-train rate being tested (Fig. 2, middle panel). For example, the MPI for a 3500-pps pulse train was 286 μsec. A single masker and the probe thus formed a pulse train consisting of two pulses. The ECAP was resolved by applying the following subtraction: (B_N-C_N)-(B_T-C_T). To resolve the ECAP in response to the third pulse in the train, the number of maskers was incremented to two, keeping the MPI and masker rate fixed (as in the aforementioned example). This procedure was repeated until the number of maskers was incremented to 12 so that the addition of the probe yielded a pulse train of 13 pulses. The right panel of Fig. 2 shows a schematic for a pulse train consisting of six pulses (five maskers and the probe).

Finally, ECAP refractory-recovery functions were obtained for the same electrode using the same three probe levels used for the pulse-train data. For each recovery function, the masker was 10 CL above the probe, which was the same as the masker and probe levels used to obtain the ECAP response to the first pulse in the train (see Fig. 2, trace B_T). MPIs ranged from 100 μsec to 10 msec. The same template subtraction method described above was used to resolve the ECAP (described further in Miller et al., 2000). In the Custom Sound EP software, this method is called Masked Response Extraction, and is the default artifact-reduction method for refractory-recovery functions.

2.4. Data Analysis

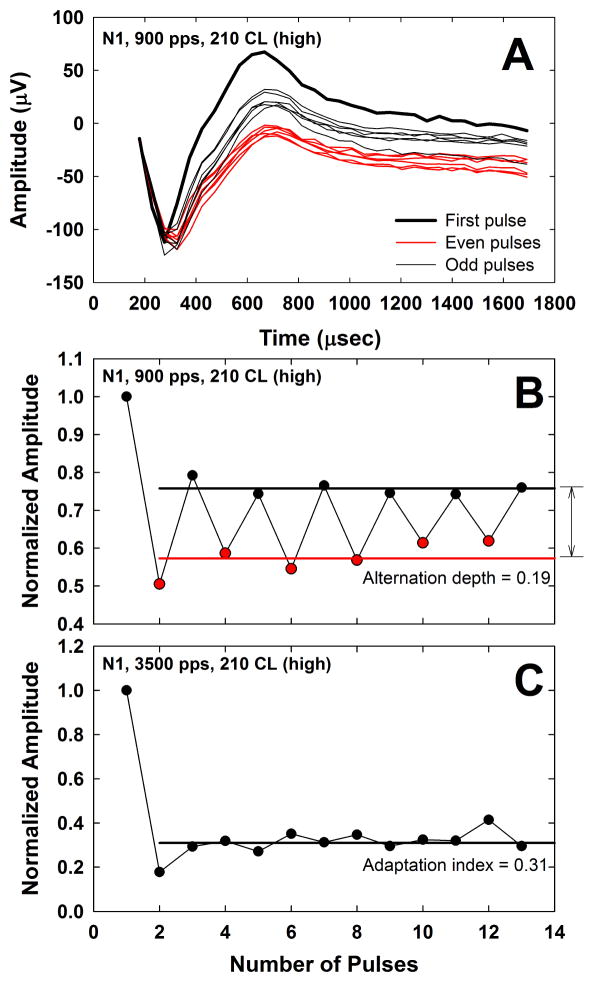
ECAP data files were exported from Custom Sound EP as Excel files, which were read into a custom Matlab (Mathworks, Inc., Natick, MA) program that applied the subtractions described in Fig. 2. The resulting waveforms were displayed, and the N1 and P2 peaks were manually marked. Fig. 3A shows an example of the ECAP waveforms from all 13 pulses in a 900-pps pulse train for subject N1 at the highest level (210 CL). The thick black line depicts the ECAP response to the first pulse, the thin red lines depict responses to the even-numbered pulses (2–12), and the thin black lines show responses to the odd-numbered pulses (3–13). The resulting peak-to-peak amplitudes were then normalized to that obtained in response to the first pulse in the train to assess the relative amplitude changes across the duration of the pulse train (Fig. 3B). The alternation depth was determined by averaging the normalized ECAP amplitudes for the odd- and even-numbered pulses separately (black and red horizontal lines in Fig. 3B, respectively), excluding the first pulse, and then taking the difference between the two averages (indicated by the vertical arrow to the right of Fig. 3B)². In Fig. 3B, the alternation depth was 0.19. The rate that yielded the largest mean difference was taken as the rate of maximum alternation.

Fig. 3.

A: ECAP waveforms for pulses 1–13 after artifact-reduction methods from Fig. 2 are applied. Data are from subject N1 for a 900-pps pulse train at the highest level (210 CL). The ECAP response to the first pulse (indicated by the thick solid line) has the largest amplitude. ECAPs obtained in response to even- and odd-numbered pulses are shown with thin red or black lines, respectively. Note that responses to the even-numbered pulses are generally the smallest. B: Peak-to-peak ECAP amplitudes from Fig. 3A normalized to that of the first pulse in the train. Data for even- and odd-numbered pulses are shown with red and black symbols, respectively. Red and black horizontal lines indicate the mean normalized amplitudes for even- and odd-numbered pulses, respectively, excluding the normalization point. The vertical arrow to the right of the graph indicates the alternation depth of 0.19. C: Normalized ECAP amplitudes at 210 CL for 3500 pps in the same subject. The horizontal black line indicates the adaptation index of 0.31, which was obtained by averaging the normalized amplitudes across pulses 2–13.

For each subject, the stochastic rate was determined as the rate at which the alternating pattern disappeared. Specifically, a paired t-test was used to compare the means of the normalized amplitudes obtained in response to the even-numbered versus odd-numbered pulses (excluding the first pulse, which was the normalization point). A Rank Sum Test was used for data that were not normally distributed (14/180 comparisons), as determined by the Shapiro-Wilk test. The rate at which the difference was no longer statistically significant (p > 0.05) was determined to be the stochastic rate.

Adaptation was characterized by an ‘adaptation index,’ calculated as the average normalized amplitude across pulses 2–13 for each rate. The adaptation index therefore represents a fraction (or percentage) of the amplitude to the first pulse in the train. An example is shown in Fig. 3C for subject N1 (3500 pps), with the average amplitude across pulses 2–13 indicated by the solid horizontal line. In this example, the adaptation index was 0.31, which means the average ECAP amplitude across the pulse train was 31% of the ECAP amplitude for the first pulse in the train. A smaller adaptation index therefore represents a greater degree of adaptation.

For refractory-recovery functions, the time constant for recovery, tau (τ), was calculated using the following formula, as described in Hughes et al. (2012):

$$\mathrm{A}={\mathrm{A}}_{max}\ast e^{-((\text{MPI-t}0)/\mathrm{\tau })}+\mathrm{C},$$

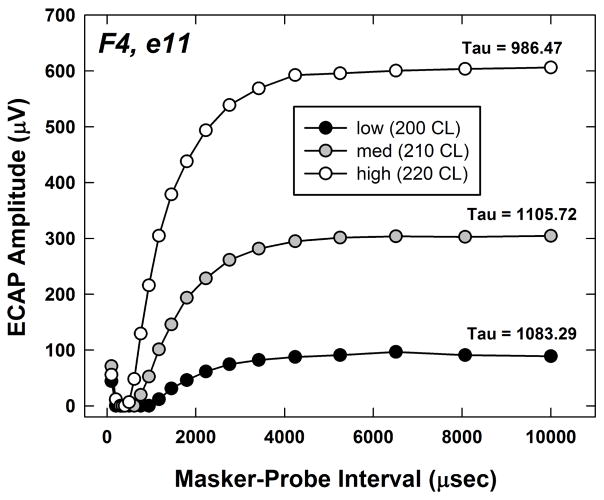
where A is the ECAP amplitude, A_max is the maximum ECAP amplitude within the refractory-recovery function, MPI is the masker-probe interval for the amplitude A, t0 is the MPI for the peak of the function (A_max), and C is the amplitude at the longest MPI measured, which served as a correction factor to account for residual masking. An example of three recovery functions for the three stimulus levels is shown in Fig. 4 for subject F4. Tau is indicated for each function. With the two-pulse forward-masking paradigm, the masker (first pulse) elicits a response from a population of neurons. For very short MPIs (less than approximately 400 μsec), neurons that are partially depolarized by the masker (i.e., elevated thresholds) will fire in response to the probe. This summative effect yields small ECAP amplitudes for the shortest MPIs. As the MPI approaches the absolute refractory period for the majority of the population, no response to the probe will be measured. Finally, as the MPI becomes longer, more fibers will recover from the relative refractory period and fire in response to the probe. The MPI for which the function reaches a plateau represents the point where the masker is no longer effective. In Fig. 4, the highest stimulus level yielded the shortest recovery time.

Fig. 4.

Individual example of ECAP refractory-recovery functions obtained for subject F4, electrode 11. The probe levels were the same as those used for the pulse-train data, representing high (220 CL), medium (210 CL), and low (200 CL) levels within the ECAP dynamic range. The masker was 10 CL above the probe to ensure adequate masking. Tau values (time course of recovery) are indicated for each function.

For all outcome measures except adaptation, a one-way repeated-measures analysis of variance (RM ANOVA) was used to examine the effect of stimulus level on each measure (rate at maximum alternation, alternation depth at the maximum alternation, stochastic rate, and refractory-recovery time constant). For the adaptation data, level effects were examined for each of the five rates tested, so a 2-way RM ANOVA was used to assess the effects of rate, level, and any potential interaction between rate and level. In cases where the data were not normally distributed, a non-parametric RM ANOVA on ranks (Friedman’s RM ANOVA) was performed, and medians are reported in addition to means. Post-hoc comparisons were made using the Holm-Sidak method for parametric comparisons and the Tukey test for non-parametric comparisons.

3. Results

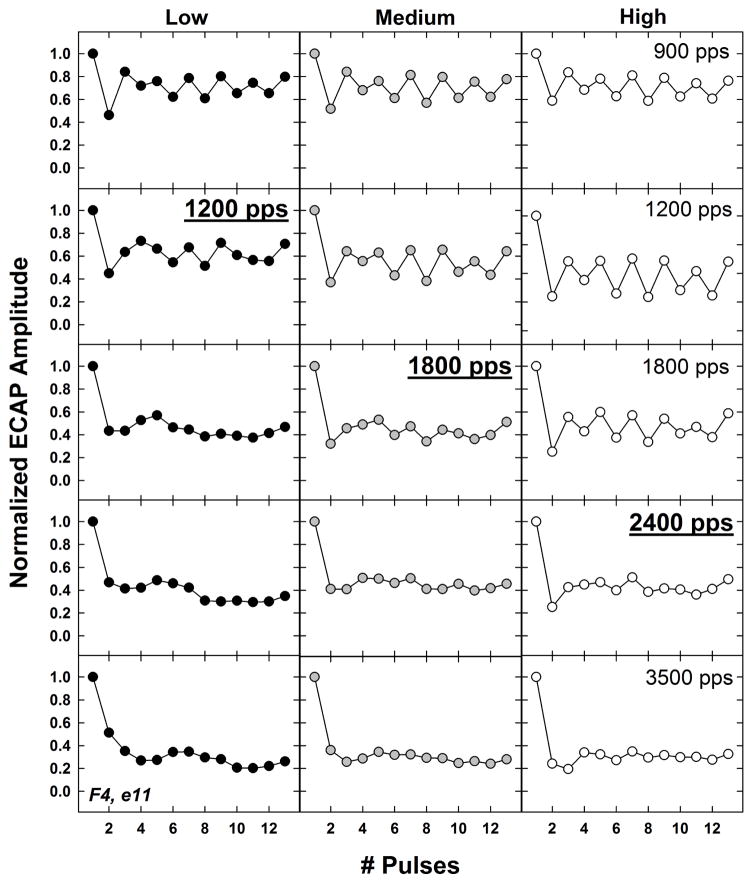
Fig. 5 shows an individual example of normalized ECAP amplitudes as a function of pulse number for low, medium, and high stimulus levels (left to right columns, respectively) across the five rates tested (top, 900 pps; bottom, 3500 pps). The data are from the same subject as shown in Fig. 3 (F4, electrode 11). For each stimulus level, the stochastic rate is indicated by underline and bold font. In this example, the stochastic rate increased with stimulus level: 1200, 1800, and 2400 pps for low, medium, and high levels, respectively. The maximum alternation occurred at 900, 1200, and 1200 pps for the low, medium, and high levels, respectively.

Fig. 5.

Individual example showing normalized ECAP amplitudes as a function of pulse number for low, medium, and high stimulus levels (left to right columns, respectively). Rows represent data for the slowest rate (900 pps, top) to the fastest rate (3500 pps, bottom). In each column (level), the stochastic rate is indicated with boldface and underline. Data are from electrode 11 in subject F4.

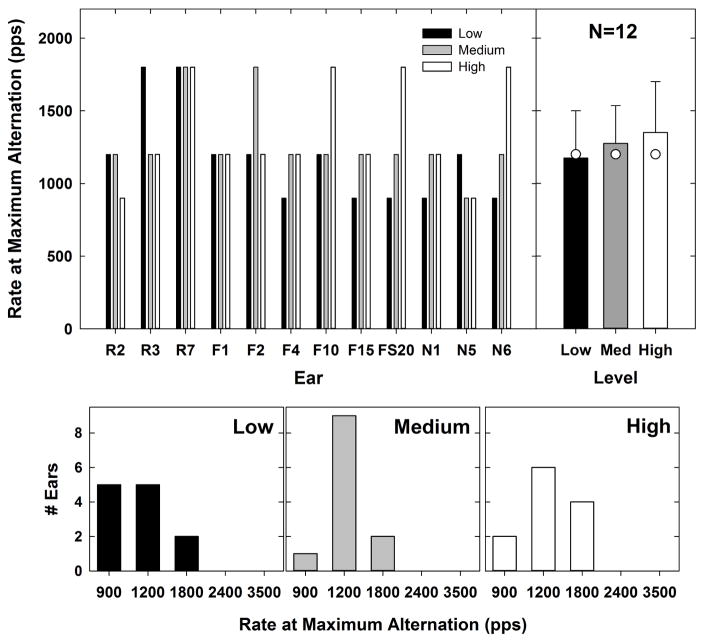
Figs. 6–10 address the first aim of the study, which was to evaluate within-subjects effects of stimulus level on ECAP responses to pulse trains and refractory-recovery time constants. The top left panel of Fig. 6 shows the rate at which the maximum alternation occurred for each subject and level. Data for low, medium, and high levels are indicated by black, gray, and white bars, respectively. The top right panel shows the mean (indicated by bar height), standard deviation (capped lines), and median (white circles) values for each stimulus level. Mean rates for the maximum alternation were 1175 pps, 1275 pps, and 1350 pps for low, medium, and high levels, respectively. The median rate for all three levels was 1200 pps. Corresponding histograms are shown in the bottom row of Fig. 6 for low to high stimulus levels (left to right, respectively). In each of those panels, the height of the bar represents the number of ears that demonstrated maximum alternation at each rate. For all ears, the maximum alternation occurred at either 900, 1200, or 1800 pps. At low levels, the maximum alternation occurred equally as often at 900 and 1200 pps (Fig. 6, bottom left panel). At medium and high levels, the maximum alternation occurred most often at 1200 pps (Fig. 6, bottom middle and right panels). A Friedman’s RM ANOVA revealed no significant effect of stimulus level on the rate at which the maximum alternation occurred [Χ² _(2,11) = 2.3, p = 0.3]. As a result, the hypothesis that the maximum alternation would occur at slower rates for lower levels was not supported. It is worth noting, however, that the mean data follow the expected trend, and that the maximum alternation occurred more often at the slowest rate (900 pps) for low levels (N = 5) than at medium (N = 1) or high levels (N = 2).

Fig. 6.

Top left: Individual data showing the rate at which the maximum alternation occurred for each subject and level. Low, medium, and high levels are indicated by black, gray, and white bars, respectively. Top right: group mean (bar height), +1 SD (lines), and median (white circles) values representing the rate at which the maximum alternation occurred for each level. Bottom row: histograms for low to high stimulus levels (left to right, respectively) indicating the number of ears that demonstrated maximum alternation at each rate.

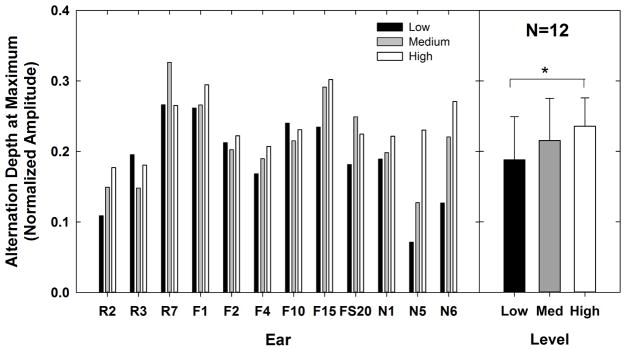
The left panel of Fig. 7 shows the alternation depth at its maximum for each subject and level. The right panel shows the mean alternation depth for the three levels tested; capped lines indicate 1 SD above the mean. In general, the alternation depth increased as the stimulus level increased. A one-way RM ANOVA showed a significant effect of stimulus level on the alternation depth [F_(2,11) = 6.4, p = 0.006]. Post-hoc pairwise comparisons (Holm-Sidak) showed a significant difference in alternation depth between low and high levels (t = 3.6, p = 0.005), but not between medium and low or medium and high levels (p > 0.1). Mean alternation depths were 0.188, 0.215, and 0.236 for low, medium, and high levels, respectively. These findings generally supported the hypothesis that the alternation depth at its maximum is smallest for lower levels and largest for higher levels.

Fig. 7.

Left: Individual data showing the alternation depth measured at its maximum for each subject and level. Low, medium, and high levels are indicated by black, gray, and white bars, respectively. Right: group mean (bar height) alternation depth for each level (lines represent +1 SD). Significant differences are indicated by the bracket and asterisk.

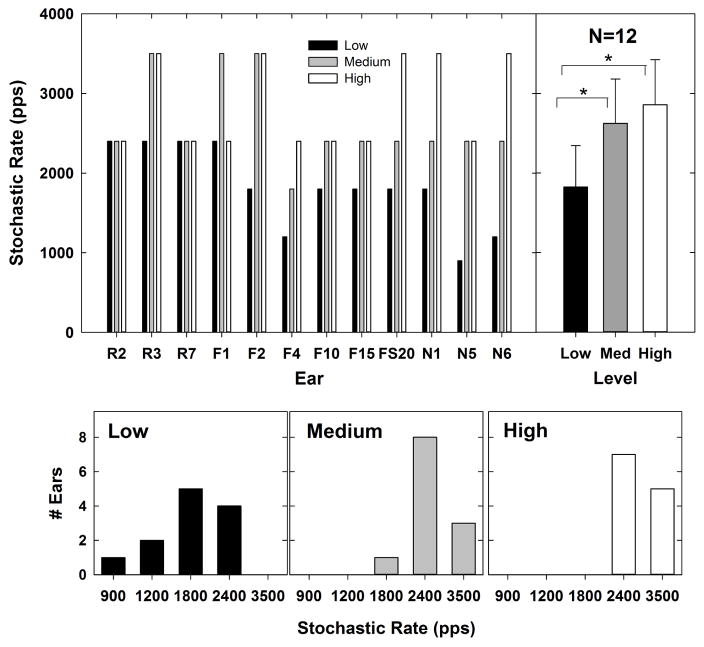
The top left panel of Fig. 8 shows the stochastic rate for each subject and level. These data are plotted similar to Fig. 6. For N5 (who also had the smallest ECAPs in the group), there was no significant alternation between even- and odd-numbered pulses at any of the rates for the lowest stimulation level, so the stochastic rate was set to 900 pps. Because this could potentially bias the results, the RM ANOVA was run with and without N5. The top right panel shows the mean (+1 SD) stochastic rate values for each stimulus level, which were 1825 pps, 2625 pps, and 2858 pps for low, medium, and high levels, respectively. Corresponding histograms are shown in the bottom row. At low levels, the stochastic rate occurred between 900 pps and 2400 pps. At medium levels, the stochastic rate occurred between 1800 and 3500 pps; and at high levels, the stochastic rate was either 2400 or 3500 pps. At low levels, the stochastic rate occurred most often at 1800 pps (Fig. 8, bottom left panel). At medium and high levels, the stochastic rate occurred most often at 2400 pps (Fig. 8, bottom middle and right panels). A one-way RM ANOVA showed a significant effect of level on stochastic rate [F_(2,11) = 16.1, p < 0.001]. Post-hoc pairwise comparisons (Holm-Sidak) showed that the stochastic rate was significantly faster for high (t = 5.4, p < 0.001) and medium (t = 4.2, p < 0.001) levels than for low levels. There was no significant difference in stochastic rate between high and medium levels (p = 0.2). The main effect [F_(2,10) = 12.85, p < 0.001] and post-hoc results (high vs. low, t = 4.88, p < 0.001; medium vs. low, t = 3.63, p = 0.003; high vs. medium, t = 1.25, p = 0.22) were similar when N5 was excluded from the analysis. In general, the stochastic rate increased with stimulus level, which was consistent with the hypothesis.

Fig. 8.

Top left: Individual data showing the rate at which the alternating pattern ceased (stochastic rate) for each subject and level. Data are plotted similar to Fig. 6. Top right: group mean (bar height) stochastic rates for each level (lines represent +1 SD). Significant differences are indicated by brackets and asterisks. Bottom row: histograms for low to high stimulus levels (left to right, respectively) indicating the number of ears that exhibited each stochastic rate.

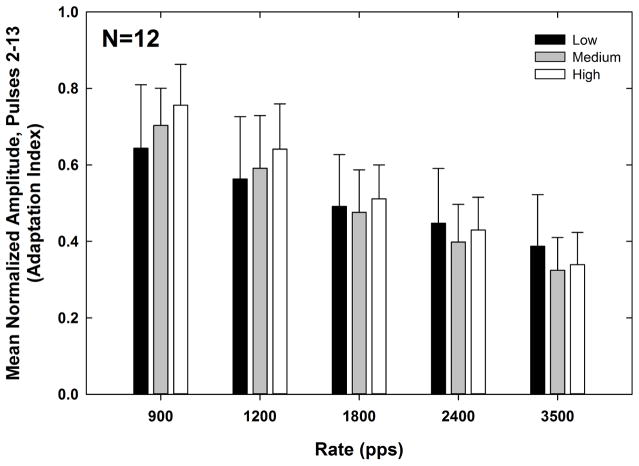
Fig. 9 shows the adaptation index for each rate (x-axis) and level (indicated by bar shading). The means (+1 SD) are indicated by bar height. Recall that a smaller adaptation index represents a greater degree of adaptation. A 2-way RM ANOVA was used to examine the effects of rate and level on the adaptation index. As expected, the degree of adaptation increased significantly with rate (F_{(4, 11)} = 165.31, p < 0.001). The mean adaptation indices (collapsed across level) were 0.70, 0.60, 0.49, 0.43, and 0.35 for pulse-train rates of 900, 1200, 1800, 2400, and 3500 pps, respectively. Pairwise comparisons (Bonferroni) showed that the adaptation index was significantly different for all rate comparisons (p < 0.001). There was no significant main effect of stimulus level (F_{(2, 11)} = 1.45, p = 0.26). The mean adaptation indices (collapsed across rate) were 0.51, 0.50, and 0.54 for low, medium, and high levels, respectively. The interaction between rate and level was significant (F_(8,11) = 6.62, p < 0.001). For the two slowest rates (900 and 1200 pps), there was significantly more adaptation (smaller adaptation index) at low levels than at high levels (p < 0.03), which was consistent with the hypothesis. However, this finding did not hold for the faster rates (1800–3500 pps).

Fig. 9.

Mean (+1 SD) adaptation indices for low, medium, and high levels (black, gray, and white bars, respectively) across pulse-train rates for all subjects. Because the adaptation index is the mean normalized amplitude across pulses 2–13, a smaller adaptation index represents a greater degree of adaptation.

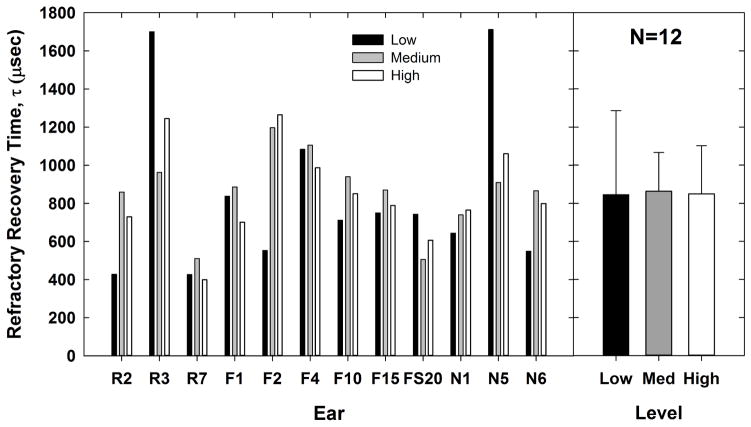
The left panel of Fig. 10 shows the refractory-recovery time constants (tau) for each subject and level. The means (+1 SD) are indicated by bar height in the right panel, which were 844.8, 862.9, and 849.5 μsec for low, medium, and high levels, respectively. A RM ANOVA showed no significant effect of stimulus level on the refractory-recovery time constant [F_(2,11) = 0.02, p = 0.98], which did not support the hypothesis that slower recovery would be observed for lower levels. However, these comparisons were under-powered (0.05). Consequently, the negative result should be considered with caution.

Fig. 10.

Left: Individual data showing the refractory-recovery time constant, τ, for each subject and level. Data are plotted similar to Figs. 7 and 9. Right: group mean (bar height) tau values for each level (lines represent +1 SD).

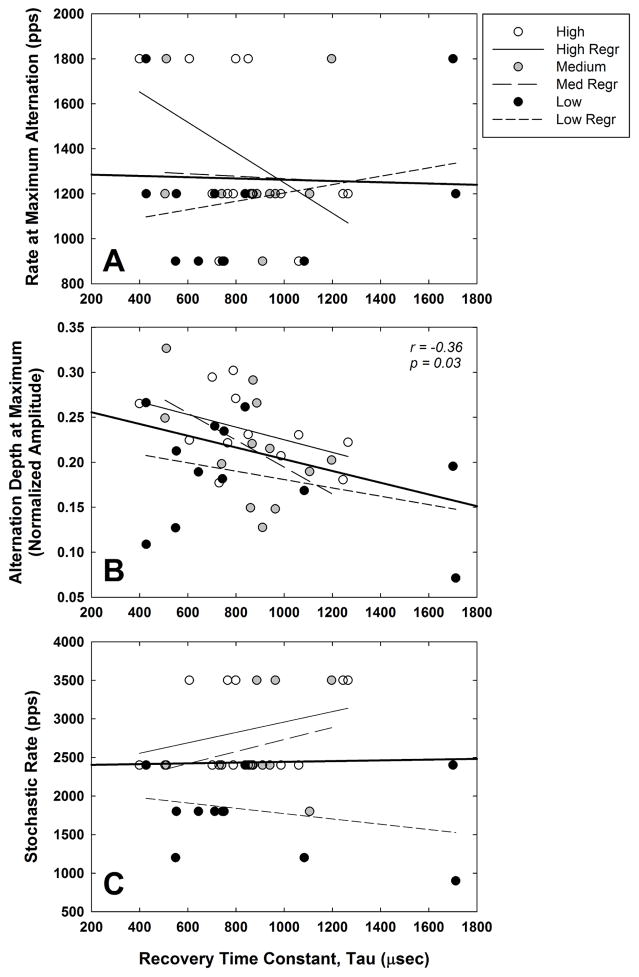
Fig. 11 addresses the second aim of the study, which was to examine how refractory-recovery time constants relate to the maximum alternation and stochastic rate. In all three panels, data from all subjects for the three stimulus levels are plotted with white, gray, and black symbols representing high, medium, and low levels, respectively. Linear regression lines for each level are represented by thin lines that are identified in the figure legend. The regression line for the data pooled across subjects and levels is shown by the thick solid line extending to the axes. Fig. 11A shows the relation between the rate at which the maximum alternation occurred and the refractory-recovery time constant tau for all subjects and levels. There was no significant correlation (Pearson) between the two measures for any of the stimulus levels or for the aggregate data (p > 0.1). Fig. 11B shows the relation between the alternation depth at its maximum versus recovery time. There was no significant correlation between the two measures for each level separately (p > 0.09), however the negative correlation across levels was significant (r = −0.36, p = 0.03). Last, Fig. 11C shows no significant relation (p > 0.3) between stochastic rate and recovery time for any of the individual stimulus levels or the aggregate data.

Fig. 11.

Scatterplots illustrating the relation between the refractory-recovery time constant and (A) the rate at which the maximum alternation occurred, (B) the alternation depth at its maximum, and (C) stochastic rate. White, gray, and black symbols represent data for high, medium, and low stimulus levels, respectively. Linear regression lines for high, medium, and low levels are represented by thin solid, long-dashed and short-dashed lines, respectively. The regression lines for the data pooled across subjects and levels (N = 36 per panel) are shown by the thick solid lines extending to the axes.

4. Discussion

4.1. Summary of Findings

The primary goal of this study was to systematically evaluate within-subjects effects of stimulus level on ECAP responses to equal-amplitude pulse trains at different rates, and to relate those measures to the time course of refractory recovery obtained with a two-pulse paradigm. Results from this study showed (1) a trend for maximum alternation to occur at slower rates for lower levels (Fig. 6), which was in the direction hypothesized although not statistically significant; (2) reduced alternation depth with reduced level, as hypothesized (Fig. 7); (3) reduced stochastic rates at lower levels, as hypothesized (Fig. 8); (4) more adaptation (smaller adaptation index) at lower levels, but only for the two slowest rates (900 and 1200 pps; Fig. 9); and (5) no significant effect of stimulus level on the time course of recovery (Fig. 10), which was unexpected. The second goal of the study was to examine how refractory-recovery time constants relate to maximum alternation and stochastic rate. When the data were pooled across stimulus levels, there was a significant negative correlation between alternation depth and refractory recovery time, suggesting that faster recovery is related to larger alternation depths.

4.2. Maximum Alternation

The alternating amplitude pattern occurs when the period of a pulse train falls within the relative refractory period of the responding neural population (e.g., Matsuoka et al., 2000). Previous studies with human CI recipients have shown that the alternating pattern typically occurs for pulse-train rates that are approximately 400—2400 pps (Hughes et al., 2012; Wilson et al., 1997). This corresponds to a range of periods between 417 μsec to 2.5 ms, which overlaps with the time course of recovery from the relative refractory period measured with a two-pulse forward-masking paradigm (e.g., Botros & Psarros, 2010; Brown et al., 1990; Cohen, 2009; Morsnowski et al., 2006). Data from the present study and from Hughes et al. (2012) showed that the maximum alternation depth occurs most often between 1200–1800 pps for stimulus levels at the upper end of participants’ dynamic ranges. These rates correspond to periods of 556–833 μsec, a range that is slightly longer than the absolute refractory period (and within the early portion of the relative refractory period) observed in humans. This result supports the theory posed by Matsuoka et al. (2000) that the maximum alternation occurs for pulse-rate periods that produce a “trade off” between a large-amplitude first pulse and a minimum-amplitude second pulse. In other words, for the second pulse, the majority of fibers that respond to the first pulse are in a relative refractory period that coincides with the stimulus inter-pulse interval.

Both animal (Matsuoka et al., 2000; Miller et al., 2008) and human (Finley et al., 1997) studies have shown that higher stimulus levels yield greater synchrony and faster recovery from the refractory period as compared with lower levels. As a result, we should see a shift in the rate that produces the maximum alternation depth as the stimulus level is changed. Specifically, if recovery is slower at lower stimulus levels, then we would expect the maximum alternation to occur at slower rates for lower levels. This is because slower rates have longer pulse periods to accommodate the slower recovery that occurs at lower levels. The findings of the present study were generally consistent with this hypothesis (Fig. 6) and with cat data from Matsuoka et al. (2000), although the trend in our data failed to reach statistical significance. One possible contributing factor is the coarse sampling of rates tested in the present study. Because the maximum alternation occurred for all subjects at only one of three rates (900, 1200, or 1800 pps; see Fig. 6), it is possible that a clearer pattern of results might have been obtained if more rates were tested between 900 pps and 1800 pps.

4.3. Stochastic Rate

The ECAP represents an aggregate response of a population of individual auditory neurons. Across the population, individual neurons have different temporal response properties, including the time course at which neurons fire and recover (e.g., Javel & Shepherd, 2000; Matsuoka et al., 2001; Miller et al., 2001, 2008). These properties are influenced by physical characteristics such as fiber diameter, degree of demyelination, peripheral loss, etc. (e.g. Shepherd et al., 2004; Sly et al., 2007). As the stimulation rate increases, the relative differences in excitability and recovery time across the population will result in a relatively stochastic state because the firing patterns of individual neurons become desynchronized and/or adapted (e.g., Boulet et al., 2016; Miller et al., 2008; Rubinstein et al., 1999). Results from the present study show that, for higher stimulus levels, faster rates are necessary to produce a stochastic state (Fig. 8). Likewise, lower levels produce a stochastic state at slower rates. These within-subjects findings are consistent with across-subjects findings in Hughes et al. (2012), who showed a significant correlation between level and stochastic rate, where higher stimulus levels yielded faster stochastic rates. Collectively, these results can be attributed to evidence that shows higher stimulus levels yield greater synchrony and faster recovery from a refractory state (e.g., Finley et al., 1997; Matsuoka et al., 2000; Miller et al., 2008). As a result, faster rates are needed to produce adaptation and to desynchronize the firing patterns of individual neurons for higher stimulus levels, producing a relatively stochastic state.

4.4. Adaptation

In the normally hearing ear, adaptation has been attributed to a depletion of neurotransmitter and/or desensitization of receptors at the synapse between the inner hair cell and auditory neuron (e.g., Zilany et al., 2009). In the electrically stimulated deaf ear (in which the synaptic junction is missing and/or otherwise bypassed), sustained stimulation of auditory neurons nonetheless produces adaption. In this case, adaptation has been attributed to a persistent shift in intracellular and extracellular concentrations of sodium and potassium, produced by changes in neural membrane conductance following sustained electrical stimulation (e.g., Boulet et al., 2016; Litvak et al., 2001). In either case, an increased stimulation rate will exacerbate these deviations from homeostasis.

In the present study, we found that adaptation increased with pulse-train rate, consistent with other studies in humans and animals (e.g., He et al., 2016; Hughes et al., 2012; Litvak et al., 2001; Zhang et al., 2007). We also found that adaptation was greater for lower stimulus levels, but only for the two slower rates (900 and 1200 pps; see Fig. 9). This finding was generally consistent with data from acutely deafened cats, as reported by Zhang et al. (2007), and from a group of five CI recipients, as reported by McKay et al. (2013). Although McKay et al. did not specify the rates at which they observed significant level effects on adaptation, they noted that it was “mostly at the lower rates” (the range of rates that they tested spanned 500–2400 pps). Data from Zhang et al. (2007) showed that adaptation can be partially overcome by increasing the stimulus level, which increases membrane excitation (Miller et al., 2008). This level effect was demonstrated for slower pulse-train rates (250 pps) but not for faster rates (5000 pps). Because adaptation increases with stimulation rate (see Fig. 9), it is likely that larger increases in level are needed to partially overcome adaptation effects as the stimulation rate increases.

4.5. Refractory Recovery

The absolute refractory period for ECAP responses in humans ranges from approximately 0.3–0.5 ms, with the relative recovery time spanning up to approximately 2–6 ms (Brown et al., 1990; Cohen, 2009; Miller et al., 2000; Morsnowski et al., 2006; Shpak et al., 2004). Several studies have shown shorter refractory-recovery time constants for higher stimulus levels, and slower recovery times for lower levels (Finley et al., 1997; Matsuoka et al., 2000; Miller et al. 2001, 2008). Single-fiber data from cats showed that the firing efficiency diminishes with level, requiring longer MPIs for the probe response to return to 100% firing efficiency (Miller et al., 2001). Additionally, increased stimulus levels produce increased membrane excitability, allowing for relative refractoriness to be overcome (Miller et al., 2008). In contrast to these earlier studies, the results from the present study showed no significant effect of level on the refractory-recovery time constants (Fig. 10). The individual data in Fig. 10 (left panel), show that only half (6 of 12) of the ears demonstrated longer recovery for low versus high levels. Our aggregate result is consistent with ECAP data from cats reported by Brown and Abbas (1990), who showed that refractory-recovery time constants are not influenced by the stimulus level, as long as the masker is equal to or higher than the probe. Finally, the level comparisons for recovery time constants in the present study were statistically underpowered, so the negative finding should be interpreted with caution.

4.6. Single-Pulse Refractory Recovery versus Pulse-Train Data

In our initial study that characterized ECAP responses to pulse trains of different rates across different cochlear regions (Hughes et al., 2012), we found that electrodes with shorter refractory-recovery times tended to demonstrate the maximum alternation at faster rates, consistent with the suggestion by Matsuoka et al. (2000). However, the trend in our earlier dataset failed to reach statistical significance (p = 0.06). There was also no significant difference in refractory-recovery times across electrodes with different stochastic rates, which supports the idea that the stochastic state reflects temporal characteristics of individual fibers more so than the whole-nerve response to a single pulse. One problem with the comparisons in our earlier study was that the refractory-recovery comparisons were made post hoc; the recovery data were obtained as part of a different study, so the stimulus levels were not well controlled. In the present study, ECAP refractory-recovery functions were obtained using the standard two pulse (masker-probe) paradigm with the same masker and probe levels that were used for the pulse-train data. As shown in Fig. 11B, there was a significant negative correlation between the two-pulse refractory-recovery time constant and the alternation depth at its maximum, but only when the data were pooled across level. This means that greater alternation is observed for neural populations that exhibit shorter recovery times, and is in general agreement with the known effects of stimulus level on refractory-recovery time (Matsuoka et al., 2000). Further, the results in Fig. 11B are also consistent with data from guinea pigs in Ramekers et al. (2015), which showed that poorer spiral ganglion cell survival was correlated with faster refractory recovery and larger alternation depths. Poorer neural survival likely leads to more homogeneous temporal responses that exhibit larger alternation depths because there is less variance in recovery times across the contributing fibers. Alternatively, smaller alternation depths would be expected for larger neural populations because of greater heterogeneity in recovery times across fibers.

4.7. Study Limitations

A potentially confounding variable in this study was that the participants with the older 24R(CS) devices (R2, R3, and R7) used the default interphase gap of 25 μsec, whereas participants with newer devices used the default interphase gap of 7 μsec. Several studies have shown that the duration of the interphase gap can affect ECAP measures such as amplitude, threshold, slope, latency, and dynamic range (e.g., Shepherd & Javel, 1999; Prado-Guitierrez et al., 2006; Ramekers et al., 2014). In animal studies, interphase gap has been shown to be sensitive to the degree of peripheral neural degeneration. As a result, ECAP measures obtained with the longer interphase gap in 24R(CS) recipients might be more likely to reflect neural health status than for recipients with the newer devices. Inspection of the individual results in Figs. 6–8 and Fig. 10, however, do not reveal any consistent differences between participants who were tested with a 7-μsec versus a 25-μsec interphase gap. Given the relatively small subject groups tested with the two different interphase gaps, this remains an area for further investigation.

A second limitation of this study was the restricted range of stimuli that were used. We did not include slower rates below 900 pps or a finer sampling within the range of rates tested. Testing rates using smaller step sizes might have exploited more subtle differences among subjects, although an increase in sample size would also be needed. Additionally, we only measured ECAP responses to 13 pulses in a pulse train, so our results do not consider the effects of stimulus level on adaptation, facilitation, recovery, and accommodation that are observed over a longer-duration pulse train (e.g., Finley et al., 1997; Hay-McCutcheon et al., 2005; Litvak et al., 2003; Miller et al., 2008; Schmidt Clay & Brown, 2007). The total pulse-train durations for the rates tested in the present study ranged from 3.7 ms (3500 pps) to 14.4 ms (900 pps), which is much shorter than the average duration of English phonemes (e.g., Umeda, 1975, 1977). In our earlier study (Hughes et al., 2012), we used slightly longer pulse trains, but this exacerbated loudness-tolerance limitations that precluded making measurements in more than one-third of the subjects enrolled in the study. Regardless, the present results provide insight to the effects of stimulus level across a range of pulse-train rates so that we can begin to understand how stimulus level affects auditory-nerve responses to electrical stimulation at the most basic level.

Along the lines of practical applicability, a third limitation of the present study is that we only measured ECAP responses to equal-amplitude pulse trains rather than amplitude-modulated pulse trains, which are used to represent speech in CIs. Several studies have evaluated ECAP (Tejani et al., 2017; Wilson et al., 1997) or single-fiber (Hu et al., 2010) responses to amplitude-modulated pulse trains, or modeled spike activity for amplitude-modulated stimuli (Goldwyn et al., 2010). As with the unmodulated pulse-train data, results show that neural activity changes over the course of the modulated pulse train. Hu and colleagues (2010) found that the effects of level on adaptation were similar for both equal-amplitude and modulated pulse trains. Clearly, neural responses to amplitude-modulated pulse trains will vary with carrier rate, modulation rate, and modulation depth. It is important to note that those studies only examined responses to a single modulation frequency at a time. Although amplitude-modulated stimuli are more complex than unmodulated pulse trains, using a single modulation frequency is still somewhat simplistic as it does not reflect the more dynamic properties of speech, such as the constantly changing temporal fine structure.

Finally, the present study only evaluated ECAP responses to stimulation on a single electrode in isolation. With monopolar stimulation, the spatial spread of excitation can span a large portion of the cochlea (e.g., Cohen et al., 2003; Hughes & Stille, 2010). In daily use, pulse trains are interleaved across multiple electrodes, so channel interaction will also play a role by effectively increasing the overall stimulation rate delivered to individual neurons.

5. Conclusions

The results from this study show that stimulus level significantly affects temporally related ECAP responses to unmodulated pulse trains in CI recipients. Stimulus level had significant effects on the alternating-amplitude pattern, stochastic rate, and degree of adaptation. In general, the results are consistent with single-fiber data from animals, which show that higher stimulus levels yield greater synchrony and faster recovery from the refractory period, as compared with lower stimulus levels. As a result, the alternating pattern becomes more pronounced at higher levels, and faster rates are necessary to produce a stochastic state. Adaptation can be partially overcome by increasing the stimulus level, but this effect was only observed for slower rates. It may be that further increases in level are needed to overcome adaptation at higher rates, but this is limited by loudness tolerance issues with human participants.

Highlights.

• Stimulus level affects auditory-nerve responses to electrical pulse trains

• The alternating amplitude pattern is more pronounced at higher levels

• Faster rates are needed to produce a stochastic state for higher levels

• Higher levels yield less adaptation than lower levels, but only for slower rates

Abbreviations

CI

cochlear implant

CL

current-level unit

ECAP

electrically evoked compound action potential

MPI

masker-probe interval

NRT

Neural Response Telemetry

pps

pulses per second

RM ANOVA

repeated-measures analysis of variance