Genetic association studies often collect a wide range of complex traits, including high-dimensional and structured omics measurements. The complex...
Keywords: dual kernels, genetic association analysis, high-dimensional traits, network structure, pleiotropy
Abstract
Many genetic association studies collect a wide range of complex traits. As these traits may be correlated and share a common genetic mechanism, joint analysis can be statistically more powerful and biologically more meaningful. However, most existing tests for multiple traits cannot be used for high-dimensional and possibly structured traits, such as network-structured transcriptomic pathway expressions. To overcome potential limitations, in this article we propose the dual kernel-based association test (DKAT) for testing the association between multiple traits and multiple genetic variants, both common and rare. In DKAT, two individual kernels are used to describe the phenotypic and genotypic similarity, respectively, between pairwise subjects. Using kernels allows for capturing structure while accommodating dimensionality. Then, the association between traits and genetic variants is summarized by a coefficient which measures the association between two kernel matrices. Finally, DKAT evaluates the hypothesis of nonassociation with an analytical P-value calculation without any computationally expensive resampling procedures. By collapsing information in both traits and genetic variants using kernels, the proposed DKAT is shown to have a correct type-I error rate and higher power than other existing methods in both simulation studies and application to a study of genetic regulation of pathway gene expressions.
LARGE-SCALE, genome-wide association studies and next generation sequencing association studies have resulted in the identification of a wide range of genetic variants, common and rare, related to a host of complex traits and disorders (McCarthy et al. 2008; Welter et al. 2014). Traditional genetic association analyses have focused on identifying associations between individual genetic variants or groups of genetic variants with a single trait of interest. However, this approach proves inadequate when a single variable does not fully capture the trait or phenotype of interest and further may result in power loss. In many situations, joint analysis of multiple traits, simultaneously, may prove advantageous as compared to single trait analysis for a number of reasons. First, joint analysis tends to be statistically more powerful than individual trait analysis, especially when many of the traits are correlated and each trait has only modest association with genotypes. Joint analysis can exploit the correlation structure by borrowing information across multiple traits and amplifying the modest marginal association signals (Klei et al. 2008; Aschard et al. 2014). Second, joint analysis facilitates the elucidation of shared genetic mechanisms and pleiotropic relationships, thus serving as an appropriate means for improving biological understanding (Chesler et al. 2005; Andreassen et al. 2015). Finally, many traits are inherently multi-phenotypic. For example, metabolic syndrome, which increases risk for heart disease, diabetes, and stroke, is defined based on the presence of three out of five conditions (Alberti et al. 2005); information can be gained by using all five conditions as trait measures rather than considering only the formal diagnosis of metabolic syndrome.
A wide range of statistical and computational methods have been developed for analyzing multiple phenotypes. Broadly speaking, these methods fall into three main categories. The first category is based on directly integrating univariate results from analyzing each trait separately (Yang et al. 2010; van der Sluis et al. 2013). Generally these methods can handle at most a moderate number of traits (e.g., <20 traits) and do not directly harness correlation and relationships among the traits. The second category of methods is based on applying classical dimension-reduction methods, e.g., principal component analysis (Klei et al. 2008) and canonical correlation analysis (Ferreira and Purcell 2009), to collapse multiple traits into a single score. However, results based on dimension-reduction methods are difficult to interpret and lose power when the weights for collapsing the multiple traits are imperfect (Aschard et al. 2014). The final category is the broadest and is based on multivariate-regression methods, which often assume a parametric model for the relationships between multiple traits and a single SNP (O’Reilly et al. 2012; Zhou and Stephens 2014; Wu and Pankow 2015; Joo et al. 2016; Ray et al. 2016; Schaid et al. 2016). The specific modeling strategies underlying each approach vary with some approaches using classical mixed models and others using alternative strategies, e.g., MultiPhen (O’Reilly et al. 2012), which uses ordinal regression to regress a SNP on multiple traits. These methods often suffer when underlying parametric assumptions are violated. Many of these methods have been extended to accommodate multiple SNPs and multiple traits (Maity et al. 2012; Hua and Ghosh 2015; Broadaway et al. 2016; Kim et al. 2016; Wu and Pankow 2016), with the understanding that the multi-SNP analysis can oftentimes improve power for the same reasons that multi-trait analysis can improve power.
There are considerable and increasing interests in high-dimensional structured phenotypes, such as imaging traits or other omics data, as they are often inherently interesting and also can serve as intermediate traits, which help in elucidating the underlying molecular mechanisms while being more directly related to etiology. However, despite interest, phenotypes such as imaging outcomes (Zhang et al. 2014) and other sources of omics data such as gene expression, metabolomics intensity (Zhan et al. 2015b), and microbiome composition (Zhao et al. 2015), continue to pose grand challenges. Beyond the intrinsic high dimensionality and scale of the data, such phenotypes are often statistically complex in that they have underlying structure that needs to be accommodated. Examples of structures include network/pathway relationships in metabolomic data and gene expression data, and phylogenetic relationships in microbiome data. Most existing multivariate-trait-association methods do not generally accommodate high-dimensional structured phenotypes. Methods based on univariate analysis and collapsing rapidly lose power as dimensionality increases (Yang et al. 2010; van der Sluis et al. 2013), since they typically suffer from power loss due to a heavy multiple-testing burden, which comes with the high-dimensional traits. Dimension reduction-based association analysis usually considers surrogate outcomes (e.g., principal components), which breaks down the inherent structures in the original phenotypes. More complicated multivariate-regression modeling strategies often become unstable or computationally intractable when dimensionality of traits increases (Maity et al. 2012; Wu and Pankow 2016). None of the methods directly consider the issue of incorporating high-dimensional structured traits, which leads to potential power loss of detecting existing associations (Freytag et al. 2014). Thus, new methods are necessary.
A powerful approach in genetic association analysis is the kernel machine regression (KMR) framework, which has proven to be a useful tool for association studies with both common and rare variants (Kwee et al. 2008; Wu et al. 2010, 2011; Ionita-Laza et al. 2013; Zhan et al. 2016). Under the original KMR framework, a single phenotype is modeled to be related to a group of genetic variants. The relationship is captured by way of a kernel function which measures similarity among the risky variants. Then testing proceeds by comparing pairwise similarity in genetic variant profiles between subjects (measured by the kernel matrix) to pairwise similarity in phenotypes (measured by the cross-product matrix of traits), with correspondence in similarity indicative of association. By intelligently choosing kernels, structure in the genetic variants can be directly accommodated (Schaid 2010a,b) while dealing with high dimensionality.
Motivated by these kernel-based genetic association tests, we propose the dual kernel-based association test (DKAT) which is designed to assess the association between high-dimensional, possibly structured, phenotypes of interest with multiple genetic variants, though the approach trivially applies to single genetic variant analysis as well. The idea of DKAT is that we propose to use not only a kernel for the genetic variants but also a kernel for the high-dimensional and structured traits. In other words, we replace the cross-product matrix for traits in the existing KMR framework with a kernel matrix to better capture the high dimensionality as well the structure of the traits. To associate the traits (now embedded within a kernel) and a group of genetic variants, we again compare similarity in genetic variant profiles to similarity in phenotypic profiles. In particular, the normalized Frobenius inner product between two kernel matrices is used as the statistic to summarize the genotype–phenotype association.
Besides being able to incorporate high-dimensional structured traits in genetic association analysis, another major contribution of DKAT is that we introduce a new test design for genetic association testing. Currently, two most popular P-value calculation methods for genetic association analysis is either based on large-sample asymptotic theory (Wu et al. 2010, 2011; Broadaway et al. 2016; Wu and Pankow 2016) or via permutations (Hua and Ghosh 2015; Pan et al. 2015; Joo et al. 2016; Kim et al. 2016). However, the large-sample asymptotic theory-based P-value calculation can lead to a conservative test with accumulated estimation error (Lee et al. 2012; Chen et al. 2016), as in studies with small samples or high-dimensional traits. On the other hand, the permutation test is inefficient when a stringent P-value is required, as in many genome-wide association studies. We propose a fast pseudopermutation technique for DKAT, which approximates the empirical distribution of all potential permuted DKAT statistics by moment matching. In this new test design, we only calculate the first three sample moments of permutations, without explicitly calculating the permutations themselves. Then, the Pearson type III density with the same moments is used to approximate the empirical distribution of all permutations, where a Pearson type III density is selected in this article due to its good approximation performance for DKAT-similar statistics (Josse et al. 2008; Minas et al. 2013; Zhan et al. 2017). Fortunately, the first three sample moments of these permutations have closed-form expressions (Kazi-Aoual et al. 1995). Thus, we can analytically calculate both the Pearson type III density and the DKAT P-value. Our DKAT test design is more efficient and accurate than those currently used for genetic association tests, since it neither requires explicit permutations nor relies on large-sample asymptotic theory.
Methods
Notations
Throughout this article, we assume a study with n unrelated individuals who have been genotyped and phenotyped. For the ith subject (), let denote the vector of genotypes, where 0, 1, or 2 represents the number of minor alleles, denote the set of p traits (e.g., the expression values of p genes in a pathway or the abundances of p metabolites in a pathway), and denote covariates such as age, gender and principal components of genotypes. The objective is to test the global association between the group of traits and the group of genetic variants after accounting for the effect of covariates, which will be accomplished by using the kernel machine framework. We emphasize that although our focus is on the setting in which we have multiple genetic variants, our method trivially applies to the scenario when that is, when we are interested in the relationship between a single variant and multiple traits.
Single kernel-based association tests
Before discussing multi-trait association analysis, we first briefly review the KMR framework, which has been widely used to test the association between a set of genetic variants and a single trait (Liu et al. 2007, 2008; Kwee et al. 2008; Wu et al. 2010, 2011; Ionita-Laza et al. 2013; Zhan et al. 2016). Specifically, the KMR relates the trait (continuous or dichotomous) to the set of genotype values using the following generalized partial linear model (Liu et al. 2007, 2008):
| (1) |
where are the regression coefficients for the covariates; is a generally specified function belonging to a space spanned by a kernel function and is a link function, such as an identity function for continuous traits and logit function for dichotomous traits. The kernel is the genotype kernel and has corresponding kernel matrix where The key to this KMR framework is usage of a positive semidefinite kernel function as a similarity measure between genotypes and (Schaid 2010a,b), which can facilitate capture of structure and relationships among genetic variants.
In the KMR model (1), the trait is related to the variants through Hence, testing the hypothesis of no association between the trait and genetic variants after adjusting for covariates is equivalent to testing Through connections between KMR and generalized linear mixed models (Liu et al. 2007, 2008), we can treat as a vector of subject-specific random effects with mean zero and variance Then testing is equivalent to testing whether the variance component τ is equal to zero, which can be easily accomplished using a variance component score test with the following test statistic
| (2) |
where is the estimated trait values under the null model of and denotes the trace of a matrix. When the trait is continuous, with being estimated under the null model. When the trait is dichotomous, Under the null, Q follows a mixture of distributions which can be approximated using exact methods (Davies 1980).
Test statistic (2) is essentially the sum of the element-wise product of two matrices. One is and the other is the cross product of the trait residuals In genetic association analysis, the kernel matrix is often used to measure the subject-pairwise similarity in terms of genotypes (Kwee et al. 2008; Wu et al. 2010, 2011), and the cross product of residuals is often used to measure subject-pairwise similarity of phenotypes (Tzeng et al. 2009, 2011). Heuristically speaking, statistic S compares the subject-pairwise similarity in the trait to that in genotypes, where a high correspondence usually leads to a large statistic value and suggests existence of association.
There are two straightforward ways to extend the single kernel-based association test statistic (2) to accommodate multiple traits One is to stack the columns of into a huge column vector and apply the statistic (2) to This approach is evaluated in Maity et al. (2012). However, a major limitation is that this approach can be computationally intractable with high-dimensional traits since it needs to eigendecompose an matrix. The other approach to incorporate multiple traits is simply to replace the univariate trait residuals cross-product matrix by the multivariate traits residuals cross-product matrix where is estimated under the null model assuming all traits are continuous. The second approach typically loses power when traits are highly or even modestly correlated with each other (Wu and Pankow 2016). Furthermore, both approaches fail to capture any complicated structures within traits (e.g., inherent regulatory network structure within transcriptomic pathway expressions), which can further lead to power loss (Freytag et al. 2014). To address this issue, we propose the DKAT approach in the following section to allow for testing association between high-dimensional, possibly structured, traits and one or more genetic variants.
A DKAT
To address the aforementioned limitations, we propose to use a phenotype kernel to model multiple traits simultaneously. Similar the genotype kernel the phenotype kernel is used to summarize the phenotypic similarity. Compared with the cross-product matrix used in some existing methods, DKAT is able to capture complex structures among the multiple phenotypes by embedding the phenotypes in a kernel.
Like the single kernel-based association tests in KMR, we test the association between multiple traits and multiple genetic variants by comparing the phenotypic similarity matrix and genotypic similarity matrix across pairs of individuals. Motivated by works of relating two matrices from the same individuals (Josse et al. 2008; Minas et al. 2013; Zhan et al. 2017), we propose the new DKAT statistic as
| (3) |
where is a centering matrix, is the nth order identity matrix, and is an n-dimensional vector of ones. Since is idempotent, the numerator is essentially the same as which is the element-wise multiplication of centered genotype kernel matrix and centered phenotype kernel matrix Hence, our DKAT statistic shares the same spirit of comparing two similarities as the single kernel-based association tests statistic (2). Moreover, if the phenotype kernel is picked as then the DKAT statistic reduces to the form of the KMR statistic in (2). Therefore, most existing kernel association tests (Liu et al. 2007, 2008; Kwee et al. 2008; Wu et al. 2010, 2011; Maity et al. 2012; Wu and Pankow 2016; Zhan et al. 2016) can be viewed as special forms of DKAT. As an alternative to comparing two kernel matrices, there exist some similar statistics either comparing two input matrices (Josse et al. 2008) or two distance matrices (Minas et al. 2013). Kernels have been widely used to capture structures among genotypes (Kwee et al. 2008; Wu et al. 2010, 2011; Ionita-Laza et al. 2013; Broadaway et al. 2016). Following this steam, specific kernels are used in this article to capture the inherent structures among both genotypes and phenotypes.
Intuitively speaking, the larger the DKAT statistic, the more likely the genotype kernel matrix resembles the phenotype kernel matrix, which further implies that the phenotypes might be associated with the genotypes in a specific way. To calculate the exact critical value of a DKAT under a given significance level, we need to study its distribution under the null hypothesis of no association. Two current standard approaches of calculating the null distribution of a genetic association test statistic are permutation-based resampling methods (Hua and Ghosh 2015; Pan et al. 2015; Joo et al. 2016; Kim et al. 2016) and large sample-based asymptotic methods (Kwee et al. 2008; Wu et al. 2010, 2011; Broadaway et al. 2016; Wu and Pankow 2016). However, both methods have potential limitations. On one hand, it is computationally expensive to use permutations to achieve genome-wide significance. On the other hand, it is observed that asymptotic methods can be conservative when the sample size is small or modest (Lee et al. 2012; Chen et al. 2016). To overcome these potential limitations, we calculate the P-value of DKAT using a fast-pseudopermutation method, closely following the strategy being used in the RV-coefficient literature (Josse et al. 2008; Minas et al. 2013; Zhan et al. 2017), where a typical RV coefficient shares the same form of the DKAT statistic but uses totally different matrices other than and (both introduced in the next section) as used in this article. Specifically, a Pearson type III distribution is used to approximate the permutation null distribution of DKAT by matching the first three moments. Technical details of calculating the Pearson type III density are presented in Supplemental Material, Section S.1 in File S1. The advantages of the new DKAT P-value calculation strategy are twofold. First, no explicit permutation is required as the finite-sample empirical moments can be analytically calculated. Second, closed-form expression of the Pearson type III density is available, and thus our method allows a fast and analytic P-value calculation for genetic association analysis.
Choices of kernels
A key aspect of DKAT is the kernels, which appropriately summarize the phenotypic and genotypic similarities between pairwise subjects; although DKAT is statistically valid in protecting the correct type I error, irrespective of the kernels being used. However, good choice of kernels, which better reflect the unique data features, can improve the test power (Freytag et al. 2014; Zhao et al. 2015). In this section, we first briefly review some genotype kernels widely used in existing kernel-based association tests and some kernels that could potentially be used for phenotypes. Then we propose a specific phenotype kernel for the high-dimensional structured phenotypes considered in this article.
In the literature, many kernels have been proposed for genotype data (Schaid 2010a,b). Some popular examples include the linear kernel and the identity-by-state (IBS) kernel:
Linear kernel:
IBS kernel:
The linear kernel assumes a linear association pattern. That is, the function in model (1) is of a linear form. It is simple and can be powerful when the true underlying association pattern is linear. The IBS kernel measures the similarity based on identity-by-state (IBS) allele sharing and is positive definite (Kwee et al., 2008). However, the space spanned by an IBS kernel is less studied. Both the linear kernel and the IBS kernel are additive forms, which makes it easy to incorporate weights for each genetic variant (Wu et al. 2011).
On the other hand, few studies have described the use of kernels for the complex multi-dimensional traits as considered in this article. In general, if all traits are continuous, then the Gaussian kernel and the dth-order polynomial kernel are often used. Also, the binary kernel was shown to be a valid kernel function for all multivariate binary traits.
Gaussian kernel:
Polynomial kernel:
Binary kernel:
If the traits are mixed (a combination of continuous variables and binary variables), then we can define kernels for both the continuous and binary parts separately and then multiply them together as the final kernel function, which has been shown to be valid for association analysis (Zhan et al. 2016).
No matter how large the dimension p is, the information in all traits is pooled into a scalar by using the phenotype kernel. In this sense, DKAT is robust against high-dimensional phenotypes, which can be a major advantage over most existing multivariate regression-based testing methods (Maity et al. 2012; Wu and Pankow 2016). Besides the robustness to high-dimensional traits, another major concern of this article is to address the network-type traits, such as expression of genes belonging to the same pathway. For such gene pathway data, a network-based kernel has been proposed of the form (Freytag et al. 2014), where is the undirected adjacency matrix, represents that gene i and gene j interact with each other in an activating fashion, and represents an inhibition pattern.
In reality, it is difficult to know the functional relationship between each gene pair within the pathway. Hence, we replace the adjacency matrix with the precision matrix (also called inverse covariance matrix ), which can be estimated from the data without any prior biological knowledge. The precision matrix is useful in estimating partial correlations, which incorporates the functional mechanism of the whole pathway. For example, under the Gaussian assumption, indicates that gene i and gene j are conditionally independent given all other genes in the network/pathway, or equivalently speaking, gene i and j are unconnected in the gene network/pathway (Friedman et al. 2008). Similar to the undirected adjacency matrix can also incorporate the underlying network structure. Thus, we propose the phenotype kernel matrix as where is the estimated precision matrix. A simple estimator is the sample precision matrix and the corresponding phenotype kernel matrix is proportional to the so-called projection similarity matrix in the literature (Wessel and Schork 2006; Broadaway et al. 2016). When the dimension of traits is high, the sample precision matrix is unstable or even not estimable. In such a high-dimensionality scenario, we estimate the precision matrix via regularization. For example, a graphical lasso estimator can be derived by maximizing the lasso-penalized log likelihood (Friedman et al. 2008).
In practice, it is often true that multiple kernels and are available for testing in DKAT. Without knowing the true underlying association model, it is of importance to accommodate multiple candidate kernels. In general, there are two approaches to tackle this issue. The first average-type strategy is to calculate an omnibus which is usually a linear combination of and another omnibus which is usually a linear combination of Then a final DKAT() test is applied. The other minimum-type approach to accommodate multiple candidate kernels is to pick the most significant kernel pair. That is, and are selected such that DKAT() has the smallest P-value over all kernel pairs However, the minimum P-value is no longer a genuine P-value and permutations are often needed to establish the final significance. Details of these two approaches of accommodating multiple candidate kernels, along with numerical evaluations, can be found in Section S.2 of File S1.
Besides the kernels, another important practical issue is to adjust for the confounding covariates effects, such as age, gender, and principal components of genotypes (for adjusting population structures). In genetic association tests, a common strategy of adjusting for covariates is the residual-based approach (Tzeng et al. 2009, 2011; Wu et al. 2010, 2011; Hua and Ghosh 2015; Broadaway et al. 2016). That is, we first fit the null model with covariates only: and then calculate the residuals of the null model. Next, one can construct the phenotype kernel on the residuals as the subject-wise trait similarity after adjusting for covariates. That is, the phenotype kernel matrix is used in DKAT, where is the estimated precision matrix of residuals. Existing numerical studies have shown that it can have the correct type I error as long as the number of covariates is much smaller than the sample size (Wu et al. 2010, 2011; Hua and Ghosh 2015; Broadaway et al. 2016).
Simulation studies
We conducted extensive simulation studies under different scenarios to evaluate the performance of DKAT in testing the association between high-dimensional structured traits and genotypes. To mimic a relatively high-dimensional scenario, traits (e.g., expressions of genes belonging to a pathway) were considered in our simulation. As a comparison, most existing multivariate association tests usually considered <20 traits (Klei et al. 2008; Maity et al. 2012; van der Sluis et al. 2013; Broadaway et al. 2016; Ray et al. 2016; Schaid et al. 2016; Wu and Pankow 2016). Two different correlation structures were used in this simulation. One was the compound symmetry covariance structure as commonly used in the literature (Maity et al. 2012; Broadaway et al. 2016; Ray et al. 2016; Schaid et al. 2016; Wu and Pankow 2016). That was and for all where was the covariance matrix of the traits. The other correlation structure was the banded inverse covariance (precision) matrix with and zero otherwise, where was the precision matrix of traits. Assuming all traits were continuous, then where was the partial correlation between trait i and j given all other traits. Thus, the banded precision matrix represented such a pathway that each gene was only related to its nearby genes conditional on all other genes in the pathway. In contrast to the compound symmetry covariance structure, the banded inverse covariance structure mimicked the complicated functional-regulatory mechanisms in a gene pathway. For simplicity, we denoted these two covariance structures as and in the rest of the simulation section. To guarantee positive definiteness of and we simply simulated ρ from uniform (0, 0.5) distribution. Finally, we conducted three different simulation studies, where simulation I was for a single SNP, simulation II was for multiple SNPs, and simulation III was for multiple rare variants. Under each simulation scenario, we considered a sample size of either 500 or 1000 subjects.
Simulation I:
This simulation was designed to mimic the pleiotropy effect, where a common SNP affected multiple traits. The data were generated from the model
| (4) |
where was the expression value of gene j for subject i and was a single SNP taking values 0, 1, and 2, with a minor allele frequency (MAF) of 0.3. For each i, was distributed as multivariate Gaussian with mean zero and covariance matrix where or For simplicity, we did not consider covariates in the model since they could be easily adjusted via the residual-based approach described previously. Under the null model, all Under the alternative model, we set a proportion () of traits to be truly associated with the SNP (with nonzero β-coefficients). Without loss of generality, we set the first traits as relevant ones with coefficients generated from a uniform (0,) distribution, for and for The effect sizes [following uniform (0,) distribution] changed with sample size and hence it was meaningless to compare test powers under different sample sizes. These effect sizes were selected to better distinguish different tests under each scenario.
Simulation II:
In the second simulation scenario, we tested the association between multiple SNPs and multiple traits. The multiple SNPs were generated based on the linkage disequilibrium (LD) structure of gene acid ceramidase 1 (ASAH1), as used in Wu et al. (2010). A total of 93 HapMap SNPs are located within this gene. Based on the LD structure of the ASAH1 gene, we used HAPGEN (Spencer et al. 2009) to generate SNP genotype data at each of the 93 loci. After the SNPs were simulated, we generated the traits from the following model:
| (5) |
where relevant model parameters (e.g., ) were the same as the previous Simulation I. We selected 29 typed SNPs on Affy6 to calculate the genotype kernel in the analysis. Under the null model Under the alternative model, we selected the first traits as causal ones which were truly associated with the SNPs. For each causal trait, we randomly selected 3 SNPs from the 93 SNPs as the causal SNPs for that trait, and simulated the nonzero βkj-coefficient from uniform (0,) distribution for and where different traits could have different causal SNPs. Finally, to allow for the heterogeneous effect of different loci, we randomly assigned a sign for the β-coefficient of each SNP with even probability.
Simulation III:
For the simulation of rare variants, we considered the design of Wu et al. (2011) to generate rare variants. We simulated 10,000 haplotypes for a 1-Mb region on the basis of COSI (Schaffner et al. 2005) to mimic the LD pattern, local recombination rate, and population history of European descent. Only those variants with MAF were included in the analysis. After rare variants being simulated, we generated the traits according to model (5). Under the alternative model, we randomly selected 10% of the rare variants as causal ones and simulated the nonzero β-coefficients from uniform Other simulation settings were the same as Simulation II.
Competing methods:
After the data were generated, DKAT was applied to test the association between genotypes and phenotypes. The phenotype kernel used in DKAT was where was the phenotypes’ sample mean and the graphical lasso regularization parameter was set as in our simulation. The graphical lasso method was used for illustrative purposes of constructing the phenotype kernel, incorporating the high dimensionality as well as network structures in traits. An optimal graphical lasso regularization parameter was beyond the scope of this article.
Along with DKAT, we also evaluated other methods for comparison. Among existing multivariate-trait association tests, both multiple testing-adjusted univariate trait methods (Yang et al. 2010; van der Sluis et al. 2013) and dimension reduction-based methods (Klei et al. 2008; Ferreira and Purcell 2009) can be limited with high-dimensional traits. Other multivariate traits–single SNP association testing methods (O’Reilly et al. 2012; Joo et al. 2016) suffer from power loss when there are systematic but weak marginal effects for each SNP. To make the comparison fair, we focus on existing methods that test association between multivariate traits and multiple SNPs/rare variants. Two of such methods are the gene association with multiple traits (GAMuT) test (Broadaway et al. 2016) and the multivariate sequence kernel association tests (MSKAT) (Wu and Pankow 2016), which are briefly introduced in the following paragraph.
The GAMuT test statistic (Broadaway et al. 2016) is actually the numerator of the DKAT statistic in (3). However, it calculates the P-value differently, using large-sample results (Broadaway et al. 2016). The asymptotic distribution of the GAMuT statistic is where are eigenvalues of and respectively, and are independent and identically distributed with 1 degree of freedom. Then, the GAMuT P-value is calculated based on this asymptotic distribution with quadratic form approximations (Davies 1980). To make a fair comparison, the same phenotype kernel in DKAT was applied in GAMuT in our simulations. The other method, MSKAT, assumes a linear model between each individual trait with multiple genetic variants, and considers the score test statistics between the kth trait and jth variant, where Let be the score vector between the jth variant and all traits. Ignoring the weights, the MSKAT statistic has been proposed as (Wu and Pankow 2016), where is the sample precision matrix. Unlike -based DKAT and GAMuT, the MSKAT statistic uses which requires To avoid this potential limitation, another variant of statistic is also considered (Wu and Pankow 2016), which is termed as MSKAT2 in our simulations. MSKAT2 represents a broad class of multivariate-trait association testing methods that ignore the correlation structures among outcomes [such as DKAT and GAMuT with the linear phenotype kernel MSKAT and MSKAT2 P-values are calculated in a similar way as GAMuT, which is based on its asymptotic quadratic form approximation (Wu and Pankow 2016).
As pointed out in Wu and Pankow (2016), MSKAT and MSKAT2 implicitly used the (weighted) linear kernel for genetic variants. To make the comparison fair, the same linear kernels were used in DKAT and GAMuT. In particular, we used the same linear kernel for the SNPs simulations (Simulation I and Simulation II) and the weighted linear kernel for the rare variants simulation (Simulation III). The weight for each rare variant was specified as Beta(MAF,1,25) as suggested in SKAT (Wu et al. 2011). Finally, under each simulation scenario, we evaluated the type-I error of each test with 1,000,000 replicates under the null model, and the power with 1000 replicates under the alternative model. The empirical type-I error rate and power were calculated as the proportion of replicates with a P-value smaller than the nominal significance level.
Real data application
We applied the newly proposed DKAT approach to a Grady Trauma Project data set that was collected as part of a larger study investigating the role of genetic and environmental factors in predicting response to stressful life events (Gillespie et al. 2009). A total of 337 individuals were recruited from the Grady Memorial Hospital in Atlanta, Georgia. Blood samples were collected from these individuals who provided informed consent and participated in a verbal interview. For each individual, both gene expressions and genotypes were measured. Demographic data such as gender, age, and race were also collected. Details on data collection and preprocessing can be obtained from previous publications (Gillespie et al. 2009). Previous studies have shown that genetic risk factors may account for up to 30–40% of the heritability of developing post-traumatic stress disorder (PTSD) following a trauma, and many gene pathways that are associated with PTSD have been identified (Almli et al. 2014b). In this analysis, we further studied the genetic regulation of expressions of genes belonging to these pathways. In particular, we were particularly interested in the cis-regulation, that was, whether pathway gene expressions were associated with the SNPs in the same pathway. Expressions of 8588 genes belonging to 224 pathways (with more than one gene in each pathway) were measured. In each pathway analysis, the phenotypes were the gene expression values and the genotypes were the SNPs in that pathway. A total of 164,503 SNPs were mapped to the 8588 genes in 224 pathways. The median number of genes in a pathway was 27, with the first and third quantiles being 14 and 48, respectively.
Two different sets of association analyses were conducted. In the first set of association analysis, we evaluated the association between the multiple gene expressions in a pathway and all SNPs in the same pathway using DKAT, GAMuT, MSKAT, and MSKAT2. In the second set of association analysis, we evaluated the importance of each individual gene for certain pathways that might be of interest based on results of the first analysis. In other words, we examined the association between the pathway gene expressions and SNPs in each individual gene belonging to the pathway. For all association analyses, we adjusted the covariate effects of gender, age, race, and the top 10 principal components of the genotype data.
Data availability
An R software implementing the proposed DKAT method is available at https://github.com/xyz5074/DKAT. The expression data are available at Gene Expression Omnibus accession number GSE58137. Details about the genotype data are available in Almli et al. (2014a).
Results
Simulation results
Type-I error results:
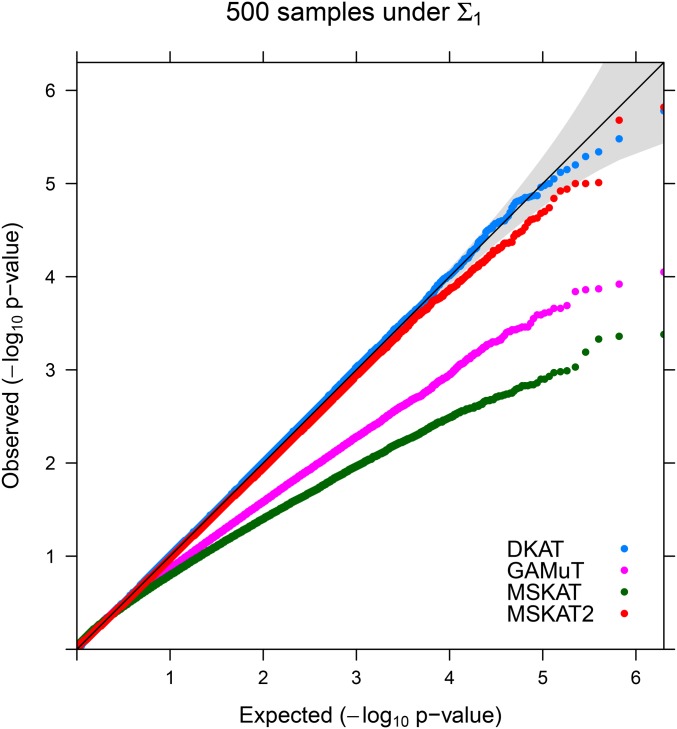
The empirical type-I error rates under Simulation I are reported in Table 1. Based on the table, DKAT is always able to protect the correct type-I error across different scenarios. On the other hand, GAMuT and MSKAT are conservative under each simulation scenario, especially when the sample size is relatively small (). MSKAT2 seems to be more conservative under than To further explore the type-I error of all tests at more stringent significance levels, we present the QQ plots of P-values under the configuration of and in Figure 1. As we can see, the P-values of DKAT stick with the 45° line, which indicates that the type-I error of DKAT is well controlled under different significance levels. For GAMuT and MSKAT, we can see a clear departure from the 45° line with plots skewing downward, implying these tests are very conservative, which are all consistent with the results from Table 1. QQ plots under other simulation configurations are qualitatively similar and hence are not reported. Similar empirical type-I error results have also been observed in Simulation II and Simulation III (Tables S2 and S3in File S1).
Table 1. Empirical type-I error rates (divided by the nominal significance level α) under simulation I.
| n | α | DKAT | GAMuT | MSKAT | MSKAT2 | |
|---|---|---|---|---|---|---|
| 500 | 1.04 | 0.09 | 0.01 | 0.87 | ||
| 1.06 | 0.01 | 0 | 0.67 | |||
| 0.90 | 0 | 0 | 0.50 | |||
| 1000 | 0.92 | 0.31 | 0.19 | 0.93 | ||
| 1.07 | 0.13 | 0.12 | 0.56 | |||
| 1.00 | 0 | 0 | 0.80 | |||
| 500 | 0.96 | 0.10 | 0.01 | 0.21 | ||
| 1.03 | 0.02 | 0 | 0.12 | |||
| 0.90 | 0 | 0 | 0.10 | |||
| 1000 | 1.06 | 0.23 | 0.27 | 0.37 | ||
| 0.89 | 0.14 | 0.10 | 0.23 | |||
| 0.90 | 0 | 0 | 0.30 |
Figure 1.
QQ plots: QQ plots for DKAT, GAMuT, MSKAT, and MSKAT2 with under simulation I. The shading area is the 95% confidence band for P-values.
It has been observed in single trait kernel association tests that estimation error (due to small sample size) can lead to conservative tests (Lee et al. 2012; Chen et al. 2016), which also explains the conservativeness of GAMuT and MSKAT in this simulation. Taking GAMuT as an example, the asymptotic null distribution of GMAuT depends on the eigenvalues of matrix where which further requires accurate estimation of the precision matrix. Given the high dimensionality of traits, many parameters in the precision matrix need to be estimated. The accumulated estimation errors in GAMuT deteriorate the performance of the test, resulting in overprotected (conservative) P-values (Lee et al. 2012; Chen et al. 2016). Unlike GAMuT and MSKAT, which need to estimate the whole precision matrix MSKAT2 only needs to estimate the diagonals The accumulated estimation errors in MSKAT2 is much smaller and hence it is less conservative than GAMuT and MSKAT. Finally, the way DKAT calculates its P-value is more robust to these estimation errors (Section S.1 in File S1), and hence DKAT is robust to small samples and high-dimensional traits. To summarize, the proposed DKAT always has the correct type-I error rate even under a very stringent nominal significance level. On the other hand, GAMuT, MSKAT, and MSKAT2 can be conservative especially when the sample size is relatively small or modest.
Power results:
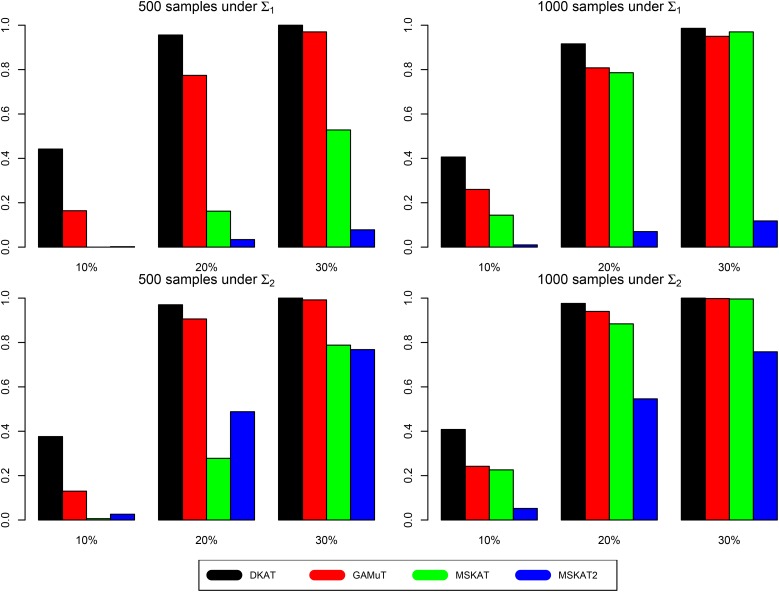
Without loss of generality, we compare the power of all tests under significance level (reflecting a genome-wide Bonferroni correction for 20,000 genes). The power under Simulation I is presented in Figure 2. It is clear to see that DKAT is always the most powerful test under each scenario. On the other hand, MSKAT2 always tends to be the least powerful test (except for the small-sample scenario, where MSKAT can have lower power due to the its conservativeness as seen in the previous type-I error simulation results section). This is because the phenotype kernel used in DKAT and GAMuT (or used in MSKAT) can incorporate the inherent correlation structure among the multivariate traits, while MSKAT2 simply ignores the correlations among traits. The power gain of DKAT/GAMuT/MSKAT over MSKAT2 increases with the (partial) correlation strength among traits (i.e., ρ value in or ). For each test considered in this simulation study, the power of the test increases as the proportion (γ) of associated traits increases (i.e., as the genes are increasingly pleiotropic). This is because it can further amplify the association signal by including more relevant traits into the multi-trait association analysis. Qualitatively similar empirical power results are also observed in Simulation II (Figure S2in File S1) and Simulation III (Figure S3 in File S1).
Figure 2.
Power under simulation I: x-axis represents proportion of relevant traits () and y-axis represents power.
To summarize, DKAT is always more powerful than GAMuT, MSKAT, and MSKAT2. The power gain probably comes from two aspects. One is the usage of phenotype kernel to incorporate the complex structure of traits into association analysis (compared to MSKAT2). The other is from the new efficient and robust P-value calculation (compared to GAMuT and MSKAT).
Data application results
To account for multiple testing, we set family-wise significance level of which corresponds to a Bonferroni correction based on the number of pathways being tested. Under this significance level, 18, 17, 16, and 1 pathways have been found where their gene expressions were significantly associated with their SNPs by DKAT, GAMuT, MSKAT, and MSKAT2, respectively. Compared with MSKAT2, it is clear that incorporating the network-type gene regulatory structure via the precision matrix (as in DKAT/GAMuT/MSKAT) can largely enhance the discovery power of association analysis between pathway gene expressions and SNPs. The DKAT is slightly more powerful than GAMuT and MSKAT, which is probably because the test design of DKAT is more efficient for this data set.
Under the family-wise significance level, the only pathway that was detected as associated with its SNPs by all DKAT, GAMuT, MSKAT, and MSKAT2 methods was asthma (KEGG: hsa05310). A further interesting analysis was to test which individual gene regulates the asthma pathway gene expressions. To this end, we tested the association between asthma pathway gene expressions and all SNPs in a single gene belonging to that pathway. In this data, a total of 167 SNPs were detected in 10 genes in the asthma pathway. Under the gene-level SNPs and pathway-level expression association analysis, DKAT, GAMuT, and MSKAT all detected four genes (HLA-DRA, HLA-DRB1, HLA-DQA1, and HLA-DQB1) which regulated the asthma pathway expressions while MSKAT2 only detected two of them (HLA-DRB1 and HLA-DQA1). Further functional study of these genes on asthma may be of biological interest.
Discussion
In this article, we have proposed DKAT for evaluating the association between high-dimensional structured traits and multiple SNPs or rare variants. Compared with most existing kernel association tests (e.g., SKAT), the novelties of DKAT are twofold. First, an additional phenotype/trait kernel is used, which can incorporate the inherently complex structure of the traits and thereby improve the statistical power for detecting an existing association signal. The numerical studies in this article are mainly designed to mimic the scenario of high-dimensional, structured traits, where we propose a network-type phenotype kernel by replacing the adjacency matrix in Freytag et al. (2014) with the precision matrix. We emphasize that it is possible to design new appropriate kernels for other data types, which can lead to a useful and powerful association analysis. Second, unlike existing association tests, DKAT provides a new robust strategy to compute P-values in genetic association testing. The DKAT P-value is less sensitive to estimating errors in covariance terms compared to other methods (e.g., GAMuT and MSKAT), and is extremely appealing with high-dimensional traits, where it is difficult to accurately estimate the trait covariance matrix given the dimensionality. Thus, DKAT is more robust than most existing methods in testing the association between high-dimensional structured traits and genotypes.
As an association test, DKAT has four advantages. First, DKAT is methodologically flexible in testing the association between an arbitrary set of traits and an arbitrary set of genetic variants. It can test the association between multiple traits and either single/multiple SNPs or multiple rare variants, without making parametric assumptions. On the contrary, many existing multivariate-trait association tests can only handle a single SNP (O’Reilly et al. 2012; Zhou and Stephens 2014; Wu and Pankow 2015; Joo et al. 2016; Ray et al. 2016; Schaid et al. 2016). Others often assume that traits are associated with SNPs through a linear model (Maity et al. 2012; Wu and Pankow 2016). Second, DKAT can evaluate biologically meaningful hypotheses. The phenotype kernel in DKAT can capture pleiotropy effects among the phenotypes and the genotype kernel can capture epistasis effects among SNPs. With prior biological knowledge, it can be of interest to apply DKAT to test associations between a prespecified set of traits and a prespecified region of genetic variants, the results of which may further lead to meaningful biological insights. Third, DKAT is also statistically very powerful. As illustrated previously in the SNP-set association test (Kwee et al. 2008; Wu et al. 2010), a SNP kernel can amplify the association signal by collapsing information across multiple SNPs. Moreover, the phenotype kernel in DKAT can further amplify the association signal by collapsing information across multiple traits. After amplifying twice, DKAT can greatly improve the statistical power to detect any existing association signal. Fourth, DKAT is also computationally scalable. Only matrix multiplication is required in DKAT. However, both GAMuT and MSKAT requires eigendecomposition of matrices, which can be computationally unstable for a large sample size. Furthermore, the asymptotic P-value calculation in GAMuT and MSKAT requires large n or small p, otherwise it can be conservative due to estimation error (Lee et al. 2012; Chen et al. 2016). On the other hand, DKAT is applicable to any sample size n and trait dimension p. In this regard, DKAT is appropriate for the large p small n problems frequently encountered in modern scientific studies.
The design of simulation II (SNPs set) and simulation III (rare variants) is in vein with previous simulation studies in the literature (Wu et al. 2010, 2011). For example, the same ASAH1 gene/LD structure is used in the article. Since no relevant assumptions are made, we believe that our method should also work well with other genes/LD structures. In this article, we only considered an association study for unrelated populations. Another important scenario is cohorts with population relatedness, such as family-based association studies (Chen and Abecasis 2007; Schifano et al. 2012; Wang et al. 2016). It is of future interest to extend the current DKAT to incorporate the family structure. As indicated in our numerical studies, including more relevant traits in DKAT increases the power to a large extent. However, when more noise traits (not associated with the SNP set) are added, it may lead to power loss. In practice, the true association signal may not be known. Adaptive testing strategies could be used to address this uncertainty (Pan et al. 2015; Zhan et al. 2015a; Kim et al. 2016). Finally, to aid interpretation of which genetic variants or which traits are associated, it is of interest to prioritize individual genetic variants/traits by incorporating variable selection in DKAT (He et al. 2016). We believe these issues are of importance and warrant further investigation.
Supplementary Material
Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.116.199646/-/DC1.
Acknowledgments
Comments by two referees and the communicating editor helped improve this article and are highly appreciated. This research was supported by National Institutes of Health grants U10 CA-180819 and R01 HG-007508 and the Hope Foundation.
Footnotes
Communicating editor: C. Sabatti
Literature Cited
- Alberti K. G. M., Zimmet P., Shaw J., IDF Epidemiology Task Force Consensus Group , 2005. The metabolic syndrome–a new worldwide definition. Lancet 366: 1059–1062. [DOI] [PubMed] [Google Scholar]
- Almli L. M., Duncan R., Feng H., Ghosh D., Binder E. B., et al. , 2014a Correcting systematic inflation in genetic association tests that consider interaction effects: application to a genome-wide association study of posttraumatic stress disorder. JAMA Psychiatry 71: 1392–1399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almli L. M., Fani N., Smith A. K., Ressler K. J., 2014b Genetic approaches to understanding post-traumatic stress disorder. Int. J. Neuropsychopharmacol. 17: 355–370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andreassen O. A., Harbo H. F., Wang Y., Thompson W., Schork A., et al. , 2015. Genetic pleiotropy between multiple sclerosis and schizophrenia but not bipolar disorder: differential involvement of immune-related gene loci. Mol. Psychiatry 20: 207–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aschard H., Vilhjálmsson B. J., Greliche N., Morange P.-E., Trégouët D.-A., et al. , 2014. Maximizing the power of principal-component analysis of correlated phenotypes in genome-wide association studies. Am. J. Hum. Genet. 94: 662–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broadaway K. A., Cutler D. J., Duncan R., Moore J. L., Ware E. B., et al. , 2016. A statistical approach for testing cross-phenotype effects of rare variants. Am. J. Hum. Genet. 98: 525–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J., Chen W., Zhao N., Wu M. C., Schaid D. J., 2016. Small sample kernel association tests for human genetic and microbiome association studies. Genet. Epidemiol. 40: 5–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W.-M., Abecasis G. R., 2007. Family-based association tests for genomewide association scans. Am. J. Hum. Genet. 81: 913–926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chesler E. J., Lu L., Shou S., Qu Y., Gu J., et al. , 2005. Complex trait analysis of gene expression uncovers polygenic and pleiotropic networks that modulate nervous system function. Nat. Genet. 37: 233–242. [DOI] [PubMed] [Google Scholar]
- Davies R. B., 1980. Algorithm as 155: the distribution of a linear combination of χ2 random variables. J. R. Stat. Soc. Ser. C Appl. Stat. 29: 323–333. [Google Scholar]
- Ferreira M. A., Purcell S. M., 2009. A multivariate test of association. Bioinformatics 25: 132–133. [DOI] [PubMed] [Google Scholar]
- Freytag S., Manitz J., Schlather M., Kneib T., Amos C. I., et al. , 2014. A network-based kernel machine test for the identification of risk pathways in genome-wide association studies. Hum. Hered. 76: 64–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J., Hastie T., Tibshirani R., 2008. Sparse inverse covariance estimation with the graphical lasso. Biostatistics 9: 432–441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillespie C. F., Bradley B., Mercer K., Smith A. K., Conneely K., et al. , 2009. Trauma exposure and stress-related disorders in inner city primary care patients. Gen. Hosp. Psychiatry 31: 505–514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Q., Cai T., Liu Y., Zhao N., Harmon Q. E., et al. , 2016. Prioritizing individual genetic variants after kernel machine testing using variable selection. Genet. Epidemiol. 40: 722–731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hua W.-Y., Ghosh D., 2015. Equivalence of kernel machine regression and kernel distance covariance for multidimensional phenotype association studies. Biometrics 71: 812–820. [DOI] [PubMed] [Google Scholar]
- Ionita-Laza I., Lee S., Makarov V., Buxbaum J. D., Lin X., 2013. Sequence kernel association tests for the combined effect of rare and common variants. Am. J. Hum. Genet. 92: 841–853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joo J. W. J., Kang E. Y., Org E., Furlotte N., Parks B., et al. , 2016. Efficient and accurate multiple-phenotype regression method for high dimensional data considering population structure. Genetics 204: 1379–1390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Josse J., Pagès J., Husson F., 2008. Testing the significance of the RV coefficient. Comput. Stat. Data Anal. 53: 82–91. [Google Scholar]
- Kazi-Aoual F., Hitier S., Sabatier R., Lebreton J.-D., 1995. Refined approximations to permutation tests for multivariate inference. Comput. Stat. Data Anal. 20: 643–656. [Google Scholar]
- Kim J., Zhang Y., Pan W., 2016. Powerful and adaptive testing for multi-trait and multi-SNP associations with GWAS and sequencing data. Genetics 203: 715–731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klei L., Luca D., Devlin B., Roeder K., 2008. Pleiotropy and principal components of heritability combine to increase power for association analysis. Genet. Epidemiol. 32: 9–19. [DOI] [PubMed] [Google Scholar]
- Kwee L. C., Liu D., Lin X., Ghosh D., Epstein M. P., 2008. A powerful and flexible multilocus association test for quantitative traits. Am. J. Hum. Genet. 82: 386–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S., Emond M. J., Bamshad M. J., Barnes K. C., Rieder M. J., et al. , 2012. Optimal unified approach for rare-variant association testing with application to small-sample case-control whole-exome sequencing studies. Am. J. Hum. Genet. 91: 224–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu D., Lin X., Ghosh D., 2007. Semiparametric regression of multidimensional genetic pathway data: least-squares kernel machines and linear mixed models. Biometrics 63: 1079–1088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu D., Ghosh D., Lin X., 2008. Estimation and testing for the effect of a genetic pathway on a disease outcome using logistic kernel machine regression via logistic mixed models. BMC Bioinformatics 9: 292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maity A., Sullivan P. F., Tzeng J.-Y., 2012. Multivariate phenotype association analysis by marker-set kernel machine regression. Genet. Epidemiol. 36: 686–695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarthy M. I., Abecasis G. R., Cardon L. R., Goldstein D. B., Little J., et al. , 2008. Genome-wide association studies for complex traits: consensus, uncertainty and challenges. Nat. Rev. Genet. 9: 356–369. [DOI] [PubMed] [Google Scholar]
- Minas C., Curry E., Montana G., 2013. A distance-based test of association between paired heterogeneous genomic data. Bioinformatics 29: 2555–2563. [DOI] [PubMed] [Google Scholar]
- O’Reilly P. F., Hoggart C. J., Pomyen Y., Calboli F. C., Elliott P., et al. , 2012. MultiPhen: joint model of multiple phenotypes can increase discovery in GWAS. PLoS One 7: e34861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan W., Kwak I.-Y., Wei P., 2015. A powerful pathway-based adaptive test for genetic association with common or rare variants. Am. J. Hum. Genet. 97: 86–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ray D., Pankow J. S., Basu S., 2016. USAT: a unified score-based association test for multiple phenotype-genotype analysis. Genet. Epidemiol. 40: 20–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaffner S. F., Foo C., Gabriel S., Reich D., Daly M. J., et al. , 2005. Calibrating a coalescent simulation of human genome sequence variation. Genome Res. 15: 1576–1583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaid D. J., 2010a Genomic similarity and kernel methods i: advancements by building on mathematical and statistical foundations. Hum. Hered. 70: 109–131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaid D. J., 2010b Genomic similarity and kernel methods ii: methods for genomic information. Hum. Hered. 70: 132–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaid D. J., Tong X., Larrabee B., Kennedy R. B., Poland G. A., et al. , 2016. Statistical methods for testing genetic pleiotropy. Genetics 204: 483–497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schifano E. D., Epstein M. P., Bielak L. F., Jhun M. A., Kardia S. L., et al. , 2012. SNP set association analysis for familial data. Genet. Epidemiol. 36: 797–810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer C. C., Su Z., Donnelly P., Marchini J., 2009. Designing genome-wide association studies: sample size, power, imputation, and the choice of genotyping chip. PLoS Genet. 5: e1000477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzeng J.-Y., Zhang D., Chang S.-M., Thomas D. C., Davidian M., 2009. Gene-trait similarity regression for multimarker-based association analysis. Biometrics 65: 822–832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzeng J.-Y., Zhang D., Pongpanich M., Smith C., McCarthy M. I., et al. , 2011. Studying gene and gene-environment effects of uncommon and common variants on continuous traits: a marker-set approach using gene-trait similarity regression. Am. J. Hum. Genet. 89: 277–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Sluis S., Posthuma D., Dolan C. V., 2013. TATES: efficient multivariate genotype-phenotype analysis for genome-wide association studies. PLoS Genet. 9: e1003235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X., Zhang Z., Morris N., Cai T., Lee S., et al. , 2016. Rare variant association test in family-based sequencing studies. Brief. Bioinform. bbw083 DOI: 10.1093/bib/bbw083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welter D., MacArthur J., Morales J., Burdett T., Hall P., et al. , 2014. The NHGRI GWAS catalog, a curated resource of SNP-trait associations. Nucleic Acids Res. 42: D1001–D1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wessel J., Schork N. J., 2006. Generalized genomic distance–based regression methodology for multilocus association analysis. Am. J. Hum. Genet. 79: 792–806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu B., Pankow J. S., 2015. Statistical methods for association tests of multiple continuous traits in genome-wide association studies. Ann. Hum. Genet. 79: 282–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu B., Pankow J. S., 2016. Sequence kernel association test of multiple continuous phenotypes. Genet. Epidemiol. 40: 91–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu M. C., Kraft P., Epstein M. P., Taylor D. M., Chanock S. J., et al. , 2010. Powerful SNP-set analysis for case-control genome-wide association studies. Am. J. Hum. Genet. 86: 929–942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu M. C., Lee S., Cai T., Li Y., Boehnke M., et al. , 2011. Rare-variant association testing for sequencing data with the sequence kernel association test. Am. J. Hum. Genet. 89: 82–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Q., Wu H., Guo C.-Y., Fox C. S., 2010. Analyze multivariate phenotypes in genetic association studies by combining univariate association tests. Genet. Epidemiol. 34: 444–454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhan X., Epstein M. P., Ghosh D., 2015a An adaptive genetic association test using double kernel machines. Stat. Biosci. 7: 262–281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhan X., Patterson A. D., Ghosh D., 2015b Kernel approaches for differential expression analysis of mass spectrometry-based metabolomics data. BMC Bioinformatics 16: 77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhan X., Girirajan S., Zhao N., Wu M. C., Ghosh D., 2016. A novel copy number variants kernel association test with application to autism spectrum disorders studies. Bioinformatics 32: 3603–3610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhan X., Plantinga A., Zhao N., Wu M. C., 2017. A fast small-sample kernel independence test for microbiome community-level association analysis. Biometrics DOI: 10.1111/biom.12684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y., Xu Z., Shen X., Pan W., 2014. Testing for association with multiple traits in generalized estimation equations, with application to neuroimaging data. Neuroimage 96: 309–325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao N., Chen J., Carroll I. M., Ringel-Kulka T., Epstein M. P., et al. , 2015. Testing in microbiome-profiling studies with mirkat, the microbiome regression-based kernel association test. Am. J. Hum. Genet. 96: 797–807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou X., Stephens M., 2014. Efficient algorithms for multivariate linear mixed models in genome-wide association studies. Nat. Methods 11: 407. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
An R software implementing the proposed DKAT method is available at https://github.com/xyz5074/DKAT. The expression data are available at Gene Expression Omnibus accession number GSE58137. Details about the genotype data are available in Almli et al. (2014a).