Genetics of Genome-Wide Recombination Rate Evolution in Mice from an Isolated Island

Abstract

Recombination rate is a heritable quantitative trait that evolves despite the fundamentally conserved role that recombination plays in meiosis. Differences in recombination rate can alter the landscape of the genome and the genetic diversity of populations. Yet our understanding of the genetic basis of recombination rate evolution in nature remains limited. We used wild house mice (Mus musculus domesticus) from Gough Island (GI), which diverged recently from their mainland counterparts, to characterize the genetics of recombination rate evolution. We quantified genome-wide autosomal recombination rates by immunofluorescence cytology in spermatocytes from 240 F₂ males generated from intercrosses between GI-derived mice and the wild-derived inbred strain WSB/EiJ. We identified four quantitative trait loci (QTL) responsible for inter-F₂ variation in this trait, the strongest of which had effects that opposed the direction of the parental trait differences. Candidate genes and mutations for these QTL were identified by overlapping the detected intervals with whole-genome sequencing data and publicly available transcriptomic profiles from spermatocytes. Combined with existing studies, our findings suggest that genome-wide recombination rate divergence is not directional and its evolution within and between subspecies proceeds from distinct genetic loci.

MEIOTIC recombination is a fundamental part of genetic transmission in most eukaryotes. The sets of chromosomes gametes receive undergo an exchange of genetic material through a process known as crossing over. Crossovers, long recognized cytologically as chiasmata (Janssens 1909), fuse alleles into new haplotypic combinations. Recombination thus forms a knob that tunes the speed with which haplotypic diversity enters a population. The settings on this knob—recombination rates—are heritable, and they vary between individuals, populations, and species (True et al. 1996; Kong et al. 2004; Coop et al. 2008; Smukowski and Noor 2011; Comeron et al. 2012; Ritz et al. 2017).

The production of genetic variation among offspring by meiotic recombination is theorized to provide an advantage to organismal fitness by improving the efficacy of selection (Weismann et al. 1891; Kondrashov 1993; Burt 2000). Many models attribute the evolutionary advantage of recombination to its ability to dispel negative, nonrandom allelic combinations in a population (“negative linkage disequilibrium”) produced by epistatic interactions (Feldman et al. 1980; Barton 1995) or by genetic drift (Hill and Robertson 1966; Felsenstein 1974; Otto and Barton 1997). In this theoretical framing, the advantages of eliminating negative linkage disequilibrium lead to indirect selection favoring recombination. Increased recombination rate in response to artificial selection on a variety of phenotypes (Flexon and Rodell 1982; Burt and Bell 1987; Gorlov et al. 1992; Korol and Iliadi 1994) provides evidence supporting this hypothesis, though some studies reveal no such increase (Bourguet et al. 2003; Muñoz-Fuentes et al. 2015). In nature, indirect selection on recombination rate is likely to be strongest in populations subject to directional selection, including those populations experiencing new environments (Otto and Barton 2001).

Another possibility is that recombination rate itself is targeted by selection. Chiasmata generate physical tension between homologous chromosome pairs in meiosis, a necessity for proper chromosome disjunction (Roeder 1997; Hassold and Hunt 2001). This process leads to the constraint that each chromosome, or chromosome arm, harbor at least one crossover (Pardo-Manuel de Villena and Sapienza 2001; Fledel-Alon et al. 2009). It has also been suggested that the number of recombination events is limited to reduce the chances of aberrant exchange, which can lead to deleterious chromosomal rearrangements (Inoue and Lupski 2002; Coop and Przeworski 2007). In the laboratory, artificial selection targeting recombination rate often generates a response (Chinnici 1971; Kidwell and Kidwell 1976; Charlesworth and Charlesworth 1985). Furthermore, there is some evidence that human mothers with higher average rates of crossing over have more children (Kong et al. 2004; Coop et al. 2008).

Understanding how recombination rate differences are inherited illuminates the evolution of this key genomic parameter. Multiple loci that shape recombination rate variation have been identified (Murdoch et al. 2010; Dumont and Payseur 2011a; Balcova et al. 2016; Hunter et al. 2016), including variants in specific genes (Kong et al. 2008, 2014; Sandor et al. 2012; Ma et al. 2015; Johnston et al. 2016). In addition to confirming that recombination rate is a genetically complex trait with the capacity to respond to evolutionary forces, these findings provide a window into the evolutionary history of recombination rate. Current recombination rates capture only a single moment in evolutionary time, but each allele that increases or decreases recombination rate documents a genetic change in an ancestral population.

Despite this progress, the existing picture of the genetics of recombination rate variation suffers from important biases. First, loci have either been identified through genome-wide association studies within populations (Kong et al. 2008, 2014; Sandor et al. 2012; Ma et al. 2015; Hunter et al. 2016; Johnston et al. 2016) or in crosses between strains from different subspecies or species (Murdoch et al. 2010; Dumont and Payseur 2011a). Second, work has focused on humans and domesticated animals. As a result, the genetic basis of evolutionary differences in recombination rate between wild populations remains largely unprofiled.

In this study, we use an unusual population of wild house mice (Mus musculus domesticus) from the isolated Gough Island (GI) to address this challenge. Organisms that colonize islands often evolve extreme phenotypes in response to the substantial environmental changes they experience (Foster 1964; Case 1978; Grant and Grant 2002; Lomolino 2005). GI mice are exceptionally large—at approximately twice the weight of their mainland counterparts, they are the largest wild house mouse in the world (Rowe-Rowe and Crafford 1992; Jones et al. 2003). Historical records (Verrill 1895; Wace 1961) and population genetic analysis (Gray et al. 2014) indicate that this phenotypic change occurred over the short time span of 130–200 years, and genetic mapping suggests that directional selection was responsible for this case of rapid evolution (Gray et al. 2015). This context provides a special opportunity to examine the indirect effects of selection on the genetic architecture of recombination rate evolution in a natural population.

Extensive knowledge about recombination also positions the house mouse as an especially powerful system for understanding its evolution. Genome-wide recombination rates are known to vary among inbred mouse strains (Koehler et al. 2002; Dumont and Payseur 2011b), and dense genetic maps are available (Cox et al. 2009; Liu et al. 2014). Molecular and genetic mechanisms of recombination, including the regulation of crossover hotspots (Baudat et al. 2010; Parvanov et al. 2010; Grey et al. 2011), have been elucidated in the mouse (Paigen and Petkov 2010; Bolcun-Filas and Schimenti 2012; Cole et al. 2014; Hunter 2015). Finally, an immunofluorescence-cytology technique developed in the mouse enables the total number of crossovers during meiosis to be measured in individuals. Collectively, these resources and tools make it possible to characterize the genetic architecture of recombination rate evolution in nature.

Materials and Methods

Mice and crosses

GI is an uninhabited volcanic island in the South Atlantic Ocean, more than 2500 km away from the nearest continental landmass. Mice were live trapped from GI and brought to the Charmany Instructional Facility at the University of Wisconsin–Madison. A breeding colony was established from 25 mature females (♀) and 21 mature males (♂). Details on the transportation, housing, and establishment of this colony can be found in Gray et al. (2015). Mice derived from GI were crossed with WSB/EiJ, a North American wild-derived inbred strain purchased from the Jackson Laboratory (Bar Harbor, ME). All mice were housed in micro-isolator cages, separated by sex, and kept in a temperature-controlled room (68–72°F) with a 12-hr light/dark cycle. Food and water were provided ad libitum. Animals were cared for according to protocols approved by the University of Wisconsin School of Veterinary Medicine Animal Care and Use Committee.

Several partially inbred lines were created by brother-sister mating in our breeding colony. We selected a pair of full siblings from one of these lines to cross with WSB/EiJ. This brother-sister pair was separated from wild GI mice by four generations of full-sib mating in the laboratory. From this pair, we produced two independent sets of F₁’s and two independent F₂ intercrosses (Supplemental Material, Figure S1 in File S1). We generated 877 F₂ mice: 383 with the GI grandmother and 494 with the WSB/EiJ grandmother. We omitted mice with no genotype data or with obvious genotyping errors (see below), leaving 793 F₂ individuals (♀GI × ♂WSB: 341 and ♀WSB × ♂GI: 452) for subsequent analyses.

Chromosome spreads and immunostaining

Spermatocyte spreads were prepared from five WSB/EiJ mice, five GI mice, and a subset of F₂ males to characterize individual recombination rates (following Peters et al. 1997; Dumont and Payseur 2011a). Mice were euthanized at ∼16 weeks of age and the left testis from each individual was collected and processed based on established protocols. Prepared spreads were either immediately stained or stored at −20°C.

We adapted the immunostaining protocol from Anderson et al. (1999), de Boer et al. (2009), and Dumont and Payseur (2011a). Primary antibodies against MLH1 (rabbit polyclonal; Calbiochem, San Diego, CA) and SYCP3 (goat polyclonal; Santa Cruz Biotechnology) were diluted 1:50 while the primary antibody against centromeres (purified from CREST patient serum; Antibodies Incorporated, Davis, CA) was diluted 1:200. For secondary antibodies, Alexa 488 donkey anti-rabbit (Molecular Probes, Eugene, OR) and Alexa 568 donkey anti-goat were diluted 1:100, and A350/A280 donkey anti-human (Jackson ImmunoResearch) was diluted 1:200. All incubations were carried out at 37°C in an enclosed humid chamber.

Following established immunostaining protocols, slides to be stained were first blocked in a Coplin jar with 1× antibody dilution buffer for 30 min before receiving 60 μl of the diluted primary antibody cocktail. Slides were sealed with a coverslip and rubber cement before being incubated for 48 hr. After a wash step on the incubated slides, 60 μl of diluted secondary antibodies (donkey anti-rabbit and donkey anti-human) was applied to each slide for an overnight incubation. The final incubation involved 60 μl of diluted secondary antibody (donkey anti-goat), which lasted 2 hr. Stained slides were then washed and allowed to air dry before fixing with Prolong Gold Antifade reagent (Invitrogen, Carlsbad, CA).

Microscopy and scoring

All slides were imaged on a Carl Zeiss (Thornwood, NY) AxioPlan 2 microscope with an AxioCam HR3 camera and AxioVision 4.8.2 software. Images were captured with a 100× objective and stored as 1030 × 1300 or 1388 × 1040 TIFF files at 150 pixels/in.

Cells were selected for scoring based on the morphology of the synaptonemal complex and the robustness of the MLH1 signal. We included cells for which the full set of 20 chromosomes was clearly condensed and indicative of the pachytene stage. Cells were omitted if defects in synapsis or damage from handling were obvious. We counted only MLH1 foci that appeared on autosomes, as recombination on the XY chromosome pair is not synchronous with the autosomes (Kauppi et al. 2012). We also omitted cells for which an MLH1 focus could not be detected on each autosome. The absence of a crossover from an autosome is rare and this omission minimized the influence of staining artifacts on MLH1 focus counts. For each cell counted, we also recorded an image-quality value based on the robustness of the MLH1 signal and the difficulty of scoring. This quality value ranged from 1 (weak MLH1 signal and difficult to score) to 6 (strong MLH1 signal and easy to score). For subsequent analyses, we included only cells with quality values of 2 or higher.

Genotyping

All mice were genotyped with the Mega Mouse Universal Genotyping Array (MegaMUGA) (Morgan et al. 2015). This Illumina Infinium array contains 77,808 markers covering the autosomes, sex chromosomes, and mitochondria. Liver tissue from killed mice was extracted and sent to GeneSeek (Neogene, Lincoln, NE) for genotyping on 16 96-well plates. Several steps were taken to control for errors and ensure data quality. This included the replication of parental WSB and GI samples across different plates of the array to account for plate extraction effects. After a comparison between plates and controls, markers with high rates of missing genotypes as well as mice with high rates of missing data were removed. A small number of individuals with many Mendelian inconsistencies were also removed. To simplify our analysis, we retained 11,833 informative single nucleotide polymorphisms (SNPs) that were fixed in GI mice and whose segregation patterns were consistent with a standard F₂ intercross.

Genetic distances were estimated from this marker information using the Lander–Green hidden Markov model (Lander and Green 1987) as implemented in the R/qtl est.map() function (Broman et al. 2003). We assumed a genotyping error rate of 0.2% and converted recombination fractions to map distances with the Carter–Falconer function (Carter and Falconer 1951). We also estimated the number of crossovers inherited by each F₂ individual by fitting this marker data to a hidden Markov model. This model removed implausibly close crossovers by including the probability of genotyping errors. Crossovers were counted on the underlying genotype, imputed with the Viterbi algorithm while assuming a genotyping error rate of 0.2%.

Quantitative trait loci analysis

We calculated the mean number of MLH1 foci among spermatocytes for each individual. The average individual was represented by counts from >20 spermatocytes; we omitted individuals with counts from <5 spermatocytes. We performed Haley–Knott regression to identify quantitative trait loci (QTL) for the mean MLH1 focus count using data from 240 F₂ individuals. Thresholds for significance were derived by randomly permuting phenotypes and repeating QTL scans (Churchill and Doerge 1994). Thresholds for genome-wide significance, α = 0.05, were established from 1000 permutation replicates.

We investigated the effects of cross direction by adding it as an interactive covariate and by performing separate analyses on each cross direction. The addition of cross direction as an interactive covariate is similar to performing the QTL analysis separately in each direction, but with constraints on residual variation based on the combined data (Broman and Sen 2009). We established significance thresholds for the covariate analysis by performing two sets of permutations. Using the same random seed, we performed 1000 permutations treating cross direction as an additive covariate, and 1000 permutations treating cross direction as an interactive covariate. When the analysis was split by cross direction, (♀GI × ♂WSB: 86 and ♀WSB × ♂GI: 154), we performed two separate sets of 1000 permutation replicates.

We fit several multiple QTL models to look for additional QTL and to test for interactions between them. We tested for pointwise interactions between detected QTL, calculating a P-value under the null hypothesis that LOD scores follow a χ² distribution. We also applied a forward/backward stepwise search algorithm with penalized LOD scores (Manichaikul et al. 2009). Penalties for additional QTL and interactions in this search were derived from 1000 permutations of a two-dimensional, two-QTL scan over the genome. Because of the computational costs of two-dimensional scans, the stepwise search and the permutation replicates were performed on a fixed 0.5-cM grid of pseudomarkers.

In addition to analyzing the mean number of MLH1 foci, we estimated and mapped QTL for variance in the number of MLH1 foci among spermatocytes from the same individual. Because of the greater difficulty in estimating variance, we omitted individuals with <15 counts for this analysis, leaving 214 F₂ individuals. As with the mean, we performed Haley–Knott regression and established thresholds from 1000 permutation replicates. However, mapping the estimated variance is likely insufficient to characterize variance QTL (vQTL) because of confounding between the mean and variance (Rönnegård and Valdar 2011; Geiler-Samerotte et al. 2013). For example, if there was a Poisson-like crossover number, variance in crossover number would be linearly proportional to its mean. An analysis that tries to identify QTL from raw values of variance will capture this mean-variance relationship. To decouple this relationship, we transformed the raw counts with a generalized linear model, fitting an appropriate power-variance function. This transformation preserves the mean for each individual, but removes the mean-variance relationship by explicitly parameterizing it. We sought a variance function of the form

$$V\left(Y_i\right)=\phi {\left[E\left(Y_i\right)\right]}^{\theta },$$

where E(Y_i) and V(Y_i) are the mean and variance for individual Y_i, φ is a constant dispersion parameter, and θ is the power parameter that characterizes the mean-variance relationship. We employed the eql() function from the R/EQL package to numerically fit a power-variance function that maximized the extended quasi-likelihood (Nelder and Pregibon 1987). The error variance from this model, estimated by the mean square residuals, represents each individual’s departure from the modeled mean-dependent variance. We performed Haley–Knott regression to map error variance and established genome-wide significance thresholds with 1000 permutation replicates.

Candidate genes and parental sequences

We overlapped multiple types of data to identify candidate genes under QTL peaks responsible for recombination rate variation. Studies of gene expression in mouse spermatocytes suggest that most transcripts involved in meiotic recombination are expressed before midpachytene, the point when transcription switches to spermiogenesis-related genes (Fallahi et al. 2010; Margolin et al. 2014; Ball et al. 2016; da Cruz et al. 2016). We merged two RNA-sequencing (RNA-seq) data sets that characterized temporal patterns of gene expression in mouse spermatocytes. From da Cruz et al. (2016), where RNA-seq was performed on spermatocytes sorted by flow cytometry, we included transcripts that were expressed in pachytene or leptotene/zygotene at a higher level than in secondary spermatocytes. From Ball et al. (2016), where RNA-seq and cytological data were integrated to stage transcripts, we included transcripts that were concordant with preleptotene, early leptotene, late leptotene/zygotene, and early pachytene. We omitted noncoding RNAs due to their poor annotation across databases.

Variants in the GI parents were identified by whole-genome sequencing at an average depth of 10×. Sequencing was performed on an Illumina HiSequation 2500 with 100-bp, paired-end reads. These reads were mapped with the Burrows–Wheeler Aligner (Li and Durbin 2009) to the C57BL/6 mouse reference genome. Variants were called with SAMtools 1.0 (Li et al. 2009) and compared to those found in the WSB/EiJ whole-genome sequence (Keane et al. 2011). We included variants that were 1-kb upstream and downstream of the transcription start and end sites. Transcription start and end sites were assigned from University of California, Santa Cruz annotations on the GRCm38/mm10 build. We also included genes that were associated with any gene ontology (GO) terms containing “recombination” (MouseMine; Motenko et al. 2015). From this list of 8501 genes related to meiotic recombination, we selected candidates that were within the 1.5 LOD intervals of our QTL peaks. To prioritize candidates, we employed the Ensembl Variant Effect Predictor (McLaren et al. 2016) and examined the predicted consequence of each variant.

Data availability

All genotype and phenotype data used in this study are available from the QTL Archive at the Jackson Laboratory, http://phenome.jax.org. File S1 contains Figures S1 and S2. File S2, File S3, File S4, and File S5 contain the complete list of candidate mutations under the QTL peaks on chromosomes 5, 6, 10, and 14 respectively. Sequence data for the two GI parents in this study can be accessed at the National Center for Biotechnology Information Sequence Read Archive under accessions SRX2339878 and SRX2339880.

Results

Genome-wide recombination rates

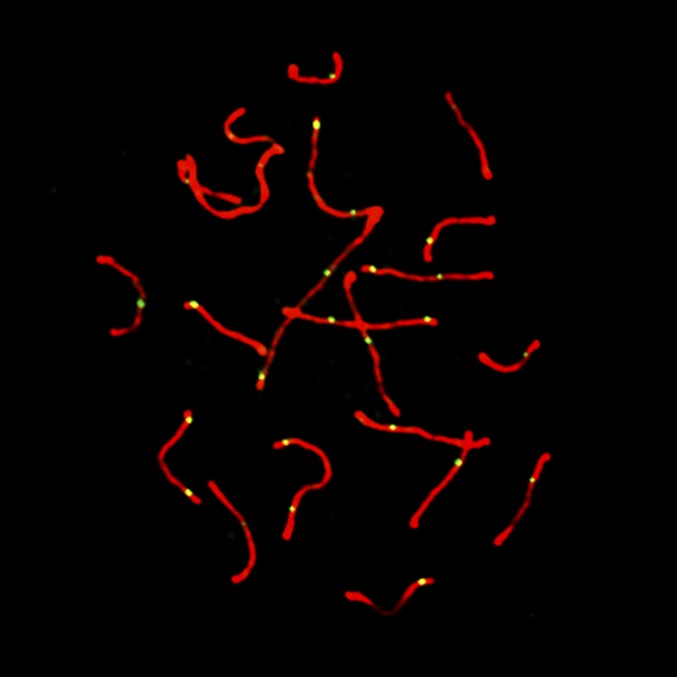
We used fluorescent immunocytology to measure recombination rates in individual mice from GI, WSB, and our F₂ intercross. We focused on spermatocytes in pachytene, the third stage of meiotic prophase during which crossovers become apparent and antibodies against the MLH1 protein localize to sites of crossover, forming punctate foci against the condensed chromosomes (Figure 1). By counting the number of MLH1 foci in multiple spermatocytes from each individual, we estimated the mean autosomal recombination rate in each of 240 F₂ animals.

Figure 1.

Representative image of pachytene spermatocyte. In red, fluorescent antibodies localizing to SYCP3 show the synaptonemal complex. In green, fluorescent antibodies localizing to MLH1 indicate sites of meiotic crossover.

While outbred GI mice were previously shown to have an average of two more crossovers per spermatocyte than WSB/EiJ (Dumont and Payseur 2011b), the derived GI line featured in our intercross exhibits only a modest elevation in recombination rate (GI mean = 22.63 foci, SE = 0.14; WSB/EiJ mean = 22.29, SE = 0.16; t-test P = 0.11). Notably, the distribution of F₂ crossover numbers shows transgressive segregation: a large number of individuals display recombination rates that lie outside the range of both parental means (Figure 2). This pattern is consistent with the presence of QTL alleles that have opposing effects within lines (Lynch and Walsh 1998; Rieseberg et al. 1999). We also detected a significant difference in F₂ recombination rates between cross directions. F₂’s with the GI grandmother produce spermatocytes with more crossovers (mean = 22.76, SE = 0.09) than F₂’s with the WSB/EiJ grandmother (mean = 22.47, SE: 0.06) (t-test P = 0.01).

Figure 2.

Distribution of the number of crossovers in F₂ animals. Plot points show the means for each F₂ individual, with error bars indicating ±1 SE. Also included are the parental means with ±1 SE for GI (in red), and for WSB/EiJ (in gray).

In addition to cytological characterization of recombination rates in the gametes of F₂’s, we tracked recombination events by analyzing F₂ genotypes at informative SNPs. The resulting estimates of recombination rate, from inference of crossovers under a hidden Markov model, differ in two important ways from our cytological estimates. First, F₂ genotypes track crossovers that occurred during gametogenesis in F₁’s. Since the parent from which a crossover originated is ambiguous, these estimated rates are sex-averaged. Second, interference-independent crossovers, a small proportion of crossovers that do not rely on the MLH1 pathway (Hollingsworth and Brill 2004; Holloway et al. 2008), are detected in the genotypic analysis. We estimated a mean of 25.79 (SE = 0.15) crossovers per F₁ individual from the genotypes of 793 F₂’s. We again noticed a significant difference in crossover number between cross directions. F₁’s with GI mothers produce spermatocytes with more crossovers (mean = 26.24; SE = 0.23) than F₁’s with WSB/EiJ mothers (mean = 25.46; SE = 0.19) (t-test P < 0.01).

QTL for genome-wide recombination rate evolution

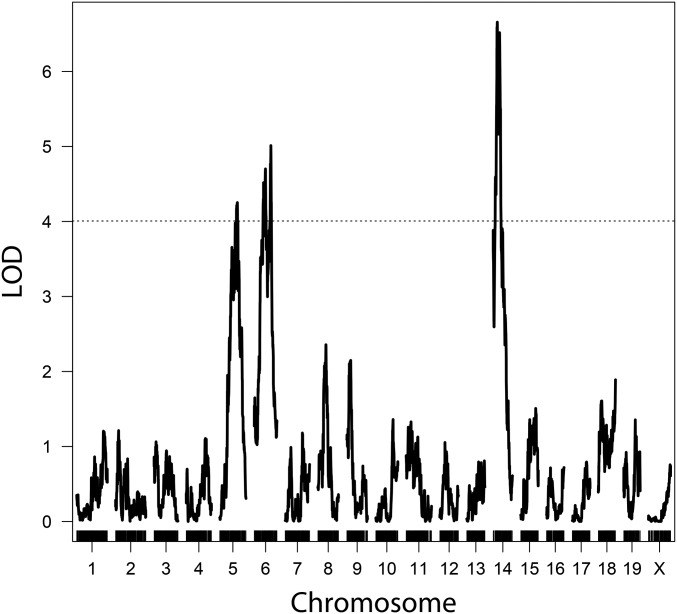
We detected three genomic regions linked to variation in mean MLH1 count (Figure 3). The strongest of these QTL, in terms of effect size and LOD score, localizes to the proximal end of chromosome 14. Genomic regions on chromosomes 5 and 6 also contribute to mean MLH1 count (Table 1). We repeated the scan for QTL with image quality (see Materials and Methods) and cross direction as additive covariates, but did not find a substantial difference in the results. Given the elevated crossover number detected in F₁ individuals with GI mothers from the genotypic analysis, we added cross direction as an interactive covariate in our QTL mapping analysis. We found evidence for an additional QTL on chromosome 10, whose effects significantly differ between the two cross directions (Figure S2 in File S1). These results suggest a QTL on chromosome 10 for mean crossover number that is either segregating within the GI line, interacting with loci segregating within the GI line, or interacting with a maternal effect. Model-based multiple QTL mapping (Broman and Speed 2002) did not identify new QTL or interactions between QTL, though QTL positions were refined (Table 1).

Figure 3.

LOD plot of QTL for mean MLH1 count. Mapping the mean number of MLH1 foci from spermatocytes of each F₂ animal revealed three QTL on chromosomes 5, 6, and 14. Genome-wide significance threshold, α = 0.05, shown as dashed line.

Table 1. QTL for the genome-wide recombination rate.

Chr.	Single QTL model		Multiple QTL model		Pos.a (Mb)	1.5 LOD intervalb (Mb)	Var. (%)c	Estimated phenotypic means (SE)
	Pos. (cM)	LOD	Pos. (cM)	LOD				GG	GW	WW
5	53.5	4.39	36.9	4.61	83.8	74.3–132.5	6.1	22.91 (0.11)	22.58 (0.07)	22.30 (0.10)
6	50.3	5.12	29.8	4.50	81.4	73.5–134.7	5.9	22.88 (0.10)	22.55 (0.07)	22.23 (0.11)
14	12.5	6.66	20.0	7.57	56.5	28.2–60.9	10.4	22.12 (0.11)	22.55 (0.07)	22.90 (0.09)
10d	55.1	4.54	58.0	5.12	122.8	114.5–123.8	6.9	22.68 (0.19)	23.06 (0.12)	22.21 (0.16)
								22.33 (0.13)	22.45 (0.09)	22.62 (0.12)

Chr., chromosome; pos., position; var., variance; G, Gough; W, WSB/EiJ.

^aEstimated from position of LOD peak in a multiple QTL model.

^bEstimated from single QTL model (a more conservative estimate).

^cPercentage of phenotypic variance among F₂’s explained.

^dSingle QTL model position and LOD from G×W cross alone; estimated phenotypic means for the G×W cross (first row) and W×G cross (second row).

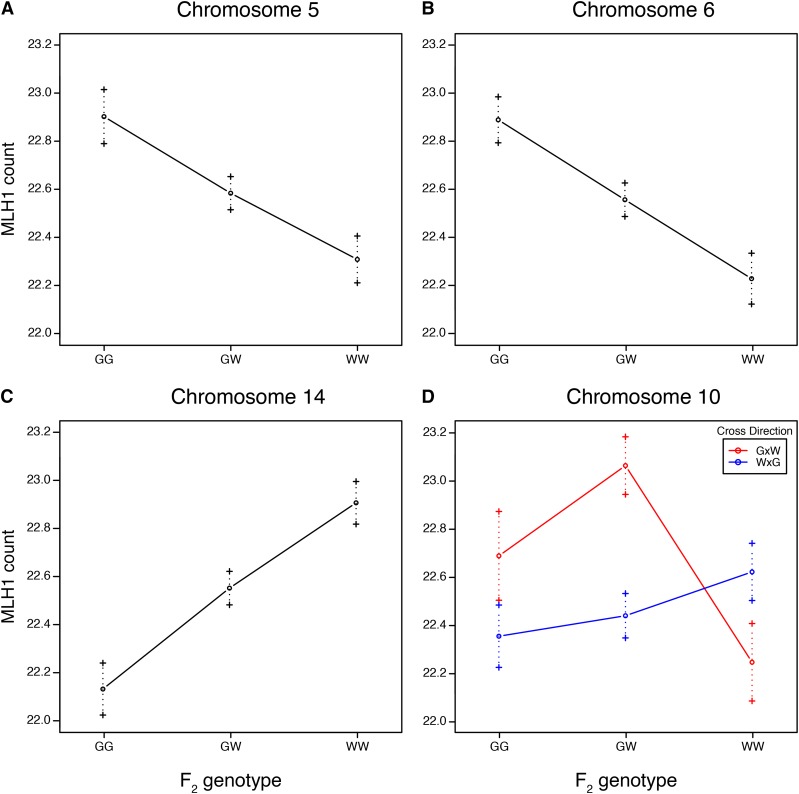
As predicted from the transgressive distribution of mean crossover number, we found a QTL with phenotypic effects opposite of the parental-trait difference. The GI allele at the QTL on chromosome 14 confers a reduction in mean crossover number. In contrast, GI alleles at the QTL on chromosomes 5, 6, and 10 are associated with increases in mean crossover number. Alleles at three QTL act additively; the QTL on chromosome 10 shows signs of overdominance (Figure 4 and Table 1).

Figure 4.

Estimated effects by genotype for genome-wide recombination rate QTL on (A) chromosome 5, (B) chromosome 6, (C) chromosome 14, and (D) chromosome 10. Error bars show ±1 SE. G, Gough; W, WSB/EiJ.

Together, detected QTL explain an estimated 33% of the variance in mean crossover number among F₂’s. While this percentage is almost certainly inflated by the Beavis effect (Beavis 1994; Xu 2003), the detected QTL may explain a majority of the genetic variance. The narrow-sense heritability of recombination rate has been estimated at 0.46 for mice (Dumont et al. 2009).

QTL for within-animal variance in the genome-wide recombination rate

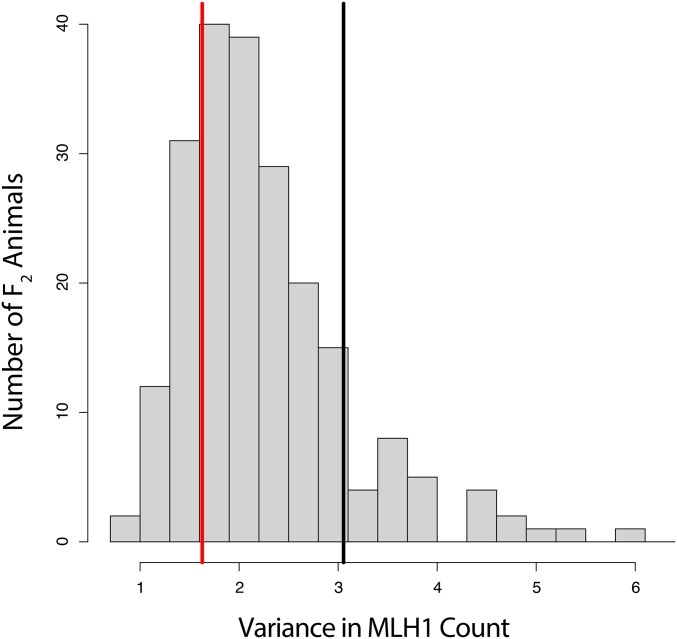
The distribution of within-animal variances in crossover number is shown in Figure 5. GI mice display significantly lower variance in crossover number among spermatocytes than WSB/EiJ (Levene’s test, P < 0.005), and the center of the F₂ distribution is closer to the GI value.

Figure 5.

Distribution of within-animal variance for MLH1 count among spermatocytes. Within-animal variances of the parental strains are indicated by the vertical lines in red for GI and black for WSB/EiJ.

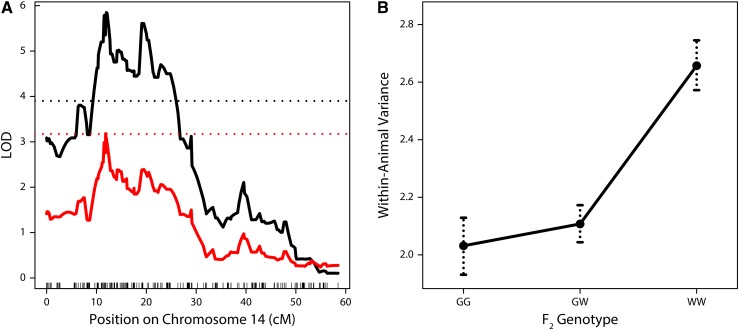
We detected a single region on chromosome 14 that confers differences in within-animal variance (peak = 33.8 Mb, LOD = 5.85; Figure 6A). The 1.5 LOD interval of this QTL (29.1–68.4 Mb) overlaps substantially with the previously identified QTL on this chromosome for mean crossover number.

Figure 6.

(A) LOD plots showing QTL for within-animal variance in MLH1 count on chromosome 14. In black, raw variance is being mapped and an α = 0.05 genome-wide significance threshold is shown as a dashed line. In red, the transformed error variance is being mapped and an α = 0.20 genome-wide significance threshold is shown as a dashed line. (B) Estimated effects on within-animal variance by genotype for the QTL on chromosome 14.

The distribution of crossover number among F₂ individuals is highly heteroscedastic: the variance is positively correlated with the mean (Pearson’s r = 0.50). We mapped QTL for MLH1 count variance within individuals, applying an approach to deconvolve the mean-variance relationship (see Materials and Methods). Using this approach, the LOD score for the QTL on chromosome 14 for variance dropped but remained suggestive, reaching the 20% threshold for genome-wide significance (peak = 33.3 Mb, LOD = 3.18; Figure 6A). From these results, it is difficult to ascertain whether the QTL on chromosome 14 has an effect on variance independent of its effect on the mean. Nevertheless, this QTL explains an estimated 10% of the variation in within-animal crossover-number variance and the GI allele at this locus dominantly reduces this variance (Figure 6B). The effect of this GI allele could partially account for the shift in the F₂ distribution of crossover number variance toward the GI parent.

Candidate genes for genome-wide recombination rate evolution

Using knowledge of temporal expression patterns and GO terms (see Materials and Methods), we identified a total of 590 candidate genes under the detected QTL peaks on chromosomes 5, 6, 10, and 14. To prioritize this list, we examined the SNP and short indel differences between the GI and WSB/EiJ lines for the candidate genes. The complete list of candidate genes and their associated variants can be found in File S1, File S2, File S3, and File S4. Here, we focus on the most compelling candidates: those genes with a recombination-associated GO term that contain a variant conferring a change to either a nonsynonymous site or a transcription factor binding site. We identified strong candidate genes for QTL on chromosomes 5, 6, and 14 (Table 2), including DNA helicases that mediate homologous recombination (Bugreev et al. 2007; De Muyt et al. 2012) and E3 ligases thought to regulate the crossover/noncrossover decision (Reynolds et al. 2013; Qiao et al. 2014).

Table 2. Candidate genes and mutations for QTL.

Gene symbol	Chr.	Positiona	Baseb change	AA change	Zygosity in GI parents	Variant effectc
Helq	5	100,768,573	A → G	S → P	Homo; Homo	SIFT: 1
Helq	5	100,770,406	T → C	I → V	Homo; Homo	SIFT: 0.63–1
Helq	5	100,778,820	T → C	N → S	Homo; Homo	SIFT: 0.57–0.6
Helq	5	100,779,195	A → T	V → A	Homo; Homo	SIFT: 1
Helq	5	100,783,056	T → G	E → D	Homo; Homo	SIFT: 1
Helq	5	100,783,139	T → C	I → V	Homo; Homo	SIFT: 0.36–0.43
Helq	5	100,785,420	C → T	G → E	Homo; Homo	SIFT: 0.11–0.14
Helq	5	100,791,815	T → C	S → G	Homo; Homo	SIFT: 1
Helq	5	100,794,483	Indel	—	Homo; Homo	Low info TF site
Helq	5	100,798,458	T → G	T → P	Homo; Homo	SIFT: 0.1–0.33
Hfm1	5	106,853,422	T → C	—	Homo; Homo	Low info TF site
Hfm1	5	106,871,789	T → G	Y → S	Homo; Homo	SIFT: 0.04
Hfm1	5	106,904,814	T → C	T → A	Homo; Homo	SIFT: 0.74
Hfm1	5	106,911,653	A → G	C → R	Homo; Homo	SIFT: 0.08
Rnf212	5	108,729,476	T → C	I → V	Homo; Homo	SIFT: 0.49
Rnf212	5	108,744,012	C → T	—	Homo; Het	Low info TF site
Rnf212	5	108,770,595	C → T	V → I	Homo; Het	SIFT: 0.05
Rad18	6	112,649,678	A → G	L → S	Homo; Homo	SIFT: 0.02–0.1
Rad18	6	112,649,714	A → G	L → S	Homo; Homo	SIFT: 0.07–0.11
Rad18	6	112,664,108	G → A	R → W	Homo; Homo	SIFT: 0.01–0.03
Rad51ap1	6	126,928,176	T → C	H → R	Homo; Homo	SIFT: 0.79–0.84
Rad51ap1	6	126,928,188	C → T	G → D	Homo; Homo	SIFT: 0.6–0.62
Rad51ap1	6	126,928,206	T → C	E → G	Homo; Homo	SIFT: 0.22
Rad51ap1	6	126,939,497	G → A	T → I	Homo; Homo	SIFT: 0.17–0.22
Ccnb1ip1	14	50,791,413	T → C	—	Het; Het	Low info TF site
Tep1	14	50,824,479	G → A	—	Het; Het	High info TF site
Tep1	14	50,824,758	T → G	N → H	Het; Het	SIFT: 0.2
Tep1	14	50,837,421	G → A	R → C	Het; Het	SIFT: 0.16
Tep1	14	50,837,421	G → A	—	Het; Het	Low info TF site
Tep1	14	50,839,000	C → T	G → D	Homo; Het	SIFT: 0.4
Tep1	14	50,853,017	T → C	D → G	Homo; Homo	SIFT: 0.09
Tep1	14	50,855,613	C → T	V → I	Homo; Homo	SIFT: 1
Tep1	14	50,860,668	T → C	S → G	Homo; Homo	SIFT: 0.02
Tep1	14	50,863,639	T → G	I → L	Homo; Homo	SIFT: 0
Tep1	14	50,868,186	A → G	S → P	Homo; Homo	SIFT: 0.29
Tep1	14	50,868,261	G → T	H → N	Homo; Homo	SIFT: 0.05
Apex1	14	50,925,294	G → A	A → T	Het; Het	SIFT: 0.14–0.6
Rec8	14	55,625,075	C → T	A → V	Het; Het	SIFT: 0.31

Homo, homozygous; TF, transcription factor; het, heterozygous.

^aPosition in GRCm38/mm10.

^bBase change and AA change in GI with WSB/EiJ as reference.

^cPredicted variant effect for nonsynonymous changes as SIFT score 0.0 (deleterious) to 1.0 (tolerated) (Kumar et al. 2009); for variants at predicted TF binding sites, variants are classified as being in high or low information regions.

Discussion

While most genetic mapping studies feature parental lines with notable differences between trait means, the absence of a large difference does not rule out the possibility of historic divergence. In this study, the genome-wide recombination rate showed transgressive segregation and was linked to multiple QTL. Not only were QTL alleles with antagonistic effects harbored in the same line, but the allele with the strongest effect opposed the phenotypic pattern seen in the parents. Transgressive segregation may be a relatively common phenomenon, especially in crosses where the difference between parental trait means is small (Lynch and Walsh 1998; Rieseberg et al. 2003). What is remarkable is the observation of transgressive segregation and complementary QTL effects in all three studies that have mapped QTL for genome-wide recombination rate variation in mice (Murdoch et al. 2010; Dumont and Payseur 2011a). Furthermore, in both cases in which only wild-derived mice were used (this study and Dumont and Payseur 2011a), the leading QTL displayed antagonistic effects. This finding suggests that an antagonistic genetic architecture may be a common feature of genome-wide recombination rate evolution (at least in mice).

The distribution of QTL effects can be used to draw inferences about the role of natural selection (Coyne 1996; True et al. 1997; Orr 1998). When the direction of QTL effects consistently matches the direction of parental phenotypic differences, a history of directional selection may be hypothesized. The repeated finding of antagonistic loci therefore argues against scenarios that invoke consistent directional selection on the genome-wide recombination rate.

The proposal that recombination rate may evolve in response to rapid shifts in the selective optima of multiple traits, as in the case of domestication (Burt and Bell 1987; Ross-Ibarra 2004), has previously been challenged by examples from mammals and insects (Wilfert et al. 2007; Muñoz-Fuentes et al. 2015). Alternative explanations include genetic drift, stabilizing selection, and fluctuating selection. From a molecular genetics standpoint, the case for boundaries on genome-wide recombination rate evolution seems strong (Ritz et al. 2017). Meiotic requirements appear to set a lower limit based on the increased risk of aneuploidy in crossover-deficient meiotic cells (Roeder 1997; Hassold and Hunt 2001), and an upper limit based on the presumed risks to genome integrity from an excess of crossovers (Inoue and Lupski 2002; Coop and Przeworski 2007). Perhaps recombination rate evolution is primarily governed by drift (with no optimum value) within these bounds (Dumont and Payseur 2008). The possibility that the direction of selection on recombination rate has shifted over time is less explored. Meiotic constraints may evolve as chromosome structure changes, shifting the acceptable bounds for genome-wide recombination rate (Borodin et al. 2008; Dumont 2017). Whether episodic shifts in selection could explain the repeated observation of antagonistic loci for recombination rate in mice would depend on their timing and frequency.

Our sample size was similar to those in other genetic mapping studies of genome-wide recombination rate variation in mice, enabling straightforward comparisons between the results. We detected fewer QTL, an outcome potentially explained by the much higher phenotypic divergence between the lines used in the other studies (both of which involved intersubspecific crosses; Murdoch et al. 2010; Dumont and Payseur 2011a). The absence of X-linked QTL in GI × WSB/EiJ is also notable because the X chromosome has been repeatedly linked to genome-wide recombination rate divergence between lines from different mouse subspecies (Murdoch et al. 2010; Dumont and Payseur 2011a; Balcova et al. 2016). The QTL we discovered on chromosome 14 lies near a QTL found in the C57BL/6J × M. m. castaneus cross (Murdoch et al. 2010). Intriguingly, this QTL showed antagonistic effects in both crosses. This coincidence raises the possibility that a shared locus reduces recombination rate in GI and C57BL/6J. The lack of overlapping QTL with the wild-derived M. m. musculus × M. m. castaneus cross in Dumont and Payseur (2011a) suggests that different loci are responsible for recombination rate evolution within and between subspecies. Nevertheless, our list of candidate genes supports the notion that the number of loci contributing to natural variation in recombination rate is limited. Our most promising candidates include Rnf212, Rec8, and Ccnb1ip1 (Hei10); genes that have been linked to variation in recombination rate within multiple mammalian species (Kong et al. 2008, 2014; Sandor et al. 2012; Qiao et al. 2014; Ma et al. 2015; Johnston et al. 2016).

Our observation of significantly more crossovers among F₂ mice from the cross direction with GI mothers can mostly be explained by the QTL on chromosome 10. Since the GI parents were not completely inbred, our observation that this QTL confers direction-specific effects suggests it segregates within the GI line. The antagonistic allele on chromosome 14 may actually be polymorphic within GI mice as well, since higher genome-wide recombination rates were observed in outbred mice from the island (Dumont and Payseur 2011b).

Our experimental design provided a rare opportunity to characterize the genetics of differences in within-animal recombination rate variance. The identification of QTL affecting phenotypic variation, or vQTL, in multicellular organisms typically requires a comparison of variance between different genotypic groupings of individuals. This is often achieved by measuring the variance among individuals from different inbred lines (Mackay and Lyman 2005; Shen et al. 2012; Ayroles et al. 2015). Unlike most quantitative traits, biological replicates for the number of crossovers per spermatocyte can be collected from the same individual using the MLH1 approach. We found significantly lower variation in genome-wide recombination rate in GI compared to WSB/EiJ. We also mapped a QTL that reduces crossover number variance in GI mice to chromosome 14. Genetically controlled reduction of phenotypic variability may increase developmental consistency and robustness to environmental fluctuations (Waddington 1942; Rutherford and Lindquist 1998; Mackay and Lyman 2005; Levy and Siegal 2008). Alternatively, increased phenotypic variability can be advantageous and may contribute to adaptation (Losick and Desplan 2008; Beaumont et al. 2009; Eldar and Elowitz 2010). Although QTL that control variance have been previously identified for several traits (Shen et al. 2012; Hulse and Cai 2013; Mulder et al. 2016), ours is the first report of such a QTL for recombination rate. The causative variant(s) underlying this QTL might act by modulating the stringency of meiotic checkpoints, which ensure consistency among gametes (Hochwagen and Amon 2006; Li and Schimenti 2007; Jaramillo-Lambert et al. 2010; Kauppi et al. 2013). However, patterns of natural variation in the consistency of recombination rate among gametes are poorly understood. Our results, along with the abundance of meiotic surveillance mechanisms, raise the prospect that gamete consistency plays a role in the evolution of recombination rate.

Supplementary Material

Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.117.202382/-/DC1.