A Unified Characterization of Population Structure and Relatedness

Abstract

Many population genetic activities, ranging from evolutionary studies to association mapping, to forensic identification, rely on appropriate estimates of population structure or relatedness. All applications require recognition that quantities with an underlying meaning of allelic dependence are not defined in an absolute sense, but instead are made “relative to” some set of alleles other than the target set. The 1984 Weir and Cockerham $F_{\mathrm{ST}}$ estimate made explicit that the reference set of alleles was across populations, whereas standard kinship estimates do not make the reference explicit. Weir and Cockerham stated that their $F_{\mathrm{ST}}$ estimates were for independent populations, and standard kinship estimates have an implicit assumption that pairs of individuals in a study sample, other than the target pair, are unrelated or are not inbred. However, populations lose independence when there is migration between them, and dependencies between pairs of individuals in a population exist for more than one target pair. We have therefore recast our treatments of population structure, relatedness, and inbreeding to make explicit that the parameters of interest involve the differences in degrees of allelic dependence between the target and the reference sets of alleles, and so can be negative. We take the reference set to be the population from which study individuals have been sampled. We provide simple moment estimates of these parameters, phrased in terms of allelic matching within and between individuals for relatedness and inbreeding, or within and between populations for population structure. A multi-level hierarchy of alleles within individuals, alleles between individuals within populations, and alleles between populations, allows a unified treatment of relatedness and population structure. We expect our new measures to have a wide range of applications, but we note that their estimates are sensitive to rare or private variants: some population-characterization applications suggest exploiting those sensitivities, whereas estimation of relatedness may best use all genetic markers without filtering on minor allele frequency.

WE offer here a unified treatment of relatedness and population structure with an underlying framework of allelic dependence, where the degree of dependence can be quantified as the probability the alleles are identical by descent (ibd) or as the correlation of allelic-state indicators. We follow Thompson (2013) in regarding ibd for a set of alleles as being relative to some other, reference, set: “There is no absolute measure of ibd: ibd is always relative to some reference population.” In other words, ibd implies a reference point, and ibd status for different alleles at this point is often implicitly assumed to be zero. The need for a reference set for allelic-state correlations was made explicitly by Wright (1951): “the correlation between random gametes, drawn from the same subpopulation, relative to the total, is given by …” (emphasis added), and for inbreeding by Wright (1943): “The inbreeding coefficient is zero relative to the unit groups, $F_i$ relative to the intermediate groups and $F_t$ relative to the total.”

A function of allelic dependence of particular interest to us is $F_{\mathrm{ST}},$ which we will show below can be expressed as the probability of ibd of pairs of alleles within populations relative to that for pairs of alleles from different populations. The uses of estimates of this quantity are widespread, and here we note, for instance, a recent discussion by McTavish and Hillis (2015) who used “pairwise $F_{\mathrm{ST}}$ for all pairs of populations using Weir and Cockerham’s method.” We suggest that a more informative analysis may result from our population-specific $F_{\mathrm{ST}}$ estimates (Weir and Hill 2002; Weir et al. 2005; Browning and Weir 2010). Other authors (e.g., Balding and Nichols 1995; Beaumont and Balding 2004; Shriver et al. 2004; Gaggiotti and Foll 2010) have also discussed the advantages of working with population-specific $F_{\mathrm{ST}}$ values instead of single values for a set of populations, or of values for each pair of populations, and our recognition of allele frequency correlations among populations extends their work. Interpopulation correlations have also been considered by Fu et al. (2003), and in the Bayesian treatments of Fu et al. (2005), Song et al. (2006), Karhunen and Ovaskainen (2012) and Günther and Coop (2013). Here we allow for correlations in providing explicit moment estimates that apply to both populations and individuals.

The usual global $F_{\mathrm{ST}}$ measure can be regarded as an unweighted average of population-specific values, and, because it is an average, it masks the variation among populations that can indicate the effects of past selection (Beaumont and Balding 2004; Weir et al. 2005). The global measure can diminish signals of population history, and this diminution has become more pronounced as genetic marker data have become richer, and real differences among populations have become more evident.

As Astle and Balding (2009) noted “population structure and [cryptic] relatedness are different aspects of a single confounder: the unobserved pedigree defining the (often distant) relationships among the study subjects.” A similar point was made by Kang et al. (2010): “The presence of related individuals within a study sample results in sample structure, a term that encompasses population stratification and hidden relatedness.” Our goal is to provide a unified approach to characterizing population structure and individual relatedness and inbreeding, in terms of both the underlying parameters and the methods of estimation. By working with proportions of pairs of alleles that match, or are the same type, we can give a single estimator for $F_{\mathrm{ST}},$ where the pairs are from the same or different populations, and for inbreeding or coancestry, where the pairs are from the target individual(s) or from all pairs of individuals in a study. Measures of population structure are seen to be averages of coancestry measures for individuals within those populations as has been noted by Karhunen and Ovaskainen (2012).

Ibd refers to the history of pairs of alleles, and a consideration of historical “genetic sampling” (Weir 1996) shows that ibd measures allow quantification of the variance of allele frequencies among evolutionary replicates of these histories. Data from a single population or a single individual have no information about this variance, and so do not allow estimation of ibd probabilities. We might regard multiple loci as providing replication of the genetic sampling process, or we might collect data from multiple populations. An exception is when allele frequencies and ibd status in the reference population are assumed known, as is implied for standard methods for estimating relatedness and inbreeding (e.g., Ritland 1996; Purcell et al. 2007; Yang et al. 2011; Wang 2014) or in forensic science if the frequencies are taken from databases (e.g., Balding 2003). If, instead, estimation methods make use of frequencies from a sample of individuals, they are providing estimates of the inbreeding or relatedness ibd measures relative to those measures for all individuals in the sample. This point was also made by Yu et al. (2006), who spoke of “adjusting the probability of identity by state between two individuals with the average probability of identity by state between random individuals” in order to address ibd. Existing relatedness estimation methods that do not use allele frequencies (e.g., KING-robust, Manichaikul et al. 2010) estimate ibd between individuals (coancestry) relative to that within individuals (inbreeding).

For both population structure and relatedness, we propose the use of allelic matching proportions within and between individuals or populations in order to characterize ibd for an individual or a population relative to a reference set of ibd values. We use allele matching, equivalent to homozygosity and complementary to heterozygosity as used by Nei (1973), rather than components of variance (Weir and Cockerham 1984: hereafter WC84). Although our matching proportions can be translated into the sums of squares used by WC84 we believe they may have more intuitive appeal. Our present treatment also differs from that in WC84 by using unweighted averages of statistics over populations instead of the weighted averages that were more appropriate for the WC84 model of independent populations. We return to this aspect in the Discussion.

The size of current genetic studies requires computationally feasible methods for estimating relatedness between all pairs of individuals, potentially 5 billion pairs for the TOPMed project (http://www.nhlbiwgs.org). The scale of the task may well rule out maximum likelihood approaches (e.g., Thompson 1975; Ritland 1996; Milligan 2003) and Bayesian methods (e.g., Gaggiotti and Foll 2010), and Karhunen and Ovaskainen (2012) have reviewed the challenges of selecting the allele frequency distributions needed for likelihood- and Bayesian-based methods. Moment estimates seem still to be relevant, therefore, and will be presented here.

Materials and Methods

Allele-pair dependencies

Our discussion involves two dualities: the dependencies between pairs of alleles expressed either as correlations or as probabilities of ibd; and the identification of allele pairs either by the individuals or the populations from which they are drawn. Although we generally sample individuals and score genotypes, we begin with allelic descriptors: for a locus of interest, and allele A identified by individual and population (see Table 1), we assign the allelic indicator $x_u$ the value 1 if A is of type u, and the value 0 if it is of not of type u. We will assume alleles within diploids are defined unambiguously, although we have previously (Hill and Weir 2004) discussed the situation when they are not, as have others (e.g., Holsinger et al. 2002). We write the dosage $X_u$ of allele u for a diploid individual as the sum of the x’s for the two alleles carried by the individual, and for haploids the dosage is $X_u=x_u.$ For SNPs, we write X as the dosage of the reference allele.

Table 1. Notation.

Quantity	Notation
Allele	$A_{jk}^i$ for allele $k\in \left\{1,2\right\},$ individual $j\in \left\{1,2,\dots .n_i\right\},$ population $i\in \left\{1,2,\dots r\right\}$
Allelic indicator	$x_{jku}^i$ for allele $A_{jk}^i$ being of type u
Allele frequency	${\pi }_u$ expected value of $x_{jku}^i$ for all $i,j,k$
	$p_{iu}$ actual frequency for allele type u in population i
	${\stackrel{\sim }{p}}_{iu}$ observed frequency for allele type u in sample from population i
Theta	${\theta }_{jk,j^{\prime }{k}^{\prime }}^{i{i}^{\prime }}$ is probability of ibd between allele k in individual j from population i and allele $k^{\prime }$ in individual $j^{\prime }$ from population $i^{\prime }$
Inbreeding coefficient	$F_j^i$ is the ibd probability for the two alleles for individual j in population i: $F_j^i=\frac{1}{2}{\displaystyle {\sum }_{k=1}^2{\displaystyle {\sum }_{k^{\prime }=1,k^{\prime }\ne k}^2{\theta }_{jk,j{k}^{\prime }}^{ii}}}$
Coancestry coefficient	Coancestry ${\theta }_{j{j}^{\prime }}^i$ is the ibd probability for a pair of alleles drawn from individuals $j,j^{\prime }$ in population i: ${\theta }_{j{j}^{\prime }}^i=\frac{1}{4}{\displaystyle {\sum }_{k=1}^2{\displaystyle {\sum }_{k^{\prime }=1}^2{\theta }_{jk,j^{\prime }{k}^{\prime }}^{ii}}}.$ ${\theta }_S^i$ is the average of ${\theta }_{j{j}^{\prime }}^i$ for all pairs $j,j^{\prime }.$ ${\theta }^S$ is the average over populations of ${\theta }_S^i.$ For any two distinct alleles drawn from population i, the ibd probability is ${\theta }_W^i.$ The average over populations of ${\theta }_W^i$ is ${\theta }^W.$ ${\theta }^B$ is the average of ibd probabilities for alleles from different populations
Relative inbreeding	The relative inbreeding coefficient for individual j in population i is ${\beta }_j^i=\left(F_j^i-{\theta }_R\right)/\left(1-{\theta }_R\right):$ reference ${\theta }_R$ is ${\theta }_S^i$ or ${\theta }^B$
Relative coancestry	The relative coancestry coefficient for individuals $j,j^{\prime }$ in population i is ${\beta }_{j{j}^{\prime }}^i=\left({\theta }_{j{j}^{\prime }}^i-{\theta }_R\right)/\left(1-{\theta }_R\right):$ reference ${\theta }_R$ is ${\theta }_S^i$ or ${\theta }^B$
Population-specific $F_{\mathrm{ST}}$	${\beta }_{\mathrm{WT}}^i=\left({\theta }_W^i-{\theta }^B\right)/\left(1-{\theta }^B\right)$ is probability two alleles drawn from population i are ibd, relative to the probability an allele drawn from one population is ibd to an allele drawn from another population. ${\beta }_{\mathrm{ST}}^i=\left({\theta }_S^i-{\theta }^B\right)/\left(1-{\theta }^B\right)$ is for alleles drawn from two individuals in population i

We stipulate that the expected value of $x_u,$ where expectation is over replicates of the evolutionary history of that allele, is ${\pi }_u,$ the probability a random allele is of type u, regardless of which individual carries that allele or which population contains that individual. The essence of our treatment rests on the expectation of the products of two x_u’s, or the probabilities that pairs of alleles are both of type u. For alleles A and $A^{\prime },$ with indicators $x_u$ and ${x^{\prime }}_u^{},$ we stipulate the expectation to be

$$\mathrm{ℰ}\left(x_u{x^{\prime }}_u^{}\right)={\pi }_u^2+{\pi }_u\left(1-{\pi }_u\right)\theta .$$ (1)

As $\mathrm{ℰ}\left(x_u^2\right)$ is also ${\pi }_u,$ we see that the variance of $x_u$ is ${\pi }_u\left(1-{\pi }_u\right)$ for any allele at the locus of interest. We also see, from Equation 1, that the covariance of $x_u$ and ${x^{\prime }}_u^{}$ is ${\pi }_u\left(1-{\pi }_u\right)\theta ,$ and it follows that the quantity θ is the correlation of the indicators for pairs of alleles as in the writing of Cockerham (e.g., Cockerham 1969). There is no requirement in Equation 1 for θ to be positive, and, for example, negative values are expected for the two alleles carried by one individual in populations for which there is avoidance of mating between relatives. We add individual and population identifiers to θ in Table 1.

Following the work of Malécot (see review by Epperson 1999), we can also interpret Equation 1 with θ defined as the probability that alleles $A,A^{\prime }$ are ibd. It is then the case that θ cannot be negative. Either of the two alleles has probability ${\pi }_u$ of being of type u. The other allele has probability θ of being ibd to the first, and so is also of type u, and it has probability $\left(1-\theta \right)$ of not being ibd to the first, and so is of type u with probability ${\pi }_u.$ If we follow Thompson (2013), and regard ibd alleles as those that descend from a single allele in a reference population, the allele probability ${\pi }_u$ refers to the reference population. We distinguish the expected value ${\pi }_u$ from the actual allele frequency $p_u$ in a population, and from the frequency ${\stackrel{\sim }{p}}_u$ in a sample from the population, as listed in Table 1.

We will phrase much of our subsequent discussion in terms of ibd probabilities, but will return to the allelic indicator correlations on occasion. Our estimation procedures rest on Equation 1 and so will hold for both interpretations. We turn first, however, to some predictions of ibd probabilities.

Predicted ibd probabilities

Individuals:

For a single diploid individual j, the inbreeding coefficient $F_j$ is the probability its two alleles are ibd. The coancestry, or kinship, coefficient ${\theta }_{j{j}^{\prime }}$ for individuals $j,j\prime$ is defined here as the average of the four ibd probabilities for one allele from each individual. It follows that the coancestry of individual j with itself is $\left(1+F_j\right)/2.$ Generally, however, we will follow WC84 and reserve the term coancestry for distinct individuals. For haploids, inbreeding coefficients are not needed, and kinship is the ibd probability of the allele in individual j with the allele in individual $j\prime .$ We will have occasion to use ${\theta }_S,$ the average over pairs of individuals of the coancestries for (samples from) a population. In Table 1, we have added superscripts to indicate the populations from which the individuals are drawn.

If diploid individual J is ancestral to both j and $j\prime ,$ and if there are n individuals in the pedigree path joining j to $j\prime$ through J, including j and $j\prime ,$ then ${\theta }_{jj\prime }={\displaystyle \sum {\left(0.5\right)}^n\left(1+F_J\right)},$ where $F_J$ is the inbreeding coefficient of J, and the sum is over all ancestors J and all paths joining j to $j\prime$ through J (Wright 1922). The coancestry ${\theta }_{jj\prime }$ is also the inbreeding coefficient for an individual with parents $j,j\prime .$ If ancestor J is further back in time than the reference time, then it does not contribute to the relatedness of individuals j and $j^{\prime }.$

Populations:

For a single population, the average coancestry coefficient ${\theta }_S$ will refer to pairs of distinct alleles, one in each of two distinct individuals. For populations in which there is random union of gametes $F_j={\theta }_{j{j}^{\prime }}$ for all j and $j^{\prime }\ne j$ and θ will refer to a random pair of distinct alleles in the population regardless of the individuals in which they are carried. If we wish to distinguish this allele-based quantity from genotype-based ${\theta }_S,$ as we do below, then we write it as ${\theta }_W.$ In Table 1, we show superscripts to denote population, and we adopt that convention now to describe the accrual of ibd in random-mating population i with constant population size $N_i.$ Without mutation, ${\theta }^i\equiv {\theta }_W^i$ values for t discrete generations after the time when the population had ibd probability ${\theta }^i\left(0\right),$ satisfy

$${\theta }^i\left(t\right)=1-\left[1-{\theta }^i\left(0\right)\right]{\left(1-\frac{1}{2N_i}\right)}^t.$$ (2)

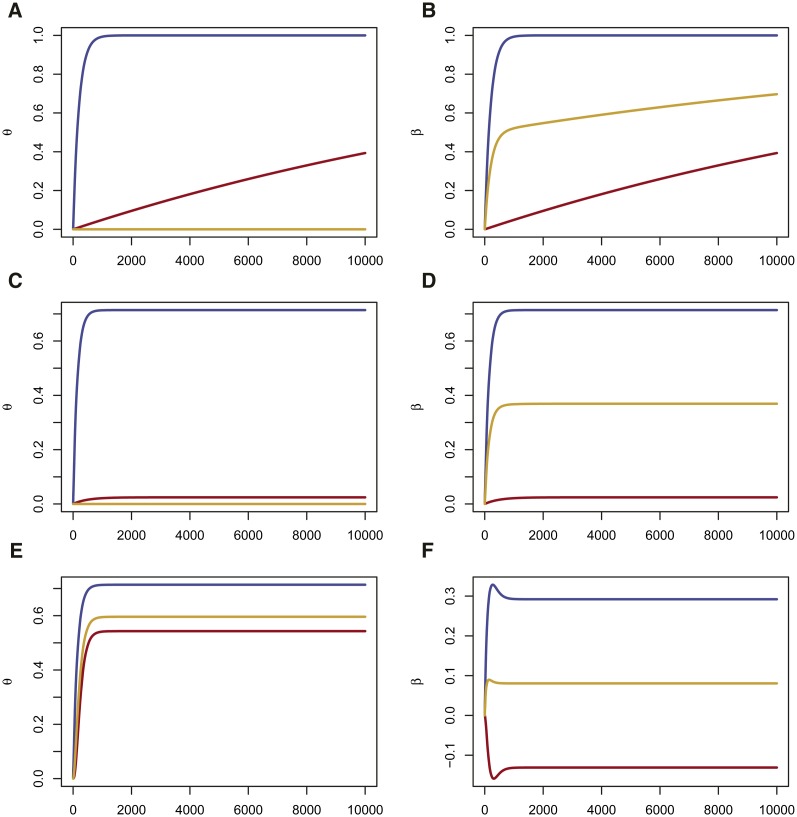
This result was discussed by Wright (1931), although not quite in this form, with ${\theta }^i\left(0\right)$ shown explicitly. We plot θ from Equation 2 in the first row of Figure 1.

Figure 1.

Effects of Drift, Mutation and Migration on θ and β as a function of generation. For all panels, $N_1=10,000\hspace{0.17em}\text{and}\hspace{0.17em}{N}_2=100$. Left column (A, C, E) ${\theta }^1$ in red, ${\theta }^2$ in blue, ${\theta }^{12}$ in orange. Right column (B, D, F) ${\beta }_{\mathrm{WT}}^1$ in red, ${\beta }_{\mathrm{WT}}^2$ in blue, ${\beta }_{\mathrm{WT}}$ in orange. (A, B) Drift only (no mutation nor migration). ${\theta }^1,{\theta }^2$ and β tend to 1, ${\theta }^{12}=\mathrm{0.000.}$ (C, D) Drift and Mutation $\mu ={10}^{-3},m_1=m_2=0.$ θ and β have positive limits <1. At equilibrium, ${\theta }^1=0.024,{\theta }^2=0.714,{\theta }^{12}=0.000,{\beta }_{\mathrm{WT}}^1=0.024,{\beta }_{\mathrm{WT}}^2=0.714,{\beta }_{\mathrm{WT}}=\mathrm{0.369.}$ (E, F) Drift, Mutation and Migration. $\mu ={10}^{-3},m_1={10}^{-2},m_2=0.$ θ positive and <1, ${\beta }_{\mathrm{WT}}$ is positive but ${\beta }_{\mathrm{WT}}^1$ is negative. At equilibrium, ${\theta }^1=0.543,{\theta }^2=0.714,{\theta }^{12}=0.596,{\beta }_{\mathrm{WT}}^1=-0.131,{\beta }_{\mathrm{WT}}^2=0.292,{\beta }_{\mathrm{WT}}=\mathrm{0.080.}$

As for pairs of individuals, the coancestry for pairs of populations is defined here as the average ibd probability for pairs of alleles, one in each population. For populations $i,i^{\prime }$ the quantity ${\theta }_B^{i{i}^{\prime }}$ is the average over all such pairs of alleles and it does not matter whether or not there is random mating within each population. If there is random mating within each of two populations $i=1,2$ with constant population sizes $N_1,N_2,$ however, then genetic drift in the t distinct generations since they diverged from a common ancestral population where ${\theta }^{12}\left(0\right)$ was the ibd probability provides

$$\begin{array}{c}{\theta }^i\left(t\right)=1-\left[1-{\theta }^{12}\left(0\right)\right]{\left(1-\frac{1}{2N_i}\right)}^t,\hspace{1em}i=1,2.\\ {\theta }^{12}\left(t\right)={\theta }^{12}\left(0\right)\end{array}$$

In the absence of mutation and migration, the between-population ibd probability ${\theta }^{12}\left(t\right)$ at present time t is the same as it was, ${\theta }^{12}\left(0\right),$ in the common ancestral population. To avoid having to specify the ancestral value ${\theta }^{12}\left(0\right),$ we define the relative coancestries within populations as ${\beta }^i\left(t\right)=\left[{\theta }^i\left(t\right)-{\theta }^{12}\left(t\right)\right]\left[1-{\theta }^{12}\left(t\right)\right]$ for $i=1,2.$ It is pairs of alleles, one from each of populations 1 and 2, that serve as a reference for describing the ibd status for alleles within each of populations 1 and 2, and there is zero ibd between the two populations relative to this reference. For a study in which there are only these two populations, we write ${\theta }^W=\left({\theta }^1+{\theta }^2\right)/2$ and ${\beta }^W=\left({\beta }^1+{\beta }^2\right)/2.$ We also write ${\theta }^B={\theta }^{12},$ and we could write ${\beta }^B=\left({\theta }^B-{\theta }^{12}\right)/\left(1-{\theta }^{12}\right)$ but this is zero for two populations.

For a set of r populations, we make use of the average over populations of the between-individual, within-population, coancestries, ${\theta }^S={\displaystyle {\sum }_{i=1}^r{\theta }_S^i/r},$ and the average over pairs of populations of the population-pair coancestries, ${\theta }^B={\displaystyle {\sum }_{i=1}^r{\displaystyle {\sum }_{i^{\prime }=1,i^{\prime }\ne i}^r{\theta }_B^{i{i}^{\prime }}/\left[r\left(r-1\right)\right]}}.$ We now have two possible reference sets for within-population coancestries. Relative to all pairs of individuals in population i, the coancestry for individuals $j,j^{\prime }$ is $\left({\theta }_{j{j}^{\prime }}^i-{\theta }_S^i\right)/\left(1-{\theta }_S^i\right),$ and this has an average value of zero. Relative to all pairs of alleles, one in each of two distinct populations, the coancestry is $\left({\theta }_{j{j}^{\prime }}^i-{\theta }^B\right)/\left(1-{\theta }^B\right),$ and we write the average of these quantities over all pairs of individuals as ${\beta }_{\mathrm{ST}}^i=\left({\theta }_S^i-{\theta }^B\right)/\left(1-{\theta }^B\right),$ the “population-specific F_ST.” Averaging over populations gives the usual “population-average F_ST,” now written as

$$F_{\mathrm{ST}}={\beta }_{\mathrm{ST}}=\frac{{\theta }^S-{\theta }^B}{1-{\theta }^B},$$ (3)

to stress it is the within-population coancestry relative to the between population-pair coancestry. Recall that our use of ${\theta }_S^i,{\theta }^S$ for within-population pairs of alleles indicates that we are referring to genotypes, whereas, if we work only with alleles, we write ${\theta }_W^i,{\theta }^W={\displaystyle {\sum }_i{\theta }_W^i/r}$ and allele-based $F_{\mathrm{ST}}$ is

$$F_{\mathrm{ST}}={\beta }_{\mathrm{WT}}=\frac{{\theta }^W-{\theta }^B}{1-{\theta }^B}.$$ (4)

This is the average over populations of the ${\beta }_{\mathrm{WT}}^i=\left({\theta }_W^i-{\theta }^B\right)/\left(1-{\theta }^B\right).$ This expression has been given previously (e.g., Karhunen and Ovaskainen 2012). For random-mating populations, there will be no need for this distinction between ${\beta }_{\mathrm{ST}}$ and ${\beta }_{\mathrm{WT}}.$

We acknowledge a notational difficulty in our use of superscript B rather than T and the loss of an immediate similarity to the work of Sewall Wright (e.g., Wright 1951). We use B to stress that our reference set of alleles is between pairs of populations or individuals, whereas T would suggest a total of all pairs, including those within populations or individuals, and the subsequent need to specify population size for the proportion of pairs from the same allele in one individual. Our formulation is simpler by having a reference be “between” rather than “total.”

In WC84, we had set ${\theta }^B$ to zero but we do not need that restriction to extend the result of Reynolds et al. (1983) that $F_{\mathrm{ST}}$ for a set of populations provides a measure of the time since those populations separated from an ancestral population under a pure drift model. Population-specific and population-average F_ST values are defined for a set of populations, and are not defined when the set has a single population. For a single population i, we still have the ibd probability ${\theta }^i,$ and we note that Balding (2003) refers to this as $F_{\mathrm{ST}}.$

This development with the θ values regarded as ibd probabilities can be replicated with θ regarded as a correlation of allelic state indicators. Transition equations can be established for $P_{u,u}^{i{i}^{\prime }},$ the probability a random pair of alleles, one from population i and one from population $i^{\prime },$ are both of type u. Adding over allele types leads to the same transition equation for correlations as for ibd probabilities, so that Equation 4 applies to correlations, and brings us back to Wright’s original definition of $F_{\mathrm{ST}}$ (Wright 1951).

F-statistics:

The quantity $F_{\mathrm{ST}}$ is one of a set of three functions of allelic-state correlations introduced by Wright (1951) for alleles within individuals I within subpopulations S of a total population T. The three quantities $F_{\mathrm{IS}},F_{\mathrm{ST}},\hspace{0.17em}\text{and}\hspace{0.17em}{F}_{\mathrm{IT}}$ are collectively referred to in population genetics as F-statistics. Reich et al. (2009) worked with functions of allele frequencies in two, three, or four populations. For a SNP reference allele, their two-population functions involved the squared difference of allele frequencies in the two populations, and were termed f-statistics. Subsequently, Peter (2016) defined “F-statistics” with, for example, $F_2\left(i,i^{\prime }\right)=\mathrm{ℰ}{\left(p_i-p_{i^{\prime }}\right)}^2$ where p is the actual allele frequency in population i. In our notation, omitting W subscripts, $F_2\left(1,2\right)=\pi \left(1-\pi \right)\left({\theta }^1+{\theta }^2-2{\theta }^{12}\right).$

Drift, mutation, and migration:

Nontrivial equilibria for populations drifting apart are obtained when there is mutation and migration, and we illustrate some aspects of our population-specific approach by considering the case of two randomly mating populations exchanging alleles each generation when there is infinite-alleles mutation. A similar treatment (Rousset 1996) allows for symmetric mutation rates among a fixed finite set of alleles. The ibd probability transition equations for an arbitrary number of populations, but with equal population sizes and equal migration rates between all pairs of populations, were given by Maruyama (1970). In our case of two unequal population sizes and unequal migration rates, they are, omitting W subscripts,

$$\begin{array}{c}{\theta }^1\left(t+1\right)={\left(1-\mu \right)}^2\left[{\left(1-m_1\right)}^2{\phi }^1\left(t\right)+2m_1\left(1-m_1\right){\theta }^{12}\left(t\right)+m_1^2{\phi }^2\left(t\right)\right]\\ {\theta }^2\left(t+1\right)={\left(1-\mu \right)}^2\left[m_2^2{\phi }^1\left(t\right)+2m_2\left(1-m_2\right){\theta }^{12}\left(t\right)+{\left(1-m_2\right)}^2{\phi }^2\left(t\right)\right]\\ {\theta }^{12}\left(t+1\right)={\left(1-\mu \right)}^2\left[\left(1-m_1\right)m_2{\phi }^1\left(t\right)+\left[\left(1-m_1\right)\left(1-m_2\right)+m_1{m}_2\right]{\theta }^{12}\left(t\right)+m_1\left(1-m_2\right){\phi }^2\left(t\right)\right],\end{array}$$ (5)

where ${\phi }^i\left(t\right)=1/\left(2N_i\right)+\left(2N_i-1\right){\theta }^i\left(t\right)/\left(2N_i\right),$ the mutation rate is μ, and population $i:i=1,2$ receives a fraction $m_i$ of its alleles each generation from population $i^{\prime }:i^{\prime }\ne i.$ A consequence of these equations is that ${\theta }^1\left(t\right)+{\theta }^2\left(t\right)\ge 2{\theta }^{12}\left(t\right),$ or that ${\theta }^W\ge {\theta }^B$ and ${\beta }_{\mathrm{WT}}=F_{\mathrm{ST}}$ is positive. However, it is not necessary that each of ${\theta }^1,{\theta }^2$ exceeds ${\theta }^{12}.$ In Figure 1, second row, we show that mutation leads to equilibrium values of ${\theta }^i$ different from 1, and, in the third row, that migration can lead to cases where ${\theta }^1>{\theta }^{12}>{\theta }^2.$ In the absence of migration, mutation drives ${\theta }^{12}$ to zero, so that ${\beta }_{\mathrm{WT}}^i=\left({\theta }^i-{\theta }^{12}\right)/\left(1-{\theta }^{12}\right)={\theta }^i$ are both positive. For two populations, ${\beta }_{\mathrm{WT}}^{12}$ is always zero.

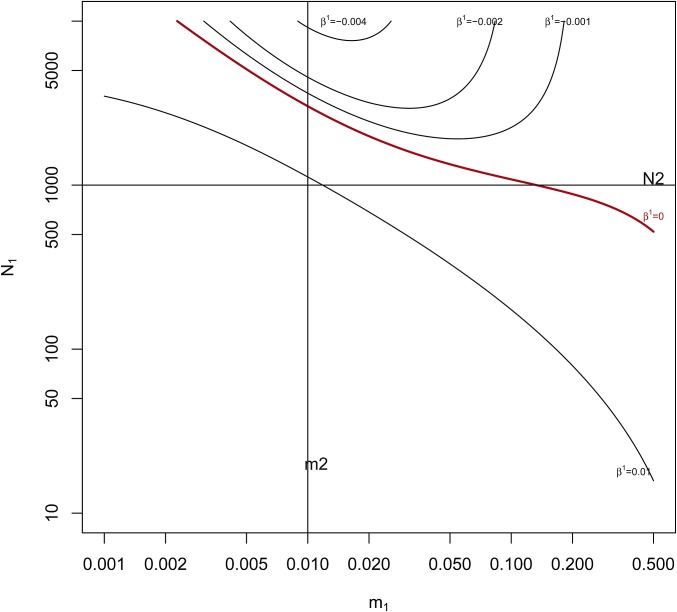
We used numerical methods to find the equilibria for Equation 5, and in Figure 2 we show the region in the space of $N_1,m_1$ values where ${\beta }_{\mathrm{WT}}^1\le 0\le {\beta }_{\mathrm{WT}}^2$ for fixed $N_2,m_2,\hspace{0.17em}\text{and}\hspace{0.17em}\mu .$ Averaging over the two ${\beta }_{\mathrm{WT}}^i$ to work with $F_{\mathrm{ST}}$ hides any difference in the sign of ${\beta }_{\mathrm{WT}}^i$. We note that, in this model, migrants do not come from a “unique and common migrant pool,” as is assumed in the F-model of Balding (2003), Beaumont (2005) and Gaggiotti and Foll (2010).

Figure 2.

Contour plots for ${\beta }_{\mathrm{WT}}^1$ at equilibrium obtained by solving the system of Equation 5. $N_2$ and $m_2$ fixed at 1000 and 0.01 respectively (solid horizontal and vertical black lines). The region above and to the right of the red line has equilibrium values of ${\theta }^1\le {\theta }^{12}\le {\theta }^2,$ i.e., ${\beta }_{WT}^1\le 0\le {\beta }_{\mathrm{WT}}^2.$ In that region, a pair of alleles within population 1 has a smaller probability of ibd than does an allele from population 1 with an allele from population 2.

Actual vs. predicted θ:

The probabilities of ibd calculated from path-counting methods for pedigrees of individuals, or from transition equations for populations, can be regarded as the expected values, over evolutionary replicates, of the actual identity status of a pair of alleles. We have previously discussed the variation of actual identity about the predicted value (Hill and Weir 2011, 2012), as did Speed and Balding (2015). The variance of an actual ibd measure for two alleles, whose predicted value is θ, is $\text{Δ}-{\theta }^2$ (Cockerham and Weir 1983), where $\text{Δ}$ is the joint probability of ibd for each of two pairs of alleles. The coefficient of variation of the actual coancestry for two individuals is >1 for individuals with predicted coancestry θ <0.125, and it increases as the degree of relationship decreases. The implication of this is that, for a particular pair of populations or individuals, estimated values may not match those expected from pedigrees or transition equations. Evaluation of estimation procedures should, therefore, be performed over many replicates.

Estimation

Allelic matching:

We find intuitive appeal in working with proportions of pairs of alleles that are identical by state (ibs). The matching (allele sharing) proportion for pairs of distinct alleles $k,k^{\prime }$ drawn from individual j in a sample from population i is ${\stackrel{\sim }{M}}_{jj}^i={\displaystyle {\sum }_u{\displaystyle {\sum }_{k=1}^2{\displaystyle {\sum }_{k^{\prime }=1,k^{\prime }\ne k}^2{x}_{jku}^i{x}_{j{k}^{\prime }u}^i/2}}},$ using the notation in Table 1. From Equation 1 this matching proportion has expected value $M+\left(1-M\right)F_j^i$ where $M={\displaystyle {\sum }_u{\pi }_u^2}.$ Similarly, the matching proportion for pairs of alleles $k,k^{\prime }$ drawn from distinct individuals $j,j^{\prime }$ respectively in population i is ${\stackrel{\sim }{M}}_{j{j}^{\prime }}^i={\displaystyle {\sum }_u{\displaystyle {\sum }_{k=1}^2{\displaystyle {\sum }_{k^{\prime }=1}^2{x}_{jku}^i{x}_{j^{\prime }{k}^{\prime }u}^i/4}}},$ and this has expectation $M+\left(1-M\right){\theta }_{j{j}^{\prime }}^i.$ In Table 2 we display all the matching proportions needed for data consisting of genotypes from $n_i$ individuals drawn from the ith of r populations, along with expected values of these proportions. Within populations, it is convenient to express matching proportions in terms of individual allelic dosages rather than allelic indicators. Between populations, it is convenient to use sample allele frequencies.

Table 2. Allele-pair matching proportions.

Matching of two distinct alleles within individual j in population i ${\stackrel{\sim }{M}}_j^i=(1/2){\displaystyle {\sum }_u{X}_{ju}^i\left(X_{ju}^i-1\right)},\hspace{1em}\mathrm{ℰ}\left({\stackrel{\sim }{M}}_j^i\right)=M+\left(1-M\right)F_j^i$

Average within-individual matching in population i ${\stackrel{\sim }{M}}_I^i=(1/n_i){\displaystyle {\sum }_{j=1}^{n_i}{\stackrel{\sim }{M}}_j^i},\hspace{1em}\mathrm{ℰ}\left({\stackrel{\sim }{M}}_I^i\right)=M+\left(1-M\right)F_I^i$

Average over populations of within-individual matching ${\stackrel{\sim }{M}}^I=(1/r){\displaystyle {\sum }_{i=1}^r{\stackrel{\sim }{M}}_I^i},\hspace{1em}\mathrm{ℰ}\left({\stackrel{\sim }{M}}^I\right)=M+\left(1-M\right)F^I$

Matching of one allele from each of individuals $j,j^{\prime }$ in population i ${\stackrel{\sim }{M}}_{j{j}^{\prime }}^i=(1/4){\displaystyle {\sum }_u{X}_{ju}^i{X}_{j^{\prime }u}^i},\hspace{1em}\mathrm{ℰ}\left({\stackrel{\sim }{M}}_{j{j}^{\prime }}^i\right)=M+\left(1-M\right){\theta }_{j{j}^{\prime }}^i$

Average between-individual matching in population i ${\stackrel{\sim }{M}}_S^i=1/\left[n_i\left(n_i-1\right)\right]{\displaystyle {\sum }_{j=1}^{n_i}{\displaystyle {\sum }_{j^{\prime }=1,j^{\prime }\ne j}^{n_i}{\stackrel{\sim }{M}}_{j{j}^{\prime }}^i}},\hspace{1em}\mathrm{ℰ}\left({\stackrel{\sim }{M}}_S^i\right)=M+\left(1-M\right){\theta }_S^i$

Average over populations of between-individual within-population matching ${\stackrel{\sim }{M}}^S=(1/r){\displaystyle {\sum }_{i=1}^r{\stackrel{\sim }{M}}_S^i},\hspace{1em}\mathrm{ℰ}\left({\stackrel{\sim }{M}}^S\right)=M+\left(1-M\right){\theta }^S$

Matching of two distinct alleles, ignoring genotypes, within population i ${\stackrel{\sim }{M}}_W^i=\left[2n_i/(2n_i-1\right)]{\displaystyle {\sum }_u{\stackrel{\sim }{p}}_{iu}^2}-\left[1/(2n_i-1\right)],\hspace{1em}\mathrm{ℰ}\left({\stackrel{\sim }{M}}_W^i\right)=M+\left(1-M\right){\theta }_W^i$

Average over populations of within-population allele matching, ignoring genotypes ${\stackrel{\sim }{M}}^W=(1/r){\displaystyle {\sum }_{i=1}^1{\stackrel{\sim }{M}}_W^i},\hspace{1em}\mathrm{ℰ}\left({\stackrel{\sim }{M}}^W\right)=M+\left(1-M\right){\theta }^W$

Matching of an allele from individual j in population i with an allele from individual $j^{\prime }$ in population $i^{\prime }.$ ${\stackrel{\sim }{M}}_{j{j}^{\prime }}^{i{i}^{\prime }}=(1/4){\displaystyle {\sum }_u{X}_{ju}^i{X}_{j^{\prime }u}^{i^{\prime }}},\hspace{1em}\mathrm{ℰ}\left({\stackrel{\sim }{M}}_{j{j}^{\prime }}^{i{i}^{\prime }}\right)=M+\left(1-M\right){\theta }_{j{j}^{\prime }}^{i{i}^{\prime }}$

Matching of one allele from each of populations $i,i^{\prime }$ ${\stackrel{\sim }{M}}_B^{i{i}^{\prime }}=[1/(n_i{n}_{j^{\prime }})]{\displaystyle {\sum }_{j=1}^{n_i}{\displaystyle {\sum }_{j^{\prime }=1}^{n_{i^{\prime }}}{\stackrel{\sim }{M}}_{j{j}^{\prime }}^{i{i}^{\prime }}}}={\displaystyle {\sum }_u{\stackrel{\sim }{p}}_{iu}{\stackrel{\sim }{p}}_{i^{\prime }u}},\hspace{1em}\mathrm{ℰ}\left({\stackrel{\sim }{M}}_B^{i{i}^{\prime }}\right)=M+\left(1-M\right){\theta }_B^{i{i}^{\prime }}$

Average over pairs of populations of between-population-pair matching ${\stackrel{\sim }{M}}^B=\left\{1/[r\left(r-1\right)\right]\}{\displaystyle {\sum }_{i=1}^r{\displaystyle {\sum }_{i^{\prime }=1,i^{\prime }\ne i}^r{\stackrel{\sim }{M}}_B^{ii\prime }}},\hspace{1em}\mathrm{ℰ}\left({\stackrel{\sim }{M}}^B\right)=M+\left(1-M\right){\theta }^B$

Individuals:

If data are available only from a single population, it is possible to estimate only the probability of two alleles, within or between individuals, being ibd relative to the ibd probability of pairs of alleles in a reference set defined by these data. We take the reference set to be an allele from one individual in the sample, paired with an allele from another individual in the sample, averaged over all pairs of distinct individuals in the sample. The estimates are shown in Table 3, and for SNPs they are as shown in Equation 6 without designating the population:

$$\begin{array}{c}\text{Relative}\hspace{0.17em}\text{inbreeding}\hspace{0.17em}\text{for}\hspace{0.17em}\text{individual}\hspace{0.17em}j:\hspace{1em}{\widehat{\beta }}_j=\frac{{\left(X_j-1\right)}^2-{\stackrel{\sim }{M}}_S}{1-{\stackrel{\sim }{M}}_S}\\ \text{Relative}\hspace{0.17em}\text{coancestry}\hspace{0.17em}\text{for}\hspace{0.17em}\text{individuals}\hspace{0.17em}j,j^{\prime }:\hspace{1em}{\widehat{\beta }}_{j{j}^{\prime }}=\frac{\frac{1}{2}\left[1+\left(X_j-1\right)\left(X_{j^{\prime }}-1\right)\right]-{\stackrel{\sim }{M}}_S}{1-{\stackrel{\sim }{M}}_S},\end{array}$$ (6)

where, for a sample of n individuals, ${\stackrel{\sim }{M}}_S={\displaystyle {\sum }_{j=1}^n{\displaystyle {\sum }_{j^{\prime }=1,j^{\prime }\ne j}^n\left[1+\left(X_j-1\right)\left(X_{j^{\prime }}-1\right)\right]/\left[2n\left(n-1\right)\right]}}.$ Recall that $X_j$ is the reference-allele dosage for individual j. Averaging the inbreeding coefficient over individuals in the sample gives an estimate of the within-population inbreeding coefficient $F_{\mathrm{IS}}$ for the sampled population, whereas the average coancestry is zero by construction.

Table 3. Estimates of inbreeding, coancestry, and relatedness.

Allele matching in individual j of population i, relative to individual-pair matching in population i. ${\widehat{\beta }}_j^i=({\stackrel{\sim }{M}}_j^i-{\stackrel{\sim }{M}}_S^i)/(1-{\stackrel{\sim }{M}}_S^i),\hspace{1em}\mathrm{ℰ}\left({\widehat{\beta }}_j^i\right)={\beta }_j^i=(F_j^i-{\theta }_S^i)/(1-{\theta }_S^i)$

Average within-individual matching in population i, relative to individual-pair matching in population i ${\widehat{\beta }}_{\mathrm{IS}}^i=({\stackrel{\sim }{M}}_I^i-{\stackrel{\sim }{M}}_S^i)/(1-{\stackrel{\sim }{M}}_S^i),\hspace{1em}\mathrm{ℰ}\left({\widehat{\beta }}_{\mathrm{IS}}^i\right)=F_{\mathrm{IS}}^i={\beta }_{\mathrm{IS}}^i=(F_I^i-{\theta }_S^i)/(1-{\theta }_S^i,)$ population-specific $F_{\mathrm{IS}}$

Population average of within-individual matching, relative to individual-pair matching in each population. ${\widehat{\beta }}_{\mathrm{IS}}=({\stackrel{\sim }{M}}^I-{\stackrel{\sim }{M}}^S)/(1-{\stackrel{\sim }{M}}^S),\hspace{1em}\mathrm{ℰ}\left({\widehat{\beta }}_{\mathrm{IS}}\right)=F_{\mathrm{IS}}={\beta }_{\mathrm{IS}}=(F^I-{\theta }^S)/(1-{\theta }^S)$

Population average of within-individual matching, relative to allele matching between populations. ${\widehat{\beta }}_{\mathrm{IT}}=({\stackrel{\sim }{M}}^I-{\stackrel{\sim }{M}}^B)/(1-{\stackrel{\sim }{M}}^B),\hspace{1em}\mathrm{ℰ}\left({\widehat{\beta }}_{\mathrm{IT}}\right)=F_{\mathrm{IT}}={\beta }_{\mathrm{IT}}=(F^I-{\theta }^B)/(1-{\theta }^B)$

Allele matching between individuals $j,j^{\prime }$ in population i relative to between-individual matching in that population. ${\widehat{\beta }}_{j{j}^{\prime }}^i={(\stackrel{\sim }{M}}_{j{j}^{\prime }}^i-{\stackrel{\sim }{M}}_S^i)/(1-{\stackrel{\sim }{M}}_S^i),\hspace{1em}\mathrm{ℰ}\left({\widehat{\beta }}_{j{j}^{\prime }}^i\right)={\beta }_{j{j}^{\prime }}^i=({\theta }_{j{j}^{\prime }}^i-{\theta }_S^i)/(1-{\theta }_S^i,)$ with zero average over pairs of individuals.

Average individual matching within population i, relative to allele matching between populations. ${\widehat{\beta }}_{\mathrm{ST}}^i={(\stackrel{\sim }{M}}_S^i-{\stackrel{\sim }{M}}^B)/(1-{\stackrel{\sim }{M}}^B),\hspace{1em}\mathrm{ℰ}\left({\widehat{\beta }}_{\mathrm{ST}}^i\right)={\beta }_{\mathrm{ST}}^i=({\theta }_S^i-{\theta }^B)/(1-{\theta }^B),$ population-specific $F_{\mathrm{ST}}$ for genotypic data.

Population average of within-population individual-pair matching, relative to allele matching between populations. ${\widehat{\beta }}_{\mathrm{ST}}={(\stackrel{\sim }{M}}^S-{\stackrel{\sim }{M}}^B)/(1-{\stackrel{\sim }{M}}^B),\hspace{1em}\mathrm{ℰ}\left({\widehat{\beta }}_{\mathrm{ST}}\right)={\beta }_{\mathrm{ST}}=F_{\mathrm{ST}}=({\theta }^S-{\theta }^B)/(1-{\theta }^B),$ overall $F_{\mathrm{ST}}$ for genotypic data.

Distinct allele matching within population i, ignoring genotypes, relative to allele matching between populations. ${\widehat{\beta }}_{\mathrm{WT}}^i=({\stackrel{\sim }{M}}_W^i-{\stackrel{\sim }{M}}^B)/(1-{\stackrel{\sim }{M}}^B),\mathrm{ℰ}\left({\widehat{\beta }}_{\mathrm{WT}}^i\right)={\beta }_{\mathrm{WT}}^i=({\theta }_W^i-{\theta }^B)/(1-{\theta }^B),$ population-specific $F_{\mathrm{ST}}$ for allelic data.

Population average of within-population allele matching, relative to allele matching between populations. ${\widehat{\beta }}_{\mathrm{WT}}=({\stackrel{\sim }{M}}^W-{\stackrel{\sim }{M}}^B)/(1-{\stackrel{\sim }{M}}^B),\mathrm{ℰ}\left({\widehat{\beta }}_{\mathrm{WT}}\right)=F_{\mathrm{ST}}={\beta }_{\mathrm{WT}}=({\theta }^W-{\theta }^B)/(1-{\theta }^B),$ overall $F_{\mathrm{ST}}$ for allelic data.

Matching of one allele from each of populations $i,i^{\prime },$ relative to allele matching between all populations. ${\widehat{\beta }}_B^{i{i}^{\prime }}=({\stackrel{\sim }{M}}_B^{i{i}^{\prime }}-{\stackrel{\sim }{M}}^B)/(1-{\stackrel{\sim }{M}}^B),\hspace{1em}\mathrm{ℰ}\left({\widehat{\beta }}_{\mathrm{BT}}^{i{i}^{\prime }}\right)={\beta }_B^{i{i}^{\prime }}=({\theta }_B^{i{i}^{\prime }}-{\theta }^B)/(1-{\theta }^B),$ with zero average over pairs of populations.

Notice that we construct estimates as the ratio of expressions that each have expected values proportional to $1-M={\displaystyle {\sum }_u{\pi }_u\left(1-{\pi }_u\right)}.$ As we did in WC84, we assume the expected value of the ratio of two expressions is approximately the ratio of their expectations. The $\left(1-M\right)$ values cancel, and we are left with expected values that are our “relative to” functions of ibd probabilities. This first-order Taylor series approximation to the expectation of a ratio has proven robust for $F_{\mathrm{ST}}$ since 1984 (e.g., Goudet et al. 1996), and the results shown in Figure 7 below suggest it is also robust for relatedness estimation. Being able to cancel the M terms means we avoid having to know, or estimate, (squares of) the allele frequencies ${\pi }_u,$ and so we avoid having to specify ancestral populations or individuals. Our work results in ranking populations or individuals by estimates of their ibd status.

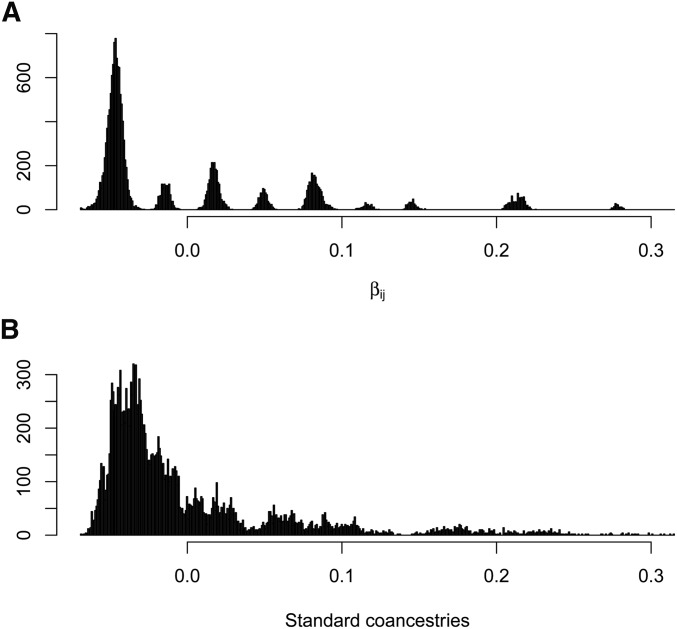
Figure 7.

Comparison of β (A) and standard coancestry (B) estimates, when founders are drawn from a single population.

The new estimators we display in Equation 6 differ from the standard estimators (e.g., Ritland 1996; Yang et al. 2011; Wang et al. 2017). For biallelic loci these estimators are

$${\widehat{\theta }}_{j{j}^{\prime }}=\frac{\left(X_j-2\stackrel{\sim }{p}\right)\left(X_{j^{\prime }}-2\stackrel{\sim }{p}\right)}{4\stackrel{\sim }{p}\left(1-\stackrel{\sim }{p}\right)}$$ (7)

for all $j,j^{\prime }.$ These estimators use the sample allele frequencies for the sampled population, and are intended to estimate $\left(1+F_j\right)/2$ when $j=j^{\prime }$ and ${\theta }_{j{j}^{\prime }}$ when $j\ne j^{\prime }.$ There is no simple translation from these estimates to those we propose in Equation 6.

Ochoa and Storey (2016a,b) have estimates equivalent to those in Equation 6. Their expressions are a little different because their reference is for all pairs of alleles in a sample, including those within individuals, whereas ours are for pairs of alleles in different individuals. Astle and Balding (2009) (Equation 2.3) gave similar estimates although, in effect, they set ${\theta }^B,$ the average coancestry of all pairs of individuals in a sample, to zero.

We estimate inbreeding and coancestry relative to the average coancestry of all pairs of individuals in a study. Yang et al. (2010) also discuss estimates relative to the study population, and say “Estimates of relationships are always relative to an arbitrary base population in which the average relationship is zero. We use the individuals in the sample as the base so that the average relationship between all pairs of individuals is 0 and the average relationship of an individual with him- or herself is 1.” Although our estimates of pairwise relationship sum to zero when we use data from a single population, we retain the unknown value ${\theta }_S$ in their expectations. We cannot estimate ${\theta }_S,$ and we may prefer to report estimates relative to those for the least related pairs as described below in Equation 11.

Populations:

With data from a set of r populations, the matching proportions and estimates are also shown in Table 2 and Table 3. In each table these population-based entries reduce to individual-based entries if the sample sizes are one, $n_i=1,i=1,2,\dots ,r.$ Regardless of sample size, we can estimate inbreeding and coancestry relative to pairs of alleles, one from each of all pairs of populations in the study. In that case, we would replace a population-specific ${\stackrel{\sim }{M}}_S$ in Equation 6 by a population-pair average ${\stackrel{\sim }{M}}^B.$ The average inbreeding coefficient estimate over individuals in a population i is now an estimate of the population-specific $F_{\mathrm{IT}}^i$ value, and averaging these over populations gives an estimate of $F_{\mathrm{IT}}.$ Averaging the coancestries for pairs of individuals in population i gives an estimate of the population-specific $F_{\mathrm{ST}}^i,$ and averaging those over populations gives an estimate of $F_{\mathrm{ST}}.$

With genotypic data, the estimates in Table 3 provide the usual relationship

$$\left(1-F_{\mathrm{IT}}\right)=\left(1-F_{\mathrm{ST}}\right)\left(1-F_{\mathrm{IS}}\right)$$ (8)

although our use of the whole set of populations as a reference does not allow alleles to be drawn from the same population for the matching proportion ${\stackrel{\sim }{M}}^B.$ This shows the composite nature of $F_{\mathrm{IT}},$ and we note that, if one is interested in an overall inbreeding coefficient, it might be better estimated by not accounting for the subpopulations. Note that Equation 8 holds for the overall ${\beta }_{\mathrm{IT}},{\beta }_{\mathrm{ST}},\hspace{0.17em}\text{and}\hspace{0.17em}{\beta }_{\mathrm{IS}}$ quantities as well as the population-specific ${\beta }_{\mathrm{IT}}^i,{\beta }_{\mathrm{ST}}^i,\hspace{0.17em}\text{and}\hspace{0.17em}{\beta }_{\mathrm{IS}}^i$ quantities.

If we ignore genotypes and use only allelic data, then we return to estimation of population-specific and population-average $F_{\mathrm{ST}}$ with ${\stackrel{\sim }{M}}_W^i$ and ${\stackrel{\sim }{M}}^W$ compared to ${\stackrel{\sim }{M}}^B:$

$${\widehat{F}}_{\mathrm{ST}}^i={\widehat{\beta }}_{\mathrm{WT}}^i=\frac{{\stackrel{\sim }{M}}_W^i-{\stackrel{\sim }{M}}^B}{1-{\stackrel{\sim }{M}}^B},{\widehat{F}}_{\mathrm{ST}}={\widehat{\beta }}_{\mathrm{WT}}=\frac{{\stackrel{\sim }{M}}^W-{\stackrel{\sim }{M}}^B}{1-{\stackrel{\sim }{M}}^B}.$$

The population-average value has been given previously by Hudson et al. (1992) (Equation 3).

For SNPs, where the sample frequency of the reference allele for population i is ${\stackrel{\sim }{p}}_i,$ the allele-based population-specific, and population-average $F_{\mathrm{ST}}$ estimates for large sample sizes can be written as

$$\begin{array}{c}{\widehat{\beta }}_{\mathrm{WT}}^i=\frac{\overline{p}\left(1-\overline{p}\right)-{\stackrel{\sim }{p}}_i\left(1-{\stackrel{\sim }{p}}_i\right)+\frac{1}{r}{s}_p^2}{\overline{p}\left(1-\overline{p}\right)+\frac{1}{r}{s}_p^2}\\ {\widehat{\beta }}_{\mathrm{WT}}=\frac{s_p^2}{\overline{p}\left(1-\overline{p}\right)+\frac{1}{r}{s}_p^2},\end{array}$$ (9)

where $\overline{p}={\displaystyle {\sum }_{i=1}^r{\stackrel{\sim }{p}}_i/r}$ and $s_p^2={\displaystyle {\sum }_{i=1}^r{\left({\stackrel{\sim }{p}}_i-\overline{p}\right)}^2/\left(r-1\right)}.$ For a large number of sampled populations, and only then, ${\widehat{\beta }}_{\mathrm{WT}}$ is the common $F_{\mathrm{ST}}$ estimate $s_p^2/\overline{p}\left(1-\overline{p}\right)$ (e.g., Hartl and Clark 1997, Equation 4.6). For all r it is an estimate of $\left({\theta }^W-{\theta }^B\right)/\left(1-{\theta }^B\right).$ For the case $r=2,$ the single-population and population-pair estimates are

$$\begin{array}{c}{\widehat{\beta }}_{\mathrm{WT}}^1=\frac{\left({\stackrel{\sim }{p}}_1-{\stackrel{\sim }{p}}_2\right)\left(2{\stackrel{\sim }{p}}_1-1\right)}{{\stackrel{\sim }{p}}_1\left(1-{\stackrel{\sim }{p}}_2\right)+{\stackrel{\sim }{p}}_2\left(1-{\stackrel{\sim }{p}}_1\right)}\\ {\widehat{\beta }}_{\mathrm{WT}}^2=\frac{\left({\stackrel{\sim }{p}}_2-{\stackrel{\sim }{p}}_1\right)\left(2{\stackrel{\sim }{p}}_2-1\right)}{{\stackrel{\sim }{p}}_1\left(1-{\stackrel{\sim }{p}}_2\right)+{\stackrel{\sim }{p}}_2\left(1-{\stackrel{\sim }{p}}_1\right)}\\ {\widehat{\beta }}_{\mathrm{WT}}=\frac{{\left({\stackrel{\sim }{p}}_1-{\stackrel{\sim }{p}}_2\right)}^2}{{\stackrel{\sim }{p}}_1\left(1-{\stackrel{\sim }{p}}_2\right)+{\stackrel{\sim }{p}}_2\left(1-{\stackrel{\sim }{p}}_1\right)}.\end{array}$$ (10)

Each of the estimates in Equation 10 reflects difference of the two sample allele frequencies. Either ${\widehat{\beta }}_{\mathrm{WT}}^1$ or ${\widehat{\beta }}_{\mathrm{WT}}^2$ can be negative as shown in Figure 2 for predicted values, but ${\widehat{\beta }}_{\mathrm{WT}}$ is positive.

Note that the pairwise coancestry estimates ${\widehat{\beta }}_{j{j}^{\prime }},j\ne j^{\prime },$ and population-pair estimates ${\widehat{\beta }}^{i{i}^{\prime }},i^{\prime }\ne i,$ sum to zero by construction. Although it is not possible to find estimates for each θ when the sampled individuals within a population are related, or when sampled populations have correlated sample allele frequencies, or when there is just a single sampled population, it is possible to rank $\widehat{\beta }$ values, and, we expect these to have the same ranking as their expected values θ.

Combining over loci:

Single-locus analyses do not provide meaningful results, and combining estimates over loci l has often been considered in the literature. In a parallel discussion of weighting over alleles u at a single locus, Ritland (1996) considered weights $w_u$ chosen to minimize variance.

If the locus-l estimates ${\widehat{\beta }}_l,$ for individuals (Equations 6 and 7) or populations (Equations 9 and 10), are written as $N_l/D_l,$ then a weighted average over loci is ${\displaystyle {\sum }_l{w}_l{\widehat{\beta }}_l}/{\displaystyle {\sum }_l{w}_l}.$ Two extreme weights are $w_l=1$ and $w_l=D_l.$ The first may be called “unweighted” and the second “weighted.” For population structure, Bhatia et al. (2013) refer to the first estimate as the “average of ratios” and the second as the “ratio of averages.” WC84 advocated the second, with justification given in the Appendix to that paper, as did Bhatia et al. (2013).

The unweighted estimate is unbiased for all allele frequencies, but is susceptible to the effects of rare variants, when the denominators $D_l$ of the single-locus estimates can be very small. Rare variants may have little effect on the weighted average, and the variance of the estimate is seen in simulations to be less than for the unweighted average, but it is unbiased only if every locus has the same β value. A more extensive discussion was given in the Appendix of WC84 for population structure, and by Ritland (1996) for inbreeding and relatedness. More recently, Ochoa and Storey (2016b) discussed weights for their estimates, and Wang et al. (2017) discuss weighting in the context of known allele frequencies.

Regardless of weighting scheme, the use of several loci allows us to use bootstrapping over loci (Weir 1996) to generate empirical sampling distributions for our estimates. We used bootstrapping for confidence intervals in the Results section. We discussed sampling properties previously (Weir and Hill 2002; Weir et al. 2005), and will give more details elsewhere. We note here that it is increasing the number of loci, rather than the number of individuals, that lead to the greatest reduction in variance—providing the parametric values do not vary too much over loci.

Private alleles:

Current sequence-based studies are revealing large numbers of low-frequency variants, including those found in only one population. These private alleles were identified by Slatkin (1985) and Mathieson and McVean (2012) as being of particular interest. They are very frequent in the 1000 genomes project data (1000 Genomes Project Consortium 2010). We show estimates in Table 4 for the case of an allele observed in only one of a set of r populations.

Table 4. Population-level estimates for private alleles.

Quantity	Observation or estimate
Private allele frequency	${\stackrel{\sim }{p}}_1$ in population 1, zero in populations $2,3,\dots ,r$
Sample matching proportions	${\stackrel{\sim }{M}}_W^1=1-2{\stackrel{\sim }{p}}_1\left(1-{\stackrel{\sim }{p}}_1\right)2n_i/(2n_i-1)$
	${\stackrel{\sim }{M}}_W^i=1,\hspace{1em}i\ne 1$
	${\stackrel{\sim }{M}}^W=1-2{\stackrel{\sim }{p}}_1\left(1-{\stackrel{\sim }{p}}_1\right)2n_1/[r\left(2n_1-1\right)]$
	${\stackrel{\sim }{M}}_B^{1i}=1-{\stackrel{\sim }{p}}_1,\hspace{1em}i\ne 1$
	${\stackrel{\sim }{M}}_B^{i{i}^{\prime }}=1,\hspace{1em}i,i^{\prime }\ne 1,i\ne i^{\prime }$
	${\stackrel{\sim }{M}}^B=1-2{\stackrel{\sim }{p}}_1/r$
β estimates	$F_{\mathrm{ST}}^1={\widehat{\beta }}_{\mathrm{WT}}^1=1-r\left(1-{\stackrel{\sim }{p}}_1\right)2n_1/(2n_{\mathrm{i}}-1)\approx 1-r\left(1-{\stackrel{\sim }{p}}_1\right)$
	$F_{\mathrm{ST}}^i={\widehat{\beta }}_{\mathrm{WT}}^i=1,\hspace{1em}i\ne 1$
	$F_{\mathrm{ST}}={\widehat{\beta }}_{\mathrm{WT}}=(2n_1-{\stackrel{\sim }{p}}_1-1)/(2n_1-1)\approx {\stackrel{\sim }{p}}_1$
	${\widehat{\beta }}_{\mathrm{WT}}^{1i}=1-r/2,i\ne 1$
	${\widehat{\beta }}_{\mathrm{WT}}^{i{i}^{\prime }}=1,\hspace{1em}i,i^{\prime }\ne 1$

The estimate of ${\beta }_{\mathrm{WT}}=F_{\mathrm{ST}}$ for a private allele is, approximately, its own-population sample frequency, but the population-specific value ${\widehat{\beta }}_{\mathrm{WT}}^1$ for its own population ranges from approximately $-r+1$ when ${\stackrel{\sim }{p}}_1$ is very small to 1 when ${\stackrel{\sim }{p}}_1=1.$ This amplifies the comment “populations can display spatial structure in rare variants, even when Wright’s fixation index $F_{\mathrm{ST}}$ is low” of Mathieson and McVean (2012). A population with many private alleles at low to intermediate frequencies will thus likely have a negative ${\widehat{\beta }}_{\mathrm{WT}},$ and how negative will depend on how many populations have been sampled. Note that this implies ${\widehat{\beta }}_{\mathrm{WT}}^i$ must be allowed to go negative, whereas Bayesian and maximum likelihood estimators of population specific $F_{\mathrm{ST}}$ are often forced to belong to $\left[0,1\right],$ although this assumption can be relaxed (Ritland 1996).

Data availability

The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article.

Results

Population structure

We conducted a series of simulations to evaluate the performance of our $F_{\mathrm{ST}}$ estimates, and we looked at 1000 Genomes SNP data to explore the role of rare variants on the estimates. Some of the simulations were conducted with sim.genot.metapop.t available in the hierfstat package (Goudet 2005). The migration model we used allows for a matrix of migration rates between each pair of populations, and the mutation model allows for multiple alleles at a locus. The notation for a two-population model was given above. Our approach of estimating $F_{\mathrm{ST}}$ values that are population-specific, and of allowing allele frequencies to be correlated among populations, means that we are estimating different (combinations of) parameters than have other authors (e.g., Gaggiotti and Foll 2010).

Drift with mutation

We first simulated genotypic data under a scenario of pure genetic drift from a common ancestral population. Populations of different sizes ($100,1000$ and $10,000$) were investigated, and 50 diploid individuals, each genotyped at 1000 loci with up to 20 alleles were sampled from each population at three time points: $t=50,500,\text{and}5000$ generations. The results are reported in Table 5. In all situations, the estimates ${\widehat{\beta }}_{\mathrm{WT}}^i$ are close to their expectations, and the 95% confidence intervals obtained by bootstrapping over loci include the expected value ${\beta }_{\mathrm{WT}}^i.$ The credible intervals for ${\widehat{F}}_{\mathrm{ST}}^i$ obtained from Bayescan 2.1 (Foll and Gaggiotti 2008) include the expected values ${\beta }_{\mathrm{WT}}^i$ for only three of the nine reported situations. The Bayescan estimate ${\widehat{F}}_{\mathrm{ST}}^i$ tends to overestimate ${\beta }_{\mathrm{WT}}^i$ when it is large, and to underestimate it when it is small. A possible reason for this discrepancy is that the Dirichlet distribution used in Bayescan is an approximation of allele frequency distribution under an equilibrium island model (Gaggiotti and Foll 2010). We note that an alternative to the Dirichlet distribution often used, the truncated normal distribution (Nicholson et al. 2002), might be more appropriate for the simulated data, but we are unaware of available implementations of such estimator of $F_{\mathrm{ST}}.$ Moreover, both the Dirichlet and the truncated normal are just convenient approximations of the true distribution of allele frequencies [see figure S1 and file S2 in Karhunen and Ovaskainen (2012)].

Table 5. Predicted and estimated population-specific $F_{\mathrm{ST}}$ values for two populations without migration.

t	N	${\beta }_{\mathrm{WT}}^i={\theta }^i$	${\widehat{\beta }}_{\mathrm{WT}}^i$	${\widehat{F}}_{\mathrm{ST}}^i$
50	100	0.221	0.222 (0.215, 0.229)	0.332 (0.325, 0.340)
50	1,000	0.025	0.026 (0.024, 0.028)	0.026 (0.025, 0.027)
50	10,000	0.002	0.003 (0.001, 0.005)	0.0003 (0.0001, 0.0005)
500	100	0.891	0.887 (0.875, 0.899)	0.918 (0.911, 0.925)
500	1,000	0.211	0.211 (0.204, 0.219)	0.289 (0.283, 0.296)
500	10,000	0.023	0.025 (0.021, 0.029)	0.002 (0.001, 0.002)
5000	100	0.962	0.958 (0.950, 0.965)	0.958 (0.953, 0.964)
5000	1,000	0.693	0.698 (0.684, 0.713)	0.683 (0.673, 0.694)
5000	10,000	0.143	0.145 (0.138, 0.152)	0.056 (0.053, 0.058)

Mutation rate $\mu ={10}^{-4};$ 1000 multi allelic loci. 95% confidence intervals for ${\widehat{\beta }}_{\mathrm{WT}}^i$ from bootstrapping over loci. 95% credible intervals obtained with Bayescan 2.1 for ${\widehat{F}}_{\mathrm{ST}}^i.$

Drift with mutation and migration

Model 1. Same migration rates, different population sizes:

We considered two populations under the model described by Equation 5, with sizes $N_1=100,N_2=1,000,$ and migration rates $m_1=m_2=\mathrm{0.01.}$ The mutation rate was $\mu ={10}^{-6}.$ After 400 generations, β has expected values ${\beta }_{\mathrm{WT}}^1=0.156\text{and}{\beta }_{\mathrm{WT}}^2=-0.037,$ and ${\theta }_{\mathrm{WT}}^{12}=\mathrm{0.059.}$ We simulated 50 individuals from each population under this scenario, with 1000 loci and up to 20 alleles per locus. From the resulting allelic data we obtained estimates, and 95% confidence intervals by bootstrapping over loci. The results are shown in Table 6. The predicted values are contained in the confidence intervals, and there are negative values for both the parametric and the estimated value of ${\beta }_{\mathrm{WT}}^2.$ Note that we cannot estimate ${\beta }_{\mathrm{WT}}^{12}$ with data from two populations.

Table 6. Predicted and estimated population-specific $F_{\mathrm{ST}}$values for two populations with migration.

Model	$N_1$	$N_2$	$m_1$	$m_2$	${\beta }_{\mathrm{WT}}^1$	${\widehat{\beta }}_{\mathrm{WT}}^1$	${\beta }_{\mathrm{WT}}^2$	${\widehat{\beta }}_{\mathrm{WT}}^2$	${\theta }_{\mathrm{WT}}^{12}$
1	100	1000	0.01	0.01	0.156	0.159 (0.148, 0.169)	−0.037	−0.031 (−0.038, −0.023)	0.059
2	100	1000	0.01	0.01	0.198	0.203 (0.196, 0.211)	0.024	0.025 (0.022, 0.027)	0
3	100	1000	0.01	0.01	0.277	0.268 (0.254, 0.282)	−0.061	−0.059 (−0.067, −0.050)	0.112
4	10,000	100	0.01	0	−0.281	−0.269 (−0.292, −0.248)	0.461	0.448 (0.419, 0.477)	0.090

Mutation rate $\mu ={10}^{-6};$ Generation $t=400;$ 1000 multiallelic loci. 95% confidence intervals from bootstrapping over loci. For Model 2, using Bayescan 2.1, ${\widehat{F}}_{\mathrm{ST}}^1=0.206\left(0.201,0.211\right),$ ${\widehat{F}}_{\mathrm{ST}}^2=0.001\left(0.000,0.002\right).$

Model 2. Continent-island model:

In this scenario we have an infinite continent supplying a proportion $m=0.01$ of the alleles independently to populations 1 and 2, still with sizes $N_1=100\text{and}{N}_2=1,000.$ There is no migration between the two populations, so ${\theta }^{12}=0.$ Table 6 shows that the predicted values are contained in the confidence intervals of their estimated values. For this situation, the F-model is suitable, and at the bottom of Table 6 we report ${\widehat{F}}_{\mathrm{ST}}^1,{\widehat{F}}_{\mathrm{ST}}^2$ with their 95% credible intervals. ${\widehat{F}}_{\mathrm{ST}}^1$ slightly overestimates ${\beta }_{\mathrm{WT}}^1$ and ${\widehat{F}}_{\mathrm{ST}}^2$ underestimates ${\beta }_{\mathrm{WT}}^2.$

Model 3. Migrant-pool island model:

In this model, each population contributes to a migrant pool, from which migrant alleles are drawn. Among the migrant alleles in the case of two populations, half of the “migrant alleles” will in fact be resident alleles if the gametic pool is composed of the same proportion of alleles from each island, independent of its size. With otherwise the same parameter values, the predicted values, and our estimates after 400 generations, are shown in Table 6, and are in good agreement.

Model 4. Different population sizes, different migration rates:

We return to the two-populations model described by Equation 5, but now with $N_1=10,000\text{and}{N}_2=100,$ and different migration rates $m_1=0.01$ and $m_2=0.$ Predicted values after 400 generations are given in Table 6.

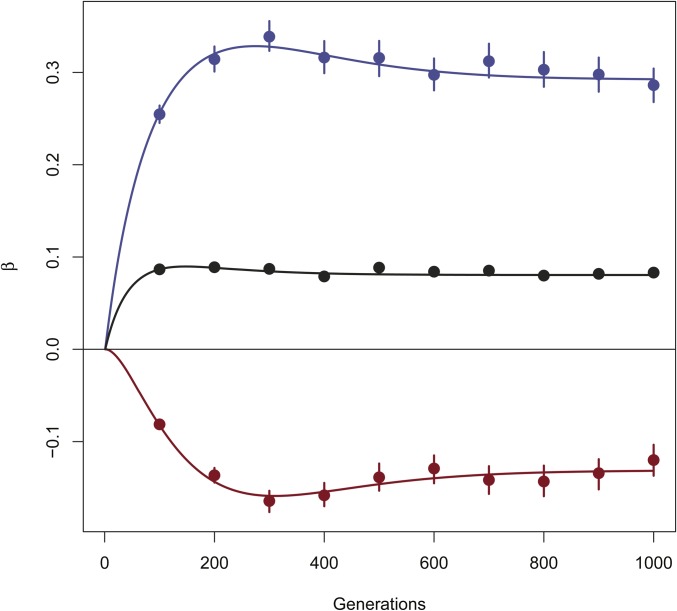
The results in Table 5 and Table 6 show good behavior of ${\beta }_{\mathrm{WT}}^i$ estimates with low bias. In Figure 3 we show the estimates for 10 different time points (independent replicates) for Model 4 with a mutation rate of ${10}^{-3}$ in order to maintain sufficient levels of polymorphism. Again, expected values and estimates are in good agreement throughout the simulations.

Figure 3.

Estimated ${\beta }_{\mathrm{WT}}$ for independent simulations of the two-population model described by the system of Equation 5, at different times. Population sizes $N_1=10,000\text{and}\hspace{0.17em}{N}_2=100.$ Migration rates $m_1=0.01\text{and}\hspace{0.17em}{m}_2=\mathrm{0.0.}$ Mutation rate $\mu ={10}^{-3}.$ ${\beta }_{\mathrm{WT}}^1$ in red, ${\beta }_{\mathrm{WT}}^2$ in blue, ${\beta }_{\mathrm{WT}}$ in black. Lines are expectations, points are estimates, and bars represent the 95% confidence intervals obtained by bootstrapping over loci.

Rare alleles:

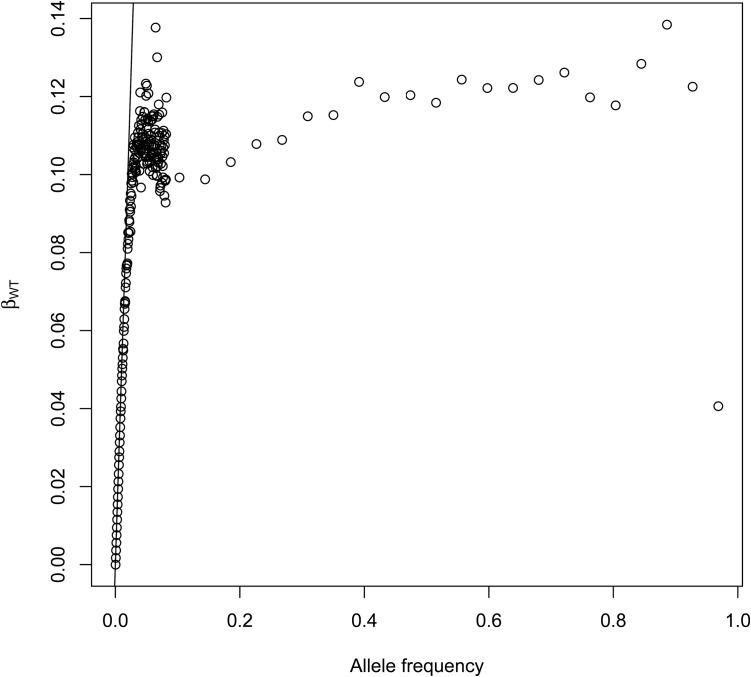
For r populations with total sample size $n_T,$ and with $x_1$ copies of an allele private to population 1, the total count for this alleles is $x_T=x_1$ and ${\stackrel{\sim }{p}}_T=n_1{\stackrel{\sim }{p}}_1/n_T,$ so ${\widehat{\beta }}_{WT}=n_T{\stackrel{\sim }{p}}_T/n_1\approx r{\stackrel{\sim }{p}}_T,$ assuming similar sample sizes for each sample. In Figure 4 we display ${\widehat{\beta }}_{\mathrm{WT}}=F_{\mathrm{ST}}$ as a function of allele frequencies for SNPs located on chromosome 2 in the 1000 Genomes project. Individuals were grouped by regions (Africa, Europe, South Asia, East Asia and the Americas). The drawn line corresponds to ${\beta }_{\mathrm{WT}}=5p_T.$ The initial linear segment corresponds to alleles that are present in one continent only. ${\beta }_{\mathrm{WT}}$ starts departing from this line for allele counts >80, or equivalently, for worldwide sample frequencies >$\approx 0.01,$ given the sampled chromosome number of $2426.$

Figure 4.

${\beta }_{\mathrm{WT}}$ as a function of allele frequencies ($n_u/n_T$) for SNPs located on chromosome 2. Data from the 1000 genomes project, individuals were grouped by regions (Africa, Europe, South Asia, East Asia, and Americas). The drawn line corresponds to $5n_u/n_T.$ The initial linear segment corresponds to alleles that are present in one continent only. ${\beta }_{\mathrm{WT}}$ starts departing from this line for allele counts >80, or equivalently, for worldwide frequencies > $\approx 0.01,$ given the sampled chromosome number of 2426.

When a new allele appears, it will be present in one population only. We expect most, if not all, rare alleles to be private alleles, and thus the expected values for $F_{\mathrm{ST}}$ (${\beta }_{\mathrm{WT}}$) for these rare alleles are their own-population frequencies. When ${\widehat{\beta }}_{\mathrm{WT}}$ starts departing from the allele frequency, it implies that some scattering has been happening. In species with a lot of migration, this will happen at low frequencies, whereas the species that are more sedentary should show a 1:1 relation between subpopulation allele frequencies and ${\beta }_{\mathrm{WT}}$ for a larger range of their site frequency spectrum.

Reference populations:

In Buckleton et al. (2016) we gave population-specific $F_{\mathrm{ST}}$ estimates for a set of 446 populations, using published data for 24 microsatellite loci collected for forensic purposes. We showed in that paper how the choice of a reference set of populations can affect results. Here, we illustrate this point with data from the 1000 genomes, using 1,097,199 SNPs on chromosome 22. For the samples originating from Africa, there is a larger $F_{\mathrm{ST}},$ ${\widehat{\beta }}_{\mathrm{WT}}=0.013,$ with Africa as a reference set than there is, ${\widehat{\beta }}_{\mathrm{WT}}=-0.099,$ with the world as a reference set. African populations tend to be more different from each other on average than do any two populations in the world on average. The opposite was found for the collection of East Asian populations: there is a smaller $F_{\mathrm{ST}},$ ${\widehat{\beta }}_{\mathrm{WT}}=0.013$ with East Asia as a reference set than there is, ${\widehat{\beta }}_{\mathrm{WT}}=0.225$ with the world as a reference set. East Asian populations are more similar to each other than are any pair of populations in the world.

Inbreeding and coancestry

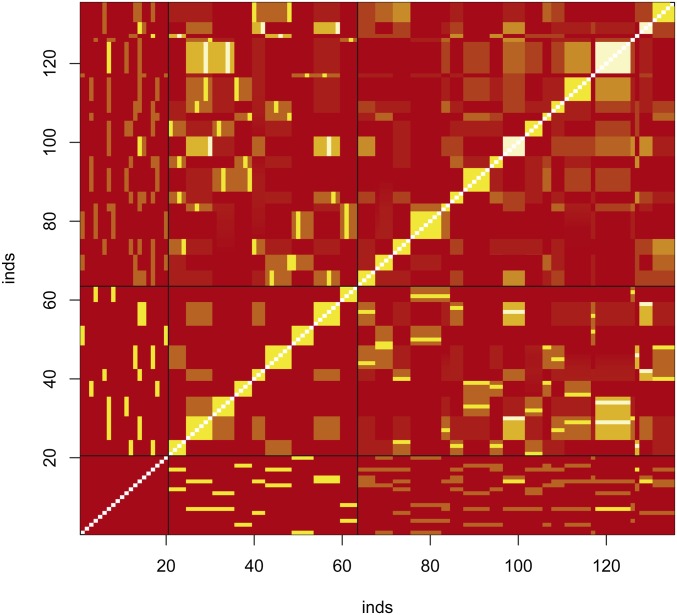
To check on the validity of our estimators of individual inbreeding and coancestry coefficients, we simulated data for a range of nine coancestries: $\left(i/32:i=0,1,\dots ,6,8,10\right).$ Using the ms software (Hudson 2002), we generated data from an island model with two populations exchanging $Nm=1$ migrant per generation. We simulated 5000 independent loci, read either as haplotypes (5000) or as SNPs (∼80,000 polymorphic sites for the founders). We then chose 20 individuals from one of these populations and let them mate at random, without selfing. We did not assign or consider sex for these 20 founders. In order to generate a sufficient number of pairs of related individuals, we drew the number of offspring per mating from a Poisson distribution with a mean of five. These offspring were also allowed to mate at random, without selfing, and produced families with sizes drawn from a Poisson distribution with mean three. By keeping records of all matings we could generate the pedigree-based inbreeding and coancestry values for all 135 individuals: founders, their offspring, and their grand-offspring. The pedigree-based coancestries for all 9045 pairs of individuals are shown in Figure 5, although we note (Hill and Weir 2011) that the actual values have variation about expected or pedigree values.

Figure 5.

Pedigree-based coancestry coefficients for simulated data for 135 individuals with 20 founders. Red correspond to low values, yellow to high values of coancestry, white are missing data (unknown inbreeding coefficient of the founders). Black horizontal and vertical lines separate generations in the pedigree. The yellow blocks along the main diagonal correspond to sibships.

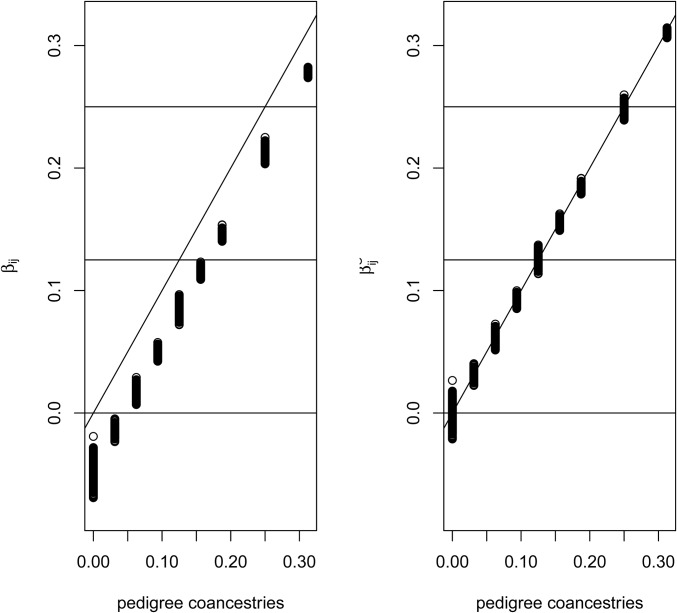
The left-hand plot of Figure 6 compares the coancestry estimates ${\widehat{\beta }}_{j{j}^{\prime }},$ with the pedigree values for all pairs of individuals in the pedigree, and reflects the summing to zero by construction of the ${\widehat{\beta }}_{j{j}^{\prime }},j\ne j^{\prime }$ coancestries, whereas the pedigree coancestries are necessarily non-negative. The right-hand plot shows a “correction” of the estimates: we took the set of smallest ${\widehat{\beta }}_{j{j}^{\prime }}$ values in the left-hand plot to represent the unrelated (relative to the assumed-unrelated) founders. If we write ${\widehat{\beta }}_0$ as the average value of the set of least-related pairs of individuals then our corrected values ${\widehat{\beta }}_{j{j}^{\prime }}^c$ are

$${\widehat{\beta }}_{j{j}^{\prime }}^c=\frac{{\widehat{\beta }}_{j{j}^{\prime }}-{\widehat{\beta }}_0}{1-{\widehat{\beta }}_0}.$$ (11)

The corrected estimates are clearly close to the pedigree values. However, we are not sure if it is necessary, in general, to undertake this correction process. Whether or not it is applied, the $\widehat{\beta }$ values are still relative to those among all pairs of individuals in a study sample. In general, we will not have any individuals identified for which it is justified to assume zero relatedness or zero inbreeding, and we note the comment by Thompson (2013) “in most populations IBD within individuals is at least as great as IBD between.”

Figure 6.

Comparison of estimated and pedigree coancestries. Uncorrected estimates (Equation 6) on left, corrected estimates (Equation 11) on right.

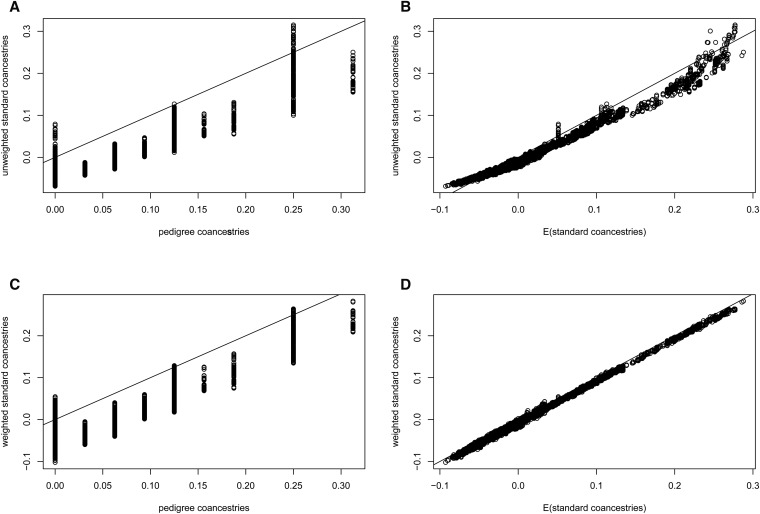
The distributions of estimates in Figure 7A are tightly clustered around nine values, corresponding to the nine distinct pedigree values $i/32,i=0,1,2\dots 6,8,10.$ A contrasting result is shown in Figure 7B, for the standard estimates (Equation 7), calculated as weighted averages over loci (i.e., taking the ratio of the sums over loci of the single-locus estimator numerators and denominators).

There is a current tendency in genome wide association studies (GWAS) to restrict the SNPs used in relatedness estimation to having a minor allele frequency (MAF) above some threshold. For example, the KING manual (http://people.virginia.edu/$\sim$wc9c/KING/manual.html) lists a parameter minMAF to specify the minimum minor allele frequency to select SNPs for relationship inference in homogeneous populations. The thought is that lesser frequencies give rise to biased values, but that is not likely the case if “ratio of averages” estimates are used. To illustrate the effect of MAF filtering, we applied four different thresholds to our simulated data, and we show the means and SDs for estimates for each of nine pedigree values in Table 7. The estimates are the corrected values – i.e., relative to an assigned value of zero for the least-related class. There is clear evidence for the merits of retaining all SNPs, both in terms of bias and variance: all filtered estimates are downwardly biased, and the stronger the filter, the stronger the downward bias.

Table 7. Effects of filtering to L SNPs on coancestry estimate means (and SDs $\times 100$).

Pedigree value	$L=79,069$	$L=72,012$	$L=56,979$	$L=44,061$
	All SNPs	MAF$\ge 0.01$	MAF$\ge 0.05$	MAF$\ge 0.10$
0	0.000 (0.50)	0.000 (1.00)	0.000 (1.99)	0.000 (2.43)
0.03125	0.031 (0.30)	0.026 (0.30)	0.010 (0.89)	0.003 (1.45)
0.06750	0.061 (0.34)	0.056 (0.35)	0.041 (1.13)	0.036 (1.79)
0.09375	0.092 (0.27)	0.087 (0.27)	0.069 (0.72)	0.061 (1.13)
0.12500	0.124 (0.41)	0.120 (0.46)	0.112 (1.90)	0.109 (2.69)
0.15625	0.156 (0.29)	0.151 (0.29)	0.133 (0.65)	0.122 (1.15)
0.18750	0.184 (0.26)	0.179 (0.27)	0.157 (1.07)	0.144 (1.64)
0.25000	0.249 (0.42)	0.245 (0.45)	0.241 (1.87)	0.239 (2.62)
0.31250	0.311 (0.20)	0.307 (0.20)	0.285 (0.77)	0.271 (1.23)

We continued a comparison of our proposed coancestry estimates $\widehat{\beta }$ by applying the estimates described by Wang (2014), listed in Table 8, and computed using the related R package (Pew et al. 2015). Additionally, related offers maximum likelihood estimators, derived by Milligan (2003) and Wang and Santure (2009). They are not computed here, because they require substantial computing time, which may rule them out for genomic data.

Table 8. Other estimates of relatedness.

Method	Description
ped	The pedigree based relatedness
bij	${\beta }_{ij},$ developed here (Equation 4). These values are relative to the mean of the population and hence the mean of these relatedness must be 0
stand.u	The standard estimator, Equation 7 average of ratios
	Identical to the estimator derived by Ritland (1996) [Equation (4) in Wang (2014)] and also used in GCTA Yang et al. (2011)
stand.w	Equation 7, ratio of averages
wang	The estimator developed by Wang (2002)
lynchli	The estimator derived by Lynch (1988) and improved by Li et al. (1993), Equation (7)in Wang (2014)
lynchrd	The estimator derived by Lynch and Ritland (1999) [Equations (5 and 6) in Wang (2014)]
quellergt	The estimator derived by Queller and Goodnight (1989) [Equations (2 and 3) in Wang (2014)]

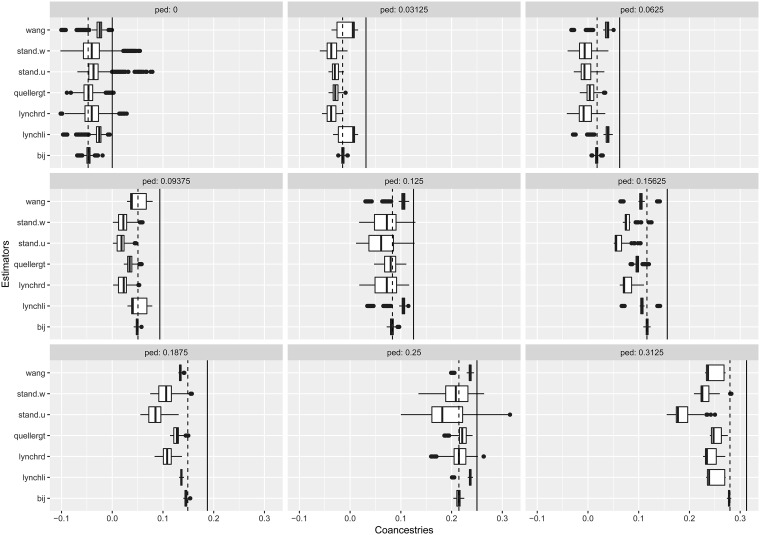
In Figure 8 we display box plots of coancestry estimates for seven alternative estimates, displayed according to nine pedigree values. The solid line for each panel corresponds to the pedigree value. The dashed line corresponds to an adjusted pedigree value, where the adjustment is obtained by subtracting the mean pedigree coancestry from the pedigree values, and dividing this by 1 – the mean pedigree value to insure that the range of possible values are covered. In Figure 6, we used estimates from the least related individuals to adjust the estimates, whereas here we adjusted the pedigree values to have an overall mean of zero.

Figure 8.

Boxplots of coancestry estimates for seven alternative estimates, displayed according to nine pedigree values. Vertical solid black line on each panel shows the pedigree coancestry, and vertical dashed line shows the mean-adjusted pedigree coancestry (see text). Estimators are defined in Table 6. ${\beta }_{j{j}^{\prime }}$ shows very good statistical properties for all mean-adjusted pedigree coancestries.

All the estimates are negatively biased when compared to the pedigree values. When compared to the adjusted pedigree value, the β estimates show extremely good properties, with no bias, and very small variances. Other estimates, while also closer to these adjusted values, mostly underestimate, but sometimes overestimate (e.g., wang, lynchli) the adjusted pedigree values. The standard estimators (weighted or unweighted) consistently underestimate the adjusted pedigree values, except for the unrelated class.

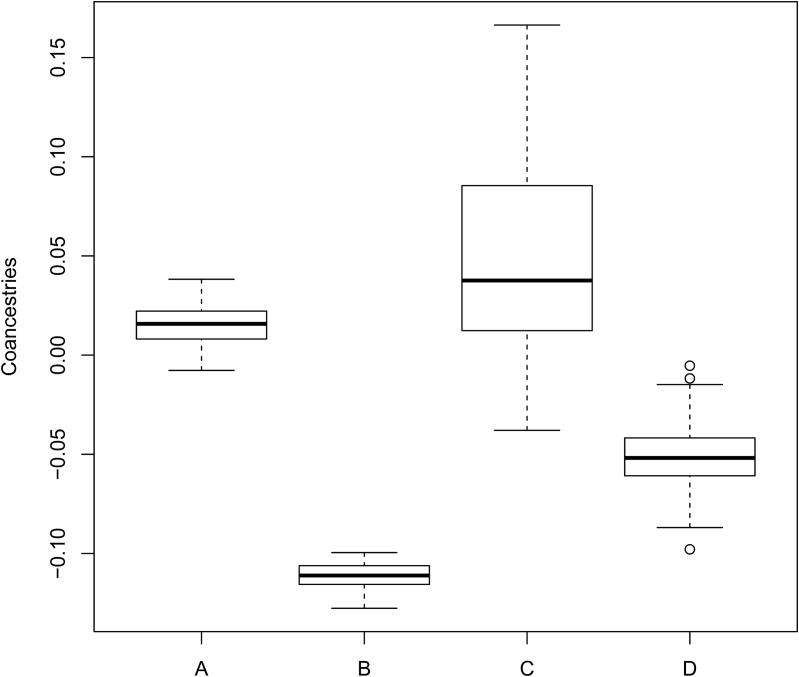
Next, we illustrate how we can recover the average $F_{\mathrm{ST}}$ from the individual coancestries. For this, we use the pedigree described above, but take as founders 10 individuals from each of the two populations (mean $F_{\mathrm{ST}}$ between these two populations is ${\widehat{\beta }}_{\mathrm{ST}}=0.114$). Figure 9 illustrates the accuracy of our β estimates (Equation 6) compared with the standard estimates (Equation 7), for the coancestries of pairs of founders (but with the whole pedigree as the reference population). The $\widehat{\beta }$ values for pairs of founders from the same population (Boxplot A in Figure 9) are tightly distributed around 0.016, while $\widehat{\beta }$’s for pairs of individuals one from each population (boxplot B) are tightly distributed around $-\mathrm{0.111.}$ The distribution for the same two categories for the standard estimator (boxplots C and D) is wider, in particular for pairs of individuals originating from the same population.

Figure 9.

Boxplots of coancestry estimates β (A and B) and the standard estimates (C and D) when the founders come from two populations. Coancestries were estimated for all the individuals in the pedigree shown in Figure 5, but only coancestries between founders are shown. (A and C): pairs of founders from the same population (B and D) pairs when the two members come from different populations.

The ${\widehat{\beta }}_{\mathrm{ST}},$ i.e., the average ${\widehat{F}}_{\mathrm{ST}}$ for the two populations from which the founders originated, is recovered from the individual coancestries as follows: each individual pair coancestry is calculated as ${\widehat{\beta }}_{j{j}^{\prime }}^p=\left({\stackrel{\sim }{M}}_{j{j}^{\prime }}^p-{\stackrel{\sim }{M}}_S^p\right)/\left(1-{\stackrel{\sim }{M}}_S^p\right)$ (Table 3; the superscript p highlights that the estimates are taken over all pairs in the pedigree). We are seeking ${\widehat{\beta }}_{\mathrm{S}{\mathrm{T}}_{f0}}=\left({\stackrel{\sim }{M}}^{S_{f0}}-{\stackrel{\sim }{M}}^{B_{f0}}\right)/\left(1-{\stackrel{\sim }{M}}^{B_{f0}}\right),$ the overall $F_{\mathrm{ST}}$ among the founders only. The mean coancestry of founders from the same population in Figure 9 (boxplot A) corresponds to ${\stackrel{\sim }{S}}_{f0}=\left({\stackrel{\sim }{M}}^{S_{f0}}-{\stackrel{\sim }{M}}_S^p\right)/\left(1-{\stackrel{\sim }{M}}_S^p\right),$ and the mean coancestry of founders, one from each population in the same figure (boxplot B) corresponds to ${\stackrel{\sim }{B}}_{f0}=\left({\stackrel{\sim }{M}}^{B_{f0}}-{\stackrel{\sim }{M}}_S^p\right)/\left(1-{\stackrel{\sim }{M}}_S^p\right).$ Subtracting ${\stackrel{\sim }{B}}_{f0}$ from ${\stackrel{\sim }{S}}_{f0},$ and dividing by $\left(1-{\stackrel{\sim }{B}}_{f0}\right)$ allows elimination of ${\stackrel{\sim }{M}}_S^p$ and recovery of the expression of ${\widehat{\beta }}_{\mathrm{S}{\mathrm{T}}_{f0}}.$ For our situation, this gives ${\widehat{\beta }}_{\mathrm{S}{\mathrm{T}}_{f0}}=\left(0.016-\left(-0.111\right)\right)/\left(1-\left(-0.111\right)\right)=0.114={\widehat{\beta }}_{\mathrm{ST}},$ as expected.

Discussion

A unified approach

Although there has been general recognition that family and evolutionary relatedness are just two ends of a continuum, we are not aware of previous moment estimates of population structure quantities such as $F_{\mathrm{ST}}$ or individual-pair coancestries that rest on this common framework. We have presented estimates that apply equally well to populations and individuals. While their statistical properties remain to be fully explored, it is reassuring to see how well they performed in the few simulations presented here.

Although individual-specific inbreeding coefficient, and individual-pair-specific coancestry coefficient moment estimates, are used routinely in association studies, we have not seen widespread adoption of population-specific $F_{\mathrm{ST}}$ moment estimates in evolutionary studies. We have shown here, theoretically and empirically, that these values can differ substantially among populations. This may simply reflect population size and migration rate differences, but different values for specific loci may also provide signatures of natural selection: see Balding and Nichols (1995), Beaumont and Balding (2004), Foll and Gaggiotti (2008) and Weir et al. (2005) for example. There is a growing literature for Bayesian analyses that address population-specific parameters (e.g., Karhunen and Ovaskainen 2012; Günther and Coop 2013), although these may not be amenable to analyses of genome-wide variant data.

There is also general understanding that identity by descent is a relative concept, rather than an absolute concept. This understanding has not led to an apparent recognition that the standard estimates of inbreeding and kinship are not unbiased for expected or pedigree values. Replacing population allele frequencies by sample values leads to bias in the usual estimates, regardless of sample size. Whenever sample allele frequencies from a study are used to estimate inbreeding or coancestry coefficients, the estimators are affected by the inbreeding and coancestry values for all study individuals. We will come back to this point in the section containing Equation 13

We also stress that all allelic variants, whatever their frequencies, need to be included in the estimation of population structure and inbreeding or relatedness. The estimates certainly depend on the allele frequencies, and restricting the range of frequencies used may reveal features of interest, but the underlying ibd parameters do not depend on the frequencies (see Equation 1 with the ibd interpretation). Exclusion of some alleles based on their frequencies will lead to biased estimates of the parameters as shown in Table 7.

Previous estimates

Weir and Cockerham estimates of $F_{\mathrm{ST}}$:

The $F_{\mathrm{ST}}$ estimate of WC84 has been widely adopted, and it performs well for the model stated in that paper: data from a series of independent populations with equivalent histories and sizes. In the present notation, WC84 assumed ${\theta }^i=\theta ,{\theta }^{i{i}^{\prime }}=0$ for all populations i and all $i^{\prime }\ne i.$ The estimate was designed to be unbiased for any number of sampled populations, any sample sizes and any number of alleles per locus. The analysis was a weighted one over populations: the average allele frequencies ${\overline{p}}_u$ for a study had sample size weights, ${\overline{p}}_u={\displaystyle {\sum }_i{n}_i{\stackrel{\sim }{p}}_{iu}}/{\displaystyle {\sum }_i{n}_i}$ for $n_i$ alleles sampled from population i. Although our β estimates do not make explicit mention of allele frequencies, there is implicit use of sample frequencies that are unweighted averages over populations.

Weighting over populations has been discussed by Tukey (1957) and Robertson (1962). Those authors were concerned with bias and variance, and they used the language of variance components, within and between populations. For allele u, these components were given as $\left(1-\theta \right)p_u\left(1-p_u\right)$ and $\theta p_u\left(1-p_u\right),$ respectively, by WC84. Tukey said “In practice, we select two quadratic functions by some scheme involving intuition, find how their average values are expressed linearly in terms of the variance components, and then form two linear combinations of the original quadratics whose average values are the variance components. These linear combinations are then our estimates. Much flexibility is possible.” The estimates of WC84, Weir and Hill (2002) and Bhatia et al. (2013) all have this structure, although ratios of linear combinations are taken to remove the allele frequency parameters. Tukey went on to say that the weights $w_i=n_i$ (in the present notation) “gives the customary analyses, which treat observations as important and columns [i.e. populations] as unimportant.” Further, “the choice $w_i=1$ … treat the columns as important. This [unweighted] approach is appropriate when the column variance component is large compared with the within variance component.” Robertson (1962) also pointed to sample-size weights for small between-population variance components and equal weights for large values. Bhatia et al. (2013) were concerned with unequal $F_{\mathrm{ST}}$ values so their use of equal weights is consistent with Turkey’s statements. Their work provides simple averages of the different $F_{\mathrm{ST}}$ values as opposed to averages weighted by sample sizes. For unequal $F_{\mathrm{ST}}$ and unequal sample sizes, Weir and Hill (2002) said “the usual moment estimate [with sample-size weights] is of a complex function [of the $F_{\mathrm{ST}}$’s].” In our current model of unequal ${\theta }^i$ and nonzero ${\theta }^{i{i}^{\prime }},$ we agree that unweighted analyses (population weights of 1) are appropriate, and that is what we have used in this paper. We note that Tukey’s “flexibility” in the choice of moment estimators, phrased in terms of weights, does not arise with maximum likelihood approaches. If sample allele frequencies are taken to be approximately normally distributed, then REML methods give appropriate and unique estimates.

What are the consequences of using the WC84 estimates when the current model of unequal ${\theta }^i$ and nonzero ${\theta }^{i{i}^{\prime }}$ is more appropriate? We can show that the expected value of the Weir and Cockerham estimate ${\widehat{\theta }}_{\mathrm{WC}}$ is

$$\mathrm{ℰ}\left({\widehat{\theta }}_{\text{WC}}\right)=\frac{{\theta }^{W\ast }-{\theta }^{B\ast }+Q}{1-{\theta }^{B\ast }+Q}.$$

This expression uses three functions of sample sizes: $\overline{n}={\displaystyle {\sum }_{i=1}^r{n}_i/r},$ $n_i^c=n_i-n_i^2/{\displaystyle {\sum }_i{n}_i}$ and $n_c={\displaystyle {\sum }_i{n}_i^c/\left(r-1\right)}.$ The two weighted averages are ${\theta }^W\ast ={\displaystyle {\sum }_i{n}_i^c{\theta }^i}/{\displaystyle {\sum }_i{n}_i^c}$ and

${\theta }^B\ast ={\displaystyle {\sum }_i{\displaystyle {\sum }_{i^{\prime }\ne i}{n}_i{n}_{i^{\prime }}{\theta }^{i{i}^{\prime }}}}/{\displaystyle {\sum }_i{\displaystyle {\sum }_{i^{\prime }\ne i}{n}_i{n}_{i^{\prime }}}}.$ The quantity Q is $\left[{\displaystyle {\sum }_i\left(n_i/\overline{n}-1\right){\theta }^i}\right]/\left[n_c\left(r-1\right)\right].$ For equal sample sizes, $n_i=n,$ or, for equal values of $F_{\mathrm{ST}},$ ${\theta }_W^i={\theta }^W={\theta }^W\ast =\theta ,$ and $Q=0.$ Under these circumstances $\mathrm{ℰ}\left({\widehat{\beta }}_{\mathrm{WC}}\right)=\left({\theta }^W-{\theta }^B\right)/\left(1-{\theta }^B\right),$ and we find the WC84 estimator performs well unless ${\theta }^i$ and/or $n_i$values are quite different. We stress though that it is $\left({\theta }^W-{\theta }^B\right)/\left(1-{\theta }^B\right)$ being estimated.

Nei estimates of $F_{\mathrm{ST}}$:

Although we have phrased estimates in terms of matching proportions, we note that they are the complements of “heterozygosities” $\stackrel{\sim }{M}=1-\stackrel{\sim }{H}.$ Our approach uses ${\stackrel{\sim }{M}}^B,$ the average population-pair allele matching, whereas most previous treatments, from Nei (1973) onwards, use total heterozygosities ${\stackrel{\sim }{H}}^T=1-{\displaystyle {\sum }_u{\overline{p}}_u^2}$ where ${\overline{p}}_u$ is the average sample allele frequency over populations: ${\overline{p}}_u={\displaystyle {\sum }_{i=1}^r{\stackrel{\sim }{p}}_{iu}/r}.$ For large sample sizes, ${\stackrel{\sim }{H}}^T=\left(r-1\right){\stackrel{\sim }{H}}^B/r+{\stackrel{\sim }{H}}^W/r$ and Nei’s $G_{\mathrm{ST}}$ quantity and its expectation, in our notation, are

$$\begin{array}{c}{G}_{\mathrm{ST}}=1-\frac{{\stackrel{\sim }{H}}^W}{{\stackrel{\sim }{H}}^B-\frac{1}{r}\left({\stackrel{\sim }{H}}^B-{\stackrel{\sim }{H}}^W\right)},\\ \mathrm{ℰ}\left(G_{\mathrm{ST}}\right)=\frac{{\theta }^W-{\theta }^B}{1-{\theta }^B+\frac{1}{r-1}\left(1-{\theta }^W\right)},\end{array}$$ (12)

which reduce to ${\widehat{\beta }}_{\mathrm{WT}}$ and $\mathrm{ℰ}\left({\widehat{\beta }}_{\mathrm{WT}}\right)$ as r becomes large. Otherwise, the expectation of $G_{\mathrm{ST}}$ depends on the number r of populations. This expectation is bounded above by one, contrary to the claim of Bhatia et al. (2013). Nei and Chesser (1983) and Nei (1987) modified Nei’s earlier approach to remove the effects of the number of populations. Bounds on $F_{\mathrm{ST}},$ when that is defined as $\left(1-{\stackrel{\sim }{H}}^W/{\stackrel{\sim }{H}}^T\right),$ were given by Jakobsson et al. (2013).

Jost (2008) pointed out that $G_{\mathrm{ST}}$ does not provide a good measure of differentiation among populations, where differentiation reflects the collection of allele frequencies $p_{iu},$ or their sample values ${\stackrel{\sim }{p}}_{iu}.$ We regard θ as an indicator of evolutionary history, rather than of allele frequencies, and we interpret it as probabilities of pairs of alleles being identical by descent. Jost introduced $D=\left(H^B-H^W\right)/\left(1-H^W\right)$ or $D=\left({\theta }^W-{\theta }^B\right)/{\theta }^W$ as a measure of differentiation among populations. For the two-population drift scenario without mutation, D, unlike ${\beta }_{\mathrm{WT}},$ does not have a simple dependence on time, and so does not serve as a measure of evolutionary distance.

Standard coancestry estimates:

The expressions in Equation 7 provide unbiased estimates of ${\theta }_{jj}=\left(1+F_j\right)/2$ and ${\theta }_{j{j}^{\prime }},j\ne j^{\prime }$ when the allele frequencies are known. When study sample allele frequencies are used, however, the expectations of these expressions, for one locus, are

$$\mathrm{ℰ}\left({\widehat{\theta }}_{j{j}^{\prime }}\right)=\frac{\left({\theta }_{j{j}^{\prime }}-{\psi }_j-{\psi }_{j^{\prime }}+{\theta }_S\right)-\frac{1}{n}\left({\theta }_{jj}+{\theta }_{j^{\prime }{j}^{\prime }}-{\psi }_j-{\psi }_{j^{\prime }}-F_S+{\theta }_S\right)}{\left(1-{\theta }_S\right)-\frac{1}{n}\left(F_S-{\theta }_S\right)}$$ (13)

where $F_S={\displaystyle {\sum }_{j=1}^n{\theta }_{jj}/n}$ is the average of all within-individual coancestries $\left(1+F_j\right)/2,$ ${\psi }_j={\displaystyle {\sum }_{j^{\prime }=1,j^{\prime }\ne j}^n{\theta }_{j{j}^{\prime }}/\left(n-1\right)}$ is the average coancestry of individual j to all other individuals, and ${\theta }_S={\displaystyle {\sum }_{j=1}^n{\psi }_j/n}.$ These expectations also hold for both the average over loci of the ratios for each locus, and for the ratio of averages when each locus has the same values of ${\theta }_{j{j}^{\prime }}.$ Note the difference with the expected values of ${\widehat{\beta }}_{i{i}^{\prime }}$ shown in Table 2.

The differences diminish for studies with large numbers of individuals:

$$\mathrm{ℰ}\left({\widehat{\theta }}_{j{j}^{\prime }}\right)\approx \frac{{\theta }_{j{j}^{\prime }}-{\psi }_j-{\psi }_{j^{\prime }}+{\theta }_S}{1-{\theta }_S}$$

They diminish further for low average coancestries ${\psi }_{j\prime },{\psi }_{j^{\prime }}$ of the target individuals with other study individuals. An equivalent expression was given by Ochoa and Storey (2016b). The extent of bias of ${\widehat{\theta }}_{j{j}^{\prime }}$ depends on the number of individuals in the sample, and how different the average coancestry of a target individual with all other study individuals ${\psi }_j$ is from the average coancestry of all pairs of study individuals. However, the standard ${\widehat{\theta }}_{j{j}^{\prime }}$ estimates are not unbiased for ${\theta }_{j{j}^{\prime }}.$ This is illustrated in Figure 10, which displays, for the pedigree discussed previously (Figure 5) with founders originating from one population, the relation between the unweighted or weighted standard coancestry estimates (Equation 7) and pedigree coancestries in the left column, and the relation between the unweighted or weighted standard coancestries estimates and their expectation given by Equation 13 in the right column (B and D). The estimated standard coancestries do not match well the pedigree coancestries (Figure 10, A and C), contrary to the good match for ${\widehat{\beta }}_{ij}$ (see Figure 6), which leads to the overdispersion of standard coancestry estimates seen in Figure 7B. But, standard coancestries match very well their expected values given by Equation 13, particularly so for the weighted standard coancestries (Figure 10D).

Figure 10.

Comparison of standard coancestry estimates (Equation 7) against pedigree coancestries (A and C) or against their expected values from Equation 13 (B and D), using the pedigree shown in Figure 5 and genotypes derived from founders originating from a single population. (A and B): unweighted standard coancestries; (C and D): weighted standard coancestries.

The standard estimates of Equation 7 appear as elements of the Genetic Relatedness Matrix (GRM) of Yang et al. (2011). We are grateful to P. Visscher (personal communication) for pointing out that the GRM was not designed for the purpose of kinship estimation, but was for estimating genetic variances in association mapping.

Population history

We commented earlier that $F_{\mathrm{ST}}$ can serve as a measure of genetic distance among populations in the sense that, for the genetic drift model, it depends on the time since the sampled populations diverged from an ancestral population. We see the need for further exploration of the role of population-specific $F_{\mathrm{ST}}$ estimates in evolutionary genetic studies, given the generally unrecognized prevalence of negative expected values for populations with correlated allele frequencies shown in Figure 1, and the relationship of estimates with the site-frequency spectrum suggested in Figure 4.

Conclusion

We have presented moment estimators for the probabilities that pairs of alleles, taken from individuals or from populations, are ibd relative to the ibd probabilities for alleles from all pairs of individuals or populations in a study. By identifying the reference set of alleles as those in the current study, we allow for negative values of measures of population structure or relatedness and their estimates. Alleles may have smaller ibd probabilities within some populations than between all pairs of populations in a study, for example. Some pairs of individuals in a study will be less related than the average for all pairs. Our estimates are phrased in terms of the proportions of pairs of alleles, within and between populations or individuals, that are of the same type (ibs).

For sets of populations, we advocate the use of population-specific $F_{\mathrm{ST}}$ values, as these more accurately reflect population history. For sets of individuals, our estimates seem to behave at least as well as those given previously. We note that our estimates have the same logical basis, and algebraic expressions, for populations and for individuals. The chief novelty of our method-of-moments approach is in allowing for allele frequencies to be correlated among populations when characterizing population structure, and correlated among all individuals when characterizing individual-pair relatedness.