Abstract
Mobile genetic elements can be found in almost all genomes. Possibly the most common nonautonomous mobile genetic elements in bacteria are repetitive extragenic palindromic doublets forming hairpins (REPINs) that can occur hundreds of times within a genome. The sum of all REPINs in a genome can be viewed as an evolving population because REPINs replicate and mutate. In contrast to most other biological populations, we know the exact composition of the REPIN population and the sequence of each member of the population. Here, we model the evolution of REPINs as quasispecies. We fit our quasispecies model to 10 different REPIN populations from 10 different bacterial strains and estimate effective duplication rates. Our estimated duplication rates range from ∼5 × 10−9 to 15 × 10−9 duplications per bacterial generation per REPIN. The small range and the low level of the REPIN duplication rates suggest a universal trade-off between the survival of the REPIN population and the reduction of the mutational load for the host genome. The REPIN populations we investigated also possess features typical of other natural populations. One population shows hallmarks of a population that is going extinct, another population seems to be growing in size, and we also see an example of competition between two REPIN populations.
Keywords: REP sequences, mobile genetic elements, evolution, bacteria, quasispecies
REPETITIVE sequences are common in most bacterial genomes, but rare compared to their prevalence in most eukaryotic genomes (Versalovic et al. 1991; Jurka et al. 2007). A large proportion of repetitive sequences in bacterial genomes are the result of self-replicating DNA sequences. These sequences usually encode an enzyme called a transposase that specifically copies its own sequence (Mahillon and Chandler 1998). There are also repetitive sequences that do not encode a transposase themselves, but are copied by a transposase that is encoded elsewhere in the genome. These elements are referred to as miniature inverted repeat transposable elements (MITEs) (Wessler et al. 1995). MITEs were first described in plant genomes (Bureau and Wessler 1994) and later also in bacteria (Oggioni and Claverys 1999). Recently, it has been shown that repetitive extragenic palindromic (REP) sequences (Higgins et al. 1982) or more specifically REP doublets forming hairpins (REPINs) (Bertels and Rainey 2011b), one of the most abundant repeat families in bacteria, are also MITEs (Nunvar et al. 2010; Bertels and Rainey 2011a,b; Ton-Hoang et al. 2012).
REP sequences are ∼25-bp-long, highly abundant sequences in bacterial genomes (Higgins et al. 1982; Aranda-Olmedo et al. 2002; Silby et al. 2009). They contain a short imperfect palindromic sequence that can form hairpins in single-stranded DNA or RNA. REP sequences mostly occur in noncoding DNA between genes and are part of REPINs. REPINs in most Pseudomonas strains consist of two REP sequences in inverted orientation separated by a highly diverse nucleotide sequence (Bertels and Rainey 2011b). REPINs are a replicative unit and are mobilized by REP-associated tyrosine transposases (RAYTs) (Nunvar et al. 2010; Bertels and Rainey 2011b; Ton-Hoang et al. 2012). Although the structure of REPINs in Pseudomonas is well defined, for REPINs in Escherichia coli there has not been an extensive study on what exactly comprises the replicative unit. Nevertheless, RAYTs in E. coli have been shown to bind to REP sequences and cleave DNA once they are bound (Messing et al. 2012; Ton-Hoang et al. 2012). Thus, in a fashion similar to IS200 sequences (Barabas et al. 2008; Ton-Hoang et al. 2010) and almost every other known insertion sequence (Mahillon and Chandler 1998), RAYTs presumably transpose REPINs by cutting them out of the genome and pasting them into another part of the genome. This implies that REPINs do not acquire additional mutations as they are copied, which is an important insight for modeling REPIN evolution.
The occurrence of REP sequences and associated functions have been described in many different bacterial genomes (Higgins et al. 1982; Aranda-Olmedo et al. 2002; Silby et al. 2009). REP evolution has not been studied in detail before the description of REPINs (Bertels and Rainey 2011a,b) and nothing is known about the duplication rates of REPINs. Although we know that closely related E. coli strains contain varying numbers of REP sequences, this may not be a direct result of replication. Instead it may be more likely that it is a consequence of the extremely dynamic genome composition of E. coli (Touchon et al. 2009), where REP sequences get deleted or inserted together with other parts of the genome. However, the lack of evidence for novel REPIN insertions probably means that duplication rates are low, despite the presence of hundreds of REPINs in some genomes (Bertels and Rainey 2011b).
As it is difficult to study the evolution of the complete REPIN sequence due to the highly diverse loop region (which is probably strongly affected by recombination), we model the evolution of the most conserved 25 bp at each end of the REPIN. The beauty of studying REPINs in bacterial genomes is that we know the exact composition of the population at the time of genome sequencing, something that is impossible to achieve for almost any other population study.
We model the evolution of REPINs with a quasispecies model. To infer duplication rates, we first fit the equilibrium of our quasispecies model for a REPIN population from Pseudomonas fluorescens SBW25 and later for nine other bacterial genomes. Our results show that despite the large divergence between the bacterial strains, our inferred effective duplication rates are very similar and very low. All rates fall into a narrow margin between one REPIN duplication in ∼65 × 106 and host divisions. Hence, if a bacterium were to divide every 40 min, it would take ∼5000 years for a specific REPIN duplication to fix in the population. The astonishing rarity of these events may explain the lack of evidence for novel REPIN insertions in bacterial genomes.
Materials and Methods
Quasispecies model
The quasispecies model describes the mutation–selection balance of a set of similar sequences that evolve on a fitness landscape. Sequences with high fitness leave many offspring, sequences with low fitness leave few offspring. The fitness landscape is traversed by acquiring mutations (Eigen 1971; Eigen and Schuster 1977; Nowak 1992).
The quasispecies model has been applied previously, mostly to model viral populations (Seifert et al. 2015; Domingo and Schuster 2016). Here, we model REPIN sequences that mutate and duplicate: the fitness in the quasispecies model corresponds to the REPIN duplication rate, and the model’s mutation rate to the genome mutation rate (Figure 1). We assume that the REPIN population in our genome is a quasispecies in equilibrium. The most abundant sequence in our population is our master sequence. With increasing genetic distance to the master sequence, fitness changes. For our model, we assume five discrete mutation classes (Supplemental Material, File S10). The zeroth class contains the master sequence. Sequences differing in one, two, or three positions are in the next three classes. All remaining sequences are in the fourth mutation class. The frequencies of the sequences belonging to each of these classes i are given by The population evolves to a mutation–selection balance as described by the standard quasispecies equation (Page and Nowak 2002; Bull et al. 2005)
| (1) |
In our case, n equals 4. The fitness of sequences belonging to each class j is given by and the average fitness of the population is given by The probability that a sequence from class j mutates into class i is given by In our model, sequences can only acquire a single mutation per time step. Hence, is a tridiagonal matrix with nonzero entries in the main diagonal (no mutation), the first diagonal above (sequence acquires an additional mutation), and the first diagonal below (sequence loses a mutation and reverts to the previous class). For a mutation rate μ and a sequence length L, the probability of transitioning to the next mutation class is and to the previous mutation class is For the fourth mutation class, we assume a back mutation rate of zero. We also assume that the mutation rate of REPINs only depends on the host mutation rate. Mutations that occur during the duplication process are assumed to be negligible.
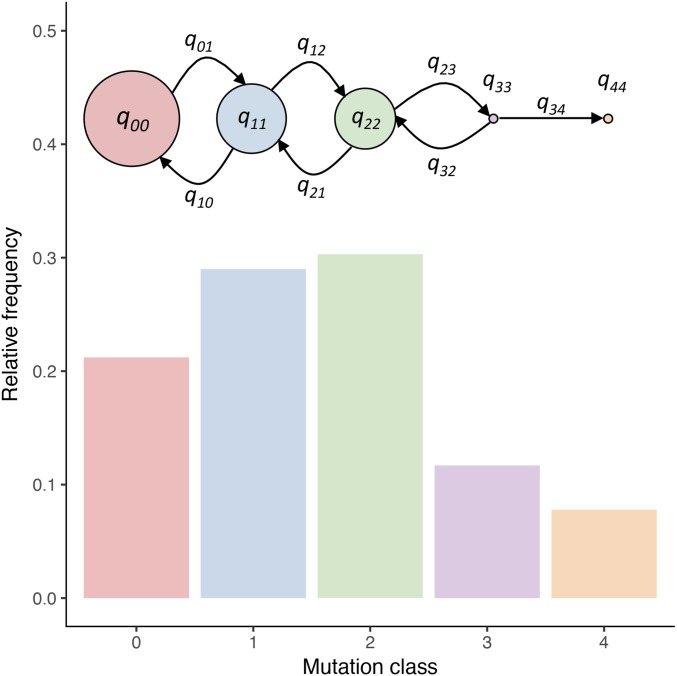
Figure 1.
Exemplar results for a quasispecies model. For a mutation rate of and the fitnesses as given in Table 2 (1 + scaled duplication rate), we illustrate the equilibrium distribution of the relative frequencies of P. fluorescens SBW25 REPINs. The radii of the circles indicate the duplication rate (see Equation 2). Note that the actual fitness differences are extremely minute at the level of The cartoon merely illustrates the architecture of the fitness landscape. The mutation probabilities are given by while self-replication occurs with probability
Parameterizing the quasispecies model
We set the fitness of the highest mutation class to one: For a given set of equilibrium sequence frequencies, we can then calculate the relative fitness of the remaining four mutation classes for a given mutation rate (see File S6 and File S7). For all our bacteria we assume a host mutation rate of which was inferred for E. coli (Wielgoss et al. 2011). The duplication rates for fitness values are then
| (2) |
Stochastic simulations
For each REPIN population, we performed a finite population simulation to determine the extent of stochastic fluctuation on the equilibrium frequencies. These fluctuations mainly depend on the REPIN population size. As we cannot simulate evolution for the genome mutation rate, we adjusted our fitness values to fit a mutation rate of With the new mutation rate, each discrete time step corresponds to bacterial generations. The equilibrium frequencies for the new mutation rate remain similar if we scale up the fitness values to which holds as long as (File S8).
We start the simulation with a clonal population of the master sequence at carrying capacity, which is set to the number of REPINs observed in the genome. The number of offspring each sequence leaves in each generation is equal to the sequence’s fitness. If the number of offspring exceeds the carrying capacity, a random selection of the same size as the carrying capacity survives to the next time point. We simulated a total of generations.
To infer confidence intervals for our fitness estimates, we computed fitness values from sequence frequencies at various time points during the simulation. We sampled the sequence frequencies of each mutation class every 100 time steps, starting from time point 1000 and ending at time step 20,000 in our simulations.
We repeated each simulation 100 times and measured the proportion of simulations where the zeroth mutation class did not persist (i.e., the master sequence had completely decayed).
Determining REPIN populations
We extracted REPIN populations from 10 bacterial genomes in the following manner: For each of the genomes we determined the most common 25-bp-long sequence. We then recursively searched the entire genome for all sequences that have a Hamming distance of up to two to all identified sequences until no more sequences were found. We call these sequences REP sequences. For all REP sequences, we determined whether they were part of a sequence cluster by checking whether there were any additional occurrences in a vicinity of 130 bp. From these sequence clusters we extracted REPINs. REPINs consist of two adjacent REP sequences that are found in opposite directions (one on the positive and one on the negative DNA strand, also called inverted repeats) in the DNA sequence. The REPINs we found were extracted and joined together. REP sequences found as direct repeats or as singlets in the genome were also extracted (as single sequences). We added another 25 bp of adenine nucleotides at the end of each REP singlet in our data to make them easily comparable with REPINs. Hence the Hamming distance between REP singlet and REP doublet is at least 25.
Clustering REPIN sequences
REPIN populations can be represented as sequence networks. In these networks, each node represents a sequence. An edge between nodes exists if the Hamming difference between the sequence pair is one. Because REPIN populations in Pseudomonas do not always evolve on a single peak due to the presence of multiple RAYTs (transposases) in the genome, we extracted subpopulations clustered around the master sequence. We determined these subpopulations for all Pseudomonas strains by applying a Markov clustering algorithm implemented in the MCL package (van Dongen 2000) with the inflation parameter set to 1.2 to the sequence network. The MCL algorithm simulates random walks on a stochastic graph by alternating between expansion and inflation operations, where larger inflation parameters will lead to more fragmented networks.
We used the largest REPIN cluster for our analyses. Since these clusters exclude decayed sequences far from the master sequences, we also included all sequences with a Hamming distance of up to two to any sequence in the cluster. Of the sequences identified in the last step, we only included instances that occurred less than three times in the genome. Sequences that occur more than three times in the genome are likely to have been duplicated by other RAYTs.
Inferring an error threshold
The error threshold defines a critical point in a quasispecies where, with the given fitness values and mutation rate, it is impossible to maintain the master sequence for a single peaked fitness landscape. Here we deviate slightly from this definition as we define the error threshold as the point where the master sequence cannot be maintained at a relative frequency of >1%. To determine the duplication rate at which we reach our error threshold, we reduced all fitness values in decrements of As soon as one of the five fitness parameters reaches one, this parameter will remain constant for the remainder of the procedure. We performed this procedure for the fitness landscape of each species separately.
Data availability
All genomes are publicly available on GenBank (https://www.ncbi.nlm.nih.gov/genbank/) under the accession numbers listed in Table 1.
Table 1. List of accession numbers for genomes used in this study.
| Species name | NCBI accession no. |
|---|---|
| P. syringae pv. tomato DC3000 | NC_004632.1 |
| P. synxantha BG33R | CM001514 |
| P. fluorescens A506 | NC_017911 |
| P. fluorescens SBW25 | NC_012660.1 |
| P. putida GB1 | NC_010322.1 |
| E. coli 536 | NC_008253.1 |
| E. coli K-12 MG1655 | CP014225.1 |
| E. coli UTI89 | NC_007946.1 |
| E. coli B REL606 | NC_012967.1 |
| E. coli UMN026 | NC_011751.1 |
NCBI, National Center for Biotechnology Information.
We included eight supplemental files: File S1 contains detailed descriptions of all supplemental files. File S2 contains the sequence and frequency of the most common 25-bp-long sequence, the gene name of the flanking RAYT and the number of RAYTs, in all of the bacteria analyzed in this study. File S3 contains the modeling and simulation results for all 10 REPIN populations we analyzed in our study. File S4 contains the proportion of symmetric REPINs in all identified sequences from all studied strains. File S5 contains the effective duplication rates and equilibrium frequencies for each of the 10 REPIN populations at the error threshold. File S6 provides the Mathematica code for calculating equilibrium frequencies, fitness values, and error thresholds for all 10 REPIN populations. File S7 contains the same Mathematica code as a PDF. File S8 contains a figure showing that the adjusted equilibrium frequencies remain constant for small mutation rates. File S9 contains the sequence frequencies of the different mutation classes for all 10 REPIN populations. File S10 presents data showing that choosing five mutation classes is optimal for our data sets.
Results and Discussion
REPINs in P. fluorescens SBW25
In P. fluorescens SBW25, REPINs consist of two inverted highly conserved sequences that are 25 bp in length and are separated by a sequence of varying length that shows low levels of conservation (Bertels and Rainey 2011a,b). The processes that lead to the varying levels of conservation in REPINs are not well understood. Hence, we focus our analysis only on the most conserved 25 bp flanking the REPIN. These sequences were discovered a long time ago in E. coli and have been called REP sequences (Stern et al. 1984). The most common 25-bp-long sequence occurs 265 times in the SBW25 genome and is usually part of a REPIN (Bertels and Rainey 2011b). If we allow for nucleotide changes in the REP sequence, we end up with a REP population that contains 932 REP sequences. For all these 932 sequences, we determined whether they were part of a REPIN or not and displayed the resulting sequences as a sequence network and (Figure 2).
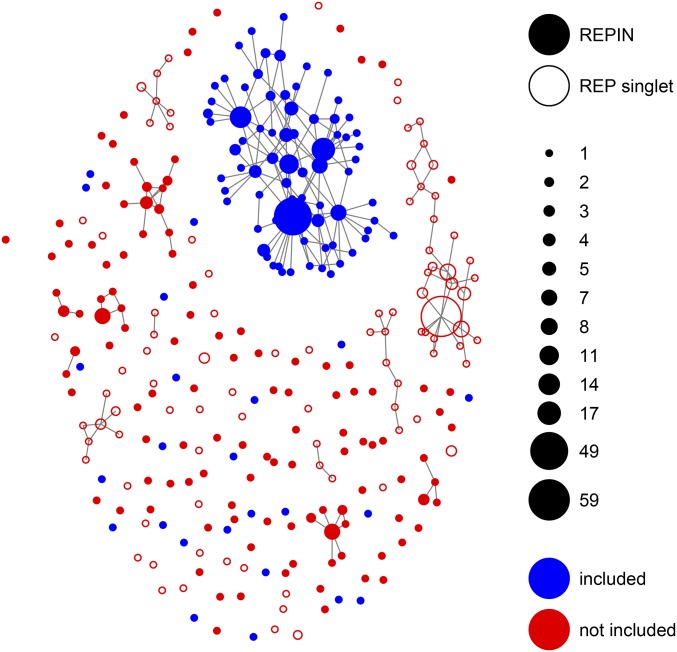
Figure 2.
Structure of the REPIN population in SBW25. REPINs that differ in exactly one position are connected. REP sequences that do not form REPINs (e.g., singlets) are shown as ○. Blue included nodes belong to the REPIN population for which we infer duplication rates. Red (“not included”) nodes were excluded from the analysis because they likely evolve on a more complex fitness landscape that is more difficult to model. The size of the nodes indicates the frequency of the corresponding sequence in the SBW25 genome.
The population network in Figure 2 has many sequence hubs distantly related and not connected to the master sequence. Instead of a very rugged activity landscape of a single RAYT (the transposase responsible for duplicating REPINs), we hypothesize that it is more likely that these hubs were manifested by the concurrent activities of multiple RAYT transposases (the SBW25 genome contains three RAYT genes). As it is impossible to accurately model this complexity for small REPIN populations, we decided to reduce the REPIN population to all sequences that are part of the largest cluster as well as all sequences that are at most 2-bp different from any sequence that is part of the cluster.
The “included” subpopulation selected in Figure 2 has 243 members. We model this subpopulation as a quasispecies, with five sequence classes, that are 0, 1, 2, 3, and >3 mutations away from the master sequence. Modeling five mutation classes is optimal for our data sets, as it represents a trade-off between robustness and accuracy of the inferred fitness values (see File S10). To infer fitness values for our quasispecies model in SBW25, we assume that the population is in equilibrium and the frequencies of the sequences we observe are steady state frequencies (Table 2).
Table 2. Inferred REPIN duplication rates in P. fluorescens SBW25.
| Mutation class | Inferred duplication rate (× 10−9)a | Scaled duplication rate (× 10−9)b | Mean duplication rate (simulation) | SD duplication rate (simulation) |
|---|---|---|---|---|
| 0 | 10.9 | 11.3 | 13.1 | 2.4 |
| 1 | 7.6 | 8.1 | 10.3 | 2.5 |
| 2 | 6.7 | 7.1 | 9.4 | 2.4 |
| 3 | −0.4 | 0 | 2.0 | 2.5 |
| 4 | 0.0 | 0.4 | 1.4 | 2.5 |
We identified the master sequence 5′-ATGTGGGAGGGGGCTTGCCCCCGAT-3′ in the data and inferred the frequency of the different mutation classes. We use the equilibrium of our quasispecies model to calculate the associated fitness values and set to 1, where is
The scaled duplication rate is:
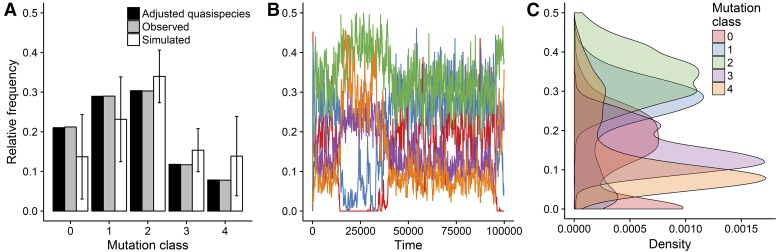
The quasispecies equation provides us with a set of fitness values that perfectly recapitulate the observed frequencies for infinitely large populations (Figure 3A). However, REPIN populations are relatively small, which means that population size will have a strong effect during REPIN evolution. To estimate stochastic effects, we used the calculated fitness parameters for each mutation class to perform a stochastic simulation with a maximum of 243 individuals (Figure 3B). Our simulation shows that the distributions of the mutation classes are wide, particularly for the master sequence, which is an effect of the small population size (Figure 3C).
Figure 3.
Inferred and observed steady state REPIN frequencies in P. fluorescens SBW25. (A) The observed frequencies of each mutation class are identical to the equilibrium frequencies for our quasispecies model at a mutation rate of (observed). We adjusted time to allow us to do simulations at a mutation rate of i.e., each time step lasts long enough to allow for ∼10−4 mutations to occur for an underlying mutation rate of (adjusted quasispecies). The resulting adjusted quasispecies equilibria agree almost perfectly with the observed frequencies. A simulation of a simulation (105 generations) with the same fitness values allows us to infer the variation of these frequencies (simulated). (B) Relative frequencies obtained from the simulation using the adjusted fitness values for generations. (C) Density plot of the relative frequencies of the mutation classes from our simulation.
Inferred duplication rates of REPINs are low
The rate at which duplications occur can be calculated from the inferred fitness values (see Equation 2). The duplication rate we inferred for the master sequence in SBW25 is per generation and per sequence. However, this means that for the third mutation class, we infer negative duplication rates (Table 2). Unless there is an active deletion process for these mutation classes, these duplication rates are unlikely to be accurate. Alternatively, it is possible that members of the fourth mutation class are more likely to replicate than members of the third mutation class. This could be true as it is possible that these sequences are also recognized by a second RAYT transposase in the SBW25 genome. To alleviate this problem, we can scale up all mutation classes so that the lowest fitness is one. This scaling does not affect the equilibrium frequencies of the different mutation classes. The rescaled fitness values result in a higher duplication rate of the master sequence’s mutation class of instead of (Table 2).
Our data also show that the duplication rates of mutation class 4 is very low compared to that of mutation classes 0, 1, and 2 to This raises the possibility that these values are not significantly different from zero. To test this possibility, we inferred duplication rates for mutation class frequencies at 200 time points during our simulation. We then inferred fitness values for each of these 200 samples, which allowed us to determine confidence intervals for our duplication rates (Table 2). The confidence intervals show that both mutation classes 3 and 4 are not significantly different from zero and may not actively be duplicated in the genome.
To understand how low the inferred mutation rates are, we can calculate how long it would take for a single REPIN duplication to spread through a large bacterial population. If we assume one cell division takes 40 min and novel REPIN insertions to be selectively neutral, then it would take ∼7000 years until a novel REPIN master sequence fixes in the SBW25 population. This would explain, why, to our knowledge, there is no report of novel REPIN insertions within genomes of experimental SBW25 (or other bacterial) populations. It may also explain why REPINs can be maintained for long times within a genome without being selected against. Due to the rarity of duplication events, the negative fitness effects resulting from transposition [e.g., transposition is likely to disrupt genes because ∼88% of the SBW25 genome are coding regions (Silby et al. 2009)] are probably negligible.
Limitations of our quasispecies model
As for any mathematical model of a complex biological system there are also limitations for our quasispecies model.
For example, we cannot infer fitness values for any specific sequence except for the master sequence. For all other mutation classes, our model only infers average fitness values. Across one mutation class there may be many reasons for why the fitness of one sequence may be different to another sequence’s fitness. For example, biochemical interactions could make it more likely that some sequences within a mutation class are more likely to duplicate than others.
Another complication not taken into account by our model is the fact that the SBW25 genome contains three different RAYT genes, each associated with a specific REPIN (Bertels and Rainey 2011b). Although associated with three distinct master sequences, these three RAYT genes may also transpose a set of sequences in parallel, which could lead to a more rugged fitness landscape.
Furthermore, our quasispecies model only estimates effective duplication rates, which is the fraction of duplications that do not incur a significant fitness cost to the host and are therefore selected against at the level of the host. The fact that we only observe a fraction of the duplications is evident in the almost exclusive presence of REPINs in extragenic space (Bertels and Rainey 2011b). This is presumably because a REPIN insertion into a gene would immediately destroy the open reading frame of the gene, which would have detrimental fitness effects for the host. To estimate the proportion of the genome that is permissive of REPIN insertion, we can rely on recent estimates of neutrally evolving sites in the extragenic space of a bacterial genome (Thorpe et al. 2016). If these estimates are similar among bacteria and also hold for REPIN insertions, then it is safe for REPINs to transpose into ∼4% of the genome. If there is no mechanism to increase the likelihood of inserting into neutral sites [there is some evidence that such mechanisms may exist (Bertels and Rainey 2011a)], then the true duplication rate would be ∼25 times higher than the one we inferred with our quasispecies model.
The inferred duplication rates also depend on the choice of the mutation rate. A higher mutation rate will lead to higher duplication rates and vice versa. The mutation rate we chose is conservative at the lower end of the scale for E. coli. Other studies have inferred higher mutation rates for E. coli as well as most other bacteria (Lynch et al. 2016). However, these measurements determine mutation rates for one particular strain with a certain genetic background at one particular point in time. Over evolutionary timescales the mutation rate of a particular strain can change significantly (Wielgoss et al. 2013). This may also be true for duplication rates. So the inferred values should serve as an orientation to compare REPIN populations with each other, but also to get an idea about the approximate scale of the duplication rates.
REPIN duplication rates in other bacteria
We also calculated duplication rates for four more Pseudomonas strains and five more E. coli strains. The E. coli strains we chose were quite distantly related to each other and belong to phylogroups A, B2, and D. The Pseudomonas strains we chose are very distantly related to each other as well as to E. coli (Figure 4A). To get an idea about how distantly related the individual strains are, we gauge the time that has passed since the strains diverged by measuring the 16S ribosomal DNA (rDNA) divergence (Ochman and Wilson 1987; Ochman et al. 1999). Ochman et al. (1999) estimated that it takes ∼50 MY for the 16S rDNA to diverge by 1%. According to these estimates, the most recent common ancestor (MRCA) of the E. coli strains lived ∼15 MYA. The MRCA of the Pseudomonas strains lived ∼100 MYA and E. coli and Pseudomonas diverged ∼600 MYA. Hence, the REPIN populations in our selected bacteria have been evolving independently of each other for a very long time. RAYTs, the genes that mobilize REPINs in E. coli and Pseudomonas, are also very different in E. coli and Pseudomonas and belong to two different gene classes (Bertels and Rainey 2011b). There is no detectable sequence conservation in the nucleotide sequence and very little sequence conservation in the amino acid sequence apart from the catalytic center of the protein.
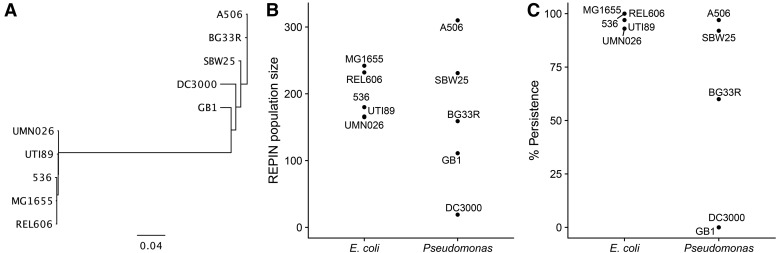
Figure 4.
REPIN populations in other bacteria. (A) 16S tree showing the phylogenetic relationship between REPIN-containing bacteria selected in our study. The scale bar shows the number of substitutions per nucleotide site. (B) REPIN population sizes in E. coli and Pseudomonas. (C) Proportion of 100 simulations where one or more sequences are left in mutation class 0 after time steps.
Divergent bacteria have divergent REPIN populations
The divergence between the different bacterial strains is also reflected in the similarity between the most abundant 25-bp-long sequences (REP sequences). The most common sequences in E. coli are almost all identical, except for that of UTI89, where the most common sequence is shifted by 1 nt with respect to the other E. coli sequences (File S2). But all E. coli REP sequences are very different to all of the Pseudomonas REP sequences. Among the Pseudomonas strains, the REP sequences from P. fluorescens A506 and P. fluorescens BG33R are almost identical (again shifted by 1 nt), which are also the most closely related strains. Despite this similarity, the population sizes and structures are completely different between the two strains (see population networks in File S3). This observation highlights the opportunity to study the evolution of entire populations. As bacterial populations diverge, the REPIN populations diverge. In one bacterial lineage, a certain REPIN population may prosper whereas in another, it declines.
Not only do REPINs differ in their sequences, the populations in Pseudomonas and E. coli also differ in the population structure. In contrast to Pseudomonas, REPIN populations in E. coli form relatively simple networks, consistent with a single fitness peak (see sequence networks in File S3). The differences in the complexity of the sequence network may stem from the fact that there is only a single RAYT gene encoded in E. coli, but there are usually multiple RAYT genes in Pseudomonas (Bertels and Rainey 2011b). If we assume that the activities of multiple RAYT genes can interfere with each other, then generalist sequences that can be moved by multiple RAYT genes will evolve, and give rise to a complex sequence network.
Although the divergence between E. coli and Pseudomonas is very large and the differences between the structure of the REPIN (File S4; the REPIN is symmetric in Pseudomonas but is asymmetric in E. coli) and the corresponding transposase are tremendous (Bertels and Rainey 2011b), the inferred REPIN population sizes are surprisingly similar (Figure 4B). REPIN populations in E. coli range between 165 (UMN026) and 242 (MG1655) members. REPIN populations in Pseudomonas are spread more widely and range between 23 (DC3000) and 309 (A506) members. The population size has a strong effect on whether the master sequence can persist for long times within the population, or whether it will die out. Our simulations show that among all Pseudomonas REPIN populations, only that of P. fluorescens A506 and P. fluorescens SBW25 are large enough to persist over long periods of time. In E. coli, in contrast, most populations persist over time steps (Figure 4C).
Small REPIN populations in Pseudomonas
P. syringae DC3000 is different from the other Pseudomonas strains. The REPIN population is particularly small (only 23 members), which leads to a particularly unstable REPIN population (Figure 4C). Another notable feature of the DC3000 REPIN population is that a large part of the repetitive sequences does not form REPINs (File S4). Furthermore, the only RAYT in DC3000 is not flanked by the most common 25-bp-long sequence in the genome, which is the case for all other population we have analyzed (File S2) and has been a defining feature of the REPIN–RAYT system (Bertels and Rainey 2011b). This suggests to us that the DC3000 REPIN population may be a dead or dying population, which is slowly disintegrating due to genetic drift. Hence the population is probably not in equilibrium, which means that the inferred duplication rates may not be accurate.
The populations found in BG33R and GB1 are also too small to persist for extended periods of time. However, in contrast to DC3000, they are also the two populations with the highest inferred duplication rate, and in both cases the most common 25-bp-long sequence does flank a RAYT gene and both populations consist mostly of REPINs (File S4). Hence there is no sign of population disintegration. High duplication rates are likely to evolve for small populations, because the mutation load is comparatively small. This suggests that these two populations may be growing.
REPIN populations in competition
The population network in BG33R is particularly interesting as it contains two similar sized populations (126 and 147 members) and the REPIN master sequence consists, in both cases, of two identical 25-mers that both occur exactly 160 times in the genome and differ in 5 nt positions (i.e., the REPIN master sequence differs in 10 positions). When inferring the fitness of the master sequence for both populations, then we also get very similar and extremely high duplication rates of ∼15 × 10−9. One would expect the evolution of high duplication rates not only for growing populations but also for populations that are competing for space in the genome. With space we are referring to regions in the genome that, when inserted into, incur no fitness cost.
REPIN populations in E. coli
In E. coli, the most abundant 25-bp-long sequences do not form symmetric REPINs as observed in Pseudomonas (File S4). This could lead us to the conclusion, as for DC3000, that E. coli does not contain REPIN populations that are alive. However, there are a few differences to DC3000. First of all, RAYTs in E. coli are very distantly related to RAYTs in most Pseudomonas, which leaves the possibility that REPINs in E. coli are structured differently to REPINs in Pseudomonas. Second, there is not a single instance of a REPIN in any of the five E. coli populations. If E. coli REPIN populations were dying populations, then all populations in E. coli would already be dead. This either happened ∼15 MYA, when the last common ancestor of the five E. coli strains lived, or it happened recently simultaneously. If it happened 15 MYA, then we would expect the population to have vanished by now and not consist of up to 242 members. It also seems unlikely that it happened recently in all strains at the same time and within the same time frame. Finally, the most common 25-bp-long sequences in the five strains does still flank the RAYT gene, something that is not the case for DC3000 but is for all other REPIN populations in our study (File S2). Hence REPIN populations in E. coli, in contrast to DC3000, are very likely alive and replicating.
REPIN duplication rate is close to the error threshold
The duplication rates of the master sequences are in the range of and Considering that the rates were inferred for very different species and the species contain very different transposases that disperse the REPIN populations, these values are very similar. This may be due to at least two reasons.
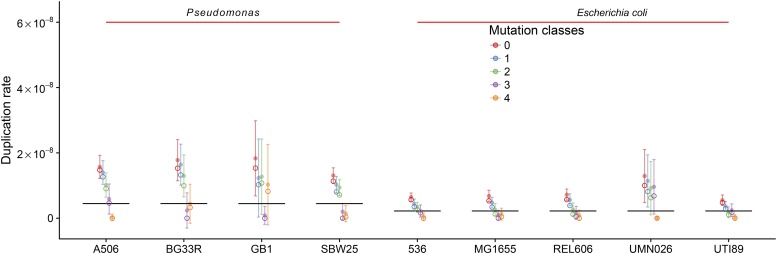
First, the duplication rate is very close to its lower possible limit, because the number of mutations that occur on average between two duplication events is between 0.29 and 0.45 for 50-bp-long REPINs in Pseudomonas, and between 0.22 and 0.46 for 25-bp REP(IN)s in E. coli. If one or more mutations occur between consecutive duplication events then it is impossible to maintain a master sequence; this occurs when duplication rates fall below (E. coli) or for Pseudomonas (Figure 5 and File S5). Hence, if REPIN duplication rates were much lower, then REPIN populations would very quickly go extinct.
Figure 5.
REPIN duplication rates in Pseudomonas and E. coli strains. The figure shows duplication rates for the largest REPIN populations in various Pseudomonas and E. coli strains. The ●’s indicate the mean duplication rate and their variance inferred from the frequencies of the aforementioned simulation every 100 time points between time point 1000 and 20,000. For BG33R, GB1, and UMN026, values from the simulation are not reliable as the master sequence did not persist until the end of the simulation. The DC3000 population was excluded as it died out almost immediately after the simulation was started. ○’s indicate the inferred duplication rate from the observed sequences. The black lines indicate error thresholds. If the duplication rate of the master sequence falls below the black horizontal lines, then it is impossible to maintain the master sequence above a frequency of 1% in the population. All error thresholds among Pseudomonas strains and among E. coli strains only differ at a level of which cannot be seen in the figure as it is less than the line width. The full organism names from left to right are: P. fluorescens A506, P. synxantha BG33R, P. putida GB1, P. fluorescens SBW25, E. coli 536, E. coli K-12 MG1655, E. coli B REL606, E. coli UMN026, and E. coli UTI89.
Second, each duplication event is equivalent to an insertion introduced at a random position in the genome. Therefore, an increase in the duplication rate would also increase the mutational load for the host organism. Hence, similar to selection for replication fidelity (Lynch et al. 2016), selection will favor organisms with decreased REPIN duplication rates.
The REPIN duplication rates we inferred are probably the result of these two opposing forces.
Maintenance of the REPIN–RAYT system
The low duplication rate we inferred for all REPIN populations also suggests that REPIN sequences have been part of bacterial genomes for a very long time. This again raises the question of how and why they are maintained. There are two explanations: (1) the REPIN–RAYT system is frequently transmitted horizontally, or (2) the REPIN–RAYT system provides a benefit to the host organism (Bichsel et al. 2013).
It is possible that the REPIN–RAYT system does get horizontally transferred from time to time. However, horizontal transfers are likely to be rare, because to establish a novel REPIN population in a new host both the transposase (RAYT) and the REPIN have to be transferred. This process is probably facilitated by the fact that RAYTs are usually flanked by REPINs (Bertels and Rainey 2011b). However, the rarity of these events is consistent with the observation that the establishment of a population that is as diverse as the REPIN population in SBW25 will take thousands of years. Hence it seems unlikely that horizontal transfers are frequent enough to explain the ubiquitous presence of the REPIN–RAYT system in bacteria.
Alternatively, the REPIN–RAYT system may be maintained because it provides a selective advantage to the host bacterium (Bertels and Rainey 2011a,b; Bertels et al. 2017;). There have been many studies on potential benefits for individual REP sequences (Higgins et al. 1988; Espéli et al. 2001; Liang et al. 2015). Similar to why bacterial mutator populations are not maintained in constant environments over long periods of time (Wielgoss et al. 2013), local benefits of REPINs cannot explain the maintenance of the REPIN–RAYT system over long periods of time. Hence the REPIN–RAYT system probably possesses a function other than the dispersion of REPINs that is beneficial for the host bacterium.
Supplementary Material
Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.117.201160/-/DC1.
Acknowledgments
We thank Paul Rainey for his insightful comments on the manuscript. All authors acknowledge generous funding from the Max Planck Society.
Footnotes
Communicating editor: L. M. Wahl
Literature Cited
- Aranda-Olmedo I., Tobes R., Manzanera M., Ramos J. L., Marqués S., 2002. Species-specific repetitive extragenic palindromic (REP) sequences in Pseudomonas putida. Nucleic Acids Res. 30: 1826–1833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barabas O., Ronning D. R., Guynet C., Hickman A. B., Ton-Hoang B., et al. , 2008. Mechanism of IS200/IS605 family DNA transposases: activation and transposon-directed target site selection. Cell 132: 208–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertels F., Rainey P. B., 2011a Curiosities of REPINs and RAYTs. Mob. Genet. Elements 1: 262–268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertels F., Rainey P. B., 2011b Within-genome evolution of REPINs: a new family of miniature mobile DNA in bacteria. PLoS Genet. 7: e1002132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertels F., Gallie J., Rainey P. B., 2017. Identification and characterization of domesticated bacterial transposases. bioRxiv 119735. https://doi.org/10.1101/119735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bichsel M., Barbour A. D., Wagner A., 2013. Estimating the fitness effect of an insertion sequence. J. Math. Biol. 66: 95–114. [DOI] [PubMed] [Google Scholar]
- Bull J. J., Meyers L. A., Lachmann M., 2005. Quasispecies made simple. PLOS Comput. Biol. 1: 450–460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bureau T. E., Wessler S. R., 1994. Stowaway: a new family of inverted repeat elements associated with the genes of both monocotyledonous and dicotyledonous plants. Plant Cell 6: 907–916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Domingo, E., and P. Schuster (Editors), 2016 Quasispecies: From Theory to Experimental Systems (Current Topics in Microbiology and Immunology, Vol. 392). Springer, Berlin. [PubMed] [Google Scholar]
- Eigen M., 1971. Selforganization of matter and the evolution of biological macromolecules. Naturwissenschaften 58: 465–523. [DOI] [PubMed] [Google Scholar]
- Eigen M., Schuster P., 1977. The hypercycle. a principle of natural self-organization. part a: emergence of the hypercycle. Naturwissenschaften 64: 541–565. [DOI] [PubMed] [Google Scholar]
- Espéli O., Moulin L., Boccard F., 2001. Transcription attenuation associated with bacterial repetitive extragenic BIME elements. J. Mol. Biol. 314: 375–386. [DOI] [PubMed] [Google Scholar]
- Higgins C. F., Ames G. F.-L., Barnes W. M., Clement J. M., Hofnung M., 1982. A novel intercistronic regulatory element of prokaryotic operons. Nature 298: 760–762. [DOI] [PubMed] [Google Scholar]
- Higgins C. F., McLaren R. S., Newbury S. F., 1988. Repetitive extragenic palindromic sequences, mRNA stability and gene expression: evolution by gene conversion? — a review. Gene 72: 3–14. [DOI] [PubMed] [Google Scholar]
- Jurka J., Kapitonov V. V., Kohany O., Jurka M. V., 2007. Repetitive sequences in complex genomes: structure and evolution. Annu. Rev. Genomics Hum. Genet. 8: 241–259. [DOI] [PubMed] [Google Scholar]
- Liang W., Rudd K. E., Deutscher M. P., 2015. A role for REP sequences in regulating translation. Mol. Cell 58: 431–439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M., Ackerman M. S., Gout J.-F., Long H., Sung W., et al. , 2016. Genetic drift, selection and the evolution of the mutation rate. Nat. Rev. Genet. 17: 704–714. [DOI] [PubMed] [Google Scholar]
- Mahillon J., Chandler M., 1998. Insertion sequences. Microbiol. Mol. Biol. Rev. 62: 725–774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Messing S. A. J., Ton-Hoang B., Hickman A. B., McCubbin A. J., Peaslee G. F., et al. , 2012. The processing of repetitive extragenic palindromes: the structure of a repetitive extragenic palindrome bound to its associated nuclease. Nucleic Acids Res. 40: 9964–9979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowak M. A., 1992. What is a quasispecies? Trends Ecol. Evol. 7: 118–121. [DOI] [PubMed] [Google Scholar]
- Nunvar J., Huckova T., Licha I., 2010. Identification and characterization of repetitive extragenic palindromes (REP)-associated tyrosine transposases: implications for REP evolution and dynamics in bacterial genomes. BMC Genomics 11: 44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ochman H., Wilson A. C., 1987. Evolution in bacteria: evidence for a universal substitution rate in cellular genomes. J. Mol. Evol. 26: 74–86. [DOI] [PubMed] [Google Scholar]
- Ochman H., Elwyn S., Moran N. A., 1999. Calibrating bacterial evolution. Proc. Natl. Acad. Sci. USA 96: 12638–12643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oggioni M. R., Claverys J.-P., 1999. Repeated extragenic sequences in prokaryotic genomes: a proposal for the origin and dynamics of the RUP element in Streptococcus pneumoniae. Microbiology 145: 2647–2653. [DOI] [PubMed] [Google Scholar]
- Page K. M., Nowak M. A., 2002. Unifying evolutionary dynamics. J. Theor. Biol. 219: 93–98. [PubMed] [Google Scholar]
- Seifert D., Di Giallonardo F., Metzner K. J., Günthard H. F., Beerenwinkel N., 2015. A framework for inferring fitness landscapes of patient-derived viruses using quasispecies theory. Genetics 199: 191–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silby M. W., Cerdeño-Tárraga A. M., Vernikos G. S., Giddens S. R., Jackson R. W., et al. , 2009. Genomic and genetic analyses of diversity and plant interactions of Pseudomonas fluorescens. Genome Biol. 10: R51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stern M. J., Ames G. F.-L., Smith N. H., Robinson E. C., Higgins C. F., 1984. Repetitive extragenic palindromic sequences: a major component of the bacterial genome. Cell 37: 1015–1026. [DOI] [PubMed] [Google Scholar]
- Thorpe H. A., Bayliss S. C., Hurst L. D., Feil E. J., 2016. The large majority of intergenic sites in bacteria are selectively constrained, even when known regulatory elements are excluded. bioRxiv 069708. https://doi.org/10.1101/069708. [Google Scholar]
- Ton-Hoang B., Pasternak C., Siguier P., Guynet C., Hickman A. B., et al. , 2010. Single-stranded DNA transposition is coupled to host replication. Cell 142: 398–408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ton-Hoang B., Siguier P., Quentin Y., Onillon S., Marty B., et al. , 2012. Structuring the bacterial genome: Y1-transposases associated with REP-BIME sequences. Nucleic Acids Res. 40: 3596–3609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Touchon M., Hoede C., Tenaillon O., Barbe V., Baeriswyl S., et al. , 2009. Organised genome dynamics in the Escherichia coli species results in highly diverse adaptive paths. PLoS Genet. 5: e1000344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Dongen S., 2000. A cluster algorithm for graphs. Report - Inf. Syst. 10: 1–40. [Google Scholar]
- Versalovic J., Koeuth T., Lupski J. R., 1991. Distribution of repetitive DNA sequences in eubacteria and application to fingerprinting of bacterial genomes. Nucleic Acids Res. 19: 6823–6831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wessler S. R., Bureau T. E., White S. E., 1995. LTR-retrotransposons and MITEs: important players in the evolution of plant genomes. Curr. Opin. Genet. Dev. 5: 814–821. [DOI] [PubMed] [Google Scholar]
- Wielgoss S., Barrick J. E., Tenaillon O., Cruveiller S., Chane-Woon-Ming B., et al. , 2011. Mutation rate inferred from synonymous substitutions in a long-term evolution experiment with Escherichia coli. G3 (Bethesda) 1: 183–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wielgoss S., Barrick J. E., Tenaillon O., Wiser M. J., Dittmar W. J., et al. , 2013. Mutation rate dynamics in a bacterial population reflect tension between adaptation and genetic load. Proc. Natl. Acad. Sci. USA 110: 222–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All genomes are publicly available on GenBank (https://www.ncbi.nlm.nih.gov/genbank/) under the accession numbers listed in Table 1.
Table 1. List of accession numbers for genomes used in this study.
| Species name | NCBI accession no. |
|---|---|
| P. syringae pv. tomato DC3000 | NC_004632.1 |
| P. synxantha BG33R | CM001514 |
| P. fluorescens A506 | NC_017911 |
| P. fluorescens SBW25 | NC_012660.1 |
| P. putida GB1 | NC_010322.1 |
| E. coli 536 | NC_008253.1 |
| E. coli K-12 MG1655 | CP014225.1 |
| E. coli UTI89 | NC_007946.1 |
| E. coli B REL606 | NC_012967.1 |
| E. coli UMN026 | NC_011751.1 |
NCBI, National Center for Biotechnology Information.
We included eight supplemental files: File S1 contains detailed descriptions of all supplemental files. File S2 contains the sequence and frequency of the most common 25-bp-long sequence, the gene name of the flanking RAYT and the number of RAYTs, in all of the bacteria analyzed in this study. File S3 contains the modeling and simulation results for all 10 REPIN populations we analyzed in our study. File S4 contains the proportion of symmetric REPINs in all identified sequences from all studied strains. File S5 contains the effective duplication rates and equilibrium frequencies for each of the 10 REPIN populations at the error threshold. File S6 provides the Mathematica code for calculating equilibrium frequencies, fitness values, and error thresholds for all 10 REPIN populations. File S7 contains the same Mathematica code as a PDF. File S8 contains a figure showing that the adjusted equilibrium frequencies remain constant for small mutation rates. File S9 contains the sequence frequencies of the different mutation classes for all 10 REPIN populations. File S10 presents data showing that choosing five mutation classes is optimal for our data sets.