Abstract
We report on the development of a technique for differentiating between biological micro-objects using a rigorous, full-wave model of OCT image formation. We model an existing experimental prototype which uses OCT to interrogate a microfluidic chip containing the blood cells. A full-wave model is required since the technique uses light back-scattered by a scattering substrate, rather than by the cells directly. The light back-scattered by the substrate is perturbed upon propagation through the cells, which flow between the substrate and imaging system’s objective lens. We present the key elements of the 3D, Maxwell equation-based computational model, the key findings of the computational study and a comparison with experimental results.
OCIS codes: (110.4500) Optical coherence tomography, (170.3880) Medical and biological imaging, (170.1470) Blood or tissue constituent monitoring, (170.3660) Light propagation in tissues, (050.1755) Computational electromagnetic methods
1. Introduction
Blood cell detection and differentiation lie at the heart of a complete blood count (CBC), which is a complex blood test used to evaluate the composition and concentration of the various cellular components of blood [1]. While effective differentiation between various cell types is an essential mechanism required to count the individual cells, the significance of a blood cell count, however, results directly from the diverse functions of the cells in the organism. The red blood cells (RBCs) and the white blood cells (WBCs) are two of the main components of human blood and they have completely different functions in the body. A low RBC count, for example, is an indicator of anemia, while a reduced number of WBCs may be caused by a medical condition, such as an autoimmune disorder or cancer [1, 2].
Hematology analyzers, employing optical [3] or impedance [4] methods to count single blood cells, have been the gold standard in CBC for decades. Recently, new methods that employ modern optical imaging to count various blood cells have been developed, such as spectrally encoded flow cytometry [5], lens-free holographic microscopy [6], and cell-phone based fluorescent microscopy [7]. Furthermore, new devices combining microfluidics [8] with optical methods have been reported to count and discriminate between blood cells [9–16]. However, only a few existing optical methods perform differentiation between RBCs and WBCs using the phase information, together with magnitude, to count the cells [6, 12]. New counting techniques based on the impedance method also have been presented in recent years, such as those reported in [17, 18]. They do not, however, enable direct differentiation between RBCs and WBCs.
We have previously developed a novel method for the detection and differentiation of moving micro-objects, such as RBCs and WBCs, based upon experimental measurements and knowledge of cell morphology [19]. Phase-sensitive optical coherence tomography (OCT), and a dedicated microfluidic chip, which is depicted in Fig. 1(a), lie at the heart of this system. The key advance which enables this microfluidic setup to perform blood cell differentiation is the embedding of the microchannels in polydimethylsiloxane (PDMS) mixed with titanium dioxide (TiO2), resulting in a highly scattering substrate (TiO2-PDMS); the depth-resolved structure of the chip is presented schematically in Fig. 1(b). The cells are made to flow over the top of the substrate, within the microchannel, and cell identification is based upon the OCT signal corresponding to the TiO2-PDMS layer, rather than the signal corresponding to light directly back-scattered by cell. The advantage of this approach over using a high numerical aperture objective, high spectral bandwidth source, optical coherence microscopy system to directly image sub-cellular components is reduced system complexity and, therefore resulting in a cheaper and more robust system. Furthermore, the approach employed in this paper takes advantage of the property that biological cells tend to scatter light predominantly in the forward direction. Moreover, unlike conventional hematology analyzers, our method provides additional quantitative information at the single-cell level, as a result of a statistical analysis of the phase perturbation introduced by flowing cells. In other words, this technique enables single-cell statistics (additional information at the single-cell level), instead of statistics applicable to the entire sample of cells analyzed by a conventional device. Criteria for cell differentiation are based upon differential parameters derived from the measured signals (Fig. 1(d)) which depend on the size, shape and sub-cellular components of the targeted blood cells. In the experiments, we separately studied the flowing blood cells—i.e., erythrocytes and leukocytes—as two separate samples. We did not perform experiments on whole blood since the ratio of erythrocytes to leukocytes is on the order of 1000:1 [1, 19]. This makes numerical simulation an important tool for verification of this technique. Moreover, the relative quantitative agreement between experimental and simulated results allows for additional, otherwise inaccessible, information about both cells and the experimental system to be obtained in silico. For example, simulating how the OCT illumination beam is scattered by the blood cells is important for understanding the physical basis of the differentiation technique. Further, isolating specific optical properties of each cell, in a noise free environment, allows the physical origin of differentiation criteria to be probed in a manner that would be impossible using experiment.
Fig. 1.
Schematic diagram of the image formation model composed of an OCT system and a microfluidic chip; a) a photo of the microfluidic chip and b) its depth resolved structure; c) the scattering volume design (TiO2 scatterers are not displayed); and d) an example OCT image showing the signals of interest.
In this work, we present a comprehensive, highly realistic, three-dimensional model of image formation for the experimental system described above. Additionally, we perform a quantitative comparison between simulated and experimental results. Figure 1(c) outlines the operation of the experimental system including the OCT beam, blood cell models and simulation coordinate system. Figure 1(d) shows an example experimental measurement consistent with the scenario depicted in Fig. 1(c), except that the signals of interest derive from two RBCs. The microscope coverslip is neglected in the model since it is used in the experiments only as the upper cover of the microchannel and does not impact upon experimental measurements.
Modelling of image formation for the combination of OCT system and microfluidic chip depicted in Fig. 1 is challenging. This is because the signals of interest, as shown in Fig. 1(d), correspond to the region containing the TiO2 scatterers. Information about cells in the microchannel is obtained indirectly since light contributing to the signals of interest propagates through a particular cell twice during its round trip from the optical fiber to the TiO2 scattering region and back. By definition then, models based on the first Born approximation [20] are not appropriate for this application. Under this approximation, light within an extended scatterer is assumed to be equivalent to the light that would be incident on the space occupied by the scatterer but in the absence of the scatterer. This approximation is invalid for highly scattering regions such as the TiO2-PDMS region, furthermore, it implies that the light incident upon the TiO2-PDMS layer will be assumed to not be perturbed by cells in the microchannel. Models based upon the extended Huygens-Fresnel [21] formalism (EHF) are not appropriate either. The EHF could be used to model the attenuation of the OCT signal in the TiO2-PDMS region, and a multiple scattering contribution, but not the perturbation due to cells in the microchannel of the light incident upon the TiO2-PDMS. Monte Carlo based models [22] are also not appropriate for this application since they do not model image formation due to deterministic refractive index distributions, as is required for this application.
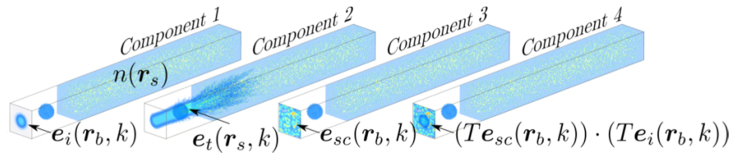
A highly realistic model of image formation in OCT has recently been introduced [23], based upon one for high numerical aperture coherent optical imaging systems [24]. This model is based on Maxwell’s equations and thus treats light propagation and scattering entirely using a full-wave formalism. We first give a brief overview of the model before explaining each component in further detail in Section 2. The components of the model are outlined diagrammatically in Fig. 2. Component 1 shows how, for the simulation of a particular A-scan, the focused incident field is calculated on a transverse plane. This incident field is denoted by where k is the wavenumber of the illumination. The details of the optical system are incorporated in the equation used to calculate where the subscripts i and b denote incident and boundary, respectively. We model image formation for an arbitrary refractive index distribution throughout the sample, denoted where the subscript s denotes sample. A numerical method is used in component 2 to determine how the incident focused beam is scattered by the sample. Although a variety of numerical techniques could be used, our model uses the pseudo-spectral time-domain (PSTD) method because it allows for reduced spatial sampling requirements [25] compared with, for example, the finite-difference time-domain (FDTD) and finite element methods. Another important feature of the PSTD method is that it allows for broadband simulation of the scattered field in a single simulation, by introducing a temporal pulse into the simulation. The PSTD simulation yields the total field within the sample space which we denote by where the subscript t denotes total. The scattered field is ultimately required to model image formation, which is isolated from the total field by subtracting the known incident field. This is performed in component 3 where the scattered field is evaluated, for each wavenumber of interest, on a transverse plane in the simulation space as where the subscript sc denotes scattered. Component 4 of the model calculates how the scattered light is coupled into the system’s optical fiber. An approach more computationally efficient than simply propagating to the fiber, is used to perform this coupling calculation within the sample space [26]. This is performed by integrating the product of the focused illumination and scattered field on a transverse plane. This is illustrated in Fig. 2 where the quantity to be integrated is given as where T = diag(a1,a2,0) is a diagonal matrix for which enables the Cartesian coordinates of the field to be selected in line with the modeled experimental system.
Fig. 2.
An illustration of the four key components of the three-dimensional full-wave model of OCT image formation.
2. Description of the model
2.1 Blood cell models
The development of refractive index models of the RBCs and WBCs, for specifying for input to the PSTD method, was a crucial aspect of this work. This was performed by drawing on our knowledge of blood cell morphology and using parameters found in the literature [27–34]. The erythrocyte was modeled as a biconcave, homogeneous disc of diameter 7.7 μm and a maximum thickness of ~2μm [27], using the equation [28]:
| (1) |
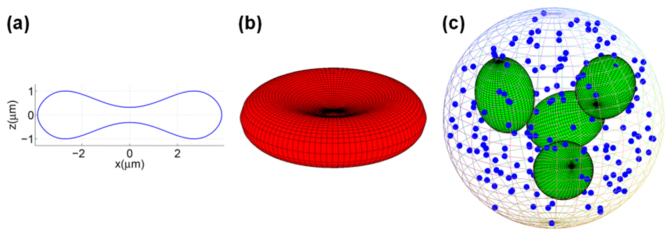
where d is a diameter of RBC. Since water and hemoglobin constitute the bulk of RBC content, we used the absolute refractive index ne = 1.41 [28] for the central wavelength of illumination λ0 = 790nm; the imaginary part was neglected for this wavelength. Fig. 3(a) depicts a two-dimensional plot of the RBC shape, that is z2 = (f(x))2, according to Eq. (1), while Fig. 3(b) depicts a three-dimensional plot as z2 = (f(r))2, where
Fig. 3.
Renders of the RBC and WBC refractive index models; a) a plot of the erythrocyte model topology; b) a three-dimensional rendering of the modeled erythrocyte surface, and c) a 3D rendering of the leukocyte (neutrophil) model.
Because of the diversity of WBCs occurring in human blood, we have selected the mature neutrophil as representative since they are the most abundant WBC subpopulation (46−73%) of the entire population of leukocytes [29]. This choice is further supported by the unimodal nature of the experimental results presented in Section 3 for samples containing all WBC subtypes. Figure 3(c) is a three-dimensional depiction of a WBC model. We introduced a sphere (dn = 11μm) as a model for a body of mature neutrophil. The sphere contains four ellipsoids (random position and orientation inside the cytoplasm) representing a 4-lobe nucleus and spherical granules that are identical (dg = 0.3μm) and randomly distributed inside the cell. In the following we briefly describe other parameters of the model. We set the volume fraction of the nucleus (ellipsoids) and granules (spheres) to be fn = 0.11 and fg = 0.09, respectively, which agree with the literature data on neutrophil morphology [30, 31]. For the lobed nucleus we set the refractive index to nn = 1.5 (protein), while for granules we set it to the upper limit for dried proteins, ng = 1.58 [34]. For the cytoplasm we chose nc = 1.36 [30], and the medium surrounding the cells in microchannel (1% PBS, phosphate-buffered saline) was approximated by water, giving nw = 1.33 for λ0 = 790nm [35] (Supporting Information).
2.2 Modelling the focused illumination
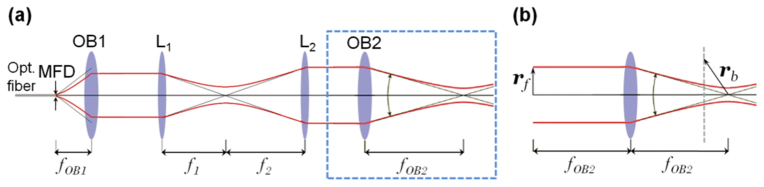
The simulations presented in this paper employ parameters based upon the experimental system, which was used to generate experimental results presented in Section 3. An Fd-OCT setup with Thorlabs LSM02-BB objective lens (axial resolution: ∼3.5µm in tissue, lateral resolution: 8.4µm) was used for these experiments. The setup includes a fiber coupler with optical fibers (70/30, AC Photonics); a dedicated spectrometer with a line scan camera (sp4096-140k, Sprint, Basler); dispersion compensation elements; a mirror in the reference arm and microfluidic chip (the measured sample) [19] which is shown in Figs. 1(a)–1(b). A light source comprised of a broadband femtosecond laser with a spectrum of FWHM = 142nm was employed. We used a spectrum centered on wavelength λ0 = 790nm spanning a total bandwidth of 250nm (ΔλMAX) in the simulation to ensure that the simulated spectrum contains the spectrum used in experiment. Figure 4(a) depicts the object arm of the OCT system and Table 1 contains a listing of the values of selected parameters describing this system, including all parameters defined in Fig. 4(a). These parameters were employedthroughout the simulation. To simplify the model, we also approximate the reference arm of the simulated setup in the same way as the object arm, except with a mirror as the sample.
Fig. 4.
a) The Fd-OCT system sample arm; MFD – mode field diameter, OB1 – objective lens of the collimator, L1, L2 – lenses, OB2 – objective lens; b) A zoomed-in, annotated, depiction of the objective lens shown in the boxed region of (a), illustrating the parameters used to calculate the focused illumination using Eq. (2).
Table 1. Parameters of the numerical simulation. Most of symbols are defined in Fig. 4; ΔλMAX stands for maximum spectral width (wavelength width) and NAOB2 indicates numerical aperture of the objective lens OB2.
| Parameter | Value |
|---|---|
| λ0 | 790nm |
| ΔλMAX | 250nm |
| NAOB2 | 0.11 |
| fOB1 | 9mm |
| fOB2 | 18mm |
| f1 | 53.5mm |
| f2 | 75mm |
| Optical fiber | Single mode fiber Corning HI 780 (MFD = 5.5μm) |
The focused illumination due to the system depicted in Fig. 4(a) is calculated by projecting the field emitted by the fiber into the back focal plane of OB2, resulting in the simpler system of Fig. 4(b). The focused illumination, is then calculated using the Debye-Wolf integral [36] according to:
| (2) |
where is the normalized position within the objective’s pupil, F is a parameter specifying the diameter of the Gaussian beam assumed to be incident upon the objective’s back focal plane, and is a unit vector which describes refraction by the lens and is readily calculated using the generalized Jones matrix formalism [37]. Note that and are the unit vectors parallel to the x and y axes, respectively. In this case, [23], which is found by projecting the Gaussian beam exiting the optical fiber onto the focal plane common to lenses L1 and L2. This value of F assumes that the lenses in Fig. 4(a) are arranged as a series of 4f systems, which, although not being strictly correct, proves to be a satisfactory assumption.
2.3 Calculation of light scattered by the sample
We consider the sample to be composed of the microfluidic chip possibly with a blood cell present within the microchannel. The PSTD method calculates how light is scattered by the refractive index distribution by partitioning the computational space into cubic cells of side λ0/6 (PSTD cells). All six components of the electromagnetic field are sampled once for each cell. The PSTD simulation employed a total of 150×150×1500 cells in the computational grid and a perfectly matched layer (PML), as proposed by Berenger [38], of 10 cells was positioned around the grid. A time step of 20.4 fs was employed requiring a total of 10000 iterations to complete the simulation. The transverse size of the computational grid (150×150 cells) was chosen to ensure that the magnitude of the incident beam, did not exceed 1% of its peak at the transverse plane in which it is introduced, ensuring an appropriate tradeoff between computation time and accuracy [23]. The axial extent of the computational grid was chosen to ensure that A-scans are simulated to an experimentally relevant depth, as shown in Figs. 1(c)–1(d).
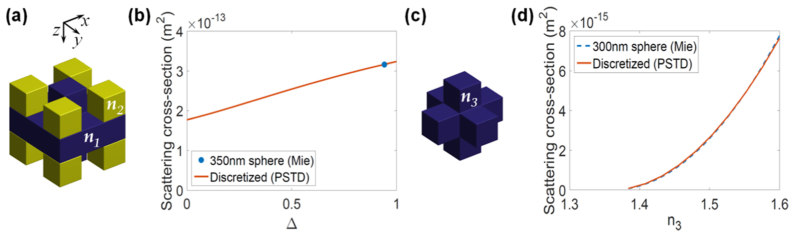
A limitation of the PSTD method is that scatterers must be constructed using a so-called staircase approximation of the cubic cells making up the computational grid. This can be problematic when trying to model objects with dimensions of only a few PSTD cells. The TiO2 scatterers and the WBC granules, both assumed to be spherical with diameters of 350nm and 300nm, respectively, were difficult to model using the PSTD cell size of λ0/6 = 131.7nm. Figure 5(c) shows, arguably, the simplest staircase approximation to spheres of diameter 300 and 350 nm. It is obtained by choosing only PSTD cells with a center contained within the surface of the sphere to be approximated and setting n3 to be equal to the refractive index of the sphere to be modelled. However, this shape with n3 = 2.52 underestimates the scattering cross-section of the TiO2 spheres, yet is appropriate for the granules contained within the WBCs, as is shown in Fig. 5(d). To rectify this problem for the TiO2 spheres, a modified staircase approximation was employed as shown in Fig. 5(a), which, relative to the shape in Fig. 5(c), has an additional four cells colored blue (refractive index n1 = 2.52) and an additional eight yellow cells (refractive index n2). The value of n2 was set according to where n0 = 1.41 is the refractive index of the PDMS medium in which the TiO2 spheres are embedded and n1 = 2.52 is the refractive index of the spheres. The value of Δ = 0.9414 was obtained, as shown in Fig. 5(b), using the PSTD method to match the scattering cross-section of the modified staircase approximation to that of a sphere (diameter 350nm) according to Mie theory. As has been pointed out previously [23], this method of scatterer design neglects the angular distribution of scattering. We have plotted the magnitude of the scattered electric field for discrete and spherical scatterers in Fig. 6 in order to illustrate the discrepancy between the two cases. It is clear from these plots that there is a discrepancy between the profiles of the scattered field, the resolution of which is an important subject of future work.
Fig. 5.
Rendering of the staircase approximation to the TiO2 (a) and WBC granule (c), the result of simulations used to calculate the required value of Δ for modelling the TiO2 scatterers (b) and verification (d) that the granules are well represented by the shape in (c) for n3 ranging between nc and 1.6.
Fig. 6.
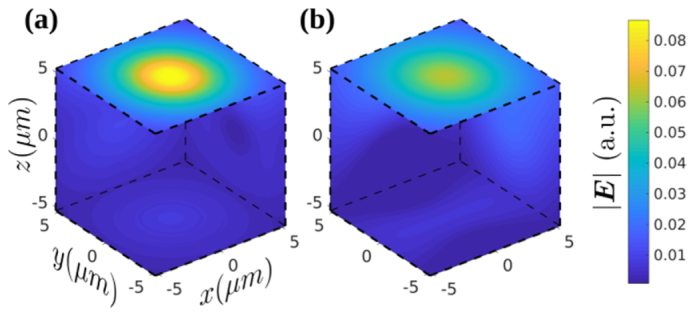
Rendering of the magnitude of electric field scattered by the discretized approximation to the TiO2 spheres using the PSTD method (a), and that of an ideal TiO2 sphere using Mie theory (b) for a plane wave polarized in the x-direction and propagating the z-direction. The field is normalized by the magnitude of the incident plane wave.
A similar calculation was performed for the WBC granules. The granules and cytoplasm were assumed to have refractive indices of ng = 1.58 and nc = 1.36, respectively (see Section 2.1). The simulations plotted in Fig. 5(d) confirm that the 7-cell shape in Fig. 5(c) results in a scattering cross-section very close to that of a sphere for n3 between nc and 1.6. This means that n3 = ng results in the granules being accurately represented by the shape in Fig. 5(c).
The staircase representations of the TiO2 spheres and granules were combined with that of the other refractive index variations resulting in a model representing the WBC, RBC and microfluidic chip. The discrete representations of TiO2 spheres, granules and nucleus lobes were arranged randomly in a non-overlapping fashion within the appropriate model sub-volumes. Only the refractive index of PSTD cells representing the RBC and WBC varied between simulations. A-scans were simulated for varying transverse blood cell positions, differing by integer multiples of the width of a single PSTD cell, i.e., each blood cell was approximated by a fixed staircase approximation that was rigidly translated through the computational space. For a given discrete refractive index distribution (i.e., scattering geometry), the PSTD simulation executes by introducing the incident illumination through a time-varying magnetic current density of the form [39]:
| (3) |
where k0 is the central wavenumber, ω0 is the central angular frequency, is the unit vector aligned with the optical axis, t0 ensures that the value of is vanishingly small and W controls the temporal width of the incident pulse and therefore the spectral width of the simulation.
2.4 Calculation of light coupled into the optical fiber
The PSTD method allows for the light scattered back towards lens OB2 (see Fig. 4) to be calculated on a transverse plane in the vicinity of the focus of OB2, as illustrated in component 3 of Fig. 2. Supposing that scattered field, is known on this plane, we have previously shown [26] that the coupling of this scattered light into the fiber used to illuminate the sample can be rigorously evaluated as:
| (4) |
where and is the modal coefficient of the light coupled into the optical fiber. We note that since is required to be calculated for a large number of values of k, it is desirable to evaluate Eq. (4) as the PSTD simulation progresses, rather than storing in computer memory for each value of k. This is achieved by recognizing that is evaluated from its time domain form, as the PSTD simulation progresses according to: where ∆t is the time step and is the total number of time steps employed by the PSTD simulation. It is then easy to see how the summation over the time step n can be moved outside of the integral in Eq. (4), allowing to be evaluated for a range of values of k without needing to store each
2.5 OCT reconstruction
Once is evaluated for a particular scattering geometry, the OCT A-scan can be evaluated according to:
| (5) |
where is the modal coefficient of reference arm light simulated in the same way as except that a mirror at location zref is modelled as the sample and is the effective system spectrum.
2.6 Differential parameters
Differential parameters are obtained as is described in reference [19] for experimental data. Both magnitude-based and phase-based differential parameters employed in this study are calculated for experimentally acquired and simulated M-scan ROIs (regions of interest; 43μm high for the magnitude data and 27μm high for the phase data) which are wide enough to horizontally cover the signal of interest. The axial position of the ROI remains constant for RBCs and WBCs, for both the simulated and experimental data.
This section summarizes the differential parameters employed in the comparative quantitative analysis presented in Section 3.3. Differential parameters are collated in Table 2, of which the differential parameters: 1–2 and 4–5 were previously described in [19]. For clarity we provide a mathematical definition of differential parameter 5 (Phase 2DFT/Contrast Top-Middle) to supplement the description given in [19]. This parameter is evaluated by first performing a two-dimensional discrete Fourier transform of the phase gradient ROIs depicted in Fig. 7 which results in a matrix with elements [aij] and dimension Nv × Nh, where we assume that Nv and Nh are both even, for simplicity. The Phase 2DFT differential parameter is then found as:
| (6) |
where Nthresh is an integer set such that |Nthresh/(Nv/2-Nthresh)-3| is minimized.
Table 2. Differential parameters.
|
Magnitude-based differential parameters
|
Phase-based differential parameters
|
||
|---|---|---|---|
| No. | Differential parameter | No. | Differential parameter |
| 1 | Standard deviations (a.u.) | 4 | Standard deviations (rad) |
| 2 | Axial (vertical) speckle size (μm) | 5 | Phase 2DFT (Contrast Top-Middlea) (a.u.) |
| 3 | Speckle contrast (‒) | 6 | Slope (‒) |
The identifier of Phase 2DFT differential parameter used in [19].
Fig. 7.
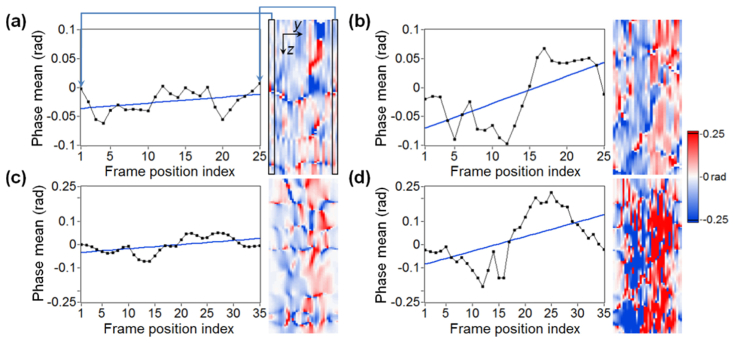
Plots of the phase-based differential parameter Slope; a) a horizontal profile through the experimentally acquired RBC signal; the blue line indicates a linear fit; b) a profile through the WBC signal plus linear fit; (c-d) simulated RBC and WBC profiles with linear fits. The black frame on the phase gradient ROI shown in (a) indicates the values used to calculate the first or last sample in the plot on the left. The label ‘Phase mean’ in the plots refers to the mean, taken over a rectangular frame, of phase gradient calculated for different positions of the frame.
It is difficult to obtain absolute quantitative agreement between differential parameters originating from experimental and simulated data sets. The reasons for this are explained in detail in Section 4, however, it is essentially due to imperfect knowledge of experimental conditions, or, an inability to precisely model them. Despite this, the simulation successfully replicates the relative separation of differential parameters corresponding with RBCs and WBCs. Thus, in order to compare differential parameters originating from experimental and simulated data, the simulated values in Section 3.3 are scaled to bring the mean of WBC and RBC values into relative agreement with the corresponding experimental means. In particular, the mean of the differential parameter values for both RBCs and WBCs combined was calculated for the experimental and simulated cases, resulting in a single scaling factor for each differential parameter. We also emphasize that only differential parameters 1 and 5 were scaled in this manner and that the same scaling factor is applied to both the WBC and RBC differential parameters. We developed a new magnitude-based unitless differential parameter (parameter 3) which does not require scaling. It is denoted as Speckle contrast, and is defined as:
| (7) |
where is the standard deviation of the signal magnitude and is the mean value of the signal magnitude, both calculated for the selected ROIs.
Additionally, we introduce differential parameter 6 to emphasize the difference between RBC and WBC signals observed in phase gradient M-scans (see Section 3.2 for definition), which is partially based on previously introduced differential parameter 4. Figure 7 demonstrates how the Slope is calculated, based on four examples, which refer to different ROIs selected from the phase gradient M-scans shown in Section 3.2. The plots shown in Figs. 7(a)–7(b) present horizontal (lateral) profiles of the corresponding ROIs (the adjacent images) for RBC and WBC signals, respectively. The mean calculated for the values indicated by the black frame (two A-scans wide and 27μm high) on the phase gradient ROI in Fig. 7(a), is used as the first or last sample shown in the plot on the left. Subsequent samples are obtained for different positions of this frame, shifted line by line until reaching the right limit of the ROI. The slope (tangent of angle of inclination; the angle is provided in radians) of the fitted line in the plot (blue color) is the value of the Slope differential parameter. Figures 7(c)–7(d) show the profiles, plus linear fits, and the corresponding phase gradient ROIs for simulated RBC and WBC signals, respectively. The Slope parameter measures the differences in transverse phase gradient contrast between RBC and WBC signals for both simulated and experimental data. The transverse phase contrast can be observed in the phase gradient ROIs in Fig. 7 and is due to the shape of the measured cell.
3. Results
Each A-scan evaluated using the full-wave model required approximately 13 hours to compute using a 12-core Intel Xeon CPU (E5-2670 v3, 2.30GHz) and approximately 4Gb of RAM. Since the full M-scan simulation contains 407 A-scans, one for each sampled position of the blood cells relative to the optical axis, we utilized the Pawsey Supercomputing Centre’s Magnus, a Cray XC40 series supercomputer with 1488 nodes, each containing two CPUs (as specified above) and 64 GB RAM.
3.1 Simulated electric field distribution
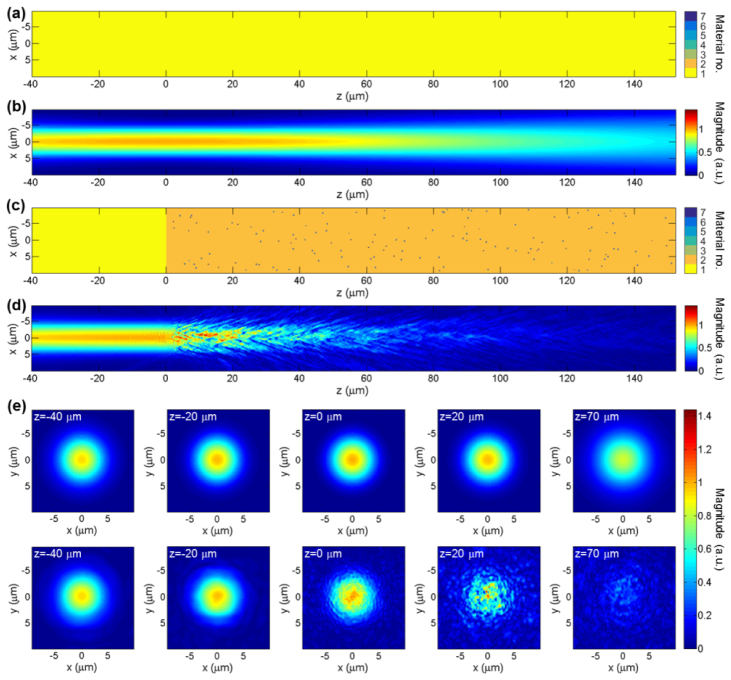
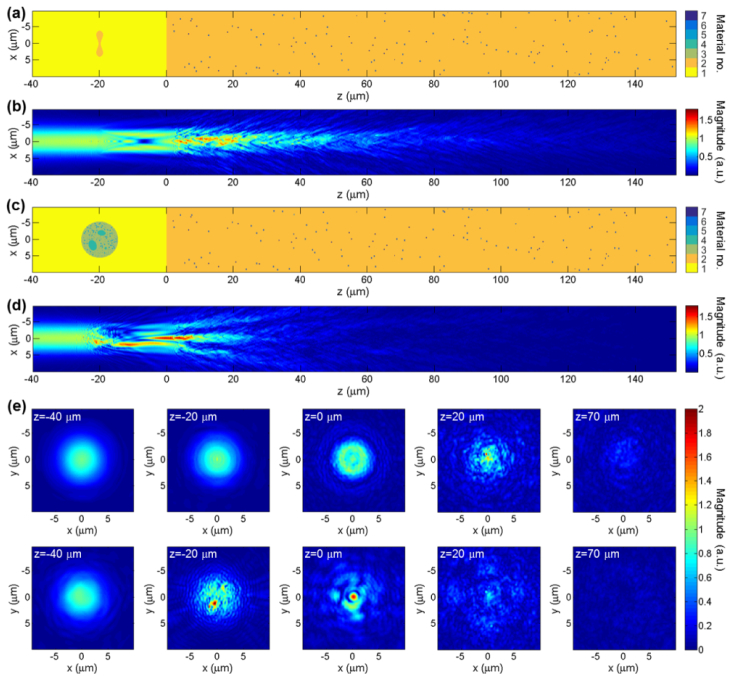
Four different scattering geometries are considered: the homogeneous case of water only (Fig. 8(a)), the microchannel without a blood cell (Fig. 8(c)), the microchannel with a RBC (Fig. 9(a)) and the microchannel with a WBC (Fig. 9(c)). In each case, the magnitude of the x-component of the electric field, |Ex|, is plotted. The color in each of Fig. 8(a), Fig. 8(c), Fig. 9(a) and Fig. 9(c) represents an index into a global list of refractive indices given as: 1.33, 1.41, 1.36, 1.5, 1.58, 2.455 and 2.52. Where available, the refractive index values are provided at λ0 = 790nm. The scattering geometries are plotted in the x-z plane containing the optical axis. Field quantities are plotted either in this plane, or in x-y planes spaced about the beam’s focus. In particular, the plane z = −40μm refers to the x-y plane located 40μm before focus. For reference, the scattering geometry of Fig. 8(c) is common to all of the 407 A-scans simulated to construct Fig. 10. The first and last of these A-scans used precisely this scattering geometry. A-scan numbers 106 and 290, in Fig. 10, used the scattering geometries of Fig. 9(a) and Fig. 9(c) respectively.
Fig. 8.
Plots of the magnitude of the x-component of electric field, |Ex|; the plots shown in (a-d) are plotted in x-z plane containing the optical axis; a) the 3D homogeneous geometry for water only; b) a plot of |Ex| for the case presented in (a); c) the scattering geometry for the empty microchannel; d) a plot of |Ex| for the case presented in (c); e) plots of |Ex| in x-y planes spaced about the beam’s focus: the top row of images shows the plots associated with (a-b), and the lower shows those associated with (c-d).
Fig. 9.
Magnitude plots of the x-component of electric field, |Ex|, for the cases of an RBC and WBC present in the microchannel; the plots shown in (a-d) are plotted in x-z plane containing the optical axis; a) the scattering geometry for the RBC included in the microchannel; b) a plot of |Ex| for the case (a); (c-d) the plots corresponding to (a-b) but with a WBC in the microchannel; e) plots of |Ex| in x-y planes: the top row of images for the RBC case (i.e., a-b), and the lower row corresponds to the WBC case (i.e., c-d).
Fig. 10.
a) Simulated magnitude M-scans constructed from 407 A-scans; b) the M-scan from (a) with static background subtracted (differential magnitude M-scan); c) phase gradient M-scan based on complex M-scan shown as magnitude in (a). The left signal of interest in all M-scans refers to the RBC, while the right one to the WBC.
Figure 8(b) shows a plot of |Ex| for the beam focused in water only. The top row of Fig. 8(e) shows |Ex| at five transverse planes spaced about the beam’s focus, again in water only. These plots are useful for comparison with subsequent plots where scatterers have been included (Fig. 9). All values of |Ex| are normalized by the peak value of |Ex| in the case of water only. Accordingly, the maximum value of |Ex| in Fig. 8(b) and the top row of Fig. 8(e) is 1. Figure 8(d) shows |Ex| for the case with microfluidic chip in place. The peak value of |Ex| exceeds that of the homogeneous case due to constructive interference of light scattered by the TiO2 particles. The attenuation of the beam is readily observed in this plot. Plots of |Ex| in transverse planes are shown in the lower row of Fig. 8(e). These plots show a weak backscattered field (z = −40μm and −20μm) and beam which becomes increasingly perturbed as z increases (z = 0μm, 20μm and 70μm).
Figure 9 represents the case where blood cells are included within the microchannel. In particular, Fig. 9(a) and Fig. 9(c) show how the refractive index distributions change when the RBC and WBC, respectively, are included in the microchannel. Figure 9(b) and the top row of images in Fig. 9(e) show the field distribution when the RBC is included. The scattering geometry in Fig. 9(a) is slightly idealized since the RBC is centered upon the optical axis, leading to the highly symmetrical field structure in Fig. 9(b), immediately after the RBC. Figure 9(d) and the lower row of images in Fig. 9(e) show the field distribution when the WBC is included. The field plots show that the WBC scatters the field significantly more than the RBC.
3.2 Comparison of simulated and experimentally acquired OCT images
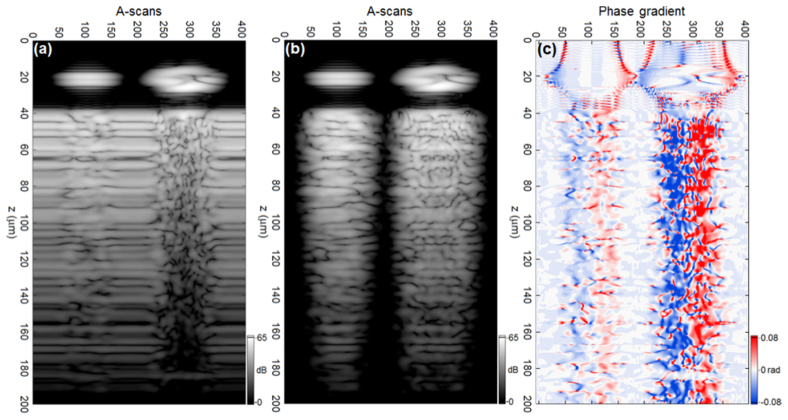
This section contains several examples of simulated and experimentally acquired M-scans. For brevity, in what follows, we abbreviate “experimentally acquired M-scans” as “experimental M-scans”. Figure 10(a) shows the magnitude of a simulated OCT M-scan (we define this M-scan as “magnitude M-scan”) obtained as a result of computing 407 A-scans for a set of 407 scattering geometries, which together represent the movement of cells through the microchannel. Note that the horizontal speckle line visible in Fig. 10(a), around z = 185μm, and the corresponding effect noticeable at the same depth in Fig. 10(c), is due to an erroneous reflection from the PML. This erroneous reflection occurs because field quantities and material properties have only a finite spatial sampling and can be reduced by reducing the PSTD cell dimension [38]. M-scans presented in Figs. 10(b)–10(c) represent the difference between the complex valued A-scans for the cases with and without cells. Figure 10(b) is the differential magnitude M-scan, i.e. the magnitude of complex valued M-scan (Fig. 10(a)) after subtracting the constant signal originating from TiO2-PDMS layer (Fig. 4(b) in the reference [19] depicts the procedure of background subtraction). Figure 10(c) is the phase gradient M-scan which is constructed across the lateral (transverse) direction, so that the ith A-scan of the phase gradient M-scan is obtained by subtracting phase of the (i-1)th raw, complex valued, A-scan (including background) from that of the ith. The phase gradient M-scan is represented on a divergent, or bipolar, colormap which represents negative phase values by blue, zero with white and positive values with red. Characteristic speckle fields are observed in all images beneath the signal associated with each cell localized in the microchannel (the left signal comes from RBC and the right one from WBC). This is because a cell in the microchannel perturbs both the light incident upon the substrate and the light scattered back by the substrate before reaching the detection fiber. For a fixed illumination beam (M-scan mode), this signal perturbation is clearly visible on the static background as a perturbed, or new, speckle pattern in both the magnitude and phase gradient M-scans. Moreover, this perturbation results in a marked visual difference between the simulated signals in Fig. 10. This difference is visually evident also in the experimentally acquired OCT images shown in Fig. 11, Fig. 12 as well as Fig. 13, and is due to the differing scattering properties of the cells presented in Fig. 9.
Fig. 11.
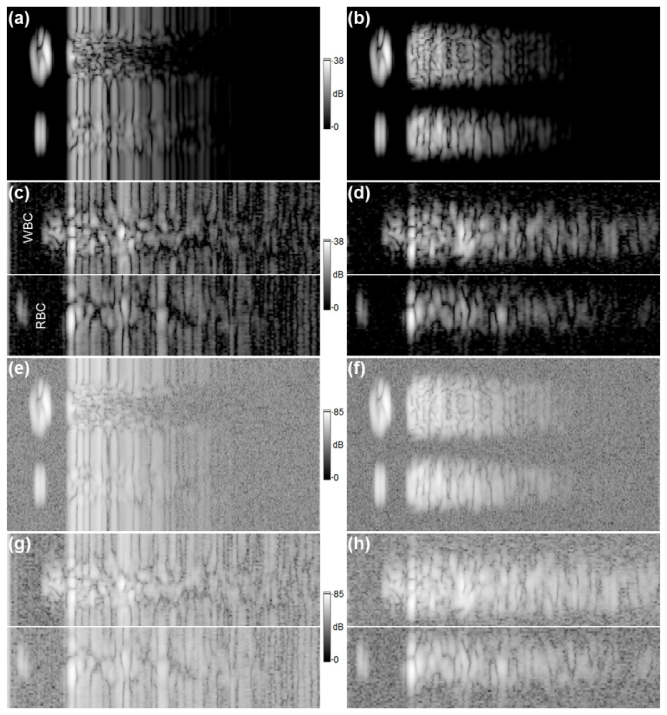
Comparison of simulated and experimental M-scans for data set 1; a) a simulated magnitude M-scan; b) the M-scan from (a) with background subtracted; c) an experimental M-scan created by fusing two independent M-scans (the top image shows a part of M-scan including a signal coming from the WBC and the lower image shows a signal derived from the RBC); d) the M-scans from (c) with background subtracted; e) the simulated M-scan from (a) divided by its dynamic range and with white noise, of standard deviation taken from (g), added; f) the simulated M-scan from (b) processed in the same way as (e) with noise derived from (h); g) the experimental M-scan from (c), divided by its dynamic range; h) the experimental M-scan from (d) processed in the same way as (g).
Fig. 12.
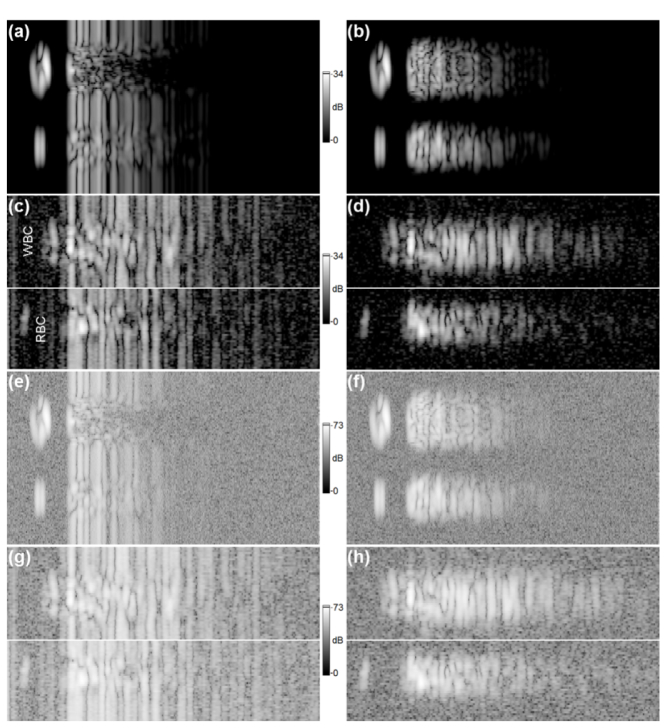
An identical analysis to that presented in Fig. 11, but for data set 2. All images (a-h) directly correspond to that presented in Fig. 11. The SNR for data set 2 is 34dB.
Fig. 13.
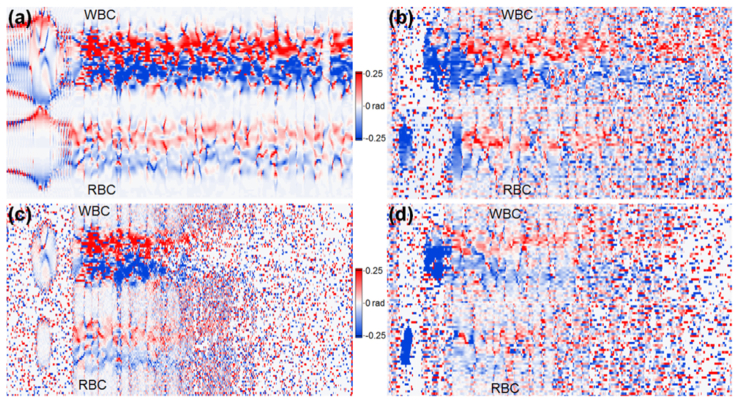
Simulated and experimental phase gradient M-scans; a) a simulated phase gradient M-scan corresponding with the M-scans depicted in Fig. 11(a) and Fig. 12(a); b) an experimental phase gradient M-scan corresponding with the M-scan of Fig. 11(c) (data set 1); c) a simulated phase gradient M-scan with noise added, derived directly from data shown as magnitude in Fig. 11(e) and Fig. 12(e); d) an experimental phase gradient M-scan corresponding with the M-scan of Fig. 12(g) (data set 2).
Figure 11 and Fig. 12 show a comparison of simulated and experimental magnitude M-scans for two different experimental data sets: data set 1 and data set 2, respectively; all M-scans in each figure depict 200μm of the sample depth. Both experimental data sets were adopted from our previous study [19] and refer to different experimental measurements conducted by means of the OCT setup with LSM02-BB objective lens (see Table 1 in the reference [19]). The same simulated data set is considered in both figures. The sampling rate of the position of blood cells in the microchannel for the experimental case depends on the velocity of flowing cells and the parameters of the spectrometer camera. Because the simulation sampling rate exceeds the experimental one, all simulated M-scans used in the comparative study (Fig. 11, Fig. 12, Fig. 13 and Fig. 14) are constructed by choosing every 4th A-scan from the set of 407 shown in Fig. 10, giving 102 A-scans per M-scan.
Fig. 14.
Illustration of the attenuation of the OCT signal (magnitude); all plots and images are presented in decibel scale; a) profiles (A-scans) through the signals of interest for: experimental RBC (red line, depicted as an image in (e), data set 2), experimental WBC (black line, data set 2), simulated RBC (green line, also depicted in (f)) and simulated WBC (blue line). The dashed lines (magenta) indicate the SNR level for data set 2 (34dB); b) the corresponding profiles for data set 1 (SNR 38dB); (c-d) the profiles through the TiO2-PDMS layer in the absence of cells: experimental (orange lines, shown as the images in (g-h)), for experimental data set 2 (c) and data set 1 (d), and simulated profiles (brown lines) also depicted in (i). The vertical lines in images (e-f) indicate the origin of the associated profile plots.
The simulated M-scans (the magnitude and differential magnitude M-scans) shown in Figs. 11(a)–11(b) are displayed on a logarithmic scale such that the peak OCT signal in the simulated image corresponds to the peak value of the signal-to-noise ratio (SNR) in the experimental images (38dB), presented in Figs. 11(c)–11(d). The simulated and experimental images differ significantly in terms of the noise level. In particular, the simulated images are free of noise. Therefore, the magnitude M-scans shown in Figs. 11(a)–11(d) were modified by dividing by their respective dynamic ranges (DR) [40], and the simulated complex valued M-scans shown as magnitude in Figs. 11(e)–11(f) had complex white noise added, with standard deviation values sampled from the modified (DR corrected) experimental intensity M-scans depicted as magnitudes in Figs. 11(g)–11(h). In particular, the standard deviation of complex valued noise added to the simulated complex M-scan shown as magnitude in Fig. 11(e) was obtained from the experimental intensity M-scan presented as magnitude in Fig. 11(g), for a specially selected M-scan ROI which includes the noise signal. The above analysis is based upon our previous treatment [40]. The image set shown in Fig. 12 is presented in the same way as the set shown in Fig. 11 for images obtained from data set 2. Note that the experimental M-scans from each data set have different SNR levels, which affects data processing and the final result. Figure 11 and Fig. 12 show that the signal attenuates faster for simulated images than for their experimental counterparts, even if noised simulated images are considered.
The influence of the noise on the phase gradient M-scan quality is clearly visible in Fig. 13, which presents a comparison of simulated and experimental phase gradient M-scans. The top signal of interest in each phase gradient M-scan in this figure is derived from the WBC, while the lower one corresponds to the RBC. Fig. 13(a) shows a simulated phase gradient M-scan derived from the simulated M-scan depicted in the magnitude plot in Fig. 11(a). The experimental phase gradient M-scan obtained from data set 1 is depicted in Fig. 13(b). The simulated phase gradient M-scan (with noise added) is shown in Fig. 13(c) to justify the loss of quality observed in experimental phase gradient M-scans presented in Fig. 13(b) and Fig. 13(d), where the latter one was computed from experimental data set 2. The simulated image presented in Fig. 13(c) also indicates faster attenuation of the phase gradient signal in comparison to the experimental M-scans shown in Fig. 13(b) and Fig. 13(d). All phase gradient M-scans in Fig. 13 are displayed in a way presented in Fig. 10(c), covering the range of ± 0.25 radians. Since all phase gradient M-scans in Fig. 13 are computed directly from the corresponding complex valued M-scans, presented as a magnitude in Fig. 11 and Fig. 12, they also visualize 200μm of the sample depth.
3.3 Comparative quantitative analysis
As a validation step we analyzed selected A-scans to quantify the differences in attenuation of the signal between simulated and experimental results, observed in Fig. 11 and Fig. 12. The A-scans include a 160μm deep TiO2-PDMS section of the sample. Figures 14(a)–14(b) show the magnitudes of the A-scans (profiles) through the WBC and RBC centers, for both data set 2 and data set 1, respectively. Each of the figures depicts four profiles: experimental RBC (red line) and WBC (black line) signals, compared with corresponding simulated RBC (green line) and WBC (blue line) signals. Each line profile is part of an M-scan shown in Fig. 11 or Fig. 11. In particular, the experimental RBC profile of Fig. 14(a) is derived from the M-scan depicted in Fig. 14(e), while the simulated RBC profile is derived from the M-scan depicted in Fig. 14(f). Figs. 14(c)–14(d) compare experimental and simulated A-scans due to the TiO2-PDMS layer, in the absence of cells, for the two data sets. Each of the experimental profiles, shown as orange lines in Fig. 14(c)–14(d) and depicted in Figs. 14(g)–14(h), were calculated by averaging 16 neighboring A-scans. The simulated profile in each plot (brown) corresponds to the first and last A-scans (which are identical) shown in Fig. 11(a) and Fig. 12(a) and is depicted in Fig. 14(i).
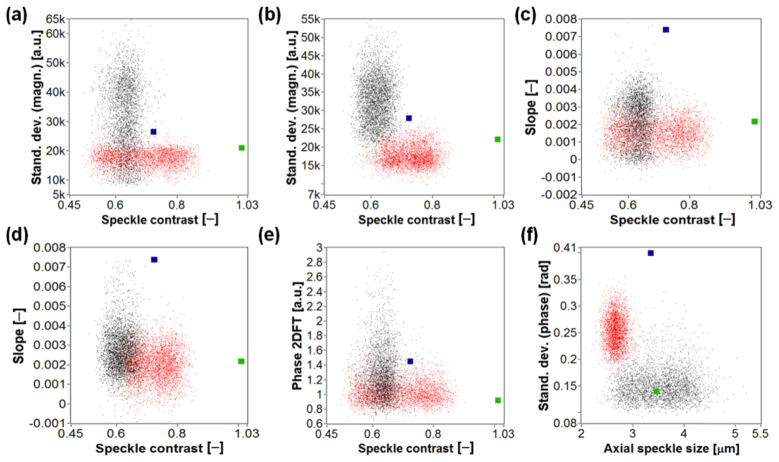
In order to show the potential of our technique to differentiate cells we considered two-dimensional scatter plots of various sampled differential parameter values originating from both experimental data sets, and both types of blood cell in the microchannel (the RBCs or WBCs). We compared these differential parameters with simulated values, as shown in Fig. 15. In each plot, experimental measurements for RBCs and WBCs are indicated by red dots and black dots, respectively, while the simulated values are indicated by a green dot for the RBC and by a dark blue dot in case of the WBC. Differential parameters presented in Fig. 15 are described in Section 2.6, where we also explain why some of the differential parameter values are scaled. The scaling factors are provided in parentheses in the caption of Fig. 15. Each plot in Fig. 15 corresponds to a different combination of two differential parameters taken from those collated in Table 2. Each differential parameter is calculated for M-scan ROIs with an upper limit located 68μm below the microchannel (for both experimental and synthetic data). This value corresponds to the axial position of the ROIs considered in our previous study [19] and was obtained experimentally.
Fig. 15.
Two-dimensional scatter plots of differential parameter values for RBC (red dots) and WBC (black dots) signals of interest combined with simulated differential parameter values (green dot: RBC, dark blue dot: WBC). Experimental values shown in (b) and (d) were calculated for experimental data set 1, while the remainder of the plots were calculated using data set 2; a) Speckle contrast [‒] (not scaled) vs. Standard deviations (magnitude) [a.u.] (×235); b) Speckle contrast [‒] (not scaled) vs. Standard deviations (magnitude) [a.u.] (×247); (c-d) Speckle contrast [‒] vs. Slope [‒] (both not scaled); e) Speckle contrast [‒] (not scaled) vs. Phase 2DFT [a.u.] (×2.2); f) Axial (vertical) speckle size [μm] vs. Standard deviations (phase) [rad] (both not scaled). The scaling factors are provided in parentheses.
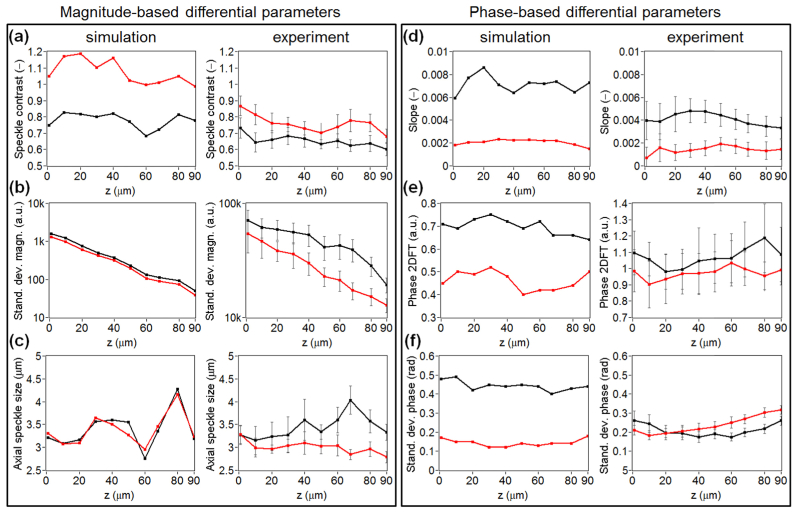
The plots presented in Fig. 15 reveal that the separation of differential parameter values is largely superior for simulated differential parameters, which we believe results from the idealized blood cell optical models and imaging conditions as considered further in Section 4. Moreover, Fig. 15(f) shows that differential parameters: Axial (vertical) speckle size and phase-based Standard deviations, are not confirmed by the simulated results. The identifier “Standard deviations” is due to standard deviation calculated several times for different sections of the ROI [19].
Figure 16 presents differential parameters calculated for different axial positions of the ROI. The analysis was performed for the simulated and exemplar experimental data derived from data set 2. The plots in Fig. 16 demonstrate the sensitivity of differential parameters collated in Table 2, with respect to ROI position. The left frame in this figure includes the plots of magnitude-based differential parameters, while the right one includes the plots of phase-based differential parameters. The left column in each frame contains simulated results and the right one includes experimental results. The red line in each plot indicates differential parameters obtained for the RBC signals, while the black line corresponds to the WBCs.
Fig. 16.
Plots illustrating the sensitivity of the differential parameters to axial position of the ROI, calculated for simulated (the left column in each frame) and exemplar experimental data (the right columns), which consists of 130 RBC signals and 130 WBC signals, derived from experimental data set 2. The parameter values shown in row (b) in the left frame are presented in logarithmic scale. The red line in each plot indicates differential parameters obtained for the RBC signals, while the black line corresponds to the WBCs.
The analysis shown in Fig. 16 allows us to choose the most reliable differential parameters in terms of effective differentiation. In particular, the most stable differential parameters with respect to the axial position of the ROI are: magnitude-based Speckle contrast and Standard deviations, as well as phase-based Slope. These differential parameters are also the most effective in differentiating between cells. Figure 16 also reveals some discrepancies between simulation and experiment. A discrepancy in the magnitude-based differential parameters, corresponding to WBCs, can be observed in Figs. 16(b)–16(c). In particular, the WBC magnitude signal is attenuated more rapidly in simulation than in experiment. Moreover, the speckle size is noticeably different between simulated and experimental results for WBC signals. We believe that this is due to the sub-optimal refractive index distribution model of the WBC and possibly the TiO2 scatterers. In particular, the TiO2 scatterers match only scattering cross-section, but not the direction of scattering. This issue will be addressed in future work. Furthermore, the WBC refractive index model is obtained by combining several sources of data. To the best of our knowledge, such a rigorous theoretical validation of the optical properties of WBCs has not previously been performed. There are also some discrepancies in the phase-based differential parameters shown in Figs. 16(e)–16(f). We believe this is due to pixels in the complex OCT data being set to zero when their SNR is less than a defined threshold. This is performed as it leads to a reduction in noise in the experimentally acquired phase gradient M-scans. This has the effect of reducing the standard deviation phase, yet maintaining the mean phase. This can be understood by noting that this step essentially transforms the distribution of pixel phase values, of those with a low SNR, from a Gaussian with zero mean to one where the only possible value is 0. This discrepancy is not observed for the Slope differential parameter, shown in Fig. 16(d), since it is obtained using a line of best fit, which remains unaffected by thresholding due to the same reason that the mean is unaffected.
4. Discussion and conclusion
We applied a rigorous, full-wave, model of OCT image formation to an experimental, microfluidic chip based, biological micro-objects differentiation technique. We explained the components of the image formation model and presented example data resulting from each component of the model. This is the first instance, to our knowledge, that a model of this degree of realism has been applied to validating experimental OCT images of medical or biological significance. Additionally, as far as we know, the examples of modelling blood cell’s scattering properties measured by the OCT system have not yet been presented. A particularly novel aspect of the model is the generation of optical models, i.e., refractive index distributions, for erythrocytes and leukocytes and the simulation of the OCT image of these cell models. We simulated M-scans for such erythrocytes and leukocytes flowing through the microfluidic chip and compared the result with experimentally obtained M-scans. Differential parameters were extracted from experimental and simulated M-scans. Moreover, there was relative quantitative agreement between the differential parameters obtained from experimental and simulated M-scans in the sense that the relative magnitudes of the differential parameters agree for the experimental and simulated cases. We believe that refinement of the model will allow for absolute quantitative agreement, which remains one of the foci of future work.
The model still possesses some weaknesses which require further investigation. First, the axial attenuation of the signal observed in simulated M-scans is greater than in case of experimental M-scans. The analysis presented in Section 3.3 outlines this discrepancy quantitatively. Second, the simulated lateral speckle size is significantly lower when measured for the signal derived from the WBC than obtained from the RBC. This is not the case for experimental results since no significant difference was measured between WBC and RBC signals.
We performed a number of additional simulations to ascertain the cause of the discrepancies mentioned above. In particular, we varied the effective spectral width of the simulation and found that, as expected, reducing the spectral width leads to an increase in both vertical and horizontal speckle sizes. However, reducing the spectral width within the range of plausible values is insufficient to bring the simulated lateral speckle size into agreement with experiment, even though the axial speckle size approximately agrees with experiment. We varied the position of the axial focus of the objective to check whether this was influencing the greater axial attenuation of the simulated M-scans. These simulations confirmed that the axial position of the focus has only a negligible effect on the axial attenuation observed in the simulated M-scans. Individual scatterers were designed, via simulation, to match the scattering cross-sections of the assumed spherical scatterers. We thus believe that scatterer representation is not the cause of the higher simulated axial attenuation. The diameter of TiO2 scatterers used in the experiment is, however, not known precisely, and these simulations suggest that the previously assumed diameter of 350nm may be incorrect. The proportion by mass of the TiO2, relative to PDMS, is known. Mie theory based calculations show that, at a fixed proportion by mass, a lower scattering coefficient can be obtained if the diameter of the TiO2 is reduced below 275nm. Therefore, improved estimation of the diameter of the TiO2 scatterers is an important aspect of future work.
In this work we model two single blood cells as the examples of RBCs and WBCs. Although a single RBC model seems to be sufficient to represent the population of normal erythrocytes, the neutrophil model represents only one of five leukocyte subpopulations appearing in human blood [1]. Thus, modeling other WBCs, such as lymphocyte and monocyte, is another important aspect of our future work, as well as refining the neutrophil model by, for example, changing its diameter, the number of nucleus lobes or refractive index contrast between intracellular components, regardless of the refractive index values reported in the literature. Furthermore, since the locations and orientations of the RBC and WBC models were idealized, parametric studies, including varying positions, orientations (including rotation), mechanical deformation and sizes, are also considered for further investigation.
Acknowledgments
This work was supported by resources provided by the Pawsey Supercomputing Centre with funding from the Australian Government and the Government of Western Australia. P.O. acknowledges fruitful discussions with Maciej Szkulmowski (Nicolaus Copernicus University).
Funding
Australian Research Council Discovery Early Career Research Award (DE120101331); Royal Society University Research Fellowship (UF130304); National Science Center within the MAESTRO Programme (DEC-2011/02/A/ST2/00302); European Union’s Horizon 2020 research and innovation programme grant No. 666295.
References and links
- 1.Lokwani D., The ABC of CBC: Interpretation of Complete Blood Count and Histograms (Jaypee Brothers Medical Publishers, 2013). [Google Scholar]
- 2.Bain B. J., Bates I., Laffan M. A., Lewis S. M., Dacie and Lewis Practical Haematology: Expert Consult: Online and Print (Elsevier Health Sciences, 2011). [Google Scholar]
- 3.Shapiro H. M., Practical Flow Cytometry (John Wiley & Sons, 2005). [Google Scholar]
- 4.Coulter W. H., “High speed automatic blood cell counter and cell size analyzer,” Proc. Natl. Electron. Conf. 12, 1034–1040 (1956). [Google Scholar]
- 5.Golan L., Yeheskely-Hayon D., Minai L., Dann E. J., Yelin D., “Noninvasive imaging of flowing blood cells using label-free spectrally encoded flow cytometry,” Biomed. Opt. Express 3(6), 1455–1464 (2012). 10.1364/BOE.3.001455 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Seo S., Isikman S. O., Sencan I., Mudanyali O., Su T.-W., Bishara W., Erlinger A., Ozcan A., “High-throughput lens-free blood analysis on a chip,” Anal. Chem. 82(11), 4621–4627 (2010). 10.1021/ac1007915 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zhu H., Sencan I., Wong J., Dimitrov S., Tseng D., Nagashima K., Ozcan A., “Cost-effective and rapid blood analysis on a cell-phone,” Lab Chip 13(7), 1282–1288 (2013). 10.1039/c3lc41408f [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Godin J., Chen C. H., Cho S. H., Qiao W., Tsai F., Lo Y. H., “Microfluidics and photonics for Bio-System-on-a-Chip: a review of advancements in technology towards a microfluidic flow cytometry chip,” J. Biophotonics 1(5), 355–376 (2008). 10.1002/jbio.200810018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yun H., Bang H., Min J., Chung C., Chang J. K., Han D.-C., “Simultaneous counting of two subsets of leukocytes using fluorescent silica nanoparticles in a sheathless microchip flow cytometer,” Lab Chip 10(23), 3243–3254 (2010). 10.1039/c0lc00041h [DOI] [PubMed] [Google Scholar]
- 10.Shi W., Guo L., Kasdan H., Tai Y.-C., “Four-part leukocyte differential count based on sheathless microflow cytometer and fluorescent dye assay,” Lab Chip 13(7), 1257–1265 (2013). 10.1039/c3lc41059e [DOI] [PubMed] [Google Scholar]
- 11.Vercruysse D., Dusa A., Stahl R., Vanmeerbeeck G., de Wijs K., Liu C., Prodanov D., Peumans P., Lagae L., “Three-part differential of unlabeled leukocytes with a compact lens-free imaging flow cytometer,” Lab Chip 15(4), 1123–1132 (2015). 10.1039/C4LC01131G [DOI] [PubMed] [Google Scholar]
- 12.Wu T.-F., Mei Z., Lo Y.-H., “Optofluidic device for label-free cell classification from whole blood,” Lab Chip 12(19), 3791–3797 (2012). 10.1039/c2lc40560a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ramoji A., Neugebauer U., Bocklitz T., Foerster M., Kiehntopf M., Bauer M., Popp J., “Toward a spectroscopic hemogram: Raman spectroscopic differentiation of the two most abundant leukocytes from peripheral blood,” Anal. Chem. 84(12), 5335–5342 (2012). 10.1021/ac3007363 [DOI] [PubMed] [Google Scholar]
- 14.Hebert C. G., Terray A., Hart S. J., “Toward label-free optical fractionation of blood--optical force measurements of blood cells,” Anal. Chem. 83(14), 5666–5672 (2011). 10.1021/ac200834u [DOI] [PubMed] [Google Scholar]
- 15.Kummrow A., Theisen J., Frankowski M., Tuchscheerer A., Yildirim H., Brattke K., Schmidt M., Neukammer J., “Microfluidic structures for flow cytometric analysis of hydrodynamically focussed blood cells fabricated by ultraprecision micromachining,” Lab Chip 9(7), 972–981 (2009). 10.1039/b808336c [DOI] [PubMed] [Google Scholar]
- 16.Wang Z., Chin S. Y., Chin C. D., Sarik J., Harper M., Justman J., Sia S. K., “Microfluidic CD4+ T-cell counting device using chemiluminescence-based detection,” Anal. Chem. 82(1), 36–40 (2010). 10.1021/ac902144w [DOI] [PubMed] [Google Scholar]
- 17.van Berkel C., Gwyer J. D., Deane S., Green N. G., Holloway J., Hollis V., Morgan H., “Integrated systems for rapid point of care (PoC) blood cell analysis,” Lab Chip 11(7), 1249–1255 (2011). 10.1039/c0lc00587h [DOI] [PubMed] [Google Scholar]
- 18.Holmes D., Pettigrew D., Reccius C. H., Gwyer J. D., van Berkel C., Holloway J., Davies D. E., Morgan H., “Leukocyte analysis and differentiation using high speed microfluidic single cell impedance cytometry,” Lab Chip 9(20), 2881–2889 (2009). 10.1039/b910053a [DOI] [PubMed] [Google Scholar]
- 19.Ossowski P., Raiter-Smiljanic A., Szkulmowska A., Bukowska D., Wiese M., Derzsi L., Eljaszewicz A., Garstecki P., Wojtkowski M., “Differentiation of morphotic elements in human blood using optical coherence tomography and a microfluidic setup,” Opt. Express 23(21), 27724–27738 (2015). 10.1364/OE.23.027724 [DOI] [PubMed] [Google Scholar]
- 20.Ralston T. S., Marks D. L., Carney P. S., Boppart S. A., “Inverse scattering for optical coherence tomography,” J. Opt. Soc. Am. A 23(5), 1027–1037 (2006). 10.1364/JOSAA.23.001027 [DOI] [PubMed] [Google Scholar]
- 21.Schmitt J., Knüttel A., “Model of optical coherence tomography of heterogeneous tissue,” J. Opt. Soc. Am. A 14(6), 1231–1242 (1997). 10.1364/JOSAA.14.001231 [DOI] [Google Scholar]
- 22.Pan Y., Birngruber R., Rosperich J., Engelhardt R., “Low-coherence optical tomography in turbid tissue: theoretical analysis,” Appl. Opt. 34(28), 6564–6574 (1995). 10.1364/AO.34.006564 [DOI] [PubMed] [Google Scholar]
- 23.Munro P. R., “Three-dimensional full wave model of image formation in optical coherence tomography,” Opt. Express 24(23), 27016–27031 (2016). 10.1364/OE.24.027016 [DOI] [PubMed] [Google Scholar]
- 24.Török P., Munro P. R., Kriezis E. E., “High numerical aperture vectorial imaging in coherent optical microscopes,” Opt. Express 16(2), 507–523 (2008). 10.1364/OE.16.000507 [DOI] [PubMed] [Google Scholar]
- 25.Liu Q. H., “The PSTD algorithm: A time‐domain method requiring only two cells per wavelength,” Microw. Opt. Technol. Lett. 15(3), 158–165 (1997). [DOI] [Google Scholar]
- 26.Munro P. R., “Exploiting data redundancy in computational optical imaging,” Opt. Express 23(24), 30603–30617 (2015). 10.1364/OE.23.030603 [DOI] [PubMed] [Google Scholar]
- 27.Lim J., Ding H., Mir M., Zhu R., Tangella K., Popescu G., “Born approximation model for light scattering by red blood cells,” Biomed. Opt. Express 2(10), 2784–2791 (2011). 10.1364/BOE.2.002784 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Yurkin M. A., Semyanov K. A., Tarasov P. A., Chernyshev A. V., Hoekstra A. G., Maltsev V. P., “Experimental and theoretical study of light scattering by individual mature red blood cells by use of scanning flow cytometry and a discrete dipole approximation,” Appl. Opt. 44(25), 5249–5256 (2005). 10.1364/AO.44.005249 [DOI] [PubMed] [Google Scholar]
- 29.Perkins S. L., “Normal blood and bone marrow values in humans,” in Wintrobe's Clinical Hematology, 11th ed., Greer J. P., Foerster J., Lukens J. N., eds. (Lippincott Williams & Wilkins, 2003). [Google Scholar]
- 30.Yurkin M. A., Semyanov K. A., Maltsev V. P., Hoekstra A. G., “Discrimination of granulocyte subtypes from light scattering: theoretical analysis using a granulated sphere model,” Opt. Express 15(25), 16561–16580 (2007). 10.1364/OE.15.016561 [DOI] [PubMed] [Google Scholar]
- 31.Ruban G. I., Kosmacheva S. M., Goncharova N. V., Van Bockstaele D., Loiko V. A., “Investigation of morphometric parameters for granulocytes and lymphocytes as applied to a solution of direct and inverse light-scattering problems,” J. Biomed. Opt. 12(4), 044017 (2007). 10.1117/1.2753466 [DOI] [PubMed] [Google Scholar]
- 32.Fung Y. C., Tong P., “Theory of the sphering of red blood cells,” Biophys. J. 8(2), 175–198 (1968). 10.1016/S0006-3495(68)86484-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lewis S. M., Bain B. J., Bates I., Dacie J. V., Dacie and Lewis Practical Haematology (Elsevier Health Sciences, 2006). [Google Scholar]
- 34.Dunn A. K., “Modeling of light scattering from inhomogeneous biological cells,” in Optics of Biological Particles, Hoekstra A. G., Maltsev V. P., Videen G., eds. (Springer, 2007). [Google Scholar]
- 35.Schoch R. L., Kapinos L. E., Lim R. Y., “Nuclear transport receptor binding avidity triggers a self-healing collapse transition in FG-nucleoporin molecular brushes,” Proc. Natl. Acad. Sci. U.S.A. 109(42), 16911–16916 (2012). 10.1073/pnas.1208440109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Richards B., Wolf E., “Electromagnetic diffraction in optical systems. II. Structure of the image field in an aplanatic system,” Proc. R. Soc. Lond. A Math. Phys. Sci. 253(1274), 358–379 (1959). 10.1098/rspa.1959.0200 [DOI] [Google Scholar]
- 37.Török P., Munro P., “The use of Gauss-Laguerre vector beams in STED microscopy,” Opt. Express 12(15), 3605–3617 (2004). 10.1364/OPEX.12.003605 [DOI] [PubMed] [Google Scholar]
- 38.Berenger J. P., “A perfectly matched layer for the absorption of electromagnetic waves,” J. Comput. Phys. 114(2), 185–200 (1994). 10.1006/jcph.1994.1159 [DOI] [Google Scholar]
- 39.Munro P. R., Engelke D., Sampson D. D., “A compact source condition for modelling focused fields using the pseudospectral time-domain method,” Opt. Express 22(5), 5599–5613 (2014). 10.1364/OE.22.005599 [DOI] [PubMed] [Google Scholar]
- 40.Szkulmowski M., Wojtkowski M., “Averaging techniques for OCT imaging,” Opt. Express 21(8), 9757–9773 (2013). 10.1364/OE.21.009757 [DOI] [PubMed] [Google Scholar]