Similarity regularized sparse group lasso for cup to disc ratio computation

Abstract

Automatic cup to disc ratio (CDR) computation from color fundus images has shown to be promising for glaucoma detection. Over the past decade, many algorithms have been proposed. In this paper, we first review the recent work in the area and then present a novel similarity-regularized sparse group lasso method for automated CDR estimation. The proposed method reconstructs the testing disc image based on a set of reference disc images by integrating the similarity between testing and the reference disc images with the sparse group lasso constraints. The reconstruction coefficients are then used to estimate the CDR of the testing image. The proposed method has been validated using 650 images with manually annotated CDRs. Experimental results show an average CDR error of 0.0616 and a correlation coefficient of 0.7, outperforming other methods. The areas under curve in the diagnostic test reach 0.843 and 0.837 when manual and automatically segmented discs are used respectively, better than other methods as well.

1. Introduction

Glaucoma is the second leading cause of blindness, predicted to affect around 80 million people by 2020 [1]. Since glaucoma is a chronic eye disease occurs without easily noticeable symptoms over a long period of time, most of the patients are not aware of it until too late [2]. Therefore, glaucoma is also called the silent thief of sight. One major reason that glaucoma can result in vision loss is that it cannot be cured currently. However, the progression of the disease can be slowed down or even stopped if it is detected and treated timely. Thus, the screening of high risk population is vital for glaucoma control and disease management.

The current clinical approaches for glaucoma assessment consist of visual field test, optic nerve head (ONH) assessment and the air-puff intraocular pressure (IOP) measurement. The limitation of IOP measurement by tonometry is that the value is dependent on the thickness of subject’s central cornea [3], thus using IOP for glaucoma detection is not accurate. On the other hand, visual field examination is unsuitable for population screening as dedicated equipments for such examination are only available in specialized hospitals. Though ONH assessment is promising for glaucoma screening, manual assessment by trained professionals is not only time consuming and costly but also can be subjective due to inter-grader variance. With the recent development of technologies, automatic ONH assessment has received much attention lately. Researchers have reported 3D-image-based methods for automated cup to disc ratio (CDR) [4] detection, for examples, via optical coherence tomography images [5–7] or stereo images [8]. However, the expense of 3D image acquisition makes it unsuitable for low cost large-scale screening [9]. On the other hand, the 2D retinal fundus images are much inexpensive as fundus cameras are extensively available in eye centers, polyclinics, hospitals and even in optical shops. Introducing a fundus-image-based glaucoma screening programme would induce minimal additional cost with the current setup.

Many researchers worked on automatic glaucoma detection from 2D retinal fundus images. Several groups proposed methods for binary classification between normal and glaucomatous images using features at image level [10–12], where classification and feature selection strategies can be challenging [9]. Recently, deep learning is also applied to detect glaucoma [13, 14]. These methods work as black box technology without giving clinically meaningful measurements. Some other researchers follow clinical indicators, such as CDR, disc diameter [15], compliance of ISNT [16] rule, etc. Although the usefulness of these factors could be debatable for some ophthalmologists, CDR is mostly used by clinicians. In general, a larger CDR suggests a higher risk of glaucoma and vice versa. This papers focuses on the automatic CDR computation from known discs.

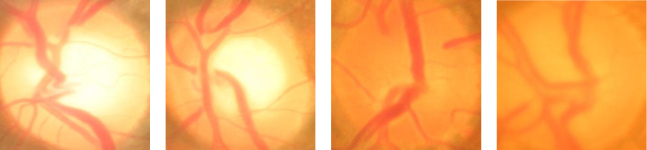
A number of algorithms have been proposed by various researchers to segment the optic disc (in short, disc) and/or optic cup (in short, cup) in order to compute CDR. In [17], Wong et al. proposed an automatic algorithm based on a variational level set to detect cup boundary. Later, they further detect blood vessel kinks for cup segmentation [18]. Joshi et al. used a similar concept but named as vessel bend to aid in cup detection [9]. The main challenge in detecting kinks or vessel bending for cup segmentation is the large number of false alarms. Narasimhan and Vijayarekha [19] used K-means clustering technique to extract the disc and cup and also an elliptical fitting technique to calculate the CDR. In [20], Gabor wavelet transform is further incorporated. Ho et al. [21] and Mishra et al. [22] used active contour to detect the cup boundary. Yin et al. [23] introduced a statistical model based method for disc and cup segmentation by integrating prior knowledge into contour deformation. Ingle and Mishra [24] explored the cup segmentation based on gradient method. We have proposed superpixel based classification approach [25] which exploits using features at superpixel level to enhance the detection accuracy of disc and cup. A common limitation of these algorithms is that they relied on obvious contrast between the neuroretinal rim and the cup. Therefore, they do not work well when the contrast is weak. Figure 1 gives four disc images where first two are samples with obvious cup boundary and last two are samples with unclear cup boundary.

Fig. 1.

Sample Images: two images with obvious cup boundary and two disc images with unclear cup boundary.

To overcome the above limitations, reconstruction based approaches were recently proposed [26, 27]. In these methods, a disc is first reconstructed from a set of reference discs. Then its CDR is estimated by a weighted combination of the CDRs of these reference discs. Mathematically, given a set of n discs X = [x₁, ⋯, x_n] and a testing disc image y, we want to reconstruct y as $\hat{y}=Xw$, where w = [w₁, ⋯, w_n]^T denotes the reconstruction coefficients. Then, we estimate the CDR of y as

$$\hat{r}=\frac{1}{{\mathbf{1}}_n^{T}w}{r}^{T}w,$$ (1)

where r = [r₁, r₂, ⋯, r_n]^T denotes the CDR values of discs in X, 1_n is a vector of 1s with length n. Figure 2 illustrates the reconstruction based method.

Fig. 2.

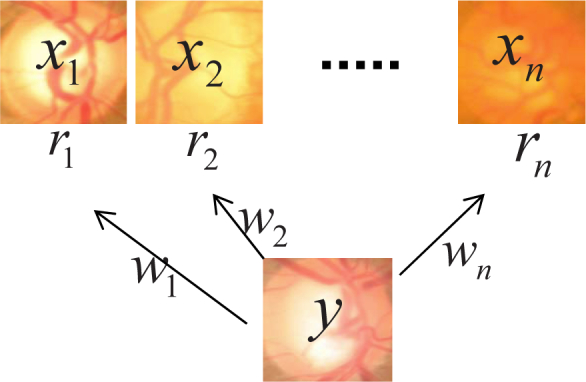
Illustration of reconstruction based CDR computation

The computation of CDR based on (1) does not rely on the segmentation of the cup boundary. Instead, it relies on the reference disc images X and corresponding reconstruction coefficients w. Intuitively, we want to minimize the difference between y and Xw. However, pixel-wised distance between y and Xw is insufficient to yield a good solution for accurate CDR estimation. To improve CDR estimation, Xu et al. [26] used a Gaussian distance to regularize the reconstruction. However, the ℓ₂-norm regularization yield a non-sparse solution, which leads to a bias due to too many reference images with non-uniform CDR distribution. Recently, we proposed sparse dissimilarity-constrained coding with ℓ₁-norm regularization to achieve a sparse solution. It improves the results over [26]. However, it might reconstruct the testing disc using discs with a wide range of CDRs. Although this might lead to the minimal reconstruction error between y and Xw, it is not optimal for our purpose of CDR estimation. Intuitively, to achieve an optimal CDR estimation from the reconstruction, we hope to find a set of reference disc images which are similar to the testing disc image. In addition, these discs shall have CDRs similar to the testing image. This implies that discs with non-zero weights shall have CDRs with small range. Correspondingly, the coefficients w shall have non-zero elements for a few similar reference discs with close CDRs. To achieve this, we propose a novel reconstruction method, namely, similarity regularized sparse group lasso (SSGL), which integrates sparse group lasso constraints with similarity regularization for CDR estimation.

Besides proposing a new method for CDR computation, we also introduce our data set for public research use in this paper. Public data sets have been rare resources in medical imaging research. Previously, the DRIVE [28] database with 40 images has been established to enable comparative studies on segmentation of blood vessels in retinal images. DRIONS-DB [29] is a database of 110 images dealing with the segmentation of ONH. Neither of the data sets is for glaucoma study. RIM-One [30] data set deals with glaucoma study. However, only disc margins and the cropped region of interest were given in the first and second releases. In the third release, 159 stereo retinal fundus images were provided with 85 from healthy subjects and 74 from glaucoma and glaucoma suspects. DRISHTI-GS is a data set consists of 101 images only [31]. It has been recognized that larger and ‘real life’ data sets are important [32]. Although many groups have been worked on automatic CDR computation, different groups use different data sets. Very often, these data sets are not publicly available. For example, Xiong et al. [33] use a private date set of 597 images including 297 glaucomatous and 300 normal images. Our team use a data set of 650 images from Singapore Eye Research Institute. Therefore, it is difficult for different researchers to compare their algorithms. In this paper, we introduce our data set for public use. It contains 650 images from different eyes including 168 glaucomatous eyes and 482 normal eyes. It is noted that our data set is obtained from a population based study and is therefore a ‘real life’ data set. For the convenience of subsequent research, we have partitioned the data set into two subsets A and B so that different researchers have the same partition of the data set for training and testing.

The main contributions of this paper include:

1. we formulate the CDR computation problem as a sparse group lasso problem and propose similarity-regularized sparse group lasso to reconstruct the disc images and to compute CDR;

2. results from the proposed method outperforms the state-of-the-art approaches by a more accurate CDR detection;

3. introduce a population based data set for public research use. This provides a great convenience for the society to develop, validate and compare the algorithms.

The rest of the paper is organized as follows. In section 2, we introduce the proposed SSGL method for CDR computation including the formulation of SSGL, its solution and detailed implementations including disc similarity computation. Section 3 introduces our data set in details and the experimental results. In the last section, we conclude the study.

2. Similarity regularized sparse group lasso

In this section, we introduce the proposed SSGL method. As discussed in the introduction, we want to reconstruct a testing disc image y as Xw, where w = [w₁, ⋯, w_n]^T is the reconstruction coefficients. To achieve a good reconstruction, we want to minimize the error ‖y − Xw‖². Since our final objective is to compute the CDR of y, we want to reconstruct y based on discs that are closest to y with similar CDRs. Very often, a few such discs are enough while too many references might lead to a bias [27]. Therefore, a sparsity constraint is added to penalize the number of reference images with non-zero weights [27]. However, even though the ℓ₁ sparse term posts a constraint in the number of non-zero elements in w, it does not consider the range of the CDRs of discs with non-zero weights. Therefore, the resultant reconstruction might come from discs with significantly different CDRs. Since our objective of reconstruction is to predict the CDR, we intend to reconstruct from discs with similar CDRs. It implies that the reference discs used to reconstruct a target disc shall have a small range of CDRs.

Obviously, one can post a lower and upper limit on CDRs of the reference images in the reconstruction, however, it is practically challenging to get the range as we do not know the CDR of the testing image yet. Since a potential solution of w shall satisfy the following conditions: 1) it is sparse; 2) the non-zero items of w comes from a group of references with a small range of CDRs, we need to consider the CDRs of the reference images during the reconstruction. Assuming that we have partitioned the reference images into groups of images with similar CDRs, the solution w shall satisfy the group lasso constraint, i.e., the reconstruction shall choose one or a few more groups in the reconstruction. This becomes a sparse group lasso problem [34, 35]. In this paper, we propose to use the sparse group lasso as a constraint. In addition, we integrate the similarity cost term into the objective function so that more similar discs have higher weights. Denoting the similarity cost between X and y as a vector s = [s₁, ⋯, s_n]^T, we also want to minimize the similarity cost term ‖s ⊙ w‖, where s_i denotes the similarity cost between x_i and y, ⊙ denotes the element-wise product.

To take the CDRs into consideration, we divide the n reference discs into many non-overlapping groups, where each group contains the discs with CDRs within a small range. In this paper, we form N non-overlapping groups:

$$G_i=\{x_j|t_i<x_j\le t_{i+1}\},$$ (2)

where t = [t₀, t₁, ⋯, t_N] denotes the thresholds to obtain the non-overlapping groups. In this paper, we set N = 15. Considering the fact that CDRs are in the range of [0,1] with majority of values from 0.4 to 0.75, we set t₀ = 0, t_i = 0.4 + 0.025 · i, i = 1, ⋯ 14, tN = 1.

2.1. Formulation of SSGL

Integrating the sparsity term ‖w‖₁ and the group lasso term ${\displaystyle {\sum }_{i=1}^N{\psi }_i{\Vert x_{G_i}\Vert }_2}$ and the similarity cost term ‖s ⊙ w‖² with the data term ‖y − Xw‖², we obtain the SSGL objective function:

$${\Vert y-Xw\Vert }^2+{\lambda }_1\cdot {\Vert s\odot w\Vert }^2+{\lambda }_2\cdot {\Vert w\Vert }_1+{\lambda }_3\cdot {\displaystyle \sum _{i=1}^N{\psi }_i{\Vert x_{G_i}\Vert }_2},$$ (3)

where λ₁, λ₂ and λ₃ control the weights of the regularization items, and the group lasso term is based on the above partitioning of non-overlapping groups G_i, i = 1, ⋯ N.

Merging the first two items in (3), we get

$$\begin{array}{l}{\Vert y-Xw\Vert }^2+{\lambda }_1\cdot {\Vert s\odot w\Vert }^2+{\lambda }_2\cdot {\Vert w\Vert }_1+{\lambda }_3\cdot {\displaystyle \sum _{i=1}^N{\psi }_i{\Vert x_{G_i}\Vert }_2}\\ ={\Vert y-Xw\Vert }^2+{\lambda }_1\cdot {\Vert Sw\Vert }^2+{\lambda }_2\cdot {\Vert w\Vert }_1+{\lambda }_3\cdot {\displaystyle \sum _{i=1}^N{\psi }_i{\Vert x_{G_i}\Vert }_2}\\ ={\Vert \left[\begin{array}{c}y\\ \mathbf{0}\end{array}\right]-\left[\begin{array}{c}X\\ \sqrt{{\lambda }_{1}S}\end{array}\right]w\Vert }^2+{\lambda }_2\cdot {\Vert w\Vert }_1+{\lambda }_3\cdot {\displaystyle \sum _{i=1}^N{\psi }_i{\Vert x_{G_i}\Vert }_2}\\ ={\Vert \hat{y}-\hat{X}w\Vert }^2+{\lambda }_2\cdot {\Vert w\Vert }_1+{\lambda }_3\cdot {\displaystyle \sum _{i=1}^N{\psi }_i{\Vert x_{G_i}\Vert }_2}\end{array}$$ (4)

where S = diag (s) denotes a diagonal matrix with main diagonal element s(i, i) = s_i, i = 1, ⋯, n, 0 is a vector of 0s with length n, $\hat{y}=\left[\begin{array}{c}y\\ \mathbf{0}\end{array}\right]$ and $\hat{X}=\left[\begin{array}{c}X\\ \sqrt{{\lambda }_{1}S}\end{array}\right]$.

2.2. Solution

Minimizing the objective function in (4) is a standard sparse group lasso problem. We solve the problem using the sparse learning with efficient projection (SLEP) package [36]. In SLEP, the solver ‘sgLeastR’ solves the standard sparse group lasso problem.

2.3. Disc similarity

To use the above reconstruction based methods effectively, we need to segment the disc and compute the disc similarity score. The overall flowchart to process an image for CDR computation is summarized in Fig. 3.

Fig. 3.

Flowchart of the processing

Effective computation of the disc similarity such that it reflects the relative cup size is important. There are many factors that might affect the similarity computation. For example, the blood vessels within the disc vary largely among different individuals, but the difference in vessels is not quite related with the CDRs. Inhomogeneous background across the optic disc also affects the similarity computation and the reconstruction. Very often, we observe a change of background intensity from one side to another side of the disc. Therefore, the disc similarity score computation is not a trivial task. In the following, we give details of our implementation on overcoming the above issues in disc similarity computation.

2.3.1. Vessel removal

The vessels within the disc vary largely among different individuals. However, the vessel distribution is minimally affected by glaucoma itself. The disc reconstruction and the similarity computation without removing vessels would lead to the emphasis of vessels. Therefore, it is important to remove the blood vessels. To overcome this, the vessels within the disc are first segmented.

A number of automated vessel detection methods [37–39] have been developed. In this paper, we use the newly developed vessel detection algorithm which is obtained through deep learning [40]. After that, image inpainting technique is utilized to replace the pixels of the vessel mask by those of the neighborhood in a visually pleasing way. Many image inpainting algorithms [41] have been proposed such as absolute minimizing Lipschitz extension inpainting [42], harmonic inpainting [43], Mumford-Shah-Euler inpaiting [44], Cahn-Hilliard inpainting [45]. In this paper, we use the harmonic inpainting [43] as it performs fast. In addition, we find the algorithm works well for retinal images from our visual inspection. After applying a harmonic inpainting, we obtain a vessel-free disc image. An example of effect of vessel removal is illustrated in Fig. 4.

Fig. 4.

Effects of vessel impainting.

2.3.2. Illumination Correction

Due to inconsistent image acquisition angles, the color funds image might have inhomogeneous background. This might affect the computation of disc similarity. Very often, one side of the disc is brighter than the other side while the unbalance varies from one disc image to another. In this paper, we correct the unbalance by a linear mapping. As illustrated in Fig. 5, we compute the average pixel intensity from first and last p columns, then we compute the balance corrected disc x_b as:

$$x_b(i,j)=\frac{(j-j_{max}/2)}{j_{max}-p}({\overline{x}}_l-{\overline{x}}_r)+\hat{x}(i,j),$$ (5)

where j_max is width of the disc. ${\overline{x}}_l$ and ${\overline{x}}_r$ denote the mean intensity from pixels of the first p columns and last p columns respectively. In our implementation, p = 0.1 · j_max. It should be noted that the computation of the disc similarity is not sensitive to p.

Fig. 5.

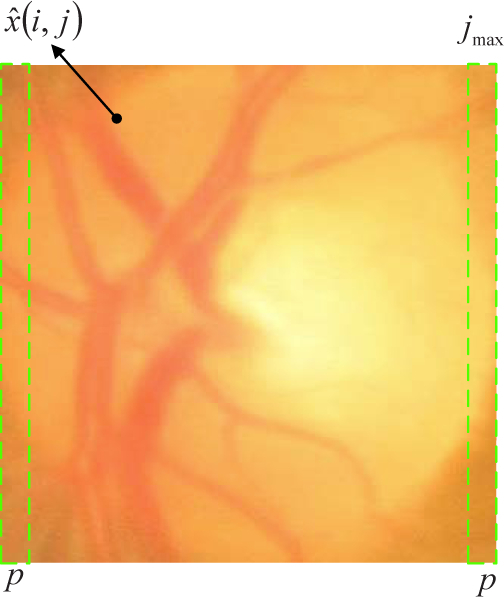
Linear mapping for illumination correction

2.3.3. Disc similarity computation

As the final objective is to estimate the CDR, it is important to compute a similarity that reflects difference in CDR, i.e., the two discs with similar CDR is expected to be similar and vice versa. Xu et al. [26] use Gaussian distance $d_i=\exp (\frac{{\Vert y-x_i\Vert }^2}{2{\sigma }^2})$, however, the pixel-wise difference does not represent the actual CDR difference between two discs. In many cases, discs with similar CDRs might have a large Gaussian distance due to the presence of vessels, mis-alignment etc. In this paper, we compute the similarity based on overall intensity change.

It is observed that the CDR is often reflected by the overall intensity change in the disc. Motivated by this, we have proposed to extract features that reflects the overall intensity change previously [27]. To achieve the robustness over noise and disturbance from blood vessels, we use surface fitting from non-vessel pixels within the disc. Here we avoid pixels from the segmented vessels as the image inpainting does not work perfectly to obtain the ideal vessel free disc image. Similar to that in [27], we compute a second order two-dimensional polynomial surface U(j, k). It is defined by $\overrightarrow{a}={[a_1,a_2,a_3,a_4,a_5]}^T\in {ℝ}^5$:

$$U(j,k)=a_1{j}^2+a_{2}j+a_3{k}^2+a_{5}k+a_5={(\overrightarrow{q})}^T\cdot \overrightarrow{a}$$ (6)

where $\overrightarrow{q}={[j^2,j,k^2,k,1]}^T$. The matrix form of (6) is given as:

$$\overrightarrow{u}=Q\overrightarrow{a}$$ (7)

where $\overrightarrow{u}$ is obtained by stringing out U(j, k) into a column, and Q is determined by $\overrightarrow{q}$. The coefficient $\overrightarrow{a}$ is then obtained by minimizing the error $E(\overrightarrow{v})={(\overrightarrow{x}-Q\overrightarrow{a})}^2$. It can be seen that

$$\overrightarrow{a}={(Q^{T}Q)}^{-1}{Q}^T\hspace{0.17em}\overrightarrow{x}$$ (8)

Since the overall intensity change of the disc is mostly reflected by the second order coefficients a₁ and a₃, we compute similarity cost between x_i and y as

$$s_i=\sqrt{{(a_{1,x_i}-a_{1,y})}^2+{(a_{3,x_i}-a_{3,y})}^2},$$ (9)

where a_j,z denotes the j^th coefficient from z.

3. Experimental results

3.1. Data set

We use the ORIGA data set of 650 images from the Singapore Malay Eye Study (SiMES) acquired using Canon CR-DGi in our study [46]. The SiMES was a population based study conducted from 2004 to 2007 by Singapore Eye Research Institute, aiming to assess the risk factors of visual impairment in Singapore Malay community. In this study, the clinicians examined 3,280 Malay adults aged 40 to 80. Our data set consists of 168 images from all glaucomatous eyes and 482 images from randomly selected normal eyes. As mentioned, the data set is obtained from a population based study and is therefore suitable for evaluating the performance of glaucoma screening.

Manual CDRs computed from manually segmented disc and cup boundaries are necessary to evaluate the proposed method. Two sets of manually segmented disc and cup boundaries are obtained. The first set is marked by a group of 3-6 well trained graders in previous studies [25]. The graders work daily in retinal image grading at local hospitals. At least three graders examine the image simultaneously and determine the disc and cup boundaries based on mutual agreement. After that, a glaucoma specialist examines and adjusts all the marked results to control the quality of the marking. The second set is marked by a single well trained independent senior glaucoma specialist. A grading software is designed to mark a free number of points along the boundaries of the optic disc and optic cup. Then, a polynomial fitting is adopted to connect the points to boundaries. The specialist is able to modify the points and adjust the boundaries until a satisfactory result is obtained. We then compute the vertical disc and cup diameters to compute the manual CDRs. For convenience, we denote the first set of manual demarcations as ‘Expert A’ and the second set as ‘Expert B’.

In this paper, we introduce the data set for public research use, together with the two sets of manually segmented disc/cup boundaries and the corresponding CDRs. The data set will be made available online upon the publication of this paper. For convenience, the 650 images have been divided into set A and set B with 325 images in each set randomly based on patient, i.e., the eyes from same patient are put in either set A or set B only. A two-fold cross validation strategy is adopted to obtain the results for all 650 images: in the methods where a training set or a reference set is required, we first use set A as training or reference set and set B as testing set to get the results in set B. Then we use set B as training or reference set and set A as testing set to3 get the results in set A. Therefore the results by all 650 images are obtained.

3.2. Evaluation criteria

The following criteria are used in our evacuation:

1. mean absolute CDR error: $\delta =\frac{1}{M}{\displaystyle {\sum }_i^M|G{T}_i-CD{R}_i|}$ where GT_i and CDR_i denote the manual and automated CDR of sample i;

2. The correlation: the Pearson’s correlation coefficient between the manual CDRs and the automated CDRs is used.

3. The area under the receiver operating characteristic (ROC) curve in the glaucoma detection: The ROC curve plots the sensitivity against 1-specificity for all possible values. The area under the curve (AUC) is computed as the overall measure of the diagnostic strength.

3.3. Results from manually segmented disc

As this paper focuses on the cup size estimation, the disc is assumed known or has been segmented. We first conducts experiments using manually segmented discs. Even though this is only an ideal scenario, it prevents the error propagation from the disc localization & segmentation step to the cup size or CDR computation step. Therefore, it isolates the error from previous steps and shows how the proposed SSGL works for CDR estimation in ideal scenario.

3.3.1. Performance evaluation under different parameters settings

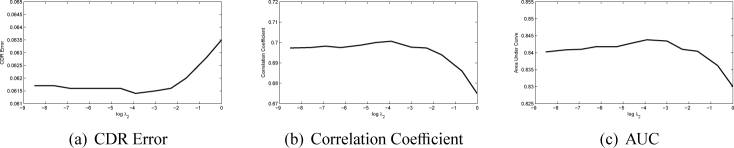
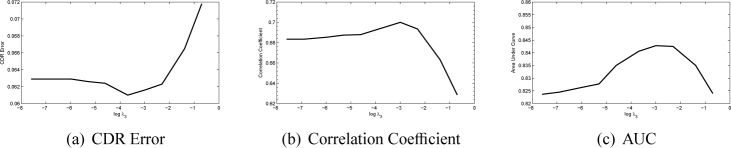
There are three main parameters λ₁, λ₂ and λ₃ in the SSGL. In this paper, we first show how these parameters affect the performance. The first parameter λ₁ controls the weight of the similarity cost. In Fig. 6, we plot the CDR error, correlation and AUC with a wide range of λ₁ values at log scale with the other two parameters fixed heuristically (λ₂ = 0.01 and λ₃ = 0.05). The figure shows that when log λ₁ is in the range of 1 to 5, the proposed method achieves good results. However, further increases λ₁ will make the performance drop rapidly as the similarity term will dominate the results. We also plot the CDR error, correlation and AUC with a wide range of λ₂ and λ₃ values at log scale in Fig. 7 and Fig. 8. Similarly, large λ₂ and λ₃ will make the sparse group lasso items dominate the results as well. In following, we fix λ₁ = 100, λ₂ = 0.01 and λ₃ = 0.05.

Fig. 6.

Performance changes as λ₁ changes

Fig. 7.

Performance changes as λ₂ changes

Fig. 8.

Performance changes as λ₃ changes

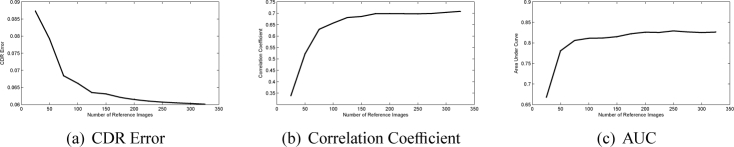
The number of reference images n is another factor. In our experiments, we choose n images from set A as reference images to construct the 325 images in set B and compute their CDRs. The results as n increases from 25 to 325 are shown in Fig. 9. As we can see, the proposed method improves as n increase. The results become stable with n no less than 150.

Fig. 9.

Performance changes as the number of reference images n changes.

3.3.2. Comparison with other methods

Three competitive state-of-the-art algorithms using superpixel classification [25], locality constrained coding (LLC) [26] and sparse dissimilarity coding (SDC) [27] are first included for comparison. In addition, we have also implemented two other possible reconstruction based approaches, namely, the sparse coding (SC) [47] and the locally linear embedding (LLE) [48] for comparison. Moreover, we use the manual CDRs ‘Expert B’ as a second opinion to compute inter-observer error.

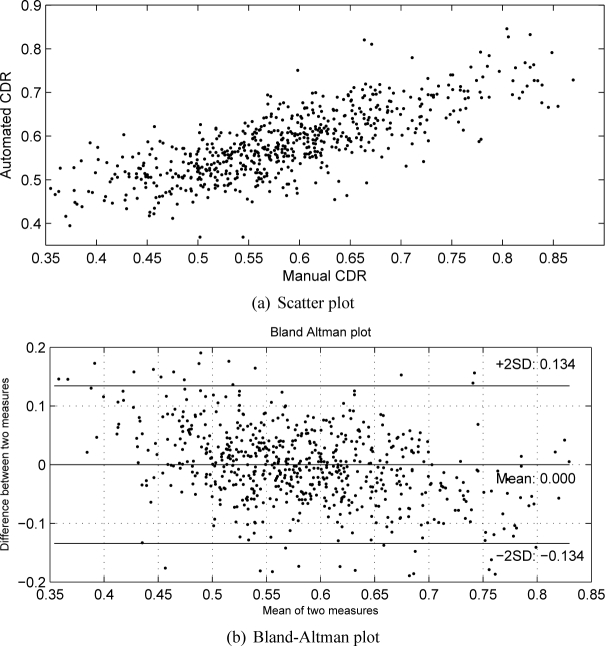
A two-fold cross validation is adopted to get the results for 650 images. The automated CDRs are compared with the manual CDRs from ‘Expert A’ and the diagnostic outcomes. Table 1 shows the results. From Table 1, we observe that the proposed method outperforms other methods. Compared with the superpixel classification [25], LLC method [26] and SDC method [27], the proposed SSGL method reduces the CDR error relatively by 21.5%, 11.0% and 6.7% respectively. At the same time, it improves the correlation by 17.3% and 16.7% and 8.0% respectively. We have also conducted t-test to compare the CDR error between the proposed method and other methods and obtained p < 0.0001 for all t-tests, which shows that the reduction in CDR error is significant. Figure 10 shows the scatter plot between manual and automated CDR by the proposed method as well as Bland-altman plot for a visual assessment.

Table 1.

Performance by various methods.

	CDR Error	p-value(t-test)	Correlation	p-value(correlation)	AUC	p-value (ROC)
Superpixel [25]	0.0785	p < 0.0001	0.597	p < 0.0001	0.793	p = 0.0090
LLE [48]	0.0794	p < 0.0001	0.530	p < 0.0001	0.764	p < 0.0001
SC [47]	0.0746	p < 0.0001	0.598	p < 0.0001	0.803	p = 0.0242
LLC [26]	0.0692	p < 0.0001	0.600	p < 0.0001	0.811	p = 0.0241
SDC [27]	0.0660	p < 0.0001	0.648	p < 0.0001	0.821	p = 0.0441
Expert B	0.0679	p < 0.0001	0.679	p < 0.0001	0.819	p = 0.1315
Expert A	–	–	–	–	0.838	p = 0.7702
Proposed	0.0616	–	0.700	p < 0.0001	0.843	–

Fig. 10.

Scatter plot and Bland-Altman plot between manual and automated CDR by the proposed method.

The improvement in AUC is relatively smaller. Figure 11 shows the ROC curves by various methods. To evaluate the significance level of the change in ROC, we also compare the ROC curves using the Delong’s method [51]. The p-values of the ROC comparisons between proposed method and other methods are computed and included in the last column in Table 1. According to Delong’s method, p < 0.05 indicates a significant difference. As we can see, the proposed method achieves a diagnosis test significantly better than state-of-the-art methods while there is no significant difference between the ROC curves by the proposed method and manual demarcations by ‘Expert A’ and ‘Expert B’. The proposed SSGL method also outperforms other reconstruction based methods. This justifies the benefits of the similarity cost term and the sparse group lasso items in SSGL.

Fig. 11.

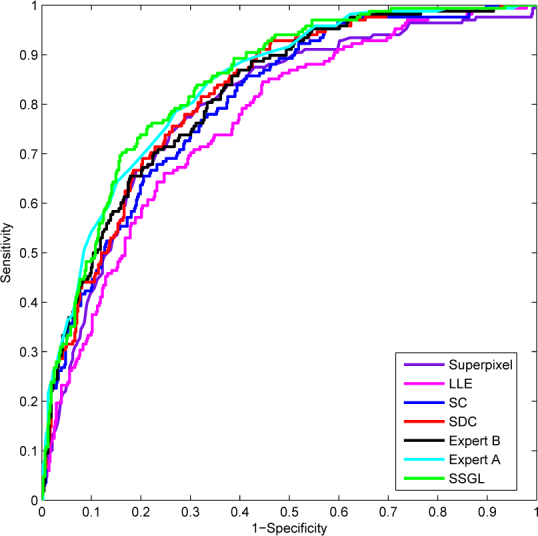
Comparison of ROC by different methods.

The computational cost is also evaluated. It takes around 0.06 second for a new disc image tested with 325 reference images using a dual core 3.0 GHz PC with 3.25 GB RAM. This is faster than the state-of-the-art SDC [27] method which takes 0.17 second under same setting.

3.4. Results from automatically segmented disc

After presenting the results from manually segmented discs, we next present how the proposed method works on automatically segmented discs. In this paper, we use three different disc segmentation methods including the template matching approach [49], the superpixel classification approach [25] and self-assessed approach [50] to segment the disc. Then the proposed SSGL is used to compute the CDR from these automatically segmented discs. Similar to previous settings, we also use the two-fold cross validation strategy. In our experiments, we first use the manually segmented discs in set A to reconstruct the automatically segmented discs for images in set B. Then, we use the manually segmented discs in set B to reconstruct the automatically segmented discs in set A. When different disc segmentation methods are used to obtain the automatically segmented discs, the reference disc images are fixed to be the manually segmented discs. Table 2 summarizes the results. The replacement of manually segmented discs with automatically segmented discs in testing will increase the CDR error by 6.5% to 14.0% based on ‘Expert A’, 5.7% to 9.0% based on ‘Expert B’ and 6.2% to 13.6% based on their average. Figure 12 gives a visual comparison of the ROCs obtained from discs generated by different disc segmentation methods. This is partially because of the presence of other diseases. For example, the bright lesions in age-related macular degeneration may obstruct the detection of the optic disc.

Table 2.

Performance from different discs.

	Expert A			Expert B			Average
	CDR Error	Correlation	AUC	CDR Error	Correlation	AUC	CDR Error	Correlation	AUC
Template Matching Disc [49]	0.0702	0.604	0.812	0.0704	0.621	0.798	0.0583	0.684	0.806
Superpixel Disc [25]	0.0658	0.662	0.837	0.0683	0.657	0.824	0.0545	0.730	0.831
Self-Assessed Disc [50]	0.0670	0.640	0.829	0.0689	0.650	0.815	0.0553	0.715	0.823
Manually Segmented Disc	0.0616	0.700	0.843	0.0646	0.688	0.826	0.0513	0.765	0.835

Fig. 12.

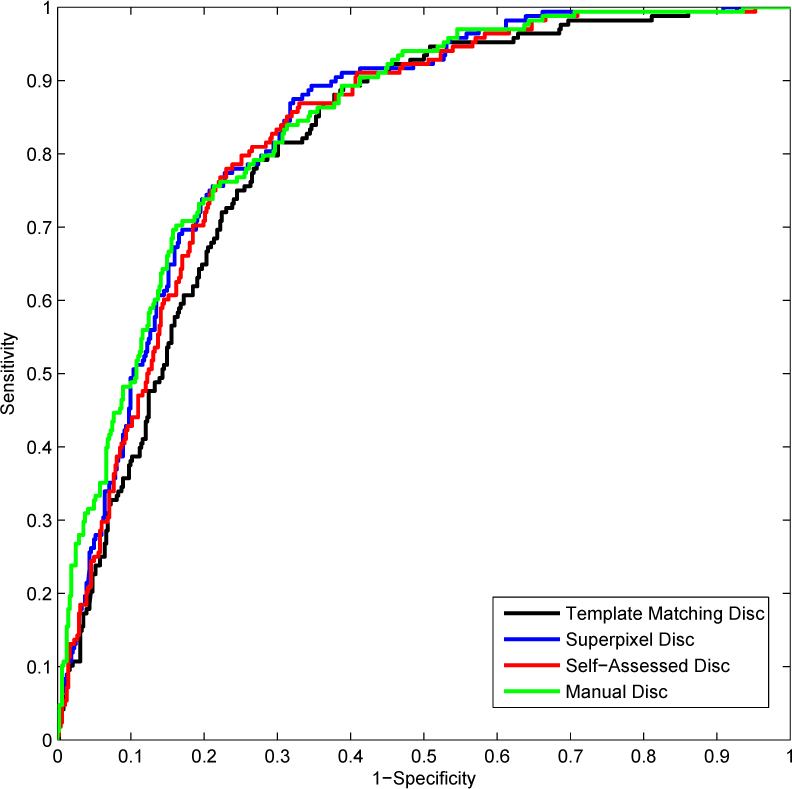
Comparison of ROC curves from automated and manually segmented discs

In order to evaluate the significance of the change in ROC, we also compare the ROC curves obtained from manual and automatically segmented discs using the Delong’s method [51]. The p-values of the ROC comparisons are given in Table 3. Based on the p values, there is no significant difference between ROC curves from manually segmented disc and automatically segmented discs by superpixel disc or self-assessed disc. The template matching disc performs the worst, leading to a significant change in ROC. This suggests that the previous superpixel classification based disc segmentation or the self-assessed disc segmentation algorithm can be used to replace manual disc demarcation without significant loss in diagnosis accuracy.

Table 3.

p values of ROCs based on automatically segmented disc in comparison with manually segmented disc.

	Template Matching	Superpixel	Self-Assessed
p	0.0048	0.4538	0.0720

4. Conclusions

In this paper, we formulate the CDR estimation problem as a sparse group lasso problem and propose SSGL for automatic CDR computation. The proposed SSGL integrates the similarity cost and sparse group lasso term with data term. The results show that such integration improves the accuracy in CDR estimation. SSGL achieves an error smaller than inter-observer error. This implies that we can replace manual CDR demarcation with automatic CDR computation algorithms without sacrificing much the accuracy. Our results also show that the automatically segmented discs work slightly worse than manually segmented discs for CDR computation, therefore, there are still room for improvement in disc segmentation. Besides the technical contribution, we also introduce our data set for public research use and the detailed settings are given. We believe this will benefit the society and bring the accuracy of automatic glaucoma diagnosis into a higher level.

Funding

This work was supported in part by the Agency for Science, Technology and Research, Singapore, under SERC Grant 121-148-0007 and Australian Research Council FT-130101457, DP-140102164 and LP-150100671.

Disclosures

The authors declare that there are no conflicts of interest related to this article.